Сложные интегралы: Сложные интегралы, примеры решений - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Примеры решения сложных интегралов с ответами

Алгоритм решения сложных интегралов

Сложными являются интегралы, которые нельзя вычислить, используя таблицу интегралов.

Сложные интегралы вычисляются методом введения дополнительной переменной. Этот приём позволяет преобразовать подынтегральную функцию к виду, характерному для табличных интегралов.

При вычислении сложных интегралов также применяются свойства интеграла и таблица основных интегралов.

– постоянная величина

Примеры решений сложных интегралов

Пример 1

Задача

Вычислить интеграл:

при помощи подстановки

Решение

Найдём dx:

Преобразуем подынтегральную функцию c учётом подстановки :

Искомый интеграл преобразуется к следующему виду:

Перейдём к переменной , для этого из подстановки выразим через :

В итоге получим:

Преобразуем полученный результат с учётом, что

Считая, что , получим

Индекс можно обозначить через

Окончательно, получим:

Ответ

Пример 2

Задача

Вычислить интеграл:

при помощи подстановки

Решение

Найдём dx:

Преобразуем подынтегральную функцию c учётом подстановки :

Искомый интеграл преобразуется к следующему виду:

Перейдём к переменной , для этого из подстановки выразим через :

В итоге получим:

Ответ

Пример 3

Задача

Вычислить интеграл от дроби:

Решение

Ответ

Пример 4

Задача

Вычислить интеграл:

при помощи тригонометрической подстановки

Решение

Найдём dx:

Преобразуем подынтегральную функцию c учётом подстановки :

Искомый интеграл преобразуется к следующему виду:

Интеграл вида относится к табличным и равен:

Поэтому:

Перейдём к переменной , для этого из подстановки выразим через :

В итоге получим:

Ответ

Пример 5

Задача

Вычислить интеграл:

при помощи тригонометрической подстановки

Решение

Найдём dx:

Преобразуем подынтегральную функцию c учётом подстановки :

Искомый интеграл преобразуется к следующему виду:

Интеграл вида относится к табличным и равен:

Поэтому:

Перейдём к переменной , для этого из подстановки выразим через :

В итоге получим:

Ответ

Пример 6

Задача

Вычислить интеграл:

при помощи подстановки

Решение

Найдём dx:

Преобразуем подынтегральную функцию c учётом подстановки :

Искомый интеграл преобразуется к следующему виду:

Перейдём к переменной , для этого из подстановки выразим через :

В итоге получим:

Т. к. , то

Ответ

Пример 7

Задача

Вычислить интеграл:

при помощи подстановки

Решение

Найдём dx:

Преобразуем подынтегральную функцию c учётом подстановки :

Искомый интеграл преобразуется к следующему виду:

Перейдём к от к переменной :

Ответ

Пример 8

Задача

Вычислить интеграл:

при помощи подстановки

Решение

Выразим подынтегральную функцию через переменную :

Разделим обе части равенства на :

В правой части равенства заменим на :

Переходя к переменной , получаем:

Ответ

Пример 9

Задача

Вычислить интеграл:

при помощи подстановки

Решение

Выразим подынтегральную функцию через переменную :

Переходя к переменной , и учитывая, что получаем:

Ответ

Пример 10

Задача

Вычислить интеграл:

при помощи подстановки

Решение

Выразим подынтегральную функцию через переменную :

Переходя к переменной , и учитывая, что получаем:

Ответ

Средняя оценка 4 / 5.

4+tan(x), в качестве пределов интегрирования указываем 1, 2.

Если определить вид интегрирования, подробное решение будет доступно в MS Word:
Интегрирование по частям: ∫xe^xdx, ∫xcos(x)dx, ∫ln(x²-1)dx, ∫arcsin(4x)dx Примеры
Интегрирование простейших иррациональности вида , Примеры
Интегрирование простейших иррациональности вида
Интегрирование рациональных дробей вида Примеры
Интегрирование тригонометрических функции вида Примеры
Не знаю (по возможности определяется метод решения, например, подведение под знак дифференциала)

Примечание: число “пи” (π) записывается как pi; знак “бесконечность” (∞) ≡ infinity

Примеры правильной записи некоторых выражений

	`sqrt(6-x)`
	`(6+2*x)^(1/3)`
log₅(1+x)	`log(1+x,5)`
	`(2/3+x^2)/(x^3+x)`

Таблица интегралов

Вместе с этим калькулятором также используют следующие:
Точки разрыва функции

Производная функции:

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление пределов

Способы нахождения неопределенных интегралов:

Подведение под знак дифференциала:
Интегрирование по частям: ∫xe^xdx
Простейшие преобразования подынтегрального выражения (пример):
Интегрирование рациональных дробей:
Интегрирование простейших иррациональностей:
Интегрирование выражений, содержащих тригонометрические функции: ∫cos⁴(x)sin³(x)dx

Приближенное вычисление определенного интеграла по формуле прямоугольников.
см. также Задача интегрирования в конечном виде, Несобственные интегралы

Пример 1. Вычислить ∫(3x+15)¹⁷dx.
Решение.
Возводить двучлен в 17-ю степень нецелесообразно. Исходя из табличного интеграла , получаем
= .
Пример 2. Вычислить .
Решение.
Аналогично предыдущему,
=

Пример 3. .
Решение. Поскольку
, то .

Пример 4. Вычислить
Решение. Так как
, то .

Пример 5. Вычислить .
Решение.
Применим подстановку . Отсюда x-5=t², x=t²+5, dx=2tdt.
Подставив в интеграл, получим

Пример 6. Вычислить ∫x²e^xdx.
Решение.
Положим u=x², dv=e^xdx; тогда du=2xdx, v=e^x. Применим формулу интегрирования по частям:
∫x²e^xdx=x²e^x-2∫xe^x.
Мы добились понижения степени x на единицу. Чтобы найти ∫xe^x, применим еще раз интегрирование по частям. Полагаем u=x, dv=e^xdx; тогда du=dx, v=e^x и
∫xe^x=x²e^x-2xe^x+2e^x+C.

Пример 7. Вычислить .
Решение. Выделяя целую часть, получим: .
Учитывая, что x⁴+5x²+4=(x²+1)(x²+4), для второго слагаемого получаем разложение

Приводя к общему знаменателю, получим равенство числителей:
-5x²–4=(Ax+B)(x²+4)+(Cx+D)(x²+1).
Приравнивая коэффициенты при одинаковых степенях x, получаем
x³: 0=A+C
x₂: -5=B+D
x: 0=4A+C
x⁰: -4=4B+D

Отсюда находим A=C=0, B=¹/₃, D=-¹⁶/₃.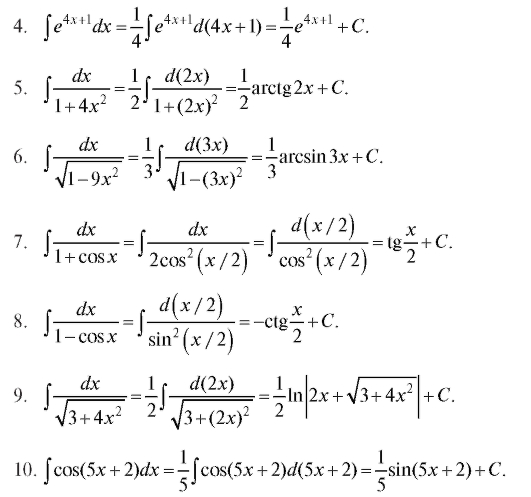
Подставляя найденные коэффициенты в разложение и интегрируя его, получаем:

Пример 8. Вычислить .
Решение. Так как
,
то подынтегральное выражение есть рациональная функция от x и ; поэтому введем подстановку:
; ,
откуда
; ; ;.
Следовательно,

Пример 9. Вычислить .
Решение.
Подынтегральная функция рационально зависит от sinx(x) и cos(x); применим подстановку tg^x/₂=t, тогда
, , и
=
Возвращаясь к старой переменной, получим
= .

Пример 10. Вычислить .
Решение.
Произведем замену 1+3x⁸ = z². Тогда , ;
таким образом,
.
Следует обратить внимание, что при замене переменной в определенном интеграле пределы интегрирования в общем случае изменяются.

Пример 11.Вычислить несобственный интеграл или доказать его расходимость.
Решение. Подынтегральная функция не ограничена в окрестности точки x=1. На любом же отрезке [1+ε;e] она интегрируема, так как является непрерывной функцией. Поэтому

Пример 12. Вычислить несобственный интеграл или доказать его расходимость.
Решение.
Подынтегральная функция непрерывна и интегрируема на R. По определению Интеграл сходится.

Пример 13. Найти площадь фигуры, ограниченной параболой y=x² и прямой x+y=2.
Решение.
Найдем абсциссы точек пересечения параболы y=x² и прямой y=2-x. Решая уравнение x²=2-x, находим x₁=-2, x₂=1. Так как фигура ограничена сверху прямой, а снизу параболой, по известной формуле находим
.

Приемы взятия сложных интегралов – Dmitri Nesteruk

Интегралы, что может быть веселее? Ну, возможно не для всех, но все же, я уже давно ничего не постил такого сугубо математического, так что попробую. Этот пост – про то как брать «сложные» интегралы. Этот пост подразумевает что читатель учился таки в школе и знает тривиальные подходы (например, интегрирование по частям). В посте мы будем обсуждать только интегралы Римана, а не интегралы Лебега-Стилтьеса, Ито, Скорохода и так далее (хотя я бы с удовольствием, чесслово).

Весь этот пост — маленькая выборка рецептов или «паттернов» которые можно взять в копилку и потом применять. Пост рекомендуется читать на high-DPI дисплее дабы предотвратить глазное кровотечение. Я предупредил.

Переход к полярным координатам

Начнем с немного избитого метода — перехода к полярным координатам. Примечательно, что переход к полярным координатам можно применять даже там где, казалось бы, речь о декартовых координатах не идет вообще. Например, неопределенный интеграл Гаусса не имеет аналитического решения, а вот определенный интеграл .

Доказать это можно вот как: сначала, чтобы применить преобразование координат, мы вводим две переменные интегрирования и так что

Декартовы координаты можно выразить через полярные вот так:

Интегрирование от до в декартовой системе координат — это то же, что интегрирование от до и от до .

В результате получим следующее:

Этот же подход может применять и в 3-х измерениях с использованим сферических координат .

Геометрические интерпретации

Вообще, «скатывание в геометрию» порой приносит плоды. Вот например допустим вам надо посчитать

Уверен, многие из вас знают что у этого интеграла есть аналитическое решение , поэтому посчитать определенный интеграл не составляет труда. Но на самом деле, этот интеграл можно посчитать даже без этого знания.

Представьте круг с радиусом с центром . Длина дуги этого круга с центральным углом равна , а если круг единичный – то просто . Тогда

где — это произвольная переменная интегрирования.

При таком раскладе, подынтегральное выражение равно , но мы можем его усложнить, например

Далее, делаем подстановку

Тем самым, получаем

Допустим что . Тогда , а поскольку отмеряет нам ровно четверть круга (длина всего единичного круга ), мы моментально получаем результат

По аналогии с этим результатом можно получить и другие, разбивая круг на разное количество отрезков, например

и так далее.

Разбиение диапазона интегрирования

Допустим вам надо посчитать

Для взятия этого интеграла, разобъем диапазон интегрирования на два, т.к. .

Займемся сначала первым интегралом, т.е. . Сделаем подстановку . Получим

То есть внезапно оказалось, что поставленная переменная выполняет такую же функцию что и . Другими словами, а это значит что мы автоматически получаем значение искомого интеграла:

Разбиениe на четное и нечетное

Вот нужно вам например посчитать

Давайте сделаем несколько замен:

Теперь нам нужно посчитать , и вот тут начинается самое интересное. Мы переписываем как сумму четной и нечетной функции:

Многие спросят «а так вообще можно?» — на самом деле да, и вот почему. Возьмите и воткните в определение выше вместо . Вы получите

благодаря свойствам четности и нечетности функций. Следовательно, мы можем выразить четную и нечетную сторону функции как

Так-то. Соответственно, наш интеграл можно переписать как

Как видно выше, нечетная функция пропала полностью, осталась только четная сторона, т. к.

Ладно, вам уже наверное надоело ждать сути этого примера. Так вот, у нас есть формула , дайвате воткнем в эту формулу . Мы получим

Но мы-то знаем, что — четная функция, поэтому можно переписать как

Это какое-то месиво и непонятно что с ним делать. Но с другой стороны посмотрите, у нас в формуле присутствует . Давайте вспомним, что и мы получим

Ну вот и всё — наша страшная дробь выше уже совсем не страшная т.к. числитель и знаменатель равны, а это значит что

а сам интеграл теперь легко посчитать:

Хотите ещё?

Я на самом деле понял, что по объему для одного поста вполне достаточно. Сорри если что написал не так — я по-русски прочитал ровно нуль математических книг (чего и вам советую), так что терминология может страдать.

Существует еще вагон разных трюков, так что, если интересно, советую глянуть соответствующую литературу. Удачи! ■

Rate this:

Like this:

Like Loading…

Новости

ТАСС

ДВФУ для достижения углеродной нейтральности внедрит «зеленую» энергетику

ТАСС

ДВФУ и харбинский вуз запустят совместную медицинскую образовательную программу

Большая Азия

Российско-китайский центр технологического и инвестиционного сотрудничества появится в ДВФУ

ТАСС

Власти Чукотки будут сотрудничать с ДВФУ в трудоустройстве учителей в регион

РИА Новости

Чернышенко отметил четкую связь ДВФУ с передовыми компаниями

ТАСС

ДВФУ запустил центр климатических и экологических проектов «Карбонлайф»

ТАСС

ИТ-компании Дальнего Востока подписали кодекс этики в сфере ИИ

Аргументы и факты

Сбер и ДВФУ представили книгу о регулировании искусственного интеллекта

ТАСС

Во Владивостоке открыли Дальневосточный центр искусственного интеллекта

Газета. Ru

Сбер и ДВФУ открыли Дальневосточный центр искусственного интеллект

Аргументы и факты

На ВЭФ обсудили вопросы подготовки кадров для IT

ТАСС

Во Владивостоке откроется первый на Дальнем Востоке аддитивный центр общего доступа

Большая Азия

ДВФУ представил идею создания плавучего университета

Lenta. ru

«Роснефть» и Дальневосточный федеральный университет создадут Центр компетенций

Атомная энергия 2.0

«РусАТ» и ДВФУ откроют во Владивостоке первый Аддитивный центр общего доступа

Аргументы и факты

ДВФУ и ХК «Адмирал» наладили спортивные отношения

Газета.ru

«Роснефть» и Дальневосточный федеральный университет создадут Центр компетенций

Life.ru

На ВЭФ обсудили подготовку кадров для обеспечения технологического прорыва России

Аргументы и факты

Учёба в море. В России начал работу «Плавучий университет»

ТАСС

ТАСС и ДВФУ договорились о сотрудничестве в подготовке журналистских кадров

Аргументы и факты

Компания «РусГидро» открыла Научно-исследовательский центр на острове Русский

Комсомольская правда

Выставку «Многоликая в цвете. Российская империя на фотографиях Прокудина-Горского» открыли в Пушкинском театре ДВФУ

ТАСС

В ДВФУ расширят работы по созданию спин-орбитроники

Российская газета

Дальневосточный федеральный университет делает ставку на потребности рынка

ТАСС

На острове Русском создадут центр исследования блокчейна

ТАСС

Тихоокеанский плавучий университет планируют создать во Владивостоке

Российская газета

На острове Русском запустили уникальный энергетический полигон

Сделано в России

ДВФУ на ВЭФ подпишет с Индией и Китаем контракты в области образования

ТАСС

Компания “Русгидро” открыла научно-исследовательский центр во Владивостоке

ТАСС

Обучающую программу для стартапов Приморья по привлечению инвестиций запустили на ВЭФ

ТАСС

Школьники со всей России на площадке «ВЭФ. Юниор» разработают четыре стратегии для ДФО

Российская газета

Почему молодежь Дальнего Востока все чаще делает выбор в пользу родного края

ТАСС

ИНТЦ «Русский» предложит бизнесу инвестиционные лоты с объектами инфраструктуры

Большая Азия

В ДВФУ пройдет международный симпозиум по магнетизму

ТАСС

ИНТЦ «Русский» на ВЭФ подпишет соглашения с крупными фармацевтическими и IT-компаниями

Восток России

Синергия науки и бизнеса даст прорыв в биотехнологиях

Научная Россия

Ученые ИМО ДВФУ проверили тихоокеанского лосося на токсканты

Научная Россия

Ученые создают молекулы-лидеры для новых антибиотиков и противоопухолевых препаратов

Sciencepop

Это любовь: древние собаки стали есть злаки, чтобы понравиться людям

ТАСС

Технопарк «Русский» запустит на ВЭФ программу для стартапов Приморья

Что такое интеграл простым языком

Содержание

Интегралы – что это, как решать, примеры решений и объяснение для чайников
Почему вы не знаете, как решать интегралы
Интеграл – что это?
Объясняем понятие «Интеграл»
Неопределённый интеграл
Определённый интеграл
Таблица интегралов для студентов (основные формулы)
Как вычислять интеграл правильно
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Заключение
Интеграл простыми словами
Простыми словами…
Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.
Зачем нужен интеграл
Еще примеры из жизни
Интегралы для чайников: как решать, правила вычисления, объяснение
Изучаем понятие « интеграл »
Неопределенный интеграл
Полная таблица интегралов для студентов
Определенный интеграл
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Свойства определенного интеграла
Примеры решения интегралов
Видео

Интегралы – что это, как решать, примеры решений и объяснение для чайников

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов

Почему вы не знаете, как решать интегралы

Внимание!

Если вам нужна помощь с академической работой, то рекомендуем обратиться к профессионалам. Более 70 000 экспертов готовы помочь вам прямо сейчас.

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Если вы не уверены, что справитесь с работой, обратитесь за помощью к профессионалам. Работу могут написать преподаватели, доцены вузов

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Когда нет времени!

Помощь в написании работы от 1 дня. Гарантируем сдачу работу к сроку без плагиата, только авторский текст. Оформление + сопровождеие в подарок!

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Источник

Интеграл простыми словами

Интегралы начинают изучать еще в школе. Но никто из учителей не говорит, зачем это нужно, как использовать эти знания в жизни. Мало кто вообще способен объяснить простыми словами, что такое интеграл, даже в университете. А мы попробуем.

Простыми словами…

Если коротко — интеграл, это сумма маленьких частей. Да, точно так же как и сложение 2+2, только части бесконечно маленькие, естественно и количество их — бесконечно.

Знак интеграла ∫ — это вытянутая буква s (длинная «эс» существовала до начала 19-ого века писалась так — ſ). Первая буква слова summa.

Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.

Почему обычного «плюсования» не достаточно? Просто в алгебре нет никаких бесконечно малых или больших.

Бесконечно малая величина, это не какое-то конкретное число. Это абстракция, в реальном мире аналогов просто нет. Мы придумали так для удобства. Что-то настолько маленькое, что измерять его бессмысленно, но в расчетах использовать можно.

Слово «интеграл» происходит от латинского integer, что означает «целый». Даже в названии есть намек некое действие, что-то вроде восстановления чего-то целого.

Лучше всего показать «на пальцах», точнее на примере. Предположим, мы хотим узнать площадь фигуры как на картинке (она называется криволинейная трапеция, потому, что одна из сторон создана кривой линией). Зачем нам это нужно? Например, это часть крыла самолета и нужно знать его площадь.

Можно, конечно, разбить фигуру на две, прямоугольник и треугольник.

Но останется «пробел», площадь которого будет неизвестна. Чтобы увеличить точность, можно разделять на большее количество фигур, но все равно будет оставаться какая-то, пусть и небольшая, но «не закрашенная» область. Фигуры будут становиться все меньше и меньше… Очевидно, что процесс измельчения будет бесконечным, по крайней мере в воображении.

Но, в реальности, бесконечный процесс попросту не нужен. На самом деле вычислить такие вещи как площадь круга, длину диагонали квадрата или объем пирамиды невозможно, значение будет бесконечным, естественно, практического смысла бесконечные числа не имеют и мы их «округляем» до нужного предела точности — приблизительно.

Такой метод в Древней Греции назывался «исчерпание». Аналогия с водой тут очень уместна, если представить, что черпаешь из ведра при помощи кружки, то сначала кружки будут полные, но чем ближе ко дну, тем меньший объем будет попадать в кружку. Первой известной личностью «взявшей интеграл» был Архимед, он фактически решил задачу по нахождению площади круга и площади параболы ничего не зная ни про пределы, но даже про число «пи».

Чем больше будет фигур, тем больше будет и точность расчета и тем меньше будут сами фигурки. Если площадь маленьких фигурок будет бесконечно малой, то есть стремится к нулю (но не равняться ему), сумма всех этих площадей будет равна сумме большой фигуры с бесконечно большой точностью.

То же самое происходит при интегрировании:

Фигура на картинке разбивается на столбцы бесконечно маленькой ширины. Ширина у нас Х. Бесконечно малое число обозначается d. То есть dx — это бесконечно малый «икс».

Сложение бесконечного числа частей бесконечно маленького размера это и есть интегрирование.

Чтобы узнать площадь фигуры нужна еще высота, а это y. Высота везде не одинаковая, она постоянно меняется. И мы знаем как именно! Ведь кривая может быть (а может и не быть, но в нашем случае так и есть) функцией y=f(x), то есть значение у меняется по закону (буква f об этом говорит) зависимому от х.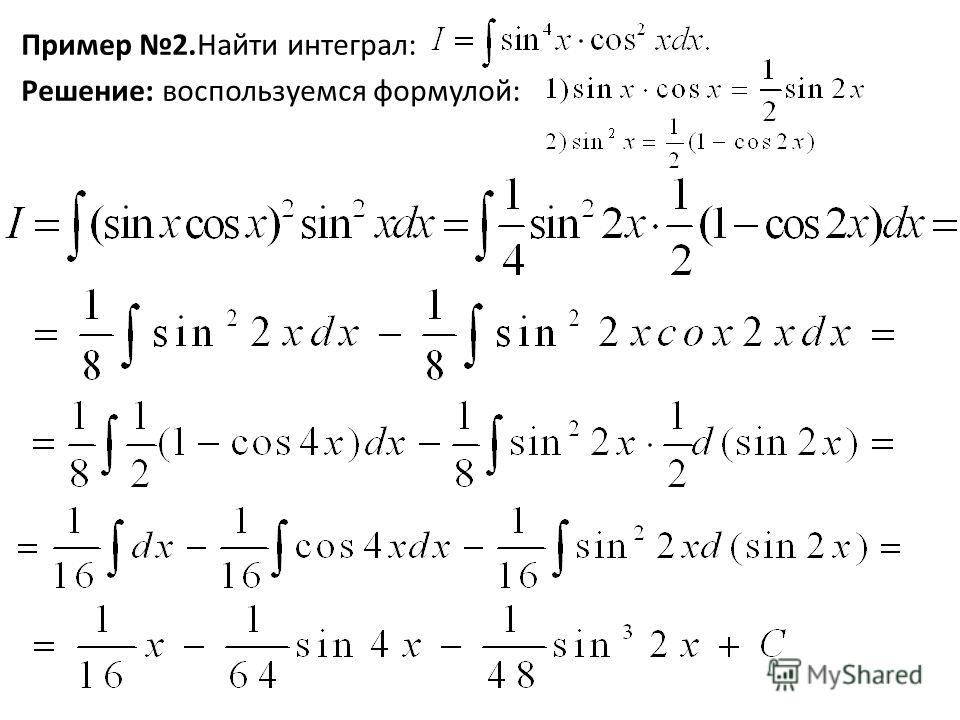 Поэтому «эф от икс». Значит высота это f(x). Функция, кстати, тоже бесконечная.

Высота конкретного прямоугольничка, это значение функции в этой конкретной точке (почему точке, потому, что ширина полоски у нас бесконечно маленькая, мы так договорились в самом начале).

Площадь, это высота умноженная на ширину. За высоту можем брать и y и f(x), они равны. За ширину у нас играет dx. Итак, момент истины:

f(x)dx — площадь нашего маленького столбика. В если собрать из все вместе, будет сумма бесконечно маленьких столбиков.

А площадь нужна не бесконечной фигуры, а той что начинается от 1 и закачивается на 5. Если написать эти цифры над и под значком интеграла, получится определенный интеграл.

Собственно и все, интеграл — это сумма бесконечно малых приращений (то есть значений) какой-то функции. Не сложно и не страшно, если не усложнять.

Что мы делаем? Разрезаем фигуру на «ленточки» изменяем площадь этих ленточек и собираем все обратно (суммируем).

Интересно, везде идет речь о сумме, а площадь считается умножением. Парадокс? Нет, умножение это ведь то же самое, что и сложение: 2+2+2+2=2*4. То же самое происходит и с площадью. Чтобы выяснить какова площадь прямоугольника со сторонами 5 и 4, перемножаем 5 на 4, или разделяем прямоугольник на 5 полосок шириной в «единицу» и складываем 4+4+4+4+4=5*4=20.

Никакого противоречия здесь нет. Вот только умножение работает в случае одинаковых величин, простых фигур или прямолинейного движения без ускорения. В остальных случаях — интегрирование.

Зачем нужен интеграл

Из примера выше уже понято, что одна из полезных задач интегрирования — это расчет площади криволинейных фигур. В любой сложной ситуации, если сложность эта заключается криволинейности или неравномерности мы используем интеграл.

Но лучший способ объяснить, что такое интеграл простыми словами — показать еще пару примеров. Как когда-то в детстве объяснили сложение на яблоках. Для чего интеграл может понадобиться?

Предположим, нужно построить храм кому-то из древнегреческих богов, такой чтобы место в нем хватило всем, крыша была прямоугольной, а колоны круглыми, ведь так красивее (а еще прочнее).

Давление колонны на фундамент легко посчитать, если она квадратного сечения, делим силу на площадь и вуаля. А если колонна круглого сечения? Какова площадь круга?

Можно конечно, не напрягаться, и заменить круг эквивалентным квадратом (квадратура круга), но каким? На всякий случай побольше, чтобы наверняка ничего не развалилось. Но это не наш метод, особенно, если ни бесконечного числа рабочих, ни бесконечного числа мрамора в действительности нет и взять негде, а казнить за неэффективное использование бюджета никто не запрещает.

Прием с эквивалентом площади на самом деле простой, использовался древними людьми. Очень-очень древние греки ничего не знали об интегрировании, а Архимед еще не родился, тем не менее, чтобы рассчитать площадь круга, в него выкладывались камешки. Когда круг заполнялся, камешки собирались и раскладывались в виде квадрата. Чем меньше камешки тем… Ничего не напоминает?

Еще примеры из жизни

Конечно, в физике интеграл «берут» постоянно. Вместо Х, может быть время, и тогда мы будем иметь дело с функцией времени, такой, например, как скорость. Ускорение — это скорость изменения скорости. Скорость, это скорость изменения координат. Пробежавшись от ускорения к скорости мы уже дважды использовали интеграл.

В обратную сторону: первая производная пути, это скорость, вторая производная — ускорение. Если ускорение равно нулю, значит скорость не менялась.

Интегрирование и дифференцирование, такие же «парочка» как и умножение и деление, суммирование и вычитание, только не с цифрами, а с функциями. Это взаимно-обратные операции. В случае производной, мы не «складываем», а «отнимаем».

Если проинтегрировав функцию изменения скорости (ускорение) получим константу (число, например, 60, а не формулу y=2x), значит, скорость не изменялась со временем, ускорения не было. Если, взяв приводную (дифференциал) функции скорости по времени, получим ноль — скорость не менялась, ускорение равно нулю.

То есть, имея в своем распоряжении какую-то функцию (зависимость чего-то от чего-то), мы можем ее дифференцировать или интегрировать. Точно также как если бы умножали и или, вычитали и складывали обычные числа.

Например, у нас есть функция изменения координат от времени. В реальном мире мы вышли на пробежку. Бежал наш виртуальный спортсмен 30 минут, первые 10 минут очень быстро, вторые 10 минут уже с одышкой, ну а последние 10 прошел пешком.

Очевидно, что координаты бегуна в начале и в конце разные (он же не стоял на месте). Если координаты менялись — скорость не равнялась нулю.

Скорость не была одинаковой, а менялась в зависимости от времени (больше времени, больше усталость, меньше скорость).

Итак, у нас есть функция изменения координат. Первая производная даст нам новую функцию — изменения координат, вторая производная — функцию ускорения. И первая и вторая функции зависят от одной и той же переменной — времени.

Еще один пример, вычисление массы. Масса, это произведение плотности на объем. Если плотность и объем одинаковы (это стакан воды) никаких проблем нет. А если плотность меняется (тот же стакан, только с коктейлем в несколько слоев)? В таком случае нужно знать закон (зависимость с которой изменяться плотность жидкости в стакане).

Если вам такие примеры не близки, то представьте себе, что взяли кредит под сложный процент. Тогда ваш долг будет расти не линейно. И вы будете интегрировать…

Если нужно узнать какую работу нужно затратить на перемещение предмета не по прямой, а если, нужно рассчитать лучшую цену, зная зависимость спроса от предложения, а если нужно посчитать за какое время рабочие выкопают яму, если это не роботы, а живые люди, которые устают со временем, а если…

Если посмотреть вокруг, не найдется в реальном мире ни идеальных фигур, ни ровных графиков, ни равномерного движения без ускорения, ни линейных зависимостей в поведении человека «разумного».

Все эти простые штуки из науки, просто частные случаи. А значит, в реальном мире интеграл более полезен, чем кажется. Конечно, кривые сложнее прямых и именно поэтому всю свою историю люди упрощали себе жизнь: делили поле прямыми, на квадраты и прямоугольники при помощи натянутой веревки. Считали среднюю скорость, а не мгновенную в каждой точке маршрута, полагали, что тело прошенное под углом к горизонту летит по параболе, а не баллистической кривой… Но, просто — не значит точно.

Говоря простым языком, интегрирование — это такой же инструмент, как и суммирование, в нем нет никаких особых тайн и сложностей. Кроме одной — представить себе бесконечность сложнее, чем натуральные числа, у которых есть наглядные представления в природе. Но справляемся же мы как-то с представлениями таких абстракций как «ноль» или «отрицательное число». С матанализом просто нужно чуть больше воображения.

Ну а если уж совсем просто, для гуманитариев, то производная винограда — это вино. Интеграл вина — это виноград.

Источник

Интегралы для чайников: как решать, правила вычисления, объяснение

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Свойства определенного интеграла

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Видео

ИНТЕГРАЛ С НУЛЯ | определенный интеграл | ТАБЛИЦА ИНТЕГРАЛОВ | сумма Римана

Математика без ху{a47c00a1996a64a2145764bc9f608acb943865b2eadd21c2af8fa308981ee3ea}!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.

Зачем нужен ИНТЕГРАЛ. Объяснение математического смысла.

Определенные и неопределенные интегралы для чайников. Свойства интегралов.

✓ Формула Ньютона-Лейбница. Что такое первообразная и интеграл | Осторожно, спойлер! | Борис Трушин

Смысл интеграла и производной. В помощь студенту

05. Что такое интеграл?

ЧТО ТАКОЕ ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ. Артур Шарифов

Интеграл: Азы интегрирования. Высшая математика

Определенный интеграл. 11 класс.

Неопределенный интеграл. Основные методы интегрирования

4.2.

Неопределенный интеграл. Основные методы интегрирования

Сегодня вы изучите вопросы

Метод интегрирования неопределенного интеграла по частям
Интегрирование рациональных дробей
Интегрирование некоторых классов тригонометрических функций
Интегрирование иррациональных функций

Изучив тему занятия, вы сможете

найти нетабличные неопределенные интегралы;
найти интегралы от рациональных дробей;
найти интегралы от некоторых классов тригонометрических функций;
найти интегралы от иррациональных функций.

Основные понятия

4.2.1.

Метод интегрирования неопределенного интеграла по частям

Пусть u и v — две дифференцируемые функции одного и того же аргумента.

Известно, что:

(177)

Возьмем от обеих частей равенства (177) неопределенный интеграл:

Отсюда находим:

. (178)

Равенство (178) называется формулой интегрирования неопределенного интеграла по частям.

Если подынтегральные выражения в равенстве (178) рассматривать как произведение двух сомножителей, то формула интегрирования по частям переводит один интеграл в другой, где дифференцирование от одного множителя подынтегрального выражения переведено на другой множитель.

Действительно, подынтегральное выражение интеграла слева в равенстве (178) равно , а подынтегральное выражение интеграла правой части равенства (178) равно .

Следует заметить, что разбиение подынтегрального выражения должно быть таким, чтобы интегрирование дифференциала не представляло трудностей и чтобы замена на и на в итоге упрощала подынтегральное выражение.

Приведем некоторые типы интегралов, которые удобно раскрывать методом интегрирования по частям:

,

где — многочлен, .

В этом случае удобно положить , а остаток подынтегрального выражения обозначить dv.
В этом случае удобно положить , а остаток подынтегрального выражения принять за u.
где .

В этом случае можно принять за и повторно интегрировать по частям.

Замечание. В первом случае формулу интегрирования по частям применяют n раз, понижая каждый раз показатель степени многочлена на единицу.

Ко второму случаю можно отнести также интегралы, у которых отсутствует многочлен, а аргументы логарифмической или обратных тригонометрических функций более сложные.

Рассмотрим конкретные примеры применения метода интегрирования по частям.

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Пример 5.

Пусть . В этом обозначении равенство

перепишем так:

то есть относительно F(x) мы получили линейное уравнение.

Отсюда находим:

Возвращаясь к прежнему обозначению, окончательно находим:

4.2.2.

Интегрирование рациональных дробей

Под рациональной дробью понимается отношение двух многочленов:

(179)

х — независимая переменная,

, — действительные числа.

Если , то дробь (179) является неправильной. В этом случае делением числителя на знаменатель дробь (179) можно представить в виде суммы целого многочлена и правильной рациональной дроби.

Действительно, пусть .

Разделив на , будем иметь:

Следовательно, дробь можно представить в следующем виде:

В дальнейшем будем полагать, что дробь (179) является правильной и несократимой.

По основной теореме алгебры корнями (или нулями) многочлена являются либо действительные числа, либо комплексные (сопряженные) числа, суммарное число корней равно степени многочлена, причем каждый корень считается столько раз, какова его кратность.

По теореме Безу, если x = a является нулем многочлена f (x), то справедливо равенство , где — многочлен, степень которого на единицу меньше степени f (x).

Также легко доказать, что если f (x) имеет комплексный корень , то он имеет и сопряженный корень .

Следовательно, по теореме Безу f (x) можно представить в виде:

Действительно, перемножив линейные множители получим квадратный трехчлен с действительными коэффициентами. Покажем это:

где .

То есть , где — многочлен, степень которого на две единицы меньше, чем степень f (x).

Отсюда следует по основной теореме алгебры, что всякий многочлен степени n можно представить так:

В этой связи рациональную дробь можно рассматривать как отношение

Рассмотрим частный случай, когда

Покажем, что в этом случае правильную рациональную дробь можно представить в следующем виде:

где A₁ — действительное число, отличное от нуля;

— многочлен, степень которого меньше степени знаменателя .

Действительно,

Подберем такое чтобы многочлен в точке x = a обратился в нуль:

. (180)

Таким образом, если определить равенством (180), то по теореме Безу .

Отсюда находим, что:

или

. (181)

Применяя заданное разложение повторно раз, получим:

По аналогии, если , то получим:

где являются действительными числами. Таким образом, правильную несократимую рациональную дробь, знаменатель которой имеет действительные и комплексные корни, можно представить в следующем виде:

(182)

Из разложения (182) следует, что интегрирование правильной несократимой рациональной дроби всегда можно привести к интегрированию рациональных дробей следующих видов:

;
,

называемых простейшими.

Перейдем к интегрированию простейших рациональных дробей.

1. .

2. .

где . (183)

Интеграл (183) берется методом понижения порядка, по так называемой рекуррентной формуле, основная идея которой заключается в выражении интеграла (183) аналогичным интегралом, степень знаменателя которого будет меньше на единицу (183).

Имеем:

(184)

Второй интеграл в равенстве (184) возьмем по частям:

. (185)

Равенство (183) с учетом полученного равенства (185) перепишется так:

или . (186)

Применяя формулу (186) последовательно k — 1 раз, придем к интегралу:

. (187)

Подставляя затем вместо t и а их соответствующие выражения, получим выражение интеграла (183) через действительные числа M, N, p и q.

Примеры.

.

Отсюда находим, что . Ввиду тождественности последнего равенства положим

.

Пусть , получим . Следовательно, заданный интеграл можно разбить на два интеграла:

Заданный интеграл можно раскрыть, если воспользоваться табличным интегралом
.

Воспользуемся табличным интегралом:

.

Имеем:

.
.

Для раскрытия последнего интеграла воспользуемся табличным интегралом:

.

В нашем случае . Имеем:

.
Рассмотрим интеграл:

По формуле (186), где , имеем:

4.2.3.

Интегрирование некоторых классов тригонометрических функций

Так как все тригонометрические функции рационально выражаются через синус и косинус, следовательно, всякая функция, рационально зависящая от тригонометрических функций, может быть преобразована в соответствующую рациональную функцию только синуса и косинуса.

Поэтому достаточно будет рассмотреть интегрирование функций, рационально зависящих от синуса и косинуса.

Рассмотрим интеграл:

, (188)

где является рациональной функцией и .

Интегралы типа (188) называются тригонометрическими интегралами.

Интеграл (188) приводится к интегралу от рациональной функции переменной при помощи универсальной подстановки:

. (189)

Действительно, если воспользоваться известными из школьного курса тригонометрическими формулами, то легко выразить , и через переменную :

(190)

Подставляя найденные выражения и , и в выражение подынтегральной функции (1), получим интеграл от рациональной функции переменной :

(191)

Пример.

В некоторых частных случаях быстрее приводят к цели другие подстановки, так как универсальная подстановка на практике в большинстве случаев приводит к интегрированию сложных рациональных дробей.

Рассмотрим следующие частные случаи.

, где является рациональной функцией .

Подстановка приводит этот интеграл к интегралу от рациональной функции переменной :
Пример.
.

Подстановка приводит этот интеграл к интегралу от рациональной функции переменной : .
Пример.
.

Подстановкой данный интеграл сводится к интегралу от рациональной функции переменной :

Пример.
где подынтегральная функция является рациональной функцией от четных степеней синуса и косинуса переменной интегрирования.

Заданный интеграл приводится к интегралу от рациональной функции переменной подстановкой :

Пример.

4.2.4.

Интегрирование иррациональных функций

Рассмотрим наиболее распространенные неопределенные интегралы от иррациональных функций, которые с помощью подстановок приводятся к интегралам от рациональных функций и, следовательно, выражаются через элементарные функции.

Интегралы, подынтегральные функции которых содержат различные радикалы переменной :

где являются целыми положительными числами.

Заданный интеграл приводится к интегралу от рациональной функции с помощью замены переменной , где — общий знаменатель всех показателей степеней.
Пример.
Интегралы, содержащие различные радикалы от дробно-линейной функции.

Дробно-линейной функцией от переменной называется функция от дроби , где — действительные числа. Следовательно, мы рассматриваем интегралы следующего типа:

где являются целыми положительными числами.

Данные интегралы приводятся к интегралам от рациональной дроби путем подстановки , где — общий знаменатель всех показателей степеней.

Пример.

Рассмотрим интегралы от иррациональной функции, которые приводятся к рациональным функциям с помощью замены переменной и подстановки. Данные интегралы нами приведены как табличные.

В правой части последнего равенства мы имеем исходный интеграл. Переносом этого интеграла в левую часть окончательно находим:

, или

Для привития навыков интегрирования рассмотрим дополнительный перечень интегралов, заданных не по типам, чтобы в каждом конкретном случае читатель мог сам выбрать тот или иной эффективный способ интегрирования.

Пример 1.

Пример 2.

Пример 3.

Последнее вытекает из табличного интеграла .

Пример 4.

Пример 5.

Пример 6.

Пример 7.

Рассмотрим пример, где потребуется дважды применять интегрирование по частям.

Пример 8.

Пример 9.

Пример 10.

Пример 11.

Пример 12.

В числителе выделим дифференциал знаменателя:

Пример 13.

Полагаем х = 2: 2 = — А; А = — 2.

Полагаем х = 3: 3 = В.

Таким образом, имеем: .

Следовательно, заданный интеграл можно переписать так:

Пример 14.

Найти .

Разложим знаменатель на линейные множители:

Представим рациональную дробь в виде трех слагаемых с линейными знаменателями:

Отсюда, полагая х = 0, получим: 2 = -8А; .

Полагая х = 2, получим: 4 — 4 + 2 = 12В; .

Полагая х = -4, получим: 16 + 8 + 2 = 24С; .

Отсюда находим, что:

Пример 15.

Для раскрытия последнего интеграла воспользуемся табличным интегралом:

В нашем случае а = 6; u = х — 5. Имеем:

Пример 16.

В заключение остановимся на понятии «неберущиеся интегралы». Как известно, интегралы от непрерывных функций существуют. Однако этим не утверждается, что первообразная непременно будет одна из основных элементарных функций или функция, полученная из элементарных функций путем всевозможных комбинаций образования сложных функций. Весьма вероятно, что произвольно взятый нами интеграл может иметь первообразную, которая не является элементом известного нам множества функций. Например, первообразные интегралы

, , , ,

не могут быть образованы из основных элементарных функций и любого способа образования сложных функций. В этом случае говорят, что интеграл является неберущимся. По сути дела, приведенные интегралы это абсолютно новые функции.

Контрольные вопросы

Какие вы знаете методы интегрирования и в чем заключается идея этих методов?
В чем заключается различие метода замены переменной от метода подстановки?
Как вы понимаете понятие «неберущиеся интегралы»?
Каким условиям должна удовлетворять подынтегральная функция, чтобы существовал неопределенный интеграл (или первообразная)?
Напишите формулу интегрирования по частям для неопределенного интеграла.
Какие дроби называются простейшими рациональными дробями и чему равны интегралы от таких функций?

Задания для самостоятельной работы

Применяя метод интегрирования по частям, найдите следующие интегралы:
Найдите интегралы от выражений, содержащих квадратный трехчлен:
Найдите интегралы от рациональных дробей:

Комплексный анализ

←Комплексный анализ→

Магия и сила исчисления в конечном итоге основываются на том удивительном факте, что дифференцирование и интеграция являются взаимно обратными операциями. И так же, как сложные функции обладают замечательной дифференцируемостью свойства, которых нет у их реальных аналогов, поэтому возвышенная красота сложной интеграции далеко выше своего реального прародителя.

Питер Дж. b v(t)\,dt \end{эквнаррай}

Теперь запишем подынтегральную функцию $$f(z)= u(x,y)+ iv(x,y)$$ через его действительную и мнимую части, а также дифференциал $$dz=\frac{dz}{dt}dt = \left(\frac{dx}{dt}+ i \frac{dy}{dt}\right)dt = dx+ i dy$$ Тогда комплексный интеграл (\ref{contour-integral}) распадается на пару вещественных линейных интегралов: \begin{eqnarray}\label{действительные интегралы} \int_C f(z)\,dz = \int_C\left(u+iv\right)\left(dx+idy\right) = \int_C\left(u\,dx-v\,dy\right) + i \int_C\влево(v\,dx+u\,dy\вправо). \end{эквнаррай} 9{2\пи} dt= 2\пи \,я. \end{выравнивание*}

Численная оценка комплексных интегралов

Разведка 1

Используйте следующий апплет для численного исследования интеграла $$\int_C \overline{z}\, dz$$ с разными контурами $C$:

Сегменты линий.
Полукруги.
Круги, позитивно и негативно ориентированные.

Вы также можете изменить параметр отображения цвета домена. Перетаскивайте точки и внимательно наблюдайте, что происходит. затем решить упражнение 1 ниже. 92 . Затем проанализируйте значения $I_2$ в следующих случаях:

$C$ — любой контур от $z_0=-i$ до $z_1 = i$. Что происходит, когда вы выбираете Line Segment в апплете? Что случается когда вы выбираете Полукруги ?

$C$ — окружность с центром $z_0$ и радиусом $r\gt 0$, $|z-z_0|= г$; позитивно или негативно ориентированы. В этом случае выберите Circle ↺ или Circle ↻ . Что произойдет, если $z = 0$ окажется внутри или вне круга? Что произойдет, если $z=0$ лежит на контуре, например когда $z_0=1$ и $r=1$? 92}$ от это?
Антидеривативы
Хотя значение контурного интеграла функции $f (z)$ от фиксированной точки $z_0$ до фиксированная точка $z_1$ зависит, вообще говоря, от выбранного пути, существуют определенные функции, интегралы которых от $z_0$ до $z_1$ имеют значения, не зависящие от пути, как вы видели в упражнениях 2 и 3. Эти примеры также иллюстрируют тот факт, что значения интегралов вокруг замкнутых путей иногда, но не всегда, нуль. Следующая теорема полезна для определения того, когда интегрирование является независимым. пути и, тем более, когда интеграл по замкнутому пути имеет нулевое значение. Это известно как сложная версия 9{b} \frac{d}{dt} F \left(z(t)\right) dt \\ &=& F\влево(z(b)\вправо) – F\влево(z(a)\вправо) \\ &=& F\влево(z_1\вправо) – F\влево(z_0\вправо) \end{выравнивание*} где $z_0= z(a)$ и $z_1= z(b)$ — концы контура $C$. $\черный квадрат$
СЛЕДУЮЩАЯ: Интегралы функций с ветвями
страница не найдена – Колледж Уильямс
’62 Центр театра и танца, ’62 Центр
Касса 597-2425
Магазин костюмов 597-3373
Менеджер мероприятий/помощник менеджера 597-4808 597-4815 факс
Производство 597-4474 факс
Магазин сцен 597-2439
’68 Центр изучения карьеры, Мирс 597-2311 597-4078 факс
Академические ресурсы, Парески 597-4672 597-4959 факс
Служба поддержки инвалидов, Парески 597-4672
Приемная, Уэстон Холл 597-2211 597-4052 факс
Позитивные действия, Хопкинс-холл 597-4376
Африканские исследования, Голландия 597-2242 597-4222 факс
Американские исследования, Шапиро 597-2074 597-4620 факс
Антропология и социология, Холландер 597-2076 597-4305 факс
Архивы и специальные коллекции, Sawyer 597-4200 597-2929 факс
Читальный зал 597-4200
Искусство (История, Студия), Spencer Studio Art/Lawrence 597-3578 597-3693 факс
Архитектурная студия, Spencer Studio Art 597-3134
Студия фотографии, Spencer Studio Art 597-2030
Студия гравюры, Spencer Studio Art 597-2496
Скульптурная студия, Spencer Studio Art 597-3101
Senior Studio, Spencer Studio Art 597-3224
Видео/фотостудия, Spencer Studio Art 597-3193
Азиатские исследования, Голландия 597-2391 597-3028 факс
Астрономия/астрофизика, Физика Томпсона 597-2482 597-3200 факс
Отделение легкой атлетики, физического воспитания, отдыха, Ласелл 597-2366 597-4272 факс
Спортивный директор 597-3511
Лодочная пристань, озеро Онота 443-9851
Вагоны 597-2366
Фитнес-центр 597-3182
Хоккейный каток Ice Line, Lansing Chapman 597-2433
Очные занятия, Спортивный центр Чендлера 597-3321
Физкультура 597-2141
Мокрая линия бассейна, Спортивный центр Чандлера 597-2419
Информация о спорте, Хопкинс-холл 597-4982 597-4158 факс
Спортивная медицина 597-2493 597-3052 факс
Корты для сквоша 597-2485
Поле для гольфа Taconic 458-3997
Биохимия и молекулярная биология, Биология Томпсона 597-2126
Биоинформатика, геномика и протеомика, Бронфман 597-2124
Биология, Биология Томпсона 597-2126 597-3495 факс
Безопасность и безопасность кампуса, Хопкинс-холл 597-4444 597-3512 факс
Карты доступа/Системы сигнализации 597-4970/4033
Служба сопровождения, Хопкинс-холл 597-4400
Офицеры и диспетчеры 597-4444
Секретарь, удостоверения личности 597-4343
Распределительный щит 597-3131
Центр развития творческого сообщества, 66 Stetson Court 884-0093
Центр Экономики Развития, ул. Мэйн 1065, 597-2148 597-4076 факс
Компьютерный зал 597-2522
Вестибюль 597-4383
Центр экологических исследований, выпуск 1966 г. Экологический центр 597-2346 597-3489 факс
Лаборатория наук об окружающей среде, Морли 597-2380
Экологические исследования 597-2346
Лаборатория ГИС 597-3183
Центр иностранных языков, литературы и культуры, Голландия 597-2391 597-3028 факс
Арабистика, Голландия 597-2391 597-3028 факс
Сравнительная литература, Hollander 597-2391
Critical Languages, Hollander 597-2391 597-3028 факс
Языковая лаборатория 597-3260
Русский, Голландец 597-2391
Центр обучения в действии, Brooks House 597-4588 597-3090 факс
Библиотека редких книг Чапина, Сойер 597-2462 597-2929 факс
Читальный зал 597-4200
Офис капелланов, Парески 597-2483 597-3955 факс
Еврейский религиозный центр, Stetson Court 24 597-2483
Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) 597-2483
Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) 597-2483
Химия, Химия Томпсона 597-2323 597-4150 факс
Классика (греческая и латинская), голландская 597-2242 597-4222 факс
Когнитивные науки, Бронфман 597-4594
College Marshal, Thompson Physics 597-2008
Отношения с колледжами 597-4057
25-я программа воссоединения, Фогт 597-4208 597-4039 факс
50-я программа воссоединения, Фогт 597-4284 597-4039 факс
Операции по развитию, Мирс-Уэст 597-4154 597-4333 факс
Мероприятия для выпускников, Фогт 597-4146 597-4548 факс
Фонд выпускников 597-4153 597-4036 факс
Отношения с выпускниками, Мирс-Уэст 597-4151 597-4178 факс
Почтовые службы для выпускников и разработчиков, Mears West 597-4369
Развитие, Фогт 597-4256
Связи с донорами, Фогт 597-3234 597-4039 факс
Отдел планирования подарков, Фогт 597-3538 597-4039 факс
Отдел грантов, Мирс-Уэст 597-4025 597-4333 факс
Программа крупных подарков, Vogt 597-4256 597-4548 факс
Родительский фонд, Фогт 597-4357 597-4036 факс
Prospect Management & Research, Mears 597-4119 597-4178 факс
Начало и академические мероприятия, Jesup 597-2347 597-4435 факс
Коммуникации, Хопкинс Холл 597-4277 597-4158 факс
Информация о спорте, Хопкинс-холл 597-4982 597-4158 факс
Веб-группа, Southworth Schoolhouse
Williams Magazines (ранее Alumni Review), Hopkins Hall 597-4278
Информатика, Химия Томпсона 597-3218 597-4250 факс
Конференции и мероприятия, Парески 597-2591 597-4748 факс
Справки о домике на дереве вяза, ферма Маунт-Хоуп 597-2591
Офис контролера, Хопкинс-холл 597-4412 597-4404 факс
Кредиторская задолженность и ввод данных, Hopkins Hall 597-4453
Касса и кассовые чеки, Hopkins Hall 597-4396
Финансовые информационные системы, Хопкинс Холл 597-4023
Карточки для закупок, Хопкинс Холл 597-4413
Студенческие ссуды, Хопкинс Холл 597-4683
Танец, ’62 Центр 597-2410
Центр Дэвиса (ранее Мультикультурный центр), Дженнесс 597-3340 597-3456 факс
Харди Хаус 597-2129
Дженнес Хаус 597-3344
Райс Хаус 597-2453
Декан колледжа, Хопкинс-холл 597-4171 597-3507 факс
Декан факультета, Хопкинс-холл 597-4351 597-3553 факс
Обеденные услуги, капельницы 597-2121 597-4618 факс
’82 Гриль, Парески 597-4585
Пекарня, Парески 597-4511
Питание, Факультет 597-2452
Обеденный зал Дрисколла, Дрисколл 597-2238
Эко-кафе, Научный центр 597-2383
Grab ‘n Go, Парески 597-4398
Закусочная Lee, Парески 597-3487
Обеденный зал Mission Park, Mission Park 597-2281
Уитменс, Парески 597-2889
Экономика, Шапиро 597-2476 597-4045 факс
английский, голландский 597-2114 597-4032 факс
Помещения, Сервисное здание 597-2301
Запрос автомобиля для колледжа 597-2302
Вечерние/выходные чрезвычайные ситуации 597-4444
Запросы на работу объектов 597-4141 факс
Особые события 597-4020
Склад 597-2143 597-4013 факс
Факультетский клуб, Факультетский дом/Центр выпускников 597-2451 597-4722 факс
Бронирование 597-3089
Офис стипендий, Хопкинс-холл 597-3044 597-3507 факс
Финансовая помощь, Weston Hall 597-4181 597-2999 факс
Геофизические науки, Кларк Холл 597-2221 597-4116 факс
немецкий-русский, голландский 597-2391 597-3028 факс
Глобальные исследования, Холландер 597-2247
Программа магистратуры по истории искусств, The Clark 458-2317 факс
Health and Wellness Services, Thompson Ctr Health 597-2206 597-2982 факс
Санитарное просвещение 597-3013
Услуги комплексного благополучия (консультации) 597-2353
Экстренные ситуации, угрожающие жизни Звоните 911
Медицинские услуги 597-2206
История, Холландер 597-2394 597-3673 факс
История науки, Бронфман 597-4116 факс
Хопкинс Форест 597-4353
Центр Розенбурга 458-3080
Отдел кадров, здание B&L 597-2681 597-3516 факс
Услуги няни, здание B&L 597-4587
Преимущества 597-4355
Программа помощи сотрудникам 800-828-6025
Занятость 597-2681
Расчет заработной платы 597-4162
Ресурсы для супругов/партнеров 597-4587
Трудоустройство студентов 597-4568
Погодная линия (ICEY) 597-4239
Гуманитарные науки, Шапиро 597-2076
Информационные технологии, Джесуп 597-2094 597-4103 факс
Пакеты для чтения курса, почтовый ящик Office Services 597-4090
Центр кредитования оборудования, Додд, приложение 597-4091
Служба поддержки преподавателей/персонала, [email protected] 597-4090
Мультимедийные услуги и справка для занятий 597-2112
Служба поддержки студентов, [электронная почта защищена] 597-3088
Телекоммуникации/телефоны 597-4090
Междисциплинарные исследования, Hollander 597-2552
Международное образование и учеба вне дома, Хопкинс-холл 597-4262 597-3507 факс
Инвестиционный офис, Хопкинс-холл 597-4447
Офис в Бостоне 617-502-2400 617-426-5784 факс
Еврейские исследования, Мазер 597-3539
Справедливость и право, Холландер 597-2102
Latina/o Studies, Hollander 597-2242 597-4222 факс
Исследования лидерства, Шапиро 597-2074 597-4620 факс
Морские исследования, Бронфман 597-2297
Математика и статистика, Bascom 597-2438 597-4061 факс
Музыка, Бернхард 597-2127 597-3100 факс
Concertline (записанная информация) 597-3146
Неврология, Биология Томпсона 597-4107 597-2085 факс
Центр Окли, Окли 597-2177 597-4126 факс
Управление институционального разнообразия и справедливости, Хопкинс-холл 597-4376 597-4015 факс
Бухгалтерия студентов, Хопкинс Холл 597-4396 597-4404 факс
Исследования производительности, ’62 Центр 597-4366
Философия, Шапиро 597-2074 597-4620 факс
Физика, Физика Томпсона 597-2482 597-4116 факс
Планетарий/Обсерватория Хопкинса 597-3030
Старый театр обсерватории Хопкинса 597-4828
Бронирование 597-2188
Политическая экономия, Шапиро 597-2327
Политология, Шапиро 597-2168 597-4194 факс
Офис президента, Хопкинс-холл 597-4233 597-4015 факс
Дом Президента 597-2388 597-4848 факс
Услуги печати/почты для преподавателей/сотрудников, ’37 House 597-2022
Программа обучения, Бронфман 597-4522 597-2085 факс
Офис проректора, Хопкинс-холл 597-4352 597-3553 факс
Психология, психологические кабинеты и лаборатории 597-2441 597-2085 факс
Недвижимость, здание B&L 597-2195/4238 597-5031 факс
Ипотека преподавателей/сотрудников 597-4238
Аренда жилья для преподавателей/сотрудников 597-2195
Офис ЗАГСа, Хопкинс Холл 597-4286 597-4010 факс
Религия, голландец 597-2076 597-4222 факс
Романские языки, голландский 597-2391 597-3028 факс
Планировщик помещений 597-2555
Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 House 597-3003
Библиотека Сойера, Сойер 597-2501 597-4106 факс
Услуги доступа 597-2501
Приобретения/Серийные номера 597-2506
Услуги каталогизации/метаданных 597-2507
Межбиблиотечный абонемент 597-2005 597-2478 факс
Исследовательские и справочные услуги 597-2515
Стеллаж 597-4955 597-4948 факс
Системы 597-2084
Научная библиотека Шоу, Научный центр 597-4500 597-4600 факс
Научные и технологические исследования, Бронфман 597-2239
Научный центр, Бронфман 597-4116 факс
Магазин электроники 597-2205
Машиностроительный/модельный цех 597-2230
Безопасность 597-4444
Специальные академические программы, Hardy 597-3747 597-4530 факс
Информация о спорте, Хопкинс-холл 597-4982 597-4158 факс
Студенческая жизнь, Парески 597-4747
Планировщик помещений 597-2555
Управление студенческими центрами 597-4191
Планирование студенческих мероприятий 597-2546
Студенческое общежитие, Парески 597-2555
Участие студентов 597-4749
Жилищные программы высшего класса 597-4625
Студенческая почта, Почта Парески 597-2150
Устойчивое развитие/Zilkha Center, Harper 597-4462
Коммутатор, Хопкинс Холл 597-3131
Книжный магазин Уильямс 458-8071 458-0249 факс
Театр, ’62 Центр 597-2342 597-4170 факс
Управление траста и недвижимости, Sears House 597-4259
Учебники 597-2580
Вице-президент Campus Life, Хопкинс-холл 597-2044 597-3996 факс
Вице-президент по связям с колледжами, Мирс 597-4057 597-4178 факс
Вице-президент по финансам и администрации, Хопкинс Холл 597-4421 597-4192 факс
Центр визуальных ресурсов, Лоуренс 597-2015 597-3498 факс
Детский центр колледжа Уильямс, Детский центр Уильямс 597-4008 597-4889 факс
Художественный музей колледжа Уильямс (WCMA), Лоуренс 597-2429 597-5000 факс
Подготовка музея 597-2426
Служба безопасности музея 597-2376
Музейный магазин 597-3233
Уильямс Интернэшнл 597-2161
Выездной клуб Williams, Парески 597-2317
Аппаратная/стол для учащихся 597-4784
Проект Уильямса по экономике высшего образования, Мирс-Уэст 597-2192
Уильямс Рекорд, Парески 597-2400 597-2450 факс
Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет 011-44-1865-512345
Программа Williams-Mystic, Музей Mystic Seaport 860-572-5359 860-572-5329 факс
Женские, гендерные и сексуальные исследования, Шапиро 597-3143 597-4620 факс
Написание программ, Хопкинс-холл 597-4615
Центр экологических инициатив Зилха, Харпер 597-4462
Научное предложение
Научное предложение
Научный Приговор Научный Калькуляторы Решения за Уравнения

     Предисловие

     Проф Аджайя

     Книги
     Школа Аль-Аджуррумья
Средняя школа
Математика 2 | Чими 2 | Преобразования
Механик 2 | Электричество 2 | Лес Энтье
Алг. линейный | Графики | Астрономия
Математика Египта | Оптик2 | Полиномы
Науки и техно. | Цвета | СВТ
Математика 3 | Математика 4 | Математика 5 | Факт. лестница
Проблемы CD | 436 Редакции, раздел 4
Тесты знаний | Калькуляторы
Альгебр | Геометрия | Функции
Статистика | Вероятность | Графы
Проц. де голос | П. условные
Векторы | Коники | Каре Расина
Лес Перспективы | Тригонометрия
Лин. Оптимизация | Проблемы SD

Колледж
Алгебра | Оптимизация
Геометрия | Аналитическая геометрия
Чими | Статистика inferentielles
Предварительный расчет | Исчисление I | Исчисление II
Исчисление III | Вероятность и статистика
Физика и измерения | Лес силы
Механика | Квантовая механика
Ядерная физика | Специальная теория относительности
Оптика | Электростатика | Телосложение 1S
Математика 1С | Проблема двух корпусов
Хими Органик | Леа Ароматики
Анализ | Вероятность | Математика
Математика TS | Наук ТС | Логарифмы
Алгоритмический | Бакалавриат
Отправьте домашнее задание сейчас
Научное предложение Интернет
© Научный приговор. 1993 – 2020. сообщите об этом объявлении
Комплексная интеграция
1. Введение 2. Теорема Коши 3. Тейлора и Лорана64 4. Особенности 5. Остатки 6. Вычисление вещественных определенных интегралов как интегралов по контуру. 7. Приложения
Комплексная интеграция
1. Введение
2. Теорема Коши
3. Тейлор и Лоурент 64
4. Сингулярности
5. Остатки
6. Оценка реальных интеграл как интегрированные. контурные интегралы
7. Applications

COMPLEX INTEGRATION

1 Prerequisites

Before starting this Студенты темы должны уметь проводить интегрирование простых вещественных функций и быть знакомы с основными понятиями функций комплексного переменного. Студенты также должны быть знакомы с линейными интегралами.

2 Введение

Комплексная интеграция является интуитивно понятным расширением реальной интеграции. Поскольку комплексное число представляет собой точку на плоскости, а действительное число — это число на прямой, аналогом единственного действительного интеграла в комплексной области всегда является континуальный интеграл. Для некоторых специальных функций и доменов интеграция не зависит от пути, но в целом это не следует рассматривать. Учитывая чувствительность пути для данного интеграла и его результата, параметризация часто является наиболее удобным способом оценки таких интегралов. Методы сложных переменных использовались в самых разных областях техники. Это особенно верно в таких областях, как теория электромагнитного поля, гидродинамика, аэродинамика и упругость.

3 Cauchy’s Theorem

3. 1 De nitions

3.1.1Connected Region

A connected region есть такая, любые две точки которой можно соединить кривой, полностью лежащей в области.

3.1.2 Односвязная область

Кривая, не пересекающая сама себя, называется простой замкнутой кривой. Область, в которой каждая замкнутая кривая в ней охватывает только точки области, называется односвязной областью.

3.1.3 Контурный интеграл

Интеграл по простой замкнутой кривой называется контурным интегралом.

3.1.4 Интегральная теорема Коши
Если функция f(z) является аналитической и ее производная f0(z) непрерывна во всех точках внутри и на простой замкнутой кривой c, то c f(z)dz = 0:
3.1.5 Интегральная формула Коши.
интегрирование по c ведется в положительном направлении.

3.1.6 Интегральная формула Коши для производной
Если функция f(z) аналитична внутри и на простой замкнутой кривой c и a есть любая точка, лежащая на ней, то

3

3,2 ОБРАБОТКИ Примеры

3,3 Учебный0003

4 Расширение ряда Тейлора и Лорана.
4.1 Ряд Тейлора.

Функция F (Z), аналитическая внутри A Circle C с центром A, может быть расширена в серии

4.2

Пусть C1; C2 — две концентрические окружности jz aj = R1 и jz aj = R2, где R2 < R1: Пусть функция f(z) аналитична на C1 и C2 и в кольцевой области R между ними. Затем для любой точки z в R

, где интегралы берутся против часовой стрелки.

4.3 Разработанные примеры

1. Разложите ez в ряд Тейлора относительно z = 0
0002 Решение.

4.4 Tutorial Problems

5 Singularities

5.1 De nitions

5.1.2 Нули аналитической функции:
Если функция f(z), аналитическая в области R, равна нулю в точке z = z0 в R, то z0 называется нулем f(z).

5.1.3 Простой нуль:
Если f(z0) = 0 и f0(z0) 6= 0, то z = z0 называется простым нулем f(z) или нулем первого порядка. .

5.1.4 Нуль порядка n:

Говорят, что аналитическая функция f(z) имеет нуль порядка n, если f(z) может быть выражена как f(z) z) = (z z0)m (z), где (z) является аналитическим и (z0) 6 = 0

5. 1.5 Особые точки:
Точка z = z0, в которой функция f(z) не является аналитической, называется особой точкой.
5.1.6 ВСЕГО ФУНКЦИЯ
Функция F (z), которая является аналитической везде в плоскости NITE, называется целой функцией.

5.1.7 Мероморфная функция

Функция f(z), аналитическая всюду на конечной плоскости, кроме конечного числа полюсов, называется мероморфной функцией.

5.2 Типы особенностей

5.2.1. Изолированная особенность
Точка z = z0 называется изолированной особенностью функции f(z), если не содержащий другой особенности.

5.2.2. Устранимая особенность:

Если главная часть f(z) в разложении f(z) в ряд Лорана относительно точки z0 равна нулю, то точка z = z0 называется устранимой особенностью.

5.2.3. Полюс:
Если мы можем найти натуральное число n такое, что limz!a(z a)nf(z) 6= 0, то z = a называется полюсом порядка n для f(z).

5.2.4. Существенная особенность:

Если главная часть f(z) в разложении f(z) в ряд Лорана относительно точки z0 содержит бесконечное число ненулевых членов, то точка z = z0 называется существенной особенностью .

5.5.3 Примеры разработки

функция f(z) не определена при z = 0.0003
By, правило Лопиталя

Поскольку предел существует и конечен, особенность в точке z = 0 является устранимой особенностью.
Поскольку предел существует и конечен, особенность в точке z = 0 является устранимой особенностью     .

5.5.4 Проблемы с учебным пособием

6 Остатки

6 Остатки

6 Остатки

0025

6. 1 Definitions:

6.1.2 Worked out Examples

6.1.3 Tutorial Problems

6.2. Теорема Коши о вычетах0003
за исключением конечного числа изолированных особенностей z1; з2; з3; :: затем

6.2.1. РАЗРЕШЕНИЯ.
7 Вычисление действительных определенных интегралов как интегралов по контуру.

7.1 Интегрирование по контуру:

Комплексное интегрирование по скро-кривой, используемое при вычислении определенного интеграла, называется интегрированием по контуру. Здесь мы увидим под тремя типами. Они
7.2 Тип I
7.2.1 Проработанные примеры

0003
7. 2.2 Проблемы с учебным пособием

7.3 Тип II
7.3.1 Проработайте примеры

, где C, состоящий из SEMI Circle: JZJ = R и RABING DI-DI-DI-DI-DI-DI-DI-DI-DI-DI-DI-DI-di- аметр [ R ; Р].
где z = i; 2i — простые полюса лежат внутри и z = I; 2i — простые полюса, лежащие снаружи

, полуокружность становится очень большой, а действительная и мнимая части любой точки, лежащей на полуокружности, становятся очень большими, так что

где c — верхняя половина полуокружности T с граничным диаметром [ R; Р].

Полукруга становится очень большим, и реальные и мнимые части любой точки, лежащей на полукруге, становятся очень большими, так что

7.4.2.

8 Применения:
Blasius Theorem.

На следующем рисунке показано поперечное сечение цилиндра (не обязательно круглого) с границей С, помещенного в устойчивый невязкий поток идеальной жидкости; течение происходит в плоскостях, параллельных плоскости xy. Цилиндр находится вне плоскости бумаги. Поток жидкости воздействует на цилиндр силами и крутящими моментами. Пусть X, Y будут составляющими в направлениях x и y соответственно силы, действующей на цилиндр, и пусть M будет моментом против часовой стрелки (на цилиндре) относительно начала координат.

, где Re обозначает действительную часть, представляет собой (постоянную) плотность жидкости, а w = u + iv представляет собой комплексный потенциал потока, оба из которых считаются известными. Мы найдем X; Y и M, если цилиндр имеет круглое поперечное сечение, а граница определяется выражением jzj = a: Пусть течение представляет собой однородный поток со скоростью U:
Теперь, используя стандартный результат, комплексный потенциал, описывающий эту ситуацию, равен :

Опять же, используя ключевую точку выше, это приводит к 4 a2U2i, и это имеет нулевую действительную часть. Следовательно, также М = 0. Подразумевается, что на цилиндр не действует ни результирующая сила, ни момент. На практике это не так. Несоответствие возникает из-за пренебрежения вязкостью жидкости.

Учебный материал, Конспект лекций, Задание, Справочник, Вики-описание, краткие подробности интересно, но, строго говоря, не является необходимым условием для понимания квантовой механики. Это еще один пример того, как можно заблудиться в математике при изучении или преподавании физики.
Исходное сообщение :
Роджер Пенроуз много рассказывает в своей главе об исчислении комплексных чисел ( Дорога к реальности , глава 7). Он кратко вводит понятие интегрирования по контуру, а затем сразу же переходит к обсуждению представлений комплексных функций степенными рядами, а также довольно продвинутых способов работы с сингулярностями (см. раздел об аналитическом продолжении). Браун и Черчилль используют для этого не менее трех глав («Интегралы» (глава 4), «Ряды» (глава 5) и «Вычеты и полюсы» (глава 6)), и это, вероятно, то, что необходимо для хоть какого-то понимания всего этого. Начнем с интегралов. Однако позвольте мне сначала отметить, что WordPress, похоже, не имеет редактора формул (поэтому он не похож на MS Word), и, следовательно, я должен сохранить простоту обозначений: я буду использовать символ ∫ _C для контурного (или линейного) интеграла вдоль кривой C и символ ∫ _{[a, b]} для интеграла на (замкнутом) интервале [a, b].
ОК. Вот так. Во-первых, важно отметить, что Пенроуз, Браун и Черчилль говорят о комплексных интегралах, т. е. интегралах от комплекснозначных функций, само значение которых тоже (обычно) является комплексным числом. Это сильно отличается от линейных интегралов, с которыми я столкнулся, читая «Лекции Фейнмана по физике». Действительно, Лекции Фейнмана (том II, по электромагнетизму) предлагают прекрасное введение в контурные интегралы, где интегрируемая функция представляет собой либо скалярное поле (например, электрический потенциал), либо некоторое векторное поле (например, магнитное поле, гравитационное поле). . Теперь векторные поля — это двумерные вещи: они имеют координаты x и y, и, следовательно, мы можем думать, что функции, включающие векторы, тоже сложны. Да, но, как уже было сказано, все задействованные интегралы дают действительные числа, потому что подынтегральная функция, скорее всего, будет скалярное произведение векторов (а скалярное произведение векторов, в отличие от перекрестного произведения, дает действительное число). Я не буду вдаваться в подробности здесь, но для тех, кто хотел бы иметь такие подробности, статья в Википедии предлагает прекрасное описание (включая несколько очень хороших анимаций) того, что на самом деле означает интеграция по линии или кривой в таких полях. . Поэтому я не буду повторяться здесь. Могу только отметить, что говорят о них Браун и Черчилль: эти интегралы (вещественные) можно интерпретировать как площади под кривой, и обычно они также имеют тот или иной очевидный физический смысл, а комплексные интегралы обычно имеют , а не имеют такую «полезную геометрическую или физическую интерпретацию».
Так что же это такое? Давайте сначала начнем с нескольких примеров кривых.
Рисунок выше показывает, что на практике кривые, с которыми мы имеем дело, обычно являются параметрическими кривыми. Другими словами, координаты всех точек z кривой C можно представить как некоторую функцию вещественно-числового параметра: z(t) = x(t) + i y(t). Тогда мы можем определить комплексный интеграл как интеграл от комплекснозначную функцию f(z) комплексной переменной z вдоль кривой C от точки z ₁ до точки z ₂ и запишем такой интеграл в виде ∫ _C f(z)dz.
Более того, если C можно параметризовать как z(t), у нас будут некоторые (вещественные) числа a и b такие, что z ₁ = z(a) и z ₂ = z(b) и, взяв принимая во внимание, что dz = z'(t)dt с z'(t)=dz/dt (т. е. производной (комплекснозначной) функции z(t) по (вещественному) параметру t), мы можем написать ∫ _C f(z)dz как:
∫ _C f(z)dz = ∫ _{[a, b]} f[z(t)]z'(t)dt
Ну и что? Что ж, об этом можно сказать много интересного, но позвольте мне просто резюмировать некоторые основные теоремы. Первая важная теорема, по-видимому, не связана с каким-либо конкретным математиком (в отличие от Коши или Гурса, которых я представлю через минуту), но она весьма центральна: если у нас есть некоторая (комплекснозначная) функция f(z), которая имела бы место быть непрерывным в некоторой области D, то все следующих утверждений будут истинны, если одно из из них истинно:
(I) f(z) имеет первообразную F(z) в D ; (II) интегралы от f(z) по контурам, целиком лежащим в D и простирающимся от любой фиксированной точки z ₁ до любой фиксированной точки z ₂, имеют одинаковое значение; и, наконец, (III) все интегралы от f(z) вокруг замкнутых контуров, целиком лежащих в D, имеют нулевое значение.
Это в основном означает, что интегрирование f(z) от z ₁ — z ₂ — это , а не , в зависимости от выбранного пути. Но когда же у нас будет такая независимость пути ? Ну… Вы, наверное, уже догадались об ответе на этот вопрос: это когда функция аналитическая или, другими словами, когда эти уравнений Коши-Римана u _x = v _y и u _y = – v _x удовлетворяются (см. мой другой пост об аналитических (или голоморфных) комплекснозначных функциях). Это, вкратце, то, что утверждается в так называемой теореме Коши-Гурса, и следует отметить, что это действительно эквивалентность, поэтому мы также имеем наоборот утверждение: если интегралы от f(z) по замкнутым контурам в некоторой области D равны нулю, то мы знаем, что f(z) голоморфна.
Короче говоря, мы всегда будем иметь дело с «хорошими» функциями, и тогда мы сможем показать, что так называемая «фундаментальная» теорема исчисления (т. е. та, которая связывает интегралы с производными, или, если быть более точным, с первообразной подынтегральной функции) также применяется к комплекснозначным функциям. У нас есть:
∫ _C f(z)dz = ∫ _{[a, b]} f[z(t)]z'(t)dt = F[z(b)] – F[z(a)]
или больше в общее: ∫ _C f(z)dz = F(z ₂ ) – F(z ₁ )
Нам также необходимо отметить интегральную формулу Коши : если у нас есть функция f, которая является аналитической внутри и на замкнутом контуре C, то значение этой функции для любой точки z ₀ будет равно: (г)/(г – г ₀ )]dz
Это может выглядеть как еще одна формула, но на самом деле она весьма эффектна: в основном она говорит, что значение функции любой точки z ₀ в пределах области, заключенной в кривую, полностью определяется значениями эта функция на эта кривая. Более того, многократное интегрирование обеих частей этого уравнения приводит к аналогичным формулам для производных первого, второго, третьего и более высоких порядков от f: f'(z ₀ ) = (1/2π i ) ∫ _C [f(z)/(z – z ₀ ) ² ]dz, f”(z ₀ ) = (1/2π i )(∫ _{C [ 93 z)/(z – z ₀ ) ³ ]dz или, в более общем виде:}
f ⁽ⁿ⁾ (z ₀ ) = (n!/2π i ) ∫ _{C ∫ _{[f(z)/(z – z ₀ ) ⁿ⁺¹ ]dz (n = 1, 2, 3,…)}}
Эта формула также известна как формула дифференцирования Коши . На самом деле это центральная теорема комплексного анализа, поскольку она ведет ко многим другим интересным теоремам, включая теорему Гаусса о среднем значении, теорему Лиувилля, принцип максимума (и минимума) модуля. Это также важно для следующей главы курса Брауна и Черчилля: Представления сложных функций в степенных рядах. Однако я остановлюсь здесь, потому что полагаю, что это «введение» в комплексные интегралы уже достаточно запутанно.
Post scriptum : Я часто задавался вопросом, почему одну теорему называют «фундаментальной», поскольку это подразумевает, что все остальные теоремы могут быть важными, но, очевидно, несколько менее фундаментальными. Я проверил это, и оказалось, что здесь есть какая-то случайность. Статья в Википедии смело заявляет, что фундаментальная теорема алгебры (которая утверждает, что каждый непостоянный многочлен от одной переменной с комплексными коэффициентами имеет хотя бы один комплексный корень) не так уж и «фундаментальна» для современной алгебры: ее название просто отражает тот факт, что было время, когда алгебра была сосредоточена почти исключительно на изучении многочленов. То же самое может быть верно для фундаментальной теоремы арифметики (т. е. теоремы об уникальной (-простой) факторизации), которая утверждает, что каждое целое число больше 1 равно либо само простое число , либо произведение простых чисел, например 1200 = (2 ⁴ )(3 ¹ )(5 ² ).
При этом фундаментальная теорема исчисления, очевидно, действительно довольно «фундаментальна». Это приводит ко многим результатам, которые действительно являются ключевыми для понимания и решения проблем в физике. Одной из них является теорема о дивергенции (или теорема Гаусса), которая утверждает, что внешний поток векторного поля через замкнутую поверхность равен объемному интегралу от дивергенции по области внутри поверхности. А? Ну… Да. Это всплывает в любой стандартной трактовке электромагнетизма. Есть и другие (например, теорема Стокса), но я пока остановлюсь на этом, особенно потому, что это теоремы, включающие вещественных интегралов из .
Нравится:
Нравится Загрузка…
Контурные интегралы от аналитических функций, заданных на сетке в комплексной плоскости | Журнал численного анализа IMA
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisЭтот выпускIMA JournalsNumerical AnalysisBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisЭтот выпускIMA JournalsNumerical AnalysisBooksJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
Бенгт Форнберг
Бенгт Форнберг
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Журнал численного анализа IMA , том 41, выпуск 2, апрель 2021 г. , страницы 814–825, https://doi.org/10.1093/imanum/draa024
Опубликовано:
20 июля 2020 г.
3 История статьи
Получено:
08 февраля 2020 г.
Получена редакция:
10 марта 2020 г.
Опубликовано:
20 июля 2020 г.
Цитировать
Процитируйте
Бенгт Форнберг, Контурные интегралы аналитических функций, заданные на сетке в комплексной плоскости, Журнал численного анализа IMA , том 41, выпуск 2, апрель 2021 г. , страницы 814–825, https://doi. org/10.1093/imanum/draa024
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Разрешения
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisЭтот выпускIMA JournalsNumerical AnalysisBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisЭтот выпускIMA JournalsNumerical AnalysisBooksJournalsOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Способность вычислять контурные интегралы занимает центральное место как в теории, так и в использовании аналитических функций. Мы представляем здесь комплексную плоскую реализацию формулы Эйлера-Маклорена, которая включает веса также в некоторых точках сетки, смежных с каждым концом отрезка (состоящего из точек сетки, расположенных на равном расстоянии друг от друга, вдоль которых мы используем правило трапеций). Например, при |$5\times 5$| «корректирующий шаблон» (с весами примерно на два порядка меньше, чем у правила трапеций), точность увеличивается с |$2$|го до |$26$|го порядка.
© Автор(ы), 2020. Опубликовано Oxford University Press от имени Института математики и его приложений. Все права защищены.
© Автор(ы), 2020. Опубликовано Oxford University Press от имени Института математики и его приложений. Все права защищены.
Раздел выпуска:
Статьи
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
Нажмите Войти через свое учреждение.
Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Щелкните Войти через сайт сообщества.
При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Кратковременный доступ
Чтобы приобрести краткосрочный доступ, войдите в свою учетную запись Oxford Academic выше.

’62 Центр театра и танца, ’62 Центр
Касса	597-2425
Магазин костюмов	597-3373
Менеджер мероприятий/помощник менеджера	597-4808	597-4815 факс
Производство		597-4474 факс
Магазин сцен	597-2439
’68 Центр изучения карьеры, Мирс	597-2311	597-4078 факс
Академические ресурсы, Парески	597-4672	597-4959 факс
Служба поддержки инвалидов, Парески	597-4672
Приемная, Уэстон Холл	597-2211	597-4052 факс
Позитивные действия, Хопкинс-холл	597-4376
Африканские исследования, Голландия	597-2242	597-4222 факс
Американские исследования, Шапиро	597-2074	597-4620 факс
Антропология и социология, Холландер	597-2076	597-4305 факс
Архивы и специальные коллекции, Sawyer	597-4200	597-2929 факс
Читальный зал	597-4200
Искусство (История, Студия), Spencer Studio Art/Lawrence	597-3578	597-3693 факс
Архитектурная студия, Spencer Studio Art	597-3134
Студия фотографии, Spencer Studio Art	597-2030
Студия гравюры, Spencer Studio Art	597-2496
Скульптурная студия, Spencer Studio Art	597-3101
Senior Studio, Spencer Studio Art	597-3224
Видео/фотостудия, Spencer Studio Art	597-3193
Азиатские исследования, Голландия	597-2391	597-3028 факс
Астрономия/астрофизика, Физика Томпсона	597-2482	597-3200 факс
Отделение легкой атлетики, физического воспитания, отдыха, Ласелл	597-2366	597-4272 факс
Спортивный директор	597-3511
Лодочная пристань, озеро Онота	443-9851
Вагоны	597-2366
Фитнес-центр	597-3182
Хоккейный каток Ice Line, Lansing Chapman	597-2433
Очные занятия, Спортивный центр Чендлера	597-3321
Физкультура	597-2141
Мокрая линия бассейна, Спортивный центр Чандлера	597-2419
Информация о спорте, Хопкинс-холл	597-4982	597-4158 факс
Спортивная медицина	597-2493	597-3052 факс
Корты для сквоша	597-2485
Поле для гольфа Taconic	458-3997
Биохимия и молекулярная биология, Биология Томпсона	597-2126
Биоинформатика, геномика и протеомика, Бронфман	597-2124
Биология, Биология Томпсона	597-2126	597-3495 факс
Безопасность и безопасность кампуса, Хопкинс-холл	597-4444	597-3512 факс
Карты доступа/Системы сигнализации	597-4970/4033
Служба сопровождения, Хопкинс-холл	597-4400
Офицеры и диспетчеры	597-4444
Секретарь, удостоверения личности	597-4343
Распределительный щит	597-3131
Центр развития творческого сообщества, 66 Stetson Court	884-0093
Центр Экономики Развития, ул. Мэйн 1065,	597-2148	597-4076 факс
Компьютерный зал	597-2522
Вестибюль	597-4383
Центр экологических исследований, выпуск 1966 г. Экологический центр	597-2346	597-3489 факс
Лаборатория наук об окружающей среде, Морли	597-2380
Экологические исследования	597-2346
Лаборатория ГИС	597-3183
Центр иностранных языков, литературы и культуры, Голландия	597-2391	597-3028 факс
Арабистика, Голландия	597-2391	597-3028 факс
Сравнительная литература, Hollander	597-2391
Critical Languages, Hollander	597-2391	597-3028 факс
Языковая лаборатория	597-3260
Русский, Голландец	597-2391
Центр обучения в действии, Brooks House	597-4588	597-3090 факс
Библиотека редких книг Чапина, Сойер	597-2462	597-2929 факс
Читальный зал	597-4200
Офис капелланов, Парески	597-2483	597-3955 факс
Еврейский религиозный центр, Stetson Court 24	597-2483
Мусульманская молитвенная комната, часовня Томпсона (нижний уровень)	597-2483
Католическая часовня Ньюмана, часовня Томпсона (нижний уровень)	597-2483
Химия, Химия Томпсона	597-2323	597-4150 факс
Классика (греческая и латинская), голландская	597-2242	597-4222 факс
Когнитивные науки, Бронфман	597-4594
College Marshal, Thompson Physics	597-2008
Отношения с колледжами	597-4057
25-я программа воссоединения, Фогт	597-4208	597-4039 факс
50-я программа воссоединения, Фогт	597-4284	597-4039 факс
Операции по развитию, Мирс-Уэст	597-4154	597-4333 факс
Мероприятия для выпускников, Фогт	597-4146	597-4548 факс
Фонд выпускников	597-4153	597-4036 факс
Отношения с выпускниками, Мирс-Уэст	597-4151	597-4178 факс
Почтовые службы для выпускников и разработчиков, Mears West	597-4369
Развитие, Фогт	597-4256
Связи с донорами, Фогт	597-3234	597-4039 факс
Отдел планирования подарков, Фогт	597-3538	597-4039 факс
Отдел грантов, Мирс-Уэст	597-4025	597-4333 факс
Программа крупных подарков, Vogt	597-4256	597-4548 факс
Родительский фонд, Фогт	597-4357	597-4036 факс
Prospect Management & Research, Mears	597-4119	597-4178 факс
Начало и академические мероприятия, Jesup	597-2347	597-4435 факс
Коммуникации, Хопкинс Холл	597-4277	597-4158 факс
Информация о спорте, Хопкинс-холл	597-4982	597-4158 факс
Веб-группа, Southworth Schoolhouse
Williams Magazines (ранее Alumni Review), Hopkins Hall	597-4278
Информатика, Химия Томпсона	597-3218	597-4250 факс
Конференции и мероприятия, Парески	597-2591	597-4748 факс
Справки о домике на дереве вяза, ферма Маунт-Хоуп	597-2591
Офис контролера, Хопкинс-холл	597-4412	597-4404 факс
Кредиторская задолженность и ввод данных, Hopkins Hall	597-4453
Касса и кассовые чеки, Hopkins Hall	597-4396
Финансовые информационные системы, Хопкинс Холл	597-4023
Карточки для закупок, Хопкинс Холл	597-4413
Студенческие ссуды, Хопкинс Холл	597-4683
Танец, ’62 Центр	597-2410
Центр Дэвиса (ранее Мультикультурный центр), Дженнесс	597-3340	597-3456 факс
Харди Хаус	597-2129
Дженнес Хаус	597-3344
Райс Хаус	597-2453
Декан колледжа, Хопкинс-холл	597-4171	597-3507 факс
Декан факультета, Хопкинс-холл	597-4351	597-3553 факс
Обеденные услуги, капельницы	597-2121	597-4618 факс
’82 Гриль, Парески	597-4585
Пекарня, Парески	597-4511
Питание, Факультет	597-2452
Обеденный зал Дрисколла, Дрисколл	597-2238
Эко-кафе, Научный центр	597-2383
Grab ‘n Go, Парески	597-4398
Закусочная Lee, Парески	597-3487
Обеденный зал Mission Park, Mission Park	597-2281
Уитменс, Парески	597-2889
Экономика, Шапиро	597-2476	597-4045 факс
английский, голландский	597-2114	597-4032 факс
Помещения, Сервисное здание	597-2301
Запрос автомобиля для колледжа	597-2302
Вечерние/выходные чрезвычайные ситуации	597-4444
Запросы на работу объектов		597-4141 факс
Особые события	597-4020
Склад	597-2143	597-4013 факс
Факультетский клуб, Факультетский дом/Центр выпускников	597-2451	597-4722 факс
Бронирование	597-3089
Офис стипендий, Хопкинс-холл	597-3044	597-3507 факс
Финансовая помощь, Weston Hall	597-4181	597-2999 факс
Геофизические науки, Кларк Холл	597-2221	597-4116 факс
немецкий-русский, голландский	597-2391	597-3028 факс
Глобальные исследования, Холландер	597-2247
Программа магистратуры по истории искусств, The Clark		458-2317 факс
Health and Wellness Services, Thompson Ctr Health	597-2206	597-2982 факс
Санитарное просвещение	597-3013
Услуги комплексного благополучия (консультации)	597-2353
Экстренные ситуации, угрожающие жизни	Звоните 911
Медицинские услуги	597-2206
История, Холландер	597-2394	597-3673 факс
История науки, Бронфман		597-4116 факс
Хопкинс Форест	597-4353
Центр Розенбурга	458-3080
Отдел кадров, здание B&L	597-2681	597-3516 факс
Услуги няни, здание B&L	597-4587
Преимущества	597-4355
Программа помощи сотрудникам	800-828-6025
Занятость	597-2681
Расчет заработной платы	597-4162
Ресурсы для супругов/партнеров	597-4587
Трудоустройство студентов	597-4568
Погодная линия (ICEY)	597-4239
Гуманитарные науки, Шапиро	597-2076
Информационные технологии, Джесуп	597-2094	597-4103 факс
Пакеты для чтения курса, почтовый ящик Office Services	597-4090
Центр кредитования оборудования, Додд, приложение	597-4091
Служба поддержки преподавателей/персонала, [email protected]	597-4090
Мультимедийные услуги и справка для занятий	597-2112
Служба поддержки студентов, [электронная почта защищена]	597-3088
Телекоммуникации/телефоны	597-4090
Междисциплинарные исследования, Hollander	597-2552
Международное образование и учеба вне дома, Хопкинс-холл	597-4262	597-3507 факс
Инвестиционный офис, Хопкинс-холл	597-4447
Офис в Бостоне	617-502-2400	617-426-5784 факс
Еврейские исследования, Мазер	597-3539
Справедливость и право, Холландер	597-2102
Latina/o Studies, Hollander	597-2242	597-4222 факс
Исследования лидерства, Шапиро	597-2074	597-4620 факс
Морские исследования, Бронфман	597-2297
Математика и статистика, Bascom	597-2438	597-4061 факс
Музыка, Бернхард	597-2127	597-3100 факс
Concertline (записанная информация)	597-3146
Неврология, Биология Томпсона	597-4107	597-2085 факс
Центр Окли, Окли	597-2177	597-4126 факс
Управление институционального разнообразия и справедливости, Хопкинс-холл	597-4376	597-4015 факс
Бухгалтерия студентов, Хопкинс Холл	597-4396	597-4404 факс
Исследования производительности, ’62 Центр	597-4366
Философия, Шапиро	597-2074	597-4620 факс
Физика, Физика Томпсона	597-2482	597-4116 факс
Планетарий/Обсерватория Хопкинса	597-3030
Старый театр обсерватории Хопкинса	597-4828
Бронирование	597-2188
Политическая экономия, Шапиро	597-2327
Политология, Шапиро	597-2168	597-4194 факс
Офис президента, Хопкинс-холл	597-4233	597-4015 факс
Дом Президента	597-2388	597-4848 факс
Услуги печати/почты для преподавателей/сотрудников, ’37 House	597-2022
Программа обучения, Бронфман	597-4522	597-2085 факс
Офис проректора, Хопкинс-холл	597-4352	597-3553 факс
Психология, психологические кабинеты и лаборатории	597-2441	597-2085 факс
Недвижимость, здание B&L	597-2195/4238	597-5031 факс
Ипотека преподавателей/сотрудников	597-4238
Аренда жилья для преподавателей/сотрудников	597-2195
Офис ЗАГСа, Хопкинс Холл	597-4286	597-4010 факс
Религия, голландец	597-2076	597-4222 факс
Романские языки, голландский	597-2391	597-3028 факс
Планировщик помещений	597-2555
Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 House	597-3003
Библиотека Сойера, Сойер	597-2501	597-4106 факс
Услуги доступа	597-2501
Приобретения/Серийные номера	597-2506
Услуги каталогизации/метаданных	597-2507
Межбиблиотечный абонемент	597-2005	597-2478 факс
Исследовательские и справочные услуги	597-2515
Стеллаж	597-4955	597-4948 факс
Системы	597-2084
Научная библиотека Шоу, Научный центр	597-4500	597-4600 факс
Научные и технологические исследования, Бронфман	597-2239
Научный центр, Бронфман		597-4116 факс
Магазин электроники	597-2205
Машиностроительный/модельный цех	597-2230
Безопасность	597-4444
Специальные академические программы, Hardy	597-3747	597-4530 факс
Информация о спорте, Хопкинс-холл	597-4982	597-4158 факс
Студенческая жизнь, Парески	597-4747
Планировщик помещений	597-2555
Управление студенческими центрами	597-4191
Планирование студенческих мероприятий	597-2546
Студенческое общежитие, Парески	597-2555
Участие студентов	597-4749
Жилищные программы высшего класса	597-4625
Студенческая почта, Почта Парески	597-2150
Устойчивое развитие/Zilkha Center, Harper	597-4462
Коммутатор, Хопкинс Холл	597-3131
Книжный магазин Уильямс	458-8071	458-0249 факс
Театр, ’62 Центр	597-2342	597-4170 факс
Управление траста и недвижимости, Sears House	597-4259
Учебники	597-2580
Вице-президент Campus Life, Хопкинс-холл	597-2044	597-3996 факс
Вице-президент по связям с колледжами, Мирс	597-4057	597-4178 факс
Вице-президент по финансам и администрации, Хопкинс Холл	597-4421	597-4192 факс
Центр визуальных ресурсов, Лоуренс	597-2015	597-3498 факс
Детский центр колледжа Уильямс, Детский центр Уильямс	597-4008	597-4889 факс
Художественный музей колледжа Уильямс (WCMA), Лоуренс	597-2429	597-5000 факс
Подготовка музея	597-2426
Служба безопасности музея	597-2376
Музейный магазин	597-3233
Уильямс Интернэшнл	597-2161
Выездной клуб Williams, Парески	597-2317
Аппаратная/стол для учащихся	597-4784
Проект Уильямса по экономике высшего образования, Мирс-Уэст	597-2192
Уильямс Рекорд, Парески	597-2400	597-2450 факс
Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет	011-44-1865-512345
Программа Williams-Mystic, Музей Mystic Seaport	860-572-5359	860-572-5329 факс
Женские, гендерные и сексуальные исследования, Шапиро	597-3143	597-4620 факс
Написание программ, Хопкинс-холл	597-4615
Центр экологических инициатив Зилха, Харпер	597-4462

Примеры решения сложных интегралов с ответами

Примеры решений сложных интегралов

Приемы взятия сложных интегралов – Dmitri Nesteruk

Переход к полярным координатам

Геометрические интерпретации

Разбиение диапазона интегрирования

Разбиениe на четное и нечетное

Хотите ещё?

Rate this:

Like this:

Новости

Что такое интеграл простым языком

Интегралы – что это, как решать, примеры решений и объяснение для чайников

Почему вы не знаете, как решать интегралы

Интеграл – что это?

Объясняем понятие «Интеграл»

Неопределённый интеграл

Определённый интеграл

Таблица интегралов для студентов (основные формулы)

Как вычислять интеграл правильно

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Заключение

Интеграл простыми словами

Простыми словами…

Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.

Зачем нужен интеграл

Еще примеры из жизни

Интегралы для чайников: как решать, правила вычисления, объяснение

Изучаем понятие « интеграл »

Неопределенный интеграл

Полная таблица интегралов для студентов

Определенный интеграл

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Свойства определенного интеграла

Примеры решения интегралов

Видео

Неопределенный интеграл. Основные методы интегрирования

Комплексный анализ

Численная оценка комплексных интегралов

Разведка 1

Антидеривативы

страница не найдена – Колледж Уильямс

Научное предложение

Комплексная интеграция

3

Нравится:

Контурные интегралы от аналитических функций, заданных на сетке в комплексной плоскости | Журнал численного анализа IMA

Abstract

Войти

Получить помощь с доступом

Доступ для учреждений

Доступ на основе IP

Войдите через свое учреждение

Войти с помощью читательского билета

Члены общества

Войти через сайт сообщества

Войти через личный кабинет

Личный кабинет

Просмотр учетных записей, вошедших в систему

Выполнен вход, но нет доступа к содержимому

Ведение счетов организаций

Покупка

Кратковременный доступ

Оставить комментарий Отменить ответ