Сложные пределы примеры – tjqokjl
14 Mar 15 – 03:52
Сложные пределы примерыСкачать Сложные пределы примеры
Информация о файле:
Добавлен: 14.03.2015
Скачали: 294
Рейтинг: 130 из 1317
Скорость загрузки: 38 Mbit/s
Файлов в категории: 331
Часто встречаются пределы: ; . Более сложные случаи, так называемые неопределённости вида: рассмотрим на примерах. Найти пределы функций
Тэги: пределы сложные примеры
Недавние поисковые запросы:
смк управление документацией ворд
скачать пример дневника практики экономиста
содержание документации для электронного аукциона
Замечательные пределы – подробные и понятные образцы решений. настоятельно рекомендую ознакомиться со статьей Пределы. Примеры решений. . читайте 2-ой параграф заключительной статьи Сложные пределы.В ролике разбираются простые примеры решения пределов. Более сложные ролики вы найдете в других моих видео на канале или на Типовые варианты рейтинговых работ по теме «Пределы» Кроме того, наряду с простыми примерами разбираются и более сложные.
Сложные пределы Кроме того, мы рассмотрим примеры с более редкими замечательными пределами, которые до сей поры были обделены моим Учимся решать пределы. Подробные, понятные примеры решений. А поэтому переходим к рассмотрению более сложных пределов. Пределы с?Замечательные пределы -?Методы решения пределовМетоды решения пределов. Неопределённости www.mathprofi.ru/metody_resheniya_predelov_neopredelennosti.htmlСохраненнаякопияПохожиеНа уроках Пределы. Примеры решений, Замечательные пределы мы рассмотрели которые возникают в ходе решения более сложных пределов. Бесплатные примеры решения задач по математическому анализу: пределы функций и последовательностей. Безумно сложный предел. Практически не решить. В этом видео рассматривается решение невозможно сложного предела.
скипофит для похудения инструкция, смешанные посадки примеры
Руководство по эксплуатации stiga 75 r-h, Инструкция для epson lx-1050+, Програмаа платёжных бланков, Фирменные бланки 7, Временная инструкция пограничных войск.

Пределы роста. 30 лет спустя
Пределы роста. 30 лет спустя (Limits to growth. The 30-year update) вышла на английском в 2004-м году и на русском в начале 2008-го. Как ясно из названия, эта монография — прямое развитие знаменитого «Доклада римскому клубу» 1972-го года. За три десятка прошедших лет авторы получили в своё распоряжение множество новых фактов, разработали более сложные и продуманные математические модели, прогресс информационных технологий предоставил им большие вычислительные мощности.
Как и
в исходной книге, основной идеей является то что для существующей
модели развития с её относительно быстрым ростом всех показателей
естественным станет ограничение возможностей биосферы и других земных
оболочек. Авторы не занимаются футуризмом и не пытаются предсказывать
будущее (и активно возражают против такого понимания их книг), но
представляют читателям набор сценариев развития (известный как модель
World3).
Первоначально предполагалось что в запасе у человечества до момента прекращения роста есть ещё около полувека. Уже во втором издании книги (За пределами роста, 1992) авторам пришлось скорректировать свою точку зрения в пессимистическую сторону. По их мнению, человечество уже к концу семидесятых или началу восьмидесятых годов перешагнуло границы самоподдержания биосферы.
Кратко
перечислю основные тезисы авторов. По некоторым показателям пределы
роста уже достигнуты (производство с/х продукции на душу населения,
вылов рыбы), по другим будет достигнут в ближайшее время. Скорость
потери сельскохозяйственных земель возрастает, приходится включать в
оборот всё менее и менее ценные участки, при этом современные методы
сельскохозяйственного производства не способствуют сохранению почвы.
Всё хуже становится и ситуация с пресной водой. Подробно анализируются
также ситуация с невозобновимыми источниками сырья и энергии. Большое
внимание уделяется экономическим механизмам регулирования и
показывается их неспособность управлять развитием в глобальных
масштабах.
|
| |||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||
Кассовые сборы уик-эндов (США) | ||||||||||||||||||||||||||||||||||||||
| Первый уик-энд → | ||||||||||||||||||||||||||||||||||||||
Ежедневные кассовые сборы (США) | ||||||||||||||||||||||||||||||||||||||
| Первый день проката → | ||||||||||||||||||||||||||||||||||||||
Насколько безграничны возможности нашей памяти?
- Адам Хадхази
- BBC Future
Автор фото, Thinkstock
Подпись к фото,Наш мозг – не карта памяти, в него влезает гораздо больше, чем нам кажется
Есть люди, которые обладают талантом запоминать огромные объемы информации.
В отличие от цифровых камер с заполненной до конца картой памяти, которые больше не могут сохранять новые снимки, наш мозг, похоже, никогда не испытывает недостатка в свободных объемах для хранения информации. И все же обыденная логика не может примириться с тем, что мозг взрослого человека, “пропитанная кровью губка”, как выразился в свое время писатель Курт Воннегут, способен без ограничений сохранять новые факты и опыты.
Нейрофизиологи давно пытаются измерить максимальный объем нашей памяти. Однако все усилия, направленные на то, чтобы вычислить, какими возможностями обладает человеческая память, сводятся к неким когнитивным подвигам, совершаемым отдельными индивидами и людьми с атипичным мозгом.
Многие из нас прилагают нечеловеческие усилия, чтобы запомнить номер телефона. А если нужно запомнить 67980 цифр? Именно столько цифр числа “пи” после запятой сумел назвать Чао Лу из Китая в 2005 году, когда он был 24-летним студентом выпускного курса. Чао выдавал цифры в течение 24-часового марафона, не отрываясь даже на посещение туалета, и побил мировой рекорд.
А если нужно запомнить 67980 цифр? Именно столько цифр числа “пи” после запятой сумел назвать Чао Лу из Китая в 2005 году, когда он был 24-летним студентом выпускного курса. Чао выдавал цифры в течение 24-часового марафона, не отрываясь даже на посещение туалета, и побил мировой рекорд.
Саванты, люди с необыкновенными способностями памяти, порой устраивали еще более впечатляющие представления, проявляя чудеса запоминания, начиная от имен и дат до воспроизведения сложных визуальных композиций. Так, например, художник-аутист Стивен Уилтшир в 2013 году в мельчайших подробностях изобразил вид Лондона со смотровой площадки, расположенной на высоте 224 м, чтобы можно было представить себе, как будет выглядеть окрестный пейзаж с верхних этажей небоскреба “Шард” (The Shard) – самого высокого здания британской столицы. В отдельных, довольно редких, случаях, травмы, перенесенные прежде вполне здоровыми людьми, давали толчок развитию приобретенного “синдрома саванта”. Его носители, которые в иных областях могут отличаться отставанием в развитии, порой обладают феноменальными способностями в изобразительном искусстве, музыке, математических и календарных расчетах, картографии.
Автор фото, Thinkstock
Подпись к фото,Запомнить расклад карт – это не самая сложная задача для некоторых людей
Орландо Серреллу, например, было 10 лет, когда бейсбольный мяч попал ему в голову с левой стороны. После того происшествия он внезапно обнаружил, что помнит бесчисленное множество автомобильных номеров и способен производить сложные календарные исчисления. Так, он может вычислить, какой день недели приходился на тот или иной день много десятилетий назад.
Каким же образом варят “котелки” этих людей, что им удается посрамить возможности памяти среднестатистического индивида? И что говорят способности декламаторов числа пи и савантов об истинном потенциале человеческого мозга?
Байты мозга
На уровне, поддающемся исчислению, потенциал нашей памяти в определенной степени обоснован физиологией мозга. Если обратиться к базовым, но, пожалуй, полезным данным, касающимся этой темы, то мы вспомним, что наш мозг состоит примерно из 100 млрд нейронов. И только один миллиард из них имеет отношение к долговременному хранению информации в памяти. Эти клетки называются пирамидальными.
И только один миллиард из них имеет отношение к долговременному хранению информации в памяти. Эти клетки называются пирамидальными.
Если допустить, что каждый нейрон содержит по одной единице памяти, тогда можно прийти к заключению, что наш мозг уже полон до краев. “Если бы можно было иметь столько воспоминаний, сколько существует нейронов, то окажется, что это число не так уж велико, – говорит Пол Ребер, профессор психологии из Северо-Западного университета в Эванстоне, штат Иллинойс. – Место для хранения (данных) в вашем мозгу закончилось бы довольно быстро”.
Автор фото, Thinkstock
Подпись к фото,Как именно работают шестеренки нашей памяти? Пока мы этого не знаем
Вместо этого, как полагают исследователи, воспоминания формируются путем соединений между нейронами и по нейронным сетям. Каждый нейрон имеет отростки, которые можно представить себе в виде линий пригородной железнодорожной сети. Они переплетаются примерно с одной тысячей других нервных клеток нейронов. Такая архитектура, как представляется, позволяет элементам памяти возникать и воспроизводиться по всей запутанной клеточной паутине мозга. Как таковая, например, концепция голубого неба может возникать в бесчисленных, отвлеченно дискретных воспоминаниях об эпизодах, связанных с пребыванием на открытом воздухе.
Такая архитектура, как представляется, позволяет элементам памяти возникать и воспроизводиться по всей запутанной клеточной паутине мозга. Как таковая, например, концепция голубого неба может возникать в бесчисленных, отвлеченно дискретных воспоминаниях об эпизодах, связанных с пребыванием на открытом воздухе.
Ребер называет этот эффект “экспоненциальным хранением” данных, благодаря которому потенциал памяти мозга “перехлестывает через край”.
“Разумно будет предположить, что речь идет о диапазоне в несколько петабайтов”, – говорит Ребер. Один петабайт равен 2000 лет звучания музыкальных файлов в формате MP3. Мы пока не знаем, сколько нейронных соединений требуется для одной отдельной отдельно взятой памяти, как не знаем, можно ли вообще уподобить ее цифровому компьютеру, поэтому все сравнения такого рода нужно воспринимать с известной долей сомнения. Достаточно сказать, если воспользоваться выражением Ребера, что “в нашем распоряжении есть тонны и тонны свободного объема” (памяти).
И маленькая тележка?
Действительно ли те люди, которые наделены суперпамятью, имеют какой-то исключительный мозг?
Короткий ответ: нет. Рекордсмены по запоминанию цифр после запятой в числе пи, вроде Чао Лу, также как и большинство других победителей соревнований по запоминанию чего-либо, клянутся, что они – самые обычные люди, посвятившие себя тому, чтобы натренировать свой мозг на хранение и воспроизведение избранных фрагментов информации.
Нелсон Деллис, победитель чемпионатов США по запоминанию 2011, 2012 , 2014 и 2015 гг., говорит, что его память была просто ужасной, прежде чем он стал выступать на состязаниях в качестве ментального атлета. Однако тренировки сделали свое дело. “За несколько недель тренировок, а может и меньше, вы начинаете делать то, что кажется почти невозможным для обычного человека, – говорит Деллис. – Эта способность скрыта в каждом из нас”.
Автор фото, Thinkstock
Подпись к фото,С помощью давно известных трюков и упражнений можно довольно быстро натренировать свою память
Несколько лет назад, когда Деллис только начал тренировать мозг, ему требовалось 20 минут, чтобы запомнить порядок карт в колоде. Сегодня он способен сохранить в памяти все 52 карты менее чем за 30 секунд, другими словами он запоминает их за время одной раздачи. Деллис тренировался считать карты по пять часов день, когда готовился отстоять свой титул на чемпионате США 29 марта 2015 года.
Сегодня он способен сохранить в памяти все 52 карты менее чем за 30 секунд, другими словами он запоминает их за время одной раздачи. Деллис тренировался считать карты по пять часов день, когда готовился отстоять свой титул на чемпионате США 29 марта 2015 года.
Подобно другим чемпионам соревнований по запоминанию Деллис полагается на проверенные временем способы. Один из популярных трюков заключается в том, чтобы построить своего рода “дворец памяти”. Как объясняет Деллис, он воочию представляет себе некое жилье, хорошо ему знакомое, например, дом, в котором он жил ребенком. Он переводит элементы, которые ему нужно запомнить, в зрительные образы, после чего размещает их на столе у двери, затем на кухонном столе и так далее. “Вы перемещаетесь по этому пространству в своем воображении, берете те образы, которые вы там разложили, и снова переводите их в те элементы, которые вы запомнили”, – рассказывает Деллис.
Декламаторы числа пи часто пользуются “дворцом памяти” или другими похожими приемами. Например, они переводят большие объемы цифр в цепочки слов, образующие определенное повествование, напоминающие подсказки для угадывания слов в кроссвордах.
Например, они переводят большие объемы цифр в цепочки слов, образующие определенное повествование, напоминающие подсказки для угадывания слов в кроссвордах.
Включить внутреннего саванта
Широкомасштабный успех таких методик тренировки памяти дает основания полагать, что каждый может стать феноменом, если настроится на достижение такой цели. Но можно ли достичь тех же результатов без большого объема черновой работы? Именно эту цель ставит перед собой Аллен Снайдер, директор Центра по изучению разума при Университете Сиднея, Австралия. Он проповедует довольно спорную теорию о том, что каждый из нас носит в себе “внутреннего саванта”, которого можно “включить” с помощью “правильных” технологий.
Если верить Снайдеру, разум нормального человека по большей части оперирует скорее на уровне концептуального мышления, чем дает себе труд озаботиться мириадами деталей низшего порядка. “Мы осознаем целое, а не те части, которые его составляют”, – говорит он.
Автор фото, Thinkstock
Подпись к фото,Узелок на память – это, конечно, бывает удобно. А если нужно завязать сто узелков?
В качестве моментальной демонстрации нашей “встроенной” системы умственного программирования концепций, Снайдер произвел такой опыт со своими коллегами. Он поставил им задачу запомнить длинный список необходимых покупок, в котором фигурировали такие предметы, как рулевое колесо, дворники, фары и т.д. и т.п. “Людям никак не удавалось запомнить список, просто кошмар”, – рассказывает Снайдер. Каждый из них утверждал, что он говорил: “автомашина”, хотя на самом деле это слово не произносилось. “Они собрали из частей целое”, – подводит логический итог Снайдер.
Вполне вероятно, что эволюция заточила наш мозг, чтобы он работал именно так. Например, вместо того, чтобы забивать себе голову тем, как выглядит каждая черточка на морде льва, вроде оттенка той или иной шерстинки, наш мозг мгновенно догадывается – бум! это хищник!, – и реагировать на это озарение нужно не мешкая.
Другими словами, большинство данных от наших органов чувств передается в мозг, не доходя до уровня анализа и осмысления. У савантов такое концептуальное мышление высокого уровня не включается, что обеспечивает им “привилегированный доступ” буквально к безбрежному морю деталей. Запоминая список предстоящих покупок, они зафиксируют в своем мозгу все запчасти по отдельности, не сводя их в единую концепцию – автомобиль.
Случаи приобретенного синдрома саванта, как это было у Орландо Серрелла, который, будучи ребенком, получил удар бейсбольным мячом по голове, подтолкнули Снайдера к поискам физиологических основ такого явления. Кандидатом в подозреваемые оказалась левая височная доля, т.е. тот отдел мозга, который расположен у нас над левым ухом. Исследователи обратили внимание на ее дисфункцию у людей с аутизмом, синдромом саванта, а также у тех, кто страдает старческим слабоумием. Эта дисфункция нередко сопровождается проявлением вновь открывшихся художественных и музыкальных способностей. (Этот отдел находится именно в том месте, в котором Серреллу была в детстве нанесена травма).
(Этот отдел находится именно в том месте, в котором Серреллу была в детстве нанесена травма).
Снайдер деликатно подавлял нейронную активность в этом участке мозга волонтеров-участников его экспериментов с помощью медицинского прибора, который он окрестил “мыслительным колпаком”, генерирующим магнитные поля. Интригует то, что, как он утверждает, эти люди временно демонстрировали улучшение навыков рисования, проверки текстов на предмет ошибок, а также счета в уме.
Автор фото, Thinkstock
Подпись к фото,Почему мы не запоминаем все подряд? Не хватает скорости переработки
Впрочем, вопреки всем амбициям Снайдера, любой, кто надеется ускоренными темпами стать гением, будет вынужден немного подождать. Вполне возможно, что другие факторы, такие как повышенная уверенность в себе или настороженность при наличии на головах испытуемых футуристических штуковин, выливаются в очевидные успехи обычного мозга. Более того, задачи, которые ставились в ходе экспериментов, были относительно скромны (Снайдеру еще только предстоит протестировать крайние состояния, относящиеся к долгосрочной памяти, например), поэтому успехи его волонтеров едва ли дотягивают до головокружительных высот, достигнутых признанными савантами, такими как Серрелл.
С учетом этих ограничений некоторые ученые просто саркастически фыркают, когда слышат об утверждениях Снайдера. Несмотря на то, что интерес к стимуляции мозга растет, амбиции исследователей, работающих в этой области, как правило, гораздо скромнее. Однако даже самые предварительные результаты работ Снайдреа намекают на то, что наш мозг сможет удивлять нас все больше по мере того, как мы будем углубляться в тайны его функционирования.
“Бутылочное горлышко” памяти
Ясно одно: человеческая память, как таковая, имеет одно существенное ограничение. Итак, почему мы не запоминаем абсолютно все?
“Не знаю, – говорит Снайдер, – но можно предположить, что дело тут в экономии средств переработки информации”.
Пол Ребер из Северо-Западного университета полагает, что мозг, интерпретируя окружающий мир, просто не в состоянии поспевать за потоком внешних раздражителей. “Именно поэтому мы не запоминаем все. Между нашими чувствами и нашей памятью расположено своего рода бутылочное горлышко”, – говорит он.
Обращаясь к привычным для нас аналогиям из мира компьютеров, Ребер говорит, что ограничение человеческой памяти на протяжении жизни – это не емкость жесткого диска, а скорость загрузки. “Дело не в том, что наш мозг переполнен, – объясняет Ребер. – Просто информация, с которой мы сталкиваемся, поступает быстрее, чем наша система памяти способна всю ее записать”.
Типы данных JavaScript и структуры данных – JavaScript
Все языки программирования содержат встроенные типы данных, но они часто отличаются друг от друга в разных языках. Эта статья — попытка описать встроенные структуры (типы) данных, доступные в JavaScript, и их свойства. На их основе строятся другие структуры данных. Когда это возможно, то мы будем сравнивать типы данных в разных языках.
JavaScript является слабо типизированным или динамическим языком. Это значит, что вам не нужно определять тип переменной заранее. Тип определится автоматически во время выполнения программы. Также это значит, что вы можете использовать одну переменную для хранения данных различных типов:
Также это значит, что вы можете использовать одну переменную для хранения данных различных типов:
var foo = 42;
foo = "bar";
foo = true;
Стандарт ECMAScript определяет 9 типов:
- 6 типов данных являющихся примитивами:
- Undefined (Неопределённый тип) :
typeof instance === "undefined" - Boolean (Булев, Логический тип) :
typeof instance === "boolean" - Number (Число) :
typeof instance === "number" - String (Строка) :
typeof instance === "string" - BigInt :
typeof instance === "bigint" - Symbol (в ECMAScript 6) :
typeof instance === "symbol"
- Undefined (Неопределённый тип) :
- Null (Null тип ) :
typeof instance === "object". Специальный примитив, используемый не только для данных но и в качестве указателя на финальную точку в Цепочке Прототипов; - Object (Объект) :
typeof instance === "object". Простая структура, используемая не только для хранения данных, но и для создания других структур, где любая структура создаётся с использованием ключевого слова
Простая структура, используемая не только для хранения данных, но и для создания других структур, где любая структура создаётся с использованием ключевого слова new: new Object, new Array, new Map (en-US), new Set, new WeakMap, new WeakSet, new Date и множество других структур; - и Function :
typeof instance === "function". Специальный случай, упрощающий определение типа для Функций, несмотря на то, что все функции конструктивно унаследованы от Object.
И здесь нам необходимо сделать предостережение относительно использования оператора typeof для определения типа структур, т.к. все структуры будут возвращать "object" при его использовании, так как назначение typeof — проверка типа данных, но не структур. Если проверить тип структуры всё же необходимо, то в этом случае желательно использовать оператор instanceof, так как именно он отвечает на вопрос о том, какой конструктор был использован для создания структуры.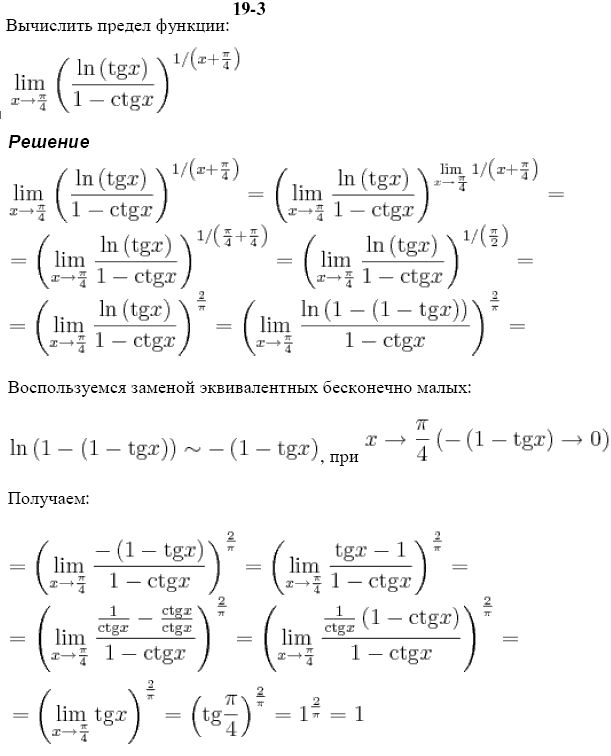
Все типы данных в JavaScript, кроме объектов, являются иммутабельными (значения не могут быть модифицированы, а только перезаписаны новым полным значением). Например, в отличии от C, где строку можно посимвольно корректировать, в JavaScript строки пересоздаются только полностью. Значения таких типов называются «примитивными значениями».
Булевый тип данных
Булевый тип представляет логическую сущность и имеет два значения: true (истина) и false (ложь). Смотрите Boolean и Boolean для получения подробностей.
Null
Этот тип данных имеет всего одно значение: null. Смотрите null и Null для получения подробностей.
Undefined
Переменная, которой не было присвоено значение, будет иметь значение undefined. Смотрите undefined и undefined для получения подробностей.
Числа
В соответствии со стандартом ECMAScript, существует только один числовой тип, который представляет собой 64-битное число двойной точности согласно стандарту IEEE 754. Другими словами, специального типа для целых чисел в JavaScript нет. Это означает, что при числовых операциях вы можете получить неточное (округлённое) значение. В дополнение к возможности представлять числа с плавающей запятой, есть несколько символических значений:
Другими словами, специального типа для целых чисел в JavaScript нет. Это означает, что при числовых операциях вы можете получить неточное (округлённое) значение. В дополнение к возможности представлять числа с плавающей запятой, есть несколько символических значений: +Infinity (положительная бесконечность), -Infinity (отрицательная бесконечность), и NaN (не число).
Для получения самого большого или самого меньшего доступного значения в пределах +/-Infinity, можно использовать константы Number.MAX_VALUE или Number.MIN_VALUE. А начиная с ECMAScript 2015, вы также можете проверить, находится ли число в безопасном для целых чисел диапазоне, используя метод Number.isSafeInteger(), либо константы Number.MAX_SAFE_INTEGER и Number.MIN_SAFE_INTEGER. За пределами этого диапазона операции с целыми числами будут небезопасными, и возвращать приближённые значения.
Ноль в JavaScript имеет два представления: -0 и +0. («0» это синоним +0). На практике это имеет малозаметный эффект. Например, выражение +0 === -0 является истинным. Однако, это может проявиться при делении на ноль:
> 42 / +0
Infinity
> 42 / -0
-InfinityХотя число в большинстве случаев представляет только своё значение, JavaScript предоставляет несколько бинарных операций. Они могут использоваться для того, чтобы представлять число как несколько булевых значений, с помощью битовой маски. Это считается плохой практикой, так как JavaScript предлагает другие способы представления булевых значений (например, массив элементов с булевыми значениями или объект, содержащий набор булевых свойств). Кроме того, битовые маски часто делают код более трудным для чтения, понимания и дальнейшей поддержки. Эта техника может быть необходима в условиях технических ограничений, таких как объём локального хранилища данных, или в такой экстремальной ситуации, когда каждый бит передаваемый по сети на счету. Данный подход следует использовать как крайнюю меру, когда не остаётся других путей для необходимой оптимизации.
Данный подход следует использовать как крайнюю меру, когда не остаётся других путей для необходимой оптимизации.
Текстовые строки
В JavaScript для представления текстовых данных служит тип String. Он представляет собой цепочку «элементов» 16-битных беззнаковых целочисленных значений. Каждый такой элемент занимает свою позицию в строке. Первый элемент имеет индекс 0, следующий — 1, и так далее. Длина строки — это количество элементов в ней.
В отличие от языков подобных C, строки в JavaScript являются иммутабельными. Это означает, что после того, как строковое значение создано, его нельзя модифицировать. Остаётся лишь создать новую строку путём совершения некой операции над исходной строкой. Например:
- Получить часть исходной строки выборкой отдельных символов, либо применением метода
String.substr(). - Объединить две строки в одну, применив оператор (
+) или методString.concat().
Избегайте повсеместного использования строк в своём коде!
Иногда может показаться соблазнительным использование строк для представления сложных структур данных. Это даст небольшие краткосрочные выгоды:
Это даст небольшие краткосрочные выгоды:
- Легко соединять данные в кучу сложением строк.
- Легко отлаживать (данные выглядят «как есть», в читаемом текстовом виде).
- Строки — это распространённый формат данных, используемый разнообразными API (поля ввода, значения локального хранилища,
XMLHttpRequestвозвращает ответ в виде строки, и т. д.) и использовать только строки может показаться заманчивым.
Несмотря на то, что в строке можно выразить данные любой сложности, делать это — не самая лучшая идея. Например, используя разделитель, строку можно использовать как список элементов (массив JavaScript будет более подходящим решением). К сожалению, если такой сепаратор встретится в значении одного из элементов, такой список будет сломан. Выходом может стать добавление символа экранирования, и т. д. Всё это потребует добавления множества ненужных правил, и станет обременительным при поддержке.
Используйте строки только для текстовых данных. Для составных структур преобразуйте строки в подобающие конструкции.
Для составных структур преобразуйте строки в подобающие конструкции.
Тип данных Символ (Symbol)
Символы являются нововведением JavaScript начиная с ECMAScript 2015. Символ — это уникальное и иммутабельное примитивное значение, которое может быть использовано как ключ для свойства объекта (смотрите ниже). В некоторых языках программирования символы называются атомами. Их также можно сравнить с именованными значениями перечисления (enum) в языке C. Подробнее смотрите Symbol и Symbol.
Тип данных Большое целое (BigInt)
BigInt является встроенным объектом, который предоставляет способ представления целых чисел, которые больше 2 53, что является наибольшим числом, которое JavaScript может надёжно представить с помощью Number примитива.
> let bigInt = 19241924124n;
> console.log(bigInt);
19241924124n
> console.log(typeof bigInt);
"bigint"В компьютерной терминологии, объект — это значение в памяти, на которое возможно сослаться с помощью идентификатора.
Свойства
В JavaScript объект может расцениваться как набор свойств. Литеральная инициализация объекта задаёт определённое количество начальных свойств, и в процессе работы приложения поля могут добавляться и удаляться. Значения свойств могут иметь любой тип, включая другие объекты, что позволяет строить сложные, разветвлённые иерархии данных. Каждое свойство объекта идентифицируется ключом, в качестве которого может выступать значение с типом Строка или Символ.
Есть два типа свойств: свойство-значение и свойство-акцессор (свойство, обёрнутое в геттер и сеттер). Они отличаются определёнными атрибутами.
Свойство-значение
Ассоциирует ключ со значением, и имеет следующие атрибуты:
| Атрибут | Тип | Описание | Значение по умолчанию |
|---|---|---|---|
| [[Value]] | Любой тип JavaScript | Значение, возвращаемое при обращении к свойству. | undefined |
| [[Writable]] | Boolean | Если false, то [[Value]] свойства не может быть изменено. | false |
| [[Enumerable]] | Boolean | Если true, свойство будет перечислено в цикле for…in. Смотрите подробнее Перечисляемость и владение свойствами. | false |
| [[Configurable]] | Boolean | Если false, то свойство не может быть удалено, а его атрибуты, кроме [[Value]] и [[Writable]] не могут быть изменены. | false |
| Атрибут | Тип | Описание |
|---|---|---|
| Read-only | Boolean | Зарезервировано по атрибуту [[Writable]] ES5. |
| DontEnum | Boolean | Зарезервировано по атрибуту [[Enumerable]] ES5. |
| DontDelete | Boolean | Зарезервировано по атрибуту [[Configurable]] ES5. |
Свойство-акцессор
Ассоциирует ключ с одной из двух функций-акцессоров (геттер и сеттер) для получения или изменения значения свойства, и имеет следующий атрибуты:
| Атрибут | Тип | Описание | Значение по умолчанию |
|---|---|---|---|
| [[Get]] | Function или undefined | Функция вызывается без параметров и возвращает значение свойства каждый раз, когда происходит чтение свойства. Смотрите также get (en-US). | undefined |
| [[Set]] | Function или undefined | Функция вызывается с одним аргументом, содержащим присваиваемое значение, каждый раз, когда происходит попытка присвоить свойству новое значение. Смотрите также set (en-US). | undefined |
| [[Enumerable]] | Boolean | Если true, свойство будет перечислено в цикле for. ..in. ..in. | false |
| [[Configurable]] | Boolean | Если false, то свойство не может быть удалено, и не может быть преобразовано в свойство-значение. | false |
Примечание: Атрибуты обычно используются движком JavaScript, поэтому вы не можете обратиться к ним напрямую (смотрите подробнее Object.defineProperty()). Вот почему в таблицах выше они помещены в двойные квадратные скобки вместо одиночных.
«Обычные» объекты и функции
Объект JavaScript — это таблица соотношений между ключами и значениями. Ключи — это строки (или Symbol), а значения могут быть любыми. Это делает объекты полностью отвечающими определению хеш-таблицы.
Функции — это обычные объекты, имеющие дополнительную возможность быть вызванными для исполнения.
Даты
Для работы с датами служит встроенный глобальный объект Date.
Массивы общие и типизированные
Массив — это обычный объект с дополнительной связью между целочисленными ключами его свойств и специальным свойством length. Вдобавок ко всему, массивы наследуют
Вдобавок ко всему, массивы наследуют Array.prototype, предоставляющий исчерпывающий набор методов для манипуляции массивами. Например, метод indexOf (служит для поиска значения в массиве), push (en-US) (добавляет элемент в конец массива) и т. д. Всё это делает массив идеальным кандидатом для представления списков и перечислений.
Типизированный массив является новинкой ECMAScript Edition 6 и является массивоподобным представлением для лежащего в его основе бинарного буфера памяти. Следующая таблица поможет вам найти соответствующие типы языка C:
Объекты TypedArray
| Размер (байты) | |||||
Int8Array | -128 до 127 | 1 | 8-битное целое со знаком с дополнением до двух | byte | int8_t |
Uint8Array | 0 до 255 | 1 | 8-битное беззнаковое целое | octet | uint8_t |
Uint8ClampedArray | 0 до 255 | 1 | 8-битное беззнаковое целое (фиксированное от 0 до 255) | octet | uint8_t |
Int16Array | -32768 до 32767 | 2 | 16-битное целое со знаком с дополнением до двух | short | int16_t |
Uint16Array | 0 до 65535 | 2 | 16-битное беззнаковое целое | unsigned short | uint16_t |
Int32Array | -2147483648 до 2147483647 | 4 | 32-битное целое со знаком с дополнением до двух | long | int32_t |
Uint32Array | 0 до 4294967295 | 4 | 32-битное беззнаковое целое | unsigned long | uint32_t |
Float32Array | 1. 2×10-38 to 3.4×1038 2×10-38 to 3.4×1038 | 4 | 32-битное число с плавающей точкой IEEE-стандарта (7 значащих цифр, например 1.123456) | unrestricted float | float |
Float64Array | 5.0×10-324 to 1.8×10308 | 8 | 64-битное число с плавающей точкой IEEE-стандарта (16 значащих цифр, например, 1.123…15) | unrestricted double | double |
Коллекции: Maps, Sets, WeakMaps, WeakSets
Эти наборы данных используют ссылку на объект в качестве ключа, и введены в JavaScript с приходом ECMAScript Edition 6. Set и WeakSet являют собой набор уникальных объектов, в то время как Map и WeakMap ассоциируют с объектом (выступающим в качестве ключа) некоторое значение. Разница между Map и WeakMap заключается в том, что только у Map ключи являются перечисляемыми. Это позволяет оптимизировать сборку мусора для WeakMap.
Это позволяет оптимизировать сборку мусора для WeakMap.
Можно было бы написать собственную реализацию Map и Set на чистом ECMAScript 5. Однако, так как объекты нельзя сравнивать на больше или меньше, то производительность поиска в самодельной реализации будет вынужденно линейной. Нативная реализация (включая WeakMap) имеет производительность логарифмически близкую к константе.
Обычно, для привязки некоторых данных к узлу DOM, приходится устанавливать свойства этому узлу непосредственно, либо использовать его атрибуты data-*. Обратной стороной такого подхода является то, что эти данные будут доступны любому скрипту, работающему в том же контексте. Maps и WeakMaps дают возможность приватной привязки данных к объекту.
Структурированные данные: JSON
JSON (JavaScript Object Notation) — это легковесный формат обмена данными, происходящий от JavaScript, но используемый во множестве языков программирования. JSON строит универсальные структуры данных. Смотрите JSON и JSON для детального изучения.
Больше объектов и стандартная библиотека
JavaScript имеет стандартную библиотеку встроенных объектов. Пожалуйста, обратитесь к справочнику, чтобы найти описание всех объектов доступных для работы.
Оператор typeof может помочь определить тип вашей переменной. Смотрите страницу документации, где приведены его детали и случаи использования.
Пределы оказания юридической помощи по назначению
10 октября 2019 г. 13:30
На сайте ФПА РФ размещено Разъяснение Совета АП города Москвы об обеспечении непрерывности защиты по назначению
Адвокатская палата города Москвы опубликовала
Разъяснение № 13 по вопросам профессиональной этики адвоката «Об обеспечении непрерывности защиты по назначению», утвержденное Советом палаты от 30 сентября 2019 г. (Документ также размещен на сайте
ФПА РФ.) Советник ФПА РФ, вице-президент АП Ставропольского края Нвер Гаспарян отметил важность Разъяснения, принятого в связи с необходимостью обеспечить конституционное право граждан на получение от адвокатов по назначению квалифицированной юридической помощи. По его мнению, было бы целесообразным принятие аналогичного разъяснения и другими адвокатскими палатами. Советник ФПА РФ, член Совета АП города Москвы Евгений Рубинштейн пояснил, что причиной обсуждения вопроса о непрерывности оказания юридической помощи в уголовном судопроизводстве по назначению и в дальнейшем разработки и принятия Разъяснения послужили дисциплинарные производства, в которых в целом был поднят вопрос объема обязательств защитника по назначению. По его словам, Совет палаты, обсуждая эту проблему, исходил из сложившихся традиций в адвокатуре и главной цели – наиболее эффективного оказания юридической помощи по защите обвиняемого (подозреваемого) по уголовному делу.
По его мнению, было бы целесообразным принятие аналогичного разъяснения и другими адвокатскими палатами. Советник ФПА РФ, член Совета АП города Москвы Евгений Рубинштейн пояснил, что причиной обсуждения вопроса о непрерывности оказания юридической помощи в уголовном судопроизводстве по назначению и в дальнейшем разработки и принятия Разъяснения послужили дисциплинарные производства, в которых в целом был поднят вопрос объема обязательств защитника по назначению. По его словам, Совет палаты, обсуждая эту проблему, исходил из сложившихся традиций в адвокатуре и главной цели – наиболее эффективного оказания юридической помощи по защите обвиняемого (подозреваемого) по уголовному делу.
Как отмечается в документе, Совет Адвокатской палаты города Москвы неоднократно давал разъяснения по вопросам, отнесенным к его компетенции и касающимся порядка и качества оказания юридической помощи адвокатами, участвующими в качестве защитников в уголовном судопроизводстве по назначению органов дознания, органов предварительного следствия, прокурора или суда. Вместе с тем анализ дисциплинарной практики Адвокатской палаты города Москвы показывает, что в профессиональной деятельности адвокатов продолжают встречаться и неоднозначно разрешаются сложные ситуации, связанные, в том числе, с обеспечением непрерывности оказания юридической помощи при защите по назначению. В связи с указанными обстоятельствами Совет АП города Москвы принял данное Разъяснение.
Вместе с тем анализ дисциплинарной практики Адвокатской палаты города Москвы показывает, что в профессиональной деятельности адвокатов продолжают встречаться и неоднозначно разрешаются сложные ситуации, связанные, в том числе, с обеспечением непрерывности оказания юридической помощи при защите по назначению. В связи с указанными обстоятельствами Совет АП города Москвы принял данное Разъяснение.
В п. 1 Разъяснения указывается, что в соответствии с п. 17 Стандарта осуществления защиты в уголовном судопроизводстве, принятого VIII Всероссийским съездом адвокатов 20 апреля 2017 г., адвокат участвует в уголовном деле до полного исполнения принятых на себя обязательств, за исключением случаев, предусмотренных законодательством и (или) разъяснениями Комиссии Федеральной палаты адвокатов РФ по этике и стандартам, утвержденными Советом Федеральной палаты адвокатов РФ. В соответствии с п. 8 ст. 10 Кодекса профессиональной этики адвоката «Обязанности адвоката, установленные действующим законодательством, при оказании им юридической помощи бесплатно в случаях, предусмотренных законодательством, или по назначению органа дознания, органа предварительного следствия или суда не отличаются от обязанностей при оказании юридической помощи за гонорар».
На основании перечисленных требований отмечается, что действующий в городе Москве порядок назначения адвокатов в качестве защитников и осуществления ими защиты основан на принципе непрерывности защиты, который, в частности, означает участие одного и того же адвоката в уголовном деле с момента назначения до полного исполнения принятых им на себя обязательств.
В п. 2 Разъяснения указывается, что адвокат, принявший поручение по осуществлению защиты по назначению в досудебном производстве, обязан участвовать не только в процессуальных действиях, проводимых следователем (дознавателем), но и в судебно-контрольном производстве в первой и апелляционной инстанциях (при избрании, изменении и продлении меры пресечения, мер процессуального принуждения, обжаловании действий (бездействия) и решений в порядке, предусмотренном ст. 125 УПК РФ, и др.).
Пункт 3 содержит разъяснение о том, что адвокат, принявший поручение на защиту по назначению в суде первой инстанции, обязан участвовать в апелляции при обжаловании промежуточных решений суда.
Согласно п. 4 адвокат, принявший поручение на защиту по назначению, обязан явиться к инициатору заявки, предъявить ордер и удостоверение, после чего выяснить о наличии у обвиняемого (подозреваемого, подсудимого) защитника по назначению или соглашению. При наличии защитника по соглашению адвокат должен руководствоваться Разъяснениями Совета АП города Москвы от 18 января 2016 г. № 11.
В п. 5 документа указывается, что вступившему в дело адвокату рекомендуется подать письменное заявление лицу, в производстве которого находится уголовное дело, об обязательном надлежащем уведомлении защитника обо всех планируемых следственных (судебных) и иных процессуальных действиях с участием подзащитного, а также иных любых иных действиях, затрагивающих права последнего.
В заключительном пункте разъясняется, что освобождение адвоката от участия в деле в качестве защитника по назначению допускается в исключительных случаях, предусмотренных законодательством (принятие мотивированного процессуального решения о замене либо отводе защитника при наличии законных оснований, отказ подзащитного, приостановление статуса адвоката и др. ), разъяснениями Комиссии ФПА РФ по этике и стандартам и Совета АП города Москвы, а также при наличии иных уважительных причин (например, тяжелая продолжительная болезнь, препятствующая осуществлению профессиональных обязанностей, и т.п.).
), разъяснениями Комиссии ФПА РФ по этике и стандартам и Совета АП города Москвы, а также при наличии иных уважительных причин (например, тяжелая продолжительная болезнь, препятствующая осуществлению профессиональных обязанностей, и т.п.).
В комментарии пресс-службе ФПА РФ советник ФПА РФ, вице-президент АП Ставропольского края Нвер Гаспарян отметил, что считает Разъяснение Совета АП города Москвы полезным и важным. По его мнению, оно может быть принято и иными палатами страны. Как подчеркнул Нвер Гаспарян, настоящее Разъяснение продиктовано необходимостью обеспечить конституционное право граждан на получение от адвокатов по назначению квалифицированной юридической помощи. По его словам, отсутствие непрерывности в осуществлении защиты по назначению приводит к тому, что в ходе досудебного производства при выполнении различных следственных действий обвиняемого могут защищать поочередно несколько адвокатов. Такая практика приводит к ослаблению позиции защиты, ее непоследовательности и хаотичности. «Адвокаты могут занимать разные позиции и пытаться их навязать своему подзащитному. Такая дисгармония не может не отразиться на качестве защиты. Поэтому документ направлен на обеспечение участия по возможности одного адвоката на одной стадии уголовного судопроизводства. В п. 6 Разъяснения обоснованно прописаны случаи освобождения адвоката по назначению от участия в уголовном деле, которые часто имеют место на практике. Пункт 4 Разъяснения имеет важное внутрикорпоративное значение, поскольку позволяет избежать возможные коллизии между участвующим адвокатом по назначению и вновь вступающим его коллегой. Вместе с тем, как мне представляется, именно этот аспект реализации непрерывной защиты по назначению требует наибольшего внимания, поскольку таит в себе нежелательные конфликты между коллегами», – пояснил Нвер Гаспарян.
«Адвокаты могут занимать разные позиции и пытаться их навязать своему подзащитному. Такая дисгармония не может не отразиться на качестве защиты. Поэтому документ направлен на обеспечение участия по возможности одного адвоката на одной стадии уголовного судопроизводства. В п. 6 Разъяснения обоснованно прописаны случаи освобождения адвоката по назначению от участия в уголовном деле, которые часто имеют место на практике. Пункт 4 Разъяснения имеет важное внутрикорпоративное значение, поскольку позволяет избежать возможные коллизии между участвующим адвокатом по назначению и вновь вступающим его коллегой. Вместе с тем, как мне представляется, именно этот аспект реализации непрерывной защиты по назначению требует наибольшего внимания, поскольку таит в себе нежелательные конфликты между коллегами», – пояснил Нвер Гаспарян.
Комментируя
документ для «Адвокатской газеты», советник ФПА РФ, член Совета АП города Москвы Евгений Рубинштейн отметил, что причиной обсуждения вопроса о непрерывности оказания юридической помощи в уголовном судопроизводстве по назначению и в дальнейшем разработки и принятия Разъяснения послужили дисциплинарные производства, в которых в целом был поднят вопрос объема обязательств защитника по назначению (в отношении защитников по соглашению подобное Разъяснение Совета действует с 2007 г. ).
).
«Адвокаты, начинавшие свою практику до принятия Закона об адвокатуре, отдавали себе отчет, что должны оказывать юридическую помощь доверителю по назначению в полном объеме на каждой стадии уголовного судопроизводства до вступления приговора в силу, – пояснил он. – В современных условиях этот подход к пониманию пределов оказания юридической помощи по назначению “размылся” как в адвокатской среде, так и в среде правоприменителей. Поэтому и возникло недопонимание, и обнаружился нормативный пробел в этом вопросе».
Евгений Рубинштейн добавил, что Совет палаты, обсуждая эту проблему, исходил из сложившихся традиций в адвокатуре и главной цели – наиболее эффективного оказания юридической помощи по защите обвиняемого (подозреваемого) по уголовному делу: «Ни у кого не возникло сомнений, что фрагментарная юридическая помощь, оказываемая разными адвокатами на разных этапах и в разных формах работы защитника по уголовному делу, не может считаться удовлетворяющей потребностям эффективной защиты. В связи с этим Совет положил в основу Разъяснения традицию ведения дела защитником по назначению с момента принятия поручения до вступления приговора в силу, являющуюся одновременно наиболее эффективной формой оказания юридической помощи в уголовном судопроизводстве, а также принципиальные требования КПЭА и Стандарта уголовной защиты».
В связи с этим Совет положил в основу Разъяснения традицию ведения дела защитником по назначению с момента принятия поручения до вступления приговора в силу, являющуюся одновременно наиболее эффективной формой оказания юридической помощи в уголовном судопроизводстве, а также принципиальные требования КПЭА и Стандарта уголовной защиты».
Между тем, подчеркнул он, Совет отдавал себе отчет в том, что одномоментное и серьезное изменение требований о пределах участия в уголовном деле защитника по назначению может повлечь объективные сложности и недопонимание адвокатов и правоприменителей, способное породить множество конфликтных ситуаций, включая дисциплинарные жалобы. Поэтому на данном этапе он ограничился требованием непрерывной защиты по назначению в рамках каждой стадии судопроизводства.
«Следует, однако, еще раз оговориться, что на данном этапе Разъяснение не требует от защитника по назначению участвовать в нескольких или во всех стадиях уголовного судопроизводства по одному уголовному делу», – резюмировал Евгений Рубинштейн.
В заключение он добавил, что Совет АП города Москвы будет внимательно анализировать складывающуюся практику (в том числе в вопросе замены защитников по назначению) и при создании соответствующих условий примет решение о переходе ко второму этапу – обеспечению «сплошной» защиты по назначению на всех стадиях уголовного судопроизводства адвокатом, принявшим поручение на защиту.
Примечание: Разъяснение № 13 Совета Адвокатской палаты города Москвы по вопросам профессиональной этики адвоката «Об обеспечении непрерывности защиты по назначению» опубликовано также на сайте ФПА РФ.
Урок 18. Символьные вычисления в Mathcad
Mathcad представляет из себя WYSIWYG-редактор, в котором можно размещать математические и текстовые области. До этого урока в математических областях мы проводили только численные расчеты. Однако расчеты в Mathcad могут быть и символьными (аналитическими) – это позволяет совершать операции дифференцирования, интегрирования, вычисления пределов, разложение в ряд и т. д. и записать результат вычисления в привычном виде.
д. и записать результат вычисления в привычном виде.
Если Вы только начинаете работу с символьными вычислениями, лучше проводите их в отдельных файлах. Если Вы используете одинаковые имена переменных для символьных и численных вычислений, то они могут взаимодействовать и мешать друг другу. Вы можете вставлять результаты из одного файла в другой.
В этом уроке мы будем в основном использовать те инструменты, которые уже изучили, но с той большой разницей, что вычисления будут символьными.
Оператор «Аналитическое преобразование»
Мы уже знаем пять различных знаков «равно» в Mathcad:
Добавим в этот список еще один знак – аналитическое преобразование:
Этот оператор достаточно важен, поэтому будет полезным запомнить его сочетание клавиш.
Там, где это возможно, аналитическое преобразование дает точный результат, без округления. Примеры:
Если параметры известны, аналитическое преобразование вставит их в результат:
Интегрирование
В качестве первого примера возьмем интеграл: вкладка Математика –> Операторы и символы –> Операторы –> Математический анализ –> Интеграл:
Введите в местозаполнители следующее:
Аналитическое преобразование даст:
Это вычисление динамично – если Вы меняете функцию, результат также меняется. Чтобы найти определенный интеграл, введите в местозаполнители пределы интегрирования:
Чтобы найти определенный интеграл, введите в местозаполнители пределы интегрирования:
Таким же образом можно вычислить результат численно:
Mathcad может брать достаточно сложные интегралы, где численное вычисление не работает:
Mathcad может брать двойные и тройные интегралы:
Дифференцирование
Введите оператор дифференцирования, затем переменную, затем функцию:
Пример:
Чтобы найти производную более высокого порядка, введите в дополнительный местозаполнитель за переменной в знаменателе (щелкните по оператору, чтобы увидеть этот местозаполнитель):
Таким же образом можно найти частную производную:
Пределы
Для вычисления предела введите оператор со вкладки Математика –> Операторы и символы –> Операторы –> Математический анализ, введите в местозаполнители точку и функцию и вычислите символьно:
Оператор предела содержит четвертый местозаполнитель (щелкните по оператору, чтобы увидеть его). Используйте этот местозаполнитель, чтобы вычислять предел слева (с [-]) или предел (с [+]). Мы проиллюстрируем все три предела на примере функции тангенса:
Используйте этот местозаполнитель, чтобы вычислять предел слева (с [-]) или предел (с [+]). Мы проиллюстрируем все три предела на примере функции тангенса:
Резюме
В этом уроке мы познакомились с символьными вычислениями.
- Символьные вычисления дают точный результат (там, где возможно). При этом используется оператор аналитического преобразования с сочетанием клавиш [Ctrl+.].
- Проводите символьные вычисления в отдельных файлах; если необходимо, вставляйте результат в изначальный документ.
- Оператор интегрирования можно использовать как символьно, так и численно.
- Оператор дифференцирования может вычислить производную любого порядка. Этот оператор производит символьные и численные вычисления.
- Результат интегрирования и дифференцирования можно использовать в качестве функции.
- Оператор предела вычисляет обычный предел, предел справа и предел слева. Предел можно вычислить только символьно.
Другие интересные материалы
Комплекс делящихся дрожжей Stn1-Ten1 ограничивает активность теломеразы посредством мотива, взаимодействующего с SUMO, и способствует репликации теломер
G-хвост для удлинения теломер ( 2 , 3 ). У людей рекрутирование теломеразы на теломеры опосредуется взаимодействием между доменом TEN каталитической субъединицы теломеразы TERT ( 4 ) и участком TEL TPP1 ( 5 , 6 ).После удлинения G-хвоста теломераза ингибируется комплексом CST (CTC1-STN1-TEN1) ( 7 , 8 ), который взаимодействует с комплексом primase-Polα (Prim-Polα) для синтеза комплементарного C богатая нить ( 9 , 10 ). Считается, что ингибирование теломеразы достигается секвестрацией праймеров, а также физическим взаимодействием с POT1-TPP1 (8). В общем, CST также облегчает репликацию теломерной ДНК и других хрупких участков, вероятно, способствуя перезапуску репликации застопорившихся вилок репликации ( 11 , 12 ).Однако молекулярный механизм действия CST на теломеры остается неясным ( 13 ). Делящиеся дрожжи Schizosaccharomyces pombe стали привлекательной моделью в области теломер с момента открытия шелтериноподобной структуры ( 14 ), что подчеркивает эволюционное сохранение состава теломер у делящихся дрожжей и млекопитающих.
У людей рекрутирование теломеразы на теломеры опосредуется взаимодействием между доменом TEN каталитической субъединицы теломеразы TERT ( 4 ) и участком TEL TPP1 ( 5 , 6 ).После удлинения G-хвоста теломераза ингибируется комплексом CST (CTC1-STN1-TEN1) ( 7 , 8 ), который взаимодействует с комплексом primase-Polα (Prim-Polα) для синтеза комплементарного C богатая нить ( 9 , 10 ). Считается, что ингибирование теломеразы достигается секвестрацией праймеров, а также физическим взаимодействием с POT1-TPP1 (8). В общем, CST также облегчает репликацию теломерной ДНК и других хрупких участков, вероятно, способствуя перезапуску репликации застопорившихся вилок репликации ( 11 , 12 ).Однако молекулярный механизм действия CST на теломеры остается неясным ( 13 ). Делящиеся дрожжи Schizosaccharomyces pombe стали привлекательной моделью в области теломер с момента открытия шелтериноподобной структуры ( 14 ), что подчеркивает эволюционное сохранение состава теломер у делящихся дрожжей и млекопитающих. Комплекс шелтерина делящихся дрожжей состоит из Taz1, который специфически связывается с дуплексной теломерной ДНК, белка Pot1, связывающего G-хвост, и четырех теломерных белков Tpz1, Rap1, Poz1 и Ccq1, которые связывают Taz1 и Pot1 через сеть белково-белковых связей. взаимодействия ( 15 , 16 ).Taz1 является гомологом TRF1-2 и взаимодействует с Rap1. Оба белка действуют как негативный регулятор теломеразы ( 17 ), но только Taz1 способствует полуконсервативной репликации теломер ( 18 ). Pot1, гомолог POT1 человека, связывается с выступающим G-тяжем и связывается с Tpz1, ортологом TPP1 млекопитающих. Несмотря на отсутствие какой-либо очевидной гомологии с белком других видов, Poz1 соединяет Pot1-Tpz1 с Taz1-Rap1 и может подходить на роль ортолога TIN2, соединяющего TRF2 с POT1-TPP1 ( 14 ).Ccq1, который взаимодействует с Tpz1, не имеет четкого ортолога в других организмах; однако он выполняет несколько теломерных функций, таких как защита теломер и рекрутирование теломеразы ( 19 ).
Комплекс шелтерина делящихся дрожжей состоит из Taz1, который специфически связывается с дуплексной теломерной ДНК, белка Pot1, связывающего G-хвост, и четырех теломерных белков Tpz1, Rap1, Poz1 и Ccq1, которые связывают Taz1 и Pot1 через сеть белково-белковых связей. взаимодействия ( 15 , 16 ).Taz1 является гомологом TRF1-2 и взаимодействует с Rap1. Оба белка действуют как негативный регулятор теломеразы ( 17 ), но только Taz1 способствует полуконсервативной репликации теломер ( 18 ). Pot1, гомолог POT1 человека, связывается с выступающим G-тяжем и связывается с Tpz1, ортологом TPP1 млекопитающих. Несмотря на отсутствие какой-либо очевидной гомологии с белком других видов, Poz1 соединяет Pot1-Tpz1 с Taz1-Rap1 и может подходить на роль ортолога TIN2, соединяющего TRF2 с POT1-TPP1 ( 14 ).Ccq1, который взаимодействует с Tpz1, не имеет четкого ортолога в других организмах; однако он выполняет несколько теломерных функций, таких как защита теломер и рекрутирование теломеразы ( 19 ). Теломеразный комплекс делящихся дрожжей включает каталитическую субъединицу Trt1 TERT , регуляторную субъединицу Est1 и РНК TER1 TERC . После фосфорилирования Ccq1 с помощью киназы Rad3 ATR и рекрутирования теломеразы ( 20 , 21 ) Tpz1 сумоилируется на Lys 242 с помощью E3-лигазы Pli1 для ингибирования теломеразного действия Stn1. Комплекс Ten1 ( 22 – 24 ).Stn1-Ten1 выполняет важную функцию защиты теломер ( 25 ), хотя третий компонент комплекса CST, CTC1, отсутствует у S. pombe (или еще не идентифицирован). N-концевая часть Stn1 (NStn1) содержит олигонуклеотид-связывающий (OB)-складчатый домен, необходимый для взаимодействия с Ten1, тогда как его C-концевой домен демонстрирует два мотива «крылатая спираль-поворот-спираль» (Wh2-2) ( 26 ). Известно, что домены WH обеспечивают интерфейс для связывания субстрата, обычно ДНК ( 27 ). stn1 и ten1 являются важными генами, и делеционные мутанты в конечном итоге выживают за счет циркуляризации своих хромосом, что позволяет предположить, что оба белка выполняют важные функции для поддержания теломер ( 25 ).
Теломеразный комплекс делящихся дрожжей включает каталитическую субъединицу Trt1 TERT , регуляторную субъединицу Est1 и РНК TER1 TERC . После фосфорилирования Ccq1 с помощью киназы Rad3 ATR и рекрутирования теломеразы ( 20 , 21 ) Tpz1 сумоилируется на Lys 242 с помощью E3-лигазы Pli1 для ингибирования теломеразного действия Stn1. Комплекс Ten1 ( 22 – 24 ).Stn1-Ten1 выполняет важную функцию защиты теломер ( 25 ), хотя третий компонент комплекса CST, CTC1, отсутствует у S. pombe (или еще не идентифицирован). N-концевая часть Stn1 (NStn1) содержит олигонуклеотид-связывающий (OB)-складчатый домен, необходимый для взаимодействия с Ten1, тогда как его C-концевой домен демонстрирует два мотива «крылатая спираль-поворот-спираль» (Wh2-2) ( 26 ). Известно, что домены WH обеспечивают интерфейс для связывания субстрата, обычно ДНК ( 27 ). stn1 и ten1 являются важными генами, и делеционные мутанты в конечном итоге выживают за счет циркуляризации своих хромосом, что позволяет предположить, что оба белка выполняют важные функции для поддержания теломер ( 25 ). Совсем недавно был выделен и охарактеризован термочувствительный аллель ( ts ) stn1 ( stn1-1 ) ( 28 ). При рестриктивной температуре клетки stn1-1 теряют свои теломерные и субтеломерные последовательности, указывая на то, что Stn1 также необходим для полуконсервативной репликации этих областей.Несмотря на эти наблюдения, механизм действия гетеродимера Stn1-Ten1 до конца не ясен. Как показано на посттрансляционной модификации Tpz1, регуляция длины теломер у делящихся дрожжей зависит от SUMOylation. Делеция генов pmt3 и pli1 , кодирующих пептид малого убиквитин-подобного модификатора (SUMO) и Е3-лигазу, соответственно, вызывает удлинение теломер ( 29 , 30 ). Модификация SUMO часто распознается по последовательности аминокислот, которая содержит гидрофобные остатки (V/IXV/IV/I) плюс полярные/кислые остатки, называемые SUMO-взаимодействующими мотивами (SIM) или SUMO-связывающими мотивами ( 31 – 33 ).Недавние исследования показали, что Stn1 взаимодействует с SUMO ( 22 , 23 ), предполагая, что Stn1 имеет домен SIM.
Совсем недавно был выделен и охарактеризован термочувствительный аллель ( ts ) stn1 ( stn1-1 ) ( 28 ). При рестриктивной температуре клетки stn1-1 теряют свои теломерные и субтеломерные последовательности, указывая на то, что Stn1 также необходим для полуконсервативной репликации этих областей.Несмотря на эти наблюдения, механизм действия гетеродимера Stn1-Ten1 до конца не ясен. Как показано на посттрансляционной модификации Tpz1, регуляция длины теломер у делящихся дрожжей зависит от SUMOylation. Делеция генов pmt3 и pli1 , кодирующих пептид малого убиквитин-подобного модификатора (SUMO) и Е3-лигазу, соответственно, вызывает удлинение теломер ( 29 , 30 ). Модификация SUMO часто распознается по последовательности аминокислот, которая содержит гидрофобные остатки (V/IXV/IV/I) плюс полярные/кислые остатки, называемые SUMO-взаимодействующими мотивами (SIM) или SUMO-связывающими мотивами ( 31 – 33 ).Недавние исследования показали, что Stn1 взаимодействует с SUMO ( 22 , 23 ), предполагая, что Stn1 имеет домен SIM. Здесь мы идентифицировали SIM-домен в Stn1 и показали, что этот мотив имеет решающее значение для взаимодействий SUMO и Tpz1-SUMO. Мутации в SIM Stn1 ( stn1-226 ) вызывают фенотип с длинными теломерами. Этот фенотип является результатом сниженного рекрутирования Stn1-Ten1 на теломеры и, как следствие, удержания теломеразы на теломерах. Кроме того, мы обнаружили неожиданную важную функцию Stn1 в репликации теломерных и субтеломерных областей.Наши данные также предполагают, что Stn1-Ten1 способствует продвижению вилки репликации через эти регионы. Вместе наши результаты показывают, что комплекс Stn1-Ten1 выполняет двойную функцию на теломерах: во-первых, он ограничивает действие теломеразы, а во-вторых, способствует репликации концов хромосом.
Здесь мы идентифицировали SIM-домен в Stn1 и показали, что этот мотив имеет решающее значение для взаимодействий SUMO и Tpz1-SUMO. Мутации в SIM Stn1 ( stn1-226 ) вызывают фенотип с длинными теломерами. Этот фенотип является результатом сниженного рекрутирования Stn1-Ten1 на теломеры и, как следствие, удержания теломеразы на теломерах. Кроме того, мы обнаружили неожиданную важную функцию Stn1 в репликации теломерных и субтеломерных областей.Наши данные также предполагают, что Stn1-Ten1 способствует продвижению вилки репликации через эти регионы. Вместе наши результаты показывают, что комплекс Stn1-Ten1 выполняет двойную функцию на теломерах: во-первых, он ограничивает действие теломеразы, а во-вторых, способствует репликации концов хромосом.Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно.Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
 Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. \mathbf {L} A_ n \to K_ n$.я (К_ п) \к 0 \]
\mathbf {L} A_ n \to K_ n$.я (К_ п) \к 0 \]
Условие Миттаг-Леффлера гарантирует, что левые члены равны нулю (лемма 15.86.1), и мы заключаем, что лемма верна. $\квадрат$
Последовательности и пределы комплексных чисел – Комплексные функции и итерация
Добро пожаловать на лекцию 2, на второй неделе нашего курса Анализ сложного вида. В этой лекции мы будем изучать последовательности и пределы комплексных чисел. Обе эти темы необходимы нам для понимания множеств Жюлиа и множества Мандельброта.Итак, начнем с последовательностей комплексных чисел. Рассмотрим, например, следующую последовательность комплексных чисел. Это для перечисления 1, 1 половины, 1 3, 1 4, 1 5 и так далее. Это последовательность комплексных чисел. Что происходит, когда эти числа уходят все дальше и дальше вправо? Если бы вы изобразили их на графике, мы могли бы изобразить сложную плоскость и сказать, скажем, 1 здесь, 1 половина здесь, 1 3 здесь, 1 4, 1 5, так что кажется, что эти точки накапливаются около начала координат. Давайте посмотрим на другой пример: я, я больше 2, я больше 3, я больше 4 и так далее.Где эти цифры? Ну, я здесь, я над 2 здесь, я над 3, я над 4, я над 5. Таким образом, эти точки будут проходить на воображаемой оси, но опять же они, кажется, очень близко подходят к началу координат, поскольку идем все дальше и дальше вправо по последовательности. Давайте посмотрим на другую последовательность, я минус 1 половина. Минус i больше 3 и так далее, так что я снова здесь. Минус 1 половина, вроде бы вот. Минус я больше 3 здесь. 1 4, я больше 5, минус 1 6, минус я больше 7.Таким образом, эти точки как бы закручиваются вокруг начала координат, но опять же. Они все ближе и ближе к источнику. Мы говорим, что все эти три последовательности сходятся к нулю. Неформально мы говорим, что последовательность {sn} сходится к пределу s, если эта последовательность в конце концов лежит в любом (даже очень маленьком) круге с центром в s. Это означает, что независимо от того, насколько маленький диск я нарисую вокруг начала координат в этом примере, например, достаточно далеко вправо, каждый элемент моей последовательности будет находиться где-то в этом маленьком диске.
Давайте посмотрим на другой пример: я, я больше 2, я больше 3, я больше 4 и так далее.Где эти цифры? Ну, я здесь, я над 2 здесь, я над 3, я над 4, я над 5. Таким образом, эти точки будут проходить на воображаемой оси, но опять же они, кажется, очень близко подходят к началу координат, поскольку идем все дальше и дальше вправо по последовательности. Давайте посмотрим на другую последовательность, я минус 1 половина. Минус i больше 3 и так далее, так что я снова здесь. Минус 1 половина, вроде бы вот. Минус я больше 3 здесь. 1 4, я больше 5, минус 1 6, минус я больше 7.Таким образом, эти точки как бы закручиваются вокруг начала координат, но опять же. Они все ближе и ближе к источнику. Мы говорим, что все эти три последовательности сходятся к нулю. Неформально мы говорим, что последовательность {sn} сходится к пределу s, если эта последовательность в конце концов лежит в любом (даже очень маленьком) круге с центром в s. Это означает, что независимо от того, насколько маленький диск я нарисую вокруг начала координат в этом примере, например, достаточно далеко вправо, каждый элемент моей последовательности будет находиться где-то в этом маленьком диске. И если бы я выбрал меньший диск, мне просто пришлось бы подождать немного дольше. И в конце концов последовательность будет найдена внутри этого диска. Как сделать это математически точным? На самом деле нам не нужно иметь математически точное понятие, но я хочу показать вам, как сделать это математически точным, если вам интересно. Итак, вот собственно определение. Последовательность {sn} комплексных чисел сходится к s, еще одному комплексному числу, если для каждого эпсилон оно будет описывать радиус того маленького диска, о котором мы говорили.Существует индекс N, точка в последовательности, начиная с которой xn минус s меньше эпсилон. Итак, что такое sn минус s? Вот как далеко sn от s. Итак, если бы я нарисовал картинку и предположил, что s не обязательно является началом координат, но предположим, что это мой предел, и я нарисовал круг радиусом эпсилон вокруг этой точки, тогда s является центром круга. И если я хочу, чтобы sn минус s было меньше эпсилон, это означает, что sn должно быть внутри этого круга.
И если бы я выбрал меньший диск, мне просто пришлось бы подождать немного дольше. И в конце концов последовательность будет найдена внутри этого диска. Как сделать это математически точным? На самом деле нам не нужно иметь математически точное понятие, но я хочу показать вам, как сделать это математически точным, если вам интересно. Итак, вот собственно определение. Последовательность {sn} комплексных чисел сходится к s, еще одному комплексному числу, если для каждого эпсилон оно будет описывать радиус того маленького диска, о котором мы говорили.Существует индекс N, точка в последовательности, начиная с которой xn минус s меньше эпсилон. Итак, что такое sn минус s? Вот как далеко sn от s. Итак, если бы я нарисовал картинку и предположил, что s не обязательно является началом координат, но предположим, что это мой предел, и я нарисовал круг радиусом эпсилон вокруг этой точки, тогда s является центром круга. И если я хочу, чтобы sn минус s было меньше эпсилон, это означает, что sn должно быть внутри этого круга. Таким образом, это определение просто делает математически точным то, что мы хотим, и мы хотим, чтобы sn находилась внутри этого диска радиуса эпсилон, достаточно далеко вдоль с.В этом случае мы также используем обозначение предел, lim, предел, sn равен s. И мы помещаем n, уходящее в бесконечность, под этим знаком ограничения, чтобы указать, какое n мы хотим довести до бесконечности. Вот пример, например с предыдущей страницы, предел, когда n стремится к бесконечности от 1 до n, равен 0. Как бы мы это показали? Ну, мы должны показать, что предел равен 0, а это означает, что независимо от того, насколько мал диск радиуса эпсилон, который показывает вокруг начала координат, в конечном итоге моя последовательность будет в нем.Так что мне придется показать, что в конце концов 1 больше n минус 0. Вам не обязательно это записывать, но я просто запишу это для полноты картины. Меньше, чем эпсилон для данного эпсилон, поэтому мы выберем некоторое число эпсилон. И кстати, этот эпсилон снова является одним из тех греческих символов, и математики часто используют греческий символ эпсилон для обозначения действительно небольшого числа.
Таким образом, это определение просто делает математически точным то, что мы хотим, и мы хотим, чтобы sn находилась внутри этого диска радиуса эпсилон, достаточно далеко вдоль с.В этом случае мы также используем обозначение предел, lim, предел, sn равен s. И мы помещаем n, уходящее в бесконечность, под этим знаком ограничения, чтобы указать, какое n мы хотим довести до бесконечности. Вот пример, например с предыдущей страницы, предел, когда n стремится к бесконечности от 1 до n, равен 0. Как бы мы это показали? Ну, мы должны показать, что предел равен 0, а это означает, что независимо от того, насколько мал диск радиуса эпсилон, который показывает вокруг начала координат, в конечном итоге моя последовательность будет в нем.Так что мне придется показать, что в конце концов 1 больше n минус 0. Вам не обязательно это записывать, но я просто запишу это для полноты картины. Меньше, чем эпсилон для данного эпсилон, поэтому мы выберем некоторое число эпсилон. И кстати, этот эпсилон снова является одним из тех греческих символов, и математики часто используют греческий символ эпсилон для обозначения действительно небольшого числа. Если вы действительно хотите запутать математика, сделайте эпсилон большим числом. Так что же означает, что 1 на n меньше эпсилон? На самом деле это просто упрощается до 1 на n, меньше, чем эпсилон, и может решить это уравнение.Для каких значений n это верно, это верно, когда n больше 1 по эпсилону, поэтому для моего данного эпсилон. Я вычисляю единицу по эпсилону, а затем просто выбираю индекс, который больше, чем тот, что по эпсилону, и мне гарантировано, что начиная с этого индекса вся моя последовательность будет находиться внутри этого диска. Другим примером является последовательность 1 над n в некоторой степени p, p может быть чем угодно, это может быть 2s, 3, 4, это может быть половина. Так, например, когда p равно 2, мы будем рассматривать последовательность 1 на 1 в квадрате, 1 на 2 в квадрате, 1 на 3 в квадрате и так далее, то есть 1, 1 на 4, 1 на 9.Эта последовательность сходится к 0, но также, когда p равно 1, половина. Что значит возвести число в половинную степень? Это значит извлечь из этого числа квадратный корень.
Если вы действительно хотите запутать математика, сделайте эпсилон большим числом. Так что же означает, что 1 на n меньше эпсилон? На самом деле это просто упрощается до 1 на n, меньше, чем эпсилон, и может решить это уравнение.Для каких значений n это верно, это верно, когда n больше 1 по эпсилону, поэтому для моего данного эпсилон. Я вычисляю единицу по эпсилону, а затем просто выбираю индекс, который больше, чем тот, что по эпсилону, и мне гарантировано, что начиная с этого индекса вся моя последовательность будет находиться внутри этого диска. Другим примером является последовательность 1 над n в некоторой степени p, p может быть чем угодно, это может быть 2s, 3, 4, это может быть половина. Так, например, когда p равно 2, мы будем рассматривать последовательность 1 на 1 в квадрате, 1 на 2 в квадрате, 1 на 3 в квадрате и так далее, то есть 1, 1 на 4, 1 на 9.Эта последовательность сходится к 0, но также, когда p равно 1, половина. Что значит возвести число в половинную степень? Это значит извлечь из этого числа квадратный корень. Таким образом, в этом случае последовательность будет равна единице на квадратный корень из единицы, единице на квадратный корень из двух, единице на квадратный корень из трех и так далее, и эта последовательность также будет равна 0, и мы можем показать это очень похожим образом. Как мы показываем, последовательность один на n сходится к 0. И вообще, для любой степени P вы фиксируете эту степень, и последовательность будет равна 8.Переход к 8 займет больше времени, будет медленнее, когда P — очень маленькое число, и будет быстрее, когда P — большое число. Кроме того, я мог бы поместить константу в числитель, я мог бы умножить всю последовательность на комплексное число, и она все равно будет равна 0. Поскольку все, что идет к 0, я могу умножить это на 2, но это займет вдвое больше времени. до 0, оно все равно переходит в 0. Другой пример — последовательность чисел q в степени n, где q — число от 0 до 1. Так, например, если q равно, скажем, 1 3-му, то последовательность мы бы посмотрели на это, 1 3 в степени 1, 1 3 в квадрате, что равно 1 9.
Таким образом, в этом случае последовательность будет равна единице на квадратный корень из единицы, единице на квадратный корень из двух, единице на квадратный корень из трех и так далее, и эта последовательность также будет равна 0, и мы можем показать это очень похожим образом. Как мы показываем, последовательность один на n сходится к 0. И вообще, для любой степени P вы фиксируете эту степень, и последовательность будет равна 8.Переход к 8 займет больше времени, будет медленнее, когда P — очень маленькое число, и будет быстрее, когда P — большое число. Кроме того, я мог бы поместить константу в числитель, я мог бы умножить всю последовательность на комплексное число, и она все равно будет равна 0. Поскольку все, что идет к 0, я могу умножить это на 2, но это займет вдвое больше времени. до 0, оно все равно переходит в 0. Другой пример — последовательность чисел q в степени n, где q — число от 0 до 1. Так, например, если q равно, скажем, 1 3-му, то последовательность мы бы посмотрели на это, 1 3 в степени 1, 1 3 в квадрате, что равно 1 9. 1 3 в кубе, всего 1 на 27. 1 3 на 4, то есть 1 на 81, и так далее. Итак, пока q является числом меньше единицы, всякий раз, когда вы возводите это число во все большую и большую степень, числа будут становиться все меньше и меньше и меньше, и снова они будут приближаться к 0. Если бы q было числом 1, вы бы возводить 1 в степень n, это было бы постоянно равно 1, это не сходилось бы к 0. И если бы q было больше 1, эти числа взорвались бы, определенно не сходились бы к 0. В более общем случае, если бы вместо a действительное число, q между 0 и 1, мы подставляем сюда комплексное число, длина которого меньше 1.Это все равно будет сходиться к 0, поэтому давайте посмотрим на картину того, почему это происходит. Итак, предположим, что это круг радиуса 1, а мой z — это какое-то число. Если я возведу в квадрат это число z, произойдет следующее: мы возведем в квадрат расстояние до начала координат, что уменьшит это число, потому что расстояние от начала координат меньше 1, и мы удвоим аргумент, так что, возможно, z в квадрате будет сюда.
1 3 в кубе, всего 1 на 27. 1 3 на 4, то есть 1 на 81, и так далее. Итак, пока q является числом меньше единицы, всякий раз, когда вы возводите это число во все большую и большую степень, числа будут становиться все меньше и меньше и меньше, и снова они будут приближаться к 0. Если бы q было числом 1, вы бы возводить 1 в степень n, это было бы постоянно равно 1, это не сходилось бы к 0. И если бы q было больше 1, эти числа взорвались бы, определенно не сходились бы к 0. В более общем случае, если бы вместо a действительное число, q между 0 и 1, мы подставляем сюда комплексное число, длина которого меньше 1.Это все равно будет сходиться к 0, поэтому давайте посмотрим на картину того, почему это происходит. Итак, предположим, что это круг радиуса 1, а мой z — это какое-то число. Если я возведу в квадрат это число z, произойдет следующее: мы возведем в квадрат расстояние до начала координат, что уменьшит это число, потому что расстояние от начала координат меньше 1, и мы удвоим аргумент, так что, возможно, z в квадрате будет сюда. Z в кубе, мы утроим аргумент и даже приблизимся к началу координат. Z до четвертого и так далее.Таким образом, эти числа будут как бы спирально вращаться вокруг начала координат, приближаясь к началу координат, потому что расстояние от начала координат просто стремится к 0, еще один пример. Предположим, мы ищем n-й корень из 10. Итак, эта последовательность начинается с первого корня из 10. Что такое первый корень из 10? Ну, это 10. Второй корень из 10 — это просто квадратный корень из 10. Итак, это 3 пункта, а затем кубический корень из 10. Итак, это число, куб которого равен 10. Итак, это между 2 и 3 и четвертым корень из 10, так что это число, поэтому, когда это увеличивает степень 4, оно равно 10.Вы можете видеть, что эти числа становятся все меньше и меньше и меньше, и они на самом деле приближаются к числу 1 при достаточно большом значении N. И, наконец, корень n-й степени из n, это интересная последовательность, и здесь мы не совсем уверены, где он на самом деле. бывает. Давайте посмотрим, что происходит, когда n равно 1, это первый корень из 1, так что это просто 1.
Z в кубе, мы утроим аргумент и даже приблизимся к началу координат. Z до четвертого и так далее.Таким образом, эти числа будут как бы спирально вращаться вокруг начала координат, приближаясь к началу координат, потому что расстояние от начала координат просто стремится к 0, еще один пример. Предположим, мы ищем n-й корень из 10. Итак, эта последовательность начинается с первого корня из 10. Что такое первый корень из 10? Ну, это 10. Второй корень из 10 — это просто квадратный корень из 10. Итак, это 3 пункта, а затем кубический корень из 10. Итак, это число, куб которого равен 10. Итак, это между 2 и 3 и четвертым корень из 10, так что это число, поэтому, когда это увеличивает степень 4, оно равно 10.Вы можете видеть, что эти числа становятся все меньше и меньше и меньше, и они на самом деле приближаются к числу 1 при достаточно большом значении N. И, наконец, корень n-й степени из n, это интересная последовательность, и здесь мы не совсем уверены, где он на самом деле. бывает. Давайте посмотрим, что происходит, когда n равно 1, это первый корень из 1, так что это просто 1. Если n равно 2, мы получаем квадратный корень из 2, мы знаем, что это 1,4 с чем-то, затем мы получаем куб корень из 3. Корень 4-й степени из 4, корень 5-й степени из 5, и это довольно неясно, потому что число, которое мы берем, становится все больше и больше, но мы также берем все больше и больше корней этих чисел, и это требует некоторого больше мысли.Что можно доказать, что последовательность сходится к 1. Вот некоторые правила и факты о пределах, один факт заключается в том, что сходящиеся последовательности ограничены. Помните, что значит быть ограниченным? Это означает, что последовательность содержится в каком-то большом диске вокруг начала координат. Итак, почему это так, ну вот наши координатные оси и предположим, что у нас есть последовательность, которая сходится к некоторой точке s. Это означает, что для любого диска, который мы выберем вокруг этой точки s, в конце концов весь остаток последовательности будет лежать внутри диска радиуса s.Таким образом, только несколько элементов этой последовательности могут находиться за пределами диска радиуса s, и это только последнее меню, то есть одно самое большое.
Если n равно 2, мы получаем квадратный корень из 2, мы знаем, что это 1,4 с чем-то, затем мы получаем куб корень из 3. Корень 4-й степени из 4, корень 5-й степени из 5, и это довольно неясно, потому что число, которое мы берем, становится все больше и больше, но мы также берем все больше и больше корней этих чисел, и это требует некоторого больше мысли.Что можно доказать, что последовательность сходится к 1. Вот некоторые правила и факты о пределах, один факт заключается в том, что сходящиеся последовательности ограничены. Помните, что значит быть ограниченным? Это означает, что последовательность содержится в каком-то большом диске вокруг начала координат. Итак, почему это так, ну вот наши координатные оси и предположим, что у нас есть последовательность, которая сходится к некоторой точке s. Это означает, что для любого диска, который мы выберем вокруг этой точки s, в конце концов весь остаток последовательности будет лежать внутри диска радиуса s.Таким образом, только несколько элементов этой последовательности могут находиться за пределами диска радиуса s, и это только последнее меню, то есть одно самое большое. И мы можем просто выбрать диск, достаточно большой, чтобы содержать все эти конечные [НЕРАЗБОРЧИВО] элементы, плюс диск вокруг точки s, и тогда этот диск покажет нам, что последовательность ограничена. Другой факт заключается в том, что если у вас есть две сходящиеся последовательности, одна по имени sn, которая сходится к s, а другая по имени tn, предположим, что ее пределы равны t, то я могу сложить эти две последовательности друг с другом, и сумма сходится к s плюс t.Давайте рассмотрим пример, мы знаем, что если sn равно 1/n. Затем эта последовательность сходится к 0. Мы также знали, что если tn равно, скажем, 1/3-му числу n. Тогда tn также сходится к 0. Теперь, согласно этому факту, я могу сложить эти две вещи. Я могу посмотреть на s и плюс tm, что равно 1 на m плюс 1 3-я в степени n, и вместе это все равно будет сходиться к 0. Еще один факт заключается в том, что sn, умноженное на tn, будет сходиться к s, умноженному на t, поэтому я мог бы перемножить эти числа. две последовательности или любые другие две сходящиеся последовательности.
И мы можем просто выбрать диск, достаточно большой, чтобы содержать все эти конечные [НЕРАЗБОРЧИВО] элементы, плюс диск вокруг точки s, и тогда этот диск покажет нам, что последовательность ограничена. Другой факт заключается в том, что если у вас есть две сходящиеся последовательности, одна по имени sn, которая сходится к s, а другая по имени tn, предположим, что ее пределы равны t, то я могу сложить эти две последовательности друг с другом, и сумма сходится к s плюс t.Давайте рассмотрим пример, мы знаем, что если sn равно 1/n. Затем эта последовательность сходится к 0. Мы также знали, что если tn равно, скажем, 1/3-му числу n. Тогда tn также сходится к 0. Теперь, согласно этому факту, я могу сложить эти две вещи. Я могу посмотреть на s и плюс tm, что равно 1 на m плюс 1 3-я в степени n, и вместе это все равно будет сходиться к 0. Еще один факт заключается в том, что sn, умноженное на tn, будет сходиться к s, умноженному на t, поэтому я мог бы перемножить эти числа. две последовательности или любые другие две сходящиеся последовательности. И их произведение будет сходиться к произведению пределов, в частности, я могу умножить сходящуюся последовательность на некоторое число. И эта новая последовательность будет сходиться к старому пределу, умноженному на это число. Я также могу составить частное двух последовательностей, и оно будет сходиться к частному пределов. Очевидно, что я не могу делить на 0, поэтому я не могу сделать это для примера, который мы рассматривали выше. 1 3-й к n не годится, он сходится к 0, и поэтому 0 в знаменателе — это не то, что нам бы хотелось.Итак, здесь нам понадобится другой пример, например, что-то, что сходится к 1. Итак, давайте применим эти факты, которые мы только что узнали, и найдем некоторые ограничения. Давайте посмотрим на последовательность n на n плюс 1, ну, n само по себе не является последовательностью сходимости, X просто увеличивается, 1, 2, 3, 4, 5. Последовательность n плюс 1 также становится все больше и больше, так что посмотрите на нее как это бесполезно, но мы можем вытащить n как из числителя, так и из знаменателя.
И их произведение будет сходиться к произведению пределов, в частности, я могу умножить сходящуюся последовательность на некоторое число. И эта новая последовательность будет сходиться к старому пределу, умноженному на это число. Я также могу составить частное двух последовательностей, и оно будет сходиться к частному пределов. Очевидно, что я не могу делить на 0, поэтому я не могу сделать это для примера, который мы рассматривали выше. 1 3-й к n не годится, он сходится к 0, и поэтому 0 в знаменателе — это не то, что нам бы хотелось.Итак, здесь нам понадобится другой пример, например, что-то, что сходится к 1. Итак, давайте применим эти факты, которые мы только что узнали, и найдем некоторые ограничения. Давайте посмотрим на последовательность n на n плюс 1, ну, n само по себе не является последовательностью сходимости, X просто увеличивается, 1, 2, 3, 4, 5. Последовательность n плюс 1 также становится все больше и больше, так что посмотрите на нее как это бесполезно, но мы можем вытащить n как из числителя, так и из знаменателя.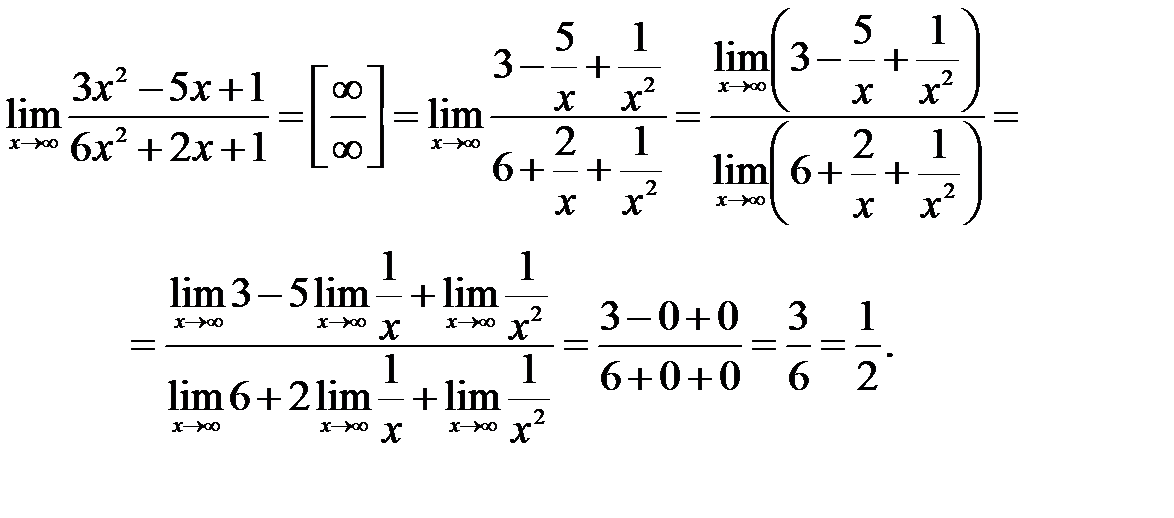 И если мы это сделаем, числитель станет 1, а знаменатель станет 1 плюс 1 над n.И вдруг мы оказываемся с постоянной последовательностью в числителе, которая, очевидно, сходится к 1, потому что она постоянна. И в знаменателе есть последовательность 1 над n, которая, как мы знаем, сходится к 0. Мы добавляем к этому число 1, которое представляет собой постоянную последовательность, которая разбивается на 1. Итак, знаменатель сходится к 1. 1 разделить на 1 равно 1. Итак, вся последовательность сходится к 1. Итак, здесь этот знаменатель, как мы знаем, сходится к 1. числитель постоянный, поэтому он сходится к 1.Итак, предел частного равен 1. Вот еще один пример, если мы снова посмотрим на него в исходной форме: 3 в квадрате плюс пять, деленное на in в квадрате плюс 2 в минус 1, трудно понять, каков предел. Потому что и числитель, и знаменатель, похоже, уходят в бесконечность. Они не ограничены, они не сходящиеся последовательности, сходящиеся последовательности не ограничены. Но если я возьму n в квадрате из числителя и знаменателя, мне нужно сделать это правильно.
И если мы это сделаем, числитель станет 1, а знаменатель станет 1 плюс 1 над n.И вдруг мы оказываемся с постоянной последовательностью в числителе, которая, очевидно, сходится к 1, потому что она постоянна. И в знаменателе есть последовательность 1 над n, которая, как мы знаем, сходится к 0. Мы добавляем к этому число 1, которое представляет собой постоянную последовательность, которая разбивается на 1. Итак, знаменатель сходится к 1. 1 разделить на 1 равно 1. Итак, вся последовательность сходится к 1. Итак, здесь этот знаменатель, как мы знаем, сходится к 1. числитель постоянный, поэтому он сходится к 1.Итак, предел частного равен 1. Вот еще один пример, если мы снова посмотрим на него в исходной форме: 3 в квадрате плюс пять, деленное на in в квадрате плюс 2 в минус 1, трудно понять, каков предел. Потому что и числитель, и знаменатель, похоже, уходят в бесконечность. Они не ограничены, они не сходящиеся последовательности, сходящиеся последовательности не ограничены. Но если я возьму n в квадрате из числителя и знаменателя, мне нужно сделать это правильно. Мне нужно извлечь это из каждого члена, чтобы числитель стал 3 плюс 5 на n в квадрате, а знаменатель стал i плюс 2 i, деленное на n.Здесь только одно n, поэтому нам нужно вытащить второе n прямо здесь, минус 1 на n в квадрате. Теперь я знаю, что 1 на n в квадрате сходится к 0, поэтому 5 на n в квадрате сходится к 0, поэтому весь числитель сходится к 3. В знаменателе i на n в квадрате равняется 0, а 2 на n приближается к 0 и поэтому знаменатель идет к i. Таким образом, весь предел равен 3 над i, а это не то, как мы записываем комплексные числа, как мы уже знаем. Представьте, что единственное число находится в знаменателе, поэтому оно равно минус 3i, поэтому предел последовательности равен минус 3i.Вот еще один пример. n в квадрате над n плюс 1. Опять же, и числитель, и знаменатель стремятся к бесконечности, поэтому мы пытаемся получить n. Если я вытащу одно n, у меня останется другое n в числителе. Знаменатель равен 1 плюс 1 к n. Так что знаменатель ведет себя очень хорошо. Он сходится к 1.
Мне нужно извлечь это из каждого члена, чтобы числитель стал 3 плюс 5 на n в квадрате, а знаменатель стал i плюс 2 i, деленное на n.Здесь только одно n, поэтому нам нужно вытащить второе n прямо здесь, минус 1 на n в квадрате. Теперь я знаю, что 1 на n в квадрате сходится к 0, поэтому 5 на n в квадрате сходится к 0, поэтому весь числитель сходится к 3. В знаменателе i на n в квадрате равняется 0, а 2 на n приближается к 0 и поэтому знаменатель идет к i. Таким образом, весь предел равен 3 над i, а это не то, как мы записываем комплексные числа, как мы уже знаем. Представьте, что единственное число находится в знаменателе, поэтому оно равно минус 3i, поэтому предел последовательности равен минус 3i.Вот еще один пример. n в квадрате над n плюс 1. Опять же, и числитель, и знаменатель стремятся к бесконечности, поэтому мы пытаемся получить n. Если я вытащу одно n, у меня останется другое n в числителе. Знаменатель равен 1 плюс 1 к n. Так что знаменатель ведет себя очень хорошо. Он сходится к 1. Таким образом, знаменатель можно рассматривать как почти равный 1, с погрешностью n. Однако числитель становится все больше и больше, больше и больше. И если я разделю очень большое число на число, это будет почти 1.Действительно большое число мало что меняет. Так что эта последовательность не ограничена, она просто становится все больше и больше. Просто числитель сильнее знаменателя. Последовательность не ограничена, а значит, не сходится. На самом деле последовательности сходимости ограничены. Поскольку это число не ограничено, оно не может сходиться, и, наконец, давайте посмотрим на этот пример 3n плюс 5, деленное на в квадрате плюс 2yn минус 1. Опять же, давайте возведем n в квадрат из числителя и знаменателя, тогда числитель станет 3 над n плюс 5 над n в квадрате.Знаменатель становится i, плюс 2 i на n минус один на n в квадрате. В числителе 3 на n равняется нулю, 5 на n в квадрате равняется 0. В знаменателе единица на n в квадрате равняется нулю, 2 i на n равняется 0 I, ios постоянная, равная i.
Таким образом, знаменатель можно рассматривать как почти равный 1, с погрешностью n. Однако числитель становится все больше и больше, больше и больше. И если я разделю очень большое число на число, это будет почти 1.Действительно большое число мало что меняет. Так что эта последовательность не ограничена, она просто становится все больше и больше. Просто числитель сильнее знаменателя. Последовательность не ограничена, а значит, не сходится. На самом деле последовательности сходимости ограничены. Поскольку это число не ограничено, оно не может сходиться, и, наконец, давайте посмотрим на этот пример 3n плюс 5, деленное на в квадрате плюс 2yn минус 1. Опять же, давайте возведем n в квадрат из числителя и знаменателя, тогда числитель станет 3 над n плюс 5 над n в квадрате.Знаменатель становится i, плюс 2 i на n минус один на n в квадрате. В числителе 3 на n равняется нулю, 5 на n в квадрате равняется 0. В знаменателе единица на n в квадрате равняется нулю, 2 i на n равняется 0 I, ios постоянная, равная i. 2 равно -1.4, то есть один и так далее. Итак, мы хотели бы применить наши факты, но i в степени n, умноженной на последовательность 1 над n. Мы знаем, что последовательность от 1 до n стремится к 0, но последовательность от i до степени n просто прыгает. Один я минус один минус я, один я, минус один, минус я, оно скачет. Он никогда не приближается только к одной точке, он всегда находится в разных местах. Эта последовательность не сходится, хотя она и ограничена, она никогда не остается в пределах маленького диска только с одной точкой, потому что вы просто продолжаете идти, и она окажется за пределами этого диска.Итак, как мы относимся к этому продукту? Последовательность, как нам показалось, сходится к 0, потому что, вы знаете, мы начали с i и имеем минус одну половину, минус i над 3, одну четвертую и так далее. Кажется, что последовательность движется по спирали к 0. Итак, кажется, что она сходится к 0, но как мы это покажем? Вот некоторые дополнительные факты; последовательность комплексных чисел сходится к 0 тогда и только тогда, когда последовательность абсолютных значений сходится к 0.
2 равно -1.4, то есть один и так далее. Итак, мы хотели бы применить наши факты, но i в степени n, умноженной на последовательность 1 над n. Мы знаем, что последовательность от 1 до n стремится к 0, но последовательность от i до степени n просто прыгает. Один я минус один минус я, один я, минус один, минус я, оно скачет. Он никогда не приближается только к одной точке, он всегда находится в разных местах. Эта последовательность не сходится, хотя она и ограничена, она никогда не остается в пределах маленького диска только с одной точкой, потому что вы просто продолжаете идти, и она окажется за пределами этого диска.Итак, как мы относимся к этому продукту? Последовательность, как нам показалось, сходится к 0, потому что, вы знаете, мы начали с i и имеем минус одну половину, минус i над 3, одну четвертую и так далее. Кажется, что последовательность движется по спирали к 0. Итак, кажется, что она сходится к 0, но как мы это покажем? Вот некоторые дополнительные факты; последовательность комплексных чисел сходится к 0 тогда и только тогда, когда последовательность абсолютных значений сходится к 0. Что ж, если вы можете взять здесь абсолютные значения, мы имеем золотой I к n над n, абсолютное значение i к n всего 1.Итак, это становится последовательностью 1 на n, и мы знаем, что она сходится к 0. Итак, это один из способов показать, что последовательность сходится к 0. Это работает только для сходится к 0, однако последовательности сходящихся абсолютных значений недостаточно. для сходимости другой последовательности к какому-то другому числу она работает только при 0. Другой факт состоит в том, что последовательность комплексных чисел сходится к пределу, если действительные части последовательности сходится к действительной части предела, а мнимые части сходится к мнимой части часть лимита.Таким образом, действительные части должны сходиться, а мнимые части должны сходиться, и это приводит к сходимости всей последовательности. Вот еще один действительно интересный факт, вы, возможно, слышали об этом в исчислении, это называется теоремой сжатия. Предположим, у вас есть три последовательности rn, sn и tn.
Что ж, если вы можете взять здесь абсолютные значения, мы имеем золотой I к n над n, абсолютное значение i к n всего 1.Итак, это становится последовательностью 1 на n, и мы знаем, что она сходится к 0. Итак, это один из способов показать, что последовательность сходится к 0. Это работает только для сходится к 0, однако последовательности сходящихся абсолютных значений недостаточно. для сходимости другой последовательности к какому-то другому числу она работает только при 0. Другой факт состоит в том, что последовательность комплексных чисел сходится к пределу, если действительные части последовательности сходится к действительной части предела, а мнимые части сходится к мнимой части часть лимита.Таким образом, действительные части должны сходиться, а мнимые части должны сходиться, и это приводит к сходимости всей последовательности. Вот еще один действительно интересный факт, вы, возможно, слышали об этом в исчислении, это называется теоремой сжатия. Предположим, у вас есть три последовательности rn, sn и tn. И предположим, что они все [НЕРАЗБОРЧИВО] выстроены так, что r n всегда внизу меньше или равно s n, это то, что посередине, и меньше или равно t n справа. Если бы вам нужно было нарисовать числовую линию, у нас было бы r n, а затем s n и t n.Теперь предположим, что и rn, и t сходятся, хорошо? Итак, r n сходится к некоторому пределу, а t n сходится к некоторому пределу. И предположим, что это число, предположим, что все они сходятся к пределу L. Что ж, тогда у sn, застрявшего между ними, нет другого выбора, кроме как также сходиться к L, и это то, что говорит теорема о сжатии, и вот последний факт. Что-то вроде эквивалента бегущей по стене последовательности, предположим, что у вас есть ограниченная и монотонная последовательность. Ограниченный означает, что он никуда не уйдет, а монотонный означает, что он продолжает увеличиваться или становится меньше, но вы должны выбрать один из этих двух.Итак, речь идет о последовательности действительных чисел, то есть о последовательности, которая постоянно увеличивается.
И предположим, что они все [НЕРАЗБОРЧИВО] выстроены так, что r n всегда внизу меньше или равно s n, это то, что посередине, и меньше или равно t n справа. Если бы вам нужно было нарисовать числовую линию, у нас было бы r n, а затем s n и t n.Теперь предположим, что и rn, и t сходятся, хорошо? Итак, r n сходится к некоторому пределу, а t n сходится к некоторому пределу. И предположим, что это число, предположим, что все они сходятся к пределу L. Что ж, тогда у sn, застрявшего между ними, нет другого выбора, кроме как также сходиться к L, и это то, что говорит теорема о сжатии, и вот последний факт. Что-то вроде эквивалента бегущей по стене последовательности, предположим, что у вас есть ограниченная и монотонная последовательность. Ограниченный означает, что он никуда не уйдет, а монотонный означает, что он продолжает увеличиваться или становится меньше, но вы должны выбрать один из этих двух.Итак, речь идет о последовательности действительных чисел, то есть о последовательности, которая постоянно увеличивается. Но вы не можете выйти за пределы, тогда вам нужно где-то накапливаться. Она могла скапливаться у той стены, а может быть вы, стена выбрана слишком большой, собирается скапливаться где-то перед стеной, и уж точно не может убежать в бесконечность. Но она должна сходиться, поэтому монотонная последовательность действительных чисел сходится. Итак, давайте применим эти 2 факта к последовательности от i до n над n. Я уже показал вам, как применить первый факт, i к n над n, абсолютное значение которого равно 1 над n, которое стремится к 0, и, таким образом, первая теорема говорит нам, что i от n над n также должно переходить в 0.Но теперь давайте посмотрим на действительную и мнимую части. Какова действительная часть i относительно n над n? Смотря как. Я помню, что это просто i1, и это равно 1. Это минус 1, 1 и это равно 2. Это минус i1, и это равно 3. Это 1, 1 и это равно 4. Опять же, я минус 1 минус я, 1 и так далее. Таким образом, действительная часть может быть 0, 1 или минус 1. Действительная часть равна 0 в случаях i, минус i и 1 или минус 1 в двух других случаях.
Но вы не можете выйти за пределы, тогда вам нужно где-то накапливаться. Она могла скапливаться у той стены, а может быть вы, стена выбрана слишком большой, собирается скапливаться где-то перед стеной, и уж точно не может убежать в бесконечность. Но она должна сходиться, поэтому монотонная последовательность действительных чисел сходится. Итак, давайте применим эти 2 факта к последовательности от i до n над n. Я уже показал вам, как применить первый факт, i к n над n, абсолютное значение которого равно 1 над n, которое стремится к 0, и, таким образом, первая теорема говорит нам, что i от n над n также должно переходить в 0.Но теперь давайте посмотрим на действительную и мнимую части. Какова действительная часть i относительно n над n? Смотря как. Я помню, что это просто i1, и это равно 1. Это минус 1, 1 и это равно 2. Это минус i1, и это равно 3. Это 1, 1 и это равно 4. Опять же, я минус 1 минус я, 1 и так далее. Таким образом, действительная часть может быть 0, 1 или минус 1. Действительная часть равна 0 в случаях i, минус i и 1 или минус 1 в двух других случаях. И вы знаете, я разделил это здесь, когда это 0, когда это 1 и когда это минус 1, вы можете это проверить.И точно так же мнимая часть равна либо 1, либо минус 1, либо 0, и я записал это прямо здесь. Таким образом, действительные части всегда находятся между минус 1 над n и 1 над n, как и мнимые части. Поскольку и 1 над n, и минус 1 над n сходятся к 0, теорема о сжатии подразумевает, что действительные части и мнимые части преобразуются в 0, поэтому принуждают i к n над n, чтобы сходиться к 0. Нам также нужно поговорить о пределы сложных функций, мы говорим, что функция комплексного значения f имеет предел l, когда z приближается к 0.Если значения f близки к l. Se переходит в z0. Это означает, что если это точка L и значения f должны быть близки к L, это означает, что если я нарисую достаточно маленький диск вокруг L и диск радиуса эпсилон, то в конечном итоге все значения f окажутся в этом диск. Если значения z были достаточно близки к z0. Так. Я могу найти другой диск вокруг z0, такой, что, если мои значения z находятся внутри этого диска, а значения f значений z будут на диске радиуса эпсилон.
И вы знаете, я разделил это здесь, когда это 0, когда это 1 и когда это минус 1, вы можете это проверить.И точно так же мнимая часть равна либо 1, либо минус 1, либо 0, и я записал это прямо здесь. Таким образом, действительные части всегда находятся между минус 1 над n и 1 над n, как и мнимые части. Поскольку и 1 над n, и минус 1 над n сходятся к 0, теорема о сжатии подразумевает, что действительные части и мнимые части преобразуются в 0, поэтому принуждают i к n над n, чтобы сходиться к 0. Нам также нужно поговорить о пределы сложных функций, мы говорим, что функция комплексного значения f имеет предел l, когда z приближается к 0.Если значения f близки к l. Se переходит в z0. Это означает, что если это точка L и значения f должны быть близки к L, это означает, что если я нарисую достаточно маленький диск вокруг L и диск радиуса эпсилон, то в конечном итоге все значения f окажутся в этом диск. Если значения z были достаточно близки к z0. Так. Я могу найти другой диск вокруг z0, такой, что, если мои значения z находятся внутри этого диска, а значения f значений z будут на диске радиуса эпсилон. Итак, если бы вы хотели сделать это точным, вы бы сказали, вы знаете, для каждого эпсилон это диск вокруг этой единицы, есть дельта, это второй диск вокруг 0, так что всякий раз, когда z минус 0, меньше, чем дельта , z находятся в дельта-диске, тогда f от z минус l меньше эпсилон.Конечно, вы знаете, что f от z должно быть определено рядом с z0, чтобы это определение имело хоть какой-то смысл, но мы не обязательно требуем, чтобы f определялось как z 0. Используйте пример. Предположим, f от z — это функция z, возведенная в квадрат минус один по z минус 1. Эта функция не определена как z, равная единице, потому что я буду делить на 0. Но мы могли бы спросить, приближается ли f от z к пределу, когда z приближается к 1? Это немного неясно, давайте посмотрим на это. Мы смотрим на предел f для z, когда z приближается к 1, и замечаем, что числитель фактически включает z минус 1, умноженное на z плюс 1, и мы можем отменить один из этих z минус один множителей, и мы остаемся с пределом z плюс 1, когда z становится 1.
Итак, если бы вы хотели сделать это точным, вы бы сказали, вы знаете, для каждого эпсилон это диск вокруг этой единицы, есть дельта, это второй диск вокруг 0, так что всякий раз, когда z минус 0, меньше, чем дельта , z находятся в дельта-диске, тогда f от z минус l меньше эпсилон.Конечно, вы знаете, что f от z должно быть определено рядом с z0, чтобы это определение имело хоть какой-то смысл, но мы не обязательно требуем, чтобы f определялось как z 0. Используйте пример. Предположим, f от z — это функция z, возведенная в квадрат минус один по z минус 1. Эта функция не определена как z, равная единице, потому что я буду делить на 0. Но мы могли бы спросить, приближается ли f от z к пределу, когда z приближается к 1? Это немного неясно, давайте посмотрим на это. Мы смотрим на предел f для z, когда z приближается к 1, и замечаем, что числитель фактически включает z минус 1, умноженное на z плюс 1, и мы можем отменить один из этих z минус один множителей, и мы остаемся с пределом z плюс 1, когда z становится 1. Но z плюс 1 по мере того, как z приближается к 1, в основном равно 1 плюс 1, то есть 2, поэтому предел этой функции равен 2. Таким образом, у нее есть предел, даже если сама функция не определена при z равном единице. Давайте посмотрим на другой пример, предположим, что f от z — это функция, аргумент z, где аргумент — это аргумент в верхнем регистре. Помните, аргумент z в верхнем регистре — это угол, который z образует с положительной вещественной осью, и мы должны выбрать угол между минусом pi и pi. Итак, давайте посмотрим на аргумент z, когда z приближается к i, i прямо здесь.И когда z приближается к i, независимо от того, откуда z приближается к i, я могу нарисовать целый маленький диск вокруг i, и все эти значения Z здесь имеют аргумент, который довольно близок к числу пи больше двух. И чем меньше я нарисую диск, тем ближе все эти аргументы будут к pi больше 2. Итак, мы говорим, что предел аргумента z при приближении z к I равен pi при 2. Как насчет аргумента z при приближении z один? Один здесь, и снова я могу нарисовать небольшой диск вокруг 1.
Но z плюс 1 по мере того, как z приближается к 1, в основном равно 1 плюс 1, то есть 2, поэтому предел этой функции равен 2. Таким образом, у нее есть предел, даже если сама функция не определена при z равном единице. Давайте посмотрим на другой пример, предположим, что f от z — это функция, аргумент z, где аргумент — это аргумент в верхнем регистре. Помните, аргумент z в верхнем регистре — это угол, который z образует с положительной вещественной осью, и мы должны выбрать угол между минусом pi и pi. Итак, давайте посмотрим на аргумент z, когда z приближается к i, i прямо здесь.И когда z приближается к i, независимо от того, откуда z приближается к i, я могу нарисовать целый маленький диск вокруг i, и все эти значения Z здесь имеют аргумент, который довольно близок к числу пи больше двух. И чем меньше я нарисую диск, тем ближе все эти аргументы будут к pi больше 2. Итак, мы говорим, что предел аргумента z при приближении z к I равен pi при 2. Как насчет аргумента z при приближении z один? Один здесь, и снова я могу нарисовать небольшой диск вокруг 1. И аргументы над реальной осью будут немного больше, чем 0, а ниже реального доступа к меньшему, чем 0.Но все они довольно близки к 0 здесь. Чем меньше я нарисую свой диск, тем ближе эти аргументы будут к 0. Таким образом, предел аргумента равен 0. Но теперь давайте посмотрим на минус 1, я нарисую маленький диск вокруг минус 1. Что произойдет? Для точек в верхней половине этого диска аргумент приближается к числу пи. Это немного меньше числа Пи, но его аргумент довольно близок к числу Пи. С другой стороны, для точек в нижней половине диска мы измеряем отрицательно, аргумент почти минус пи.Итак, здесь аргумент действительно близок к минус пи, так что если я буду делать свой диск все меньше и меньше и меньше. Ниже оси X аргумент указывает на приближение к минус 5, но выше оси X аргумент хочет приблизиться к пи, они не могут согласиться, поэтому нет предела. Этого предела не существует. Из предыдущих фактов о пределах последовательностей следуют аналогичные факты о пределах функций. Я просто очень быстро перечислю их и напомню вам об этих фактах, когда они нам понадобятся.
И аргументы над реальной осью будут немного больше, чем 0, а ниже реального доступа к меньшему, чем 0.Но все они довольно близки к 0 здесь. Чем меньше я нарисую свой диск, тем ближе эти аргументы будут к 0. Таким образом, предел аргумента равен 0. Но теперь давайте посмотрим на минус 1, я нарисую маленький диск вокруг минус 1. Что произойдет? Для точек в верхней половине этого диска аргумент приближается к числу пи. Это немного меньше числа Пи, но его аргумент довольно близок к числу Пи. С другой стороны, для точек в нижней половине диска мы измеряем отрицательно, аргумент почти минус пи.Итак, здесь аргумент действительно близок к минус пи, так что если я буду делать свой диск все меньше и меньше и меньше. Ниже оси X аргумент указывает на приближение к минус 5, но выше оси X аргумент хочет приблизиться к пи, они не могут согласиться, поэтому нет предела. Этого предела не существует. Из предыдущих фактов о пределах последовательностей следуют аналогичные факты о пределах функций. Я просто очень быстро перечислю их и напомню вам об этих фактах, когда они нам понадобятся. Если f имеет предел в точке z0, то f ограничено точно так же, как сходящаяся последовательность должна быть ограничена.Если функция f приближается к пределу L, а предел g приближается к пределу M. Когда z приближается к 0, то сумма двух функций приближается к L плюс M, или произведение функций приближается к произведению пределов, а частное приближается к частному предела, при условии, что вам действительно разрешено делить на знаменатель. Вы не можете делить на 0. Наконец, функция непрерывна, если f от z приближается к f от z 0, когда z приближается к 2 0. Это непрерывность при z 0, это определение подразумевает много вещей неявно.Итак, мы говорим, что f должно быть определено в z 0. Потому что иначе мы не могли бы записать f z0 прямо здесь. Мы также говорим, что f имеет предел, когда z обращается к 0, потому что мы говорим, что f из z преобразуется во что-то, когда z обращается к 0. И, наконец, мы говорим, что эти два значения должны быть равны, потому что мы говорим f z не просто преобразуется в некоторый предел l.
Если f имеет предел в точке z0, то f ограничено точно так же, как сходящаяся последовательность должна быть ограничена.Если функция f приближается к пределу L, а предел g приближается к пределу M. Когда z приближается к 0, то сумма двух функций приближается к L плюс M, или произведение функций приближается к произведению пределов, а частное приближается к частному предела, при условии, что вам действительно разрешено делить на знаменатель. Вы не можете делить на 0. Наконец, функция непрерывна, если f от z приближается к f от z 0, когда z приближается к 2 0. Это непрерывность при z 0, это определение подразумевает много вещей неявно.Итак, мы говорим, что f должно быть определено в z 0. Потому что иначе мы не могли бы записать f z0 прямо здесь. Мы также говорим, что f имеет предел, когда z обращается к 0, потому что мы говорим, что f из z преобразуется во что-то, когда z обращается к 0. И, наконец, мы говорим, что эти два значения должны быть равны, потому что мы говорим f z не просто преобразуется в некоторый предел l. Но этот предел на самом деле должен быть f от z0. Таким образом, F необходимо определить в точке z0. У него должен быть предел, когда z стремится к 0. И этот предел должен равняться f от z0.Вы, наверное, уже встречали определения непрерывности для функций от r до r, которые часто описываются как то, что вы можете нарисовать функцию, не поднимая карандаша, что не совсем точно, есть некоторые другие непрерывные функции, но этого достаточно для нашего понимания. Понимание, у вас не может быть функции, которая делает прыжок, например. Эта функция не будет непрерывной, потому что у нее не будет предела. И поэтому функция, которая непрерывна в точке Z0, должна быть определена там, иметь предел, и этот предел равен f от z 0.Примерами непрерывных функций являются постоянные функции, функция f от z равна z, многочлены, f от z равна модулю z. И f от z — это многочлен, деленный на некоторые другие многочлены, но вы можете смотреть только на точки, где знаменатель не равен 0, потому что иначе вы бы делили на 0, и тогда у вас не было бы предела.
Но этот предел на самом деле должен быть f от z0. Таким образом, F необходимо определить в точке z0. У него должен быть предел, когда z стремится к 0. И этот предел должен равняться f от z0.Вы, наверное, уже встречали определения непрерывности для функций от r до r, которые часто описываются как то, что вы можете нарисовать функцию, не поднимая карандаша, что не совсем точно, есть некоторые другие непрерывные функции, но этого достаточно для нашего понимания. Понимание, у вас не может быть функции, которая делает прыжок, например. Эта функция не будет непрерывной, потому что у нее не будет предела. И поэтому функция, которая непрерывна в точке Z0, должна быть определена там, иметь предел, и этот предел равен f от z 0.Примерами непрерывных функций являются постоянные функции, функция f от z равна z, многочлены, f от z равна модулю z. И f от z — это многочлен, деленный на некоторые другие многочлены, но вы можете смотреть только на точки, где знаменатель не равен 0, потому что иначе вы бы делили на 0, и тогда у вас не было бы предела. Итак, на сегодня достаточно, к следующей лекции мы, наконец, будем готовы начать разговор о множествах Джулии квадратичных многочленов, которые, как мы только что узнали, являются непрерывными функциями.
Итак, на сегодня достаточно, к следующей лекции мы, наконец, будем готовы начать разговор о множествах Джулии квадратичных многочленов, которые, как мы только что узнали, являются непрерывными функциями.
Ограничения службы для уровней и SKUS — Когнитивный поиск Azure
- Статья
- 10 минут на чтение
Пожалуйста, оцените свой опыт
да Нет
Любая дополнительная обратная связь?
Отзыв будет отправлен в Microsoft: при нажатии кнопки отправки ваш отзыв будет использован для улучшения продуктов и услуг Microsoft.Политика конфиденциальности.
Представлять на рассмотрение
Спасибо.
В этой статье
Максимальные ограничения на хранилище, рабочие нагрузки и количество индексов и других объектов зависят от того, предоставляете ли вы Azure Cognitive Search в ценовых категориях Free , Basic , Standard или Storage Optimized .
Бесплатно — это многопользовательская общая служба, которая входит в вашу подписку Azure.
Basic предоставляет выделенные вычислительные ресурсы для производственных рабочих нагрузок в меньшем масштабе, но совместно использует некоторую сетевую инфраструктуру с другими арендаторами.
Standard работает на выделенных машинах с большей емкостью хранения и обработки на каждом уровне. Стандарт поставляется в четырех уровнях: S1, S2, S3 и S3 HD. S3 High Density (S3 HD) разработан для мультитенантности и большого количества небольших индексов (три тысячи индексов на службу).
 S3 HD не предоставляет функцию индексатора, и для приема данных должны использоваться API-интерфейсы, которые передают данные из источника в индекс.
S3 HD не предоставляет функцию индексатора, и для приема данных должны использоваться API-интерфейсы, которые передают данные из источника в индекс.Storage Optimized работает на выделенных машинах с большим объемом хранилища, пропускной способностью и объемом памяти, чем Standard . Этот уровень предназначен для больших медленно меняющихся индексов. Storage Optimized поставляется на двух уровнях: L1 и L2.
Лимиты подписки
В подписке можно создать несколько служб.Каждый из них может быть предоставлен на определенном уровне. Вы ограничены только количеством сервисов, разрешенных на каждом уровне. Например, вы можете создать до 12 служб на уровне «Базовый» и еще 12 служб на уровне S1 в рамках одной подписки. Дополнительные сведения об уровнях см. в статье Выбор SKU или уровня для Azure Cognitive Search.
Максимальные лимиты услуг могут быть увеличены по запросу. Если вам нужно больше служб в рамках одной подписки, обратитесь в службу поддержки Azure.
| Ресурс | Бесплатно 1 | Базовый | С1 | С2 | С3 | S3 HD | Л1 | Л2 |
|---|---|---|---|---|---|---|---|---|
| Максимум услуг | 1 | 16 | 16 | 8 | 6 | 6 | 6 | 6 |
| Максимальный масштаб в единицах поиска (SU) 2 | н/д | 3 шт. | 36 шт. | 36 шт. | 36 шт. | 36 шт. | 36 шт. | 36 шт. |
1 Бесплатное использование общих, а не выделенных ресурсов.Масштабирование не поддерживается для общих ресурсов.
2 Единицы поиска — это единицы выставления счетов, выделенные либо как реплика , либо как раздел . Вам нужны оба ресурса для хранения, индексирования и выполнения запросов. Дополнительные сведения о вычислениях SU см. в разделе Масштабирование уровней ресурсов для рабочих нагрузок запросов и индексов.
в разделе Масштабирование уровней ресурсов для рабочих нагрузок запросов и индексов.
Пределы хранения
Служба поиска ограничена дисковым пространством или жестким ограничением на максимальное количество индексов или индексаторов, в зависимости от того, что наступит раньше.В следующей таблице указаны пределы хранения. Максимальные ограничения объектов см. в разделе Ограничения по ресурсам.
| Ресурс | Бесплатно | Базовый 1 | С1 | С2 | С3 | S3 HD | Л1 | Л2 |
|---|---|---|---|---|---|---|---|---|
| Соглашение об уровне обслуживания (SLA) 2 | № | Да | Да | Да | Да | Да | Да | Да |
| Память на раздел | 50 МБ | 2 ГБ | 25 ГБ | 100 ГБ | 200 ГБ | 200 ГБ | 1 ТБ | 2 ТБ |
| Разделов на службу | н/д | 1 | 12 | 12 | 12 | 3 | 12 | 12 |
| Размер раздела | н/д | 2 ГБ | 25 ГБ | 100 ГБ | 200 ГБ | 200 ГБ | 1 ТБ | 2 ТБ |
| Реплики | н/д | 3 | 12 | 12 | 12 | 12 | 12 | 12 |
1 Базовая версия имеет один фиксированный раздел. Дополнительные единицы поиска можно использовать для добавления реплик для больших объемов запросов.
Дополнительные единицы поиска можно использовать для добавления реплик для больших объемов запросов.
2 Соглашения об уровне обслуживания действуют для оплачиваемых услуг на выделенных ресурсах. Бесплатные сервисы и предварительные версии не имеют соглашения об уровне обслуживания. Для оплачиваемых услуг соглашения об уровне обслуживания вступают в силу, когда вы обеспечиваете достаточную избыточность для своей службы. Для запросов (чтения) SLA требуются две или более реплик. Для запросов и индексации (чтение-запись) SLA требуется три или более реплик. Количество разделов не является фактором SLA.
Пределы индекса
| Ресурс | Бесплатно | Базовый 1 | С1 | С2 | С3 | S3 HD | Л1 | Л2 |
|---|---|---|---|---|---|---|---|---|
| Максимальные индексы | 3 | 5 или 15 | 50 | 200 | 200 | 1000 на раздел или 3000 на службу | 10 | 10 |
| Максимальное количество простых полей на индекс | 1000 | 100 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| Максимальное количество сложных полей коллекции на индекс | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 |
| Максимальное количество элементов во всех сложных коллекциях на документ 2 | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 |
| Максимальная глубина сложных полей | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Максимальное количество предложений на индекс | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Максимальное количество профилей оценки на индекс | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Максимальное количество функций на профиль | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
1 Базовые службы, созданные до декабря 2017 года, имеют более низкие ограничения (5 вместо 15) на индексы. Базовый уровень — это единственный SKU с нижним пределом в 100 полей на индекс.
Базовый уровень — это единственный SKU с нижним пределом в 100 полей на индекс.
2 Для элементов существует верхний предел, поскольку их большое количество значительно увеличивает объем хранилища, необходимый для вашего индекса. Элемент сложной коллекции определяется как член этой коллекции. Например, предположим, что документ Hotel содержит комплексную коллекцию Rooms, каждая комната в коллекции Rooms считается элементом. Во время индексирования механизм индексирования может безопасно обрабатывать не более 3000 элементов документа в целом.Это ограничение было введено в api-version=2019-05-06 и применяется только к сложным коллекциям, а не к коллекциям строк или сложным полям.
Ограничения документа
С октября 2018 г. больше нет ограничений на количество документов для любой новой услуги, созданной на любом оплачиваемом уровне (базовый, S1, S2, S3, S3 HD) в любом регионе. Для старых сервисов, созданных до октября 2018 г., могут по-прежнему действовать ограничения на количество документов.
Чтобы определить, есть ли у вашей службы ограничения на количество документов, используйте REST API статистики службы GET.Ограничения документа отражаются в ответе, где null указывает на отсутствие ограничений.
Примечание
Несмотря на то, что служба не накладывает ограничения на количество документов, существует ограничение сегмента примерно в 24 миллиарда документов на индекс в службах поиска Basic, S1, S2 и S3. Для S3 HD ограничение сегмента составляет 2 миллиарда документов на индекс. Каждый элемент сложной коллекции считается отдельным документом с точки зрения ограничений сегментов.
Ограничения размера документа на вызов API
Максимальный размер документа при вызове Index API составляет примерно 16 мегабайт.
Размер документа фактически ограничивает размер тела запроса Index API. Поскольку вы можете одновременно передать пакет из нескольких документов в Index API, ограничение размера реально зависит от того, сколько документов находится в пакете. Для пакета с одним документом максимальный размер документа составляет 16 МБ в формате JSON.
Для пакета с одним документом максимальный размер документа составляет 16 МБ в формате JSON.
При оценке размера документа не забывайте учитывать только те поля, которые могут использоваться службой поиска. Любые двоичные данные или данные изображения в исходных документах должны быть исключены из ваших расчетов.
Ограничения индексатора
Максимальное время работы существует для обеспечения сбалансированности и стабильности службы в целом, но для больших наборов данных может потребоваться больше времени для индексации, чем позволяет максимальное значение. Если задание индексирования не может быть завершено в течение максимально допустимого времени, попробуйте запустить его по расписанию. Планировщик отслеживает статус индексации. Если запланированное задание индексирования прерывается по какой-либо причине, индексатор может продолжить с того места, где оно было остановлено в последний раз, при следующем запланированном запуске.
| Ресурс | Бесплатно 1 | Базовый 2 | С1 | С2 | С3 | S3 HD 3 | Л1 | Л2 |
|---|---|---|---|---|---|---|---|---|
| Максимальные индексаторы | 3 | 5 или 15 | 50 | 200 | 200 | н/д | 10 | 10 |
| Максимальное количество источников данных | 3 | 5 или 15 | 50 | 200 | 200 | н/д | 10 | 10 |
| Максимальный набор навыков 4 | 3 | 5 или 15 | 50 | 200 | 200 | н/д | 10 | 10 |
| Максимальная нагрузка индексации на вызов | 10 000 документов | Ограничено только максимальным количеством документов | Ограничено только максимальным количеством документов | Ограничено только максимальным количеством документов | Ограничено только максимальным количеством документов | н/д | Без ограничений | Без ограничений |
| Минимальный график | 5 минут | 5 минут | 5 минут | 5 минут | 5 минут | 5 минут | 5 минут | 5 минут |
| Максимальное время работы | 1-3 минуты | 24 часа | 24 часа | 24 часа | 24 часа | н/д | 24 часа | 24 часа |
| Максимальное время работы индексаторов с набором навыков 5 | 3-10 минут | 2 часа | 2 часа | 2 часа | 2 часа | н/д | 2 часа | 2 часа |
| Индексатор больших двоичных объектов: максимальный размер большого двоичного объекта, МБ | 16 | 16 | 128 | 256 | 256 | н/д | 256 | 256 |
| Индексатор больших двоичных объектов: максимальное количество символов содержимого, извлекаемого из большого двоичного объекта | 32 000 | 64 000 | 4 миллиона | 8 миллионов | 16 миллионов | н/д | 4 миллиона | 4 миллиона |
1 Максимальное время выполнения индексатора бесплатных служб составляет 3 минуты для источников BLOB-объектов и 1 минута для всех остальных источников данных.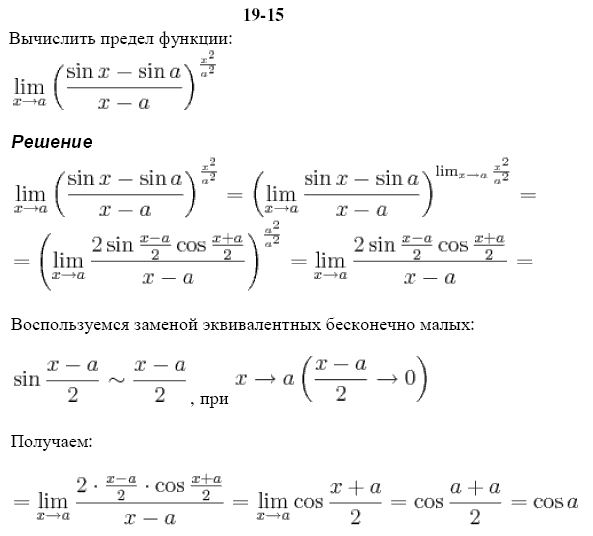 Для индексации ИИ, которая вызывает Cognitive Services, бесплатные услуги ограничены 20 бесплатными транзакциями в день, где транзакция определяется как документ, который успешно проходит через конвейер обогащения.
Для индексации ИИ, которая вызывает Cognitive Services, бесплатные услуги ограничены 20 бесплатными транзакциями в день, где транзакция определяется как документ, который успешно проходит через конвейер обогащения.
2 Базовые службы, созданные до декабря 2017 г., имеют более низкие ограничения (5 вместо 15) на индексаторы, источники данных и наборы навыков.
3 Службы S3 HD не включают поддержку индексатора.
4 Максимум 30 навыков на набор навыков.
5 Обогащение ИИ и анализ изображений требуют больших вычислительных ресурсов и потребляют непропорционально большое количество доступной вычислительной мощности. Время выполнения этих рабочих нагрузок было сокращено, чтобы дать другим заданиям в очереди больше возможностей для выполнения.
Примечание
Как указано в ограничениях индекса, индексаторы также будут применять верхний предел в 3000 элементов для всех сложных коллекций на документ, начиная с последней версии GA API, которая поддерживает сложные типы ( 2019-05-06 ) и выше. Это означает, что если вы создали свой индексатор с предыдущей версией API, на вас не распространяется это ограничение. Чтобы сохранить максимальную совместимость, индексатор, который был создан с использованием предыдущей версии API, а затем обновлен с помощью API версии
Это означает, что если вы создали свой индексатор с предыдущей версией API, на вас не распространяется это ограничение. Чтобы сохранить максимальную совместимость, индексатор, который был создан с использованием предыдущей версии API, а затем обновлен с помощью API версии 2019-05-06 или более поздней версии, по-прежнему будет исключен из ограничений. Клиенты должны знать о неблагоприятном влиянии очень больших сложных коллекций (как указано ранее), и мы настоятельно рекомендуем создавать любые новые индексаторы с последней версией GA API.
Ограничения ресурсов общей частной ссылки
Индексаторы могут получать доступ к другим ресурсам Azure через частные конечные точки, управляемые через общий API ресурса частной ссылки. В этом разделе описываются ограничения, связанные с этой возможностью.
| Ресурс | Бесплатно | Базовый | С1 | С2 | С3 | S3 HD | Л1 | Л2 |
|---|---|---|---|---|---|---|---|---|
| Поддержка частного индексатора конечных точек | № | Да | Да | Да | Да | № | Да | Да |
| Поддержка частных конечных точек для индексаторов с набором навыков 1 | № | № | № | Да | Да | № | Да | Да |
| Максимальное количество частных конечных точек | н/д | 10 или 30 | 100 | 400 | 400 | н/д | 20 | 20 |
| Максимальное количество различных типов ресурсов 2 | н/д | 4 | 7 | 15 | 15 | н/д | 4 | 4 |
1 Обогащение ИИ и анализ изображений требуют больших вычислительных ресурсов и потребляют непропорционально большое количество доступной вычислительной мощности. По этой причине частные подключения отключены на нижних уровнях, чтобы избежать негативного влияния на производительность и стабильность самой службы поиска.
По этой причине частные подключения отключены на нижних уровнях, чтобы избежать негативного влияния на производительность и стабильность самой службы поиска.
2 Количество различных типов ресурсов вычисляется как количество уникальных значений groupId , используемых во всех общих ресурсах частных ссылок для данной службы поиска, независимо от состояния ресурса.
Пределы синонимов
Максимальное количество карт синонимов зависит от уровня. Каждое правило может иметь до 20 расширений, где расширение является эквивалентным термином.Например, при заданном «кошке» ассоциация с «кошачьим», «кошачьим» и «фелисом» (родом кошек) будет считаться тремя расширениями.
| Ресурс | Бесплатно | Базовый | С1 | С2 | С3 | S3-HD | Л1 | Л2 |
|---|---|---|---|---|---|---|---|---|
| Максимальные карты синонимов | 3 | 3 | 5 | 10 | 20 | 20 | 10 | 10 |
| Максимальное количество правил на карту | 5000 | 20000 | 20000 | 20000 | 20000 | 20000 | 20000 | 20000 |
Пределы данных (обогащение AI)
Конвейер обогащения ИИ, который вызывает ресурсы Azure Cognitive Services для языка для распознавания сущностей, связывания сущностей, извлечения ключевых фраз, анализа тональности, определения языка и обнаружения личной информации, ограничен данными. Максимальный размер записи должен составлять 50 000 символов, измеренный
Максимальный размер записи должен составлять 50 000 символов, измеренный String.Length . Если вам нужно разбить данные перед отправкой в анализатор тональности, используйте навык «Разделение текста».
Пределы регулирования
Запросы API регулируются по мере того, как система приближается к пиковой мощности. Регулирование ведет себя по-разному для разных API. API-интерфейсы запросов (поиск/предложение/автозаполнение) и API-интерфейсы индексации динамически регулируются в зависимости от нагрузки на службу. API-интерфейсы индексов и API операций служб имеют статические ограничения скорости запросов.
Пределы запроса статической скорости для операций, связанных с индексом:
- Список индексов (GET /indexes): 3 в секунду на единицу поиска
- Получение индекса (GET /indexes/myindex): 10 в секунду на единицу поиска
- Создать индекс (POST/indexes): 12 в минуту на единицу поиска
- Создать или обновить индекс (PUT /indexes/myindex): 6 в секунду на единицу поиска
- Удалить индекс (DELETE /indexes/myindex): 12 в минуту на единицу поиска
Пределы запроса статической скорости для операций, связанных с услугой:
- Сервисная статистика (GET /servicestats): 4 в секунду на единицу поиска
Ограничения запросов API
- Максимум 16 МБ на запрос 1
- Максимальная длина URL-адреса 8 КБ
- Максимум 1000 документов на пакет загрузки, слияния или удаления индекса
- Максимум 32 поля в предложении $orderby
- Максимальный размер условия поиска составляет 32 766 байт (32 КБ минус 2 байта) текста в кодировке UTF-8
1 В Azure Cognitive Search тело запроса имеет верхний предел в 16 МБ, что накладывает практическое ограничение на содержимое отдельных полей или коллекций, которые иначе не ограничены теоретическими ограничениями (см.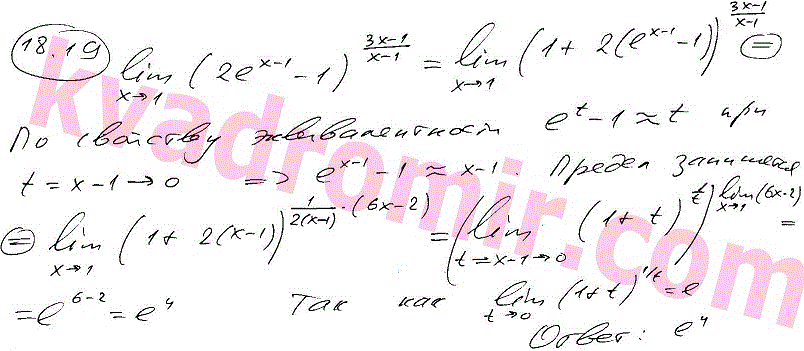 Поддерживаемые типы данных для получения дополнительной информации о составе полей и ограничениях).
Поддерживаемые типы данных для получения дополнительной информации о составе полей и ограничениях).
Ограничения ответов API
- Максимум 1000 документов, возвращаемых на страницу результатов поиска
- Максимум 100 предложений, возвращаемых на запрос Suggest API
Ограничения ключей API
Ключи APIиспользуются для аутентификации службы. Есть два типа. Ключи администратора указываются в заголовке запроса и предоставляют полный доступ для чтения и записи к сервису. Ключи запроса доступны только для чтения, указаны в URL-адресе и обычно распространяются среди клиентских приложений.
- Максимум 2 ключа администратора на службу
- Максимум 50 ключей запроса на службу
PURE MTH 4119 – Комплексный анализ – Награды
PURE MTH 4119 — комплексный анализ — с отличием
Кампус North Terrace – 1 семестр – 2020
2022202120202012017201620152014 Когда действительные числа заменяются комплексными числами в определении производной функции, получающиеся (комплексно) дифференцируемые функции оказываются обладающими многими замечательными свойствами, которыми не обладают их действительные аналоги. Эти функции, обычно называемые голоморфными функциями, имеют множество приложений в таких областях, как инженерия, физика, дифференциальные уравнения и теория чисел, и это лишь некоторые из них. Основное внимание в этом курсе уделяется изучению голоморфных функций и их важнейших основных свойств. Рассматриваемые темы: комплексные числа и функции; комплексные пределы и дифференцируемость; элементарные примеры; аналитические функции; комплексные линейные интегралы; теорема Коши и интегральная формула Коши; теорема Тейлора; нули голоморфных функций; Теорема Руша; теорема об открытом отображении и теорема об обратной функции; лемма Шварца; автоморфизмы шара, плоскости и сферы Римана; изолированные особенности и их классификация; серия Лорана; теорема об остатках; вычисление определенных интегралов и вычисление бесконечных рядов с помощью вычетов; Теорема Монтеля и теорема Римана об отображении.
Эти функции, обычно называемые голоморфными функциями, имеют множество приложений в таких областях, как инженерия, физика, дифференциальные уравнения и теория чисел, и это лишь некоторые из них. Основное внимание в этом курсе уделяется изучению голоморфных функций и их важнейших основных свойств. Рассматриваемые темы: комплексные числа и функции; комплексные пределы и дифференцируемость; элементарные примеры; аналитические функции; комплексные линейные интегралы; теорема Коши и интегральная формула Коши; теорема Тейлора; нули голоморфных функций; Теорема Руша; теорема об открытом отображении и теорема об обратной функции; лемма Шварца; автоморфизмы шара, плоскости и сферы Римана; изолированные особенности и их классификация; серия Лорана; теорема об остатках; вычисление определенных интегралов и вычисление бесконечных рядов с помощью вычетов; Теорема Монтеля и теорема Римана об отображении.
Детали курса
Код курса ЧИСТЫЙ МТН 4119 Курс Комплексный анализ – Награды Координатор Школа математических наук Срок Семестр 1 Уровень Бакалавриат Местоположение/я Кампус Северной Террасы Единицы 3 Контакт До 3 часов в неделю Доступно для обучения за границей и обмена Д Предпосылки MATHS 2100 или MATHS 2101 или MATHS 2202 или ELEC ENG 2106 Предполагаемые знания МАТЕМАТИКА 2101 Ограничения Только отличники Описание курса Когда действительные числа заменяются комплексными числами в определении производной функции, получающиеся (комплексно) дифференцируемые функции оказываются обладающими многими замечательными свойствами, которыми не обладают их действительные аналоги.  Эти функции, обычно называемые голоморфными функциями, имеют множество приложений в таких областях, как инженерия, физика, дифференциальные уравнения и теория чисел, и это лишь некоторые из них. Основное внимание в этом курсе уделяется изучению голоморфных функций и их важнейших основных свойств.
Эти функции, обычно называемые голоморфными функциями, имеют множество приложений в таких областях, как инженерия, физика, дифференциальные уравнения и теория чисел, и это лишь некоторые из них. Основное внимание в этом курсе уделяется изучению голоморфных функций и их важнейших основных свойств.Рассматриваемые темы: комплексные числа и функции; комплексные пределы и дифференцируемость; элементарные примеры; аналитические функции; комплексные линейные интегралы; теорема Коши и интегральная формула Коши; теорема Тейлора; нули голоморфных функций; Теорема Руша; теорема об открытом отображении и теорема об обратной функции; лемма Шварца; автоморфизмы шара, плоскости и сферы Римана; изолированные особенности и их классификация; серия Лорана; теорема об остатках; вычисление определенных интегралов и вычисление бесконечных рядов с помощью вычетов; Теорема Монтеля и теорема Римана об отображении.
Персонал курса
Координатор курса: Д-р Дэвид Баралья
Расписание занятий
Полное расписание всех занятий по этому курсу можно найти в Планировщике курсов.

Результаты обучения по курсу
1.Продемонстрировать понимание основных концепций, лежащих в основе сложного анализа.2. Продемонстрировать знакомство с рядом примеров этих понятий.
3. Доказать основные результаты комплексного анализа.
4. Применять методы комплексного анализа для вычисления определенных интегралов и бесконечных рядов.
5. Продемонстрировать понимание и оценку более глубоких аспектов комплексного анализа, таких как теорема об отображении Римана.
6. Демонстрировать навыки общения по математике устно и письменно.
Атрибуты выпускника университета
Этот курс предоставит учащимся возможность развить следующие атрибуты выпускника:
Атрибут выпускника университета Результаты обучения по курсу Глубокие дисциплинарные знания - информированы и основаны на передовых исследованиях, поддерживаются на протяжении всей программы обучения
- приобретены в результате личного общения с преподавателями-исследователями, начиная с 1 года
- аккредитованы или подтверждены в соответствии с национальными или международными стандартами ( для соответствующих программ)
1,2,3,4,5 Критическое мышление и решение проблем - погружены в исследовательские методы и строгость
- основаны на эмпирических данных и научном подходе к развитию знаний
1,2,3,4
Командная работа и коммуникативные навыки - развиты благодаря SGDE, с его помощью и с помощью SGDE
- отточены путем оценивания и практики на протяжении всей программы обучения
- поощряются и ценятся во всех аспектах обучения
6 Готовность к карьере и лидерству - технологический здравый смысл
- профессиональный и, где применимо, полностью аккредитованный
- дальновидный и хорошо осведомленный
5,6
Требуемые ресурсы
Рекомендуемые ресурсы
В BSL доступны следующие книги в порядке возрастания сложности. Ближайшим к уровню данного курса является 2.
Ближайшим к уровню данного курса является 2.1. Churchhill & Brown: Complex Variables and Applications; 517.53 C563
2. Марсден и Хоффман: базовый комплексный анализ; 517.54 M363b
3. Конвей: Функции одной комплексной переменной; 517.53 C767f
4. Альфорс: Введение в теорию аналитических функций одной комплексной переменной; 517.53 А28Онлайн-обучение
Этот курс использует MyUni исключительно для предоставления электронных ресурсов, таких как конспекты лекций, рабочие задания, примеры решений, доски обсуждений и т. д.Учащимся рекомендуется надлежащим образом использовать эти ресурсы.
Режимы обучения и обучения
В течение 30 лекций лектор представляет материал студентам и ведет их через него.
 Ожидается, что в течение этого времени студенты будут заниматься материалом, представленным на лекциях, выявляя любые трудности, которые могут возникнуть в их понимании, и взаимодействуя с лектором для преодоления этих трудностей.Ожидается, что студенты будут посещать все лекции, но лекции будут записываться (когда это позволяют условия), чтобы помочь в случае случайного пропуска и в целях повторения. На двухнедельных занятиях студенты представляют свои решения заданных упражнений и обсуждают их с лектором и своими сверстниками. Каждые две недели домашние задания помогают учащимся укрепить свое понимание теории и навыки ее применения, что позволяет им оценить свой прогресс.
Ожидается, что в течение этого времени студенты будут заниматься материалом, представленным на лекциях, выявляя любые трудности, которые могут возникнуть в их понимании, и взаимодействуя с лектором для преодоления этих трудностей.Ожидается, что студенты будут посещать все лекции, но лекции будут записываться (когда это позволяют условия), чтобы помочь в случае случайного пропуска и в целях повторения. На двухнедельных занятиях студенты представляют свои решения заданных упражнений и обсуждают их с лектором и своими сверстниками. Каждые две недели домашние задания помогают учащимся укрепить свое понимание теории и навыки ее применения, что позволяет им оценить свой прогресс.Рабочая нагрузка
Приведенная ниже информация предоставляется в качестве руководства, чтобы помочь учащимся надлежащим образом изучить требования курса.
Деятельность Количество часов рабочей нагрузки Лекции 30 90 Учебники 5 18 Задания 5 50 Всего 158 Сводка по учебной деятельности
Расписание лекций Неделя 1 Комплексные числа, функции и дифференцирование. 
Неделя 2 Уравнения Коши-Римана. Элементарные функции. Неделя 3 Другие примеры, гармонические функции, комплексные ряды. Неделя 4 Аналитические функции. Комплексные первообразные. Неделя 5 Интеграция сложных функций. Неделя 6 Теорема Коши-Гурса. Интегральная формула Коши. Неделя 7 Следствия интегральной формулы Коши. Неделя 8 Теорема Тейлора. Нули голоморфных функций. Неделя 9 Теоремы об открытом отображении и обратной функции. Изолированные особенности голоморфных функций. Неделя 10 Мероморфные функции, ряды Лорана; остатки. Неделя 11 Применение остатков.Просто связанные домены. Неделя 12 Теорема Римана об отображении. 
Политика университета в отношении оценивания курсовых работ основана на следующих четырех принципах:
- Оценка должна поощрять и укреплять обучение.
- Оценивание должно обеспечивать надежные и справедливые суждения об успеваемости учащихся.
- Практика оценивания должна быть честной и равноправной по отношению к учащимся и давать им возможность продемонстрировать, чему они научились.
- Оценка должна соответствовать академическим стандартам.
Резюме оценки
Задача оценки Тип задачи Из-за Утяжеление Результаты обучения Экзамен Суммарный Период экзамена 70% Все Тест в середине семестра Суммарный Неделя 6 10% 1,2,3,6 Учебники Формирующая и суммативная Недели 2,4,8,10,12 5% Все Задания Формирующая и суммативная Недели 3,5,7,9,11 15% Все
В связи с текущей ситуацией с COVID-19 были внесены изменения в порядок оценивания, чтобы облегчить дистанционное обучение и преподавание. Сведения об оценке, представленные здесь, отражают последние обновления.
Сведения об оценке, представленные здесь, отражают последние обновления. Чтобы поддержать изменения в преподавании, были внесены следующие изменения в оценивание: –
В этом семестре университет не будет проводить экзамены, как обычно. В связи с этим возникла необходимость изменить оценку
этого курса. Новая оценка выглядит следующим образом:Обычный экзамен будет заменен онлайн-экзаменом, проводимым через MyUni. Это будет стоить 50% баллов.
Будет по-прежнему 5 заданий, но теперь они будут стоить 30% от вашей общей оценки (6% за задание).
Участие в обучении 10%. Как мы уже делали, каждому студенту назначается вопрос в одном из уроков. Вы получаете оценку за то, что представили мне решение этого вопроса.
Наконец, через MyUni будет проведена онлайн-викторина, которая будет стоить 10%.
Более подробная информация об экзамене и онлайн-викторине будет опубликована в установленном порядке.
Требования, связанные с оценкой
Для успешного прохождения курса необходимо набрать 50% общего балла.

Деталь оценки
Оценка Комплект Из-за Утяжеление Учебник 1 Неделя 1 Неделя 2 1% Назначение 1 Неделя 2 Неделя 3 3% Учебник 2 Неделя 3 Неделя 4 1% Назначение 2 Неделя 4 Неделя 5 3% Тест в середине семестра Неделя 6 Неделя 6 10% Назначение 3 Неделя 6 Неделя 7 3% Учебник 3 Неделя 7 Неделя 8 1% Назначение 4 Неделя 8 Неделя 9 3% Учебник 4 Неделя 9 Неделя 10 1% Назначение 5 Неделя 10 Неделя 11 3% Учебник 5 Неделя 11 Неделя 12 1% Представление
Максимальный срок выполнения заданий для обратной связи со студентами составляет две недели.

Оценка курса
Оценки за вашу работу по этому курсу будут выставляться в соответствии со следующей схемой:
м11 (схема отличия отметки) класс класс отражает следующие критерии для распределения класса , зарегистрированных на официальном транскрипта сбой Отчет между 1-49 F Третье Класс Отчет от 50 до 59 3 Отчет между 60-69 2B второго класса Div A Отчет между 70-79 2A Первый класс Отчет между 80-100 1 Временный результат Промежуточный результат RP Продолжение Продолжение CN Более подробную информацию об оценках/результатах можно получить на экзаменах.
Доступны дескрипторы классов
, которые предоставляют общее руководство по стандартам работы, ожидаемым на каждом уровне обучения. Дополнительные сведения см. в разделе «Оценка программ курсовых работ».
Окончательные результаты этого курса будут доступны через Access Adelaide.
Университет уделяет большое внимание подходам к обучению и преподаванию, которые расширяют возможности студентов. От студентов требуется обратная связь различными способами, включая постоянное взаимодействие с персоналом, использование онлайн-дискуссий и использование опросов «Студенческий опыт обучения и преподавания» (SELT), а также опросов GOS и обзоров программ.
SELT являются важным источником информации для информирования об индивидуальной практике преподавания, решениях о преподавательских обязанностях, а также о разработке учебных курсов и программ. Они позволяют университету оценить, насколько эффективно его учебная среда и методы преподавания способствуют вовлечению студентов и результатам обучения.
 В соответствии с действующей Политикой SELT (http://www.adelaide.edu.au/policies/101/) курсы SELT являются обязательными и должны проводиться в конце каждого триместра/семестра/триместра для каждого предлагаемого курса.Отзывы по вопросам, поднятым в ходе опросов SELT курса, предоставляются зачисленным студентам через различные ресурсы (например, MyUni). Кроме того, доступны сводные данные курса SELT.
В соответствии с действующей Политикой SELT (http://www.adelaide.edu.au/policies/101/) курсы SELT являются обязательными и должны проводиться в конце каждого триместра/семестра/триместра для каждого предлагаемого курса.Отзывы по вопросам, поднятым в ходе опросов SELT курса, предоставляются зачисленным студентам через различные ресурсы (например, MyUni). Кроме того, доступны сводные данные курса SELT.В этом разделе содержатся ссылки на соответствующие политики и рекомендации, связанные с оцениванием — все политики университета.
Напоминаем учащимся, что для поддержания академической честности всех программ и курсов университет придерживается абсолютной нетерпимости к студентам, предлагающим деньги или ценные товары или услуги любому сотруднику, который участвует в их обучении или оценке.Студенты, предлагающие лекторам, репетиторам или профессиональным сотрудникам что-то большее, чем небольшой знак признательности, абсолютно неприемлемы ни при каких обстоятельствах.
 Сотрудники обязаны сообщать обо всех таких инцидентах своему руководителю/менеджеру, который направляет их для принятия мер в соответствии с дисциплинарными процедурами университета в отношении студентов.
Сотрудники обязаны сообщать обо всех таких инцидентах своему руководителю/менеджеру, который направляет их для принятия мер в соответствии с дисциплинарными процедурами университета в отношении студентов.Университет Аделаиды регулярно проводит обзоры курсов и программ, предлагаемых студентам.Таким образом, Университет Аделаиды оставляет за собой право прекращать или изменять программы и курсы без предварительного уведомления. Пожалуйста, прочитайте важную информацию, содержащуюся в отказе от ответственности.
Городские власти решают проблемы правоприменения, ограничивающего доступ к спортивному комплексу Янгсвилля
Городские власти Янгсвилля решают проблемы одного из родителей по поводу недавнего изменения политики в спортивном комплексе, которое ограничивает доступ населения.

Сообщение родителей привлекло внимание в социальных сетях….
По данным городских властей, дети со всей Акадианы могут использовать спортивный комплекс Янгсвилля для проведения лиг и спортивных программ.
Однако для игры в закрытый неорганизованный волейбол и баскетбол требуется проживание.
А осенью соблюдение этого правила ужесточили.
Дочь Рэйчел Мутон играет в университетский баскетбол в средней школе Саутсайда, но говорит, что ей отказали в бросках, потому что она не живет в городе Янгсвилл.
«…Я поставил под сомнение это, потому что моя дочь пошла играть, и ей не разрешили стрелять», — сказал Мутон. -мотивирован.
“Моя самая большая проблема заключалась в том, что вы говорите о городе, в котором более 81 процента населения составляют белые, и они запретили спорт, привлекающий наибольшее количество черных. И это сильно повлияет на чернокожих учеников средней школы Саутсайда. И в Саутсайде не так много чернокожих студентов, — сказал Мутон.

Мэр Янгсвилля Кен Риттер, отвечая на расистские обвинения, сказал: «Я разочарован, что это было бы инсинуацией, потому что более половины детей, которые играют в баскетбол в нашем спортивном комплексе, не являются жителями города Янгсвилл, и если эта юная леди была связана со спортивной программой или любой другой спортивной программой, которую мы предлагали, мы были бы рады приветствовать ее». для баскетбола и волейбола было разрешено только жителям из-за ограниченной доступности, места и надзора.
«Это не имеет ничего общего с черным или белым, но неправильно и правильно. И это правильно, чтобы защитить инвестиции города Янгсвилля», — продолжил Будро. «У нас было граффити в ванной, вешалки для туалетной бумаги, которые были стены оторвались, у нас было место, где они сидели на столешницах, и это было вытащено из стены. И сидеть там и говорить: «Ты сделал это». когда 10 человек вошли туда в этот период времени… как вы можете вернуться и точно определить? Потому что никто не собирается признаваться в этом», — сказал он.


 5% (% от сборов)
5% (% от сборов)  Простая структура, используемая не только для хранения данных, но и для создания других структур, где любая структура создаётся с использованием ключевого слова
Простая структура, используемая не только для хранения данных, но и для создания других структур, где любая структура создаётся с использованием ключевого слова  Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором. S3 HD не предоставляет функцию индексатора, и для приема данных должны использоваться API-интерфейсы, которые передают данные из источника в индекс.
S3 HD не предоставляет функцию индексатора, и для приема данных должны использоваться API-интерфейсы, которые передают данные из источника в индекс. Эти функции, обычно называемые голоморфными функциями, имеют множество приложений в таких областях, как инженерия, физика, дифференциальные уравнения и теория чисел, и это лишь некоторые из них. Основное внимание в этом курсе уделяется изучению голоморфных функций и их важнейших основных свойств.
Эти функции, обычно называемые голоморфными функциями, имеют множество приложений в таких областях, как инженерия, физика, дифференциальные уравнения и теория чисел, и это лишь некоторые из них. Основное внимание в этом курсе уделяется изучению голоморфных функций и их важнейших основных свойств.
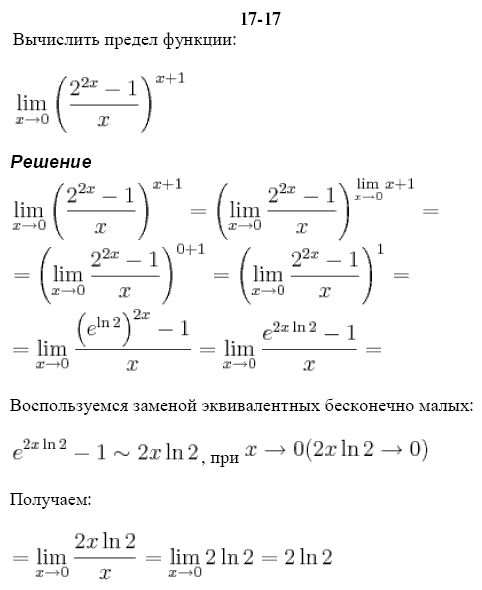 Ближайшим к уровню данного курса является 2.
Ближайшим к уровню данного курса является 2. Ожидается, что в течение этого времени студенты будут заниматься материалом, представленным на лекциях, выявляя любые трудности, которые могут возникнуть в их понимании, и взаимодействуя с лектором для преодоления этих трудностей.Ожидается, что студенты будут посещать все лекции, но лекции будут записываться (когда это позволяют условия), чтобы помочь в случае случайного пропуска и в целях повторения. На двухнедельных занятиях студенты представляют свои решения заданных упражнений и обсуждают их с лектором и своими сверстниками. Каждые две недели домашние задания помогают учащимся укрепить свое понимание теории и навыки ее применения, что позволяет им оценить свой прогресс.
Ожидается, что в течение этого времени студенты будут заниматься материалом, представленным на лекциях, выявляя любые трудности, которые могут возникнуть в их понимании, и взаимодействуя с лектором для преодоления этих трудностей.Ожидается, что студенты будут посещать все лекции, но лекции будут записываться (когда это позволяют условия), чтобы помочь в случае случайного пропуска и в целях повторения. На двухнедельных занятиях студенты представляют свои решения заданных упражнений и обсуждают их с лектором и своими сверстниками. Каждые две недели домашние задания помогают учащимся укрепить свое понимание теории и навыки ее применения, что позволяет им оценить свой прогресс.

 Сведения об оценке, представленные здесь, отражают последние обновления.
Сведения об оценке, представленные здесь, отражают последние обновления. 


 В соответствии с действующей Политикой SELT (http://www.adelaide.edu.au/policies/101/) курсы SELT являются обязательными и должны проводиться в конце каждого триместра/семестра/триместра для каждого предлагаемого курса.Отзывы по вопросам, поднятым в ходе опросов SELT курса, предоставляются зачисленным студентам через различные ресурсы (например, MyUni). Кроме того, доступны сводные данные курса SELT.
В соответствии с действующей Политикой SELT (http://www.adelaide.edu.au/policies/101/) курсы SELT являются обязательными и должны проводиться в конце каждого триместра/семестра/триместра для каждого предлагаемого курса.Отзывы по вопросам, поднятым в ходе опросов SELT курса, предоставляются зачисленным студентам через различные ресурсы (например, MyUni). Кроме того, доступны сводные данные курса SELT. Сотрудники обязаны сообщать обо всех таких инцидентах своему руководителю/менеджеру, который направляет их для принятия мер в соответствии с дисциплинарными процедурами университета в отношении студентов.
Сотрудники обязаны сообщать обо всех таких инцидентах своему руководителю/менеджеру, который направляет их для принятия мер в соответствии с дисциплинарными процедурами университета в отношении студентов.

