Смещение физика это: Колебательные движения — урок. Физика, 7 класс.

Гармонические колебания — формулы, законы, примеры

Покажем, как применять знание физики в жизни

Начать учиться

121.1K

Современный мир невозможен без гармонических колебаний — любая электромагнитная волна их распространяет. Не было бы телефонов, интернета и других электронных средств. О том, что такое гармонические колебания — в этой статье.

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Полезные подарки для родителей

В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием. 

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника. 

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний T  = t/N T — период [с] t — время [с] N — количество колебаний [—]

Также есть величина, обратная периоду — частота.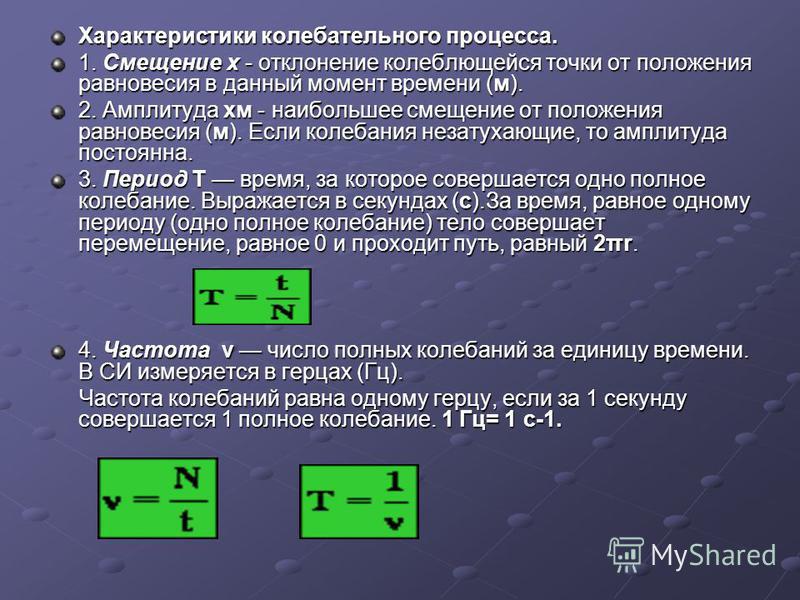 Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты ν  = N/t = 1/T ν — частота [Гц] t — время [с] T — период [с] N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x^max.

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением: 

Уравнение гармонических колебаний x = xmaxcos(2πνt) x — координата в момент времени t [м] xmax — амплитуда [м] ν — частота [Гц] t — момент времени [с] π = 3,14

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний φ = 2πνt φ — фаза [рад] ν — частота [Гц] t — момент времени [с] π = 3,14

Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.  

На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

• В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

• Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника T — период [с] l — длина нити [м] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 π = 3,14

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника T — период [с] m — масса маятника [кг] k — жесткость пружины [Н/м] π = 3,14

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии. 

Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Карина Хачатурян

К предыдущей статье

Кинематика

К следующей статье

114.5K

Механическое движение

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2. 1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4. 1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5. 5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

Расстояние и смещение

Расстояние и смещение — это две величины, которые могут показаться одним и тем же, но имеют совершенно разные определения и значения.

• Расстояние — это скалярная величина, которая относится к тому, «сколько земли преодолел объект» во время своего движения.
• Смещение — это векторная величина, которая указывает на то, «насколько далеко находится объект от места»; это общее изменение положения объекта.

Чтобы проверить свое понимание этого различия, рассмотрите движение, изображенное на диаграмме ниже. Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.

Несмотря на то, что учительница физики прошла в общей сложности 12 метров, ее перемещение равно 0 метрам. За время своего движения она «преодолела 12 метров земли» (расстояние = 12 м). Тем не менее, когда она заканчивает идти, она не находится «не на своем месте», т. Е. Для ее движения нет смещения (смещение = 0 м). Смещение, будучи векторной величиной, должно учитывать направление. 4 метра на восток отменяет 4 метра на запад; а 2 метра южнее отменяет 2 метра на север. Векторные величины, такие как смещение, осведомлены о направлении . Скалярные величины, такие как расстояние, не знают направления. При определении общего расстояния, пройденного учителями физики, можно не учитывать различные направления движения.

 

 

Теперь рассмотрим другой пример. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем в пункт С и затем в пункт D.

С помощью диаграммы определите результирующее перемещение и расстояние, пройденное лыжником за эти три минуты. Затем нажмите кнопку, чтобы увидеть ответ.

В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, тренер перемещается из позиции A в B, затем в C и затем в D.

Каково результирующее перемещение и пройденное расстояние автобуса? Нажмите кнопку, чтобы увидеть ответ.

 

Чтобы понять разницу между расстоянием и смещением, вы должны знать определения. Вы также должны знать, что векторная величина, такая как смещение, учитывает направление , а скалярная величина, такая как расстояние, не знает направления . Когда объект меняет направление движения, смещение учитывает это изменение направления; движение в противоположном направлении фактически начинается с отменить независимо от того, какое смещение когда-то было.

Проверьте свое понимание

1. Каково перемещение команды по кроссу, если они начинают в школе, пробегают 10 миль и заканчивают обратно в школе?

2. Какова дистанция и смещение гонщиков в Indy 500?

Следующий раздел:

Перейти к следующему уроку:

Устали от рекламы?
Получите бесплатную рекламу на 1 год

Смещение | Физика

Положение

Чтобы описать движение объекта, вы должны сначала уметь описать его положение — где он находится в любой конкретный момент времени. Точнее, нужно указать его положение относительно удобной системы отсчета. Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к неподвижным объектам в этой системе отсчета. Например, запуск ракеты может быть описан с точки зрения положения ракеты относительно Земли в целом, а положение профессора может быть описано с точки зрения того, где он находится по отношению к ближайшей доске. (См. рис. 2.) В других случаях мы используем системы отсчета, которые не стационарны, а находятся в движении относительно Земли. Например, для описания положения человека в самолете в качестве системы отсчета мы используем самолет, а не Землю. (См. рис. 3.)

Смещение

Если объект перемещается относительно системы отсчета (например, если профессор движется вправо относительно белой доски или пассажир движется к задней части самолета), то положение объекта изменяется. Это изменение положения известно как смещение . Слово «смещение» подразумевает, что объект сдвинулся или был смещен.

Смещение

Смещение изменение позиции Объекта:

Δ x = x _F – x _O,

, где Δ x – это смещение x

0. ₀ — начальная позиция.

В этом тексте заглавная греческая буква Δ (дельта) всегда означает «изменение» любой величины, следующей за ней; таким образом, Δ x означает изменение позиции . Всегда находите смещение, вычитая начальную позицию x ₀ от конечной позиции x _f .

Обратите внимание, что единицей СИ для перемещения является метр (м) (см. Физические величины и единицы), но иногда используются километры, мили, футы и другие единицы длины. Имейте в виду, что когда в задаче используются единицы измерения, отличные от метра, вам может потребоваться преобразовать их в метры, чтобы завершить расчет.

Рис. 2. Профессор ходит влево и вправо во время лекции. Ее положение относительно Земли задается x. Смещение профессора относительно Земли представлено стрелкой, указывающей вправо.

Рис. 3. Пассажир перемещается со своего места в заднюю часть самолета. Его положение относительно самолета задается x. Смещение пассажира на -4,0 м относительно самолета показано стрелкой в ​​направлении задней части самолета. Обратите внимание, что стрелка, представляющая его смещение, в два раза длиннее стрелки, представляющей смещение профессора (она перемещается в два раза дальше) на рисунке 3.

Обратите внимание, что смещение имеет не только величину, но и направление. Перемещение профессора — 2,0 м вправо, перемещение авиапассажира — 4,0 м назад. В одномерном движении направление может быть указано со знаком плюс или минус. Когда вы начинаете решать задачу, вы должны выбрать положительное направление (обычно это будет вправо или вверх, но вы можете выбрать любое положительное направление). Начальная позиция профессора x ₀ = 1,5 м и ее конечное положение x _f = 3,5 м. Таким образом, ее перемещение равно

Δ x = x _f − x _o = 3,5 м − 1,5 м = +2,0 м

В этой системе координат движение положительно. слева отрицательный. Аналогично, начальное положение пассажира самолета x ₀ = 6,0 м, а его конечное положение x _f = 2,0 м, поэтому его перемещение равно

Δ x = x _f  − x _o  = 2,0 м − 6,0 м =-4,0 м отрицательное направление x в нашей системе координат.

Расстояние

Хотя смещение описывается в терминах направления, расстояние — нет. Расстояние определяется как величина или размер смещения между двумя положениями . Обратите внимание, что расстояние между двумя положениями не равно расстоянию, пройденному между ними. Пройденное расстояние равно общей длине пути, пройденного между двумя позициями . Расстояние не имеет направления и, следовательно, не имеет знака. Например, расстояние, которое проходит профессор, равно 2,0 м. Расстояние, которое проходит пассажир самолета, равно 4,0 м.

Предупреждение о неправильном представлении: пройденное расстояние и величина смещения

Важно отметить, что пройденное расстояние , однако, может быть больше, чем величина смещения (под величиной мы понимаем просто величину смещения без учета его направления, то есть просто число с единицей). Например, профессор может ходить взад и вперед много раз, возможно, пройти расстояние 150 м во время лекции, но все же оказаться всего в 2,0 м справа от своей начальной точки. В этом случае ее перемещение составило бы +2,0 м, величина ее смещения составила бы 2,0 м, а пройденное ею расстояние составило бы 150 м. В кинематике мы почти всегда имеем дело с перемещением и величиной смещения и почти никогда с пройденным расстоянием. Один из способов подумать об этом — предположить, что вы отметили начало и конец движения. Смещение — это просто разница в положении двух меток, и оно не зависит от пути, пройденного при перемещении между двумя метками. Однако пройденное расстояние — это общая длина пути, пройденного между двумя отметками.

 

Проверьте правильность понимания

Велосипедист проезжает 3 км на запад, затем разворачивается и едет 2 км на восток. а) Каково ее перемещение? б) Какое расстояние она проехала? в) Какова величина ее смещения?

Рис. 4.

Решения

(а) Перемещение всадника Δ x = x _f  –

x 4 900,0 км (Смещение отрицательно, потому что мы принимаем восток за положительное значение, а запад за отрицательное.)

(b) Пройденное расстояние равно 3 км + 2 км = 5 км.

(c) Величина смещения 1 км.

Краткое описание раздела

• Кинематика — это изучение движения без учета его причин. В этой главе оно ограничивается движением по прямой линии, называемым одномерным движением.
• Смещение — это изменение положения объекта.
• В символах смещение Δ x определяется как

Δ х = x _f − x _o,

, где x _o — начальная позиция, а x _f — конечная позиция.