10.3. Производная и ее геометрический смысл.
Автор Татьяна Андрющенко На чтение 4 мин. Просмотров 10.1k. Опубликовано
В координатной плоскости хОу рассмотрим график функции y=f (x). Зафиксируем точку М(х0; f (x0)). Придадим абсциссе х0 приращение Δх. Мы получим новую абсциссу х0+Δх. Это абсцисса точки N, а ордината будет равна f (х0+Δх). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy.
Δy=f (х0+Δх) — f (x0). Через точки M и N проведем секущую MN, которая образует угол φ с положительным направлением оси Ох. Определим тангенс угла φ из прямоугольного треугольника MPN.
Определим тангенс угла φ из прямоугольного треугольника MPN.
Пусть Δх стремится к нулю. Тогда секущая MN будет стремиться занять положение касательной МТ, а угол φ станет углом α. Значит, тангенс угла α есть предельное значение тангенса угла φ:
Определение производной. Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:
Смотрите видео 10.3. Определение производной. Геометрический смысл производной.
Примеры.
1. Найти приращение аргумента и приращение функции y=x2, если начальное значение аргумента было равно 4, а новое –4,01.
Решение.
Новое значение аргумента х=х0+Δx. Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх=4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х0+Δх) – f (x0). Так как у нас функция y=x2, то Δу=(х0+Δx)2— (х0)2=(х0)2+2x0 · Δx+(Δx)2— (х0)2=2x0 · Δx+(Δx)2=
=2 · 4 · 0,01+(0,01)2=0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх=0,01; приращение функции Δу=0,0801.
Можно было приращение функции найти по-другому: Δy=y (х0+Δx) -y (х0)=у(4,01) -у(4)=4,012-42=16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х0, если f ‘(х0) = 1.
Решение.
Значение производной в точке касания х0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f ‘(х0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45°.
3. Вывести формулу производной функции y=xn.
Смотрите видео: «10.3.0. Вывод формулы производной степени».
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (xn)’ = nxn-1.
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования.
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
9) Производная. Геометрический и физический смысл производной
8) Некоторые важные пределы |
Если угол а выражен в радианах, то При нахождении многих пределов применяются следующие пределы: (13. (13.20) (13.21) Частными случаями формул (13.19) и (13.20) являются соответственно формулы: (13.22) (13.23) При нахождении пределов видаНеобходимо иметь В виду следующее: 1) если существуют конечные пределы 3) еслиТо, положивГде ПриПолучим Пример 13.12. Найти ПриВыражениеПолучаем неопределенность ВидаЧтобы раскрыть ее, введем новую переменную по формулеОткудаКогдаПереходя к пределу С использованием формул (13.13) и (13.18), находим В частности, приПолучаем Пример 13.13. Найти Разделив числитель и знаменатель наИ воспользовавшись результатом примера 13.12, получим Пример 13.14. НайтиПреобразуя эту дробь и применяя первую из формул (13.17), находим Пример 13.15. Найти Преобразуя данную функцию, вводя новую переменнуюИ применяя Формулу
(13. |
Перейти к списку задач и тестов по теме “Производная. Геометрический и физический смысл производной”
Определение: Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение , стремящемся к нулю.
Производные элементарных функций.
Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то
Производная сложной функции:
Геометрический
смысл производной. Производная
в точке x
Уравнение касательной к графику функции y=f(x) в точке x0 :
Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
10) Производные некоторых основных элементарных функций
В
этом пункте мы найдем производные следующих
основных элементарных функций:
постоянной (константы) степенной функции с
натуральным
показателем , показательной функции логарифмической функции и тригонометрических функций .
Производные остальных основных элементарных функций будут найдены в последующих пунктах. 1. Производная постоянной Так как функция сохраняет постоянное значение на всей числовой оси, то в произвольно выбранной точке любому приращению аргумента соответствует приращение функции , равное нулю. Поэтому
Итак,
2. Производная степенной функции с натуральным показателем . Пусть х — произвольно выбранная точка, -приращение аргумента в этой точке и — соответствующее приращение данной функции. Тогда по формуле бинома Ньютона
или
Следовательно,
Таким образом,
3. Производная показательной функции Давая приращение произвольно выбранному значению аргумента получим следующее приращение показательной функции:
Следовательно,
так
как (см.
гл. V, § 2, п. 2, пример 3).
Таким образом,
В частности, при получим
так как
4. Производная логарифмической функции Возьмем любое значение из области определениялогарифмической функции и дадим ему приращение Тогда приращение функции
Поэтому
Для того чтобы найти этот предел, сделаем следующее преобразование:
Принимая во внимание, что величина постоянна и что при также и по формуле (25) гл. V, § 2 получим
Итак,
(19)
или
так как
В частности, при получим
так как
5. Производные функций Пусть — приращение произвольно выбранного значения аргумента функции Тогда приращение этой функции
Следовательно,
так как по формуле (18) гл. V, § 1, п. 7
Аналогично выводится формула для производной функции
11) Основные правила дифференцирования
Установим
правила, по которым можно было бы
находить производные суммы,
произведения и частного функций, зная
производные слагаемых, сомножителей,
делимого и делителя.
Эти правила мы сформулируем в следующих теоремах.
Теорема I. Если функции дифференцируемы в данной точке , то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:
Доказательство. Рассмотрим функцию . Приращению аргумента соответствуют приращения
функций и и и. Тогда функция у получит приращение
Следовательно,
Так как по предложению функции и и v дифференцируемы, то
и, следовательно, .
Итак,
Замечание. Формула (23) легко обобщается на случай любого конечного числа слагаемых:
Пример 1. Найти производную функции Решение. Применяя вначале формулу (24), а затем формулы (16), (21) и (20), получим
Теорема
2. Если функции и дифференцируемы
в данной точке ,
то в той же точке дифференцируемо и их
произведение.
Доказательство. Пусть
Если получит приращение то функции и, v и у будут иметь соответственно некоторые приращения причем
Следовательно,
Так как при фиксированном постоянны, то их можно вынести за знак предела. Поэтому
Кроме того,
так как функция v по условию дифференцируема, а следовательно, и непрерывна, и поэтому
Таким образом,
Следствие. Постоянный множитель можно вынести за знак производной:
Действительно, если (с — постоянная), то по формуле (25)
В частности, можно выносить за знак производной множитель, равный —1, что равносильно вынесению за знак производной знака
На этом основании можно получить формулу для производной разности двух функций:
Пример
2. Найти производную функции .
Найти производную функции .
Решение. По формулам (25), (18) и (22) получим
Пример 3. Найти производную многочлена Решение. Применяя последовательно формулы (24), (26), (16) и (15), получим
Замечание. Формулу (25) можно обобщить на случай любого конечного числа сомножителей. Если, например, , то
В самом деле,
Теорема 3. Если в данной точке функции дифференцируемы и , то в той точке дифференцируемо и их частное причем
Доказательство. Пусть — приращение аргумента а — соответствующие приращения функций . Тогда функция будет иметь приращение
Следовательно,
или
Мы считали, что вследствие предположения о дифференцируемости, а следовательно, инепрерывности функции у.
Пример 4. Найти производную функции .
Решение. Представив данную функцию в виде частного
получим по формуле (29):
Таким образом,
При этом условие выполняется для любого принадлежащего области определения функции
Аналогично выводится формула для производной функции :
Смысл производной.
 Производная функции. Геометрический смысл производной
Производная функции. Геометрический смысл производнойМногие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины . Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные , в том числе производные сложных функций . Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования , даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо . Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции , а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью . И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто , чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Скорость изменения функцииИдея состоит в следующем: возьмём некоторое значение (читается «дельта икс») , которое назовём приращением аргумента , и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание! Обозначение являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже.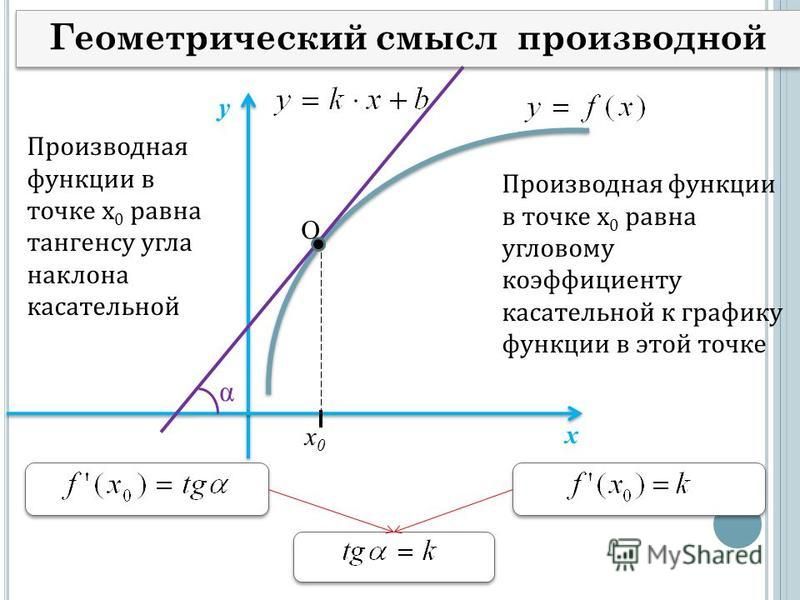 Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной :
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела . Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».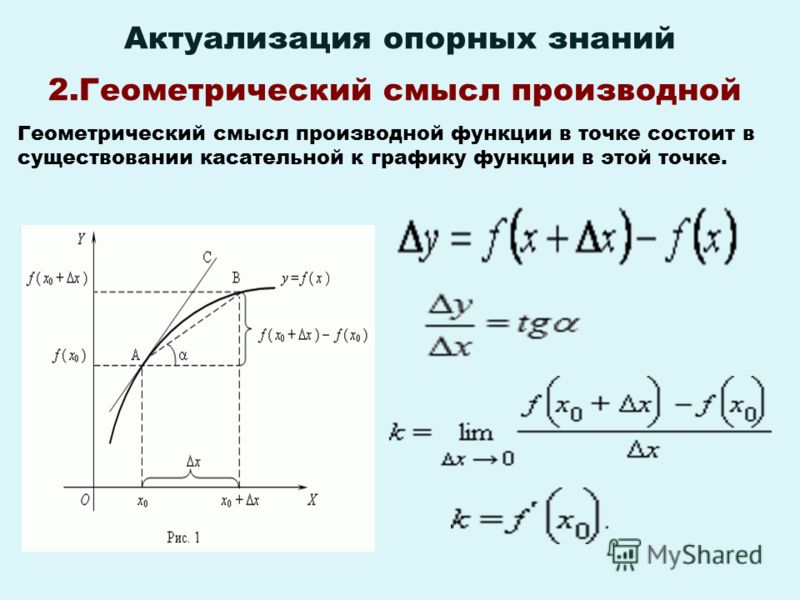
Ускорение тела – это скорость изменения скорости, поэтому: . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом
Тот
процесс, с помощью которого из данной
функции f(x) получают новую функцию f
” (x) ,
называют дифференцированием и состоит он из следующих трех шагов:
1)
даем аргументу x приращение x и определяем соответствующее приращение
функции y
= f(x+ x)
-f(x) ;
2)
составляем отношение
3)
считая x постоянным, а x 0,
находим
,
который обозначаем черезf
” (x) ,
как бы подчеркивая тем самым, что
полученная функция зависит лишь от того
значения x ,
при котором мы переходим к
пределу. Определение : Производной
y ” =f ” (x) данной
функции y=f(x) при
данном x называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю, если, конечно, этот
предел существует, т.е. конечен.
Таким
образом,
Определение : Производной
y ” =f ” (x) данной
функции y=f(x) при
данном x называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю, если, конечно, этот
предел существует, т.е. конечен.
Таким
образом,
,
или
Заметим,
что если при некотором значении x ,
например при x=a ,
отношение
при x 0
не стремится к конечному пределу, то в
этом случае говорят, что функция f(x) при x=a (или в точке x=a )
не имеет производной или не дифференцируема
в точке x=a .
2. Геометрический смысл производной.
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x 0
f(x)
Рассмотрим
произвольную прямую, проходящую через
точку графика функции – точку А(x 0 ,
f
(х 0))
и пересекающую график в некоторой точке
B(x;f(x)).
Такая прямая (АВ) называется секущей.
Из ∆АВС: АС = ∆x;
ВС =∆у; tgβ=∆y/∆x
.
Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO – это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k – угловой коэффициент прямой АВ.
Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.
Если
перейти к пределу при ∆х → 0 в равенстве
tgβ
=∆y/∆x,
то получим
илиtg
=f
“(x 0),
так как
-угол
наклона касательной к положительному
направлению оси Ох
,
по определению производной. Но tg
= k – угловой коэффициент касательной,
значит, k = tg
= f
“(x 0).
Итак, геометрический смысл производной заключается в следующем:
Производная функции в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .
3.
 Физический смысл производной.
Физический смысл производной.Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.
Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.
lim Vср (t) = (t 0) – мгновенная скорость в момент времени t 0 , ∆t → 0.
а lim = ∆x/∆t = x”(t 0) (по определению производной).
Итак, (t) =x”(t).
Физический смысл производной заключается в следующем: производная функции y = f (x ) в точке x 0 – это скорость изменения функции f (х) в точке x 0
Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.
(t) = x”(t) – скорость,
a(f) = ”(t) – ускорение, или
Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:
φ = φ(t) – изменение угла от времени,
ω = φ”(t) – угловая скорость,
ε
= φ”(t)
– угловое ускорение, или ε
= φ”(t).
Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:
m = m(х) – масса,
x , l – длина стержня,
р = m”(х) – линейная плотность.
С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука
F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω 2 =k/m, получим дифференциальное уравнение пружинного маятника х”(t) + ω 2 x(t) = 0,
где ω = √k/√m частота колебаний (l/c), k – жесткость пружины (H/m).
Уравнение вида у” + ω 2 y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция
у = Asin(ωt + φ 0) или у = Acos(ωt + φ 0), где
А – амплитуда колебаний, ω – циклическая частота,
φ 0 – начальная фаза.
{\large\bf Производная функции}
Рассмотрим функцию y=f(x) , заданную на интервале (a, b) . Пусть x – любое фиксированная точка интервала (a, b) , а Δx – произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b) . Это число Δx называют приращением аргумента.
Пусть x – любое фиксированная точка интервала (a, b) , а Δx – произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b) . Это число Δx называют приращением аргумента.
Определение . Приращением функции y=f(x) в точке x , соответствующим приращению аргумента Δx , назовем число
Δy = f(x+Δx) – f(x) .
Считаем, что Δx ≠ 0 . Рассмотрим в данной фиксированной точке x отношение приращения функции в этой точке к соответствующему приращению аргумента Δx
Это отношение будем называть разностным отношением. Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx . Эта функция определена для всех значений аргумента Δx , принадлежащих некоторой достаточно малой окрестности точки Δx=0 , за исключением самой точки Δx=0 . Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .
Определение . Производной функции y=f(x) в данной фиксированной точке x называется предел при Δx → 0 разностного отношения, то есть
При условии, что этот предел существует.
Обозначение . y′(x) или f′(x) .
Геометрический смысл производной : Производная от функции f(x) в данной точке x равна тангенсу угла между осью Ox и касательной к графику этой функции в соответствующей точке:
f′(x 0) = \tgα .
Механический смысл производной : Производная от пути по времени равна скорости прямолинейного движения точки:
Уравнение касательной к линии y=f(x) в точке M 0 (x 0 ,y 0) принимает вид
y-y 0 = f′(x 0) (x-x 0) .
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f′(x 0)≠ 0 , то уравнение нормали к линии y=f(x) в точке M 0 (x 0 ,y 0) записывается так:
Понятие дифференцируемости функции
Пусть функция y=f(x) определена на некотором интервале (a, b) , x – некоторое фиксированное значение аргумента из этого интервала, Δx – любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b) .
Определение . Функция y=f(x) называется дифференцируемой в данной точке x , если приращение Δy этой функции в точке x , соответствующее приращению аргумента Δx , может быть представимо в виде
Δy = A Δx +αΔx ,
где A – некоторое число, не зависящее от Δx , а α – функция аргумента Δx , являющая бесконечно малой при Δx→ 0 .
Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:
Δy = A Δx +o(Δx) .
Теорема . Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x , необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x) , то есть
Δy = f′(x) Δx +o(Δx) .
Операцию нахождения производной обычно называют дифференцированием.
Теорема .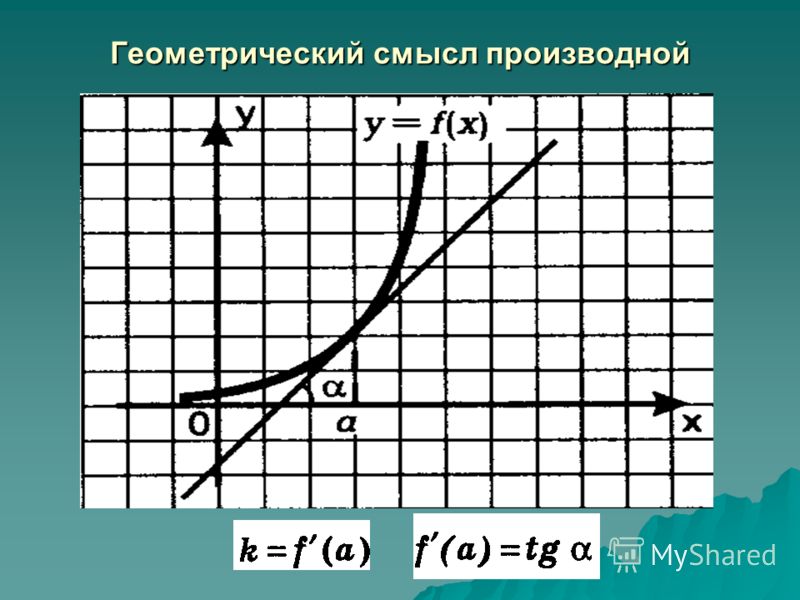 Если функция y=f(x) x , то она непрерывна в этой точке.
Если функция y=f(x) x , то она непрерывна в этой точке.
Замечание . Из непрерывности функции y=f(x) в данной точке x , вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| – непрерывна в точке x=0 , но не имеет производной.
Понятие дифференциала функции
Определение . Дифференциалом функции y=f(x) называется произведение производной этой функции на приращение независимой переменной x :
dy = y′ Δx, df(x) = f′(x) Δx .
Для функции y=x получаем dy=dx=x′Δx = 1· Δx= Δx , то есть dx=Δx – дифференциал независимой переменной равен приращению этой переменной.
Таким образом, можем записать
dy = y′ dx, df(x) = f′(x) dx
Дифференциал dy и приращение Δy функции y=f(x) в данной точке x , оба отвечающие одному и тому же приращению аргумента Δx , вообще говоря, не равны друг другу.
Геометрический смысл дифференциала : Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение Δx .
Правила дифференцирования
Теорема . Если каждая из функций u(x) и v(x) дифференцируема в данной точке x , то сумма, разность, произведение и частное этих функций (частное при условии, что v(x)≠ 0 ) также дифференцируемы в этой точке, причем имеют место формулы:
Рассмотрим сложную функцию y=f(φ(x))≡ F(x) , где y=f(u) , u=φ(x) . В этом случае u называют промежуточным аргументом , x – независимой переменной .
Теорема . Если y=f(u) и u=φ(x) – дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.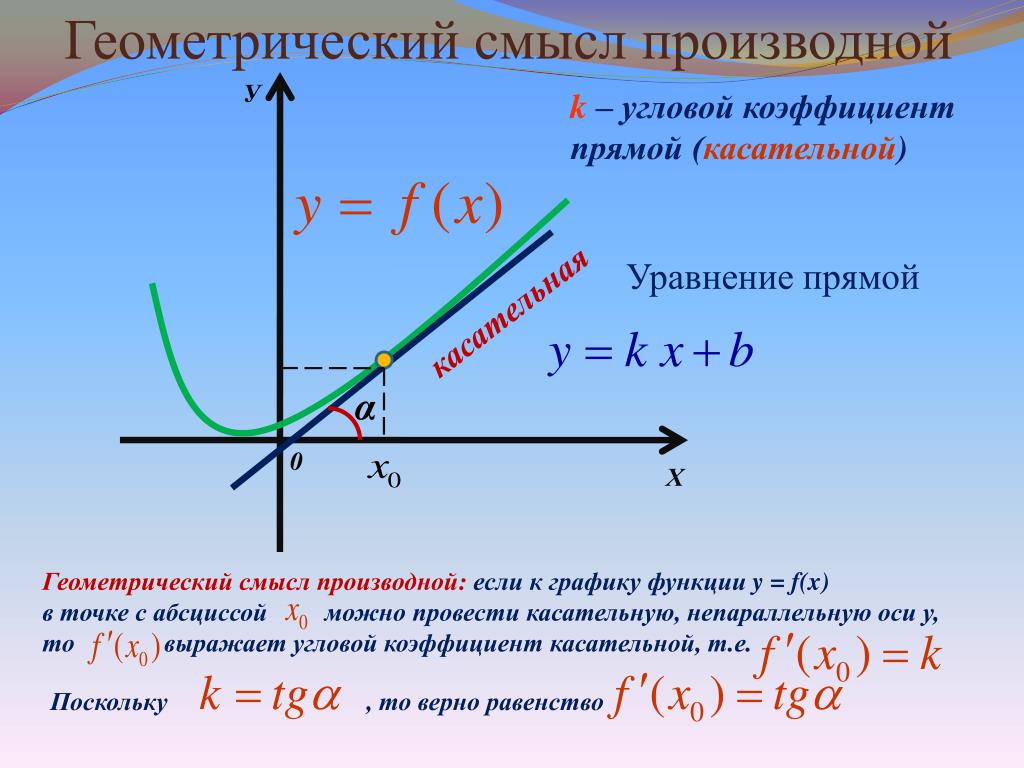 е.
е.
Замечание . Для сложной функции, являющейся суперпозицией трех функций y=F(f(φ(x))) , правило дифференцирования имеет вид
y′ x = y′ u u′ v v′ x ,
где функции v=φ(x) , u=f(v) и y=F(u) – дифференцируемые функции своих аргументов.
Теорема . Пусть функция y=f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x 0 . Пусть, кроме того, эта функция дифференцируема в указанной точке x 0 и ее производная в этой точке f′(x 0) ≠ 0 . Тогда в некоторой окрестности соответствующей точки y 0 =f(x 0) определена обратная для y=f(x) функция x=f -1 (y) , причем указанная обратная функция дифференцируема в соответствующей точке y 0 =f(x 0) и для ее производной в этой точке y справедлива формула
Таблица производных
Инвариантность формы первого дифференциала
Рассмотрим дифференциал сложной функции. Если y=f(x) , x=φ(t) – дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой
y′ t = y′ x x′ t .
По определению dy=y′ t dt , тогда получим
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx ,
dy = y′ x dx .
Итак, доказали,
Свойство инвариантности формы первого дифференциала функции : как в случае, когда аргумент x является независимой переменной, так и в случае, когда аргумент x сам является дифференцируемой функцией новой переменной, дифференциал dy функции y=f(x) равен производной этой функции, умноженной на дифференциал аргумента dx .
Применение дифференциала в приближенных вычислениях
Мы показали, что дифференциал dy функции y=f(x) , вообще говоря, не равен приращению Δy этой функции. Тем не менее с точностью до бесконечно малой функции более высокого порядка малости, чем Δx , справедливо приближенное равенство
Δy ≈ dy .
Отношение называют относительной погрешностью равенства этого равенства. Так как Δy-dy=o(Δx) , то относительная погрешность данного равенства становится как угодно малой при уменьшении |Δх| .
Учитывая, что Δy=f(x+δ x)-f(x) , dy=f′(x)Δx , получим f(x+δ x)-f(x) ≈ f′(x)Δx или
f(x+δ x) ≈ f(x) + f′(x)Δx .
Это приближенное равенство позволяет с ошибкой o(Δx) заменить функцию f(x) в малой окрестности точки x (т.е. для малых значений Δx ) линейной функцией аргумента Δx , стоящей в правой части.
Производные высших порядков
Определение . Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.
Обозначение второй производной функции y=f(x) :
Механический смысл второй производной . Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная f″(x) равна ускорению движущейся точки в момент времени x .
Аналогично определяется третья, четвертая производная.
Определение . n -й производной (или производной n -го порядка) функции y=f(x) называется производная от ее n-1 -й производной:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′ .
Обозначения: y″′ , y IV , y V и т.д.
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x 0 ,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
- Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями.
 Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0. - Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2.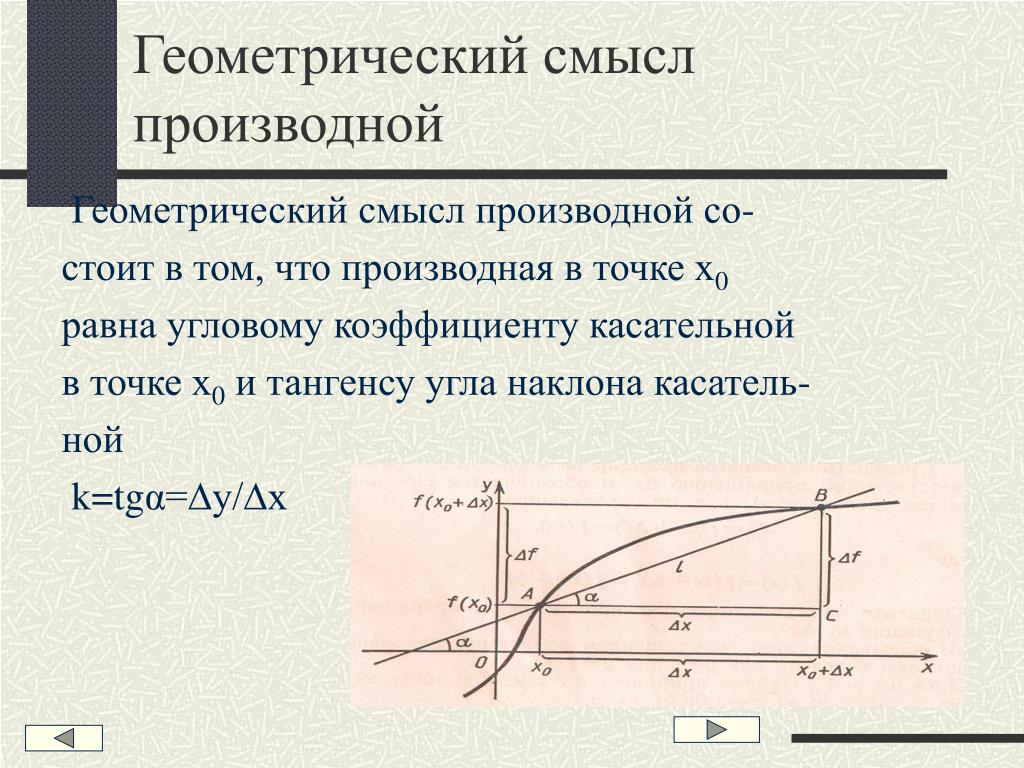 Именно в ней знак производной меняется с плюса на минус.
Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2).
 Т.е. большему значению аргумента соответствует меньшее значение функции.
Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.

- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.
Производная функции одной переменной.
Введение.
Настоящие методические разработки предназначены для студентов факультета промышленное и гражданское строительство. Они составлены применительно к программе курса математики по разделу «Дифференциальное исчисление функций одного переменного».
Разработки представляют собой единое
методическое руководство, включающее
в себя: краткие теоретические сведения;
«типовые» задачи и упражнения с подробными
решениями и пояснениями к этим решениям;
варианты контрольной работы.
В конце каждого параграфа дополнительные упражнения. Такая структура разработок делает их пригодными для самостоятельного овладения разделом при самой минимальной помощи со стороны преподавателя.
Механический и геометрический смысл
производной.
Понятие производной является одним из самых важных понятий математического анализа.Оно возникло еще в 17 веке. Формирование понятия производной исторически связано с двумя задачами: задачей о скорости переменного движения и задачей о касательной к кривой.
Эти задачи, несмотря на их различное содержание, приводят к одной и той же математической операции, которую нужно провести над функцией.Эта операция получила в математике специальное название. Она называется операцией дифференцирования функции. Результат операции дифференцирования называется производной.
Итак, производной функцииy=f(x)
в точкеx0 называется
предел (если он существует) отношения
приращения функции
к приращению аргумента
при
.
Производную принято обозначать
так:
.
Таким образом, по определению
Для обозначения производной употребляются
также символы
.
Механический смысл производной.
Если s=s(t)
– закон прямолинейного движения
материальной точки, то
есть скорость этой точки в момент времениt.
Геометрический смысл производной.
Если функция y=f(x)
имеет производную в точке,
то угловой коэффициент касательной к
графику функции в точке
равен
.
Пример.
Найдите производную функции
в точке=2:
1) Дадим точке
=2
приращение
.
Заметим, что.
2) Найдем приращение функции в точке =2:
3) Составим отношение приращения функции к приращению аргумента:
Найдем предел отношения при
:
.
Таким образом,
.
§ 2. Производные от некоторых
простейших функций.
Студенту необходимо научиться вычислять производные конкретных функций: y=x,y=и вообщеy=.
Найдем производную функции у=х.
т.е. (x)′=1.
Найдем производную функции
Производная
Пусть
тогда
Легко заметить закономерность в
выражениях производных от степенной
функции
приn=1,2,3.
Следовательно,
. (1)
Эта формула справедлива для любых действительных n.
В частности, используя формулу (1), имеем:
;
.
Пример.
Найдите производную функции
.
.
Данная функция является частным случаем функции вида
при
.
Используя формулу (1), имеем
.
Производные функций y=sin x и y=cos x.
Пусть y=sinx.
Разделим на ∆x, получим
Переходя к пределу при ∆x→0, имеем
Пусть y=cosx .
Переходя к пределу при ∆x→0, получим
;
.
(2)
§3. Основные правила дифференцирования.
Рассмотрим правила дифференцирования.
Теорема 1 . Если
функцииu=u(x)
иv=v(x)
дифференцируемы в данной точкеx,то в этой точке дифференцируема и их
сумма, причем производная суммы равна
сумме производных слагаемых: (u+v)”=u”+v”. (3)
(3)
Доказательство: рассмотрим функцию y=f(x)=u(x)+v(x).
Приращению ∆x аргумента x соответствуют приращения ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) функций u и v. Тогда функция y получит приращение
∆y=f(x+∆x)-f(x)=
=–=∆u+∆v.
Следовательно,
Итак, (u+v)”=u”+v”.
Теорема 2. Если функцииu=u(x) иv=v(x) дифференцируемы в данной точкеx, то в той же точке дифференцируемо и их произведение.При этом производная произведения находится по следующей формуле: (uv)”=u”v+uv”. (4)
Доказательство: Пусть y=uv, где u и v – некоторые дифференцируемые функции от x. Дадим x приращение ∆x;тогда u получит приращение ∆u, v получит приращение ∆v и y получит приращение ∆y.
Имеем y+∆y=(u+∆u)(v+∆v), или
y+∆y=uv+u∆v+v∆u+∆u∆v.
Следовательно, ∆y=u∆v+v∆u+∆u∆v.
Отсюда
Переходя к пределу при ∆x→0 и учитывая, чтоuиvне зависят от ∆x, будем иметь
Теорема 3 .
Производная частного двух функций равна
дроби, знаменатель которой равен квадрату
делителя, а числитель- разности между
произведением производной делимого на
делитель и произведением делимого на
производную делителя, т. е.
е.
Если
то
(5)
Теорема 4. Производная постоянной равна нулю, т.е. если y=C, где С=const, то y”=0.
Теорема 5. Постоянный множитель можно выносить за знак производной, т.е. если y=Cu(x), где С=const, то y”=Cu”(x).
Пример 1.
Найдите производную функции
.
Данная функция имеет вид
,
гдеu=x,v=cosx. Применяя правило
дифференцирования (4), находим
.
Пример 2.
Найдите производную функции
.
Применим формулу (5).
Здесь
;
.
Задачи.
Найдите производные следующих функций:
;
11)
2)
;
12)
;
3)
13)
4)
14)
5)
15)
6)
16)
7 )
17)
8)
18)
9)
19)
10)
20)
Производное определение и значение | Dictionary.com
- Основные определения
- Викторина
- Связанный контент
- Примеры
- Британский
- Медицинский
- Научный
Уровень сложности этого слова.
[ dih-riv-uh-tiv ]
/ dɪˈrɪv ə tɪv /
Сохранить это слово!
См. синонимы для: деривативный / деривативный на Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
прилагательное
производное.
не оригинал; вторичный.
существительное
то, что было получено.
Также называется производной формой .Grammar. форма, которая произошла от другой, как атом от атома.
Химия. вещество или соединение, полученное или рассматриваемое как производное от другого вещества или соединения.
Также называется дифференциальным коэффициентом; особенно британский, дифференциальный коэффициент .Математика. предел отношения приращения функции к приращению переменной в ней при стремлении последнего к 0; мгновенное изменение одной величины по отношению к другой, как скорость, которая является мгновенным изменением расстояния по отношению ко времени. Сравните первую производную, вторую производную.
Сравните первую производную, вторую производную.
финансовый контракт, стоимость которого определяется стоимостью базовых акций, облигаций, валюты, товаров и т. д. “ДОЛЖЕН” ВЫЗОВ?
Должны ли вы пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма обычно используется с другими глаголами для выражения намерения?
Иногда der·i·vate [der-uh-veyt] /ˈdɛr əˌveɪt/ .
Происхождение производного
Впервые записано в 1400–1450 гг.; позднесреднеанглийское производное от позднелатинского dērīvātīvus, эквивалентное латинскому dērīvāt(us) (см. происхождение) + суффикс -īvus; см. -ive
ДРУГИЕ СЛОВА ИЗ производного
производное, наречие, производное, существительное, не производное, прилагательное, существительное, не производное, ·tive·ly, наречие
un·de·riv·ative, прилагательноеun·de·riv·a·tive·ly, наречие
Слова рядом с производным
насмешка, насмешка, насмешка, производная, производная, производная , производная, производная, производная кривая, производная ископаемая, производная единица измерения
Dictionary. com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
Слова, относящиеся к производным
побочный продукт, родственный, вторичный, подчиненный, ответвление, результат, побочный эффект, волна, приобретенный, предковый, вызванный, родственный , скопированный, развитый, наследственный, подражательный, выведенный, выведенный, полученный, плагиат
Как использовать дериватив в предложении
Рони Исраэлов, президент инвестиционной компании Ndvr и автор нескольких научных статей о деривативах, говорит 2020 привел к значительному росту опционных контрактов на отдельные акции.
«Отправляемся в Вегас:» начинающим трейдерам опционов грозит расплата по мере того, как ралли акций технологических компаний угасает техническая коррекция в значительной степени может быть связана с «без сомнения, тем фактом, что все стало очень, очень дорого».
Куда дальше идут акции технологических компаний?|Энн Срейдерс|10 сентября 2020 г.
 |Fortune
|FortuneПозднее FT сообщила, что SoftBank получил торговую прибыль в размере около 4 миллиардов долларов от ставок основателя Масаеши Сона на деривативы на акции, ссылаясь на людей с непосредственным знанием дела.
Акции SoftBank упали после того, как их разоблачили как «кита Nasdaq»|Клэр Зиллман, репортер|7 сентября 2020 г.|Fortune
The Financial Times, Wall Street Journal и Zero Hedge сообщили, что SoftBank делал огромные ставки на технологические акции, используя деривативы на акции.
Акции SoftBank упали после того, как их разоблачили как «кита Nasdaq»|Клэр Зиллман, репортер|7 сентября 2020 г.|Fortune
Это производные контракты, которые инвестор, обычно страховая компания, может купить как способ дальнейшее хеджирование рисков, связанных со стихийными бедствиями.
Страховщики нервничают, поскольку ураган Лаура должен обрушиться на сушу как мощный шторм категории 4|Джереми Кан|26 августа 2020 г.
 |Fortune
|FortuneЭти фильмы следуют ряду рецептов производных боевиков.
Адаптация романов для молодежи посрамила популярные блокбастеры|Эми Циммерман|14 июня 2014|DAILY BEAST
По данным Национального института по борьбе со злоупотреблением наркотиками, производное морфина является наркотиком, вызывающим наибольшее привыкание в своем классе.
Галлюцинации избавления от героиновой зависимости|Эбби Хэглейдж|4 мая 2014|DAILY BEAST
Конечно, они тоже производные, как если бы Серра был его собственным учеником или фальсификатором своих собственных произведений.
Железный человек XVII|Блейк Гопник|24 января 2014|DAILY BEAST
Новая идея сделать вышеупомянутую оболочку Dorito более острой и добавить немного лайма в лучшем случае является производной.
У Америки закончились идеи?|Дэниел Гросс|27 августа 2013 г.|DAILY BEAST
Некоторые из этих владельцев находятся за пределами вашей страны, поэтому вы даже не получаете производных преимуществ.

Ответ Рогоффа и Рейнхарта|Меган МакАрдл|17 апреля 2013|DAILY BEAST
Те, кто считает, что виды были основой древних ладов или гармоний, должны рассматривать тональности как производные.
Лады древнегреческой музыки|Дэвид Биннинг Монро
Производное право в этом случае зависит не только от законов, но и от словосочетаний; и словосочетания не могут быть сведены ни к какому закону.
Система логики: рациональная и индуктивная|Джон Стюарт Милль
В рассматриваемом примере мы знаем причины, от которых зависит единообразие производной.
Логическая система: рациональная и индуктивная|Джон Стюарт Милль
Одни свойства являются конечными, другие производными; у одних невозможно указать причину, но другие явно зависят от причин.
Система логики: рациональная и индуктивная|Джон Стюарт Милль
Это производное слово от алгонкинского, а ган — предпоследний слог оджибвского термина Са-г—ган, озеро.

Индеец в своем вигваме|Генри Р. Скулкрафт
Британский словарь определений производных
производных
/ (dɪˈrɪvətɪv) /
производных19; полученный
на основе или с использованием других источников; неоригинальный или первичный
скопированный у других, особенно рабски; плагиат
существительное
термин, идея и т. д., которые основаны на другом слове того же класса или происходят от него
слово, происходящее от другого слова структурно родственное соединение хлороформ является производным метана
математика
- Также называется: дифференциальный коэффициент, первая производная изменение функции f(x) относительно бесконечно малого изменения независимой переменной x; предел [f(a + Δ x)–f(a)] / Δ x при x = a, поскольку приращение Δ x стремится к 0. Обозначения: df(x)/d x, f′(x ), Df(x) производная от x n равна nx n–1
- скорость изменения одной величины по отношению к другой скорости является производной от расстояния по времени
финансирование финансового инструмента, такого как фьючерсный контракт или опцион, цена которого во многом определяется товаром, валютой
психоанальная деятельность, представляющая собой выражение скрытых побуждений и желаний путем направления их в социально приемлемые формы
Производные формы производного
производного, наречие Английский словарь Коллинза – полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins
Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
© William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins
Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Медицинские определения производных
производных
[dĭ-rĭv′ə-tĭv]
2 90.
Что-то полученное или произведенное путем модификации чего-то другого.
Химическое соединение, которое может быть получено из другого соединения аналогичной структуры в одну или несколько стадий.
прил.
Полученный в результате, охарактеризованный или использующий производное.
Медицинский словарь Стедмана The American Heritage® Copyright © 2002, 2001, 1995, компания Houghton Mifflin. Опубликовано компанией Houghton Mifflin.
Научные определения производной
производной
[ di-rĭv’ə-tĭv ]
В исчислении – наклон касательной к кривой в определенной точке кривой. Поскольку кривая представляет собой функцию, ее производную также можно рассматривать как скорость изменения соответствующей функции в данной точке. Производные вычисляются с помощью дифференцирования.
Производные вычисляются с помощью дифференцирования.
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Определение производной
Определение производной Производная
Наклон секущей линии
Пример:
Рассмотрим функцию
у = f(х) = х 2
затем секущая линия от x = 2 до x = 4 определяется линией, соединяющей две точки (2,f(2)) и (4,f(4)). Эта линия имеет наклон
f(4) – f(2) 16 –
4
подъем/бег =
знак равно
= 6
4 –
2
4 – 2
В общем случае мы даем следующее определение
| Определение наклона секущей линии Пусть
y = f(x) — функция. е(б) – е(а) |
Производная
Если вместо выбора (4,f(4)), мы выберем (2 + h,f(2 + h)) в качестве второго мы имеем, что наклон секущей равен
f(2 + h) – f(2) f(2 + h) –
f(2)
=
(2 + ч) –
2
ч
(2 + ч) 2 – 2 2 4 + 4ч + ч 2 –
4
знак равно
=
час
ч
4h + h 2
знак равно
= 4 + ч
час
Что произойдет, если мы позволим h приблизиться к 0? Геометрически это называется
наклон касательной к f(x)
при x = 2. Аналитически это называется Производная от f(x) при x =
2. В приведенном выше примере ограничение равно 4.
Мы говорим, что f'(2) = 4.
Аналитически это называется Производная от f(x) при x =
2. В приведенном выше примере ограничение равно 4.
Мы говорим, что f'(2) = 4.
Определение производной Производная (f ‘(х) или df/dx) функции f(x) при x = c определяется по |
Упражнения: Найти f следующих функций
А. f(x) = 2x – 1 при x = 2
Б. f(x) = x 2 при x = 1
C. f(x) = 1/x при x = 3
D. f(x) = при x = 4
Мы вызываем функцию, которая переводит значение x в производную по значению x производная функции.
Пример
Найдите производную от
3
f(x) =
Икс
Решение
Находим предел
Теперь умножьте числитель и знаменатель на x(x + з) чтобы получить
Упражнения: Найти f'(x) для следующих функций
А. f(x) = x 3
f(x) = x 3
Б. f(x) = 4 – x
C. f(x) =
Альтернативная форма производной
Есть это еще один способ записать производную. Так как производная есть ограничивающий наклон секущей, мы можем считать, что первая точка в точке c фиксирована. а затем второй точкой будет переменное значение x, стремящееся к c. Тогда наклон касательной будет
Если функция не является непрерывной, то числитель либо не существует, либо не будет стремиться к нулю, а знаменатель будет приближаться нуль. Это приводит нас к следующей теореме.
Теорема Если f(x) — дифференцируемая функция при x = c
тогда f (х)
непрерывна в точке x =
в. |
Обратная теорема не всегда верна. Что существуют непрерывные функции, которые не являются дифференцируемыми. За например, пусть
f(x) = | х |
От на графике мы видим, что наклон секущей будет равен -1 влево 0 и 1 справа от 0. В начале координат производная не определена хотя f(x) непрерывна в нуле.
Когда функция дифференцируема?
Ответ: Если он непрерывен, не имеет острых краев и касательная линия не вертикальная.
Назад на главную страницу исчисления
Назад к математике домашняя страница отдела
электронная почта Вопросы и предложения
Что такое производная? Производные Определение и значение
Explore Derivatives
Если у вас есть вопросы о деривативах — например, что это такое, почему они используются и как их найти — вы попали по адресу! Производные являются фундаментальной концепцией в вашем путешествии по исчислению, поэтому не стесняйтесь потратить на это некоторое время.
Мы не хотим переусердствовать, но мы думаем, что вы извлечете большую пользу из приведенных ниже деталей (извините, нам пришлось).
Впрочем, хватит шуток! Время сосредоточиться на наших сильных сторонах.
Давайте научимся математике, хорошо?
Что такое производная?
Производная — один из важнейших инструментов дифференциального исчисления. Производные дают нам гибкий способ измерения точных скоростей изменений, что действительно здорово!
Вы можете использовать производные инструменты во многих различных сценариях, в том числе:
- Производные функций
- Производные выражения
- Производные интегралов
- Первые производные и вторые производные
- Производные высшего порядка
Значение производных
Проще говоря, производные показывают нам мгновенную скорость изменения в конкретной точке на графике функции. Это означает, что мы можем с относительной легкостью получить довольно надежную информацию (в зависимости от уровня вычислений, которые вы выполняете!).
Кроме того, возможность находить производные дает нам возможность более точно моделировать такие вещи, как скорость, сила, ускорение и т. д., поэтому они используются не только для того, чтобы бросить вам вызов во время выполнения домашних заданий. Производные на самом деле имеют решающее значение для внутренней работы очень многих вещей вокруг нас.
Например: допустим, вы находитесь на бейсбольном матче и хотите узнать скорость изменения скорости мяча, когда он покидает руку питчера. В этом случае вы захотите взять производную!
Производная и наклон
Трудно говорить о производных, не связывая их с наклоном.
Почему? Потому что нахождение производной на самом деле эквивалентно нахождению наклона касательной в определенной точке функции.
Забавный факт: то, как мы вычисляем производную, зависит от того, как мы вычисляем наклон! Это подъем над пробегом, но с несколькими интересными поворотами.
Определение производной
Итак, зная контекст производных и то, что они нам говорят, как мы определяем «производную»? Это наше определение:
Производная : ( n ) скорость изменения количества по отношению к изменению переменной; результат дифференцирования
Достаточно просто, правда?
Производные в математике и деривативы в финансах
Для ясности: мы здесь, чтобы рассказать вам о деривативах в математике, но вы также можете найти информацию о деривативах в финансах или инвестициях.
Если это то, что вы ищете, вам нужно знать, что «дериватив» в финансах — это контракт, стоимость которого определяется динамикой актива, процентной ставкой или другим «базовым активом».
Но мы здесь, чтобы учить математику, так что давайте займемся уравнениями!
Как будут выглядеть уравнения с производными?
Мы можем говорить о «почему» деривативов до посинения, но теперь пришло время сосредоточиться на «как» и посмотреть, как деривативы будут выглядеть на странице.
В зависимости от того, берете ли вы производную функции, интеграла или выражения, ваш точный порядок действий будет отличаться. Но ваши стартовые задачи, вероятно, будут выглядеть примерно так: 92}$$
Примечание. Это всего лишь примеры, а НЕ решения этих проблем!
Пока вы работаете с этими уравнениями, не забывайте о правилах дифференцирования, которые помогут вам более стратегически манипулировать вычислениями!
| Постоянное кратное свойство производных | $$\frac{d}{dx}\left(c\times f(x)\right)=c\times\frac{d}{dx}\left(f(x) \right)$$ |
| Правило сумм для производных | $$\frac{d}{dx}\left(f(x) + g(x)\right)=\frac{d}{dx}\left( f(x) \right)+\frac{d }{dx}\left( g(x) \right)$$ |
| Разностное правило для производных | $$\frac{d}{dx}\left(f(x) – g(x)\right)=\frac{d}{dx}\left( f(x) \right)-\frac{d }{dx}\left( g(x) \right)$$ |
| Правило произведения для производных | $$\frac{d}{dx}\left(f(x)\times g(x)\right)=\frac{d}{dx}\left( f(x) \right)\times g( x)+f(x)\times\frac{d}{dx}\left( g(x) \right) $$ |
| Частное правило для производных | $ $ \ frac {d} {dx} \ left (\ frac {f (x)} {g (x)} \ right) = \ frac {\ frac {d} {dx} \ left (f (x) \right)\times g(x)-f(x)\times\frac{d}{dx}\left( g(x) \right)}{(g(x))^{2}}$$ 9{-1}\влево(х\вправо)\вправо)}$$ |
Как вы понимаете, существует множество уравнений для производных, так что давайте уточним!
Производная функции
Нахождение производных функций обычно является отправной точкой вашего приключения с дифференцированием, поэтому обязательно освойте эти процедуры, прежде чем переходить к ограничениям и более сложным задачам дифференцирования.
Как и во всем в жизни, во время работы полезно помнить о своих целях! Итак, какова наша цель с производными функций?
Когда мы берем производную функции, это потому, что мы хотим найти:
- Скорость изменения функции
- Наклон касательной в определенной точке функции
Вскоре мы рассмотрим, как это сделать; но сначала давайте расшифруем кое-что еще, что вы можете услышать при изучении производных функций.
Производная по x
Возможно, вы слышали, как учитель математики говорил о производной «по» переменной (вначале это обычно $$x$$), и вы не совсем уверены, что это действительно означает.
Если мы работаем с функцией — $$f(x)$$ — и хотим найти «производную по $$x$$», это просто означает, что мы ищем скорость при который $$f$$ изменяется при изменении $$x$$. По сути, это означает, что мы действительно фокусируемся на переменной $$x$$ и на том, как она влияет на нашу функцию.
Процесс нахождения производной функции
Если вы помните ключевые термины из своего словаря, то помните, что процесс нахождения производной называется «дифференцированием». (Мы можем помочь, если вам нужно освежить словарный запас!)
(Мы можем помочь, если вам нужно освежить словарный запас!)
Забавный факт: производная функции — это тоже функция, а ее значения — соответствующие производные в точке. По существу, если мы определяем производную функции $$f$$ при любом значении $$x$$, то наша производная $$f'(x)$$ представляет собой функцию, которая выводит значение $$f'(x )$$ для любого входа $$x$$ (по крайней мере, для которого эта производная существует).
Фактические шаги дифференциации будут варьироваться в зависимости от индивидуальной проблемы и сложности — мы можем подробно объяснить в приложении! — но вот обзор:
- Возьмите производную от обеих частей уравнения
- Использование правил дифференцирования (также называемых «формулами производных»)
- Найдите производную
- Упростите выражение, если необходимо
Нужно больше? Перейдите, чтобы глубже погрузиться в производные функций.
Не забывайте: Вы также можете найти производные от выражений и интегралов, которые будут выглядеть немного иначе.
Что такое f’(x)?
$$f’(x)$$ обозначает производную. Итак, когда вы начнете брать производную функции $$f(x)$$, ваше решение — производная — будет помечено как $$f’(x)$$. Вы также можете увидеть $$f’(x)$$ в виде $$\frac{dy}{dx}$$ в определенных сценариях.
Будьте осторожны при чтении, потому что легко пропустить этот маленький апостроф. Когда мы видим $$f’(x)$$, мы видим производную, но $$f(x)$$ говорит нам, что это функция!
Производная и предельная: в чем разница?
Производные и лимиты не являются взаимозаменяемыми терминами, но есть некоторое совпадение.
Разница зависит от того, говорите ли вы о производных и пределах определенного значения функции или о функции в целом. Поясним:
- Производная функции в точке — это особый вид предела в этой точке — другими словами, всякая производная есть предел!
- Численно значение производной в определенной точке функции говорит нам о мгновенной скорости изменения функции в этой точке.

- Геометрически значение производной в определенной точке функции представляет собой наклон линии, проходящей касательной к графику функции в этой точке.
- Численно значение производной в определенной точке функции говорит нам о мгновенной скорости изменения функции в этой точке.
- Предел функции в точке представляет поведение функции вокруг этой точки. По сути, если поведение предсказуемо, то предел существует. 92дт$$
Вот как мы решаем первую практическую задачу в приложении:
/
Застряли на других производных практических задачах? Отсканируйте проблему с помощью приложения Photomath, чтобы мы могли помочь вам с каждым шагом!
Часто задаваемые вопросы
Каковы два определения производной?
Производная описывается либо как скорость изменения функции, либо как наклон касательной в определенной точке функции.
Что такое производная простыми словами?
Производная говорит нам о скорости изменения определенной переменной.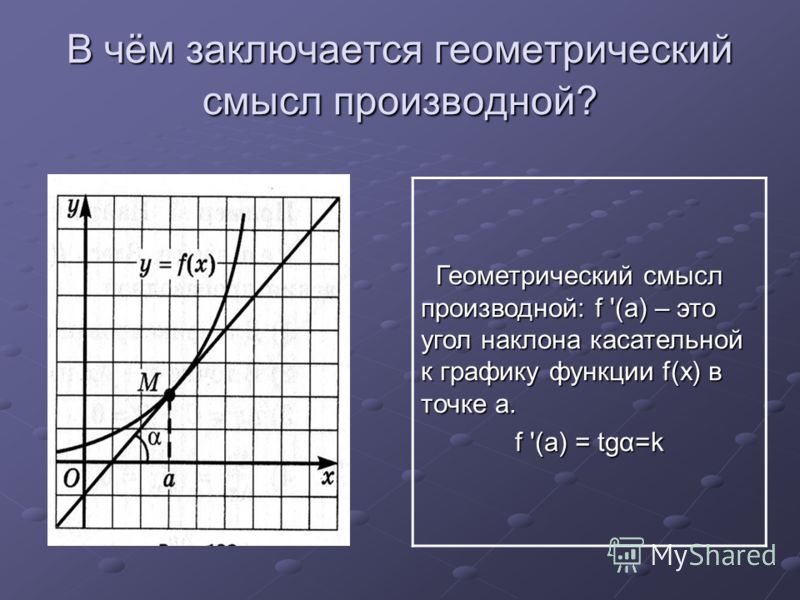

 19)
19) 21), находим
21), находим
 Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0. Т.е. большему значению аргумента соответствует меньшее значение функции.
Т.е. большему значению аргумента соответствует меньшее значение функции.
 |Fortune
|Fortune |Fortune
|Fortune

 затем
наклон секущей между x
= а и х
= б равно
затем
наклон секущей между x
= а и х
= б равно 
