Главная
Собственный момент инерции это: Национальный исследовательский университет «Высшая школа экономики»

Собственный момент инерции это: Национальный исследовательский университет «Высшая школа экономики»

3}{48}[/math]

Содержание

Момент инерции двутавра и профилей

Дополнительная информация

В приложенном файле – геометрические характеристики других сечений (из справочника по сопротивлению материалов /Фесик С.П. – 1982)


Связанные статьи

Момент инерции цилиндра, теория и примеры

Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:

   

где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.

Для получения формулы расчета момента инерции однородного цилиндра, мы его представим как совокупность бесконечно тонких дисков, а диск, в свою очередь – совокупность бесконечно тонких колец. Поэтому мы сначала получим выражение для момента инерции кольца, затем диска и только в самом окончании цилиндра.

Момент инерции тонкого кольца

Пусть кольцо имеем радиус R. Его называют бесконечно тонким, если его ширина и толщина много меньше радиуса. Пусть кольцо вращается относительно оси Z, перпендикулярной плоскости кольца и проходит через центр кольца (рис.1).

Выделим на кольце элементарную массу (), – плотность кольца; – элементарный объем кольца. Для нахождения момента инерции кольца нам следует найти интеграл (1). Все элементарные массы находятся на одном расстоянии от оси, то есть распределение массы кольца имеет цилиндрическую (осевую) симметрию.

   

Момент инерции бесконечно тонкого однородного диска

Пусть диск имеет радиус R. Он вращается относительно оси, которая проходит через его центр инерции, перпендикулярно его плоскости. Диск представим как систему бесконечно тонких колец, радиусы которых изменяются от нуля до R. Одно из таких колец изображено на рис.2.

Так как момент инерции тонкого кольца мы уже нашли, то его возьмем за элементарный:

   

где – масса выделенного кольца, равная:

   

Найдем момент инерции бесконечно тонкого диска, учитывая: :

   

массу бесконечно тонкого диска можно считать равной:

   

тогда момент инерции диска равен:

   

Момент инерции цилиндра

Для того, чтобы найти момент инерции однородного цилиндра, вращающегося относительно своей оси, представим его как совокупность дисков, толщиной .

Формула (7) справедлива для диска имеющего толщину, поэтому в качестве элементарной массы мы возьмем диск. Тогда имеем:

   

где – высота цилиндра. Тогда момент инерции цилиндра относительно его собственной оси равен:

   

где масса цилиндра равна:

   

Примеры решения задач

Новосибирский государственный архитектурно-строительный университет – Сибстрин

НГАСУ (Сибстрин) занял 17 призовых мест во Всероссийском конкурсе выпускных квалификационных работ в области строительства

Подведены итоги Всероссийского конкурса выпускных квалификационных работ в области строительства, защищенных в 2020 году. Его организатором является Международная общественная организация содействия строительному образованию (АСВ) при содействии Федерального учебно-методического объединения в системе высшего образования по укрупненной группе специальностей и направлений подготовки 08.
00.00 «Техника и технологии строительства». На конкурс, который проводится в дистанционном формате на базе НИУ МГСУ, от НГАСУ (Сибстрин) было направлено 37 работ. По результатам участия университета во Всероссийском конкурсе, выпускные квалификационные работы в области строительства…

Студенты направления «Социология» отчитались о практике в солнечной Турции

23 ноября 2021 года состоялась конференция по итогам летней учебной практики студентов направления «Социология». Благодаря соглашению между нашим университетом и туристической компанией Kilit Global с 2020 года в учебном процессе кафедры Экономики, управления, социологии и педагогики НГАСУ (Сибстрин) задействованы ведущие туроператоры Новосибирска. Это дало возможность студентам-социологам продуктивно провести лето в солнечной Турции. В работе конференции принимали участие директор института международной деятельности Наталья Синеева, директор института цифровых и инженерных технологий Лилия Ильина и заведующая кафедрой Экономики, социологии и педагогики Наталья Нижальская, а также студенты разных групп и курсов института цифровых и инженерных технологий.

7 декабря пройдут встречи кандидатов на должность ректора с сотрудниками и студентами университета

7 декабря 2021 года (вторник) пройдут встречи кандидатов на должность ректора Новосибирского государственного архитектурно-строительного университета (Сибстрин) с сотрудниками и студентами. Встреча Косолаповой Ирины Анатольевны: в 12.00 в ауд. 362 Встреча Сколубовича Юрия Леонидовича: в 14.00 в ауд. 239 Напоминаем, что 10 декабря 2021 года (пятница) состоится конференция научно-педагогических работников, представителей других категорий работников и обучающихся НГАСУ (Сибстрин) по выборам ректора университета. Начало регистрации: в 13.30 Начало конференции: в 14.00

Как рассчитать момент инерции балки?

font-size:15px;
}
]]>

How to Calculate Moment of Inertia of a Beam Section
(Второй момент области)

Before we find the moment of inertia of a beam section (or second moment of area of a beam section) , его центроид (или центр масс) должен быть известен. Например, если момент инерции сечения относительно его горизонтали (XX) ось требовалась тогда вертикальная (и) сначала потребуется центроид (Пожалуйста, просмотрите наш учебник о том, как вычислить центр тяжести луча Раздел).

Прежде чем мы начнем, если вы искали наш Калькулятор свободного момента инерции пожалуйста, нажмите на ссылку, чтобы узнать больше. Это вычислит центр тяжести, меня, и другие результаты и даже покажут вам пошаговые расчеты! Но сейчас, давайте посмотрим на пошаговое руководство и пример того, как рассчитать момент инерции:

шаг 1: Сегментируйте сечение балки на части

При расчете площади момента инерции, мы должны рассчитать момент инерции меньших сегментов. Попробуйте разбить их на простые прямоугольные секции. Например, рассмотрите раздел I-луча ниже, который также был показан в нашем Centroid Tutorial. Мы решили разделить этот раздел на 3 прямоугольные сегменты:

шаг 2: Рассчитать нейтральную ось (Не Доступно)

Нейтральная ось (Не Доступно) или горизонтальная ось ХХ находится в центре тяжести или центре масс. В нашем Centroid Tutorial, ранее было установлено, что центр тяжести этого участка 216.29 мм от нижней части секции.

Попробуйте наш бесплатный калькулятор момента инерции:

Калькулятор свободного момента инерции

шаг 3: Рассчитать момент инерции

Для расчета общего момента инерции сечения нам нужно использовать “Теорема о параллельной оси”:

Так как мы разделили его на три прямоугольные части, мы должны рассчитать момент инерции каждого из этих участков. Широко известно, что момент уравнения инерции прямоугольника относительно его оси центроида просто:

Момент инерции других форм часто указывается на лицевой / оборотной стороне учебников или в этом руководстве. момент инерции формы. Однако прямоугольная форма очень распространена для секций балки, так что, наверное, стоит запомнить.

Теперь у нас есть вся информация, необходимая для использования “Теорема о параллельной оси” и найти общий момент инерции сечения двутавровой балки. В наш момент инерции пример:

Итак, у нас есть руководство по расчету площади момента для сечений балок.. Этот результат имеет решающее значение в проектировании конструкций и является важным фактором в отклонении луча. Мы надеемся, что вам понравился урок, и с нетерпением ждем ваших комментариев.. (Проверить moment of inertia formula)

БОНУС: Используя наш Калькулятор Момента Инерции

There are many ways in terms of how to calculate moment of inertia, one of them is using software to make the process easier.

Аккаунт SkyCiv показывает полные расчеты момента инерции. Этот интерактивный модуль покажет вам пошаговые расчеты того, как найти момент инерции.:

альтернативно, вы можете увидеть результаты нашего Калькулятор свободного момента инерции проверить свою работу. Это позволит вычислить все свойства вашего поперечного сечения и является полезным справочным материалом для расчета центроида., Площадь, и момент инерции секций вашей балки!

Калькулятор свободного момента инерции

Часть 16 — Свойства тензора инерции твердого тела / Хабр


  1. Что такое тензор и для чего он нужен?
  2. Векторные и тензорные операции. Ранги тензоров
  3. Криволинейные координаты
  4. Динамика точки в тензорном изложении
  5. Действия над тензорами и некоторые другие теоретические вопросы
  6. Кинематика свободного твердого тела. Природа угловой скорости
  7. Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
  8. О свертках тензора Леви-Чивиты
  9. Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
  10. Получаем вектор угловой скорости. Работаем над недочетами
  11. Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
  12. Параметры Родрига-Гамильтона в кинематике твердого тела
  13. СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
  14. Нестандартное введение в динамику твердого тела
  15. Движение несвободного твердого тела
  16. Свойства тензора инерции твердого тела
  17. Зарисовка о гайке Джанибекова
  18. Математическое моделирование эффекта Джанибекова

Начав рассматривать

динамику твердого тела мы столкнулись интересной тензорной величиной, а именно

называемой

тензором инерции твердого тела

. Кроме того,

мы выяснили

, что привычный из курса теоретической механики момент инерции твердого тела, при его вращении вокруг неподвижной оси, получается из тензора инерции с помощью простой формулы

Рассмотрим подробнее свойства тензора инерции твердого тела. И для начала изучим механические величины, вычисление которых, так же как и приведение сил инерции к данному центру, приводит к понятию тензора инерции.

Моментом количества движения материальной точки (МКД) относительно данного центра

называют вектор, равный

Для твердого тела, при вращении вокруг полюса МКД элементарного объема

или в тензорной форме

Интегрируя (3) получим МКД твердого тела относительно центра

В соответствии с (4), тензор инерции есть линейный оператор, связывающий МКД твердого тела с его угловой скоростью.

Кинетическая энергия элементарного объема тела

что эквивалентно тензорному соотношению

Интегрируя последнее выражение по всему объему тела получаем выражение кинетической энергии

В выражении (5), как видно, снова фигурирует тензор инерции

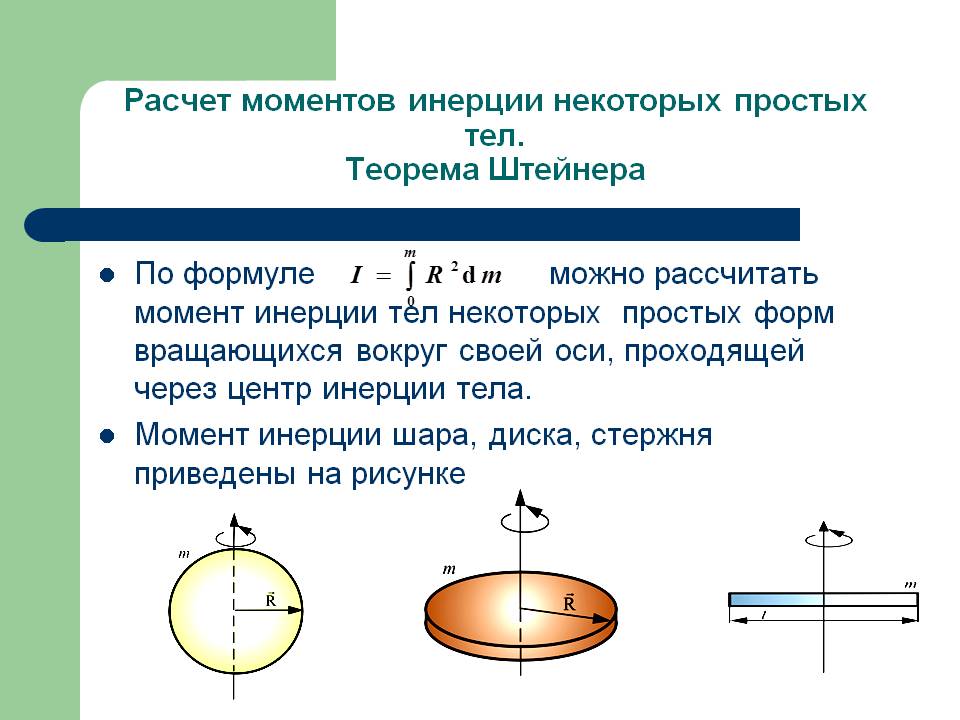. При вращении тела вокруг неподвижной оси, в соответствии с выражением угловой скорости через конечный поворот тела

выражение (5) трансформируется в

Формула (6) — кинетическая энергия твердого тела при вращательном движении, а

, в соответствии с (2), момент инерции тела относительно оси, задаваемой ортом

.

Легко показать, что тензор (1) не является симметричным. Однако, в декартовых координатах тензор инерции есть симметричный тензор, и исходя из этого факта выводятся все основные его свойства. Вместе с тем, мы не могли не заметить, что в выражениях (2) и (5) фигурирует величина вида

Полученный тензор (7) является симметричным ковариантным тензором 2-го ранга, так как нетрудно убедится в справедливости равенства

. Будем называть тензор (7)

ковариантным тензором инерции

. С учетом выражения (7) можно переписать выражение (2) для осевого момента инерции через контравариантные компоненты орта оси вращения

Автор не встретил в литературе только что введенного термина, но поскольку из симметричности (7) вытекают все основные свойства тензора инерции, ввод данного понятия, как будет показано ниже, вполне оправдан.

Покажем, для начала, что тензор (7), в силу своей симметричности, имеет действительные собственные значения. Пусть

— произвольное собственное число, которому соответствует собственный вектор

. Тогда справедливо соотношение

Допустив комплексные собственные числа и собственные векторы, умножим (9) слева на сопряженнй собственный вектор

Выполним комплексное сопряжение (10)

Здесь мы учитываем что компоненты (7) — действительные числа, а значит операция сопряжения эквивалентна транспонированию. Так как тензор (7) симметричный,

, то есть, с учетом (10)

или, окончательно

Равенство (12) справедливо, если

— действительное число.

Так как тензор (7) представлен матрицей в трехмерном пространстве, он имеет три действительных собственных числа , которым соответствуют действительные же собственные векторы , соответственно, можно записать тензорные соотношения

Умножим скалярно каждое из уравнений (13) на соответствующий собственный вектор

Поделив обе части уравнений (14) на квадрат модуля соответствующего собственного вектора, получим

Очевидно, что

контравариантные компоненты некоторых ортов. Значит в (15), согласно (8), в качестве собственных чисел ковариантного тензора инерции, представлены моменты инерции тела относительно осей

и

Кроме того, собственные векторы

и

образуют ортогональную тройку векторов. Действительно, проведем цепочку преобразований, с участием любой пары собственных векторов

Учитывая, что

, получаем условие

которое, в силу того, что в общем случае

, справедливо, когда скалярное произведение собственных векторов равно нулю

Это означает, что

. Повторяя доказательство для любой пары собственных векторов, получим, что они действительно ортогональны друг другу.

По результатам предыдущего параграфа можно сказать, что с твердым телом связана ортогональная система координат, оси которой

и

направлены вдоль собственных векторов ковариантного тензора инерции. В этих осях, в соответствии с определением собственных значений, ковариантный тензор инерции приводится к диагональному виду

В диагонали стоят моменты инерции, вычисляемые по формулам (17). Эти моменты инерции называют

главными моментами инерции твердого тела

, а оси, направление которых задается векторами

и

—

главными осями инерции

.

Предположим, что нам известен центральный (вычисленный относительно центра масс тела) тензор инерции

. Допустим, что мы хотим вычислить тензор инерции относительно точки

, отстоящей от центра масс в направлении известного вектора

. В этом случае радиус-вектор элементарного объема тела относительно точки

можно определить как сумму

где

— радиус вектор элементарного объема тела относительно центра масс

Подставим (18) в (1)

Здесь мы учитываем, что интегралы вида

задают положение центра масс тела относительно центра масс, то есть равны нулю. Окончательно получаем выражение для тензора инерции

определяющее тензор инерции относительно произвольной точки

через тензор инерции относительно центра масс. Выражение (19) называют

теоремой Гюйгенса-Штейнера

. Приведенное доказательство этой теоремы выполнено в самой общей форме.

В декартовых координатах метрика задается единичной матрицей, то есть формально

В этом случае совпадают выражения для тензора инерции и ковариантного тензора инерции

Поэтому в декартовых координатах симметричен и тензор инерции, и для него справедливы вышеперечисленные свойства, связанные с собственными значениями и собственными векторами. В декартовых координатах тензор инерции представляется матрицей

или

где диагональные элементы называют осевыми моментами инерции, а прочие элементы — центробежными моментами инерции.

Материал данной статьи — авторская работа. В литературе господствует подход к изучению тензора инерции связанный с использованием декартовых координат. Нами же рассмотрен самый общий подход и мы убедились, что свойства тензора инерции и теорема Гюйгенса-Штейнера могут быть получены в произвольных координатах. Все приведенные в статье формулы переходят в общеизвестные из курса теоретической механики при использовании декартовой метрики.

Upd: Нашел упоминание о ковариантном тензоре инерции на каком-то богом забытом сайте. Что ж, это подтверждает идею, использованную мной в данной статье

Продолжение следует…

Проектирование прямоугольного перекрытия. Подбор профилей балок, образующих перекрытие. Расчет напряжения, страница 3

Проектирование прямоугольного перекрытия. Подбор профилей балок, образующих перекрытие. Расчет напряжения, страница 3 Другие предметы \ Проектирование

Обозначения к таблице

h

п – высота профиля;

b – ширина головки;

s – толщина стенки;

f – площадь сечения;

I

x – собственный момент инерции;

у

0 – отстояние нейтральной оси от нижней кромки профиля.

Подбор профиля БГН

Это несколько больше требуемого.

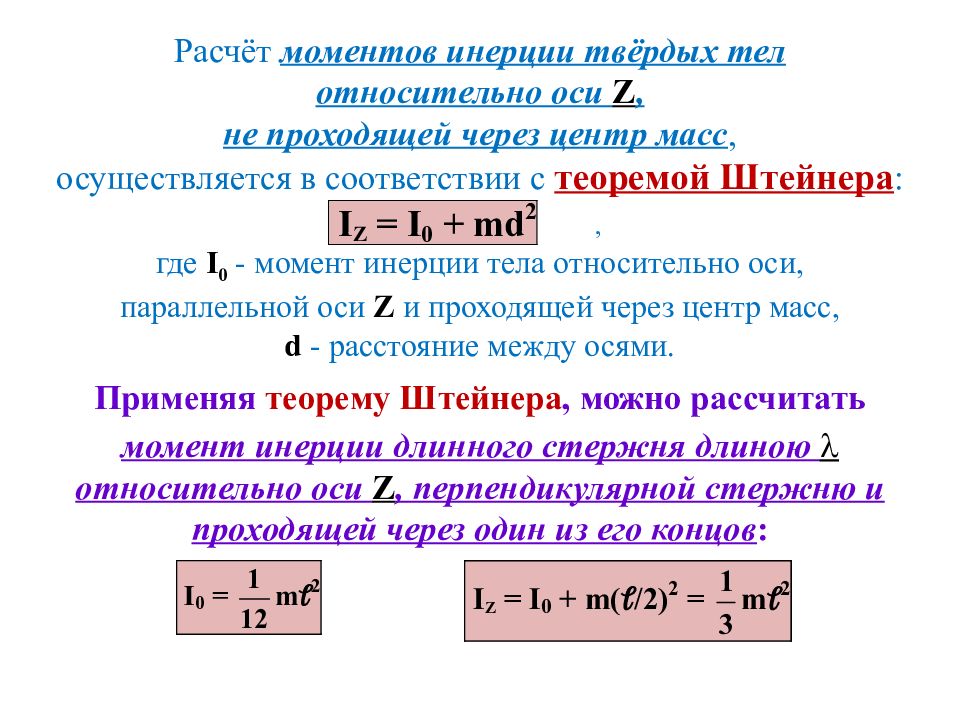
Рассчитаем момент сопротивления полособульба № 18б с присоединённым пояском. Ширина пояска принимается равной меньшей из двух величин: расстояния между двумя соседними БГН (в нашем примере 0,5 м) или 1/6 длины пролёта БГН (которая равна половине ширины перекрытия, т.е. 3 м; 1/6 длины пролёта составляет также 0,5 м).

Расчёт ведём в стандартной табличной форме.

Расчёт геометрических характеристик балки главного направления

Пояснения к таблице.

f – площадь связи,

z – отстояние от оси сравнения, которая у нас принята на линии соединения профиля с пластиной,

i – собственный момент инерции,

А – площадь профиля с пояском,

В – статический момент относительно оси сравнения,

С – момент инерции относительно этой оси.

Положение нейтральной оси е = В/А.

Наименования

f, см2

z, см

fz

fz2

i

Профиль

25,8

10,81

278,9

3015

837

Поясок

45

-0,45

-20,3

9

3

Суммы

А = 70,8

е = 3,65

В = 258,6

С = 3864

Подбор профиля перекрёстной связи в первом приближении

 Подбор профиля перекрёстной связи

Величина коэффициента с определяется по таблице из справочника в зависимости от числа перекрёстных связей m и от условий закрепления балок главного направления.

Если m = 1, с = 0,932 – при шарнирном опирании обоих концов, с = 1,310 – при жёсткой заделке, с = 1,165 – если один конец балки главного направления опирается шарнирно, а другой жёстко заделан.

Заметим, что прочность ПС пока не учитывается.

 

Одинаковый момент инерции могут иметь различные профили. Наиболее рациональным из них будет тот, который обладает наибольшим моментом сопротивления. Для этого профиль должен иметь максимальную высоту h. С точки зрения восприятия изгибающих моментов выгоднее всего увеличивать площадь меньшего пояска при минимально возможной площади стенки. Но площадь стенки должна, во-первых, обеспечивать восприятие касательных усилий (перерезывающих сил), во-вторых, не должна терять устойчивость при изгибе. У балок с большим отношением длины к высоте (а можно предполагать, что в нашей задаче так и будет) касательные напряжения обычно (при нормальных соотношениях между площадями стенки и поясков) бывают невелики.

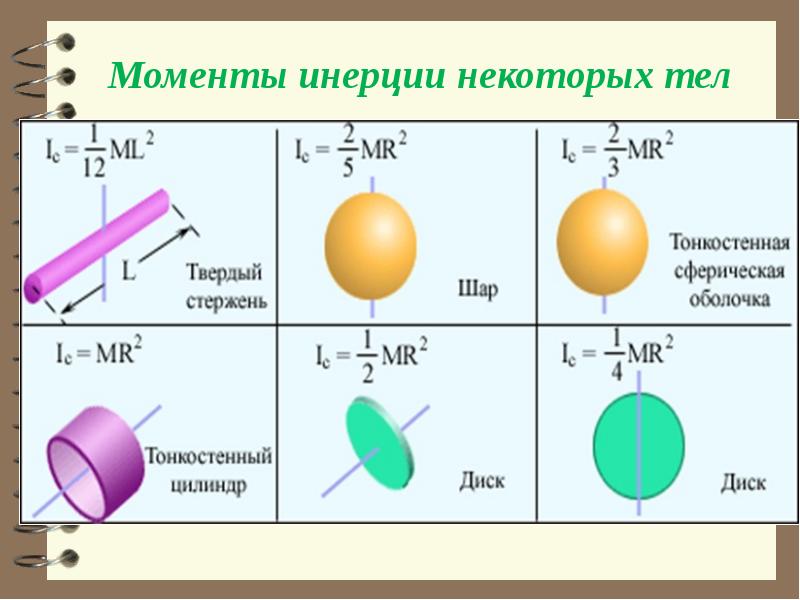Правда, нужно отметить, что перекрёстная связь является балкой на упругом основании; основанием для неё служат балки главного направления. В этом случае влияние перерезывающих сил значительно возрастает. В работе учёт касательных напряжений не требуется.

Согласно рекомендациям справочника по строительной механике корабля под ред. Ю.А. Шиманского, т. 3, отношение высоты стенки к её толщине для стали с пределом текучести 2500 кгс/см

2 при работе балки на изгиб со сдвигом не должно превышать 59. Отношение ширины полки к её толщине должно быть не больше 33 (при пределе текучести 3000 кгс/см2). При соблюдении этих соотношений будет обеспечиваться устойчивость пластин, из которых составлен профиль.

Обычно отношение высоты стенки к её толщине берётся в пределах 30 – 50, а отношение ширины полки к её толщине – 10 – 15. На эти значения мы и будем ориентироваться. Важной величиной является отношение площади полки S к площади стенки w, оптимальные значения этого отношения лежат в пределах 0,45 – 1,0.

Ориентировочно можно считать, что площадь полки должна быть примерно в 1,5 раза меньше, чем площадь стенки.

Отсюда требуемая высота h = 110 см.

Принимаем предварительно h = 120 см; толщину стенки = 2,2 см; толщину полки = 3,0 см; ширину полки = 60 см. Соотношение площадей полки и стенки получилось равным 1,47.

По принятым размерам в таблице рассчитаем момент инерции перекрёстной связи вместе с присоединённым пояском, ширина которого выбирается с учётом указаний п. 3, и сравним его с предварительно полученным. В нашем случае присоединённый поясок имеет ширину 3,0 м.

© 2021 ВУнивере.ру

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

2 {/ экв}. Его угловая скорость 40,0 рад / с. Если сила действует на астероид в течение 0,100 с, увеличивая угловую скорость до 48,0 рад / с, найдите ее величину.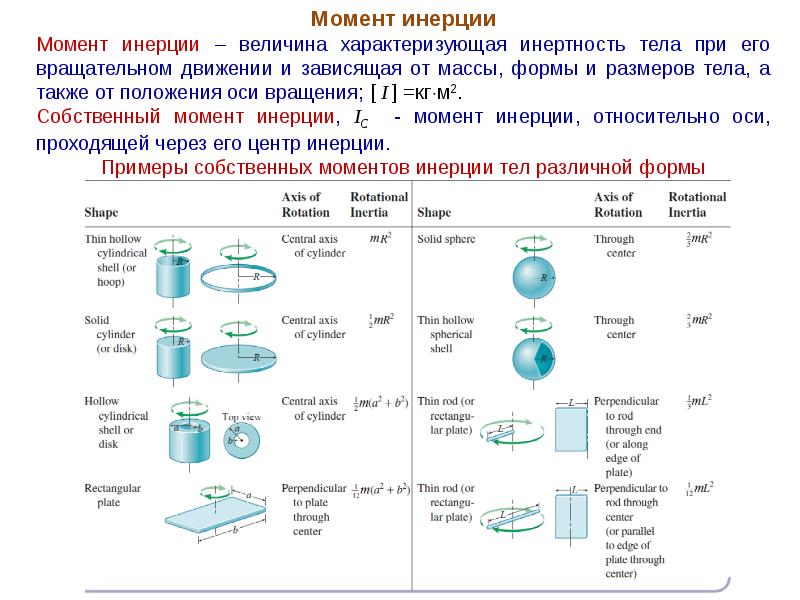

Крутящий момент:

При вращательном движении крутящий момент, приложенный к вращающемуся объекту, равен скорости изменения его углового момента. Это аналог силы, действующей на объект при поступательном движении. Крутящий момент, создаваемый во вращающемся объекте, также определяется как перекрестное произведение вектора положения (где приложена сила) от оси вращения и приложенной силы в данном положении от оси вращения.Математически величина крутящего момента выражается следующим образом:

{eq} \ tau = r F \ sin \ theta {/ eq}

Где:

  • {eq} \ tau {/ eq} – крутящий момент, создаваемый вращающимся объектом.
  • {eq} F {/ eq} – это сила, приложенная к объекту для его вращения.
  • {eq} r {/ eq} – это величина вектора положения от оси вращения до точки воздействия (где применяется сила).

Сейчас,

Математически взаимосвязь между угловым моментом и крутящим моментом, создаваемым во вращающемся объекте, может быть выражена следующим образом:

{eq} \ tau = \ dfrac {dL} {dt} {/ eq}

Где:

  • {eq} \ dfrac {dL} {dt} {/ eq} – скорость изменения углового момента. {4} \, …

См. Полный ответ ниже.

Асимметричный станок Этвуда. Некоторые физические задачи можно решить несколькими разными методами. Часто учебные задачи идеализируются, предполагая, что трение и другие процессы рассеивания энергии имеют незначительное влияние, все тела ведут себя как твердые тела, любые соединительные шнуры имеют незначительную массу, совершенно гибкие, но не растягиваются. Очень часто эти проблемы решаются одним из нескольких методов.

  1. Динамический анализ с использованием только законов Ньютона и геометрических ограничений.
  2. Энергетический анализ.
  3. Импульсный анализ.
Это хороший способ проверить результаты. Какой бы действительный метод ни использовался, ответы должны быть согласованы. Не думайте, что сами методы или законы физики, на которых они основаны, излишни. Вы столкнетесь с другими ситуациями, когда необходимо применить несколько методов вместе, чтобы выжать все важные результаты.
Система. Диаграммы сил свободного тела
трех частей системы.
Шкив с тремя радиусами.

Шкив вверху состоит из двух или более шкивов разного радиуса, скрепленных вместе на общей оси. Мы относимся к нему как к не имеющему трения и имеющему незначительную массу. Поскольку он безмассовый, его момент инерции равен нулю.Поддерживающие струны невесомые, нерастягивающиеся, но при этом идеально гибкие. Обозначим натяжение левой струны T 1 . Натяжение правой струны будет обозначено T 2 .

Динамический анализ.

Мы примем соглашение о том, что вверх слева положительно, а справа внизу – положительно. Вращение по часовой стрелке положительное. Моменты по часовой стрелке положительные. (У нас есть очень веские основания предполагать, что шкив вращается по часовой стрелке, но любое согласованное соглашение о знаках также подойдет и даст те же физические ответы.)

Сначала мы сделаем это «по книге», используя подход «разделяй и властвуй». Мы мысленно разделяем систему на части. Затем мы применяем второй закон Ньютона к каждой части системы по очереди, создавая столько уравнений, сколько частей в системе. Затем эти уравнения решаются одновременно, устраняя нежелательные величины, чтобы получить интересующие ответы. Затем, если вы действительно хотите узнать значения исключенных вами величин, вы можете вернуть ответы в уравнения, чтобы сгенерировать их.

На каждом этапе будьте очень осторожны, чтобы определить все силы, действующие на выбранную вами часть системы, а – только на эту часть. При написании F = ma для одной части игнорируйте силы, которые действуют на другие части системы. Если две части системы соединены шнурами или прижимаются друг к другу, третий закон Ньютона используется для связи этих сил действия / противодействия.

Бывают ситуации, когда вы можете сократить процесс, объединив несколько частей системы, если они имеют одинаковое движение и их взаимные силы взаимодействия вас не интересуют.Эти силы, будучи равными по величине и противоположно направленными, тогда являются «внутренними силами» и «выпадают» из расчета чистой силы, чистого крутящего момента и чистого импульса. Мы увидим пример этого по мере продвижения. Итак, приступим. Это будет не только весело, но и поучительно.

По второму закону Ньютона на левую массу m действуют две силы. Восходящая сила T 1 и нисходящая гравитационная сила mg. Таким образом, F net = ma дает T 1 – mg = ma.

Правая масса 2m имеет направленную вверх силу T 2 и направленную вниз силу (2m) g, поэтому (2m) g – T 2 = (2m) a.

Первый закон Ньютона для крутящих моментов на шкиве: -T 1 (R) + T 2 (2R) = 0, поскольку массой шкива можно пренебречь.

Следовательно, T 1 = 2 (T 2 )

T 1 – мг = m (a 1 )
(2m) g – T 2 = (2m) (a 2 )
Т 1 = 2 (Т 2 )
a 2 = 2 (a 1 ) по геометрическому ограничению.

Итак:

2 (T 2 ) – mg = m (a 1 ) (1)
2 мг – (T 2 ) = 2 м (a 2 ) (2)

Умножьте вторую на 2.

4 мг – 2 (T 2 ) = 4 м (a 2 ) (3)

Складываем 1 и 3, чтобы исключить T 2 :

– мг + 4 мг = m ( 1 ) + 4m ( 2 )
– мг + 4 мг = m ( 1 ) + 4 м2 ( 1 ) = 9m ( 1 )
3 мг = 9 м ( 1 )
3g = 9 (а 1 )
а 1 = (3/9) г = г / 3
2 = (2/3) г (вдвое больше, чем у 1 )

(T 1 ) – мг = мг / 3
– (T 2 ) + 2 мг = (2 м) (2/3) г = (4/3) мг

(T 1 ) = (4/3) мг

Это больше, чем мг, поэтому m ускоряется вверх.

(T 2 ) = 2 мг – (4/3) мг = (2/3) мг

Это половина T 1 и меньше 2 мг, поэтому 2 м ускоряется вниз.

Энергетический анализ.

Что могут сказать нам уравнения энергии?

Предположим, что левая сторона движется вверх на расстояние y. Затем правая сторона опускается на расстояние 2y. Изменение потенциальной энергии плюс изменение кинетической энергии равно нулю для замкнутой системы.

mg2y – mgy = ½mv 1 2 + ½mv 2 2

mgy = ½mv 1 2 + ½m (2v 1 ) 2

gy = (3/2) v 1 2

v 1 = √ [(2/3) gy]

В этом примере нет необходимости явно использовать концепцию работы.Это сделало бы вывод более беспорядочным. Гравитационная сила действует на массы, силы натяжения тоже действуют, но, используя концепцию потенциальной энергии, мы можем рассматривать эту систему так, как если бы она была замкнутой, а работа, выполняемая силами натяжения, является внутренней. Таким образом, увеличение кинетической энергии можно рассматривать как результат чистой работы силы тяжести, передаваемые системе.

Какова кинетическая энергия объектов по прошествии определенного времени?

Если m перемещается вверх на расстояние y по вертикали, то 2m перемещается на 2y вниз по геометрическим параметрам.

(2m) g (2y) – mgy = (1 / 2m (v 1 ) 2 + (1/2) 2m (v 2 ) 2

(Изменение гравитационного потенциала = изменение кинетической энергии из положения покоя.)

3mgy = (1/2) m (v 1 ) 2 + (1/2) 2m [2 (v 1 )] 2

(Изменение кинетической энергии – это конечная кинетическая энергия m плюс конечная кинетическая энергия 2m.)

3mgy = (1/2) m (v 1 ) 2 + 4m [(v 1 )] 2

Но по геометрическим ограничениям (v 2 ) = 2 (v 1 ), поэтому:

3 мгги = (9/2) м (v 1 ) 2

gy = (3/2) (v 1 ) 2

v 1 = √ [(2/3) gy]

v 2 = √ [2 (2/3) gy]

Кинетическая энергия m равна (1/2) m (2/3) gy = (1/3) mgy

. Кинетическая энергия 2m равна (1/2) 2m4 (2/3) gy = (8/3) mgy

. Общая кинетическая энергия обоих вместе составляет (1/3 + 8/3) mgy = (9/3) mgy = 3mgy, что равно общему изменению потенциальной энергии.Это служит проверкой математики.

Гравитационная потенциальная энергия изменяется по мере движения тел. Он уменьшается, потому что центр масс системы перемещается вниз. Это ничем не отличается от случая, когда тело свободно падает, и его гравитационная потенциальная энергия уменьшается на ту же величину, на которую увеличивается его кинетическая энергия, таким образом, общая энергия системы остается постоянной.

Обратите внимание, что нам никогда не нужно было слишком рассматривать систему в целом, когда мы использовали F = ma для ее отдельных частей.Как говорили мои профи по физике, метод решения таких задач – «разделяй и властвуй», то есть смотреть на каждую часть системы и применять F = ma к каждой по очереди.

Теперь один может рассматривать систему в целом, обнаруживая движение центра масс системы при движении масс вниз, а затем вычисляя его ускорение. Затем используйте F (net) = (m + 2m) a. В этом случае силы натяжения не входят в расчет, поскольку все они являются парами действие / противодействие и выпадают из-за третьего закона Ньютона.

Наконец, можно очистить свободные концы, используя кинематические законы для нахождения других величин. Например, ускорение (которое мы так легко обнаружили с помощью динамического анализа).

Используйте v 1 2 = 2a 1 y 1

(2/3) gy 1 = 2a 1 y 1

a 1 = g / 3, как мы обнаружили из динамического анализа.

Возникает важный вопрос.Как мы узнаем, что в этой системе ускорение каждой части постоянно, что позволяет нам использовать кинематические уравнения «Галилео», которые были выведены в предположении постоянного ускорения? Это можно рассматривать как «скрытое предположение» в большинстве учебников по анализу таких динамических систем. Фактически, существует короткий период времени, когда система освобождается, в течение которого силы натяжения быстро изменяются, а ускорение быстро изменяется. Например, когда система удерживается в состоянии покоя (ускорение равно нулю), напряжение на m составляет всего мг, но когда систему отпускают, это напряжение очень быстро увеличивается до (4/3) мг, и за это время его ускорение быстро увеличивается от нуля до г / 2.Фактически мы игнорируем этот короткий (хотя и интересный) процесс, в течение которого система движется очень мало, и проводим анализ гораздо большей продолжительности процесса, в течение которого ускорение почти постоянно. Вопрос: Можете ли вы описать ситуацию, когда этот ярлык не будет оправдан для этой системы?

Импульсный анализ.

Есть еще один способ решить эту проблему. Используйте Impulse = изменение импульса. В учебниках это делается редко.Однако все ответы должны совпадать.

Импульс равен ∫ F (t) dt = Δ (мВ) в течение времени, в течение которого действует сила. Время не должно быть коротким.

Пусть система ускоряется с постоянной скоростью в течение времени t.

Чистый гравитационный импульс в системе равен изменению количества движения системы.

(2m) gt – mgt) = 2mv 2 – mv 1

mgt = (2m2 – m) v 1 = 3mv 1

Для сравнения с предыдущими результатами в нашем наборе инструментов есть кинематические уравнения для постоянного ускорения (иногда называемые «уравнениями движения Галилея»).Используйте это.

y 1 = (1/2) a 1 t 2

и

v 1 2 = 2a 1 y 1

Таким образом, gt = 3v 1 и, следовательно, t = 3v 1 / g

v 1 2 = 2a 1 y 1

y 1 = (1/2) (3v 1 / g) 2 = (a 1 /2) (3 / g) 2 2a 1 y 1

1 = 9 (а 1 / г) 2

Наконец, 1 = г / 3, что удовлетворительно согласуется с предыдущими методами.

Метод углового момента.

Эту проблему также можно проанализировать, рассматривая угловой момент системы. Это тривиальное упражнение для ученика. Но давайте воспользуемся творческим сокращением, возможно, потому что мы предположили, что момент инерции шкива пренебрежимо мал.

Возьмите центр шкива как центр крутящего момента. Считайте крутящий момент по часовой стрелке положительным, а против часовой стрелки – отрицательным. Это не обычное соглашение в учебниках, но вы можете поменять знаки без вреда, если будете последовательны.

Крутящий момент, создаваемый силой тяжести на mg, равен mgR. Крутящий момент из-за силы тяжести на 2 м составляет (2 м) g (2R). До тех пор, пока грузы на струнах не достигают шкива, система ведет себя так же, как если бы грузы были прикреплены в точках R и 2R на самом шкиве, и движение происходило под очень маленьким углом.

Используйте τ net = I α и I = ∫ r 2 дм

Мы рассматриваем систему как единое целое с двумя действующими на нее гравитационными моментами.

-mgR + 4mgR = (mR 2 + 2m (2R) 2 ) α

Итак, 3mR = 9mR 2 α

И 3g = 9Rα

Но по геометрии αR = a 1

Итак, 1 = (3/9) g = g / 3

Неудивительно, правда? Этот метод самый простой из-за того, что масса шкива незначительна. Если масса шкива незначительна, то и его момент инерции незначителен, и, следовательно, чистый крутящий момент на нем равен нулю, даже если он вращается, и мы можем с уверенностью сказать, что натяжения левой и правой струны находятся в соотношении 1: 2. .Эти силы являются внутренними по отношению к системе и не обеспечивают ей работы и импульсов. Поэтому нам не нужно использовать напряжения в расчетах. Однако теперь, когда у нас есть ускорения каждой массы, мы можем легко вычислить напряжения, используя F net = ma для каждой.

ma 1 = T – мг

мг / 3 = T 1 – мг

Т 1 = (4/3) г

Как мы выяснили предыдущими методами.

Масса шкива, которой нельзя пренебречь.

Это говорит о том, что мы можем так же легко проанализировать эту систему, когда масса шкива значительна. Просто измените наше предыдущее уравнение:

-mgR + 4mgR = (mR 2 + 2m (2R) 2 ) α

Добавив член для углового момента шкива (I):

-mgR + 4mgR = (mR 2 + 2m (2R) 2 + I) α

Или в более общем виде:

-m 1 gR 1 + m 2 gR 2 = (m 1 R 1 2 + m 2 R 2 2 + I) α

Это уравнение лежит в основе нескольких поучительных упражнений.Момент инерции шкива можно измерить напрямую. Шкив снимается и взвешивается. Подвесьте шкив за какую-нибудь точку. Эти шкивы обычно имеют фланец на ободе, который является удобной точкой подвески. Затем позвольте ему колебаться в простом гармоническом движении, измеряя период его движения с помощью секундомера. По этим данным можно рассчитать его момент инерции относительно точки подвеса. Затем теорему о параллельности оси можно использовать для определения его момента инерции относительно собственной оси вращения.Это можно примерно проверить по измерениям размеров, если его геометрия проста. Этот результат вставлен в формулу. 2, которая решается, как и раньше, предсказывая ускорение асимметричной машины Атвуда, которое затем может быть подтверждено экспериментально.

Или, ускорение системы может быть измерено, и уравнение. 2 используется для расчета I.

Некоторые студенты не понимают, что тело, движущееся по прямой линии, может иметь угловую скорость, угловое ускорение и угловой момент относительно точки.Векторная форма определения угловой скорости: ω = R × V , поэтому угловой момент тела массы m, подвешенного на веревке, прикрепленной к шкиву радиусом R от его оси, имеет угловой момент размера mvR. . Его момент инерции относительно этой оси равен mR 2 .

Историческая справка.

Этот проблемный пример показывает, почему в истории физики понадобилось так много времени, чтобы развить концепции энергии и импульса. Вопрос был в том, «Какова правильная мера движения?» Кандидатами были «vis viva» (mv 2 ) и импульс (mv).Некоторые физические ситуации могут быть проанализированы с использованием любого из них. Но для некоторых других проблем требовалось использование и вместе. Теперь мы понимаем, что нам нужно и то, и другое, чтобы адекватно справляться со всеми возможными взаимодействиями между материальными телами. Теперь мы также понимаем, что энергия – это скалярная величина, а импульс – это векторная величина. Они не взаимозаменяемы.

Сравнение поступательного и углового перемещения.

Как правило, учебники физики сначала вводят прямолинейное движение с постоянным ускорением в отдельную главу.Далее рассматривается движение с постоянным ускорением в плоскости на примерах траекторий снарядов. Для этого нужна векторная алгебра. Наконец, рассматривается особый случай кругового движения, и это может показаться повторением процесса и выводов, уже изученных для работы с прямолинейным движением. Но для неосторожных есть ловушки. Движение по прямой начинается с переменных времени, расстояния, скорости и ускорения. Круговое движение начинается с времени, угла, угловой скорости и углового ускорения.Хотя процесс получения результатов из них кажется идентичным для кинематических уравнений, сюрпризы ждут, когда переходишь к работе, энергии, импульсу и импульсу.

Я не буду здесь делать выводы, их можно найти в любом хорошем учебнике физики. Но учебник может не подводить итоги и не сравнивать их критически, как я сделаю здесь.

название линейной величины линейный символ и определение название угловой величины угловой символ и определение геометрическая связь между угловыми и линейными величинами для кругового движения комментарий
время t т
расстояние x угловое положение θ рад ≡ L / R θR = L (длина дуги)
скорость s = d x / dt угловая скорость ω = d θ / dt ωR = s (скорость вокруг дуги)
ускорение a = d v / dt Угловое ускорение α = dω / dt αR = a (ускорение вокруг дуги)
сила F крутящий момент τ = FR Сила и крутящий момент НЕ равны.
работа dW = ∫ F · dx работа dW = τ · dθ Они равны для кругового движения!
масса M момент инерции I = ∫ r 2 дм Масса и момент инерции не равны.
Второй закон Ньютона F = m a τ = I α Аналогия сохраняется, но законы физически не те же.
Третий закон Ньютона F 12 =
-F 21 		τ 12 = – τ 21 Аналогия верна, но законы физически не такие.
кинетическая энергия K = mv 2 /2 кинетическая энергия K = Iω 2 /2 Они равны для кругового движения.
момент импульса P = м v момент импульса M = м v × R линейный момент и угловой момент НЕ равны .

Обратите внимание, что угловое положение, скорость и ускорение не равны их линейным аналогам. Единственные, в которых аналогичные величины равны, это , энергия, (и работа). Они чудаки.

Угловые величины и их уравнения необходимо независимо выводить из первых принципов. Эта таблица представляет собой лишь сводку результатов, которая служит путеводителем по уравнениям и помогает запоминать.

Нас совсем не удивляет аналогия, которая сохраняется, когда мы выводим угловые аналоги кинематических уравнений «Галилея» для движения с постоянным ускорением.

Кинематические уравнения для постоянного ускорения.
Линейное ускорение a и угловое ускорение α постоянны. Тело покоится в момент времени t = 0, но его начальная скорость равна v 0 .
d и θ – линейные и угловые перемещения соответственно.		 d = (v + v 0 ) t / 2
d = v 0 t + ½ при 2
v 2 = v 0 2 + 2ad		 θ = (ω – ω 0 ) т / 2
θ = ω 0 t + ½αt 2
ω 2 = ω 0 2 + 2αθ

Но помните, что это , а не , вывод угловых уравнений из линейных.Это лишь их параллельное сравнение.

В двух измерениях, со скоростью и ускорением, выраженными как векторы, эти паттерны по-прежнему аналогичны, но члены первых двух являются векторами, поэтому они складываются путем сложения векторов. Последнее уравнение имеет скалярные члены, и произведение «as» становится a • d , скалярное произведение вектора ускорения, a и смещения d .

В двух измерениях, когда угол, угловая скорость и угловое ускорение выражаются векторами, эти модели по-прежнему аналогичны.Все члены первых двух являются векторами, поэтому они складываются путем сложения векторов. Последнее уравнение имеет скалярные члены, и произведение «αθ» становится α • θ , скалярным векторным произведением векторов углового ускорения α и углового смещения θ .

Инерция.

Студенты часто слышат слово «инерция», но многие ли знают, что оно означает? Какая мера инерции? Инерция – это мера «сопротивления» или «медлительности» тела, которое приводится в движение при приложении силы.Закон Ньютона F = ma в преобразованном виде a = F / m показывает, что ускорение тела массы m в результате приложения силы обратно пропорционально массе тела. Масса – это мера поступательной инерции. Уравнение α = τ / I показывает, что вращательное ускорение тела обратно пропорционально его моменту инерции. Момент инерции – это мера его вращательной инерции.

В классической физике масса не зависит от того, насколько быстро тело ускоряется.Даже если он находится в состоянии покоя, он имеет массу. Масса – это свойство тела. Его момент инерции зависит только от распределения его массы относительно потенциальной оси вращения. Но даже если он не вращается, его момент инерции можно рассчитать по формуле I = ∫ r 2 дм. Нужно ли нам движение для измерения инерции? Один из способов измерения массы – это приложение известной силы к массе и измерение результирующего ускорения массы, а затем использование закона Ньютона F = ma. Это измеряет «динамическую массу».Но мы также можем использовать балочные весы для сравнения силы тяжести, действующей на массу, с силой на калиброванном эталоне массы. Это называется «гравитационная масса». Есть два вида массы? Все эксперименты на сегодняшний день показывают, что при использовании любого метода результаты всегда идентичны, поэтому мы обычно называем это просто «массой». С философской точки зрения можно утверждать, что движение необходимо в любом методе. При взвешивании чего-либо на весах как узнать, что баланс был достигнут? Вы знаете это, когда весы не двигаются, и вы проверяете это, немного подстраивая весы, так что они немного колеблются, а затем останавливаются.

    Дональд Э. Симанек, 3 сентября 2010 г.

Перейдите к следующей главе, «Механическая вселенная».
Вернуться на страницу содержания Краткий курс классической механики .
Вернитесь на главную страницу Дональда Симанека.

22A: Центр масс, момент инерции

Довольно часто, когда требуется определение положения центра масс распределения частиц, распределение частиц представляет собой совокупность частиц, составляющих жесткую тело.Самым простым твердым телом, для которого можно вычислить центр масс, является тонкий стержень, потому что он простирается только в одном измерении. (Здесь мы обсуждаем идеальный тонкий стержень. Физический тонкий стержень должен иметь некоторый ненулевой диаметр. Однако идеальный тонкий стержень является хорошим приближением к физическому тонкому стержню, если диаметр стержня мал по сравнению с его длиной. .)

В простейшем случае вычисление положения центра масс тривиально. В простейшем случае используется однородный тонкий стержень.Однородный тонкий стержень – это стержень, у которого линейная массовая плотность \ (\ mu \), масса на длину стержня, имеет одно и то же значение во всех точках стержня. Центр масс однородного стержня находится в центре стержня. Так, например, центр масс однородного стержня, который простирается вдоль оси x от \ (x = 0 \) до \ (x = L \), находится в (L / 2, 0).

Линейная массовая плотность \ (\ mu \), обычно называемая линейной плотностью, когда контекст ясен, является мерой того, насколько плотно упакованы элементарные частицы, составляющие стержень.При высокой линейной плотности частицы расположены близко друг к другу.

Чтобы представить себе, что подразумевается под неоднородным стержнем, стержнем, линейная плотность которого является функцией положения, представьте тонкий стержень, сделанный из сплава, состоящего из свинца и алюминия. Далее представьте, что процентное содержание свинца в стержне плавно изменяется от 0% на одном конце стержня до 100% на другом. Линейная плотность такого стержня будет функцией положения по длине стержня. Одномиллиметровый сегмент стержня в одном положении будет иметь массу, отличную от массы миллиметрового сегмента стержня в другом положении.

Людям, имеющим некоторое отношение к исчислению, легче понять, что такое линейная плотность, чем людям без исчисления, потому что линейная плотность – это просто отношение количества массы в сегменте стержня к длине сегмента, в пределе длина сегмента стремится к нулю. Рассмотрим стержень, который простирается от \ (0 \) до \ (L \) вдоль оси \ (x \). Теперь предположим, что \ (m_s (x) \) – это масса того сегмента стержня, который простирается от \ (0 \) до \ (x \), где \ (x \ ge0 \), но \ (x

Теперь, когда у вас есть хорошее представление о том, что мы понимаем под линейной плотностью массы, мы собираемся проиллюстрировать на примере, как определить положение центра масс неоднородного тонкого стержня.

Найдите положение центра масс тонкого стержня, который простирается от \ (0 \) до \ (. 890 \) м вдоль оси \ (x \) декартовой системы координат и имеет линейную плотность, задаваемую \ (\ му (х) = 0.2 \).

Решение

Чтобы иметь возможность определить положение центра масс стержня с заданной длиной и заданной линейной плотностью как функцию положения, сначала необходимо найти массу стержня. такой стержень. Для этого у кого-то может возникнуть соблазн использовать метод, который работает только для частного случая однородного стержня, а именно, попробовать использовать \ (m = \ mu L \), где \ (L \) – длина стержня. . Проблема в том, что \ (\ mu \) меняется по всей длине стержня.Какое значение использовать для \ (\ mu \)? У кого-то может возникнуть соблазн оценить данное \ (\ mu \) в \ (x = L \) и использовать его, но это будет действовать так, как если бы линейная плотность была постоянной в \ (\ mu = \ mu (L) \ ). Нет. Фактически, в данном случае \ (\ mu (L) \) – это максимальная линейная плотность стержня, она имеет это значение только в одной точке стержня.

Что мы можем сделать, так это сказать, что бесконечно малое количество массы \ (dm \) в сегменте \ (dx \) стержня равно \ (\ mu dx \). Здесь мы говорим, что в некоторой позиции \ (x \) на стержне, количество массы на бесконечно малой длине \ (dx \) стержня является значением \ (\ mu \) при этом \ (x \) значение, умноженное на бесконечно малую длину \ (dx \).Здесь нам не нужно беспокоиться о том, что \ (\ mu \) изменяется с положением, поскольку сегмент \ (dx \) бесконечно мал, что означает, по сути, что он имеет нулевую длину, поэтому весь сегмент по существу находится на одна позиция \ (x \) и, следовательно, значение \ (\ mu \) при этом \ (x \) хорошо для всего отрезка \ (dx \).

\ [dm = \ mu (x) dx \ label {22-2} \]

Теперь это верно для любого значения \ (x \), но оно просто покрывает бесконечно малый сегмент стержня на \(Икс\). Чтобы получить массу всего стержня, нам нужно сложить все эти вклады в массу.Конечно, поскольку каждый \ (dm \) соответствует бесконечно малой длине стержня, у нас будет бесконечное количество членов в сумме всех \ (dm \) ‘s. Бесконечная сумма бесконечно малых членов есть интеграл.

\ [\ int dm = \ int_ {0} {L} \ mu (x) dx \ label {22-3} \]

, где значения \ (x \) должны начинаться с \ (0 \ ) к \ (L \), чтобы покрыть длину стержня, отсюда и пределы справа. Теперь математики предоставили нам богатый набор алгоритмов для вычисления интегралов, и нам действительно нужно будет обратиться к этому набору инструментов, чтобы вычислить интеграл справа, но чтобы вычислить интеграл слева, мы не можем, не должны и не буду обращаться к такому алгоритму.Вместо этого мы используем здравый смысл и наше концептуальное понимание того, что означает интеграл слева. В контексте рассматриваемой проблемы \ (\ int dm \) означает «сумму всех бесконечно малых бит массы, составляющих стержень». Теперь, если вы сложите все бесконечно малые части массы, составляющие стержень, вы получите массу стержня. Итак, \ (\ int dm \) – это просто масса стержня, который мы назовем \ (m \). Уравнение \ (\ ref {22-3} \) тогда принимает вид

\ [m = \ int_ {0} {L} \ mu (x) dx \ label {22-4} \]

Замена \ (\ mu (x) \) с заданным выражением для линейной плотности \ (\ mu = 0.3} {3} \]

\ [m = 0.1527kg \]

Это значение пригодится при вычислении положения центра масс. Теперь, когда мы вычислили центр масс набора дискретных частиц (где дискретная частица – это та, которая сама по себе, в отличие, например, от того, чтобы быть частью твердого тела), мы просто выполнили взвешенную сумму, в которой каждый член был положением частицы, умноженным на ее весовой коэффициент, а весовой коэффициент был той долей от общей массы, представленной массой частицы.Мы выполняем аналогичную процедуру для непрерывного распределения массы, такой как та, которая составляет рассматриваемый стержень. Начнем с написания одного члена суммы. Мы рассмотрим бесконечно малую длину стержня \ (dx \) в точке \ (x \) по длине стержня. Положение, как только что было сказано, равно \ (x \), а весовой коэффициент – это та доля от общей массы \ (m \) стержня, которая равна массе \ (dm \) бесконечно малой длины \ (dx \) представляет. Это означает, что весовой коэффициент равен \ (\ frac {dm} {m} \), поэтому член в нашей взвешенной сумме позиций выглядит так:

\ [\ frac {dm} {m} x \]

Теперь , \ (dm \) можно выразить как \ (\ mu \) \ (dx \), поэтому наше выражение для члена взвешенной суммы можно записать как

\ [\ frac {\ mu dx} {m} x \]

Это один член взвешенной суммы положений, сумма, которая дает положение центра масс.Дело в том, что, поскольку значение \ (x \) не указано, этот один член подходит для любого бесконечно малого сегмента полосы. Каждый член в сумме выглядит точно так же. Итак, у нас есть выражение для каждого члена суммы. Конечно, поскольку выражение предназначено для бесконечно малой длины стержня \ (dx \), в сумме будет бесконечное количество членов. Итак, снова у нас есть бесконечная сумма бесконечно малых членов. То есть снова у нас есть интеграл. Наше выражение для положения центра масс:

\ [\ bar {x} = \ int_ {0} {L} \ frac {\ mu dx} {m} x \]

Подставляем данное выражение \ (\ му (х) = 0.3} {3} \), которое мы вывели для массы, а не значения, которое мы получили при вычислении этого выражения, наше выражение для \ (\ bar {x} \) упростилось бы до \ (\ frac {3} { 4} L \), который оценивается как \ (\ bar {x} = 0,668m \), тот же результат, что и выше.

Страница не найдена – Субхасиш Чандра

Это слово произносит средний человек во всех ситуациях от рождения до смерти.

(Ну, я просто использую родовое имя на английском языке. Вы можете использовать звук, который описывает его / ее на вашем языке.Содержание этого блога останется прежним.)

Самый первый метод, которым мы учимся понимать Бога, – это религия. Каждая религия может иметь разные процессы понимания, процессы, которые передавались из поколения в поколение (с изменениями, производимыми людьми по мере необходимости) . Немногие религии имеют пантеон , в то время как немногие верят в « единственный ». Как бы то ни было, все религии согласны с тем, что Бог является высшей силой, контролирующей работу Вселенной.Хотя теисты полагают, что эта сила является сверхчеловеческой , атеисты сомневаются в самой правдивости этого аргумента. Но тем не менее все верят в существование сверхдержавы .

В детстве я всегда сталкивался с дилеммой выбора между Богами. Например, я, будучи бенгальцем, узнал кое-что о богине Дурге. Но я был удивлен, узнав, что пока «наша бенгальская Дурга» ехала на тигре, в Тумсаре ехали на льве! Меня смутила эта «дуальность Вагана».Как Дурга справилась с этой сменой «ваханов»? Правдоподобный ответ был таков, что она была богиней. И даже сейчас большинство вопросов, связанных с Богами, обычно заканчивается этим фантастическим аргументом.

В то время я прочитал в одной из книг о морали «Ананд Марг», сокращенно обозначенной БОГОМ,

.

G энератор

О ператор

D эстроератор

Это был очень хороший ответ. Я снова спросил значение этих слов в контексте.Мне сказали, что Бог создал все, что присутствует в этой вселенной, контролировал, как все эти творения должны были функционировать, а затем творения в конечном итоге были уничтожены. ( У моего дяди было фактически три имени для каждой задачи: Генератор – Господь Брахма, Оператор – Господь Вишну и Разрушитель – Господь Шива. )

Мое понимание Богов продолжало оставаться в тумане. Чем больше я читал, видел, обсуждал и думал, тем больше сбивался с толку. В какой-то момент я фактически стал агностиком.Я нашел это занятие бесплодным. Но потом «Пуна» случилась в жизни. Университет не только дал мне лучшее образование по физике, но и предоставил мне людей, которые были готовы обсуждать разные темы. Эти обсуждения могли показаться другим аргументами и спорами, но мы дорожили ими. Сумеру Гондане (в Яшаде, Пуне) сказал мне позже, что первые ответы на все вопросы были даны религией, затем философией и, наконец, наукой.

Вы можете выбрать свой собственный метод, но в конце концов вы просто пытаетесь найти ответ на самый простой вопрос: « Какова причина того, что это происходит вот так? ».Я тоже прошел через эти обсуждения, чтобы узнать ответ. Что ж, невозможно получить конечный ответ на вопрос, имеющий бесконечное количество разветвлений. Но эти обсуждения в сочетании с изучением физики и особенно космологии заставляют меня поверить в Высшую Силу .

Мы можем называть его любым именем; мы можем придать ему любую форму, какую захотим, но функция силы – это, в конце концов, то, что я прочитал в книге Ананда Марга. Исследования во всех науках показали, что эти процессы работают одинаково: Генерация → Работа → Разрушение → Генерация →… Круг продолжается и указывает на высшую силу, эффекты которой мы видим в наших соответствующих микрокосмосах.Если вы посмотрите на эти вещи в режиме от микро до макро, вы обнаружите бесконечную симметрию. Я думаю, эта симметрия побудила Эйнштейна сказать, что Бог не играет в кости.

Мы можем назвать эту сверхдержаву Богом, अल्लाह, भगवान, Природой, Сингулярностью, पूर्ण ब्रह्म, Ad Infinitum или как угодно. В конце концов, эта высшая сила является высшей истиной, и все, что изучается где-либо в этой вселенной, является пониманием проявления этой силы.

Итак, хотя мы не можем точно сказать точную форму или внешний вид Бога, его существование неоспоримо.

Свойства поперечного сечения | MechaniCalc

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

Поведение элемента конструкции определяется его материалом и геометрией. Эта ссылка сосредоточена на влиянии геометрии на поведение элемента конструкции. Поперечное сечение и длина конструктивного элемента влияют на то, насколько этот элемент отклоняется под нагрузкой, а поперечное сечение определяет напряжения, которые существуют в элементе при данной нагрузке.

Недвижимость участков

Центроид

Центроид формы представляет собой точку, вокруг которой равномерно распределена площадь сечения. Если область дважды симметрична относительно двух ортогональных осей, центр тяжести лежит на пересечении этих осей. Если область симметрична только относительно одной оси, то центр тяжести лежит где-то вдоль этой оси (необходимо вычислить другую координату). Если точное местоположение центроида не может быть определено путем осмотра, его можно рассчитать следующим образом:

где dA представляет собой площадь бесконечно малого элемента, A – общая площадь поперечного сечения, а x и y – координаты элемента dA относительно интересующей оси.

Центроидальные положения общих поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать местоположение с помощью приведенных выше уравнений.

Если поперечное сечение состоит из набора основных форм, центроидальное положение которых известно относительно некоторой контрольной точки, то центральное положение составного поперечного сечения можно рассчитать как:

где x c, i и y c, i – прямоугольные координаты центроидного положения секции i th относительно опорной точки, а A i – площадь i th раздел.

Центроидное расстояние

Центроидное расстояние , c – это расстояние от центра тяжести поперечного сечения до крайнего волокна. Центроидное расстояние в направлении y для прямоугольного поперечного сечения показано на рисунке ниже:

Обычно центроидное расстояние используется:

Первый момент области

Первый момент области указывает распределение области относительно некоторой оси.Первый момент области относительно интересующей оси рассчитывается как:

Q x = ∫ y dA Q y = ∫ x dA

где Q x – это первый момент относительно оси x, а Q y – это первый момент относительно оси y. Значения x и y указывают положения относительно оси интереса бесконечно малых областей, dA, каждого элемента при выполнении интегрирования.

Если область состоит из набора основных форм, чьи центроидные положения известны относительно интересующей оси, то первый момент составной области можно рассчитать как:

Если вы сравните приведенные выше уравнения для Q с уравнениями для вычисления центроида (обсуждавшимися в предыдущем разделе), вы увидите, что мы фактически используем первый момент площади при вычислении местоположения центроида по отношению к интересующей нас точке.

Первый момент также используется при вычислении значения напряжения сдвига в определенной точке поперечного сечения. Напомним, что напряжение сдвига в любой точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения, рассчитывается как:

где Q – первый момент области между точкой y 1 и крайним волокном (верхним или нижним) поперечного сечения. Рассмотрим рисунок ниже. Нас интересует расчет напряжения сдвига в точке, находящейся на расстоянии y 1 от центра тяжести поперечного сечения.Мы можем вычислить первый момент области либо выше, либо ниже этого местоположения. В этом случае интересующая точка находится выше нейтральной оси, поэтому проще рассмотреть верхнюю область, которая на рисунке ниже заштрихована синим цветом. Эта область простирается от точки y 1 до крайнего волокна в верхней части поперечного сечения.

Первый момент относительно оси x области, заштрихованной синим на рисунке выше, вычисляется относительно центроида поперечного сечения (точка O на рисунке) как:

Если центроидное положение интересующей области известно, то первый момент области относительно центроида упрощается до (см. Рисунок выше):

Q cx = y c1 A 1

Следует отметить, что первый момент области является положительным или отрицательным в зависимости от положения области относительно оси интереса.Следовательно, первый момент всей площади поперечного сечения относительно его собственного центроида равен нулю.

Момент инерции площади

Второй момент площади, более известный как момент инерции , I, поперечного сечения, является показателем способности конструктивного элемента сопротивляться изгибу. (Примечание 1) I x и I y – моменты инерции относительно осей x и y, соответственно, и рассчитываются по формуле:

I x = ∫ y 2 dA I y = ∫ x 2 dA

где x и y – координаты элемента dA относительно интересующей оси.

Чаще всего моменты инерции рассчитываются относительно центра тяжести сечения. В этом случае они обозначаются как центроидных моментов инерции и обозначаются как I cx для инерции относительно оси x и I cy для инерции относительно оси y.

Моменты инерции общих поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать их с помощью приведенных выше уравнений. Свойства нескольких общих сечений приведены в конце этой страницы.

Если поперечное сечение состоит из набора основных форм, все центроиды которых совпадают, то момент инерции составного сечения является просто суммой отдельных моментов инерции. Примером этого является балка коробчатого сечения, состоящая из двух прямоугольных секций, как показано ниже. В этом случае внешняя часть имеет «положительную площадь», а внутренняя часть имеет «отрицательную площадь», поэтому составной момент инерции представляет собой вычитание момента инерции внутренней части из внешней части.

В случае более сложного составного поперечного сечения, в котором центральные положения не совпадают, момент инерции может быть вычислен с помощью теоремы о параллельных осях .

Важно не путать момент инерции поверхности с моментом инерции твердого тела. Момент инерции площади указывает на сопротивление поперечного сечения изгибу, тогда как момент инерции массы указывает на сопротивление тела вращению.

Теорема о параллельной оси

Если известен момент инерции поперечного сечения относительно центральной оси, то для вычисления момента инерции относительно любой параллельной оси можно использовать теорему о параллельных осях :

I параллельная ось = I c & plus; А д 2

где I c – момент инерции относительно центральной оси, d – расстояние между центральной осью и параллельной осью, а A – площадь поперечного сечения.

Если поперечное сечение состоит из набора основных форм, центроидные моменты инерции которых известны вместе с расстояниями центроидов до некоторой контрольной точки, то теорема о параллельных осях может использоваться для вычисления момента инерции составного поперечного сечения.

Например, двутавровую балку можно аппроксимировать 3 прямоугольниками, как показано ниже. Поскольку это составное сечение симметрично относительно осей x и y, центр тяжести сечения можно определить путем осмотра на пересечении этих осей.Центроид находится в начале координат O на рисунке.

Момент инерции составной секции можно рассчитать с помощью теоремы о параллельности осей. Центроидный момент инерции секции относительно оси x, I cx , рассчитывается как:

I cx.IBeam = I cx.W & plus; (I cx.F1 & plus; A F1 d 1 2 ) & plus; (I cx.F2 & plus; A F2 d 2 2 )

где члены I cx представляют собой моменты инерции отдельных секций относительно их собственных центроидов в ориентации оси x, члены d представляют собой расстояния от центроидов отдельных секций до центроида составной секции, а Термины – это площади отдельных разделов.Поскольку центроид сечения W и центроид составного сечения совпадают, d для этого сечения равно нулю, поэтому член Ad 2 отсутствует.

Важно отметить, что из теоремы о параллельности осей следует, что по мере того, как отдельная секция перемещается дальше от центра тяжести составной секции, вклад этой секции в момент инерции составной секции увеличивается в d 2 . Следовательно, если намерение состоит в том, чтобы увеличить момент инерции секции относительно определенной оси, наиболее эффективно расположить область как можно дальше от этой оси.Это объясняет форму двутавровой балки. Фланцы вносят основной вклад в момент инерции, а перегородка служит для отделения фланцев от оси изгиба. Однако полотно должно сохранять некоторую толщину, чтобы избежать коробления, а также потому, что полотно принимает на себя значительную часть напряжения сдвига в сечении.

Полярный момент инерции

Полярный момент инерции , J, поперечного сечения является показателем способности конструктивного элемента противостоять скручиванию вокруг оси, перпендикулярной сечению.Полярный момент инерции для сечения относительно оси можно рассчитать следующим образом:

J = ∫ r 2 dA = ∫ (x 2 & plus; y 2 ) dA

где x и y – координаты элемента dA относительно интересующей оси, а r – расстояние между элементом dA и интересующей осью.

Хотя полярный момент инерции может быть вычислен с использованием приведенного выше уравнения, обычно удобнее рассчитывать его, используя теорему о перпендикулярной оси , которая гласит, что полярный момент инерции области является суммой моментов инерции относительно любые две ортогональные оси, проходящие через интересующую ось:

J = I x и плюс; Я y

Чаще всего интересующая ось проходит через центр тяжести поперечного сечения.

Модуль упругости сечения

Максимальное изгибающее напряжение в балке рассчитывается как σ b = Mc / I c , где c – расстояние от нейтральной оси до крайнего волокна, I c – центроидный момент инерции, а M – изгибающий момент. Модуль упругости сечения объединяет члены c и I c в уравнении напряжения изгиба:

S = I c / c

Используя модуль упругости сечения, напряжение изгиба рассчитывается как σ b = M / S.Полезность модуля сечения заключается в том, что он характеризует сопротивление сечения изгибу одним термином. Это позволяет оптимизировать поперечное сечение балки, чтобы противостоять изгибу, за счет максимального увеличения одного параметра.

Радиус вращения

Радиус вращения представляет собой расстояние от центра тяжести секции, на котором вся площадь может быть сосредоточена без какого-либо влияния на момент инерции. Радиус вращения формы относительно каждой оси определяется выражением:

Полярный радиус вращения также может быть вычислен для задач, связанных с кручением вокруг центральной оси:

Прямоугольные радиусы вращения также можно использовать для вычисления полярного радиуса вращения:

r p 2 = r x 2 & plus; г г 2

PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице сечений.Этот курс можно использовать для выполнения требований к кредитам PDH для поддержания вашей лицензии PE.

Теперь, когда вы прочитали эту справочную страницу, получите за нее кредит!

Свойства общих сечений

В таблице ниже приведены свойства обычных поперечных сечений. Более подробные таблицы можно найти в перечисленных ссылках.

Свойства, вычисленные в таблице, включают площадь, центроидный момент инерции, модуль упругости сечения и радиус вращения.


Банкноты


Примечание 1: Прогиб балки

Прогиб балки при изгибе определяется моментом инерции поперечного сечения, длиной балки и модулем упругости материала. Более подробная информация представлена ​​в этом обсуждении отклонения балки.

Список литературы

  1. Гир, Джеймс М., “Механика материалов”, 6-е изд.
  2. Линдебург, Майкл Р., “Справочное руководство по машиностроению для экзамена на физическую форму”, 13-е изд.

Моменты инерции (включая 3D-печатную модель) – MAE 206 Engineering Statics Materials

Площадь моментов инерции интегрированием

Моменты инерции (как площади, так и массы) могут быть трудными для понимания или запоминания. Этот и последующие модули помогут вам проработать концепции и расчеты для моментов инерции площади.

Материалы:

  • Деревянная линейка 12 дюймов
  • 3D-принтер с гибкими материалами
  • 3 прямых штифта или гвоздя
  1. Чтение : Момент области инерции, фон и мотивация (3 страницы)
  2. Видео : https://youtu.be/omrmA-QGkcw (7 минут)
  3. Практическое руководство : Согните свою линейку. Есть три оси: одна по длине, одна по дюймовым отметкам и одна по толщине. Помните, что когда мы говорим о том, чтобы что-то согнуть, ось, вокруг которой вы наклоняетесь, – это то место, где будет находиться ваш большой палец.Таким образом, момент по длине балки скручивает балку. Момент в любой из двух других осей (по плоскости или по ширине) изгибает линейку.
    1. В каком направлении легче сгибаться?
  4. Чтение : Примечание о топорах (1 страница)
    1. Нарисуйте оси вдоль линейки так, чтобы z находился вдоль балки. (Сделайте свои оси правой системой координатных осей. Если вы посмотрите на поперечное сечение, вы должны увидеть обычную систему координатных осей x-y.)
    2. Какой момент изгибается больше: тот, который вращается вокруг оси x, или тот, который вращается вокруг оси y?
    3. Каким способом вы хотите установить линейку в конструкции, чтобы выдерживать больший вес?
    4. Что меняется, поскольку материал и длина не меняются?
  5. Чтение : Линейка изгибается вокруг своего собственного центроида (чуть больше 1 страницы)
  6. Пример (прочтите или посмотрите): прямоугольный луч, изгибающийся вокруг центроидных осей (2 страницы) или https: // youtu.be / BvEu0fpLfdc (чуть больше 1 минуты)
  7. Напишите краткий абзац для собственных заметок с объяснением осей и изгибающих нагрузок на линейку своими руками.
  8. Распечатайте 3D-гибкий i-beam.stl. Распечатайте это с плотностью 100% гибким материалом.
    1. Если позволяют средства, распечатайте копию на негибком материале, чтобы почувствовать разницу.
  9. Практическое руководство : Согните двутавр своими руками в двух направлениях.
    1. Нарисуйте оси прямо на распечатанном луче так, чтобы ось z была вдоль луча.В качестве альтернативы вставьте булавки в балку, чтобы вы могли видеть, где находятся топоры. (Убедитесь, что это правая система координат, чтобы, когда вы смотрите на поперечное сечение, вы видели обычную систему осей x-y.)
    2. Нарисуйте FBD балки, чтобы указать, в каком направлении действуют ваши нагрузки, когда вы изгибаете балку в каждом из направлений. Свяжите свои нагрузки с балкой с простой опорой.
    3. В какую сторону балка больше изгибается? О какой оси это? (Помните, что направление приложения момента находится там, где указывает ваш большой палец.)
    4. О каком моменте инерции области мы говорим для каждого направления изгиба? (Ix и Iy)
  10. Практическое руководство : Проведите линию в один дюйм сверху и снизу двутавровой балки. Согните двутавровую балку вокруг оси абсцисс. Обратите внимание, что одна из ваших дюймовых линий длиннее другой.
  11. Чтение : Нейтральная ось (1 страница)
  12. Видео : посмотрите видео-анимацию напряжения в изгибаемой двутавровой балке в обоих направлениях. Гибка как двутавровая балка и гибка такой же балки как двутавровая балка.
    1. Положите напечатанную двутавровую балку поверх карандаша, чтобы вы могли надавить на нее с обеих сторон и согнуть балку над карандашом, как показано на видео.
    2. В каком направлении легче отклоняться?
  13. Пример : Изгиб прямоугольной балки относительно базовой линии (2 страницы) или https://youtu.be/nD1ZMlrgJ_k (2 минуты)
  14. Практическое руководство : Положите гибкую двутавровую балку на стол. Если надавить на два верхних конца, балка испытывает изгибающий момент; верхняя поверхность балки будет немного изгибаться, но нижняя поверхность не деформируется.На нейтральной оси деформация равна нулю.
  15. Напишите краткий абзац для собственных заметок, объясняющий, почему момент инерции относительно базовой линии прямоугольника больше, чем относительно его центра тяжести. Соотнесите это с линейкой и своей двутавровой балкой.
  16. Чтение : Теорема о параллельной оси (1 страница)
  17. Практика : Найдите момент инерции треугольника относительно его базовой линии. Решение (смотрите только после того, как разобрались сами): https: // youtu.be / UjC4xjr0jCc (2 минуты)
    1. Сравните это с треугольной балкой в ​​голове, где вы пытаетесь согнуть балку с треугольным поперечным сечением, которая также находится на столе.
  18. Практика : подумайте, что потребуется, чтобы найти момент инерции площади относительно центральных осей треугольника. Решение: https://youtu.be/MApovKX7CIc (чуть более 4 минут)
    1. Объясните себе, почему момент инерции относительно центроида формы ниже.
  19. Практика : используйте теорему о параллельных осях, чтобы связать момент инерции относительно базовой линии в № 17 с моментом инерции относительно центра тяжести в № 18. Решение (1 страница)
  20. Практика : Найдите момент инерции зеленой фигуры относительно осей x и y. Показаны единицы измерения в см; рисунок выполнен не в масштабе. Решение: область между двумя кривыми (2 страницы).
  21. Практика : Найдите момент инерции бирюзовой формы относительно оси y.4.
  22. Примечание: найти момент инерции относительно оси x для этой формы сложно. (Студенты иногда могут проявить творческий подход. Будьте осторожны.)

Как только вы сможете найти момент инерции площади путем интегрирования, следующая часть – изучить метод составных тел. Это будет в следующем посте.

Разница между моментом инерции и полярным моментом инерции

Главное отличие – момент инерции vs.Полярный момент инерции

Момент инерции (который относится к массе второй момент инерции) и полярный (второй) момент инерции – обе величины, которые описывают способность объекта сопротивляться изменениям из-за приложенных к нему крутящих моментов. Основное различие между моментом инерции и полярным моментом инерции состоит в том, что момент инерции измеряет, насколько объект сопротивляется угловому ускорению , тогда как полярный момент инерции измеряет, насколько объект сопротивляется кручению .

Что такое момент инерции

Момент инерции тела определяется следующим интегралом:

где – расстояние массового элемента от оси вращения.

Физически момент инерции дает телу способность сопротивляться угловому ускорению (аналогично тому, как масса сопротивляется линейному ускорению) при воздействии крутящего момента. Если момент инерции велик, то угловое ускорение, создаваемое данным крутящим моментом, будет меньше.Единица момента инерции равна кг · м 2 .

Момент инерции используется для расчета кинетической энергии вращения, а также для расчета крутящего момента с точки зрения массы и углового ускорения.

Что такое полярный момент инерции

Полярный второй момент инерции дает объекту способность противостоять кручению (т. Е. «Скручиванию») вокруг заданной оси из-за приложенного крутящего момента. Если полярный момент инерции велик, кручение, создаваемое данным крутящим моментом, будет меньше.Полярный момент инерции определяется как:

где – расстояние элемента области от оси вращения. Полярный момент инерции равен м 4 .

Разница между моментом инерции и полярным моментом инерции – Определение полярного момента инерции (здесь показано в 2D)

Второй полярный момент площади часто путают со вторым моментом инерции площади, который определяется:

, где – расстояние элемента площади от определенной плоскости .Он также имеет единицы измерения m 4 , однако физически эта величина указывает на сопротивление объекта изгибу относительно определенной плоскости при воздействии крутящего момента.

Разница между моментом инерции и полярным моментом инерции

Математическое определение момента инерции и полярного момента инерции

Момент инерции определяется как.

Полярный момент инерции определяется как.

Физический смысл

Момент инерции – это измерение сопротивления объекта угловому ускорению.

Полярный момент инерции – это измерение сопротивления объекта кручению (скручиванию).

Оставить комментарий