Белорусский государственный университет транспорта – БелГУТ (БИИЖТ)
Регистрация на «Что? Где? Когда?»
Регистрация на конференцию «Транспорт в интеграционных процессах мировой экономики»
Регистрация на конференцию «Композиты в машиностроении и транспорте»
Регистрация на конференцию
«Научные и методические аспекты математической подготовки в университетах технического профиля»
Как поступить в БелГУТ
Как получить место
в общежитии БелГУТа
Как поступить иностранному гражданину
События
Все события
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
1 | 2 Дата : 2023-03-02 | 3 Дата : 2023-03-03 | 4 Дата : 2023-03-04 | 5 | ||
6 Дата : 2023-03-06 | 7 | 8 | 9 | 10 | 11 Дата : 2023-03-11 | 12 |
13 Дата : 2023-03-13 | 14 | 15 Дата : 2023-03-15 | 16 Дата : 2023-03-16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 | 31 | ||
Все анонсы
- ЕДИ «80 лет трагедии в Хатыни.
Результаты расследо… - Заседание совета университета…
- Открытая лекция «Постоянный электрический ток»…
- С праздником, дорогие женщины!…
- XXХII университетская олимпиада по сопротивлению м…
- Конкурс «Лучший лектор БелГУТа»…
- Студенческая лига киберспорта по дисциплинам CS:GO…
- IV Международная научно-практическая онлайн-конфер…
- I Международная научно-практическая конференция «К…
- Медицинские услуги санатория РУП «Гомельское отдел…
Результаты расследо…Анонсы
Университет
Абитуриентам
Студентам
Конференции
Приглашения
ЕДИ «80 лет трагедии в Хатыни. Результаты расследо…
Заседание совета университета…
Открытая лекция «Постоянный электрический ток»…
С праздником, дорогие женщины!…
Новости
Университет
Международные связи
Спорт
Воспитательная работа
Жизнь студентов
Новости подразделений
- Студенческая жизнь
..10 марта 2023
- Спорт
Первенство области по вольной борьбе
09 марта 2023
- Студенческая жизнь
Сюрприз коллегам по учебе
08 марта 2023
- Воспитательная работа
Самые прекрасные женщины
07 марта 2023
- Университет
Я выпускник ПГС! – встреча студентов факультета ПГС с выпускником 1969…
07 марта 2023
- Студенческая жизнь
Парни БелГУТа поздравляют с праздником прекрасных дам…
07 марта 2023
- Университет
Встреча с представителем Гуандунского союза по научно-техническому сот.
..
07 марта 2023
- Университет
Новый номер газеты «Вести БелГУТа»
07 марта 2023
- Университет
День открытых дверей строительного факультета…
07 марта 2023
Другие новости
- Встреча девушек БелГУТа и БТЭУ ПК в волейбольном зале …
- Победители межвузовского конкурса «Военный переводчик – 2023»…
- Победа команды БелГУТа
- Новополоцк – Молодёжная столица 2023!
- Памяти Коваля Олега Степановича
- Ученые БелГУТа на заседании российско-белорусской рабочей группы в обл…
- Инновационная разработка для «100 идей для Беларуси»…
- Олимпиада – путь к успеху!
- Второй этап сезона 2022/2023 учебного года «Что? Где? Когда?» среди пр…
- Не поддавайтесь на провокации, молодежь!. ..
- 1 марта – международный день борьбы с наркотиками…
..БелГУТ на Доске почета
Достижения университета
КУДА ПОСТУПАТЬ
Все факультеты
Предложения
Все предложения
Видеотека
Все видео
Фотогалерея
Все фото
3.23. Эффект Доплера . Новый физический фейерверк
Если вы встанете на железнодорожном переезде, когда поезд будет проноситься мимо и при этом гудеть, вам покажется, что частота гудка меняется. Почему? Будет ли она меняться от высокой частоты к низкой или наоборот?
ОТВЕТ • Движение источника звука относительно наблюдателя (в данном случае — слушателя, а им можете быть как вы, так и любой другой детектор звука) меняет частоту звука. Этот эффект называется 
Так что вы слышите ту же самую частоту звука, которую производит источник, и никакого сдвига нет. Если, напротив, источник движется на вас, он излучает волну, которая направляется на вас, скорость пролета областей высокого давления мимо вас теперь больше, чем их скорость относительно источника, и вы слышите более высокую частоту. Если же источник звука движется от вас, эффект обратный: вы слышите звук более низкой частоты, чем та, на которой он испущен источником. Так что движение источника на вас сдвигает частоту вверх, а от вас — вниз, и величина сдвига зависит от скорости источника. Если источник звука движется под углом к линии, соединяющей источник и вас, эффект (величина сдвига) меньше, а если этот угол прямой, сдвига вообще нет.
Если вы поместите детектор звука между железнодорожными рельсами, вы сможете замерить доплеровский сдвиг гудка поезда. Частота гудка будет сдвинута на определенную величину вверх в течение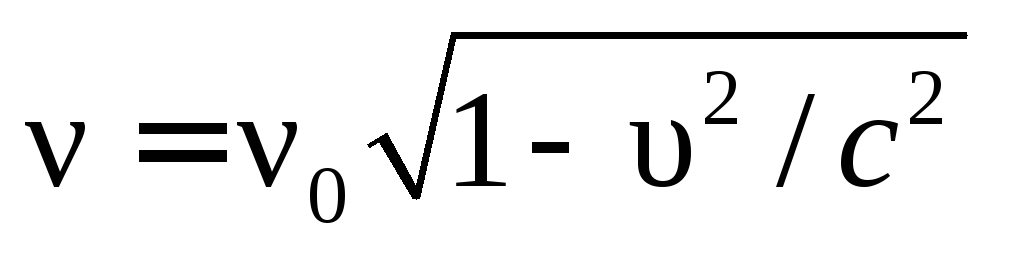 
Если же вы поместите детектор на некотором безопасном расстоянии, скажем, 20 м от железнодорожного пути, измерения покажут другое значение, и вот почему. Когда поезд приближается к детектору, его скорость относительно детектора будет постепенно уменьшаться, поэтому будет уменьшаться и доплеровский сдвиг. В результате б
Однако на наблюдения влияет и ваша психофизиология. Представьте себе, что вы детектор и стоите близко к железнодорожным путям, так что геометрический эффект не влияет.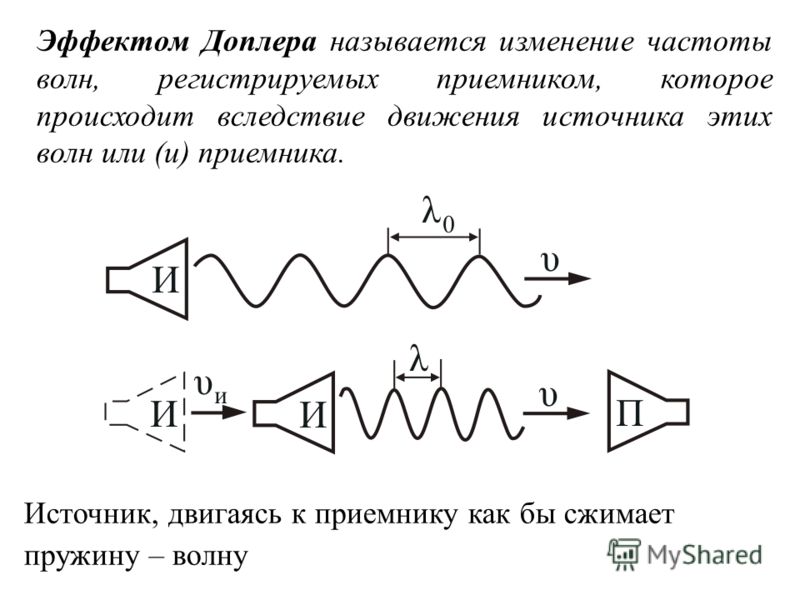
17.7 Эффект Доплера | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Объяснять изменение наблюдаемой частоты при приближении или удалении движущегося источника звука от неподвижного наблюдателя
- Объясните изменение наблюдаемой частоты по мере того, как наблюдатель движется к стационарному источнику звука или от него
Характерный звук проезжающего мимо мотоцикла является примером Эффект Доплера .
В частности, если вы стоите на углу улицы и наблюдаете, как машина скорой помощи со звуком сирены проезжает с постоянной скоростью, вы заметите два характерных изменения в звуке сирены. Во-первых, громкость звука увеличивается по мере приближения машины скорой помощи и уменьшается по мере ее удаления, что и ожидалось. Но, кроме того, высокий звук сирены резко меняется на более низкий звук. Когда машина скорой помощи проезжает, частота звука, слышимого стационарным наблюдателем, изменяется с постоянной высокой частоты на постоянную более низкую частоту, даже если сирена излучает постоянную частоту источника. Чем ближе проезжает скорая помощь, тем резче сдвиг. Кроме того, чем быстрее движется машина скорой помощи, тем больше смещение. Мы также слышим этот характерный сдвиг частоты для проезжающих автомобилей, самолетов и поездов.
Эффект Доплера — это изменение наблюдаемой частоты звука из-за движения источника или наблюдателя. Хотя этот эффект менее известен, он легко заметен для стационарного источника и движущегося наблюдателя.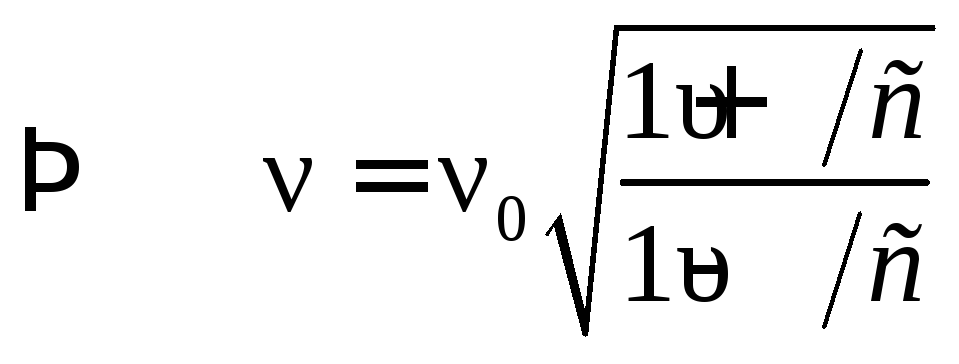
Например, если вы проедете в поезде мимо стационарного звукового сигнала, вы услышите, как частота звукового сигнала смещается с высокой на низкую, когда вы проходите мимо. Фактическое изменение частоты из-за относительного движения источника и наблюдателя называется доплеровским сдвигом . Эффект Доплера и доплеровский сдвиг названы в честь австрийского физика и математика Кристиана Иоганна Доплера (1803–1853), который проводил эксперименты как с движущимися источниками, так и с движущимися наблюдателями. Допплер, например, заставил музыкантов играть в движущемся открытом вагоне поезда, а также играть стоя рядом с железнодорожными путями, когда поезд проезжал мимо. Их музыку наблюдали как в поезде, так и вне его, и измеряли изменения частоты.
Что вызывает доплеровский сдвиг? (Рисунок) иллюстрирует звуковые волны, излучаемые стационарными и движущимися источниками в неподвижной воздушной массе. Каждое возмущение распространяется сферически от точки, в которой излучается звук.
Если источник неподвижен, то центр всех сфер, представляющих сжатие воздуха в звуковой волне, находится в одной точке, и неподвижные наблюдатели с обеих сторон слышат ту же длину волны и частоту, что и источник (случай а). Если источник движется, ситуация иная. Каждое сжатие воздуха движется по сфере из точки, в которой он был выпущен, но точка выброса движется. Эта движущаяся точка выброса заставляет сжатия воздуха быть ближе друг к другу с одной стороны и дальше друг от друга с другой. Таким образом, длина волны меньше в направлении движения источника (справа в случае б) и длиннее в противоположном направлении (слева в случае б). Наконец, если наблюдатели перемещаются, как в случае (с), частота, с которой они получают сжатия, изменяется. Наблюдатель, движущийся к источнику, принимает их с более высокой частотой, а человек, удаляющийся от источника, принимает их с более низкой частотой.
Рисунок 17.30 Звуки, излучаемые источником, распространяющимся сферическими волнами.
(а) Когда источник, наблюдатели и воздух неподвижны, длина волны и частота одинаковы во всех направлениях и для всех наблюдателей. (б) Звуки, излучаемые источником, движущимся вправо, распространяются от точек, в которых они излучались. Длина волны уменьшается, и, следовательно, частота увеличивается в направлении движения, так что наблюдатель справа слышит более высокий звук. Противоположное верно для наблюдателя слева, где длина волны увеличивается, а частота уменьшается. в) Тот же эффект возникает при движении наблюдателей относительно источника. Движение к источнику увеличивает частоту, поскольку наблюдатель справа проходит через большее количество гребней волны, чем если бы он оставался неподвижным. При движении от источника частота уменьшается, поскольку наблюдатель слева проходит через меньшее количество гребней волны, чем если бы он оставался неподвижным.
Мы знаем, что длина волны и частота связаны соотношением [latex] v=f\lambda , [/latex] где v — фиксированная скорость звука.
Звук движется в среде и имеет в этой среде одну и ту же скорость v независимо от того, движется источник или нет. Таким образом, f , умноженное на [латекс] \лямбда [/латекс], является константой. Поскольку наблюдатель справа в случае (b) получает более короткую длину волны, частота, которую он принимает, должна быть выше. Точно так же наблюдатель слева получает более длинную волну и, следовательно, слышит более низкую частоту. То же самое происходит и в случае (c). Наблюдатель, движущийся к источнику, принимает более высокую частоту, а наблюдатель, удаляющийся от источника, принимает более низкую частоту. В общем, относительное движение источника и наблюдателя друг к другу увеличивает принимаемую частоту. Относительное движение врозь снижает частоту. Чем больше относительная скорость, тем больше эффект.
Эффект Доплера возникает не только для звука, но и для любой волны, когда существует относительное движение между наблюдателем и источником. Доплеровские сдвиги возникают, например, в частоте звуковых, световых и водных волн.
Доплеровские сдвиги можно использовать для определения скорости, например, когда ультразвук отражается от крови при медицинской диагностике. Относительные скорости звезд и галактик определяются сдвигом частот света, получаемого от них, и многое говорят о происхождении Вселенной. На современную физику глубоко повлияли наблюдения доплеровских сдвигов.
Получение наблюдаемой частоты из-за доплеровского сдвига
Рассмотрим двух стационарных наблюдателей X и Y на (рис.), расположенных по обе стороны от стационарного источника. Каждый наблюдатель слышит одну и ту же частоту, и эта частота является частотой, создаваемой стационарным источником.
Рисунок 17.31 Неподвижный источник излучает звуковые волны с постоянной частотой [латекс] {f}_{\text{s}}, [/латекс] с постоянной длиной волны [латекс] {\lambda}_{\ text{s}}, [/latex] со скоростью звука v. Два стационарных наблюдателя X и Y по обе стороны от источника наблюдают частоту [latex] {f}_{\text{o}}={ f}_{\text{s}} [/латекс], с длиной волны [латекс] {\lambda}_{\text{o}}={\lambda}_{\text{s}}.
[/латекс]
Теперь рассмотрим стационарного наблюдателя X с источником, удаляющимся от наблюдателя с постоянной скоростью [латекс] {v}_{\text{s}}
. ] {f}_{\text{s}}, [/latex] с постоянной длиной волны [латекс] {\lambda }_{\text{s}} [/latex], со скоростью звука v.
Моментальные снимки источник с интервалом [латекс] {T}_{\text{s}} [/латекс] показан по мере того, как источник удаляется от стационарного наблюдателя X. Сплошные линии представляют положение звуковых волн после четырех периодов с начального времени. Пунктирные линии используются для отображения положения волн в каждый период времени. Наблюдатель слышит длину волны [латекс] {\ lambda} _ {\ text {o}} = {\ lambda} _ {\ text {s}} + \ text {Δ} x = {\ lambda} _ {\ text {s}}+{v}_{\text{s}}{T}_{\text{s}} [/латекс].
Используя тот факт, что длина волны равна произведению скорости на период, а период обратно пропорционален частоте, мы можем получить наблюдаемую частоту:
[латекс] \begin{array}{ccc}\hfill { \ lambda } _ {\ text {o}} & = \ hfill & {\ lambda } _ {\ text {s}} + \ text {Δ} x \ hfill \\ \ hfill v {T} _ {\ text { о}} & =\ hfill & v {T} _ {\ text {s}} + {v} _ {\ text {s}} {T} _ {\ text {s}} \ hfill \\ \ hfill \ frac {v} {{f} _ {\ text {o}}} & = \ hfill & \ frac {v} {{f} _ {\ text {s}}} = \ frac {{v} _ {\ текст {s}}} {{f} _ {\ text {s}}} = \ frac {v + {v} _ {\ text {s}}} {{f} _ {\ text {s}}} \ hfill \\ \hfill {f} _ {\ text {o}} & = \ hfill & {f} _ {\ text {s}} (\ frac {v} {v + {v} _ {\ text {s} }}).
\hfill \end{массив} [/latex]
По мере удаления источника от наблюдателя наблюдаемая частота становится ниже частоты источника.
Теперь рассмотрим источник, движущийся с постоянной скоростью [латекс] {v}_{s}, [/латекс] движущийся к неподвижному наблюдателю Y , также показанному на (Рисунок). Длина волны определяется Y как [латекс] {\ lambda} _ {\ text {o}} = {\ lambda} _ {\ text {s}} – \ text {Δ} x = {\ lambda} _ {\ text {s}} – {v} _ {\ text {s}} {T} _ {\ text {s}}. [/latex] Еще раз, используя тот факт, что длина волны равна скорости, умноженной на период, а период обратно пропорционален частоте, мы можем вывести наблюдаемую частоту:
[латекс] \begin{array}{ccc}\hfill {\lambda}_{\text{o}}& =\hfill & {\lambda}_{\text{s}}-\text{Δ} х \ hfill \\ \ hfill v {T} _ {\ text {o}} & = \ hfill & v {T} _ {\ text {s}} – {v} _ {\ text {s}} {T } _ {\ text {s}} \ hfill \\ \ hfill \ frac {v} {{f} _ {\ text {o}}} & = \ hfill & \ frac {v} {{f} _ {\ text{s}}}-\frac{{v}_{\text{s}}}{{f}_{\text{s}}}=\frac{v-{v}_{\text{s }}}{{f}_{\text{s}}}\hfill \\ \hfill {f}_{\text{o}}& =\hfill & {f}_{\text{s}}( \frac{v}{v-{v}_{\text{s}}}).
\hfill \end{массив} [/latex]
Когда источник движется, а наблюдатель неподвижен, наблюдаемая частота равна
[латекс] {f}_{\text{o}}={f}_{\text{s}}(\frac{v} {v\mp {v}_{\text{s}}})\text{‘} [/latex]
, где [latex] {f}_{\text{o}} [/latex] — частота наблюдаемый неподвижным наблюдателем, [латекс] {f}_{\text{s}} [/латекс] — частота, создаваемая движущимся источником, v — скорость звука, [латекс] {v}_{ \text{s}} [/latex] — постоянная скорость источника, причем верхний знак указывает на приближение источника к наблюдателю, а нижний знак — на источник, удаляющийся от наблюдателя.
Что произойдет, если наблюдатель движется, а источник неподвижен? Если наблюдатель движется к стационарному источнику, наблюдаемая частота выше, чем частота источника. Если наблюдатель удаляется от стационарного источника, наблюдаемая частота ниже частоты источника. Рассмотрим наблюдателя X на (рис.), когда наблюдатель движется к стационарному источнику со скоростью [латекс] {v}_{\text{o}} [/латекс].
Источник излучает тон с постоянной частотой [латекс] {f}_{\текст{с}} [/латекс] и постоянным периодом [латекс] {Т}_{\текст{с}}. [/latex] Наблюдатель слышит первую волну, излучаемую источником. Если бы наблюдатель был неподвижен, время прохождения одной длины волны звука должно быть равно периоду источника [латекс] {T}_{\text{s}}. [/latex] Поскольку наблюдатель движется к источнику, время прохождения одной длины волны меньше, чем [latex] {T}_{\text{s}} [/latex], и равно наблюдаемому периоду [latex ] {T} _ {\ text {o}} = {T} _ {\ text {s}} – \ text {Δ} t. [/latex] В момент времени [latex] t=0, [/latex] наблюдатель начинает с начала длины волны и движется ко второй длине волны по мере того, как длина волны удаляется от источника. Длина волны равна расстоянию, пройденному наблюдателем, плюс расстояние, пройденное звуковой волной до встречи с наблюдателем:
[латекс] \begin{array}{ccc}\hfill {\lambda}_{\text{s}}& =\hfill & v{T}_{\text{o}}+{v}_{ \text{o}}{T}_{\text{o}}\hfill \\ \hfill v{T}_{\text{s}}& =\hfill & (v+{v}_{\text{ о}}) {T} _ {\ text {o}} \ hfill \\ \ hfill v (\ frac {1} {{f} _ {\ text {s}}}) & = \ hfill & (v + { v} _ {\ text {o}}) (\ frac {1} {{f} _ {\ text {o}}}) \ hfill \\ \ hfill {f} _ {\ text {o}} & = \hfill & {f}_{\text{s}}(\frac{v+{v}_{\text{o}}}{v}).
\hfill \end{массив} [/latex]
Рис. 17.33 Стационарный источник излучает звуковую волну с постоянной частотой [латекс] {f}_{\text{s}} [/латекс], с постоянной длиной волны [латекс] {\lambda}_{\text{s }} [/latex] движущийся со скоростью звука v. Наблюдатель X движется к источнику с постоянной скоростью [latex] {v}_{\text{o}} [/latex], а на рисунке показаны начальная и конечное положение наблюдателя X. Наблюдатель X наблюдает частоту выше, чем частота источника. Сплошные линии показывают положение волн при [латексе] t=0 [/латекс]. Пунктирные линии показывают положение волн в точке [латекс] t={T}_{\text{o}} [/латекс].
Если наблюдатель удаляется от источника ((Рисунок)), можно найти наблюдаемую частоту:
[латекс] \begin{array}{ccc}\hfill {\lambda }_{\text{s} } & = \ hfill & v {T} _ {\ text {o}} – {v} _ {\ text {o}} {T} _ {\ text {o}} \ hfill \\ \ hfill v {T } _ {\ text {s}} & = \ hfill & (v- {v} _ {\ text {o}}) {T} _ {\ text {o}} \ hfill \\ \ hfill v (\ frac {1}{{f}_{\text{s}}})& =\hfill & \hfill (v-{v}_{\text{o}})(\frac{1}{{f}_ {\text{o}}})\\ \hfill {f}_{\text{o}}& =\hfill & {f}_{\text{s}}(\frac{v-{v}_ {\text{o}}}{v}).
\hfill \end{массив} [/latex]
Рисунок 17.34 Неподвижный источник излучает звуковую волну с постоянной частотой [латекс] {f}_{\text{s}} [/латекс], с постоянной длиной волны [латекс] {\lambda}_{\ text{s}} [/latex] движущийся со скоростью звука v. Наблюдатель Y удаляется от источника с постоянной скоростью [latex] {v}_{\text{o}} [/latex], а фигура показывает начальное и конечное положение наблюдателя Y. Наблюдатель Y наблюдает частоту ниже частоты источника. Сплошные линии показывают положение волн при [латексе] t=0 [/латекс]. Пунктирные линии показывают положение волн в точке [латекс] t={T}_{\text{o}} [/латекс].
Уравнения для наблюдателя, движущегося к стационарному источнику или от него, можно объединить в одно уравнение:
[латекс] {f}_{\text{o}}={f}_{\text{s}} (\frac{v±{v}_{\text{o}}}{v}), [/latex]
, где [latex] {f}_{\text{o}} [/latex] – наблюдаемая частота, [latex] {f}_{\text{s}} [/latex] – частота источника, [latex] {v}_{\text{w}} [/latex] – скорость звука, [latex] {v}_{\text{o}} [/latex] — скорость наблюдателя, верхний знак — для наблюдателя, приближающегося к источнику, а нижний — для наблюдателя, удаляющегося от источника.
(рисунок) и (рисунок) могут быть суммированы в одном уравнении (верхний знак означает приближение) и дополнительно проиллюстрировано на (рисунок):
[латекс] {f}_{\text{o}}={ f} _ {\ text {s}} (\ frac {v ± {v} _ {\ text {o}}} {v \ mp {v} _ {\ text {s}}}), [/latex]
” The fourth row contains “source moving away from observer”, “f subscript o equals f subscript s times v over v plus v subscript s”, “f subscript o equals f subscript s times v plus v subscript o over v plus v subscript s”, and f subscript o equals f subscript s times v minus v subscript o over v plus v subscript s.””>[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v ± {v} _ {\ text {o}}} {v \ mp { v}_{\text{s}}}) [/латекс]
где [латекс] {f}_{o} [/латекс] — наблюдаемая частота, [латекс] {f}_{s} [/латекс] — исходная частота, [латекс] {v}_ {w} [/latex] — скорость звука, [latex] {v}_{o} [/latex] — скорость наблюдателя, [latex] {v}_{s} [/latex] — скорость звука.
скорость источника, верхний знак соответствует приближению, а нижний — удалению.
Эффект Доплера связан с движением, и видео поможет визуализировать эффекты движущегося наблюдателя или источника. В этом видео показаны движущийся источник и неподвижный наблюдатель, а также движущийся наблюдатель и неподвижный источник. Также обсуждается эффект Доплера и его применение к свету.
Пример
Расчет доплеровского сдвига
Предположим, поезд с рупором на 150 Гц движется со скоростью 35,0 м/с в неподвижном воздухе в день, когда скорость звука составляет 340 м/с.
а) Какие частоты наблюдает человек, стоящий на обочине пути, при приближении поезда и после его прохождения?
(b) Какую частоту наблюдает машинист, едущий в поезде?
Стратегия
Чтобы найти наблюдаемую частоту в (а), мы должны использовать [латекс] {f} _ {\ text {obs}} = {f} _ {\ text {s}} (\ frac {v} {v\mp {v}_{\text{s}}}) [/latex], потому что источник движется. Знак «минус» используется для приближающегося поезда, а знак «плюс» — для удаляющегося поезда.
В (b) есть два доплеровских смещения — одно для движущегося источника и другое для движущегося наблюдателя.
Решение
- Введите известные значения в [латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v- {v} _ {\ text { с}}}): [/латекс]
[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v- {v} _ {\ text {s}}}) = (150\,\text{Гц})(\frac{340\,\text{м/с}}{340\,\text{м/с}-35,0\,\text{м/с}}). [/латекс]
Вычислите частоту, наблюдаемую неподвижным человеком при приближении поезда:
[латекс] {f}_{\text{o}}=(150\,\text{Гц})(1.11)=167\,\text{Гц}\text{.} [/latex]
Используйте то же уравнение со знаком плюс, чтобы найти частоту, слышимую неподвижным человеком при удалении поезда:
[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v + {v} _ {\ text {s}}}) = ( 150\,\text{Гц})(\frac{340\,\text{м/с}}{340\,\text{м/с}+35,0\,\text{м/с}}). [/латекс]
Вычислить вторую частоту:
[латекс] {f}_{\text{o}}=(150\,\text{Гц})(0,907)=136\,\text{Гц}\text{.
} [/latex] - Определить известные:
- Кажется разумным, что инженер получит ту же частоту, что и рупор, потому что относительная скорость между ними равна нулю.
- Относительно среды (воздуха) скорости равны [латексу] {v}_{\text{s}}={v}_{\text{o}}=35,0\,\text{м/с}\ текст{.} [/латекс]
- Первое доплеровское смещение для движущегося наблюдателя; второй для движущегося источника.
Используйте следующее уравнение:
[латекс] {f} _ {\ text {o}} = [{f} _ {\ text {s}} (\ frac {v ± {v} _ {\ text {o}}} {v}) ] (\ frac {v} {v \ mp {v} _ {\ text {s}}}). [/латекс]
Величина в квадратных скобках представляет собой частоту, сдвинутую Доплером из-за движущегося наблюдателя. Фактор справа — это эффект движущегося источника.
Поскольку машинист движется в направлении к звуковому сигналу, мы должны использовать знак плюс для [латекса] {v}_{\text{obs}}; [/latex] однако, поскольку рупор также движется в направлении от инженера, мы также используем знак плюс для [latex] {v}_{\text{s}}.
[/latex] Но поезд везет машиниста и гудок с одинаковой скоростью, поэтому [латекс] {v}_{\text{s}}={v}_{\text{o}}. [/latex] В результате все, кроме [latex] {f}_{\text{s}} [/latex] отменяется, что дает[латекс] {f}_{\text{o}}={f}_{\text{s}}. [/латекс]
} [/latex]
[/latex] Но поезд везет машиниста и гудок с одинаковой скоростью, поэтому [латекс] {v}_{\text{s}}={v}_{\text{o}}. [/latex] В результате все, кроме [latex] {f}_{\text{s}} [/latex] отменяется, что даетЗначение
Для случая, когда источник и наблюдатель не движутся вместе, рассчитанные числа действительны, когда источник (в данном случае поезд) находится достаточно далеко, чтобы движение происходило почти вдоль линии, соединяющей источник и наблюдатель. В обоих случаях сдвиг значителен и легко заметен. Обратите внимание, что сдвиг составляет 17,0 Гц для движения вперед и 14,0 Гц для движения назад. Сдвиги не симметричны.
Для машиниста, едущего в поезде, мы можем ожидать, что частота не изменится, поскольку источник и наблюдатель движутся вместе. Это соответствует вашему опыту. Например, нет доплеровского сдвига частоты разговоров водителя и пассажира на мотоцикле. Люди, разговаривающие, когда ветер перемещает воздух между ними, также не наблюдают в своем разговоре доплеровского сдвига.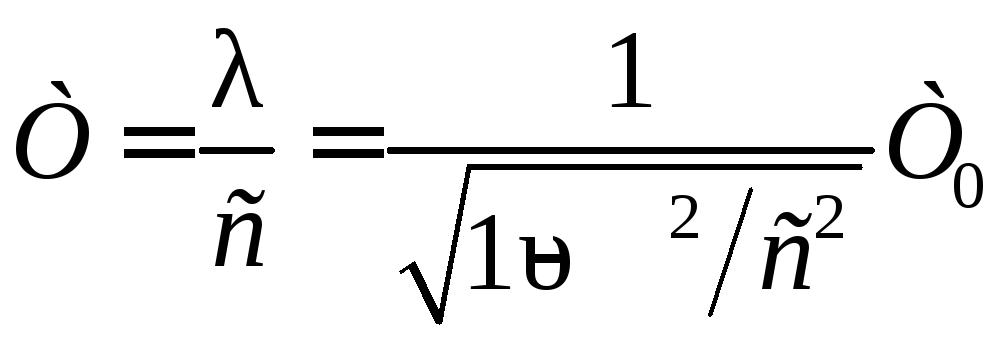
Важным моментом является то, что источник и наблюдатель не движутся друг относительно друга.
Проверьте свое понимание
Опишите ситуацию в вашей жизни, когда вы могли бы положиться на доплеровский сдвиг, чтобы помочь вам, когда вы ведете машину или идете рядом с транспортным потоком.
Показать решение
Эффект Доплера и сдвиг Доплера имеют множество важных применений в науке и технике. Например, доплеровский сдвиг в ультразвуке можно использовать для измерения скорости кровотока, а полиция использует доплеровский сдвиг в радаре (микроволне) для измерения скорости автомобиля. В метеорологии доплеровский сдвиг используется для отслеживания движения грозовых облаков; такой «доплеровский радар» может определить скорость и направление дождя или снега на погодном фронте. В астрономии мы можем исследовать свет, излучаемый далекими галактиками, и определять их скорость относительно нашей. По мере того, как галактики удаляются от нас, их свет смещается в сторону более низкой частоты и, следовательно, в сторону большей длины волны — так называемое красное смещение.
Такая информация от далеких-далеких галактик позволила нам оценить возраст Вселенной (с момента Большого взрыва) примерно в 14 миллиардов лет.
Резюме
- Эффект Доплера — это изменение наблюдаемой частоты звука из-за движения источника или наблюдателя.
- Фактическое изменение частоты называется доплеровским сдвигом.
Концептуальные вопросы
Доплеровский сдвиг реален или это просто сенсорная иллюзия?
Три стационарных наблюдателя наблюдают доплеровское смещение от источника, движущегося с постоянной скоростью. Наблюдатели располагаются, как показано ниже. Какой наблюдатель будет наблюдать наибольшую частоту? Какой наблюдатель будет наблюдать самую низкую частоту? Что можно сказать о частоте, наблюдаемой наблюдателем 3?
Показать ответ
Ниже показаны стационарный источник и движущиеся наблюдатели. Опишите частоты, наблюдаемые наблюдателями для этой конфигурации.
До 1980 года синоптики использовали обычный радар.
В 1960-х синоптики начали экспериментировать с доплеровским радаром. Как вы думаете, в чем преимущество использования доплеровского радара?
Показать решение
Задачи
(a) Какую частоту улавливает человек, наблюдающий за приближающейся машиной скорой помощи, движущейся со скоростью 110 км/ч и излучающей устойчивый звук сирены частотой 800 Гц? Скорость звука в этот день 345 м/с. б) Какую частоту она получает после того, как проехала машина скорой помощи?
Показать решение
(a) На авиашоу реактивный самолет летит прямо к трибунам со скоростью 1200 км/ч, излучая частоту 3500 Гц, в день, когда скорость звука составляет 342 м/с. Какая частота принимается наблюдателями? б) Какую частоту они получают, когда самолет летит прямо от них?
Какую частоту принимает мышь непосредственно перед тем, как ястреб летит на нее со скоростью 25,0 м/с и издает визг частотой 3500 Гц? Примем скорость звука равной 331 м/с.
Показать решение
Зритель на параде слышит тон 888 Гц от приближающегося трубача, который играет ноту 880 Гц. С какой скоростью приближается музыкант, если скорость звука 338 м/с?
Пригородный поезд гудит в гудок на 200 Гц, приближаясь к переезду. Скорость звука 335 м/с. (a) Наблюдатель, ожидающий на перекрестке, принимает частоту 208 Гц. Какова скорость поезда? б) Какую частоту получает наблюдатель при удалении поезда?
Показать решение
Можете ли вы ощутить изменение частоты, возникающее, когда вы тянете на себя камертон со скоростью 10,0 м/с в день, когда скорость звука составляет 344 м/с? Чтобы ответить на этот вопрос, рассчитайте коэффициент, на который смещается частота, и посмотрите, больше ли он 0,300%.
Два орла летят прямо навстречу друг другу, первый со скоростью 15,0 м/с, а второй со скоростью 20,0 м/с. Оба визжат, первый издает частоту 3200 Гц, а второй – частоту 3800 Гц.
Какие частоты они принимают, если скорость звука 330 м/с?
Показать решение
Студент A бежит по коридору школы со скоростью [латекс] {v}_{\text{o}}=5,00\,\text{м/с,} [/латекс] неся звон Камертон 1024,00 Гц в сторону бетонной стены. Скорость звука [латекс] v=343.00\,\текст{м/с}\текст{.} [/латекс] Студент B стоит неподвижно у стены. (a) Какую частоту слышит студент B ? (b) Какова частота ударов, которую слышит учащийся A ?
Машина скорой помощи с ревущей сиреной [латекс] (f=1.00\text{кГц}) [/латекс] приближается к месту аварии. Машина скорой помощи движется со скоростью 70,00 миль в час. Медсестра приближается к месту происшествия с противоположной стороны, бежит со скоростью [латекс] {v}_{o}=7.00\,\text{м/с}\text{.} [/latex] Какую частоту наблюдает медсестра? Предположим, что скорость звука равна [латекс] v=343,00\,\текст{м/с}\текст{.} [/латекс]
Показать решение
Частота сирены скорой помощи 900 Гц и приближается к вам.
Вы стоите на углу и наблюдаете частоту 960 Гц. Какова скорость машины скорой помощи (в милях в час), если скорость звука [латекс] v=340,00\,\текст{м/с?} [/латекс]
Какова минимальная скорость, с которой должен двигаться источник к вам, чтобы вы могли услышать, что его частота сдвинута доплеровским методом? То есть, какая скорость производит сдвиг [латекс] 0,300\текст{%} [/латекс] в день, когда скорость звука равна 331 м/с?
Показать решение
Глоссарий
- Эффект Доплера
- изменение наблюдаемой частоты звука из-за движения либо источника, либо наблюдателя
- Доплеровский сдвиг
- фактическое изменение частоты из-за относительного движения источника и наблюдателя
17.4 Эффект Доплера и звуковые удары
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Определение эффекта Доплера, доплеровского сдвига и звукового удара
- Рассчитать частоту звука, слышимого человеком, наблюдающим доплеровский сдвиг
- Опишите звуки, издаваемые объектами, движущимися быстрее скорости звука
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 6. B.5.1 Учащийся может создать или использовать диаграмму волнового фронта, чтобы продемонстрировать или качественно интерпретировать наблюдаемую частоту волны, зависящую от относительных движений источника и наблюдателя. (СП 1.4)
B.5.1 Учащийся может создать или использовать диаграмму волнового фронта, чтобы продемонстрировать или качественно интерпретировать наблюдаемую частоту волны, зависящую от относительных движений источника и наблюдателя. (СП 1.4) Характерный звук проезжающего мимо мотоцикла является примером эффекта Доплера. Высокий крик резко сменяется более низким ревом, когда мотоцикл проезжает мимо неподвижного наблюдателя. Чем ближе проезжает мотоцикл, тем резче переключение передач. Чем быстрее движется мотоцикл, тем больше смещение. Мы также слышим этот характерный сдвиг частоты для проезжающих гоночных автомобилей, самолетов и поездов. Оно настолько знакомо, что используется для обозначения движения, и дети часто имитируют его в игре.
Эффект Доплера — это изменение наблюдаемой частоты звука из-за движения источника или наблюдателя. Хотя этот эффект менее известен, он легко заметен для стационарного источника и движущегося наблюдателя.
Например, если вы проедете поезд мимо стационарного предупредительного звонка, вы услышите, как частота звонка смещается с высокой на низкую, когда вы проходите мимо. Фактическое изменение частоты из-за относительного движения источника и наблюдателя называется доплеровским сдвигом. Эффект Доплера и доплеровский сдвиг названы в честь австрийского физика и математика Кристиана Иоганна Доплера (1803–1853), который проводил эксперименты как с движущимися источниками, так и с движущимися наблюдателями. Допплер, например, заставил музыкантов играть в движущемся открытом вагоне поезда, а также играть стоя рядом с железнодорожными путями, когда поезд проезжал мимо. Их музыку наблюдали как в поезде, так и вне его, и измеряли изменения частоты.
Что вызывает доплеровский сдвиг? На рис. 17.15, рис. 17.16 и рис. 17.17 сравниваются звуковые волны, излучаемые стационарными и движущимися источниками в неподвижной воздушной массе. Каждое возмущение распространяется сферически от точки, где был испущен звук.
Если источник неподвижен, то все сферы, представляющие сжатие воздуха в звуковой волне, центрируются в одной и той же точке, и неподвижные наблюдатели с обеих сторон видят ту же длину волны и частоту, которые излучает источник, как на рис. 17.15. Если источник движется, как на рис. 17.16, то ситуация иная. Каждое сжатие воздуха движется по сфере из точки, где он был испущен, но точка выброса движется. Эта движущаяся точка выброса заставляет сжатия воздуха быть ближе друг к другу с одной стороны и дальше друг от друга с другой. Таким образом, длина волны короче в направлении движения источника (справа на рис. 17.16) и длиннее в противоположном направлении (слева на рис. 17.16). Наконец, если наблюдатели перемещаются, как показано на рис. 17.17, частота, с которой они получают компрессию, меняется. Наблюдатель, движущийся к источнику, принимает их с более высокой частотой, а человек, удаляющийся от источника, принимает их с более низкой частотой.
Рис. 17.15 Звуки, излучаемые источником, распространяются сферическими волнами.
Поскольку источник, наблюдатели и воздух неподвижны, длина волны и частота одинаковы во всех направлениях и для всех наблюдателей.
Рис. 17.16 Звуки, издаваемые источником, движущимся вправо, распространяются от точек, в которых они были изданы. Длина волны уменьшается и, следовательно, частота увеличивается в направлении движения, так что наблюдатель справа слышит более высокий звук. Противоположное верно для наблюдателя слева, где длина волны увеличивается, а частота уменьшается.
Рис. 17.17 Тот же эффект возникает, когда наблюдатели перемещаются относительно источника. Движение к источнику увеличивает частоту, поскольку наблюдатель справа проходит через большее количество гребней волны, чем если бы он оставался неподвижным. При движении от источника частота уменьшается, поскольку наблюдатель слева проходит через меньшее количество гребней волны, чем если бы он оставался неподвижным.
Мы знаем, что длина волны и частота связаны соотношением vw=fλ,vw=fλ, size 12{v rSub { size 8{w} } =fλ} {}, где vwvw size 12{v rSub { size 8{w}} } {} — фиксированная скорость звука.
Звук движется в среде и имеет одинаковую скорость vwvw size 12{v rSub { size 8{w} } } {} в этой среде независимо от того, движется источник или нет. Таким образом, ff size 12{f} {}, умноженный на λλ size 12{λ} {}, является константой. Поскольку наблюдатель справа на рис. 17.16 принимает более короткую длину волны, частота, которую он принимает, должна быть выше. Точно так же наблюдатель слева получает более длинную волну и, следовательно, слышит более низкую частоту. То же самое происходит и на рис. 17.17. Наблюдатель, движущийся к источнику, принимает более высокую частоту, а наблюдатель, удаляющийся от источника, принимает более низкую частоту. В общем, относительное движение источника и наблюдателя друг к другу увеличивает принимаемую частоту. Относительное движение врозь снижает частоту. Чем больше относительная скорость, тем больше эффект.
Эффект Доплера
Эффект Доплера возникает не только для звука, но и для любой волны, когда существует относительное движение между наблюдателем и источником.
Например, существуют доплеровские сдвиги частоты звука, света и водных волн. Доплеровские сдвиги можно использовать для определения скорости, например, когда ультразвук отражается от крови при медицинской диагностике. Разбегание галактик определяется сдвигом частот получаемого от них света и многое говорит о происхождении Вселенной. На современную физику глубоко повлияли наблюдения доплеровских сдвигов.
Для стационарного наблюдателя и движущегося источника можно показать, что частота f obs , принимаемая наблюдателем, равна 8{“obs”} } =f rSub { размер 8{s} } слева ( { {v rSub { размер 8{w} } } над {v rSub { размер 8{w} } +- v rSub { размер 8{ s} } } } right )} {}
где fsfs size 12{f rSub { size 8{s} } } } {} — частота источника, vsvs size 12{v rSub { size 8{s} } } {} — скорость источника вдоль линии, соединяющей источник и наблюдатель, а vwvw — скорость звука. Знак «минус» используется для движения к наблюдателю, а знак «плюс» — для движения от наблюдателя, производя соответствующие сдвиги вверх и вниз по частоте.
Обратите внимание, что чем больше скорость источника, тем больше эффект. Аналогично, для стационарного источника и движущегося наблюдателя частота принимаемых наблюдателем fobsfobs size 12{f rSub { size 8{“obs”} } } {} определяется как
17.21 fobs=fsvw±vobsvw,fobs=fsvw±vobsvw, размер 12{f rSub { размер 8{“obs”} } =f rSub { размер 8{s} } левый ( { {v rSub { размер 8{w } } +- v rSub { size 8{“obs”} } } over {v rSub { size 8{w} } } } right )} {}
где vobsvobs size 12{v rSub { size 8{“obs” } } } {} — скорость наблюдателя вдоль линии, соединяющей источник и наблюдатель. Здесь знак «плюс» соответствует движению к источнику, а «минус» — движению от источника.
Пример 17.4 Расчет доплеровского сдвига: звуковой сигнал поезда
Предположим, что поезд со звуковым сигналом частотой 150 Гц движется со скоростью 35,0 м/с в неподвижном воздухе в день, когда скорость звука составляет 340 м/с.
а) Какие частоты наблюдает человек, стоящий на обочине пути, при приближении поезда и после его прохождения?
(б) Какую частоту наблюдает машинист, едущий в поезде?
Стратегия
Чтобы найти наблюдаемую частоту в (a), fobs=fsvwvw±vsfobs=fsvwvw±vs size 12{f rSub { size 8{“obs”} } =f rSub { size 8{s} } left ( {{v rSub { size 8{w} } } over {v rSub { size 8{w} } +- v rSub { size 8{s} } } } right )} {} должен использоваться, поскольку источник движущийся.
Знак «минус» используется для приближающегося поезда, а знак «плюс» — для удаляющегося поезда. В (b) есть два доплеровских смещения — одно для движущегося источника и другое для движущегося наблюдателя.
Решение для (a)
(1) Введите известные значения в fobs=fsvwvw–vs.fobs=fsvwvw–vs. size 12{f rSub { size 8{“obs”} } =f rSub { size 8{s} } left ( { {v rSub { size 8{w} } } over {v rSub { size 8{w} } + – v rSub { размер 8{s} } } } правый )} {}
17,22 fobs=fsvwvw-vs=150 Гц340 м/с340 м/с – 35,0 м/sfobs=fsvwvw-vs=150 Гц340 м/с340 м /с – 35,0 м/с размер 12{f rSub { размер 8{“obs”} } =f rSub { размер 8{s} } слева ( { {v rSub { размер 8{w} } } над {v rSub { размер 8{w} } – v rSub { размер 8{s} } } } правый )= левый (“150″” Гц” правый) левый ({{“340″” м/с”} более {“340 м/с” с-35″ “.” “0 м/с”} } справа )} {}
(2) Вычислите частоту, которую наблюдает неподвижный человек при приближении поезда.
17,23 fobs=(150 Гц)(1,11)=167 Гцfobs=(150 Гц)(1,11)=167 Гц размер 12{ {}= \(“150” итал.
“Гц” \) \( 1 “.” ” 11″ \) =”167″ ital “Hz”} {}
(3) Используйте то же уравнение со знаком плюс, чтобы найти частоту, слышимую неподвижным человеком при удалении поезда.
17,24 fobs=fsvwvw+vs=150 Гц340 м/с340 м/с+35,0 м/sfobs=fsvwvw+vs=150 Гц340 м/с340 м/с+35,0 м/с размер 12{f rSub {размер 8{” obs”} } =f rSub { размер 8{s} } слева ( { {v rSub { размер 8{w} } } над {v rSub { размер 8{w} } +v rSub { размер 8{s} } } } справа )= слева (“150″” Гц” справа ) слева ({{“340″” м/с”} свыше {“340 м/с-35” “.” “0 м/с”} } справа ) } {}
(4) Рассчитать вторую частоту.
17,25 fobs=(150 Гц)(0,907)=136 Гцfobs=(150 Гц)(0,907)=136 Гц размер 12{ {}= \(“150” итал. “Гц” \) \( 0 “.” ” 97″ \) =”136″ ital “Hz”} {}
Обсуждение (a)
Вычисленные числа действительны, когда поезд находится достаточно далеко, чтобы движение происходило почти вдоль линии, соединяющей поезд и наблюдателя. . В обоих случаях сдвиг значителен и легко заметен. Обратите внимание, что сдвиг составляет 17 Гц для движения вперед и 14 Гц для движения назад.
Сдвиги не симметричны.
Решение для (b)
(1) Определите известные:
- Кажется разумным, что инженер получит ту же частоту, что и рупор, потому что относительная скорость между ними равна нулю.
- Относительно среды (воздуха) скорости vs=vobs=35 м/с. vs=vobs=35 м/с.
- Первое доплеровское смещение для движущегося наблюдателя; второй для движущегося источника.
(2) Используйте следующее уравнение:
17,26 fobs=[fsvw±vobsvw]vwvw±vs.fobs=[fsvw±vobsvw]vwvw±vs. size 12{f rSub { size 8{“obs”} } = left [f rSub { size 8{s} } left ( { {v rSub { size 8{w} } +- v rSub { size 8{“obs” } } } над {v rSub { размер 8 {w} } } } справа ) справа ] rSub { размер 8 {s} } слева ( { {v rSub { размер 8 {w} } } над {v rSub { размер 8 { w} } +v rSub { size 8{s} } } } right )} {}
Величина в квадратных скобках представляет собой частоту с доплеровским сдвигом из-за движущегося наблюдателя. Фактор справа — это эффект движущегося источника.