Второй закон термодинамики может нарушаться в квантовом мире
Закон неубывания энтропии в замкнутых системах, который является одной из формулировок знаменитого второго начала термодинамики, может нарушаться: как оказалось, в квантовых системах энтропия может убывать, выяснила международная группа учёных под руководством ведущего научного сотрудника Лаборатории квантовой теории информации МФТИ и Института теоретической физики им. Л.Д. Ландау РАН Гордея Лесовика. Результаты исследования опубликованы в журнале Scientific Reports (входит в группу Nature).
«Мы нашли квантового демона Максвелла, который может уменьшить энтропию в системе, причём даже не измеряя её состояние», — говорит Гордей Лесовик.
Рисунок. Демон Максвелла — микроскопическое разумное существо, которое придумал Джеймс Максвелл для иллюстрации парадокса Второго начала термодинамики.
Большинство процессов в рамках классической физики независимы от направления «стрелы времени»: любой из них можно развернуть в обратную сторону и никакие законы не будут нарушены.
В 1870-х годах принцип роста энтропии был сформулирован в более строгой форме Людвигом Больцманом в его так называемой H-теореме (произносится «аш-теорема»). Она гласит, что величина энтропии в замкнутой системе, состояние которой описывается кинетическим уравнением (называемым теперь уравнением Больцмана), либо растёт, либо остаётся постоянной. Долгое время эту теорему не удавалось доказать в рамках традиционной статистической физики без привлечения дополнительных ограничений. После появления квантовой механики учёные предположили, что «корни» H-теоремы связаны с квантовыми явлениями. В квантовой теории информации были получены важные результаты, описывающие условия, при которых энтропия системы не убывает.
Группа под руководством Лесовика впервые сформулировала H-теорему на языке квантовой физики и в течение нескольких лет пыталась найти её доказательство.
«Мы пытались доказывать: вроде бы, получалось, потом обнаруживалась „дырка“, мы её закрывали, затем „дырки“ появлялись опять, и в конце концов мы поняли, что это неспроста, что, может быть, эта теорема и не верна для квантовой системы и, даже если система энергетически изолирована, этого недостаточно, чтобы энтропия не убывала», — говорит учёный.
В результате учёные обнаружили условия, при которых второй закон термодинамики может локально нарушаться. Это может происходить в квантовых системах относительно небольшого, но макроскопического размера — сантиметры и даже метры. Существенное различие состоит в том, что если в классической физике уменьшение энтропии связано с передачей тепловой энергии, то в квантовом мире снижение энтропии может происходить без передачи энергии — за счёт квантовой запутанности.
«Представьте себе Золушку, которую мачеха заставляет разобрать перемешанную чечевицу и горох, то есть понизить энтропию в системе. Классическая Золушка в изолированной системе не смогла бы это сделать, а квантовая — может. Мы можем „вычистить“ состояния за счёт квантовых эффектов», — объясняет Лесовик.
Второе начало термодинамики
| на главную | доп. материалы | физика как наука и предмет | молекулярная физика и термодинамика |
Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.
Первое начало термодинамики, выражая закон сохранения и
превращения энергии, не позволяет установить направление протекания
термодинамических процессов.
Используя понятие энтропии и неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.
Можно дать более краткую формулировку второго начала
термодинамики: в процессах, происходящих в замкнутой системе, энтропия не
убывает. Здесь существенно, что речь идет о замкнутых системах, так как в
незамкнутых системах энтропия может вести себя любым образом (убывать,
возрастать, оставаться постоянной).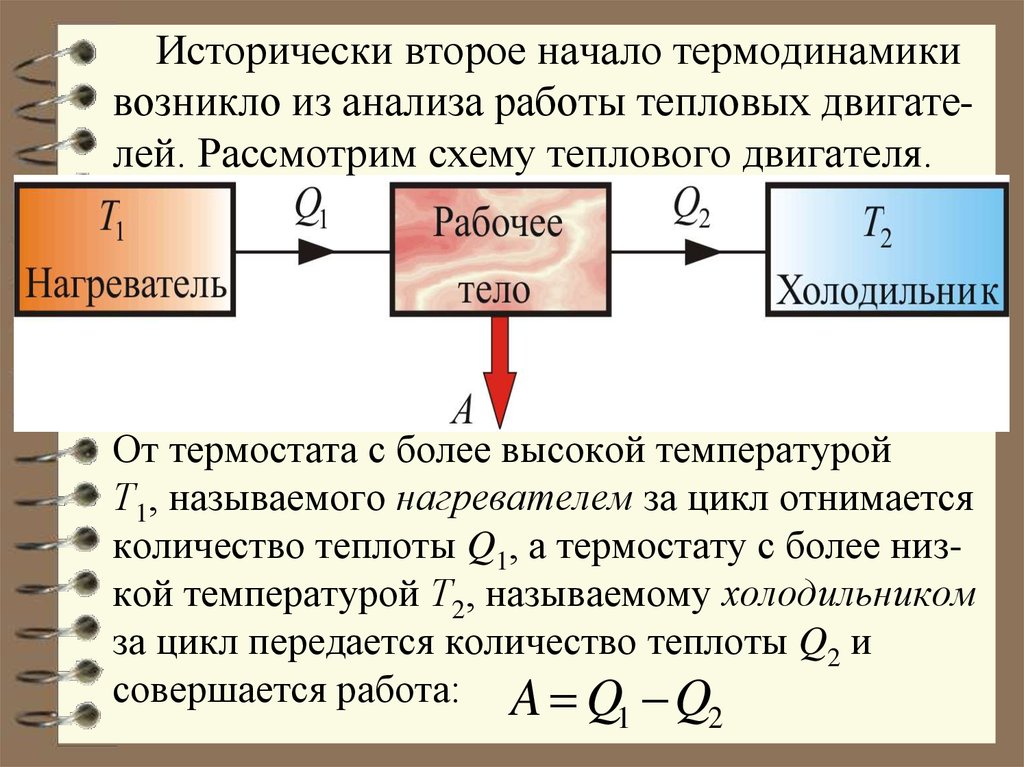
Кроме того, отметим еще раз, что энтропия
остается постоянной в замкнутой системе только при обратимых процессах. При
необратимых процессах в замкнутой системе энтропия всегда возрастает.
Формула Больцмана (57.8) позволяет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Таким образом, формула Больцмана позволяет дать статистическое толкование второго начала термодинамики. Оно, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему.
Укажем еще две формулировки второго начала термодинамики:
1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;
2) по Клаузиусу: невозможен круговой процесс,
единственным результатом которого является передача теплоты от менее нагретого
тела к более нагретому.
Можно довольно просто доказать (предоставим это читателю) эквивалентность формулировок Кельвина и Клаузиуса. Кроме того, показано, что если в замкнутой системе провести воображаемый процесс, противоречащий второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это же доказывает эквивалентность формулировки Клаузиуса (а следовательно, и Кельвина) и статистической формулировки, согласно которой энтропия замкнутой системы не может убывать.
В середине XIX в. возникла проблема так называемой тепловой
смерти Вселенной. Рассматривая Вселенную как замкнутую систему и применяя к
ней второе качало термодинамики, Клаузиус свел его содержание к утверждению, что
энтропия Вселенной должна достигнуть своего максимума. Это означает, что со
временем все формы движения должны перейти в тепловую. Переход же теплоты от
горячих тел к холодным приведет к тому, что температура всех тел во Вселенной
сравняется, т. е. наступит полное тепловое равновесие и все процессы во
Вселенной прекратятся — наступит тепловая смерть Вселенной.
Первые два начала термодинамики дают недостаточно сведений о поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом термодинамика, или теоремой Нернста* — Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:
Так как энтропия определяется с точностью до аддитивной
постоянной, то эту постоянную удобно взять равной нулю. Отметим, однако, что это
произвольное допущение, поскольку энтропия по своей сущности всегда
определяется с точностью до аддитивной постоянной. Из теоремы Нернста — Планка
следует, что теплоемкости Ср и СV
при 0 К равны нулю.
Второй закон термодинамики (в пересчете на энтропию)
спросил
Изменено 2 месяца назад
Просмотрено 4к раз
$\begingroup$
Является ли второй закон термодинамики (с точки зрения энтропии) для закрытых систем или изолированных систем? Я думал, что это должно быть справедливо для изолированных систем, таких как Вселенная. Но в книге «Основы физики» (Холлидей, Резник, Уокер) сформулирован закон для закрытых систем. Я смущен.
- термодинамика
- энтропия
- терминология
$\endgroup$
8
$\begingroup$
По вашим ссылкам изолированная система:
В физической науке изолированной системой может быть одно из следующих:
1) физическая система, настолько удаленная от других систем, что не взаимодействует с ними.
2) термодинамическая система, окруженная жесткими неподвижными стенами, через которые не могут пройти ни материя, ни энергия.
Закрытая система
В термодинамике замкнутая система может обмениваться с окружающей средой энергией (теплотой или работой), но не материей. Изолированная система не может обмениваться теплом, работой или веществом с окружающей средой, в то время как открытая система может обмениваться энергией и веществом
Я неравнодушен ко второму закону, сформулированному в терминах энтропии и энтропии, определяемой статистической механикой
Толкование энтропии в статистической механике — это мера неопределенности или путаницы в формулировке Гиббса, которая остается относительно системы после того, как были приняты во внимание ее наблюдаемые макроскопические свойства, такие как температура, давление и объем. Для данного набора макроскопических переменных энтропия измеряет степень, в которой вероятность системы распределена по различным возможным микросостояниям.
В отличие от макросостояния, которое характеризует легко наблюдаемые средние величины, микросостояние определяет все молекулярные детали системы, включая положение и скорость каждой молекулы. Чем больше таких состояний доступно системе с заметной вероятностью, тем больше энтропия. В статистической механике энтропия — это мера количества способов организации системы, часто принимаемая за меру «беспорядка» (чем выше энтропия, тем выше беспорядок). Это определение описывает энтропию как пропорциональную натуральному логарифму числа возможных микроскопических конфигураций отдельных атомов и молекул системы (микросостояний), которые могут привести к наблюдаемому макроскопическому состоянию (макросостоянию) системы. Константой пропорциональности является постоянная Больцмана. 9−23 Дж/К. Суммирование ведется по всем возможным микросостояниям системы, а p_i — вероятность того, что система находится в i-м микросостоянии
Поскольку все определения энтропии эквивалентны, эта формулировка делает ясным, что утверждение второго закона относится к изолированным системам, определенным выше.
Следуя второму закону термодинамики, энтропия изолированной системы всегда возрастает . Разница между изолированной системой и закрытой системой заключается в том, что тепло не может поступать в изолированную систему и из нее, но возможно тепловое движение в замкнутую систему и из нее.
При рассмотрении микросостояний тепловым и энергетическим обменом считаются взаимодействия, которые увеличивают количество микросостояний для изолированной системы, но могут оставить закрытую систему.
Таким образом, в отличие от другого ответа, я заключаю, что второй закон касается изолированных систем. Возможно, закрытый считается синонимом изолированного для книги, которую вы цитируете.
$\endgroup$
$\begingroup$
Второй закон термодинамики имеет много почти эквивалентных формулировок. Традиционные всегда предполагают закрытую систему, изоляция не требуется – допускается передача энергии как через тепло, так и через работу.
9A \frac{dU-dW}{T}
$$
, где $R$ – некоторое подходящее, согласованное исходное состояние, $U$ – внутренняя энергия, $W$ – работа, совершаемая системой, а $T$ – ее температура; интегрирование производится по любому пути в пространстве термодинамических состояний системы, соединяющему $A$ с $R$.
$\endgroup$
$\begingroup$
2-й закон в терминах энтропии: Второй закон термодинамики можно сформулировать в терминах энтропии. Если имеет место обратимый процесс, чистое изменение энтропии. В необратимом процессе энтропия всегда возрастает, поэтому изменение энтропии положительно. Общая энтропия Вселенной постоянно увеличивается
$\endgroup$
$\begingroup$
Я иногда задавался вопросом, используется ли иногда термин закрытая система для обозначения изолированной системы.
Но если это и так, то не везде. Возвращаясь ко второму закону с точки зрения энтропии, второй закон применим только к изолированной системе, находящейся в равновесии. Например, если кристаллизация происходит в закрытой системе (например, в металлическом ящике), энергия передается в окружающую среду, и энтропия закрытой системы падает. Только если ящик и его окружение рассматриваются как единое целое (то есть изолированная система), общая энтропия увеличивается.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
2-й закон термодинамики – Химия LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1923
Второй закон термодинамики гласит, что состояние энтропии всей вселенной как изолированной системы всегда будет увеличиваться с течением времени. Второй закон также гласит, что изменения энтропии во Вселенной никогда не могут быть отрицательными.
Введение
Почему, если оставить кубик льда при комнатной температуре, он начинает таять? Почему мы становимся старше и никогда не моложе? И почему всякий раз, когда комнаты убираются, они снова становятся грязными в будущем? Определенные вещи происходят в одном направлении, а не в другом, это называется «стрелой времени» и охватывает все области науки.
Термодинамическая стрела времени (энтропия) является мерой беспорядка в системе. Обозначаемое как \(\Delta S\), изменение энтропии предполагает, что само время асимметрично по отношению к порядку изолированной системы, что означает: система будет становиться более неупорядоченной по мере увеличения времени.
Основные участники разработки Второго закона
- Николя Леонар Сади Карно был французским физиком, которого считают «отцом термодинамики», поскольку он ответственен за происхождение Второго закона термодинамики, а также различные другие понятия. Текущая форма второго закона использует энтропию, а не калорию, которую Сади Карно использовал для описания закона. Калория связана с теплом, и Сади Карно пришел к выводу, что часть калорий всегда теряется в цикле движения. Таким образом, концепция термодинамической обратимости оказалась ошибочной, доказав, что необратимость является результатом любой системы, включающей работу.
- Рудольф Клаузиус был немецким физиком, и он разработал утверждение Клаузиуса, которое гласит: «Тепло вообще не может спонтанно течь от материала с более низкой температурой к материалу с более высокой температурой».
- Уильям Томпсон, также известный как лорд Кельвин, сформулировал утверждение Кельвина, в котором говорится: « невозможно полностью преобразовать тепло в циклическом процессе». Это означает, что невозможно преобразовать всю энергию системы в работу без потери энергии.
- Константин Каратеодори, греческий математик, создал свое собственное утверждение второго закона, утверждая, что «вблизи любого начального состояния есть состояния, к которым нельзя приблизиться сколь угодно близко через адиабатические изменения состояния».
Вероятности
Если данное состояние может быть выполнено больше способов, то это более вероятно, чем состояние, которое может быть достигнуто только меньшим количеством/одним способом.
Предположим, что коробка, заполненная деталями головоломки, была перемешана в своей коробке, вероятность того, что часть головоломки приземлится случайным образом, не там, где она идеально подходит, очень высока.
Почти каждый фрагмент головоломки приземлится где-то далеко от своего идеального положения. Вероятность того, что часть головоломки правильно приземлится на свое место, очень мала, так как это может произойти только в одном случае. Таким образом, неуместные кусочки мозаики имеют гораздо более высокую множественность, чем правильно расположенные кусочки мозаики, и мы можем правильно предположить, что неуместные кусочки мозаики представляют более высокую энтропию.
Вывод и объяснение
Чтобы понять, почему энтропия увеличивается и уменьшается, важно понимать, что всегда необходимо учитывать два изменения энтропии. Изменение энтропии окружения и изменение энтропии самой системы. Учитывая, что изменение энтропии Вселенной эквивалентно суммам изменений энтропии системы и окружающей среды:
\[\Delta S_{univ}=\Delta S_{sys}+\Delta S_{surr}=\dfrac {q_{sys}}{T}+\dfrac{q_{surr}}{T} \label{1}\]
При изотермическом обратимом расширении теплота q, поглощаемая системой из окружающей среды, равна
\[q_{rev}=nRT\ln\frac{V_{2}}{V_{1}}\label{2} \]
Поскольку теплота, поглощаемая системой, равна количеству тепла, теряемому окружающей средой, \(q_{sys}=-q_{surr}\).
Следовательно, для действительно обратимого процесса изменение энтропии равно
\[ \Delta S_{univ}=\dfrac{nRT\ln\frac{V_{2}}{V_{1}}}{T}+\dfrac{-nRT\ln\frac{V_{2}}{V_{ 1}}}{T}=0 \label{3}\]
Однако если процесс необратим, изменение энтропии равно
\[\Delta S_{univ}=\frac{nRT\ln \frac{V_{2}}{V_{1}}}{T}>0 \label{4}\]
Если мы поместим два уравнения для \(\Delta S_{univ}\) вместе для обоих типов процессов, у нас остается второй закон термодинамики,
\[\Delta S_{univ}=\Delta S_{sys}+\Delta S_{surr}\geq0 \label{5}\]
где \(\Delta S_{univ}\) равно нулю для действительно обратимого процесса и больше нуля для необратимого процесса. В действительности, однако, по-настоящему обратимые процессы никогда не происходят (или для их осуществления требуется бесконечно много времени), поэтому можно с уверенностью сказать, что все термодинамические процессы, с которыми мы сталкиваемся каждый день, необратимы в том направлении, в котором они происходят.
Второй закон термодинамики можно также сформулировать так: «Все спонтанные процессы производят увеличение энтропии Вселенной».
Свободная энергия Гиббса
При другом уравнении:
\[\Delta S_{total}=\Delta S_{univ}=\Delta S_{surr}+\Delta S{sys} \label{6}\]
Формула изменения энтропии в окружающей среде: \(\Delta S_{surr}=\Delta H_{sys}/T\). Если это уравнение заменить в предыдущей формуле, а затем уравнение умножить на T и на -1, получится следующая формула.
\[-T \, \Delta S_{univ}=\Delta H_{sys}-T\, \Delta S_{sys} \label{7}\]
Если заменить левую часть уравнения на \(G\), которая известна как энергия Гиббса или свободная энергия, уравнение принимает вид
\[\Delta G_{}=\Delta H-T\Delta S \label{8}\]
Теперь намного проще сделать вывод о том, является ли система спонтанной, неспонтанной или равновесной.
- \(\Delta H\) относится к изменению теплоты реакции. Положительное \(\Delta H\) означает, что тепло берется из окружающей среды (эндотермическое). Отрицательное значение \(\Delta H\) означает, что тепло выделяется или отдается окружающей среде (экзотермическое).
- \(\Delta G\) есть мера изменения свободной энергии системы, в которой протекает реакция при постоянном давлении (\(P\)) и температуре (\(T\)).
Согласно уравнению, когда энтропия уменьшается, а энтальпия увеличивается, изменение свободной энергии \(\Delta G_{}\) является положительным и не спонтанным, и не имеет значения, какова температура системы. Температура вступает в игру, когда энтропия и энтальпия увеличиваются или уменьшаются. Реакция не идет самопроизвольно, когда и энтропия, и энтальпия положительны, и при низких температурах, и реакция идет самопроизвольно, когда и энтропия, и энтальпия положительны, и при высоких температурах. Реакции протекают самопроизвольно, когда энтропия и энтальпия отрицательны при низких температурах, и реакция не является самопроизвольной, когда энтропия и энтальпия отрицательны при высоких температурах. Поскольку все спонтанные реакции увеличивают энтропию, можно определить, изменяется ли энтропия в соответствии со спонтанным характером реакции (уравнение \(\ref{8})).
| Чемодан | \(\Дельта H\) | \(\Дельта S\) | \(\Дельта G\) | Ответить |
|---|---|---|---|---|
| высокая температура | – | + | – | Спонтанный |
| низкотемпературный | – | + | – | Спонтанный |
| высокая температура | – | – | + | Несамопроизвольный |
| низкотемпературный | – | – | – | Спонтанный |
| высокая температура | + | + | – | Спонтанный |
| низкотемпературный | + | + | + | Несамопроизвольный |
| высокая температура | + | – | + | Несамопроизвольный |
| низкотемпературный | + | – | + | Несамопроизвольный |
Пример \(\PageIndex{1}\)
Начнем с простой реакции:
\[2 H_{2(g)}+O_{2(g)} \rightarrow 2 H_2O_{(g )}\]
Энтальпия, \(\Delta H_{}\), для этой реакции составляет -241,82 кДж, а энтропия, \(\Delta S_{}\), этой реакции составляет -233,7 Дж/К .
Если температура равна 25º C, то информации достаточно для расчета стандартного изменения свободной энергии \(\Delta G_{}\).
Первым шагом является преобразование температуры в Кельвины, поэтому прибавьте 273,15 к 25 и получите температуру 298,15 К. Затем подключите \(\Delta H_{}\), \(\Delta S_{}\) и температуры в \(\Delta G=\Delta H-T \Delta S_{}\).
\(\Delta G\)= -241,8 кДж + (298,15 К)(-233,7 Дж/К)
= -241,8 кДж + -69,68 кДж (не забудьте перевести джоули в килоджоули)
= – 311,5 кДж
Пример \(\PageIndex{2}\)
Вот немного более сложная реакция:
\[2 ZnO_{(s)}+2 C_{(g)} \rightarrow 2 Zn_{(s)}+2 CO_{(g)}\]
Если эта реакция протекает при комнатной температуре (25ºC) а энтальпия \(\Delta H_{}\) и стандартная свободная энергия \(\Delta G_{}\) составляют -957,8 кДж и -935,3 кДж соответственно. Нужно действовать несколько в обратном направлении, используя то же уравнение из примера 1 для приведенной свободной энергии.
-935,3 кДж = -957,8 кДж + (298,15 К) (\(\Delta S_{}\))
22,47 кДж = (298,15 К) (\(\Delta S_{}\)) (Добавить -957,8 кДж в обе стороны)
0,07538 кДж/К = \(\Delta S_{}\) (Разделите на 298,15 К в обе стороны)
Умножьте энтропию на 1000, чтобы преобразовать ответ в Джоули, и новый ответ будет 75,38 Дж/К.
Пример \(\PageIndex{3}\)
Для следующей реакции диссоциации
\[O_{2(g)} \rightarrow 2 O_{(g)}\]
при каких температурных условиях она будет происходить спонтанно?
Решение
Просто наблюдая за реакцией, можно определить, что в реакции увеличивается количество молей, поэтому энтропия увеличивается. Теперь осталось вычислить энтальпию реакции. Энтальпия положительна, потому что ковалентные связи разорваны. При разрыве ковалентных связей энергия поглощается, а это означает, что энтальпия реакции положительна. Другой способ определить, является ли энтальпия положительной, заключается в использовании данных о пласте и вычитании энтальпии реагентов из энтальпии продуктов для расчета общей энтальпии. Таким образом, если температура низкая, вероятно, что \(\Delta H_{}\) больше, чем \(T*\Delta S_{}\), что означает, что реакция не является самопроизвольной. Если температура велика, то \(T*\Delta S_{}\) будет больше, чем энтальпия, что означает, что реакция идет самопроизвольно.
Пример \(\PageIndex{4}\)
Следующая реакция
\[CO_{(г)} + H_2O_{(г)} \rightleftharpoons CO_{2(г)} + H_{2(г) }\]
возникает самопроизвольно при каких температурных условиях? Энтальпия реакции -40 кДж.
Раствор
Возможно, потребуется рассчитать энтальпию реакции, но в данном случае она дана. Если энтальпия отрицательна, то реакция экзотермическая. Теперь нужно найти, больше ли энтропия нуля, чтобы ответить на вопрос. Используя данные об энтропии образования и данные об энтальпии образования, можно определить, что энтропия реакции составляет -42,1 Дж/К, а энтальпия -41,2 кДж. Поскольку и энтальпия, и энтропия отрицательны, самопроизвольный характер реакции зависит от температуры реакции. Температура также определяла бы самопроизвольный характер реакции, если бы и энтальпия, и энтропия были положительными. Когда реакция протекает при низкой температуре, изменение свободной энергии также отрицательно, что означает, что реакция идет самопроизвольно.
Однако, если реакция происходит при высокой температуре, реакция становится неспонтанной, поскольку изменение свободной энергии становится положительным, когда высокая температура умножается на отрицательную энтропию, поскольку энтальпия не так велика, как произведение.
Пример \(\PageIndex{5}\)
При каких температурных условиях самопроизвольно происходит следующая реакция?
\[H_{2(g)} + I_{(g)} \rightleftharpoons 2 HI_{(g)}\]
Решение
Только после расчета энтальпии и энтропии реакции можно можно ответить на вопрос. Расчетная энтальпия реакции составляет -53,84 кДж, а энтропия реакции составляет 101,7 Дж/К. В отличие от двух предыдущих примеров температура не влияет на самопроизвольный характер реакции. Если реакция происходит при высокой температуре, изменение свободной энергии по-прежнему отрицательно, а \(\Delta G_{}\) по-прежнему отрицательно, если температура низкая. Глядя на формулу спонтанного изменения, можно легко прийти к тому же заключению, поскольку нет никакого способа, чтобы изменение свободной энергии было положительным.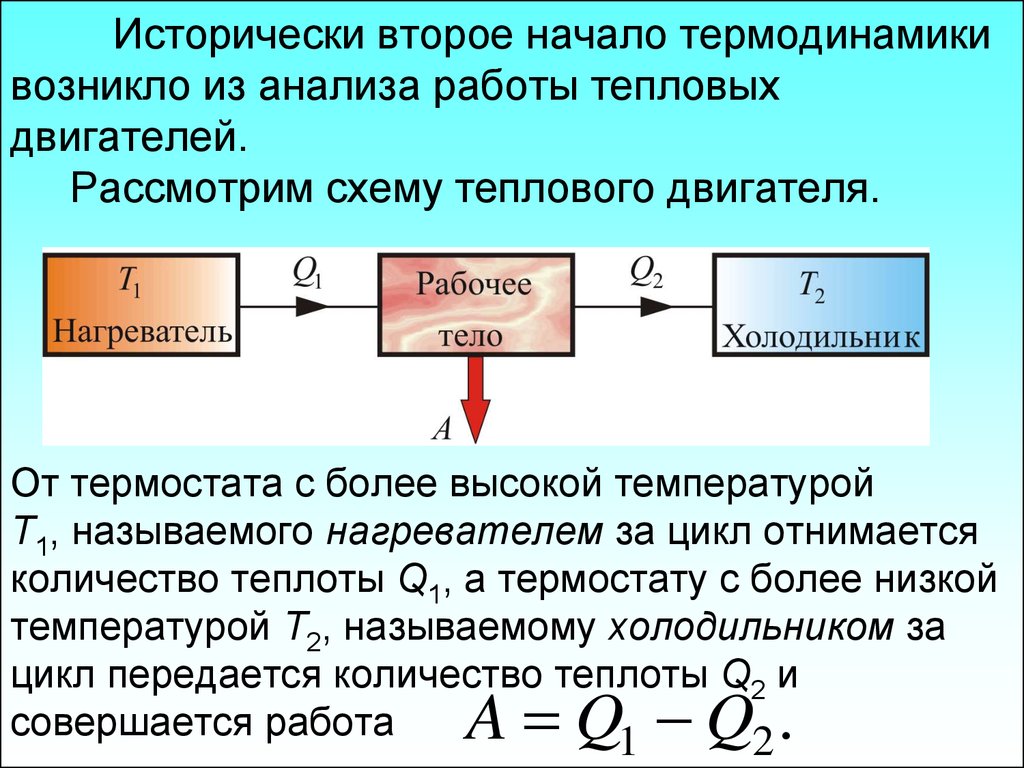
Следовательно, реакция идет самопроизвольно при любой температуре.
Применение Второго закона
Второй закон постоянно встречается вокруг нас, существуя как самая большая, самая мощная общая идея во всей науке.
Объяснение возраста Земли
Когда ученые пытались определить возраст Земли в 1800-х годах, им не удалось даже приблизиться к значению, принятому сегодня. Они также были неспособны понять, как трансформировалась земля. Лорд Кельвин, о котором упоминалось ранее, первым выдвинул гипотезу о том, что поверхность земли чрезвычайно горячая, подобная поверхности Солнца. Он считал, что земля остывает медленно. Используя эту информацию, Кельвин применил термодинамику, чтобы прийти к выводу, что Земле не менее двадцати миллионов лет, поскольку примерно столько же времени потребуется Земле, чтобы остыть до ее нынешнего состояния. Двадцать миллионов лет даже близко не соответствовали фактическому возрасту Земли, но это потому, что ученые во времена Кельвина не знали о радиоактивности.
Несмотря на то, что Кельвин ошибался в отношении возраста планеты, использование им второго закона позволило ему предсказать более точное значение, чем другие ученые того времени.
Эволюция и второй закон
Некоторые критики утверждают, что эволюция нарушает второй закон термодинамики, поскольку организация и сложность возрастают в процессе эволюции. Однако этот закон относится только к изолированным системам, а Земля не является изолированной или закрытой системой. Это очевидно для постоянного увеличения энергии на Земле из-за тепла, исходящего от Солнца. Таким образом, порядок может становиться более организованным, вселенная в целом становится более дезорганизованной, поскольку солнце высвобождает энергию и становится беспорядочной. Это связано с тем, как связаны второй закон и космология, что хорошо объяснено в видео ниже.
Задачи
- Предсказать изменение энтропии при преобразовании SO2 в SO3: 2 SO2 (г) + O2 (г) –> 2 SO3 (г)
- True/False: \(\Delta G\) > 0, процесс самопроизвольный
- Укажите условия, при которых \(\Delta G\) не является самопроизвольным.
- Верно/неверно: самопроизвольный процесс не может происходить при внешнем вмешательстве.
Ответы
- Энтропия уменьшается
- Ложь
- Случай 3, Случай 6, Случай 7, Случай 8 (Таблица выше)
- Правда
Ссылки
- Чанг, Рэймонд. Физическая химия для биологических наук. Саусалито, Калифорния: Университетские научные книги, 2005. .
- Как была создана Земля . Реж. Питер Чин. Домашнее видео A&E, 2008. DVD.
- Петруччи, Ральф Х., Уильям С. Харвуд, Ф. Г. Херринг и Джеффри Д. Мадура. Общая химия: принципы и современные приложения. 9-е изд. Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall, 2007. 791-796.
Условное содержание (участник Pro)
Авторы и авторство
- Константин Малли, Равнит Сингх (UCD), Тяньюй Дуан (UCD)
Второй закон термодинамики распространяется по незадекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts.