Соотношения Максвелла – Справочник химика 21
Уравнения Гиббса—Гельмгольца и соотношения Максвелла [c.118]Соотношения такого типа называют соотношениями Максвелла. Они будут подробно рассмотрены в 24. [c.94]
Затем берем перекрестную производную от выражения йО=УйР — 8йТ и получаем соотношение Максвелла в таком виде [c.104]
Соотношения Максвелла. Теплоемкости как функции давления и объема. [c.145]
Если производная содержит энтропию, то ее переводят в числитель и или исключают при помощи соотношений Максвелла, или посредством выражения (25.8) (при ы) = Т) приводят к стандартным производным. [c.125]
В этом случае энтропию нельзя исключить посредством соотношений Максвелла [ср. (24.17)]. [c.125]
Выражение в правой части можно легко свести к стандартным производным, используя (25.
При помощи соотношения Максвелла (24.24) и определений [c.130]
Далее, из соотношения Максвелла (24.11) следует [c.209]
ИЛИ, используя соотношения Максвелла (24.11), [c.218]
Кроме того, измеряемая приборами температура характеризует среднюю энергию броуновского колебания частиц. В реальности же в любой системе существует широкое распределение частиц по кинетическим энергиям, которое описывается соотношением Максвелла-Больцмана. Характер этого несимметричного распределения представлен на рис. 1.10. График показывает, что велика доля частиц, кинетическая энергия которых больше энергии, рассчитываемой по средней температуре.
В предыдущем параграфе показано, что электромагнитные ПОЛЯ описываются в общем случае следующей системой интегральных соотношений Максвелла [c.192]
Из (1. 38) можно найти соотношения, аналогичные соотношениям Максвелла [c.33]
38) можно найти соотношения, аналогичные соотношениям Максвелла [c.33]
Учитывая значения первых производных термодинамических потенциалов согласно (У.4), (У.5), (У.14), (У.15), (У.22), (У.23), (У.ЗО), (У.31), записанных в форме, аналогичной (УП.40) и (УП.41) при учете (УП.55), и беря вторые производные по соответствующим параметрам состояния аналогично тому, как это делалось при выводе соотношений Максвелла, получим группу уравнений, определяющих частные производные термодинамического сродства
Согласно соотношению Максвелла (V.85) [c.188]
Далее из уравнения (1Х.66) вытекает следующее соотношение Максвелла [c.218]
Ряд важных с точки зрения физического содержания соотношений, называемых соотношениями Максвелла, получается из (2.66), (2.70) и (2.73), а также из выражения для (1Н, если использовать свойство смешанных вторых производных. Например, из (2.72) при постоянстве всех Хк получим  84]
84]
Выражения (2.76) и (2.77) являются примерами соотношений Максвелла. Из (2.76), например, можно получить уравне- [c.84]
Соотношения Максвелла могут быть записаны для каждой пары слагаемых в правой части фундаментального уравнения (2,66) или уравнений (2.69а, 2.72, 2.73), а также уравнений для дифференциалов любых других функций состояния. [c.85]
Значение соотношений Максвелла состоит не только в том, что для ряда явлений они приводят к законам, описывающим эти явления (как это было показано на примере получения уравнения Клаузиуса—Клапейрона), но и в том важном для получения различных соотношений обстоятельстве, что с их помощью можно выразить не измеряемые на опыте величины (например, стоящие в правой части равенств (2.76) и (2.77) производные от энтропии) через измеряемые.
Здесь расположенные накрест величины всегда относятся к одной (i-й или k-vi) степени свободы, поскольку с помощью преобразований Лежандра производится замена переменных только в пределах каждого отдельного слагаемого в фундаментальном уравнении Гиббса и не может затрагиваться распределение термодинамических параметров между различными слагаемыми.

Заметим, что тот же результат получается и из соотношений Максвелла (2.76) и (2.77). [c.86]
Ряд важных с точки зрения физического содержания соотноше ний, называемых соотношениями Максвелла, получается из (2.58) [c.72]
Выражение (2.68) является одним из соотношений Максвелла. Из него, например, можно получить уравнение Клаузиуса—Кла- [c.72]
В качестве примера термодинамических соотношений, очень простых с математической точки зрения, но имеющих далеко не тривиальное физическое содержание, прежде всего следует указать на соотношения Максвелла.
Все же первое уравнение Максвелла не очень удобно для использования, поскольку обе входящие в него частные производные трудно сопоставить с опытными данными. Однако соотношения Максвелла, получаемые с помощью функций Р м О, имеют наиболее важное значение и широко применяются в химической термодинамике.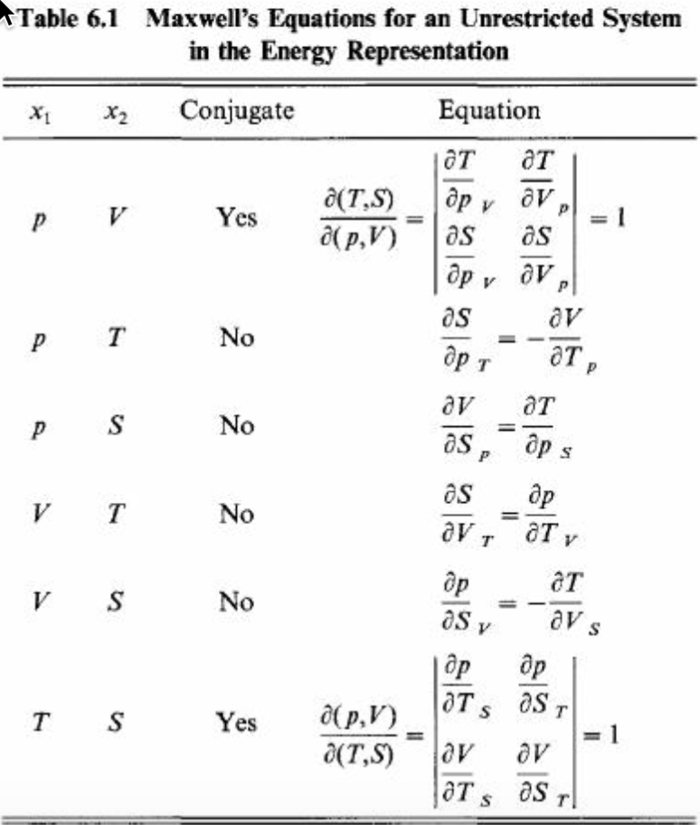
Уравнение (П.13) называют уравнением Клапейрона—Клаузиуса. Оно играет большую роль в теории фазовых переходов, но при математическом построении теории вытекает непосредственно из соотношений Максвелла. Исторически оно было получено гораздо сложнее. На основании анализа экспериментальных данных Клапейрон пришел к соотношению [c.57]
Искомое выражение легко получить из соотношения Максвелла для функции О дЮ да / де -
Отсюда, с применением соотношения Максвелла, получаем [c.59]
Входящую сюда частную производную легко найти из соотношений Максвелла [c.95]
Что такое соотношения Максвелла Напишите 4 основных уравнения Максвелла и расскажите о других видах соотношений Максвелла. Используйте соотношение Максвелла для вывода уравнения электрокапиллярности Липпмана и адсорбционного уравнения Гиббса. [c.297]
Примените одно из соотношений Максвелла к фазовым переходам и получите с его помощью уравнения Клапейрона — Клаузиуса.
Используйте соотношение Максвелла для вычисления внутренней энергии системы при различных объемах и энтальпии при различных давлениях. Запишите уравнение, определяющее внутреннюю энергию как функцию объема и температуры. Сделайте то же самое для энтальпии как функции давления и температуры. [c.297]
Используйте соотношения Максвелла для определения энтропии как функции давления и температуры. Найдите значение энтропии системы при произвольных давлении и температуре. Какие экспериментальные данные необходимы для такого расчета [c.297]
Соотношение (695) называется соотношением Максвелла . Например, для алмаза при v 10 Гц величина е 5,7, а 5,76. Однако соотношение Максвелла, как правило, перестает быть верным в области видимого света у таких тел, которые в инфракрасной части показывают избирательные области поглощения. Противоречие это, однако, весьма просто разрешается с позиций электронной теории (см.
Эти уравнения называются соотношениями Максвелла. Важнейшими частными случаями (для однокомпонентной системы) являются [c.121]
Согласно уравнению (25.8) для каждого класса достаточно знать девять величин дх1дт) , чтобы сконструировать все частные производные класса. Таким образом, задача сводится к нахождению 90 уравнений. Использование соотношений Максвелла ( 24) уменьшает это число еще вдвое, так что остается 45 основных уравнений, которые Бриджмен свел в таблицы.
Как МЫ ВИДИМ, Р1екоторые из соотношений Максвелла были открыты исходя из опытных данных, хотя нри последовательном термодинамическом рассмотрении их можно сразу записать, разбирая математические свойства функций состояния 1/, Р, О или С. К числу соотношений Максвелла относится также знаменитое адсорбционное уравнение Гиббса [c.58]
МАКСВЕЛЛА СООТНОШЕНИЯ – это… Что такое МАКСВЕЛЛА СООТНОШЕНИЯ?
- МАКСВЕЛЛА СООТНОШЕНИЯ
- МАКСВЕЛЛА СООТНОШЕНИЯ
-
– соотношения между производными термодинамич.
 ф-ций:
ф-ций:где P– давление, T– абс. темп-pa, V– объём, S– энтропия.M. с. можно получить из второго начала термодинамики. Напр., из термодинамич. равенства где U– внутр. энергия, следует первое M. с. как условие того, что dU есть полный дифференциал. Остальные M. с. следуют из того, что энтальпия H, энергия Гельмгольца F и энергия Гиббса G являются характеристическими функциями или термодинамическими потенциалами в переменных S, P; V, T; P, T. Иногда M. с. наз. соотношениями взаимности.
Лит.: Стенли Г., Фазовые переходы и критические явления, пер. с англ., M., 1973, гл. 2; Новиков И. И., Термодинамика, M., 1984, p 2, 8. Д. H. Зубарев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А.
 М. Прохоров.
1988.
М. Прохоров.
1988.
.
- МАКРОСКОПИЧЕСКИЕ КВАНТОВЫЕ ЭФФЕКТЫ
- МАКСВЕЛЛА ТЕНЗОР НАТЯЖЕНИЙ
Смотреть что такое “МАКСВЕЛЛА СООТНОШЕНИЯ” в других словарях:
МАКСВЕЛЛА УРАВНЕНИЯ — фундаментальные ур ния классич. макроскопич. электродинамики, описывающие эл. магн. явления в любой среде (и в вакууме). Сформулированы в 60 х гг. 19 в. Дж. Максвеллом на основе обобщения эмпирич. законов электрич. и магн. явлений и развития идеи … Физическая энциклопедия
Максвелла распределение — Функция плотности распределения Распределение Максвелла распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и… … Википедия
Максвелла уравнения — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
Уравнения Максвелла — Классическая электродинамика … Википедия
Распределение Максвелла — Функция плотности распределения Распределение Максвелла распределение вероятности, встречающееся в физике и химии.
 Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и… … Википедия
Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и… … ВикипедияРаспределение Максвелла — Больцмана — Функция плотности распределения Распределение Максвелла распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и… … Википедия
Уравнение максвелла — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
ЭЛЕКТРОДИНАМИКА — классическая, теория (неквантовая) поведения электромагнитного поля, осуществляющего взаимодействие между электрич. зарядами (электромагнитное взаимодействие). Законы классич. макроскопич. Э. сформулированы в Максвелла уравнениях, к рые позволяют … Физическая энциклопедия
Максвелл, Джеймс Клерк — В Википедии есть статьи о других людях с такой фамилией, см.
 Максвелл. Джеймс Клерк Максвелл James Clerk Maxwell … Википедия
Максвелл. Джеймс Клерк Максвелл James Clerk Maxwell … ВикипедияЭлектромагнитная теория света — 1. Характерные свойства луча света. 2. Свет не есть движение упругого твердого тела механики. 3. Электромагнитные явления как механические процессы в эфире. 4. Первая Максвеллова теория света и электричества. 5. Вторая Максвеллова теория. 6.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Книги
- Научные основы материаловедения стекол. Учебное пособие, Немилов Сергей Владимирович. Материаловедение стёкол – веществ, находящихся в стеклообразном состоянии, – имеет как теоретический, так и практический аспекты. В настоящее время отсутствует учебная литература, которая… Подробнее Купить за 2585 руб
- Научные основы материаловедения стекол, Немилов С.В.. Материаловедение стёкол веществ, находящихся в стеклообразном состоянии, имеет как теоретический, так и практический аспекты. В настоящее время отсутствует учебная литература, которая… Подробнее Купить за 1777 грн (только Украина)
- Научные основы материаловедения стекол, Немилов С.
 В.. Материаловедение стёкол — веществ, находящихся в стеклообразном состоянии, — имеет как теоретический, так и практический аспекты. В настоящее время отсутствует учебная литература, которая… Подробнее Купить за 1374 руб
В.. Материаловедение стёкол — веществ, находящихся в стеклообразном состоянии, — имеет как теоретический, так и практический аспекты. В настоящее время отсутствует учебная литература, которая… Подробнее Купить за 1374 руб
Вывод соотношений Максвелла – Энциклопедия по машиностроению XXL
Ж-4.2. Вывод соотношений Максвелла [c.336]Рассматриваются общие методы преобразования переменных в термодинамических уравнениях. Выводятся соотношения Максвелла и термодинамические уравнения состояния. Рассматривается вопрос [c.85]
Важнейшим выводом теории Максвелла явилось положение, согласно которому скорость распространения электромагнитного поля в вакууме равняется отношению электромагнитных и электростатических единиц силы тока второй, не менее важный вывод гласил, что показатель преломления электромагнитных волн равняется У ер, где е — диэлектрическая, ар — магнитная проницаемости среды. Таким образом, скорость распространения электромагнитной волны, в частности света, оказалась связанной с константами вещества, в котором распространяется свет. Эти константы первоначально вводились в уравнения Максвелла формально и имели чисто феноменологический характер. Напомним, что в механической (упругой) теории никакой связи между оптическими характеристиками среды (скорость света) и ее механическими свойствами (упругость, плотность) установлено не было. Известно, что для целого ряда газообразных и жидких диэлектриков соотношение Максвелла п = Уе х е (ибо р. близко к 1) выполняется достаточно хорошо
[c.539]
Таким образом, скорость распространения электромагнитной волны, в частности света, оказалась связанной с константами вещества, в котором распространяется свет. Эти константы первоначально вводились в уравнения Максвелла формально и имели чисто феноменологический характер. Напомним, что в механической (упругой) теории никакой связи между оптическими характеристиками среды (скорость света) и ее механическими свойствами (упругость, плотность) установлено не было. Известно, что для целого ряда газообразных и жидких диэлектриков соотношение Максвелла п = Уе х е (ибо р. близко к 1) выполняется достаточно хорошо
[c.539]
Уравнение Клаузиуса — Клапейрона представляет собой полезное соотношение между температурой и давлением некоторого вещества, находящегося в состоянии насыщения. Мы приведем его строгий вывод с помощью одного из соотношений Максвелла. [c.323]
Вывод обобщенных соотношений Стефана-Максвелла методами термодинамики необратимых процессов.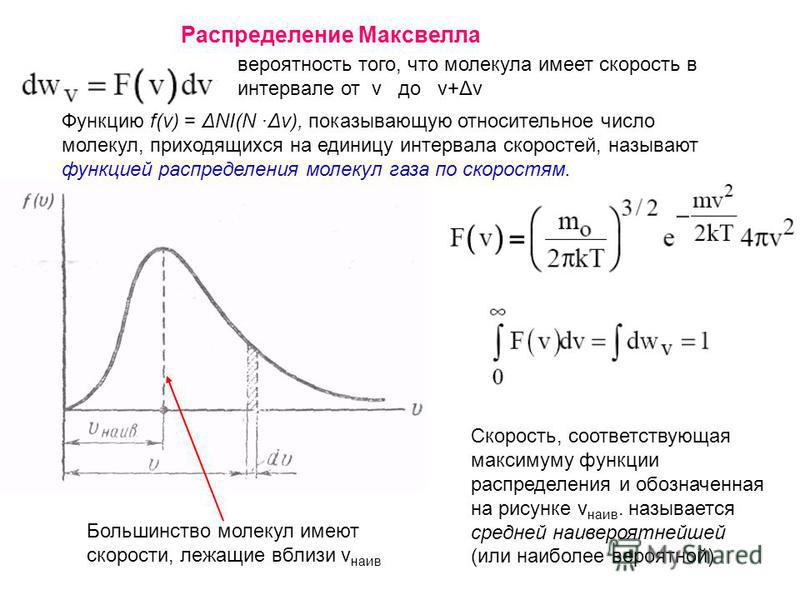 Для феноменологического вывода соотношений Стефана-Максвелла (для регулярных движений смеси) разрешим уравнения (2.3.16) и (2.3.17) относительно обобщенных термодинамических сил XQJ и X J =- p/n )d J (р = 1,2,…,//) через потоки J J и (1,2,…,//)
[c.99]
Для феноменологического вывода соотношений Стефана-Максвелла (для регулярных движений смеси) разрешим уравнения (2.3.16) и (2.3.17) относительно обобщенных термодинамических сил XQJ и X J =- p/n )d J (р = 1,2,…,//) через потоки J J и (1,2,…,//)
[c.99]
Важнейший вывод из полученных соотношений — частота й)о, при которой наступает заметное поглощение, лежит в видимой или ультрафиолетовой области спектра и при всех частотах со [c.201]
Два параметра их являются константами, характеризующими оптические свойства металла. Выводя волновое уравнение из уравнений Максвелла для металла, мы получим соотношения [c.491]
Это уравнение выводится аналогично тому, как получено уравнение (6.3.9). Величины Ji , как обычно, определяю ся из соотношений Стефана—Максвелла, а Jis , ные потоки компонентов конденсированной фазы и выше определяются по формулам [c.264]
Этот фокус главным или вторичным. Пределы применимости принципа Гюйгенса и соотношений, получаемых с помощью преобразования Фурье, при рассмотрении образования изображения станут совершенно очевидными, если при выводе этих соотношений исходить из уравнений Максвелла [4, 5]. [c.18]
[c.18]
Соотношения Стефана-Максвелла. Для вывода обобщенных соотношений Стефана-Максвелла (см. разд. 2.3.3.) для турбулентных многокомпонентных смесей, разрешим относительно термодинамических сил через потоки [c.228]
Определение вида функции / представляет собой задачу статистической механики. Именно эту задачу оказалось невозможно решить с помощью классической теории. Выводы термодинамики [соотношения (5.24), (5.26) и (5.41)], напротив, имеют неограниченную применимость, ибо основаны лишь на двух положениях механики системы, а именно на формуле Максвелла (5.20) для давления излучения и понятии параметрической инвариантности, которые сохраняют силу и в квантовой теории. [c.97]
Квантовые свойства С., обнаружившиеся при изучении спектров и действий С., не объяснимы теорией Максвелла. Для создания единой теории С., обнимающей как законы распространения, так и процессы излучения и поглощения С., необходима новая квантовая электродинамика. Отсутствие таковой заставило наряду с волновым представлением о С. пользоваться во многих случаях видоизмененной корпускулярной теорией С. Помимо объяснения спектральных закономерностей и действий С. теория фотонов совместима с рядом явлений, которые ранее рассматривались ка1 очевидное доказательство волновой природы С. При этом необходимо помимо квантовых соотношений пользоваться выводами теории относительности. Примером может служить классический опыт Фуко, доказавший, что вопреки корпускулярной механич. теории Ньютона скорость С. в веществе меньше, чем в пустоте. Если корпускула Ньютона с массой т и скоростью с падает под углом г на границу раздела пустоты и среды и, преломляясь под углом г, движется со скоростью и, то тангенциальная слагающая количества движения корпускулы должна остаться неизменной при переходе границы, откуда следует, что
[c.148]
Отсутствие таковой заставило наряду с волновым представлением о С. пользоваться во многих случаях видоизмененной корпускулярной теорией С. Помимо объяснения спектральных закономерностей и действий С. теория фотонов совместима с рядом явлений, которые ранее рассматривались ка1 очевидное доказательство волновой природы С. При этом необходимо помимо квантовых соотношений пользоваться выводами теории относительности. Примером может служить классический опыт Фуко, доказавший, что вопреки корпускулярной механич. теории Ньютона скорость С. в веществе меньше, чем в пустоте. Если корпускула Ньютона с массой т и скоростью с падает под углом г на границу раздела пустоты и среды и, преломляясь под углом г, движется со скоростью и, то тангенциальная слагающая количества движения корпускулы должна остаться неизменной при переходе границы, откуда следует, что
[c.148]
Из рис. 2 видно, что кривые Максвелла и Релея лежат внутри области, даваемой соотношениями (9) и (10), достаточно близко подходя к верхней границе.
 Это указывает на то, что истинная кривая должна лежать ближе к верхней границе, чем к нижней. Этот вывод подтверждают и экспериментальные данные [101 и [И].
[c.54]
Это указывает на то, что истинная кривая должна лежать ближе к верхней границе, чем к нижней. Этот вывод подтверждают и экспериментальные данные [101 и [И].
[c.54]Уравнения Максвелла имеют вид уравнений (1а) и (2а) разд. 9.12. Мы опять выразим Е и Н с помощью уравнения (10) разд. 9.21 через четыре вектора М , N , М , N , получаемых из двух решений и и v) скалярного волнового уравнения. Эти векторы подчиняются тем же соотношениям (8) и (9) разд. 9.21, однако вывод их из функций и и v иной. Определение, которым здесь следует пользоваться и которое заменяет уравнение (7) разд. 9.21, имеет вид [c.346]
Поскольку полное представление о распространении волн СВЧ-диапазона здесь дать невозможно, ограничимся рассмотрением наиболее важных соотношений, необходимых для понимания применения СВЧ-излучения в неразрушающем контроле. Вывод этих соотношений основан на решении уравнений Максвелла, приводимом в любом курсе электродинамики.
[c. 429]
429]
Распределение числа молекул по скоростям согласно уравнению Максвелла является формой равновесия теплового движения. Растворимость тоже равновесное явление. Поэтому соотношение Максвелла послужило автору основой для вывода уравнения растворимости газов жидкостя.х, которое обеспечило вычисление растворимости газов в жидкостях определение энергии взаимодействия газовы.х молекул с молекулами растворителей позволило раскрыть физическую природу константы закона Генри и привело к обоснованию других эмпирических и полуэмпирических закономерностей. Оно же позволило раскрыть физическую природу двух констант, входящих в полуэмпирическое уравнение И. Р. Кричевского и Я. С. Казарновского и теоретически рассчитать их значения. Полученные расчетным путем значениу двух констант уравнения И. Р. Кричевского и Я. С. Казарновского близостью теоретически вычисленных величин к экспериментально найденным И. Р. Кричевским и Я. С. Казарновским и др. подтверждают справедливость уравнения автора и указывают на раскрытие физической природы констант известного полуэмпирического уравнения. [c.123]
[c.123]
Карр и Цимм [27] произвели весьма тщательные измерения коэффициента рассеяния для нескольких жидкостей. Они получили значения, существенно (приблизительно на 40%) превышающие опубликованные ранее данные ). Рассмотрев величину aIAii RTК , Карр и Цимм пришли к выводу, что ни формула Лорентц — Лоренца, ни предложенное Бхагавантамом [14] так называе юе соотношение Максвелла, связывающее показатель преломления с плотностью, не соответствуют экспериментальным данным даже для жидкостей типа четыреххлористого углерода. [c.108]
В этой главе выводятся выражения для распределения оптического поля в направлении, перпендикулярном плоскости р — п-перехода в гетеролазерах, и даны характерные численные примеры для GaAs—Al.,Gai-.tAs-reTepo TpyKTyp. Рассмотрение распределения оптического поля вдоль плоскости перехода проводится после обсуждения в гл. 7 лазеров с полосковой геометрией, Уравнения Максвелла приведены в 2 настоящей главы, где также выводятся соотношения, связывающие проводимость и диэлектрическую проницаемость с коэффициентом поглощения и показателем преломления. Вывод этих соотношений помогает лучше понять процесс распространения волн и позволяет
[c.32]
Вывод этих соотношений помогает лучше понять процесс распространения волн и позволяет
[c.32]
Распространение принципа относительности на электромагнитные явления — на все физические явления — означало, что необходимо было найти такие преобразования зравнений Максвелла, чтобы при переходе от одной инерциальной системы к другой их вид не менялся и скорость света оставалась постоянной. Эйнштейн строго показывает, что этим требованиям удовлетворяют преобразования Лоренца (83). При этом из формальных математических выводов они приобретают ясный физический смысл преобразований координат и времени при переходе от одной инерциальной системы к другой. Отметим разницу в пути, которым шли к соотношениям (83j Лоренц и Эйнштейн. Лоренц нашел их… как гипотезу о сокращении размеров тел в процессе их движения. Эйнштейн показал, что в постулате относительности речь идет не только о гипотезе сокращения тел, но и о новой трактовке времени [67]. Время, бывшее незыблемым, абсолютным, меняет свое течение в различных системах отсчета. В движущихся системах течение времени замедляется
[c.134]
В движущихся системах течение времени замедляется
[c.134]
ФРЕНЕЛЯ ФЙРМУЛЫ—определяют отношения амплитуды, фазы и состояния поляризации отражённой и преломлённой световых волн, возникающих при прохождении света через границу раздела двух прозрачных диэлектриков, к соответствующим характеристикам падающей волны. Установлены О. Ж. Френелем в 1823 на основе представлений об упругих поперечных колебаниях эфира. Однако те же самые соотношения—Ф. ф.— следуют в результате строгого вывода из эл.-магн. теории света при решении ур-ний Максвелла. [c.375]
В этой вводной главе дается обзор и вывод некоторых основных соотношений для классических электромагнитных полей. Исходя из у ивнений Максвелла и материальных уравнений, мы получим выражения для плотности и потока энергии электромагнитного поля. Будет доказана теорема Пойнтинга, а также выведены законы сохранения и волновые уравнения. Мы подробно рассмотрим распространение монохроматических плоских волн и некоторые их важные свойства, а также обсудим понятия фазовой скорости и групповой скорости волнового пакета, распространяющегося в среде с дисперсией.
[c.9]
Мы подробно рассмотрим распространение монохроматических плоских волн и некоторые их важные свойства, а также обсудим понятия фазовой скорости и групповой скорости волнового пакета, распространяющегося в среде с дисперсией.
[c.9]
TO получается положительное значение времени до разрушения. Если k растет так, что выражение в фигурных скобках, – О, то 4 -> оо. Если k таково, что моделью Максвелла. При использовании другой модели соответствующие соотношения и вытекающие из них выводы будут другими. [c.220]
Наиболее полная попытка феноменологического вывода определяющих соотношений (включая соотношения Стефана-Максвелла для многокомпонентной диффузии) для неидеальных многокомпонентных сплошных сред была предпринята в работе Колесниченко, Тирский, 1976). Определяющие соотношения, полученные в этой работе, по структуре тождественны аналогичным соотношениям, выведенным методами газовой кинетики в широко цитируемой до настоящего времени книге Гиршфельдера, Кертисса и Берда Гиршфельдер и др. , 1961). Однако в этой книге приняты весьма неудачные определения коэффициентов многокомпонентной диффузии (как несимметричных по индексам величин) и коэффициентов термодиффузии, не согласующиеся с соотношениями взаимности Онзагера-Казимира в неравновесной термодинамике Де Гроот, Мазур, 1964 Дьярмати, 1974). Этот эмпирически установленный принцип взаимности (который может быть выведен также на основе методов статистической механики), носит фундаментальный характер и может быть назван четвертым законом термодинамики (третий закон о недостижимости абсолютного нуля температуры не обсуждается в этой книге). По этой причине соответствие коэффициентов молекулярного обмена принципу взаимности Онзагера-
[c.85]
, 1961). Однако в этой книге приняты весьма неудачные определения коэффициентов многокомпонентной диффузии (как несимметричных по индексам величин) и коэффициентов термодиффузии, не согласующиеся с соотношениями взаимности Онзагера-Казимира в неравновесной термодинамике Де Гроот, Мазур, 1964 Дьярмати, 1974). Этот эмпирически установленный принцип взаимности (который может быть выведен также на основе методов статистической механики), носит фундаментальный характер и может быть назван четвертым законом термодинамики (третий закон о недостижимости абсолютного нуля температуры не обсуждается в этой книге). По этой причине соответствие коэффициентов молекулярного обмена принципу взаимности Онзагера-
[c.85]
Эта программа (по наведению указанного соответствия) в рамках кинетического подхода наиболее последовательно была осуществлена Ферцигером и Капером в монографии Ферцигер, Капер, 1976), в которой, в частности, коэффициенты многокомпонентной диффузии определены как симметричные. В данной книге предложен феноменологический вывод определяющих соотношений для термодинамических потоков (в частности, соотношений Стефана-Максвелла для многокомпонентной диффузии и скоррелированного с ними выражения для полного потока тепла), а также всех важнейших алгебраических формул, связывающих между собой кинетические коэффициенты переноса. При этом все полученные результаты (определяющие соотношения, формулы связи для коэффициентов переноса) полностью тождественны соответствующим результатам кинетической теории, приведенным в монографии Ферцигер, Капер, 1976). Однако, развитый здесь термодинамический вывод доказывает их универсальный характер, т.е. пригодность использования для описания не только одноатомных газов, но и более сложных сплошных сред, например многоатомных химически активных газовых смесей или жидких растворов (электролитов, суспензий и т.п.), для которых не разработан соответствующий кинетический аппарат.
[c.86]
В данной книге предложен феноменологический вывод определяющих соотношений для термодинамических потоков (в частности, соотношений Стефана-Максвелла для многокомпонентной диффузии и скоррелированного с ними выражения для полного потока тепла), а также всех важнейших алгебраических формул, связывающих между собой кинетические коэффициенты переноса. При этом все полученные результаты (определяющие соотношения, формулы связи для коэффициентов переноса) полностью тождественны соответствующим результатам кинетической теории, приведенным в монографии Ферцигер, Капер, 1976). Однако, развитый здесь термодинамический вывод доказывает их универсальный характер, т.е. пригодность использования для описания не только одноатомных газов, но и более сложных сплошных сред, например многоатомных химически активных газовых смесей или жидких растворов (электролитов, суспензий и т.п.), для которых не разработан соответствующий кинетический аппарат.
[c.86]
Трусделл, 1962) было высказано предположение, что во втором приближении матрица несимметрична (другими словами, по мнению Трусделла соотношения Стефана-Максвелла (2. 3.29) не носят универсального термодинамического характера, а являются математическим феноменом, присущим лишь первому приближению теории Чепмена-Энскога). Позднее, в работе Макенфус, 1973) предпринималась попытка получить соотношения (2.3.28) из кинетической теории газов в любом приближении, но был сделан неверный вывод о том, что поправочные множители к бинарным коэффициентам диффузии (учитывающие высшие приближения при разложении возмущенных функций распределения отдельных компонентов в ряды по полиномам Сонина-Лаггера) зависят только от числа приближений теории Чепмена-Энскога и числа N (количество компонентов в системе), но не зависят от самих взаимодействующих компонентов кроме того не был получен явный вид этой поправки. Обобщенные соотношения Стефана-Максвелла и формулы для поправок к бинарным коэффициентам диффузии в любом приближении коэффициентов молекулярного переноса были выведены для частично ионизованных смесей впервые в работе Колесниченко, 1979) (в которой был рассмотрен предельный случай нулевого магнитного поля) и в работах Колесниченко, 1982 Колесниченко, Маров, 1982) (с учетом сильного магнитного поля, вносящего анизотропию в коэффициенты переноса).
3.29) не носят универсального термодинамического характера, а являются математическим феноменом, присущим лишь первому приближению теории Чепмена-Энскога). Позднее, в работе Макенфус, 1973) предпринималась попытка получить соотношения (2.3.28) из кинетической теории газов в любом приближении, но был сделан неверный вывод о том, что поправочные множители к бинарным коэффициентам диффузии (учитывающие высшие приближения при разложении возмущенных функций распределения отдельных компонентов в ряды по полиномам Сонина-Лаггера) зависят только от числа приближений теории Чепмена-Энскога и числа N (количество компонентов в системе), но не зависят от самих взаимодействующих компонентов кроме того не был получен явный вид этой поправки. Обобщенные соотношения Стефана-Максвелла и формулы для поправок к бинарным коэффициентам диффузии в любом приближении коэффициентов молекулярного переноса были выведены для частично ионизованных смесей впервые в работе Колесниченко, 1979) (в которой был рассмотрен предельный случай нулевого магнитного поля) и в работах Колесниченко, 1982 Колесниченко, Маров, 1982) (с учетом сильного магнитного поля, вносящего анизотропию в коэффициенты переноса). Там же была показана симметрия коэффициентов сопротивления в полном согласии с соответствующим результатом термодинамики необратимых процессов Колесниченко, Тирский, 1976).
[c.99]
Там же была показана симметрия коэффициентов сопротивления в полном согласии с соответствующим результатом термодинамики необратимых процессов Колесниченко, Тирский, 1976).
[c.99]
В аэрономических исследованиях при моделировании процессов тепло- и массопереноса удобно гшеть подобные определяющие соотношения в виде соотношений Стефана-Максвелла, в которые, вместо многокомпонентных коэффициентов диффузии (для которых кинетическая теория разреженных газов дает чрезвычайно громоздкие расчетные формулы), входят коэффициенты диффузии в бинарных смесях газов. Эти соотношения и соответствующее им выражение для полного потока тепла в многокомпонентной смеси получены в монографии методами термодинамики необратимых процессов с использованием принципа взаимности Онзагера-Казимира. Феноменологический вывод обобщенных соотношений Стефана-Максвелла обосновывает законность их использования с полу эмпирическими выражениями для бинарных коэффициентов диффузии (и коэффициентов термодиффузии), что важно с точки зрения практических приложений, [c.
 113]
113]Вывод обобщенных соотношений Стефана-Максвелла для многокомпонентной диффузии позволяет также получить очень важные алгебраические уравнения для расчета многокомпонентных коэффициентов диффузии через бинарные коэффициенты диффузии формулы, связывающие термодиффузионные отношения с коэффициентами термодиффузии и многокомпонентной диффузии смеси формулы, связывающие истинный и парциальный коэффициенты теплопроводности. Все найденные (феноменологически) формулы по структуре полностью тождественны выражениям, полученным в рамках первого приближения метода Чепмена-Энскога в кинетической теории многокомпонентных смесей одноатомных газов (сопоставление проведено с результатами, представленными в уникальной книге Ферцигера и Капера). Однако, в отличие от газокинетического подхода (до конца разработанного только для газов умеренной плотности, когда известен потенциал взаимодействия между частицами газа), феноменологический подход не связан с постулированием конкретной микроскопической модели среды и потому полученные здесь результаты носят универсальный характер, т. е. пригодны для описания широкого класса сред, например, многоатомных газовых смесей (что важно для аэрономических приложений), плотных газов, жидких растворов и т.п.
[c.113]
е. пригодны для описания широкого класса сред, например, многоатомных газовых смесей (что важно для аэрономических приложений), плотных газов, жидких растворов и т.п.
[c.113]
Обратимся к результатам моделирования структуры и энергетики верхней атмосферы Земли в области высот 70-400 км, полученным с использованием одномерных уравнений гидродинамики смеси Маров, Колесниченко, 1987). Модель содержит аккуратное описание процессов тепло- и массопереноса в термосфере (области положительного температурного градиента выше уровня мезо-наузы) на основе использования соотношений Стефана-Максвелла для многокомпонентной молекулярной диффузии, термодинамический вывод которых дан в 2.3, и реологических соотношений для потоков турбулентной диффузии и тепла, полученных в 3.3. [c.237]
Эти соотношения образуют систему замкнутых дифференщ1альных уравнений в частных производных. Уравнение Пуассона, являющееся одним из уравнений Максвелла, описывает распределение заряда в полупроводниковом приборе. Уравнения непрерывности описывают локальное равновесие между приходом и уходом электронов и дырок. Выражения для токов задают абсолютное значение, направление и ориентацию электронного и дырочного токов. Уравнения непрерывности и формулы для токов совсем не тривиально выводятся из уравнения Больцмана. Из-за ограниченности места привести здесь этот вывод нет возможности. Интересующихся читателей можно отослать к [15.172] и к литературе или монографиям по полупроводниковым приборам, например [15.18, 15.78, 15.136, 15.148].
[c.392]
Уравнения непрерывности описывают локальное равновесие между приходом и уходом электронов и дырок. Выражения для токов задают абсолютное значение, направление и ориентацию электронного и дырочного токов. Уравнения непрерывности и формулы для токов совсем не тривиально выводятся из уравнения Больцмана. Из-за ограниченности места привести здесь этот вывод нет возможности. Интересующихся читателей можно отослать к [15.172] и к литературе или монографиям по полупроводниковым приборам, например [15.18, 15.78, 15.136, 15.148].
[c.392]
2.75 Цветовые системы. История вопроса (часть 19)
Тема лекции: Цветовые системы 19 века. Система Джеймса Кларка Максвелла.Джеймс Кларк Максвелл
Источник – Википедия
Джеймс Клерк (Кларк) Максвелл (англ. James Clerk Maxwell; 13 июня 1831, Эдинбург – 5 ноября 1879, Кембридж) – британский физик и математик. Шотландец по происхождению. Член Лондонского королевского общества (1861). Максвелл заложил основы современной классической электродинамики (уравнения Максвелла), ввёл в физику понятия тока смещения и электромагнитного поля, получил ряд следствий из своей теории (предсказание электромагнитных волн, электромагнитная природа света, давление света и другие). Он является одним из основателей кинетической теории газов, установил распределение молекул газа по скоростям (распределение Максвелла). Максвелл одним из первых ввёл в физику статистические представления, показал статистическую природу второго начала термодинамики (“демон Максвелла”), получил ряд важных результатов в молекулярной физике и термодинамике (термодинамические соотношения Максвелла, правило Максвелла для фазового перехода жидкость – газ и другие). Он является пионером количественной теории цветов, автором принципа цветной фотографии. Среди других работ Максвелла – исследования по устойчивости колец Сатурна, теории упругости и механике (фотоупругость, теорема Максвелла), оптике, математике.
Максвелл заложил основы современной классической электродинамики (уравнения Максвелла), ввёл в физику понятия тока смещения и электромагнитного поля, получил ряд следствий из своей теории (предсказание электромагнитных волн, электромагнитная природа света, давление света и другие). Он является одним из основателей кинетической теории газов, установил распределение молекул газа по скоростям (распределение Максвелла). Максвелл одним из первых ввёл в физику статистические представления, показал статистическую природу второго начала термодинамики (“демон Максвелла”), получил ряд важных результатов в молекулярной физике и термодинамике (термодинамические соотношения Максвелла, правило Максвелла для фазового перехода жидкость – газ и другие). Он является пионером количественной теории цветов, автором принципа цветной фотографии. Среди других работ Максвелла – исследования по устойчивости колец Сатурна, теории упругости и механике (фотоупругость, теорема Максвелла), оптике, математике. Он подготовил к публикации рукописи работ Генри Кавендиша, много внимания уделял популяризации науки, сконструировал ряд научных приборов.
Он подготовил к публикации рукописи работ Генри Кавендиша, много внимания уделял популяризации науки, сконструировал ряд научных приборов.
Теория цветов Максвелла
После сдачи экзамена Максвелл решил остаться в Кембридже для подготовки к профессорскому званию. Он занимался с учениками, принимал экзамены в Челтенхем-колледже, заводил новых друзей, продолжал сотрудничать с Рабочим колледжем, по предложению редактора Макмиллана начал писать книгу по оптике (она так и не была закончена), а в свободное время посещал в Гленлэре отца, здоровье которого резко ухудшилось. К этому же времени относится шуточное экспериментальное исследование по “котоверчению”, вошедшее в кембриджский фольклор: его целью было определение минимальной высоты, падая с которой, кошка встаёт на четыре лапы.
Однако главным научным интересом Максвелла в это время была работа по теории цветов. Она берёт начало в творчестве Исаака Ньютона, который придерживался идеи о семи основных цветах. Максвелл выступил как продолжатель теории Томаса Юнга, выдвинувшего идею трёх основных цветов и связавшего их с физиологическими процессами в организме человека. Важную информацию содержали свидетельства больных цветовой слепотой, или дальтонизмом. В экспериментах по смешиванию цветов, во многом независимо повторявших опыты Германа Гельмгольца, Максвелл применил “цветовой волчок”, диск которого был разделён на окрашенные в разные цвета секторы, а также “цветовой ящик”, разработанную им самим оптическую систему, позволявшую смешивать эталонные цвета. Подобные устройства использовались и раньше, однако лишь Максвелл начал получать с их помощью количественные результаты и довольно точно предсказывать возникающие в результате смешения цвета. Так, он продемонстрировал, что смешение синего и жёлтого цветов даёт не зелёный, как часто полагали, а розоватый оттенок. Опыты Максвелла показали, что белый цвет не может быть получен смешением синего, красного и жёлтого, как полагали Дэвид Брюстер и некоторые другие учёные, а основными цветами являются красный, зелёный и синий.
Максвелл выступил как продолжатель теории Томаса Юнга, выдвинувшего идею трёх основных цветов и связавшего их с физиологическими процессами в организме человека. Важную информацию содержали свидетельства больных цветовой слепотой, или дальтонизмом. В экспериментах по смешиванию цветов, во многом независимо повторявших опыты Германа Гельмгольца, Максвелл применил “цветовой волчок”, диск которого был разделён на окрашенные в разные цвета секторы, а также “цветовой ящик”, разработанную им самим оптическую систему, позволявшую смешивать эталонные цвета. Подобные устройства использовались и раньше, однако лишь Максвелл начал получать с их помощью количественные результаты и довольно точно предсказывать возникающие в результате смешения цвета. Так, он продемонстрировал, что смешение синего и жёлтого цветов даёт не зелёный, как часто полагали, а розоватый оттенок. Опыты Максвелла показали, что белый цвет не может быть получен смешением синего, красного и жёлтого, как полагали Дэвид Брюстер и некоторые другие учёные, а основными цветами являются красный, зелёный и синий. Для графического представления цветов Максвелл, следуя Юнгу, использовал треугольник, точки внутри которого обозначают результат смешения основных цветов, расположенных в вершинах фигуры.
Для графического представления цветов Максвелл, следуя Юнгу, использовал треугольник, точки внутри которого обозначают результат смешения основных цветов, расположенных в вершинах фигуры.
Более детально о работах Максвелла в области цвета
1859 год – один из выдающихся годов в истории науки: англичанин Чарльз Дарвин изложил свои идеи происхождения видов и таким образом проложил дорого теории эволюции; и в том же самом году шотландский физик Джеймс Кларк Максвелл (1831-1879) опубликовал свою “Кинетическую теорию газов”, в которой он представил статистические подсчёты молекулярных движений и их математическую обработку, известную сегодня как “распределение Максвелла” и внёсшую огромный вклад в наши фундаментальные знания физики.
В том же году Максвелл, тогда 28-летний, представил свою “Теорию цветного зрения”, признанную основательницей количественного цветового измерения (колориметрии). В этой работе Максвелл показывает, что все цвета возникают из смеси трёх спектральных цветов – красного (red – R), зелёного(green -G), и синего (blue – B), например – на предположении, что возбудитель света может быть как добавляем, так и вычитаем. Он располагает каждый из трёх основных цветов в углах треугольника, в который мы поместили кривую спектральных цветов, которая установленна с помощью технических данных. Линия этого типа вновь появится позже в системе CIE. Это важно, так как все связанные способы проникновения в суть вопроса берут начало у Максвелла, который со своим треугольником представил первую двухмерную цветовую систему, основанную на психофизических измерениях.
В этой работе Максвелл показывает, что все цвета возникают из смеси трёх спектральных цветов – красного (red – R), зелёного(green -G), и синего (blue – B), например – на предположении, что возбудитель света может быть как добавляем, так и вычитаем. Он располагает каждый из трёх основных цветов в углах треугольника, в который мы поместили кривую спектральных цветов, которая установленна с помощью технических данных. Линия этого типа вновь появится позже в системе CIE. Это важно, так как все связанные способы проникновения в суть вопроса берут начало у Максвелла, который со своим треугольником представил первую двухмерную цветовую систему, основанную на психофизических измерениях.
Постороннему наблюдателю трудно объяснить, насколько известен Максвелл среди физиков. В дополнение к максвеллианскому распределению, его имя также связано с четырьмя так называемыми уравнениями поля, которые объясняют, как распространяется свет и указывают на существование электромагнитных волн. Мы используем приём этих волн сегодня, например, когда слушаем радио. Максвелл показал, что волны света нужно понимать как вибрирующие электрические и магнитные поля, и он объясняет, как волны света могут проходить сквозь общирные пустоты Вселенной и обнаруживать звёзды.
Мы используем приём этих волн сегодня, например, когда слушаем радио. Максвелл показал, что волны света нужно понимать как вибрирующие электрические и магнитные поля, и он объясняет, как волны света могут проходить сквозь общирные пустоты Вселенной и обнаруживать звёзды.
Перед тем, как подойти ещё ближе к пониманию истинной природы света, Максвелл попытался получить более точный доступ к цветам. Физика и измерение света и цвета вновь возникают в пост-ньютоновской истории как результат этого участия, будучи со своим треугольником частью попыток улучшить методы Ньютона по смешиванию света. В предыдущем десятилетии физики научились определять длину волн в районе 10-7 метров с помощью микроскопических дифракционных решёток. Сегодня длина волн может быть более точно выражена в нанометрах (1 нанометр равен 10-9 метрам). Длина волн видимого спектра света – от 760 нанометров для красного до 380 нанометров для синего цвета, с зелным цветом примерно в районе 550 нанометров. (Эти значения располагаются вдоль длины кривой.)
(Эти значения располагаются вдоль длины кривой.)
Наблюдения Максвелла за цветами основаны на предложениях, сделанных Томасом Юнгом, который уже заметил, что нужно не более 3-х цветов спектра, чтобы воспроизвести все остальные. В то время, когда Юнг представлял свою трихроматическую теорию, многие художники уже давно знали, что они могут намешать любые оттенки, используя три первичных пигмента. Физики, однако, всё ещё находились под влиянием утверждения Ньютона о том, что семь цветов, излучаемых сквозь призму – первичны (элементарны), и поэтому несмешиваемы.
Три рецептора Юнга приобрели убедительность, когда в 1855 году Джордж Уилсон из Эдинбурга представил свой первый статистический анализ цветовой слепоты. В приложении Максвелл смог показать, что подобные наблюдения имели смысл, если наблюдаемый предположительно имел один или два неработающих рецептора.
Максвелл начал свои эксперименты по цветовому смешиванию в Эдинбурге, в лаборатории Дж. Д. Форбса, который работал с быстро вращающимися дисками. Используя этот метод, Форбс хотел смешать спектральные цвета, чтобы получить серый, однако он не смог получить серый смешиванием красного, жёлтого и синего. И вскоре он увидел почему: в этих обстоятельствах синий и жёлтый не образовывали зелёного, но вместо него получился своего рода ярко-розовый. В результате этого Максвелл выбрал красный, зелёный и синий в качестве своих основных цветов, однако чётко подчёркивая, что любое другое трио цвета может быть избрано, и в комбинации они дадут белый цвет. Мы вновь находим эти базовые цвета в его треугольнике.
В свои эксперименты по измерению цвета Максвелл вовлекал подопытных тестируемых, которые судили о том, как цвет образца сравнивался со смесью трёх базовых цветов – красного, зелёного и синего – с помощью стандартизированных источников света до тех пор, пока впечатление от цвета не совпадёт с цветом образца (“подборка цвета”). Относительные пропорции смеси могут быть записаны с помощью трёх чисел, идентифицируемых как R,G,B и известных со времён Максвелла как “трёхцветное значение”.
Максвелл сейчас понял, что отражательная способность полихромной поверхности относительно нечувствительна к изменениям яркости, и смог полностью убрать этот фактор из своих расчетов, введя новые параметры r, g, b, прийдя к ним путём деления каждого трёхцветного значения на их общую сумму r = R/(R+G+B), g = G/(R+G+B), and b = B/(R+G+B). Эти новые координаты цвета выполняют простое условие – их сумма равна 1 (r + g + b = 1). Это значит, что все их возможные комбинации могут быть представлены как вершины равностороннего треугольника – треугольника Максвелла.
Поскольку трёхцветные значения цветов, или их цветовые координаты приводятся к единице, треугольник позволяет нам предвидеть результат смеси двух цветов. Все возможные комбинации любых двух цветов будут лежать на линии, связывающей их соответствующие положения внутри треугольника. Естественно, круг Ньютона уже определил результаты цветового смешивания. Но достижение Максвелла было в том, что геометрическое отношение и расположение цветов в его треугольнике имело точное значение, базируемое на психофизических измерениях.
В своих экспериментах по смешиванию цветов Максвелл сумел продемонстрировать, что семицветный круг Ньютона с белым цветом в его середине, безоговорчно удовлетворил требованиям трихроматической теории, поскольку он равнозначен модели, в которой выделена точка для каждого цвета внутри трёхмерного пространства. Введя экспериментальные результаты в свой треугольник, он установил точку для белого цвета. С помощью этой точки Максвелл смог выделить три вариации – похожие на вариации у Гельмгольца – которые характеризуют цвет (“hue” – оттенок (на основе серого), “tint” – светлый тон (на основе белого), “shade” – тёмный тон (на основе черного)). Максвелл также показал, как просто связывать эти три вариации друг с другом и изображать цвета, как сумму трёх основных цветов.
Ограничения этого треугольника, в данном случае, вскоре стали очевидными: его значения базируются на сравнениях пигментов, но свет спектральных цветов может быть намного более интенсивным. Например, если мы ищем месторасположение насыщенного жёлтого, мы обнаружим, что оно должно лежать за пределами линии между G и R. Если нужно вписать все спектральные цвета, включая пурпурные, в диаграмму Максвелла, тогда этот треугольник нужно либо расширить, либо реконструировать. Подобная попытка берёт начало у Гельмгольца. Сейчас мы обращаемся к мудрёному методу, где линия в треугольнике уже настроена (система CIE). Даже сегодня, поскольку машины сами по себе не могут различить между жёлтым и красным, измерение цветов продолжает оставаться сложной задачей. Как всегда, только человек обладает способностью решать. Именно в его глаза падает свет, и из его глаз виден мир.
Что такое ню? Пересмотр аргумента Максвелла о «соотношении единиц», от механической теории электромагнитного поля до «Об элементарных отношениях между электрическими измерениями»
. Октябрь-декабрь 2017 г .; 65-66: 87-98. DOI: 10.1016 / j.shpsa.2016.08.005. Epub 2017 14 августа.Принадлежности Расширять
Принадлежность
- 1 Кембриджский университет, факультет истории и философии науки, Free School Lane, Кембридж, CB2 3RH, Великобритания.
Элемент в буфере обмена
Дэниел Джон Митчелл. Stud Hist Philos Sci. Октябрь-декабрь 2017 г.
Показать детали Показать вариантыПоказать варианты
Формат АннотацияPubMedPMID
.Октябрь-декабрь 2017 г .; 65-66: 87-98. DOI: 10.1016 / j.shpsa.2016.08.005. Epub 2017 14 августа.Принадлежность
- 1 Кембриджский университет, факультет истории и философии науки, Free School Lane, Кембридж, CB2 3RH, Великобритания.
Элемент в буфере обмена
Полнотекстовые ссылки Опции CiteDisplayПоказать варианты
Формат АннотацияPubMedPMID
Абстрактный
Этот пересмотр самой ранней версии самого важного аргумента Максвелла в пользу электромагнитной теории света – равенства между скоростью распространения волн в электромагнитном эфире и соотношением электростатических и электромагнитных величин электрической величины – устанавливает непредвиденные связи между теоретическими расчетами Максвелла. электрическая метрология и его механическая теория электромагнитного поля.Электрическая метрология не была нейтральной по сравнению с теоретико-полевой концепцией электромагнитного взаимодействия по сравнению с концепцией действия на расстоянии. Взаимное согласование между этими концепциями было достигнуто Максвеллом в Комитете по электрическим стандартам Британской ассоциации развития науки (BAAS) путем использования измерения параметров среды – электрической индуктивной емкости и магнитной проницаемости – в произвольном масштабе. Хотя он всегда работал в рамках этого ограничения при разработке аргумента «отношения единиц» математически, я утверждаю, что Максвелл пришел к пониманию отношения «как скорости», рассматривая параметры среды как физические величины, которые можно измерить абсолютно, что было возможно только через соответствие между электрическими и механическими величинами, установленное в механической теории.Тем самым я исправляю два тесно связанных заблуждения относительно аргумента отношения единиц – парадоксальное, но широко распространенное представление о том, что отношение естественно является скоростью, и предположение, что Максвелл либо вывел, либо доказал это из своей размерной формулы.
Ключевые слова: Абсолютное измерение; Электрическая метрология; Электродинамика; Электромагнитная теория света; Джеймс Клерк Максвелл; Единицы и размеры.
Авторские права © 2017. Издано Elsevier Ltd.
Похожие статьи
- По замыслу: Джеймс Клерк Максвелл и евангельское объединение науки.
Стэнли М. Стэнли М. Br J Hist Sci. 2012 Март; 45 (164 Pt 1): 57-73. DOI: 10,1017 / s0007087410001548. Br J Hist Sci. 2012 г. PMID: 22702031
- «… Статья… я считаю себя великим оружием»: комментарий к Максвеллу (1865 г.) «Динамическая теория электромагнитного поля».
Лонгэр М. Лонгэр М. Философия Trans A Math Phys Eng Sci. 2015 13 апреля; 373 (2039): 20140473. DOI: 10.1098 / rsta.2014.0473. Философия Trans A Math Phys Eng Sci. 2015 г. PMID: 25750155 Бесплатная статья PMC.
- Роль Максвелла в превращении концепции модели в методологию моделирования.
Hon G, Goldstein BR. Hon G, et al. Stud Hist Philos Sci.2021 августа; 88: 321-333. DOI: 10.1016 / j.shpsa.2021.03.010. Epub 2021 20 июля. Stud Hist Philos Sci. 2021 г. PMID: 34298278
- О вкладе Хевисайда в теорию линий передачи: волны, диффузия и поток энергии.
Донахи-Спарго К. Донахи-Спарго К. Философия Trans A Math Phys Eng Sci. 2018 29 октября; 376 (2134): 20170457. DOI: 10.1098 / rsta.2017.0457. Философия Trans A Math Phys Eng Sci.2018. PMID: 30373946 Рассмотрение.
- Электромагнетизм Максвелла как возникающее явление в конденсированных средах.
Рен Дж, Месснер Р. Рен Дж. И др. Философия Trans A Math Phys Eng Sci. 2016 28 августа; 374 (2075): 20160093. DOI: 10.1098 / rsta.2016.0093. Философия Trans A Math Phys Eng Sci. 2016 г. PMID: 27458263 Рассмотрение.
LinkOut – дополнительные ресурсы
Источники полных текстов
Источники другой литературы
Материалы исследований
цитировать
КопироватьФормат: AMA APA ГНД NLM
Распределения произведения и отношения случайных величин Максвелла и Рэлея
Абрамовиц М., Стегун И.А. (1970) Справочник по математическим функциям с формулами, графиками и математическими таблицами.Дувр, Нью-Йорк
Google ученый
Балакришнан Н., Невзоров В.Б. (2003) Праймер статистических распределений. Уайли, Нью-Джерси
Google ученый
Бхаргава Р.П., Хатри К.Г. (1981) Распределение произведения независимых бета-случайных величин с применением к многомерному анализу. Ann Inst Statist Math 33: 287–296
Статья MathSciNet МАТЕМАТИКА Google ученый
Cigizoglu HK, Bayazit M (2000) Обобщенная сезонная модель для кривой продолжительности потока.Hydrol Process 14: 1053–1067
Статья Google ученый
Frisch U, Sornette D (1997) Крайние отклонения и приложения. J Phys I France 7: 1155–1171
Статья Google ученый
Галамбос Дж., Симонелли И. (2005) Произведения случайных величин – приложения к проблемам физики и арифметическим функциям. CRC Press, Бока-Ратон
Google ученый
Градштейн И.С., Рыжик И.М. (2000) Таблица интегралов, рядов и произведений, 6-е изд.Академик, Сан-Диего
Google ученый
Grubel HG (1968) Портфели, диверсифицированные на международном уровне: благосостояние увеличивает потоки капитала. Am Econ Rev 58: 1299–1314
Google ученый
Корхонен П.Дж., Нарула С.К. (1989) Распределение вероятностей отношения абсолютных значений двух нормальных переменных. J Statist Comput Simul 33: 173–182
Статья MathSciNet МАТЕМАТИКА Google ученый
Ladekarl M, Jensen V, Nielsen B (1997) Общее количество ядер раковых клеток и митозов в опухолях молочной железы, оцененное с помощью оптического дисектора.Anal Quant Cyto Histol 19: 329–337
Google ученый
Lee RY, Holland BS, Flueck JA (1979) Распределение отношения коррелированных гамма-случайных величин. SIAM J Appl Math 36: 304–320
Статья MathSciNet МАТЕМАТИКА Google ученый
Малик HJ, Trudel R (1986) Функция плотности вероятности произведения и частного двух коррелированных экспоненциальных случайных величин.Can Math Bull 29: 413–418
MathSciNet МАТЕМАТИКА Google ученый
Marsaglia G (1965) Отношения нормальных переменных и отношения сумм однородных переменных. J Am Statist Assoc 60: 193–204
Статья MathSciNet МАТЕМАТИКА Google ученый
Надараджа С. (2005) О произведении и соотношении случайных величин Лапласа и Бесселя. J Appl Math 4: 393–402
Статья MathSciNet Google ученый
Надараджа С., Али М.М. (2005) О произведении и соотношении t и случайных величинах Лапласа.Пак Дж. Статист 21: 1–14
MathSciNet МАТЕМАТИКА Google ученый
Надараджа С., Гупта А.А. (2005) О произведении и соотношении случайных величин Бесселя. Int J Math Math Sci 18: 2977–2989
Статья MathSciNet Google ученый
Надараджа С., Коц С. (2005) О произведении и соотношении случайных величин типа VII Пирсона и Лапласа. Aust J Statist 34 (1.1): 11–23
Google ученый
Pham-Gia T (2000) Распределения отношений независимых бета-переменных и приложений. Коммунальный статистик – методы теории 29: 2693–2715
Статья MathSciNet МАТЕМАТИКА Google ученый
Press SJ (1969) Распределение t-отношения. J Am Statist Assoc 64: 242–252
Статья MathSciNet Google ученый
Прудников А.П., Брычков Ю.А., Маричев О.И. (1986).Интегралы и ряды, том 1, 2 и 3. Gordon and Breach Science Amsterdam
Рати П.Н., Рорер Х.Г., (1987) Точное распределение произведений независимых случайных величин. Метрон 45: 235–245
MathSciNet МАТЕМАТИКА Google ученый
Рокич М., Клиюнас П. (1972) Поведение как функция отношения к объекту и отношения к ситуации. J Pers Social Psychol 22: 194–201
Статья Google ученый
Сакамото Х. (1943) О распределениях продукта и частном независимых и равномерно распределенных случайных величин.Tohoku Math J 49: 243–260
MathSciNet МАТЕМАТИКА Google ученый
Шеннон CE, (1948) Математическая теория коммуникации. Bell System Tech J 27: 379–432
MathSciNet Google ученый
Сорнетт Д. (1998) Мультипликативные процессы и степенные законы. Phys Rev E, 57: 4811–4813
Статья Google ученый
Сорнетт Д. (2004) Критические явления в естественных науках, хаос, фракталы, самоорганизация и дозоупорядочение: концепции и инструменты, 2-е изд.Серия Springer в синергетике, Гейдельберг
Google ученый
Springer MD, Thompson WE (1970) Распределение произведений бета-, гамма- и гауссовских случайных величин. SIAM J Appl Math 18: 721–737
Статья MathSciNet МАТЕМАТИКА Google ученый
Тан Дж., Гупта А.К. (1984) О распределении произведения независимых бета-случайных величин.Statist Probab Lett 2: 165–168
Статья MathSciNet МАТЕМАТИКА Google ученый
Wallgren CM (1980) Распределение произведения двух коррелированных t вариаций. J Am Statist Assoc 75: 996–1000
Статья MathSciNet МАТЕМАТИКА Google ученый
Программы магистратуры | Школа Максвелла
Экономический факультет предлагает отдельные программы, ведущие к М.А. и к.т.н. градусов. Преподаватели кафедры ориентированы на прикладную экономику и экономику, связанную с политикой, которая построена на прочном фундаменте экономической теории, статистических и эконометрических методов.
На кафедре низкое соотношение аспирантов и преподавателей. Среднее количество студентов в поступающей докторантуре. класс колеблется от 8 до 12 с несколько большим числом, поступающим на программу MA. Этот небольшой размер обеспечивает большее взаимодействие между преподавателями и студентами, чем в других программах с большим количеством студентов.Кафедра пользуется большой лояльностью со стороны многих выдающихся выпускников, занимающих должности в академических кругах, бизнесе и правительстве.
Последние исследования в аспирантуре
Двум аспирантам, Гуанью Лю и Тяньюнь Чжу, была присуждена стипендия Мелвина Эггерса по экономике для аспирантов для докторантов. Эта стипендия, учрежденная в 1994 году, предоставляет стипендии аспирантам, изучающим экономику в Школе гражданства и связей с общественностью Максвелла, причем предпочтение отдается студентам, обучающимся на докторскую степень, которые намерены преподавать на уровне колледжа.Фонд, который чествует бывшего канцлера и председателя экономического факультета Мелвина Эггерса, позволяет Максвеллу привлекать высококвалифицированных студентов к докторской программе экономического факультета.
Гуанью Лю применяет методы усреднения моделей для оценки эффектов лечения с помощью продольных данных. Показано, что его новая оценка модели усреднения для эффектов лечения непротиворечива, и установлено его асимптотическое распределение . Также показано, с помощью моделирования, чтобы генерировать более точные прогнозы и лучший статистический вывод (на основе подвыборки).Он применил свою новую оценку для анализа экономических последствий украинского конфликта в 2013 году.
В исследовании Тяньюнь Чжу предлагается новый подход к восстановлению неявной ценовой эластичности спроса на удобства. Он выводит основанную на правдоподобии оценку неявной ценовой эластичности на основе теории торгов и сортировки. Его подход учитывает как наблюдаемую, так и ненаблюдаемую неоднородность предпочтений и избегает эндогенности. Оценщик также позволяет охарактеризовать равновесие сортировки и частично восстановить функцию предложения, что важно при проведении анализа благосостояния.Он применяет свой новый подход к оценке неявной ценовой эластичности спроса на качество государственных средних школ и этнический состав жителей района в Кливленде, штат Огайо.
Для получения дополнительной информации о стипендии Мелвина Эггерса свяжитесь с Нормой Шеннон по адресу [email protected].
- Хоанг Фам недавно защитил диссертацию. Он изучили, как экономическая открытость для торговли влияет на конкуренцию в сфере домашнего труда рынок. Кроме того, Хоанг изучает влияние глобализации на рост производительности. и мобильность между поколениями в развивающихся странах.Три Главы его диссертации будут представлены в виде трех отдельных статей в экономические журналы. Он будет работать в Университете штата Орегон в качестве доцента кафедры Экономика осенью.
- Исследование Росс Джестраб изучает мотивы торговли соглашения. Он исследует влияние мобильности домашней рабочей силы на формирование торговых соглашений. В текущем проекте он изучает, могут ли страны использовать торговые соглашения, чтобы понять их мотивы или манипулировать торговлей цена партнеров.
- Yimin Yi изучил связь между устранением неопределенности торговой политики предоставление США статуса постоянных нормальных торговых отношений (PNTR) Китаю. Конгресс. Он дополнительно изучил эволюцию производства в Китае. трудоустройство. У него есть еще два текущих проекта: (а) оценка динамического стохастическая структурная модель решений по импорту и экспорту на уровне фирмы, включая будущую траекторию производительности этой фирмы; и (б) влияние 2018 г. Торговая война между США и Китаем против глобальных цепочек поставок.
- Нам Сеок Ким , в статье в соавторстве с Лейлой Каракас и Девашиш Митра, использовали шведское национальное исследование выборов для изучения отношения к торговле и иммиграция, изучая их влияние на поведение избирателей. Бумага была отправлено в журнал. В настоящее время он работает над другим документом, в котором изучается влияние торговля и иммиграция на результаты выборов.
- Дэн Чжан в настоящее время анализирует, как ПИИ либерализация в Китае влияет на уценку заработной платы (заработная плата / предельный доход). продукта) по уровням образования работников.Либерализация ПИИ может привлечь некоторых иностранные фирмы, которые платят более высокую заработную плату, особенно высокообразованным работникам, тем самым меняются уровни занятости в местных компаниях и их уценка.
- Huong Tran проводит исследования, связанные с к оценке распределения заработной платы. Во многих странах распределение доходов смещено вправо. Есть экономические теории которые могут объяснить эту правую асимметрию, которую можно разделить на три группы: шанс, выбор экономических агентов и институциональные факторы, такие как минимальная заработная плата.Какая экономическая теория дает функцию плотности вероятности (лог) зарплата, которая ближе всего к истине? Ответ на этот вопрос важные последствия для справедливого распределения и государственной политики, поскольку вопросы в этих областях полагаются на оценку контрфактической плотности (журнал) заработная плата. Однако эта задача не была выполнена в реальных эмпирических условиях. параметр. Хуонг оценивает функцию плотности вероятности предполагаемой (логарифмической) заработной платы. экономическими теориями распределения доходов и ранжирует теории используя статистические меры близости между подобранной плотностью и истинной плотность.Использование национально репрезентативного бразильского домохозяйства исследование за 2001 год, она считает, что минимальная заработная плата должна быть смоделирована явно на любом рынке труда, где проводится политика минимальной заработной платы, поскольку, в противном случае результирующая прогнозируемая плотность значительно отличается от истинной плотность (лог) заработной платы.
- Dahae Choo изучает влияние пронаталистов политика, введенная местными органами власти в Южной Корее, стране с одним из самые низкие показатели рождаемости в мире.Учитывая, что в Южной Корее брак в значительной степени предварительное условие для деторождения, Дахэ объясняет совместное решение жениться и иметь детей. Ее настройки богаты по сравнению с другими настройками в какие подобные политики были оценены (в других странах устанавливаются на национальном уровне): в Южной Корее местный характер политики подразумевает что существует большой разброс сумм переводов, которые можно использовать для идентификация. Кроме того, Дахэ может оценить реакцию фертильности на разные уровни передачи.Ее результаты показывают, что политика не имеет существенное влияние на общее количество детей или вероятность рождения ребенок, вызывающий некоторые сомнения в эффективности проводимой политики. Ее результаты предполагают, что дополнительный перевод в размере 1000 долларов США из программы увеличится вероятность рождения всего на 0,26 процентных пункта, что означает, что только 0,89% больше замужних женщин будут вступать в материнство из-за политики. Дахэ также анализирует время до материнства, которое может привести к увеличению фертильности в длинный пробег.Она обнаружила, что перевод в размере 1000 долларов от программы побудил женщин родить первого ребенка на восемь месяцев раньше, но время рождения второго ребенка доставка не пострадала. В совокупности результаты показывают, что политика похоже, не достигает своей цели.
SketchUp – Камера – Документация Maxwell
Для каждой сцены в вашей модели SketchUp плагин создает и поддерживает связанную камеру Maxwell.
Выходное разрешение
В этом разделе определяются выходные размеры визуализированного изображения.Он работает в двух основных режимах: Viewport и Custom.
В режиме видового экрана подключаемый модуль сопоставляет выходное разрешение камеры с размером связанного окна просмотра SketchUp. В пользовательском режиме выходное разрешение камеры может быть определено независимо от физического размера области просмотра. Список стандартных размеров разрешения представлен в раскрывающемся списке «Предустановка». Кроме того, есть еще два параметра, которые используются в пользовательском режиме.
Заблокировать соотношение сторон
Если этот параметр включен, соотношение сторон выходного разрешения будет поддерживаться во время настройки любого из его значений.
Показать соотношение сторон в окне просмотра
При использовании пользовательского режима вполне вероятно, что соотношение сторон вывода Maxwell не будет соответствовать соотношению сторон окна просмотра SketchUp. Чтобы вы могли точно предсказать композицию вашего изображения, плагин предоставляет функцию «Показать соотношение сторон в окне просмотра». Если этот параметр включен, в окне просмотра SketchUp появятся серые полосы, обрамляющие область, которая будет отображаться при визуализации.
Видео, показывающее, как можно изменить разрешение как для Fire, так и для RenderПримечания по выходному разрешению в автономном плагине
Плагин может визуализировать изображения с помощью Maxwell Fire или Maxwell Render.Если выходное разрешение, указанное в камере, больше, чем Maxwell Fire’s Max. Разрешение будет изменено с сохранением соотношения сторон. Без лицензии Fire позволяет макс. Разрешение 800 х 800 пикселей; по лицензии разрешает 1920 x 1080 пикселей. Однако при рендеринге через Maxwell Render (лицензированный) ограничение практически отсутствует: 65000×65000, что больше, чем может выдержать любая машина.
Оптика
Экспозиция камеры является результатом комбинации значений fStop, Shutter и ISO.По мере уменьшения значения fStop в камеру попадает больше света, увеличивая экспозицию. И наоборот, при увеличении значения выдержки пленка экспонируется в течение более короткого времени, затемняя экспозиция. По мере увеличения значения ISO пленки ее светочувствительность увеличивается, что позволяет достичь заданной экспозиции за более короткий промежуток времени. Камера может быть сфокусирована вручную или автоматически плагином, используя одну из трех различных стратегий.
Фокус
По умолчанию фокус камеры определяется вручную с помощью инструмента «Установить фокусное расстояние».При желании вы можете настроить плагин для автоматической фокусировки камеры. Доступны три режима выборки автофокуса:
Пятно | В этом режиме измеряется фокусное расстояние с помощью одного луча, расположенного в центре плоскости просмотра. |
Среднее значение | В этом режиме фокусное расстояние измеряется с помощью кругового набора лучей, диаметр которых примерно вдвое меньше размера плоскости обзора, и расположенных вокруг его центра. |
Среднее + DOF | Этот режим идентичен среднему режиму, но также берет на себя управление fStop камеры, автоматически устанавливая ближнее и дальнее фокусное расстояние камеры. |
Таким образом, режим точечной выборки будет фокусироваться на расстоянии до объекта, находящегося непосредственно перед камерой. Режим «Среднее» будет фокусироваться на среднем расстоянии до объектов, которые он находит рядом с центром изображения.В режиме «Среднее значение + глубина резкости» выполняется выборка «Среднее значение» и используются ближайшие и самые дальние расстояния для установки значения fStop камеры; в результате при использовании этого режима прямая регулировка fStop отключена.
В крайних случаях в режиме «Среднее + DOF» могут возникнуть трудности с нахождением желаемого диапазона фокусировки; когда это происходит, обычно лучше вернуться к использованию ручного или точечного режима.
Экспозиция
Значения fStop, Shutter и ISO можно объединить математически, чтобы выразить число EV (значение экспозиции), которое описывает общую экспозицию камеры в виде одного числа.Более низкие значения EV обычно подходят для сценариев с низким освещением, и наоборот. Там, где для сцены при свечах может потребоваться EV 4-6, для яркой солнечной сцены может потребоваться что-то большее порядка 13-16. Таблицу электромобилей для различных сценариев можно найти в конце этого руководства.
Кроме того, если выдержка и ISO в первую очередь влияют на яркость экспозиции, fStop камеры также влияет на ее глубину резкости (то есть глубину резкости: расстояние между ближайшим и самым дальним расстояниями, которые будут в фокусе на изображении).Это часто становится проблемой, потому что часто бывает желательно отрегулировать fStop для достижения желаемой глубины резкости в композиции; однако, когда это делается, это также влияет на экспозицию из-за изменения fStop, даже если это не является частью желаемого эффекта.
Для решения этой проблемы в камере предусмотрена функция блокировки экспозиции по EV. При активации невозможно напрямую изменить выдержку и ISO; этими значениями будет управлять плагин при изменении fStop или EV, поддерживая постоянную конечную экспозицию.Это позволяет регулировать глубину резкости камеры, не влияя также на экспозицию, или регулировать экспозицию напрямую, регулируя EV, не беспокоясь о довольно сложной взаимосвязи между fStop, Shutter и ISO.
Более подробное знакомство с камерой Maxwell см. На странице «Камера» в документации Maxwell.
Объектив
Поддерживаются несколько типов объективов. Для достижения наилучших результатов обязательно используйте тип Parallel при использовании камеры SketchUp с параллельной проекцией.Дополнительную информацию об объективах см. Здесь.
Диафрагма
Диафрагма относится к типу диафрагмы, используемой камерой; есть два типа: круговой и многоугольный. Когда используется многоугольник, форма так называемых эффектов боке будет определяться числом и углом лепестков диафрагмы. Пожалуйста, смотрите страницу камеры в документации Maxwell для получения более подробной информации.
Пользовательское боке
Эти настройки позволяют настраивать эффекты боке объектива. Подробнее см. Здесь.
Z-Clip Ples
При желании вы можете выбрать обрезку геометрии во время рендеринга, используя ближнюю и дальнюю плоскости, которые установлены перпендикулярно направлению камеры. Ближайшее расстояние указывает, как далеко от камеры находится ближняя плоскость; любая геометрия между этой плоскостью и камерой будет вырезана из поля зрения. Точно так же любая геометрия дальше от камеры, чем Дальняя плоскость, также будет вырезана из поля зрения. Пожалуйста, смотрите страницу Z-clip plane в документации Maxwell для получения более подробной информации.
Плоскости Z-Clip можно установить интерактивно с помощью инструментов Set DOF, Z-Clip или Z-Buffer Tool; для этого нажмите SHIFT, выбирая точки с помощью инструмента.
Сдвиг объектива
Пленку камеры можно смещать по осям X и Y относительно объектива. Это часто бывает полезно при рендеринге высоких зданий; камеру можно настроить так, чтобы ее направление было параллельно земле, а ее высота была на метр или два над землей. Затем пленку можно сдвинуть вниз, перемещая здание ближе к центру обзора, избегая при этом искажения перспективы, которое могло бы возникнуть в результате наклона камеры вверх для достижения аналогичной композиции.Пожалуйста, обратитесь к странице Shift Lens в документации Maxwell для получения более подробной информации.
Хотя это похоже на использование двухточечной перспективы SketchUp, эффект сдвига линзы не может быть визуализирован в окне просмотра SketchUp из-за ограничений API SketchUp. Однако это можно визуализировать с помощью Maxwell Fire.
Показатель преломления
Показатель преломления Показатель преломления
Детлеф Смилджис
Уравнения Максвелла в присутствии среды приведены в СИ.
единицы
(м кг с A) как:
∇⋅ D = 0
∇ × E = – ∂ / ∂t B
∇⋅ B = 0 ∇ × H = ∂ / ∂t D
Кроме того, существуют феноменологические отношения между поля
D = ε ε 0 E B = μ μ 0 H
В вакууме ε = μ = 1, в среде для определения ε и μ.Распространение электромагнитный волна через среду определяется волновым уравнением, которое может быть полученное из приведенных выше уравнений, учитывая:
∇ × (∇ × E) = – ∇ × (∂ / ∂t B )
Левая часть упрощается с помощью ∇ D = 0 до
∇ × (∇ × E ) = ∇ × (∇ E ) – (∇ 2 ) E =- 2 E
Правую часть можно переписать как
– ∇ × ∂ / ∂t B = ∂ / ∂t ∇ × μ μ 0 H = μ μ 0 ∂ 2 / ∂t 2 D = ε ε 0 мкм мкм 0 ∂ 2 ∂t 2 E
урожайности
∇ 2 E = 1 / c 2 ∂ 2 / ∂t 2 E
со скоростью света в среде c = 1 / sqrt (ε ε 0 μ μ 0 ).
Тогда показатель преломления n определяется как отношение между скорость света в вакууме (ε = μ = 1) и скорость света в среде:
n = c 0 / c = sqrt (ε μ).
Решения волнового уравнения – плоские волны.
E = E 0 exp (i k r – ωt)
, которые должны удовлетворять дисперсионному соотношению
ω = c k = (c 0 / n) k
где k = || к ||.
Граничные условия для k вектор
Рассмотрим волну, бегущую через среду 1 и попадающую в самолет интерфейс со средой 2. Самая общая ситуация будет с той частью из падающая волна отражается и часть ее преломляется в среду 2. Решения волнового уравнения в обеих средах подвержены граница условия на интерфейсе.Прежде всего, частоты трех волна должна быть одинаковой по обе стороны от интерфейса:
ω = ω ‘Из этого условия сразу следует для волновых векторов:
к ‘= n кСледующее условие – компоненты волнового вектора параллельны интерфейс равны – только так мы можем иметь непрерывность полей по в интерфейс:
к ‘ || = k ||Теперь мы можем вычислить связь между z-компонентами волны вектор:
k ‘ z 2 = k’ 2 – k ‘ || 2 = (n k) 2 – k || 2 = (n k) 2 – (к 2 – к z 2 ) = (n 2 -1) k 2 – к z 2
Томас Максвелл, прокурор Индианаполиса | Барнс и Торнбург
Заместитель председателя группы практики финансовых институтов фирмы, Том обладает более чем тридцатилетним опытом оказания помощи финансовым учреждениям в решении сложных транзакционных и нормативных вопросов.В течение девяти лет, до прихода в фирму, Том работал советником в федеральных банковских агентствах, включая Федеральную корпорацию страхования вкладов и Управление по надзору за сбережениями.
Том регулярно консультирует клиентов по широкому кругу стратегических сделок, которые включают практически все типы финансовых учреждений, такие как банки, сберегательные ассоциации, кредитные союзы и ипотечные компании. Он организовывал банки и трастовые компании, представлял покупателей и продавцов в сделках по приобретению, создавал холдинговые компании для депозитарных учреждений, представлял финансовые учреждения в качестве эмитентов при размещении ценных бумаг, структурировал и получал разрешение регулирующих органов на приобретения и представлял клиентов финансовых учреждений в регулирующих процедурах.
Том также консультирует клиентов финансовых учреждений по всему спектру нормативных вопросов, включая вопросы, возникающие в соответствии с федеральным Законом о банковской тайне, включая Закон о корпоративной прозрачности, и федеральными законами штата и законами о соблюдении требований потребителей, такими как Закон о процедурах урегулирования сделок с недвижимым имуществом и Истина в кредитовании. Действовать. Он регулярно консультируется с представителями государственных и федеральных банковских агентств, чтобы помочь клиентам решить сложные нормативные вопросы.
Том также занимается консультированием клиентов нефинансовых организаций по общим вопросам, связанным с ценными бумагами и корпоративным правом.Он выступал в качестве советника эмитента и андеррайтера при многочисленных размещениях ценных бумаг, включая первичное публичное размещение и частное размещение. Он также регулярно консультирует публичные компании и их директоров по вопросам корпоративного управления, обязательствам по раскрытию информации и другим вопросам в соответствии с федеральными законами о ценных бумагах. Том также консультирует корпорации, партнерства и компании с ограниченной ответственностью по различным сложным сделкам, включая слияния, поглощения, продажу активов и финансирование под обеспечение.
До прихода в Barnes & Thornburg Том работал советником в Федеральной корпорации по страхованию вкладов в Бостоне и Чикаго, а также в Управлении по надзору за сбережениями и его предшественнике в Чикаго и Вашингтоне, округ Колумбия. нормативные и контрольные вопросы, с которыми сталкиваются клиенты финансовых учреждений, и процесс их решения.
Участие специалистов и общества
Член правления Reach For Youth, Inc.
Награды
Лучшие юристы Америки, 2012-2021 гг.
Индианаполис
11 С.Meridian StreetIndianapolis, IN 46204-3535
Заместитель председателя группы практики финансовых институтов фирмы Том обладает более чем тридцатилетним опытом оказания помощи финансовым учреждениям в решении сложных транзакционных и нормативных вопросов. В течение девяти лет, до прихода в фирму, Том работал советником в федеральных банковских агентствах, включая Федеральную корпорацию страхования вкладов и Управление по надзору за сбережениями.
maxwell technologies inc (MXWL) Анализ коэффициента текущей ликвидности
Этот отчет поможет вам изучить недавние и исторические значения коэффициента текущей ликвидности для maxwell technologies inc. Временной интервал данных, используемых в этом анализе, – между 2010 и 2019 годами. В этом диапазоне вы найдете как годовые, так и квартальные значения коэффициента текущей ликвидности, а также лучшие и худшие кварталы.
В этом отчете четыре раздела. Ниже приводится содержание, которое поможет вам.
- maxwell technologies inc Коэффициент текущей ликвидности по годам
- MXWL Коэффициент текущей ликвидности по кварталам
- 5 самых высоких квартальных показателей коэффициента текущей ликвидности компании maxwell technologies inc 5 самых низких квартальных показателей коэффициента текущей ликвидности
- MXWL
Примечание. Коэффициент текущей ликвидности – это важный «коэффициент заемного капитала», который помогает вам узнать способность компании рефинансировать свои краткосрочные долги.Под краткосрочными мы подразумеваем те обязательства, которые необходимо погасить в течение одного года. Возможность исходит из оборотных активов, которые обозначают те активы, которые являются денежными или легко конвертируемыми.
1 maxwell technologies inc Коэффициент текущей ликвидности по годам
Первый раздел поможет вам узнать исторические годовые значения коэффициента текущей ликвидности MXWL. Вы можете задаться вопросом, какое значение имеют ценности, отличные от ценностей последних лет, в анализе финансового здоровья. Ниже указано значение.
Тенденцию «коэффициента текущей ликвидности» можно узнать, посмотрев, увеличивается или уменьшается значение с течением времени. Постоянно снижающийся коэффициент текущей ликвидности может указывать на то, что компания все больше заимствует для поддержания своей жизнеспособности. Точно так же увеличение коэффициента может свидетельствовать об улучшении финансового состояния компании. Поэтому, вместо просмотра снимка, просмотр тренда (с помощью графика и таблицы, которые вы увидите ниже) поможет вам получить четкое представление.
Ниже представлена гистограмма, содержащая годовые значения коэффициента текущей ликвидности maxwell technologies inc.Вы можете интерпретировать тенденцию, посмотрев, увеличиваются или уменьшаются полосы по высоте со временем.
Ниже представлена таблица, которая содержит числовые значения коэффициента текущей ликвидности компании maxwell technologies inc. Помимо числовых цифр, вы также увидите, как значения меняются из года в год. Вы увидите как абсолютное, так и процентное изменение.
| Год | Коэффициент текущей ликвидности | Изменение коэффициента по сравнению с предыдущим годом | ||
|---|---|---|---|---|
| 2010 | 2,45 | |||
| 2011 | 1.89 | -0,56 ( -22,86% ) | ||
| 2012 | 2,18 | 0,29 ( 15,34% ) | ||
| 2013 | 2,43 | 113570,235 2014 | 2,15 | -0,28 (-11,52% ) |
| 2015 | 2,5 | 0,35 ( 16,28% ) | ||
| 2016 | 2,81 | 01 2,81%|||
| 2017 | 2.41 | -0,4 ( -14,23% ) | ||
| 2018 | 4,03 | 1,62 ( 67,22% ) |
В качестве дополнительной информации ниже приводится разбивка формулы, используемой для расчета коэффициента текущей ликвидности для MXWL. В качестве примера вы найдете расчет для 2018 года.
Вот разбивка расчета.
Текущие активы maxwell technologies inc в 2018 году = 114,46 миллиона долларов.
Текущие обязательства MXWL в течение 2018 года = 28 долларов США.38 миллионов.
Соотношение между двумя вышеуказанными значениями = (оборотные активы / текущие обязательства) = 4,03.
В зависимости от временного диапазона нашего анализа maxwell technologies inc достигла наивысшего коэффициента текущей ликвидности 4,03 в течение 2018 года. Tweet This
2 MXWL Current Ratio by Quarter
Во втором разделе вы увидите квартал- поквартальный коэффициент текущей ликвидности maxwell technologies inc. В отличие от годовых значений, квартальные значения отражают краткосрочные изменения.
Ниже линейный график отображает квартальные значения коэффициента текущей ликвидности MXWL.Тенденция линии поможет вам наблюдать за тем, как компания ежеквартально поддерживала финансовое здоровье.
Теперь давайте посмотрим на таблицу, содержащую квартальные цифры, соответствующие графику, который вы видели. Наряду с числовыми цифрами вы также увидите, как каждое квартальное значение соответствует предыдущему.
| Квартал | Коэффициент текущей ликвидности | Изменение коэффициента по сравнению с предыдущим кварталом | |||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q4-2010 | 2,45 | ||||||||||||||||||||||||||||||||||||||
| Q1-2011 | 2.24 | -0,21 (-8,45% ) | |||||||||||||||||||||||||||||||||||||
| 2 квартал 2011 г. | 2,13 | -0,11 ( -4,86% ) | |||||||||||||||||||||||||||||||||||||
| 3 квартал 2011 г. | 2,06 -0362 3,21% ) | ||||||||||||||||||||||||||||||||||||||
| 4 кв. 2011 г. | 1,89 | -0,17 ( -8,48% ) | |||||||||||||||||||||||||||||||||||||
| 1 кв. 2012 | 1,94 | -0,01 (-0.49% ) | |||||||||||||||||||||||||||||||||||||
| 3 кв. 2012 г. | 2 | 0,06 ( 3,25% ) | |||||||||||||||||||||||||||||||||||||
| 4 кв. | 2,03 | -0,15 ( -6,8% ) | |||||||||||||||||||||||||||||||||||||
| Q2-2013 | 1,99 | -0,04 ( -1,76% ) | |||||||||||||||||||||||||||||||||||||
| Q3-2013 | 2,32 | 2,32 903 % ) | |||||||||||||||||||||||||||||||||||||
| Q4-2013 | 2.43 | 0,11 ( 4,78% ) | |||||||||||||||||||||||||||||||||||||
| 1 кв. 2014 г. | 2,32 | -0,11 ( -4,56% ) | |||||||||||||||||||||||||||||||||||||
| 2 кв. | |||||||||||||||||||||||||||||||||||||||
| 3 кв. 2014 г. | 2,16 | -0,2 ( -8,61% ) | |||||||||||||||||||||||||||||||||||||
| 4 кв. | 2,31 | 0,16 ( 7.43% ) | |||||||||||||||||||||||||||||||||||||
| 2 кв. 2015 г. | 2,8 | 0,49 ( 21,4% ) | |||||||||||||||||||||||||||||||||||||
| 3 кв. 2015 | 2,5 | -0,13 ( -4,78% ) | |||||||||||||||||||||||||||||||||||||
| кв. -5.06% ) | |||||||||||||||||||||||||||||||||||||||
| Q2-2017 | 2.1 | -0,71 ( -25,18% ) | |||||||||||||||||||||||||||||||||||||
| Q3-2017 | 2,57 | 0,47 ( 22,4% ) | |||||||||||||||||||||||||||||||||||||
| Q4-2017 | 2,41 -0362 9070,21 ) | ||||||||||||||||||||||||||||||||||||||
| 1 квартал 2018 г. | 2,23 | -0,18 ( -7,55% ) | |||||||||||||||||||||||||||||||||||||
| 2 квартал 2018 г. | 2,21 | -0,02 ( -0,72 -0,02) 2018| 3,22 | 1,01 ( 45.58% ) | 4 квартал 2018 г. | 4,03 | 0,81 ( 25,27% ) | 1 квартал 2019 г. -2018. MXWL достиг самого высокого квартального коэффициента текущей ликвидности 4,03. Tweet This | 3 maxwell technologies inc. 5 самых высоких квартальных показателей коэффициента текущей ликвидности.Этот раздел является интересным, где вы увидите лучшие пять кварталов относительно текущего отношения maxwell technologies inc.Знание лучших мест служит одной цели. Вы будете знать те периоды, когда у компании было больше возможностей рефинансировать свои краткосрочные долги. Вы можете проанализировать основные причины, по которым компании удалось зафиксировать высокие значения коэффициента текущей ликвидности в течение этих кварталов. Вы также можете попытаться выяснить, могут ли аналогичные хорошие финансовые результаты повториться в будущем. Во-первых, давайте посмотрим на график, представляющий лучшие пять кварталов MXWL. Ниже представлена таблица, содержащая данные, использованные для построения вышеуказанного графика.Помимо числовых значений, вы также увидите, как все кварталы по сравнению с лучшим кварталом maxwell technologies inc.
4 MXWL 5 самых низких квартальных значений коэффициента текущей ликвидности за предыдущий периодза предыдущий периодвы увидели пять лучших четвертей компаний maxwell technologies inc. Теперь пришло время увидеть кварталы с самым низким коэффициентом текущей ликвидности. Опять же, мы рекомендуем вам проанализировать эти кварталы на предмет причин, по которым компания отставала в своем потенциале по управлению текущими обязательствами. Как и в предыдущем разделе, вы увидите график и таблицу, отражающие кварталы с низкой производительностью.
ЗаключениеМы надеемся, что отчет помог вам глубоко проанализировать потенциал или возможности maxwell technologies inc для управления краткосрочными обязательствами с использованием легко конвертируемых активов. |

 ф-ций:
ф-ций: М. Прохоров.
1988.
М. Прохоров.
1988.
 Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и… … Википедия
Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и… … Википедия Максвелл. Джеймс Клерк Максвелл James Clerk Maxwell … Википедия
Максвелл. Джеймс Клерк Максвелл James Clerk Maxwell … Википедия В.. Материаловедение стёкол — веществ, находящихся в стеклообразном состоянии, — имеет как теоретический, так и практический аспекты. В настоящее время отсутствует учебная литература, которая… Подробнее Купить за 1374 руб
В.. Материаловедение стёкол — веществ, находящихся в стеклообразном состоянии, — имеет как теоретический, так и практический аспекты. В настоящее время отсутствует учебная литература, которая… Подробнее Купить за 1374 руб