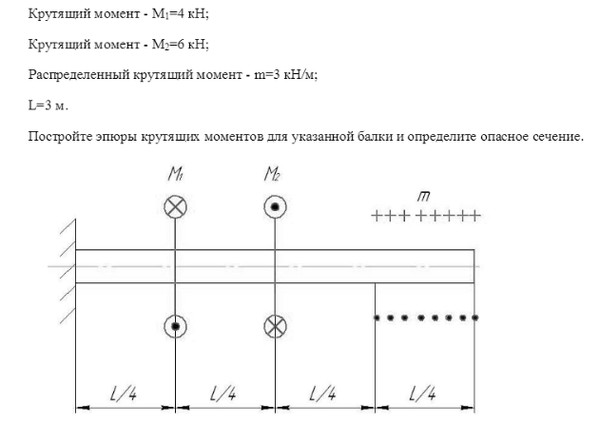
Расчет балки
построение эпюр в балках
Расчетная схема №1835278
Для более удобной и быстрой оплаты Вы можете зарегистрироваться, пополнить счет на сайте и оплачивать со своего счета
Почему не бесплатно? – Сайт создан исключительно на энтузиазме автора и дабы этот энтузиазм не угас, хотелось бы его подкрепить хоть каким-нибудь материальным поощрением. Кроме того, возросшее количество пользователей вынудило перейти на платный хостинг.
Условия оплаты? – Взнос денег считаем спонсорским взносом, поэтому ни о каком возврате речь идти не может, тем более суммы мизерные – практически не о чем спорить.
Но! Если Вы оплатили взнос, но недовольны результатом, Вы всегда можете обратиться за помощью к автору –
Telegram: sopromat_xyz
WhatsApp
А Ваш сайт не сворует мой номер карты, пароли и т.д.??? – Это невозможно! После того, как Вы нажмете “Перевести”, Вы будете направлены на страницу Яндекса (можете проверить в адресной строке), и все дальнейшие операции будете производить на сервисе Яндекса, так что со стороны сайта Вам ничего не грозит.
Слева Справа
Расстояние от левого края балки, м
Шарнирно неподвижная опора
Расстояние от левого края балки, м
Расстояние от левого края балки, м
Значение, кН
плюс – вверх
минус – вниз
Значение, кНм
плюс – по часовой
минус – против
Координата начала, м
Координата конца, м
Значение в начале, кН/м
Значение в конце, кН/м
Название схемы
Общая длина балки, м
Эпюра М на сжатых волокнах (для механиков)
Подбор сечения и прогибы
подобрать двутавр [σ] = МПа
подобрать круг [σ] = МПа
подобрать квадратное сечение [σ] = МПа
подобрать трубчатое сечение [σ] = МПа при d/D=
подобрать прямоугольное сечение [σ] = МПа при h/b=
записать уравнения начальных параметров для каждого участка и посчитать прогибы и углы поворота в промежуточных точках
Какие балки можно здесь расчитать?
Как поставить треугольную нагрузку?
Добавить нагрузки / опоры
Заменим распределенную нагрузку равнодействующей
Q1 = 6·2 = 12кН
Составим уравнения равновесия для определения реакций опор
Σ MA = + P · 2 + M + Q1 · 3 – RE · 6= + 12 · 2 + 8 + 12 · 3 – RE · 6=0
Σ ME = – P · 4 + M – Q1 · 3 + RA · 6= – 12 · 4 + 8 – 12 · 3 + RA · 6=0
Из этих уравнений находим реакции опор
RA = 12.
RE = 11.33кН.
Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений
На участке AB: (0 ≤ z1 ≤ 2 м )
Q(z1) = + RA = + 12.67 = 12.667 кН
M(z1) = + RA · z = + 12.67 · z
M(0) = 0 кНм
M(2) = 25.333 кНм
На участке BC: (2 ≤ z2 ≤ 4 м )
Q(z2) = + RA – P – q1·(z – 2) = + 12.67 – 12 – 6·(z – 2)
Q(2) = 0.667 кН
Q(4) = -11.333 кН
M(z2
M(2) = 25.333 кНм
M(4) = 14.667 кНм
Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M
M(2.11) = 25.4 кНм
На участке CD: (4 ≤ z3 ≤ 5 м )
Q(z3) = + RA – P – Q1 = + 12. 67 – 12 – 12 = -11.333 кН
67 – 12 – 12 = -11.333 кН
M(z3) = + RA · z – P·(z – 2) – Q1·(z – 3) = + 12.67 · z – 12·(z – 2) – 12·(z – 3)
M(4) = 14.667 кНм
M(5) = 3.333 кНм
На участке DE: (5 ≤ z4 ≤ 6 м )
Q(z4) = + RA – P – Q1 = + 12.67 – 12 – 12 = -11.333 кН
M(z4) = + RA · z – P·(z – 2) + M – Q1·(z – 3) = + 12.67 · z – 12·(z – 2) + 8 – 12·(z – 3)
M(5) = 11.333 кНм
M(6) = 0 кНм
Максимальный момент в балке составляет Mmax = 25.4 кНм. По этому значению подбираем сечение балки.
Условие прочности при изгибе σ = Mmax / W ≤ [σ]
Отсюда, минимально необходимый момент сопротивления вычисляем по формуле Wmin=Mmax / [σ]
Посмотреть примеры
Не получается решить задачу? Есть вопросы? Нужна помощь? Обратитесь к авторам сайта через ВКонтакте Telegram: sopromat_xyz WhatsApp: +380936422175
Расчёт балки задачи по сопромату примеры и решения
Содержание:
- Напряжения в поперечных сечениях
- Касательные напряжения
- Пример решения задачи 1.

- Пример решения задачи 2
- Расчет на прочность
- Пример решения задачи 3
- Пример решения задачи 4
В инженерной практике часто применяются балки с поперечным сечением, имеющим вертикальную ось симметрии. Если внешняя нагрузка и реактивные усилия лежат в одной плоскости, которая совпадает с осью симметрии сечения, то балка будет изгибаться в той же плоскости. Такой изгиб называется плоским (рис.1).
При плоском поперечном изгибе в сечениях балки возникают два внутренних усилия – поперечная сила и изгибающий момент (рис.2).
Напряжения в поперечных сечениях
Поскольку поперечная сила является равнодействующей касательных напряжений (рис.3), а изгибающий момент – равнодействующей нормальных напряжений (рис.4), то, следовательно, в поперечных сечениях балки в общем случае возникают и нормальные напряжения и касательные
 5). Линия, во всех точках которой называется нейтральной линией. В рассматриваемом случае плоского вертикального изгиба нейтральная линия совпадает с осью
5). Линия, во всех точках которой называется нейтральной линией. В рассматриваемом случае плоского вертикального изгиба нейтральная линия совпадает с осьюПо мере удаления от нее напряжения возрастают по модулю, достигая наибольших по модулю значений в крайних точках сечения, наиболее удаленных от нейтральной линии.
Чтобы определить нормальные напряжения в произвольной точке используется следующая формула
где – величина изгибающего момента в рассматриваемом сечении, определяется по эпюре
– осевой момент инерции поперечного сечения, табличная величина;
– координата точки, в которой определяется напряжение.
Возможно вам будут полезны данные страницы:
Задачи на сжатие и растяжение по сопромату примеры и решения |
Задачи на кручение по сопромату примеры и решения |
Задачи на эпюры по сопромату построение примеры и решения |
Задачи с двутавром по сопромату примеры и решения |
Знак определяется с помощью эпюры Подробнее это будет рассмотрено при решении конкретных задач.
Преобразуя формулу (1), можно получить формулу для определения максимальных напряжений
где – осевой момент сопротивления сечения, табличная величина.
Касательные напряжения
Касательные напряжения в поперечном сечении балки определяются по формуле Журавского:
где – величина поперечной силы в рассматриваемом сечении, определяется по эпюре
– осевой момент инерции всего сечения, табличная величина;
– статический момент отсеченной части сечения, определяется по формуле:
– координата отсеченной части сечения;
ее площадь; – ширина сечения на уровне отсеченной части. Распределение касательных напряжений по высоте поперечного сечения зависит от формы самого сечения. На рис.6 приведены эпюры касательных напряжений для некоторых часто встречающихся форм поперечных сечений балки.
Как видно из этих рисунков, максимальной величины касательные напряжения достигают на нейтральной линии, а в крайних точках сечения они равны нулю. Рассмотрим примеры определения нормальных и касательных напряжений.
Рассмотрим примеры определения нормальных и касательных напряжений.
Пример решения задачи 1.
1) Пусть в опасном сечении балки, сечение которой изображено на рис.7, возникают изгибающий момент растягивающий нижние волокна и Определить нормальные и касательные напряжения в точке а также наибольшие нормальные и касательные напряжения. Построить эпюру распределения нормальных напряжений по высоте сечения. Решение:
1) Покажем на чертеже сечения положение центра тяжести и проводим оси Это будет система главных центральных осей, так как ось совпадает с осью симметрии сечения.
2) Выпишем из справочника [3, табл.5] формулу для определения момента инерции для треугольного сечения и подставим численные значения
3) Найдем нормальные напряжения в точке используя формулу (1)
Эти напряжения будут отрицательными, так как согласно условию задачи растягиваются нижние волокна сечения, то есть выше нейтральной линии (ось лежит зона сжатия, а ниже – зона растяжения.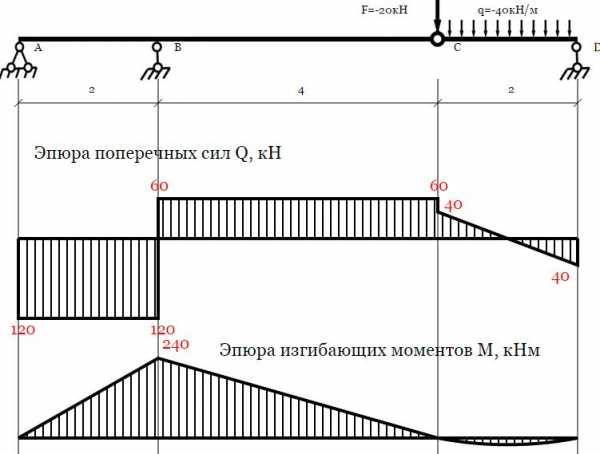 Точка находится в зоне сжатия, поэтому
Точка находится в зоне сжатия, поэтому
4) Найдем наибольшее нормальное напряжение. Поскольку сечение несимметрично относительно оси то целесообразно пользоваться формулой (1). Из чертежа видно, что наибольшие сжимающие напряжения возникают в точке 1, так как эта точка является наиболее удаленной от нейтральной линии в зоне сжатия. Наибольшие растягивающие напряжения возникают в нижних точках сечения
По полученным данным построим эпюру (рис.7).
5) Найдем касательное напряжение в точке Сначала проведем через точку линию, параллельную оси и назовем отсеченной часть сечения, лежащую выше этой линии. Обозначим через точку центр тяжести отсеченной части и вычислим его координату Из чертежа видно
статический момент отсеченной части.
Используем формулу (3):
Здесь ширина основания отсеченной части.
Пример решения задачи 2
Пусть в сечении балки возникают поперечная сила и изгибающий момент растягивающий верхние волокна. Определить наибольшие нормальные и касательные напряжения.
Определить наибольшие нормальные и касательные напряжения.
Решение:
1) Покажем положение главной центральной системы координат
2) Найдем осевой момент сопротивления используя справочник
3) Так как сечение симметрично относительно оси и удобнее использовать формулу (2).
Согласно условию задачи растягиваются верхние волокна, поэтому
4) Из рис.6 следует, что наибольшие касательные напряжения возникают в точках, лежащих на нейтральной линии, поэтому проводим линию, совпадающую с осью Отсеченной будет, например, верхняя часть сечения, т. -центр тяжести этой части, т.е. полукруга.
Найдем используя формулу из [3, табл.5]:
Найдем момент инерции всего сечения (т.е. круга) [3, табл.5]:
Используем формулу (3)
Построим эпюры (рис.8).
Расчет на прочность
Расчет на прочность начинается с построения эпюр внутренних усилий балки Сечение, в котором величина достигает наибольшего значения, считается опасным сечением. Именно для такого сечения и делается расчет на прочность.
Именно для такого сечения и делается расчет на прочность.
Если балка выполнена из пластического материала, который одинаково работает на растяжение и сжатие, то условие прочности записывается в виде:
где – расчетное сопротивление, заданная величина .
Если балка выполнена из хрупкого материала, который неодинаково работает на растяжение и сжатие, то используются два условия прочности.
где расчетное сопротивление на растяжение,
расчетное сопротивление на сжатие.
Как правило, расчет балки на прочность производится только по нормальным напряжениям, так как в подавляющем большинстве балок величина нормальных напряжений намного превосходит величину напряжений касательных. Однако в следующих случаях проверяется и условие прочности по касательным напряжениям:
- 1) если рассчитываемая балка выполнена из дерева, так как дерево плохо сопротивляется скалыванию вдоль волокон;
- 2) если балка короткая;
- 3) если на балку действуют большие сосредоточенные силы, приложенные на наибольших расстояниях от опор.

В последних двух случаях поперечные сечения в балке достигают большой величины, в то время как изгибающие моменты за счет малых плеч сравнительно невелики.
Условие прочности по касательным напряжениям записывается в виде:
где расчетное сопротивление на срез.
Пример решения задачи 3
Проверить выполнение условий прочности по нормальным и касательным напряжениям для деревянной балки (рис.9), если
Решение:
1) Строим эпюры Опасным является сечение в заделке, (рис.9).
2) Проверим условие прочности по нормальным напряжениям
Величина была определена в примере 2:
Условие прочности по нормальным напряжениям выполняется.
3) Проверим условие прочности по касательным напряжениям
Величину берем из примера 2:
Условие прочности по касательным напряжениям выполняется. Замечание.
Во всех последующих примерах будем использовать только условие прочности по нормальным напряжениям.
Пример решения задачи 4
Проверить выполнение условия прочности для балки, выполненной из чугуна, если
Решение: 1) Построим эпюры внутренних усилий Опасным является сечение в заделке (рис.10). 2) Так как балка выполнена из хрупкого материала, то проверяем два условия прочности (5):
Значения напряжений были определены в примере 1.
Условие прочности на сжатие выполняется.
Условие прочности на растяжение не выполняется.
Примеры решения задач по сопромату
На этой странице собраны ссылки на примеры решения задач по сопромату (сопротивлению материалов), которые размещены на сайте – ssopromat.ru. Я решил собрать все примеры в одном месте, со всех статей, для удобства навигации и поиска нужного решения задачи. Эта страница будет постоянно обновляться, по мере развития сайта и публикации новых примеров.
Навигация по примерам
Для поиска нужных примеров, можешь воспользоваться данными ссылками:
- Построение эпюр при растяжении (сжатии).

- Расчёты на прочность при растяжении (сжатии).
- Построение эпюр при кручении.
- Определение реакций опор.
- Построение эпюр при поперечном (плоском) изгибе.
- Расчёт сечений из простых фигур.
Примеры решения задач на растяжение (сжатие)
В этом разделе собраны ссылки на примеры решения задач на растяжение (сжатие). Здесь можно найти примеры построения эпюр при чистом растяжении или сжатии, а также различные прочностные расчёты при этом виде деформации.
Построение эпюр
Здесь можно найти примеры построения эпюр: продольных сил, нормальных напряжений и углов закручивания (углов поворотов) поперечных сечений для стержней, работающих на чистое растяжение (сжатие).
Задача №1
Для стального ступенчатого бруса (E=2·105 МПа), загруженного силами F1 = 5 кН, F2 = 8 кН требуется построить эпюры: продольных сил, нормальных напряжений и осевых перемещений поперечных сечений. Площадь поперечного сечения первой ступени равна 2 см2, второй — 4 см2.
Площадь поперечного сечения первой ступени равна 2 см2, второй — 4 см2.
Перейти к примеру
Задача №2
Для ступенчатого бруса требуется построить эпюры: продольных сил, нормальных напряжений и осевых перемещений поперечных сечений. Модуль упругости: E=2·105 МПа, нагрузка: F1 = 5 кН, F2 = 8 кН, q = 2 кН/м, площади поперечных сечений: A1 = 2 см2, A2 = A3= 4 см2.
Перейти к примеру
Расчёты на прочность
В этом разделе можно найти ссылки на примеры расчётов на прочность при растяжении (сжатии): проверочные и проектировочные.
Задача №1
Для стального стержня, нагруженного сжимающей силой F = 100 кН, с размерами: d1 = 50 мм, d2 = 70 мм, необходимо проверить прочность, если σт = 260 МПа, nт = 2.
Перейти к примеру
Задача №2
Для бруса, загруженного силами: F1 = 60 кН, F2 = 80 кН необходимо подобрать размеры поперечных сечений (d1, d2), если [σ] = 160 МПа. Расчётные диаметры округлить по ГОСТ 6636-69 (Ra40) до ближайших больших значений.
Расчётные диаметры округлить по ГОСТ 6636-69 (Ra40) до ближайших больших значений.
Перейти к примеру
Примеры решения задач на кручение
Здесь можно найти ссылки на примеры решения задач, связанные с чистым кручением, где рассчитываются и строятся эпюры и проводятся прочностные расчёты для валов.
Построение эпюр
В этих примерах рассчитываются и строятся эпюры при чистом кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов) поперечных сечений.
Задача №1
Для ступенчатого стального стержня (G = 8 · 1010 Па) загруженного вращающими моментами: M1 = 30 кН·м, M2 = 70 кН·м, M3 = 90 кН·м, требуется построить эпюры крутящих моментов, максимальных касательных напряжений и углов закручивания.
Перейти к примеру
Примеры решения задач на поперечный изгиб
Здесь будут публиковаться ссылки на примеры решения задач, связанных с поперечным (плоским) изгибом. В этом разделе можно найти примеры определения опорных реакций, расчёт и построение эпюр для статически определимых балок и рам, а также различные прочностные расчёты данных элементов конструкций.
В этом разделе можно найти примеры определения опорных реакций, расчёт и построение эпюр для статически определимых балок и рам, а также различные прочностные расчёты данных элементов конструкций.
Определение реакций опор
В этом разделе собраны ссылки на примеры определения реакций опор для плоских статически определимых систем.
Задача №1
Для двухопорной балки, загруженной посередине пролёта сосредоточенной силой (F = 2 кН), требуется определить реакции в опорах и выполнить проверку решения.
Перейти к примеру
Задача №2
Для балки на двух опорах, загруженной распределённой нагрузкой (q) с интенсивностью – 10 кН/м, требуется найти опорные реакции и провести проверку найденных реакций.
Перейти к примеру
Задача №3
Для консольной балки, загруженной распределённой нагрузкой (q = 5 кН/м) и силой (F = 2 кН) направленной под углом (α = 30°) к продольной оси балки, необходимо найти реакции в жёсткой заделке и провести проверку решения.
Перейти к примеру
Задача №4
Для плоской статически определимой рамы, загруженной нагрузкой: F1 = 2 кН, F2 = 4 кН, M = 3 кН∙м, q = 2 кН/м, необходимо рассчитать реакции в опорах и проверить решение.
Перейти к примеру
Построение эпюр
В этом разделе собраны ссылки на примеры построения эпюр при поперечном изгибе – поперечных сил и изгибающих моментов. В примерах строятся эпюры для статические определимых плоских систем – балок и рам.
Задача №1
Для консольной балки, к которой приложены нагрузки: M = 10 кН·м; F1 = 5 кН; F2 = 15 кН, необходимо рассчитать и построить эпюры поперечных сил и изгибающих моментов.
Перейти к примеру
Задача №2
Для двухопорной балки, загруженной распределённой нагрузкой (q = 5 кН/м), моментом (M = 10 кН·м) и силой (F = 12 кН) требуется построить эпюры поперечных сил и изгибающих моментов.
Перейти к примеру
Примеры расчёта геометрических характеристик
В этом разделе можно найти ссылки на примеры расчётов геометрических характеристик плоских сечений (фигур) – положение центра тяжести, моментов инерции, моментов сопротивления.
Сечения из простых фигур
Здесь собраны ссылки на расчёты плоских сечений, состоящих из простейших фигур.
Задача №1
Для плоского сечения, состоящего из простых фигур, необходимо определить положение центра тяжести.
Перейти к примеру
Задача №2
Для симметричного сечения, имеющего две оси симметрии, необходимо определить положение центра тяжести, а также определить осевые моменты инерции.
Перейти к примеру
Бесплатный калькулятор луча | ClearCalcs
Калькулятор балки ClearCalcs позволяет пользователю ввести геометрию и нагрузку балки для анализа за несколько простых шагов. Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов. ClearCalcs позволяет выполнять проектирование из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
- «Основные свойства», где пользователь вводит геометрию выбранного сечения и опор балки.
- «Нагрузки», где можно вводить распределенные, точечные и моментные нагрузки,
- «Сводка», в которой отображаются основные выходные данные и диаграммы.
Также имеется раздел «Комментарии», в котором пользователь может оставить любые примечания к дизайну. Щелчок по любой из меток ввода/свойства дает описательное справочное объяснение.
1. Свойства клавиш ввода
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.
Длина балки общая сумма, включая все пролеты балки, в мм или футах. пользователь.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию соответствует значениям для обычной стальной балки.
Второй момент площади (или момент инерции) также относится к выбранному сечению балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других сечений балки можно получить из библиотеки свойств сечений ClearCalcs. Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю ввести любое количество опор и указать их положение по длине балки. Тип опоры может быть фиксированным (фиксированным при перемещении, свободным при вращении) или фиксированным (фиксированным как при перемещении, так и при вращении) и выбирается из раскрывающегося меню. Требуется как минимум одна фиксированная опора или две опоры на штифтах.
Калькулятор балки также позволяет использовать консольные пролеты на каждом конце, поскольку положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются при добавлении, изменении или удалении опор в зависимости от заданной нагрузки.
2. Входные нагрузки
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждая загрузка может быть названа пользователем.
Для нагрузки используются следующие знаки (показаны положительные значения):
Распределенные нагрузки указаны в единицах силы на единицу длины, кН/м или pf, вдоль балки и могут быть приложены между любыми двумя точками. В калькуляторе можно применять два разных типа:
Равномерные нагрузки имеют постоянную величину по длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны совпадать.
Линейные нагрузки имеют различную величину по длине применения. Различные начальные и конечные величины должны быть указаны пользователем, и их можно использовать для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указаны в единицах силы, кН или тысяч фунтов, и площади, приложенной в дискретных точках вдоль балки. Например, они могут представлять реакции других элементов, соединяющихся с балкой. Пользователь вводит имя, величину и местоположение слева от луча.
На приведенной ниже примерной диаграмме из сводного раздела показана двухпролетная неразрезная балка с линейной распределенной патч-нагрузкой и точечной нагрузкой.
3. Итоговые результаты расчетов
После задания нагрузки и геометрии калькулятор автоматически использует механизм анализа методом конечных элементов ClearCalcs для определения моментов, поперечных сил и прогибов. Максимальные значения каждого выводятся как «Запрос момента» , «Запрос на сдвиг» и «Отклонение» вместе со схемами по длине балки.
Положительные значения означают отклонение вниз, а отрицательные значения означают отклонение вверх. На диаграммах поперечной силы и изгибающего момента используются следующие знаки (показаны положительные значения):
При наведении курсора на любую точку на диаграммах изгибающего момента, поперечной силы или прогиба отображаются конкретные значения в этом месте вдоль балки. В приведенном ниже примере показаны выходные данные для двухпролетной неразрезной балки с линейной распределенной патч-нагрузкой и точечной нагрузкой.
Простой калькулятор луча | Calcresource
Прыжки до
-Калькулятор
-Фон
СОДЕРЖАНИЕ
-Калькулятор
-Фон
-Введение
-Asplactions
-Согласование
-Символы
– СОДЕРЖАНИЯ СОДЕРЖА равномерная распределенная нагрузка
– Свободно опертая балка с сосредоточенной силой в середине
– Свободно опертая балка с точечной силой в произвольном положении
– Свободно опертая балка с точечным моментом
– Свободно опертая балка с треугольной нагрузкой
– Свободно опертая балка с трапециевидной нагрузкой
– Свободно опертая балка с трапециевидным распределением нагрузки плитного типа
– Свободно опертая балка с частично распределенной равномерной нагрузкой load
– Свободно опертая балка с частично распределенной трапециевидной нагрузкой
– Статьи по теме
Поделиться
См. также
также
Калькулятор балки с простой опорой
– Д-р Минас Э. Лемонис, доктор философии – Обновлено: 11 мая 2022 г.
Главная > Статика > Балка с простой опорой
Этот инструмент вычисляет статическую реакцию балки с простой опорой при различных сценариях нагрузки. Инструмент рассчитывает и строит диаграммы для следующих величин:
- реакции
- изгибающие моменты
- поперечные силы сдвига
- прогибы
- уклоны
Пожалуйста, имейте в виду, что приняты предположения теории балок Эйлера-Бернуля. является упругим, а поперечное сечение постоянным на всем пролете балки (призматическая балка).
- Вместо этого переходите к теории и формулам!
Units: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Структура | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L = | mcmmmydftin | 94|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассчитайте момент инерции балок различных сечений с помощью наших специальных калькуляторов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT |
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Imposed loading: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Uniform distributed loadUniform распр. нагрузка (суммарная)Точечная нагрузка (по центру)Точечная нагрузкаТочечный моментТреугольная нагрузкаТрапециевидная нагрузкаТрапециевидная нагрузка (плита)Частичная равномерная нагрузкаЧастичная треугольная нагрузкаЧастичная трапециевидная нагрузка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculate | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reactions: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R A = | kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R B = | kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bending Moment: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M u = | kNmNmkg. mt.mlbf.ftlbf.inkip.ftkip.in mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x m = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Transverse Shear Force: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V u = | kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x v = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deflection: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d u = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x d = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Наклоны: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ A = | DEGRADMRAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ B = | 61616169θ B = | 1616169θ B = θ B θ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Request results at a specific point: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M(x) = | kNmNmkg. mt.mlbf.ftlbf.inkip.ftkip.in mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V(x) = | kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d(x) = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ(x) = | degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT |
| 1 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagrams | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kN/mN/mkg/mt /mlbf/ftlbf/inkip/ft | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
РЕКЛАМА
Лучшие страницы
Поделиться
Справочная информация
Содержание
-4 Предположение 9– 5 Введение0005
– Условные знаки
– Обозначения
– Свободно опертая балка с равномерно распределенной нагрузкой
– Свободно опертая балка с точечной силой в середине
– Свободно опертая балка с точечной силой в произвольном положении
– Свободно опертая балка с точечным моментом
– Свободно опертая балка с треугольной нагрузкой
– Свободно опертая балка с трапециевидной нагрузкой
– Свободно опертая балка с трапециевидным распределением нагрузки плитного типа
– Свободно опертая балка с частично распределенной равномерной нагрузкой
– Свободно опертая балка с частично распределенной трапециевидной нагрузкой
– Статьи по теме
Введение
Свободно опертая балка является одной из самых простых конструкций. Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.
Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.
Удаление любой из опор или вставка внутреннего шарнира превратит свободно опертую балку в механизм, который будет перемещаться без ограничений в одном или нескольких направлениях. Очевидно, что это нежелательно для несущей конструкции. Таким образом, свободно опертая балка не предлагает избыточности опор. Если произойдет локальный отказ, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются критическими или детерминантными 9.0662 конструкции. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией.
РЕКЛАМА
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для свободно опертой балки, которая воспринимает только поперечные нагрузки, осевая сила всегда ноль, поэтому им часто пренебрегают. Расчетные результаты на странице основаны на следующих предположениях:
- Материал однородный и изотропный (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
- Материал линейно-упругий
- Нагрузки действуют статически (они не меняются со временем) )
- Сечение одинаковое по всей длине балки
- Прогибы малы
- Каждое поперечное сечение, изначально плоское и перпендикулярное к продольной оси, остается плоским и нормальным также к отклоненной оси.
 Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).
Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).
Последние два предположения удовлетворяют кинематическим требованиям теории балки Эйлера-Бернулли, которая также принята здесь.
Правила знаков
Для расчета внутренних сил и моментов в любом сечении балки необходимо соблюдать правила знаков. Здесь приняты следующие значения:
- Осевая сила считается положительной, если она вызывает растяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хоть и не обязательны, но достаточно универсальны. Другой набор правил, если им следовать последовательно, также приведет к тем же физическим результатам.
Символы
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опорная реакция
- d: прогиб
- M: изгибающий момент
- V: поперечная поперечная сила Нагрузка w распределяется по всему пролету балки, имея постоянную величину и направление.
 Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}
Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}РЕКЛАМА
Свободно опертая балка с точечной силой посередине
Сила сосредоточена в одной точке, расположенной в середине балки. Однако на практике сила может быть распределена по небольшой площади, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической теорией балки, может быть неточной. Однако это лишь локальное явление. По мере того, как мы удаляемся от места действия силы, результаты становятся достоверными в силу принципа Сен-Венана. 92)}{16 E I} &, x>L/2 \end{выровнено}\right.
где:
\acute{x}=L-x
Свободно поддерживаемая балка с точечной силой в произвольном месте
Сила сосредоточена в одной точке, в любом месте поперек пролета балки.
 Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенную точечную силу P, приложенную на случайном расстоянии a от левого конца.
Simply supported beam with point load at random position
Quantity Formula Reactions: R_A={Pb\over L}
R_B={Pa\ более L}
 3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.
3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.где:
b=L-a
\acute{x}=L-x
Свободно опертая балка с точечным моментом
, в любом месте на пролете балки. С практической точки зрения это может быть пара сил или элемент при кручении, соединенный вне плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину балки, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке. Несмотря на то, что в непосредственной близости от области применения предсказанные результаты с помощью классической теории балок, как ожидается, будут неточными (из-за концентрации напряжений и других локализованных эффектов), по мере удаления предсказанные результаты совершенно достоверны, как заявил Святой – Принцип Венана.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенный точечный момент M, приложенный на расстоянии a от левого конца.

просто поддержанный луч с точечным моментом
LOUTITION Формула Реакция: . } Концевые уклоны: 92}{2 E I} &, x>a\end{выровнено} \right. где:
b=L-a
\acute{x}=L-x
Просто опертая балка с треугольной нагрузкой, однако, ее нагрузка не распределяется по всему пролету
постоянна, но изменяется линейно, начиная с нуля на левом конце и заканчивая пиковым значением w_1 на правом конце. Размеры w_1 – это сила на длину. Суммарная сила, приложенная к балке, равна W={1\over2}w L, где L – длина пролета.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на линейно изменяющуюся (треугольную) распределенную нагрузку, возрастающую слева направо.
Simply supported beam with linearly varying distributed load (triangular)
Quantity Formula Reactions: R_A={1\over6}w_1L
R_B={ 1\over3}w_1L 94} {24EIL}
где:
C=\sqrt{15-\sqrt{120}}\left(\sqrt{15}+\sqrt{50}\right)\приблизительно 22,01237
Свободно опертая балка с трапециевидной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце до w_2 на правом конце.
 Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L – длина пролета.
Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L – длина пролета.В следующей таблице представлены формулы, описывающие статическую реакцию простой балки трапециевидной формы на переменную распределенную нагрузку.
Simply supported beam with linearly varying distributed load (trapezoidal)
Quantity Formula Reactions: R_A={(2w_1+w_2)L\over6}
R_B={(w_1+2w_2)L\over6}
где:
w_x=w_1+{(w_2-w_1)x\over L}
Опорная балка с трапециевидным распределением нагрузки характерны для балок по периметру плиты. Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах она становится равной нулю. Размеры (\w\) представляют собой силу на длину.
 Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L – длина пролета, а a, b – длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93
Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L – длина пролета, а a, b – длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93Свободно опертая балка с частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет не нагружен. Размеры w представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=\left(L-a-b\right)w, где L – длина пролета, а a, b – ненагруженные длины левой и правой сторон балки соответственно.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную равномерную нагрузку. 92}{2 E I} &,x\ge L-b \end{выровнено}\right.
Где:
\ Острый {x} = L-X
x_a = x-a
L_W = L-A-B
просто нагружен нагрузкой.
 пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L – длина пролета, а a, b – ненагруженные длины левой и правой сторон балки соответственно.
пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L – длина пролета, а a, b – ненагруженные длины левой и правой сторон балки соответственно.Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок могут быть получены путем соответствующей установки значений w_1 и w_2. Кроме того, соответствующие случаи для полностью загруженного пролета могут быть получены путем установки a и b равными нулю.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную трапециевидную нагрузку.
Свободно опертая балка с частично распределенной линейно-переменной нагрузкой (трапециевидная) 93
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
РЕКЛАМА
Смотрите также
Пять бесплатных программ для разработчика металлоконструкций.
 Онлайн-калькуляторы и программы для расчета конструкций
Онлайн-калькуляторы и программы для расчета конструкцийОдним из популярных решений для проектирования деревянного дома на персональном компьютере является комплекс специализированных программ KZ-Cottage. Эти приложения значительно облегчают работу по черчению и оцилиндровке. Программа позволяет создавать подробные чертежи для разных этапов строительства жилого дома.
Проект двухэтажного коттеджа из оцилиндрованного бревна с гаражом
Благодаря использованию данной программы значительно сокращаются затраты времени на изготовление проектной документации и ее оформление в государственном учреждении.
Основной целью работы приложений на базе «КЗ-Коттедж» является создание разного рода проектно-сметной документации, которая будет использоваться на всех этапах и участках текущего строительства. В самой программе разработан типовой акт, позволяющий обеспечить каждую часть конструкции необходимыми чертежами:
- проведение подготовительных работ перед монтажом здания;
- заказ или производство материалов, необходимых для строительства;
- поставка деталей и окончательная подготовка;
- строительство или монтаж жилых зданий.

Основным отличием программного обеспечения KZ-Cottage является его универсальность и многофункциональность.
Проектирование деревянного дома в программе К3-Дача
В отличие от других программ, не только позволяет создавать, помимо основных рабочих чертежей и моделей будущего здания, дополнительные спецификации и управляющие программы для ЧПУ, но также делает большую часть работы автоматически. Благодаря этому дизайнер может избежать большинства проблем, связанных с созданием того или иного документа. Ошибки в основном связаны с человеческим фактором.
Онлайн-калькуляторы
Россия и страны СНГ
Единственный в своем роде сайт практикующего инженера, предоставляющий калькуляторы проектирования зданий с расчетами по СП, СНиП, здесь есть калькуляторы расчета железобетона, металлоконструкций, калькуляторы расчета фундаментов и фонды.
Назначение Калькулон – автоматизировать подготовку коммерческого предложения на выполнение проектных работ, согласно справочников базовых цен, утвержденных Правительством Москвы и России.
 Калькулон полезен руководителям и сметчикам проектных организаций, он позволяет быстро определить примерную стоимость любых проектных работ, которые указаны в справочниках базовых цен.
Калькулон полезен руководителям и сметчикам проектных организаций, он позволяет быстро определить примерную стоимость любых проектных работ, которые указаны в справочниках базовых цен.Онлайн-калькулятор на этом сайте поможет вам произвести следующие расчеты: расход материалов, необходимых для возведения всех основных элементов здания; расчет необходимых размеров и параметров элементов; расчет необходимых характеристик строительных материалов.
Интересно выполненные калькуляторы помогут в строительстве вашего каркасного дома, решат необходимость подсчитать количество стройматериалов или рассчитать размеры той или иной конструктивной детали.
Удобный бесплатный онлайн-калькулятор матриц. На сайте реализованы все основные операции матричного калькулятора над матрицами, а также методы, использующие матрицы для решения систем линейных уравнений.
Преобразование легко и просто!
Иностранный
На сайте более нескольких сотен калькуляторов для решения сложных уравнений и формул в области электричества, механики, химии, электроники, гражданского строительства, металлургии, нефти и газа, оптики, физики, математики и т.
 д.
д.Вы инженер-механик, инженер-строитель, чертежник, техник или студент? Необходимо работать с профессиональными вычислительными системами? Но вы не готовы или не можете платить тысячи рублей за неадекватно сложные или непонятные решения? Тогда вам просто необходим MITCalc
Хорошие строительные онлайн калькуляторы, статические расчеты балок и т.д.
Расчет деревянных конструкций. Эти интерактивные инструменты доступны бесплатно, чтобы помочь инженерам и архитекторам проектировать здания с использованием дерева в качестве конструкционного материала.
Диаграмма изгибающего момента — это бесплатный онлайн-калькулятор, который создает диаграммы поперечной силы и изгибающего момента для большинства простых балок. Калькулятор полностью настраивается для соответствия большинству конструкций балок, чего нет в большинстве других калькуляторов.
Красиво оформленная версия калькуляторов для расчета балок из стали, дерева и опорных плит с анкерными болтами.

Быстрое решение технических проблем. Выберите калькулятор ниже, чтобы начать!
Отличный выбор калькуляторов для расчета строительных конструкций из различных материалов.
Xcalcs представляет собой набор инструментов для инженерных расчетов в области расчета конструкций, для непосредственного использования в веб-среде. Вы найдете ее в списке под заголовком «библиотека» в оглавлении. Часто проверяйте этот список, расчетные листы и инструменты регулярно обновляются!
Инструменты и основная информация для проектирования, проектирования и строительства.
Сайт инженеров-практиков содержит калькуляторы расчета ветровых нагрузок, сейсмостойкости, фундаментов, рам и отдельно балок и колонн.
Большой выбор калькуляторов с разнообразной тематикой для расчета строительных конструкций, очень качественные калькуляторы, сделанные инженерами-практиками.
Большой выбор строительных калькуляторов!
Здесь вы найдете отличный выбор калькуляторов для расчетов по математике, финансам, строительству, статистике, физике, калькуляторы перевода единиц измерения.

Проектирование металлоконструкций- одно из важнейших направлений строительной деятельности. Для определения необходимых параметров профиля используется дорогостоящее лицензионное программное обеспечение, требующее профильного образования и навыков работы с конкретным программным комплексом.
В то же время бывают ситуации, когда нужно сделать чертеж «на коленке», подобрать нужный прокат, рассчитать вес бруса для определения стоимости и заказать металл. В случаях, когда использовать специальные программы нет возможности, удобными помощниками в расчете металлоконструкций могут стать бесплатные онлайн и настольные программы:
- калькулятор металлопроката Арсенал;
- онлайн калькулятор Metalcalc;
- онлайн-программа sopromat.org для расчета балок и ферм;
- расчет балок в Сопроматгуру онлайн;
- настольная программа “Ферма”.
Компания Арсенал предоставляет всем желающим возможность сэкономить свое время, используя фирменную настольную программу для расчета теоретического веса металлопрофиля любого вида, в том числе черного и нержавеющего, а также цветного металла.
 Сайт доступен и онлайн-версия программы .
Сайт доступен и онлайн-версия программы .Для расчета профиля необходимо ввести информацию о толщине металла, длине сегмента, высоте и ширине. Также вы можете выбрать марку прокатного профиля из ассортимента и задать необходимую длину. В этом случае программа автоматически определит его габариты и вес.
2. Metalcalc онлайн калькуляторОнлайн калькулятор metalcalc – удобный ресурс для определения веса и длины металлопроката. При задании основных технических параметров изделия (номер сортамента или габаритные размеры профиля, его длина) программа определит его вес. Расчеты выполняются на основе действующих ГОСТов и отличаются максимальной точностью.
В программе также есть функция пересчета. Если указать вес и размер профиля, сервис рассчитает его длину. Ресурс абсолютно бесплатный и простой в использовании.
3. Бесплатная онлайн программа sopromat.org для расчета балок и фермНа сайте sopromat.
 org представлена бесплатная онлайн программа для расчета балок и ферм методом конечных элементов. Расчет может производиться, в том числе, и для статически неопределимых фреймов.
org представлена бесплатная онлайн программа для расчета балок и ферм методом конечных элементов. Расчет может производиться, в том числе, и для статически неопределимых фреймов.Сервис может быть полезен как студентам для выполнения курсовых работ, так и практикующим инженерам для определения параметров реальных металлоконструкций. Интернет-ресурс позволяет:
- определять перемещения в узлах;
- рассчитать реакции опор;
- участок Q, M, N
- сохранить результаты расчетов и схему нагрузок;
- экспортировать результаты в формат чертежа DXF.
На сайте всегда самая последняя версия программы. Есть версия Mini для скачивания и работы на мобильных устройствах. Мобильная программа обладает всеми преимуществами полной версии.
4. Расчет балок в СопроматгуруВ ближайшее время авторы планируют добавить в программу функцию расчета ферм. Сегодня онлайн-ресурс позволяет бесплатно задать параметры балки, опоры, нагрузки и получить схему.
5. Бесплатная настольная программа “Ферма” Для доступа к подробному расчету авторы программы просят вас перевести символический платеж. Стоит отметить, что онлайн-сервис красиво оформлен и оснащен понятным интерфейсом.
Для доступа к подробному расчету авторы программы просят вас перевести символический платеж. Стоит отметить, что онлайн-сервис красиво оформлен и оснащен понятным интерфейсом.Малая программа Ферма позволяет рассчитать плоскую статически определимую ферму и сохранить результаты. Для начала необходимо указать геометрические параметры фермы (размеры стержней, высоты, положения раскосов, нагрузки).
Расчет выполняется методом раскроя узлов. Определяются усилия в стержнях фермы, а также реакции опор. Максимальное количество панелей фермы – 16, количество нагрузок – не более 20. Программный комплекс также может быть использован для расчета статически неопределимых ферм.
Программа «Проектирование и расчет деревянных конструкций
с соединениями на металлических зубчатых пластинах»Программа разработана ЗАО «Техкомплект» совместно с ООО «Научно-технический центр АПМ» для деревянных каркасно-стропильных конструкций, применяемых в жилом и промышленном строительстве.
 (Совместные авторские и имущественные права на Программу подтверждены Свидетельством об официальной регистрации программ для ЭВМ № 2007610917 от 27 февраля 2007 г., выданным Федеральной службой России по интеллектуальной собственности, патентам и товарным знакам). Программа сертифицирована в системе ГОСТ Р Органом по сертификации программных продуктов в строительстве (Сертификат соответствия № РОСС RU.СП15.Н00087 от 20.03.2007)
(Совместные авторские и имущественные права на Программу подтверждены Свидетельством об официальной регистрации программ для ЭВМ № 2007610917 от 27 февраля 2007 г., выданным Федеральной службой России по интеллектуальной собственности, патентам и товарным знакам). Программа сертифицирована в системе ГОСТ Р Органом по сертификации программных продуктов в строительстве (Сертификат соответствия № РОСС RU.СП15.Н00087 от 20.03.2007) Соединение элементов конструкции в узлах осуществляется на металлических зубчатых пластинах (МЗП) по ТУ 5369-026-02495282-97 и испытан в ЦНИИСК им. В.А. Кучеренко (Сертификат соответствия № РОСС RU.СЛ71. Н00402 от 08.02.2007).
Программа предназначена для создания 2-х, 3-х мерных моделей, комплексного расчета и анализа деревянных каркасных конструкций с МЗП.
В программном продукте используется параметрическая библиотека типовых наиболее часто используемых конфигураций для ускорения построения моделей деревянных конструкций.
 В состав системы также входит библиотека типовых сечений балок и база данных размеров и несущих способностей МЗП с длинным зубом высотой 14 мм и малым зубом высотой 8 мм.
В состав системы также входит библиотека типовых сечений балок и база данных размеров и несущих способностей МЗП с длинным зубом высотой 14 мм и малым зубом высотой 8 мм.Имеются специальные функции для рисования и редактирования стержней в 2D пространстве, которые позволяют быстро обрезать, сращивать, удлинять стержни для быстрого создания произвольных сложных конструкций.
Для выполнения прочностного расчета конструкции в диалоговом режиме можно задавать статические распределенные и сосредоточенные нагрузки, а также сейсмические нагрузки и их комбинации. В расчете учитываются растягивающие-изгибные и сжимающе-изгибные напряжения, а также устойчивость сжатых стержней; в трехмерном пространстве можно получить картину напряженно-деформированного состояния строительной конструкции. Анализируя результаты расчетов, можно принять решение об изменении и уточнении проектируемого варианта модели, внести необходимые изменения и произвести перерасчет.
В программе реализованы два вида расчета соединений на металлических зубчатых пластинах: расчетный и проверочный.
 При расчете конструкции выбор параметров и расположение зубчатых пластин относительно узла осуществляется автоматически. При поверочном расчете пользователь устанавливает металлические зубчатые пластины в узлы соединения и выбирает их параметры из библиотеки в ручном режиме. После завершения расчета система выдаст предупреждение о возможности использования пользовательских номеров. Такой расчет целесообразно проводить, когда требуется проверить пригодность к подключению существующих МЗП.
При расчете конструкции выбор параметров и расположение зубчатых пластин относительно узла осуществляется автоматически. При поверочном расчете пользователь устанавливает металлические зубчатые пластины в узлы соединения и выбирает их параметры из библиотеки в ручном режиме. После завершения расчета система выдаст предупреждение о возможности использования пользовательских номеров. Такой расчет целесообразно проводить, когда требуется проверить пригодность к подключению существующих МЗП.В случае, когда для обеспечения возможности транспортировки конструкция должна состоять из отдельных подконструкций с последующим их соединением на строительной площадке в единое целое, предусмотрена функция установки и расчета дюбельных соединений.
Расчеты выполняются в соответствии с нормативными документами: стандарт организации. СТО 3654501-002-2006. Деревянные клееные и цельнодеревянные конструкции. Методы проектирования и расчета. ЦНИИСК, Москва, 2006
По результатам расчета возможно получение автоматического формирования детальных чертежей элементов конструкции и параметров соединений в узлах с металлическими зубчатыми пластинами, в том числе размеров и ориентации МЗП.
 Технологически все это необходимо для правильной резки каждого из брусков, входящих в состав строительного объекта; составление спецификаций на МРОТ и пиломатериалы и документации на сборку деревянной конструкции.
Технологически все это необходимо для правильной резки каждого из брусков, входящих в состав строительного объекта; составление спецификаций на МРОТ и пиломатериалы и документации на сборку деревянной конструкции.Программа работает как приложение к чертежно-графическому редактору APM Graph. Все необходимые расчеты действующих сил, прочности и устойчивости выполняются расчетным ядром системы APM Structure3D.
Программа позволяет импортировать файлы с расширением DXF, разработанные в системе AutoCAD.
Предназначен для персональных компьютеров с частотой процессора не менее 0,5 ГГц, с минимальным объемом оперативной памяти (ОЗУ) 64 МБ. Система работает в операционных средах MS Windows 2000, XP.
Группа компаний «ИНФАРС» всегда находится на острие технического прогресса в области автоматизации проектирования, что является принципиально важным этапом на пути к созданию новых структур, производств и объектов инфраструктуры.
Мы предлагаем самые современные, технологичные программы расчета конструкций различного назначения, которые позволят производить моделирование, расчет зданий и сооружений любой сложности.






 Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).
Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение). Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}
Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I} Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным. 3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.
3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.
 Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L – длина пролета.
Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L – длина пролета. Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L – длина пролета, а a, b – длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93
Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L – длина пролета, а a, b – длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93 пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L – длина пролета, а a, b – ненагруженные длины левой и правой сторон балки соответственно.
пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L – длина пролета, а a, b – ненагруженные длины левой и правой сторон балки соответственно. Онлайн-калькуляторы и программы для расчета конструкций
Онлайн-калькуляторы и программы для расчета конструкций
 Калькулон полезен руководителям и сметчикам проектных организаций, он позволяет быстро определить примерную стоимость любых проектных работ, которые указаны в справочниках базовых цен.
Калькулон полезен руководителям и сметчикам проектных организаций, он позволяет быстро определить примерную стоимость любых проектных работ, которые указаны в справочниках базовых цен.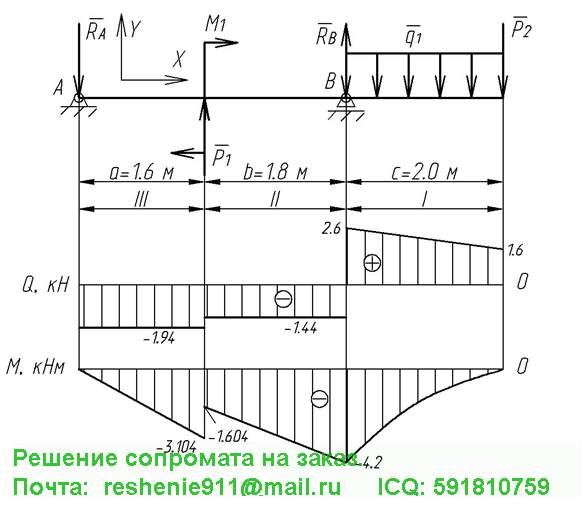 д.
д.

 Сайт доступен и онлайн-версия программы .
Сайт доступен и онлайн-версия программы . org представлена бесплатная онлайн программа для расчета балок и ферм методом конечных элементов. Расчет может производиться, в том числе, и для статически неопределимых фреймов.
org представлена бесплатная онлайн программа для расчета балок и ферм методом конечных элементов. Расчет может производиться, в том числе, и для статически неопределимых фреймов. Для доступа к подробному расчету авторы программы просят вас перевести символический платеж. Стоит отметить, что онлайн-сервис красиво оформлен и оснащен понятным интерфейсом.
Для доступа к подробному расчету авторы программы просят вас перевести символический платеж. Стоит отметить, что онлайн-сервис красиво оформлен и оснащен понятным интерфейсом. (Совместные авторские и имущественные права на Программу подтверждены Свидетельством об официальной регистрации программ для ЭВМ № 2007610917 от 27 февраля 2007 г., выданным Федеральной службой России по интеллектуальной собственности, патентам и товарным знакам). Программа сертифицирована в системе ГОСТ Р Органом по сертификации программных продуктов в строительстве (Сертификат соответствия № РОСС RU.СП15.Н00087 от 20.03.2007)
(Совместные авторские и имущественные права на Программу подтверждены Свидетельством об официальной регистрации программ для ЭВМ № 2007610917 от 27 февраля 2007 г., выданным Федеральной службой России по интеллектуальной собственности, патентам и товарным знакам). Программа сертифицирована в системе ГОСТ Р Органом по сертификации программных продуктов в строительстве (Сертификат соответствия № РОСС RU.СП15.Н00087 от 20.03.2007)  В состав системы также входит библиотека типовых сечений балок и база данных размеров и несущих способностей МЗП с длинным зубом высотой 14 мм и малым зубом высотой 8 мм.
В состав системы также входит библиотека типовых сечений балок и база данных размеров и несущих способностей МЗП с длинным зубом высотой 14 мм и малым зубом высотой 8 мм.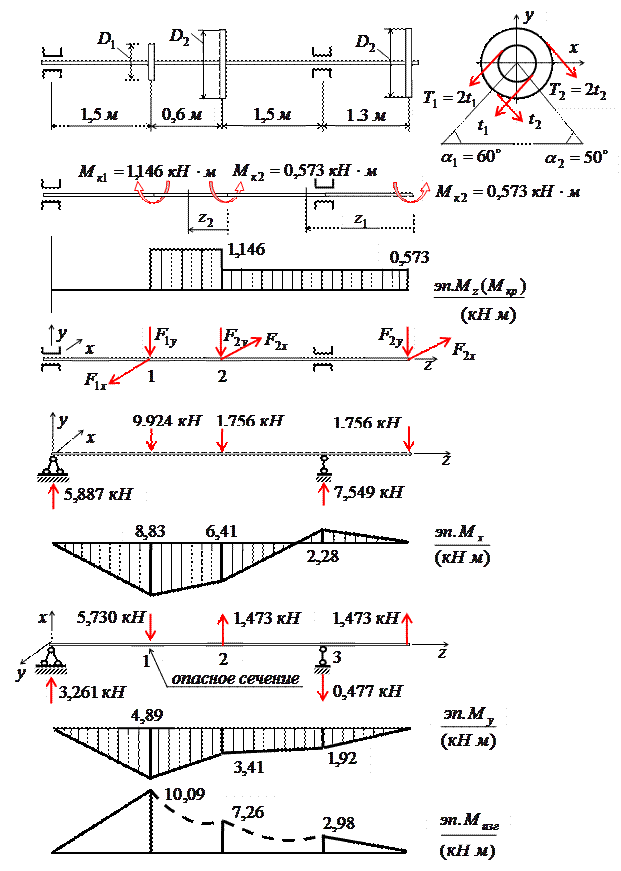 При расчете конструкции выбор параметров и расположение зубчатых пластин относительно узла осуществляется автоматически. При поверочном расчете пользователь устанавливает металлические зубчатые пластины в узлы соединения и выбирает их параметры из библиотеки в ручном режиме. После завершения расчета система выдаст предупреждение о возможности использования пользовательских номеров. Такой расчет целесообразно проводить, когда требуется проверить пригодность к подключению существующих МЗП.
При расчете конструкции выбор параметров и расположение зубчатых пластин относительно узла осуществляется автоматически. При поверочном расчете пользователь устанавливает металлические зубчатые пластины в узлы соединения и выбирает их параметры из библиотеки в ручном режиме. После завершения расчета система выдаст предупреждение о возможности использования пользовательских номеров. Такой расчет целесообразно проводить, когда требуется проверить пригодность к подключению существующих МЗП. Технологически все это необходимо для правильной резки каждого из брусков, входящих в состав строительного объекта; составление спецификаций на МРОТ и пиломатериалы и документации на сборку деревянной конструкции.
Технологически все это необходимо для правильной резки каждого из брусков, входящих в состав строительного объекта; составление спецификаций на МРОТ и пиломатериалы и документации на сборку деревянной конструкции.