Сопромат решение задач геометрические характеристики плоских сечений: Геометрические характеристики плоских сечений - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Геометрические характеристики плоских сечений

Рассмотрим формулы для определения геометрических характеристик плоских сечений: статического момента площади фигуры, осевых моментов инерции и радиуса инерции сечения.

При расчете элементов конструкций на прочность, жесткость и устойчивость приходится кроме общеизвестной характеристики – площади поперечного сечения A, оперировать такими геометрическими характеристиками сечений, как статический момент площади, момент инерции, момент сопротивления, радиус инерции.

Статический момент площади

Интегралы вида:

называются статическими моментами площади сечения A относительно осей X и Y соответственно.

В тех случаях, когда сечение может быть разделено на простейшие фигуры площади A_i и координаты центров тяжести x_i и y_i которых известны, статические моменты площади сложной фигуры определяются через суммирование

Статические моменты площади имеют размерность [м³] и могут принимать любые числовые значения.

Для осей X_C, Y_C, проходящих через центр тяжести сечения C (центральные оси), статические моменты равны нулю:

Координаты центров тяжести сечения определяются относительно так называемых вспомогательных осей по формулам:

Если сечение имеет ось симметрии, то центр тяжести находится на этой оси и его положение определяется одной координатой.

При наличии двух и более осей симметрии центр тяжести совпадает с точкой пересечения этих осей.

Моменты инерции

Моментами инерции площади сечения называют интегралы вида:

где:
I_x, I_y — осевые моменты инерции площади сечения относительно осей OX, OY соответственно;

I_xy — центробежный момент инерции;
I_ρ — полярный момент инерции.

Размерность момента инерции [м⁴], I_x, I_y, I_ρ всегда положительны, I_xy может принимать любые значения, при этом, если хотя бы одна из осей является осью симметрии, I_xy=0.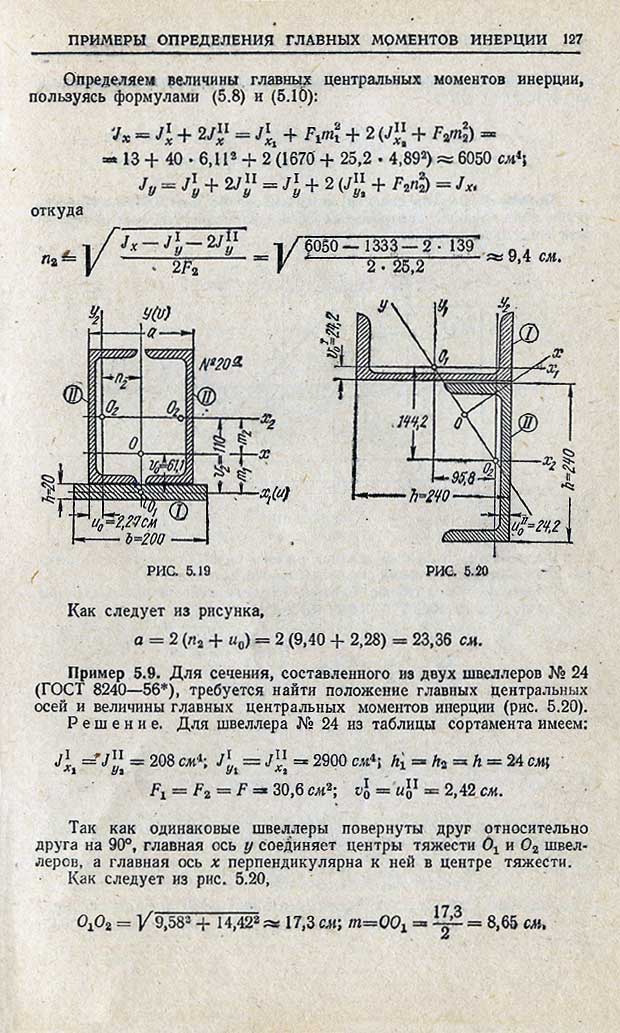

Зависимости между моментами инерции относительно параллельных осей выражаются формулами:

где a, b – расстояния между осями X, X_C и Y, Y_C.

Оси, относительно которых I_xy=0, называют главными, а осевые моменты инерции относительно них – главными моментами инерции.

Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а соответствующие им моменты инерции – главными центральными моментами инерции.

Главные оси характерны тем, что их моменты инерции принимают экстремальные значения (I_max, I_min).

Момент инерции сложного сечения относительно какой-либо оси находится суммированием моментов инерции составляющих его частей относительно той же оси:

Радиусы инерции

Величины

называют радиусами инерции сечения относительно осей OX и OY соответственно.

Эллипс, построенный в главных осях, с полуосями, равными главным радиусам инерции

называют эллипсом инерции.

Лекции по сопромату >
Примеры решения задач >

Геометрические характеристики плоских сечений – Энциклопедия по машиностроению XXL

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ [c.11]

Геометрические характеристики плоских сечений [c.131]

Введем еще одну геометрическую характеристику плоского сечения. [c.220]

Теория напряженного состояния и гипотезы прочности > Геометрические характеристики плоских сечений [c.1]

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИИ [c.24]

Между преподавателями нередко возникают споры о том, что целесообразно изучать раньше — кручение или геометрические характеристики плоских сечений. Это вопрос не принципиальный, но некоторые аргументы в защиту изучения кручения до моментов инерции приведены в следующей главе. [c.101]

Нередко возникает спор о том, что изучать раньше — кручение или геометрические характеристики плоских сечений.

Про- [c.112]

Учебное пособие по курсу Сопротивление материалов предназначено для студентов заочной и вечерней форм обучения всех технических специальностей. В пособии более детально, нем в других источниках, описываются простые виды деформаций с приведением конечных формул с тем, чтобы студент-заочник легче их запомнил при усвоении основ курса и умело пользовался ими при подготовке к экзаменам и в дальнейшей самостоятельной практике инженерных расчетов. Подробно, с большим количеством решенных типовых задач, рассмотрены геометрические характеристики плоских сечений, растяжение, сжатие, сдвиг, смятие, основы напряженного и деформированного состояний, теории прочности, кручение, поперечный изгиб. Вышеназванные темы можно отнести к первой части курса.

[c.3]

Для определения деформаций и напряжений в каком-либо сечении стержня или балки приходится использовать моменты инерции плоских фигур. Для полной геометрической характеристики плоского сечения необходимо знать три типа моментов инерции осевой, или экваториальный, полярный и центробежный. [c.20]

Учебник имеет ряд особенностей, отличающих его от большинства учебников, ранее изданных другими авторами. Учитывая затруднения, которые испытывают студенты при изучении курса и преследуя цель равномерно распределить домашние расчетнопроектировочные работы, авторы сочли целесообразным изменить обычно принятую последовательность изложения материала. В частности, такой раздел, как Геометрические характеристики плоских сечений , носящий вспомогательный характер, помещен в начале курса, что позволяет уже в первые дни выдавать студентам домашнее расчетно-проектировочное задание. Затем в самостоятельную главу выделены вопросы построения эпюр внутренних усилий — раздел, усвоение которого вызывает у студентов определенные трудности. Особенность книги состоит также в том, что решение основных задач сопротивления материалов в ней излагается по единому плану сначала рассматривается статическая сторона задачи, затем — геометрическая, физическая и, наконец, их синтез.

[c.3]

Практические работы: Сопротивление материалов

государственное автономное учреждение

Калининградской области

профессиональная образовательная организация

Колледж сервиса и туризма

Методические рекомендации

по выполнению практических работ

«Сопротивление материалов»

по дисциплине Техническая механика

для студентов 3 курса

специальности 20.02.04 Пожарная безопасность

Калининград

УТВЕРЖДАЮ

Заместитель директора по УР ГАУ КО ПОО КСТ Н.Н. Мясникова

ОДОБРЕНО

Методическим советом ГАУ КО ПОО КСТ

РАССМОТРЕНО

На заседании ПЦК технологических дисциплин

Редакционная коллегия:

Колганова А. А., методист

Фалалеева А.Б., преподаватель русского языка и литературы

Цветаева Л.В.., председатель ПЦК общематематических и естественнонаучных дисциплин

Составитель:

Незванова И.В. преподаватель ГАУ КО ПОО КСТ

Содержание

Практическое занятие 6: Расчёты на прочность и жёсткость при растяжении и сжатии

Практическая работа 7: Геометрические характеристики плоских сечений

Практическая работа 8: Кручение. Расчёты на прочность и жесткость при кручении

Практическая работа 9: Расчёты на прочность при изгибе

Практическая работа 10: Расчёты бруса круглого поперечного сечения при сочетании основных деформаций.

Приложение

Список литературы

Практическое занятие 6

Расчёты на прочность и жёсткость при растяжении и сжатии

Необходимые формулы

Нормально напряжение

где N- продольная сила; А- площадь поперечного сечения.

Удлинение (укорочение) бруса

Е-модуль упругости; l- начальная длина стержня.

Допускаемое напряжение

[s]-допускаемые запасы прочности.

Условие прочности при растяжении и сжатии:

Примеры расчётов на прочность и сжатие

Пример 1: Груз закреплён на стержнях и находится в равновесии (рисунок 6.1). Материал стержней – сталь, допускаемое напряжение 160 МПа. Вес груза 100кН. Длина стержней: первого – 2м, второго – 1м. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения – круг.

Рисунок 6.1

Решение:

1. Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статики (закон действия и противодействия) реакция стержня численно равна нагрузке на стержень.

Наносим реакции связей, действующих в точке В. Освобождаем точку В от связей. (рисунок 6.1)

Выбираем систему координат так, чтобы одна из осей координат совпадала с неизвестной силой. (рисунок 6.1. б)

Составим систему уравнений равновесия для точки В:

Решим систему уравнений и определяем реакции стержней.

Направление реакций выбрано верно. Оба стержня сжаты. Нагрузки на стержни: F₁=57,4kH; F₂=115,5kH.

2. Определяем потребную площадь поперечного сечения стержней из условий прочности.

Условие прочности на сжатие:

откуда

Стержень 1 (N₁=F₁)

Для круга

Стержень 2 (N₂=F₂)

Полученные диаметры округляем: d₁=25мм, d₂=32мм.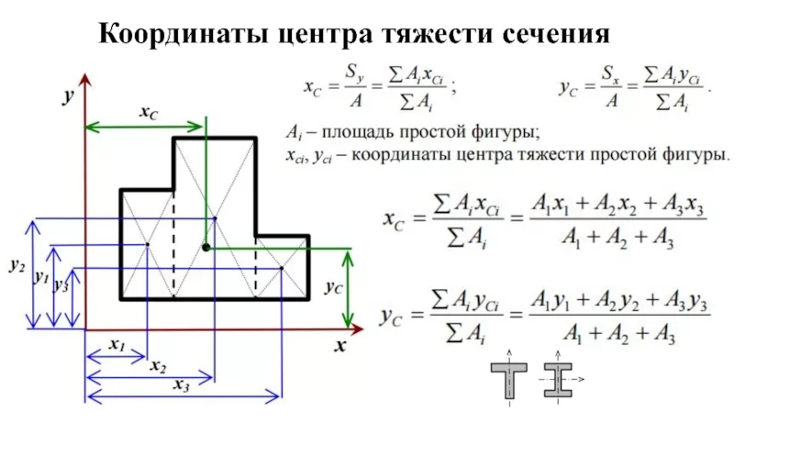

3. Определяем удлинение стержней

Укорочение стержня 1:

Укорочение стержня 2:

Пример 2: Однородная жесткая плита с силой тяжести 10кН, нагруженная силой F=4,5кН и моментом m=3 кН*м, оперта в точке А и подвешена на стержень ВС (рисунок 6.2). Подобрать сечение стержня в виде швеллера и определить его удлинение, если длина стержня 1м, материал – сталь, предел текучести 570 МПа, запас прочности для материала 1,5.

Решение:

1. Определить усилие в стержне под действием внешних сил.

Система находится в равновессии, можно использовать уравнение равновессия для плиты:

R_B – реакция стержня, реакции шарнира А не рассматриваем.

Откуда

По третьему закону динамики реакция в стержне равна силе, действующей от стержня на плиту. Усилие в стержне равно 14 кН.

Рисунок 6.2

2. По условию прочности определяем потребную величину площади поперечного сечения:

, откуда

Допускаемое напряжение для материала стержня:

Следовательно

3. Подберём сечение стержня по ГОСТ (Приложение 1)

Минимальная площадь швелера 6,16см²

Целесообразнее оспользовать равнополочный уголок №2 (d=3мм), площадь поперечного сечения которого 1,13 см².

4. Определить удлинение стержня

Расчётно-графическая работа

Задание 1: Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брос нагружен силами F₁, F_2,F₃. Площадь поперечного сечения А₁ и А₂.

Принять

Рисунок 6.3

Задание 2: Балка АВ, на которую действуют указанные нагрузки, удерживается в равновесии тягой ВС. Определить размеры поперечного сечения тяги для двух случаев: 1) сечение – круг; 2)сечение – уголок равнополочный. Принять . Собственный вес конструкции не учитывать.

Рисунок 6.4

Практическая работа 7

Геометрические характеристики плоских сечений

Моменты инерции простейших сечений

Прямоугольник и квадрат (Рисунок 7.1)

Осевые:

J_x-относительно оси хх

J_y-относительно оси yy

Полярный: J_p=J_x+J_y

Рисунок 7. 1

Круг и кольцо (рисунок 7.2)

Осевые: – круг;

–кольцо

Полярные – круг;

– кольцо.

Рисунок 7.2

Моменты инерции относительно параллельных прямых (рисунок 7.3)

где J_x– момент инерции относительно оси хх;

J_x₀– момент инерции относительно оси х₀х₀;

Рисунок 7.3

А-площадь сечения; а- расстояние между осями.

Рекомендации для решения задач расчетно–графической работы.

1. Момент инерции сложной фигуры является суммой моментов инерции частей, на которые ее разбивают. Разбить заданную фигуру на простейшие части, для каждой определить главные центральные моменты инерции по известным формулам.

2. Моменты инерции вырезов и отверстий можно представить отрицательными величинами.

3. Заданные сечения симметричны, главные центральные оси совпадают с осями симметрии составного сечения.

4. Моменты инерции частей, чьи главные центральные оси не совпадают с главными центральными осями сечения в целом, пересчитывают с помощью формулы для моментов инерции относительно параллельных осей. Расстояние между параллельными осями определить по чертежу.

5. При выполнении задания 2 главные центральные моменты инерции отдельных стандартных профилей определить по таблицам ГОСТ (Приложение 1).

Для использованных в составных сечениях полос моменты инерции определить по известной формуле для прямоугольника.

Расчетно-графическая работа

Геометрические характеристики плоских сечений

Задание 1: Вычислить главные центральные моменты инерции сечений, представленных на схемах (рисунок 7.4). При расчётах воспользоваться данными таблицы, выбрав необходимые значения.

Рисунок 7.4

Практическая работа 8

Кручение. Расчёты на прочность и жёсткость при кручении.

Основные положения расчётов при кручении

Распределение касательных напряжений по сечению при кручении (рисунок 8.1).

Касательное напряжение в точке А:

, где ρ_А–расстояние от точки А до центра сечения.

Условие прочности при кручении

Рисунок 8.1

М_к– крутящий момент в сечении, Н*м

W_p – момент сопротивления при кручении, м³

– допускаемое напряжение при кручении, Н/м²

Проектировочный расчёт, определение размеров поперечного сечения

Сечение-круг:

Сечение – кольцо:

где d – наружный диаметр круглого сечения;

d_вн– внутренний диаметр кольцевого сечения; с= d_вн/ d

Определение рационального расположения колёс на валу

Рациональное расположение колес – расположение, при котором максимальное значение крутящего момента на валу – наименьшее из возможных.

Для экономии металла сечение бруса рекомендуется выполнять кольцевым.

Условие жесткости при кручении

G – модуль упругости при сдвиге, Н/м²

E – модуль упругости при растяжении, Н/м²

– допускаемый угол закручивания,

– полярный момент инерции в сечении, м⁴

Проектировочный расчёт, определение наружного диаметра сечения

Рекомендации по выполнению расчетно-графической работы

1. Построить эпюру крутящих моментов по длине вала для предложенной в задании схемы.

2. Выбрать рациональное расположение колес на валу и дальнейшие расчеты проводить для вала с рационально расположенными шкивами.

3. Определить потребные диаметры вала круглого сечения из расчета на прочность и жесткость и выбрать наибольшее из полученных значений, округлив величину диаметра. 4. Сравнить затраты металла для случая круглого и кольцевого сечений. Сравнение провести по площадям поперечных сечений валов.

Площади валов рассчитать в наиболее нагруженном сечении (по максимальному крутящему моменту на эпюре моментов).

Расчетно-графическая работа

Для стального вала круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.

Построить эпюру крутящих моментов по длине вала.

Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.

Построить эпюру крутящих моментов для этого случая.

Дальнейшие расчеты вести для вала с рациональным расположением шкивов.

Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного или оканчивающегося на 5 числа.

При расчете использовать следующие данные: вал вращается с угловой скоростью 25 рад/ с; материал вала — сталь, допускаемое напряжение кручения 30 МПа, модуль упругости при сдвиге 8-104 МПа; допускаемый угол закручивания = 0, 02 рад/ м.

Провести расчет для вала кольцевого сечения, приняв с = 0,9.

Сделать выводы о целесообразности выполнения вала круглого или кольцевого сечения, сравнив площади поперечных сечений.

Рисунок 8.2

Практическая работа 9

Расчёты на прочность при изгибе

Основные положения и расчётные формулы при изгибе

Распределение нормальных и касательных напряжений при изгибе

где М_и – изгибающий момент в сечении;

Q-поперечная сила в сечении;

Рисунок 9.1

у – расстояние до нейтрального слоя;

J_x– осевой момент инерции сечения (рисунок 9.1)

W_x – осевой момент сопротивления сечения; А-площадь сечения\

Условие прочности при изгибе

где – допускаемое напряжение\

Знаки изгибающих моментов и поперечных сил (рисунок 9. 2)

Рисунок 9.2

Расчётно-графическая работа

Задание 1: Для одноопорной балки, нагруженной сосредоточенными силами и парой сил с моментом m, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и из условия прочности подобрать поперечное сечение для балки в виде двутавра и прямоугольника с отношением сторон h=2b. Материал – сталь, допускаемое напряжение 160 МПа. Рассчитать площади поперечных сечений и сделать вывод о целесообразности применения сечения. Для выбора профелей балок использовать приложение 1.

Рисунок 9.3

Задание 2: Для двухопорной балки, нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах. Найти максимальный изгибающий момент и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 Мпа. Сечение – швелер.

Рисунок 9.4

Практическая работа 10

Расчёты бруса круглого поперечного сечения при сочетании основных деформаций.

Основные положения и расчётные формулы

Геометрические характеристики круга и кольца

Круг (рисунок 10.1)

– круг;

Рисунок 10.1

Кольцо (рисунок 10.2)

Рисунок 10.2

Моменты сопротивления:

Площади сечения

Условие прочности при совместном действии изгиба и кручения.

Эквивалентные моменты

Расчетно-графическая работа

Для промежуточного вала редуктора, передающего мощность Р при угловой скорости ω, определить вертикальную и горизонтальную составляющие реакции подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметры вала по сечениям, приняв [σ] – 60 МПа и полагая F_T– 0,364 F_t. Расчёт произвести по гипотезе максимальных касательных напряжений.

Рисунок 10.3

Указание: Окружную силу определить по формуле

Приложение № 1

Сталь горячекатная. Швеллеры.

Обозначение:

h- высота швеллера; b- ширина швеллера

d- толщина стенки; t-средняя толщина полки

А- площадь швеллера

J- момент инерции

W- момент сопротивления

i – радиус инерции

S – статический момент полусечения

Z₀– расстояние от оси у до наружной грани стенки

Таблица 1

Сталь горячекатная. Балки двутавровые.

Обозначение:

h- высота балки ;b- ширина балки

d- толщина стенки; t-средняя толщина полки

А- площадь сечения; J- момент инерции

W- момент сопротивления

i – радиус инерции

S – статический момент полусечения

Таблица 2

Сталь прокатная угловая равнополочная.

Обозначение:

b- ширина полки;

d- толщина полки;

А- площадь уголка;

W- момент сопротивления

i – радиус инерции

Z₀– расстояние от оси у до наружной грани полки

J- момент инерции

Таблица 3

Продолжение таблицы 3

Список литературы

Олофинская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: учебное пособие / В.П.Олофинская – 3-е издание – М.: ФОРУМ, 2012 – 352 стр.

Геометрические характеристики плоских сечений – презентация онлайн

ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Инженерно-технический институт
Кафедра прикладной механики
Решение задач
по дисциплине «Техническая механика»
270800 – Строительство

2. Геометрические характеристики плоских сечений

Определить величины главных моментов инерции и моментов
сопротивления сечения прямоугольного бруса, ослабленного
круглым отверстием, при заданных размерах b=12 см, h=20 см,
d=5 см.

x
d
h
y
b
Решение:
Центральные оси x и y являются главными, так как они
являются осями симметрии сечения.
Моменты инерции относительно осей:
bh4 bd 3 12 203 12 53
I X I X1 I X 2
7875см4
12
12
12
12
bh4 db3 20 123 5 123
IY IY1 IY2
2160см4
12
12
12
12
Соответственно, моменты сопротивления:
Ix
IX
7875
Wx
787,5см3 ;
ymax h / 2
10
WY
Iy
xmax
IY
2160
360см3 .
b/2
6
Вычислить, как изменяется момент инерции и момент
сопротивления квадрата со стороной а, относительно оси x,
если сечение повернуть на угол =450, оставив ось x
горизонтальной .
а)
б)
y1
o
a
x1
x
h
a
h
y
b
Решение
Осевой момент инерции и момент сопротивления
квадрата относительно оси x в положении а) будут равны:
bh 3 a a 3 a 4
IX
0,0833a 4
12
12
12
IX
a3
WX
0,16667a 3
a/2 6
Осевой момент инерции и момент сопротивления повернутого
на 450 квадрата (рис.

б) относительно горизонтальной оси x1
будут равны:
3
3
bh
1,414a (0,707a)
I X1 2
2
0,0833a 4
12
12
h 0,707a.
где b 2 a Cos450 a 2 0,707 1,414a;
W X1
I X1
0,0833a 4
0,11787a 3
h
0,707a
Моменты инерции IX и IХ1 равны, т.е. не изменяются,
момент сопротивления WX1 уменьшается на 29,3%.
Сравнить величины моментов инерции относительно
центральной оси x сечений прямоугольника, квадрата и круга
при условии, что площади А всех трех сечений одинаковы.
б)
x
a
в)
x
x
b
2a
a)
b
d
Решение
Для сравнения величин моментов инерции, выражаем
.
их через площади сечения, так как у всех сечений площади
одинаковые.
d 2
A A( a ) a 2a 2a 2 , A A( б ) b b b 2 , A A(b )
Моменты инерции сечений относительно оси x:
I X(a)
I X (б )
I X (b)
4
a ( 2a ) 3
8 4 2 ( 2a 2 ) ( 2a 2 )
a
0,1667 Aa2 0,1667 A 2 ;
12
12
12
b b3 b4 b2 b2
0,08333 Aб2 0,08333 A 2 ;
12
12
12
d 4 d 2 d 2
1
Ab2 0,0796 A 2 .

64
4 4 4
4
Момент инерции прямоугольника больше, чем квадрата в 2
раза, а круглого сечения – в 2,1 раза. Момент инерции
квадратного сечения больше, чем круглого в 1,05 раза.
Для сечений, показанных на рис., определить:
•положение центра тяжести;
•вычислить осевые моменты инерции IX и IY ;
•осевые моменты сопротивления
•вычислить
осевые и центробежный момент инерции
относительно осей, повернутых на угол α а) =300
б)
=-450
в) =600 г) =-600.
5a
б)
3a
г)
в)
4a
3a
2a
1,
5a
8a
9a
9a
8a
2a
а)
5a
4a
9a
Решение
Сечение
а
.
Положение центра тяжести фигуры относительно оси x1:
1,5a 2
0,424. 1,5a
S x1 5a 8a 4a
2
yC
4,326a
2
A
1,5a
y0
5a 8a
y2
2
Моменты инерции фигуры относительно
2
центральных осей x0, y0:
x
5a (8a)
2
I x0
4,326a 4a (5a 8a)
12
2
3
I y0
x0
1,
5a
8a
(1,5a) 2
4
2
0,11 (1,5a)
(4,326a 0,424 1,5a )
2
168,929a 4 ;
8a (5a) 3 (1,5a) 4
81,346a 4
12
8
=30 0
1
1
3a
5a
x1
Моменты сопротивления
соответствующих точках 1 и 2.

W
(1)
x
сечения
относительно
оси
x0
в
I x0 168,929a 4
168,929a 4
( 2)
3
45,98a 3
39,05a Wx
y2
3,674a
y1
4,326a
I x0
где y1=4,326a, y2=h-y1=3,674а.
В сечении ось y0 является осью симметрии, следовательно,
.
центробежный момент инерции I x у 0
0 0
Осевые моменты инерции относительно осей x2 и y2 , повернутых на
угол =300:
I x2 I x0 Cos 2 300 I y0 Sin 2 300
168,929a 4 Cos 2 300 81,346a 4 Sin 2 300 147,033a 4
I y2 I x0 Sin 2 300 I y0 Cos 2 300
168,929a 4 Sin 2 300 81,346a 4 Cos 2 300 103,242a 4
Центробежный момент инерции относительно осей x2 и y2:
I x2 y 2
I x0 I y0
2
168,929a 4 81,346a 4
Sin 2
Sin 60 0 37,923a 4
2
Вычислить главные центральные моменты инерции.
Решение: Сечение имеет 2 оси симметрии,
которые и являются его главными центральными осями.
Разбиваем сечение на 2 прямоугольника:
b*h = 140*8 мм и 2 прокатных швеллера
№16.

Из табл. сортамента имеем:
I x1 I x 747см4 ; I y1 I y 63,3см4 ;
A1 18,1см2 ; z0 1,8см.
Вычислим Ix и Iy
bh4
I x 2( I x1
a22bh)
12
14 0,83
2(747
8,4 2 14 0,8) 3080см4 ;
12
hb3
I y 2( I y1 b A
)
12
0,8 143
2
2(63,3 5,2 18,1
) 1470см4 ;
12
2
1 1
Определить на каком расстоянии друг от друга нужно
расположить два швеллера №14, чтобы осевые моменты
инерции сечения были равны между собой.
у
х
а-?
а) 4,63 см
б) 20,4 см
в) 7,35 см
г) 16,0 см
Определить на каком расстоянии друг от друга нужно
расположить два двутавра №20, чтобы осевые моменты
инерции сечения были равны между собой.
у
А) 20,2 см ;
В) 12,24см;
Б) 16,04см;
Г) 32,24см;
х
а-?
Для сечения, составленного из двух неравнобоких уголков
100*63*10, определить момент инерции Jx
.
80 мм
x
А) 1059,4 см4;
Б) 308 см4;
В) 483 см4;
Г) 683 см4

Геометрические характеристики плоских сечений – PDF, страница 2

Определить моменты инерции прямоугольникаотносительно осей Х1 и У1, совпадающих с его сторонами (рис.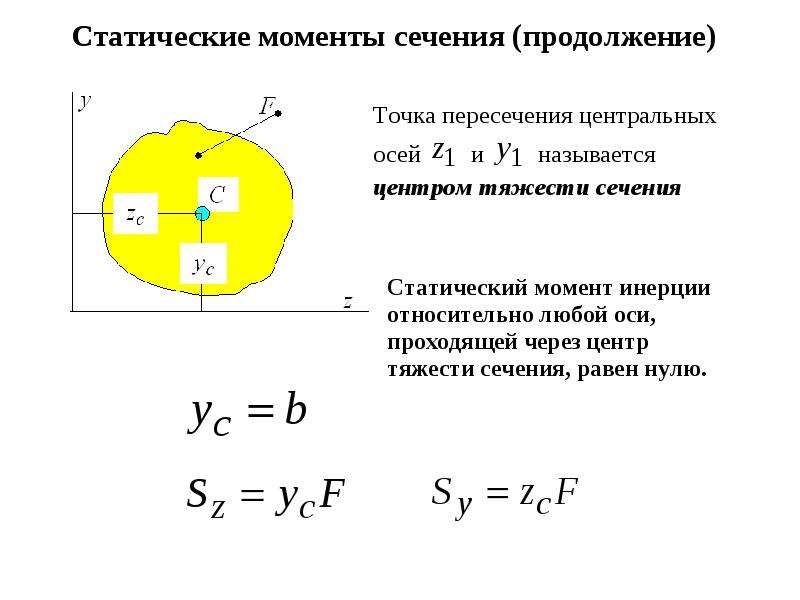 9).Решение. Используем формулы (7) ,переходакосям,параллельнымцентральным:2I x1bh4bh4h Ix  а A  bh  1232I y1hb3hb3b Iy  b A  bh  1232222I x1y1  I xy  аbA  0  bhРис.9h b b2h32 2411Справедливы также зависимости обратные формулам (7):I x  I x1  а 2 A; I y  I y1  b 2 A; I xy  I x1 y1  abA, (8)т.е.

с помощью формул (8) осуществляется переход от некоторыхпроизвольных осей X1 и Y1 к центральным осям X и Y.Задача 5. Определитьмоментинерцииполукругаотносительно центральной оси x (рис. 7).Решение. Положение центра тяжести фигуры известно (см. задачу3),тогда:2πR 4 πR 2  4 R   π 8  4I x  I x1  a A     R82  3 π   8 9π 2Задача 6. Определить моменты инерции сечения (см. рис.6) относительно центральных осей Хс С Ус.Решение. Используя зависимости (7) получим:8 10 34  63 (8 10) 1,43 2  [ (4  6)  2,43 2 ]  616,54 см 412128 3 1043  6Iy  (8 10)  0,57 2  [ (4  6)  0,43 2 ]  416,2 2 см 41212Ix Рассмотримособенности использования формул (7) длявычисления моментов инерции при параллельном переносе осейприменительно к тонкостенным стержням, поперечное сечениекоторых состоит из сочетания узких прямоугольников, каждый изкоторых имеет постоянную толщину. На рис.10 показан элемент сечения такого тонкостенногостержня в виде прямоугольника шириной в и толщиной , (  в).Вычислимосевыемоментыинерциипрямоугольникаотносительно оси X с использованием формулы (7) Анализформул (7) показывает 1;2;3;4;5;6;7  , что в большинствеслучаев cобственным моментом инерции узкого прямоугольника,относительно оси, параллельной, длинной стороне,можно, пренебречь.

Дляслучая, изображенного нарис.10 можно считать, чтоРис.10.I x1  a 2 A12Задача 7. Для коробчатого сечения (рис.11), вычислитьмоменты инерции относительно центральных осей Х и У.Решение.2δ h4hI x  2bδ 2    2 1122bh 2 δ 2 h 3 δ126Рис. 11.2δ b3hb 2 δ1δ b3bI y  2hδ1    2 2 2.12262При повороте осей Х и У на некоторый угол  моменты инерцииотносительно повернутых осей u и v (рис. 12)определяются по формулам:I u  I x Сos 2  I y Sin 2  I xy Sin 2I u , I v , I uvI v  I x Sin 2  I y Cos 2  I xy Sin 2Рис.12.Ix  IySin 2  I xy Cos 2 (9)2где  – угол поворота осей Х и У. Положительный угол  отсчитывается от оси Х против хода часовойстрелки.

Известно 1, что(10)I u  I v  I x  I y  constI uv Это соотношение, показывает, чтопри поворотеосейсумма осевых моментов остаетсянеизменной и равной полярному моменту инерции.Задача 8. Для прямоугольника, (рис.13), вычислить осевые ицентробежный моменты инерции., относительно осей u и v.Ось u совпадает с диагональю прямоугольника, а ось vперпендикулярна к ней.Решение. Используя, рис.13 найдем, Sin и Сos :hbSin , Cos 222h bh  b2Определим осевые I u I v и центробежный I uv моменты инерции132I u  I x Cos 2 α  I y Sin α  I xy Sin2α bh123b 22 h bРис.132 0 2bh 3I v  I x Sin α  I y Cos α  I xy Sin2α 1222hb 3122 hb 3 h 212  h  b 2h 3b 3,26(h  b 2 ) h3  b2 h344  0  hb(h  b ) ,12(h 2  b 2 )h3  b2 b bh 3 hb 3I uv  (I x  I y ) Sin α Cos α  I xy Cos 2α  12 122 222 hbh b (h  b )0  .2222 12(h 2  b 2 ) h b   h b  4.

Главные оси и главные моменты инерции. Главнымиосямиинерцииназываютдвевзаимноперпендикулярные оси, относительно которых центробежныймомент инерции равен нулю.Направление главных осей инерции определяется выражениемtg 2a  2I xy / ( I x  I y )(11)/По этой формуле определяются два значения угла a 0 иa0// 0 a0/  90 0 , отличающиеся друг от друга на 90 , и положениеглавных осей, которые взаимно перпендикулярны.Главными моментами инерции называют осевые моментыинерции, вычисленные относительно главных осей инерции,которые имеют экстремальные значения.I max minIx  Iy21( I x  I y ) 2  4 I 2 xy2(12)14Здесь знак плюс перед вторым слагаемым соответствуетмаксимальному, а знак минус – минимальному моменту инерции.Главные оси, проходящие через центр тяжести сечения,называют главными центральными осями, а моменты инерцииотносительно этих осей – главными центральными моментамиинерции.Ось симметрии плоского сечения является главнойцентральной осью инерции.Положение главных осей инерции находят с помощьювыражений:I xyI xy,(13)tg 1  ;tg 2  I max  I yI min  I yгде 1 – угол между осью xинерции равенI max , аи осью, относительно которой момент2 -угол между осьюx иосью,относительно которой момент инерции равен I min .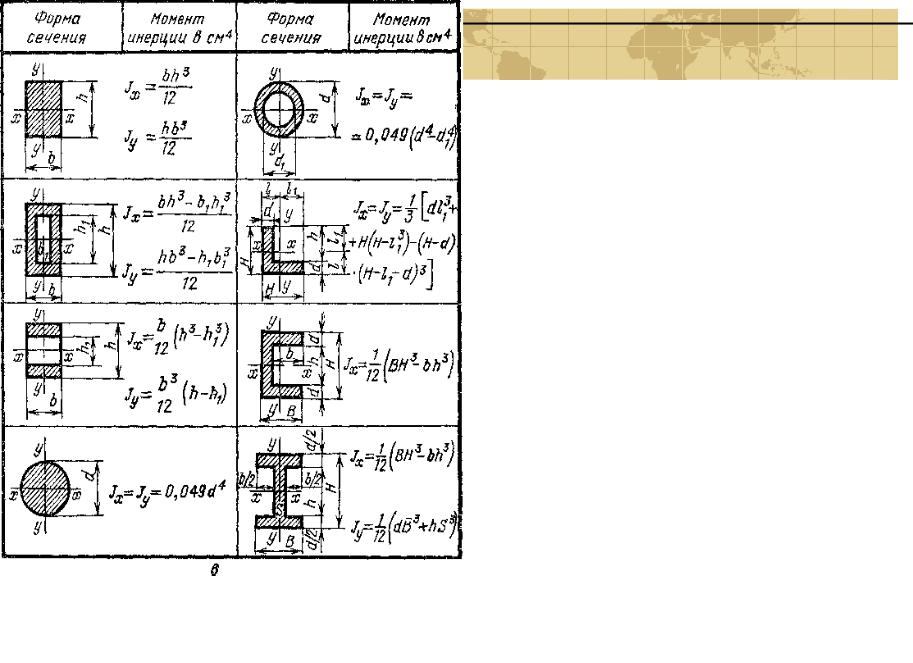 Положительные значения углов отсчитываются от осипротив хода часовой стрелки.

Напомним, что 1   2  90 0xРадиусы инерции, соответствующие главным осям, называютсяглавными радиусами инерции и определяются по формулам:(14)imax  I max / A; imin  I min / A .5. Примеры вычисления геометрических характеристиксоставных сечений.Задача 9. Определить положение главных центральных осей ивычислить относительно этих осей моменты инерции (рис. 14).Решение.

Заданное поперечное сечение, рассматривается каксочетание двух простейших фигур: прямоугольника 50х40 см, изкоторого вырезан (удален) полукруг R = 15 см.Выберем положение осей координат, в которых определимположение центра тяжести всей фигуры. Пусть начальные осикоординатпроходят, через центр тяжести прямоугольника.Вследствие симметрии фигурыотносительно вертикальнойоси, главная центральная ось поперечного сечения У совпадает сосью симметрии, и абсцисса центра тяжести фигуры x c= 0.Ординаты центров тяжести частей, составляющих сечение, атакже их площади равны для прямоугольника: y I c1  0 ;AI  bh  40  50  2000 см 2 ,15для полукруга:y II c1  18,63cм. 2AIIπRπ1522Ординатусечениявыражения: 353,25 см2центратяжестиопределимизyc Рис.

14.2SAxc1=AI yc1I  AII yc1II 0  353,25(18,63) 3,92 см.AI  AII2000  353,25Определение главных осевых моментов инерции.Как уже отмечалось, в параграфе один, моменты инерциисоставногопоперечногосеченияопределяютсякакалгебраическая сумма моментов инерции простейших фигур,составляющих это сечение:nIx nIy I xi ;i 1Iyii 1Моменты инерции каждой отдельной фигуры относительноцентральных осей вычисляются с использованием формул (7). bh 3IIII x  I xI  I xII  I x1 a12 A I  I x2 a22 A II   a12 A I   12 (9π 2  64) 4 40  50 32II R  a2 A    3,92 2  2000  72π  12424 0,108 15  22,6  353,25  236319 см .bhπR50  40π  154 246796 см 4 .128128Сравнивая величины, Iх и Iу, устанавливаем, что Imax = I1 = Iу ==246796 cм 4; Imin = I2 = Ix = 236319 см 4 .I y  I y1I  I y2II 343Задача 10.

Вычислить величины главных центральныхмоментов инерции сечения, изображенного на рис. 5.16Решение. Из анализа полученного ранее решения устанавливаем(cм. задачу 1), что одной из главных осей рассматриваемогосечения, является ось симметрии у, вторая главная ось хспроходит через центр тяжести сечения, и перпендикулярна кпервой. Вычислим моменты инерции. Момент инерцииотносительно оси х определим, применив формулу перехода коси, параллельной центральной:I xc  I xcI  I xcII  I xI1  a12 A1  I xII2  a22 A2IIIгде – I x1; I x 2 – моменты инерции I и II прямоугольниковотносительно собственных центральных осей х1 и х2 ;а1 и а2 – расстояние между собственными центральными осями иосью х.Ось у является, одновременно, как главной осьюпрямоугольников I и II, так и всего сечения, тогда:I y  I yI  I yIIВыполнив, вычисления получим:14  3 33  30 3 (31,5  20,25) 2  14  3 1212 (20,25  15) 2  3  30  14560 см 4 ;I xc Iy 3  14 3 30  3 3 686  67,5  753,5 см 4 .1212На основании выполненных вычислений устанавливаемI 1  I xc  14560 см 4 ;I 2  I y  753,5 см 4 .Задача 11.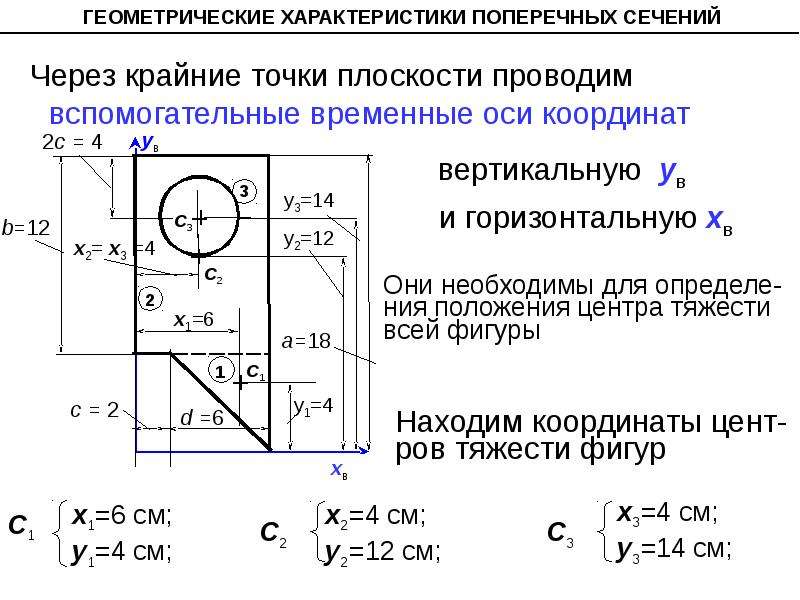

На сколько процентов уменьшаются I1 и I2 послеослабления квадрата симметричными вырезами, отмеченныепунктиром (см. рис. 16).Решение. Для квадрата I x = I y = I1= I2 . Вычислим осевой моментинерцииIx bh 3 h 4 50 4см412 12 1217Дляослабленногосечениямомент инерции относительно осих будет достигать максимальногозначения.50 412,5  25 3 21212 488281,25см 4I x  I1 Рис. 16.Тогда, уменьшение I1 составляет:δ520833,33  488281,25 100%  6,25%520833,33Воспользуемся зависимостью (7),устанавливающую связьмежду моментами инерции относительно параллельных осей у иу1, тогда:50 425 12,5 337,5 2 2 [()  25 12,5]  292968,75 см 412122Уменьшение I2 составляет:I y  I2 δ520833,33  292968,75100%  43,75%520833,33Задача 12.

Для сечения, рис.17,определитьмоментыинерцииотносительно осей, проходящих черезцентр тяжести.Решение. Проведем произвольныеоси х и у и разобьем сечение на частитак, чтобы положение центра тяжестикаждой из них было известно. Дляопределениякоординатцентратяжести всего сечения, вычислимплощадь А и статические моменты S xРис. 17и S y всего сечения.А = А 1 + А 2= 14∙1 + 8∙1 = 22 см2;3S x = S x 1 + S x 2 = 14∙1∙7 + 8∙1∙0,5 = 102 cм3S y = S y 1 + S y 2 = 14∙1∙0,5 + 8∙1∙5 = 47 cм .Тогда координаты центра тяжести всего сечения можновычислить следующим образом:18xc SyA47 2,14 cм ;22S102yc  x  4,64 cм .A22Определим центральные осевые и центробежный моментыинерции.I xo  I x1  A1  a12  I x2  A2  a 22 1 14 3 1 14  (7  4,64) 2 128 13 8 1  (4,64  0,5) 2  444,42 cм 41214 13I yo  I y1  A1  b12  I y2  A2  b22  14 1  (2,14  0,5) 2 1231 8 8 1  (5  2,14) 2  146,92 cм 412I xoyo  I x1y1  A1 a1b1  I x2y2  A2 a 2 b2  0  14 1  2,36  (1,64)  0  8 1  2,86  (4,14)  148,91cм 4  148,91cм 4Полученные значения сравним с данными ГОСТ 8510 – 86 длянеравнополочного уголка 140х90х10.Данный угловой профиль отличается от рассматриваемогосечения закруглениями.

Из сортамента устанавливаем, чтоxo  2,12 cм ; y o  4,58 cм ;I x  444 cм 4 ; I y  146 cм 4 ; I xy  147 cм 4 .Результаты, сравнения показывают, что выполненные по ГОСТзакругления прокатных профилей не оказывают существенноговлияния на величины моментов инерции и положения центратяжести. Задача 13. Вычислить главные центральные моменты инерциисечения изображенного на рис. 17.Решение. Определим координаты центра тяжести сечения, длячего проведем оси хоу и рассмотрим сечение, состоящее из двухфигур:19Рис. 17.Двутавра – I и швеллера – II, все необходимые данные,имеются в сортаменте, (смотри приложение 1, 2).Геометрические характеристики для двутавра принимаем поГОСТ 8239-89: площадь сечения А1= 40,2см2; моменты инерциисечения Iх1 = 5010 см4; Iу1 = 260 см4.Для швеллера по ГОСТ 8240-89 – площадь сечения А2 = 23,4см2; моменты инерции сечения Iх2 = Iy ГОСТ = 113 см4; Iy2 = Ix ГОСТ == 1520 см4; zo = 2,07 cм.Вследствие симметрии фигуры относительно вертикальнойоси, главная центральная ось поперечного сечения У совпадает сосью симметрии и, следовательно, абсцисса центра тяжестифигуры Хс = 0.Определим ординату центра тяжести сечения.

По формуле (6)находим:yc S x A y  A y 40,2  13,5  23,4  (27  0,52  2,07) 17,9 cмAAA40,2  23,4112122Центр тяжести сечения (точка Ос) показан на рис. 17.Проведем через него главные центральные оси инерции YcОсX с .Определим главные моменты инерции относительно этих осей.20I xc  I x1  A1  a12  I x2  A2  a 22  5010  40,2  (17,9  13,5) 2  113  23,4  (25,45  17,9) 2  7235,13 cм 4I y c  I y1  I y2  260  1520  1780 cм 4Ось х с является осью максимума, так как Ix c > Iy c, а ось уc – осьюминимума, следовательно:I 1  I xc  7235,13 cм 4 ; I 2  I yc  1780 cм 4 .Задача 14. Определить положение главных центральныхосей и вычислить моменты инерции относительно этих осейдлясоставногокоробчатого сечения (рис.

расчет моментов инерции составного сечения

Промежуточные результаты в короткой форме

Элемент	x	y	A	x-xc	y-yc	Ix	Iy	Ixy

Расчет составного сечения

Определим собственные характеристики каждого элемента, характеристики прокатных профилей выписываем из сортамента, характеристики простых фигур вычисляем по формулам

Общая площадь сечения равна сумме площадей отдельных фигур

A = = см²

Проводим дополнительные оси, относительно которых определим центр тяжести всей фигуры.

Показываем на чертеже центры тяжести каждой фигуры и находим их координаты в дополнительных осях.

Центр тяжести сечения определим по формуле

Xc = ΣX_i*A_i / A

Yc = ΣY_i*A_i / A

X_C = () / A = () / = см

Y_C = () / A = () / = см

Используя эти значения, указываем положение центра тяжести всей фигуры и проводим через него центральные оси

Находим координаты центров тяжести элементов в центральных осях

Центральные осевые моменты инерции сечения находим, используя формулу перехода между параллельными осями

I_x = Σ(I_X^{собств.} + b² *A) = = см⁴

I_y = Σ(I_Y^{собств.} + a² *A) = = см⁴

I_xy = Σ(I_XY^{собств.} + a*b*A) = = см⁴

Угол наклона главных центральных осей

tg2α=2*I_xy / (I_y-I_x)=2* / (-)=

α = arctg() / 2 = °

Главные моменты инерции – это моменты инерции относительно главных осей.

I_X0 = I_x*cos²(α) + I_y*sin²(α) – I_xy*sin(2*α) =

= *cos²(°) + *sin²(°) – 2**sin(2*°) = см⁴

I_Y0 = I_y*cos²(α) + I_x*sin²(α) + I_xy*sin(2*α) =

= *cos²(°) + *sin²(°) + 2**sin(2*°) = см⁴

Радиусы инерции

i_x² = I_X0 / A = / = 0

i_x = см

i_y² = I_Y0 / A = / = 0

i_y = см

Геометрические характеристики и вес трубы и воды в трубе. Диаметр наружный 50-1420 мм, толщина стенок 1-30 мм, Площадь сечения, осевой момент инерции, полярный момент инерции, осевой момент сопротивления, полярный момент сопротивления, радиус инерции

Адрес этой страницы (вложенность) в справочнике dpva. ru: главная страница / / Техническая информация / / Материалы / / Сопротивление материалов. Сопромат. Таблицы строительных конструкций. / / Геометрические характеристики и вес трубы и воды в трубе. Диаметр наружный 50-1420 мм, толщина стенок 1-30 мм, Площадь сечения, осевой момент инерции, полярный момент инерции, осевой момент сопротивления, полярный момент сопротивления, радиус инерции

Подробные численные данные

А.Г.КАМЕРШТЕЙН, В. В. РОЖДЕСТВЕНСКИЙ, М.Н.РУЧИМСКИЙ “РАСЧЕТ ТРУБОПРОВОДОВ НА ПРОЧНОСТЬ” СПРАВОЧНАЯ КНИГА, 1969

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Прямоугольное сечение – обзор

4.1.1 Пластометрические тесты

В этом разделе обсуждаются основные типы пластометрических тестов, а также указываются их преимущества и ограничения. Знание устойчивости материалов к деформации и их способности безопасно выдерживать нагрузку до разрушения имело первостепенное значение для людей с тех пор, как были построены конструкции. В шестнадцатом веке обнаружены документальные свидетельства из работ Леонардо да Винчи, которые показывают, что количественные методы использовались для измерения различий в свойствах материалов [352].Галилео Галилей [95] представил первую серьезную математическую интерпретацию упругой прочности материала в конструкции, подвергаемой изгибу. В течение последующих столетий продолжались поиски зависимости между приложенной нагрузкой и деформацией материала, и были разработаны машины для измерения прочности на растяжение. Испытания на растяжение были основным методом, применяемым в то время. Среди ряда вкладов в разработку методов испытания материалов следует упомянуть вклад Уильяма Фэйрберна [85] в Англии, а затем Адольфа Мартенса [222] в Германии.Бывший ученый внес значительный вклад в систематическую оценку прочности материалов при высоких температурах.

Иоганн Баушингер [27] был еще одним участником испытаний материалов, которому приписывают введение двусторонних экстензометров, которые позволяют компенсировать кривизну или перекос испытуемого образца. Это значительно улучшило измерение деформации при растяжении и обеспечило достаточную точность измерений, чтобы заметить, что предел текучести снижается, когда за деформацией в одном направлении следует деформация в противоположном направлении.Теперь это известно как эффект Баушингера. В течение следующих десятилетий были предприняты многочисленные исследования и сопоставления по испытаниям на растяжение, и результаты впоследствии были обобщены Анвином [358]. ASTM E8-24T «Стандартные методы испытаний металлических материалов на растяжение» был опубликован в 1924 году.

В настоящее время испытания на растяжение считаются наиболее распространенными и простыми в выполнении. Прочность материала при растяжении долгое время считалась одной из наиболее важных характеристик, необходимых для проектирования, производства, контроля качества и прогнозирования срока службы промышленного оборудования.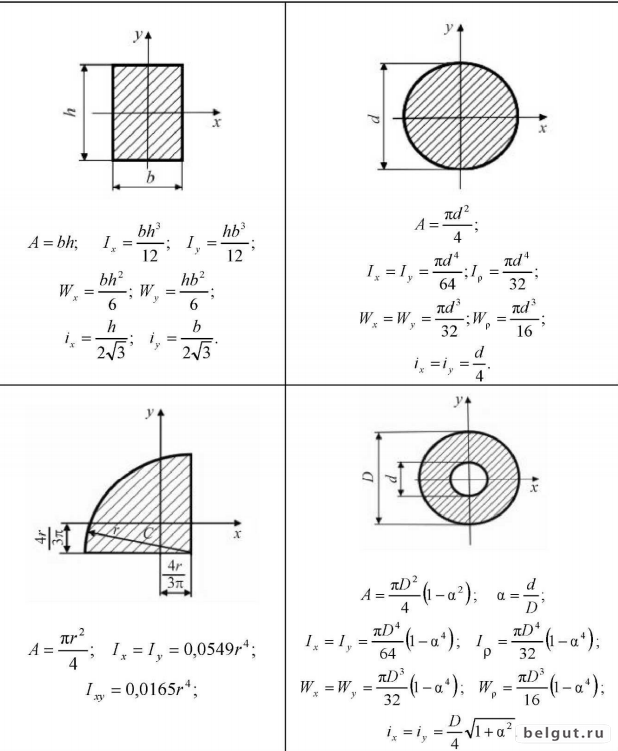 Стандарты испытаний на растяжение были одними из первых опубликованных стандартов, и разработка таких стандартов продолжается и сегодня. Эти тесты широко разрабатывались в течение почти столетия, и было опубликовано большое количество научных статей и руководств по передовой практике. Последние собраны в отчете по проекту 6-й рамочной программы «Испытания металлических материалов на растяжение: обзор», аббревиатура TENSTAND.

Для испытаний на растяжение используются образцы цилиндрического или прямоугольного сечения.Преимущества этих испытаний можно резюмировать следующим образом:

•: нет проблем с трением, которые следует учитывать,
•: испытания регулируются стандартами, поэтому межлабораторная изменчивость сводится к минимуму.

Недостатки указывают на то, что испытание на растяжение не является наиболее подходящим испытанием, когда информация, которая должна использоваться, касается изучения процессов объемного формования металла. Они следующие:

•: возможны низкие деформации, не более 40–50%,
•: одноосный характер распределения напряжений теряется, когда начинается локализованное деформирование.

Теперь доступна обширная информация о методах и стандартах испытаний на растяжение, и читатель может перейти к обзорным публикациям в Refs. [118,212] [118] [212], стандарты ASTM E8 / E8M-13a «Стандартные методы испытаний металлических материалов на растяжение» и к упомянутому отчету проекта 6-й рамочной программы TENSTAND.

Испытание на сжатие было разработано намного позже, чем испытание на растяжение. Этот тест определяет поведение материалов при сжимающих нагрузках.Подробный обзор процедуры и стандартов испытаний на сжатие можно найти в работе. [178]. Испытание может проводиться на цилиндрических или плоских образцах. Первое называется одноосным сжатием (UC), а второе – PSC. В некоторых практических приложениях также используется испытание на сжатие кольца (RC). Схематическое изображение основных испытаний на сжатие представлено на рисунке 4.1. Сжатие в канальных штампах также показано на рисунке 4.1, но этот тест посвящен, скорее, исследованию механизма деформации при плоском состоянии деформации.Общие преимущества всех тестов на сжатие:

Рисунок 4.1. Схематическое изображение пластометрических тестов.

•: возможны более высокие деформации, чем при растяжении, обычно более 1 при сжатии цилиндров и до 2 при испытании плоских образцов
•: состояние напряжения в основном сжимающее, как в объемных формирование.

Недостатки испытаний на сжатие:

•: Силы трения на границе раздела поршень-образец растут по мере выполнения испытания, и их влияние необходимо устранять.
•: Деформация при растяжении на цилиндрических поверхностях или краях плоских образцов ограничивает степень деформации.
•: Достижение постоянных истинных скоростей деформации во время испытаний требует тщательного контроля с обратной связью, что делает неизбежным использование кулачкового пластометра или сервогидравлической испытательной системы.
•: Распределение деформаций в нормальном направлении неравномерно. Когда выполняется сжатие с плоской деформацией, трудно достичь изотермических условий.

В тесте UC образец помещается между двумя параллельными плитами (рис. 4.1). Образцы обрабатываются с учетом минимизации остаточных напряжений. Следует записать ориентацию образца по отношению к исходному исходному материалу. Рекомендуемое соотношение сторон (высота к диаметру) должно быть около 1,5. Перед горячей деформацией образец следует подвергнуть определенному циклу предварительного нагрева. Целью предварительного нагрева является гомогенизация микроструктуры и получение однородной температуры в начале испытания.Применение разных температур предварительного нагрева позволяет получить различную микроструктуру перед деформацией [270]. Образец сжимается между плитами, и во время испытания регистрируются силы, текущая высота и температура. Напряжение течения рассчитывается как отношение силы к контактной поверхности ( F / A ), а деформация рассчитывается по изменению высоты как ε = ln ( h ₁/ h 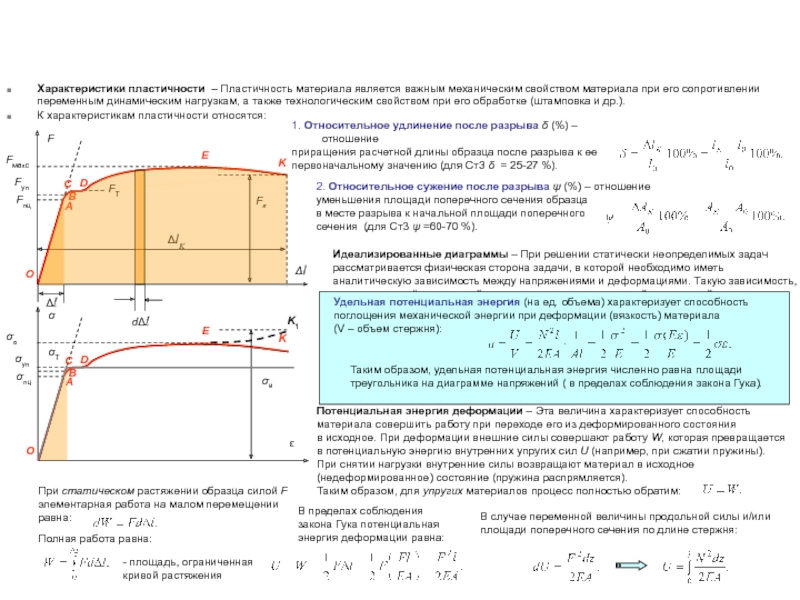_{). 2}), где h ₁ и h ₂ – начальная и конечная высота соответственно.

Трение является основным фактором, влияющим на результаты этого теста. Из-за трения деформация неоднородна. Помимо этого, деформационный нагрев и передача тепла на плиту и в окружающую среду еще больше затрудняют интерпретацию результатов испытаний. Неоднородность теста хорошо видна на рисунке 4.2. На этом рисунке видно, что распределение деформаций и температуры неравномерно. Таким образом, прямая интерпретация результатов теста может привести к ошибкам.

Рисунок 4.2. Распределение деформаций (а) и температур (б) в испытании UC для стали C-Mn.

PSC – это один из пластометрических тестов, который используется в основном для физического моделирования многоступенчатых процессов формовки, но также часто применяется для определения напряжения течения. В этом испытании кубовидный образец сжимается между двумя плоскими штампами; см. Рисунок 4.1. Это испытание допускает большую пластическую деформацию, а состояние деформации аналогично тому, которое происходит в процессе плоской прокатки. Плоскодеформированное состояние достигается за счет двух факторов. Малая ширина (b) отношения образца к ширине фильеры (w) препятствует течению материала в направлении ширины. Это похоже на плоскую прокатку, где малое отношение длины контакта к ширине полосы способствует удлинению и предотвращает растекание. Влияние так называемых жестких концов – еще один фактор, ограничивающий распространение и связанный с состоянием плоской деформации. Жесткие концы – это части образца за пределами области под штампом. Эти части не сжимаются, поэтому у них нет тенденции к растеканию.Более того, когда образцы нагреваются резистивным нагревом (например, на симуляторе Gleeble 3800), эти детали имеют более низкую температуру, чем область под штампом, и их сопротивление деформации выше. В связи со всеми этими обсуждаемыми фактами PSC часто используется в качестве физического моделирования процесса плоской прокатки.

Плоское состояние штаммов, недостижимое в других пластометрических тестах, в течение многих лет вдохновляло ученых на различные применения тестов PSC. Идентификация модели напряжения течения – одно из таких приложений, а исследование эволюции микроструктуры – другой пример.Среди нескольких исследовательских лабораторий, участвующих в исследованиях на основе тестов PSC, группа под руководством К.М. Следует упомянуть Селларса из Университета Шеффилда. В течение 1950-х и 1960-х годов этот тест широко использовался там для исследования материалов, и результатом этого исследования стали фундаментальные работы по эволюции микроструктуры [322] и по моделям напряжения течения [58].

Некоторые аспекты теста PSC, такие как подготовка образца, предварительный нагрев и т. Д., Аналогичны тем, которые используются в тестах UC.Однако следует подчеркнуть, что различные нарушения очень затрудняют интерпретацию результатов тестов PSC. Эти испытания характеризуются большой неоднородностью деформации (рис. 4.3а), которая вызвана сложной формой зоны деформации (рис. 4.1) и эффектом трения. Помимо этого, тепло, выделяемое из-за пластической работы и трения, а также передача тепла инструментам и окружающей среде, вызывает сильную неоднородность температуры в образце (Рисунок 4. 3б).

Рисунок 4.3. Распределение деформаций (а) и температур (б) в тесте PSC для медного сплава.

Метод RC, первоначально разработанный для холодной штамповки, был адаптирован Мале и Кокрофтом [218] для горячей обработки. Течение металла в этом испытании зависит от трения. Для снижения трения увеличиваются как внутренний, так и внешний диаметр. При большом трении внутренний диаметр течет внутрь, а внешний – наружу, и возникает нейтральная точка без проскальзывания. Это хорошо видно на рисунке 4.4, где показаны результаты расчетов формы кольца для различных коэффициентов трения в модели Треска. Поскольку положение нейтральной точки зависит от трения, этот тест обычно используется для измерения коэффициента трения. Для определения этого коэффициента достаточно измерить только изменение формы кольца. Традиционный метод интерпретации RC основан на измерении только внутреннего диаметра после сжатия. Специальные диаграммы, см., Например, Schey [317], используются для определения коэффициента трения на основе этого измерения. Однако тест RC дает больше информации, чем изменения внутреннего диаметра кольца. Обратный анализ позволяет учесть эту информацию, которая обычно включает результаты измерений внутреннего и внешнего диаметра в нескольких местах по высоте кольца. Кроме того, измерение нагрузок при деформации кольца дает информацию, которая дополнительно позволяет оценить параметры напряжения течения. Следовательно, этот тест может быть выбран для оценки как параметров трения, так и реологических параметров.

Рисунок 4.4. Форма четверти поперечного сечения кольца, измеренная до и после сжатия (сплошные линии) и рассчитанная после сжатия для различных коэффициентов трения.

Тщательный анализ преимуществ и недостатков тестов UC и PSC, а также стандарты для этих тестов можно найти в Руководствах по передовой практике Национальной физической лаборатории [197,304] [197] [304]. Применение обратного анализа к интерпретации результатов тестов UC, RC и PSC представлено в разделе 4.2.2.

Испытания на кручение проводятся с материалами для определения таких свойств, как модуль упругости при сдвиге, предел текучести при кручении и модуль разрыва. Эти испытания особенно полезны для определения технологических характеристик пластичности материалов, которые отражают свойства материалов в процессах обработки металлов давлением. Они также используются для сравнительной оценки пластичности материала в зависимости от его химического состава, фазового состава и технологии производства.Результаты испытаний на кручение могут быть использованы для оценки сило-силовых параметров в процессах обработки металлов давлением и определения оптимальных диапазонов технологических параметров в этих процессах. Эти испытания также позволяют оценить влияние условий деформации на эволюцию микроструктуры.

Испытания на кручение также часто используются для испытания хрупких материалов и для испытаний полноразмерных деталей, то есть валов, осей и спиральных сверл, которые подвергаются крутильной нагрузке в процессе эксплуатации.При испытании на кручение стандартные цилиндрические образцы на кручение обрабатываются из поставляемого исследуемого материала и подвергаются испытаниям на специализированном торсионном аппарате, оборудованном излучающей печью.

Испытания на кручение лучше всего подходят для процессов с большими деформациями. Можно получить конечную деформацию 5, что позволяет моделировать полную историю горячей прокатки, включая явления на черновом стане и чистовой линии станов горячей прокатки. Преимущества испытаний на кручение:

•: возможны очень большие деформации,
•: постоянную скорость деформации легко достичь,
•: проблем с трением не существует.

Недостатки:

•: крутильные напряжения и деформации изменяются по поперечному сечению, и для извлечения данных одноосного нормального напряжения-деформации требуется значительный объем анализа,
•: изменение во времени. В результате для разных участков поперечного сечения требуется разное время, чтобы испытать металлургические явления, в частности динамическую рекристаллизацию (DRX).

Крутящий момент является основным выходным показателем при испытании на кручение.Есть несколько нарушений, которые затрудняют надежное измерение крутящего момента. На ускорение скорости скручивания от нуля до номинального значения требуется некоторое время. Во время испытания температура образца увеличивается. Эти два явления вызывают необходимость выполнения коррекции записанного теста. Типичное уравнение коррекции имеет вид:

(4.1) M = Mrec (N˙NN˙) m

, где M _rec – зарегистрированный крутящий момент, M – скорректированный крутящий момент, м – чувствительность скорости деформации. , N˙N – номинальная скорость крутки, а N˙ – записанная скорость крутки.

Расчет истинной деформации ε , скорости деформации ε˙ и напряжения течения σ _p по измеренному крутящему моменту – еще одна проблема при интерпретации результатов испытаний. В работе [5] были предложены следующие соотношения. [127]:

(4.2) ε = 23πRNL

(4.3) ε˙ = 23πRN˙L

(4.4) σp = (3M2πR3) 2 (3 + p + m) 2+ (FπR2) 2

где L, – длина образца, R, – радиус образца, M, – крутящий момент, N, – количество скручиваний, N˙ – скорость скручивания, м, – чувствительность скорости деформации, и p. дифференциальная составляющая, определяемая по уравнению:

(4.5) p = NM∂M∂N

В литературе можно найти несколько других методов интерпретации испытания на кручение, которые позволяют рассчитать напряжение течения на основе крутящего момента, зарегистрированного во время испытания [117]. Моделирование этого теста методом конечных элементов (КЭ) представлено в работе. [257], а попытка применения обратного анализа к интерпретации результатов испытаний на кручение представлена в [257]. [157]. КЭ модель испытания на кручение также использовалась в качестве модели прямой задачи в этой публикации. Поскольку КЭ моделирование деформации материала во время кручения, которое связано со значительным напряжением сдвига, было затруднено, применение обратного анализа к интерпретации результатов испытаний на кручение представляло трудности и никогда не становилось таким популярным, как испытания на сжатие.Обзор методов расчета напряжения течения по крутящему моменту, зарегистрированному во время испытания, был разработан Хадасиком [127], и они не описываются в этой книге.

Подводя итог, можно констатировать, что разнообразие в конструкции торсионных пластометров, гибкость метода тестирования и трудности в учете теплового эффекта и неоднородности красителя привели к значительным расхождениям между результатами, полученными в различных лабораториях. Это также затрудняет сравнение результатов испытаний на кручение с результатами испытаний на сжатие.Все эти трудности с интерпретацией результатов испытаний на кручение являются основными ограничениями в применении испытания на кручение для количественного определения напряжения течения. Тест скорее посвящен сравнению различных материалов и физическому моделированию многоступенчатых процессов.

Детальная ошибка IIS 7.5 – 404.11

Resumen de error

Ошибка HTTP 404.11 – не найдено

El módulo Solicitar filtrado est configurado for denegar una solicitud que contiene una secuencia de doble escape.

Подробная информация об ошибках

Módulo

RequestFilteringModule

Notificación

BeginRequest

Controlador

StaticFile

Código

Método de inicio de inicio aún
Dirección URL solicitada	http://materiales.azc.uam.mx:80/gjl/clases/ma10_i/roark’s%20formulas%20for%20stress%20and%20strain.pdf
Ruta de Acceso física	E: \ web \ materiales \ gjl \ clases \ ma10_i \ roark’s% 20formulas% 20for% 20stress% 20and% 20strain.pdf
Usuario de inicio de sesión	Не определено

Вероятные причины:

La solicitud contenía una secuencia de doble escape y Solicitar filtrado está configurado en el servidor web for denegar secuencias de doble escape.

Qué puede intentar:

Compruebe la configuración configuration/system.webServer/security/requestFiltering@allowDoubleEscaping del archivo applicationhost.config или web.config.

Vínculos y más información Se trata de una característica de seguridad. No la cambie salvo que conozca con excitud el alcance del cambio. Debe realizar un seguimiento de la red antes de cambiar este valor para confirmar que no es una solicitud maliciosa. Si el servidor permite secuencias de doble escape, modifique la configuración configuration / system.webServer / security / requestFiltering @ allowDoubleEscaping. Esto podría estar causado por una dirección URL mal formada enviada al servidor por un usuario malicioso.

Дополнительная информация »

Эксперимент по испытанию на растяжение | Материаловедение и инженерия

Одним из широко используемых и признанных свойств материала является прочность материала. Но что означает слово «сила»? “Сила” может иметь много значений, поэтому позвольте Давайте подробнее рассмотрим, что подразумевается под прочностью материала.Мы будем смотреть в очень простом эксперименте, который дает много информации о силе или механическое поведение материала, называемое испытанием на растяжение.

Основная идея испытания на растяжение заключается в размещении образца материала между двумя креплениями. так называемые «захваты», которые зажимают материал. Материал имеет известные размеры, например длину. и площадь поперечного сечения.Затем мы начинаем прикладывать вес к материалу, захваченному за один конец, а другой конец закреплен. Мы продолжаем увеличивать вес (часто называемый нагрузку или силу), одновременно измеряя изменение длины образца.

Испытание на растяжение

Очень упрощенный тест можно сделать дома.

Если у вас есть способ подвесить один конец какого-либо материала к твердой точке, которая не двигаться, то на другой конец можно повесить гири.

Измерьте изменение длины при добавлении веса, пока деталь не начнет растягиваться и наконец ломается.

Результатом этого теста является график зависимости нагрузки (количества веса) от смещения. (количество растянутых). Поскольку вес, необходимый для растяжения материала, зависит от по размеру материала (и конечно свойствам материала), сравнение между материалами может быть очень сложно.Умение провести правильное сравнение может быть очень важно для тех, кто занимается проектированием конструкций, в которых материал должен выдерживать определенные силы.

Площадь поперечного сечения

Нам нужен способ напрямую сравнивать различные материалы, чтобы определить «прочность» мы сообщаем независимо от размера материала.Мы можем сделать это, просто разделив нагрузка, приложенная к материалу (вес или сила) начальным поперечным сечением площадь. Мы также делим величину его перемещения (смещение) на начальную длину материал. Это создает то, что ученые-материаловеды называют инженерным стрессом (нагрузка деленное на начальную площадь поперечного сечения) и инженерной деформации (смещение деленное на исходную длину).Глядя на инженерный отклик на напряжение-деформацию материал, мы можем сравнивать прочность различных материалов, независимо от их размеры.

Чтобы использовать реакцию “напряжение-деформация” для проектирования конструкций, мы можем разделить нагрузку мы хотим с помощью инженерного напряжения определить площадь поперечного сечения, необходимую для уметь удерживать этот груз.Например, стальная проволока 4340 диаметром 1/8 дюйма может удерживать маленькая машина. Опять же, не всегда все так просто. Нам нужно понять разные значения «силы» или инженерного напряжения.

Теперь все становится сложнее. Давайте посмотрим, что подразумевается под разными значения прочности, а также посмотрите на другие важные свойства, которые мы можем получить с помощью этого простого тестовое задание.Самый простой способ – изучить график зависимости инженерного напряжения от инженерного. напряжение. Ниже показан график испытания на растяжение обычного стального резьбового стержня. являясь хорошим примером общего испытания металла на растяжение. Единицы техники Напряжение составляет тысяч фунтов на квадратный дюйм , что означает тысячу фунтов на квадратный дюйм. Обратите внимание на ссылку на область в единицы. Единицы измерения деформации, конечно, безразмерны, поскольку мы делим расстояние по расстоянию.

Расположение графика 1: эластичная область

Давайте обсудим некоторые важные области графика.Во-первых, точка на графике цифра 1 обозначает конец упругой области кривой. До этого точка, материал растягивается эластично или обратимо.

Все материалы состоят из набора атомов. Эластичность лучше всего понять посредством изображения атомы связаны пружинами.Когда мы натягиваем материал, пружины между атомами удлиняется, и материал удлиняется. Эластичная часть кривая – прямая линия. Прямая линия означает, что материал вернется до первоначальной формы после снятия нагрузки.

Расположение графика 2: 0.Предел текучести смещения 2%

Следующая часть интересующей кривой – это точка 2. В этой точке кривая имеет начал наклоняться или больше не является линейным. Эта точка известна как смещение 0,2%. предел текучести. Он указывает на прочность материала, когда он начинает постоянно изменить форму.Он определяется как значение напряжения, при котором линия того же наклон как начальная часть (упругая область) кривой, которая смещена деформацией 0,2% или значение 0,002 деформации пересекает кривую.

В нашем примере предел текучести смещения 0,2% составляет 88 тысяч фунтов на квадратный дюйм.

Это очень важный аспект силы.Это в основном говорит нам о количестве стресса мы можем нанести до того, как материал начнет постоянно менять форму, надев его путь к возможной неудаче. Те, кто проектирует детали, которые используются в стрессовых ситуациях, должны убедитесь, что напряжение или сила со стороны детали никогда не превышают этого значения.

Местоположение графика 3: Максимальное выдерживаемое напряжение

По мере продвижения от точки 2 нагрузка или «напряжение» на материал увеличивается, пока мы не достигают максимального приложенного напряжения, при этом материал деформируется или меняет форму равномерно по всей длине колеи.Когда мы достигаем точки 3, мы можем определить растяжение прочность или максимальное напряжение (или нагрузка), которую может выдержать материал. Это не очень полезный свойство, так как материал в этот момент необратимо деформировался. После того, как мы достигнем в этот момент напряжение начинает резко снижаться. Это соответствует локализованному деформация, которая наблюдается по заметному «сужению» или уменьшению диаметра и соответствующее поперечное сечение образца в очень маленькой области.Если мы выпустим нагрузка в этой области, материал будет немного пружинить, но все равно пострадает постоянное изменение формы.

Местоположение графика 4: Отказ или перелом

Наконец, следуя кривой, мы в конечном итоге достигаем точки, где материал разрывается. или терпит неудачу.Здесь интересна конечная степень изменения формы материала. Это «пластичность» материала. Определяется пересечением линии номер 4, имеющий тот же наклон, что и линейный участок кривой, с деформацией ось.

Наш пример показывает деформацию 0.15. Изменение длины на 15% – это величина «пластичности».

Когда образец раскалывается или ломается, нагрузка снимается. Следовательно, атомы упруго растянутые вернутся в свои ненагруженные положения. Другая информация о механическом реакцию материала также можно получить из испытания на излом.

Испытания на растяжение – композиты

Если тянуть за материал до разрыва, можно найти много информации о различная прочность и механическое поведение материала.В этом виртуальном эксперименте мы исследуем поведение при растяжении трех различных композитных волокнистых материалов. У них схожее использование, но очень разные свойства.

Процедура

Материал захватывается с обоих концов устройством, которое медленно тянет в продольном направлении. на кусок, пока он не сломается.Сила тяги называется нагрузкой, которая наносится на график против изменения длины материала или смещения. Нагрузка преобразуется в напряжение значение, а смещение преобразуется в значение деформации.

О материалах

Материалом для испытаний являются композиты из стекловолокна, кевлара® и углеродного волокна.Композиты представляют собой комбинации двух или более отдельных материалов с целью производства материал, обладающий уникальными свойствами, которых нет ни в одном материале.

Все эти композиты используют эпоксидную смолу в качестве матрицы, которая «склеивает» ткань, как композиция. волокон соответствующих материалов.

Эпоксидные смолы – это термореактивные сетчатые полимеры, которые очень твердые и прочные, но не хрупкая сторона.

Все ткани имеют одинаковый «вес», который является мерой размера или веса ткани. квадратного двора.Пример волокнистого материала из стекловолокна показан выше. левый. Кевлар очень похож, за исключением того, что он имеет желтый цвет. Углерод имеет черный цвет цвет. Образцы, используемые в этом случае, представляют собой плоские прутки, вырезанные из более крупного материала с использованием водоструйная пила. Три образца показаны внизу слева.

Свойства материала

Свойства материала	Стекловолокно	Кевлар®	Углеродное волокно
Плотность	-п.	E	E
Прочность на разрыв	Ф	G	E
Прочность на сжатие	G	-п.	E
Жесткость	Ф	G	Ф
Сопротивление усталости	G-E	E	G
Сопротивление истиранию	Ф	E	Ф
Шлифование / обработка	E	-п.	E
Электропроводность	-п.	-п.	E
Термостойкость	E	Ф	E
Влагостойкость	G	Ф	G
Совместимость смол	E	Ф	E
Стоимость	E	Ф	-п.

P = плохо, G = хорошо, F = удовлетворительно, E = отлично

Эксперимент

Описание: Аппарат тянет за каждый конец материала, пока он не сломается.

Стекловолокно 00:00
Кевлар 01:10
Углеродное волокно 03:09

Видео продолжительностью 5 минут 5 секунд без звука.

Исполнительный продюсер Эд Лайтила
Ведущий Стивен Форселл
Видеограф Бритта Лундберг

Окончательные данные

Исходные данные для стекловолокна

Смещение увеличивается от нуля до немногим более 5 мм.Нагрузка увеличивается почти линейно от 0 до примерно 12 кН перед почти вертикальным падением.

Исправленные данные для стекловолокна

Инженерное напряжение увеличивается от нуля до примерно 0.10. Инженерное напряжение возрастает. линейно от нуля до примерно 170 МПа, предел прочности. Модуль составляет 1,7 ГПа.

Исправленные данные для кевлара

Инженерное напряжение увеличивается от нуля до примерно 0.11. Инженерное напряжение возрастает. линейно от нуля до примерно 265 МПа, предел прочности. Модуль составляет 2,3 ГПа.

Исправленные данные для углеродного волокна

Инженерное напряжение увеличивается от нуля до примерно 0.10. Инженерное напряжение возрастает. линейно от нуля до примерно 580 МПа, предел прочности. Модуль составляет 5,7 ГПа.

Выводы

Композитный материал из углеродного волокна имеет гораздо более высокий предел прочности и модуль упругости. эластичности, чем другие материалы.Обратите внимание, что все они ломаются «хрупко», так как кривая является линейной до тех пор, пока она не разорвется или не сломается без изгиба кривой при высокие нагрузки. Следовательно, при этом не происходит постоянного изменения первоначальной формы. тест, и, следовательно, никакой пластичности.

Виртуальные примеры

Вы видели эксперименты с композитными материалами.Сравните композитный материал Кривые напряжения-деформации с кривыми для полимера и стали.

Сталь для испытаний на растяжение

Стальной образец с шейкой имеет непрерывную зависимость между напряжением и деформацией.Стресс увеличивается почти вертикально, затем постепенно опускается.

Полимер для испытаний на растяжение

Образец растягивающегося полимера имеет разрывную зависимость напряжения от деформации.В напряжение увеличивается почти вертикально, затем падает и неравномерно увеличивается.

Фото галерея

Ниже представлены оптические фотографии разбитых или расколотых образцов, а также крупные планы. поверхности излома, снятые с помощью растрового электронного микроскопа.Изучение этих поверхности излома также являются очень важной частью материаловедения и инженерии, что делает это областью специализации.

(PDF) Формулировка прочности материалов для тонкостенных композитных балок с кручением

wkh prvw frpprq vwuxfwxudo frpsrqhqw / duh vxemhfwhg wr frpelqhg ordglqj

lqfoxglqj ir dhrdurl durlql ylhz / wkhuh lv frqvlghudeoh lqwhuhvw lq ghyhorslqj d ehdp wkhru | lqfoxglqj

wruvlrq излучающих uhvxowv LQ vlpsoh htxdwlrqv vlplodu wkrvh dydlodeoh сог ира ehdpv

pdgh ри д vlqjoh lvrwurslf DQG krprjhqhrxv pdwhuldo1 EHDP wkhrulhv dW0

whpswlqj dgguhvv WKH сог fdvh ри jhqhudoo | odplqdwhg vhfwlrq zlwk duelwudu |

jhrphwu | uhvxow lq frpsoh {irupxodwlrqv iru zklfk vroxwlrqv fdq eh rewdlqhg

rqo | LQ d olplwhg qxpehu рите vlpsoh fdvhv1 D jhqhudo irupxodwlrq лв suhvhqwhg

LQ ^ 5` / DQG WKH htxdwlrqv Духа vroyhg ира d vrolg uhfwdqjxodu спосы | huhg vhfwlrq1

Dqdo | wlfdo vroxwlrqv ч {LVW иру WKH fdvh ри wzr0od | х lvrwurslf ^ 6` / v | pphwulf

vdqgzlfk lvrwurslf ^ 7` / krprjhqhrxv dqlvrwurslf ^ 8` / DQG odplqdwhg eduv ^ 9` /

^: `> zlwk ду wkhvh vroxwlrqv olplwhg сог uhfwdqjxodu vrolg vhfwlrqv1

Lqwurgxflqj dssur {lpdwlrqv uhjduglqj WKH nlqhpdwlfv ri ghirupdwlrq lq

wkh odplqdwh / lw lv srvvleoh wr rewdlq vlpsohu vroxwlrqv wr pruh jhqhudo fdvhv /

dowkrxjk wkh | pd | vxhu iru fdvhv ri vwurqj pdwhuldo frxsolqj1 Ds0

sur {lpdwh irupxodwlrqv duh ghyhorshg lq ^; `/ vhsdudwho | iru wkh fdvhv ri uhfw0

dqjxodu / wxexodu / dqg rshq vhfwlrqv1 Dq dssur {lpdwh irupxodwlrq iru uhfw0

dqjxodu ehdpv lv

dqjxodu ehdpv lg lv suhvhq для ^ whldwhdwh

dqjxodu ehdpv lv lv suhvhq ruwkrwurslf odplqdwhg ehdp1 Xvlqj uvw rughu vkhdu ghirupd0

wlrq wkhru | + IVGW, wr prgho wkh nlqhpdwlfv ri wkh odplqdwh / d forvhg irup

vroxwlrq wr d jhqhudo ruwkrwurslf odplqdwh lv ghyhorshg lq ^ 43` iru uhfwdq5 jhrphrwur 9000 | htxd0

wlrqv jryhuqlqj WKH ЭГФД ehkdylru ри wklq0zdoohg odplqdwhg vhfwlrqv zklfk

Дух wkhq vroyhg LQ иру WKH fdvh flufxodu е | olqgulfdo vkhoov1 D vlpsoh irupx0

odwlrq зидовудин suhvhqwhg LQ ^ 5; `сог frpsxwh WKH ehqglqj DQG vkhdu vwlqhvv ри

Wlprvkhqnr * v ehdp wkhru | iru wklq0zdoohg odplqdwhg ehdpv zlwkrxw wruvlrq1

Iruwxqdwho | / pdq | sudfwlfdo hqjlqhhulqj dssolfdwlrqv h {lvw iru zklfk wkh ds0

sur {lpdwlrqv pdgh lq wkhvh wkhrulhv duh uhdvrqdeoh2 Wkhvh lqfoxgh wkh fdvkxv

xvhg lq flylo lqiudvwuxfwxuh dssolfdwlrqv /

dqg prvw odplqdwhg ehdpv zkhuh wklfn odplqdwhv / yhu | glvvlplodu pdwhuldov /

ru vhyhuho | xqv | pphwulfdo / xqedodqfhg спосо | 0xsv Дух ч {foxghg сог dyrlg WKH xq0

ghvludeoh hhfwv излучающие wkrvh frqjxudwlrqv surgxfh / lqfoxglqj zduslqj gxh сог

fxulqj uhvlgxdo vwuhvvhv / hwf1

Ri frxuvh / vshfldo dssolfdwlrqv гр ч { LVW / vxfk DV kholfrswhu urwru eodghv

^ 45` / DQG vzhsw iruzdug dlufudiw zlqjv ^ 46` / zhuh vwurqj frxsolqj hhfwv Дух gh0

vludeoh2 Qr dwwhpsw лв pdgh LQ wklv zrun сог dgguhvv wkhvh frpsoh {vlwxdwlrqv1

Vroxwlrqv Дух довр dydlodeoh iru vshfldo jhrphwulhv / vshfldoo | f | olqgulfdo vkhoov

^ 47`1 Frqwrxu dqdo | vhv iru dhurhodvwlfdoo | wdloruhg frpsrvlwh urwru eodghv duh

Прочность материалов – основы и уравнения

В механике материалов прочность материала – это его способность выдерживать приложенную нагрузку без разрушения или пластической деформации. Прочность материалов в основном учитывает взаимосвязь между внешними нагрузками , приложенными к материалу, и результирующей деформацией или изменением размеров материала. При проектировании конструкций и машин важно учитывать эти факторы, чтобы выбранный материал имел достаточную прочность, чтобы противостоять приложенным нагрузкам или силам, и сохранять свою первоначальную форму. Прочность материала – это его способность выдерживать эту приложенную нагрузку без разрушения или пластической деформации.

Однако мы должны отметить, что нагрузка, которая деформирует небольшой компонент, будет меньше нагрузки, необходимой для деформации более крупного компонента из того же материала. Следовательно, нагрузка (сила) не является подходящим термином для описания прочности . Вместо этого мы можем использовать силу (нагрузку) на единицу площади (σ = F / A), называемую напряжением , которое является постоянным (до появления деформации) для данного материала независимо от размера составной части. В этой концепции деформация также является очень важной переменной, поскольку она определяет деформацию объекта.Таким образом, механическое поведение твердых тел обычно определяется конститутивным соотношением напряжение-деформация . Деформация называется упругой деформацией, если напряжение является линейной функцией деформации. Другими словами, напряжение и деформация подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Такое неупругое поведение называется пластической деформацией.

Напряжение

В механике и материаловедении напряжение (представленное строчной греческой буквой сигма – σ ) – это физическая величина, которая выражает внутренние силы, которые соседние частицы сплошного материала оказывают друг на друга при деформации. является мерой деформации материала, которая не является физической величиной.

Хотя невозможно измерить интенсивность этого напряжения, можно измерить внешнюю нагрузку и площадь, к которой она приложена. Напряжение (σ) может быть приравнено к нагрузке на единицу площади или силе (F), приложенной к площади поперечного сечения (A) перпендикулярно силе, как:

Когда металл подвергается нагрузке (сила ), он искажается или деформируется, независимо от того, насколько прочен металл или легкая нагрузка. Если нагрузка небольшая, искажение, вероятно, исчезнет при снятии нагрузки.Интенсивность или степень искажения известна как деформация . Деформация называется упругой деформацией , если напряжение является линейной функцией деформации. Другими словами, напряжение и деформация подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Это неупругое поведение называется пластической деформацией .

Напряжение – это внутреннее сопротивление или противодействие материала искажающим эффектам внешней силы или нагрузки.Эти противодействующие силы стремятся вернуть атомы в их нормальное положение. Полное развиваемое сопротивление равно внешней нагрузке.

Типы напряжений

Напряжения возникают в любом материале, который подвергается нагрузке или любой приложенной силе. Существует множество типов напряжений , но все они могут быть классифицированы по одной из шести категорий:

Структурные напряжения – это напряжения, возникающие в элементах конструкции из-за веса, который они поддерживают.Вес обеспечивает нагрузки. Эти напряжения обнаруживаются в фундаментах и каркасах зданий, а также в деталях машин.
Остаточные напряжения – это напряжения, вызванные производственными процессами. Напряжение этого типа остается в твердом материале после устранения первопричины напряжений. Например, сварка оставляет в свариваемых металлах остаточные напряжения. Тепло от сварки может вызвать локальное расширение, которое во время сварки поглощается либо расплавленным металлом, либо размещением свариваемых деталей.
Напряжения давления – это напряжения, возникающие в сосудах, содержащих материалы под давлением. Нагрузка обеспечивается той же силой, что и давление. В реакторной установке корпус реактора является ярким примером корпуса высокого давления. Одной из проблем безопасности, которая является долгосрочной проблемой, вызванной старением ядерных установок, является тепловой удар под давлением (PTS) . PTS – это удар, который испытывает толстостенный сосуд из-за комбинированных напряжений от быстрого изменения температуры и / или давления.
Термические напряжения существуют всякий раз, когда в материале присутствуют градиенты температуры. Разные температуры вызывают разное расширение и подвергают материалы внутреннему напряжению. Этот тип напряжения особенно заметен в механизмах, работающих при высоких температурах и охлаждаемых холодной жидкостью. Одной из проблем безопасности, которая является долгосрочной проблемой, вызванной старением ядерных установок, является тепловой удар под давлением (СТВ). PTS – это удар, который испытывает толстостенный сосуд из-за комбинированных напряжений от быстрого изменения температуры и / или давления.
Напряжения потока возникают, когда масса текущей жидкости вызывает динамическое давление на стенку трубы. Сила удара жидкости о стену действует как нагрузка. Этот тип напряжения может проявляться неустойчиво при колебаниях расхода. Гидравлический удар является примером кратковременного напряжения течения. Гидравлический удар в трубе или трубе – это скачок давления, вызванный внезапным изменением скорости потока. и энергия скорости преобразуется в энергию давления.
Усталостные напряжения.Fatique – это ослабление материала, вызванное циклической нагрузкой, которое приводит к прогрессирующим и локализованным повреждениям конструкции и росту трещин. Как только трещина возникла, каждый цикл нагружения будет немного увеличивать трещину. Напряжения могут быть вызваны вибрацией или термоциклированием.

Прикладное напряжение

С внутренней точки зрения интенсивность напряжения в теле компонента выражается как один из трех основных типов внутренней нагрузки, а именно: растяжение , сжатие и сдвиг .В инженерной практике многие нагрузки являются скорее скручивающими, чем чисто сдвиговыми. Математически существует только два типа внутренней нагрузки, поскольку растягивающее и сжимающее напряжение можно рассматривать как положительную и отрицательную версии одного и того же типа нормальной нагрузки.

Напряжение растяжения . Одно из наиболее распространенных механических нагрузочно-деформационных испытаний проводится при растяжении. Растягивающее напряжение – это такой тип напряжения, при котором две части материала по обе стороны от плоскости напряжения имеют тенденцию разъединяться или удлиняться.Способность материала или конструкции выдерживать нагрузки, имеющие тенденцию к удлинению, известна как предел прочности при растяжении (UTS) . Предел прочности на разрыв измеряется максимальным напряжением, которое может выдержать материал при растяжении или растяжении перед разрушением. При исследовании прочности материалов прочность на растяжение, прочность на сжатие и сдвиг может быть проанализирована независимо. Поскольку растягивающие и сжимающие нагрузки создают напряжения, которые действуют поперек плоскости, в направлении, перпендикулярном (перпендикулярном) плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями .
Напряжение сжатия . Напряжение сжатия противоположно растягивающему. Соседние части материала имеют тенденцию давить друг на друга через типичную плоскость напряжений. Напряжение сжатия стержней, колонн и т. Д. Приводит к укорачиванию. Напряжение сжатия определяется так же, как и растягивающее напряжение, но оно имеет отрицательные значения, чтобы выразить сжатие, поскольку дельта L имеет противоположное направление. Можно увеличивать сжимающее напряжение до тех пор, пока не будет достигнута прочность на сжатие.Тогда материалы будут реагировать пластично или разрушаться в случае хрупких материалов. Поскольку растягивающие и сжимающие нагрузки создают напряжения, которые действуют поперек плоскости, в направлении, перпендикулярном (перпендикулярном) плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями . Способность материала реагировать на сжимающее напряжение или давление называется сжимаемостью.
Напряжение сдвига . Напряжение сдвига возникает, когда две части материала имеют тенденцию скользить друг по другу в любой типичной плоскости сдвига при приложении силы, параллельной этой плоскости.Кручение – это разновидность чистого сдвига, при котором элемент конструкции скручивается. Торсионные силы вызывают вращательное движение вокруг продольной оси одного конца элемента относительно другого конца. Напряжение сдвига также имеет большое значение в природе, поскольку оно тесно связано с движением грунта вниз по склону (как в случае лавин).

Деформация

В материаловедении деформация также является очень важной переменной, поскольку она определяет деформацию объекта.В отличие от напряжения в объекте, которое вы на самом деле не видите, деформация – это видимая и измеримая величина. Когда вы тянете за натяжной стержень, вы можете увидеть, как стержень физически увеличивается в длину (или удлиняется). Когда вы изгибаете балку, вы видите ее кривую. Деформации – прямой показатель деформации. Механическое поведение твердых тел обычно определяется определяющими соотношениями напряжение-деформация . Когда металл подвергается нагрузке (силе), он деформируется или деформируется, независимо от того, насколько прочен металл или легкая нагрузка.Если нагрузка небольшая, искажение, вероятно, исчезнет при снятии нагрузки. Такое пропорциональное изменение размеров (интенсивность или степень искажения) называется деформацией и измеряется как полная деформация (удлинение) на эталонную длину материала из-за некоторого приложенного напряжения.

В механике материалов мы можем определить два основных типа деформации:

Нормальные деформации . Нормальная деформация возникает в результате растягивающего напряжения и представляет собой деформацию, вычисляемую из относительных смещений, которые измеряются перпендикулярно двум опорным плоскостям.Нормальные деформации измеряют относительное перпендикулярное движение одной базовой плоскости по отношению к другой. Символом нормальной деформации обычно является греческий символ эпсилон (ε) в нижнем регистре.
Деформации сдвига. Деформация сдвига возникает в результате напряжения сдвига, и это деформация, вычисляемая на основе относительных смещений, измеренных параллельно двум опорным плоскостям. Деформация сдвига измеряет относительное параллельное движение одной базовой плоскости по отношению к другой. Символом деформации сдвига обычно является греческий символ гаммы в нижнем регистре (γ).

Деформация

Деформация – это мера того, насколько объект деформируется относительно своих исходных размеров или размеров в заданном направлении. В зависимости от того, какую деформацию вы измеряете, вы можете рассчитать различные типы деформации.

Деформация называется упругой деформацией, если напряжение является линейной функцией деформации. Другими словами, напряжение и деформация подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение.Такое неупругое поведение называется пластической деформацией.

Упругая деформация . Упругая деформация и Упругая деформация – это временное изменение размеров, которое существует только при приложении исходного напряжения и исчезает сразу после снятия напряжения. Когда металл подвергается нагрузке (силе), он деформируется или деформируется, независимо от того, насколько прочен металл или легкая нагрузка. Эта деформация может быть или не быть постоянной. До предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки.Приложенные напряжения заставляют атомы в кристалле перемещаться из положения равновесия. Все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и остаточная деформация не происходит.
Пластическая деформация. Пластическая деформация и Пластическая деформация – это изменение размеров, которое не исчезает при снятии инициирующего напряжения. Это происходит, если превышение предельной нагрузки приводит к необратимой деформации тела при снятии нагрузки.Пластическая деформация происходит в материальных телах после того, как напряжения достигли определенного порогового значения, известного как предел упругости или предел текучести , и являются результатом скольжения или механизмов дислокации на атомном уровне.

Кривая напряжения – деформации

Прочность материалов в основном учитывает взаимосвязь между внешними нагрузками , приложенными к материалу, и результирующей деформацией или изменением размеров материала.При проектировании конструкций и машин важно учитывать эти факторы, чтобы выбранный материал имел достаточную прочность, чтобы противостоять приложенным нагрузкам или силам, и сохранять свою первоначальную форму. Прочность материала – это его способность выдерживать эту приложенную нагрузку без разрушения или пластической деформации.

Однако мы должны отметить, что нагрузка, которая деформирует небольшой компонент, будет меньше нагрузки, необходимой для деформации более крупного компонента из того же материала. Следовательно, нагрузка (сила) не является подходящим термином для описания прочности .Вместо этого мы можем использовать силу (нагрузку) на единицу площади (σ = F / A), называемую напряжением , которое является постоянным (до появления деформации) для данного материала независимо от размера составной части. В этой концепции деформация также является очень важной переменной, поскольку она определяет деформацию объекта. Таким образом, механическое поведение твердых тел обычно определяется конститутивным соотношением напряжение-деформация . Деформация называется упругой деформацией, если напряжение является линейной функцией деформации.Другими словами, напряжение и деформация подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Такое неупругое поведение называется пластической деформацией.

Принципиальная диаграмма кривой напряжения-деформации низкоуглеродистой стали при комнатной температуре показана на рисунке. Есть несколько стадий, демонстрирующих разное поведение, что предполагает разные механические свойства. Для пояснения, материалы могут пропускать одну или несколько стадий, показанных на рисунке, или иметь совершенно разные стадии.В этом случае необходимо различать деформационные характеристики пластичных материалов и хрупких материалов . Следующие пункты описывают различные области кривой напряжения-деформации и важность нескольких конкретных мест.

Предел пропорциональности . Пропорциональный предел соответствует местоположению напряжения в конце линейной области , поэтому график напряжения-деформации представляет собой прямую линию, а градиент будет равен модулю упругости материала.Для растягивающего и сжимающего напряжения наклон той части кривой, где напряжение пропорционально деформации, обозначается как модуль Юнга и применяется закон Гука . Между пределом пропорциональности и пределом текучести закон Гука становится спорным, и деформация увеличивается быстрее.
Предел текучести . Предел текучести – это точка на кривой напряжения-деформации, которая указывает предел упругого поведения и начало пластического поведения. Предел текучести или предел текучести – это свойство материала, определяемое как напряжение, при котором материал начинает пластически деформироваться, тогда как предел текучести – это точка, в которой начинается нелинейная (упругая + пластическая) деформация. До достижения предела текучести материал будет упруго деформироваться и вернется к своей исходной форме, когда приложенное напряжение будет снято. После достижения предела текучести некоторая часть деформации будет постоянной и необратимой. Некоторые стали и другие материалы демонстрируют поведение, называемое явлением предела текучести.Предел текучести варьируется от 35 МПа для алюминия с низкой прочностью до более 1400 МПа для высокопрочных сталей.
Предел прочности на разрыв . Предел прочности на растяжение является максимальным на инженерной кривой зависимости напряжения от деформации. Это соответствует максимальному напряжению , которое может выдержать конструкция при растяжении. Предел прочности на разрыв часто сокращают до «прочности на разрыв» или даже до «предела». Если это напряжение приложить и поддерживать, в результате произойдет разрушение.Часто это значение значительно превышает предел текучести (на 50–60 процентов больше, чем предел текучести для некоторых типов металлов). Когда пластичный материал достигает предела прочности, он испытывает образование шейки, где площадь поперечного сечения локально уменьшается. Кривая “напряжение-деформация” не содержит напряжения, превышающего предел прочности. Несмотря на то, что деформации могут продолжать увеличиваться, напряжение обычно уменьшается после достижения предела прочности. Это интенсивное свойство; поэтому его значение не зависит от размера испытуемого образца.Однако это зависит от других факторов, таких как подготовка образца, наличие или отсутствие поверхностных дефектов, а также температура температуры испытательной среды и материала. Предел прочности на разрыв варьируется от 50 МПа для алюминия до 3000 МПа для очень высокопрочных сталей.
Точка разрушения : Точка разрушения – это точка деформации, в которой материал физически разделяется. В этот момент деформация достигает максимального значения, и материал фактически разрушается, даже если соответствующее напряжение может быть меньше, чем предел прочности в этой точке.У пластичных материалов прочность на излом ниже, чем предел прочности при растяжении (UTS), тогда как в хрупких материалах прочность на излом эквивалентна UTS. Если пластичный материал достигает предела прочности на растяжение в ситуации с контролируемой нагрузкой, он будет продолжать деформироваться без приложения дополнительной нагрузки до тех пор, пока не разорвется. Однако, если нагрузка регулируется смещением, деформация материала может уменьшить нагрузку, предотвращая разрыв.

Во многих ситуациях предел текучести используется для определения допустимого напряжения, которому может подвергаться материал.Для компонентов, которые должны выдерживать высокое давление, таких как те, которые используются в реакторах с водой под давлением (PWR), этот критерий неадекватен. Чтобы охватить эти ситуации, теория максимального напряжения сдвига разрушения была включена в Кодекс ASME (Американское общество инженеров-механиков) по котлам и сосудам под давлением, раздел III, Правила строительства ядерных сосудов под давлением. Эта теория утверждает, что отказ компонента трубопровода происходит, когда максимальное напряжение сдвига превышает напряжение сдвига в пределе текучести при испытании на растяжение.

Хрупкость и вязкость – кривые напряжение-деформация

Некоторые материалы ломаются очень резко, без пластической деформации, что называется хрупким разрушением. Другие, более пластичные, в том числе большинство металлов, испытывают некоторую пластическую деформацию и, возможно, образование шейки перед разрушением. Среди кривых растяжения различных групп материалов можно выделить некоторые общие характеристики. Исходя из этого, можно разделить материалы на две большие категории; а именно:

Пластичные материалы . Пластичность – это способность материала растягиваться при растяжении. Пластичный материал деформируется (удлиняется) больше, чем хрупкий. Пластичные материалы перед разрушением деформируются. При пластическом разрушении перед разрушением происходит обширная пластическая деформация (образование шейки). Вязкое разрушение (разрушение при сдвиге) лучше, чем хрупкое разрушение, потому что есть медленное распространение и поглощение большого количества энергии до разрушения. Пластичность желательна при высоких температурах и высоком давлении в реакторных установках из-за дополнительных напряжений на металлах.Высокая пластичность в этих применениях помогает предотвратить хрупкое разрушение.
Хрупкие материалы . Хрупкие материалы под воздействием напряжения разрушаются с небольшой упругой деформацией и без значительной пластической деформации. Перед разрушением хрупкие материалы поглощают относительно мало энергии, даже если они обладают высокой прочностью. При хрупком разрушении (трансгранулярный раскол) до разрушения не происходит явной пластической деформации. Трещины быстро распространяются.

На следующем рисунке показана типичная кривая напряжения-деформации для пластичного и хрупкого материалов.Пластичный материал – это материал с небольшой прочностью и большой пластической областью. Материал будет выдерживать большее напряжение (деформацию) перед разрушением. Хрупкий материал – это материал, в котором пластичная область мала, а прочность материала высокая. Испытание на растяжение дает три описательных факта о материале. Это напряжение, при котором начинается наблюдаемая пластическая деформация или «податливость»; предел прочности при растяжении или максимальная интенсивность нагрузки, которую можно нести при растяжении; и относительное удлинение или деформация (степень растяжения материала) и соответствующее процентное уменьшение площади поперечного сечения, вызванное растяжением.Также можно определить точку разрыва или перелома.

Деформационное упрочнение

Одной из стадий на кривой напряжения-деформации является область деформационного упрочнения . Эта область начинается, когда деформация выходит на за предел текучести , и заканчивается в точке предела прочности, которая представляет собой максимальное напряжение, показанное на кривой зависимости напряжения от деформации. В этой области напряжение в основном увеличивается по мере удлинения материала, за исключением того, что вначале имеется почти плоский участок. Деформационное упрочнение также называется деформационным упрочнением или холодным деформированием .Это называется холодной обработкой, потому что пластическая деформация должна происходить при достаточно низкой температуре, чтобы атомы не могли перегруппироваться. Это процесс повышения твердости и прочности металла за счет пластической деформации. Когда металл пластически деформируется, дислокации перемещаются и возникают дополнительные дислокации. Дислокации могут двигаться, если атомы из одной из окружающих плоскостей разрывают свои связи и повторно соединяются с атомами на конечном крае. Плотность дислокаций в металле увеличивается с деформацией или холодной обработкой из-за размножения дислокаций или образования новых дислокаций.Чем больше дислокаций в материале, тем больше они будут взаимодействовать и запутываться. Это приведет к снижению подвижности дислокаций и упрочнению материала.

Закон Гука

Большинство поликристаллических материалов в пределах их диапазона упругости имеют почти постоянную зависимость между напряжением и деформацией. В 1678 году английский ученый по имени Роберт Гук провел эксперименты, которые предоставили данные, которые показали, что в диапазоне упругости материала деформация пропорциональна напряжению .Роберт Гук пришел к выводу, что сила F в любой пружине пропорциональна растяжению (деформации из расслабленного состояния) x следующим образом:

F = k · x

, где член k означает жесткость пружина и x малы по сравнению с полной возможной деформацией пружины. Он должен в конечном итоге выйти из строя, как только силы превысят некоторый предел, поскольку никакой материал не может сжиматься сверх определенного минимального размера или растягиваться сверх максимального размера без некоторой остаточной деформации или изменения состояния.

В случае напряжения растяжения однородного стержня (кривая напряжения-деформации), закон Гука описывает поведение стержня в упругой области. В этой области удлинение стержня прямо пропорционально растягивающей силе и длине стержня и обратно пропорционально площади поперечного сечения и модулю упругости . С точностью до предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки. Приложенные напряжения заставляют атомы в кристалле перемещаться из положения равновесия.Все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и остаточная деформация не происходит. Согласно закону Гука , напряжение пропорционально деформации (в упругой области), а наклон равен модулю Юнга .

Мы можем расширить ту же идею соотношения напряжения и деформации к приложениям сдвига в линейной области, соотнося напряжение сдвига с деформацией сдвига, чтобы создать закон Гука для напряжения сдвига :

Для изотропных материалов в упругой области вы может соотносить коэффициент Пуассона (ν), модуль упругости Юнга (E) и модуль упругости при сдвиге (G):

Модули упругости, относящиеся к поликристаллическим материалам:

Модуль упругости Юнга. Модуль упругости Юнга представляет собой модуль упругости для растягивающего и сжимающего напряжения в режиме линейной упругости при одноосной деформации и обычно оценивается с помощью испытаний на растяжение.
Модуль упругости при сдвиге. Модуль сдвига или модуль жесткости определяется скручиванием цилиндрического образца для испытаний. Он описывает реакцию материала на напряжение сдвига. Его символ – G. Модуль сдвига – одна из нескольких величин для измерения жесткости материалов, и он возникает в обобщенном законе Гука.
Объемный модуль упругости. Объемный модуль упругости описывает объемную упругость или тенденцию объекта деформироваться во всех направлениях при равномерной нагрузке во всех направлениях. Например, он описывает упругую реакцию на гидростатическое давление и равностороннее растяжение (например, давление на дне океана или в глубоком бассейне). Это также свойство материала, которое определяет упругую реакцию на приложение напряжения. Для жидкости значение имеет только модуль объемной упругости.

Механика материалов: деформация »Механика тонких конструкций

Штамм

До сих пор мы сосредоточились на напряжении внутри структурных элементов. Когда вы прикладываете напряжение к объекту, он деформирует . Представьте себе резинку: вы тянете за нее, и она становится длиннее – она тянется на . Деформация – это мера того, насколько объект растянут, а деформация , деформация – это соотношение между деформацией и исходной длиной.Думайте о деформации как о -процентном удлинении – насколько больше (или меньше) объект при его нагрузке.

Как и напряжение, конструкция может испытывать два типа деформации: 1. Нормальная деформация и 2. Деформация сдвига . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она вызывает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.

Рассмотрим стержень при одноосном растяжении.Стержень удлиняется под этим натяжением до новой длины, и нормальная деформация представляет собой отношение этой небольшой деформации к исходной длине стержня.

Деформация – это безразмерная мера того, насколько объект становится больше или меньше от приложенной нагрузки. Нормальная деформация возникает, когда удлинение объекта происходит в ответ на нормальное напряжение (т.е. перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует деформации при растяжении , отрицательное – при сжатии .Деформация сдвига возникает, когда деформация объекта является ответом на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой , гамма .

Механическое поведение материалов

Ясно, что напряжение и напряжение связаны. Напряжение и деформация связаны основополагающим законом , и мы можем определить их взаимосвязь экспериментально, измерив, сколько напряжения требуется для растяжения материала. Это измерение можно выполнить с помощью теста на растяжение . В простейшем случае, чем сильнее вы тянете за объект, тем сильнее он деформируется, а для малых значений деформации эта зависимость является линейной. Эта линейная упругая связь между напряжением и деформацией известна как закон Гука . Если вы построите график зависимости напряжения от деформации, для малых деформаций этот график будет линейным, а наклон линии будет свойством материала, известного как Модуль упругости . Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали.Для большинства конструкционных материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые являются линейно-эластичными (т.е. они подчиняются закону Гука) и изотропными (они ведут себя одинаково независимо от того, в каком направлении вы их тянете).

Из закона Гука и наших определений напряжения и деформации мы можем легко получить простую зависимость для деформации материала.

Интуитивно этот экзамен имеет некоторый смысл: приложите больше нагрузки, получите большую деформацию; приложите ту же нагрузку к более жесткому или толстому материалу, получите меньшую деформацию.Если конструкция меняет форму или материал, или по-разному нагружается в разных точках, то мы можем разделить эти множественные нагрузки, используя принцип наложения .

Обобщенный закон Гука

На последнем уроке мы начали узнавать, как связаны стресс и напряжение – через закон Гука. Но до этого момента мы рассматривали только очень упрощенную версию закона Гука: мы говорили о напряжении или деформации только в одном направлении.В этом уроке мы собираемся рассмотреть обобщенный закон Гука для однородных, изотропных и упругих материалов, подвергающихся действию сил по более чем одной оси.

Перво-наперво, даже простое вытягивание (или толкание) большинства материалов в в одном направлении на самом деле вызывает деформацию в во всех трех ортогональных направлениях . Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что при натяжении объекта в осевом направлении он сжимает в поперечном направлении в поперечных направлениях:

Таким образом, если потянуть за него в направлении x , он сожмется в направлениях y и z .Это свойство материала известно как коэффициент Пуассона , и обозначается греческой буквой nu и определяется как:

Или, более математически, используя осевую нагрузку, показанную на изображении выше, мы можем записать это в виде уравнения:

Поскольку коэффициент Пуассона представляет собой отношение двух деформаций, а деформация безразмерна, коэффициент Пуассона также безразмерен. Коэффициент Пуассона – это свойство материала . Коэффициент Пуассона может находиться в диапазоне от -1 до 0.5. Для большинства конструкционных материалов, например стали или алюминия, коэффициент Пуассона составляет около 0,3, а у каучуков коэффициент Пуассона составляет около 0,5, и они называются «несжимаемыми». Несжимаемый просто означает, что любая сумма, которую вы сжимаете в одном направлении, будет расширяться на такую же величину в других направлениях – следовательно, его объем не изменится.

За последнее десятилетие было проведено несколько очень интересных исследований по созданию структурированных материалов , которые используют геометрию и упругую нестабильность (тема, которую мы кратко рассмотрим в следующей лекции) для создания ауксетических материалов – материалов с отрицательным коэффициентом Пуассона.Физически это означает, что когда вы тянете материал в одном направлении, он расширяется во всех направлениях (и наоборот):

Этот принцип может быть применен в 3D для создания расширяемых / складных оболочек:

Благодаря коэффициенту Пуассона у нас теперь есть уравнение, которое связывает деформацию в направлении y или z с деформацией в направлении z. Мы, в свою очередь, можем связать это со стрессом с помощью закона Гука.Это важное замечание: если тянуть за объект в в одном направлении, это вызывает напряжение только в этом направлении , а вызывает деформацию во всех трех направлениях . Итак, сигма _y = сигма _z = 0. Давайте запишем деформации в направлении y и z через напряжение в направлении x .

Помните, что до этого момента мы рассматривали только одноосную деформацию . В действительности конструкции могут быть одновременно нагружены в нескольких направлениях, вызывая напряжение в этих направлениях.Полезный способ понять это – представить очень крошечный «кубик» материала внутри объекта. Этот куб может иметь напряжений , которые на перпендикулярны каждой поверхности , например:

Таким образом, приложение нагрузки в направлении x вызывает нормальное напряжение в этом направлении, и то же самое верно для нормальных напряжений в направлениях y и z . И, как мы теперь знаем, напряжение в одном направлении вызывает напряжение во всех трех направлениях .Итак, теперь мы включили эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как:

Эти уравнения выглядят сложнее, чем они есть на самом деле: деформация в каждом направлении (или каждый компонент деформации) зависит от нормального напряжения в этом направлении, а коэффициент Пуассона умножается на деформацию в двух других направлениях. Теперь у нас есть уравнения того, как объект изменит форму в трех ортогональных направлениях. Что ж, если объект меняет форму во всех трех направлениях, это означает, что он изменит свой объем на .Простую меру этого изменения объема можно найти, сложив три нормальных компонента деформации:

Теперь, когда у нас есть уравнение для изменения объема или расширения в терминах нормальных деформаций, мы можем переписать его в терминах нормальных напряжений.

Очень распространенный тип стресса, вызывающий расширение, известен как гидростатический стресс. Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:

Итак, в случае гидростатического давления мы можем свести наше окончательное уравнение для расширения к следующему:

Это последнее соотношение важно, потому что оно является определяющим соотношением того, как объем материала изменяется под действием гидростатического давления.Префактор p может быть переписан как модуль объемной упругости материала , K .

Наконец, вернемся к идее «несжимаемых» материалов. Что происходит с K – мерой изменения объема материала при заданном давлении – если коэффициент Пуассона для материала равен 0,5?

Закон Гука при сдвиге

В предыдущем разделе мы разработали взаимосвязь между нормальным напряжением и нормальной деформацией.Теперь поговорим о сдвиге. Вернемся к этому воображаемому кубу материала. Помимо внешних сил, вызывающих напряжения, нормальные к каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба. А, как известно, напряжения, параллельные поперечному сечению, равны касательным напряжениям

Теперь этот куб материала выглядит намного сложнее, но на самом деле это не так уж плохо. На каждой поверхности есть два напряжения сдвига, а нижние индексы говорят вам, в каком направлении они указывают и какой поверхности параллельны.Например, возьмем правую грань куба. Напряжения, нормальные к этой грани, являются нормальными напряжениями в направлении x . Есть два напряжения, параллельных этой поверхности, одно направлено в направлении y (обозначено tau _xy), а второе направлено в направлении z (обозначено tau _xz). Чтобы куб был в равновесии, tau _xy = tau _yx (в противном случае куб вращался бы). Таким образом, теперь существует шесть напряжений (сигма _x, sigmay, sigmaz, tau _xy, tau _yz, tau _xz), которые характеризуют состояние напряжения в однородном, изотропном, упругом материале.

Итак, как эти напряжения сдвига связаны с деформациями сдвига? Закон Гука для сдвига очень похож на уравнение, которое мы видели для нормального напряжения и деформации:

В этом уравнении пропорциональность между напряжением сдвига и деформацией сдвига известна как модуль сдвига материала . Это уравнение в его общей форме, но мы можем переписать его более явно в терминах его компонентов: x, y и z . Это даст нам обобщенный закон Гука для однородных, изотропных, эластичных материалов.

В нашем обобщенном законе Гука есть шесть компонентов напряжения и деформации и три свойства материала. Возникает естественный вопрос: как эти три свойства материала соотносятся друг с другом? Это соотношение задается следующим уравнением:

Сводка

В этой лекции мы представили концепцию напряжения. Деформация – это деформация материала под действием напряжения. Это просто отношение изменения длины к исходной длине.Деформации, приложенные перпендикулярно поперечному сечению, составляют нормальных деформаций , а деформации, приложенные параллельно поперечному сечению, составляют деформаций сдвига . Для линейных упругих материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как модуль упругости материала . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под воздействием внешней нагрузки.

Кроме того, в этом разделе мы узнали о многоосном нагружении .В частности, мы узнали, что напряжение в одном направлении вызывает деформацию в трех направлениях . Это происходит из-за свойства материала, известного как коэффициент Пуассона – соотношение между поперечной и осевой деформациями. Деформации, возникающие в трех ортогональных направлениях, могут дать нам меру расширения материала в ответ на многоосную нагрузку. В частности, материал может обычно изменять объем в ответ на изменение внешнего давления или гидростатического напряжения .Это привело к определению устойчивости материалов к изменению объема под действием гидростатического напряжения – объемному модулю . Изучив воображаемый кубический элемент в произвольном материале, мы смогли представить себе напряжения, возникающие нормально и параллельно каждой грани куба. Это дало нам шесть напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы связали друг с другом, используя обобщенный закон Гука для гомогенных материалов , изотропных и упругих материалов.Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости , модулем сдвига и коэффициентом Пуассона .

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Научный фонд.

Как спроектировать жесткость с использованием свойств материала

‍В моей прошлой статье мы обсуждали методы улучшения жесткости детали за счет геометрических изменений и почему это важный инструмент. Во второй части серии «Проектирование с учетом жесткости» мы рассмотрим изменение жесткости детали за счет свойств материала. Мы будем использовать многие из тех же формул, но сосредоточимся на свойствах, которыми мы можем управлять, просто выбрав материал.

В следующих параграфах подробно описаны конкретные свойства материала, которые мы будем исследовать, и то, как они применяются к жесткости детали.Кроме того, мы рассмотрим несколько примеров задач, которые помогут нам понять, как именно мы можем применить эти знания.

Основы материалов

Когда мы намереваемся увеличить или уменьшить жесткость детали путем изменения свойств материала, мы на самом деле говорим, что нам нужно выбрать материал с более высоким или более низким модулем упругости. Модуль упругости – это особое свойство данного материала, определяющее его жесткость. В этой статье мы также кратко рассмотрим предел текучести и предел прочности материалов, поскольку они в некоторой степени взаимосвязаны.

Модуль упругости

Модуль упругости материала, также известный как модуль Юнга, определяется как наклон кривой напряжения-деформации в линейной (упругой) области. Чтобы объяснить это, мы рассмотрим некоторые цифры, но сначала давайте вспомним, что такое напряжение и деформация:

Напряжение – Напряжение – это сила, приложенная к детали на единицу площади. Если мы подвесим вертикальную штангу размером 1 квадратный дюйм и повесим на ее дно гирю весом 100 фунтов, напряжение в штанге будет 100 фунтов на квадратный дюйм (psi).Деформация – деформация определяется как изменение длины, деленное на исходную длину образца под напряжением. Возвращаясь к нашему примеру с подвесной штангой, предположим, что изначально штанга была 100 дюймов, а в общей сложности она растянулась на 0,25 дюйма. Это означает, что наша деформация составляла 0,0025 дюйма / дюйм.

Теперь, когда мы разобрались с этим, мы можем начать говорить о кривой напряжения-деформации. Это кривая, которая обычно создается при испытании материалов путем их «растягивания» на специализированных машинах.Ось x кривой – это значение деформации, а ось y – значение напряжения. На приведенном ниже рисунке из Техасского университета в Арлингтоне показаны основные компоненты простой кривой напряжения-деформации.

Компоненты простой кривой напряжения-деформации
На этом изображении наклон считается равным жесткости, что справедливо для самого материала. То есть материал с более крутым уклоном будет жестче, чем материал с более пологим уклоном. Например, у ABS будет более крутой наклон, чем у резиновой ленты.Этот наклон сегмента черной линии и есть модуль упругости, о котором упоминалось ранее. До предела текучести материал ведет себя упруго, что означает, что он вернется к своей первоначальной форме и размеру после снятия напряжения. Если мы превысим предел текучести, материал будет постоянно деформироваться, что обычно плохо, если только деталь не предназначена для деформации, например, заклепки. Наклон красной линии не будет использоваться в этой статье, потому что он не используется в формулах или исследованиях FEA, которые мы собираемся исследовать.
Предел текучести и предела прочности на растяжение
Теперь, когда мы разобрались с основами кривой напряжения-деформации, давайте рассмотрим два наиболее важных значения напряжения из этих кривых. Первый – это предел текучести материала, который является самым высоким напряжением, которое мы можем приложить к материалу без постоянной деформации (обозначено пределом текучести выше). Затем следует предел прочности материала при растяжении (UTS), который определяется как максимальное напряжение, которое может выдержать материал. На приведенной ниже кривой “напряжение-деформация” обозначены эти значения.
Самыми важными значениями напряжения из кривых напряжения-деформации являются предел текучести и предел прочности на растяжение.
Если мы проведем горизонтальную линию от точки с надписью «Предел текучести» к вертикальной оси, она пересечется при значении напряжения, которое будет определять предел текучести материала. То же самое и с UTS. Наши кривые не имеют числовых значений, присвоенных осям, поэтому мы не можем получить физические значения, но мы определим, какие из этих значений будут в примерах далее в этой статье.
Объяснение основной проблемы
Основная причина, по которой нам нужно понимать эти свойства, – это знать, как мы можем использовать их при проектировании компонентов. Нам нужно, чтобы некоторые компоненты были очень жесткими, чтобы они не деформировались под нагрузкой. В некоторых случаях мы хотим, чтобы материал легко деформировался, не требуя слишком больших усилий. Эта статья решит эту основную проблему с обеих сторон спектра.
Прикладные примеры
В этом разделе мы рассмотрим, как на самом деле можно применить то, что мы узнали из кривых напряжения-деформации.Но сначала нам нужно рассмотреть некоторые формулы, которые мы обсуждали в Часть 1 этой серии.
Интересующие формулы
Первая формула, которую мы повторим, определяет прогиб консольной балки с нагрузкой на одном конце, как подробно описано ниже.
Где:
δ = прогиб
P = сила, приложенная на конце
L = длина стержня
E = модуль упругости
I = момент инерции площади (MOI)
Далее , мы вернемся к нашей формуле жесткости, как показано ниже:
Мы можем увидеть, насколько модуль упругости соответствует жесткости с математической точки зрения с помощью этой формулы.Отношение является линейным, поэтому, если мы удвоим наш модуль упругости, мы удвоим жесткость. Удвоение жесткости означает, что для отклонения детали потребуется вдвое больше силы по сравнению с исходной. Этот принцип лежит в основе нашей статьи.
Материалы для рассмотрения
Следующим шагом в применении этой концепции является определение материалов, которые мы можем использовать, и их модуля упругости. В приведенном ниже списке подробно описаны пластмассы, предлагаемые Fictiv для 3D-печати, и их модуль упругости:
Модуль упругости материала (фунт / кв. Дюйм)
FDM PLA от 293000 до 514000
FDM ABS 319000
VeroWhite / VeroBlack от 2
до 9 435000 SL 12 185,000
VisiClear 186,083 до 212,190
Эти значения опубликованы в разделе материалов Stratasys и в некоторых случаях могут зависеть от ориентации сборки деталей.В следующем примере мы будем использовать два материала, которые не указаны в таблице, но обладают известными свойствами. Эти материалы – нейлон 12 (FDM) и нейлон 12 со стекловолокном (SLS). Эти материалы используются в приведенном ниже примере, чтобы обеспечить лучший контраст между материалом с большей и меньшей жесткостью. Нейлон 12 (FDM) имеет модуль упругости 185 000 фунтов на квадратный дюйм, в то время как нейлон 12 со стеклянным наполнением (SLS) имеет модуль упругости 420 000 фунтов на квадратный дюйм. Мы видим, что Nylon 12 Glass Filled в 2,27 раза жестче обычного нейлона 12.Мы воспользуемся этими свойствами, чтобы увидеть, что это означает, в приведенных ниже примерах.
Пример конструкции – увеличение жесткости
В этом первом примере мы рассмотрим простую трубку, которая закреплена на консоли с силой, приложенной к одному концу. На рисунке ниже показан фиксированный конец с изображением замка и загруженный конец со стрелкой, направленной вниз.
Консольная трубка с усилием, приложенным к одному концу
Приложенная нагрузка составляет 10 фунтов-силы, а первым моделирующим материалом является нейлон 12 с модулем упругости 185 000 фунтов на квадратный дюйм.На рисунке ниже показано, что мы увидим 0,934 дюйма деформации в конце с приложенной нагрузкой.
Приложенная нагрузка создает деформацию в 0,934 дюйма на конце.
Затем мы заменим материал на стеклонаполненный нейлон 12 GF и посмотрим, действительно ли мы видим увеличение жесткости в 2,27 раза. На рисунке ниже показаны результаты этого исследования.
Результаты при замене материала на стеклонаполненный нейлон 12 GF
Новое отклонение составляет всего 0.4114 дюйма, и если мы разделим исходные 0,934 дюйма на новые 0,4114 дюйма, мы получим ровно 2,27. Это говорит нам о том, что наше исследование FEA полностью согласуется с нашим увеличением жесткости материала в результате изменения модуля упругости.
В этом примере мы используем простую фигуру, но у этой концепции есть реальные приложения. Возможно, мы захотим увеличить жесткость пластикового крючка, который будет удерживать предметы, чтобы они не упали под нагрузкой. Другим примером может быть увеличение жесткости ограждений и корпусов, чтобы стены не деформировались или не разрушались так легко.Вероятно, что большое количество пластиковых деталей, которые вы используете в повседневной жизни, было тщательно разработано для достижения соответствующей жесткости.
Пример конструкции – уменьшение жесткости
В следующем примере мы рассмотрим случай, в котором мы действительно можем уменьшить жесткость . Вернемся к примеру с защелкиванием из моей статьи о механических крепежах, как показано ниже.
Пример защелкивания
На этом изображении мы видим, что защелкивание должно деформироваться на 0.018 дюймов, чтобы очистить удерживающий элемент. Однако, если материал действительно жесткий, напряжения в этом компоненте будут слишком высокими, когда он действительно будет отклоняться на 0,018 дюйма. Давайте посмотрим, каковы напряжения, когда защелка так сильно деформируется, а деталь сделана из нейлона 12 GF с модулем упругости 420 000 фунтов на квадратный дюйм. Первое изображение ниже демонстрирует нагрузку 4,136 фунта-силы, создающую 0,018 дюйма деформации.
Нагрузка 4,136 фунта-силы, создающая деформацию 0,018 дюйма
Как только мы достигли необходимого нам прогиба, мы можем посмотреть на напряжения, которые будут присутствовать, когда деталь так сильно прогибается.На изображении ниже изображена такая же симуляция, но теперь мы смотрим на напряжения в детали.
То же моделирование, теперь с учетом напряжений в детали.
Этот анализ показывает, что мы наблюдаем напряжения, значительно превышающие наш предел текучести 5250, поэтому мы, вероятно, повредим эту деталь, просто установив и сняв эту крышку. Мы почти наверняка увидим образование трещин под напряжением в углах после нескольких циклов.
Что, если бы мы пришли с материалом с более низким модулем упругости, как наш оригинальный нейлон 12 (185 000 фунтов на квадратный дюйм)? Если вы помните из обсужденных нами кривых напряжение-деформация, материал с более низким модулем упругости будет подвергаться большей деформации при заданном значении напряжения.Проще говоря, это означает, что мы можем ожидать, что защелка будет перемещаться на те же 0,018 дюйма с гораздо меньшими напряжениями.
И снова мы проведем исследование методом FEA, но на этот раз с нашим более низким модулем упругости – нейлоном 12. Приведенные ниже результаты относятся к тому же исследованию; однако нагрузка на защелку была уменьшена до 1,822 фунта-силы, поскольку материал с более низким модулем упругости требует меньшего усилия для отклонения на ту же величину.
FEA-исследование с более низким модулем упругости Нейлон 12
Мы достигли необходимого отклонения 0,018 дюйма, поэтому давайте посмотрим на напряжения, с которыми мы сталкиваемся на изображении ниже.
Область, которая ранее подвергалась нагрузке до 6 643 фунтов на квадратный дюйм, теперь составляет только 2 926 фунтов на квадратный дюйм
Область, которая ранее подвергалась нагрузке до 6 643 фунтов на квадратный дюйм, теперь составляет всего 2 926 фунтов на квадратный дюйм.
Оставить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Поиск:
Рубрики
Вакансии
Востребованные вакансии
Обучение в Европе
Обучение за границей
Работа
Работа для всех
Советы абитуриенту
Студенту
Студенческие будни
Разное
2019 © Все права защищены. Карта сайта
Меню
Поиск:
Советы абитуриенту
Работа для всех
Востребованные вакансии
Студенческие будни
Обучение за границей