Первый закон Ньютона | 9 класс
Содержание
На прошлом уроке мы говорили о важности выбора системы отсчета, когда мы рассматриваем то или иное движение. Многие физические величины, описывающие движение, являются относительными. Так, рассматривая перемещение, путь, траекторию и скорость тела в разных системах отсчета, мы можем получить различные значения этих величин.
Есть и другая важная особенность при выборе системы отсчета, связанная с инерцией. Именно о ней и пойдет речь на данном уроке, что позволит нам в итоге сформулировать первый закон Ньютона.
Инерция и инертность
Из курса 7 класса вам уже известны понятия инерции и инертности тела.
Инерция — это явление сохранения скорости тела при отсутствии действия на него других тел.
Так, неподвижное тело будет стремиться остаться и дальше в состоянии покоя, а тело, которое движется прямолинейно и равномерно, будет стремиться двигаться точно так же.
Инертность — это свойство тела сохранять состояние движения.
Само свойство инертности характеризуется такой величиной, как масса. Говорят, что она является мерой инертности тела. В чем смысл? Чем больше масса тела, тем большей инертностью оно обладает. То есть, чем тело тяжелее, тем его труднее сдвинуть с места или, наоборот, остановить.
{"questions":[{"content":"Как движется тело, если на него не действуют другие тела?[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["прямолинейно и равномерно или находится в состоянии покоя","прямолинейно и равноускоренно","криволинейно и равномерно","прямолинейно и равноускоренно или находится в состоянии покоя"],"answer":[0]}}}]}Закон инерции в изложениях Аристотеля, Галилея и Ньютона
Закон инерции формулировался в течение не одного века. Давайте заглянем в глубь истории и посмотрим, как этот закон изменялся.
Начнем с древнегреческого ученого Аристотеля.
Согласно его взглядам, при отсутствии внешнего воздействия тело может только покоиться. А для того, чтобы тело двигалось с постоянной скоростью, нужно, чтобы на него непрерывно действовало другое тело.
Согласно Аристотелю все движения можно разбить на два вида: естественные и вынужденные. Самый простой пример естественного движения — это свободное падение тела на Землю (рисунок 1). В этом случае Земля сообщает телу скорость.
Рисунок 1. Падающее с дерева яблоко как пример естественного движения АристотеляПримером вынужденного движения может быть ситуация, когда лошадь тянет телегу. Пока лошадь прилагает силу, телега движется (рисунок 2). Как только лошадь останавливается, останавливается и телега. Нет силы — нет скорости.
Рисунок 2. Пример вынужденного движения АристотеляВ начале XVII века взгляды Аристотеля были опровергнуты. Галилео Галилей опубликовал работу, в которой была изложена суть закона инерции.
Чем отличаются взгляды Галилея от взглядов Аристотеля в вопросе об условиях равномерного движения тел?
Великий итальянский ученый пришел к выводу о том, что при отсутствии внешних воздействий тело может не только покоиться, но и двигаться прямолинейно и равномерно. Сила же, которую нужно прикладывать к телу для поддержания его движения, нужна лишь для того, чтобы уравновесить другие силы. Например, силу трения.
В конце XVII века английский ученый Исаак Ньютон обобщил все ранние выводы и сформулировал закон инерции. Он включил его в качестве первого из трех законов в основу механики. Именно поэтому этот закон принято называть первым законом Ньютона.
Было сказано, что тело продолжает находиться в состоянии покоя или двигаться равномерно и прямолинейно, если на него не действуют другие тела.
Но нам уже известно, что движение относительно и его характеристики связаны с выбранной системой отсчета.
Ведь в одной системе отсчета тело может покоиться, а в другой — двигаться. Значит, такой закон инерции будет выполняться далеко не во всех системах отсчета.
{"questions":[{"content":"Первый закон Ньютона — это[[choice-6]]","widgets":{"choice-6":{"type":"choice","options":["закон инерции","закон всемирного тяготения","закон сохранения энергии","закон Ома"],"answer":[0]}}}]}Первый закон Ньютона
Убедимся на опыте в том, что вышеприведенный закон инерции Ньютона выполняется не во всех системах отсчета. Возьмем тележку и поместим на нее два металлических шарика. Один из них просто положим на тележку, а второй подвесим на нити. Затем сделаем так, чтобы тележка двигалась равномерно и прямолинейно относительно земли (рисунок 3, а).
Рисунок 3. Опыт с тележкой и шарикамиСилы, действующие на шарики по вертикали, уравновешены. По горизонтали же на них не действуют никакие силы (силу сопротивления воздуха мы не учитываем). Поэтому шарики будут оставаться неподвижными относительно тележки все время ее движения при любой ее скорости ($\upsilon_1$, $\upsilon_2$, $\upsilon_3$).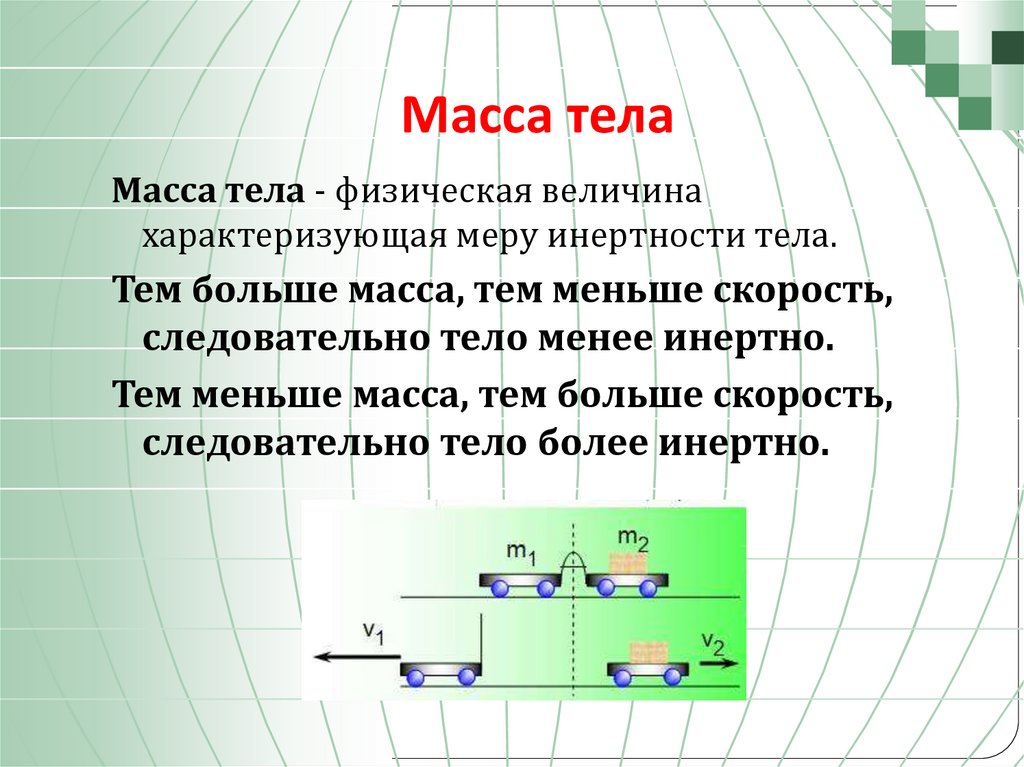
Дальше наша тележка попадает на песочную насыпь (рисунок 3, б). Скорость ее движения резко уменьшается, и тележка останавливается. Когда она начинает тормозить, оба шарика приходят в движение. Их скорость изменяется относительно тележки. При этом никакие новые силы на них не действуют.
Какой вывод следует из этого опыта?
В данном случае закон инерции не работает. Нам необходимо добавить к формулировке этого закона, что он выполняется не во всех системах отсчета.
Так мы получили современную формулировку первого закона Ньютона.
Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел компенсируются.
Обратите внимание, что в этом законе речь идет о телах, которые мы можем принять за материальные точки.
{"questions":[{"content":"Как выглядит современная формулировка первого закона Ньютона?[[choice-11]]","widgets":{"choice-11":{"type":"choice","options":["Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел компенсируются.
","Тело продолжает находиться в состоянии покоя или двигаться равномерно и прямолинейно, если на него не действуют другие тела.","При отсутствии внешних воздействий тело может не только покоиться, но и двигаться прямолинейно и равномерно.","При отсутствии внешнего воздействия тело может только покоиться. А для того, чтобы тело двигалось с постоянной скоростью, нужно, чтобы на него непрерывно действовало другое тело."],"explanations":["","Это формулировка закона инерции Ньютона, нуждающаяся в одном важном уточнении.","Это формулировка закона инерции Галилея.","Это формулировка закона инерции Аристотеля."],"answer":[0]}}}]}
","Тело продолжает находиться в состоянии покоя или двигаться равномерно и прямолинейно, если на него не действуют другие тела.","При отсутствии внешних воздействий тело может не только покоиться, но и двигаться прямолинейно и равномерно.","При отсутствии внешнего воздействия тело может только покоиться. А для того, чтобы тело двигалось с постоянной скоростью, нужно, чтобы на него непрерывно действовало другое тело."],"explanations":["","Это формулировка закона инерции Ньютона, нуждающаяся в одном важном уточнении.","Это формулировка закона инерции Галилея.","Это формулировка закона инерции Аристотеля."],"answer":[0]}}}]}Инерциальные и неинерциальные системы отсчета
А теперь мы определим системы отсчета, в которых будет выполняться первый закон Ньютона. Их назвали инерциальными.
Какие системы отсчета называются инерциальными, а какие — неинерциальными?
Инерциальная система отсчета — это такая система отсчета, в которой выполняется закон инерции.
Неинерциальная система отсчета — это такая система отсчета, в которой закон инерции не выполняется.
В курсе 9 класса мы изучим новые законы движения и взаимодействия тел. Все они будут сформулированы для инерциальных систем отсчета. Поэтому, каждый раз применяя тот или иной закон для решения задачи, не забывайте выбрать такую систему отсчета, которую мы можем считать инерциальной!
К слову, не существует такой системы, которую мы бы могли назвать инерциальной для любых процессов, которые мы будем в ней рассматривать. Тем не менее, мы будем считать инерциальной гелиоцентрическую систему — в большинстве задач мы будем рассматривать движение тел относительно поверхности нашей планеты.
Но в некоторых случаях система отсчета, связанная с Землей, будет являться неинерциальной. Например, если мы будем рассматривать движение Земли относительно своей оси или относительно звезд, то это движение совершается с некоторым ускорением.
А система, которая движется с ускорением не может считаться инерциальной.
Также инерциальной системой отсчета мы можем называть такую систему, которая связана с покоящимся или движущимся прямолинейно и равномерно телом относительно поверхности земли.
Если же какая-то система отсчета движется с ускорением относительно инерциальной системы (например, поверхности земли), то такая система будет неинерциальной.
{"questions":[{"content":"Система отсчета, в которой не выполняется первый закон Ньютона (закон инерции), называется[[choice-18]]","widgets":{"choice-18":{"type":"choice","options":["неинерциальной","инерциальной","абсолютной","относительной"],"explanations":["","В инерциальных системах отсчета первый закон Ньютона выполняется. ","",""],"answer":[0]}}}]}
","",""],"answer":[0]}}}]}Упражнение
На столе в равномерно и прямолинейно движущемся поезде стоит легкоподвижный игрушечный автомобиль. При торможении поезда автомобиль без внешнего воздействия покатился вперед, сохраняя свою скорость относительно земли.
Выполняется ли закон инерции:
а) в системе отсчета, связанной с землей;
б) в системе отсчета, связанной с поездом, во время его прямолинейного и равномерного движения; во время торможения?
Можно ли в описанном случае считать инерциальной систему отсчета, связанную с землей; с поездом?
Посмотреть ответ
Скрыть
Ответ:
В системе отсчета, связанной с землей, закон инерции выполняется. Игрушечный автомобиль во время торможения поезда покатился вперед, сохраняя свою скорость относительно земли, хотя на него не действовали никакие дополнительные силы. Значит, систему отсчета, связанную с землей, мы можем считать инерциальной.
В системе отсчета, связанной с поездом, закон инерции выполнялся, пока поезд двигался равномерно и прямолинейно. Когда поезд начал тормозить, закон инерции перестал выполняться в этой системе отсчета. Такую систему отсчета мы можем назвать неинерциальной.
Часто задаваемые вопросы
Как движется тело, если на него не действуют другие тела?
Движется равномерно и прямолинейно или находится в состоянии покоя.
Чем отличаются взгляды Галилея от взглядов Аристотеля в вопросе об условиях равномерного движения тел?
Аристотель считал, что при отсутствии внешнего воздействия тело может только покоиться, а для того, чтобы тело двигалось с постоянной скоростью, на него непрерывно должно действовать другое тело.
Галилей же заявил о том, что при отсутствии внешних воздействий тело может не только покоиться, но и двигаться прямолинейно и равномерно.
Сила же, которую нужно прикладывать к телу для поддержания его движения, нужна лишь для того, чтобы уравновесить другие силы.
Как проводился опыт, изображенный на рисунке 3, и какие выводы из него следуют?
Тележка с двумя шариками (один лежит на горизонтальной поверхности, а другой подвешен на нити) двигается равномерно и прямолинейно относительно земли. Шарики находятся в состоянии покоя относительно тележки.
Когда тележка попадает на песчаную насыпь и начинает замедляться, шарики приходят в движении, хотя на них не действуют какие-то дополнительные силы.
Отсюда мы делаем вывод, что в системе отсчета, связанной с движущейся тележкой, закон инерции не выполняется. То есть этот закон справедлив не для всех систем отсчета.
Дайте современную формулировку первого закона Ньютона.
Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел компенсируются.
Какие системы отсчета называются инерциальными, а какие — неинерциальными?
Инерциальные системы отсчета — это такие системы отсчета, в который выполняется закон инерции. В неинерциальных системах отсчета закон инерции не выполняется.
2.2. Первый закон Ньютона
• Существуют такие системы отсчета, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если действие на них сил скомпенсировано. Это инерциальные системы отсчета (ИСО).
Современная формулировка первого закона Ньютона:
• существуют такие системы отсчета, в которых свободная частица (на которую не действуют никакие силы) движется неускоренно (т.е. прямолинейно и равномерно). Такие СО называются инерциальными, а движение свободной частицы в них – движением по инерции.
ИСО
существует бесконечное множество.
Любая
СО, движущаяся относительно некоторой
ИСО прямолинейно и равномерно, является
инерциальной, что вытекает из правила
сложения скоростей. Опытным путем
установлено, что СО, центр которой
совмещен с Солнцем, а оси направлены на
соответствующие звезды, является
инерциальной. Эта система называется
Земля движется относительно Солнца и звезд по криволинейной траектории, имеющей форму эллипса. Криволинейное движение всегда происходит с некоторым ускорением. Кроме того, Земля совершает вращение вокруг своей оси. Таким образом, СО, связанная с земной поверхностью, движется с ускорением относительно гелиоцентрической СО и не является инерциальной. Однако ее ускорение настолько мало, что в большом числе случаев ее можно считать практически инерциальной.
2.3. Преобразование координат Галилея
Рассмотрим две
СО: инерциальную К и систему К,
которая движется относительно К с постоянной скоростью
.
Будем считать, что в начальный момент
времениt=0 начало
координат системы К (т. О)
находится на удалении
от начала координатО системы К.
Тогда радиус-векторы любой частицы
массы m в моменты
времени t и t
в системах К и К связаны соотношениями
.
• Последнее преобразование ниоткуда не следует, а вводится как постулат классической механики: время абсолютно, т.е. не зависит от состояния движения и течет одинаково во всех СО. Пространство в классической механике также абсолютно.
Преобразования Галилея в координатной форме:
после дифференцирования по времени получим классическую формулу сложения скоростей:
или, как она была записана в кинематике:
• Все
ИСО движутся друг относительно друга
с постоянными скоростями.
2.4. Второй и третий законы Ньютона
• Скорость изменения импульса частицы в ИСО равна результирующей силе, действующей на частицу:
.
Следует иметь в виду, что второй закон Ньютона не является определениемсилы, он только устанавливает связь между кинематическими и динамическими величинами, позволяет найти траекторию частицы. Поэтому его называют уравнением движения частицы.
Т.к. m = const,
• Опыты показывают, что законы классической механики, а также следствия преобразований Галилея справедливы только для частиц или тел с достаточно большими массами, много большими масс атомов, которые движутся с малыми скоростями (по сравнению со скоростью света).
• Уравнения
движения классической динамики одинаковы
во всех ИСО, т.е. все ИСО эквивалентны
(равноправны) по отношению к механическим
явлениям.
• Третий закон Ньютона:
силы взаимодействия двух частиц равны по величине, противоположны по направлению и направлены по прямой, соединяющей частицы:
.
м2. Значение первого закона Ньютона – Основы физики
Исаак Ньютон сформулировал свой первый закон так
Каждое тело сохраняется в своем состоянии покоя или равномерного движения по прямой [прямой] линии, если оно не вынуждено изменить это состояние силами, наложенными на него.
При поверхностном рассмотрении этот закон кажется лишь частным случаем второго закона и вряд ли заслуживает отдельного описания. Если a ~ F (второй закон Ньютона) 2 , то в отсутствие силы нет ускорения (первый закон Ньютона). Почему же первый закон заслуживает отдельного утверждения как один из основных законов механики?
На этот вопрос можно дать несколько ответов, некоторые из них были оценены Ньютоном, другие являются результатом более поздних и более глубоких открытий.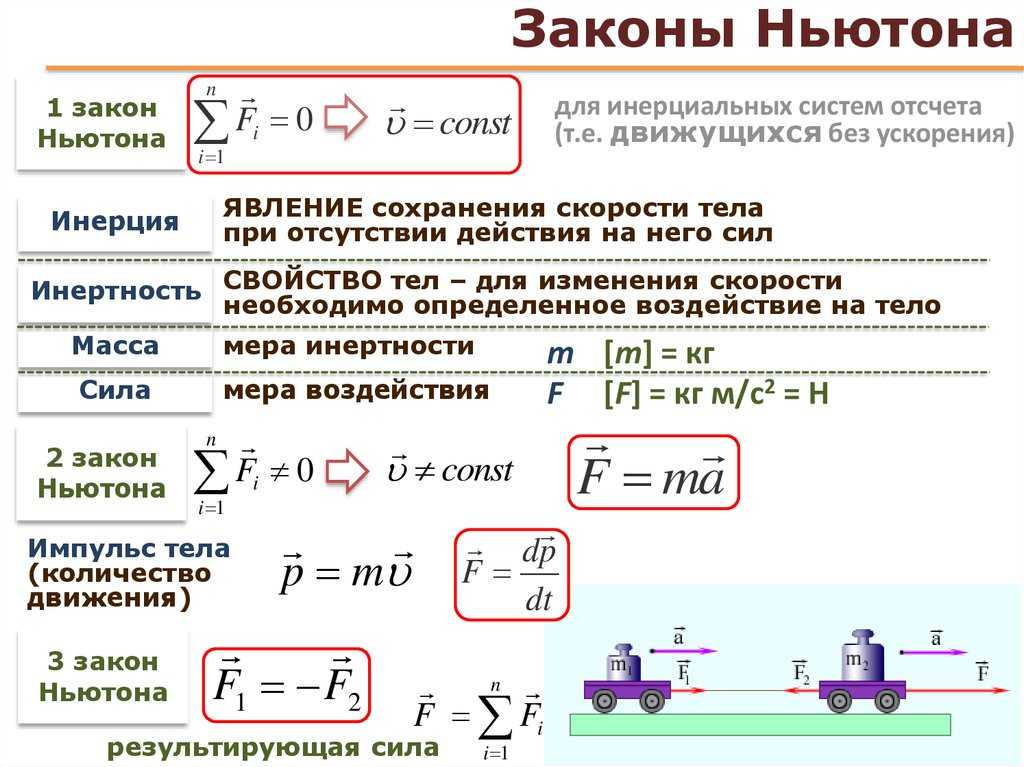
(1) Первый закон Ньютона определяет какое движение является «естественным» или невозмущенным движением, и тем самым определяет, какое движение требует дальнейшего объяснения. По Аристотелю, видимое круговое движение Солнца вокруг Земли не требует объяснения, потому что для небесных тел круговое движение является естественным движением. С другой стороны, утверждал Аристотель, продвижение стрелы вперед по воздуху требует ли объяснения с точки зрения какой-то движущей силы, потому что, по его мнению, «естественным» состоянием движения стрелы является состояние покоя или вертикального падения. 
(2) Существует современный взгляд на первый закон Ньютона, который делает его действительно независимым от второго закона, взгляд, который уже имплицитно присутствовал в размышлениях Ньютона о законах движения. Современное изложение первого закона можно сформулировать так: центр масс изолированной системы, свободной от внешних воздействий, движется с постоянной скоростью. Это утверждение содержит два улучшения по сравнению с исходным изложением закона Ньютоном 9.0003 4 Во-первых, он заменяет его слово «тело» на «центр масс». Не все части свободного тела движутся с постоянной скоростью; только его центр масс делает это. Во-вторых, в новой редакции закона вообще отсутствует понятие силы. Именно этот аспект нового утверждения существенно отличает его от оригинала. Как первоначально сформулировал Ньютон, первый закон предполагал, что сначала нужно знать, что такое сила, чтобы знать, когда ее нет. Сейчас предпочтительнее говорить об «изолированной системе, свободной от внешних воздействий».
Если рассматривать законы движения Ньютона с этой точки зрения, возникает разница между автомобилем, движущимся по прямой дороге с постоянной скоростью, и метеоритом, летящим с постоянной скоростью в глубинах пустого пространства. У автомобиля нет ускорения, потому что сумма всех сил, действующих на него, равна нулю. Его постоянная скорость просто иллюстрирует частный случай второго закона Ньютона. С другой стороны, метеорит напрямую иллюстрирует первый закон Ньютона. То, что оно должно иметь постоянную скорость, следует из его изолированности, даже если бы мы ничего не знали о силе или даже если бы сила была определена непоследовательно.
(3) История оправдала раздельную формулировку первого закона, чего Ньютон не мог предвидеть. Теперь мы знаем, что второй закон Ньютона перестает действовать в субмикроскопическом мире, управляемом квантовой механикой, и в мире высоких скоростей, управляемом теорией относительности; и что в современной физике понятие силы больше не играет центральной роли. С другой стороны, первый закон, по крайней мере когда он выражен в терминах количества движения, остается в силе, насколько нам известно, во всей природе. Его универсально верная формулировка такова: полный импульс изолированной системы, свободной от всех внешних воздействий, есть константа. В областях, где действует ньютоновская механика, постоянный полный импульс и постоянная скорость центра масс эквивалентны. Однако в теории относительности закон инерции может быть выражен только одним способом: через импульс. Поскольку закон сохранения импульса, современный эквивалент первого закона Ньютона, имеет огромное значение, мы можем сказать, что первый закон Ньютона — это не просто частный случай второго закона, а столп современной физики.
(4) Наконец, первый закон Ньютона важен тем, что он определяет инерциальные системы отсчета. Буквально верно, что ускорение объекта зависит от точки зрения. Говоря более техническим языком, это зависит от системы отсчета наблюдателя. Неподвижный объект, видимый ускоренным наблюдателем, кажется ускоренным. Ускоренный объект относительно сопровождающего его наблюдателя покоится. Эти факты означают, что изолированные системы являются неускоренными только для определенных наблюдателей. Системы отсчета этих наблюдателей называются инерциальными системами отсчета. Только в инерциальных системах отсчета действуют законы движения Ньютона.
1 Оригинал на латинице. Этот перевод сделан Эндрю Моттом и опубликован Даниэлем Ади в Нью-Йорке в 1846 году. . Скорее он формулирует второй закон просто как пропорциональность.
3 Аристотель представлял себе, как воздух перед стрелой разделяется, затем сливается за стрелой и толкает ее вперед.
4 Ньютон признал значение центра масс системы объектов; он назвал это центром тяжести.
5 Тонкости есть всегда! Центр масс системы перемещается свободно в отсутствие внешних воздействий только потому, что внутренние силы (действующие между частями системы) в сумме равны нулю — следствие третьего закона Ньютона . Таким образом, первый и третий законы связаны.
⇐ ПРЕДЫДУЩИЙ ОПИСАНИЕ | СЛЕДУЮЩЕЕ СОТРУДНИЧЕСТВО ⇒
ньютоновская механика – История толкования первого закона Ньютона
В настоящее время среди преподавателей физики, похоже, популярно представлять первый закон Ньютона как определение инерциальных систем отсчета и/или утверждение о том, что такие системы существуют. Это явно современная накладка. Вот оригинальное изложение закона Ньютоном (перевод Мотта):
Закон I. Всякое тело сохраняется в состоянии покоя или однородности. прямолинейное движение, если оно не вынуждено изменить это состояние приложенные к нему силы.
Далее текст продолжается:
Снаряды продолжают двигаться, пока не тормозится сопротивлением воздуха или толкается вниз сила притяжения. Вершина, части которой своим сцеплением вечно отклоняясь от прямолинейного движения, не прекращает своего вращения, иначе как тормозится воздухом. Большие органы планеты и кометы, встречая меньше сопротивления в более свободном пространстве, сохраняют свои движения как поступательные, так и круговые гораздо дольше время.
А потом прописан второй закон.
Здесь явно ничего о системе отсчета. На самом деле дискуссия настолько качественная и нематематическая, что многие современные учителя физики, вероятно, поставили бы на экзамене неправильную оценку.
У меня есть небольшая коллекция старых учебников по физике, и один из наиболее исторически влиятельных — «Элементы физики» Милликена и Гейла, 1927 г. (Милликен написал длинную серию учебников по физике с разными названиями.) Милликен и Гейл дают формулировка первого закона, которая читается как очень близкая парафраза перевода Мотта.
Нет упоминания о системах отсчета, инерциальных или иных.
Уважаемым и влиятельным современным учебником, нацеленным на гораздо более высокий уровень, чем книга Милликена, является «Введение в механику» Клеппнера и Коленкова 1973 года. K&K имеет это:
…всегда можно найти систему координат относительно какие изолированные тела движутся равномерно. […] Первый закон Ньютона движение есть утверждение, что инерциальные системы существуют. первый закон является частью определения и частью экспериментального факта. Изолированные тела двигаться равномерно в инерциальных системах в силу определения инерциальная система. Напротив, существование инерциальных систем является высказывание о физическом мире. Первый закон Ньютона увеличивает число вопросов, например, что мы подразумеваем под «изолированным телом», […]
На эту историко-образовательную тему есть статья: Галили и Цейтлин, «Первый закон Ньютона: текст, переводы, интерпретации и физическое образование», «Наука и образование».
Том 12, номер 1, 45–73, DOI: 10.1023/A:1022632600805. У меня был доступ к нему в свое время, и это казалось очень актуальным. К сожалению, сейчас это платный доступ. В аннотации, не защищенной платным доступом, указано:
.Обычно НФЛ интерпретируется как частный случай: тривиальный вывод из второго закона Ньютона. Некоторые продвинутые учебники заменяют НФЛ на модернизированное утверждение, которое отказывается от своего первоначального смысла.
Вопрос 1 : Кто-нибудь знает больше о том, когда учебники начали утверждать, что первый закон был констатацией определения и/или существования инерциальных систем отсчета?
Кажется, есть несколько возможных интерпретаций первого закона:
А. Ньютон сознательно записал законы движения в стиле аксиоматической системы, возможно, подражая Евклиду. Однако это лишь вопрос стиля. Очевидно, что первый закон является тривиальным выводом из второго закона. Ньютон представил его как отдельный закон лишь для того, чтобы подчеркнуть, что он работает в рамках Галилея, а не средневековой схоластики.
B. Представление Ньютоном первого и второго законов логически ошибочно, но Ньютон не смог добиться большего, потому что у него не было понятия инерциальной и неинерциальной систем отсчета. Современные авторы учебников могут сказать Ньютону: «Вот, исправил это для тебя».
C. Дать логически строгое изложение физики, описываемой первым и вторым законами, невозможно, поскольку гравитация является дальнодействующей силой, и, как указывает К&К, это вызывает проблемы при определении смысла изолированное тело. Лучшее, что мы можем сделать, это то, что в данной космологической модели, такой как ньютоновская картина бесконечной и однородной Вселенной, полной звезд, мы можем найти некоторую систему отсчета, такую как система «неподвижных звезд», которую мы хотим назвать инерционный. Другие системы отсчета, движущиеся относительно нее по инерции, также являются инерционными. Но это зависит от космологической модели. Впоследствии эта система может оказаться неинерциальной, если, например, мы узнаем, что наша галактика свободно падает во внешнем гравитационном поле, создаваемом другими массами.