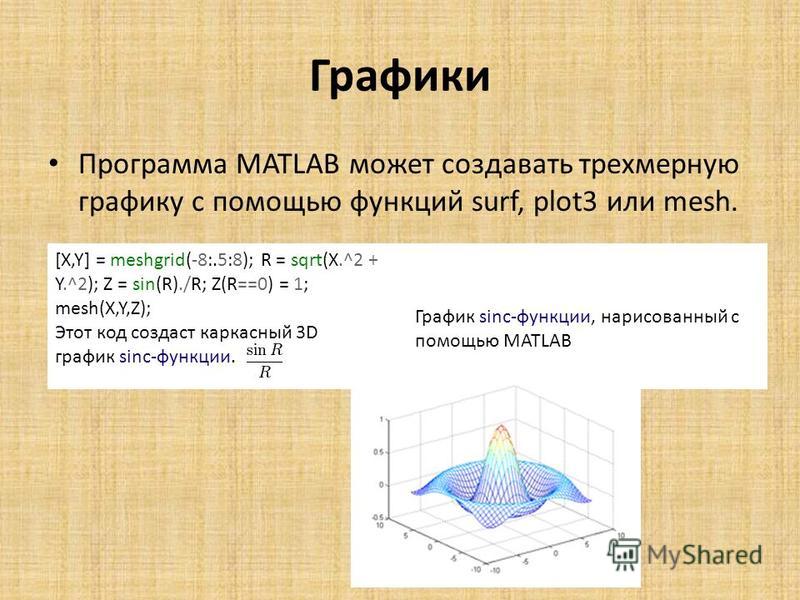
Математическая система MATLAB, создание функции пользователя y=f(x)
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Комсомольский-на-Амуре государственный
технический университет»
Электротехнический факультет
Кафедра «Промышленная электроника»
О Т Ч Е Т
по лабораторному практикуму № 1
по дисциплине «УвБС»
Математическая система MATLAB
Студент группы 0БМб-1
Преподаватель
Цель работы:
Ознакомится с математической средой MATLAB. Создать функцию
пользователя y=f(x), вычислить ее значение в точке x0 и построить график заданной функции.
Ход работы:
Создаем функцию пользователя следующим образом:
1. Вызываем окно редактора m-файлов путем нажатия кнопки New M-File (Создать m-файл).
2. Вводим строку: function Z=fun(x). Ключевое слово function объявляет новую функцию, имя которой expxp, а ее параметр – х. Символ Z определяет значение функции при аргументе x.
3. Задаем новую функцию (функцию пользователя): Z=exp(sqrt(sin(x)))-1.5
4. Сохраняем функцию пользователя на диске – кнопка Save (Сохранить).
5. Закрываем окно редактора m-файлов.
Теперь функция пользователя Z=exp(sqrt(sin(x)))-1.5 создана.
Для вычисления функции при данном аргументе x0=3,64 набираем имя функции и значение аргумента в
круглых скобках: Z=fun(3.64). На
экране получаем значение функции: Z = 0.
7296 + 0.6376i.
Рисунок 1 – Создание функции пользователя
Рисунок 2 – Значение функции в точке x0
Чтобы вывести график заданной функции зададим интервал [-5 ; 5]. Пишем исходный код программы:
>> x=-5:0.5:5; % задание промежутка
y=exp(sqrt(sin(x)))-1.5; % задание функции у
plot(x, y, [‘R’, ‘*’, ‘-.’]) % выведение графика красного цвета (R), точки в виде снежинок (*), линии штрихпунктирные (-.)
grid on % задание сетки
Рисунок 3 – Выполненная программа в окне команд
Получаем график, представленный на рисунке 4.
Рисунок 4 – График функции
Вывод:
выполнив практическую работу, мы познакомились с математической средой MATLAB,
научились писать простые программы на примере графического построения функции и
нахождения ее значение в указанной точке.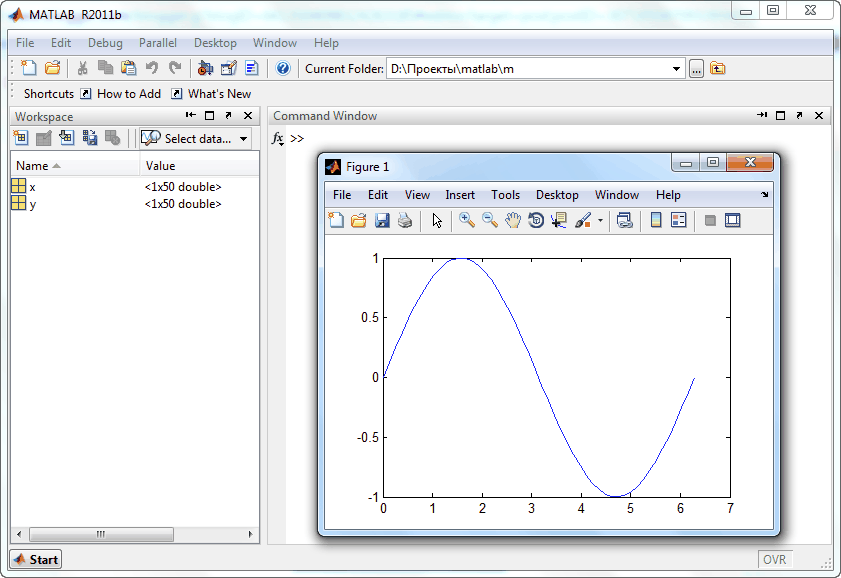
Функции с переменным числом аргументов MatLab
Урок 20. Основы программирования Основные понятия программирования
Основные средства программирования
Основные типы данных
Виды программирования
Двойственность операторов, команд и функций
Некоторые ограничения
М-файлы сценариев и функций
Структура и свойства файлов сценариев
Статус переменных в функциях
Структура М-файла-функции
Статус переменных и команда global
Частные каталоги
Обработка ошибок
Вывод сообщений об ошибках
Функция lasterr и обработка ошибок
Функции с переменным числом аргументов
Функции подсчета числа аргументов
Переменные varargin и varargout
Комментарии
Особенности выполнения m-файлов функций
Создание Р-кодов
Управляющие структуры
Диалоговый ввод
Условный оператор
Циклы типа for…end
Циклы типа while…end
Конструкция переключателя
Конструкция try.
..catch…endСоздание паузы в вычислениях
Понятие об объектно-ориентированном программировании
Проверка принадлежности объекта к заданному классу
Другие функции объектно-ориентированного программирования
Что нового мы узнали?
Функции подсчета числа аргументов
При создании функций со специальными свойствами весьма полезны две приведенные ниже функции:
nargin — возвращает число входных параметров данной функции;
nargout — возвращает число выходных параметров данной функции.
Обычный путь состоит в следующем — создаем функцию с именем sum2_5:
function f=sum2_5(x1,x2,x3,x4,x5) ;
f=x1^2+x2^2+x3^2+x4*2+x5^*2;
Теперь проверим ее в работе:
»
sum2_5(l,2.
2+x
В данной функции используется условный оператор i f…end, который будет детально описан далее. Но и без этого ясно, что благодаря применению функции nargin и условного оператора вычисления всякий раз идут по формуле с числом слагаемых, равным числу входных аргументов — от одного до пяти. Это видно из приведенных ниже примеров:
» sum2_5m(1)
ans =
1
» sum2_5m(1,2)
ans =
5
» sum2_5m( 1,2,3)
ans =
14
» sum2_5m(1,2,3,4)
ans =
30
» sum2_5m(1,2,3,4,5)
ans=
55
» sum2_5m(1,2,3,4,5,6)
??? Error using ==> sum2_5m
Too many input arguments.
Итак, при изменении числа входных параметров от 1 до 5 вычисления проходят корректно. При большем числе параметров выводится сообщение об ошибке. Этс уже действует встроенная в интерпретатор MATLAB система диагностики ошибок
Нравится
Твитнуть
Функция создания Matlab | Как создать и использовать функцию создания Matlab
Функция создания Matlab играет важную роль для реализации функции, поскольку имя функции и имя файла Matlab должны совпадать. Функция Matlab определяется как набор инструкций, которые выполняют определенные операции в Matlab, для функций требуется отдельный файл в Matlab. Это реализация, разделенная на три части: объявление функции, вызов функции и определение функции, означающей тело функции.
В объявлении функции мы объявляем имя функции, а затем объявляем, какие параметры будут работать внутри тела функции. В определении функции мы определяем функцию, здесь мы пишем фактическую логику программы и операторы, и последняя часть — это вызов функции, здесь мы просто вызываем функцию всякий раз, когда это необходимо.
Функция объявления Matlab Create Function может назначать несколько параметров, которые могут принимать несколько значений в качестве входных данных, и в определении функции может возвращать несколько значений или несколько аргументов. В Matlab есть различные функции, такие как анонимные функции, основные и подфункции, вложенные функции и частные функции. В приватной функции мы можем скрыть важные данные от нежелательных пользователей, поэтому приватные функции обеспечивают конфиденциальность кода.
Примеры и синтаксис
Ниже приведены следующие примеры и синтаксис:
Пример #1 – Простая функциональная программа
Предположим, что мы хотим решить одно математическое уравнение, и оно имеет вид )*32
Синтаксис:
имя переменной функции = имя функции (список параметров)
Определение функции (команды)
end
Следующая таблица представляет собой программную иллюстрацию приведенного выше примера 9.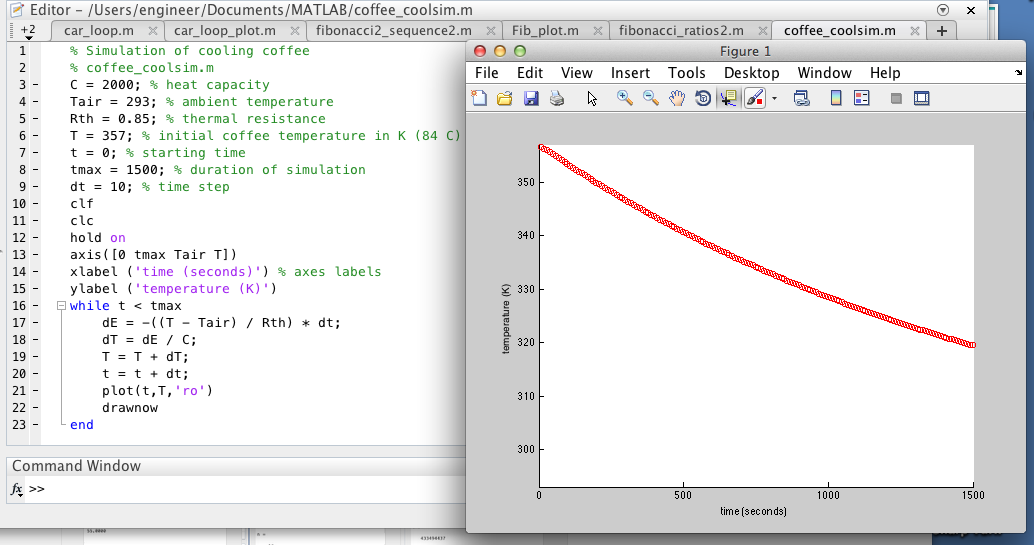
2 — log x
Чтобы решить вышеуказанную функцию, нам нужно создать анонимную функцию, а затем написать определение функции. Мы можем написать все операторы кода в командном окне.
Синтаксис:
Переменная дескриптора функции = @ входная переменная
Математическое уравнение (определение функции)
Переменная функции (значение входной переменной)
функция. 92–1 г (х)
р =
14,6137
Пример #3 – Подфункции
Если в программе более одной функции, то вторая функция называется подфункцией или основной функцией.
Синтаксис:
Функция = первое имя функции
Операторы (тело функции)
Конец
Функция = второе имя функции
Операторы
Конец
92– 4 * а1 * с1 );
end
файл хранится как quadratic.m
Пример #4 – Вложенные функции
Если вхождение какой-либо функции находится внутри другой функции, то она называется вложенной функцией.
Рассмотрим один пример. Есть две функции quadratic2 и quadratic1, здесь функция qudratic1 находится внутри функции quadratic2, поэтому она называется вложенной функцией.
Синтаксис:
Функция = имя основной функции (список параметров)
Функция = имя вложенной функции (список параметров)
Операторы (определение функции)
Конец
Конец
Следующая таблица иллюстрирует код Matlab и вывод пример 4 с использованием вложенной функции
| Окно редактора Matlab | Командное окно | Выход |
| >> квадратичный2 (45, 52, 38) | ан с = – 0,5778 + 0,7146 i |
Преимущества Matlab Create Function
Ниже описано несколько преимуществ.
- Основное преимущество функций в том, что они сохраняют программу организованной и позволяют избежать ненужных повторений.
- Разбивает длинные коды на более мелкие блоки.
- Мы можем повторно использовать код снова и снова, просто вызывая имя функции. Нет необходимости все время писать определение функции.
- Благодаря свойству повторного использования он экономит пространство, то есть память, и легко выполняет код.
- Мы можем легко управлять потоком управления, используя функции в программировании.
- Функции повышают удобочитаемость программирования.
- Изменения становятся легкими, если в программах присутствуют функции.
- Уменьшает количество ошибок.
- Уменьшает сложность программ.
Заключение
Основное свойство функций — повторное использование, потому что этот сложный код становится простым, поэтому программирование становится эффективным, если мы используем функции.
Объявить и определить любую функцию Matlab очень просто. Это повышает удобочитаемость программы, а также улучшает понимание программы.
Рекомендуемые статьи
Это руководство по функции Matlab Create. Здесь мы обсудим введение, различные примеры и синтаксис, а также преимущества. Вы также можете просмотреть другие рекомендуемые статьи, чтобы узнать больше –
- Цвета в Matlab
- Тепловая карта в MATLAB
- Диаграммы рассеяния в Matlab
- Комплексные числа в MATLAB
- Комета Matlab () | Шаги и методы
Краткое введение в создание функций в MATLAB — Techbytes
Ого, посмотрите на это! Наконец-то я собрался и написал статью в блоге о чем-то, что не является цифровым звуком! Не слишком волнуйтесь, это все еще будет статья о MATLAB, и, хотя я не собираюсь слишком углубляться в DSP, фундаментальные методы, описанные в этой статье, могут быть применены к широкому кругу задач.
А теперь позвольте мне заявить, что я не очень хороший программист.
Таким образом, если вы ищете руководство по функциональному программированию в целом, это место не для вас! Однако, если вы, возможно, студент-инженер, который изучал MATLAB в школе и, возможно, заинтересован в изучении возможностей этого языка, это хорошее место для начала. В качестве альтернативы, если вы знакомы с функциональными языками (*кашель* Python), эта статья может помочь вам начать переносить свои знания на новый язык.
Так что же такое функции?
Я уверен, что, в зависимости от того, кого вы спросите, существует множество определений того, что на самом деле представляет собой функция. Функции в MATLAB более или менее следуют стандартной модели системы сигналов и систем; это означает, что у них есть набор входов и соответствующий набор выходов. Вот и все, статья закончена, мы сделали это!
Шутки в сторону, больше нечего сказать о том, как функции используются в MATLAB; они превосходно просты. Однако функции в MATLAB обеспечивают большую гибкость, потому что они могут иметь столько входов и выходов, сколько вы выберете (и количество входов не обязательно должно совпадать с количеством выходов), а отношения между входами и выходами могут быть любыми.
Как создавать и использовать функции
Прежде чем вы начнете думать о функциях, вам понадобится сценарий MATLAB, в котором вы будете вызывать свои функции. Если вы знакомы с объектно-ориентированным языком (*кашель* Java), сценарий аналогичен вашему основному методу. Ниже я включил простой скрипт, в котором мы создаем два числа и отправляем их в функцию с именем
На самом деле не имеет значения, что делает noahFactorial, единственное, что здесь имеет значение, это то, что функция имеет два входа (здесь X и Y) и один выход (Z).
Наш фактический вызов функции noahFactorial происходит в строке 4. В этой же строке мы также присваиваем выходные данные noahFactorial переменной Z.
В строке 6 есть оператор печати, который выводит входные и выходные данные на консоль вместе с некоторыми текст.
Теперь, взглянув на noahFactorial, мы можем увидеть, как мы определяем и пишем функцию. Мы начинаем с написания «функции», а затем определяем вывод функции. Здесь выход — это всего лишь одна переменная, но если бы мы изменили «выход» на «[выход1, вывод2]», наша функция вернула бы массив 2 × 1, содержащий два выходных значения.
Некоторые из вас, более опытные программисты, могут заметить, что для «выходных данных» не указан тип данных. Это, несомненно, заставит некоторых из вас чувствовать себя некомфортно, но я обещаю, что все в порядке; MATLAB довольно хорошо знает, каким должен быть тип данных. Одним из преимуществ этого синтаксиса с большей невмешательством является то, что сам «выход» даже не обязательно должен быть одной переменной. Если вы можете отслеживать это, вы можете сделать «выход» массивом 2 × 1 и обрабатывать два значения как два отдельных вывода.
После того, как мы записали наши выходные данные, мы ставим знак равенства (как и следовало ожидать), пишем имя нашей функции и помещаем (в скобках) входные данные для нашей функции. Опять же, типизация входных данных довольно мягкая, поэтому они также могут быть массивами или отдельными значениями.
В целом объявление функции должно выглядеть так:
функция output = functionName(input)
или…
function [output1, output2, …, outputN] = functionName(input1, input2, …,inputM)
И еще раз повторюсь, N и M здесь не обязательно должны быть одинаковыми.
Оказавшись внутри нашей функции, мы можем делать все, на что способен MATLAB. В отличие от Java, операторы return не используются для отправки чего-либо на выход, а используются для остановки функции в ее следах. Обычно я назначаю вывод для сообщений об ошибках; если что-то пойдет не так, я присвою значение выходу ошибки и последую за ним с помощью «return». Это отправляет обратно сообщение об ошибке и останавливает функцию в операторе return.
Итак, если мы не используем операторы возврата, то как мы будем отправлять значения на выход? Мы убеждаемся, что в нашей функции у нас есть переменные с тем же именем, что и выходы. Мы присваиваем этим переменным значения в функции. В последней строке функции, когда функция завершается, какими бы ни были значения в выходных переменных, эти значения отправляются на выход.
Например, если мы определяем выход с именем X и где-то в нашей функции мы напишем «X=5;» и не изменим значение X до завершения функции, выход X будет иметь значение: 5. Если мы сделаем то же самое, но позже добавим еще одну строку кода в функцию, которая говорит «X=6;», то возвращаемое значение X будет: 6. Удобно и просто.
… И это так просто. Что мне действительно нравится в функциях, так это то, что они не должны быть связаны со сценарием или с объектом, вы можете просто создать их и использовать. Кроме того, если вы обнаружите, что вам нужно часто выполнять какую-то математическую операцию, напишите одну функцию и используйте ее с любым количеством различных сценариев! Эта безумная гибкость позволяет использовать некоторые безумные возможности решения проблем.