Что такое спин в квантовой физике простыми словами: бозоны, фермионы, момент импульса
Итак, полностью абстрагируемся и забываем любые классические определения. Ибо спин – это понятие, присущее исключительно квантовому миру. Попробуем разобраться в том, что это такое.
Больше полезной информации для учащихся – у нас в телеграм.
Спин и момент импульса
Спин (от английского spin – вращаться) – собственный момент импульса элементарной частицы.
Теперь вспомним, что такое момент импульса в классической механике.
Момент импульса – это физическая величина, характеризующая вращательное движение, точнее, количество вращательного движения.
В классической механике момент импульса определяется как векторное произведение импульса частицы на ее радиус вектор:
По аналогии с классической механикой спин характеризует вращение частиц.
Однако данное вращение нельзя трактовать классически. Все частицы помимо спина обладают внешним или орбитальным моментом импульса, характеризующим вращение частицы относительно какой-то точки. Например, когда частица движется по круговой траектории (электрон вокруг ядра).
Спин же является собственным моментом импульса, то есть характеризует внутреннее вращательное состояние частицы вне зависимости от внешнего орбитального момента импульса. При этом
Представить, что же там вращается внутри частицы, невозможно. Однако факт остается фактом – для заряженных частиц с разнонаправленными спинами траектории движения в магнитном поле будут различны.
Спиновое квантовое число
Для характеристики спина в квантовой физике введено спиновое квантовое число.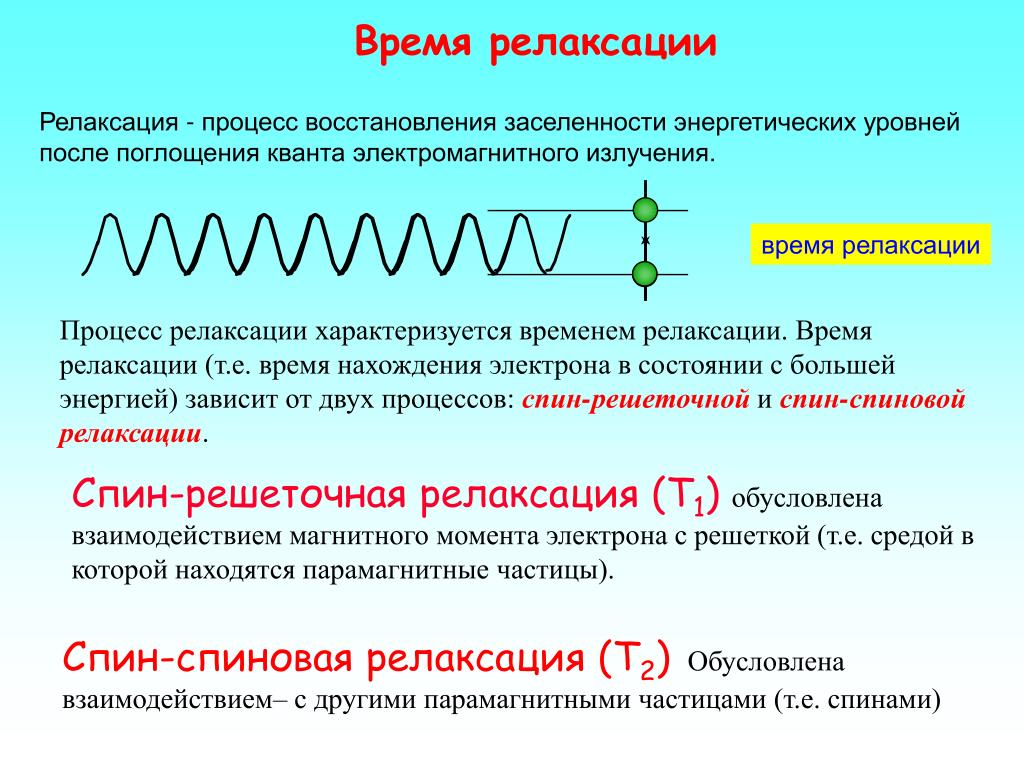
Спиновое квантовое число – одно из квантовых чисел, присущих частицам. Часто спиновое квантовое число называют просто спином. Однако следует понимать, что спин частицы (в понимании собственного момента импульса) и спиновое квантовое число – это не одно и то же. Спиновое число обозначается буквой
Бозоны и фермионы
Разным частицам присущи разные спиновые числа. Так, главное отличие состоит в том, что одни обладают целым спином, а другие – полуцелым. Частицы обладающие целым спином называются бозонами, а полуцелым – фермионами.
Бозоны подчиняются статистике Бозе-Эйнштейна, а фермионы – Ферми-Дирака. В ансамбле частиц, состоящем из бозонов, любое их количество может находиться в одинаковом состоянии. С фермионами все наоборот – наличие двух тождественных фермионов в одной системе частиц невозможно.
Бозоны: фотон, глюон, бозон Хиггса.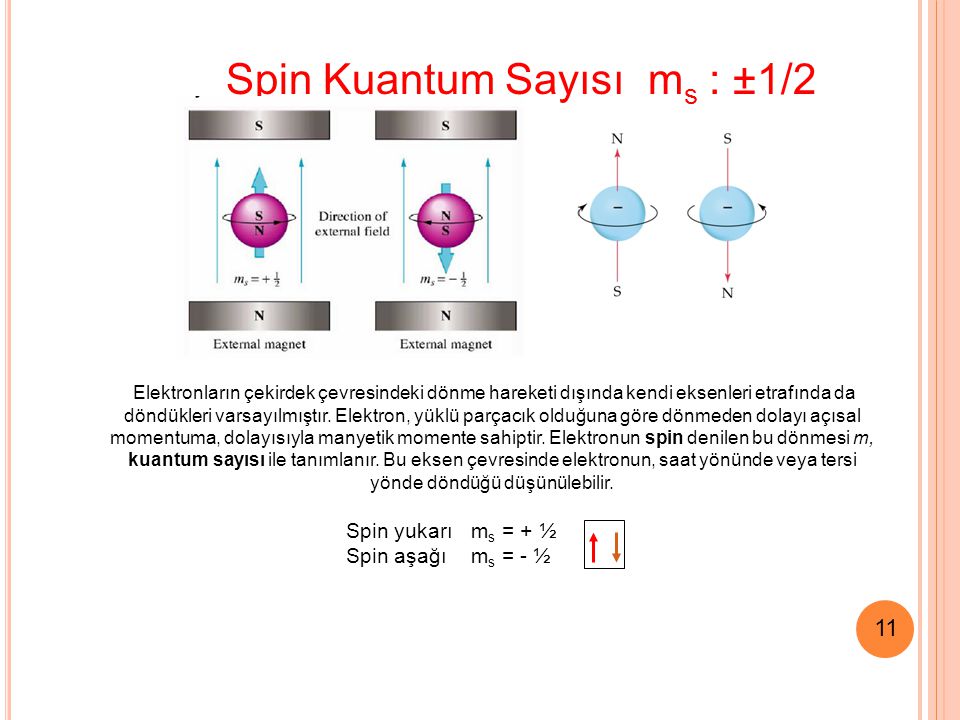
Подробнее о бозоне Хиггса – в отдельной статье.
Фермионы: электрон, лептон, кварк
Попробуем представить, чем отличаются частицы с разными спиновыми числами на примерах из макромира. Если спин объекта равен нулю, то его можно представить в виде точки. Со всех сторон, как ни вращай этот объект, он будет одинаков. При спине равном 1 поворот объекта на 360 градусов возвращает его в состояние, идентичное первоначальному состоянию.
Например, карандаш, заточенный с одной стороны. Спин равный 2 можно представить в виде карандаша, заточенного с двух сторон – при повороте такого карандаша на 180 градусов мы не заметим никаких изменений. А вот полуцелый спин равный 1/2 представляется объектом, для возвращения которого в первоначальное состояние нужно соверщить оборот в 720 градусов. Примером может служить точка, движущаяся по листу Мебиуса.
Итак, спин – квантовая характеристика элементарных частиц, которая служит для описания их внутреннего вращения, момент импульса частицы, не зависящий от ее внешних перемещений.
Надеемся, что вы осилите эту теорию быстро и сможете при случае применить знания на практике. Ну а если задачка по квантовой механике оказалось непосильно сложной или не можете не забывайте о студенческом сервисе, специалисты которого готовы прийти на выручку. Учитывая, что сам Ричард Фейнман сказал, что “в полной мере квантовую физику не понимает никто”, обратиться за помощью к опытным специалистам – вполне естественно!
Спин
СПИН
Spin
Спин (от англ. spin
– вращаться) – собственный момент количества движения элементарной частицы,
имеющий квантовую природу и не связанный с её перемещением в пространстве
как целого. Спин отвечает неотъемлемому и неизменному внутреннему вращательному
состоянию, присущему частице, хотя это вращательное состояние нельзя трактовать
классически – как вращение тела вокруг собственной оси. Наряду со спином,
любая частица, перемещаясь как целое в пространстве (например, по замкнутой
орбите) относительно некой внешней точки (центра орбиты), имеет относительно
этой точки внешний или орбитальный момент количества движения.
Спин был первоначально введен для того, чтобы объяснить экспериментально наблюдаемый факт, что многие спектральные линии в атомных спектрах состоят из двух отдельно расположенных линий. Например, первая линия серии Бальмера в атоме водорода, которая проявляется при переходах между уровнями с n = 3 и n = 2, должна наблюдаться как одиночная линия с длиной волны λ = 6563 Å, однако на самом деле наблюдались две линии с расстоянием между ними Δλ = 1.4Å. Это расщепление первоначально связывалось с еще одной дополнительной степенью свободы электрона – вращением. Предполагалось, что электрон можно рассматривать как классический вращающийся волчок, и величина спин связывалась с его характеристикой вращения. На самом деле, как выяснилось позже, спин имеет квантовую природу и не связан с какими-либо перемещениями частицы в пространстве. Величина вектора спина равна ћ[s(s + 1)]
е. характерное для каждой частицы
полуцелое или целое положительное число (оно может быть и нулевым). Частицы
с целым спином называются бозонами, с полуцелым – фермионами.Переносчики взаимодействий γ-квант, W±-, Z-бозоны и 8 глюонов имеют спин s = 1 и являются бозонами. Лептоны e, μ, τ, νe, νμ, ντ, кварки u, d, s, c, b, t имеют спин s = 1/2 и являются фермионами.
Понятие спина применяют и к сложным, составным микрообъектам – атомам, атомным ядрам, адронам. В этом случае под спином J понимают момент количества движения микрообъекта в состоянии покоя, т.е. когда орбитальный (внешний) момент количества движения микрообъекта = 0. Спины составных микрообъектов являются векторной суммой спиновых и орбитальных моментов входящих в их состав частиц – ядра и электронов в случае атома, протонов и нейтронов в случае ядра, кварков и глюонов в случае протона, нейтрона и других адронов. Спин частицы однозначно связан со статистикой, которой подчиняется ансамбль частиц с данным спином.
См. также
Спин электрона
Определение 1
Спин электрона (и других микрочастиц) — это квантовая величина, у которой нет классического аналога. Это внутреннее свойство электрона, которое можно уподобить заряду или массе. Понятие спина было предложено американскими физиками Д. Уленбеком и С. Гаудсмитом для того, чтобы объяснить существование тонкой структуры спектральных линий. Ученые предположили, что электрон имеет собственный механический момент импульса, который не связан с движением электронам в пространстве который был назван спином.
Если считать, что электрон имеет спин (собственный механический момент импульса (${\overrightarrow{L}}_s$)), то значит должен иметь собственный магнитный момент (${\overrightarrow{p}}_{ms}$). В соответствии с общими выводами квантовой физики спин квантуется как:
Помощь со студенческой работой на тему
Спин электрона
где $s$ — спиновое квантовое число.
Проводя аналогию с механическим моментом импульса, проекция спина ($L_{sz}$) квантуется таким образом, что число ориентаций вектора ${\overrightarrow{L}}_s$ равно $2s+1.$ В опытах Штерна и Герлаха ученые наблюдали две ориентации, то $2s+1=2$, следовательно, $s=\frac{1}{2}$.
При этом проекция спина на направление внешнего магнитного поля определена формулой:
где $m_s=\pm \frac{1}{2}$-магнитное спиновое квантовое число.
Получилось, что экспериментальные данные привели к необходимости введения дополнительной внутренней степени свободы. Для полного описания состояния электрона в атоме необходимы: главное, орбитальное, магнитное и спиновое квантовые числа.
Позднее Дирак показал, что наличие спина следует из полученного им релятивистского волнового уравнения.
Атомы первой валентной группы периодической системы имеют валентный электрон, находящийся в состоянии с $l=0$. При этом момент импульса всего атома равен спину валентного электрона. Поэтому когда обнаружили для подобных атомов, пространственное квантование момента импульса атома в магнитном поле это стало доказательством существования спина только двух ориентаций во внешнем поле.
Спиновое квантовое число, отличаясь от других квантовых чисел, является дробным. Количественную величину спина электрона можно найти в соответствии с формулой (1):
Для электрона имеем:
Иногда говорят, что спин электрона ориентирован по направлению или против направления напряженности магнитного поля. Такое высказывание является неточным. Так как при этом на самом деле имеется в виду направление его составляющей $L_{sz}.$
Из опытов Штерна и Герлаха получено, что $p_{ms_z}$ (проекция собственного магнитного момента электрона) равна:
где ${\mu }_B$ — магнетон Бора.
Найдем отношение проекций $L_{sz}$ и $p_{ms_z}$, применяя формулы (4) и (5), имеем:
Выражение (6) называют спиновым гиромагнитным отношением. Оно в два раза превышает орбитальное гиромагнитное отношение. В векторной записи гиромагнитное отношение записывают как:
Опыты Эйнштейна и де Гааза определили спиновое гиромагнитное отношение для ферромагнетиков. Это дало возможность определить спиновую природу магнитных свойств ферромагнетиков и получить теорию ферромагнетизма.
2.$
полуцелый спин – это… Что такое полуцелый спин?
- полуцелый спин
half-integer spiwn
Большой англо-русский и русско-английский словарь. 2001.
- полуцелый ранг
- полуцепное кольцо
Смотреть что такое “полуцелый спин” в других словарях:
полуцелый спин — pusinis sukinys statusas T sritis fizika atitikmenys: angl. half integral spin vok. halbzahliger Spin, m rus. полуцелый спин, m pranc. spin demi entier, m … Fizikos terminų žodynas
СПИН — собственный момент импульса элементарной частицы или системы, образованной из этих частиц, напр. атомного ядра. Спин частицы не связан с её движением в пространстве и не может быть объяснён с позиций классической физики он обусловлен квантовой… … Большая политехническая энциклопедия
СПИН — (от англ.
spin вращаться, вертеться) собств. момент импульса элементарной частицы или системы, образованной этими частицами (напр., атомного ядра). С. частицы имеет квантовую природу, он не связан с движением частицы в пространстве и не может… … Большой энциклопедический политехнический словарьКлассификация элементарных частиц — Это список частиц в физике элементарных частиц, включающий не только открытые, но и гипотетические элементарные частицы, а также составные частицы, состоящие из элементарных частиц. См. также «Хронология открытий элементарных частиц» … … Википедия
Список частиц — Это список частиц в физике элементарных частиц, включающий не только открытые, но и гипотетические элементарные частицы, а также составные частицы, состоящие из элементарных частиц. Содержание 1 Элементарные частицы 1.1 Стандартная модель … Википедия
Уравнение Дирака — релятивистски инвариантное уравнение движения для би спинорного классического поля электрона, применимое также для описания других точечных фермионов со спином 1/2; установлено П.
Дираком в 1928. Содержание 1 Вид уравнения 2 Физический смысл … ВикипедияДирака уравнение — Уравнение Дирака квантовое уравнение движения электрона, удовлетворяющее требованиям теории относительности, применимое также для описание других точечных фермионов со спином 1/2; установлено П. Дираком в 1928. Содержание 1 Вид уравнения 2… … Википедия
Квантовая жидкость — жидкость, свойства которой определяются квантовыми эффектами. Примером К. ж. является жидкий гелий при температуре, близкой к абсолютному нулю. Квантовые эффекты начинают проявляться в жидкости при достаточно низких температурах, когда… … Большая советская энциклопедия
Квантовая теория поля — Квантовая теория поля квантовая теория систем с бесконечным числом степеней свободы (полей физических (См. Поля физические)). К. т. п., возникшая как обобщение квантовой механики (См. Квантовая механика) в связи с проблемой описания… … Большая советская энциклопедия
ЧАСТИЦЫ ЭЛЕМЕНТАРНЫЕ — Состав материи невероятно прост.
Вся видимая материя во Вселенной на Земле и в космосе состоит из фундаментальных частиц трех разных видов: электронов и двух типов кварков. Эти три частицы (как и другие описываемые ниже) взаимно притягиваются и… … Энциклопедия КольераНЕЙТРИНО — (v), лёгкая (возможно, безмассовая) электрически нейтральная ч ца со спином 1/2 (в ед. ћ), участвующая только в слабом и гравитац. вз ствиях. Н. принадлежит к классу лептонов, а по статистич. св вам явл. фермионом. Известны три типа Н.:… … Физическая энциклопедия
spin вращаться, вертеться) собств. момент импульса элементарной частицы или системы, образованной этими частицами (напр., атомного ядра). С. частицы имеет квантовую природу, он не связан с движением частицы в пространстве и не может… … Большой энциклопедический политехнический словарь
Дираком в 1928. Содержание 1 Вид уравнения 2 Физический смысл … Википедия
Вся видимая материя во Вселенной на Земле и в космосе состоит из фундаментальных частиц трех разных видов: электронов и двух типов кварков. Эти три частицы (как и другие описываемые ниже) взаимно притягиваются и… … Энциклопедия КольераСпин (физика) – это… Что такое Спин (физика)?
Спин-орбитальное взаимодействие — Спин орбитальное взаимодействие в квантовой физике взаимодействие между движущейся частицей и её собственным магнитным моментом, известным как спин. Наиболее часто встречающимся примером такого взаимодействия является взаимодействие… … Википедия
ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф.
наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия
ФИЗИКА — наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, св ва и строение материи и законы её движения. Понятия Ф. и её законы лежат в основе всего естествознания. Ф. относится к точным наукам и изучает количеств … Физическая энциклопедия
Спин-разрушающее столкновение — Спин разрушающее столкновение в атомной физике столкновение атомов, при котором необратимо перемешиваются орбитальные моменты валентных электронов сталкивающихся атомов. В атомных парах иногда происходит столкновения атомов с друг другом.… … Википедия
Физика — I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения.
Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия
Спин-спиновое взаимодействие — взаимодействие между спиновыми магнитными моментами микрочастиц (см. Спин). Это взаимодействие является релятивистским эффектом (оно содержит множитель 1/с2, где с Скорость света). Вследствие этого С. с. в. мало по сравнению с… … Большая советская энциклопедия
Изотопический спин — Аромат в физике элементарных частиц п·Ароматы и квантовые числа: Лептонное число … Википедия
ЯДЕРНАЯ ФИЗИКА — раздел физики, посвящённый изучению структуры ат. ядра, процессов радиоактивного распада и механизма яд. реакций. К Я. ф. иногда относят также физику элементарных ч ц. Иногда разделами Я. ф. продолжают считать направления исследований, ставшие… … Физическая энциклопедия
ИЗОТОПИЧЕСКИЙ СПИН — (изоспин, I), одна из внутр. хар к (квант. чисел) адронов, определяющая число зарядовых состояний адрона (или число ч ц n в изотопич.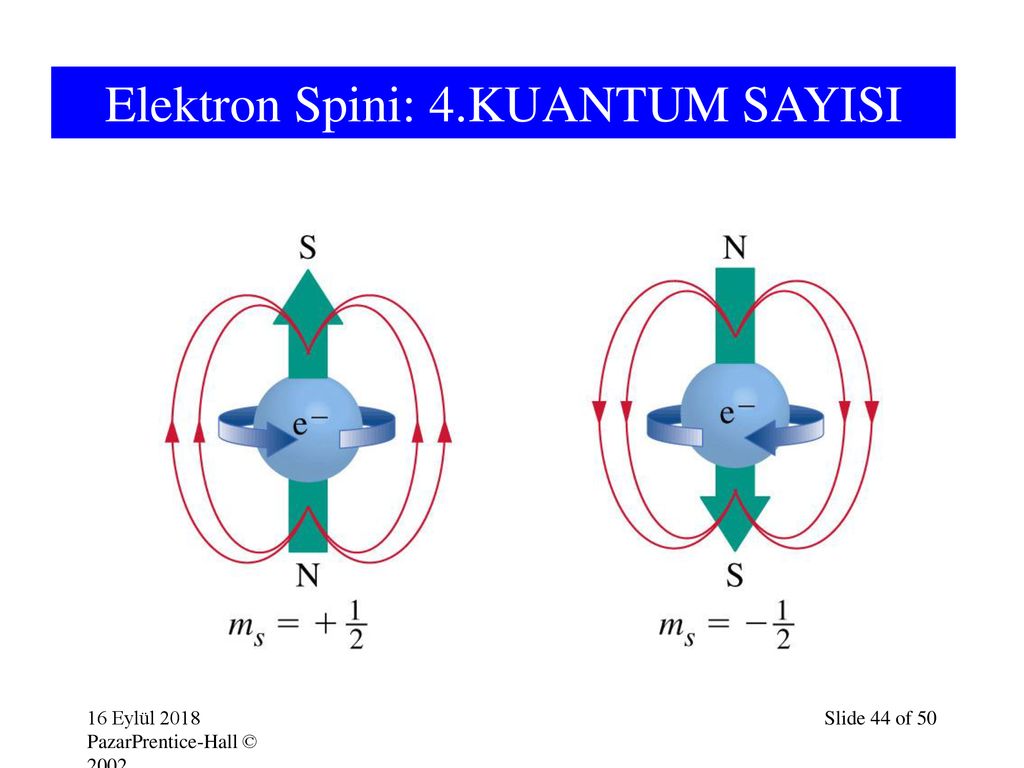
мультиплете): n=2I+1. (см. ИЗОТОПИЧЕСКАЯ ИНВАРИАНТНОСТЬ). Физический энциклопедический словарь. М.: Советская… … Физическая энциклопедия
Негатрон (физика) — Электрон Символ Масса 9,10938215(45)×10−31кг, 0,510998910(13) МэВ/c2 Античастица позитрон Классы фермион, лептон … Википедия
Так из чего всё-таки складывается спин протона?
Из чего складывается спин протона? Теоретическое обсуждение этого вопроса сопровождалось последние несколько лет нешуточными страстями, причем касалась полемика не столько ответа, сколько смысла этого вопроса. Вышедший на днях обзор попытался навести порядок в этой неразберихе.
Как уже подчеркивалось на «Элементах» (см. Детектор ALICE изучает тонкие эффекты в рождении адронов, 02.08.2013), в современной физике элементарных частиц есть разные типы трудных вопросов. Обычно внимание публики приковано к поиску новых частиц или экзотических явлений, но для самих физиков не менее интересными и трудными являются вопросы о сложном устройстве некоторых обычных частиц, например, протонов.
Главная проблема тут заключается не в том, из чего протоны состоят, а в том, как наблюдаемые характеристики протонов возникают из свойств составляющих его частиц.
Разговор о строении протона включает в себя много отдельных вопросов, каждый из которых сам по себе сложен. Этот рассказ посвящен одному из них — вопросу о том, как возникает спин протона. На первый взгляд, ситуация здесь похожа на большинство других вопросов в физике элементарных частиц: есть много экспериментальных данных, есть много теоретических работ, есть какие-то спорные моменты или необъясненные пока данные. В общем, этакая рутина в физике частиц. Но не так всё просто.
Лет пять назад теоретики вдруг резко активизировались. Пошла лавина публикаций по этому вопросу, и, в буквальном смысле слова, стали накаляться страсти. Появлялись новые статьи, комментарии к статьям, возражения к комментариям, опровержения возражений к комментариям и так далее. И вот что интересно: причиной такого всплеска стали вовсе не новые экспериментальные данные (это было бы понятно), а именно теоретические статьи! Вдруг оказалось, что некий нерешенный вопрос, над которым физики давно работали, но саму формулировку которого все они вроде бы хорошо понимали, — вот этот вопрос переворачивается с ног на голову.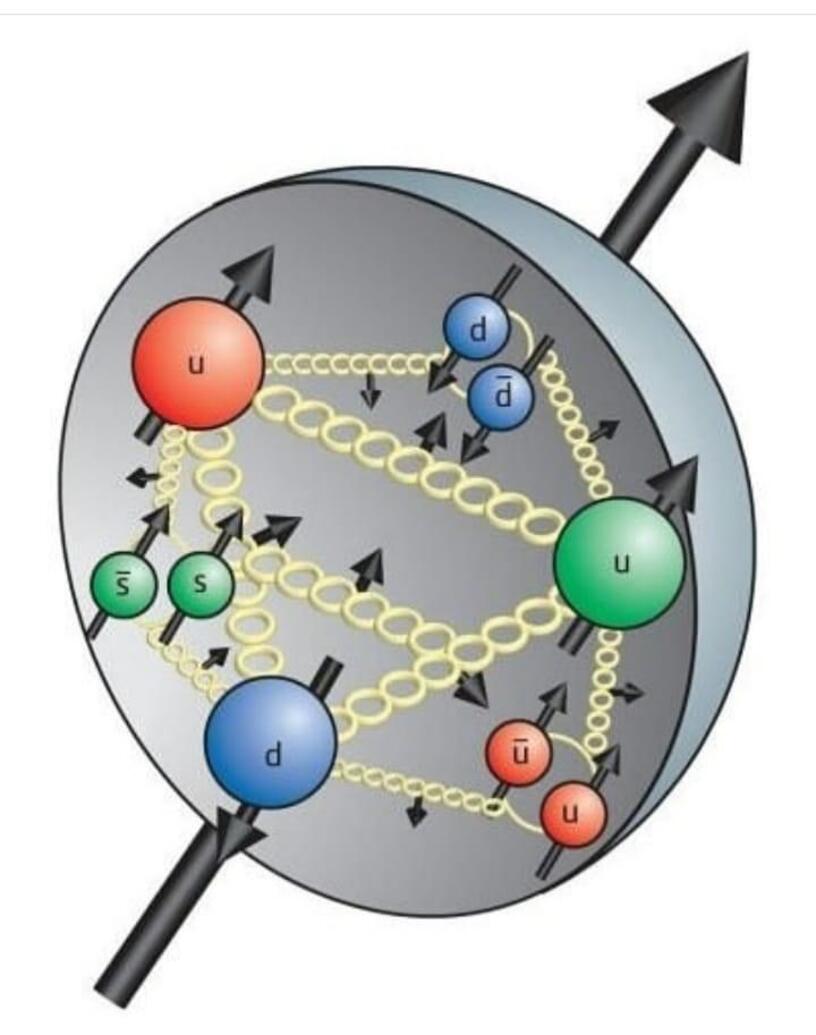
По сути, физики стали бурно спорить уже не столько о решении, сколько о смысле этого вопроса. И со стороны могло показаться, что с каждой новой статьей, с каждым новым аргументом ситуация эта только запутывается.
На днях в архиве е-принтов появился основательный обзор, в котором сделана попытка привести эту ситуацию в порядок, систематизировать полученные за последние годы результаты и направить этот спор в более конструктивное русло. Заголовок статьи говорит сам за себя: «Полемика вокруг углового момента: о чём же, собственно, спор и имеет ли он значение?»
Конечно, эта тема сложная и сам обзор полон технических деталей. Однако вопрос кажется очень интересным и злободневным, да и сама ситуация, которая сейчас сложилась вокруг него, несколько необычна. Поэтому мы рискнем рассказать о некоторых важных, но не слишком сложных аспектах этой проблемы. Даже если детали окажутся непонятными, этот рассказ можно просто воспринимать как иллюстрацию того, какого типа вопросы иногда обсуждаются в современной физике элементарных частиц.
Загадка протонного спина — стандартная версия
Что значит слово «состоит»?
Жизненный опыт говорит нам, что если сложный материальный объект состоит из более простых, то вот это понятие — «состоит» — является абсолютным, не зависящим от точек зрения или условий наблюдения. То же самое работает и в физике вплоть до отдельных атомов. Например, молекула кислорода O2 состоит из двух атомов — и никакого плюрализма мнений относительно этого факта быть не может. Та же самая абсолютность касается и физических характеристик системы, но с одним маленьким изменением. Скажем, полная энергия этой молекулы складывается из энергий покоя каждого атома и энергии их взаимодействия. И хотя эту энергию взаимодействия нельзя разбить на две части и отнести каждую половинку к отдельному атому, всё равно можно сказать, что энергия взаимодействия — это «отдельная строчка» в энергетическом балансе молекулы, и ее невозможно спутать с энергией покоя атомов.
Немножко шокирующей новостью после всего этого может стать утверждение, что в физике элементарных частиц понятие «состоит» становится относительным.
Состав сложной частицы, оказывается, кардинально зависит от того, из какой системы отсчета мы смотрим на частицу. Самый подходящий для нас пример — протон. Если мы смотрим на протон из его системы покоя, то можно сказать, что он состоит из трех кварков, которые скреплены сильным взаимодействием. Многие физические характеристики протона и других адронов получаются путем простого комбинирования характеристик кварков, иногда с добавлением скрепляющего их силового поля.
Но если на тот же протон взглянуть из системы отсчета, где он движется со скоростью, очень близкой к скорости света, то он уже будет казаться состоящим вовсе не из трех кварков, а из большого числа кварков, антикварков и глюонов, летящих рядом (рис. 2). Сколько их — сказать нельзя, как минимум потому что это число не фиксировано, а зависит от системы отсчета наблюдателя. Заметьте, мы с самим протоном ничего не делаем, он остается тем же самым объектом, что и раньше. Мы просто смотрим на него по-другому, из другой системы отсчета.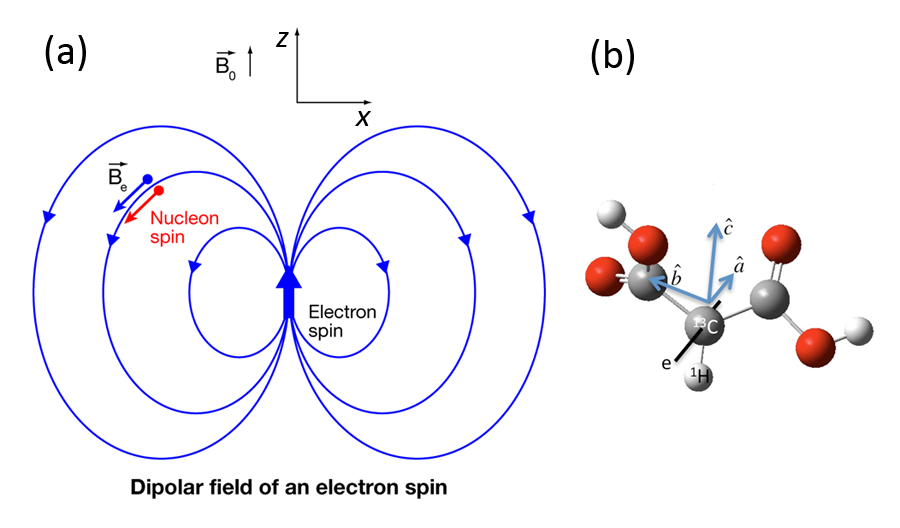
Как такое вообще может быть? Оказывается, это прямое следствие квантовой теории поля — той (единственно работающей пока!) картины квантовых процессов при околосветовых скоростях, которую дает нам современная физика. Силовые поля в ней обеспечиваются обменом частицами — квантами силовых полей. Скажем, электромагнитное взаимодействие получается из-за обмена фотонами, сильное взаимодействие между кварками — из-за обмена глюонами. В системе покоя эти фотоны или глюоны виртуальные, они не могут свободно летать, они не похожи на реальные частицы. Однако в системе отсчета, в которой весь протон пролетает мимо нас с околосветовой скоростью, эти глюоны по своим характеристикам почти не отличаются от частиц материи. И те, и другие являются «комочками полей» разного типа, несущими энергию, импульс и другие характеристики. И те, и другие считаются полноправными составными частями протона. Более развернутый рассказ на эту тему см. в популярной статье Многоликий протон.
Из чего складывается спин протона?
Теперь перейдем непосредственно к спину протона.
Протон относится к фермионам, он имеет спин 1/2. Поскольку протон является составной частицей, его спин должен как-то возникать из характеристик составных частей. С неподвижным протоном всё просто: три кварка, тоже со спинами Sq = 1/2, но направленными в разные стороны, складываются так, чтобы их спины частично компенсировались и в сумме получилось снова 1/2 (см. рис. 1, слева). В принципе, кварки могли бы двигаться внутри протона, как это делают многие электроны в атоме, и тогда появился бы новый источник для протонного спина — орбитальный угловой момент Lq. Но, к счастью, для покоящегося протона всё просто: орбитальный угловой момент кварков равен нулю.
Очень хорошо. А как обстоит дело с быстро летящим протоном? Помня про то, что силовое глюонное поле теперь является полноправной частью протона, надо честно сказать, что спин протона должен складываться из всех возможных источников (рис. 1, справа). Теперь и кварки, и глюоны могут давать вклад в спин поляризованного протона, причем как за счет своего собственного, «личного» спина, (Sq и Sg), так и за счет возможного орбитального углового момента (Lq и Lg):
Sq + Lq + Sg + Lg = 1/2
И вот вокруг этого простого разложения уже 30 лет ведутся ожесточенные бои!
В чём тут, собственно, проблема? Сначала надо упомянуть одну важную тонкость.
Выше уже было сказано, что кварков и глюонов в протоне очень много; все они несут разные доли полного импульса протона и ориентированы немножко по-разному (см. рис. 1, справа). Поэтому величина Sq в написанном выше выражении — это вовсе не спин одного кварка, а усредненное значение этого спина по всем кваркам. Аналогично и для других величин: все они представляют собой не характеристики отдельных частиц, а их усредненные значения. Кроме того, написанная выше формула относится не к полным векторам спина или орбитального момента, а к их проекциям на ось движения протона (именно поэтому все стрелочки на рис. 1 направлены в одну сторону, они показывают проекцию).
Кажется вполне естественным, что средний спин кварков всё равно получится близким к 1/2, также как и для покоящегося протона. Всё-таки мы сам протон не трогаем, мы просто переходим из одной системы отсчета в другую. Поэтому первоначальное ожидание физиков было простое: в написанной выше формуле почти вся половинка происходит из величины Sq, а остальные слагаемые будут если и не нулевые, то довольно маленькие.
Экспериментальные данные
А теперь — экспериментальные данные. Спин протона мы можем измерить напрямую, но как измерить спины или орбитальный момент кварков или глюонов по отдельности? Это очень непростая задача, ведь свойства кварков и глюонов можно почувствовать только косвенно, по характеристикам процесса столкновения протонов друг с другом или с электронами. В 1988 году коллаборация EMC в ЦЕРНе провела измерения некоторой спиновой характеристики мюон-протонного рассеяния и извлекла из них средний спин кварков в протоне. Он оказался намного меньше 1/2. Более того, первоначальные данные EMC вообще допускали нулевой вклад, что кардинально противоречило первоначальным ожиданиям. Эти результаты были сразу объявлены революционными, и началась эпопея под названием «кризис протонного спина» (proton spin crisis).
Теоретики бросились вычислять в рамках различных моделей протона вклады других слагаемых. Экспериментаторы бросились перемерять результаты EMC на своих установках, а заодно пытались придумать способы измерить и другие вклады. В том же ЦЕРНе был построен и запущен эксперимент COMPASS, одной из главных целей которого было измерение вклада глюонного спина, Sg. Аналогичные научные задачи ставились и решались в других научных лабораториях по физике частиц. В общем, спиновая физика адронов резко активизировалась.
Пропуская все промежуточные результаты, сформулируем нынешнюю ситуацию с этими экспериментальными данными: (1) подтверждено, что вклад спина кварков Sq мал, и по новым данным он составляет примерно треть от спина протона; получается, что две трети протонного спина «где-то прячутся»; (2) обнаружено, что вклад спина глюонов Sg тоже невелик; погрешности там остаются большими, но уже ясно, что списать «потерянный протонный спин» на него не получится; (3) надежных измерений орбитального момента кварков или глюонов пока нет. Таким образом, в настоящий момент нельзя сказать, что найдено какое-то общепринятое решение спинового кризиса, и вряд ли его удастся найти без спиновых экспериментов нового поколения.
Загадка протонного спина — версия современной теории
А теперь — немножко неожиданный поворот событий. Жаркие баталии физиков по этому поводу по-прежнему продолжаются, но сейчас их тон полностью переменился. Главный вопрос, вокруг которого эти битвы идут уже несколько лет, таков:
А какой вообще смысл у написанной выше формулы?
Как-то неожиданно оказалось, что у этого простого вопроса есть несколько уровней разговора. Возникло множество предметов спора и множество непримиримых точек зрения. Изначально считалось, что это разложение спина протона существует и что оно единственно. Потом — что их два. Потом — что их много. Потом — что их бесконечно много. А поскольку они неэквивалентны, возник спор, какое разложение отвечает физической истине. А если оказывается, что истинными является не одно, а несколько, то какое из них более физично. Ну а в таком случае надо определить, что вообще должно считаться критерием истинности или физичности — и по этому поводу тоже разгорелись баталии.
Вот такой тугой клубок вопросов стал вдруг предметом сотен теоретических публикаций. В результате сейчас большинство физиков, работающих над этим вопросом, разошлись на несколько враждующих лагерей. Каждый лагерь выискивает недостатки в чужой точке зрения и старается привести новые доказательства в пользу своей. А растерявшиеся экспериментаторы неожиданно оказались вообще как бы в стороне.
Главная цель появившегося на днях обзора — внести порядок в эту хаотичную битву точек зрения. Да, его авторы тоже активные участники этих битв и тоже относятся к одному из лагерей. Но они в своей работе постарались максимально дотошно сравнить различные подходы, постарались отделить требования физичности или математической самосогласованности от чистой интерпретации, попытались навести мосты и очертить четкие различия между разными точками зрения. Возможно, и по поводу этого обзора будут ломаться копья, но он, по крайней мере, хорошо систематизирует сложивший на сегодня разнобой.
О чём, собственно, спор?
Пытаться адекватно описать все тонкости разделения протонного спина на отдельные составляющие — задача, видимо, неподъемная для научно-популярной новости. Тем не менее можно дать хотя бы поверхностное представление о том, о чём идет полемика. Для этого попробуем упомянуть некоторые спорные моменты, причем далеко не самые сложные из них. Но прежде — одно маленькое, но существенное отступление.
Дисклеймер для ищущих «физическую правду»
Среди любителей физики — и особенно любителей, опровергающих современную физику, — распространена точка зрения, что физика-де оперирует какими-то заумными математическими понятиями, полностью оторвалась от реальности, и поэтому она бессмысленна и нефизична. Эта точка зрения наивна. Задача теоретической физики — строить теории, которые, во-первых, самосогласованны математически, во-вторых, позволяют вычислять реально наблюдаемые величины и не противоречат уже полученным надежным экспериментальным данным, и в-третьих, имеют предсказательную силу. При этом теориям разрешается на промежуточном этапе использовать «странные» математически объекты типа комплексных чисел, абстрактных пространств или сложных алгебраических понятий. Главное, чтобы результаты для измеряемых величин у реальных физических объектов были нормальными числами.
Теперь, наконец-то, поговорим про предмет спора.
Два разных импульса
Тонкости начинаются уже при разговоре об обычном (линейном) импульсе, а не о вращательном моменте импульса. В школьной механике импульс тела определяется просто: масса умножить на скорость. Однако в «серьезной» физике есть два импульса — кинетический и канонический. Они совпадают в школьной механике, но отличаются в чуть более сложных ситуациях, например при движении зарядов во внешнем электромагнитном поле. И тот, и другой — это полноценные физические величины, но только они входят в разные формулы и подчиняются разным законам. С этим вопросов нет; но спор может начаться, если пытаться понять, какой из них «более настоящий». В квантовой теории поля это неизбежно приводит к вопросу, что такое вообще импульс (а точнее, оператор импульса) и какие на него налагаются требования. Те же вопросы возникают и для момента импульса.
Авторы обзора показывают, что расхождение между «лагерями» состоит как раз в том, что некоторые используют кинетический момент импульса, а некоторые — канонический. Сами они предлагают свои четкие критерии физичности, и по ним выходит, что «более настоящим» является канонический. Авторы допускают, что некоторые экспериментальные результаты проще интерпретировать в терминах кинетического момента импульса, но тогда надо быть аккуратным в разложении спина протона.
Как разделять части взаимодействующей системы
Другая важная тонкость возникает из-за того, что кварки и глюоны в протоне взаимодействуют. Наш разговор про неабсолютность понятия «состоит» наводит на мысль, что само по себе разделение протонного спина на долю кварков и долю глюонов не является абсолютно четким. И действительно, если сравнивать формулы этого разделения для разных авторов, то получается, например, что одни и те же слагаемые у одних относятся к Lq, а у других — к Lg (рис. 3).
Тут полезно привести один пример, в котором перекликаются сразу две обсуждаемые тонкости. Это спор между двумя крупными физиками, Г. Минковским и М. Абрагамом, о том, чему же равен импульс фотона, который движется внутри прозрачной среды (см., например, статью в УФН 1973 года). Эта старая загадка возникла в электродинамике свыше века назад и была разрешена (и по-видимому, удовлетворительно) только недавно. Есть две формулы, каждая из которых выглядит логично, но которые приводят к разным ответам. Есть экспериментальные результаты, которые можно интерпретировать в пользу обеих формул. К математике претензий нет, спор только о том, какая отвечает «настоящему» импульсу фотона в среде. Но если фотон движется внутри среды, то он меняет ее свойства, возникает взаимодействие среды и фотона, и вот с этим взаимодействием надо что-то делать. К чему его относить, на чей импульс оно влияет — среды или фотона? В статье 2010 года показано, что два импульса отличаются как раз этой договоренностью. Более того, там же объяснено, что два выражения для импульса фотона в среде отличаются друг от друга как кинетический и канонический импульсы. Хотя справедливости ради надо сказать, что подобные точки зрения звучали и раньше (см., например, обзор 2007 года).
Видимо, в разложении протонного спина на составные части возникает нечто похожее. Правда несколько удивительно то, что ни авторы обсуждаемого здесь обзора, ни другие участники спора про спин протона не обращаются к этому примеру.
Калибровочная (не)инвариантность
Еще один предмет спора касается калибровочной инвариантности операторов момента импульса (чуть подробнее про калибровочную симметрию см., например, в статьях Большие калибры физики и Что такое цветовой заряд, или какие силы связывают кварки). В квантовой теории есть два «уровня» разговора — уровень операторов и уровень наблюдаемых величин. Сама теория строится с помощью сложных математических объектов — линейных операторов и пространства, в котором они действуют. Но к эксперименту имеют отношение не непосредственно они, а полученные из них «наблюдаемые» величины. Наблюдаемые величины должны быть физичными, и в частности, калибровочно инвариантными. Но нужно ли требовать того же от операторов? И если требовать, то нужно ли настаивать на инвариантности относительно любых калибровочных преобразований или только некоторых?
Авторы обзора резонно говорят, что нет, строгой калибровочной инвариантности от операторов требовать не нужно. Операторы (или пространства, в которых они действуют), будучи промежуточными математическими объектами теории, могут обладать некоторыми «ненормальными» свойствами; главное, чтобы вычисленные по ним наблюдаемые величины были нормальными. Зато физики из другого «лагеря» считают, что калибровочная инвариантность операторов — это важный критерий физичности формул; именно на основании этого критерия они отдают предпочтение своей формуле для разложения спина протона.
Разделение на спин и орбитальный угловой момент
Еще один момент касается того, разделяется ли полный угловой момент (величина, обозначенная буквой J на рис. 3) на спин и орбитальный угловой момент, и если да, то в каком смысле. С одной стороны, множество учебников по квантовой теории поля утверждает: это разделение векторных операторов невозможно выполнить калибровочно-инвариантным способом. Но в 2008 году была опубликована статья, продемонстрировавшая, по сути, что это утверждение неверно. Ее авторы предложили такое разделение и показали, что оно калибровочно-инвариантно. Получается, что все учебники ошибались?
Вовсе нет, но для этого надо читать мелкий текст. Учебники говорят, что калибровочно-инвариантное разделение спина и орбитального момента невозможно, если требовать, чтобы операторы были локальными. А в предложении 2008 года, как поясняет обзор, это условие нарушено, поэтому никакого противоречия нет. Эта тонкость была не сразу отслежена научным сообществом, поэтому сразу после статьи 2008 года последовали многочисленные публикации всех заинтересованных сторон, и страсти резко накалились. И именно после этой полемики стало понятно, что на самом деле разделение протонного спина можно провести бесконечным числом способов. В обсуждение этого вопроса мы вдаваться уже не будем; желающие могут самостоятельно полистать обзор.
Выводы
Так из чего всё-таки складывается спин протона? Такой простой, казалось бы, вопрос чуть ли не на ровном месте заводит физиков в дебри, полные теоретических тонкостей. Фундаментальная причина проста: в квантовой теории поля вопрос о разложении составной частицы на отдельные части не является четко определенным. И в применении к проблеме разделения спина протона на отдельные слагаемые это свойство приводит к длинному списку спорных моментов.
Насколько важно с научной точки зрения установить, какая из формул более правильна, чем другая? Один из главных выводов обзора заключается в том, что эта неопределенность не так уж и важна. Все формулы (за исключением ошибочных) работают и имеют право на существование. Но какая из них более физична, какая лучше всего отвечает интуитивным представлениям — это уже дело вкуса. Да, они могут приводить к разным ответам, но не надо считать, что это разные ответы для одной и той же величины. Это разные ответы для разных наблюдаемых величин, только, к сожалению, многие называют эти разные величины одинаковыми словами. Вот этого авторы обзора предлагают не делать.
А как тогда быть экспериментаторам? Ведь они пытаются измерить состав спина или орбитального момента кварков или глюонов на опыте. С какой формулой им сравниваться? Ответ в том, что на пути между реальным измерением и сравнением с формулами лежит интерпретация измерений, и вот для этой задачи интерпретация, к сожалению, очень неоднозначна. Это было известно и раньше, но именно в процессе спора открылись новые грани этой неоднозначности. Поэтому сравниваться им можно с чем угодно, но надо только четко указывать, что именно они измерили и в рамках какого именно разложения они делают выводы. Может быть, это несколько усложнит описание результатов эксперимента, но, по крайней мере, такой подход будет честным.
Источник: E. Leader, C. Lorce. The angular momentum controversy: What’s it all about and does it matter? // е-принт arXiv:1309.4235 [hep-ph] (17 September 2013).
Игорь Иванов
что это такое в физике, какие значения принимает, направления
Что такое спин электрона
Немецкие физики Отто Штерн и Вальтер Герлах в 1922 году провели опыт, доказавший, что у электронов есть собственный магнитный момент и связанный с ним момент импульса. Пучок атомов серебра, направленный на стеклянную пластинку, расщеплялся магнитным полем на две симметричные полоски. Этот процесс не зависел от возбуждения атомов, что противоречило теории квантовой физики. Таким образом, нечто в составе невозбужденного атома обладало магнитным моментом, достаточным, чтобы отклонять атомы в противоположные стороны.
Первоначально предполагалось, что электроны внутри атома вращаются не только вокруг ядра, но и вокруг своей оси. Собственный угловой импульс этого вращения задает направление электрона, делая его ориентированным в определенную сторону. Но модель вращающегося заряженного элемента не соответствует реальности: согласно расчетам в рамках классической механики, физическим вращением электрона невозможно индуцировать магнитный момент, наблюдавшийся при опытах.
ОпределениеСпин — собственный механический момент импульса частицы, не связанный с ее передвижением в пространстве.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кто ввел понятие
Термин «спин» ввели в научный обиход американские физики Сэмюэл Гаудсмит и Джордж Уленбек в 1925 году. Они доказали, что спин благодаря своей квантовой природе не имеет отношения к физическим перемещениям частиц в пространстве, он характеризует внутреннее свойство частицы, как масса или заряд. В процессе спин-орбитального взаимодействия внутри атома происходит изменение его полной энергии, в разных квантовых состояниях атом обладает разной энергией, что и приводит к двойным линиям в его оптическом спектре.
Формула спина электрона
Квантовое число
Спин измеряют в долях постоянной Планка (она же постоянная Дирака). Природа спина — квантовая, поэтому для каждой частицы он имеет конкретное постоянное значение.
Спиновое квантовое число всех электронов равно ½ постоянной Планка и обозначается как \(\hbar\frac{1}{2}\)
Модуль собственного момента импульса частицы определяется спиновым квантовым числом s и рассчитывается по формуле:
\(L_{s} = \hbar\sqrt{s \times (s + 1)}\)
Спиновая проекция на ось х, \(L_{sх}\), вычисляется по формуле \(L_{sх} = \hbar \times m_{s}\), где \(m_{s}\) — магнитное спиновое число. Для электрона оно равняется его спиновому квантовому числу, но может быть как положительным, так и отрицательным, так как определяет направление вектора спина. Он не является обычным вектором, поэтому может принимать только два значения относительно оси магнитного поля: «вверх» и «вниз».
Связь с релятивистским волновым уравнением
В 1928 году Поль Дирак опубликовал релятивистское уравнение для электрона. Взяв волновое уравнение Шрёдингера, Дирак применил к волновой функции процесс квантования, превратил обычные числа в квантовые, что позволило описать движение квантовых частиц во внешних полях. Координаты частиц, их импульсы, энергии и другие физические величины, описывающие переходы атомной системы из одного состояния в другое, у Дирака были представлены матрицами — квадратными таблицами (конечными или бесконечными), каждый элемент которых имеет два индекса. Так появилась квантовая теория поля, описывающая взаимодействие частиц как результат обмена квантами полей.
Каждая элементарная частица, в том числе электрон, является одновременно и частицей, и элементарной волной. У одночастичной волны, как и у обычной, можно измерить длину и частоту. В разных случаях электрон может вести себя и подобно частице, и подобно волне. В совокупности его описание как частицы и как волны дает полное представление о нем. При этом его волновая функция описывает лишь вероятность появления частицы в том или ином месте. Согласно принципу суперпозиции, волновые функции в квантовой механике складываются, и вероятности процессов определяются квадратом их модулей.
Связь спина электрона с теорией ферромагнетизма
Спин электрона, как и спин любой другой заряженной частицы, обладает магнитным моментом: реагирует на магнитное поле и сам его порождает. Явления ферромагнетизма в веществах, которые в быту называют магнитами, возникают именно благодаря спинам электронов. Когда электронные спины ориентированы упорядоченным образом, эти вещества способны намагничиваться самопроизвольно, без влияния внешнего магнитного поля.
Что такое спин субатомных частиц, таких как электроны и протоны? Имеет ли это какое-либо физическое значение, аналогичное вращению планеты?
Мортон Тавел, профессор физики в Vassar College, отвечает:“Когда некоторые элементарные частицы движутся через магнитный поле, они отклоняются таким образом, чтобы предполагать, что они свойства маленьких магнитов. В классическом мире заряженный, вращающийся объект обладает очень сильными магнитными свойствами. очень похоже на те, которые демонстрируют эти элементарные частицы.Физики любят аналогии, поэтому они описали элементарное частицы тоже с точки зрения их «спина».
“К сожалению, аналогия не работает, и мы пришли к понять, что это заблуждение – создавать образ электрон как маленький вращающийся объект. Вместо этого мы узнали просто принять наблюдаемый факт, что электрон отклоняется магнитными полями. Если настаивать на образе вращается объект, то возникают настоящие парадоксы; в отличие от брошенного софтбол, например, спин электрона никогда не меняется, и имеет только две возможные ориентации.Кроме того, само представление о том, что электроны и протоны – твердые «объекты», которые могут “вращаться” в пространстве само по себе трудно, учитывая то, что мы знать о правилах квантовой механики. Термин “вращение” тем не менее, все еще остается ».
Курт Т. Бахманн Бирмингем-Южный колледж добавляет исторический фон и другие подробности:
“Начиная с 1920-х годов Отто Штерн и Вальтер Герлах из Гамбургский университет в Германии провел ряд важных эксперименты на атомных пучках.Зная, что все движущиеся заряды производят магнитные поля, они предложили измерять магнитные поля производятся электронами, вращающимися вокруг ядер в атомах. Много Однако к своему удивлению два физика обнаружили, что электроны сами действуют так, как будто они очень быстро вращаются, производя крошечные магнитные поля, не зависящие от орбитальных полей. движения. Вскоре для описания этого кажущееся вращение субатомных частиц.
«Спин – причудливая физическая величина.Это аналог вращение планеты в том смысле, что она дает угловой момент частицы и крошечное магнитное поле, называемое магнитным моментом. На основе известны размеры субатомных частиц, однако поверхности заряженные частицы должны были бы двигаться быстрее, чем скорость света, чтобы произвести измеренные магнитные моменты. Кроме того, спин квантуется, а это означает, что только определенные Разрешены дискретные вращения. Эта ситуация создает всевозможные сложности, которые делают вращение одним из самых сложных аспектов квантовой механики.
«В более широком смысле, вращение является важным свойством, влияющим на упорядочение электронов и ядер в атомах и молекулах, придавая ему большое физическое значение в химии и физика твердого тела. Вращение также является важным фактором. во всех взаимодействиях между субатомными частицами, будь то в пучки частиц высоких энергий, низкотемпературные жидкости или разреженный поток частиц от солнца, известный как солнечный ветер. В самом деле, многие, если не большинство физических процессов, начиная от от наименьших ядерных масштабов до наибольших астрофизических расстояний, сильно зависят от взаимодействия субатомных частиц и спины этих частиц.”
Виктор Дж. Стенгер, профессор физики Гавайского университета в г. Маноа предлагает другую, более техническую перспективу:
“Спин – это полный угловой момент или собственный угловой момент . импульс тела. Спины элементарных частиц равны аналогично спинам макроскопических тел. Фактически, спин планеты – это сумма вращений и орбитального углового импульсы всех его элементарных частиц. Так спины другие составные объекты, такие как атомы, атомные ядра и протоны (которые состоят из кварков).
«В классической физике угловой момент является непрерывным Переменная. В квантовой механике угловые моменты дискретны, квантуется в единицах постоянной Планка, деленной на 4 пи. Нильс Бор предложил квантовать угловой момент в 1913 г. и использовал это, чтобы объяснить линейчатый спектр водорода.
«На нашем нынешнем уровне понимания элементарные частицы кварки, лептоны (например, электрон) и бозоны (например, фотон).Все эти частицы представляются точечными, поэтому вы можете задаться вопросом, как у них могут быть вращения. Простой ответ мог бы быть, возможно, они тоже составные. Но глубокие теоретические Причины, связанные с вращательной симметрией природы, приводят существованию спинов для элементарных объектов и их квантование. Особое значение имеет разница между фермионами, частицы, которые, как и электрон, имеют полуцелые вращения (полуцелые числа, кратные постоянной Планка делится на 2 пи), и бозоны, частицы с целыми спинами.Фермионы подчиняются принципу исключения Паули, который гласит, что два одинаковых фермиона не могут существовать в одном и том же состоянии; без принцип исключения Паули, химия не имела бы периодических Таблица. С другой стороны, бозоны, как правило, собираются в одном и том же месте. состояние, приводящее к таким явлениям, как сверхпроводимость и Конденсация Бозе-Эйнштейна.
“Спин послужил прототипом для других, еще более абстрактных понятия, которые, кажется, обладают математическими свойствами угловых импульса, но не имеют простого классического аналога.Для Например, изотопический спин используется в ядерной физике для представления два состояния «нуклона», протона и нейтрона. Точно так же кварки спарены как изоспиновые «вверх» и «вниз», что – имена, данные двум кваркам, которые составляют обычные иметь значение. Вращательная симметрия пространства и времени обобщена. включить симметрии в более абстрактные «внутренние» измерения, с в результате большая часть сложной структуры микромира можно рассматривать как результат нарушения симметрии, соединяющий глубоко к идеям, описывающим спонтанное формирование структура в макромире.
Физика тяжелых ионов и спина
Исследование фундаментальной структуры ядер в лаборатории ДжефферсонаМы используем интенсивные и энергичные пучки, доступные в Национальной лаборатории Томаса Джефферсона (JLab), для исследования внутренней структуры ядер. Мы используем спектрометр CLAS12 для проведения экспериментов, в которых электрон рассеивает кварк, который затем распространяется через ядра. Мы стремимся понять, как ядро реагирует на проходящий через него энергетический кварк.Ответ на этот вопрос откроет механизмы, с помощью которых кварки удерживаются внутри нуклонов, а также ограничит положение и импульс кварков и глюонов внутри ядер.
Электронно-ионный коллайдерДолгосрочным интересом нашей группы является будущий электронно-ионный коллайдер (EIC) в Брукхейвенской национальной лаборатории. EIC будет использовать электроны для изображения кварков и глюонов внутри ядер с беспрецедентной точностью. Действуя как мощный электронный микроскоп, он позволит нам делать томографические трехмерные изображения атомного ядра.Таким образом, это поможет нам найти источник массы и вращения протонов и нейтронов, которые являются строительными блоками всей видимой материи во Вселенной. EIC также может открыть гипотетическую новую форму «глюонной материи» и раскрыть тайну того, почему кварки никогда не наблюдаются изолированно.
группы UCR работают над НИОКР и концептуальным дизайном будущих экспериментов EIC. UCR является частью консорциума EIC Калифорнийского университета, в который входят 4 кампуса UC и все три национальные лаборатории, управляемые UC.
Почему составляющие протона ограничены?Это вопросы, которые побудили нас использовать коллайдер релятивистских тяжелых ионов (RHIC) в Брукхейвенской национальной лаборатории.
Все фазовые переходы, которые мы можем наблюдать до сих пор на Земле, связаны с электромагнитным взаимодействием, например, таяние льда, образование пара или намагничивание металлов. Мы стремимся впервые на Земле увидеть совершенно новую форму фазового перехода, включающую сильное взаимодействие или квантовую хромодинамику (КХД), в которой газ кварков и глюонов называется «кварк-глюонная плазма» (QGP). ) конденсируется с образованием протонов, нейтронов и других адронов.Это замечательный переход, потому что мы считаем, что он также дает начало протонам и нейтронам, которые составляют большую часть вещества, которое мы видим здесь, на Земле. Еще одна любопытная вещь происходит, когда протоны и нейтроны конденсируются из горячего вакуума, который составляет QGP, который предположительно создается в результате самых сильных столкновений.
Вскоре после большого взрыва Вселенная пережила период фантастического расширения, получившего название инфляции. Что могло вызвать такое катастрофическое событие? Подобно тому, как взрывная сила превращения воды в пар приводила в движение большую часть промышленной революции, считается, что какой-то фазовый переход – никто не знает, что именно – вызвал инфляцию.
Откуда берется спин протона?По некоему загадочному механизму, связанному со сложным поведением КХД, глюоны, имеющие одну единицу спина, и кварки, имеющие 1/2 единицы спина, соединяются вместе, образуя нечто, имеющее ровно 1/2 единицы. «спина».
Спин – это такое фундаментальное свойство частиц, как заряд и масса. Спин протона был впервые определен в 1927 году, но мы до сих пор не знаем, что составляет спин протона.Считалось, что спин несут кварки, составляющие протон. Однако эксперименты 1980-х годов привели к поразительному открытию, что кварки очень мало влияют на спин протона, что вызвало «кризис спина протона». Сейчас считается, что спин переносится глюонами, которые удерживают протон вместе. Измерения спина исторически давали удивительные результаты и являются строгим тестом для теорий, поскольку спин по своей сути является релятивистским и квантово-механическим аспектом взаимодействия частиц.
RHIC | Спиновая физика
RHIC – единственная в мире машина, способная сталкиваться высокоэнергетические пучки поляризованных протонов, и это уникальный инструмент для исследования загадка «недостающего» спина протона.
Помимо столкновения тяжелых ионов, RHIC может столкнуться с одиночными протоны. Хотя эти столкновения не создают кварк-глюонную плазму, они интересен физикам по другим причинам.Ученые хотят знать подробнее о свойстве частиц, называемом «спин».
Спин – это направление, в котором частица вращается вокруг оси при движении. – точно так же, как Земля вращается вокруг своей оси, когда она движется вокруг Солнца. Каждый протон имеет особый спин, который помогает придать ему характерный магнитный имущество.
На этом изображении протон-протонное столкновение, спин частиц показан стрелками вращая сферические частицы.Красные и зеленые частицы представляют продукты реакции от столкновения, которые будут “видны” и проанализированы Детекторы RHIC.
Пучки протонов в RHIC – это “спин поляризованный “, что означает, что все протоны в данном пучке вращаются в том же направлении. RHIC – первая машина в мире с способность встречать такие лучи в лоб.
Важность вращения
Почему спин протона важен для понимать? Астрономы, изучающие Вселенную, используют спин протона и магнетизм как важные измерительные свойства.Спин – это также то, что позволяет врачам использовать аппарат МРТ (магнитно-резонансной томографии), чтобы заглянуть внутрь человеческого тела, чтобы диагностировать болезнь.
По этим и другим причинам физики хотят измерить и понять, как различные факторы влияют на спин протона. Эксперименты в другом месте показали, что вращение составляющие протона кварки (и антикварки), в некоторых случаях счета только около 30% от его общего вращения.
Спиновые эксперименты RHIC предоставление первой информации о том, какой вклад вносит спин глюонов к спину протона, вклад, который недавние теоретические работы предполагают может быть большим.
Если кварк и глюон вращаются вместе все еще не учитывают спин протона, единственное оставшееся источник, доступный для “баланса книг”, – это движение кварков и глюонов. относительно друг друга. Таким образом, измерения спиновой субструктуры RHIC протона может вывести нас за пределы нашего нынешнего, все еще рудиментарного понимание того, как кварки движутся внутри протонов и других частиц.
Магниты “Змеи”
Сохранение поляризации пучков частиц при их прохождении через цепочка из пяти ускорителей, составляющих комплекс RHIC, очень трудный.Специализированные наборы магнитов «Сибирские змейки». (физик Мэй Бай показан с одним выше) используются для минимизации потеря поляризации.
Магниты в виде штопора конструкция заставляет направление магнитного поля вращаться по спирали вдоль направление луча. Когда луч проходит через двух змей в каждой колец RHIC с окружностью 2,4 мили, магнитное поле переворачивает поляризация, или направление вращения, и усредняет многие меньшие эффекты магнитов RHIC, которые в противном случае деполяризация протонных пучков.
SPINS Домашняя страница Java
Домашняя страница SPINS JavaДэвид Х. Макинтайр
Кафедра физики, Государственный университет Орегона,
SPINS – это интерактивная компьютерная программа, которая моделирует измерения Штерна-Герлаха на частицах со спином 1/2 и спином 1. Первоначальная версия для Macintosh была написана Д. В. Шредером (см. Am. J. Phys. 61 , 798 (1993)). Эта страница содержит наши Версия JAVA, которую мы разработали для использования в курсе Paradigm Ph525: Spin and Quantum Measurement (из архива в Интернете). сайт).Доступна последняя версия программы в формате HTML5.
Расширенная версия SPINS была разработана в сотрудничестве с проектом Open Source Physics (OSP). У этой версии есть отдельная домашняя страница,
, но обратите внимание, что код OSP Spins не был обновлен с поправкой кода для проблемы интерферометра спина 1, которая там отмечена.
Программа SPINS доступна в виде приложения или апплет:
|
© Дэвид Макинтайр | Частичная поддержка разработки этого программного обеспечения была
предоставлено |
(PDF) Спиновая физика в полупроводниках
Представлено в Elsevier Science 3
следствия, некоторые из которых очень
важны и определяют саму структуру
нашего мира, в то время как другие более тонкие, но
все еще довольно интересные .
2.1. Обменное взаимодействие
.
Фактически
это результат кулоновского взаимодействия
между электронами, которое становится зависимым от спина
из-за требования, чтобы
волновая функция пары электронов была
антисимметричной по отношению к
обмен электронными координатами и
спинов. Если спины электронов параллельны, то координатная часть волновой функции
должна быть антисимметричной:
ψ
↑↑
(r
2
, r
1
) = –
↑↑
(r
1
, r
2
),
, что означает, что вероятность того, что два электрона
очень близко друг к другу,
мала по сравнению с противоположным случаем, когда
спины антипараллельны, и соответственно
их координатная волновая функция симметрична.
Электроны с параллельными спинами тогда лучше
разделены в пространстве, так что их отталкивание на
меньше и, следовательно, энергия параллельных
спинов ниже.
2.2. Спин-орбитальное взаимодействие. Если наблюдатель
движется со скоростью v во внешнем электрическом поле E
, он увидит магнитное поле
B = (1 / c) v∧E, где c – скорость света
(гауссовские единицы везде в этой лекции используются
).Таким образом, когда электрон
следует по своей орбите в электрическом поле
, создаваемом ядром атома, это магнитное поле
появляется в системе отсчета электрона
. Будучи перпендикулярно как
к E, так и к v, B перпендикулярно плоскости орбиты
, таким образом, она параллельна орбитальному угловому импульсу
L. Это магнитное поле действует на
магнитного момента электрона, давая
энергия ±
µ
B, в зависимости от ориентации
спина электрона (и, следовательно, его магнитного момента
) относительно B (или L).
Это физическое происхождение спин-орбитального взаимодействия
, которое можно записать
как A (LS), константу A, зависящую от
электронного состояния в атоме. Это взаимодействие
приводит к расщеплению атомных уровней (тонкая структура
), которое сильно увеличивается для
тяжелых атомов (большое Z). Причина в том, что
существует определенная вероятность для электрона
приблизиться к ядру и, таким образом, увидеть очень сильное электрическое поле
, создаваемое неэкранированным ядерным зарядом
+ Ze в центре.
В полупроводниках спин-орбитальное взаимодействие
зависит не только от скорости
электрона (или его квазиимпульса), но и от структуры функций Блоха
, определяющих движение атома. шкала.
Спин-орбитальное взаимодействие является ключевым в нашем обсуждении
, поскольку оно обеспечивает ориентацию и обнаружение оптического вращения
(электрическое поле
световой волны не взаимодействует напрямую
со спином электрона).За спиновую релаксацию отвечает (в большинстве случаев)
. И, наконец,
делает явления переноса и вращения
взаимозависимыми.
2.3. Сверхтонкое взаимодействие с
ядерными спинами. Это магнитное взаимодействие
между электроном и
ядерными спинами, которое может быть весьма важным, если
ядер решетки в полупроводнике не имеют нулевого спина
(как в GaAs). Если ядра становятся поляризованными на
, это взаимодействие эквивалентно
существованию эффективного ядерного магнитного поля
, действующего на электронные спины.Эффективное поле
100% поляризованных ядер в GaAs
составило бы несколько тесла! Экспериментально
ядерная поляризация в несколько процентов легко достижима.
Spin (Physics) Facts for Kids
В физике вращение – это постоянное вращение объекта.
Для больших видимых объектов, таких как Земля, вращение – это угловой момент вращения Земли вокруг своей оси. Это говорит о величине вращения, которое у него есть.Угловой момент изменяется в зависимости от массы и формы объекта, а также от скорости его вращения.
Спин в квантовой теории
Эксперименты, такие как эксперимент Штерна-Герлаха, показали, что субатомные частицы, такие как электроны, похоже, имеют северный и южный полюсы так же, как магниты. Ученые когда-то думали, что это было вызвано частицей, вращающейся вокруг своей оси, как планета.
Позже было показано, что для этого электрон должен вращаться быстрее скорости света.Вот почему ученые больше не верят, что электрон действительно вращается, как планета. Однако ученые продолжают называть магнитные свойства частиц «спином».
Спин, каким бы он ни был, кажется, следует некоторым законам углового момента, но не всем. «Вращающийся» электрон (или любая другая субатомная частица со спином) может иметь только определенные значения углового момента. Электроны также могут выравниваться против магнитного поля способами, которые были бы невозможны в повседневном мире.
Спин считается фундаментальным свойством любой частицы.
Связанные страницы
Картинки для детей
Принципиальная схема, показывающая вращение нейтрона в виде черной стрелки и силовые линии магнитного поля, связанные с магнитным моментом нейтрона. Нейтрон имеет отрицательный магнитный момент. В то время как нейтрон на этой диаграмме направлен вверх, силовые линии магнитного поля в центре диполя направлены вниз.
Отдельная точка в космосе может вращаться непрерывно, не запутываясь.Обратите внимание, что после поворота на 360 градусов спираль переворачивается между ориентацией по часовой стрелке и против часовой стрелки. Он возвращается в исходную конфигурацию после полного поворота на 720 градусов.
Основы физики вращения – PubMed
Магнитно-резонансная томография – это, по сути, измерение магнетизма, присущего некоторым ядерным изотопам; из них протон или атом водорода представляет особый интерес для клинических применений.Магнетизм в каждом ядре часто называют спином. Сильное статическое магнитное поле B0 используется для выравнивания спинов, формируя магнитную плотность внутри пациента. Второе вращающееся магнитное поле B1 (РЧ-импульс) применяется на короткое время, которое поворачивает спины от B0 в процессе, называемом возбуждением. После того, как спины повернуты от B0, RF-импульс выключается, и спины прецессируют около B0. Пока все спины в любой момент времени указывают в одном и том же направлении (имеют фазовую когерентность), они действуют согласованно, создавая быстро осциллирующие магнитные поля.Эти поля, в свою очередь, создают ток в правильно размещенной катушке приемника, подобно тому, как это происходит в электрическом генераторе. Прецессирующая намагниченность быстро спадает за время, примерно определяемое постоянной времени T2. В то же время, но более медленными темпами, намагниченность снова формируется вдоль направления B0; продолжительность этого процесса приблизительно выражается постоянной времени T1. Частота прецессии каждого спина пропорциональна магнитному полю, действующему на ядро.Небольшие изменения в этом магнитном поле могут иметь драматические последствия для МР-изображения, частично вызванные потерей фазовой когерентности. Эти вариации магнитного поля могут возникать из-за конструкции магнита, магнитных свойств (восприимчивости) тканей и других материалов и ядерной среды, уникальной для различных участков внутри любой данной молекулы. Потеря фазовой когерентности может быть эффективно устранена за счет использования RF-импульсов перефокусировки. Обычные эксперименты с МР-визуализацией можно охарактеризовать как градиентное эхо или спиновое эхо, последнее указывает на использование RF-импульса перефокусировки, а также с помощью параметров TR, TE и угла поворота альфа.