6. Спиновое квантовое число
СПИНОВОЕ КВАНТОВОЕ ЧИСЛО – квантовое число, определяющее величину спина квантовой системы (атома, иона, атомного ядра, молекулы), т. е. её собств. (внутр.) момента кол-ва движения (момента импульса). Спиновый момент импульса s квантуется: его квадрат определяется выражением, где s – С. к. ч. (называемое часто просто спином). Проекция вектора s на произвольное направлениеz также квантуется: для частиц с ненулевой массой(гдеms – магнитное спиновое число), т. е. принимает 2s + 1 значений. Число s может принимать целые, нулевые или полуцелые значения.
7)Принцип
Паули: в
пределах одной квантовой системы в
данном квантовом состоянии может
находиться только одна частица, состояние
другой должно отличаться хотя бы одним
квантовым числом. Следствием принципа
является наличие электронных оболочек
в структуре атома.
8)Правило Гунда: определяет порядок заполнения орбиталей определённого подслоя и формулируется следующим образом: суммарное значение спинового квантового числа электронов данного подслоя должно быть максимальным. Сформулировано Фридрихом Хундом в 1925 году. Это означает, что в каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон. При этом на одной орбитали находятся два электрона с полуцелыми спинами противоположного знака, которые спариваются (образуют двухэлектронное облако) и, в результате, суммарный спин орбитали становится равным нулю.
9. Квантовое число
Квантовое число
n – главное. Оно определяет энергию
электрона в атоме водорода и одноэлектронных
системах (He+,
Li2+ и т. д.). В этом случае энергия электрона
д.). В этом случае энергия электрона
где n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном.
В многоэлектронных атомах электроны с одинаковыми значениями n образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.
10. Распределение электронов по энергетическим уровням
Ниже приведено распределение электронов по энергетическим уровням и подуровням у элементов, принадлежащих к группам (семействам) S, Р, D И F.
S-Элементы.
S-элементами являются элементы главных
подгрупп I и II групп, а также водород и
гелий. Водород относят к VII главной
подгруппе P-элементов, а гелий – к
VIII подгруппе инертных P-элементов. В
атомах S-элементов пополняется
электронами подуровень S Внешнего
уровня: во внешнем квантовом слое
S-подуровня они имеют 1 или 2 (S1 или S2)
электрона, удаленных на значительное
расстояние от ядра.
Квантовые числа спиновое – Справочник химика 21
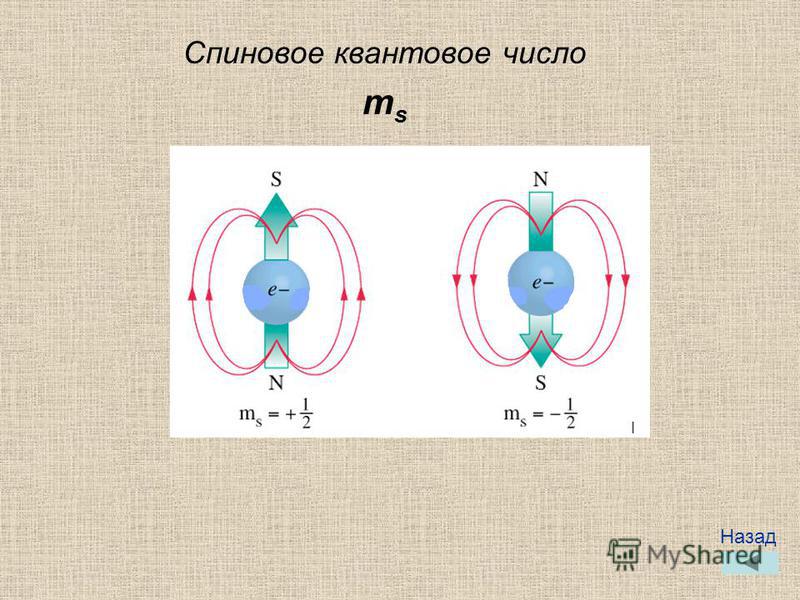
Четвертое квантовое число — спиновое (т ) — характеризует вращение электрона вокруг собственной оси. Проекция собственного момента. количества движения электрона на избранное направление (например, на ось г) называется спиновым квантовым числом. Спиновое число имеет два значения +1/2 и —1/2, их изображают в виде противоположно направленных стрелок или .Четвертое квантовое число — спиновое ( ) характеризует вращение электрона вокруг собственной оси. Подобно волчку, электрон может вращаться по часовой стрелке или против нее. Электроны, имеющие одинаковые квантовые числа п, I и т (занимаю- [c.27]
Четвертое квантовое число — спиновое число 5. Оно может иметь только два значения.
 Ведь мы уже говорили, что существует только два возможных направления вращения электрона вокруг своей оси. Принято два значения этого числа обозначать цифрами -f 7г и — /г-
Ведь мы уже говорили, что существует только два возможных направления вращения электрона вокруг своей оси. Принято два значения этого числа обозначать цифрами -f 7г и — /г- Четвертому квантовому числу — спиновому не придают какого-либо образа и считают его чисто квантово-механической величиной, принимающей два значения 1/2. [c.91]
Наличием собственных магнитных полей атома водорода удалось объяснить расщепление спектральных линий в магнитном поле (эффект Зеемана) и в электрическом поле (эффект Штарка). Для объяснения более тонких спектральных явлений введено еще одно квантовое число — спиновое квантовое число 5. Спин, или вращение электрона относительно собственной оси, может быть левым и правым [c.37]
Однако квантовое число спинового момента (х) в отличие от I может принимать лишь одно значение
Детальное изучение атомных спектров в течение первой четверти двадцатого века привело к выводу, что поведение электрона в атоме может быть полностью описано совокупностью из четырех квантовых чисел. Полное решение волнового уравнения для атома водорода привело к трем из этих квантовых чисел, совершенно идентичным соответствующим эмпирическим квантовым числам старой квантовой теории (за исключением некоторых деталей). Развитие теории показало необходимость введения четвертого квантового числа спинового квантового числа). Четыре квантовых числа определяют не только энергию электрона, но также и характер волновой функции, описывающей его орбиту — ее размер и форму.
Полное решение волнового уравнения для атома водорода привело к трем из этих квантовых чисел, совершенно идентичным соответствующим эмпирическим квантовым числам старой квантовой теории (за исключением некоторых деталей). Развитие теории показало необходимость введения четвертого квантового числа спинового квантового числа). Четыре квантовых числа определяют не только энергию электрона, но также и характер волновой функции, описывающей его орбиту — ее размер и форму.
Полное описание всех возможных орбиталей для первых трех оболочек с соответствующими квантовыми числами приведено в табл. 1-2. Существует ряд правил, которые позволяют определять возможные значения п, I и т1. Квантовое число п может иметь любое положительное целочисленное значение, за исключением нуля. Все возможные значения I, соответствующие данному п, передаются соотношением 1=п—1,. .., О, где многоточие означает все целые числа, необходимые для заполнения ряда. Возможными значениями т , соответствующими данному I, являются гп1= +1,1—1,.
Спин электрона, (механический и магнитный моменты его) характеризуется четвертым квантовым числом — спиновым (а). Последнее может принимать лишь два условных значения + Уа, —или, упрощенно, -Ь и —. [c.121]
В 1925 г. Уленбек и Гаудсмит предположили, что электрон ведет себя как вращающаяся частица и имеет внутренний угловой (спиновый) и связанный с ним магнитный моменты. Эта гипотеза позволила объяснить некоторые небольшие расщепления, наблюдавшиеся в атомных спектральных линиях. Уленбек и Гаудсмит нашли, что необходимо постулировать полуцелое квантовое число спинового углового момента (спина)
Каждый электрон кроме движения в поле ядра обладает еще и внутренним движением. Момент количества движения, связанный с внутренним движением электрона, называют спином т,. Он характеризует четвертое квантовое число. Спиновое квантовое число показывает вращение электрона вокруг своей оси, которое может иметь два противоположных направления движение по часовой стрелке и движение против часовой стрелки Значение спина 4- /г и — /г соответственно. Два электрона с противоположно направленными спинами называются спаренными электронами, а с одинаковыми спинами или ЧI — неспаренны-
Он характеризует четвертое квантовое число. Спиновое квантовое число показывает вращение электрона вокруг своей оси, которое может иметь два противоположных направления движение по часовой стрелке и движение против часовой стрелки Значение спина 4- /г и — /г соответственно. Два электрона с противоположно направленными спинами называются спаренными электронами, а с одинаковыми спинами или ЧI — неспаренны-
Квантовые числа п, I п т принадлежат орбиталям, а электрону они принадлежат постольку, поскольку он находится в данной орбитали ( занимает данную орбиталь). Кроме них существует четвертое квантовое число — спиновое, более непосредственно принадлежащее электрону, определяющее ориентацию спина электрона относительно некоторого выделенного направления и имеющее лишь два возможных значения + /2 и —72- Чаще всего его обозначают буквой 5. Таким образом, полный набор квантовых чисел для электрона в атоме содержит четыре квантовых числа п, I, т, 5. Электроны атома с одинаковыми значениями квантовых чисел п и I называются эквивалентными.
Спин электрона. В предыдущей главе было показано, что многие характерные черты водородного спектра можно объяснить на основе допущения, что состояние каждого электрона определяется тремя квантовыми числами п, I, т1. Это относится также и к спектрам многих других атомов, хотя в этом случае, конечно, имеет место значительное усложнение. Однако многие особенности спектров более сложных атомов и действие магнитного поляг на спектр водорода вызвали необходимость предположить, что электрон имеет четвертое квантовое число. Это четвертое квантовое число — спиновое квантовое число [1, 3, 4].
В 1925 г. Уленбек и Гаудсмит предположили, что электрон ведет себя как вращающаяся частица и имеет внутренний угловой (спиновый) и связанный с ним магнитный моменты. Эта гипотеза позволила объяснить некоторые небольшие расщепления, наблюдавшиеся в атомных спектральных линиях. Уленбек и Гаудсмит нашли, что необходимо постулировать по-луцелое квантовое число спинового углового момента (спина) 5 = 2 в противоположность целым значениям / = О, 1, 2,. .., которые может принимать квантовое число орбитального углового момента электрона. В предыдущей главе было показано, что орбитали с данным значением / вырождены 2/-+- 1-кратно, каждое из 2/-+- 1-состояний соответствует различным значениям т. По аналогии следует ожидать, что так как для электрона 5 = /2, то существует 25 + 1 2 разных компонент спина, т. е. Шз принимает значения /2 или — /2. Такова была гипотеза Уленбека и Гаудсмита. Позднее выяснилось, что еще за три года до их гипотезы Штерном и Герлахом были выполнены эксперименты, подтверждающие этот вывод. Эти ученые пропускали пучок атомов серебра через неоднородное магнитное поле и установили, что он расщепляется на два пучка, так как если бы атомы серебра имели именно два допустимых направления магнитных моментов относительно направления магнитного поля. Так как в атомах серебра имеется лишь один электрон на 5-орбитали сверх замкнутой (и поэтому сферической) оболочки, поведение атомов серебра в магнитном поле определяется свойствами этого электрона.
.., которые может принимать квантовое число орбитального углового момента электрона. В предыдущей главе было показано, что орбитали с данным значением / вырождены 2/-+- 1-кратно, каждое из 2/-+- 1-состояний соответствует различным значениям т. По аналогии следует ожидать, что так как для электрона 5 = /2, то существует 25 + 1 2 разных компонент спина, т. е. Шз принимает значения /2 или — /2. Такова была гипотеза Уленбека и Гаудсмита. Позднее выяснилось, что еще за три года до их гипотезы Штерном и Герлахом были выполнены эксперименты, подтверждающие этот вывод. Эти ученые пропускали пучок атомов серебра через неоднородное магнитное поле и установили, что он расщепляется на два пучка, так как если бы атомы серебра имели именно два допустимых направления магнитных моментов относительно направления магнитного поля. Так как в атомах серебра имеется лишь один электрон на 5-орбитали сверх замкнутой (и поэтому сферической) оболочки, поведение атомов серебра в магнитном поле определяется свойствами этого электрона. Поэтому расщепление, наблюдавшееся Штерном и Герлахом, очевидно, обусловлено существованием двух возможных значений Шз для электрона. [c.52]
Поэтому расщепление, наблюдавшееся Штерном и Герлахом, очевидно, обусловлено существованием двух возможных значений Шз для электрона. [c.52]
Мы ДОЛЖНЫ рассмотреть еще четвертое и последнее квантовое число — спиновое. В 1925 г. Уленбек и Гоудсмнт на основе тщательного анализа атомных спектров щелочных металлов [c.41]
У электронов со спином /г квантовое число спинового углового момента может принимать значения ms= 7г, что в отсутствие магнитного поля приводит к наличию дважды вырожденных спиновых энергетических состояний. При наложении магнитного поля это вырождение снимается. В состоянии с низщей энергией магнитный момент ориентирован по полю, что соответствует nls= —7г, тогда как в состоянии с более высокой энергией П1а= + Ч2 и магнитный момент направлен противоположно полю, в спектрах ЭПР и ЯМР имеется некоторое сходство, которое поможет нам понять основы ЭПР. В ЯМР два различных энергетических состояния возникают вследствие различной ориентации ядерных магнитных моментов относительно наложенного поля и переход Между ними происходил при наложении радиочастотного поля соответствующей частоты. В ЭПР переход между двумя различными энергетическими состояниями, различающимися ориентацией электронного спинового момента, происходит при поглощении кванта излучения в радиочастотной или микроволновой области. Энергия перехода передается выражением [c.353]
В ЭПР переход между двумя различными энергетическими состояниями, различающимися ориентацией электронного спинового момента, происходит при поглощении кванта излучения в радиочастотной или микроволновой области. Энергия перехода передается выражением [c.353]
Но электрон способен также вращаться вокруг собственной оси — эффект, именуемый спином (по-английски spin—веретено). Возможно вращение или по часовой стрелке или против. Оно характеризуется третьим квантовым числом — спиновым квантовым [c.78]
Главное кван- товое число п Орби- тальное кванто- вое число 1 Магнитное квантовое число Спиновое квантовое число Число состоя- ний элек- трона Квантовое состояние электрона Общее число состоя- ний элек- трона [c.23]
Четвертое квантовое число — спиновое (х) характеризует вращение электрона вокруг собственной оси. Подобно волчку, электрон может вращаться по часовой стрелке или против нее. ЭлеК троны, имеющие одинаковые квантовые числа /г, / и т (занимающие одну электронную орбиталь), но различающиеся спином, образуют электронную пару. Далее мы узнаем, что именно электронные пары ответственны за образование связей в молекулах органических веществ. [c.29]
Далее мы узнаем, что именно электронные пары ответственны за образование связей в молекулах органических веществ. [c.29]
Справочник квантовых чисел электронов – Электронный учебник K-tree
Существует четыре квантовых числа электронов и о каждом из них – по порядку.
Главное квантовое число N характеризует энергетический уровень, другими словами это размер энергетического уровня, чем больше число N – тем больше радиус, на котором находятся электроны.
Орбитальное квантовое число L обозначает форму той области, в которой может находится электрон, число L имеет значения s (L=0),p (L=1), d (L=2),f (L=3) и также называется энергетической оболочкой или энергетическим подуровнем.
На каждой орбитали находится «2·L + 1» орбиталей, магнитное квантовое число Ml обозначает орбиталь, на котором находится электрон. Ml может принимать значения ±L.
И последнее квантовое число – спин, он принимает два значения: +½ и -½, обозначающий соответственно
прямое и обратное вращение электрона.
Квантовые числа элемента, или квантовые числа электрона – это четыре квантовых числа, характеризующих состояние внешнего электрона в атоме, ниже дана таблица квантовых чисел электронов любого атома:
1
H
водород
1s 1
N = 1 L = 0 Ml = 0 Ms = +½
2
He
гелий
1s 2
N = 1 L = 0 Ml = 0 Ms = -½
3
Li
литий
2s 1
N = 2 L = 0 Ml = 0 Ms = +½
4
Be
бериллий
2s 2
N = 2 L = 0 Ml = 0 Ms = -½
5
B
бор
2p 1
N = 2 L = 1 Ml = -1 Ms = +½
6
C
углерод
2p 2
N = 2 L = 1 Ml = 0 Ms = +½
7
N
азот
2p 3
N = 2 L = 1 Ml = 1 Ms = +½
8
O
кислород
2p 4
N = 2 L = 1 Ml = -1 Ms = -½
9
F
фтор
2p 5
N = 2 L = 1 Ml = 0 Ms = -½
10
Ne
неон
2p 6
N = 2 L = 1 Ml = 1 Ms = -½
11
Na
натрий
3s 1
N = 3 L = 0 Ml = 0 Ms = +½
12
Mg
магний
3s 2
N = 3 L = 0 Ml = 0 Ms = -½
13
Al
алюминий
3p 1
N = 3 L = 1 Ml = -1 Ms = +½
14
Si
кремний
3p 2
N = 3 L = 1 Ml = 0 Ms = +½
15
P
фосфор
3p 3
N = 3 L = 1 Ml = 1 Ms = +½
16
S
сера
3p 4
N = 3 L = 1 Ml = -1 Ms = -½
17
Cl
хлор
3p 5
N = 3 L = 1 Ml = 0 Ms = -½
18
Ar
аргон
3p 6
N = 3 L = 1 Ml = 1 Ms = -½
19
K
калий
4s 1
N = 4 L = 0 Ml = 0 Ms = +½
20
Ca
кальций
4s 2
N = 4 L = 0 Ml = 0 Ms = -½
21
Sc
скандий
3d 1
N = 3 L = 2 Ml = -2 Ms = +½
22
Ti
титан
3d 2
N = 3 L = 2 Ml = -1 Ms = +½
23
Vd
ванадий
3d 3
N = 3 L = 2 Ml = 0 Ms = +½
24
Cr
хром
3d 5
N = 3 L = 2 Ml = 2 Ms = +½
25
Mn
марганец
3d 5
N = 3 L = 2 Ml = 2 Ms = +½
26
Fe
железо
3d 6
N = 3 L = 2 Ml = -2 Ms = -½
27
Co
кобальт
3d 7
N = 3 L = 2 Ml = -1 Ms = -½
28
Ni
никель
3d 8
N = 3 L = 2 Ml = 0 Ms = -½
29
Cu
медь
3d 10
N = 3 L = 2 Ml = 2 Ms = -½
30
Zn
цинк
3d 10
N = 3 L = 2 Ml = 2 Ms = -½
31
Ga
галлий
4p 1
N = 4 L = 1 Ml = -1 Ms = +½
32
Ge
германий
4p 2
N = 4 L = 1 Ml = 0 Ms = +½
33
As
мышьяк
4p 3
N = 4 L = 1 Ml = 1 Ms = +½
34
Se
селен
4p 4
N = 4 L = 1 Ml = -1 Ms = -½
35
Br
бром
4p 5
N = 4 L = 1 Ml = 0 Ms = -½
36
Kr
криптон
4p 6
N = 4 L = 1 Ml = 1 Ms = -½
37
Rb
рубидий
5s 1
N = 5 L = 0 Ml = 0 Ms = +½
38
Sr
стронций
5s 2
N = 5 L = 0 Ml = 0 Ms = -½
39
Y
иттрий
4d 1
N = 4 L = 2 Ml = -2 Ms = +½
40
Zr
цирконий
4d 2
N = 4 L = 2 Ml = -1 Ms = +½
41
Nb
ниобий
4d 4
N = 4 L = 2 Ml = 1 Ms = +½
42
Mo
молибден
4d 5
N = 4 L = 2 Ml = 2 Ms = +½
43
Tc
технеций
4d 5
N = 4 L = 2 Ml = 2 Ms = +½
44
Ru
рутений
4d 7
N = 4 L = 2 Ml = -1 Ms = -½
45
Rh
родий
4d 8
N = 4 L = 2 Ml = 0 Ms = -½
46
Pd
палладий
4d 10
N = 4 L = 2 Ml = 2 Ms = -½
47
Ag
серебро
4d 10
N = 4 L = 2 Ml = 2 Ms = -½
48
Cd
кадмий
4d 10
N = 4 L = 2 Ml = 2 Ms = -½
49
In
индий
5p 1
N = 5 L = 1 Ml = -1 Ms = +½
50
Sn
олово
5p 2
N = 5 L = 1 Ml = 0 Ms = +½
51
Sb
сурьма
5p 3
N = 5 L = 1 Ml = 1 Ms = +½
52
Te
теллур
5p 4
N = 5 L = 1 Ml = -1 Ms = -½
53
I
йод
5p 5
N = 5 L = 1 Ml = 0 Ms = -½
54
Xe
ксенон
5p 6
N = 5 L = 1 Ml = 1 Ms = -½
55
Cs
цезий
6s 1
N = 6 L = 0 Ml = 0 Ms = +½
56
Ba
барий
6s 2
N = 6 L = 0 Ml = 0 Ms = -½
57
La
лантан
5d 1
N = 5 L = 2 Ml = -2 Ms = +½
58
Ce
церий
4f 2
N = 4 L = 3 Ml = -2 Ms = +½
59
Pr
празеодим
4f 3
N = 4 L = 3 Ml = -1 Ms = +½
60
Nd
неодим
4f 4
N = 4 L = 3 Ml = 0 Ms = +½
61
Pm
прометий
4f 5
N = 4 L = 3 Ml = 1 Ms = +½
62
Sm
самарий
4f 6
N = 4 L = 3 Ml = 2 Ms = +½
63
Eu
европий
4f 7
N = 4 L = 3 Ml = 3 Ms = +½
64
Gd
гадолиний
5d 1
N = 5 L = 2 Ml = -2 Ms = +½
65
Tb
тербий
4f 9
N = 4 L = 3 Ml = -2 Ms = -½
66
Dy
диспрозий
4f 10
N = 4 L = 3 Ml = -1 Ms = -½
67
Ho
гольмий
4f 11
N = 4 L = 3 Ml = 0 Ms = -½
68
Er
эрбий
4f 12
N = 4 L = 3 Ml = 1 Ms = -½
69
Tm
тулий
4f 13
N = 4 L = 3 Ml = 2 Ms = -½
70
Yb
иттербий
4f 14
N = 4 L = 3 Ml = 3 Ms = -½
71
Lu
лютеций
5d 1
N = 5 L = 2 Ml = -2 Ms = +½
72
Hf
гафний
5d 2
N = 5 L = 2 Ml = -1 Ms = +½
73
Ta
тантал
5d 3
N = 5 L = 2 Ml = 0 Ms = +½
74
W
вольфрам
5d 4
N = 5 L = 2 Ml = 1 Ms = +½
75
Re
рений
5d 5
N = 5 L = 2 Ml = 2 Ms = +½
76
Os
осмий
5d 6
N = 5 L = 2 Ml = -2 Ms = -½
77
Ir
иридий
5d 7
N = 5 L = 2 Ml = -1 Ms = -½
78
Pt
платина
5d 9
N = 5 L = 2 Ml = 1 Ms = -½
79
Au
золото
5d 10
N = 5 L = 2 Ml = 2 Ms = -½
80
Hg
ртуть
5d 10
N = 5 L = 2 Ml = 2 Ms = -½
81
Tl
таллий
6p 1
N = 6 L = 1 Ml = -1 Ms = +½
82
Pb
свинец
6p 2
N = 6 L = 1 Ml = 0 Ms = +½
83
Bi
висмут
6p 3
N = 6 L = 1 Ml = 1 Ms = +½
84
Po
полоний
6p 4
N = 6 L = 1 Ml = -1 Ms = -½
85
At
астат
6p 5
N = 6 L = 1 Ml = 0 Ms = -½
86
Rn
радон
6p 6
N = 6 L = 1 Ml = 1 Ms = -½
87
Fr
франций
7s 1
N = 7 L = 0 Ml = 0 Ms = +½
88
Ra
радий
7s 2
N = 7 L = 0 Ml = 0 Ms = -½
89
Ac
актиний
7d 1
N = 7 L = 2 Ml = -2 Ms = +½
90
Th
торий
7d 2
N = 7 L = 2 Ml = -1 Ms = +½
91
Pa
протактиний
7d 1
N = 7 L = 2 Ml = -2 Ms = +½
92
U
уран
7d 1
N = 7 L = 2 Ml = -2 Ms = +½
93
Np
нептуний
7d 1
N = 7 L = 2 Ml = -2 Ms = +½
94
Pu
плутоний
7d 1
N = 7 L = 2 Ml = -2 Ms = +½
95
Am
америций
5f 7
N = 5 L = 3 Ml = 3 Ms = +½
96
Cm
кюрий
7d 1
N = 7 L = 2 Ml = -2 Ms = +½
97
Bk
берклий
7d 1
N = 7 L = 2 Ml = -2 Ms = +½
98
Cf
калифорний
5f 10
N = 5 L = 3 Ml = -1 Ms = -½
99
Es
эйнштейний
5f 11
N = 5 L = 3 Ml = 0 Ms = -½
100
Fm
фермий
5f 12
N = 5 L = 3 Ml = 1 Ms = -½
101
Md
менделеевий
5f 13
N = 5 L = 3 Ml = 2 Ms = -½
102
No
нобелий
5f 14
N = 5 L = 3 Ml = 3 Ms = -½
103
Lr
лоуренсий
6d 1
N = 6 L = 2 Ml = -2 Ms = +½
104
Rf
резерфордий
6d 2
N = 6 L = 2 Ml = -1 Ms = +½
105
Db
дубний
6d 3
N = 6 L = 2 Ml = 0 Ms = +½
106
Sg
сиборгий
6d 4
N = 6 L = 2 Ml = 1 Ms = +½
107
Bh
борий
6d 5
N = 6 L = 2 Ml = 2 Ms = +½
108
Hs
хассий
6d 6
N = 6 L = 2 Ml = -2 Ms = -½
109
Mt
мейтнерий
6d 7
N = 6 L = 2 Ml = -1 Ms = -½
110
Ds
дармштадтий
6d 8
N = 6 L = 2 Ml = 0 Ms = -½
111
Rg
рентгений
6d 9
N = 6 L = 2 Ml = 1 Ms = -½
112
Cn
коперниций
6d 10
N = 6 L = 2 Ml = 2 Ms = -½
113
Nh
нихоний
7p 1
N = 7 L = 1 Ml = -1 Ms = +½
114
Fl
флеровий
7p 2
N = 7 L = 1 Ml = 0 Ms = +½
115
Mc
московий
7p 3
N = 7 L = 1 Ml = 1 Ms = +½
116
Lv
ливерморий
7p 4
N = 7 L = 1 Ml = -1 Ms = -½
117
Ts
теннесcин
7p 5
N = 7 L = 1 Ml = 0 Ms = -½
118
Og
оганесон
7p 6
N = 7 L = 1 Ml = 1 Ms = -½
Квантовые числа | CHEMEGE.
 RU
RUМатериалы портала onx.distant.ru
Общая характеристика квантовых чисел
Принцип (запрет) Паули
Правило Хунда
Примеры решения задач
Задачи для самостоятельного решения
Общая характеристика квантовых чисел
Главное квантовое число n характеризует энергию электрона в атоме и размер электронной орбитали. Оно соответствует также номеру электронного слоя, на котором находится электрон. Совокупность электронов в атоме с одинаковым значением главного квантового числа n называют электронным слоем (энергетическим уровнем). n – принимает значения 1, 2, 3, …, ∞ . Энергетические уровни обозначают прописными латинскими буквами:
| Значение n | 1 | 2 | 3 | 4 | 5 | 6 |
| Обозначение слоя | K | L | M | N | O | P |
Различия в энергиях электронов, принадлежащих к различным подуровням данного энергетического уровня, отражает побочное (орбитальное) квантовое число l. Электроны в атоме с одинаковыми значениями n и l составляют энергетический подуровень (электронную оболочку). Максимальное число электронов в оболочке Nl:
Электроны в атоме с одинаковыми значениями n и l составляют энергетический подуровень (электронную оболочку). Максимальное число электронов в оболочке Nl:
Nl = 2(2l + 1). (1)
Побочное квантовое число принимает целые значения 0, 1, … (n – 1). Обычно l обозначается не цифрами, а буквами:
| Значение l | 0 | 1 | 2 | 3 | 4 |
| Обозначение орбитали | s | p | d | f | g |
Орбиталь – пространство вокруг ядра, в котором наиболее вероятно нахождение электрона.
Побочное (орбитальное) квантовое число l характеризует различное энергетическое состояние электронов на данном уровне, форму орбитали, орбитальный момент импульса электрона.
Таким образом, электрон, обладая свойствами частицы и волны, движется вокруг ядра, образуя электронное облако, форма которого зависит от значения l. Так, если l = 0, (s-орбиталь), то электронное облако имеет сферическую симметрию. При l = 1 (p-орбиталь) электронное облако имеет форму гантели. d-орбитали имеют различную форму: dz2 — гантель, расположенная по оси Z с тором в плоскости X – Y, dx2 — y2 — две гантели, расположенные по осям X и Y; dxy, dxz, dyz, — две гантели, расположенные под 45oк соответствующим осям.
- Формы электронных облаков для различных состояний электронов в атомах
Магнитное квантовое число ml характеризует ориентацию орбитали в пространстве, а также определяет величину проекции орбитального момента импульса на ось Z. ml принимает значения от +l до — l, включая 0. Общее число значений ml равно числу орбиталей в данной электронной оболочке.
Общее число значений ml равно числу орбиталей в данной электронной оболочке.
Магнитное спиновое квантовое число ms характеризует проекцию собственного момента импульса электрона на ось Z и принимает значения +1/2 и –1/2 в единицах h/2p (h – постоянная Планка).
Принцип (запрет) Паули
В атоме не может быть двух электронов со всеми четырьмя одинаковыми квантовыми числами. Принцип Паули определяет максимальное число электронов Nn, на электронном слое с номером n:
Nn = 2n2. (2)
На первом электронном слое может находиться не более двух электронов, на втором – 8, на третьем – 18 и т. д.
Правило Хунда
Заполнение энергетических уровней происходит таким образом, чтобы суммарный спин был максимальным. Например, три р-электрона на орбиталях р-оболочки располагаются следующим образом:
Таким образом, каждый электрон занимает одну р-орбиталь.
Примеры решения задач
Задача 1. Охарактеризовать квантовыми числами электроны атома углерода в невозбужденном состоянии. Ответ представить в виде таблицы.
Решение. Электронная формула атома углерода: 1s22s22p2. В первом слое атома углерода находятся два s-электрона с антипараллельными спинами, для которых n = 1. Для двух s-электронов второго слоя n = 2. Спины двух р-электронов второго слоя параллельны; для них m s= +1/2.
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
| 6 | 2 | 1 | 0 | +1/2 |
Задача 2. Охарактеризовать квантовыми числами внешние электроны атома кислорода в основном состоянии. Ответ представить в виде таблицы.
Охарактеризовать квантовыми числами внешние электроны атома кислорода в основном состоянии. Ответ представить в виде таблицы.
Решение. Электронная формула атома кислорода: 1s22s22p4. Во внешнем слое у этого атома находятся 6 электронов 2s22p4. Значения их квантовых чисел приведены в таблице.
| № электрона | n | l | ml | ms |
| 1 | 2 | 0 | 0 | +1/2 |
| 2 | 2 | 0 | 0 | –1/2 |
| 3 | 2 | 1 | 1 | +1/2 |
| 4 | 2 | 1 | 0 | +1/2 |
| 5 | 2 | 1 | –1 | +1/2 |
| 6 | 2 | 1 | 1 | –1/2 |
Задача 3. Охарактеризовать квантовыми числами пять электронов, находящихся в состоянии 4d. Ответ представить в виде таблицы.
Охарактеризовать квантовыми числами пять электронов, находящихся в состоянии 4d. Ответ представить в виде таблицы.
Решение. Согласно правилу Хунда электроны в квантовых ячейках располагаются следующим образом:
Значения главного, побочного и спинового квантовых чисел у электронов одинаковы и равны n=4, l=2, ms=+1/2. Рассматриваемые электроны отличаются значениями квантовых чисел ml.
| № электрона | n | l | ml | ms |
| 1 | 4 | 2 | 2 | +1/2 |
| 2 | 4 | 2 | 1 | +1/2 |
| 3 | 4 | 2 | 0 | +1/2 |
| 4 | 4 | 2 | –1 | +1/2 |
| 5 | 4 | 2 | –2 | +1/2 |
Задача 4. Рассчитать максимальное число электронов в электронном слое с n = 4.
Рассчитать максимальное число электронов в электронном слое с n = 4.
Решение. Максимальное число электронов, обладающих данным значением главного квантового числа, рассчитываем по формуле (2). Следовательно, в третьем энергетическом уровне может быть не более 32 электронов.
Задача 5. Рассчитать максимальное число электронов в электронной оболочке с l = 3.
Решение:
Максимальное число электронов в оболочке определяется выражением (1). Таким образом, максимальное число электронов в электронной оболочке с l = 3 равно 14.
Задачи для самостоятельного решения
1. Охарактеризовать квантовыми числами электроны атома бора в основном состоянии. Ответ представить в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
2. Охарактеризовать квантовыми числами d-электроны атома железа в основном состоянии. Ответ представить в виде таблиц:
Охарактеризовать квантовыми числами d-электроны атома железа в основном состоянии. Ответ представить в виде таблиц:
Расположение 3d-электронов атома железа на орбиталях:
Значения квантовых чисел этих электронов:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
Шесть 3d-электронов атома железа располагаются на орбиталях следующим образом
Квантовые числа этих электронов приведены в таблице
| № электрона | n | l | ml | ms |
| 1 | 3 | 2 | 2 | +1/2 |
| 2 | 3 | 2 | 1 | +1/2 |
| 3 | 3 | 2 | 0 | +1/2 |
| 4 | 3 | 2 | — 1 | +1/2 |
| 5 | 3 | 2 | — 2 | +1/2 |
| 6 | 3 | 2 | 2 | — 1/2 |
3. Каковы возможные значения магнитного квантового числа ml, если орбитальное квантовое число l = 3?
Каковы возможные значения магнитного квантового числа ml, если орбитальное квантовое число l = 3?
Ответ: ml = +3; +2; +1; 0, — 1, — 2, — 3.
4. Охарактеризовать квантовыми числами находящиеся во втором электронном слое электроны:
Ответ представить в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
| 7 | ? | ? | ? | ? |
Ответ: Электронная конфигурация 2s22p5. Главное квантовое число для всех электронов равно 2. Для s электронов l = 0, для р-электронов l = 1.
Главное квантовое число для всех электронов равно 2. Для s электронов l = 0, для р-электронов l = 1.
| № электрона | n | l | ml | ms |
| 1 | 2 | 0 | 0 | +1/2 |
| 2 | 2 | 0 | 0 | — 1/2 |
| 3 | 2 | 1 | 1 | +1/2 |
| 4 | 2 | 1 | 0 | +1/2 |
| 5 | 2 | 1 | — 1 | +1/2 |
| 6 | 2 | 1 | 1 | — 1/2 |
| 7 | 2 | 1 | 0 | — 1/2 |
5. Определить максимальное число электронов на электронном слое, для которого главное квантовое число n = 6.
6. Определить максимальное число электронов на электронной оболочке, для которой побочное квантовое число l = 4.
7. Определить максимальное число электронов на третьем слое.
8. Определить максимальное число электронов на 5d электронной оболочке.
9. Какие значения может принимать орбитальное (побочное) квантовое число l?
Ответ: от 0 до ( n — 1).
Полное спиновое квантовое число – Большая Энциклопедия Нефти и Газа, статья, страница 1
Полное спиновое квантовое число
Cтраница 1
Полное спиновое квантовое число S находится по тем же правилам. Для замкнутых оболочек 50 и значения полного спина любой электронной системы определяются спинами электронов лишь в незамкнутых оболочках. [1]
[1]
Полное спиновое квантовое число S находится по аналогичным правилам. Для замкнутых оболочек 5 0, и величина полного спина любой электронной системы определяется спинами электронов лишь в незамкнутых оболочках. [2]
Полное спиновое квантовое число S находится по тем же правилам. Для замкнутых оболочек 50 и значения полного спина любой электронной системы определяются спинами электронов лишь в незамкнутых оболочках. [3]
Число 5 называется полным спиновым квантовым числом группы электронов, или, более кратко, полным спином. [4]
S ( не следует путать символ 5 для полного спинового квантового числа с аналогичным символом для нулевого значения полного орбитального квантового числа), а также полный орбитальный угловой момент L атома. Для многоэлектронных атомов L и S являются лишь приближенными квантовыми числами. Квантовые числа L и 5 не поддаются прямому экспериментальному определению. Чем больше атомный номер элемента, тем хуже выполняется рассматриваемое приближение. Для заданной электронной конфигурации атома каждый индивидуальный символ терма соответствует состоянию с различающейся энергией.
[5]
Квантовые числа L и 5 не поддаются прямому экспериментальному определению. Чем больше атомный номер элемента, тем хуже выполняется рассматриваемое приближение. Для заданной электронной конфигурации атома каждый индивидуальный символ терма соответствует состоянию с различающейся энергией.
[5]
При этом / J, / 2 и Хз образуют триплетное состояние с полным спиновым квантовым числом 5 1 и с Sz 1, – 1, 0, а ул – синглетное состояние с 5 0 и Sz 0, Построение спин-орбиталей для молекулы зависит от применяемого приближенного метода. Как раз в этом отношении методы МО и ВС различаются весьма существенно. [6]
Независимость гамильтониана от спиновых координат электронов имеет важное теоретическое следствие: в этом случае гамильтониан коммутирует с оператором спина, и поэтому полное спиновое квантовое число является хорошим квантовым числом для характеристики электронных состояний.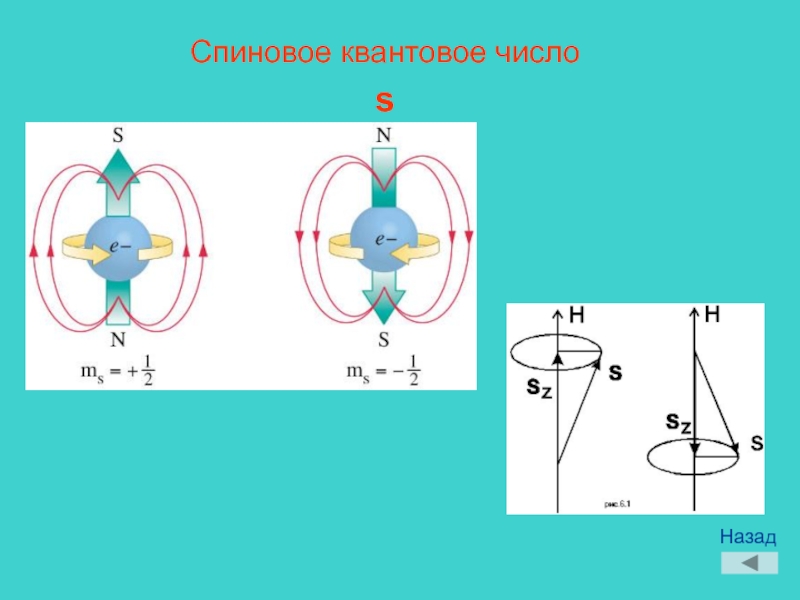 [7]
[7]
Предположим, что мы имеем атомную или молекулярную систему, для которой возможны два состояния, причем все электроны занимают одни и те же орбиты, но отличаются своими полными спиновыми квантовыми числами. Как мы видели, вследствие сил Паули электроны, имеющие одинаковый спин, стремятся избегать один другого, что повышает стабильность системы. Поэтому можно заключить, что наиболее стабильным состоянием группы электронов на данном наборе орбит будет такое состояние, в котором наибольшее возможное число электронов имеют компоненты спинов, направленные в одну сторону. S-квантовое число полного спина) является прямой мерой числа параллельных спинов, мы можем установить общее правило, согласно которому при прочих равных условиях наиболее стабильным является состояние наибольшей мультиплетности. Это известно под названием пропила мультиплетности Гунда. [8]
Обсудив важнейшие правила отбора, согласно которым должны осуществляться d – d – переходы, перейдем к исследованию причин увеличения интенсивности полос. Ранее уже было сформулировано, что в отсутствие спин-орбитального взаимодействия полное спиновое квантовое число не должно изменяться при поглощении излучения. Однако поскольку спиновое и орбитальное движения, хотя и слабо, но связаны, в интеграл момента перехода должны входить спин-орбитальные волновые функции для основного и высших состояний. Кроме того, надо учесть происходящее в небольшой степени смешивание состояний, зависящее от разности энергий орбитальных состояний и константы спин-орбитального взаимодействия. Поэтому электронные переходы, осуществляющиеся между состояниями с различной мультиплетностью, можно представить как переходы между компонентами каждого орбитального состояния с одной и той же мультиплетностью.
[10]
Ранее уже было сформулировано, что в отсутствие спин-орбитального взаимодействия полное спиновое квантовое число не должно изменяться при поглощении излучения. Однако поскольку спиновое и орбитальное движения, хотя и слабо, но связаны, в интеграл момента перехода должны входить спин-орбитальные волновые функции для основного и высших состояний. Кроме того, надо учесть происходящее в небольшой степени смешивание состояний, зависящее от разности энергий орбитальных состояний и константы спин-орбитального взаимодействия. Поэтому электронные переходы, осуществляющиеся между состояниями с различной мультиплетностью, можно представить как переходы между компонентами каждого орбитального состояния с одной и той же мультиплетностью.
[10]
Показаны также возможные конфигурации спинов d5 – HOHa же-леза ( Ш) в комплексах различной симметрии. И в октаэдриче-ском ( Oh), и в тетраэдрическом ( Td) комплексах высокоспиновое состояние соответствует пяти неспаренным электронам, а низкоспиновое состояние – одному неспаренному электрону. Поскольку электронный спин равен 1 / 2, полные спиновые квантовые числа составляют в этих двух случаях 5 / 2 и V2 соответственно.
[11]
Поскольку электронный спин равен 1 / 2, полные спиновые квантовые числа составляют в этих двух случаях 5 / 2 и V2 соответственно.
[11]
Сказанное является лишь более формальным выражением мысли, что при таких переходах не должно изменяться полное спиновое квантовое число. [12]
Существуют ионы переходных металлов, содержащие один, два, три и даже семь неспаренных электронов. Как указывалось в разд. S равно сумме спиновых квантовых чисел ( s1 / 2) отдельных электронов. Пользуясь уравнением (25.3) и подставляя в него значения S вместо s, можно вычислить магнитный момент, обусловленный только спином электронов, так называемое чисто спиновое значение момента для любого атома или иона, если для него известно полное спиновое квантовое число S. [13]
Страницы: 1
Задачи к разделу основы строения атомов
Решение: Главное квантовое число n характеризует энергию и размер орбитали и принимает значения только целых чисел от 1 до ∞.
Побочное квантовое число (орбитальное) l характеризует геометрическую форму орбитали и для каждого энергетического уровня принимает значения целых чисел от 0 до (n-1).
В многоэлектронных атомах энергия электрона зависит и от значения l. Поэтому состояние электрона, характеризующееся различными значениями l называют энергетическими подуровнями:
l=0, s-орбитали имеют форму шара
l=1, p-орбитали имеют форму гантели
l=2, d-орбитали имеют более сложную форму
l=3, f-орбитали имеют более сложную форму
Магнитное квантовое число ml характеризует направление орбитали в пространстве и принимает значение от –l … 0 … +l .
s-подуровень характеризуется значением l=0, ml= 0
p-подуровень характеризуется значением l=1, ml= -1; 0; +1 (3 орбитали)
d-подуровень характеризуется значением l=2, ml= -2; -1; 0; +1; +2 (5 орбиталей)
f-подуровень характеризуется значением l=3, ml= -3; -2; -1; 0; +1; +2; +3 (7 орбиталей)
ml определяет количество орбиталей на данном энергетическом подуровне атома.
Спиновое квантовое число ms характеризует вращение электрона вокруг своей оси и принимает значениея + ½ и – ½.
На 4 уровне для внешнего слоя атома возможны 4s, 4p, 4d энергетические состояния.
Распишем для них набор квантовых чисел:
4s: n =4, l = 0, ml= (2l+1)=1 (1 орбиталь), ms = ±½
4p: n =4, l = 1, ml= (2l+1)=3 (3 орбитали -1,0,+1), ms = ±3½
4d: n =4, l = 2, ml= (2l+1)=5 (5 орбитали -2,-1,0,+1,+2), ms = ±5½
ms указана для максимального числа электронов.
Максимальное число электронов на на p-подуровне равно 6 согласно принципу Паули:
2(2l+1)=2(2+1)=6
Что это такое Квантовые числа. Энциклопедия
Пользователи также искали:
магнитное квантовое число, квантовое, число, Магнитное, магнитное, Магнитное квантовое число, числа, квантовые, квантовые числа химия, квантовые числа физика, спиновое квантовое число, орбитальное квантовое число, главное квантовое число, определяет, определить, физика, спиновое, орбитальное, какие, значения, принимает, орбиталей, подуровня, главное, химия, Орбитальное, Орбитальное квантовое число, характеризует, квантовые числа как определить, квантовые числа пример,
Квантовое число спина: определение и пример – научный класс [видео 2021 года]
Парамагнетизм и диамагнетизм
Спин электрона заставляет его вести себя как маленький магнит, в том смысле, что спин определяет магнитные свойства атома. Электроны – очень маленькие частицы, и их движение ограничено. Однако это движение по-прежнему создает небольшое магнитное поле.
Электроны – очень маленькие частицы, и их движение ограничено. Однако это движение по-прежнему создает небольшое магнитное поле.
Например, в атоме все электроны спарены по орбиталям. Спины, поскольку они имеют значения с противоположными знаками (+1/2 и -1/2), компенсируют друг друга.Поэтому мы можем сказать, что атом диамагнитен. Диамагнетизм атомов имеют все свои электроны спаренными, и на каждой орбитали, если вы сложите их спины, общее количество будет равно нулю, и они отталкивают магнитные поля.
Теперь давайте посмотрим на атом, на орбиталях которого находятся неспаренные электроны. Эти неспаренные электроны одни на своих орбиталях. Поэтому мы можем сказать, что эти атомы с неспаренными электронами парамагнитны. Парамагнитные атомов имеют неспаренные электроны, и они притягиваются к магнитному полю. Электрон на орбитали имеет чистый спин, поэтому спины не компенсируют друг друга. Фактически, весь атом будет иметь чистый спин.
Фактически, весь атом будет иметь чистый спин.
Определение квантового числа спина
Давайте рассмотрим следующие примеры, чтобы мы могли определить значение квантового числа спина на основе информации, приведенной в вопросе:
- Пример 1: Какое правильное значение для мс для последнего электрона, который выходит на орбитали ниже? Этот атом парамагнитен или диамагнитен?
Ответ: Правильное значение для мс = +1/2, так как последний входящий электрон имеет ориентацию вращения вверх.Ни один из электронов не спарен, поэтому это показывает, что атом парамагнитен.
- Пример 2: Какое правильное значение для мс для последнего электрона, который выходит на орбитали ниже? Этот атом парамагнитен или диамагнитен?
Ответ: Правильное значение для мс = -1/2, так как последний входящий электрон имеет ориентацию со спином вниз. Все электроны спарены, поэтому этот атом диамагнитен.
Все электроны спарены, поэтому этот атом диамагнитен.
- Пример 3: Каково квантовое число спина у электрона, у которого на d-орбитали 4 электрона?
Ответ: Для 4 электронов на d-орбите орбитали будут выглядеть так:
Последний входящий электрон имеет ориентацию со спином вверх. Следовательно, ответ будет мс = +1/2
Резюме урока
Спиновое квантовое число сообщает нам ориентацию электрона на орбитали и имеет два возможных значения: мс = +1/2 для вращение вверх и мс = -1/2 для вращения вниз.Максимальное количество двух электронов может занимать орбиталь, и если есть два электрона, то их ориентации противоположны друг другу: один электрон будет вращаться вверх, а другой – вниз. Если все электроны спарены в атоме, нет чистого спина, потому что спины компенсируют друг друга. Следовательно, можно сказать, что этот атом диамагнитен и отталкивает приложенное магнитное поле. Если в атоме есть неспаренные электроны, чистый спин остается, поэтому мы можем сказать, что этот атом парамагнитен и притягивается к приложенному магнитному полю.
Если в атоме есть неспаренные электроны, чистый спин остается, поэтому мы можем сказать, что этот атом парамагнитен и притягивается к приложенному магнитному полю.
Определения, которые нужно знать
- Спиновое квантовое число: Число, которое описывает ориентацию электрона, занимающего орбиталь
- Диамагнетик: атом со спаренными электронами
- Парамагнетик: атом с неспаренными электронами
Результаты обучения
По завершении этого урока вы должны быть готовы:
- Определить квантовое число спина, парамагнитное и диамагнитное
- Вспомните два возможных значения спинового квантового числа и объясните, что они означают
- Расскажите, как вычислить значение спинового квантового числа
– Chemistry LibreTexts
- Последнее обновление
- Сохранить как PDF
- Комбинации квантовых чисел
- Ссылки
Спиновое квантовое число (\ (m_s \)) описывает угловой момент электрона.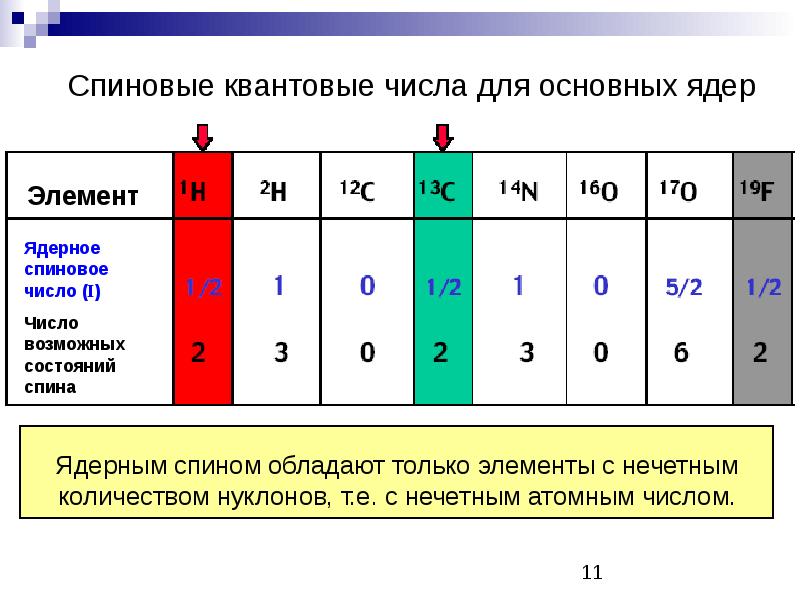 Электрон вращается вокруг оси и имеет как угловой момент, так и орбитальный угловой момент. Поскольку угловой момент является вектором, спиновые квантовые числа имеют как величину (1/2), так и направление (+ или -).
Электрон вращается вокруг оси и имеет как угловой момент, так и орбитальный угловой момент. Поскольку угловой момент является вектором, спиновые квантовые числа имеют как величину (1/2), так и направление (+ или -).
Каждая орбиталь может содержать только два электрона. Один электрон будет иметь спин +1/2, а другой – спин -1/2. Электроны любят заполнять орбитали, прежде чем они начнут образовывать пары. Следовательно, первый электрон на орбите будет иметь спин +1/2. После того, как все орбитали наполовину заполнены, электроны начинают спариваться.Этот второй электрон на орбите будет иметь спин -1/2. Если на одной орбитали находятся два электрона, они будут вращаться в противоположных направлениях.
Комбинации квантовых чисел
- Три квантовых числа ( n , l и m ), описывающие орбиталь, являются целыми числами: 0, 1, 2, 3.
- Главное квантовое число ( n ) не может быть нулевым. Допустимые значения n , следовательно, 1, 2, 3, 4 .
 ..
.. - Угловое квантовое число ( l ) может быть любым целым числом от 0 до n – 1.
- Если n = 3, l может быть 0, 1 или 2.
- Магнитное квантовое число ( м ) может быть любым целым числом от – l до + l .
- Если l = 2, m может быть -2, -1, 0, +1 или +2.
- Орбитали с одинаковым значением главного квантового числа образуют Оболочку (n).
- Орбитали внутри оболочек разделены на подоболочки (l)
- s: l = 0 p : l = 1 d : l = 2 f : l = 3
Упражнение \ (\ PageIndex {1} \): Tungsten
Что такое квантовое число спина для вольфрама (символ W)?
- Ответ
Вольфрам имеет 4 электрона на 5d-орбитали.Следовательно, на каждую орбиталь пойдет по 1 электрону (без спаривания).
 4-й электрон будет иметь спин +1/2.
4-й электрон будет иметь спин +1/2.
Упражнение \ (\ PageIndex {2} \): золото
Какое квантовое число спина у золота (символ Au)?
- Ответ
Золото имеет 9 электронов на 5d орбитали. Таким образом, электроны начнут объединяться в пары, что означает, что 9-й электрон разделится на пары, что даст ему спин -1/2.
Упражнение \ (\ PageIndex {3} \): сера
Что такое квантовое число спина для серы (символ S)?
- Ответ
Сера имеет 4 электрона на 3p-орбиталях.Четвертый электрон на этой орбитали первым образует пару с другим электроном, что дает ему спин -1/2.
Список литературы
- Хаускрофт, Кэтрин Э. и Алан Г. Шарп. Неорганическая химия . 3-е изд. Харлоу: Pearson Education, 2008. Печать. (стр.15).
- Ностранд, Ван. Энциклопедия химии. 5-е изд.
 Джон Вили и сыновья, Inc., 2005. Печать. (стр. 1396).
Джон Вили и сыновья, Inc., 2005. Печать. (стр. 1396).
Квантовые числа и электронные конфигурации
Квантовые числа и электронные конфигурацииКвантовые числа и электрон Конфигурации
Квантовые числа
Модель Бора была одномерной моделью, которая использовала одно квантовое число для описания распределение электронов в атоме.Единственная важная информация – это размер . орбиты, которая описывалась квантовым числом n . Модель Шредингера позволил электрону занять трехмерное пространство. Следовательно, потребовалось три координаты или три квантовых числа , чтобы описать орбитали, на которых электроны можно найти.
Три координаты, которые происходят из волновых уравнений Шредингера, являются главными ( n ),
угловые ( l ) и магнитные ( m ) квантовые числа.Эти квантовые числа
описывают размер, форму и ориентацию в пространстве орбиталей атома.
Главное квантовое число ( n ) описывает размер орбитали. Например, орбитали, для которых n = 2, больше, чем те, для которых n = 1. Поскольку они имеют противоположные электрические заряды, электроны притягиваются к ядру атом. Следовательно, энергия должна быть поглощена для возбуждения электрона с орбитали, на которой электрон приближается к ядру ( n = 1) на орбиталь, в которой он находится дальше из ядра ( n = 2).Таким образом, главное квантовое число косвенно описывает энергию орбитали.
Угловое квантовое число ( l ) описывает форму орбитали. Орбитали имеют форму, которую лучше всего описать как сферическую ( l = 0), полярную ( l = 0). = 1) или клеверный лист ( l = 2). Они могут даже принимать более сложные формы, поскольку углового квантового числа становится больше.
Существует только один способ ориентирования сферы ( l = 0) в пространстве. Однако орбитали полярной ( l = 1) или клеверной ( l = 2) формы могут
указывают в разные стороны. Поэтому нам нужно третье квантовое число, известное как магнитное число .
квантовое число ( м ), чтобы описать ориентацию в пространстве определенного
орбитальный. (Его называют магнитным квантовым числом , потому что влияние различных
ориентации орбиталей впервые наблюдались в присутствии магнитного поля.)
Однако орбитали полярной ( l = 1) или клеверной ( l = 2) формы могут
указывают в разные стороны. Поэтому нам нужно третье квантовое число, известное как магнитное число .
квантовое число ( м ), чтобы описать ориентацию в пространстве определенного
орбитальный. (Его называют магнитным квантовым числом , потому что влияние различных
ориентации орбиталей впервые наблюдались в присутствии магнитного поля.)
Правила, регулирующие разрешенные комбинации Квантовые числа
- Три квантовых числа ( n , l и m ), описывающие орбитальную являются целыми числами: 0, 1, 2, 3 и т. д.
- Главное квантовое число ( n ) не может быть нулевым. Допустимые значения n поэтому равны 1, 2, 3, 4 и т. д.
- Угловое квантовое число ( l ) может быть любым целым числом от 0 до n – 1. Если n = 3, например, l может быть 0, 1 или 2.

- Магнитное квантовое число ( m ) может быть любым целым числом от – l . и + l . Если l = 2, m может быть -2, -1, 0, +1 или +2.
Оболочки и подоболочки орбиталей
Орбитали с одинаковым значением главного квантового числа образуют оболочку .Орбитали внутри оболочки делятся на подоболочек , которые имеют одинаковое значение угловое квантовое число. Химики описывают оболочку и подоболочку, в которых орбитальный принадлежит с двухсимвольным кодом, например 2 p или 4 f . Первый персонаж обозначает оболочку ( n = 2 или n = 4). Второй символ обозначает подоболочка. По соглашению следующие строчные буквы используются для обозначения различных подоболочки.
| с : | л = 0 | |
п. : : | л = 1 | |
| d : | л = 2 | |
| f : | л = 3 |
Хотя в первых четырех буквах нет шаблона ( s , p , d , f ), буквы продвигаются в алфавитном порядке с этой точки ( g , h и т. д.).Некоторый допустимых комбинаций квантовых чисел n и l показаны на рисунок ниже.
Третье правило, ограничивающее допустимые комбинации n , l и m квантовые числа имеют важное следствие. Он заставляет количество подоболочек в оболочке быть равным главному квантовому числу оболочки. Оболочка n = 3, для Например, содержит три подоболочки: 3 s , 3 p и 3 d орбиталей.
Возможные комбинации квантовых чисел
В оболочке n = 1 только одна орбиталь, потому что в ней есть только один путь. который сфера может быть ориентирована в пространстве. Единственная допустимая комбинация квантовых чисел
для которого n = 1 следующее.
который сфера может быть ориентирована в пространстве. Единственная допустимая комбинация квантовых чисел
для которого n = 1 следующее.
В оболочке n = 2 четыре орбитали.
| 2 | 1 | -1 | ||||
| 2 | 1 | 0 | 2п | |||
| 2 | 1 | 1 |
В подоболочке 2 s есть только одна орбиталь.Но есть три орбитали в
подоболочка 2 p , потому что существует три направления, в которых орбитальная оболочка p может
точка. Одна из этих орбиталей ориентирована по оси X , другая – по оси Y .
ось, а третья – по оси Z системы координат, как показано на рисунке
ниже. Следовательно, эти орбитали известны как 2 p x , 2 p y ,
и 2 p z орбиталей.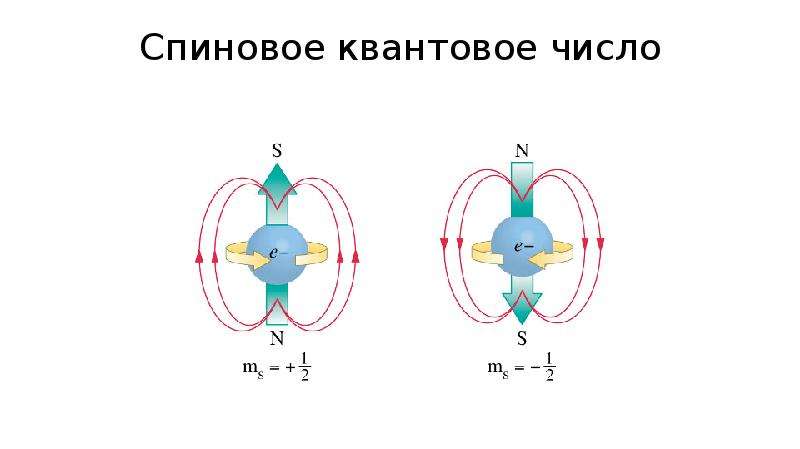
В оболочке n = 3 девять орбиталей.
| n | л | м | ||||
| 3 | 0 | 0 | 3 с | |||
| 3 | 1 | -1 | ||||
| 3 | 1 | 0 | 3 п. | |||
| 3 | 1 | 1 | ||||
| 3 | 2 | –2 | ||||
| 3 | 2 | -1 | 3 д | |||
| 3 | 2 | 0 | ||||
| 3 | 2 | 1 | ||||
| 3 | 2 | 2 |
В подоболочке 3 s имеется одна орбиталь, а в подоболочке 3 p – три орбитали. подоболочка.Однако оболочка n = 3 также включает 3 орбитали d .
Пять различных ориентаций орбиталей в подоболочке 3 d показаны на рисунок ниже. Одна из этих орбиталей лежит в плоскости XY самолета XYZ . системы координат и называется орбитальной 3 d xy . 3 d xz и 3 d yz орбитали имеют одинаковую форму, но лежат между осями система координат в плоскостях XZ и YZ .Четвертая орбиталь в этом подоболочка лежит вдоль осей X и Y и называется 3 d x 2 – y 2 орбитальный. Большая часть пространства, занимаемого пятой орбиталью, лежит вдоль оси Z и эта орбиталь называется орбиталью 3 d z 2 .
Число орбиталей в оболочке – квадрат главного квантового числа: 1 2 = 1, 2 2 = 4, 3 2 = 9.В подоболочке s ( l = 0), три орбитали в подоболочке p ( l = 1) и пять орбиталей в d подоболочка ( л = 2). Таким образом, количество орбиталей в подоболочке равно 2 ( l ) + 1.
Прежде чем мы сможем использовать эти орбитали, нам нужно знать количество электронов, которые могут занимают орбитали и как их можно отличить друг от друга. Экспериментальный данные свидетельствуют о том, что орбиталь может содержать не более двух электронов.
Чтобы различать два электрона на орбитали, нам нужен четвертый квант номер. Это называется спиновым квантовым числом ( s ), потому что электроны ведут себя как если бы они вращались либо по часовой стрелке, либо против часовой стрелки. Один из электронам на орбитали произвольно приписывается квантовое число с +1/2, другому присваивается квантовое число с -1/2. Таким образом, требуется три квантовых числа чтобы определить орбитальное, но четыре квантовых числа, чтобы идентифицировать один из электронов, который может занимают орбиталь.
Допустимые комбинации квантовых чисел n , l и m для Первые четыре оболочки приведены в таблице ниже. Для каждой из этих орбиталей есть два допустимые значения спинового квантового числа, с .
Сводка допустимых комбинаций квантовых Номера
| n | л | м | Обозначение подоболочки | Число орбиталей в подоболочке | Число электронов, необходимых для заполнения подоболочки | Общее количество электронов в подоболочке | |||||
| 1 | 0 | 0 | 1 с | 1 | 2 | 2 | |||||
| 2 | 0 | 0 | 2с | 1 | 2 | ||||||
| 2 | 1 | 1,0, -1 | 2п | 3 | 6 | 8 | |||||
| 3 | 0 | 0 | 3с | 1 | 2 | ||||||
| 3 | 1 | 1,0, -1 | 3 пол. | 3 | 6 | ||||||
| 3 | 2 | 2,1,0, -1, -2 | 3д | 5 | 10 | 18 | |||||
| 4 | 0 | 0 | 4с | 1 | 2 | ||||||
| 4 | 1 | 1,0, -1 | 4 пол. | 3 | 6 | ||||||
| 4 | 2 | 2,1,0, -1, -2 | 4д | 5 | 10 | ||||||
| 4 | 3 | 3,2,1,0, -1, -2, -3 | 4f | 7 | 14 | 32 | |||||
Относительные энергии атомных орбиталей
Из-за силы притяжения между объектами противоположного заряда наибольшая важным фактором, влияющим на энергию орбитали, является ее размер и, следовательно, значение главного квантового числа n .Для атома, содержащего только один электрон, нет разницы между энергиями различных подоболочек внутри оболочки. В 3 s , 3 p и 3 d орбиталей, например, имеют одинаковую энергию в атом водорода. Модель Бора, которая определяла энергии орбит в терминах ничего больше, чем расстояние между электроном и ядром, поэтому работает для этого атом.
Однако атом водорода необычен.Как только атом содержит более одного электрона, разные подоболочки больше не имеют одинаковой энергии. В данной оболочке орбитали s всегда имеют самую низкую энергию. Энергия подоболочек постепенно становится больше по мере увеличения значения углового квантового числа.
Относительные энергии: с < p < d < f
В результате два фактора контролируют энергию орбиты для большинства атомы: размер орбитали и ее форма, как показано на рисунке ниже.
Можно сконструировать очень простое устройство для оценки относительной энергии атомных орбиталей. Допустимые комбинации квантов n и l числа организованы в таблицу, как показано на рисунке ниже, а стрелки нарисованы на 45 углы в градусах, указывающие на нижний левый угол таблицы.
Затем считывают порядок увеличения энергии орбиталей, следуя этим стрелки, начиная с верхней части первой строки и затем переходя ко второй, третьей, четвертые строки и так далее.Эта диаграмма предсказывает следующий порядок увеличения энергии для атомных орбиталей.
1 с <2 с <2 p <3 с <3 p <4 с <3 с <4 с <5 с <4 с <5 с <6 с <4 с <5 с <6 с <7 с <5 с <6 d <7 p <8 s …
Электронные конфигурации, принцип Ауфбау, Вырожденные орбитали и правило Хунда
Электронная конфигурация атома описывает орбитали, занятые электроны на атоме. В основе этого прогноза лежит правило, известное как aufbau. принцип , который предполагает, что электроны добавляются к атому по одному, начиная с самой низкой энергетической орбиталью, пока все электроны не будут помещены в соответствующий орбитальный.
Атом водорода ( Z = 1) имеет только один электрон, который переходит в наименьшую энергию. орбитальный, 1 s орбитальный . На это указывает надстрочный индекс «1». после символа орбиты.
H ( Z = 1): 1 с 1
Следующий элемент имеет два электрона, и второй электрон заполняет орбиталь 1 s . потому что есть только два возможных значения для квантового числа спина, используемого для различения между электронами на орбитали.
He ( Z = 2): 1 с 2
Третий электрон переходит на следующую орбиталь на энергетической диаграмме 2 с орбитальный.
Li ( Z = 3): 1 с 2 2 с 1
Четвертый электрон заполняет эту орбиталь.
Be ( Z = 4): 1 с 2 2 с 2
После заполнения орбиталей 1 с и 2 с , следующая наименьшая энергия орбитали – это три орбитали 2 p .Пятый электрон, следовательно, переходит в один из эти орбитали.
B ( Z = 5): 1 с 2 2 с 2 2 p 1
Когда приходит время добавить шестой электрон, электронная конфигурация очевидна.
C ( Z = 6): 1 с 2 2 с 2 2 с 2
Однако в подоболочке 2 p есть три орбитали.Второй электрон попадает на ту же орбиталь, что и первая, или переходит на одну из других орбиталей в эта подоболочка?
Чтобы ответить на этот вопрос, нам нужно понять концепцию вырожденных орбиталей . От По определению, орбитали вырождены , когда они имеют одинаковую энергию. Энергия орбиталь зависит как от ее размера, так и от формы, потому что электрон тратит больше время дальше от ядра атома по мере того, как орбиталь становится больше или форма становится более сложным.Однако в изолированном атоме энергия орбитали не зависят от направления, в котором он указывает в пространстве. Орбитали, которые различаются только своим ориентация в пространстве, например 2 p x , 2 p y и 2 p z орбитали, поэтому вырождены.
Электроны заполняют вырожденные орбитали в соответствии с правилами, впервые сформулированными Фридрихом Хундом. Hund’s правила можно резюмировать следующим образом.
- Один электрон добавляется к каждой из вырожденных орбиталей в подоболочке перед двумя электроны добавляются к любой орбитали подоболочки.
- Электроны добавляются к подоболочке с тем же значением спинового квантового числа до тех пор, пока каждая орбиталь подоболочки имеет по крайней мере один электрон.
Когда приходит время поместить два электрона в подоболочку 2 p , мы помещаем один электрон на каждую из двух орбиталей.(Выбор между 2 p x , 2 p y и 2 p z орбитали являются чисто произвольными.)
C ( Z = 6): 1 с 2 2 с 2 2 p x 1 2 п y 1
Тот факт, что оба электрона в подоболочке 2 p имеют одинаковый спин квантовое число можно показать, представив электрон, для которого с = +1/2 с
стрелка вверх и электрон, для которого с = -1/2 со стрелкой, указывающей вниз.
Таким образом, электроны на орбиталях 2 p на углероде могут быть представлены как следует.
Когда мы дойдем до N ( Z = 7), мы должны поместить по одному электрону в каждый из трех вырожденные 2 p орбиталей.
| Н ( Z = 7): | 1 с 2 2 с 2 2 с 3 |
Поскольку каждая орбиталь в этой подоболочке теперь содержит один электрон, следующий электрон добавленный к подоболочке, должен иметь противоположное квантовое число спина, тем самым заполняя одно из орбитали 2 p .
| O ( Z = 8): | 1 с 2 2 с 2 2 с 4 |
Девятый электрон заполняет вторую орбиталь этой подоболочки.
| F ( Z = 9): | 1 с 2 2 с 2 2 с 5 |
Десятый электрон завершает подоболочку 2 p .
| Ne ( Z = 10): | 1 с 2 2 с 2 2 с 6 |
Есть что-то необычно стабильное в атомах, таких как He и Ne, у которых есть электроны. конфигурации с заполненными оболочками орбиталей.Поэтому по соглашению мы пишем сокращенные электронные конфигурации с точки зрения количества электронов за пределами предыдущий элемент с электронной конфигурацией заполненной оболочки. Электронные конфигурации следующие два элемента в периодической таблице, например, можно было бы записать следующим образом.
Na ( Z = 11): [Ne] 3 с 1
Mg ( Z = 12): [Ne] 3 с 2
Процесс aufbau можно использовать для прогнозирования электронной конфигурации элемента.Фактическая конфигурация, используемая элементом, должна быть определена экспериментально. В экспериментально определенные электронные конфигурации для элементов в первых четырех рядах периодической таблицы Менделеева приведены в таблице в следующем разделе.
Электронные конфигурации элементов
(элементы 1-го, 2-го, 3-го и 4-го ряда)
| Атомный номер | Символ | Электронная конфигурация | ||
| 1 | H | 1 с 1 | ||
| 2 | He | 1 s 2 = [He] | ||
| 3 | Li | [He] 2 с 1 | ||
| 4 | Be | [He] 2 с 2 | ||
| 5 | B | [He] 2 s 2 2 p 1 | ||
| 6 | С | [He] 2 с 2 2 с 2 | ||
| 7 | N | [He] 2 с 2 2 с 3 | ||
| 8 | O | [He] 2 с 2 2 с 4 | ||
| 9 | F | [He] 2 с 2 2 с 5 | ||
| 10 | Ne | [He] 2 s 2 2 p 6 = [Ne] | ||
| 11 | Na | [Ne] 3 с 1 | ||
| 12 | мг | [Ne] 3 с 2 | ||
| 13 | Al | [Ne] 3 с 2 3 с 1 | ||
| 14 | Si | [Ne] 3 с 2 3 с 2 | ||
| 15 | -P | [Ne] 3 с 2 3 с 3 | ||
| 16 | S | [Ne] 3 с 2 3 с 4 | ||
| 17 | класс | [Ne] 3 с 2 3 с 5 | ||
| 18 | Ar | [Ne] 3 с 2 3 p 6 = [Ar] | ||
| 19 | К | [Ar] 4 с 1 | ||
| 20 | Ca | [Ar] 4 с 2 | ||
| 21 | SC | [Ar] 4 с 2 3 d 1 | ||
| 22 | Ti | [Ar] 4 с 2 3 d 2 | ||
| 23 | В | [Ar] 4 с 2 3 d 3 | ||
| 24 | Cr | [Ar] 4 с 1 3 d 5 | ||
| 25 | Mn | [Ar] 4 с 2 3 d 5 | ||
| 26 | Fe | [Ar] 4 с 2 3 d 6 | ||
| 27 | Co | [Ar] 4 с 2 3 d 7 | ||
| 28 | Ni | [Ar] 4 с 2 3 d 8 | ||
| 29 | Cu | [Ar] 4 с 1 3 d 10 | ||
| 30 | Zn | [Ar] 4 с 2 3 d 10 | ||
| 31 | Ga | [Ar] 4 с 2 3 d 10 4 p 1 | ||
| 32 | Ge | [Ar] 4 с 2 3 d 10 4 p 2 | ||
| 33 | как | [Ar] 4 с 2 3 d 10 4 p 3 | ||
| 34 | SE | [Ar] 4 с 2 3 d 10 4 p 4 | ||
| 35 | Br | [Ar] 4 с 2 3 d 10 4 p 5 | ||
| 36 | Кр | [Ar] 4 s 2 3 d 10 4 p 6 = [Kr] | ||
Исключения из прогнозируемых электронных конфигураций
Есть несколько шаблонов в электронных конфигурациях, перечисленных в таблице в предыдущий раздел.Одним из наиболее поразительных является поразительный уровень согласия между эти конфигурации и конфигурации, которые мы могли бы спрогнозировать. Есть только два исключения среди первых 40 элементов: хром и медь.
Строгое соблюдение правил процесса aufbau предсказывает следующее: электронные конфигурации для хрома и меди.
| предсказанные электронные конфигурации: | Cr ( Z = 24): [Ar] 4 s 2 3 d 4 | |
| Cu ( Z = 29): [Ar] 4 s 2 3 d 9 |
Экспериментально определенные конфигурации электронов для этих элементов немного отличаются друг от друга. разные.
| фактических электронных конфигураций: | Cr ( Z = 24): [Ar] 4 s 1 3 d 5 | |
| Cu ( Z = 29): [Ar] 4 s 1 3 d 10 |
В каждом случае один электрон был переведен с орбитали 4 s на орбиталь 3 d орбитали, хотя предполагается, что орбитали 3 d находятся на более высоком уровне, чем 4 с по орбите.
Как только мы выйдем за пределы атомного номера 40, разница между энергиями соседних орбитали достаточно малы, чтобы переносить электрон с одной орбитально к другому. Большинство исключений из электронной конфигурации, предсказанных из поэтому показанная ранее диаграмма aufbau встречается среди элементов с атомными номерами больше 40. Хотя заманчиво сосредоточить внимание на горстка элементов, электронная конфигурация которых отличается от предсказанных с диаграммой aufbau удивительно то, что эта простая диаграмма работает для очень многих элементы.
Электронные конфигурации и периодическая таблица
Когда данные электронной конфигурации расположены так, что мы можем сравнивать элементы в одном из горизонтальные строки периодической таблицы, мы обнаруживаем, что эти строки обычно соответствуют заполнение оболочки орбиталей. Вторая строка, например, содержит элементы в которой заполнены орбитали в оболочке n = 2.
| Li ( Z = 3): | [He] 2 с 1 | |
| Be ( Z = 4): | [He] 2 с 2 | |
| B ( Z = 5): | [He] 2 s 2 2 p 1 | |
| C ( Z = 6): | [He] 2 с 2 2 с 2 | |
| Н ( Z = 7): | [He] 2 с 2 2 с 3 | |
| O ( Z = 8): | [He] 2 с 2 2 с 4 | |
| F ( Z = 9): | [He] 2 с 2 2 с 5 | |
| Ne ( Z = 10): | [He] 2 с 2 2 с 6 |
В вертикальных столбцах или группах периодических стол тоже.Элементы в группе имеют схожую конфигурацию самых внешних электроны. Это соотношение можно увидеть, посмотрев на электронные конфигурации элементы в столбцах по обе стороны периодической таблицы.
| Группа IA | Группа VIIA | |||||
| H | 1 с 1 | |||||
| Li | [He] 2 с 1 | F | [He] 2 с 2 2 с 5 | |||
| Na | [Ne] 3 с 1 | класс | [Ne] 3 с 2 3 с 5 | |||
| К | [Ar] 4 с 1 | Br | [Ar] 4 с 2 3 d 10 4 p 5 | |||
| руб. | [Kr] 5 с 1 | I | [Kr] 5 s 2 4 d 10 5 p 5 | |||
| CS | [Xe] 6 с 1 | в | [Xe] 6 s 2 4 f 14 5 d 10 6 p 5 |
На рисунке ниже показана взаимосвязь между периодической таблицей и орбиталями. заполняется во время процесса aufbau.Два столбца в левой части периодической таблица соответствует заполнению орбитали с . Следующие 10 столбцов включают элементы, в которых заполнены пять орбиталей в подоболочке d . Шесть столбцов на справа представляют заполнение трех орбиталей в подоболочке p . Наконец, 14 столбцов внизу таблицы соответствуют заполнению семи орбиталей в подоболочка f .
Спиновое квантовое число ~ ChemistryGod
Спиновое квантовое число – это квантовое число, которое описывает ориентацию собственного углового момента элементарной частицы.Обозначается он s . Спин – это внутреннее свойство элементарной частицы, которое отвечает за спиновый угловой момент. Спин можно представить как частицу, вращающуюся вокруг своей оси, как и Землю вокруг своей оси. Значение с зависит от частицы, например, электроны имеют спин 1 ⁄ 2 (или точно ℏ ⁄ 2 ), в то время как фотоны имеют спин 1 (или точно).
Спиновый момент количества движения электрона может иметь две ориентации: 1 ⁄ 2 и – 1 ⁄ 2 .Это только два возможных спина электрона, представленные стрелками: ↑ (спин вверх) и ↓ (спин вниз). Орбиталь может иметь максимум два электрона; когда орбиталь полностью заполнена двумя электронами, оба должны иметь противоположные спины, т.е. если один равен 1 ⁄ 2 , другой – 1 ⁄ 2 .
Два спина электрона
Спиновый угловой момент является векторной величиной и квантуется квантовым числом спина s .
Здесь ℏ – приведенная постоянная Планка.
Помимо спинового углового момента S , существует орбитальный угловой момент L , который вносит вклад в полный угловой момент J . Орбитальный угловой момент квантован азимутальным квантовым числом. S – результат вращения электрона вокруг своей оси, а L – результат вращения электрона вокруг своего ядра. Полный угловой момент является векторным сложением обоих: J = L + S . J сохраняется в закрытой системе.
Классическая интерпретация спина и орбитального углового моментаСпиновое квантовое число – одно из четырех квантовых чисел, которые идентифицируют электрон в атоме. Остальные три – это главное квантовое число, азимутальное квантовое число и магнитное квантовое число.
Эксперимент Штерна-Герлаха
Идея вращения возникла из эксперимента Штерна-Герлаха. В начале 1920-х годов Отто Штерн и Вальтер Герлах, оба немецкие физики, провели эксперимент.Эксперимент продемонстрировал квантованный характер собственного углового момента. В эксперименте атомы серебра испарялись в печи. Эти частицы пропускались через пространственно изменяющееся (или неоднородное) магнитное поле. Ожидается равномерное расположение атомов Ag. Однако результаты оказались противоположными. Луч разделяется на две части, как показано на схеме ниже.
Эксперимент Штерна-ГерлахаЭто показало существование собственного магнитного момента электрона. Разделение пучка на два предполагало наличие двух спиновых квантовых чисел, связанных с электронами.
У атома серебра 47 электронов. На полностью заполненной орбитали атома электроны всегда спарены, то есть оба имеют противоположные спины. В серебре 23 электрона спариваются с другими 23, в то время как один электрон остается неспаренным. Этот неспаренный электрон отвечает за спиновый магнитный момент атома Ag в эксперименте. Проще говоря, неспаренный электрон действует как небольшой магнит. Когда атомы Ag проходили через магнитное поле, атомы отклонялись вверх или вниз в зависимости от двух спинов неспаренного электрона.
Когда s = + 1 ⁄ 2 , атомы отталкивались и притягивались к полю, когда s = – 1 ⁄ 2 .
Электроны во внешнем магнитном полеПоследствия
Ученые провели аналогичные эксперименты с элементами, имеющими один неспаренный электрон в валентной оболочке в конце 1920-х годов, и наблюдали аналогичные результаты. Некоторые из них – водород ( Z = 1), натрий ( Z = 11), калий ( Z = 19), медь ( Z = 29), золото ( Z = 79).
В 1925 году Ральф Крониг первым представил идею электронных спинов, основанную на более ранних открытиях других физиков. Но он получил резкую критику со стороны Гейзенберга и Паули. Следовательно, он отказался от нее и никогда не публиковал ее. Через несколько месяцев после него Джордж Уленбек и Сэмюэл Гаудсмит, оба американо-голландские физики, опубликовали открытие.
Джордж Уленбек (слева) и Сэмюэл Гоудсмит (справа) вместе с Хендриком Крамерсом (в центре) в Анн-Арборе ок. 1928Значение
- Открытие спина принесло дополнительное квантовое число.Это также принесло принцип исключения Паули, который очень важен в химии.
- Магнитные свойства таких материалов, как парамагнетики и диамагнетики, можно объяснить спином.
- Концепция спина может объяснить дублет (две близкорасположенные линии) и триплет (три близко расположенных линии), которые наблюдались в спектрах. Эти дублет и триплет были одним из основных ограничений модели Бора.
- Тонкую и сверхтонкую структуру спектральных линий можно понять с помощью спина.
- Спиновый угловой момент был введен с существующим орбитальным угловым моментом. С этого момента вся квантовая механика изменилась.
Сопутствующие статьи
Квантовые числа | Grandinetti Group
Квантовые числа для электронной орбиты
Теперь оказывается, что если вы рассматриваете электрон, захваченный внутри сферы (а не в одномерном ящике), у него будут стоячие волны, которые очень похожи на электрон, связанный с положительно заряженным ядром электростатическим притяжением.Обычно мы работаем в 4-х измерениях (3-х пространственное и 1-временное), поэтому, как правило, нам понадобятся 4 квантовых числа, чтобы полностью указать состояние электрона (, то есть , стоячая волна).
Давайте посмотрим на квантовые числа, необходимые для обозначения возможных стоячих волн или состояний электрона, захваченного его электростатическим притяжением к положительно заряженному ядру. Для электрона, захваченного своим электростатическим притяжением к положительно заряженному ядру, мы используем три следующих квантовых числа для описания электронного состояния (орбитального).
n: главное квантовое число
Главное квантовое число имеет целые значения n = 1, 2, 3 … По мере увеличения n орбиталь электрона становится больше, и электрон проводит больше времени дальше от ядра.
ℓ: азимутальное квантовое число
Азимутальное квантовое число имеет целые значения от = 0 до ℓ = n – 1 для каждого значения n. Это квантовое число определяет форму орбитали. Каждому значению ℓ присвоены специальные буквы (см. Таблицу ниже).
Для электрона с n = 1 и ℓ = 0 мы говорим, что электрон находится в состоянии 1 с или 1 с на орбите
Для электрона с n = 2 и ℓ = 0 мы говорим … 2 с орбитальный
Для электрона с n = 2 и ℓ = 1 мы говорим … 2 p орбитальный
Для электрона с n = 3 и ℓ = 2 мы говорим … 3 d орбиталь
м
ℓ : магнитное квантовое числоМагнитное квантовое число имеет целые значения m = от – ℓ до + ℓ, включая 0.
Например, если n = 3 и ℓ = 2, то возможные значения m ℓ равны -2, -1, 0, +1, +2
m
s ,: квантовое число спинаСпиновое квантовое число имеет только два возможных значения: +1/2 или -1/2 . Если пучок атомов водорода в их основном состоянии (n = 1, ℓ = 0, m ℓ = 0) или 1s направляется через область с пространственно изменяющимся магнитным полем, тогда пучок разделяется на два пучка.
Очевидно, трех квантовых чисел n, ℓ, m 1 недостаточно для полного описания состояния H-атома. Другое квантовое число требуется для описания того, идет ли он вверх или вниз в пространственно изменяющемся магнитном поле.Это свойство называется спином , потому что, если бы электроны были зарядовыми шарами, вращающимися вокруг своей оси, они бы так себя вели в магнитном поле. На самом деле это неверная картина. Спиновое квантовое число появляется, когда волновая функция квантовой механики модифицируется с учетом эффектов теории относительности.
Электронный спин очень важен для понимания электронной структуры атомов, содержащих много электронов (а не только один, как у водорода) из-за принципа исключения Паули .
Принцип исключения Паули: Никакие два электрона в атоме не могут иметь одинаковый набор из четырех квантовых чисел n, ℓ, m ℓ , m s .
Поскольку существует только два значения m s , то любая орбиталь может удерживать только два электрона с противоположными значениями m s . Дальнейшее нарушение принципа Паули.
Таким образом, вы можете думать об электронных орбиталях как о стоячих волнах волновой функции электрона, когда он связан с положительно заряженным ядром.Однако помните, что электрон – это не просто волна. Это частица с волнообразными свойствами. Квадрат волновой функции дает вероятность нахождения электрона в любом конкретном положении.
Домашнее задание от
Chemisty, The Central Science, 10-е изд.
6,33, 6,35, 6,37, 6,39
Как узнать количество электронов всего по 4 квантовым числам?
Если вам дается полный набор квантовых чисел , то вы можете точно сказать, что имеете дело только с одним электроном .
Как вы знаете, квантовые числа используются для описания положения и спина электрона, окружающего ядро атома.
Более конкретно, четыре квантовых числа скажут вам
- уровень энергии, на котором находится электрон – задается # n #, главное квантовое число
- подоболочка, в которой находится электрон – задается # l #, квантовым числом углового момента
- точная орбиталь, на которой вы можете найти электрон – задается, # m_l #, магнитным квантовым числом
- спин электрона – задается # m_s #, квантовое число спина
Теперь каждый полный набор квантовых чисел может описывать только один электрон .Это означает, что если вам дадут что-то вроде этого
# п = 2, l = 1, m_l = 0, m_s = + 1/2 #
, то вы точно знаете, что только один электрон может иметь такой набор квантовых чисел.
Теперь предположим, что вам даны не все четыре квантовых числа. Вот несколько правил, которые помогут вам выяснить, сколько электронов может иметь неполный набор квантовых чисел
- Вам присвоено значение # n #
Если это так, то используйте тот факт, что количество электронов , которые вы получаете на один энергетический уровень, равно
# цвет (синий) (“нет.2) #
На этот раз вы знаете уровень энергии и подоболочку, в которой можно найти электроны. Чтобы определить, сколько электронов могут разделять эти квантовые числа, используйте # m_l #, которое может принимать значения от # -l # до # l #.
Как только вы узнаете, сколько орбиталей у вас на подоболочку , умножьте это значение на # 2 #, чтобы получить количество электронов
# цвет (синий) («количество электронов» = 2 xx «количество подоболочек») #
- Вы ginve # n #, # l #, и # m_l #
Теперь вы знаете энергетический уровень, подоболочку, конкретную орбиталь и , на которой могут находиться электроны.
Поскольку единственными возможными значениями для # m_s # являются # + – 1/2 #, отсюда следует, что каждая орбиталь может содержать максимум из двух электронов.
Спиновое квантовое число – обзор
Даже если спин-адаптированные CSF обеспечивают правильное спиновое квантовое число для приближенной волновой функции, существуют определенные вычислительные преимущества от применения основанного на детерминанте CI. Эти преимущества связаны с учетом расширения SD и, как следствие, эффективной оценки и хранения интегралов и коэффициентов CI [5].
Для правильного создания и хранения всех возможных SD в определенном эталонном пространстве следует применять систематическую и эффективную методологию индексации всех возможных детерминантов. Одним из методов выполнения этой задачи является графическое представление строк альфа- и бета-электронов, которое позволяет напрямую реализовать в компьютерном коде. Iβ = a1β † a2β †… aNββ †.
I α , I β , J α , J β , строка. Мы можем построить все SD, образованные расширением CI (усеченным или полным), рассматривая отдельно все возможные способы занять n орбиталей с альфа- и бета-электронами, не забывая при этом о правильном спине. Таким образом, нам нужно подумать, сколько операторов альфа-струны мы можем построить по числу N α альфа-электронов, помещенных между n орбиталями.Общее выражение для вычисления всех возможных альфа-строк дается выражением:
(75) Nstrα = nNα.
Аналогичный подход применяется для строк бета, и общее количество SD определяется как произведение количества строк альфа и бета.
(76) NSD = nNαnNβ.
Учитывая большое количество детерминантов, которые могут быть сгенерированы даже для систем среднего размера, применение систематического метода для индексации и хранения строк занятия является обязательным.Графические представления организуют все возможные строки в виде пути на диаграмме, как показано на рис. 3 [6]. Это конкретное представление показывает четыре электрона, размещенные на шести орбиталях, что дает всего 15 струн. (75). Каждая строка представлена на графике как путь; каждый путь представляет собой набор шагов от верхнего левого узла (с меткой 15) до нижнего правого узла (метка 1). Каждый узел на графе содержит метку, которая соответствует доступным путям от этого узла до нижнего правого узла (см. Ниже).Каждый узел также определяется двумя координатами ( e , o ), соответствующими его положению на графике. Координаты ( e , o ) берутся из значения электронов на оси x и орбиталей на оси y соответственно. Например, верхний левый узел имеет координаты (0, 0). Рассмотрены два разных типа ступеней: вертикальный шаг от узла ( e , o ) до ( e , o + 1), при котором орбитальная точка o + 1 остается незанятой, и диагональный шаг от узел ( e , o ) – ( e + 1, o + 1), который помещает электрон на орбитали o + 1.Рассматривая схему лексического упорядочивания , мы можем добавлять метки на каждый узел. Назначив метку, равную 1 (W- = 1) в нижнем правом узле, мы можем вычислить метки всех других узлов, применив рекурсивную формулу
Рис. 3. Графическое представление строковой диаграммы из четырех электронов в шести орбитали. Путь струны a2 † a3 † a4 † a6 † показан жирной линией .
(77) W- (e, o) = W- (e, o + 1) + W- (e + 1, o + 1).
Вес Yi (e, o) присваивается также каждому шагу от узла ( e , o ) до ( e + 1, o + 1), где индекс i для вертикального steps имеет значение i = 0 и i = 1 для диагональных шагов.Обратите внимание, что вес Y-i (e, o) соответствует выходящему узлу с координированным ( e , o ). В лексическом порядке все вертикальные шаги имеют нулевой вес (Y-0 = 0), а значения Y-1 для диагональных шагов вычисляются по формуле
(78) Y-1 (e, o ) = ∑i = 1o − eW- (e + 1, o + 2 − i).

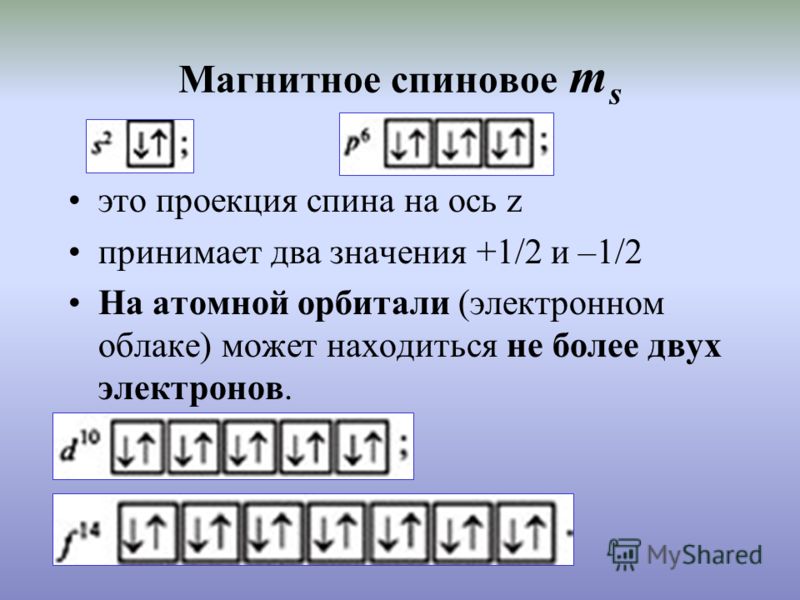 ..
.. 4-й электрон будет иметь спин +1/2.
4-й электрон будет иметь спин +1/2. Джон Вили и сыновья, Inc., 2005. Печать. (стр. 1396).
Джон Вили и сыновья, Inc., 2005. Печать. (стр. 1396).