Математики обнаружили идеальный способ перемножения чисел / Хабр
Разбивая крупные числа на мелкие, исследователи превысили фундаментальное математическое ограничение скорости
Четыре тысячи лет назад жители Вавилонии изобрели умножение. А в марте этого года математики усовершенствовали его.
18 марта 2019 два исследователя описали самый быстрый из известных методов перемножения двух очень больших чисел. Работа отмечает кульминацию давнишнего поиска наиболее эффективной процедуры выполнения одной из базовых операций математики.
«Все думают, что метод умножения, который они учили в школе, наилучший, но на самом деле в этой области идут активные исследования», — говорит Йорис ван дер Хувен, математик из Французского национального центра научных исследований, один из соавторов работы.
Сложность множества вычислительных задач, от подсчёта новых цифр числа π до обнаружения крупных простых чисел сводится к скорости перемножения. Ван дер Хувен описывает их результат как назначение своего рода математического ограничения скорости решения множества других задач.
Ван дер Хувен описывает их результат как назначение своего рода математического ограничения скорости решения множества других задач.
«В физике есть важные константы типа скорости света, позволяющие вам описывать всякие явления, — сказал ван дер Хувен. – Если вы хотите знать, насколько быстро компьютеры могут решать определённые математические задачи, тогда перемножение целых чисел возникает в виде некоего базового строительного блока, по отношению к которому можно выразить такую скорость».
Почти все учатся перемножать числа одинаково. Записываем числа в столбик, перемножаем верхнее число на каждую цифру нижнего (с учётом разрядов) и складываем результат. При перемножении двух двузначных чисел приходится проделать четыре более мелких перемножения для получения итогового результата.
Школьный метод “переноса” требует выполнения n2 шагов, где n – количество цифр в каждом из перемножаемых чисел. Вычисления с трёхзначными числами требуют девяти перемножений, а со стозначными – 10 000.
Метод переноса нормально работает с числами, состоящими из нескольких цифр, однако начинает буксовать при перемножении чисел, состоящих из миллионов или миллиардов цифр (чем и занимаются компьютеры при точном подсчёте π или при всемирном поиске больших простых чисел). Чтобы перемножить два числа с миллиардом цифр, нужно будет произвести миллиард в квадрате, или 1018, умножений, – на это у современного компьютера уйдёт порядка 30 лет.
Несколько тысячелетий считалось, что быстрее перемножать числа нельзя. Затем в 1960 году 23-летний советский и российский математик Анатолий Алексеевич Карацуба посетил семинар, который вёл Андрей Николаевич Колмогоров, советский математик, один из крупнейших математиков XX века. Колмогоров заявил, что не существует обобщённого способа умножения, требующего меньше, чем n
Анатолий Алексеевич Карацуба
Умножение Карацубы заключается в разбиении цифр числа и повторной их комбинации новым способом, который позволяет вместо большого количества умножений провести меньшее количество сложений и вычитаний.
Традиционный метод умножения 25х63 требует четыре умножения на однозначное число и несколько сложений
Умножение Карацубы 25х63 требует трёх умножений на однозначное число и несколько сложений и вычитаний.
a) разбиваем числа
b) перемножаем десятки
c) перемножаем единицы
d) складываем цифры
e) перемножаем эти суммы
f) считаем e – b – c
g) собираем итоговую сумму из b, c и f
При росте количества знаков в числах метод Карацубы можно использовать рекурсивно.
Традиционный метод умножения 2531х1467 требует 16 умножений на однозначное число.
Умножение Карацубы 2531х1467 требует 9 умножений.
«Сложение в школе проходят на год раньше, потому что это гораздо проще, оно выполняется за линейное время, со скоростью чтения цифр слева направо», — сказал Мартин Фюрер, математик из Пенсильванского государственного университета, создавший в 2007 быстрейший на то время алгоритм умножения.
Имея дело с крупными числами, умножение Карацубы можно повторять рекурсивно, разбивая изначальные числа почти на столько частей, сколько в них знаков. И с каждым разбиением вы меняете умножение, требующее выполнения многих шагов, на сложение и вычитание, требующие куда как меньше шагов.
«Несколько умножений можно превратить в сложения, учитывая, что с этим компьютеры будут справляться быстрее», — сказал Дэвид Харви, математик из Университета Нового Южного Уэльса и соавтор новой работы.
Метод Карацубы сделал возможным умножать числа с использованием лишь n1,58 умножений на однозначное число. Затем в 1971 году Арнольд Шёнхаге и Фолькер Штрассен опубликовали метод, позволяющий умножать большие числа за n × log n × log(log n) небольших умножений. Для умножения двух чисел из миллиарда знаков каждое метод Карацубы потребует 165 трлн шагов.
Йорис ван дер Хувен, математик из Французского национального центра научных исследований
Метод Шёнхаге-Штрассена используется компьютерами для умножения больших чисел, и привёл к двум другим важным последствиям. Во-первых, он ввёл в использование технику из области обработки сигналов под названием быстрое преобразование Фурье. С тех пор эта техника была основой всех быстрых алгоритмов умножения.
Во-первых, он ввёл в использование технику из области обработки сигналов под названием быстрое преобразование Фурье. С тех пор эта техника была основой всех быстрых алгоритмов умножения.
Во-вторых, в той же работе Шёнхаге и Штрассен предположили возможность существования ещё более быстрого алгоритма – метода, требующего всего n × log n умножений на один знак – и что такой алгоритм будет наибыстрейшим из возможных. Это предположение было основано на ощущении, что у такой фундаментальной операции, как умножение, ограничение операций должно записываться как-то более элегантно, чем n × log n × log(log n).
«Большинство в общем-то сошлось на том, что умножение – это такая важная базовая операция, что с чисто эстетической точки зрения ей требуется красивое ограничение по сложности, — сказал Фюрер. – По опыту мы знаем, что математика базовых вещей в итоге всегда оказывается элегантной».
Нескладное ограничение Шёнхаге и Штрассена, n × log n × log(log n), держалось 36 лет. В 2007 году Фюрер побил этот рекорд, и всё завертелось.
Их метод является улучшением большой работы, проделанной до них. Он разбивает числа на знаки, использует улучшенную версию быстрого преобразования Фурье и пользуется другими прорывами, сделанными за последние 40 лет. «Мы используем быстрое преобразование Фурье гораздо более грубо, используем его несколько раз, а не один, и заменяем ещё больше умножений сложением и вычитанием», — сказал ван дер Хувен.
Алгоритм Харви и ван дер Хувена доказывает, что умножение можно провести за n × log n шагов. Однако он не доказывает отсутствия более быстрого метода. Гораздо сложнее будет установить, что их подход максимально быстрый. В конце февраля команда специалистов по информатике из Орхусского университета опубликовала работу, где утверждает, что если одна из недоказанных теорем окажется верной, то этот метод и вправду будет скорейшим из способов умножения.
И хотя в теории этот новый алгоритм весьма важен, на практике он мало что поменяет, поскольку лишь немного выигрывает у уже используемых алгоритмов. «Всё, на что мы можем надеяться, это на трёхкратное ускорение, — сказал ван дер Хувен. – Ничего запредельного».
Кроме того, поменялись схемы компьютерного оборудования. Двадцать лет назад компьютеры выполняли сложение гораздо быстрее умножения. Разрыв в скоростях умножения и сложения с тех пор серьёзно уменьшился, в результате чего на некоторых чипах умножение может даже обгонять сложение. Используя определённые виды оборудования, «можно ускорить сложение, заставляя компьютер умножать числа, и это какое-то безумие», — сказал Харви.
Оборудование меняется со временем, но лучшие алгоритмы своего класса вечны. Вне зависимости от того, как компьютеры будут выглядеть в будущем, алгоритм Харви и ван дер Хувена всё ещё будет самым эффективным способом умножать числа.
Проект “Увлекательные способы умножения чисел”
Муниципальное казённое общеобразовательное учреждение
Баганская средняя общеобразовательная школа №2
имени героя Советского Союза Андрея Григорьевича Матвиенко
Проект
«Увлекательные способы умножения чисел»
Выполнила: Савельева Елизавета,
обучающаяся 7 класса
Руководитель: Матюшко Нина Петровна,
учитель математики
Баган, 2018 год
СОДЕРЖАНИЕ:
ВВЕДЕНИЕ……………………………………………………………. ..…..стр. 3
..…..стр. 3
1.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1. Древнерусский способ умножения на пальцах…………………..…стр.4
1.1.1. Умножение на пальцах на 9 …………………………………………стр.5
1.1.2. Как умножить на 11 любое двузначное число……………………стр.6
1.1.3. «Решётчатое умножение»……………………………………..……..стр.7
1.1.4. «Простое умножение»………………………………………………..стр.8
1.1.5. Еще один способ умножения двузначных чисел………………….стр.8
2. ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1.Выбор удобных способов умножения……………………………..….стр.9
2.2. Обучение пятиклассников применению необычных способов умножения……………………………………………………………………стр.9
ЗАКЛЮЧЕНИЕ…………………………………………………………….стр.10
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ…………………………стр.11
ВВЕДЕНИЕ
В 21 веке невозможно представить себе жизнь человека, не производящего вычислений: это и продавцы, и бухгалтера, и обыкновенные школьники.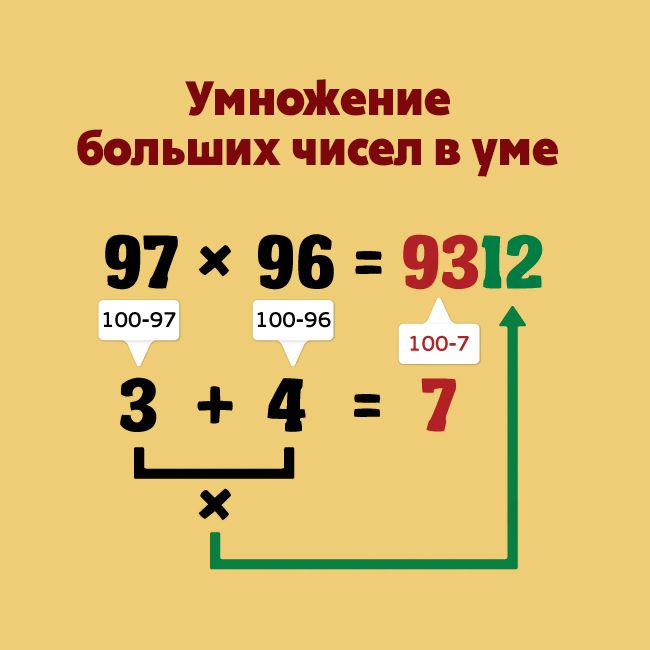 Изучение почти любого предмета в школе предполагает хорошие знания математики, и без неё нельзя освоить эти предметы. Две стихии господствуют в математике — числа и фигуры с их бесконечным многообразием свойств и действий с ними.
Изучение почти любого предмета в школе предполагает хорошие знания математики, и без неё нельзя освоить эти предметы. Две стихии господствуют в математике — числа и фигуры с их бесконечным многообразием свойств и действий с ними.
Обоснование выбора темы:
Однажды вечером, делала я алгебру. Были там и примеры и выражения… Вычислять приходилось только в столбик. И тут я подумала… Что, если решать примеры другими способами умножения? Я решила изучить «уникальные способы умножения чисел».
Цель проекта:
Изучить некоторые нестандартные приёмы умножения и показать, что их применение делает процесс вычисления рациональным и интересным и для вычисления которыми, достаточно устного счета или применения карандаша, ручки и бумаги.
Задачи проекта:
1. Найти необычные способы умножения.
2. Научиться их применять.
3. Выбрать для себя самые интересные или более лёгкие, чем те, которые предлагаются в школе, и использовать их при счёте.
Выбрать для себя самые интересные или более лёгкие, чем те, которые предлагаются в школе, и использовать их при счёте.
4. Научить одноклассников применять новые способы умножения.
Объект исследования:
Участники научно – практической конференции.
Методы исследования:
1. Работа с литературой и материалами Интернета по данной теме;
2. Изучить способы умножения.
3. Применить способы умножения в решении примеров.
1.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1. Древнерусский способ умножения на пальцах
Это один из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы.
Принцип этого способа: умножение на пальцах однозначных чисел от 6 до 9. Пальцы рук здесь служили вспомогательным вычислительным устройством.
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел больше 5.
Умножение на пальцах на 9
Очень легко воспроизводится “на пальцах” умножение для числа 9. Разведите пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки. Допустим, хотим умножить 3 на 9. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 3. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 2 пальца не загнуто, справа – 7 пальцев. Таким образом, 3·9=27.
Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки. Допустим, хотим умножить 3 на 9. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 3. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 2 пальца не загнуто, справа – 7 пальцев. Таким образом, 3·9=27.
1.1.2. Как умножить на 11 любое двузначное число
1.Напишем 43 с пробелом по серединке
4 _ 3
Теперь сложим 4 и 3.
4+3=7
И семерку вставим в серединку вместо пробела.
4 7 3
2.Так же пишем 76 с пробелом по серединке.
7 _ 6
Затем складываем между собой 7 и 6.
7 + 6 = 13
Тройку вставим вместо пробела, а единичку прибавим к семерке.
3 6.
1.1.3. «Решётчатое умножение»
Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи. Такие ставни вешались на окна венецианских домов…»
1.1.4. «Простое умножение»
умножим 95 на 88. В уме эти числа необходимо разложить на составляющие от 100.
(100-5)*(100-12)
Первые две цифры ответа – это первый множитель минус остаток второго разложенного или наоборот второй множитель минус первый остаток, кому как удобнее.
(95-12)=83 или (88-5)=83
вторые две цифры ответа – нужно просто перемножить остатки от ста
(5*12)=60
итого 95*88=8360
1.1.5. Еще один способ умножения двузначных чисел
Пример 1.
Умножим 48 на 64. Первым действием умножаем десятки с единицами (4*4=16). Вторым действием умножаем единицы на десятки (8*6=48). Складываем получившиеся произведения (16+48=64). Число 64 нужно запомнить! Теперь перемножаем десятки с десятками: 6*4=24,и сразу к 24 в разряд единиц прибавляем 6, от 64. Получается 30. Следующим действием умножаем единицы с единицами: 8*4=32, и к 32 в разряд десятков прибавляем 4= 72. Получаем два числа 30 и 72. В общем это 3072.
Пример 2.
Умножим 87 на 36.
8*6=48 + 7*3=21
69
8*3=24;24+6=30
Умножаем единицы с единицами: 7*6=42. К 42 в разряд десятков прибавляем 9, получается 13, 3 записываем в разряд единиц = 32,а 1 уходит в первое число(30+1=31).Ответ:3132.
К 42 в разряд десятков прибавляем 9, получается 13, 3 записываем в разряд единиц = 32,а 1 уходит в первое число(30+1=31).Ответ:3132.
ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1.Выбор удобных способов умножения
Работая над проектом, я рассмотрела несколько способов умножения чисел. Все они по-своему интересны. Некоторые из них являются очень лёгкими и удобными в использовании. Другие, напротив, очень трудоёмки и сложны в использовании, их сложно запомнить, а значит, и сложно будет применять на практике. Одной из задач моей работы являлась «Выбрать для себя самые интересные или более лёгкие, чем те, которые предлагаются в школе, и использовать их при счёте». Для меня такими являются умножение на пальцах на 9 и умножение двузначных чисел на 11.
2.2. Обучение пятиклассников применению необычных способов умножения
Я уже отметила, что для меня интересными и лёгкими оказались способы умножения на пальцах на 9 и умножение двузначных чисел на 11. Я предложила Нине Петровне попробовать научить пятиклассников этим способам умножения. С этой целью я пришла к ним на один из уроков математики. Ребятам очень понравились новые способы умножения. Я надеюсь, что они не забудут их и будут пользоваться ими для упрощения вычислений.
Я предложила Нине Петровне попробовать научить пятиклассников этим способам умножения. С этой целью я пришла к ним на один из уроков математики. Ребятам очень понравились новые способы умножения. Я надеюсь, что они не забудут их и будут пользоваться ими для упрощения вычислений.
ЗАКЛЮЧЕНИЕ
Работая над проектом, я выяснила, какие способы умножения существуют и где их применяют; научилась использовать новые способы умножения.
Я приходила на урок математики в 5 класс, научила их умножать на 9 и на 11. Ребятишкам понравились эти способы умножения, и, по словам Нины Петровны, на 9 таблицу умножения теперь знают все пятиклассники.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Глейзер, Г. И. История математики в школе: пособие для учителей ⁄ под редакцией В. Н. Молодшего. – М.: Просвещение, 1964. – С. 376 .
2. Перельман Я. И. Занимательная арифметика: Загадки и диковинки в мире чисел. – М.: Издательство Русанова, 1994. – С. 142.
– М.: Издательство Русанова, 1994. – С. 142.
3. Энциклопедия для детей. Т. 11. Математика /Глав. ред. М. Д. Аксенова. – М.: Авата+, 2003. – С. 130.
4. Журнал «Математика» №15 2011г.
5. Интернет-ресурсы.
11
Математический трюк для умножения на одиннадцать
(Последнее обновление: 1 июня 2018 г.)
Одиннадцать — магическое число
Вы когда-нибудь хотели иметь возможность выполнять базовые арифметические действия, используя только чистую силу своего разума? ? Ну, есть разные приемы для разных чисел, и один из самых простых расчетов, который нужно освоить, — это число одиннадцать. Понимание этого трюка также облегчит вам выполнение других видов двузначного умножения в уме. Посылка, лежащая в основе математики, та же самая, но умножение на одиннадцать позволяет очень легко увидеть и понять процесс.
To illustrate this math trick, let’s first take a look at the table below:
| 2 7 | 4 3 x 11 = 4 7 3 | 6 3 x 11 = 6 9 3 | 3 2 x 11 = 3 5 2 |
| x11 | x11 | x11 | x11 |
| 2 7 | 4 3 | 6 3 | 3 2 |
| + 2 7 0 | + 4 3 0 | + 6 3 0 | + 3 2 0 |
| = 2 9 7 | = 4 7 3 | = 6 9 3 | = 3 5 2 |
Вы, наверное, уже заметили, что в каждом из этих примеров первая и последняя цифры результата идентичны числу, которое умножается на 11 (т. е. 2 7 x 11 = 2 9 7 ). Тем не менее, остается один вопрос — что насчет среднего числа? Это не приходит из ниоткуда. Среднее число на самом деле является суммой первой и второй цифры вместе взятых.
е. 2 7 x 11 = 2 9 7 ). Тем не менее, остается один вопрос — что насчет среднего числа? Это не приходит из ниоткуда. Среднее число на самом деле является суммой первой и второй цифры вместе взятых.
Давайте снова посмотрим на пример 2 7 x 11 = 2 9 7 . Обратите внимание, как 2 + 7 = 9 ? Это так просто!
Что делать с двузначными числами?
«Хорошо, подождите минутку», — говорите вы. «Это все хорошо, когда два числа не складываются в двузначное число, но как насчет случая 67 x 11?»
Вы очень проницательны. 6 + 7 = 13 , что меняет дело, но трюк все еще работает. Вроде, как бы, что-то вроде. Вот что происходит.
Поскольку две цифры ( 6+7 ) в сумме дают 13, мы, очевидно, не можем вставить число 13 в середину, чтобы получить 6137. Это было бы очень неправильно, поэтому мы должны немного повозиться.
В этом примере мы собираемся оставить цифру 3 и снова вставить ее в середину, так что теперь у нас есть 637 (что тоже неверно). Мы забыли перенести 1 в столбец сотен. Когда мы это сделаем, мы получим 737. Это верно? ДА!
Как насчет трехзначных чисел?
Если вас интересуют трехзначные числа, значит, у вас яркий и любопытный ум. Это немного сложнее, но основная предпосылка остается той же.
123 x 11 = 1353 или (1) 35 (3)
Первая средняя цифра (в разряде сотен) разрешается путем добавления 1+2, чтобы получить 3, а вторая средняя цифра разрешается путем добавления 2 +3 или 5. Таким образом, первая и последняя цифры работают точно так же, как и при разрешении двузначных чисел, но средние числа разрешаются путем сложения первых двух цифр, чтобы получить первое среднее число в последовательности, и последние два числа чтобы получить вторую среднюю цифру в последовательности. Понял?
Хорошо, а как насчет 9-значных чисел…?
123456789 х 11 = 1358024679!
Видите, умножить на одиннадцать легко, верно? Теперь проверьте себя на умножение на одиннадцать и посмотрите, чему вы научились.
Комментарии
Комментарии
Умножение 2- и 3-значных чисел
Урок 2: Умножение 2- и 3-значных чисел
Когда вы умножаете число или сумму, вы многократно увеличиваете . В разделе «Введение в умножение» вы узнали, что умножение может быть способом понять, что происходит в реальной жизни. Например, представьте, что в магазине продаются ящики с грушами. Маленькие коробки содержат по пять груш в каждой. Вы покупаете два . Вы можете написать ситуацию следующим образом и использовать для ее решения таблицу умножения на :
Теперь представьте, что вы решили купить два большие коробки, содержащие по 14 груш в каждой. Эта ситуация будет выглядеть так:
Эту задачу решить сложнее. Подсчет груш займет некоторое время. К тому же в таблице умножения нет 14. К счастью, есть способ написать задачу так, чтобы ее можно было разбить на более мелкие части. Это называется , сложенное в стопку . Это означает, что мы будем писать числа друг над другом , а не рядом.
К счастью, есть способ написать задачу так, чтобы ее можно было разбить на более мелкие части. Это называется , сложенное в стопку . Это означает, что мы будем писать числа друг над другом , а не рядом.
Давайте потренируемся с этой задачей, 14 x 2.
Сначала напишите числа, одно над другим. Хорошая привычка всегда писать большее число сверху. Если вы этого не сделаете, решить проблему будет сложнее.
Затем запишите знак умноженный на к оставшимся числам.
Вместо знака равно поставьте черту под числом внизу.
Обратите внимание, как числа выстроены справа от ?
Когда вы пишете задачу на умножение с накоплением, всегда следите за тем, чтобы числа выстраивались таким образом.
Например, давайте рассмотрим другую задачу, 5 x 112. Видите, как 2 находится прямо над 5?
Также обратите внимание, что мы поместили большее число сверху, хотя оно было вторым числом в исходном выражении.

Всегда ставьте задачи на умножение с накоплением одинаково: с большим числом сверху…
Всегда устанавливайте задачи на умножение с накоплением одинаково: с большим числом сверху… и выстраиванием правильных цифр.
Решение задач на умножение с накоплением
На первый взгляд задачи на умножение с накоплением могут показаться довольно сложными. Не волнуйся! Если вы сможете решить задачи из раздела «Введение в умножение», вы сможете научиться решать и эти задачи. Чтобы умножать большие числа, вам понадобятся те же базовые навыки, что и для умножения маленьких. Вы даже можете использовать такие же инструменты, как умножить на таблицы .
Давайте посмотрим, как работает решение задач на умножение с накоплением.
Помните пример с двумя коробками, в каждой из которых было по 14 груш? Чтобы узнать, сколько всего груш, мы решим эту задачу: 14 x 2.
Когда вы умножаете сложенные числа, вы начинаете с правой цифры в нижнем числе задачи.
 Наше нижнее число состоит только из одной цифры: 2.
Наше нижнее число состоит только из одной цифры: 2.Мы умножим 2 на верхнее число, 14. Поскольку в таблице умножения нет 14, нам придется умножать по одной цифре за раз.
Как обычно, решим задачу от направо налево . Итак, мы умножим 2 на цифру в правом верхнем углу . Вот, это 4.
Теперь пришло время решить 2 x 4. Мы можем использовать таблицу умножения.
2 x 4 равно 8. Запишем 8 под 2 и 4.
Теперь умножим 2 на следующую цифру слева: 1.
Теперь решим 2 x 1.
Всякий раз, когда вы умножаете число на 1, это число остается тот же . Итак, 2 x 1 равно 2. Просто чтобы убедиться, мы проверим таблицу умножения.
Напишите 2 под чертой, прямо под 1.
Готово! Всего у нас 28, или двадцать восемь. 14 x 2 = 28.
Давайте потренируемся с другой задачей, 31 x 7.

Всегда начинайте с цифры внизу справа . Здесь это 7.
Сначала умножьте 7 на цифру справа вверху, 1.
7 x 1 равно 7. Напишите 7 непосредственно под цифрами, которые мы только что перемножили.
Далее мы умножим 7 на следующую цифру слева. Это 3.
Воспользуемся таблицей умножения, чтобы найти 7 x 3.
7 x 3 равно 21. Убедитесь, что числа выстроены так, чтобы правая цифра 21, 1, была прямо под 3.
Наш ответ 217. Итак, 31 x 7 = 217.
Попробуйте это!
Сложите и решите эти задачи на умножение. Затем проверьте свой ответ, введя его в поле.
31 х 3 =
24 х 2 =
40 х 8 =
Использование переноса
На последней странице вы практиковались в умножении чисел, стоящих вертикально. Некоторые проблемы требуют дополнительного шага. Давайте рассмотрим следующую задачу:
Если вы попытаетесь умножить 9 x 5, вы заметите, что нет места для записи произведения, 45. Когда произведение двух чисел равно больше, чем 9 , вам нужно будет использовать метод под названием , несущий . Если вы знаете, как складывать большие числа, возможно, вы помните и об использовании переноса. Давайте посмотрим, как это работает в умножении.
Когда произведение двух чисел равно больше, чем 9 , вам нужно будет использовать метод под названием , несущий . Если вы знаете, как складывать большие числа, возможно, вы помните и об использовании переноса. Давайте посмотрим, как это работает в умножении.
Давайте попробуем решить задачу, которую мы только что рассмотрели, 29 x 5.
Как обычно, мы начнем с умножения 5 на верхнюю правую цифру, 9.
Согласно нашей таблице умножения , 5 x 9 равно 45, но нет места для записи обеих цифр под 5 и 9.
Запишем правую цифру 5 под чертой…
Запишем правую цифру 5 под чертой… тогда запишем левую цифру , 4, до следующего набора цифр в задаче.
Видишь, как это работает? Мы умножили 5 и 9, чтобы получить 45. Мы поместили 5 под чертой, перенесли 4 и поместили ее над следующим набором цифр.
Теперь пришло время для следующего шага.
 Это то же самое, что и с любой другой задачей на умножение. Мы умножим 5 х 2,
Это то же самое, что и с любой другой задачей на умножение. Мы умножим 5 х 2,5 х 2 = 10. Но 10 под чертой пока писать не будем – есть еще один шаг.
Помните номер, который мы носили, 4?
Мы должны к добавить к нашему продукту, 10.
4 + 10 равно 14.
Мы напишем 14 под чертой.
Итого 145. Теперь мы знаем, что 29 x 5 = 145.
Давайте попробуем решить другую задачу, просто для практики. 208 х 6,
Сначала мы умножаем нижнее число 6 на цифру справа вверху. Это 8.
6 x 8 равно 48.
Запишем 8 под чертой…
Запишем 8 под чертой… и перенесем 4. Мы поместим его над следующей цифрой.
Следующая цифра 0.
Все, что умножается на ноль, равно 0, поэтому мы знаем, что 6 x 0 = 0.
Помните, мы еще не пишем этот 0 под чертой.
 Мы должны добавить его к 4, которые мы только что перенесли.
Мы должны добавить его к 4, которые мы только что перенесли.4 + 0 = 4. Под чертой напишем 4.
Наконец, мы умножаем 6 на 2.
6 x 2 = 12, поэтому мы напишем 12 под чертой.
Готово! Ответ: 1248, или одна тысяча двести сорок восемь. 208 x 6 = 1248.
Попробуйте!
Сложите и решите эти задачи на умножение. Затем проверьте свой ответ, введя его в поле.
25 х 9=
98 x 2 =
103 x 5 =
Умножение больших чисел
На последних нескольких страницах вы практиковались в умножении больших чисел на маленькие. Что произойдет, если вам нужно умножить два больших числа?
Например, представьте, что ваш счет за мобильный телефон составляет 43 доллара в месяц . В году 12 месяцев, поэтому, чтобы узнать, сколько вы платите за свой телефон каждый год, вы можете решить 43 x 12. Вы должны написать выражение следующим образом:
На первый взгляд эта проблема может показаться сложной, но не беспокойтесь. Если вы можете умножать маленькие числа, вы можете умножать и большие. Все, что вам нужно сделать, это разделить эту большую проблему на несколько более мелких. Как всегда, вы можете использовать свою таблицу умножения на , чтобы помочь.
Если вы можете умножать маленькие числа, вы можете умножать и большие. Все, что вам нужно сделать, это разделить эту большую проблему на несколько более мелких. Как всегда, вы можете использовать свою таблицу умножения на , чтобы помочь.
Чтобы решить такую большую задачу, начните с тех же шагов, которые вы используете для решения любой другой задачи на умножение.
Как всегда, вы начинаете с цифры справа внизу. Вот, это 2.
Умножим на цифру справа вверху, 3.
Благодаря нашей таблице умножения мы знаем, что 3 x 2 равно 6. линия, крайняя правая.
Далее умножаем 2 x 4.
2 x 4 равно 8.
Напишите 8 под чертой, прямо под 4.
- 90 OK. Первая половина задачи решена.
Теперь пришло время снова взглянуть на нижний номер.
Мы собираемся умножить следующую цифру. Это 1.
Сначала умножьте 1 на верхнее число справа.
 Здесь это 3.
Здесь это 3.1 x 3 равно 3… но мы не собираемся писать 3 в обычном месте.
Вместо того, чтобы писать 3 справа от , как мы обычно делаем… это на одно место левее, под вторым набором цифр.
Рекомендуется отметить место, которое вы оставили пустым. Таким образом, вы будете знать, что случайно ничего туда не запишете. Мы добавим 0, так как ноль — это то же самое, что и , и ничего .
Теперь давайте умножим последний набор чисел. Это 1 x 4.
1 x 4 = 4. Мы напишем 4 под чертой, слева от 3, которые мы только что написали.
Последний шаг. Чтобы получить окончательный ответ, нам нужно к добавить числа, которые мы только что получили в результате умножения.
Как всегда, мы начнем добавлять справа.
6 + 0 равно 6. Мы напишем 6 под чертой.
Далее, 8 + 3.
8 + 3 равно 11.
 Поскольку 11 — двузначное число, нам придется переносить.
Поскольку 11 — двузначное число, нам придется переносить.Запишите правую цифру 1 под 8 и 3…
Запишите левую цифру 1 под 8 и 3… затем перенесите правую цифру и поместите ее над цифрой слева.
Наконец, мы добавим 4 к только что перенесенной 1.
4 + 1 равно 5.
Готово! Итого 516. Другими словами, 43 x 12 = 516.
Попробуйте!
Сложите и перемножьте эти двузначные числа. Затем проверьте свой ответ, введя его в поле.
33 x 21 =
52 x 17 =
81 x 34 =
Умножение двух трехзначных чисел
Умножение больших чисел всегда работает одинаково, независимо от того, сколько цифр в числах. Когда вы умножаете, будьте осторожны, записывая числа в правильных местах. Давайте рассмотрим задачу с двумя 3-значные числа , чтобы увидеть, как это работает с еще большими числами.
Давайте попробуем решить эту задачу: 601 x 243.

Как обычно, начнем с умножения нижней правой цифры на верхнюю правую цифру. Итак, 3 x 1.
Благодаря нашей таблице умножения мы знаем, что 3 x 1 равно 3. Запишите число 3 под чертой справа.
Теперь умножьте 3 на следующее число, 0.
Любое число, умноженное на ноль, равно 0, поэтому напишите 0 под чертой, рядом с 3.
Далее, 3 x 6.
3 x 6 = 18. Напишите 18 под чертой.
Мы закончили с первой цифрой нижнего числа.
Затем умножьте на второе число внизу, 4.
4 x 1 равно 4. Помните, что вы не собираетесь писать 4 до конца вправо.
Вместо этого напишите 4 на одну позицию левее под вторым набором цифр.
Чтобы все было выровнено, мы поместим ноль в качестве заполнителя справа от четырех.
Теперь давайте перейдем к следующему числу сверху — 0.

4 x 0 равно 0. Напишите 0 под чертой.
Затем умножьте 4 на последнюю цифру верхнего числа — 6.
4 x 6 равно 24. Напишите 24 под чертой.
Мы готовы умножить на последнюю цифру нашего нижнего числа — 2.
Как всегда, начните с верхней правой цифры, 1.
2 x 1 равно 2.
Напишем 2 под чертой, через два пробела справа.
Обратите внимание, куда мы поставили 2.
Когда мы умножили на первую цифру в нижнем числе…
Когда мы умножили на первую цифру в нижнем . , мы выстроили товар до упора вправо .
Когда мы умножали на вторую цифру …
Когда мы умножали на вторую цифру … мы записывали произведение на один пробел слева.
Теперь, когда мы умножили на третью цифру .
 ..
..Теперь, когда мы умножили на третью цифру … мы поместили произведение на два пробела слева от
Возможно, вы заметили закономерность. Каждый раз, когда мы умножали на новую цифру, мы записывали произведение на одну цифру дальше влево. Это верно независимо от того, сколько цифр в числах, на которые вы умножаете.
Вернемся к нашей проблеме. Мы просто умножили 2 x 1.
Следующая цифра 0.
2 x 0 равно 0. Напишите 0 под чертой.
Наконец, умножьте 2 x 6.
2 x 6 равно 12. Напишите 12 под чертой.
Время добавить. Как всегда, начните с крайних правых цифр. Здесь это означает, что мы добавляем 3 + 0 + 0.
3 + 0 + 0 = 3. Напишите 3 непосредственно под цифрами, которые мы только что добавили.
Далее мы добавим 0 + 4 + 0.
0 + 4 + 0 равно 4.

Теперь следующий набор цифр, 8 + 0 + 2.
3
8 + 0 + 2 = 10. 10 — двузначное число, поэтому нам нужно нести . Напишите 0 под цифрами, которые мы только что добавили, и поместите 1 над следующим набором цифр.
Пришло время добавить 1, которую мы только что перенесли. Это означает, что мы находим 1 + 1 + 4 + 0.
1 + 1 + 4 + 0 = 6. Напишите 6 под чертой.
Далее, 2 + 2.
2 + 2 = 4. Напишите 4 под чертой.
Слева только одна цифра — 1.
Один плюс ничего равно 1, поэтому мы напишем 1 под чертой.
Наконец-то мы закончили! Всего у нас 146 043, или сто сорок шесть тысяч сорок три. 601 х 243 = 146 043.
Какое огромное количество! Если эта проблема показалась вам сложной, не беспокойтесь. Вам редко придется умножать такие большие числа. Когда вы это сделаете, вы всегда можете воспользоваться калькулятором.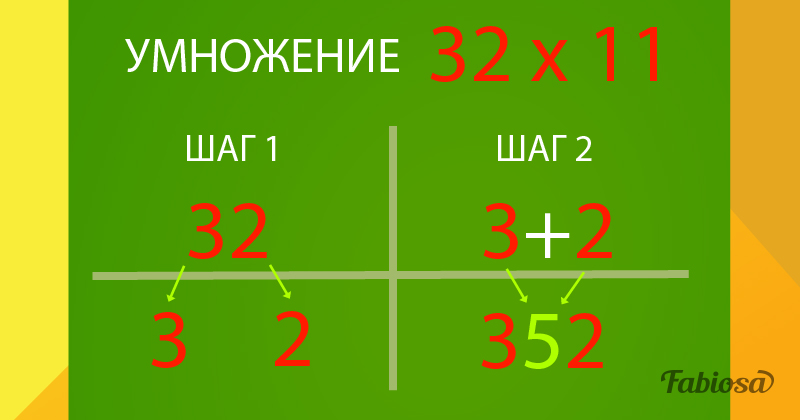


 Наше нижнее число состоит только из одной цифры: 2.
Наше нижнее число состоит только из одной цифры: 2.
 Это то же самое, что и с любой другой задачей на умножение. Мы умножим 5 х 2,
Это то же самое, что и с любой другой задачей на умножение. Мы умножим 5 х 2,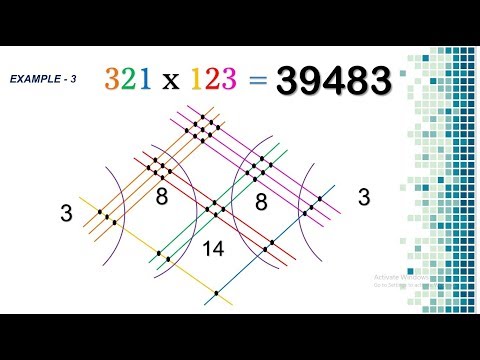 Мы должны добавить его к 4, которые мы только что перенесли.
Мы должны добавить его к 4, которые мы только что перенесли. Здесь это 3.
Здесь это 3. Поскольку 11 — двузначное число, нам придется переносить.
Поскольку 11 — двузначное число, нам придется переносить.

 ..
..