Как решить один и тот же пример разными способами: китайский метод умножения, египетский, метод решетки – 20 января 2023
Привычные нам способы решения примеров далеко не единственно верные
Фото: Александр Подопригора / 161.RU
Поделиться
Складывать, вычитать, умножать и делить мы все научились еще в школьные годы. Многие даже неплохо сохранили эти навыки и до сих пор могут что-нибудь да умножить. В уме. Но что, если приходится умножать многозначные числа? Понятно, что проще всего воспользоваться калькулятором. Но мы не ищем легких путей — вместо них мы нашли несколько способов решить одни и те же примеры. Ими до сих пор пользуются в разных странах, и это не привычное нам умножение столбиком.
В качестве примера, решить который мы попробуем семью разными методами, мы взяли не самый сложный, но и не самый простой: 223 х 304. Произведение этих множителей равняется 67 792. Нам было важно, чтобы числа были не двузначные и чтобы хотя бы в одном из них был ноль (потом объясним зачем). А теперь давайте посчитаем.
А теперь давайте посчитаем.
Чтобы решить наш пример этим способом, сперва запишем множители. После этого нужно представить число 223 в виде суммы степеней двоек — начинаем с единицы и умножаем на два, пока не получим число, которое будет больше, чем 223. Получится 256. Это уже много. А раз много, значит нам это не нужно. Остается 128.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Дальше нужно число 304 умножить на все получившиеся числа. Но понадобятся нам не все. Из чисел левого столбца нам нужно собрать число 223. Идем снизу вверх. Берем 128, прибавляем к нему 64. Получается 192. Если прибавить к этой сумме 32, получится 224, а это уже перебор. Поэтому 32 пропускаем и прибавляем все остальные. Выйдет наше 223. На те числа, что остались (а это все, кроме 32), мы и будем умножать наше 304. Теперь суммируем всё, что у нас получилось. Сумма этих чисел окажется 67 792.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Если вам кажется, что умножать 304 на 128 в такой ситуации будет полнейшим безумием, воспользуйтесь хитростью и просто умножайте каждое предыдущее число на два — так будет проще.
Всё, что вам понадобится, чтобы решить любой пример с умножением этим крестьянским методом, — это уметь умножать и делить на два.
Для начала будем последовательно делить на два первое число, пока оно не превратится в единицу. Думаете, не получится в случае с числом 223? Только не в древнерусском способе! Если в результате будет получаться число с остатком, отбрасываем эти остатки куда подальше — они нам не пригодятся.
Схема: Виталий Калистратов / Городские порталы
Поделиться
После этой нехитрой процедуры беремся за второй множитель — его будем на два умножать. Столько же раз, сколько делили первый множитель, пока он не достиг единицы. Умножили? Теперь вычеркивайте все строчки, в которых в левом столбце есть четное число. У нас такая строчка одна — с цифрой шесть.
Столько же раз, сколько делили первый множитель, пока он не достиг единицы. Умножили? Теперь вычеркивайте все строчки, в которых в левом столбце есть четное число. У нас такая строчка одна — с цифрой шесть.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Дальше — самая нелегкая задача этого метода: суммировать все числа, что стоят справа (включая 304). Сложно, но у древнерусских счетоводов не было другого выбора, и им приходилось всё считать вручную. У нас, к счастью, есть калькуляторы, так что мы с удовольствием воспользуемся этой возможностью. И калькулятор покажет 67 792. Если вы хотите проверить, действительно ли работает этот метод, можете поменять множители местами и всё пересчитать, но, забегая вперед, мы вам скажем, что от перестановки мест множителей произведение не меняется даже в этом случае.
Первым дело запишем наши числа одно над другим и подведем под ними черту. И умножим каждую цифру верхнего числа на каждую цифру нижнего. Если будут получаться двузначные числа, пишем их как есть, а вот однозначные пишем в виде «ноль и цифра» — например, 08 вместо просто 8.
И умножим каждую цифру верхнего числа на каждую цифру нижнего. Если будут получаться двузначные числа, пишем их как есть, а вот однозначные пишем в виде «ноль и цифра» — например, 08 вместо просто 8.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Получив эту хитрую комбинацию, умножаем соседние цифры (2 на 0, 2 на 4) и в обратную стороны (2 на 3 и 3 на 0). Идем еще дальше и стараемся не запутаться — перемножаем первую верхнюю цифру на третью нижнюю, а третью верхнюю — на первую нижнюю. Умножение закончилось.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Давайте складывать то, что у нас получилось. А получилось у нас 67 792.
Выписываем наших героев и подводим под ними черту, как делали это в методе треугольника. Затем перемножим крайние цифры — 2 и 4. Результат (его мы записываем как 08) будет первой строкой нашего решения. Следом за ними умножаем вторую цифру левого множителя на первую и третью — правого. Запишем их во вторую строку. Начало ромбу положено.
Следом за ними умножаем вторую цифру левого множителя на первую и третью — правого. Запишем их во вторую строку. Начало ромбу положено.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Ну а дальше умножаем друг на друга цифры из разряда сотен, десятков и единиц и так же записываем их в одну строку. Результат заносим в третью строчку.
Теперь берем вторую цифру во втором множителе и умножаем на первую и третью из первого. Четвертая строка решения готова. Последней, пятой строкой записываем произведение последней цифры первого множителя и первой цифры второго. Наш ромб готов. Осталось только суммировать цифры, расположенные друг над другом. Метод, конечно, красивый, но совсем не простой в применении.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Вот мы и добрались до того момента, где объясним, зачем нам понадобились трехзначные числа, да еще и с нулем. В китайском методе нам придется считать, чертить и рисовать. Так что для начала разберем принцип его работы на простом примере и умножим 34 на 62. Для этого нарисуем черты. Сперва три горизонтальные, потом, через промежуток, еще четыре. Это три десятка и четыре единицы нашего первого числа. А число 62 по такому же принципу превращается в шесть и две вертикальные черты. Теперь нам нужно разграничить зоны единиц, десятков и сотен.
В китайском методе нам придется считать, чертить и рисовать. Так что для начала разберем принцип его работы на простом примере и умножим 34 на 62. Для этого нарисуем черты. Сперва три горизонтальные, потом, через промежуток, еще четыре. Это три десятка и четыре единицы нашего первого числа. А число 62 по такому же принципу превращается в шесть и две вертикальные черты. Теперь нам нужно разграничить зоны единиц, десятков и сотен.
Схема: Виталий Калистратов / Городские порталы
Поделиться
После этого считаем точки пересечения всех черточек. В зоне единиц их восемь, в зоне десятков — 30, в зоне сотен — 18. Теперь нужно это сложить: 1800+300+8 = 2 108. На калькуляторе, умножая 34 на 62, получится тот же результат.
Переходим к нашему изначальному примеру и умножим 223 на 304. Рисуем две, две и три горизонтальные линии, три вертикальные слева и четыре справа. Место посередине оказывается пустым, поэтому здесь у нас будет воображаемая линия. (Цифры у нас стали крупнее, поэтому и зон будет больше.) И считаем точки пересечения.
(Цифры у нас стали крупнее, поэтому и зон будет больше.) И считаем точки пересечения.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Складываем, начиная с единиц. Там, где получились двузначные числа, оставляем единицы, а десятки перекидываем в соседнюю область. То есть там, где стояли рядом 8 и 12, оказались 9 и 2, а соседство 6 и 17 превратилось в 7 и 7. Считаем, что у нас получилось, справа налево: 67 792.
Чтобы решить наш пример методом решетки (его еще называют древнеиндийским методом), первым делом надо нарисовать таблицу, у которой будет три столбца и три строки — по количеству цифр в умножаемых числах. Потом делим каждую ячейку по диагонали на две части. Решетка готова.
Теперь по горизонтали выписываем цифры числа 223, а по вертикали — числа 304. И перемножаем каждое число сверху на каждое число справа. Результат вписываем в наши ячейки таким образом: сверху — десятки, снизу — единицы (если десятков нет, пишем ноль).
Схема: Виталий Калистратов / Городские порталы
Поделиться
Теперь складываем цифры, которые получились в наших диагоналях. По периметру, начиная с правого нижнего угла и поднимаясь до левого верхнего. Если число вышло двузначным, оставляем только единицу, а десятки плюсуются к единицам числа предыдущего — совсем как в сложении, к которому мы привыкли.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Выписываем ответ, начиная с левой стороны: 67 792. Что и требовалось доказать.
Этот метод похож на метод решетки, но есть отличия. Здесь мы снова рисуем таблицу на три столбца и три строки, но ни на какие ячейки не делим. А наши числа записываем не в виде отдельных цифр, а сотнями, десятками и единицами.
Схема: Виталий Калистратов / Городские порталы
Поделиться
Дальше начинаем умножать те цифры, что сверху, на те, что справа.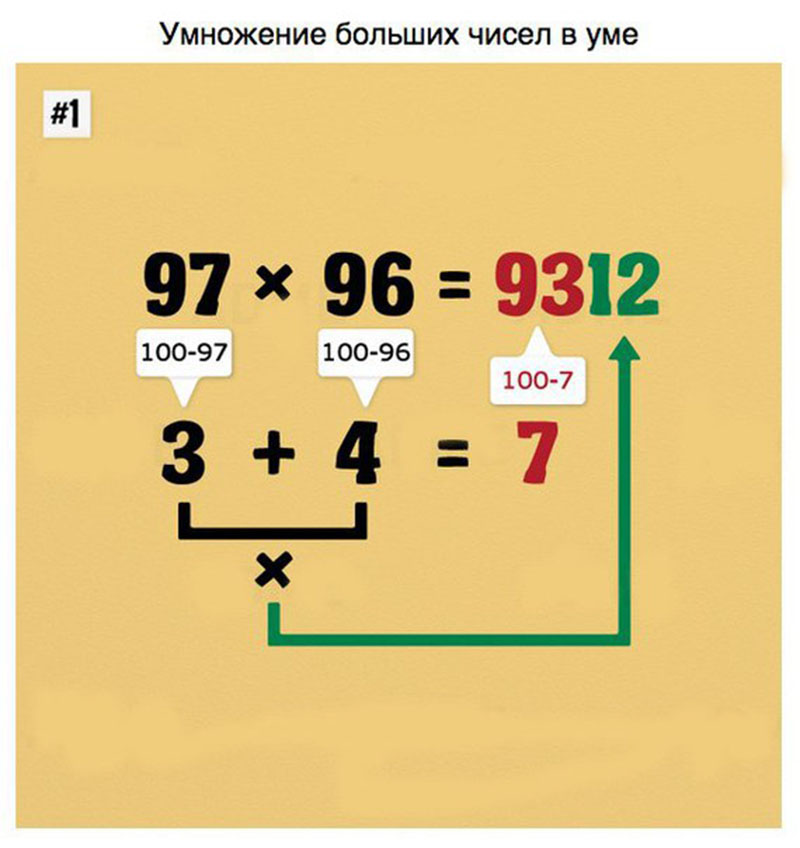
Схема: Виталий Калистратов / Городские порталы
Поделиться
Умножили? Осталось только всё сложить: 60 000 + 6000 + 900 + 800 + 80 + 12 = 67 792. Тот результат, который и получится, если умножить 223 на 304.
Разные способы решить один и тот же пример, к слову, далеко не единственная математическая причуда. На днях одна несложная на первый взгляд задачка рассорила весь интернет — скандал разгорелся из-за простого примера для 6-классников. И мы попробовали решить его с математиком.
Эффективный счёт в уме или разминка для мозга / Хабр
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10
Еще пример:
31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899.
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400; 3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68.
Аналогично выполняется умножение или деление на
600 : 25 = (600 : 100) x 4 = 6 x 4 = 24; 24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600.
Теперь не кажется невозможным умножить в уме 625 на 53:
625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = = (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125.
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. 2 = 17000 + 19000 + 2000 + 25 = 38025.
2 = 17000 + 19000 + 2000 + 25 = 38025.
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
M = 10m + n, K = 10a + 10 - n.
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим:
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77.
 Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001.
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42 = 2016.
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. 2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».
Math Tricks – Behavioral Sciences Research Core
Page MenuЭта веб-страница посвящена
невероятно умной
идее о том, что математика может быть интересной!
Попробуйте эти трюки:
- Easy Magic Addition
- Магический квадрат #15
- Магический квадрат #34
- Создайте свой собственный магический квадрат
- Перевернутый магический квадрат
- Антимагический квадрат
- Выиграйте ставки с этим квадратом
- Магический фокус с картами
- Калькулятор молний
- Таблицы забавных чисел
- Знаете ли вы.
 ..?
..? - Уловка на этот год
- Где нить?
- Огромный магический квадрат
Вот несколько интересных ссылок:
- Список книг по хитрой математике для чтения, большинство из которых я использовал для этого сайта.
- Узнайте об оригинальном компьютере: The Abacus (http://www.ee.ryerson.ca:8080/~elf/abacus/)
- Сыграйте в математическую игру (http://dev.eyecon.com/marcia) — для одного или двух игроков. (Если вы используете Netscape, Не прокручивать страницу вниз, пока загружается .
- Играйте в Shoot Balls (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Играйте в Flippo 24 (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Проверьте свои знания таблицы умножения (http://www.fi.uu.nl/wisweb/en/applets/tafels/Welcome.html)
- Попробуйте свои силы в оценке (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Исследуйте геометрию в увлекательной интерактивной форме.

- Попробуйте загадку «Ханойская башня» (http://www.eng.auburn.edu/~fwushan/Hanoi1.html).
- Посмотрите, что такое Spriographis (http://www.mainstrike.com/mstservices/handy/Spiro/).
- Посмотрите, что такое набор Мандельброта (http://www.franceway.com/java/fractale/mandel_b.htm).
- Если вы хотите больше задач по математике , попробуйте новый сайт PBS MATHLINE MATH CHALLENGES. Попробуйте, вам понравится. (Но помните, что мы были первыми.)
Волшебный трюк №1
Удивите пеонов этим. Все просто. Это эффективно. Он получает их каждый раз.
- Спросите свою оценку выберите три (3) разных номеров от 1 до 9.
- Скажите ему или ей (или ей или ему) записать три числа рядом друг с другом, начиная с самого большого и заканчивая наименьшим, чтобы получилось одно трехзначное число. Скажите ему/ей, чтобы он не говорил вам, что это за цифры.
- Затем попросите ее или его составить новое трехзначное число, переставив цифры местами, поставив наименьшее первым, а самое большое последним.

- Теперь попросите его или ее вычесть меньшее (и меньшее) трехзначное число из старшего (и большего) трехзначного числа. Скажи им, чтобы они не говорили тебе, каков результат.
- Теперь у вас есть выбор оберток:
- Попросите вашего друга сложить три цифры числа, которое получается в результате вычитания меньшего из большего трехзначного числа. Затем удивите его или ее, сказав, какова сумма этих трех чисел. Сумма трехзначного ответа всегда будет 18!
- Скажите своему другу, что если он или она скажет вам, какая первая ИЛИ последняя цифра ответа, вы скажете ей или ему, какие две другие цифры. Это возможно, потому что

Вернуться к началу
Магический квадрат #15
Каждая строка и столбец в этом магическом квадрате в сумме дают 15. Так сделайте обе диагонали!
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
Вернуться к началу
Магический квадрат #34
Каждая строка и столбец в этом магическом квадрате в сумме дают 34. Так сделайте обе диагонали!
| 1 | 15 | 14 | 4 |
| 12 | 6 | 7 | 9 |
| 8 | 10 | 11 | 5 |
| 13 | 3 | 2 | 16 |
Вернуться к началу
Рецепт собственного магического квадрата 3 X 3
Вот рецепт изготовления собственного магического квадрата 3 X 3. Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовски замечательной книги под названием 9.0004 Математика для миллиона , Ланселот Хогбен, опубликовано Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы погрузиться в приключения чисел, описанные в этой классической книге.
Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовски замечательной книги под названием 9.0004 Математика для миллиона , Ланселот Хогбен, опубликовано Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы погрузиться в приключения чисел, описанные в этой классической книге.
Некоторые необходимые правила и определения:
- Пусть буквы a , b и c обозначают целые числа (то есть целые числа).
- Всегда выбирайте a так, чтобы оно было больше суммы b и c . То есть a > b + c . Это гарантирует отсутствие записи в магический квадрат отрицательного числа.
- Не допускайте 2 X b = c . Это гарантирует, что вы не получите одно и то же число в разных ячейках.
- Используя формулы, приведенные в таблице ниже, вы можете составить магический квадрат, в котором сумма строк, столбцов и диагоналей равна 3 X независимо от числа или .

Чтобы создать первый магический квадрат #15 выше, пусть a будет равно 5, пусть b будет равно 3, и пусть c будет равно 1. Вот некоторые другие:
- а = 6, б = 3, в = 2
- а = 6, б = 3, в = 1
- а = 7, б = 3, в = 2
- а = 7, б = 4, в = 2
- а = 8, б = 6, в = 1
- а = 8, б = 5, в = 2
- а = 8, б = 4, в = 3
Попробуйте придумать что-нибудь свое.
Вернуться к началу
Перевернутый магический квадрат
Вот магический квадрат, который не только дает в сумме 264 по всем направлениям, но и делает это, даже когда он перевернут! Если не веришь мне, посмотри на это, стоя на голове! (Или просто скопируйте его и переверните вверх ногами.)
| 96 | 11 | 89 | 68 |
| 88 | 69 | 91 | 16 |
| 61 | 86 | 18 | 99 |
| 19 | 98 | 66 | 81 |
Вернуться к началу
Антимагический квадрат
Вот магический квадрат с максимально возможным количеством различных сумм .
| 5 | 1 | 3 |
| 4 | 2 | 6 |
| 8 | 7 | 9 |
Эта таблица дает 8 разных итого.
Вернуться к началу
Выиграть ставки с помощью магического квадрата
Итак, вот отличный способ выиграть ставки с помощью магического квадрата. Позвоните другу по телефону. Пусть он или она возьмет карандаш и бумагу и поднесет их к телефону, чтобы он или она могли записать цифры от 1 до 9. Скажите своему другу, что вы будете по очереди называть цифры от 1 до 9. Никто из вас не может повторить номер, который называет другой. Затем вы оба запишите числа от 1 до 9.. Затем, когда ваш друг называет одно из чисел, он обводит это число кружком, и вы тоже. Когда вы называете число, вы рисуете квадрат вокруг этого числа, и ваш друг делает то же самое. Выигрывает тот, кто первым наберет три числа, сумма которых точно равна 15.
Допустим, вы идете первым и называете 8. Ваш друг может назвать 6. Затем вы называете 2. Ваш друг называет 5, и вы называете 4. Ваш друг называет 7, а вы называете 3. Затем вы говорите своему другу, что вы только что выиграли, потому что назвали 8, 3 и 4, что в сумме дает 15.
Ваш друг снова захочет поиграть. Так что на этот раз вы можете поспорить с ним, что выиграете, с условием, что в случае ничьей (когда вы используете числа от 1 до 9, но ни один из вас не получает в сумме 15) никто ничего не должен.
Если вы знаете хитрость, вы никогда не проиграете, и, вероятно, проиграете в большинстве случаев.
Фокусы На самом деле фокус основан как на крестиках-ноликах, так и на магическом квадрате. Магический квадрат выглядит так:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Поскольку это магический квадрат, каждая строка, каждый столбец и каждая диагональ в сумме дают 15. Поэтому, если этот квадрат находится перед вами с вашим другом по телефону, вы можете поставить крестик рядом с ним. квадраты числа, которое вы называете, и O в квадратах чисел, которые называет ваш друг. Затем, как и в крестиках-ноликах, вы пытаетесь поставить три крестика подряд, потому что в сумме это всегда будет 15.
Затем, как и в крестиках-ноликах, вы пытаетесь поставить три крестика подряд, потому что в сумме это всегда будет 15.
Итак, в приведенном выше примере, когда вы называете 8, вы ставите X в верхнем левом углу. Когда ваш друг говорит 6, вы ставите ) в правом верхнем углу. И так далее.
Наверх
Математический фокус с картами
Для этого задания вам понадобится обычная колода карт. Никаких причудливых перетасовок не требуется. Просто следуйте этим простым шагам:
- Перемешайте карты, чтобы тщательно их перемешать.
- Разложите 36 карт стопкой.
- Попросите друга выбрать одну из 36 карт, посмотреть на нее и запомнить, а затем положить ее обратно в стопку, не показывая ее вам.
- Перемешайте 36 карт.
- Разложите 36 карт в 6 рядов по 6 карт в каждом. Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий.
- Попросите друга посмотреть на карточки и сказать, в каком ряду находится выбранная карточка.
 Запомните, под каким номером находится ряд.
Запомните, под каким номером находится ряд. - Аккуратно поднимите карты в том же порядке, в котором вы их положили . Таким образом, первая карта слева в верхнем ряду находится наверху стопки, а последняя карта справа в нижнем ряду — внизу стопки.
- Теперь разложите карты в 6 рядов по 6 карт в каждом, но на этот раз разложите карты по одному столбцу за раз . Вместо того, чтобы переходить от одной строки к другой, переходите от одного столбца к другому. Разложите первые шесть карт в столбце сверху вниз в крайний левый угол. Затем выложите следующие шесть карт во второй столбец из шести карт справа от первого столбца из шести карт. Продолжайте делать это, пока у вас не будет 6 столбцов по 6 карт в каждом (что выглядит так же, как 6 рядов по 6 карт в каждом, потому что это 9).0004 это то же самое).
- Еще раз спросите у друга, в каком ряду находится выбранная карта.
- Когда ваш друг говорит вам, в каком ряду находится карта, вы можете сказать, какая именно выбранная карта.
 Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Вернуться к началу
Калькулятор молний
Вот уловка, чтобы удивлять их каждый раз! Попросите кого-нибудь записать свой номер социального страхования. Затем попросите их переписать его так, чтобы все было перемешано. (Если у них нет номера социального страхования, попросите их записать любые 9 цифр от 1 до 9.) Если есть нули, попросите заменить их на любую другую цифру от 1 до 9. Затем попросите их скопировать свои девять цифр. числа в том же порядке рядом с исходными девятью числами. Это даст им число с 18 цифрами, первая половина которого такая же, как вторая половина. Далее измените вторую цифру на 7 и измените одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Вернуться к началу
Таблицы забавных чисел
Следующие забавные таблицы взяты из одной из моих любимых книг всех времен, Recreations in the Theory of Numbers , Альберт Х. Бейлер, опубликовано Dover Publications. Эта книга на самом деле объясняет математические причины, по которым эти трюки работают.
3 + 3 3 x
и 6 х
91111 1119 + 5 12345
0 987654 х 8 + 8
97 +
29044 6
 д.
д.
Наверх
Знаете ли вы…?
Каждое двузначное число, оканчивающееся на 9, представляет собой сумму, кратную двум цифрам, плюс сумму двух цифр. Так, например, 29 = (2 х 9) + (2 + 9). 2 X 9 = 18. 2 + 9 = 11. 18 + 11 = 29.
40 — уникальное число, потому что, когда оно записано как «сорок», это единственное число, буквы которого расположены в алфавитном порядке.
А премьер число — это целое число больше 1, которое не делится без остатка ни на какое другое целое число, кроме самого себя (и 1). 2, 3, 5, 7, 11, 13 и 17 являются примерами простых чисел.
139 и 149 — первые последовательные простые числа, отличающиеся на 10.
69 — единственное число, в квадрате и кубе которого между ними используются все цифры от 0 до 9 по одному разу:
69 2 = 4761 и 69 3 = 328 509.
Один фунт железа содержит примерно 4 891 500 000 000 000 000 000 000 атомов.
Существует около 318 979 564 000 возможных способов сыграть первые четыре хода с каждой стороны в игре в шахматы.
Земля проходит более полутора миллионов миль каждый день.
В Эйфелевой башне 2 500 000 заклепок.
Если бы все кровеносные сосуды в человеческом теле были сложены встык, они растянулись бы на 100 000 миль.
Вернуться к началу
Математический трюк для этого года
Предполагается, что этот трюк будет работать только в 1998 году, но на самом деле одно изменение позволит ему работать в течение любого года.
1. Выберите количество дней в неделю, когда вы хотели бы выходить на улицу (1-7).
2. Умножьте это число на 2.
3. Прибавьте 5.
4. Умножьте полученную сумму на 50.
5. В 1998 году, если у вас уже был день рождения в этом году, прибавьте 1748. Если нет , добавьте 1747. В 1999 году просто добавьте 1 к этим двум числам (поэтому добавьте 1749, если у вас уже был день рождения, и добавьте 1748, если нет). В 2000 году номер меняется на 1749 и 1748. И так далее.
В 2000 году номер меняется на 1749 и 1748. И так далее.
6. Вычтите из четырех цифр год вашего рождения (19ХХ).
Результаты:
У вас должно быть трехзначное число.
Первая цифра этого номера — это количество дней, в течение которых вы хотите выходить на улицу каждую неделю (1–7).
Последние две цифры — ваш возраст.
(Спасибо, что передали мне это, Джуди.)
Вернуться к началу
Где нить?
В следующий раз, когда вы будете с группой людей и захотите произвести на них впечатление своими экстрасенсорными способностями, попробуйте это. Пронумеруйте всех в группе от 1 до любого числа. Возьмите кусок веревки и скажите, чтобы он привязал ее кому-нибудь к пальцу, пока вы выходите из комнаты или поворачиваетесь спиной. Затем скажите, что вы можете сказать им не только, у кого он есть, но и на какой руке и на каком пальце он находится, если они просто посчитают за вас и дадут вам ответы. Затем попросите одного из них ответить на следующие вопросы:
1. Умножьте номер человека со строкой на 2.
Умножьте номер человека со строкой на 2.
2. Прибавьте 3.
3. Умножьте результат на 5.
4. Если строка справа, добавьте 8.
Если струна находится на левой руке, добавьте 9.
5. Умножьте на 10.
6. Добавьте номер пальца (большой палец = 1).
7. Добавить 2.
Попросите их сказать вам ответ. Затем мысленно вычтите 222. Остаток дает ответ, начиная с правой цифры ответа.
Например, предположим, что струна находится на безымянном пальце левой руки Игрока №6:
1. Умножить на 2 = 12.
2. Прибавить 3 = 15.
3. Умножить на 5 = 75
4. Поскольку струна находится на левой руке, прибавьте 9 = 84.
5. Умножьте на 10 = 840.
6. Прибавьте номер пальца (3) = 843.
7. Прибавьте 2 = 845.
Теперь мысленно вычтите 222 = 623. Цифра справа (3) говорит о том, что струна находится на безымянном пальце. Средняя цифра говорит о том, что он находится на левой руке (правая рука = 1). Цифра слева говорит о том, что строка принадлежит Игроку №6.
Цифра слева говорит о том, что строка принадлежит Игроку №6.
Кстати, когда номер человека больше 9, вы получите ЧЕТЫРЕХзначное число, а ДВЕ левые цифры будут номером Игрока.
В чем секрет?
(Это из замечательной книги под названием Giant Book of Puzzles & Games, Шейлы Энн Бэрри. Опубликовано Sterling Publishing Co., Inc., Нью-Йорк, 1978 г., недавно переиздано в мягкой обложке.)
Оставайтесь с нами. больше математических трюков. Они будут добавляться время от времени, так что не забудьте проверить снова.
Различные методы умножения чисел — WeTheStudy
Умножение — важный навык для изучения. Несмотря на то, что у нас есть калькуляторы и компьютеры для умножения, научиться делать это вручную — это преимущество. Иногда это даже считается искусством.
Знаете ли вы, что существует множество способов умножения чисел? Возможно, вы знаете только традиционный метод, которому обычно учат в школах. Вот некоторые из них, основанные на различных учениях по всему миру.
Новое в Stories
Традиционное умножение
Этот метод, вероятно, является обычным способом обучения умножению. По крайней мере, так я научился умножать числа. Если вам нужно освежить память, вот как это сделать (в общем, конечно):
- Сначала вы выравниваете два числа так, чтобы места оказались в одном столбце.
- Далее, вообще говоря, вы умножаете значение множителя на каждую цифру множимого на ее разряды.
- Выровняйте результаты по их местам и сложите, чтобы получить конечный продукт.
Умножение на квадрат
Недавно я узнал, что в начальных школах преподают еще один способ умножения чисел. Я обычно вижу этот метод для западных стран, и его обычно называют «методом ящика» или «методом сетки».
Это работает так, что числа разбиваются на суммы чисел. Например, 125 — это 100+20+5, а 42 — это 40+2. Затем расположите эти слагаемые в виде сетки (отсюда и название) и умножьте каждое слагаемое на другое (см.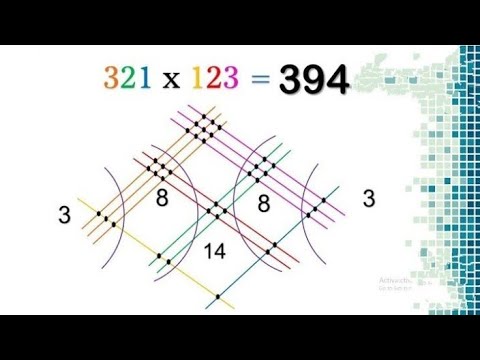 схему). Наконец, добавьте все результаты внутрь коробки, чтобы получить продукт.
схему). Наконец, добавьте все результаты внутрь коробки, чтобы получить продукт.
В некоторых странах этот метод служит отправной точкой для умножения больших чисел для учащихся начальной школы. Почему? Потому что разложение чисел на их слагаемые делает умножение более логичным подходом. Кроме того, ученики, как правило, делают меньше ошибок, используя этот способ.
Единственным недостатком является то, что это кажется ненужным из-за дополнительного шага разбиения чисел; Тем не менее, некоторые школы используют этот метод только как подготовку учеников к обучению традиционным способом.
Палочное умножение
Если вы хотите умножать числа с помощью наглядных пособий, вам подойдет китайский метод или палочное умножение. Давайте попробуем найти произведение 125 и 42. Обратите внимание на шаги и используйте диаграмму как наглядное пособие.
- Сначала нарисуйте палочки на основе значений цифр двух чисел. Для числа 125 нарисуйте 1, 2 и 5 линий слева направо и сверху вниз.
 Затем для числа 42 нарисуйте 4 и 2 линии справа вверху слева внизу (см. схему). Эти прямые должны пересекаться в точках.
Затем для числа 42 нарисуйте 4 и 2 линии справа вверху слева внизу (см. схему). Эти прямые должны пересекаться в точках. - Затем сгруппируйте точки пересечения по столбцам (см. схему). Эти столбцы представляют размещение продукта (единицы, десятки, сотни, тысячи и т. д.).
- Наконец, подсчитайте количество точек в столбце, чтобы получить значение продукта. Перенесите числа в следующий столбец, если это необходимо.
Решетчатое умножение
Другой способ визуализации умножения – использование решетки. Используя предыдущий пример, давайте умножим, используя этот метод. Пожалуйста, обращайтесь к схеме во время чтения.
- Сначала постройте решетку. Его размер зависит от количества цифр множимого и множителя. Если два числа 125 и 42, то размер решетки 3×2.
- Во-вторых, поместите значение цифр множимого (125) в столбец, а множителя (42) в строку (см. схему).
- В-третьих, проведите в решетке диагонали, как показано на рисунке.
 Они представляют размещение конечного продукта (единицы, десятки, сотни и т. д.).
Они представляют размещение конечного продукта (единицы, десятки, сотни и т. д.). - В-четвертых, умножьте каждую строку и столбец и поместите произведение на пересечение. Обратите внимание, что цифры результата разделены диагональю.
- В-пятых, добавьте числа по диагонали. Перенесите числа на следующее место, если это требуется, и разместите результат по бокам.
- Наконец, произведение вычислено. Прочитайте вычисленные суммы сверху слева вниз справа.
Лучший метод
Среди всех различных методов умножения есть лучший? Ну, если вы спросите меня, ни одного. Все зависит от ситуации. Цель этого поста — напомнить читателю, что нет стандартного способа решения проблемы . Вы можете подходить к чему-то творчески или по своему усмотрению. Естественно, некоторые методы будут зависеть от человека. Например,
- Человек скорее воспользуется традиционным методом, если ему нравятся процедуры или шаблоны.
- Тот, кто хочет более логического подхода, может использовать метод ящика для умножения чисел.



 ..?
..?


 Запомните, под каким номером находится ряд.
Запомните, под каким номером находится ряд. Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами. Затем для числа 42 нарисуйте 4 и 2 линии справа вверху слева внизу (см. схему). Эти прямые должны пересекаться в точках.
Затем для числа 42 нарисуйте 4 и 2 линии справа вверху слева внизу (см. схему). Эти прямые должны пересекаться в точках. Они представляют размещение конечного продукта (единицы, десятки, сотни и т. д.).
Они представляют размещение конечного продукта (единицы, десятки, сотни и т. д.).