Среднее ускорение формула: Среднее и мгновенное ускорение и скорость. Формулы. Пример задачи

4.Среднее ускорение. Мгновенное ускорение. Полное ускорение.

Ускорение (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления). 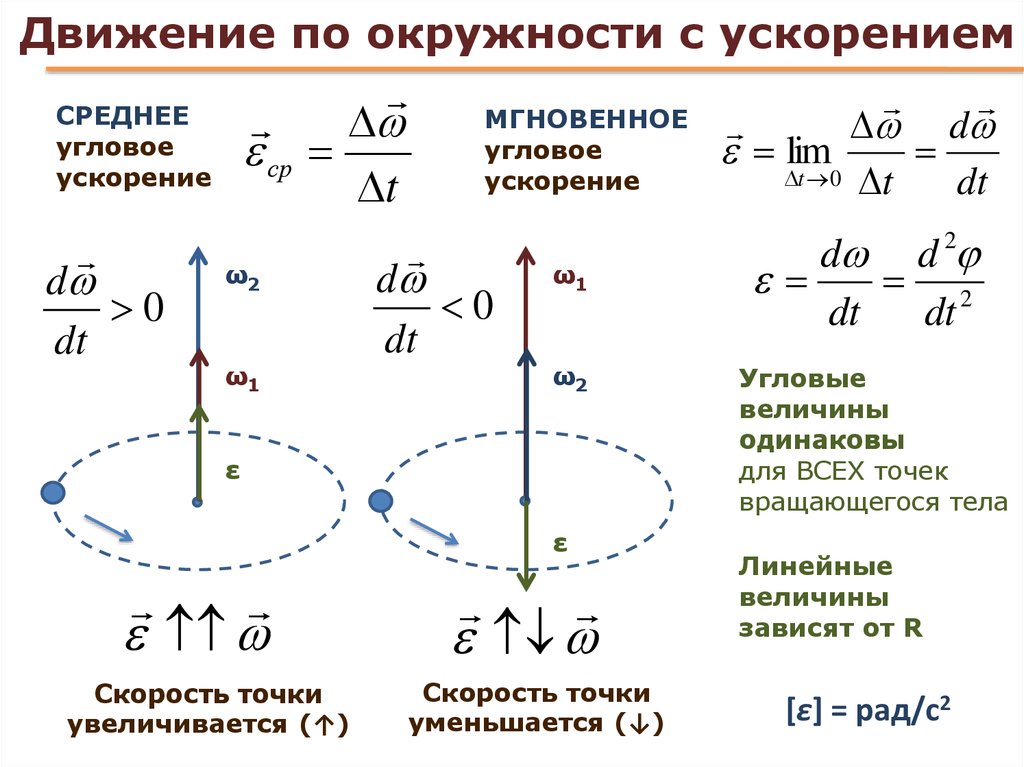Средним ускорением неравномерного движения в интервале от t до t + t называется векторная величина, равная отношению изменения скорости v к интервалу вре¬мени t Мгновенным ускорением а (ускорением) материальной точки в момент време-ни t будет предел среднего ускорения: Таким образом, ускорение a есть векторная величина, равная первой производной скорости по времени. Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющи.Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав¬ляющая ускорения — быстроту изменения скорости по направлению (направлена к цен¬тру кривизны траектории).

5.Равномерное прямолинейное движение. Ускоренное движение.(формулы, графики зависимости от времени).

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия. Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: vcp = v.

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t: = / t.

6.Вращательное движение. Угловая скорость, угловое ускорение. Формулы кинематики вращательного движения.

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. а) Угловая скорость .Быстрота вращения характеризуется угловой скоростью «омега», которая равна производной от угла поворота тела по времени – угол поворота тела за малое время . При равномерном вращении его быстроту также описывают частотой оборотов и периодом вращения .

Частота оборотов равна числу оборотов, сделанных за единицу времени, – число оборотов за время . Т.к. за один оборот тело поворачивается на угол, равный 2 , то и Период вращения – это время, за которое тело совершает один оборот. Т.к. , рад/с , об/с , с .Угловое ускорение «эпсилон» равно производной от угловой скорости по времени , – изменение угловой скорости за время . Векторы и направлены по оси вращения тела; вектор угловой скорости направлен в сторону хода правого винта при вращении винта в направлении вращения тела (рис.3). При ускоренном вращении тела направления векторов и совпадают, при замедленном – противоположны

Может ли среднее ускорение быть отрицательным: 3 важных факта

Мы знаем, что ускорение – это векторная величина; следовательно, оно может быть положительным или отрицательным, но как насчет среднего ускорения, может ли среднее ускорение быть отрицательным?

Среднее ускорение – это общее изменение скорости за заданный промежуток времени; среднее также является векторной величиной. Исходя из этого, мы можем сказать, что он может быть отрицательным или положительным. Давайте обсудим ускорение, среднее значение ускорения, мгновенное ускорение и условия, при которых среднее значение ускорения будет отрицательным..

Проще говоря, ускорение – это то, как скорость объекта изменяется во время его движения в определенный промежуток времени. Единица ускорения в системе СИ – м / с.². Ускорение – это векторная величина, поэтому оно может быть отрицательным и положительным. Математически это обозначается как,

           

 Где v – скорость 

                 t – Время

 Теперь вы знаете, что ускорение может быть отрицательным или положительным. Однако у вас возникнет вопрос: в каких условиях ускорение может быть положительным или отрицательным, и каково влияние положительного и отрицательного отрицательное ускорение на среднем разгоне? Мы обсудим эти вопросы по ходу статьи.

Среднее ускорение 

Среднее ускорение – это общее изменение скорости, которое произошло во время движения, и время, необходимое для его завершения.  Представьте себе человека, идущего по улице; он начинает двигаться с начальной скоростью «u», и через некоторое время «t» его конечная скорость равна «v». Во время движения он несколько раз меняет свою скорость между начальной и конечной скоростью. Итак, чтобы узнать полное изменение скорости во время движения, мы вычитаем его начальную скорость из конечной скорости, т. Е.

                                   Общее изменение скорости = ∆v = v – u

Мы знаем, что ускорение есть изменение скорости во времени. Итак, если мы разделим общее изменение скорости человека на время, необходимое для полного движения, то мы получим среднее ускорение человека. [латекс]\Дельта т[/латекс]

u – начальная скорость

[latex]\Delta t[/latex] – среднее время

Мгновенное ускорение

Мгновенное ускорение – это ускорение в определенный момент времени. Представьте человека, совершающего движение на улице, v1, v2, v3 …………. – скорость этого человека в момент времени t1, t2, t3 ……… Итак, если мы хотим узнать ускорение в момент t3, то, взяв соотношение скорости и ускорения в этот конкретный момент, мы можем узнать ускорение в t3. Обобщенные формулы для расчета мгновенного ускорения:

где v – конечная скорость

 где, дв – мгновенная скорость

               dt – конкретный момент времени

Условия отрицательного среднего ускорения

Давайте сначала разберемся, на что указывают отрицательные и положительные знаки. В физике, когда мы имеем дело с векторными величинами, важно знать направление этих величин, поэтому отрицательные и положительные знаки показывают направление физических величин в физическом мире.

Обычно север, юг, восток, запад, вправо, влево, вверх, вниз – все это понятия направления в физическом сценарии. В математике мы часто видим, что плоскость разделена на четыре квадранта. Знак –ve показывает левую (ось -x) или нижнюю сторону (ось -y) плоскости или знак + ve показывает правую или верхнюю сторону плоскости; мы заимствуем эту концепцию в физическом мире и говорим, что «количество» означает «лево» или «обратная сторона», а «положительное количество» означает право или положительное влияние.

 Как мы обсуждали ранее, ускорение – это векторная величина, и она может быть как положительной, так и отрицательной по направлению. И мы также знаем, что среднее ускорение – это полное изменение скорости за заданный промежуток времени.

Давайте обсудим знак среднего ускорения Итак, среднее ускорение отрицательно в следующих двух условиях:

• Когда величина скорости отрицательна –

Величина скорости отрицательна, когда объект движется в положительном направлении и замедляется. В этом состоянии объект замедляется, и направление замедления противоположно направлению скорости.  

• Когда направление скорости отрицательное – 

Когда объект совершает движение в отрицательном направлении и ускоряется, направление скорости отрицательное, а ускорение отрицательное. Представьте, что автомобиль движется в отрицательном направлении оси x и ускоряется в этом случае, ускорение происходит в направлении скорости, и оба имеют отрицательное направление. Следовательно, среднее ускорение автомобиля отрицательное, поскольку оно движется в отрицательном направлении.

различные случаи положительное и отрицательное ускорение

• Мы можем разбить эту цифру на четыре случая:
• case1: – В этом случае машина движется в положительном направлении оси x и набирает скорость, поэтому скорость и ускорение одинаковы, и оба положительны.
• Case2: – Во втором случае машина движется в отрицательном направлении и набирает скорость, поэтому ускорение идет по пути скорости и отрицательно.
• Case3: – В случае третьего автомобиля автомобиль движется в положительном направлении, но замедляется. Здесь направление скорости и ускорения противоположно, как вы можете видеть на рис. Знак ускорения отрицательный.
• Case4: – В четвертом случае машина движется отрицательно и тормозит. Здесь направление скорости отрицательное, а направление ускорения положительное, поэтому мы можем сказать, что автомобиль имеет положительное ускорение.

Калькулятор среднего ускорения

Примечание

• Введите значения трех известных переменных в текстовые поля
  
• Оставьте текстовое поле пустым для переменной, которую вы хотите вычислить.
  

Формула среднего ускорения, используемая для решения вопроса:
$a= \frac {v_f -v_i}{t}$
Здесь
$v_f$= конечная скорость
$v_i$= начальная скорость
t= временной интервал 92$
Среднее ускорение тела, движущегося прямолинейно, определяется как
$a = \frac {v_f – v_i}{t}$
Где
$v_f$ -> конечная скорость
$v_i$ -> начальная скорость
t -> Затраченное время

Пример нескольких вопросов, где вы можете использовать эту формулу среднего ускорения

Вопрос 1
Объект, движущийся по прямой линии, начал со скорости 2 м/с и достиг скорости 10 м/с за 4 сек. Найти среднее ускорение
Решение 92$

Вопрос 2
Объект начал движение со скоростью 1 м/с и имеет ускорение 5 м/с ² .Найти скорость через 5 сек.
Решение
$v_i= 1 \ м/с$, $v_f$= ? , t= 5 сек ,a = 5 м/с ²
Среднее ускорение задается как
$a = \frac {v_f – v_i}{t}$
Преобразование этого
$v_f= v_i +at$
$v_f= 1 + 5 \× 5=26 \ м/с$

Как работает калькулятор среднего ускорения

1. если $v_f$,$v_i$, t задано
Ускорение рассчитывается как
$a= \frac {v_f – v_i}{t}$
2. если $v_f$,$v_i$, a задано
время рассчитывается как
$t= \frac {v_f -v_i }{a}$
3. если $v_f$,a, t задано
Начальная скорость вычисляется как
$v_i= v_f -at$
4. если $v_i$,a, t задано
Конечная скорость рассчитывается as
$v_f= v_i +at$

Связанные калькуляторы

• Калькулятор уравнений кинематики
• Калькулятор движения снаряда
• Калькулятор углового ускорения
• Калькулятор кинетической энергии
• Калькулятор средней скорости

Связанный учебный материал

• Расстояние и смещение
• Положение частицы
• Средняя скорость и скорость
• Мгновенная скорость и скорость
• Ускорение
• Кинематические уравнения равноускоренного движения
• Ускорение свободного падения
• Относительная скорость
• Примеры задач и решений по кинематике
• Одномерные задачи движения с решением
• Рабочий лист графиков движения с ответом

сделайте ссылку на эту страницу, скопировав следующий текст

Формула среднего ускорения| Формулы и определение среднего ускорения

Ускорение объекта определяется как скорость изменения скорости.

Среднее ускорение для интервала определяется как изменение скорости для этого интервала за время.

Понимание ускорения важно в нашей повседневной жизни, а также в бескрайних просторах космоса и в микроскопическом мире субатомной физики. При нажатии на педаль тормоза автомобиль замедляется; в обычном разговоре ускориться означает поторопиться. Например, мы слишком хорошо знакомы с ускорением нашего автомобиля. Изменение скорости во времени пропорционально ускорению.

 

Ускорение — это термин, который вы, вероятно, слышали раньше, особенно в отношении автомобилей. В результате ускорение определяется как скорость изменения скорости во времени. Мы используем термин ускорение, чтобы выразить ситуацию увеличения скорости в непрофессиональных терминах. Ускорение делится на два вида: среднее и мгновенное, аналогичное скорости. Среднее ускорение рассчитывается за длительный период. Мы используем термин длина в смысле чего-то конечного, то есть чего-то, что имеет начало и конец. В результате основное внимание в этой статье будет уделено формуле среднего ускорения.

 

Среднее ускорение — определение

Изменение скорости, деленное на прошедшее время, представляет собой среднее ускорение. Например, если скорость шарика увеличивается от 0 до 60 см/с за три секунды, его среднее ускорение составляет 20 см/с. Это означает, что каждую секунду скорость шарика будет увеличиваться на 20 см/с.

 

Ускорение объекта определяется как скорость изменения скорости.

 

Среднее ускорение для интервала определяется как изменение скорости для этого интервала за время

 

Таким образом, математически

 

ускорение(a) = \[\frac{\triangle v}{\triangle t}\]

 

Если vi – начальная скорость, а vf – конечная скорость, t — время, необходимое для изменения скорости от vi до vf, тогда \[a=\frac{v_{f}-v_{t}}{t}\]

 

Аналогично, когда объект выполняет различные скоростей, таких как v1, v2, v3…vn для различных интервалов времени, таких как t1, t2, t3…tn соответственно, формула среднего ускорения записывается как:

 

= \[a_{avg}=\frac{v_{1}+v_{2}+. ….+v_{n}}{t_{1}+t_{2}+… ..+t_{n}}\]

 

Единицей среднего ускорения в системе СИ является . м/с2.

 

Примеры:

1. Если объект ускоряется с 20 м/с до 80 м/с за 3 секунды, найдите среднее ускорение объекта.

 

Sol:

Дано,

 

Начальная скорость объекта=vi=20 м/с

 

Конечная скорость объекта=vf=80 м/с

 

Время, затрачиваемое объектом = t = 3 секунды

 

Теперь нас просят рассчитать среднее ускорение объекта. Мы знаем, что среднюю скорость объекта можно рассчитать с помощью следующего уравнения:

 

\[a_{avg}=\frac{v_{f}-v_{i}}{t}\] …..( 1)

 

Где,

 

vi = Начальная скорость объекта

 

vf = Конечная скорость объекта 9{2}\]

 

Следовательно, средняя скорость объекта составляет 13 м/с2.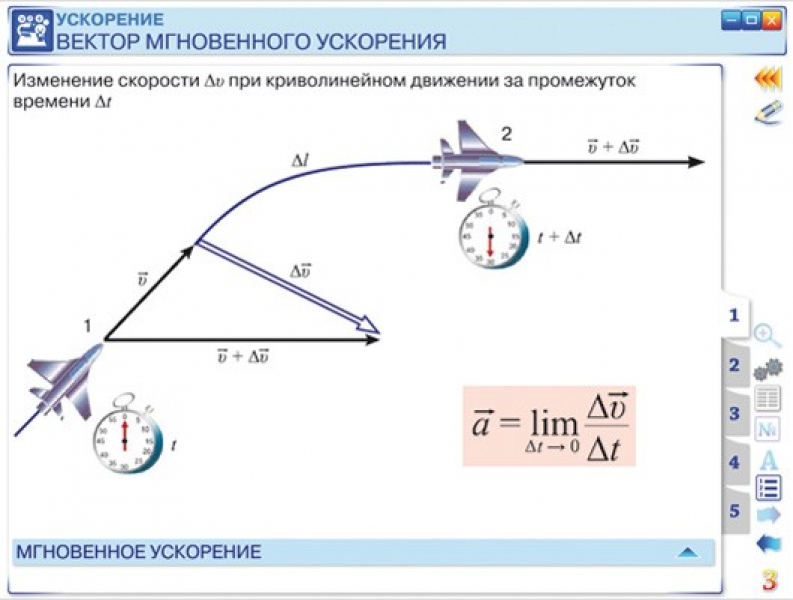

 

2. Автобус разгоняется в течение 5 секунд до скорости 10 миль в час, затем до 20 миль в час в течение 4 секунд, затем до 15 миль в час в течение 8 секунд. Что можно сказать о среднем ускорении автобуса?

 

Sol:

 

Предполагается, что скорости автобуса в определенные интервалы времени равны v1 = 10 м/с, v2 = 20 м/с, v3 = 15 м/с

 

9015 Интервалы времени, для которых предмет имеет следующие скорости: t1 = 5 с, t2 = 4 с, t3 = 8 с

 

В результате общая скорость по интервалу может быть рассчитана как сумма этих скоростей.

 

Vtotal = v1+v2+v3 = 10+20+15 = 45 м/с

 

Аналогичным образом можно рассчитать общий временной интервал, сложив эти интервалы вместе.

 

ttotal = t1+t2+t3 = 5+4+8 = 17 с

 

Теперь нас просят определить среднее ускорение автобуса.