Неравномерное прямолинейное движение
При неравномерном движении тело может за равные промежутки времени проходить как равные, так и разные пути.
Для описания неравномерного движения вводится понятие средней скорости.
|
Средняя скорость, по данному определению, величина скалярная потому, что путь и время величины скалярные.
Однако среднюю скорость можно определять и через перемещение согласно уравнению
В этом случае среднюю скорость следует считать величиной векторной потому, что она определяется через отношение векторной величины к скалярной.
Средняя скорость прохождения пути и средняя скорость перемещения – это две разные величины, которые могут характеризовать одно и то же движение.
При расчете средней скорости очень часто допускается ошибка, состоящая в том, что понятие средней скорости подменяется понятием среднего арифметического скоростей тела на разных участках движения. Чтобы показать неправомерность такой подмены рассмотрим задачу и проанализируем ее решение.
|
Пример 1Задача про половину пути и половину времени |
|
|
Движение поезда на участке AC и на участке CB равномерное.
Почему?
Да потому, что нам кажется, что для вычисления средней скорости вполне подходит формула, используемая для расчета среднего арифметического.
Давайте разберемся: можно ли использовать эту формулу и рассчитывать среднюю скорость путем нахождения полусуммы заданных скоростей.
Для этого рассмотрим несколько иную ситуацию.
Допустим, мы правы и средняя скорость действительно равна 40 км/ч.
Тогда решим другую задачу.
|
Как видно, тексты задач очень похожи, есть только «очень маленькая» разница.
Если в первом случае речь идет о половине пути, то во втором случае речь идет о половине времени.
Очевидно, что точка C во втором случае находится несколько ближе к точке A, чем в первом случае, и ожидать одинаковых ответов в первой и второй задаче, вероятно, нельзя.
Если мы, решая вторую задачу, так же дадим ответ, что средняя скорость равна полусумме скоростей на первом и втором участке, мы не можем быть уверены, что мы решили задачу правильно. Как быть?
Выход из положения следующий: дело в том, что средняя скорость не определяется через среднее арифметическое. Есть определяющее уравнение для средней скорости, согласно которому для нахождения средней скорости на некотором участке, надо весь путь, пройденный телом, поделить на все время движения:
Начинать решение задачи нужно именно с формулы, определяющей среднюю скорость, даже если нам кажется, что мы в каком-то случае можем использовать более простую формулу.
Будем двигаться от вопроса к известным величинам.
Неизвестную величину υср выражаем через другие величины – L0 и Δt0.
Оказывается, что обе эти величины неизвестны, поэтому мы должны выразить их через другие величины. Например, в первом случае: L
Подставим эти величины, соответственно, в числитель и знаменатель исходного уравнения.
Во втором случае мы поступаем точно так же. Нам не известен весь путь и все время. Выражаем их: и
Очевидно, что время движения на участке AB во втором случае и время движения на участке AB в первом случае различны.
В первом случае, поскольку нам неизвестны времена и мы попытаемся выразить и эти величины: а во втором случае мы выражаем и :
Подставляем выраженные величины в исходные уравнения.
Таким образом, в первой задаче имеем:
После преобразования получаем:
Во втором случае получаем а после преобразования:
Ответы, как и было предсказано, различны, но во втором случае мы получили, что средняя скорость действительно равняется полусумме скоростей.
Может возникнуть вопрос, а почему сразу нельзя воспользоваться этим уравнением и дать такой ответ?
Дело в том, что записав, что средняя скорость на участке AB во втором случае равна полусумме скоростей на первом и на втором участках, мы бы представили не решение задачи, а готовый ответ. Решение же, как видно, достаточно длинное, и начинается оно с определяющего уравнения. То, что мы в данном случае получили уравнение, которое хотели использовать изначально – чистая случайность.
При неравномерном движении скорость тела может непрерывно меняться. При таком движении скорость в любой последующей точке траектории будет отличаться от скорости в предыдущей точке.
Скорость тела в данный момент времени и в данной точке траектории называют мгновенной скоростью.
Чем больше промежуток времени Δt, тем средняя скорость больше отличается от мгновенной. И, наоборот, чем меньше промежуток времени, тем меньше средняя скорость отличается от интересующей нас мгновенной скорости.
|
Определим мгновенную скорость как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени:
Если речь идет о средней скорости перемещения, то мгновенная скорость является величиной векторной:
Если речь идет о средней скорости прохождения пути, то мгновенная скорость является величиной скалярной:
Часто встречаются случаи, когда при неравномерном движении скорость тела меняется за равные промежутки времени на одну и ту же величину.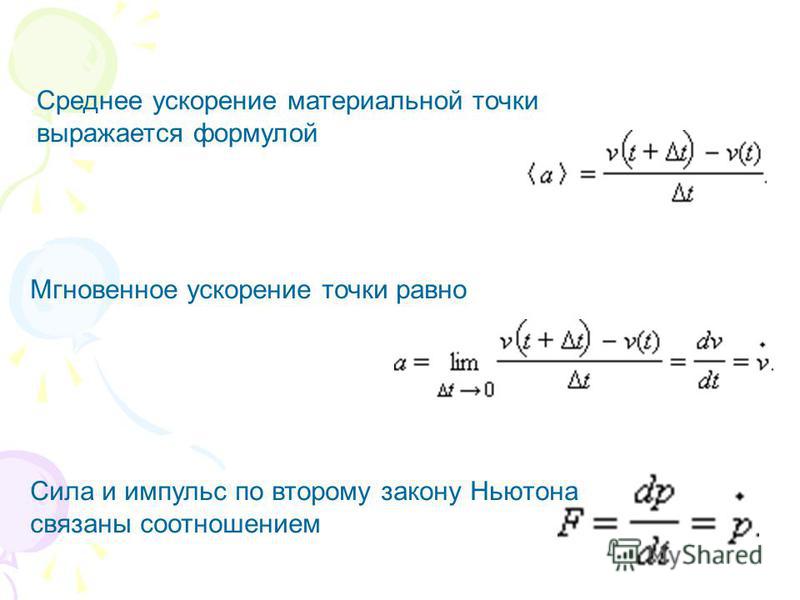
|
|
При равнопеременном движении скорость тела может, как уменьшаться, так и увеличиваться.
Если скорость тела увеличивается, то движение называется равноускоренным, а если уменьшается – равнозамедленным.
Характеристикой равнопеременного движения служит физическая величина, называемая ускорением.
|
|
Зная ускорение тела и его начальную скорость, можно найти скорость в любой наперед заданный момент времени:
В проекции на координатную ось 0X уравнение примет вид: υx = υ0x + ax ∙ Δt.
| 1. | Вопросы по теме «Скорость» | 1 вид – рецептивный | лёгкое | 1 Б. |
Предлагается ответить на вопросы по теме «Равномерное и неравномерное движение. Скорость». Скорость».
|
| 2. | Перевод км/ч в м/с, м/с в км/ч | 1 вид – рецептивный | лёгкое | 2 Б. | Перевод км/ч в м/с, м/с в км/ч. |
| 3. | Перевод м/с в см/с, м/мин | 1 вид – рецептивный | лёгкое |
2 Б.
|
Перевод м/с в см/с , м/мин. |
| 4. | Скорость | 1 вид – рецептивный | лёгкое | 1 Б. | Определение расстояния по скорости и времени. |
| 5. | Перевод км/ч в м/мин, см/с | 1 вид – рецептивный | среднее |
2 Б.
|
Перевод км/ч в м/мин, см/с. |
| 6. | Вычисление скорости | 2 вид – интерпретация | среднее | 2 Б. | Вычисление скорости. |
| 7. | Вычисление ускорения | 2 вид – интерпретация | среднее |
2 Б.
|
Вычисление ускорения. |
| 8. | Сравнение скоростей | 2 вид – интерпретация | среднее | 3 Б. | Определяются скорости движения автомобилей в км/ч и затем сравниваются. |
| 9. | Время движения парохода | 2 вид – интерпретация | среднее |
2 Б.
|
Определяется время движения парохода по течению. |
| 10. | Определение скорости тела и его пути по графику | 3 вид – анализ | сложное | 3 Б. | Анализируется график зависимости пути от времени и определяется скорость и путь. |
11.
|
Определение средней скорости движения | 2 вид – интерпретация | сложное | 3 Б. | Определяется средняя скорость транспорта при неравномерном движении. |
| 12. | Работа с графиком движения | 3 вид – анализ | сложное |
6 Б.
|
Анализируется график зависимости пути от времени, определяется скорость и путь двух тел, сравниваются результаты. |
Чем может обернуться отсутствие в КоАП трактовки термина “средняя скорость” — Российская газета
В проекте нового Кодекса об административных правонарушениях, который на днях обсуждали на межведомственной рабочей группе в минюсте, не прописано, что такое средняя скорость. Хотя предложения прописать звучали не раз. На необходимости обозначить в законе это понятие настаивает и Госавтоинспекция, и даже защитники прав автомобилистов. Почему так сложно вставить такой термин в закон, разбирался корреспондент “РГ”.
Вынесение штрафа за превышение средней скорости давно стало обыденностью. На некоторых дорогах научили комплексы фотовидеоконтроля одновременно фиксировать моментальную скорость, когда автомобиль проезжает под камерой, и высчитывать среднюю – между двух камер. Таким образом удается добиться соблюдения водителями скоростного режима на всем участке, а не только в непосредственной близости от камеры. Не обходится и без казусов, когда водитель получает сразу два штрафа: за моментальную скорость и за среднюю.
Таким образом удается добиться соблюдения водителями скоростного режима на всем участке, а не только в непосредственной близости от камеры. Не обходится и без казусов, когда водитель получает сразу два штрафа: за моментальную скорость и за среднюю.
Однако вот загвоздка: понятия средней скорости нет ни в одном законе. А у судов нет однозначного понимания, как относиться к штрафам за ее превышение. Причем, судя по судебной практике, все больше решений принимается в пользу автовладельцев.
Громкое решение Верховного суда, ставящее под большое сомнение правомерность использования комплексов, которые измеряют среднюю скорость, было принято еще в 2019 году. Тогда автомобилист обжаловал вынесенный ему штраф за среднюю скорость в Смоленской области. Впрочем, и штраф сам по себе был замечательный: среднюю скорость автовладельцу измерили на участке длиной более 70 км.
Верховный суд тогда указал, что нарушение согласно постановлению Пленума Верховного суда характеризуется в том числе местом и временем его совершения. Материалы, формируемые автоматическими камерами, должны содержать эту информацию. Указание отдельного участка дороги в качестве места совершения нарушения недопустимо, в том числе и потому, что на данный участок может распространяться юрисдикция не одного суда, а нескольких.
Материалы, формируемые автоматическими камерами, должны содержать эту информацию. Указание отдельного участка дороги в качестве места совершения нарушения недопустимо, в том числе и потому, что на данный участок может распространяться юрисдикция не одного суда, а нескольких.
В постановлении указан временной промежуток. Но превышение скорости – не длящееся нарушение. Поэтому в постановлении о штрафе должно быть указано точное время слишком быстрого движения.
Превышение скорости – не длящееся нарушение. В постановлении о штрафе должно быть указано точное время слишком быстрого движения
К тому же водитель мог остановиться или съехать на объездную дорогу, в результате скорость в какой-то момент могла быть выше, а значит, по вменяемой части данной статьи водителя привлекать нельзя, указал ВС и направил дело на новое рассмотрение в Вяземский районный суд Смоленской области.
Однако этот суд странным образом учел замечания Верховного суда. Он указал, что в законе время и место совершения нарушения не закреплены. Закреплены лишь обстоятельства. Похоже, постановление Пленума ВС для этого суда не указ. А что касается того, что скорость могла быть выше, то на это районный суд указал, что не может применять другую часть данной статьи, потому что она ухудшит положение нарушителя. Причем Смоленский областной суд это решение поддержал.
Закреплены лишь обстоятельства. Похоже, постановление Пленума ВС для этого суда не указ. А что касается того, что скорость могла быть выше, то на это районный суд указал, что не может применять другую часть данной статьи, потому что она ухудшит положение нарушителя. Причем Смоленский областной суд это решение поддержал.
Но большинство судов все-таки следуют постановлению Пленума Верховного суда. Так, Нарофоминский суд отменил постановление о превышении средней скорости водителем, а дело прекратил по истечению срока давности. Инспектор обжаловал это решение в Московском областном суде, но областной суд указал, что производство прекращено по истечению сроков давности, а в таком случае возобновить его закон не позволяет.
Ранее Чеховский районный суд выносил подобное решение. И главный аргумент в пользу отмены постановлений – не указано конкретное место и время нарушения.
Именно поэтому сейчас в МВД разрабатывают предложения для внесения в КоАП, чтобы закрепить в нем понятие “средняя скорость”.
Но главная сложность заключается в том, как обозначить место и время нарушения, раз превышение скорости – не длящееся нарушение.
Свои предложения по внесению в новый КоАП термина “средняя скорость” ранее направлял Общероссийский народный фронт. В его формулировке место и время обходилось стороной.
Но зато были указаны четкие требования: средняя скорость может измеряться на участке, где установлен единый скоростной режим, и нет примыканий, позволяющих проехать этот участок за более короткое время.
Про единый скоростной режим указано не просто так. Оказывается, к примеру, в Татарстане устанавливают камеры, которые измеряют среднюю скорость на участках, где установлены разные ограничения. Установщики камер говорят, что они замеряют среднюю скорость по максимальному ограничению. Но такое измерение в принципе неправильно. Ведь, по сути, если человек проехал с максимальной разрешенной скоростью, значит, он точно где-то нарушил.
Но предложения Общероссийского Народного Фронта в новый КоАП не были включены без объяснения причин.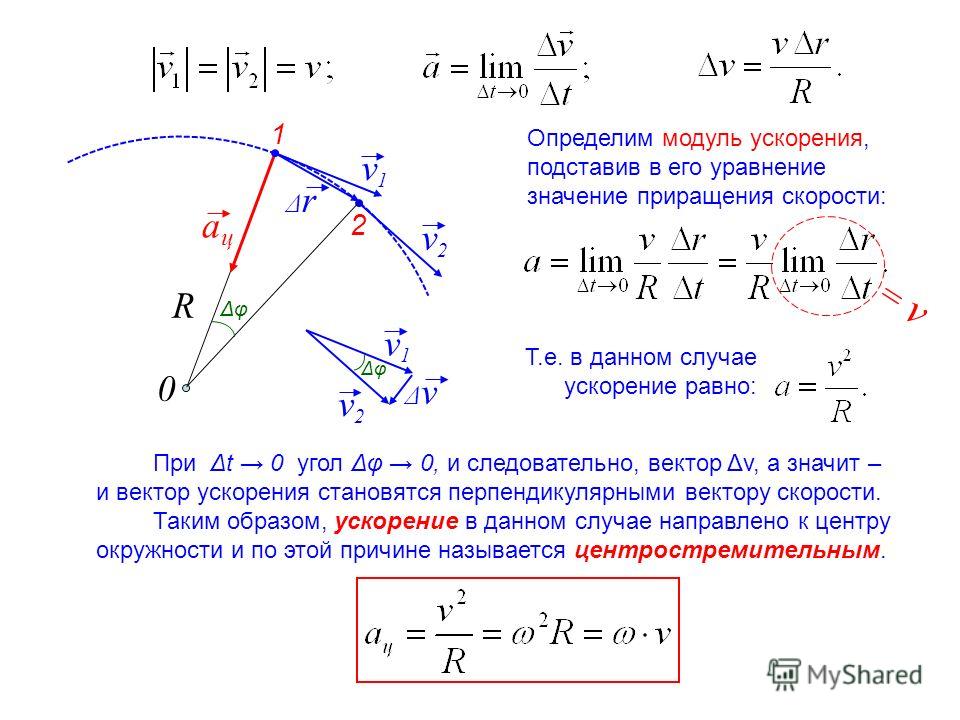 Хотя без внесения в этот документ понятия “средняя скорость”, судя по судебной практики, применять такие камеры на дорогах и выносить с их помощью штрафы незаконно.
Хотя без внесения в этот документ понятия “средняя скорость”, судя по судебной практики, применять такие камеры на дорогах и выносить с их помощью штрафы незаконно.
Средняя скорость и ускорение в физике. Ускорение. Равноускоренное движение. Зависимость скорости от времени при равноускоренном движении. Примеры задач с решением
Ско́рость в физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени.
Скорость в широком смысле – быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.
Ускоре́ние обозначается – быстрота изменения скорости, то есть первая производная от скорости по времени,векторная величина, показывающая, на сколько изменяется вектор скорости тела при его движении за единицу времени:
ускорение является вектором, то есть учитывает не только изменение величины скорости (модуля векторной величины), но и изменение её направления. В частности, ускорение тела, движущегося по окружности с постоянной по модулю скоростью, не равно нулю; тело испытывает постоянное по модулю (и переменное по направлению) ускорение, направленное к центру окружности (центростремительное ускорение).
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2),
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
Где – вектор рывка.
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Определить среднее ускорение можно формулой:
где – вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости Δ = – 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – 0. Тогда определить ускорение можно так:
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями аХ, aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости 2.
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 2. Иначе говоря, в данном случае происходитзамедление движения, при этом ускорение будет отрицательным (а
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Вопросы к экзамену по физике (ч. I, 2011 г).
Кинематика поступательного движения. Системы отсчета. Траектория, длина пути, перемещение. Скорость и ускорение. Средняя, средняя путевая, мгновенная скорость. Нормальное, тангенциальное и полное ускорение.
Кинематические характеристики вращательного движения вокруг неподвижной оси: угловая скорость, угловое ускорение.
Динамика поступательного движения. Законы Ньютона. (Савельев И.В. Т.1 § 7, 9, 11). Основные физические величины и их размерности. (Савельев И.В. Т.1 § 10). Виды сил в механике. (Савельев И.В. Т.1 § 13–16).
Кинетическая и потенциальная энергия. Механическая работа и мощность. Консервативные и неконсервативные силы. Работа в поле этих сил. Закон сохранения энергии.
Импульс механической
системы. Закон сохранения импульса.
Закон сохранения импульса.
Момент силы относительно точки и относительно оси вращения.
Момент импульса материальной точки относительно точки и относительно оси вращения. Момент импульса тела относительно оси. Закон сохранения момента импульса.
Основной закон динамики вращательного движения. Моменты инерции однородных тел правильной геометрической формы. Теорема Штейнера о параллельных осях.
Кинетическая энергия, работа и мощность при вращательном движении. Сопоставление основных формул и законов поступательного и вращательного движения.
Кинематика гармонических колебаний. Величины, характеризующие гармонические колебания: период, частота, амплитуда, фаза. Связь между периодом колебаний и циклической частотой. Зависимости смещения, скорости и ускорения от времени. Соответствующие графики.
Уравнение
гармонических колебаний в дифференциальной
форме. Зависимость смещения от времени.
Связь между циклической частотой и
массой колеблющейся точки. Энергия
гармонических колебаний (кинетическая,
потенциальная и полная). Соответствующие
графики.
Энергия
гармонических колебаний (кинетическая,
потенциальная и полная). Соответствующие
графики.
Математический и физический маятники. Формулы для периода малых колебаний. (Савельев И.В. Т.1 § 54).
Сложение гармонических колебаний одинакового направления и одинаковой частоты. Векторная диаграмма. (Савельев Т.1 § 55).
Затухающие колебания. Уравнение затухающих колебаний в дифференциальной форме. Зависимость смещения и амплитуды затухающих колебаний от времени. Коэффициент затухания. Логарифмический декремент колебаний. (Савельев И.В. Т.1 § 58).
Вынужденные колебания. Уравнение вынужденных колебаний в дифференциальной форме. Смещение, амплитуда и частота вынужденных колебаний. Явление резонанса. График зависимости амплитуды от частоты.
Волны. Распространение волн в упругой среде. Поперечные и продольные волны. Фронт волны и волновые поверхности. Длина волны. Уравнение бегущей волны. (Савельев Т.2 § 93-95).
Образование
стоячих волн. Уравнение стоячей волны.
Амплитуда стоячей волны. (Савельев
И.В. Т.2 § 99)
Уравнение стоячей волны.
Амплитуда стоячей волны. (Савельев
И.В. Т.2 § 99)
Два подхода к изучению макросистем: молекулярно-кинетический и термодинамический. Основные параметры макросистем. Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева). (Савельев И.В. Т.1 § 79–81, 86).
Уравнение состояния реального газа (уравнение Ван-дер-Ваальса). Теоретическая изотерма Ван-дер-Ваальса и экспериментальная изотерма реального газа. Критическое состояние вещества. (Савельев И.В. Т.1 § 91, § 123–124).
Внутренняя энергия системы. Внутренняя энергия идеального газа. Два способа изменения внутренней энергии. Количество теплоты. Теплоемкость. Связь удельной и молярной теплоемкостей.
Работа при изменении объема. Первое начало термодинамики. Формула Майера. Применение первого начала термодинамики к изопроцессам идеального газа.
Классическая
теория теплоемкости идеального газа.
Теорема Больцмана о равномерном
распределении энергии по степеням
свободы молекулы. Вычисление внутренней
энергии идеального газа и его
теплоемкостей через число степеней
свободы. (Савельев И.В. Т.1 § 97).
Вычисление внутренней
энергии идеального газа и его
теплоемкостей через число степеней
свободы. (Савельев И.В. Т.1 § 97).
Применение первого начала термодинамики к адиабатическому процессу. Уравнение Пуассона. (Савельев И.В. Т.1 § 88).
1. Кинематика поступательного движения. Системы отсчета. Траектория, длина пути, перемещение. Скорость и ускорение. Средняя, средняя путевая, мгновенная скорость. Нормальное, тангенциальное и полное ускорение.
Кинематика поступательного движения
При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.
Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.
Линию, по которой
движется материальная точка в
пространстве, называют траекторией .
Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r 0 , направленный от положения точки в начальный момент времени к ее положению в конечный момент.
Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
Средняя скорость – векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:
Мгновенная скорость – векторная физическая величина, равная первой производной от радиус-вектора по времени:
Мгновенная
скорость v есть
векторная величина, равная первой
производной радиуса – вектора движущейся
точки по времени. Так как секущая в
пределе совпадает с касательной,
то вектор
скорости v направлен
по касательной к
траектории в сторону движения (рисунок
1. 2).
2).
По мере уменьшение ∆t путь ∆S все больше будет приближаться к |∆r|, поэтому модуль мгновенной скорости :
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой а n . Вектор нормального ускорения направлен по радиусу кривизны траектории.
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно
теореме Пифагора для прямоугольно
прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов :
а= а τ + а n
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее
ускорение >
– это отношение изменения скорости к
промежутку времени, за который это
изменении произошло. Определить среднее
ускорение можно формулой:
Определить среднее
ускорение можно формулой:
где a – вектор ускорения .
Направление вектора ускорения совпадает с направлением изменения скорости ΔV = V – V 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость V 0 . В момент времени t2 тело имеет скорость V. Согласно правилу вычитания векторов найдём вектор изменения скорости ΔV = V – V 0 Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду
в квадрате равен ускорению прямолинейно
движущейся точки, при котором за одну
секунду скорость этой точки увеличивается
на 1 м/с. Иными словами, ускорение
определяет, насколько изменяется
скорость тела за одну секунду. Например,
если ускорение равно 5 м/с 2 ,
то это означает, что скорость тела
каждую секунду увеличивается на 5 м/с.
Можно также ввести среднюю скорость по перемещению , которая будет вектором , равным отношению перемещения ко времени, за которое оно совершено:
Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).
Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.
Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.
Тело отсчета – произвольно выбранное тело, относительно которого определяется положение остальных тел.
Система
отсчета –
совокупность системы координат и часов,
связанных с телом отсчета.
Наиболее употребительная система координат – декартовая – ортонормированный базис которой образован тремя единичными по модулю и взаимно ортогональными векторами i j k r r r , проведенными из начала координат.
Положение произвольной точки M характеризуется радиусом-вектором R r , соединяющим начало координат O с точкой M . r x i y j z k r r r r = + + , r = r = x 2 + y 2+ z 2 r
Движение материальной точки полностью определено, если декартовы координаты материальной точки заданы в зависимости от времени: x = x (t ) y = y (t ) z =z (t )
Эти уравнения
называются кинематическими
уравнениями движения точки .
Они эквивалентны одному векторному
уравнению движения точки.
Линия, описываемая движущейся материальной точкой (или телом) относительно выбранной системы отсчета называется траекторией . Уравнение траектории можно получить, исключив параметр t из кинематических уравнений. В зависимости от формы траектории движение может быть прямолинейным или криволинейным .
Длиной пути точки называется сумма длин всех участков траектории, пройденных этой точкой за рассматриваемый промежуток времени s = s (t ) . Длина пути – скалярная функция времени.
Вектор перемещения r r r 0 r r r = – вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени).
Линию,
по которой движется материальная точка
в пространстве, называют траекторией
ее движения . Иными словами, траекторией
движения называют
совокупность всех последовательных
положений, занимаемых материальной
точкой при ее движении в пространстве.
Иными словами, траекторией
движения называют
совокупность всех последовательных
положений, занимаемых материальной
точкой при ее движении в пространстве.
Одним из основных понятий механики является понятие материальной точки , что означает тело, обладающее массой, размерами которого можно пренебречь при рассмотрении его движения. Движение материальной точки – простейшая задача механики, которая позволит рассмотреть более сложные типы движений.
Перемещение
материальной точки происходит в
пространстве и изменяется со временем.
Реальное пространство трехмерно, и
положение материальной точки в любой
момент времени полностью определяется
тремя числами – ее координатами в
выбранной системе отсчета. Число
независимых величин, задание которых
необходимо для однозначного определения
положения тела, называется числом его
степеней свободы. В качестве системы
координат выберем прямоугольную, или
декартову, систему координат. Для
описания движения точки, кроме системы
координат, необходимо еще иметь
устройство, с помощью которого можно
измерять различные отрезки времени. Такое устройство назовем часами.
Выбранная система координат и связанные
с ней часы образуют систему отсчета.
Такое устройство назовем часами.
Выбранная система координат и связанные
с ней часы образуют систему отсчета.
Д
екартовы
координатыX ,Y ,Z определяют
в пространстве радиус-вектор z ,
острие которого описывает при его
изменении со временем траекторию
материальной точки. Длина траектории
точки представляет собой величину
пройденного пути S (t ).
Путь S (t )-
скалярная величина. Наряду с величиной
пройденного пути, перемещение точки
характеризуется направлением, в котором
она движется. Разность двух радиус-векторов,
взятых в различные моменты времени,
образует вектор перемещения точки
(рис.).
Для того чтобы характеризовать, как быстро меняется положение точки в пространстве, пользуются понятием скорости. Под средней скоростью движения по траектории за конечное время t понимают отношение пройденного за это время конечного пути S ко времени:
. (1.1)
Скорость
движения точки по траектории – скалярная
величина. Наряду с ней можно говорить
о средней скорости перемещения точки.
Эта скорость – величина, направленная
вдоль вектора перемещения,
Наряду с ней можно говорить
о средней скорости перемещения точки.
Эта скорость – величина, направленная
вдоль вектора перемещения,
. (1.2)
Если моменты времени t 1 , и t 2 бесконечно близки, то время t бесконечно мало и в этом случае обозначается через dt . За время dt точка проходит бесконечно малое расстояние dS . Их отношение образует мгновенную скорость точки
. (1.3)
Производная радиус-вектора r по времени определяет мгновенную скорость перемещения точки.
. (1.4)
Поскольку перемещение совпадает с бесконечно малым элементом траектории dr = dS , то вектор скорости направлен по касательной к траектории, а его величина:
. (1.5)
Н
а
рис. показана зависимость пройденного
путиS от
времени t .
Вектор скорости v (t )
направлен по касательной к кривой S (t )
в момент времени t . Из рис. видно, что угол наклона касательной
к оси t равен
Из рис. видно, что угол наклона касательной
к оси t равен
.
Интегрируя выражение (1.5) в интервале времени от t 0 до t , получим формулу, позволяющую вычислить путь, пройденный телом за время t –t 0 если известна зависимость от времени его скорости v (t )
. (1.6)
Г
еометрический
смысл этой формулы ясен из рис. По
определению интеграла пройденный путь
представляет собой площадь, ограниченную
кривойv =v (t )
в интервале от t 0 до t .В
случае равномерного движения, когда
скорость сохраняет свое постоянное
значение во все время движения, v =const ;
отсюда следует выражение
, (1.7)
где S 0 ‑ путь, пройденный к начальному времени t 0 .
Производную скорости по времени, которая является второй производной по времени от радиус-вектора, называют ускорением точки:
. (1.8)
(1.8)
Вектор ускорения а направлен вдоль вектора приращения скорости dv . Пусть а = const . Этот важный и часто встречаемый случай носит название равноускоренного или равнозамедленного (в зависимости от знака величины а) движения. Проинтегрируем выражение (1.8) в пределах от t = 0 до t :
(1.9)
(1.10)
и
используем следующие начальные условия:
.
Таким образом, при равноускоренном движении
. (1.11)
В
частности, при одномерном движении,
например вдоль оси X ,
.
Случай прямолинейного движения изображен
на рис. При больших временах зависимость
координаты от времени представляет
собой параболу.
Вобщем случае движение точки может быть криволинейным. Рассмотрим этот тип движения. Если траектория точки произвольная кривая, то скорость и ускорение точки при ее движении по этой кривой меняются по величине и направлению.
Выберем
произвольную точку на траектории. Как
всякий вектор, вектор ускорения можно
представить в виде суммы его составляющих
по двум взаимно перпендикулярным осям. В качестве одной из осей возьмем
направление касательной в рассматриваемой
точке траектории, тогда другой осью
окажется направление нормали к кривой
в этой же точке. Составляющая ускорения,
направленная по касательной к траектории,
носит название тангенциального
ускорения a t ,
а направленная ей перпендикулярно – нормального
ускорения a n .
В качестве одной из осей возьмем
направление касательной в рассматриваемой
точке траектории, тогда другой осью
окажется направление нормали к кривой
в этой же точке. Составляющая ускорения,
направленная по касательной к траектории,
носит название тангенциального
ускорения a t ,
а направленная ей перпендикулярно – нормального
ускорения a n .
Получим формулы, выражающие величины a t , и a n через характеристики движения. Для простоты рассмотрим вместо произвольной криволинейной траектории плоскую кривую. Окончательные формулы остаются справедливыми и в общем случае неплоской траектории.
Б
лагодаря
ускорению скорость точки приобретает
за времяdt малое
изменение dv .
При этом тангенциальное ускорение,
направленное по касательной к траектории,
зависит только от величины скорости,
но не от ее направления. Это изменение
величины скорости равно dv . Поэтому тангенциальное ускорение может
быть записано как производная по времени
от величины скорости:
Поэтому тангенциальное ускорение может
быть записано как производная по времени
от величины скорости:
. (1.12)
С
другой стороны, изменение dv n ,
направленное перпендикулярно к v ,
характеризует только изменение
направления вектора скорости, но не
его величины. На рис. показано изменение
вектора скорости, вызванное действием
нормального ускорения. Как видно из
рис.
,
и, таким образом, с точностью до величины
второго порядка малости величина
скорости остается неизменнойv =v” .
Найдем величину a n . Проще всего это сделать, взяв наиболее простой случай криволинейного движения – равномерное движение по окружности. При этом a t =0. Рассмотрим перемещение точки за время dt по дуге dS окружности радиуса R .
С
коростиv и v” ,
как отмечалось, остаются равными по
величине. Изображенные на рис. треугольники
оказываются, таким образом, подобными
(как равнобедренные с равными углами
при вершинах). Из подобия треугольников
следует
Из подобия треугольников
следует
,
откуда находим выражение для нормального
ускорения:
. (1.13)
Формула для полного ускорения при криволинейном движении имеет вид:
. (1.14)
Подчеркнем, что соотношения (1.12), (1.13) и (1.14) справедливы для всякого криволинейного движения, а не только для движения по окружности. Это связано с тем, что всякий участок криволинейной траектории в достаточно малой окрестности точки можно приближенно заменить дугой окружности. Радиус этой окружности, называемый радиусом кривизны траектории, будет меняться от точки к точке и требует специального вычисления. Таким образом, формула (1.14) остается справедливой и в общем случае пространственной кривой.
Движение
твердого тела, при котором две его
точки О и О ”
остаются неподвижными, называется вращательным
движением вокруг
неподвижной оси, а неподвижную прямую ОО ”
называют осью
вращения .
Пусть абсолютно твердое тело вращается
вокруг неподвижной оси ОО ”
(рис. 2.12).
2.12).
Рис. 2.12
Проследим за
некоторой точкой М этого
твердого тела. За время dt точка М совершает
элементарное перемещение d r .
При том же самом угле поворота d φ,
другая точка, отстоящая от оси на большее
или меньшее расстояние, совершает
другое перемещение. Следовательно, ни
само перемещение некоторой точки
твердого тела, ни первая производная ,
ни вторая производная не
могут служить характеристикой движения
всего твердого тела.
За это же время dt радиус-вектор R,
проведенный из точки 0 ”
в точку М ,
повернется на угол d φ.
На такой же угол повернется радиус-вектор
любой другой точки (т.к. тело абсолютно
твердое, в противном случае расстояние
между точками должно измениться).
Угол поворота d φ
характеризует перемещение всего тела
за время dt .
Удобно ввести –
вектор элементарного поворота тела,
численно равный d φ
и направленный вдоль оси вращения ОО ”
так, чтобы, глядя вдоль вектора, мы
видели вращение по часовой стрелке
(направление вектора и
направление вращения связаны «правилом
буравчика»). Элементарные повороты удовлетворяют
обычному правилу сложения векторов:
Элементарные повороты удовлетворяют
обычному правилу сложения векторов:
Угловая скорость вращения тела
Угловой скоростью тела в данный момент t называется величина, к которой стремится средняя угловая скорость , если стремится к нулю.
Угловая скорость твердого тела является первой производной от угла поворота по времени.
Размерность: [радиан/время]; ; .
Угловую скорость можно изображать вектором. Вектор угловой скорости направляют по оси вращения в ту сторону, откуда вращение видно против хода часовой стрелки.
Если угловая скорость не является постоянной величиной, то вводят еще одну характеристику вращения – угловое ускорение.
Угловое ускорение характеризует изменение угловой скорости тела с течением времени.
Если за промежуток времени угловая скорость получает приращение , то среднее угловое ускорение равно
вращение, – один
из простейших видов движения твёрдого
тела. В. д. вокруг неподвижной оси –
движение, при к-ром все точки тела,
двигаясь в параллельных плоскостях,
описывают окружности с центрами,
лежащими на одной неподвижной прямой,
перпендикулярной к плоскостям этих
окружностей и наз. осью вращения.
Скорость произвольной точки тела v =
, где w – угловая
скорость тела,
г – радиус-вектор, проведённый в точку
из центра описываемой ею окружности.Угловое
ускорение тела
e = М/I, где М – момент внеш. сил относительно
оси вращения, I – момент инерции тела
относительно той же оси.
В. д. вокруг неподвижной оси –
движение, при к-ром все точки тела,
двигаясь в параллельных плоскостях,
описывают окружности с центрами,
лежащими на одной неподвижной прямой,
перпендикулярной к плоскостям этих
окружностей и наз. осью вращения.
Скорость произвольной точки тела v =
, где w – угловая
скорость тела,
г – радиус-вектор, проведённый в точку
из центра описываемой ею окружности.Угловое
ускорение тела
e = М/I, где М – момент внеш. сил относительно
оси вращения, I – момент инерции тела
относительно той же оси.
В. д. вокруг
неподвижной точки – движение, при к-ром
все точки тела движутся по поверхностям
концентрич. сфер с центрами в неподвижной
точке. В каждый момент времени это
движение можно рассматривать как
вращение вокруг мгновенной оси вращения,
проходящей через неподвижную точку.
Скорость произвольной точки тела v =
, здесь г – радиус-вектор, проведённый
в точку из неподвижной точки тела.
Основной закон динамики: dL/dt
= М,
где L – момент
импульса тела
относительно неподвижной точки, М –
момент относительно той же точки всех
внеш. сил, приложенных к телу, наз.
главным моментом внешних сил. Этот
закон справедлив также для вращения
твёрдого тела вокруг его центра инерции
независимо от того, покоится последний
или движется произвольно. Теория В. д.
имеет многочисл. приложения в небесной
механике, внеш. баллистике, теории
гироскопа, теории машин и механизмов.
сил, приложенных к телу, наз.
главным моментом внешних сил. Этот
закон справедлив также для вращения
твёрдого тела вокруг его центра инерции
независимо от того, покоится последний
или движется произвольно. Теория В. д.
имеет многочисл. приложения в небесной
механике, внеш. баллистике, теории
гироскопа, теории машин и механизмов.
Пройденный путь S , перемещение dr, скорость v , тангенциальное и нормальное ускорение a t , и a n , представляют собой линейные величины. Для описания криволинейного движения наряду снимиможно пользоваться угловыми величинами.
Рассмотрим более подробно важный и часто встречаемый случай движения по окружности. В этом случае наряду с длиной дуги окружности движение можно характеризовать утлом поворота φ вокруг оси вращения. Величину
(1.15)
называют угловой скоростью. Угловая скорость представляет собой
вектор, направление которого связывают
с направлением оси вращения тела (рис. ).
).
Обратим внимание на то, что, в то время как сам угол поворота φ является скаляром, бесконечно малый поворот dφ – векторная величина, направление которой определяется по правилу правой руки, или буравчика, и связано с осью вращения. Если вращение является равномерным, то ω =const и точка на окружности поворачивается на равные углы вокруг оси вращения за равные времена. Время, за которое она совершает полный оборот, т.е. поворачивается на угол 2π, называется периодом движения Т. Выражение (1.15) можно проинтегрировать в пределах от нуля до Т и получить угловую частоту
. (1.16)
Число оборотов в единицу времени есть величина, обратная периоду, – циклическая частота вращения
ν =1/ T . (1.17)
Нетрудно
получить связь между угловой и линейной
скоростью точки. При движении по
окружности элемент дуги связан с
бесконечно малым поворотом соотношением dS = R·dφ. Подставив его в (1.15), находим
Подставив его в (1.15), находим
v = ω r . (1.18)
Формула (1.18) связывает величины угловой и линейной скоростей. Соотношение, связывающее векторы ω и v , следует из рис. А именно, вектор линейной скорости представляет собой векторное произведение вектора угловой скорости и радиуса-вектора точки r:
. (1.19)
Таким образом, вектор угловой скорости направлен по оси вращения точки и определяется по правилу правой руки или буравчика.
Угловое
ускорение – производная по времени от вектора
угловой скорости ω (соответственно
вторая производная по времени от угла
поворота)
Выразим тангенциальное и нормальное ускорение через угловые скорости и ускорение. Используя связь (1.18),(1.12) и (1.13), получаем
a t = β · R , a = ω 2 · R . (1.20)
Таким образом, для полного ускорения имеем
. (1.21)
(1.21)
Величина β играет роль тангенциального ускорения: если β = 0.полное ускорение при вращении точки не равно нулю, a =R·ω 2 ≠ 0.
3. Динамика поступательного движения. Законы Ньютона. (Савельев И.В. Т.1 § 7, 9, 11). Основные физические величины и их размерности. (Савельев И.В. Т.1 § 10). Виды сил в механике. (Савельев И.В. Т.1 § 13–16).
Ускорение характеризует быстроту изменения скорости движущегося тела. Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. Ускорение измеряется в метрах в секунду за секунду (м/с 2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.
Шаги
Вычисление среднего ускорения по двум скоростям
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt , где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.
Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt , где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = v к – v н и Δt = t к – t н , где v к – конечная скорость, v н – начальная скорость, t к – конечное время, t н – начальное время.
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что t н = 0.
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: . Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
Формула: . Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
- Напишите переменные: v к = 46,1 м/с, v н = 18,5 м/с, t к = 2,47 с, t н = 0 с.
- Вычисление: a = (46,1 – 18,5)/2,47 = 11,17 м/с 2 .
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
- Напишите переменные: v к = 0 м/с, v н = 22,4 м/с, t к = 2,55 с, t н = 0 с.

- Вычисление: а = (0 – 22,4)/2,55 = -8,78 м/с 2 .
Вычисление ускорения по силе
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело. Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
- Второй закон Ньютона описывается формулой: F рез = m x a , где F рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с 2).
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете.
 Масса больших тел измеряется в килограммах.
Масса больших тел измеряется в килограммах.- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно.
Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется
до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора,
то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость
его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно,
пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется,
замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните,
– это векторная величина).
Однако в физике нет термина «замедление». Если тело движется,
замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните,
– это векторная величина).
> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где – вектор ускорения .
Направление вектора ускорения совпадает с направлением изменения скорости Δ = – 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0 . В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – 0 . Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки,
при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами,
ускорение определяет, насколько изменяется скорость тела за одну секунду. Например,
если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду
увеличивается на 5 м/с.
Иными словами,
ускорение определяет, насколько изменяется скорость тела за одну секунду. Например,
если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду
увеличивается на 5 м/с.
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями а Х, a Y , a Z).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
Если скорость тела по модулю уменьшается, то есть
V 2
то направление вектора ускорения противоположно направлению вектора скорости
2 . Иначе говоря,
в данном случае происходит замедление движения , при этом ускорение
будет отрицательным (а
Иначе говоря,
в данном случае происходит замедление движения , при этом ускорение
будет отрицательным (а
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения,
направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10).
Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой
n .
Вектор нормального ускорения направлен по радиусу кривизны траектории.
То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10).
Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой
n .
Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
= τ + nПоступательное и вращательное движения
Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.
Поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями.
Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными
Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.
Скорость так же – это сумма начальной скорости и ускорения умноженного на время.
Скорость – произведение угловой скорости на радиус окружности.
v=S/t
v=v 0 +a*t
v=ωR
Ускорение тела, при равноускоренном движении – величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло.
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n . Вектор нормального ускорения направлен по радиусу кривизны траектории.
То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n . Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов :
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
v =ωR
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
Рис.3
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном – противонаправлен ему (рис. 4).
При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном – противонаправлен ему (рис. 4).
Рис.4
Тангенциальная составляющая ускорения a τ =dv/dt , v = ωR и
Нормальная составляющая ускорения
Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а τ , нормальное ускорение а n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:
s = Rφ, v = Rω, а τ = R?, a n = ω 2 R.
В случае равнопеременного движения точки по окружности (ω=const)
ω = ω 0 ± ?t, φ = ω 0 t ± ?t 2 /2,
где ω 0 – начальная угловая скорость.
Бортовой компьютер | Бортовой компьютер | Дисплеи и голосовое управление | XC90 Twin Engine 2020 Late
Экономичному вождению помогает информация о мгновенном и среднем расходе топлива. Информацию с бортового компьютера можно вывести на дисплей водителя.
Информацию с бортового компьютера можно вывести на дисплей водителя.
Пример информации с бортового компьютера на дисплее водителя. Изображение схематичное – некоторые детали могут отличаться в зависимости от модели автомобиля.
В бортовой компьютер входят следующие указатели:
- Счетчики пройденного пути
- Одометр
- Мгновенный расход топлива
- Пробег до пустого бака
- Пробег до разряженной батареи
- Туризм – альтернативный спидометр
Единицы измерения расстояния, скорости и т.п. можно изменить в системных настройках на центральном дисплее.
Счетчики пройденного пути
В автомобиле установлены два счетчика пройденного пути, ТМ и ТА.
ТМ можно обнулить вручную, а ТА обнуляется автоматически, если автомобиль не использовался более четырех часов.
Во время поездки регистрируется следующая информация:
- Отрезок пути
- Время в пути
- Средняя скорость
- Средний расход топлива
Значения рассчитываются, начиная с последнего обнуления счетчика пройденного пути.
Одометр
Одометр регистрирует общий пробег автомобиля. Это значение не обнуляется.
Мгновенный расход топлива
Этот счетчик показывает расход топлива на данный момент. Значение обновляется примерно один раз в секунду.
Пробег до пустого бака
Бортовой компьютер рассчитывает расстояние, которое можно пройти на оставшемся в баке топливе.
Для расчета используются значения среднего расхода топлива за последние пройденные 30 км (20 миль) пути и оставшегося количества топлива.
Когда счетчик показывает “—-“, количество топлива недостаточно для расчета оставшегося расстояния. Необходимо как можно быстрее залить топливо.
Примечание
Некоторые отклонения возможны при изменении манеры вождения.
Экономичный стиль вождения в общем случае увеличивает пробег автомобиля.
Пробег до разряженной батареи
Этот символ показывает примерное расстояние, которое можно пройти на энергозапасе, оставшемся в гибридном аккумуляторе.
Расчет основан на среднем расходе при обычной загрузке автомобиля в стандартном режиме движения с учетом включенной или выключенной системы кондиционирования воздуха (АС). При изменении режима вождения Hybrid на Pure расчетный пробег может увеличиться, так как в режиме Pure климатическая установка действует с ограничениями (ECO-климат).
Когда счетчик показывает “—-“, гарантированного пробега на электрической тяге не остается.
Примечание
Некоторые отклонения возможны при изменении манеры вождения.
Экономичный стиль вождения в общем случае увеличивает пробег автомобиля.
Начальное значение для полностью заряженного гибридного аккумулятора
В связи с тем, что учесть стиль вождения и другие факторы, влияющие на дальность хода на электротяге, очень сложно, компания Volvo предложила использовать начальное значение, когда автомобиль полностью заряжен. Начальное значение соответствует значению “вплоть до” вместо прогнозируемой дальности хода на электрической тяге. Разница начальных значений для режимов Hybrid и Pure связана с тем, что в режиме вождения Pure автомобилю разрешается использовать больше энергии гибридного аккумулятора, и с тем, что автомобиль переходит в режим ECO-климата.
Разница начальных значений для режимов Hybrid и Pure связана с тем, что в режиме вождения Pure автомобилю разрешается использовать больше энергии гибридного аккумулятора, и с тем, что автомобиль переходит в режим ECO-климата.
Дальность хода на электрической тяге
Чтобы обеспечить максимальную дальность хода на электрической тяге, водитель электромобиля должен также помнить и об экономии токопотребления. Чем больше потребителей (стерео, обогрев стекол, зеркал/сидений, очень холодный воздух из климатической установки и т.п.) задействованы в автомобиле, тем короче пробег.
Примечание
Пробег автомобиля снижается не только в связи с высоким потреблением тока в салоне, но и в результате высокой скорости, резкого ускорения и торможения, тяжелого груза, низкой температуры и движения вверх по склону.
Туризм – альтернативный спидометр
Вспомогательный спидометр с цифровой индикацией облегчает езду в условиях, когда ограничения скорости на знаках указываются в единицах измерения, отличающихся от приборов автомобиля.
В этом случае единицы измерения для цифровой индикации скорости противоположны установленным в аналоговом спидометре. Если в аналоговом спидометре скорость измеряется в mph, спидометр с цифровой индикацией показывает скорость в km/h и наоборот.
Скорость и ускорение при прямолинейном движении
Пусть материальная точка движется по прямой вдоль оси . Положение материальной точки в произвольный момент времени определяется выражением . Определим координату материальной точки в произвольно выбранный момент времени и обозначим ее через . Через некоторый промежуток времени координата точки измениться на . За промежуток времени материальная точка прошла путь равный . Будем считать путь положительным в случае, когда материальная точка двигалась вправо. Будем считать его отрицательным в случае, когда материальная точка двигалась влево.
Средняя скорость материальной точки
Средняя скорость материальной точки за время — отношение пройденного пути к к промежутку времени , за который этот путь был пройден.
Нужно помнить, что значение должно быть исключено.
Мгновенная скорость материальной точки
Мгновенная скорость материальной точки () — скорость прохождения материальной точкой расстояния за бесконечно малый промежуток времени .
Мгновенная скорость определяется выражением:
Предел такого типа называется производной функции по аргументу . Такая производная обозначается следующим образом:
Мгновенная скорость материальной точки () — производная координаты () по времени, или производная пройденного пути () по времени.
Таким образом, скорость материальной точки есть функция времени:
Ускорение материальной точки
Ускорение материальной точки () — производная скорости по времени:
или
Ускорение материальной точки () — это изменение скорости за бесконечно малый промежуток времени .
Принимая во внимание, что скорость материальной точки есть производная координаты по времени, то можно сделать следующий вывод.
Ускорение материальной точки () есть вторая производная координаты по времени.
Равномерное движение
является линейной функцией времени, если функцию можно привести к виду , где и — это постоянные коэффициенты. В ней — постоянная средняя скорость. Другими словами, средняя скорость не изменяется со временем и совпадает с мгновенной скоростью ().
Движение с постоянной скоростью называется равномерным.
Коэффициент есть ничто иное как начальная координата () материальной точки в начальный момент времени (). Учитывая все вышесказанное, функция равномерного движения записывается в виде:
Равноускоренное движение
Если функцию можно привести к виду , где и — это постоянные коэффициенты, то есть квадратичная функция времени .
В ней — начальная скорость движения (), определяемая в момент времени . — начальная координата движения точки (). — половина значения ускорения ().
Движение материальной точки с постоянным ускорением называется равноускоренным движением.
Учитывая все вышесказанное, функции для равноускоренного движения записываются в виде:
Координата
Мгновенная скорость
Пройденный путь
Информация предоставлена в сжатом виде. В полном виде все это можно увидеть в первом томе общего курса физики уважаемого Д.В. Сивухина. Я пользовался 4-м изданием.
Post Views: 1 492
ПохожееСкорость точки
Скоростью точки называют кинематическую меру ее движения, равную производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.
Скорость относительно выбранной системы отсчета это одна из основных характеристик движения точки.
Вектор скорости направлен по касательной к траектории точки в сторону движения.
Рассмотрим перемещение точки за малый промежуток времени Δt:
тогда
средняя скорость точки за промежуток времени Dt.
Наш видеоурок по теме:
Скорость точки в данный момент времени
Положение движущейся точки М относительно системы отсчета в момент времени t1 определяется радиус-вектором r.
Рис. 1
В другой момент времени t1=t+Δt точка займет положение М1 с радиус-вектором r1.
За время Δt радиус-вектор движущейся точки изменится на
Средней скоростью vср называется отношение изменения радиус-вектора Δr к изменению времени Δt.
Скорость точки равна первой производной по времени от ее радиус-вектора.
Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим
После дифференцирования
Отсюда следует
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.
Модуль скорости и направляющие косинусы равны:
Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда
Пусть скорость точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).
Рис. 2
Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O1
— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.
При ds>0 направления векторов τ и dr совпадают.
Если точка движется в сторону убывающих расстояний, то ds и направления векторов τ и dr противоположны.
При
вектор скорости направлен по τ, т.е. в сторону возрастающих расстояний;
при
он имеет направление, противоположное τ, т.е. в сторону убывающих расстояний.
— алгебраическая скорость точки, проекция скорости v на положительное направление касательной к траектории.
Естественное задание движения точки полностью определяет скорость по величине и направлению.
Ускорение точки >
Видеоурок поPhysics – Скорость против скорости
Видеоурок по скорости и скорости
Видеоурок «Скорость против скорости» объясняет значение скорости и скорости и различает мгновенные и средние значения каждого из них. Обсуждаются стратегии расчета средних значений скорости и скорости. В объяснениях помогают многочисленные примеры, иллюстрации и анимации.Видеоурок отвечает на следующие вопросы:
Обсуждаются стратегии расчета средних значений скорости и скорости. В объяснениях помогают многочисленные примеры, иллюстрации и анимации.Видеоурок отвечает на следующие вопросы: - Что такое скорость, мгновенная скорость и средняя скорость?
- Что такое скорость и как она связана со скоростью?
- Как рассчитывается средняя скорость и средняя скорость?
- Как можно проанализировать движение с несколькими ногами с точки зрения средней скорости и средней скорости?
Чтобы повысить эффективность обучения, The Physics Classroom предоставляет следующие инструменты:
Примечания к уроку
Заметки к уроку предназначены для распечатки и использования при просмотре видео.Они структурированы так, чтобы студенты могли следить за видео, записывать некоторые заметки и оставлять видео с документом, который можно назвать продолжением их обучения. Примечания к уроку доступны в формате PDF. Разрешается распечатать заметки или включить на них ссылку из системы управления обучением.
Просмотр заметок к уроку
Дополнительные и сопутствующие средства обучения
Обучение требует усилий. Просмотр видео – относительно пассивное занятие. Одно дело – послушать видео, представленное человеком, разбирающимся в материале.Но совсем другое дело – применить информацию из видео, чтобы лично понять материал. На этой странице перечислены различные инструменты, которые можно использовать для применения нового обучения. Инструменты включают те, которые могут использоваться учениками, и те, которые могут использоваться учителями со своими учениками в классе. Связанные ресурсы также включены в эти инструменты.Просмотреть дополнительные средства обучения
Ресурсы для учителей
Так вы этому учите? Может, мы сможем помочь… мы занимаемся этим некоторое время и у нас есть несколько ресурсов, которые могут вам пригодиться. Посетите страницу ресурсов для учителей и узнайте о некоторых инструментах, которые помогут вам преподавать и разрабатывать уроки.
Просмотреть ресурсы для учителя
Слайды из видеоурока Некоторым студентам полезно просматривать слайды презентации. Мы размещаем их здесь, на нашем сайте. Анимации, присутствующие в видео, преобразуются в одно статичное экранное изображение на слайдах.
Просмотреть слайды
Вы можете просмотреть это видео на YouTube или здесь, на нашем сайте:
Посмотреть видеоурок
Помогите нам Помогите вам Это видео является частью нашей серии видеоуроков по кинематике. Вы можете найти другие видеоуроки здесь, на нашем сайте. Чтобы получать самые свежие материалы из нашей серии видеоуроков по физике, мы предлагаем пользователям подписаться на канал The Physics Classroom на YouTube. Каждые лайков и каждые подписок помогает продвигать наше видео… так что спасибо за любую помощь, которую вы можете нам дать. Когда вы помогаете нам, мы можем помочь вам больше.
2.2 Скорость и скорость – физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Рассчитать среднюю скорость объекта
- Связать смещение и среднюю скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:
- (B) описывают и анализируют движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, лабораторное руководство по физике средней школы рассматривает содержание этого раздела лаборатории под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции.
 Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:- (В) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Раздел Основные термины
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителя
Поддержка учителя
В этом разделе учащиеся применяют то, что они узнали о расстоянии и смещении, к понятиям скорости и скорости.
[BL] [OL] Прежде чем студенты прочитают раздел, попросите их привести примеры того, как они слышали слово «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что в повседневной жизни эти слова часто используются как синонимы, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.
Объясните, что в повседневной жизни эти слова часто используются как синонимы, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.
[AL] Объясните учащимся, что скорость, как и смещение, является векторной величиной. Попросите их поразмышлять о том, чем скорость отличается от скорости.После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Какой пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение – это нечто большее, чем расстояние и перемещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и “Какая была скорость бегуна?” невозможно ответить без понимания других концепций. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, – это его скорость. Скорость – это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость является скаляром, потому что у нее есть величина, но не направление. Поскольку скорость – это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала
Скорость – это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость является скаляром, потому что у нее есть величина, но не направление. Поскольку скорость – это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала
Единицей времени в системе СИ является секунда (с), а единицей измерения скорости в системе СИ являются метры в секунду (м / с), но иногда километры в час (км / ч), мили в час (миль / ч) или другие единицы измерения. скорость используются.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость, v avg , представляет собой пройденное расстояние, деленное на время, в течение которого происходит движение.
vavg = distancetimevavg = distancetimeВы, конечно, можете изменить уравнение, чтобы найти расстояние или время
время = distancevavg. time = distancevavg.
distance = vavg × timedistance = vavg × time
time = distancevavg.
distance = vavg × timedistance = vavg × timeПредположим, что автомобиль проезжает 150 километров за 3 секунды.2 часа. Его средняя скорость за поездку –
vavg = расстояние-время = 150 км3,2 ч = 47 км / ч. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч.Скорость автомобиля, вероятно, увеличится и уменьшится во много раз за 3,2 часа поездки. Однако его скорость в определенный момент времени – это его мгновенная скорость. Спидометр автомобиля показывает его мгновенную скорость.
Поддержка учителя
Поддержка учителя
[OL] [AL] Предупредите учащихся, что средняя скорость не всегда равна средней начальной и конечной скорости объекта.Например, предположим, что автомобиль проезжает 100 км. Первые 50 км он движется со скоростью 30 км / ч, а вторые 50 км – со скоростью 60 км / ч. Его средняя скорость будет составлять расстояние / (временной интервал) = (100 км) / [(50 км) / (30 км / ч) + (50 км) / (60 км / ч)] = 40 км / ч. Если бы автомобиль на этих скоростях проехал равное время на 30 и 60 км, а не на равные расстояния, его средняя скорость составила бы 45 км / ч.
[BL] [OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» на повседневном языке часто называют просто скоростью.Подчеркните важность в науке использования правильной терминологии, чтобы избежать путаницы и правильно передавать идеи.
Рис. 2.8 За 30 минут до магазина туда и обратно общее расстояние составляет 6 км. Средняя скорость 12 км / ч. Смещение для обхода туда и обратно равно нулю, потому что не было чистого изменения положения.
Рабочий пример
Расчет средней скорости
Мрамор катится 5,2 м за 1,8 с. Какая была средняя скорость мрамора?
Стратегия
Мы знаем расстояние, на которое проходит мрамор, 5.2 м, интервал времени 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / сОбсуждение
Средняя скорость – это скаляр, поэтому мы не включаем направление в ответ. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды – это 2,5 м / с. Поскольку 2,5 м / с близко к 2,9 м / с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
8.Питчер перебрасывает бейсбольный мяч от насыпи питчера к своей тарелке за 0,46 с. Дистанция 18,4 м. Какая была средняя скорость бейсбольного мяча?
- 40 м / с
- -40 м / с
- 0,03 м / с
- 8,5 м / с
Кэсси шла к дому своей подруги со средней скоростью 1,40 м / с. Расстояние между домами 205 м. Как долго она продолжала путешествие?
- 146 с
- 0.01 с
- 2,50 мин.
- 287 с
Скорость
Векторная версия скорости – это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в определенный момент. Средняя скорость – это смещение, деленное на время, в течение которого смещение происходит.
vavg = время смещения = ΔdΔt = df − d0tf − t0vavg = время смещения = ΔdΔt = df − d0tf − t0Скорость, как и скорость, выражается в единицах СИ в метрах в секунду (м / с), но поскольку это вектор, вы также должны включить направление.Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость – это не то же самое, что средняя скорость без направления. Как мы видели в предыдущем разделе со смещением и расстоянием, изменение направления в течение определенного интервала времени оказывает большее влияние на скорость и скорость.
Предположим, что пассажир двигался к задней части самолета со средней скоростью –4 м / с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или отступил, прежде чем он добрался до задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени, такие как те, что показаны на рисунке 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, которая является скоростью в определенный момент времени.Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рис. 2.9. На диаграмме представлена более подробная запись пассажира самолета, направляющегося к задней части самолета, показаны более мелкие отрезки его полета.
Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой.Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.
Watch Physics
Расчет средней скорости или скорости
В этом видео рассматриваются векторы и скаляры и описывается, как рассчитать среднюю скорость и среднюю скорость, когда вы знаете смещение и изменение во времени. В видео также рассказывается, как преобразовать км / ч в м / с.
Проверка захвата
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его.Смещение – это пример скалярной величины, а время – пример векторной величины.
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его. Время – это пример скалярной величины, а смещение – пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору требуется только величина, чтобы полностью описать его.Смещение – это пример скалярной величины, а время – пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору требуется только величина, чтобы полностью описать его. Время – это пример скалярной величины, а смещение – пример векторной величины.
Поддержка учителя
Поддержка учителя
В этом видео хорошо показано различие между векторами и скалярами.Студент знакомится с идеей использования «s» для обозначения смещения, которое вы можете поощрять, а можете и не поощрять. Прежде чем ученики посмотрят видео, укажите, что преподаватель использует s → s → для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является обычным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часа и секунды. Напомните учащимся, что в своей работе они должны использовать сокращения h для часа и s для секунд.
Рабочий пример
Расчет средней скорости
Студент перемещается на 304 м к северу за 180 с. Какая была средняя скорость ученика?
Стратегия
Мы знаем, что смещение составляет 304 м к северу, а время – 180 с. Мы можем использовать формулу для средней скорости, чтобы решить задачу.
Решение
vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север2,1
Обсуждение
Поскольку средняя скорость является векторной величиной, вы должны включить в ответ как направление, так и величину.Обратите внимание, однако, что направление можно не указывать до конца, чтобы не загромождать проблему. Обратите внимание на значащие цифры в задаче. Расстояние 304 м состоит из трех значащих цифр, а временной интервал 180 с – только двух, поэтому частное должно состоять только из двух значащих цифр.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d обозначает расстояние и перемещение. Точно так же v обозначает скорость, а v обозначает скорость.Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Иногда векторы представлены маленькими стрелками над переменной.
Поддержка учителя
Поддержка учителя
Используйте эту задачу, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые студенты имеют тенденцию включать много цифр в свои окончательные вычисления. Они ошибочно полагают, что повышают точность своего ответа, записывая многие цифры, указанные на калькуляторе.Обратите внимание, что это приводит к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда носить с собой одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение смещения, когда известны средняя скорость и время
Лейла бегает трусцой со средней скоростью 2.4 м / с на восток. Каково ее смещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м / с на восток, а временной интервал составляет 46 секунд. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток2,2
Обсуждение
Ответ: примерно в 110 м к востоку, что является разумным смещением для чуть менее минуты бега трусцой.Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя научную нотацию, потому что мы хотели прояснить, что мы использовали только две значащие цифры.
Советы для успеха
Анализ размеров – хороший способ определить, правильно ли вы решили проблему. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают на противоположных сторонах отметки равенства. В рассмотренном примере у вас
м = (м / с) (с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица вычитает, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны смещение и средняя скорость
Филипп идет по прямой дороге от своего дома до школы. Сколько времени ему потребуется, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м / с на запад?
Стратегия
Мы знаем, что смещение Филиппа составляет 428 м к западу, а его средняя скорость составляет 1,7 м / с к западу. Мы можем рассчитать время, необходимое для поездки, переписав уравнение средней скорости.
Решение
vavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 svavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 с2,3
Обсуждение
Здесь нам снова пришлось использовать научную запись, потому что ответ мог состоять только из двух значащих цифр. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
10.Дальнобойщик проезжает 0,25 ч по прямой трассе с перемещением 16 км к югу.Какова средняя скорость дальнобойщика?
- 4 км / ч север
- 4 км / ч юг
- 64 км / ч север
- 64 км / ч юг
Птица летит со средней скоростью 7,5 м / с на восток от ветки к ветке за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м / с на восток в течение 3,5 с к другому ответвлению. Каково полное смещение птицы от начальной точки?
- 42 м запад
- 6 м запад
- 6 м на восток
- 42 м на восток
Virtual Physics
The Walking Man
В этом симуляторе вы наведете курсор на человека и переместите его сначала в одном направлении, а затем в противоположном.Не отключайте вкладку Introduction . Вы можете использовать вкладку Charts после того, как узнаете о графическом движении позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. Пока не обращайте внимания на поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость – отрицательным. Затем посмотрите, сможете ли вы сделать обратное.
Проверка захвата
Какая ситуация правильно описывает, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Мужчина удаляется от 0 слева от 0
- Человек движется от 0 справа от 0
Поддержка учителя
Поддержка учителя
Это мощная интерактивная анимация, которую можно использовать для многих уроков.На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Он также может показать, что при отрицательном смещении скорость может быть как положительной, так и отрицательной. Позже с его помощью можно будет показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется оставить учащихся на вкладке Введение . Вкладку Графики можно использовать после того, как студенты узнают о графическом движении позже в этой главе.
Проверьте свое понимание
12.Два бегуна, идущие по одному и тому же прямому пути, начинают и заканчивают свой бег одновременно. На полпути у них разные мгновенные скорости. Могут ли их средние скорости на протяжении всей поездки быть одинаковыми?
- Да, потому что средняя скорость зависит от чистого или полного смещения.
- Да, потому что средняя скорость зависит от общего пройденного расстояния.
- Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
- Нет, потому что мгновенные скорости бегунов должны оставаться такими же в средней точке, но могут изменяться в других точках.
Если вы разделите общее расстояние, пройденное за поездку на автомобиле (определенное одометром), на время поездки, вычисляете ли вы среднюю скорость или величину средней скорости, и при каких обстоятельствах эти две величины одинаковы? ?
- Средняя скорость. Оба они одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
- Средняя скорость. Оба они одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. Оба варианта одинаковы, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. И то, и другое одинаково, когда машина не меняет своего направления.
Может ли средняя скорость быть отрицательной?
- Да, если чистое смещение отрицательное.
- Да, если направление объекта меняется во время движения.
- Нет, потому что средняя скорость описывает только величину, а не направление движения.
- Нет, потому что средняя скорость описывает только величину в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание », чтобы оценить достижение учащимися учебных целей по разделам. Если учащиеся не справляются с какой-либо конкретной целью, Check Your Understanding поможет определить, кто из них и направит их к соответствующему содержанию.Тестовые задания в TUTOR позволят вам переоценить.
разница между скоростью и ускорением? [Видео]
Скорость – это скорость движения в определенном направлении. Это означает, что скорость – это вектор . Нам нужны и его величина, или значение, и его направление. Если мы знаем только скорость, это не скорость.Мы также должны знать направление. Если мы просто знаем, что едем со скоростью 30 миль в час, это только наша скорость. Если мы знаем, что идем со скоростью 30 миль в час в юго-западном направлении, то наша скорость будет 30 миль в час к юго-западу.Это вектор.
Средняя скорость
Средняя скорость – это одна из двух скоростей, которые необходимо иметь в виду. Средняя скорость определяется путем деления пройденного расстояния на пройденное время. Ваша формула: скорость равна расстоянию во времени. Вы можете начать медленно, ускориться, а затем замедлить движение по мере приближения к месту назначения. От точки А до точки Б расстояние, которое вы проехали, будет вашим расстоянием. Допустим, вы проехали 120 миль и ехали на юго-запад.
Вы добирались туда за 60 минут. Вы бы разделили это. 120 разделенное на 60 равно 2. Вы двигались на юго-запад со скоростью две мили в минуту. Это будет ваша скорость. Две мили в минуту на юго-запад. Теперь, если бы мы пытались сделать это за часы, мы могли бы просто изменить это на один час. Это было бы 120 миль в час. Это действительно быстро и маловероятно, но если бы что-то двигалось так быстро, его скорость составляла бы 120 миль в час на юго-запад или две мили в минуту на юго-запад.
Важно указать направление, иначе у вас будет только скорость. Тот факт, что у вас есть направление, делает его скоростью. Средняя скорость – это то, как далеко вы проехали, деленное на общее время всего пути. Ваша скорость постоянно увеличивается и уменьшается по мере того, как вы путешествуете.
Другой тип скорости – мгновенная скорость.
Мгновенная скорость
Это относится к скорости объекта в точную секунду во времени и обычно требует использования расчетов для определения.Если вы попали в выбоину, было бы хорошо знать, едете ли вы со скоростью одну милю в час или 60 миль в час. Было бы важно знать, как быстро вы двигаетесь и в каком направлении именно в этот второй раз. Иногда вам может потребоваться найти мгновенную скорость, но чаще всего вы слышите о средней скорости.
Теперь, ускорение – это изменение скорости объекта. Ускорение также является вектором и может иметь как величину, так и значение, и направление. Помните, мы говорили о том, что ваша скорость будет увеличиваться и уменьшаться по мере вашего путешествия.Что ж, ускорение – это изменение этой скорости. Ускорение указывает то же направление, что и скорость, пока вы поддерживаете или увеличиваете скорость. Скорость идет в этом направлении.
Ускорение происходит в этом направлении, пока вы поддерживаете или увеличиваете скорость. Deceleration – другое слово для обозначения ускорения, когда вы теряете скорость, когда ваша скорость уменьшается. Замедление будет указывать в направлении, противоположном скорости. Если вы идете в этом направлении, но замедляетесь, скорость все равно указывает в этом направлении.Вы по-прежнему едете в этом направлении, но ваше ускорение уменьшается. Ваша скорость уменьшается. Когда вы уменьшаете скорость, ускорение будет идти в направлении, противоположном скорости. Ваша скорость всегда будет оставаться неизменной, потому что вы будете двигаться вперед во времени.
Теперь замедление по-прежнему называется ускорением, потому что помните, что ускорение – это вектор с величиной и направлением. Он будет указывать назад, противоположную скорости, всякий раз, когда вы уменьшаете скорость или замедляете.
Он будет указывать вперед в том же направлении, что и скорость, всякий раз, когда вы поддерживаете или увеличиваете скорость. Иногда используется слово замедление . Иногда это не так. Иногда это просто ускорение в обе стороны. Важно знать, что это все еще можно назвать ускорением, даже когда вы уменьшаете скорость. Вот так это выглядело бы, если бы оно было представлено векторами. Теперь давайте посмотрим на наш пример.
У вас есть скорость с течением времени.Эта дуга – ваше расстояние. Вы начинаете с низкой скорости и наращиваете. Затем вы замедляете движение по мере приближения к месту назначения в конце. Вы можете видеть, что ваша скорость все еще идет в этом направлении, увеличивается, и ваше ускорение увеличивается в этом направлении. Наверху скорость и ускорение указывают в одном направлении.
Тогда, когда вы начнете замедляться, скорость все равно будет идти в том же направлении, потому что вы двигались вперед во времени. Даже когда вы замедляетесь, скорость будет указывать в том же направлении при движении вперед.Ускорение сейчас указывает назад, потому что вы замедляетесь. По мере того, как ваша скорость уменьшается, ускорение будет указывать противоположно скорости.
Это будет ваше пройденное расстояние (вся линия), и вы должны разделить это время здесь, чтобы найти вашу среднюю скорость. Мгновенная скорость была бы, если бы вы сказали: «Прямо здесь, в этот момент я хочу знать, какой была моя скорость». Скорость – это ваша скорость в определенном направлении. Средняя скорость определяется путем деления пройденного вами расстояния на время, которое вам потребовалось, чтобы его преодолеть.
Мгновенная скорость относится к скорости объекта в точный момент времени. Ускорение – это изменение скорости объекта по мере ее увеличения или уменьшения. Ускорение также является вектором и будет иметь как значение, так и направление. Он будет смотреть в том же направлении, что и ваша скорость, если вы увеличиваете скорость, и в противоположном направлении, если вы уменьшаете скорость.
В чем разница между скоростью, скоростью и ускорением?
Определения:
Скорость или скорость?
Скорость – это скорость движения или скорость изменения положения.Он выражается как пройденное расстояние (d) за единицу времени (t). Скорость – это скалярная величина с размерами расстояние / время. Скорость измеряется в тех же физических единицах измерения, что и скорость , но не содержит элемента направления. Таким образом, скорость является величиной составляющей скорости. Скорость содержит компоненты величины и направления.
Общие скорости движущихся объектов
Для людей средняя скорость ходьбы составляет около 3 миль в час (~ 5 км / ч, 1,1 км / ч).39 м / с),
Скорость бега на длинные дистанции для среднего человека составляет около 6 миль в час (~ 10 км / ч, 2,7 м / с).
Лучшие спортивные спринтеры могут бегать со скоростью 23,03 мили в час (~ 36,85 км / ч, 10,24 м / с) на короткой дистанции, например, в 200-метровом рывке.
Езда на велосипеде может в среднем 12 миль / ч (~ 20 км / ч, 5,56 м / с)
Автомобиль может в среднем 65 миль / ч (~ 104 км / ч, 28,9 м / с) на шоссе
Самолет 747 развивает среднюю скорость 565 миль / ч
Разгон
Ускорение (символ: а) определяется как скорость изменения скорости.Таким образом, это векторная величина с размерностью длина / время². В единицах СИ ускорение измеряется в метрах в секунду².
Ускорение объекта означает изменение его скорости, что достигается изменением его скорости или направления (как в случае равномерного кругового движения) в зависимости от времени. Ускорение может иметь положительные и отрицательные значения. Каждый раз, когда знак (+ или -) ускорения совпадает со знаком скорости, объект будет ускоряться. Если знаки противоположные, объект будет тормозить.Ускорение – это векторная величина. При изменении скорости или направления происходит ускорение (или замедление).
Для ускорения объекта требуется приложение силы.
График скорости и ускорения
Автомобиль разгоняется от покоя. Следующие два графика созданы с помощью Java-апплета (см. Ниже).График скорости (м / сек.) от времени (сек.) – прямая линия для ускоряющихся объектов. ускорение = скорость / время Каков наклон этого графика?
Пожалуйста, введите свой ответ в отведенное для этого поле:
График зависимости расстояния (x) от времени (t) представляет собой кривую, на которой уравнение движения имеет следующий вид: x = 1/2 ат². Какое значение (а) вы ожидаете от этого графика? Подсказка: для каждого значения t (в s) существует только одно значение x (в m).Выберите любую упорядоченную пару для t и x и подставьте их в приведенное выше уравнение. Затем решите для a.
Создайте свои собственные графики для ускорения объектов с помощью следующего java-апплета: Это приложение HTML5 от Вальтера Фендта показывает автомобиль, движущийся с постоянным ускорением. Зеленая панель управления содержит текстовые поля, в которых вы можете изменять значения начальной позиции, начальной скорости и ускорения (не забудьте нажать клавишу «Enter»!).Используя кнопки в правом верхнем углу, вы можете вернуть автомобиль в исходное положение или остановиться и возобновить симуляцию. Если вы выберете опцию «Замедленное движение», движение будет в десять раз медленнее.
Проверьте свое понимание:Среднее ускорение – Nexus Wiki
Концептуальная идея ускорения такая же, как и у нас со скоростью:
Среднее ускорение = (Насколько изменилась ваша скорость?) /
(Сколько времени потребовалось для этого изменения?)
Как и в случае со скоростью, мы должны быть осторожны, чтобы отметить, что, хотя он отражает концептуальное содержание среднего ускорения, он пропускает векторный характер ускорения.Поскольку скорость – это вектор , мы действительно имеем в виду «насколько изменилась векторная скорость» для числителя – и это делает ускорение вектором. Таким образом, ускорение связано не только с изменением скорости. Если скорость меняет направление, это тоже ускорение.
В нашем уравнении для (векторного) среднего ускорения угловые скобки «<..>» используются для обозначения «среднего», как и для скорости.
$$ \ langle \ overrightarrow {a} \ rangle = \ frac {\ Delta \ overrightarrow {v}} {\ Delta t} $$
Если мы более точно укажем начальную и конечную позиции и время, мы можем записать это как
$$ \ langle \ overrightarrow {a} \ rangle = \ frac {\ overrightarrow {v_f} – \ overrightarrow {v_i}} {t_f – t_i} $$
, где нижний индекс «i» означает «начальный», а нижний индекс «f» означает «окончательный»; так, например, $ t_i $ означает начальное (начальное) время.
Если мы умножим обе части определяющего уравнения на временной интервал, мы сможем лучше понять, что означает среднее ускорение:
$$ \ Delta \ overrightarrow {v} = \ langle \ overrightarrow {a} \ rangle \ Delta t $$
Итак, если вы изменили свою скорость на величину $ Δv $ за время $ Δt $, среднее ускорение будет «тем постоянным ускорением, которое вам придется так сильно изменить за это время». Конечно, в этот промежуток времени вы могли не двигаться с постоянным ускорением.
Размерность ускорения
Поскольку ускорение – это отношение скорости (размерность L / T) ко времени (размерность T), оно имеет размерность L / T 2 :
[$ a $] = [$ v / t $] = (L / T) / T = L / T 2 .
Постоянное ускорение
Если вы ускоряетесь с постоянной скоростью, скажем, ваше ускорение является постоянным $ a_0 $, тогда вы можете легко вычислить, насколько изменилась ваша скорость за данный интервал времени. Но вы также можете легко узнать, как далеко вы продвинулись за этот промежуток времени.Давайте сначала посмотрим, как получить изменение скорости. Как и в случае со средней скоростью, есть много разных способов написать это, в зависимости от того, что вы знаете и от того, что хотите найти. Вот несколько:
$$ \ langle \ overrightarrow {a} \ rangle = \ frac {\ Delta \ overrightarrow {v}} {\ Delta t} = \ overrightarrow {a_0} $$
$$ \ Delta \ overrightarrow {v} = \ overrightarrow {a_0} \ Delta t $$
$$ \ overrightarrow {v_2} – \ overrightarrow {v_1} = \ overrightarrow {a_0} \ Delta t $$
$$ \ overrightarrow {v} _ {final} = \ overrightarrow {v} _ {initial} + \ overrightarrow {a_0} \ Delta t $$
Обратите внимание, что, как и в случае со скоростью, если есть вектор на одной стороне уравнения, он должен быть на другой.Векторы и скаляры (числа, не имеющие направления) – это разные типы физических объектов, и их нельзя приравнивать (или складывать).
При постоянном ускорении мы также можем узнать, как изменяется положение, используя среднюю скорость. См. Следующую страницу, посвященную расчетам с постоянным ускорением.
Джулия Гувеа и Джо Редиш 20.08.13
5.2.2: Скорость и скорость – Physics LibreTexts
Средняя скорость: графическая интерпретация
Средняя скорость определяется как изменение положения (или смещения) за время движения.
цели обучения
- Контрастная скорость и скорость в физике
В повседневном использовании термины «скорость» и «скорость» используются как синонимы. Однако в физике это разные величины. Скорость – это скалярная величина, имеющая только величину. С другой стороны, скорость – это векторная величина, поэтому она имеет как величину, так и направление. Это различие становится более очевидным, когда мы вычисляем среднюю скорость и скорость.
Средняя скорость рассчитывается как расстояние, пройденное за общее время поездки.Напротив, средняя скорость определяется как изменение положения (или смещения) за общее время движения.
Средняя скорость : Кинематическая формула для расчета средней скорости – это изменение положения за время движения.
Единица измерения скорости в системе СИ – метры в секунду или м / с, но обычно используются многие другие единицы (например, км / ч, миль / ч и см / с). Предположим, например, что пассажиру самолета потребовалось пять секунд, чтобы переместиться на -4 м (отрицательный знак указывает, что смещение происходит в сторону задней части самолета).Его средняя скорость будет:
\ [\ mathrm {v = \ dfrac {Δx} {t} = \ dfrac {-4 \; m} {5 \; s} = -0,8 \ dfrac {m} {s}} \]
Знак минус указывает, что средняя скорость также направлена к задней части самолета.
Однако средняя скорость объекта ничего не говорит нам о том, что с ним происходит между начальной и конечной точкой. Например, мы не можем сказать по средней скорости, останавливается ли пассажир самолета на мгновение или отступает, прежде чем он доберется до задней части самолета.Чтобы получить больше деталей, мы должны рассматривать меньшие отрезки поездки за меньшие промежутки времени.
Чтобы проиллюстрировать разницу между средней скоростью и средней скоростью, рассмотрим следующий дополнительный пример. Представьте, что вы идете по маленькому прямоугольнику. Вы идете три метра на север, четыре метра на восток, три метра на юг и еще четыре метра на запад. Вся прогулка займет у вас 30 секунд. Если вы рассчитываете среднюю скорость, вы должны рассчитать все расстояние (3 + 4 + 3 + 4 = 14 метров) за общее время, 30 секунд.Отсюда вы получите среднюю скорость 14/30 = 0,47 м / с. Однако при вычислении средней скорости вы смотрите на смещение во времени. Поскольку вы вошли в полный прямоугольник и оказались там, где начали, ваше смещение составляет 0 метров. Следовательно, ваша средняя скорость или смещение во времени составит 0 м / с.
Средняя скорость в сравнении со средней скоростью : Если вы начали идти с одного угла и обошли прямоугольник за 30 секунд, ваша средняя скорость будет равна 0.47 м / с, но ваша средняя скорость будет 0 м / с.
Постоянная скорость: графическая интерпретация
Мгновенная скорость – это скорость объекта в одной точке времени и пространства, вычисленная по наклону касательной.
цели обучения
- Отличить мгновенную скорость от других способов определения скорости
Обычно движение не с постоянной скоростью или скоростью. Например, во время движения в машине мы постоянно ускоряемся и замедляемся.Следовательно, графическое представление нашего движения с точки зрения расстояния от времени будет более изменчивым или «извилистым», чем прямая линия, указывающая на движение с постоянной скоростью, как показано ниже. (Мы ограничиваем наше обсуждение одномерным движением. Оно должно быть простым для обобщения на трехмерные случаи.)
Движение с изменяющейся скоростью : Движение часто наблюдается с изменяющейся скоростью. Это привело бы к извилистой линии при отображении расстояния с течением времени.
Чтобы вычислить скорость объекта по графику, представляющему постоянную скорость, все, что нужно, – это найти наклон линии; это будет указывать на изменение расстояния с течением времени. Однако изменить скорость не так просто.
Поскольку наша скорость постоянно меняется, мы можем оценивать скорость по-разному. Один из способов – взглянуть на нашу мгновенную скорость, представленную одной точкой на нашей извилистой линии движения с графиком зависимости расстояния отвремя. Чтобы определить нашу скорость в любой момент, мы должны определить наклон в этой точке. Для этого мы находим линию, которая представляет нашу скорость в этот момент, показанную графически. Эта линия будет касательной к кривой в этой точке. Если мы продолжим эту линию, мы сможем легко вычислить смещение расстояния во времени и определить нашу скорость в данной точке. Скорость объекта в любой данный момент – это наклон касательной, проходящей через соответствующую точку на его оси x vs.t график.
Определение мгновенной скорости : Скорость в любой данный момент определяется как наклон касательной линии, проходящей через соответствующую точку на графике
Мгновенная скорость, ускорение, рывок, наклоны, графики в зависимости от времени : Так начинается кинематика.
В расчетах определение наклона кривой \ (\ mathrm {f (x)} \) при \ (\ mathrm {x = x_0} \) x = x 0 эквивалентно нахождению первой производной:
\ [\ mathrm {\ dfrac {df (x)} {dx} \ rvert_ {x = x_0}.} \]
Одно из толкований этого определения состоит в том, что скорость показывает, сколько метров объект пролетит за одну секунду, если он продолжит движение с той же скоростью в течение как минимум одной секунды.
Средняя скорость
Обыденное понятие скорости возникает, когда мы рассматриваем, насколько быстро или медленно движется тело. Каким-то образом мы связываем смещение тела со временем, проведенным в таком смещении. В этом разделе мы собираемся определить, что понимается в физике под средней скоростью и ее разницей со средней скоростью.
Средняя скорость
Средняя скорость тела, которое движется из точки P 1 в точку P 2 , определяется как отношение пройденного расстояния и соответствующего прошедшего времени . Это дается выражением:
Vavg = ∆s∆t = s2-s1t2 – t1
где:
- Vavg: Средняя скорость в исследуемом интервале.Единица измерения в международной системе (S.I.) – метр в секунду (м / с) .
- ∆s: Пройденное расстояние в рассматриваемом интервале. Измерено по траектории . Единицей измерения в Международной системе (S.I.) является метр (м) .
- ∆t: Время , затрачиваемое телом на переход от P 1 к P 2 . Единица измерения в международной системе (S.I.) – это секунда (ы)
- с 1 , с 2 : Расстояние, пройденное телом по траектории от начала движения до P 1 (с 1 ) , и от начала движение на P 2 (s 2 ) . Единицей измерения в Международной системе (S.I.) является метр (м) .
- t 1 , t 2 : Время , в течение которого тело находится в начальной точке P 1 и в конечной точке P 2 соответственно.Единицей измерения в Международной системе (S.I.) является секунда (с) .
Средняя скорость – это скалярная величина , в отличие от средней скорости, которая является вектором. Единица измерения в Международной системе (S.I.) для средней скорости – это метр в секунду (м / с) . С другой стороны, в отличие от средней скорости, которая зависела от векторов начального и конечного положений движения, средняя скорость зависит от расстояния, пройденного по траектории.Следовательно, движущееся тело всегда будет иметь среднюю скорость больше 0 . В общем, выполняется Vavg≥vavg →, и оба значения будут одинаковыми в случае прямолинейного движения без изменения направления.
Экспериментируйте и учитесь
Данные
Средняя скорость
На графике показана траектория, по которой следует тело, его начальное и конечное положения, а также пройденное расстояние (Δs) между двумя точками.
Перетащите точки ближе или дальше друг от друга и наблюдайте, как пройденное расстояние уменьшается или увеличивается соответственно. Кроме того, вы можете изменить время, необходимое телу для перехода от одной точки к другой (Δt), и заметить изменение средней скорости.
Что произойдет, если вы не измените положение, а уменьшите время?
Пример
Тело делает полный круг радиусом 4 метра за 1.5 секунд. Вычислить:
а) средняя скорость.
б) средняя скорость.


 Получаем: [a] = 1 м/с2.
Получаем: [a] = 1 м/с2.
 Масса больших тел измеряется в килограммах.
Масса больших тел измеряется в килограммах.

 Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент: