Как находится средняя скорость в физике. По какой формуле рассчитывается средняя скорость
Понятие скорости − одно из главных понятий в кинематике.
Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
Будем рассматривать материальную точку в системе координат x , y , z (рис. а).
Положение A точки в момент времени t характеризуем координатами x(t) , y(t) , z(t) , представляющими три составляющих радиуса-вектора (t ).
Траектория, описанная за промежуток времени от t до t + Δt , показана на рисунке б.
Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt )). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt .
Среднюю путевую скорость точки за данный промежуток времени определяют соотношением
Очевидно, что v п − скалярная величина; она характеризуется только числовым значением.
называют перемещением материальной точки за время от t до t + Δt .
Среднюю скорость по перемещению за данный промежуток времени определяют соотношением
Очевидно, что v ср − векторная величина.
Направление вектора v ср совпадает с направлением перемещения Δr .
Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от
Вопрос :
Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?
Ответ :
Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения
При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |v ср | ). Но направления перемещений (а значит, и векторов v ср ) и в данном случае будут различными для одинаковых Δt . Это видно на рисунке,
Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги
Примечание
Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко.
Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:
Научимся ее находить на примере следующей задачи:
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.
2. Два одинаковых интервала движения.
Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
| Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения. |
Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Сергей Валерьевич
Инструкция
Рассмотрим функцию f(x) = |x|. Для начала этой без знака модуля, то есть график функции g(x) = x. Этот график является прямой, проходящей через начало координат и угол между этой прямой и положительным направлением оси абсцисс составляет 45 градусов.
Так как модуль величина неотрицательная, то ту часть , которая находится ниже оси абсцисс необходимо зеркально отобразить относительно нее. Для функции g(x) = x получим, что график после такого отображения станет похож на V. Этот новый график и будет являться графической интерпретацией функции f(x) = |x|.
Видео по теме
Обратите внимание
График модуля функции никогда не будет находится в 3 и 4 четверти, так как модуль не может принимать отрицательных значений.
Полезный совет
Если в функции присутствуют несколько модулей, то их нужно раскрывать последовательно, а затем накладывать друг на друга. Результат и будет искомым графиком.
Источники:
- как построить график функции с модулями
Задачи на кинематику, в которых необходимо вычислить
Вам понадобится
- – ручка;
- – бумага для записей.
Инструкция
Самый простой случай – движение одного тела с заданной равномерной скорость ю.
Известно расстояние, которое тело прошло. Найдите в пути: t = S/v, час, где S – расстояние, v – средняя
Второй – на встречное движение тел. Из пункта А в пункт В движется автомобиль со скорость ю 50 км/ч. Навстречу ему из пункта B одновременно выехал мопед со скорость ю 30 км/час. Расстояние между пунктами А и В 100 км. Требуется найти время , через которое они встретятся.
Обозначьте точку встречи К. Пусть расстояние АК, которое автомобиль, будет х км. Тогда путь мотоциклиста составит 100-х км. Из условия задачи следует, что время в пути у автомобиля и мопеда одинаково. Составьте уравнение: х/v = (S-x)/v’, где v, v’ – и мопеда. Подставив данные, решите уравнение: x = 62,5 км. Теперь время : t = 62,5/50 = 1,25 часа или 1 час 15 минут.
Третий пример – даны те же условия, но автомобиль выехал на 20 минут позже мопеда. Определить, времени в пути будет автомобиль до встречи с мопедом.
Составьте уравнение, аналогично предыдущему.
Но в этом случае время мопеда в пути будет на 20 минут , чем у автомобиля. Для уравнивания частей, вычтите одну треть часа из правой части выражения: х/v = (S-x)/v’-1/3. Найдите х – 56,25. Вычислите время : t = 56,25/50 = 1,125 часа или 1 час 7 минут 30секунд.
Четвертый пример – задача на движение тел в одном направлении. Автомобиль и мопед с теми же скоростями двигаются из точки А. Известно, что автомобиль выехал на полчаса позже. Через какое время он догонит мопед?
В этом случае одинаковым будет расстояние, которое проехали транспортные средства. Пусть время в пути автомобиля будет x часов, тогда время в пути мопеда будет x+0,5 часов. У вас получилось уравнение: vx = v’(x+0,5). Решите уравнение, подставив значение , и найдите x – 0,75 часа или 45 минут.
Пятый пример – автомобиль и мопед с теми же скоростями двигаются в одном направлении, но мопед выехал из точки В, находящейся на расстоянии 10 км от точки А, на полчаса раньше.
Вычислить, через какое время после старта автомобиль догонит мопед.
Расстояние, которое проехал автомобиль, на 10 км больше. Прибавьте эту разницу к пути мотоциклиста и уравняйте части выражения: vx = v’(x+0,5)-10. Подставив значения скорости и решив его, вы получите : t = 1,25 часа или 1 час 15 минут.
Источники:
- какая скорость машины времени
Инструкция
Рассчитайте среднюю тела, движущегося равномерно на протяжении участка пути. Такая скорость вычисляется проще всего, поскольку она не изменяется на всем отрезке движения и равняется средней . Можно это в виде : Vрд = Vср, где Vрд – скорость равномерного движения , а Vср – средняя скорость .
Вычислите среднюю скорость равнозамедленного (равноускоренного) движения на данном участке, для чего необходимо сложить начальную и конечную скорость . Разделите на два полученный результат, который и
В школе каждому из нас попадалась задача, похожая на следующую.
Если автомобиль часть пути двигался с одной скоростью, а следующий отрезок дороги с другой, как найти среднюю скорость?
Что это за величина и зачем она нужна? Давайте попробуем в этом разобраться.
Скорость в физике — это величина, описывающая количество пути, пройденного за единицу времени. То есть когда говорят, что скорость пешехода составляет 5 км/ч, это означает, что он проходит расстояние в 5 км за 1 час.
Формула для нахождения скорости выглядит так:
V=S/t, где S — пройденный путь, t — время.
Единой размерности в этой формуле нет, поскольку с ее помощью описываются и крайне медленные, и очень быстрые процессы.
Например, искусственный спутник Земли преодолевает порядка 8 км за 1 секунду, а тектонические плиты, на которых расположены материки, по измерениям ученых, расходятся всего на несколько миллиметров за год. Поэтому и размерности у скорости могут быть разными — км/ч, м/с, мм/с и т.д.
Принцип заключается в том, что расстояние делится на время, необходимое для преодоления пути.
Не стоит забывать о размерности, если проводятся сложные расчеты.
Чтобы не запутаться и не ошибиться в ответе, все величины приводятся в одни и те же единицы измерения. Если длина пути указана в километрах, а какая-то его часть в сантиметрах, то, пока мы не получим единства в размерности, правильного ответа нам не узнать.
Постоянная скорость
Описание формулы.
Самый простой случай в физике — равномерное движение. Скорость постоянна, не меняется на протяжении всего пути. Есть даже скоростные константы, сведенные в таблицы, — неизменные величины. К примеру, звук распространяется в воздухе со скоростью 340,3 м/с.
А свет — абсолютный чемпион в этом плане, он обладает самой большой в нашей Вселенной скоростью — 300 000 км/с. Эти величины не меняются от начальной точки движения до конечной. Они зависят только от среды, в которой движутся (воздух, вакуум, вода и пр.).
Равномерное движение часто встречается нам и в повседневной жизни. Так работает конвейер на заводе или фабрике, фуникулер на горных трассах, лифт (за исключением очень коротких периодов пуска и остановки).
График такого движения очень прост и представляет собой прямую линию. 1 секунда — 1 м, 2 секунды — 2 м, 100 секунд — 100 м. Все точки находятся на одной прямой.
Неравномерная скорость
К сожалению, так идеально и в жизни, и в физике бывает крайне редко. Множество процессов проходят с неравномерной скоростью, то ускоряясь, то замедляясь.
Давайте представим движение обычного междугороднего автобуса. В начале пути он разгоняется, у светофоров тормозит, а то и вовсе останавливается. Затем уже за городом едет быстрее, но на подъемах медленнее, а на спусках вновь ускоряется.
Если изобразить этот процесс в виде графика, то получится весьма замысловатая линия. Определить скорость по графику можно только для какой-то конкретной точки, а общего принципа нет.
Потребуется целый набор формул, каждая из которых подойдет только для своего участка чертежа. Но страшного ничего нет. Для описания перемещения автобуса пользуются усредненным значением.
Найти среднюю скорость движения можно все по той же формуле.
Действительно, нам известно расстояние между автовокзалами, измерено время в пути. Поделив одно на другое, найдите искомую величину.
Для чего это нужно?
Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.
Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.
Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.
Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.
Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи ” ” и ” ” . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.
Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:
Если участков пути было два, тогда
Если три, то соответственно:
*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.
Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч.
Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:
Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:
Вторую треть пути автомобиль ехал:
Последнюю треть пути автомобиль ехал:
Таким образом
Решите самостоятельно:
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о трёх участках пути. СК будем искать по формуле:
Участки пути нам не даны, но мы можем без труда их вычислить:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
Вычисляем скорость:
Решите самостоятельно:
Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км – со скоростью 80 км/ч, а затем 150 км – со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Сказано о трёх участках пути. Формула:
Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:
Решите самостоятельно:
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км – со скоростью 90 км/ч, а затем 170 км – со скоростью 100 км/ч.
Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.
Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Скорость – это… Что такое Скорость?
Ско́рость (часто обозначается , от англ.
velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.
Скорость тела в механике
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:
Здесь — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .
Скорость направлена вдоль касательной к траектории и равна по модулю производной дуговой координаты по времени.
Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.
Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю) и тогда:
Скорость — характеристика движения точки, при равномерном движении численно равная отношению пройденного пути s к промежутку времени t, за который этот путь пройден.
Следует различать координатную и физическую скорости. При введении криволинейных или обобщённых координат положение тел описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями.
Мгновенная и средняя скорость
Иллюстрация средней и мгновенной скорости.Следует отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.
Когда говорят о средней скорости, для различения, скорость согласно выше приведённому определению называют мгновенной скоростью.
Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.
В полярных координатах
Проекции скорости в декартовой системе координат
В прямоугольной декартовой системе координат:
В то же время , поэтому
Таким образом, координаты вектора скорости — это скорости изменения соответствующей координаты материальной точки:
- .
Преобразование скорости
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела при переходе в систему отсчёта S’ будет равна .
Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:
в предположении, что скорость направлена вдоль оси х системы S.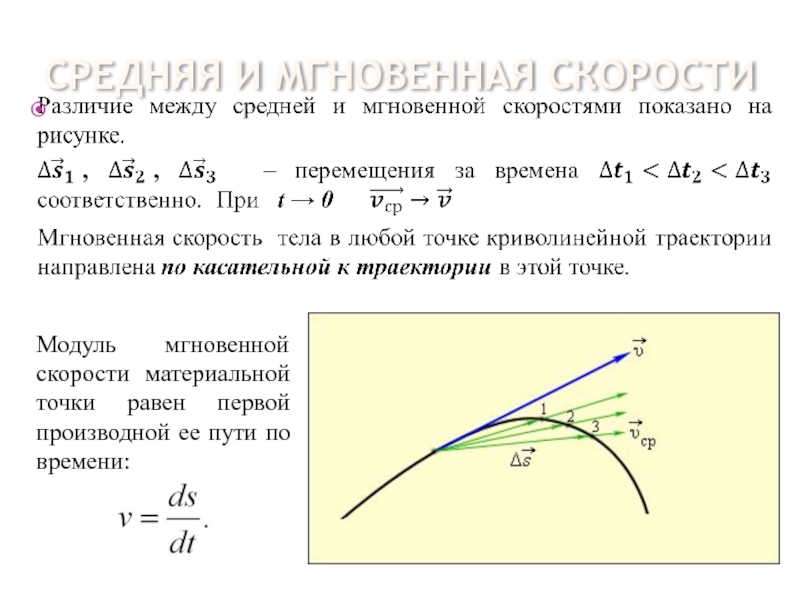
Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Единицы измерения скорости
Линейная скорость:
Угловая скорость:
- Радианы в секунду, принята в системах СИ и СГС. Физическая размерность 1/с.
- Обороты в секунду (в технике)
- градусы в секунду, грады в секунду
Соотношения между единицами скорости
- 1 м/с = 3,6 км/ч
- 1 узел = 1,852 км/ч = 0,514 м/c
- Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
- c = 299 792 458 м/c
См. также
1.1.3 Скорость материальной точки. Сложение скоростей
Видеоурок 1: Перемещение и скорость материальной точки
Видеоурок 2: Сложение скоростей
Лекция: Скорость материальной точки.
Сложение скоростейСкорость материальной точкиВсе процессы вокруг нас характеризуются тем, насколько быстро они протекают – насколько быстро двигается тело, насколько быстро протекает ток по проводам, насколько быстро изменяется магнитный поток.
При рассмотрении кинематических законов скорость характеризует быстроту изменения положения тела.
Скорость – это векторная ФВ, которая характеризует, насколько быстро изменяется положение тела, а также направление этого изменения. Основной единицей измерения является 1 м/с.
Мгновенная скорость определяется пределом изменения положения тела в пространстве к бесконечно малому интервалу времени.
На рисунке скорость можно показать, как вектор, направленный по касательной к траектории движения.
Сложение скоростейСуществуют основные правила, позволяющие складывать скорости тел для удобства во время решения задач.
1. Если тела двигаются в одном направлении, то можно воспользоваться следующей формулой:
2.
Если тела двигаются в разных направлениях вдоль одной прямой, то суммарная скорость будет равна:
3. Если перемещения тел направлены под углом друг к другу, то принято пользоваться правилом треугольника, где неизвестный суммарный вектор скорости представляется в виде неизвестной стороны треугольника, которая определяется по теореме косинусов:
4. Если тела двигаются по перпендикулярным перемещениям, то суммарная скорость равна:
Средняя скоростьЕсли за равные промежутки времени тело изменяет свою скорость, то можно воспользоваться следующей формулой:
Например, каждые 15 минут велосипедист изменял свою скорость:
Первые 15 минут его скорость была 3 м/с, вторые 15 минут – 4 м/с, а третьи – 5 м/с, то средняя скорость равна:
<v> = (3+4+5) : 3 = 4м/с.
Однако, если же тело меняло скорости не за равные промежутки времени, то следует пользоваться другой формулой:
Средняя скорость – обзор
Устойчивость на дне
Основным элементом конструкции морского трубопровода является поддержание устойчивости трубопровода на морском дне при волновых и токовых нагрузках.
Перемещение трубопровода вызовет усталость, а затем со временем выйдет из строя и может вызвать растрескивание бетонного покрытия.
В 1976 году в основу проектирования подводных трубопроводов были положены правила DNV для подводных трубопроводных систем. Нагрузки, влияющие на устойчивость трубопровода, показаны на рис.9.4.
Рисунок 9.4. Стабильность днища.
Был предпринят ряд исследовательских проектов для понимания гидродинамических сил на трубопроводах с целью разработки рациональных методологий для расчета устойчивости на дне. Двумя наиболее масштабными являются PIPESTAB (Wolfram et al., 1987) и Проект стабилизации на дне Международного совета по исследованиям трубопроводов (PRCI) (Ayers et al., 1989).
Как обсуждалось в предыдущих главах, есть сила сопротивления, F D , сила инерции, F M , подъемная сила, F L , вес в погруженном состоянии, Вт S , а сила сопротивления трения R с коэффициентом вариации μ.
Уравнение Моррисона применяется здесь для сопротивления, инерции и подъемных сил следующим образом:
Сила инерции :
FM = π (D2 / 4) ρCMa
, где подъемная сила на морском дне обеспечивает симметрию между поток через верх трубы и поток снизу. Это вызывает отсутствие потока или, возможно, более медленный поток под трубопроводом и более высокие скорости наверху с более низким давлением, что создает подъемную силу.
На практике коэффициенты гидродинамических сил равны C D = 0.7, C M = 3,29 и C L = 0,9.
Трубопровод считается устойчивым в вертикальном положении, если погруженный вес превышает максимальный подъемный вес. Погруженный вес – это вес трубы и покрытия.
Погружной вес; WS = вес трубы-плавучесть
Собственный вес трубы зависит от материала трубы (сталь, бетон), а также толщины и плотности покрытия.
Сила сопротивления вычисляется простым кулоновским трением путем умножения вертикальной нагрузки на коэффициент трения.
Коэффициент трения μ равен 0,2–0,4 в глинистом грунте и 0,5–0,9 в песчаном грунте.
В слабых глинах или илистых песках труба может врезаться в морское дно. Поэтому вполне вероятно, что в этих условиях устойчивость трубопровода будет считаться более высокой, чем предполагалось. В случае жесткой глины, плотного песка или голой породы вероятность вхождения трубы в морское дно низка. Допуск трубопровода к небольшим смещениям в защитном коридоре означает, что все еще могут быть получены улучшения по сравнению с традиционным методом анализа устойчивости.
Устойчивость трубопровода зависит от нагрузки по данным океанографии, которые имеют ту же терминологию, что и обсуждаемая в главе 2 «Нагрузки и прочность на морские конструкции» о волнах и течениях. Трубопровод отличается от фиксированной морской конструкции, поскольку магистральные линии могут составлять сотни километров, что, следовательно, изменяет океанографические данные из-за этих расстояний, а также требует числовой модели для ретроспективного прогноза или экстраполяции от известных штормов на достаточное количество мест вдоль трубопровода.
.
Как было показано ранее, необходимо определить скорость и ускорение для расчета силы сопротивления и инерции. Наиболее распространенной волновой теорией является волна Эйри, поскольку она имеет хорошую точность, поскольку трубопровод находится на морском дне, что дает лучшие результаты, чем на поверхности.
Морские течения в расчетных данных всегда учитываются на высоте 5 м над уровнем морского дна. Это используется для интегрирования скорости по высоте трубы для получения эффективного установившегося тока.
Ток может быть рассчитан согласно закону 1/7 степени, представленному в главе 2 согласно API, или по следующей формуле из DNV RP E305
UcUr = 1ln (ZrZo + 1) [(1 + ZoD ) ln (DZo + 1) −1]
, где
U c – средняя скорость по трубе с учетом шероховатости дна, Z o ; и U r – это исходная скорость на высоте, Z r над морским дном, которая измеряется измерителем течения.
Для формулы DNV, чем грубее морское дно, тем толще пограничный слой и тем ниже средняя скорость по трубопроводу.
Шероховатость дна может быть получена из таблицы 9.7 из DnV RP F109.
Таблица 9.7. Неровность морского дна.
| Морское дно | Размер зерна d 50 (мм) | Прибл. шероховатость Z o (м) | ||||||
|---|---|---|---|---|---|---|---|---|
| Ил и глина | 0.0625 | 5 × 10 −6 | ||||||
| Мелкий песок | 0,25 | 1 × 10 −5 | ||||||
| Средний песок | 0,5 | 4 × 10 −5 Крупный песок | 1,0 | 1 × 10 −4 | ||||
| Гравий | 4,0 | 3 × 10 −4 | ||||||
| Галька | 25 | 2 ×2 × | ||||||
| Cobble | 125 | 1 × 10 −2 | ||||||
| Boulder | 500 | 4 × 10 −2 |
В соответствии с DNV76, коэффициент устойчивости – коэффициент устойчивости 1.
1 как минимум. Значительная высота волны, H s , обычно используется для баланса сил для длинных трубопроводов, но в случае катушек и перемычек, которые не могут перемещаться, она используется на максимальной высоте волны, H max , в расчете стабилизации:
FS = (Ws − FL) / (FD + FM) ≥1,1
Влияние гидродинамических нагрузок на трубопровод может быть намного выше, чем у модели DnV76, которая была получены экспериментальными испытаниями.Исходя из этого, в 1981 году пересмотренные правила, опубликованные компанией DnV, предоставили более реалистичную модель гидродинамических расчетов, соответствующую экспериментальным испытаниям.
Как указано выше, трубопровод, спроектированный DNV76, вызывал некоторые опасения, но они не опасны, поскольку проводились ежегодные исследования, чтобы убедиться в отсутствии серьезных проблем.
Программное обеспечение для расчета устойчивости Американской газовой ассоциации (AGA), охватывающее результаты экспериментальных испытаний в случае шторма на трубопроводе, показывает небольшое смещение из-за волновых сил, которое приведет к постепенному углублению трубопровода в морское дно и небольшие бермы с обеих сторон, которые увеличивают сопротивление движению и обеспечивают гидродинамическую защиту.
Самый полный дизайн – это динамический анализ. Это рассматривает трубопровод как податливую конструкцию с короткими гребешковыми волнами, беспорядочно действующими по всей его длине. Определяется локальное перемещение трубопровода и рассчитываются результирующие деформации. Критерии ограничения основаны на максимально допустимом перемещении с пределом на 20 м и рабочих нагрузках. Динамический анализ потребовал использования конечного анализа. Анализ включает случайные волны, длинную совместимую модель трубопровода и реалистичную модель сопротивления морского дна, включая эффекты заделки, то есть повышенного сопротивления при движении трубопровода.Динамический анализ разрешен DNV RP E305, PRCI и AGA. Существует множество программ, которые могут выполнять этот анализ на основе используемых кодов. PRCI обеспечивает три уровня анализа. Уровень 1 представляет собой статический расчет баланса сил и проверяет FS. Уровень 2 – квазистатический подход; этот подход учитывает модель взаимодействия с грунтом и прошлую циклическую нагрузку и нарастание модельного шторма, за которым следует расчетный шторм, и вычисляет FS.
Уровень 3, представляющий собой динамический анализ, обеспечивает мгновенное значение FS, смещения трубы, заделки и напряжений.Значительная высота волны, период волны и параметры спектрального пика вводятся для получения идеализированного спектра, из которого можно получить временную диаграмму скорости донной воды на морском дне. Программное обеспечение обеспечивает лучший результат, используя только уравнение Моррисона, поскольку его простейшая форма обеспечивает точные результаты.
При проектировании необходимо учитывать два основных варианта нагружения:
- 1.
Вариант нагружения 1 : трубопровод пустой и опирается на морское дно, не подвержен коррозии, волна и течение соответствуют следующие:
- а.
Однолетняя штормовая волна с учетом значительной высоты волны и периода спектрального пика, связанного с 10-летним штормовым течением
- b.
Десятилетняя штормовая волна и однолетнее штормовое течение;
- 2.
Вариант нагружения 2 : Условия эксплуатации – трубопровод заполнен жидкостью с учетом его плотности с учетом морского роста, если это влияет на результат, и следующей комбинации анализов согласно DnV-RP-F109 осуществляются:
- а.
Столетняя штормовая волна и 10-летнее штормовое течение
- b.
Десятилетняя штормовая волна и 100-летнее штормовое течение.
Аналитические и экспериментальные средние скорости материальных точек …
Метод материальных точек (MPM) – это численный метод, который, как было продемонстрировано, подходит для моделирования многочисленных механических проблем, особенно больших проблем деформации, в то время как сохраняя массу, импульс и энергию.MPM разбивает материал на точки и решает основные уравнения на фоновой сетке, которая дискретизирует доменное пространство. Во время симуляции точки могут перемещаться по сетке. MPM является улучшением по сравнению с другими хорошо зарекомендовавшими себя численными методами, такими как метод конечных элементов (FEM), поскольку он может моделировать большие деформации и, следовательно, может моделировать механические проблемы от начала до конечного результата.
Он может стать предпочтительным числовым инструментом для анализа многих инженерных проблем.Тем не менее, в этом тезисе было продемонстрировано, что производительность MPM часто была далека от требуемого уровня точности, чтобы считаться надежным методом для обеспечения количественного анализа инженерных проблем. В этой диссертации версия неявного решения MPM была взята в качестве отправной точки для исследования и решения ее текущих основных недостатков, то есть (i) неточности при вычислении напряжений (колебаний напряжения) и (ii) взаимодействия между телами, е.грамм. грунт и конструкции. Проблема колебаний напряжения хорошо известна в сообществе MPM и связана в основном с материальными точками, пересекающими границы фоновых ячеек, что называется проблемой пересечения ячеек. В этом тезисе было показано, что пересечение клеток действительно является одним из основных источников колебаний. Однако есть и другие аспекты, способствующие наблюдаемым неточностям. В литературе пересечение клеток решается путем создания домена частиц, например в методе обобщенной интерполированной материальной точки (GIMP).
В этой диссертации было показано, что основные проблемы также включают (i) использование градиентов линейной функции формы (SF) для расчета деформаций (материальных точек) и (ii) негауссовские численные квадратуры для интегрирования жесткости материала. При использовании GIMP интеграция ухудшается. Чтобы уменьшить неточности, вызванные интеграцией, была разработана методика двойного отображения (DM), которая уменьшает ошибки при интегрировании узловых жесткостей. Показано, что это также хорошо работает с GIMP (метод DM-G).Кроме того, DM был объединен с методом лагранжевой интерполяции, который использует более крупную область решения (через комбинацию фоновых ячеек для формирования пятен) для увеличения напряжений, вычисленных в материальных точках (методы DM-C или DM-GC). Разработанные методы позволили значительно повысить точность и стабильность моделируемых задач. Это улучшение позволит более надежно использовать более продвинутые конститутивные модели. Взаимодействие тел полезно при моделировании больших деформаций, хотя MPM может приблизительно моделировать контакт без специальной обработки.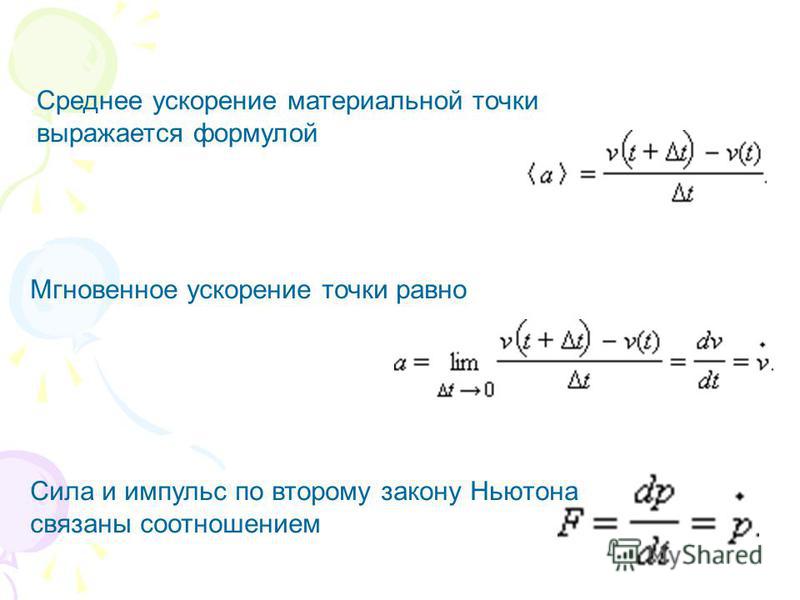
Алгоритм контакта MPM был первоначально предложен другими исследователями для схем явного интегрирования по времени, но метод не был доступен для схемы неявного интегрирования по времени. Неявная контактная схема была разработана на основе исходной (явной) контактной формулировки для расчета изменения узловой скорости во время итерационной процедуры Ньютона-Рафсона. Показано, что результаты, полученные с помощью этой контактной методологии, столь же точны, как и результаты, вычисленные с использованием явной схемы, хотя, как правило, с большим временным шагом.Кроме того, было замечено, что в большинстве случаев неявное моделирование контактов анализируется быстрее, чем явное моделирование. Однако контактные нагрузки, вычисленные с помощью этого метода, и развиваемые внутренние силы несовместимы (т. Е. Не равны), что снижает энергосбережение и остается проблемой, требующей решения. Анализ проблемы представлен как первый шаг к решению. Одна из проблем заключается в том, что любой метод, использующий постоянный контакт и внутренние силы, чувствителен к колебаниям напряжения, что может привести к крайне нереалистичным контактным силам.
Используя усовершенствования, разработанные в этой диссертации (т.е. DM-GC в сочетании с алгоритмом контакта), были успешно смоделированы проблемы взаимодействия грунт-конструкция и оползни. Включение контактного алгоритма в модель позволило смоделировать развитие сложного механизма разрушения во время разрушения откосов. Воздействие на соседние конструкции было реалистичным и отражало ожидаемое поведение, такое как скольжение и вращение жестких элементов. Было продемонстрировано, что (i) точность в MPM была улучшена за счет комбинации нескольких (существующих и новых) методов, (ii) методы, разработанные для явной схемы (или других численных методов), могут быть преобразованы и введены в неявный MPM. , поддерживая в максимально возможной степени согласованность рецептуры, и (iii) улучшая различные аспекты рецептуры, можно получить более реалистичное моделирование.Работа, представленная в этой диссертации, включает несколько шагов, способствующих совершенствованию MPM, что приведет к его использованию в инженерной практике.
Средняя скорость | Определение средней скорости, формула и разность
Термин «движение» можно описать с помощью некоторых физических величин, таких как скорость, скорость, расстояние, смещение и ускорение. Правильное описание движения было дано сэром Исааком Ньютоном. Все эти величины описываются одним параметром – временем.Здесь мы обсуждаем среднюю скорость и ее математическое представление вместе с графическим представлением.
Определение средней скорости
Среднее значение слова просто означает отношение суммы количеств к общему количеству количеств. В физике используется другой подход. Теперь, прежде чем понимать среднюю скорость, давайте разберемся, что такое скорость и что такое скорость, и как эти два понятия связаны.
Скорость объекта относится к изменению положения этого объекта во времени.С другой стороны, скорость – это не что иное, как скорость, определяемая по отношению к направлению, в котором движется объект.
Мы подробно рассмотрим разницу между скоростью и скоростью, а пока вернемся к средней скорости.
Теперь средняя скорость согласно определению – это отношение смещения объекта от точки a к точке b ко времени, которое потребовалось, чтобы сделать это перемещение от точки a к точке b. Можно отметить, что мы используем термин движение вместо расстояния, чтобы подчеркнуть направление.
Алгебраически средняя скорость определяется как, v = d / t
, где d – смещение, а t – время, затраченное на это смещение.
Для короткого промежутка времени среднюю скорость можно рассчитать следующим образом:
va = [(y0 + Δy) −y0) / [Δt]]
, где y0 – положение объекта в момент времени t, а (y0 + Δy) – его положение в том же направлении после увеличения времени на Δt.
Когда мы берем предел Δt → 0, тогда он становится dy / dt, средняя скорость превращается в мгновенную скорость в момент времени t.
Когда объект претерпевает изменение скорости в разное время, средняя скорость определяется как общая сумма всех скоростей в разных случаях, деленная на общее время. Например, если объект имеет разные скорости v1, v2, v3, vn, в моменты времени t = t1, t2, t3, tn, то средняя скорость определяется как
va = [v1 + v2 + v3 … … + вн] / [п].
Разница между средней скоростью и средней скоростью
Ранее мы объяснили, что такое скорость и что такое скорость, и в чем разница между ними.
Скорость – это скалярная величина, а скорость – это векторная величина.
Теперь, например, мы говорим о машине, движущейся со скоростью 80 миль в час, без привязки к ее направлению, тогда мы говорим о ее скорости. Если мы говорим, что автомобиль движется со скоростью 80 миль в час к северо-востоку, то мы имеем в виду его скорость. Время всегда будет скалярной величиной, а направление смещения будет направлением скорости.
Давайте рассмотрим другой пример, чтобы лучше понять эту концепцию.
Возьмем, к примеру, машину, движущуюся на восток со скоростью 80 км в час в течение 2 часов и с той же скоростью в течение одного часа, но в направлении на запад, противоположном предыдущему.
Теперь общее пройденное расстояние составляет 80 × 2 + 80 × 1 = 180 км, а общее время составляет 3 часа. Следовательно, средняя скорость 1803 = 80 км в час. Но когда вы рассчитываете смещение автомобиля, чистое смещение составляет 80 × 2 – 80 × 1 = 80 км на восток. Следовательно, средняя скорость на восток составляет 803 = 20 км в час.
Формула средней скорости
Когда мы берем среднее значение заданного числа скоростей, оно называется средней скоростью. Средняя скорость – это смещение объекта во времени. Чтобы найти среднюю скорость объекта, мы делим пройденное расстояние на прошедшее время. Мы знаем, что скорость – это векторная величина, а среднюю скорость можно найти, разделив смещение на время.
Единицы, используемые для скорости, могут быть выведены из ее определения, то есть метры в секунду (стандартная единица СИ) или любые единицы измерения расстояния в любую единицу времени.
Если скорость тела непрерывно изменяется в течение определенного периода времени, может быть очень полезно определить среднюю скорость этого объекта, чтобы получить представление о его полном путешествии.
Формула средней скорости Математическое описание
Дается Vav. Формула средней скорости включает полное смещение и общее время, затраченное на это смещение.
Для любых позиций указаны xi и xf вместе с соответствующими временными интервалами ti и tf, мы используем формулу, приведенную ниже
\ [{v_ {av}} = \ frac {{{x_f} – {x_i }}} {{{t_f} – {t_i}}} \]
Где xi = исходное положение,
xf = конечное положение,
tf –ti = временной интервал
Определение средней скорости
Для расчета средней скорости сначала нам нужно узнать чистое смещение данного объекта в течение всего его движения.
Начальное направление движения объекта, указанное в вопросе, принимается за его направление для всего курса, пока оно не указано.
Следующая диаграмма поясняет концепцию средней скорости.
Предположим, что объект движется на расстояние d1 в заданный момент времени t1, d2 за время t2 и d3 за время t3, как показано выше. Следует знать, что пройденные расстояния не совпадают. d1 + d2 + d3 – это общее расстояние, но не чистое смещение.Чистое смещение – это проекции d2 и d3 в направлении d1, равны d2 + d3 и, следовательно, чистое смещение равно d1 + d2 + d3. Следовательно, в приведенном выше случае средняя скорость может быть найдена как,
Vav = [d1 + d2 + d3] / [t1 + t2 + t3]
и в целом
Vav = [d1 + d2 +. … + dn] / [t1 + t2 + …. + tn].
Здесь следует отметить одну вещь: если скорость, обозначенная на диаграмме, принимает форму тупого угла, то указанная скорость будет иметь отрицательные значения.
Величина средней скорости
Векторные величины всегда имеют направление и величину, и, поскольку мы определили скорость как векторную величину, она имеет как величину, так и направление. Если в любом случае направление объекта игнорируется, за точку отсчета средней скорости берется величина средней скорости. Здесь следует помнить, что при вычислении средней скорости для данного объекта, где данные о скоростях были даны для разных интервалов времени, вам нужно игнорировать направление не при вычислении, а только на заключительном этапе.
Теперь вспомните формулу, которую мы вывели для вычисления средней скорости в предыдущем разделе.
Средняя скорость
Для объекта, который имеет n скоростей в n последовательных временных интервалах, величина средней скорости может быть задана как,
Величина Vav = [d1 + d2 + ..
.. + dn] / [t1 + t2 + …. + tn]
Средняя угловая скорость
До сих пор мы обсуждали средние скорости в случае линейных движений, т.е.е. объекты, движущиеся от или к заданной точке на прямой. Но изучение кругового движения не менее важно. При круговом движении объект перемещается вокруг точки по круговой траектории. Лучшим примером этого является движение вращающихся колес.
В случае кругового движения можно определить термин, называемый угловой скоростью. Угловая скорость может быть измерена как угол, под которым объект совершает круговое движение за единицу времени. Обычно мы обозначаем угловую скорость греческой буквой ω.Направление угловой скорости ограничено по часовой стрелке или против часовой стрелки. Эталон будет называться угловой скоростью в случае отсутствия направления.
Следовательно, определение средней угловой скорости таково:
ω = θ / t,
, где θ – угол, повернутый за время t
Когда мы говорим об угловой скорости, есть только два возможных результата: вычисление средней скорости проще.
Это либо два положительных, либо отрицательных.Обычно направление против часовой стрелки считается положительным, а направление по часовой стрелке – отрицательным. Базовая единица угловой скорости – радианы в единицу времени, чаще всего радианы в секунду. Следует иметь в виду, что один оборот означает покрытие угла в 2π радиан.
Также и в этом случае, когда разные угловые скорости возникают в разное время, средняя угловая скорость определяется по данной формуле.
ωav = [θ1 + θ2 + …. + θn] / [t1 + t2 + …. + tn] (если временные интервалы идут подряд.)
Измерение потока с использованием метода площади скорости
Создано Моникой З. Брукнер, Государственный университет Монтаны, Бозман
Что такое Stream Gaging?Щелкните изображение, чтобы увеличить.
Измерение потока – это метод, используемый для измерения расхода или объема воды, проходящей через канал в единицу времени в ручье.
Высота воды в канале ручья, известная как высота ступени или манометра, может использоваться для определения стока в ручье.При использовании вместе с измерениями скорости и площади поперечного сечения высота ступени может быть связана с расходом потока. Если используется водослив или желоб (устройства, обычно сделанные из бетона, расположенные в русле потока, которые имеют постоянную, известную форму и размер), математические уравнения, основанные на форме водослива или желоба, могут использоваться в сочетании с высотой сцены, что отрицает необходимость измерения скорости.
Щелкните изображение, чтобы увеличить.
Измеритель тока, подобный приведенному выше, можно использовать для измерения скорости воды, движущейся через канал. При помещении в канал гребной винт измерителя вращается со скоростью, пропорциональной скорости воды. Некоторые измерители тока записывают количество оборотов с помощью счетчика, в то время как другие издают щелкающие звуки для заданного количества оборотов.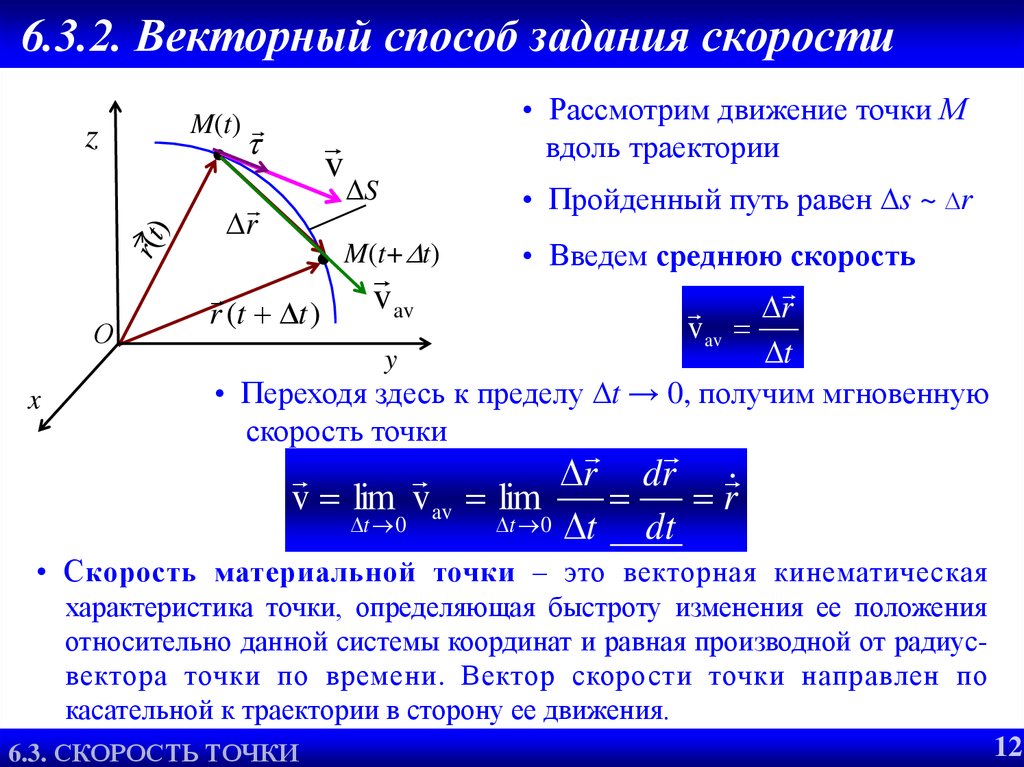
Как упоминалось выше, измерение потока может быть выполнено путем измерения высоты и скорости предметного столика в серии точек в поперечном сечении потока или путем создания желоба или водослива и регистрации высоты предметного столика.Высота столика может быть измерена с помощью линейки, датчика давления или успокоительного колодца, подключенного к регистратору данных. Более подробно методы измерения потоков будут рассмотрены ниже.
Измерительный столик и скорость для определения расхода с помощью метода «скорость-площадь»
Эта оценочная кривая относится к ручным измерениям высоты и скорости ступени для определения расхода (Q). Значения расхода по оси ординат были получены путем измерения скорости воды в канале ручья в наборе точек на поперечном разрезе потока за несколько периодов отбора проб.Скорость (измеренная измерителем тока в метрах в секунду) умножалась на площадь поперечного сечения канала (измерялась в квадратных метрах) для определения расхода (в кубических метрах в секунду или кумеках).
К точкам была нанесена линия наилучшего соответствия, чтобы получить уравнение, по которому можно определить расход в зависимости от высоты ступени.
Расход или объем воды, текущей в потоке в течение заданного интервала времени, можно определить с помощью уравнения:
Q = AV,
где Q – расход (объем / единица времени – e.грамм. м 3 / с, также называемые кумеки), A – площадь поперечного сечения потока (например, m 2 ), а V – средняя скорость (например, м / с).
Скорость воды в ручье обычно измеряется с помощью измерителя тока. Счетчики тока обычно состоят из гребного винта или горизонтального колеса с прикрепленными к нему небольшими конусообразными чашками, которые наполняются водой и поворачивают колесо при помещении в проточную воду. Число оборотов гребного винта или колесно-чашечного механизма соответствует скорости воды, текущей в ручье.Вода, текущая в потоке, подвергается трению как со стороны русла потока, так и со стороны воздуха над потоком.
Таким образом, при измерении скорости воды обычно измеряют поток на 0,6-кратной общей глубине, которая обычно представляет собой среднюю скорость потока в ручье. Это достигается путем прикрепления измерителя тока к калиброванной по высоте штанге. Стержень также можно использовать для измерения высоты ступени ручья. Если измеритель тока недоступен, для измерения скорости можно использовать другой метод, известный как метод поплавка.Хотя этот метод менее точен, он требует ограниченного и легкодоступного оборудования. Чтобы измерить скорость с помощью метода поплавка, нужно просто измерить время, которое требуется плавающему объекту (например, апельсиновой корке), чтобы пройти измеренное расстояние. Затем скорость рассчитывается путем деления пройденного расстояния на время, необходимое для прохождения этого расстояния.
Скорость также меняется в пределах поперечного сечения потока, где берега ручья связаны с большим трением и, следовательно, с более медленным движением воды.Таким образом, необходимо проводить измерения скорости вдоль поперечного сечения потока.
Поскольку русла ручья редко бывают прямыми, полезно измерить скорость на «среднем» участке протока (например, среднюю ширину и глубину) с одним каналом, относительно ровным руслом ручья с небольшим количеством растительности и камней и небольшим количеством задних водоворотов. которые затрудняют движение измерителя тока.
Расход измеряется путем интегрирования площади и скорости каждой точки поперек потока; то есть поток делится на секции в зависимости от того, где были произведены измерения скорости и высоты ступени в поперечном сечении потока.Умножив площадь поперечного сечения (ширина секции x высота ступени) на скорость, можно рассчитать расход для этой секции потока. Расход из каждой секции может быть добавлен для определения общего расхода воды из ручья.
Нагнетание и высота ступени часто эмпирически связаны, и эту взаимосвязь можно прояснить с помощью кривой оценки. Расчетная кривая строится путем графического отображения нескольких полученных вручную измерений расхода (например, измеренных с использованием метода, описанного выше) с соответствующей высотой ступени.
Кривая наилучшего соответствия соответствует этим точкам данных, а уравнение линии соответствует взаимосвязи между стадией и сбросом. Чем больше количество измерений, тем надежнее будет оценочная кривая для определения расхода на основе данных стадии.
Измерение расхода с помощью водослива
Расход в небольших ручьях можно удобно измерить с помощью водослива. Водослив – это небольшая плотина с водосбросом, обычно сделанная из эрозионно-стойкого материала, такого как бетон, определенной формы.Две распространенные формы водослива – это V-образный паз 90 ° или простой прямоугольный вырез. Этот метод измерения расхода включает создание плотины сразу после водослива. Эта плотина накапливается в водосливе, что приводит к более или менее постоянной высоте сцены (например, бассейн с более застойной водой без затруднений с определением высоты из-за волн или ряби). Используя высоту воды в водосливе, можно определить расход, используя одно из следующих эмпирически выведенных уравнений:
Прямоугольный водослив:
Q = 3.
33 (L-0,2H) H 3/2 , для измерений в футах;
Q = 1,84 (L-0,2H) H 2/3 , для измерений в метрах.
Водослив с V-образным пазом 90 °:
Q = 2,5H 5/2 , для измерений в футах;
Q = 1,379H 5/2 , для измерений в метрах.
Q представляет собой расход (футы 3 / с или м 3 / с), L – длина гребня водослива (футы или м), а H – высота воды в затонах / водосливных сооружениях.Как видите, эти уравнения исключают необходимость измерения скоростей в точках и, как правило, более надежны, поскольку бетонная конструкция водослива сопротивляется изменению формы канала, что является мешающим фактором при использовании метода площади скорости для определения расхода.
Уравнение Мэннинга
Простое уравнение, известное как уравнение Маннинга, можно использовать для оценки скорости воды в открытом канале. Уравнение Маннинга:
V = 1.
49R 2/3 S 1/2 / n , для измерений в футах
или
V = R 2/3 S 1/2 / n , для измерений в метрах,
где V – средняя скорость (фут / с или м / с), R – гидравлический радиус (отношение площади поперечного сечения потока в футах 2 или м 2 к смоченному периметру в футах или м-см. диаграмму для определения этого фактора), S – градиент энергии или наклон водной поверхности, а n – коэффициент шероховатости Мэннинга (рассчитанный на основе опубликованных значений, некоторые из которых показаны в таблице ниже).
(значения из Fetter, 2001). Анализ результатов Измерения расхода с использованием метода площади скорости и площади без использования водослива дают хорошую оценку расхода и расхода в ручье. Однако этот метод предполагает несколько вещей, в том числе постоянную площадь поперечного сечения (что не всегда так, поскольку потоки являются эрозионными, динамическими системами), сильную взаимосвязь между высотой ступени и расходом и небольшую человеческую ошибку при измерении скорости, ступени.
высота и площадь поперечного сечения.Водослив обеспечивает более надежное измерение из-за согласованности площади поперечного сечения канала и глубины, но уравнения, связанные с измерениями расхода водослива, были получены эмпирическим путем, и, таким образом, также могут иметь связанную с ними ошибку из-за изменчивости между системами водотока. В любом случае, чем больше будет измерений для построения кривой оценок, тем лучше, поскольку будет обеспечен больший диапазон измерений. Кроме того, имейте в виду, что измерения кривой рейтингов могут соответствовать ряду линий / уравнений, в зависимости от факторов окружающей среды, таких как время таяния снега, когда расход может быстро увеличиваться, или время засухи, когда расход может быть неизмеримым с помощью этого метода.
- Феттер, К.В. (2001). Прикладная гидрогеология. 4-е изд. Нью-Джерси: Прентис-Холл. 598 с.
- Weight, W.D. и Sonderegger, J.L. (2001). Руководство по прикладной полевой гидрологии. Нью-Йорк: McGraw Hill Publishing Co., 608 стр.
Нью-Йорк: McGraw Hill Publishing Co., 608 стр.- USGS Stream-Gaging Program – эта страница, размещенная на USGS, предоставляет подробное объяснение того, как выполняется потоковая регистрация.
- USGS Измерения расхода на измерительных станциях – по этой ссылке можно загрузить техническое руководство о том, как получить измерения расхода на измерительных станциях.
- USBR Water Measurements – на этом веб-сайте представлена информация об акустических расходомерах и преобразователях, включая описание, калибровку, сильные стороны, ограничения и техническое обслуживание каждого устройства.
- USGS – Как измеряется поток – эта страница, размещенная на сервере USGS, содержит краткую информацию об измерении потока, и ее можно использовать для предоставления учащимся краткого обзора процесса.
- Stream Gaging Lab – это лабораторное упражнение из Университета Колорадо в Боулдере, которое включает инструкции и дополнительные вопросы по измерению расхода воды поплавковым методом и методом площади скорости.
- USGS Поток потоков в реальном времени – этот сайт, созданный USGS, предоставляет данные в реальном времени о потоках на станциях мониторинга по всей территории Соединенных Штатов. Эти данные можно использовать для проведения лабораторных упражнений без физического измерения расхода воды (например, без необходимости оборудования и перехода к ручью).
- Количественная оценка основного стока подземных вод и улучшение математических навыков с помощью упражнения «Поток-расход». Представлено двухэтапное упражнение из семинара SERC по гидрогеологии, в котором учащиеся определяют количественный сток стока и используют данные для определения основного стока подземных вод.Сначала они используют утомительные ручные вычисления для вычисления разряда; затем разработать собственные электронные таблицы для более эффективного и точного выполнения расчетов. Наконец, учащиеся собирают полевые данные и используют свои электронные таблицы для определения разряда и расчета некоторых простых статистических данных.
- Разгрузка и перенос наносов в полевых условиях. В этой количественной полевой деятельности от SERC «Обучение количественным навыкам в модуле наук о Земле» студенты собирают полевые данные о геометрии канала, скорости потока и материалах дна.Используя эти данные, они применяют уравнения сопротивления потоку (произведение Мэннинга и крутизны глубины) и отношения переноса наносов (кривая Шилдса) для оценки полного стока и определения того, достаточно ли потока для мобилизации пласта. Это упражнение требует, чтобы студенты использовали теоретические и эмпирические уравнения, полученные в классе в контексте полевой задачи. Один должен выделить 2 часа в поле и предполагать дополнительные 2-4 часа студенческой работы вне класса.
% PDF-1.4
%
1 0 объект
> поток
2016-10-06T19: 54: 27-04: 00TeX2021-10-13T06: 18: 37-07: 002021-10-13T06: 18: 37-07: 00 Это pdfTeX, версия 3.14159265-2.6-1.40.16 (TeX Живая 2015 / Debian) Kpathsea версия 6.2.1iText 4.2.0 по 1T3XTFalseuuid: b27cd1ce-9af2-4364-b243-12b3416387bdxmp.
did: 0F41B510DBB5E6118EB9969C221E23D9xmp.did: 0F41B510DBB5E6118EB9969C221E23D9
5 / H_0Ía
XWrsN “5ЁAmgTzb &> kT3 $> 5dow – zgN ٻ oϿ |; ѹn
χ / _Ѩ? 0răI`_o & ϴDXRT {v & ķG (aԙ6G @ ύ ۨ qaћD * 9 ~! z,; 6 = JZLK \Когда можно использовать понятие материальной точки. Материальная точка
ВОПРОСЫ
1. Имеет ли материальная точка массу? Есть ли размеры?
Под материальной точкой в физике понимается тело, размерами которого можно пренебречь в условиях данной задачи. Материальная точка имеет определенную массу, но нулевые (очень маленькие) размеры.
2. Материальная точка – это реальный объект или абстрактное понятие?
Материальная точка – понятие абстрактное, потому что в природе все тела имеют определенный размер.
3. С какой целью используется понятие «материальная точка» ?
Concept материальная точка используется для упрощения условий и решения проблем. Если пренебречь размерами реального тела, то нет необходимости учитывать движение тела при его движении вокруг своей оси (летящий мяч) или движение каких-то частей тела (колеса автомобиля), если нас интересует, как быстро движется тело.
4. В каких случаях движущееся тело обычно считается материальной точкой?
В этом случае движущееся тело можно рассматривать как материальную точку, если его размеры намного меньше расстояния, на которое оно перемещается.
5. Приведите пример, показывающий, что одно и то же тело может считаться материальной точкой в одной ситуации, но не в другой.
Если рассматривать, например, движение автомобиля при движении из города A в город B, то в этом случае при определении средней скорости автомобиля его можно рассматривать как материальную точку, но если мы интересуетесь движением автомобиля более подробно, оказывается, что при движении автомобиля, например, передние и задние колеса движутся по-разному (не синхронно) из-за неровностей дороги.
6. При каком движении тело может считаться материальной точкой, даже если пройденные им расстояния сравнимы с его размерами?
Если тело движется вперед.
7. Что называется материальной точкой?
Материальная точка – абстрактное понятие, обозначающее тело, размеры которого не играют роли в условиях рассматриваемой задачи.
8. В каком случае можно указать положение движущегося тела с помощью одной координатной оси?
Если тело движется по прямой.
9. Что такое система отсчета?
Система отсчета – это опорное тело, связанная с ним система координат и инструмент для измерения времени, относительно которого учитывается движение материальных точек или тел.
УПРАЖНЕНИЯ
2. Самолет летит по маршруту Москва – Владивосток. Может ли диспетчер, наблюдая за его движением, рассматривать самолет как материальную точку? пассажир в этом самолете?
С точки зрения диспетчера, если рассматривать только маршрут полета самолета, то это возможно, но если в воздухе есть другой самолет или он садится – нет.С точки зрения пассажира, при полете по маршруту – да, а при движении пассажира внутри самолета – нет.
3. Когда говорят о скорости автомобиля, поезда и других транспортных средств, эталонное тело обычно не указывается. Что в данном случае подразумевается под эталонным телом?
Базовое тело в данном случае обычно означает поверхность Земли.
4. Мальчик стоял на земле и смотрел, как его младшая сестра каталась на карусели. После катания девушка рассказала брату, что он сам, дома и деревья быстро пронеслись мимо нее.Мальчик, напротив, стал утверждать, что он вместе с домами и деревьями неподвижен, а его сестра двигается. В отношении каких опорных тел девочка и мальчик рассматривали движение? Объясните, кто прав в споре.
Оба верны. Мальчик выбрал систему координат относительно себя (он был неподвижен), а девушку относительно себя (она была на качелях).
5. Относительно какого эталонного тела учитывается движение, когда говорят:
а) скорость ветра 5 м / с?
б) бревно плывет по реке, поэтому его скорость равна нулю;
в) скорость дерева, плывущего по реке, равна скорости потока воды в реке;
г) любая точка на колесе движущегося велосипеда описывает круг;
д) Входит ли солнце утром на востоке, движется ли по небу днем и заходит вечером на западе?
а) относительно поверхности Земли; б) относительно проточной воды; в) относительно поверхности Земли; г) относительно центра (оси) колеса; д) относительно поверхности Земли.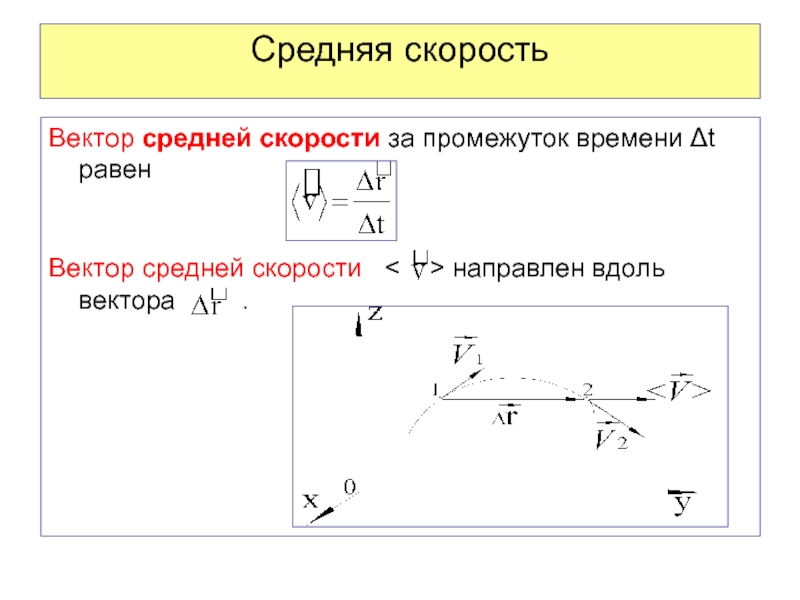
Чтобы описать движение тела, вам нужно знать, как движутся его различные точки. Однако в случае поступательного движения все точки тела движутся одинаково. Поэтому для описания поступательного движения тела достаточно описать движение одной из его точек.
Также во многих задачах механики нет необходимости указывать положение отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то это тело можно описать как точку.
ОПРЕДЕЛЕНИЕ
Материальная точка называется телом, размерами которого в этих условиях можно пренебречь.
Слово «материал» здесь подчеркивает отличие этой точки от геометрической. Геометрическая точка не имеет физических свойств. Материальная точка может иметь массу, электрический заряд и другие физические характеристики.
Одно и то же тело в одних условиях можно считать материальной точкой, а в других – нет.Так, например, рассматривая движение корабля из одного морского порта в другой, корабль можно рассматривать как материальную точку.
Однако при изучении движения шара, катящегося по палубе корабля, корабль нельзя рассматривать как материальную точку. Движение зайца, убегающего от волка по лесу, можно описать, приняв зайца за материальную точку. Но нельзя же считать зайца материальной точкой, описывая его попытки спрятаться в норе. При изучении движения планет вокруг Солнца их можно описать материальными точками, а при суточном вращении планет вокруг своей оси такая модель неприменима.
Важно понимать, что материальных точек в природе не существует. Материальная точка – это абстракция, модель для описания движения.
Примеры решения задач по теме «Существенная точка»
ПРИМЕР 1
ПРИМЕР 2
| Упражнение | Укажите, в каком из следующих случаев исследуемое тело можно принять за материальную точку: а) рассчитать давление трактора на землю; б) рассчитать высоту, на которую взлетела ракета; в) рассчитать работу при подъеме плиты перекрытия известной массы в горизонтальном положении на заданную высоту; г) определить объем стального шара с помощью мерного цилиндра (стакана). |
| Ответ | а) при расчете давления трактора на почву трактор нельзя принимать за материальную точку, так как в этом случае важно знать площадь поверхности гусениц; б) при расчете высоты подъема ракеты ракету можно рассматривать как материальную точку, так как ракета движется поступательно и расстояние, пройденное ракетой. намного больше, чем ее размер; в) в этом случае плиту перекрытия можно рассматривать как материальную точку.поскольку он совершает поступательное движение, и для решения задачи достаточно знать смещение его центра масс; г) при определении объема мяча. мяч нельзя рассматривать как материальную точку, потому что размер мяча важен в этой задаче. |
ПРИМЕР 3
| Упражнение | Можно ли принять Землю за материальную точку при расчете: а) расстояния от Земли до Солнца; б) путь, пройденный Землей по орбите вокруг Солнца; в) длина экватора Земли; г) скорость движения экваториальной точки при суточном обороте Земли вокруг оси; д) скорость обращения Земли по орбите вокруг Солнца? |
| Ответ | а) в этих условиях Землю можно принять за материальную точку, так как ее размеры намного меньше расстояния от нее до Солнца; д) в этом случае Землю можно принять за материальную точку, так как размеры орбиты намного больше размеров Земли. |
Что называется механическим движением?
Механическое движение – это изменение относительного положения тел или их частей в пространстве с течением времени.
Что называется системой отсчета?
Система отсчета – набор систем координат и часов, связанных с телом отсчета.
Что такое траектория движения? Способ?
Линия, описывающая материальную точку при движении, называется траекторией.Путь – это длина пути.
Что называется радиус-вектором?
Радиус-вектор – это вектор, соединяющий начало координат O с точкой M.
Что называется скоростью движения материальной точки? Как направлен вектор скорости?
Скорость – это векторная величина, которая определяет как скорость движения, так и его направление в данный момент времени. Вектор направлен по касательной в заданную точку траектории.
Что называется ускорением материальной точки? Как направлен вектор ускорения?
Ускорение – это векторная величина, которая характеризует скорость изменения скорости по величине и направлению.
Направлен по направлению скорости или перпендикулярно.
Что называется угловой скоростью? Как направлен вектор угловой скорости?
Угловая скорость, направленная вдоль оси вращения, т.е. по правилу правого винта
Что называется угловым ускорением? Как направлен вектор углового ускорения?
Вектор направлен по оси вращения в том же направлении, что и при ускоренном вращении, и в противоположном направлении при замедлении
Что характеризует нормальное ускорение?
Нормальное ускорение – характеризует скорость изменения скорости в направлении, перпендикулярном траектории.
Что характеризует тангенциальное ускорение?
Тангенциальное ускорение характеризует скорость изменения скорости по модулю, направленную по касательной к траектории
Что такое сила тяжести и масса тела? В чем разница между силой тяжести и массой тела?
Гравитация – это сила, с которой Земля притягивает тела к себе.
F = мг. Вес тела – сила, с которой тело давит на опору или растягивает подвеску за счет силы тяжести.P = мг. Сила тяжести действует всегда, а вес тела проявляется только тогда, когда на тело действуют другие силы помимо силы тяжести.
Что называется модулем Юнга?
Модуль Юнга численно равен напряжению при относительном удлинении, равном 1. Зависит от материала корпуса.
Что такое силы инерции?
Силы инерции – это силы, вызванные ускоренным движением неинерциальной системы отсчета (NSO) относительно инерциальной системы отсчета (IFR).
Что называется моментом силы относительно неподвижной точки? Как направлен вектор момента силы?
Момент силы относительно точки называется векторной величиной, равной: M =.
Что называется плечом силы?
Плечо силы – это кратчайшее расстояние между действием силы и точкой О.
Что называется моментом силы относительно неподвижной оси?
Момент силы вокруг оси – это скалярная величина, равная произведению модуля силы F на расстояние d от прямой линии, на которой лежит вектор F, до оси вращения.
Что называется парой сил? Какой момент у пары сил?
Пара сил – это рычаг. Сумма моментов силы равна нулю
Что называют моментом инерции тела? От чего это зависит?
Момент инерции тела – это мера инерции тела во вращательном движении, зависит от массы тела, ее распределения в объеме тела и выбора оси вращения.
Какая работа выполняется при вращательном движении?
Угол поворота
Что такое механическая работа?
Что называется механической энергией?
Энергия – универсальная мера всех форм движения материи и взаимодействия
Какова кинетическая энергия тела?
Что называется угловым моментом частицы относительно неподвижной точки? Как направлен вектор углового момента?
Момент количества движения материальной точки относительно фиксированной точки O – это физическая величина, определяемая векторным произведением: L ==.Направлено в осевом направлении в направлении, определяемом правилом правого винта
Что называется давлением?
Давление – это скалярная величина, равная силе, действующей на единицу площади, и направлена перпендикулярно.
P = F / S
Что называется резонансом?
Явление резкого увеличения амплитуды вынужденных колебаний вызывается, когда частота движущей силы приближается к частоте, равной или близкой к собственной частоте колебательной системы.
Что такое сублимация?
Процесс ухода молекул с поверхности твердого тела называется сублимацией.
Что называется потенциалом?
Потенциал – это величина, равная потенциальной энергии одиночного положительного заряда. Φ = Вт / q 0.
Что называется силой тока?
Ампер – это заряд, проходящий через единицу площади поперечного сечения за единицу времени.
Что называется стрессом?
Напряжение – это разность потенциалов.U = φ 1 -φ 2, U = A / q
Что такое индуктивность?
Индуктивность тока – это коэффициент пропорциональности между магнитным потоком и величиной тока, который создает этот магнитный поток.
Ф = LI
Что называется резонансом?
Резонанс – это явление резкого увеличения амплитуды вынужденных колебаний, когда частота движущей силы приближается к частоте, равной или близкой к собственной частоте колебательной системы.
КПД теплового двигателя
Короткое замыкание
Возникает при резком увеличении силы тока и уменьшении сопротивления.
Усилие.
Сила – это векторная величина, мера воздействия на данное тело других тел или полей, возникающих во время ускорения и деформации
Сила трения.
Сила трения – это сила, которая возникает при движении или попытке вызвать движение одного тела на поверхности другого и направлена вдоль контакта с поверхностью против движения Стоячая волна в определенной области пространства описывается уравнением … Запишите условие для точек среды, в которых амплитуда колебаний минимальна. Средняя кинетическая энергия молекул идеального газа.
Внешние силы
Внешние силы – это силы неэлектрического характера, которые могут воздействовать на электрический заряд.
Закон всемирного тяготения.
Закон Гука.
Закон Архимеда.
Закон Архимеда: выталкивающая сила, равная весу жидкости или газа перемещаемого тела, действует на тело, погруженное в жидкость или газ.F a = F прядь V t g
Закон Авогадро.
Закон Авогадро: при одинаковых p и T 1 моль любого газа занимает один и тот же объем
Закон Дальтона.
Закон Дальтона: давление смеси газов равно сумме парциальных давлений, создаваемых каждым газом в отдельности.
Закон Кулона.
Сила взаимодействия F между двумя неподвижными зарядами в вакууме пропорциональна зарядам и обратно пропорциональна квадрату расстояния между ними
Закон Видеманна-Франца
λ / γ = 3 (k / e) 2, где λ – теплопроводность, γ – удельная проводимость
Закон Ома для тока в газах
Принцип суперпозиции полей.
Правило Ленца.
Индукционный ток всегда направлен так, чтобы предотвратить причину его возникновения.
Второй закон Ньютона.
Сила, действующая на тело, равна произведению массы тела m и ускорения, передаваемого этой силой: F = ma
Волновое уравнение.
Второй закон термодинамики
Процесс самопроизвольной передачи тепла от холодного тела к горячему невозможен Вектор электрического смещения.
При переходе от одной среды к другой напряженность электрического поля резко изменяется; для характеристики непрерывного электростатического поля вводится вектор электрического смещения (D)
Теорема Штейнера.
Уравнение Бернулли.
Масса.
Масса – мера инерции тела, а также источника и объекта силы тяжести
Модель идеального газа.
Молекулы – материальные точки, не взаимодействуют друг с другом, столкновение упругое
Основные положения МКБ
Все тела состоят из атомов и молекул; молекулы непрерывно движутся и взаимодействуют друг с другом
Основное уравнение МКТ
P = 1 / 3нм 0 В q 2 = 2 / 3nE k
ЭДС – работа внешних сил по перемещению одиночного положительного заряда по электрической цепи ε = C ст / q
Распределение Максвелла.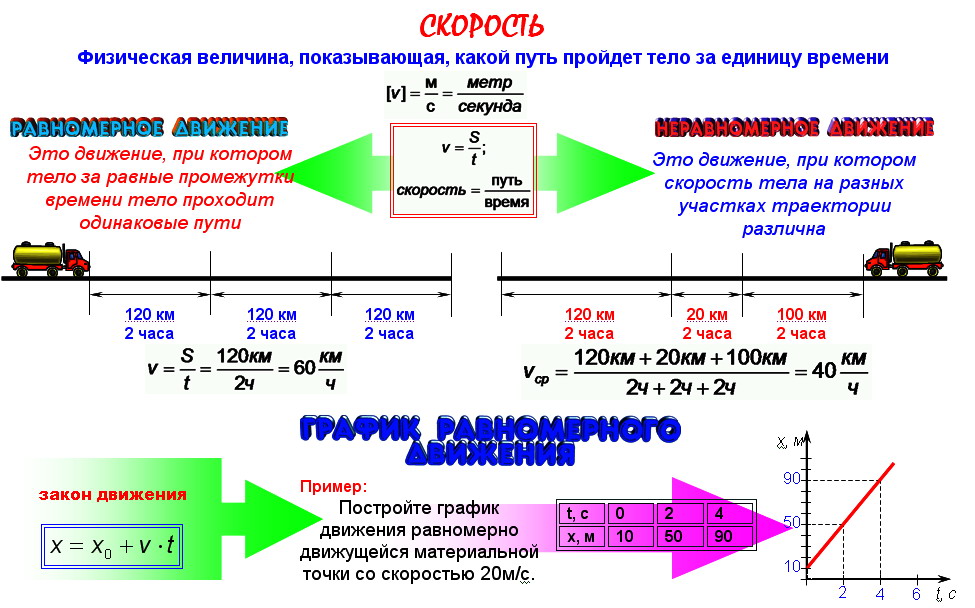
Закон Максвелла о распределении молекул идеального газа по скоростям: в газе, находящемся в равновесии при данной температуре, определенное стационарное распределение молекул по скоростям не изменяется с течением времени.
Гидростатическое давление.
Гидростатическое давление равно:
Барометрическая формула
Феномен Холла.
Явление Холла – это появление электрического поля в проводнике или полупроводнике с током, когда он движется в магнитном поле
Цикл Карно и его эффективность.
Цикл Карно состоит из двух изотерм и двух адиабат.
Циркуляция вектора напряженности электростатического поля.
Циркуляция вектора напряженности электростатического поля численно равна работе, которую электростатические силы совершают, когда одиночный положительный электрический заряд движется по замкнутому пути.
Что называется материальной точкой?
Материальная точка – это тело, размерами которого можно пренебречь по сравнению с расстоянием до другого тела, рассматриваемого в этой задаче.
Концепция материальной точки. Траектория. Путь и движение. Справочная система. Кривая скорость и ускорение. Нормальное и тангенциальное ускорение. Классификация механических движений.
Механика . Механика – раздел физики, посвященный изучению законов простейшей формы движения материи – механического движения.
Механика состоит из трех подразделов: кинематики, динамики и статики.
Кинематика изучает движение тел без учета причин, его вызывающих. Он оперирует такими величинами, как перемещение, пройденное расстояние, время, скорость движения и ускорение.
Динамика исследует законы и причины, вызывающие движение тел, т.е. изучает движение материальных тел под действием приложенных к ним сил. К кинематическим величинам добавляются величины – сила и масса.
V статика исследуют условия равновесия системы тел.
Механизм телом называется изменение его положения в пространстве относительно других тел с течением времени.
Материальная точка – тело, размером и формой которого можно пренебречь в данных условиях движения, если предположить, что масса тела сосредоточена в данной точке. Модель материальной точки – это простейшая модель движения тела в физике.Тело можно считать материальной точкой, если его размеры намного меньше характерных расстояний в задаче.
Для описания механического движения необходимо указать тело, относительно которого считается движение. Произвольно выбранное неподвижное тело, относительно которого рассматривается движение этого тела, называется опорным телом .
Справочная информация – опорное тело вместе с соответствующей системой координат и часами.
Рассмотрим движение материальной точки M в прямоугольной системе координат, поместив начало координат в точку O.
Положение точки M относительно системы отсчета можно задать не только с помощью трех декартовых координат, но и с помощью одной векторной величины – радиус-вектора точки M, проведенной в эту точку из начала координат.
системы координат (рис. 1.1). Если – единичные векторы (единичные векторы) осей прямоугольной декартовой системы координат, то
или зависимость радиус-вектора этой точки от времени
Три скалярных уравнения (1.2) или одно эквивалентное им векторное уравнение (1.3) называются кинематическими уравнениями движения материальной точки .
Траектория материальная точка – это линия, описываемая этой точкой в пространстве во время ее движения (геометрическое место концов радиус-вектора частицы). В зависимости от формы траектории различают прямолинейное и криволинейное движение точки. Если все отрезки траектории точки лежат в одной плоскости, то движение точки называется плоским.
Уравнения (1.2) и (1.3) определяют траекторию точки в так называемой параметрической форме. Роль параметра играет время t. Решая вместе эти уравнения и исключая из них время t, находим уравнение траектории.
Длинный путь материальной точки – это сумма длин всех участков траектории, пройденных точкой за рассматриваемый период времени.
Вектор смещения материальная точка – это вектор, соединяющий начальное и конечное положение материальной точки, т.е.е. приращение радиус-вектора точки за рассматриваемый интервал времени
При прямолинейном движении вектор смещения совпадает с соответствующим участком траектории. Из того факта, что смещение является вектором, следует экспериментально подтвержденный закон независимости движений: если материальная точка участвует в нескольких движениях, то результирующее смещение точки равно векторной сумме ее смещений, совершенных ею за это время. одновременно в каждом из движений отдельно
Для характеристики движения материальной точки введена векторная физическая величина – скорость , значение, которое определяет как скорость движения, так и направление движения в данный момент времени.
Пусть материальная точка движется по криволинейной траектории МN так, что в момент t она находится в точке M, а в момент – в точке N.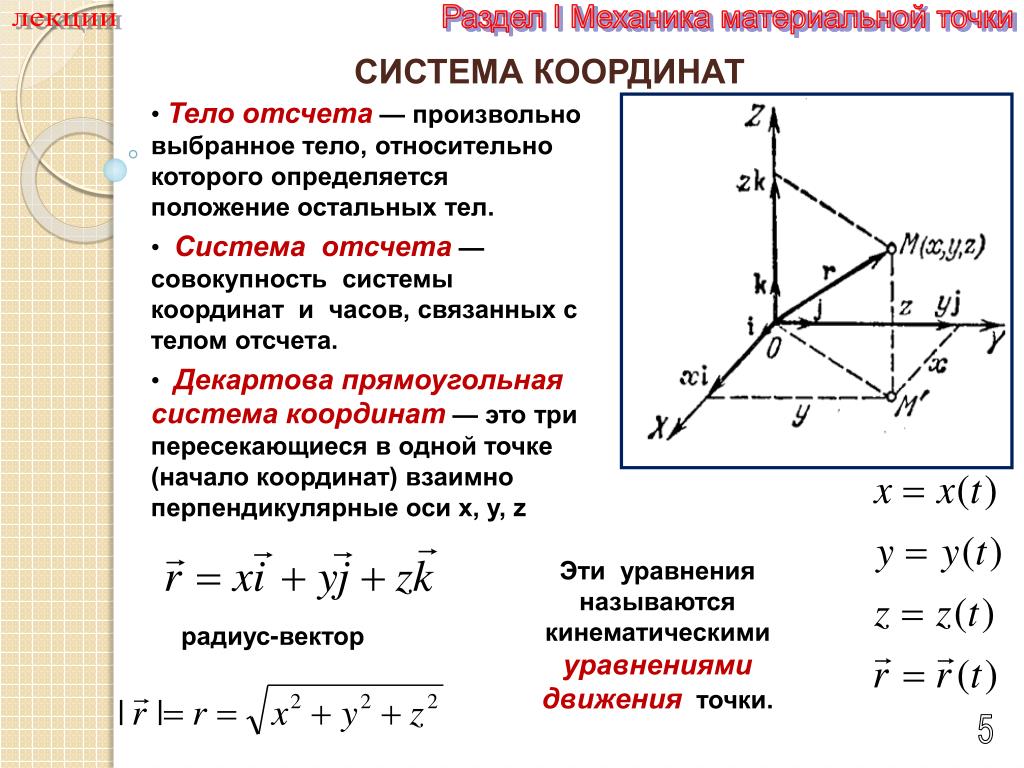
Радиус-векторы точек M и N равны соответственно, а длина дуги МN равна ( Рис. 1.3).
Вектор средней скорости точек на временном интервале от t до t + Δ t называется отношением приращения радиус-вектора точки за этот временной интервал к его значению:
Вектор средней скорости направлен так же, как вектор смещения, т.е.е. по хорде МN.
Мгновенная скорость или скорость в данный момент . Если в выражении (1.5) перейти к пределу, стремящемуся к нулю, то мы получим выражение для вектора скорости m.t. в момент времени t его прохождения через точку M траектории.
В процессе уменьшения значения точка N приближается к точке M, а хорда MN, разворачиваясь вокруг точки M, в пределе совпадает по направлению с касательной к траектории в точке M. Следовательно, вектор и скорость v движущихся точек направлены по касательной траектории в направлении движения.
Вектор скорости v материальной точки может быть разложен на три компонента, направленных вдоль осей прямоугольной декартовой системы координат.
Из сравнения выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на ось прямоугольной декартовой системы координат равны первым производным по времени соответствующих координат точки:
Движение, при котором направление скорости материальной точки не меняется, называется прямолинейным.Если числовое значение мгновенной скорости точки при движении остается неизменным, то такое движение называется равномерным.
Если за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости изменяется с течением времени. Это движение называется неравномерным.
В этом случае часто используется скалярная величина, называемая средней путевой скоростью неровного движения на заданном участке траектории. Он равен числовому значению скорости такого равномерного движения, при котором на прохождение пути затрачивается то же время, что и для данного неравномерного движения:
Потому что только в случае прямолинейного движения с постоянной скоростью по направлению, то в общем случае:
Значение пути, пройденного точкой, может быть представлено графически площадью фигуры, ограниченной кривой v знак равно f ( т ), прямой т знак равно т 1 и т знак равно т 1 и ось времени на графике скорости.
Закон сложения скоростей . Если материальная точка одновременно участвует в нескольких движениях, то результирующее движение по закону независимости движения равно векторной (геометрической) сумме элементарных движений, вызванных каждым из этих движений в отдельности:
Согласно определению (1.6):
Таким образом, скорость результирующего движения равна геометрической сумме скоростей всех движений, в которых участвует материальная точка (это положение называется законом сложения скоростей).
Когда точка движется, мгновенная скорость может изменяться как по величине, так и по направлению. Разгон характеризует скорость изменения модуля и направления вектора скорости, то есть изменение величины вектора скорости в единицу времени.
Вектор среднего ускорения . Отношение приращения скорости к интервалу времени, в течение которого произошло это приращение, выражает среднее ускорение:
Вектор среднего ускорения совпадает по направлению с вектором.
Ускорение или мгновенное ускорение равно среднему пределу ускорения, когда временной интервал стремится к нулю:
В проекциях на соответствующие координаты оси:
При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по криволинейной плоской траектории.Вектор скорости в любой точке траектории направлен по касательной к ней. Предположим, что в точке M траектории скорость была, а в точке M стала 1. В этом случае мы предполагаем, что временной интервал перехода точки на пути от M к M 1 настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Чтобы найти вектор изменения скорости, необходимо определить разность векторов:
Для этого переносим его параллельно самому себе, совмещая его начало с точкой М.Разность двух векторов равна вектору, соединяющему их концы, равному стороне АС МАС, построенной на векторах скорости, как на сторонах.
Разобьем вектор на две составляющие AB и АД, и обе соответственно через и. Таким образом, вектор изменения скорости равен векторной сумме двух векторов:
Таким образом, ускорение материальной точки можно представить как векторную сумму нормального и тангенциального ускорений этой точки
Априор:
где – путевая скорость по траектории, совпадающая с абсолютным значением мгновенной скорости в данный момент.Вектор тангенциального ускорения направлен по касательной к траектории тела.
Если использовать обозначение единичного касательного вектора, то тангенциальное ускорение можно записать в векторной форме:
Нормальное ускорение характеризует скорость изменения скорости по направлению. Рассчитаем вектор:
Для этого проведите перпендикуляр через точки M и M1 к касательным к траектории (рис.1.4) Точка пересечения обозначается буквой O. Для достаточно малого участка криволинейную траекторию можно считать частью окружности радиуса R.
Треугольники MOM1 и MVS подобны, поскольку представляют собой равнобедренные треугольники с одинаковыми углами в вершинах. . Вот почему:
Но тогда:
Переходя к пределу при и учитывая, что в этом случае, находим:
,
Поскольку под углом, направление этого ускорения совпадает с направлением нормали к скорости, т.е.е. вектор ускорения перпендикулярен. Поэтому это ускорение часто называют центростремительным.
Нормальное ускорение (центростремительное) направлено по нормали к траектории к центру ее кривизны O и характеризует скорость изменения направления вектора скорости точки.
Общее ускорение определяется векторной суммой тангенциального нормального ускорения (1.15). Поскольку векторы этих ускорений взаимно перпендикулярны, общий модуль ускорения составляет:
Направление полного ускорения определяется углом между векторами и:
Классификация движений.
Для классификации движений воспользуемся формулой для определения общего ускорения
Давайте представим, что
Следовательно,
Это случай равномерного прямолинейного движения.
Но
2)
Следовательно
Это случай равномерного движения. В данном случае
При v 0 = 0 v t = at – скорость равноускоренного движения без начальной скорости.
Криволинейное движение с постоянной скоростью.
Материальная точка
Материальная точка (частица) – простейшая физическая модель в механике – идеальное тело, размеры которого равны нулю, размеры тела также можно считать бесконечно малыми по сравнению с другими измерениями или расстояния в пределах допущений изучаемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.
На практике под материальной точкой понимается тело с массой, размером и формой которой можно пренебречь при решении этой задачи.
При прямолинейном движении тела одной координатной оси достаточно для определения его положения.
Особенности
Масса, положение и скорость материальной точки в любой момент времени полностью определяют ее поведение и физические свойства.
Последствия
Механическая энергия может храниться материальной точкой только в виде кинетической энергии ее движения в пространстве и (или) потенциальной энергии взаимодействия с полем.Это автоматически означает неспособность материальной точки к деформациям (материальной точкой можно назвать только абсолютно твердое тело) и вращению вокруг собственной оси и изменению направления этой оси в пространстве. В то же время модель движения тела, описываемого материальной точкой, заключающаяся в изменении его расстояния от некоторого мгновенного центра вращения и двух углов Эйлера, задающих направление линии, соединяющей эту точку с центром, чрезвычайно широко используется во многих отраслях механики.
Ограничения
Ограниченное применение концепции материальной точки видно из такого примера: в разреженном газе при высокой температуре размер каждой молекулы очень мал по сравнению с типичным расстоянием между молекулами. Казалось бы, этим можно пренебречь и считать молекулу материальной точкой. Однако это не всегда так: колебания и вращения молекулы являются важным резервуаром «внутренней энергии» молекулы, «емкость» которой определяется размером молекулы, ее структурой и химическими свойствами.В хорошем приближении одноатомную молекулу (инертные газы, пары металлов и т. Д.) Иногда можно рассматривать как материальную точку, но даже в таких молекулах при достаточно высокой температуре наблюдается возбуждение электронных оболочек за счет столкновений молекул, с последующей эмиссией.
Заметки (править)
Фонд Викимедиа. 2010.
- Механизм
- Абсолютно прочный
Посмотреть, что такое “Материальная точка” в других словарях:
ТОЧКА МАТЕРИАЛА – точка с массой.В механике понятие материальной точки используется в тех случаях, когда размер и форма тела не играют роли в изучении его движения, а важна только масса. Материальной точкой можно считать практически любое тело, если … … Большой энциклопедический словарь
ТОЧКА МАТЕРИАЛА – понятие, введенное в механике для обозначения объекта, который рассматривается как точка с массой. Позиция М. т. Н. In pr ve определяется как положение геометрии. очков, что значительно упрощает решение задач по механике.На практике тело можно считать … … Физическая энциклопедия
материальная точка – точка с массой. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет по научно-технической терминологии. 1984] Темы теоретическая механика EN Particle DE materialle Punkt FR point matériel … Пособие технического переводчика
ТОЧКА МАТЕРИАЛА Современная энциклопедия
ТОЧКА МАТЕРИАЛА – В механике: бесконечно маленькое тело.Словарь иностранных слов, входящих в русский язык. Чудинов А.Н., 1910 … Словарь иностранных слов русского языка
Материальная точка – Материальная точка – понятие, введенное в механике для обозначения тела, размером и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Кузов можно считать материальным … … Иллюстрированный энциклопедический словарь
материальная точка – понятие, введенное в механике для объекта бесконечно малых размеров с массой.Положение материальной точки в пространстве определяется как положение геометрической точки, что упрощает решение задач механики. Практически любой орган может … … энциклопедический словарь
Материальная точка – геометрическая точка с массой; материальная точка – это абстрактное изображение материального тела, имеющего массу и безразмерность … Начало современного естествознания
material point – materialusis taškas statusas T sritis fizika atitikmenys: angl.массовая точка; материальный пункт вок. Массенпункт, м; матчасть Пункт, м рус. материальная точка, f; точечная масса, f пранк. точечная масса, м; точечный материал, м … Fizikos terminų žodynas
материальная точка – Точка с массой … Политехнический терминологический толковый словарь
Книги
- Набор столов. Физика. 9 класс (20 таблиц). Учебный альбом из 20 листов. Материальная точка. Координаты движущегося тела. Ускорение.Законы Ньютона. Закон всемирного тяготения. Прямое и изогнутое движение. Движение тела по …
Вязкость – Гипертекст по физике
Обсуждение
определений
Неформально вязкость – это величина, которая описывает сопротивление жидкости потоку. Жидкости сопротивляются относительному движению погруженных в них объектов через них, а также движению слоев с разными скоростями внутри них.
(динамическая) вязкость
Формально вязкость (обозначенная символом η “eta”) – это отношение напряжения сдвига ( F / A ) к градиенту скорости (∆ v x / ∆ z или dv x / dz ) в жидкости.
или
Более обычная форма этой связи, называемая уравнением Ньютона , утверждает, что результирующий сдвиг жидкости прямо пропорционален приложенной силе и обратно пропорционален ее вязкости. Сходство со вторым законом движения Ньютона ( F = мА ) должно быть очевидным.
Или, если вы предпочитаете символы исчисления (а кто нет)…
Единицей вязкости в системе СИ является паскаль-секунда [Па · с], которая не имеет специального названия.Несмотря на самопровозглашенное название международной системы, Международная система единиц мало повлияла на вязкость в международном масштабе. Паскаль-секунда встречается сегодня в научной и технической литературе гораздо реже, чем следовало бы. Самая распространенная единица вязкости – дин-секунда на квадратный сантиметр [дин-с / см 2 ], получившая название пуаз [P] в честь французского физиолога Жана Пуазейля (1799–1869). Десять пуаз равны одной паскаль-секунде [Па с], что делает сантипуаз [сП] и миллипаскаль секунды [мПа с] идентичными.
| 1 Па · с = | 10-пол. |
| 1000 мПа · с = | 10-пол. |
| 1 мПа · с = | 0,01 П |
| 1 мПа · с = | 1 сП |
кинематическая вязкость
На самом деле есть две величины, которые называются вязкостью. Величина, определенная выше, иногда называется динамической вязкостью , абсолютной вязкостью или простой вязкостью , чтобы отличить ее от других величин, но обычно это просто вязкость.Другая величина, называемая кинематическая вязкость (обозначается греческой буквой ν «ню»), представляет собой отношение вязкости жидкости к ее плотности.
Кинематическая вязкость – это мера сопротивления потока жидкости под действием силы тяжести. Его часто измеряют с помощью устройства, называемого капиллярным вискозиметром – в основном это градуированная банка с узкой трубкой на дне. Когда две жидкости равного объема помещаются в одинаковые капиллярные вискозиметры и позволяют течь под действием силы тяжести, более вязкая жидкость протекает через трубку дольше, чем менее вязкая.Капиллярные вискозиметры будут рассмотрены более подробно позже в этом разделе.
Единица измерения кинематической вязкости в системе СИ – квадратных метра в секунду [м 2 / с], не имеющая специального названия. Этот агрегат настолько велик, что используется редко. Более распространенной единицей кинематической вязкости является квадратных сантиметра в секунду [см 2 / с], которому присвоено название Stokes [St] в честь ирландского математика и физика Джорджа Стокса (1819–1903).Один квадратный метр в секунду равен десяти тысячам стоек.
| 1 см 2 / с = | 1 Ст. |
| 1 м 2 / с = | 10,000 см 2 / с |
| 1 м 2 / с = | 10,000 Ст. |
Даже эта единица измерения слишком велика, поэтому наиболее распространенной единицей измерения является, вероятно, квадратных миллиметра в секунду [мм 2 / с] или сантистоксов [сСт].Один квадратный метр в секунду равен одному миллиону сантистоксов.
| 1 мм 2 / с = | 1 сСт |
| 1 м 2 / с = | 1000000 мм 2 / с |
| 1 м 2 / с = | 1000000 сСт |
Stokes – редкий пример слова в английском языке, в котором формы единственного и множественного числа идентичны. Рыба – самый непосредственный пример такого слова.1 рыба, 2 рыбы, красная рыба, синяя рыба; 1 сток, 2 стокса, несколько стоксов, несколько стоксов.
факторов, влияющих на вязкость
Вязкость в первую очередь зависит от материала. Вязкость воды при 20 ° C составляет 1,0020 миллипаскаль секунды (что удобно близко к единице только по совпадению). Большинство обычных жидкостей имеют вязкость порядка от 1 до 1000 мПа с, в то время как газы имеют вязкость от 1 до 10 мкПа с. Пасты, гели, эмульсии и другие сложные жидкости сложнее обобщить.Некоторые жиры, такие как масло или маргарин, настолько вязкие, что кажутся больше похожими на мягкие твердые вещества, чем на текущие жидкости. Расплавленное стекло чрезвычайно вязкое и по мере затвердевания приближается к бесконечной вязкости. Поскольку этот процесс не так хорошо определен, как истинное замораживание, некоторые считают (ошибочно), что стекло все еще может течь даже после полного охлаждения, но это не так. При обычных температурах стекла такие же твердые, как и настоящие твердые тела.
Из повседневного опыта должно быть известно, что вязкость зависит от температуры.Мед и сиропы могут течь легче при нагревании. Моторное масло и гидравлические жидкости значительно загустевают в холодные дни и существенно влияют на работу автомобилей и другой техники в зимние месяцы. Обычно вязкость простой жидкости уменьшается с повышением температуры. С повышением температуры средняя скорость молекул в жидкости увеличивается, а время, которое они проводят «в контакте» со своими ближайшими соседями, уменьшается. Таким образом, с повышением температуры средние межмолекулярные силы уменьшаются.Фактический способ изменения этих двух величин является нелинейным и резко меняется, когда жидкость меняет фазу.
Вязкость обычно не зависит от давления, но жидкости под экстремальным давлением часто имеют повышенную вязкость. Поскольку жидкости обычно несжимаемы, увеличение давления на самом деле не приводит к значительному сближению молекул. Простые модели молекулярных взаимодействий не могут объяснить такое поведение, и, насколько мне известно, не существует общепринятой более сложной модели, которая могла бы это сделать.Жидкая фаза, вероятно, наименее изучена из всех фаз вещества.
В то время как жидкости становятся более жидкими по мере того, как они нагреваются, газы становятся более густыми. (Если представить себе «густой» газ.) Вязкость газов увеличивается с увеличением температуры и приблизительно пропорциональна квадратному корню из температуры. Это связано с увеличением частоты межмолекулярных столкновений при более высоких температурах. Поскольку большую часть времени молекулы в газе свободно летают через пустоту, все, что увеличивает количество раз, когда одна молекула контактирует с другой, снижает способность молекул в целом участвовать в скоординированном движении.Чем больше эти молекулы сталкиваются друг с другом, тем более беспорядочным становится их движение. Физические модели, выходящие за рамки этой книги, существуют уже почти столетие, которые адекватно объясняют температурную зависимость вязкости в газах. Новые модели работают лучше, чем старые. Они также согласны с наблюдением, что вязкость газов примерно не зависит от давления и плотности. Газовая фаза, вероятно, является наиболее изученной из всех фаз материи.
Поскольку вязкость настолько зависит от температуры, без нее нельзя указывать ее.
Вязкость выбранных материалов (обратите внимание на разнообразие префиксов единиц измерения)
| простые жидкости | T (° C) | η (мПа с) |
|---|---|---|
| спирт этиловый (зерновой) | 20 | 1,1 |
| спирт изопропиловый | 20 | 2,4 |
| спирт метиловый (дерево) | 20 | 0.59 |
| кровь | 37 | 3–4 |
| этиленгликоль | 25 | 16,1 |
| этиленгликоль | 100 | 1,98 |
| фреон 11 (пропеллент) | −25 | 0,74 |
| фреон 11 (пропеллент) | 0 | 0,54 |
| фреон 11 (пропеллент) | +25 | 0,42 |
| фреон 12 (хладагент) | −15 | ? |
| фреон 12 (хладагент) | 0 | ? |
| фреон 12 (хладагент) | +15 | 0.20 |
| галлий | > 30 | 1 ~ 2 |
| глицерин | 20 | 1420 |
| глицерин | 40 | 280 |
| гелий (жидкий) | 4 К | 0,00333 |
| ртуть | 15 | 1,55 |
| молоко | 25 | 3 |
| масло растительное рапсовое | 25 | 57 |
| масло растительное рапсовое | 40 | 33 |
| масло растительное кукурузное | 20 | 65 |
| масло растительное кукурузное | 40 | 31 |
| масло растительное оливковое | 20 | 84 |
| масло растительное, оливковое | 40 | ? |
| масло растительное, соевое | 20 | 69 |
| масло растительное, соевое | 40 | 26 |
| масло машинное светлое | 20 | 102 |
| масло машинное тяжелое | 20 | 233 |
| пропиленгликоль | 25 | 40.4 |
| пропиленгликоль | 100 | 2,75 |
| вода | 0 | 1,79 |
| вода | 20 | 1,00 |
| вода | 40 | 0,65 |
| вода | 100 | 0,28 |
| газы | T (° C) | η (мкПа с) |
|---|---|---|
| воздух | 15 | 17.9 |
| водород | 0 | 8,42 |
| гелий (газ) | 0 | 18,6 |
| азот | 0 | 16,7 |
| кислород | 0 | 18,1 |
| сложные материалы | T (° C) | η (Па · с) |
|---|---|---|
| герметик | 20 | 1000 |
| стекло | 20 | 10 18 –10 21 |
| стекло, деформация ч. | 504 | 10 15,2 |
| стекло, отжиг ч. | 546 | 10 12,5 |
| стекло, смягчающее пт. | 724 | 10 6,6 |
| стекло рабочее ч. | 10 3 | |
| стекло плавки пт. | 10 1 | |
| мед | 20 | 10 |
| кетчуп | 20 | 50 |
| сало | 20 | 1000 |
| меласса | 20 | 5 |
| горчица | 25 | 70 |
| арахисовое масло | 20 | 150–250 |
| сметана | 25 | 100 |
| сироп шоколадный | 20 | 10–25 |
| сироп кукурузный | 25 | 2–3 |
| сироп кленовый | 20 | 2–3 |
| гудрон | 20 | 30 000 |
| овощной жир | 20 | 1200 |
моторное масло
Моторное масло похоже на любую другую жидкость тем, что его вязкость зависит от температуры и давления.Поскольку можно предвидеть условия, в которых будет эксплуатироваться большинство автомобилей, поведение моторного масла можно определить заранее. В Соединенных Штатах организацией, которая устанавливает стандарты характеристик моторных масел, является Общество автомобильных инженеров (SAE). Схема нумерации SAE описывает поведение моторных масел в условиях низких и высоких температур – условий, которые соответствуют температуре запуска и эксплуатации. Первое число, за которым всегда следует буква W для зимы, описывает низкотемпературное поведение масла при запуске, а второе число описывает высокотемпературное поведение масла после того, как двигатель проработал некоторое время.Более низкие значения SAE обозначают масла, которые предназначены для использования при более низких температурах. Масла с низкими числами SAE обычно более текучие (менее вязкие), чем масла с высокими числами SAE, которые имеют тенденцию быть более густыми (более вязкими).
Например, масло 10W ‑ 40 будет иметь вязкость не более 7000 мПа с в картере холодного двигателя, даже если его температура упадет до -25 ° C холодной зимней ночью и вязкость не менее 2,9 мПа с в детали двигателя под высоким давлением вблизи точки перегрева (150 ° C).
Вязкостные характеристики моторных масел марок
| sae префикс | динамическая вязкость, проворачивание максимальное | Вязкость динамическая, накачка максимальная |
|---|---|---|
| 00 Вт | 06,200 мПа · с (-35 ° C) | 60 000 мПа с (-40 ° C) |
| 05W | 06 600 мПа с (-30 ° C) | 60 000 мПа с (-35 ° C) |
| 10 Вт | 07,000 мПа · с (-25 ° C) | 60 000 мПа с (-30 ° C) |
| 15 Вт | 07,000 мПа · с (-20 ° C) | 60 000 мПа с (-25 ° C) |
| 20 Вт | 09,500 мПа · с (-15 ° C) | 60 000 мПа с (-20 ° C) |
| 25 Вт | 13000 мПа с (-10 ° C) | 60 000 мПа с (-15 ° C) |
| sae суффикс | кинематическая вязкость, низкая скорость сдвига (100 ° C) | динамическая вязкость, высокая скорость сдвига (150 ° C) |
|---|---|---|
| 08 | 04.0–6,10 мм 2 / с | > 1,7 мПа с |
| 12 | 05,0–7,10 мм 2 / с | > 2,0 мПа с |
| 16 | 06,1–8,20 мм 2 / с | > 2,3 мПа с |
| 20 | 05,6–9,30 мм 2 / с | > 2,6 мПа с |
| 30 | 09,3–12,5 мм 2 / с | > 2,9 мПа с |
| * 40 * | 12.5–16,3 мм 2 / с | > 2,9 мПа с |
| † 40 † | 12,5–16,3 мм 2 / с | > 3,7 мПа с |
| 50 | 16,3–21,9 мм 2 / с | > 3,7 мПа с |
| 60 | 21,9–26,1 мм 2 / с | > 3,7 мПа с |
вискозиметр капиллярный
Математическое выражение, описывающее течение жидкости в круглых трубках, было определено французским врачом и физиологом Жаном Пуазейлем (1799–1869).Поскольку оно было также независимо открыто немецким инженером-гидротехником Готтильфом Хагеном (1797–1884), оно должно называться уравнением Хагена-Пуазейля , но обычно его называют просто уравнением Пуазейля . Я не буду выводить это здесь (но, вероятно, когда-нибудь смогу). Для нетурбулентного, непульсирующего потока жидкости через однородную прямую трубу объемный расход ( q м ) составляет…
- прямо пропорциональна разности давлений (∆ P ) между концами трубки
- обратно пропорционально длине (ℓ) трубки
- обратно пропорционально вязкости (η) жидкости
- пропорционально четвертой степени радиуса ( r 4 ) трубки
Решите для определения вязкости, если это то, что вы хотите знать.
Капиллярный вискозиметр… продолжайте писать… извините, это неполно.
падающая сфера
Математическое выражение, описывающее силу вязкого сопротивления на сфере, было определено британским физиком XIX века Джорджем Стоуксом. Я не буду выводить это здесь (но, вероятно, когда-нибудь в будущем).
R = 6πη rv
Формула подъемной силы, действующей на сферу, была утверждена древнегреческим инженером Архимедом из Сиракуз, но тогда уравнения не были изобретены.
B = ρ жидкость гВ смещенный
Формула веса должна была быть изобретена кем-то, но я не знаю кто.
W = мг = ρ объект гВ объект
Давайте объединим все это вместе для сферы, падающей в жидкость. Вес указывает вниз, точки плавучести вверх, точки перетаскивания вверх. Через некоторое время сфера упадет с постоянной скоростью. Когда это произойдет, все эти силы аннулируются.Когда сфера падает сквозь жидкость, она полностью погружается в воду, поэтому можно говорить только об одном объеме – объеме сферы. Давайте поработаем над этим.
| B | + | R | = | Вт | |
| ρ жидкость гВ | + | 6πη rv | = | ρ объект гВ | |
| 6πη rv | = | (ρ объект – ρ жидкость ) gV | |||
| 6πη rv | = | ∆ρ г 4 3 π r 3 | |||
И вот мы.
Бросьте шар в жидкость. Если вы знаете размер и плотность шара, а также плотность жидкости, вы можете определить вязкость жидкости. Если вы не знаете плотность жидкости, вы все равно можете определить кинематическую вязкость. Если вы не знаете плотность сферы, но знаете ее массу и радиус, тогда вы можете вычислить ее плотность.
неньютоновские жидкости
Уравнение Ньютона связывает напряжение сдвига и градиент скорости с помощью величины, называемой вязкостью.Ньютоновская жидкость – это жидкость, в которой вязкость – это просто число. Неньютоновская жидкость – это жидкость, в которой вязкость является функцией некоторой механической переменной, такой как напряжение сдвига или время. Говорят, что неньютоновские жидкости, которые изменяются со временем, имеют память .
Некоторые гели и пасты ведут себя как жидкость при работе или взбалтывании, а затем переходят в почти твердое состояние в состоянии покоя. Такие материалы являются примерами жидкостей для разжижения сдвига. Краска для дома – это жидкость, разжижающая сдвиг, и это тоже хорошо.Чистка щеткой, прокатка или распыление – это средства временного приложения напряжения сдвига. Это снижает вязкость краски до точки, при которой она может вытекать из аппликатора на стену или потолок. После снятия напряжения сдвига краска возвращается к своей остаточной вязкости, которая настолько велика, что соответствующий тонкий слой ведет себя больше как твердое тело, чем жидкость, и краска не растекается и не капает. Подумайте, каково было бы рисовать водой или медом для сравнения. Первый всегда слишком жидкий, а второй – слишком липкий.
Зубная паста – еще один пример материала, вязкость которого снижается под действием нагрузки. Зубная паста, находящаяся внутри тюбика, ведет себя как твердое вещество. Он не будет вытекать самопроизвольно, когда колпачок снят, но он потечет, когда вы надавите на него. Теперь он перестает вести себя как твердое тело и начинает действовать как густая жидкость. когда она попадает на вашу зубную щетку, напряжение снимается, и зубная паста возвращается в почти твердое состояние. Вам не нужно беспокоиться о том, что он стекает с кисти, когда вы подносите ее ко рту.
Жидкости для разжижения при сдвиге можно разделить на одну из трех основных групп. Материал, вязкость которого снижается под действием напряжения сдвига, но остается постоянной во времени, называется псевдопластичным . Материал, вязкость которого снижается под действием напряжения сдвига, а затем продолжает уменьшаться со временем, называется тиксотропным . Если переход от высокой вязкости (почти полутвердой) к низкой (по существу жидкой) происходит только после того, как напряжение сдвига превышает некоторое минимальное значение, то говорят, что материал представляет собой пластик bingham .
Материалы, которые загустевают при работе или перемешивании, называются загустителями при сдвиге . Пример, который часто показывают в классах естественных наук, – это паста из кукурузного крахмала и воды (смешанная в правильных пропорциях). Получающаяся в результате странная слизь ведет себя как жидкость при медленном сжатии и как эластичное твердое вещество при быстром сжатии. Честолюбивые демонстранты науки наполнили резервуары этим веществом, а затем наткнулись на него. Пока они движутся быстро, поверхность действует как кусок твердой резины, но в тот момент, когда они перестают двигаться, паста ведет себя как жидкость, и демонстратор принимает ванну с кукурузным крахмалом.Из-за утолщения при сдвиге из ванны трудно выбраться. Чем усерднее вы работаете, чтобы выбраться, тем сильнее материал втягивает вас обратно. Единственный способ избежать этого – двигаться медленно.
Материалы, которые под воздействием стресса становятся почти твердыми, – это больше, чем просто любопытство. Они идеальные кандидаты для бронежилетов и защитной спортивной прокладки. Пуленепробиваемый жилет или наколенник, сделанный из материала, утолщающего сдвиг, будет податливым и податливым для легких нагрузок, возникающих при обычных движениях тела, но станет твердым как камень в ответ на травматическое напряжение, вызванное оружием или падением на землю.
Загустители при сдвиге также делятся на две группы: жидкости с зависящей от времени вязкостью (материалы с памятью) и жидкости с вязкостью, не зависящей от времени (материалы без памяти). Если увеличение вязкости со временем увеличивается, говорят, что материал реопектик . Если увеличение примерно прямо пропорционально напряжению сдвига и не меняется с течением времени, говорят, что материал представляет собой дилатант .
| для истончения сдвига | утолщение на сдвиг | |
|---|---|---|
| зависящий от времени (материалы памяти) | тиксотропный кетчуп, мед, зыбучие пески, змеиный яд, полимерные толстопленочные чернила | реопектик сливки взбитые |
| не зависящий от времени (материалы без памяти) | псевдопластик краска, гель для укладки, взбитые сливки, тесто для торта, яблочное пюре, чернила шариковой ручки, металлокерамические чернила | дилатант крахмальные пасты, глупая замазка, синовиальная жидкость, шоколадный сироп, вязкие связующие жидкости, жидкая броня |
| с пределом текучести | bingham plastic зубная паста, буровой раствор, кровь, масло какао, майонез, йогурт, томатное пюре, лак для ногтей, отстой сточных вод | н / д |
С небольшой корректировкой уравнение Ньютона может быть записано в виде степенного закона , который обрабатывает псевдопластику и дилантанты – уравнение Оствальда-де Ваэля …
| Ф. | = к | ⎛ ⎜ ⎝ | дв x | ⎞ n ⎟ ⎠ |
| А | дз |
, где η вязкость заменяется на k индекс консистенции потока [Па с n ], а градиент скорости повышается до некоторой степени n , называемый индексом поведения потока [безразмерный].Последнее число зависит от класса жидкости.
| n <1 | n = 1 | n > 1 |
| псевдопластический | ньютон | дилатант |
Для работы с пластиками Бингема необходима другая модификация уравнения Ньютона – уравнение Бингема …
| Ф. | = σ y + η pl | дв x |
| А | дз |
, где σ y – это предел текучести [Па], а η пл – пластическая вязкость [Па · с].Первое число отделяет пластик Бингема от ньютоновских жидкостей.
| σ y <0 | σ y = 0 | σ y > 0 |
| невозможно | ньютон | пластик bingham |
Объединение степенного закона Оствальда-де Ваэля с пределом текучести Бингема дает нам более общее уравнение Гершеля-Балкли …
| Ф. | = σ y + k | ⎛ ⎜ ⎝ | дв x | ⎞ n ⎟ ⎠ |
| А | дз |
где снова σ y – это предел текучести [Па], k – это индекс консистенции потока [Па с n ], а n – это индекс поведения потока . [безразмерный].
вязкоупругость
Когда к объекту прикладывается сила ( F ), может произойти одно из четырех событий.
- Он мог бы разогнать как целое, и в этом случае применился бы второй закон движения Ньютона …
F = ma
Этот термин сейчас нам не интересен. Мы уже обсуждали такое поведение в предыдущих главах. Масса ( м, ) – это сопротивление ускорению ( a ), которое является второй производной от положения ( x ).Перейдем к чему-то новому.
- Он мог бы течь как жидкость, что можно было бы описать этим соотношением …
F = – bv
Это упрощенная модель, в которой сопротивление прямо пропорционально скорости ( v ), первой производной от положения ( x ). Мы использовали это в задачах о конечных скоростях только потому, что они давали легко решаемые дифференциальные уравнения. Мы также использовали его в затухающем гармоническом осцилляторе, опять же потому, что он давал дифференциальные уравнения, которые было легко решить (во всяком случае, относительно легко).Константу пропорциональности ( b ) часто называют коэффициентом демпфирования.
- Он может деформировать как твердое тело в соответствии с законом Гука …
F = – kx
Константа пропорциональности ( k ) – это жесткость пружины. Позиция ( x ) не является частью какой-либо производной и не возводится в какую-либо степень.
- Может застрять …
F = – F
Этот символ f делает вид, будто мы обсуждаем статическое трение.В жидкостях (а точнее, неньютоновских жидкостях) такой термин связан с пределом текучести. Позиция ( x ) никак не задействована.
Сложите все вместе и укажите ускорение и скорость как производные от положения.
| F = м | d 2 x | – б | dx | – kx – f |
| dt 2 | дт |
Это дифференциальное уравнение суммирует возможное поведение объекта.