Столбцы и строки матрицы: Линейная алгебра

04. Матрицы и операции над ними

Матрицы и определители матриц широко используются при решении систем линейных уравнений, линейном программировании, исследовании систем дифференциальных уравнений. Аппарат теории матриц применяется в вычислительной математике, физике, моделировании практических задач в технике, экономике и бизнесе.

Матрицей называется прямоугольная таблица, составленная из элементов некоторого множества. Матрицы обычно обозначают заглавными буквами латинского алфавита в виде , если важно знать ее размеры, или буквами . Записывается матрица в следующем виде .

Элементы матрицы нумеруются двумя индексами. Первый индекс обозначает номер строки, а второй – номер столбца, на пересечении которых находится этот элемент в матрице. Матрица называется числовой, если ее элементы вещественные или комплексные числа; функциональной, если ее элементы – функции; блочной, если ее элементы – другие матрицы. Если число строк матрицы равно числу ее столбцов, то матрицу называют квадратной.

Все элементы квадратной матрицы, которые имеют одинаковые первые и вторые индексы, образуют главную диагональ матрицы. Если матрица имеет только одну строку, то ее называют матрицей – строкой или вектор – строкой. Такая матрица совпадает с арифметическим вектором, и ее элементы отделяют друг от друга запятыми. Если матрица имеет только один столбец, то ее называют матрицей – столбцом или вектор – столбцом. По соглашению, арифметические векторы записывают в виде вектор – столбцов. Например, матрица – прямоугольная числовая матрица размером две строки на три столбца, матрица – квадратная числовая матрица размером две строки на два столбца, матрица – это матрица – строка, а матрица – матрица – столбец.

Некоторые матрицы имеют специальные обозначения и названия.

Произвольная матрица называется нулевой, если все ее элементы равны нулю. Например, матрица – нулевая размером два на три.

Квадратная матрица называется единичной, если все ее элементы на главной диагонали равны единице, а все остальные элементы равны нулю. Так, матрица – единичная и имеет размеры два на два.

Квадратная матрица называется диагональной, если ее элементы, стоящие выше и ниже главной диагонали равны нулю. Например, матрица – диагональная.

Если в матрице размером заменить строки на столбцы с тем же номером, то получится новая матрица размером , которую называют транспонированной к исходной матрице . Таким образом, по определению для всех элементов транспонированной матрицы выполняются соотношения: . Например, транспонированной по отношению к матрице размером две строки на три столбца будет матрица размером три строки на два столбца. Если дважды транспонировать матрицу, то в результате получится исходная матрица.

Матрицы и Называют равными, если они имеют одинаковые размеры и все их соответствующие элементы равны, т. е. , если .

Например, числовая матрица равна квадратной, функциональной матрице , но они записаны в различных формах.

Квадратная матрица Называется симметричной, если она совпадает с транспонированной матрицей, т.

е. . Например, матрица – симметричная, и видно, что она симметрична относительно главной диагонали. Отметим также, что диагональная и единичная матрицы являются симметричными, так как они совпадают со своими транспонированными матрицами, что проверяется непосредственно.

Для матриц введены две основные операции: сложение матриц и умножение матрицы на число (вещественное или комплексное).

Суммой двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц, то есть .

Так, если и , то .

Для операции сложения матриц выполняются свойства коммутативности И ассоциативности , которые следуют из соответствующих свойств чисел. Если к любой матрице прибавить слева или справа нулевую матрицу, то исходная матрица не изменится; таким образом, выполняются равенства . Для любой матрицы существует единственная противоположная матрица , такая что , что также следует из аксиоматических свойств чисел. Разность двух матриц одинаковых размеров определяется как обычно по правилу , то есть соответствующие элементы первой и второй матриц вычитаются. Так, если

и , то .

Произведением матрицы на число (вещественное или комплексное) называется матрица , полученная из исходной матрицы умножением всех ее элементов на число , то есть .

Например, пусть . Тогда .

Для основных матричных операций выполняются, дополнительно к вышеуказанным четырем свойствам, следующие четыре свойства:

– при умножении на число 1 матрица не изменяется ,

– ассоциативность умножения на числа ,

– две дистрибутивности и . Все свойства матриц следуют из соответствующих свойств чисел.

Таким образом, для матриц относительно основных операций сложения и умножения на число выполняются все восемь аксиом линейного пространства. Это позволяет считать матрицы элементами некоторого конкретного линейного пространства и обращаться с ними как с векторами. Отметим, что арифметические векторы по их определению совпадают с матрицами – строками или матрицами – столбцами.

Следовательно, арифметические векторы также удовлетворяют всем восьми свойствам абстрактного линейного пространства и могут, как и матрицы, называться векторами.

Операция умножения первой матрицы на вторую матрицу Не является основной. Эта операция определяется только в том случае, когда число столбцов первой равно числу строк второй (длина строк первой матрицы равна высоте столбцов второй матрицы).

Произведением матрицы размера на матрицу размера называется матрица размера , все элементы которой находятся по формулам

.

Таким образом, для нахождения элементов последовательно выбираются строки и столбцы, причем при каждом выборе элементы строки умножаются на соответствующие элементы столбца и все такие парные произведения складываются. Пусть, например, первая матрица имеет размер две строки на два столбца, вторая матрица- такой же размер. Тогда матрица , равная их произведению , находится по определяющим формулам в виде и также имеет размер две строки на два столбца.

Так как матрицы И Квадратные, то их можно перемножить в обратном порядке, то есть найти

.

Мы получили в нашем случае, что . Этот контрпример доказывает, что в общем случае умножение матриц не подчиняется закону коммутативности. Существуют матрицы, для которых свойство коммутативности выполняется. Такие матрицы называют коммутирующими, и они обязательно должны быть квадратными.

Покажем, например, что матрицы и коммутирующие. Действительно

,

,

Что и доказывает наше утверждение.

Если матрица Не является квадратной, то есть , то ее нельзя умножить саму на себя, так как число столбцов первой матрицы не будет равно числу строк второй матрицы. Однако если ее транспонировать, то определено как произведение размера , так и произведение размера . Рассмотрим для примера матрицу – строку вида . Транспонированная к ней матрица будет матрицей – столбцом вида . Произведение будет иметь размер три на три, а произведение будет иметь размер одна строка на один столбец.

Сформируем далее матрицу

.

В этой формуле символом обозначен определитель матрицы , состоящей из одного элемента. Как показывается ниже, определитель такой матрицы равен значению этого единственного элемента. Полученная матрица симметричная и при умножении на себя дает единичную матрицу.

Основные свойства, связанные с умножением матриц, доказываются в общем виде на основе соответствующих свойств чисел путем непосредственного сопоставления матриц слева и справа от знака равенства:

1) ,

2) ,

3) ,

4) ,

5) ,

6) .

< Предыдущая		Следующая >

Таблица из строк и столбцов матрицы. Матрицы

Матрица обозначается заглавными латинскими буквами (А , В , С,. ..).

Определение 1 . Прямоугольная таблица вида ,

состоящая из m строк и n столбцов, называется матрицей .

Элемент матрицы, i – номер строки, j – номер столбца.

Виды матриц:

элементов, стоящих на главной диагонали:

trA=a 11 +a 22 +a 33 +…+a nn .

§2. Определители 2, 3 и n-го порядка

Пусть даны две квадратные матрицы:

Определение 1 . Определителем второго порядка матрицы А 1 называется число, обозначаемое ∆ и равное , где

Пример . Вычислить определитель 2-го порядка:

Определение 2 . Определителем 3-го порядка квадратной матрицы А 2 называется число вида:

Это один из способов вычисления определителя.

Пример. Вычислить

Определение 3 . Если определитель состоит из n-строк и n-столбцов, то он называется определителем n-го порядка.

Свойства определителей:

Определитель не меняется при транспонировании (т.е. если в нем строки и столбцы поменять местами с сохранением порядка следования).

Если в определителе поменять местами какие-либо две строки или два столбца, то определитель изменит только знак.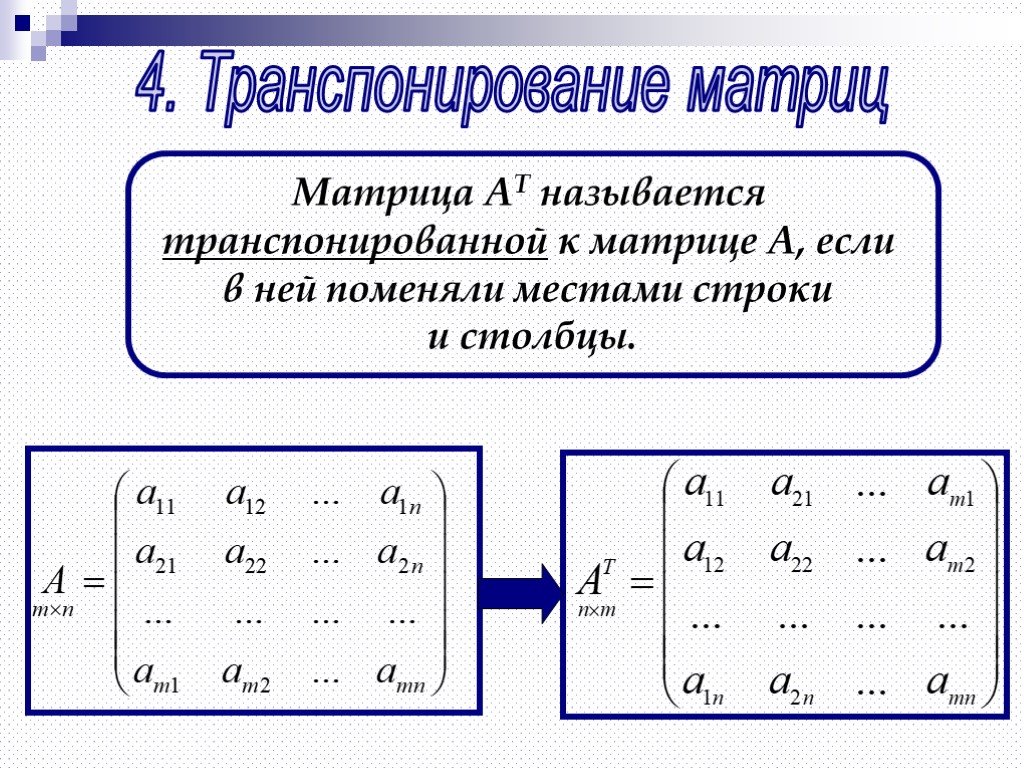

Общий множитель какой-либо строки (столбца) можно выносить за знак определителя.

Если все элементы какой-либо строки (столбца) определителя равны нулю, то определитель равен нулю.

Определитель равен нулю, если элементы каких-либо двух строк равны или пропорциональны.

Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Пример.

Определение 4. Определитель, полученный из данного путем вычеркивания столбца и строки, называется минором соответствующего элемента. М ij элемента a ij .

Определение 5. Алгебраическим дополнением элемента а ij , называется выражение

§3. Действия над матрицами

Линейные операции

1)При сложении матриц складываются их одноименные элементы.

При вычитании матриц вычитаются их одноименные элементы.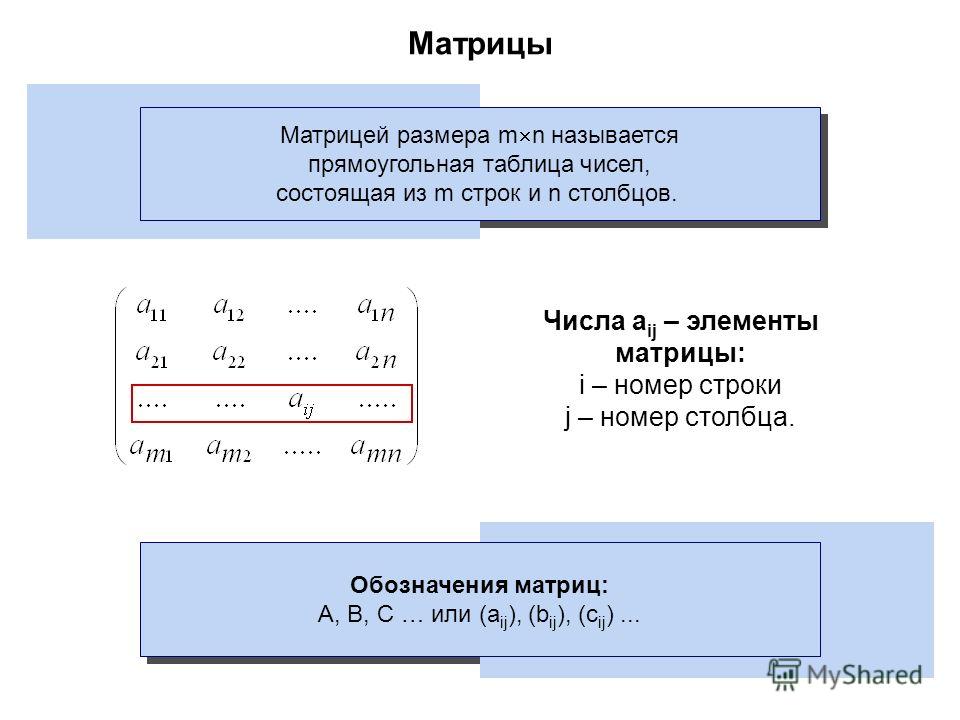

При умножении матрицы на число каждый элемент матрицы умножается на это число:

3.2.Умножение матриц.

Произведение матрицы А на матрицу В есть новая матрица , элементы которой равны сумме произведений элементовi-той строки матрицы А на соответствующие элементы j-го столбца матрицы В . Произведение матрицы А на матрицу В можно находить только в том случае, если число столбцов матрицы А равно числу строк матрицы В. В противном случае, произведение невозможно.

Замечание:

(не подчиняется свойству коммутативности)

§ 4. Обратная матрица

Обратная матрица существует только для квадратной матрицы, причем матрица должна быть невырожденной.

Определение 1. Матрица А называется невырожденной , если определитель этой матрицы не равен нулю

Определение 2. А -1 называется обратной матрицей для данной невырожденной квадратной матрицы А , если при умножении этой матрицы на данную как справа, так слева получается единичная матрица.

Алгоритм вычисления обратной матрицы

1 способ (с помощью алгебраических дополнений)

Пример 1:

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m ×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В .

В общем виде матрицу размером m ×n записывают так

.

Числа, составляющие матрицу, называются элементами матрицы . Элементы матрицы удобно снабжать двумя индексами a ij : первый указывает номер строки, а второй – номер столбца. Например, a 23 – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной , причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной . В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом .

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц . Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a ij = b ij . Так если и , то A=B , если a 11 = b 11 , a 12 = b 12 , a 21 = b 21 и a 22 = b 22 .

Транспонирование . Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей A , а переход от A к B транспонированием .

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A , обычно обозначают A T .

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры . Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B , стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C , которая определяется по правилу, например,

Примеры. Найти сумму матриц:

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B )+C =A +(B+C ).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

Примеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB , элементы которой составляются следующим образом:

Таким образом, например, чтобы получить у произведения (т.е. в матрице C ) элемент, стоящий в 1-ой строке и 3-м столбце c 13 , нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a ij) размера m ×n на матрицу B = (b ij) размера n ×p , то получим матрицу C размера m ×p , элементы которой вычисляются следующим образом: элемент c ij получается в результате произведения элементов i -ой строки матрицы A на соответствующие элементы j -го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т. е. один элемент). Действительно,

.

Примеры.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A . Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC .

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A , причём AE=EA=A .

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например , если , то

.

ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

Определителем второго порядка , соответствующим данной матрице, называется число, получаемое следующим образом: a 11 a 22 – a 12 a 21 .

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

Определителем третьего порядка , соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

.

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a 11 , a 12 , a 13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Примеры. Вычислить определитель третьего порядка.

Аналогично можно ввести понятия определителей четвёртого, пятого и т. д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки “+” и “–” у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.

Над такими матрицами производят различные действия: перемножают друг на друга, находят определители, и т.п. Матрица – частный случай массива: если массив может иметь любое количество измерений, то матрицей называют только двумерный массив.

В программировании матрицей также называют двумерный массив. Любой из массивов в программе имеет имя, как если бы это была одна переменная. Чтобы уточнить, какая из ячеек массива имеется в виду, при упоминании его в программе совместно с переменной используют номер ячейки в ней. Как двумерная матрица, так и n-мерный массив в программе может содержать не только числовую, но и символьную, строковую, булевую и иную информацию, но всегда одну и ту же в пределах всего массива.

Обозначаются матрицы заглавными буквами А:MxN, где А – имя матрицы, M– количество строк в матрице, а N– количество столбцов. Элементы – соответствующими строчными буквами с индексами, обозначающими их номер в строке и в столбце a (m, n).

Наиболее часто распространены матрицы прямоугольной формы, хотя в далеком прошлом математики рассматривали и треугольные. Если количество строк и столбцов матрицы одинаково, она называется квадратной. При этом M=N уже имеет наименование порядка матрицы. Матрица, имеющая всего одну строку, именуется строкой. Матрица с всего одним столбцом называется столбцом. Диагональная матрица – это квадратная матрица, в которой не равны нулю только элементы, расположенные по диагонали. Если все элементы равны единице, матрица называется единичной, если нулю – нулевой.

Если в матрице поменять местами строки и столбцы, она станет транспонированной. Если все элементы заменить комплексно-сопряженными, она станет комплексно-сопряженной. Кроме того, существуют и другие виды матриц, определяющиеся условиями, которые накладываются на матричные элементы. Но большинство таких условий применимо только к квадратным .

Видео по теме

Заметим, что элементами матрицы могут быть не только числа. Представим себе, что вы описываете книги, которые стоят на вашей книжной полке. Пусть у вас на полке порядок и все книги стоят на строго определенных местах. Таблица , которая будет содержать описание вашей библиотеки (по полкам и следованию книг на полке), тоже будет матрицей. Но такая матрица будет не числовой. Другой пример. Вместо чисел стоят разные функции, объединенные между собой некоторой зависимостью. Полученная таблица также будет называться матрицей. Иными словами, Матрица , это любая прямоугольная таблица , составленная из однородных элементов. Здесь и далее мы будем говорить о матрицах, составленных из чисел.

Вместо круглых скобок для записи матриц применяют квадратные скобки или прямые двойные вертикальные линии

(2. 1*)

Определение 2 . Если в выражении (1) m = n , то говорят о квадратной матрице , а если , то о прямоугольной .

В зависимости от значений m и n различают некоторые специальные виды матриц:

Важнейшей характеристикой квадратной матрицы является ее определитель или детерминант , который составляется из элементов матрицы и обозначается

Очевидно, что D E =1 ; .

Определение 3 . Если , то матрица A называется невырожденной или не особенной .

Определение 4 . Если detA = 0 , то матрица A называется вырожденной или особенной .

Определение 5 . Две матрицы A и B называются равными и пишут A = B , если они имеют одинаковые размеры и их соответствующие элементы равны, т.е .

Например, матрицы и равны, т. к. они равны по размеру и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. А вот матрицы и нельзя назвать равными, хотя детерминанты обеих матриц равны, и размеры матриц одинаковые, но не все элементы, стоящие на одних и тех же местах равны. Матрицы и разные, так как имеют разный размер. Первая матрица имеет размер 2х3, а вторая 3х2. Хотя количество элементов одинаковое – 6 и сами элементы одинаковые 1, 2, 3, 4, 5, 6, но они стоят на разных местах в каждой матрице. А вот матрицы и равны, согласно определению 5.

Определение 6 . Если зафиксировать некоторое количество столбцов матрицы A и такое же количество ee строк, тогда элементы, стоящие на пересечении указанных столбцов и строк образуют квадратную матрицу n – го порядка, определитель которой называется минором k – го порядка матрицы A .

Пример . Выписать три минора второго порядка матрицы

Определение Матрицей – называется таблица чисел содержащая определенное количество строк и столбцов

Элементами матрицы являются числа вида a ij , где i- номер строки j- номер столбца

Пример 1 i = 2 j = 3

Обозначение: А=

Виды матриц:

1. Если число строк не равно числу столбцов , то матрица называется прямоугольной:

2. Если число строк равно числу столбцов , то матрица называется квадратной:

Число строк или столбцов квадратной матрицы называется ее порядком . В примере n = 2

Рассмотрим квадратную матрицу порядка n:

Диагональ, содержащая элементы a 11 , a 22 ……., a nn , называетсяглавной, а диагональ, содержащая элементы а 12 , а 2 n -1 , …….a n 1 – вспомогательная.

Матрица, у которой отличны от нуля только элементы, находящиеся на главной диагонали, называется диагональной :

Пример 4 n = 3

3. Если у диагональной матрицы элементы равны 1, то матрица называется единичной и обозначается буквой Е:

Пример 6 n = 3

4. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается буквой О

Пример 7

5. Треугольной матрицей n-ого порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:

Пример 8 n = 3

Действия над матрицами:

Суммой матрицы А и В называется такая матрица С, элементы которой равны сумме соответствующих элементов матриц А и В.

Складывать можно только матрицы, имеющие одинаковые число строк и столбцов.

Произведением матрицы А на число k называется такая матрица kA, каждый элемент которой равен ka ij

Пример10

Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.

Произведение матриц Что бы умножить матрицу на матрицу, необходимо выбрать первую строку первой матрицы и умножить на соответствующие элементы первого столбца второй матрицы, результат сложить. Этот результат расположить в результатирующей матрице в 1-ой строке и 10ом столбце. Аналогично выполняем действия со всеми остальными элементами: 1-ую строку на второй столбец, на 3-ий и т.д., затем со следующими строками.

Пример 11

Умножение матрицы А на матрицу В возможно только в том случае, если число столбцов первой матрицы равно числу строе второй матрицы.

– произведение существует;

– произведение не существует

Примеры 12 последнюю строчку во II матрицы умножать не с чем, т. е. произведение не существует

Транспонирование матрицы называется операция замены элементов строки на элементы столбца:

Пример13

Возведением в степень называется последовательное перемножение матрицы саму на себя.

Column Matrix – определение, формула, свойства, примеры.

Матрица-столбец — это матрица, все элементы которой находятся в одном столбце. Элементы расположены вертикально, а порядок матрицы столбцов равен n x 1. Матрица столбцов имеет только один столбец и может иметь множество строк, равное количеству элементов в столбце.

Давайте узнаем больше о свойствах матрицы-столбца, матричных операциях над матрицей-столбцом, на примерах, в часто задаваемых вопросах.

1.	Что такое матрица столбцов?
2.	Свойства матрицы столбцов
3.	Операции над матрицей столбцов
4.	Примеры на матрице столбцов
5.	Практические вопросы
6.	Часто задаваемые вопросы о столбцовой матрице

Что такое матрица столбцов?

Матрица-столбец — это матрица, в которой все элементы находятся в одном столбце. Матрица столбцов имеет только один столбец и несколько строк. Порядок матрицы-столбца равен n × 1, и она состоит из n элементов. Элементы расположены вертикально, при этом количество элементов равно количеству строк в матрице-столбце. Общая форма матрицы-столбца выглядит следующим образом.

Примеры матрицы столбцов

Давайте посмотрим на три примера матриц столбцов ниже.

B = \(\begin{bmatrix}4\\5\end{bmatrix}_{2×1}\)

C = \(\begin{bmatrix}a\\b\\c\end{bmatrix }_{3×1}\)

D = \(\begin{bmatrix}8\\-2\\4\\1\end{bmatrix}_{4×1}\)

Свойства матрицы столбцов

Следующие свойства матрицы-столбца помогают глубже понять матрицу-столбец.

• Матрица столбцов имеет только один столбец.
• Матрица-столбец имеет множество строк.
• Количество элементов в матрице-столбце равно количеству строк в матрице.
• Матрица-столбец также является прямоугольной матрицей.
• Транспонирование матрицы-столбца является матрицей-строкой.
• Матрица-столбец может быть добавлена ​​или вычтена только из матрицы-столбца того же порядка.
• Матрица-столбец может быть умножена только на матрицу-строку
• Произведение матрицы-столбца на матрицу-строку дает одноэлементную матрицу.

Операции над матрицей столбцов

Над матрицами-столбцами можно выполнять следующие алгебраические операции сложения, вычитания, умножения и деления. Операции сложения и вычитания над матрицами-столбцами можно выполнять так же, как и над любыми другими матрицами. Матрица-столбец может быть добавлена ​​или вычтена только из любой другой матрицы-столбца. Здесь порядок двух матриц должен быть одинаковым.

A = \(\begin{bmatrix}7\\-3\\4\\5\end{bmatrix}\), B = \(\begin{bmatrix}3\\8\\2\\-7 \end{bmatrix}\)

A + B = \(\begin{bmatrix}7+3\\(-3)+8\\4+2\\5+(-7)\end{bmatrix}\) = \(\begin{ bmatrix}10\\5\\6\\-2\end{bmatrix}\)

Умножение матрицы-столбца возможно на матрицу-строку. При выполнении условия умножения матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. То есть количество столбцов в матрице столбцов для умножения равно количеству строк в столбце строки.

A = \(\begin{bmatrix}4\\2\\3\\1\end{bmatrix}\), B = \(\begin{bmatrix}7&4&6&5\end{bmatrix}\)

A × B = \(\begin{bmatrix}4\\2\\3\\1\end{bmatrix}\), × \(\begin{bmatrix}7&4&6&5\end{bmatrix}\)

= \(\begin{bmatrix}4×7&4×4&4×6&4×5\\2×7&2×4&2×6&2×5\\3×7&3×4&3×6&3×5\\1×7&1×4&1×6&1×5\ end{bmatrix}\)

= \(\begin{bmatrix}28&16&24&20\\14&8&12&10\\21&12&18&15\\7&4&6&5\end{bmatrix}\)

Умножение матрицы-столбца на матрицу-строку приводит к квадратной матрице . Кроме того, матрицу-столбец нельзя использовать для деления, поскольку обратной матрицы-столбца не существует.

Связанные темы

Следующие темы помогают лучше понять матрицу столбцов.

• Операции с матрицами
• Матрица трансформации
• Несингулярная матрица
• Эрмитова матрица
• Нильпотентная матрица

Примеры на матрице столбцов

1. Пример 1: Найти транспонирование матрицы-столбца \(\begin{bmatrix}5\\11\\4\\3\end{bmatrix}\).

   Решение:

   Дана матрица A = \(\begin{bmatrix}5\\11\\4\\3\end{bmatrix}\)

   Чтобы найти транспонирование этой матрицы-столбца, элементы столбца записываются как элементы строки.

   A ^T = \(\begin{bmatrix}5&11&4&3\end{bmatrix}\)

   Следовательно, транспонирование матрицы-столбца является матрицей-строкой.

2. Пример 2: Найдите произведение матрицы-столбца \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) и матрицы-строки \(\begin{bmatrix}2&6&9\end{bmatrix}\).

   Решение:

   Даны матрицы A = \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) и B = \(\begin{bmatrix}2&6&9\end{ bматрица}\).

   A × B = \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) × \(\begin{bmatrix}2&6&9\end{bmatrix}\)

   = \(\begin {bmatrix}4×2&4×6&4×9\\5×2&5×6&5×9\\3×2&3×6&3×9\\\end{bmatrix}\)

   = \(\begin{bmatrix}8&24&36\\ 10&30&45\\6&18&27\\\конец{bmatrix}\)

   Таким образом, произведение матрицы-столбца и матрицы-строки является одноэлементной матрицей.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по матрице столбцов

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о матрице столбцов

Что такое матрица столбцов?

Матрица-столбец — это матрица только с одним столбцом, все элементы которой расположены друг под другом по вертикальной линии. В матрице столбцов A = \(\begin{bmatrix}a\\b\\c\\d\end{bmatrix}\) четыре элемента размещены в одном столбце. Матрица столбцов имеет только один столбец и множество строк. Порядок матрицы-столбца равен n × 1.

Каков порядок матрицы-столбца?

Порядок матрицы-столбца равен n × 1. Матрица-столбец состоит из одного столбца и n строк. Количество строк в матрице-столбце равно количеству элементов.

Какой тип матрицы является матрицей-столбцом?

Матрица-столбец представляет собой прямоугольную матрицу. Он имеет неравное количество строк и столбцов. Матрица столбцов имеет один столбец и множество строк в зависимости от количества элементов в матрице.

Что такое транспонирование матрицы столбцов?

Транспонирование матрицы-столбца дает матрицу-строку. Матрица-столбец порядка n × 1 имеет транспонированную матрицу, которая представляет собой матрицу-строку порядка 1 × n. В матрице столбцов элементы расположены вертикально, а в матрице строк элементы расположены вертикально.

Какие операции выполняются над матрицей-столбцом?

Матричные операции сложения, вычитания и умножения можно выполнять с помощью матрицы-столбца. Обратная матрица-столбец невозможна, так как это не квадратная матрица. Сложение или вычитание матриц возможно между двумя матрицами-столбцами одного порядка. Умножение матрицы-столбца возможно на матрицу-строку. При выполнении условия умножения матриц количество столбцов в матрице-столбце должно быть равно количеству строк матрицы-строки.

В чем разница между матрицей столбцов и матрицей строк?

В матрице столбцов элементы расположены вертикально, а в матрице строк элементы расположены горизонтально. Порядок матрицы-столбца равен n × 1, а порядок матрицы-строки — 1 × n. Матрица-столбец или матрица-строка имеют одинаковое количество элементов. А произведение матрицы-столбца и матрицы-строки дает одноэлементную матрицу.

Ранг матрицы

Марко Табога, доктор философии

Ранг столбца a матрица линейный размер пространство, охваченное его столбцами.

Ранг строки матрицы — это размерность пространства, натянутого на ее строки.

Поскольку мы можем доказать, что ранг строки и ранг столбца всегда равны, мы просто говорят о ранге матрицы.

Содержание

1. Ранг столбца

2. Ранг строки

3. Ранг столбца равен рангу строки

4. Definition of rank

5. Maximum rank

6. Full-rank

7. Solved exercises

1. Exercise 1

2. Exercise 2

Column rank

Начнем с определения.

Определение Позволять быть матрица. Ранг столбца это здесь обозначает -й столбец , обозначает линейный пролет, а обозначает измерение.

Помните, что размерность линейное пространство – это количество элементы одного из его базы, то есть количество линейно независимые векторы, порождающие пространство. Итак, ранг столбца a матрица — это количество линейно независимых векторов, порождающих одинаковые пространство, порожденное столбцами матрицы.

Пример Рассмотрим матрицу и линейное пространство охватываемый двумя столбцычто есть пространство всех векторов, которое можно записать как линейные комбинации и . Любой вектор можно написать как где и два скаляра. Обратите внимание, что два столбца и линейно зависимы потому что, любой вектор можно записать как кратное : В качестве следствие, является основа для . Оно имеет элемент. Следовательно, размерность и ранг столбца равны .

Ранг строки

Определение ранга строки аналогично определению ранга столбца.

Определение Позволять быть матрица.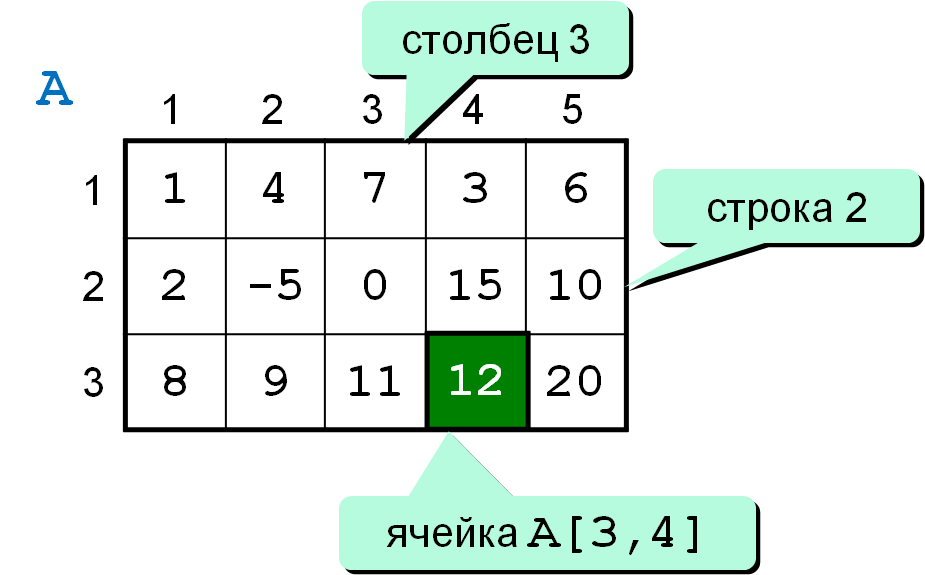 Ранг строки это здесь обозначает -й ряд , обозначает линейный пролет, а обозначает размерность.

Другими словами, ранг строки матрицы — это размерность линейного пространства порождается его строками.

Ранг столбца равен рангу строки

Важным результатом является то, что ранг столбца матрицы всегда равен ее ранг строки.

Предложение Позволять быть матрица. Тогда

Доказательство

Пусть Затем, существует основа из векторы-столбцы, которые охватывают одно и то же пространство, натянутое столбцами . Обозначим через в матрица, полученная из векторов базиса: Каждый столбец может быть выражена как линейная комбинация . Коэффициенты линейных комбинаций можно собрать в матрица такой это как мы показали в лекции о Матрица умножение и линейные комбинации. В той же лекции мы также показано, что строки произведения являются линейными комбинациями строк , с коэффициентами, взятыми из . Таким образом, размах рядов не больше размаха рядов (поскольку линейные комбинации строк могут быть записаны как линейные комбинации строк ). Там находятся ряды в . Если они линейно независимы, то их промежуток имеет размерность . В противном случае он имеет размерность меньше . Как следствие, ранг строки меньше или равно (его ранг столбца). Совершенно аналогичным образом доказывается, что столбец ранг меньше или равен рангу строки: пусть Затем, существует основа из векторы-строки, которые охватывают одно и то же пространство, натянутое строками . Обозначим через в матрица, полученная из векторов базиса: Каждый ряд может быть выражена как линейная комбинация . Коэффициенты линейных комбинаций можно собрать в матрица такой что столбцы продукта являются линейными комбинациями столбцов , с коэффициентами, взятыми из . Таким образом, размах колонн не больше размаха столбцов (поскольку линейные комбинации столбцов могут быть записаны как линейные комбинации столбцов ). Там находятся столбцы в . Если они линейно независимы, то их промежуток имеет размерность . В противном случае он имеет размерность меньше . Как следствие, ранг столбца меньше или равно (его рядовой ранг). Таким образом, мы доказали что и поэтому,

Определение ранга

Доказав, что ранг столбца и строки совпадают, теперь мы готовы предоставить определение ранга.

Определение Позволять быть матрица. Ранг , обозначается , определяется как

Другими словами, ранг матрицы — это размерность линейной оболочки матрицы. его столбцов, что совпадает с размерностью линейного пролета его ряды.

Максимальный ранг

Справедливо следующее предложение.

Предложение Позволять быть матрица. Тогда

Доказательство

У нас есть два возможных случая. Во-первых случае, что есть, число строк меньше или равно числу столбцов. Столбцы представляют собой векторы, имеющие записи. Таким образом, размер пространства, занимаемого столбцами, меньше или равно . В другом слова, но так который В секунду случае, что есть, число столбцов меньше или равно числу строк. Строки представляют собой векторы, имеющие записи. Таким образом, размер пространства, охваченного строками, меньше или равно . В другом слова, но так чтоТаким образом, в обоих случаи,

Полный ранг

Учитывая предыдущие результаты, теперь мы можем дать определение матрицы полного ранга.

Определение Позволять быть матрица. Затем называется полноранговым тогда и только тогда если

Очевидно, что если является квадратной матрицей, т. е. если , то он полноранговый тогда и только тогда если в другими словами, если является квадратным и полноранговым, то его столбцы (строки) охватывают пространство всех -размерный векторы: любой -размерный вектор можно записать как линейную комбинацию столбцов (строк) .

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Позволять быть матрица. Какой максимальный ранг он может иметь?

Решение

Максимальный ранг

Упражнение 2

Определять Что такое ранг ?

Решение

Матрица имеет два столбцы: два столбца линейно независимы, потому что ни один из них не может быть записан как скаляр, кратный другому. По сути, они не кратные. Это хорошо видно из третьей записи который : нет коэффициента, на который можно умножить чтобы получить , третья запись .