СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ – это… Что такое СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ?
- СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ
- СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ
(tend to infinity) Рост за пределы любого конечного размера, каким бы большим он ни был. То, что переменная х стремится к бесконечности, записывается как х; она становится бесконечно большой. Точно так же если х, она становится меньше, чем любое отрицательное число, однако по абсолютной величине оно может быть очень велико.
Экономика. Толковый словарь. — М.: “ИНФРА-М”, Издательство “Весь Мир”. Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М.. 2000.
Экономический словарь. 2000.
- СТРАХОВАЯ КОМПАНИЯ
- СТРЕМЛЕНИЕ К ПОЛУЧЕНИЮ РЕНТНЫХ ДОХОДОВ
Смотреть что такое “СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ” в других словарях:
СМЫСЛ ЖИЗНИ ЧЕЛОВЕКА — эйдос индивида, умопостигаемая целостность всех проявлений его души.
 Стихия С.Ж. не материя и не энергия, а информация. Догадка о чьем либо С. ж. (в т. ч. о собственном) есть попытка понять скрытую форму правления души в теле, заключить о… … Современный философский словарь
Стихия С.Ж. не материя и не энергия, а информация. Догадка о чьем либо С. ж. (в т. ч. о собственном) есть попытка понять скрытую форму правления души в теле, заключить о… … Современный философский словарьВЁБЕР — (Weber) Альфред (1868 1958) нем. философ, социолог и теоретик культуры, экономист и политолог. Начав свою научную карьеру как экономист, исследователь проблем размещения нем. промышленности, В. переходит к проблемам философии и социологии… … Философская энциклопедия
ВЕБЕР — ВЁБЕР (Weber) Альфред (1868 1958) нем. философ, социолог и теоретик культуры, экономист и политолог. Начав свою научную карьеру как экономист, исследователь проблем размещения нем. промышленности, В. переходит к проблемам философии и социологии… … Философская энциклопедия
Соотношения Эренфеста — соотношения, определяющие изменения удельной теплоёмкости и производных первого порядка удельного объёма при фазовых переходах второго рода.
 Соотношение Клапейрона Клаузиуса не имеет смысл для фазовых превращений второго рода[1], так как и… … Википедия
Соотношение Клапейрона Клаузиуса не имеет смысл для фазовых превращений второго рода[1], так как и… … ВикипедияНеевклидовы геометрии — в буквальном понимании все геометрические системы, отличные от геометрии Евклида; однако обычно термин «Н. г.» применяется лишь к геометрическим системам (отличным от геометрии Евклида), в которых определено движение фигур, причём с той… … Большая советская энциклопедия
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — в буквальном понимании все геометрич. системы, отличные от геометрии Евклида; однако обычно термин Н. г. применяется лишь к геометрич. системам (отличным от геометрии Евклида), в к рых определено движение фигур, причем с той же степенью свободы,… … Математическая энциклопедия
ИОАНН ДУНС СКОТ — [лат. Ioannes (Johannes) Duns Scotus] († 8.11.1308, Кёльн), средневек. философ и богослов, католич. священник, член монашеского ордена францисканцев; в католич. Церкви прославлен в лике блаженных (пам.
 зап. 8 нояб.). Жизнь. Иоанн Дунс Скот. 1473… … Православная энциклопедия
зап. 8 нояб.). Жизнь. Иоанн Дунс Скот. 1473… … Православная энциклопедияВЫШЕСЛАВЦЕВ — Борис Петрович (1877 1954) специалист по философии права, социальной философии, истории философии, этике, религии. Его творчество занимает видное место в рус. культурном ренессансе 20 в. В 1899 окончил юрид. ф т Моск. ун та. В 1902 В.… … Энциклопедия культурологии
КОГЕН — (Cohen) Герман (1842 1918) немецкий философ, основатель и виднейший представитель марбургской школы неокантианства. Основные работы: ‘Теория опыта Канта’ (1885), ‘Обоснование Кантом этики’ (1877), ‘Обоснование Кантом эстетики’ (1889), ‘Логика… … История Философии: Энциклопедия
БУДДИЙСКАЯ МИФОЛОГИЯ — комплекс мифологических образов, персонажей, символики, связанный с религиозно философской системой буддизма, возникшей в 6 5 вв. до н. э. в Индии, в период централизованного государства, и широко распространившейся в Южной, Юго Восточной и… … Энциклопедия мифологии
Книги
- Эротика Франции, Стефания Лукас.
 Европейского эротического искусство наиболее ярко выражено во французской гравюре этого времени. Стремление к запретному плоду в ней проявляется в полной мере.В эротике видят только забаву,… Подробнее Купить за 96 руб электронная книга
Европейского эротического искусство наиболее ярко выражено во французской гравюре этого времени. Стремление к запретному плоду в ней проявляется в полной мере.В эротике видят только забаву,… Подробнее Купить за 96 руб электронная книга
Что такое предел функции как его найти
При каком условии Вам будут совсем не страшны любые задачи, где требуется найти предел функции? Условие следующее: у Вас есть базовый навык деления одних чисел на другие, на очень-очень маленькие числа и на очень-очень большие числа. Успех придет в процессе решения.
А теперь посмотрим, что о пределе функции гласит теория. Впрочем, можно зайти чуть-чуть вперед и сразу перейти к задачам, а потом вернуться к теории. Как удобнее.
Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.
Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.
Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть . Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле
Величина, которую нам требуется найти, будет записана так:
Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.
Теперь вычислим предел, присвоив переменной x значение бесконечность (в более строгом определении это называется “доопределить функцию”, с этим определением вы можете ознакомиться в последующих частях главы “Предел”). Примем, что конечная величина, поделенная на бесконечность, равна нулю:
С рассмотренной последовательностью окружностей свяжем другую переменную величину – последовательность сумм их диаметров:
Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.
Предел функции при
Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :
(1)
сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность
(2)
и можно ставить вопрос о существовании её предела.
Это означает: чтобы найти предел функции, нужно в функцию вместо
Пример 1. Найти предел функции при .
Решение. Подставляем вместо x значение 0. Получаем:
Подставляем вместо x значение 0. Получаем:
.
Итак, предел данной функции при равен 1.
Предел функции при , при и при
Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.
Определение 2.
Символически это записывается так: .
Определение 3. Число A называется пределом функции f(x)
при (),
если для любой бесконечно большой последовательности значений аргумента, элементы
которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: ().
Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.
Пример 2. Найти предел функции при .
Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:
.
Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.
Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(3)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(4)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
(5)
Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.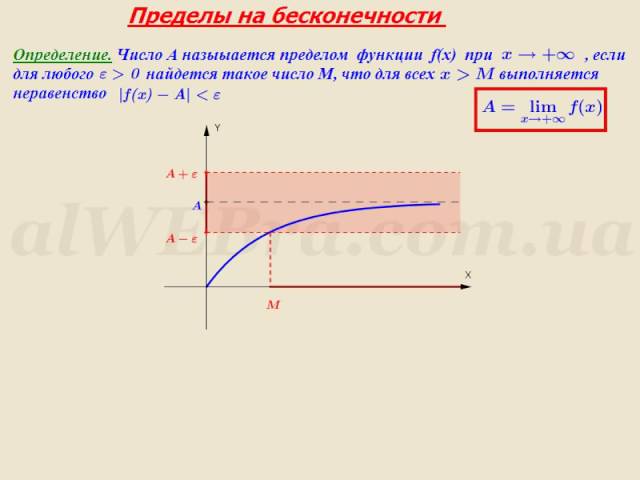
Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Пример 3. Найти предел:
Решение.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 4. Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит,
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Теорема 3 (о пределе сложной функции).
 Если существует конечный предел
Если существует конечный предела функция f(u) непрерывна в точке , то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 5. Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида – самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Освоим эти приёмы на примерах.
Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.
Неопределённость вида
Пример 12. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или “супермалому числу”.
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Проверить решение задачи на
пределы можно на калькуляторе пределов
онлайн.
Пример 13. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:
.
Комментарий к ходу решения. В числителе загоняем “икс” под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо “икса”.
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Неопределённость вида
Пример 14.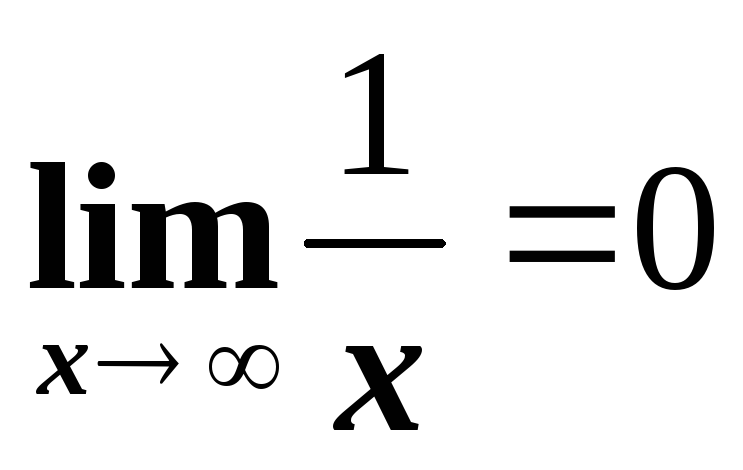 Раскрыть неопределённость и найти предел .
Раскрыть неопределённость и найти предел .
Решение. В числителе – разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
.
В знаменателе – квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):
Запишем выражение, полученное в результате преобразований и найдём предел функции:
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 15. Раскрыть неопределённость и найти предел
Решение. Теорема о пределе частного здесь неприменима, поскольку
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и
сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Пример 16. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
Продолжение темы “Предел”
Поделиться с друзьями
| Другие результаты | |
| Страны, стремящиеся в НАТО, нельзя держать на пороге до бесконечности. | |
| В частности, если функция может быть ограничена полиномом в n, то, поскольку n стремится к бесконечности, можно пренебречь членами нижнего порядка полинома. | |
Большая O нотация-это математическая нотация, которая описывает предельное поведение функции, когда аргумент стремится к определенному значению или бесконечности. | |
| Разрезание сферы по спирали шириной 1 / N и выравнивание полученной формы дает спираль Эйлера, когда N стремится к бесконечности. | |
| Благодаря модели Глауэрта эффективность находится ниже предела Бетца и асимптотически приближается к этому пределу, когда отношение скорости наконечника стремится к бесконечности. | |
| Если сферой является глобус, это создает картографическую проекцию, искажение которой стремится к нулю, как N стремится к бесконечности. | |
| В этом случае параметр μ стремится к бесконечности, и первое время прохождения для фиксированного уровня α имеет функцию плотности вероятности. | |
| Количество ey можно найти, взяв предел с обеих сторон, поскольку n стремится к бесконечности, и используя произведение Уоллиса, которое показывает, что ey = √2π. | |
Изометрическая широта равна нулю на экваторе, но быстро отклоняется от геодезической широты, стремясь к бесконечности на полюсах. | |
| Кроме того, устав от бесконечности, Дамиэль стремится к подлинности и границам человеческого существования. | |
| Поскольку n стремится к бесконечности, абсолютное значение r должно быть меньше единицы, чтобы ряды сходились. | |
| Но это не так, так как количество подходов стремится к бесконечности, а количество неучтенных приближается к 1 / бесконечности с той же скоростью. | |
| Число подходов стремится к бесконечности = по мере того, как вы движетесь бесконечно дальше от десятичного числа, бесконечно ближе к бесконечно малому. | |
| Надо заразить людей любовью к бесконечному морю, Как учёный и педагог, я люблю перефразировать эту цитату: Мы, учёные, должны учить наших студентов стремиться познать бесконечность моря, коим является наше незнание. | |
Во-первых, гравитационный потенциал сингулярен; он уходит в бесконечность, когда расстояние между двумя частицами стремится к нулю. n, на него и упрощаем n, на него и упрощаем Далее оцениваем вклад каждого слагаемого Слагаемые 3/8 стремятся к нулю при переменной направляюейся к бесконечности, поскольку 3/8<1 (свойство степенно-показательной функции).
Пример 37.Предел последовательности с факториалами раскрывается розписанням факториала к наибольшему общему множителю для числителя и знаменателя.
Пример 38.Не применяя правила Лопиталя сравниваем максимальные показатели переменной в числителе и знаменателе дроби.
Пример 39.Раскрываем особенность вида бесконечность разделить на бесконечность методом вынесения x^4 с числителя и знаменателя дроби.
Пример 41.Имеем особенность типа единица в степени бесконечность.
Пример 42.Имеем особенность типа единица в степени бесконечность.
Пример 43 В знаменателе дроби имеем неопределенность типа бесконечность минус бесконечность, фактически равное делению на ноль.
Пример 44.Найти повторные границы
Пример 45. Вычислить повторные границы |
|
Бесконечность стремится к нулю
1
Бесконечность равна нулю…
Что скрывается под этой фразой, что она означает, откуда в конце концов взялась? Спонтанна или обдумана она, имеет ли какую-то перспективу, способна ли изменить у человека представление о мире как о универсуме?
Почему она равна нулю, откуда такой смелый вывод, и стоить поверить сказавшему эту фразу? Глупа ли она по своей сути или же, наоборот, несёт в себе ничтожную частицу истинного и высокого, за выведение которого ученые годами, десятками, сотнями лет жертвовали жизнь и время науке, осознанно ставя перед собой вопросы, ответив на который, они поднимут несколько новых, оставив их без ответа?
2
Только противоборство радикальных теорий, идей, концепций и так далее способно действительно двигать общественную мысль и науку вперед. Взгляды, с помощью которых кто-то хотел бы вслепую найти экватор, затерянный между двумя полюсами, заранее обречены на провал. «Минус один» плюс «плюс один» равно нулю, как экватору. Экватор как таковой не существует, география говорит о нём лишь как об условной линии, хотя современные технологии скоро, возможно, позволят с мельчайшей погрешностью в точности провести через океаны и континенты каменную стену огромной высоты. Вопрос-то в другом: какой ущерб мы нанесем своей планете, материализовав абстрактное? Соответственно, что будет с нами, если материализуется ноль? С помощью человека, естественно. Так что не стоит пытаться воплотить божественное в жизнь, достаточно просто в совершенстве его изучить.
«Минус один» плюс «плюс один» равно нулю, как экватору. Экватор как таковой не существует, география говорит о нём лишь как об условной линии, хотя современные технологии скоро, возможно, позволят с мельчайшей погрешностью в точности провести через океаны и континенты каменную стену огромной высоты. Вопрос-то в другом: какой ущерб мы нанесем своей планете, материализовав абстрактное? Соответственно, что будет с нами, если материализуется ноль? С помощью человека, естественно. Так что не стоит пытаться воплотить божественное в жизнь, достаточно просто в совершенстве его изучить.
Можно взять что угодно, глобально-абстрактного характера: религию, государство, время, жизнь, смерть, войну – к каждому из перечисленного отношение (как преимущественно позитивное, так и преимущественно негативное) окажется весьма сложным и необъяснимым в двух словах. О таких вещах никогда не может быть сказано всё, и это «всё» по сути будет в определенном плане истиной. А истина недостижима человеку до конца, поэтому лучше много раз понемногу, чем сразу и один раз. Кстати, один из законов логики утверждает: не может одно утверждение быть одновременно истинным и ложным. Это правда. Но будет однобоким лишь в голове того, кто его услышал. Даже если его услышало несколько человек в одном месте и в одно время, все равно истинным или ложным оно будет только в отдельности для каждого из них. Человечество никогда не сможет договориться о чем-либо всем своим составом, оно не продукт конвейера, программа которого не допускает какую-либо вариацию в произведенной им продукции. Утопичны продукты человеческого разума, но не человеческая природа.
3
Давайте вспомним математику. Все в школе находили с помощью числовой прямой знак какого-либо значения переменной «х» на всем промежутке. И зажаты все числа между «минус бесконечностью» и «плюс бесконечностью». Теперь давайте в уме представим, что выпрямленная нитка, лежащая на столе – это материализованное графическое изображение числовой прямой. Соединим ее концы – получится фигура, очень похожая на ноль. Теперь складываем противоположные по знаку бесконечности, заменив значок лежащей восьмерки на любое число, пусть это будет та же восьмерка! И что мы получаем? «Минус восемь» плюс «плюс восемь» равно нулю. В итоге наблюдаем вот что: ноль мы получили и материально, и умственно. Ноль в абстракции равен нулю в реальности. Вот он, смысл: ноль существует в природе (так ли это? – на деле нет, но закончу фразу), и этот ноль есть сумма разных по знаку бесконечностей, этот ноль – ничтожная частица вечности, ощущаемая человеком, которую он называет жизнью. Стоп, а разве существует ли фактически отрицательная бесконечность? Конечно же, нет. Значит, что-то не складывается.
Однако невозможно рассуждать о бесконечности, равной нулю, руководствуясь лишь двумя составляющими данного равенства. Необходима и конкретика, то есть факты из жизни, подтверждающие верность мысли.
4
Человек рождается и умирает. В материальном смысле от него что-то, возможно, и остается. Но не от всех, конечно. А в вычислительном? Представим рождение знаком «плюс» и смерть знаком «минус». Снова возьмем любую цифру, хотя бы священную единицу. «Минус один» плюс «плюс один» равно нулю. Вот и всё, что остается от человека как от существа – ничего, ноль!
Да вот только мне думается, что я сам себе противоречу. От человека много что остается, пусть мы порой можем этого не заметить. От него остаются дети, недвижимость, следы на песке, объекты искусства, воспоминания у других… Самого же человека как биологического существа на планете после смерти не остается, хотя сохраняются его останки, то есть кости, иногда несущие функцию святых мощей. Так что остается от человека далеко не ноль, но и далеко не единица. А значит, что? А значит, что-то среднее между ними.
С самого «появления» (кавычки, потому что неизвестно, появлялся ли он когда-нибудь вообще или всегда существовал не эволюционируя)себя на планете человек осознал, что он ничтожество по сравнению с этим огромным миром. Он как капля в море, если не атом молекулы воды или, того гляди, что-то меньшее, еще не известное ученому. Полный ноль, как говорится. В одиночку он беззащитен: вокруг хищные звери, еду на блюдечке никто не поднесет, морозы скажут свое слово. Потому и начал он придумывать для себя панацею, дабы избавиться от комплекса мизерности и склонности самоунижать свое эго, ведь человек сам по себе изначально существо эгоистичное. Начал человек строить социальную дифференциацию, придумал государство, научно-технический прогресс, произошло и происходит одомашнивание животных и освоение природных богатств, начали шить теплую одежду, появился антропоцентризм. Отсюда, определенно, следует некий вывод: развитие человека происходит из-за страха перед природой и в полной мере не подчиненным ему. Не было бы страха – сидел бы и не дергался. Но долго не просидел бы… И вымер.
5
Но давайте посмотрим на ситуацию более позитивно. А раз позитивно, то по смыслу здесь ближе знак «плюс», о сакральности которого нельзя не упомянуть. Как мной уже заявлялось, рождение можно принять за прибавление человека к остальной общей массе, за «плюс». После смерти почти каждого человека всегда остается что-то, хоть капельку изменившее материю. Это следы на песке, это философские трактаты, это потомство, идеология… много можно говорить об этом, но я в силу сохранения эстетики формы этой статьи не стану уходить в сторону. Когда человек уходит в мир иной, можно характеризовать такое явление знаком «минус» (употребление в данном случае слова «процесс» вместо «явление» было бы циничным, жестоким и не в достаточной мере взвешенным). Но здесь догадываешься: за знаки «плюс» и «минус» мы приняли только стадии некого пребывания, если можно так выразиться, человека в материальном мире. Самое главное – мы оставили за бортом деятельность человека… А она будет явно положительного знака в своей основе – думаю, объяснять это подробно и с уходом в сторону не нужно. Как бы не был знаменит и хорош либо плох какой-нибудь отдельно взятый человек, какой бы масштаб ни приобрела его деятельность, но для мира все сделанное им подобно капле в море, которым мир, собственно и является. Не думаю, что возможно вычислить долю одной капли или хотя бы молекулы воды в масштабах мировых запасов воды как питьевой, так и не питьевой – такую десятичную дробь, во-первых, физически не вычислить, а во-вторых, не записать цифрами. Поэтому я бы обозначил ее, деятельность, как 0,(0)1. Потому я считаю следующее: бесконечность стремится к нулю. Я не математик или физик, чтобы выводить какую-то формулу, но методом примитивного мыслепостроения я вывожу следующее:
Бесконечность -> Коэффициент жизни – Коэффициент смерти = 0,(0)1. -> 0
Что я подразумеваю под коэффициентом жизни? На мой взгляд, это сумма рождения человека и его деятельности в течение жизни. Коэффициент жизни равен 1,(0)1, то есть «Рождение + Деятельность». Коэффициент смерти равен одному (равно как и рождение, смерть бывает только одна и одномоментна). Значит, из жизни вычесть смерть – останется деятельность? Именно так.
Из полученного значения следует, что деятельность влечет за собой ничтожно малое материальное изменение мира. Итог: бесконечность стремится к нулю и является деятельностью. Здесь может возникнуть некоторое понимание следующего: как это бесконечность стремится к чему-либо, ведь она статична. Да, она статична, но не забывайте, что абсолютно все, что находится вокруг нас – камни, трава, здания, животные, люди – и даже мы сами были кем-то когда созданы (то есть кто-то когда-то нас «сделал», то есть осуществил деятельность), а лучше считайте так и ни при каких условиях никогда не сомневайтесь в этом – зачем усложнять себе жизнь ненужным рассуждательским барахлом?
6
Ноль, как и бесконечность, являются одними из величайших тайн мира. Великая тайна – откуда взялась единица. Но еще больше великая и неразрешимая – откуда взялся ноль? Откуда взялось ничего, из чего это ничего появилось? Что было началом, когда начало началось? Всё это вопросы философского порядка, ответы на которые окончательно найти не удастся никогда. Выводы из этой главы, я боюсь, можно сделать неутешительные.
А есть ли ноль Бог? А есть ли ноль любая деятельность? А есть ли Бог деятельность. С туманом в глазах и огоньками, мерцающими в душе, мы каждый раз начинаем новый миг, ожидая пришествия того, чего хотим добиться. Кто-то хочет семью, кто-то деньги, кто-то славу, кто-то всеобщую любовь, ну, а кто-то постичь истину. Желательно, конечно, получить не один из приведенных пунктов, а несколько их вкупе, и в том числе те, которые в этом коротком списке не были найдены их искателем.
Кому истина, кому правда жизни – а кому-то бесконечность…
Некоторая интерпретация тезиса «бесконечность стремится к нулю» содержится во главе «Аксиома коэффициентарности бытия».
http://vk.com/club37892037 милости прошу)) ))))))))))) прЭлестно! Ощущение, что занять мозги больше было нечем)) Приходите в мою группу, я уже несколько лет пытаюсь через поэзию донести смысл этой фразы людям)
Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2019. Портал работает под эгидой Российского союза писателей. 18+
Давным давно, я решаю загадку бесконечности и нуля. Эту божественную загадку в решение которой, нет смысла, но одновременно смысл везде. Что же такое ноль? Это пустота, это ничего, но как не прискорбно признавать, это утверждение верно только на половину. Ноль это не только пустота, ноль это бесконечность.
Почему я решил поставить между нулем и бесконечностью знак равенства? Попробую объяснить, при деление любого числа на ноль n/0 (n-произвольное число) обычно люди говорят два ответа. Либо “на ноль дель нельзя”, либо “Бесконечность” . С первым ответом все понятно, но что делать со вторым? Почему при деление на ноль получается бесконечность?
Если рассмотреть картинку поста, то можно заметить функцию и её график (у)=1/x. Мы видим как меняется значение (у), если (х) стремится к +∞(∞-бесконечность), то (у) стремится к 0 и наоборот чем меньше (х) тем больше (у), то есть если (х) стремится к 0, то (у) стремится к +∞. Но мы забываем про отрицательные числа и отрицательную бесконечность -∞. на отрицательной стороне координат мы видим такую же ситуацию правда направленную в противоположную сторону, при(х) стремящимся к -∞ (у) стремится к 0, при (у) стремящемся к -∞ (х) стремится к 0, но здесь и появляется парадокс деления на 0. То есть
Но у нас два ответа, какой же нам выбрать? В такой ситуации можно найти среднею арифметическую, то есть
Под ∞ я беру всю прямую от -∞ до +∞.
P.S. В следующем посте попытаюсь объяснить, почему 0=n (n-произвольное число).
Дубликаты не найдены
Во-первых, если вы под нулем понимаете число (самое обыкновенное, знакомое со второго класса), то ответ тут один – неопределенность, а потому делить нельзя. Все, кто говорят иное, не понимают основ.
Во-вторых, если вам так хочется получить бесконечность, то надо под нулем понимать класс эквивалентности, вмещающий в себя все последовательности x_n/ функции f(x), стремящиеся к нулю (бесконечно малые) при n->∞ / x->x0.
При X = 0 у нас неопределенность, как уже было сказано. Можно рассматривать предел, при X->0. Первокурсникам говорят, что предела нет. Ибо предел, если существует, то единственен. Но есть односторонние пределы (если в терминах последовательностей, можно говорить о пределах частичных). К концу первого курса обычно говорят, что если пределы по всем направлениям – какая-то знаковая бесконечность, то можно сказать, что предел – просто бесконечность, без знака. Это удобно, ибо дальше, в ТФКП, бесконечностей можно придумать слишком дохрена, а точнее – как минимум континуальное множество. Потому там бесконечность одна, беззнаковая, без направления. ∞ и все.
Дальше, вы с какого-то перепугу решили сложить две разнознаковые бесконечности и получили ноль. Сложение бесконечности, если вы не понимаете, что под ней имеете в виду, с чем угодно – занятие абсурдное. Поэтому буду считать, что вы складываете две последовательности и берете предел. Чтобы сложить две бесконечно большие последовательности/функции и получить в пределе ноль, нужно, минимум, чтоб они имели одинаковый порядок роста, но этого недостаточно.2. f(x) + g(x) = x -> +∞, при x->+∞
Еще дальше. Забудем о всех этих ужасных ошибках, которые вы допускаете с бесконечностями. Вы пишите, что можно взять два результата и обобщить их с помощью среднего арифметического. Когда кто-то пользуется средним арифметическим как “лекарством от всего”, в мире рыдают все нормальные статистики. Обязательно нужно пояснять адекватность выбора метода усреднения, иначе получаем средний доход человека в 100К в доме с одним миллионером и девятью безработными.
>
Шикарно! Давайте вообще все числа будем обозначать одним и тем же знаком, это же так здорово! Сразу решаются все проблемы мирозданья.
Таким образом, я делаю вывод, что весь этот пост очередной бред из серии “Школьник доказал существование жизни после смерти с помощью матанализа.”
Рассмотрим основные типы неопределенностей пределов на бесконечности с примерами решений:
- $ [frac<0><0>] $
- $ [infty – infty] $
- $[frac<infty><infty>]^ <[infty]>и [1 ^ infty] $
| Пример 1 |
| Вычислить предел функции, стремящейся к бесконечности $ lim _limits frac$ |
| Решение |
Первым делом подставляем $ x o infty $ в предел, чтобы попытаться его вычислить.x = e qquad (1) $$
Из выражения, стоящего под знаком предела вычитаем единицу, чтобы его подстроить под формулу (1).
Перепишем предел из условия задачи в новом виде и подставим в него $x o infty$.
Пользуясь формулой (1) проведем вычисление лимита. В скобках перевернем дробь.
По условиями формулы второго замечательного предела (1) в скобках знаменатель дроби должен быть равен степени за скобкой. Выполним преобразование степени. Для этого умножим и разделим на $frac<3x+2><-6>$.
Остаётся сократить степень экспоненты и найти её предел.
Предел дроби равен отношению коэффициентов при старшей степени $x$.
Бесконечные пределы и асимптоты
Помимо конечных пределов, у последовательностей бывают бесконечные (см. раздел Пределы и ограниченность в главе 5). У функций тоже!12.1Бесконечные пределы в конечных точках
12.1.1Существование предела и ограниченность
Из лекции 5 мы знаем, что сходящаяся последовательность ограничена. Для функций можно сформулировать аналогичное утверждение. Теорема 1. Пусть функция f(x) имеет предел при x→x0. Тогда она ограничена на некоторой проколотой окрестности точки x0. Иными словами, найдутся такие C и δ∗>0, что для всех x∈˚Uδ∗(x) выполняется неравенство |f(x)|<C. Доказательство. По определению предела, для всякого ε>0 найдётся такое δ=δ(ε)>0, что для всех x из проколотой δ-окрестности x0 выполняется неравенство |f(x)−b|<ε.Положим δ∗:=δ(1) (то есть возьмём ε=1). Тогда для всех x из проколотой δ∗-окрестности точки x0 выполняется неравенство |f(x)−b|<1. По неравенству треугольника,
|f(x)|≤|f(x)−b|+|b−0|<1+|b|.
Положим C=1+|b|. Тогда ˚Uδ∗(x) — искомая окрестность точки x0. Теорема доказана.∎Доказательство очень похоже на доказательство аналогичной теоремы для последовательностей, и даже проще: в случае с последовательностями нужно было отдельно рассматривать начальный отрезок. За это мы платим тем фактом, что утверждение об ограниченности распространяется не на всю область определения функции, а лишь на некоторую проколотую окрестность точки x0.
Пример 1. Рассмотрим функцию f(x)=1/x. Она имеет предел при x→1, однако не является ограниченной на всей области определения.
12.1.2Бесконечные пределы
В том случае, когда функция не является ограниченной ни в какой проколотой окрестности точки x0, она не может иметь предела в этой точке. Однако, опять аналогично ситуациям с последовательностями, мы можем определить, что означает, что функция стремится к бесконечности в точке x0. Определение 1. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что её предел в этой точке равен бесконечности, если для всякого C найдётся такая δ>0, что для всех x из проколотой δ-окрестности точки x0 выполняется неравенство: |f(x)|>C. Формально:∀C∈R ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)|>C.
Записывают:limx→x0f(x)=∞.
Пример 2. Функция f(x)=1x стремится к бесконечности при x→0. Дейстительно, возьмём любоое C. Если C≤0, условие |1/x|>C выполнено автоматически. Если C>0, положим δ=1/C. Тогда если |x|<δ, то |1/x|=1/|x|>1/δ=C.import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
def f(x):
return 1 / x
C = 1.7
x = np.linspace(-2.7, 2.7, 211)
plt.figure(figsize=(4, 4))
plt.plot(x, np.full_like(x, C), '--', color='C1', linewidth=1)
plt.plot(x, np.full_like(x, -C), '--', color='C1', linewidth=1)
plt.plot(np.full_like(x, 1/C), x, '--', color='C2', linewidth=1)
plt.plot(np.full_like(x, -1/C), x, '--', color='C2', linewidth=1)
plt.annotate("$C$", (0.05, C + 0.05))
plt.annotate("$-C$", (0.05, -C + 0.05))
plt.annotate(r"$\delta$", (1/C + 0.05, 0 + 0.05))
plt.annotate(r"$-\delta$", (-1/C + 0.05, 0 + 0.05))
plt.plot([-1/C, 1/C], [0, 0], '-', linewidth=3, color='C2',
alpha=0.7, solid_capstyle='butt')
plt.plot([0, 0], [C, 2.7], '-', linewidth=3, color='C1',
solid_capstyle='butt')
plt.plot([0], [0], 'o', color='C2', markerfacecolor='white',
markeredgewidth=2)
plt.plot([0, 0], [-C, -2.7], '-', linewidth=3, color='C1',
solid_capstyle='butt')
plt.plot(x, f(x), label='$y=1/x$')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-2.7, xmax=2.7, ymin=-2.7, ymax=2.7,
xlabel="x", ylabel="y", axlabelshift=1.3)
# plt.xticks([1/C, -1/C], [r"$\delta$", r"$-\delta$"])
plt.xticks([])
plt.yticks([])f(x)={1/x,x∈Q,0,x∉Q,
не является ограниченной ни в какой проколотой окрестности точки x=0 (поскольку сколь угодно близко к нулю существуют рациональные числа), но при этом не стремится к бесконечности при x→0 (поскольку сколь угодно близко к нулю существуют иррациональные числа, в которых функция принимает значение 0).Опять же, аналогично последовательностям, помимо просто бесконечности, бывает плюс бесконечность и минус бесконечность:
Определение 2. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что её предел в этой точке равен плюс бесконечности (минус бесконечности), если для всякого C найдётся такая δ>0, что для всех x из проколотой δ-окрестности точки x0 выполняется неравенство: f(x)>C (соответственно, f(x)<C). Формально:Пример 4. Неверно, что 1/x→+∞ при x→0: когда x приближается к нулю слева (то есть становится очень маленьким по модулю, но отрицательным), 1/x становится большим по модулю, но тоже отрицательным. В то же время, 1/(x2)→+∞ при x→0: знаменатель всегда положительный при x≠0, и когда он маленький по модулю, дробь становится очень большой.
Наконец, можно рассматривать односторонние бесконечные пределы.
Упражнение 1. Придумайте определения для утверждений limx→x+0f(x)=+∞, limx→x+0f(x)=−∞, limx→x−0f(x)=+∞, limx→x−0f(x)=−∞ самостоятельно, объединяя определение 2 и определения 7 и 8 из лекции 10. Упражнение 2. Снова рассмотрим функцию f(x)=1/x. Докажите, чтоlimx→0+1x=+∞
иlimx→0−1x=−∞.
Определение 3. Заметим, что если функция стремится к какой-нибудь из бесконечностей (неважно, плюс, минус или просто бесконечности) когда x стремится к x0 с какой-нибудь стороны, график y=f(x) приближается к вертикальной прямой x=x0 когда x приближается к x0 (слева или справа). В этом случае прямая x=x0 называется вертикальной асимптотой функции y=f(x) (или её графика).
Пример 5. Рассмотрим функциюf(x)=x−1×2−1.
Знаменатель обнуляется в двух точках: x=1 и x=−1. При приближении к точке x=−1 знаменатель стремится к нулю, а числитель к −2. Значит, дробь стремится к бесконечности (без знака, т.к. знаменатель может быть положительным или отрицательным, в зависимости от того, с какой стороны приближаемся). У функции есть вертикальная асимптота x=−1. В точке x=1 обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке, сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел, равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции нет.import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
def f(x):
return (x - 1) / (x ** 2 - 1)
x = np.linspace(-4, 4, 161)
plt.figure(figsize=(5, 5))
plt.plot(x, f(x), label=r'$y=\frac{x-1}{x^2-1}$')
plt.plot([1], [0.5], 'o',
color='C0', markerfacecolor='white',
markeredgewidth=1.5)
plt.plot([-1, -1], [-4, 4], linewidth=1, color='C2')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-3.7, xmax=3.7, ymin=-3.7, ymax=3.7,
xlabel="x", ylabel="y") Рис. 12.2: У функции f(x)=x−1×2−1 есть единственная вертикальная асимптота: x=−1.
12.2Пределы на бесконечности
Другой тип пределов функций, связанный с бесконечностями — это предел при x стремящемся к бесконечности.12.2.1Конечные пределы на бесконечности и горизонтальные асимптоты
Определение 4. Пусть функция f(x) определена для всех достаточно больших по модулю значений x, то есть найдётся такое C∗, что f(x) определена для всех x, для которых |x|>C∗. Говорят, что предел функции f(x) при x стремящемся к бесконечности равен b, если для всякого ε>0 найдётся такое C, что для всех x, если |x|>C, то |f(x)−b|<ε.
Определение 5. Пусть функция f(x) определена для всех достаточно больших значений x, то есть найдётся такое C∗, что f(x) определена для всех x>C∗. Говорят, что предел функции f(x) при x стремящемся к плюс бесконечности равен b, если для всякого ε>0 найдётся такое C, что для всех x>C верно неравенство |f(x)−b|<ε.
Определение 6. Пусть функция f(x) определена для всех достаточно больших по модулю отрицательных значений x, то есть найдётся такое C∗, что f(x) определена для всех x<C∗. Говорят, что предел функции f(x) при x стремящемся к минус бесконечности равен b, если для всякого ε>0 найдётся такое C, что для всех x<C верно неравенство |f(x)−b|<ε.
Обозначения:
limx→∞f(x)=b,limx→+∞f(x)=b,limx→−∞f(x)=b.
Упражнение 3. Докажите, что если limx→∞f(x)=b, то limx→+∞f(x)=b и limx→−∞f(x)=b. Верно и обратное: если limx→+∞f(x)=b и limx→−∞f(x)=b, то limx→∞f(x)=b. Докажите и это.
Пример 6. Функция f(x)=1/x стремится к нулю при x→∞. (Докажите!)
Пример 7. Функция f(x)=ex стремится к нулю при x→−∞, а предел при x→+∞ не существует.
Определение 7. Если функция стремится к какому-то числу при x→+∞ или x→−∞, её график приближается к горизонтальной прямой x=b. Такая прямая называется горизонтальной асимптотой.
import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
def f(x):
return np.sin(x) / x
x = np.linspace(-40, 40, 411)
plt.figure(figsize=(6, 3))
plt.plot(x, f(x), label=r'$y=\frac{\sin x}{x}$')
plt.plot([0], [1], 'o', color='C0', markersize=4, markerfacecolor='white',
markeredgewidth=1.5)
plt.plot([-40, 40], [0, 0], '-', linewidth=2, color='C2')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-40, xmax=40, ymin=-0.5, ymax=1.2,
xlabel="x", ylabel="y", axlabelshift=1.2)
plt.xticks([])
plt.yticks([])Рис. 12.3: Прямая y=0 является горизонтальной асимптотой функции f(x)=(sinx)/x.
Вопрос 1. Сколько вертикальных асимптот может быть у функции? Вопрос 2. Рассмотрим два предела: предел функции limx→+∞sin(πx) и предел последовательности limn→∞sin(πn). Что вы можете про них сказать?12.2.2Бесконечные пределы на бесконечности
Мы рассмотрели бесконечные пределы в конечных точках и конечные пределы на бесконечности. Можно скрестить ужа с ежом и получить бесконечные пределы при x стремящемся к бесконечности. Определение 8. Пусть функция f(x) определена для всех достаточно больших значений x, то есть найдётся такое C∗, что f(x) определена для всех x>C∗. Говорят, что предел функции f(x) при x стремящемся к плюс бесконечности равен плюс бесконечности, если для всякого D найдётся такое C, что для всех x>C верно неравенство f(x)>D. Записывают:limx→+∞f(x)=+∞.
Упражнение 4. Придумайте определения для остальных комбинаций бесконечностей.
Пример 8. Функция f(x)=x2 стремится к плюс бесконечности при x→∞, а функция f(x)=x3 стремится просто к бесконечности при x→∞.
Пример 9. Рассмотрим функциюf(x)=11+e−x.
При x→+∞ функция e−x стремится к нулю (она равна 1/ex, и раз ex становится очень-очень большим, e−x становится очень близким к нулю).{-x}}$’) plt.plot([-4, 4], [0, 0], ‘-‘, linewidth=2, color=’C2’) plt.plot([-4, 4], [1, 1], ‘-‘, linewidth=2, color=’C2’) plt.legend() ob.center_spines(grid=False, minor_ticks=False) ob.settle_axes(xmin=-4, xmax=4, ymin=-0.1, ymax=1.2, xlabel=”x”, ylabel=”y”, axlabelshift=1.2) plt.xticks([]) plt.yticks([1], [‘$1$’], va=”bottom”)Рис. 12.4: У функции f(x)=1/(1+e−x) две горизонтальные асимптоты: x=0 и x=1.
12.2.3Наклонные асимптоты
Пусть limx→∞f(x)=∞. Тогда функция не может иметь горизонтальных асимптот. Однако её график по-прежнему может приближаться к какой-нибудь прямой — только не горизонтальной. Пример 10. Рассмотрим функциюf(x)=x+1x.
Её предел при x→∞ равен бесконечности, и когда x стремится к бесконечности, график функции неограниченно приближается к прямой y=x.import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
def f(x):
return x + 1 / x
x = np.linspace(-4, 4, 411)
plt.figure(figsize=(4, 4))
plt.plot(x, f(x), label=r'$y=x+\frac{1}{x}$')
plt.plot([-4, 4], [-4, 4], '-', linewidth=1, color='C2')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-4, xmax=4, ymin=-4, ymax=4,
xlabel="x", ylabel="y", axlabelshift=1.2)
plt.xticks([])
plt.yticks([], [])Рис. 12.5: У функции f(x)=x+1x есть наклонная асимптота y=x.
Действительно, давайте возьмём большое значение x=x0 и посчитаем «расстояние по вертикали» между графиком функции и прямой y=x для этого значения x. (Иными словами, мы проведём вертикальную прямую x=x0 и посмотрим на расстояние между точками пересечения этой прямой и графиков y=f(x) и y=x.) Это расстояние вычисляется как |f(x)−x|=|1/x|. Оно стремится к нулю при x→∞. Определение 9. Прямая y=kx+b называется наклонной асимптотой функции f(x) (или её графика), если хотя бы один из пределовlimx→+∞(f(x)−(kx+b)),илиlimx→−∞(f(x)−(kx+b))
равен нулю.Как искать наклонные асимптоты? На эту тему есть рецепт.
Утверждение 1. Наклонная асимптота y=kx+b при x→+∞ у функции f(x) существует тогда и только тогда, когда существуют пределы limx→+∞f(x)x=k;limx→+∞(f(x)−kx)=b.(12.1)(12.2) При этом они обязаны равняться указанным значениям (k и b).
Доказательство. Докажем в одну сторону. Пусть y=kx+b является наклонной асимптотой функции f(x) при x→+∞. Тогдаlimx→+∞f(x)x=limx→+∞f(x)−(kx+b)+(kx+b)x=limx→+∞(f(x)−(kx+b)x+k+bx)=k
Предел первого слагаемого равен нулю, поскольку числитель стремится к нулю (по предположению), а знаменатель к бесконечности.Со вторым пределом ещё проще:
limx→+∞(f(x)−kx)=limx→+∞((f(x)−(kx+b)+b)=b.
В обратную сторону. Пусть существует предел (12.2) и он равен b. Тогдаlimx→+∞(f(x)−(kx+b))=limx→+∞(f(x)−kx)−b=b−b=0.
Утверждение доказано.∎Конечно, можно сформулировать и доказать аналогичное утверждение для x→−∞.
Таким образом, чтобы найти наклонные асимптоты, нужно сперва найти предел (12.1). Если он не существует, наклонной асимптоты (для этой бесконечности) точно нет. Если существует, нужно найти предел (12.2). Если этот предел существует, прямая y=kx+b является наклонной асимптотой.
Пример 11. Может так случиться, что предел (12.1) существует, а предел (12.2) нет. Например, это верно для функции f(x)=sinx.12.3Заключение
Главная цель математического анализа — научиться «заглядывать в бесконечность». В этой лекции мы серьезно продвинулись в этом навыке.← Предыдущая глава Следующая глава →
ADDERLink INFINITY Manager | Adder Technology
Безопасный доступ и связь
Использование TLS (безопасность транспортного уровня) и HTTPS обеспечивает безопасность связи между устройствами ADDERLink ™ INFINITY (ALIF) и ADDERLink INFINITY Manager (AIM), а также между AIM и внешним миром.
Работа с резервированием
Для обеспечения круглосуточной надежности можно добавить второй «горячий» AIM, чтобы обеспечить постоянное время безотказной работы, а с двумя интерфейсами NIC на каждом устройстве ALIF можно легко спроектировать системы для обеспечения максимальной отказоустойчивости.
Управление правами доступа пользователей и контрольный журнал
Администраторы могут управлять правами доступа к каждому устройству для каждого пользователя вручную через веб-браузер или автоматически с помощью Active Directory. Отчеты, показывающие историю устройств, логинов пользователей и подключений устройств, можно просматривать и экспортировать в файл CSV или через SYSLOG.
Простое централизованное управление
Доступная через веб-браузер, приборная панель дает в реальном времени обзор системных подключений и пользователей.Вкладки позволяют перемещаться между настройками и устройствами или пользовательскими подменю.
Соединения канала управления и предустановок
AIM можно использовать для централизованного соединения между отдельной парой передающих и приемных устройств из системы управления. Используя Presets, список предустановленных подключений, многоэкранных настроек, видеостен или вывесок можно «нажать» одним щелчком мыши.
Интернационализация
Пользовательские столы могут выбирать различные конфигурации клавиатуры в соответствии со своими требованиями и в качестве глобальной настройки выбирать язык для экранного меню из более чем 14 языков.
Экранный дисплей на каждой пользовательской станции
Пользователи входят в систему и выбирают подключения каналов из интуитивно понятного экранного меню, аналогичного цифровому ТВ. Пользователи также могут использовать предустановки для переключения каналов для нескольких экранов на нескольких приемниках.
Удаленное экранное меню
Удаленное экранное меню позволяет пользователю «передавать» видео и управлять им на другую станцию, на видеостену или проектор. Избранное и переключение горячих клавиш Каждый пользователь может выбрать свои любимые каналы в экранном меню и назначить горячую клавишу для быстрого переключения между каналами.
Выбор режимов подключения
Администраторы могут предоставить пользователям возможность подключаться в четырех режимах: только просмотр, общий, частный или эксклюзивный. Затем каждый разрешенный режим становится доступным в экранном меню.
Быстрое переключение видео и USB
Время переключения между компьютерами составляет менее 1 секунды, что обеспечивает удобство работы пользователей. Многоадресная передача Многоадресная передача в сети позволяет системе одновременно передавать видео с одного передатчика на неограниченное количество приемников.Подходит для вывесок, мониторинга и совместного использования рабочих столов.
Многоадресная рассылка
Сетевая многоадресная рассылка позволяет системе передавать видео одновременно с одного передатчика на неограниченное количество приемников. Подходит для вывесок, мониторинга и совместного использования рабочих столов.
Совместное использование USB
Совместное использование USB позволяет нескольким пользователям одновременно подключаться к одному компьютеру и управлять им. Каждый передатчик может сообщать о 12 уникальных USB-устройствах (идентифицируемых кодами VID / PID), но объединяет устройства с одинаковым идентификатором, чтобы разрешить намного больше.
Каналы
Рассматриваемый как виртуальный передатчик, канал может объединять видео, аудио и USB от разных передатчиков как единый источник. Идеально подходит там, где требуются звуковые оповещения или смешанные источники видео.
Открытый API для сторонних систем управления
Adder Technology публикует простую структуру API, позволяющую легко интегрироваться с другими сторонними системами управления, поставляемыми такими компаниями, как AMX, Crestron, HRS или MediaLon на уровне HTTP.
Интеграция LDAP
Чтобы упростить настройку, система имеет интерфейс LDAP, позволяющий легко импортировать пользователей и пароли из других систем.
SNMP v3 get / walk
Внешние машины могут опрашивать AIM, чтобы узнать состояние сети и устройств ALIF. Реализована безопасность SNMP v3 с поддержкой транспорта AES / DES с аутентификацией MD5 / SHA.
Поддержка внешнего сервера NTP – NTPv4.2
Подключите до 3 серверов NTP с аутентифицированными соединениями, используя MD5 и Key ID, как определено в стандартах NTP. Все устройства ALIF в сети AIM теперь получают время с использованием аутентифицированного NTP от AIM.
Резервные копии системы
Резервные копии базы данных могут быть сохранены внутри, снаружи или автоматически отправлены по электронной почте. Автоматические обновления могут быть запланированы ежечасно, ежедневно или еженедельно.
Централизованное обновление прошивки
Помимо управления собственным обновлением прошивки, AIM управляет обновлением каждого устройства в сети и может одновременно развертывать прошивку на сотнях устройств, то есть общесистемное обновление занимает всего несколько минут.
Простая настройка матрицы
Использование нулевой конфигурации.сети, AIM автоматически получает MAC-адреса устройств расширения, когда они подключены к сети. Администратор выделяет IP-адреса, имена и местоположения, чтобы устройства было легко идентифицировать, настраивать и контролировать.
AdderLink INFINITY Manager AIM с поддержкой 24 конечных точек | AIM-24-US
Купите этот предмет и заработайте 4 033 ClubPoints.
AIM-24: Сервер матричного управления AdderLink INFINITY и встроенное программное обеспечение, поддерживающее 24 конечных точки
цифровой KVM-матричный сервер управления 19-дюймовым форм-фактором 1U обеспечивает полный контроль над всеми устройствами AdderLink INFINITY, подключенными к вашей медиасети
• Интуитивно понятный многоязычный пользовательский интерфейс
• Несколько методов переключения
• Настраиваемые права доступа пользователей
• Полный контрольный журнал
• Простое централизованное управление
• Открытый API для стороннего контроля
AdderLink INFINITY позволяют нескольким удаленным пользователям очень гибко получать доступ к хост-компьютерам.Такая гибкость требует управления и координации – вот где AdderLink INFINITY Manager (AIM) становится жизненно важным.
Сервер управленияAIM – это пакет управления, который превращает расширители AdderLink INFINITY в решение с цифровой матрицей. Используя стандартную IP-инфраструктуру, можно направить любую пользовательскую станцию на любой компьютер, подключенный к сети, без какого-либо ущерба для качества видео или управления. Это позволяет совместное использование компьютеров и многоадресную передачу видео в любое место.
AIM разработан для обеспечения наиболее эффективного использования устройств AdderLink INFINITY, позволяя централизованно управлять любым количеством передатчиков (более часто называемых «каналами» в AIM) и приемников. Используя интуитивно понятный веб-интерфейс AIM, один или несколько администраторов могут управлять потенциально тысячами пользователей, которые взаимодействуют с почти неограниченным количеством устройств.
Adder INFINITY Management работает от автономного компактного сервера, который может быть расположен в любом месте вашей сети.
СерверAIM поставляется предварительно загруженным и прост в развертывании, требуя только подключения к сети и источника питания для начала работы.
Вся конфигурация ваших передатчиков (каналов), приемников и пользователей INFINITY выполняется с помощью интуитивно понятного интерфейса браузера AIM через подключенный к сети компьютер.
Безопасный доступ и связь
Использование TLS (безопасность транспортного уровня) и HTTPS обеспечивает безопасность связи между устройствами AdderLink и AIM, а также между AIM и внешним миром.
Работа с резервированием
Для обеспечения круглосуточной надежности можно добавить второй горячий модуль AIM, чтобы гарантировать постоянное время безотказной работы, а с двумя интерфейсами NIC на каждом модуле AdderLink INFINITY можно легко спроектировать системы для обеспечения максимальной отказоустойчивости.
Управление правами доступа пользователей и контрольный журнал
Администраторы могут управлять правами доступа к каждому устройству для каждого пользователя вручную через веб-браузер или автоматически с помощью Active Directory. Отчеты, показывающие историю устройств, логинов пользователей и подключений устройств, можно просматривать и экспортировать в файл CSV или через SYSLOG.
Простое централизованное управление
Доступная через веб-браузер, информационная панель дает обзор системных подключений и пользователей в реальном времени. Вкладки позволяют перемещаться между настройками и подменю устройства или пользователя.
Соединения канала управления и предустановок
AIM можно использовать для централизованного соединения между отдельной парой передающих и приемных устройств из системы управления. Используя Presets, список предустановленных подключений, многоэкранных настроек, видеостен или вывесок можно принудительно запустить одним щелчком мыши.
Интернационализация
Пользовательские столы могут выбирать различные конфигурации клавиатуры в соответствии со своими требованиями и в качестве глобальной настройки выбирать язык для экранного меню из более чем 14 языков.
Отображение на экране на каждой пользовательской станции
Пользователи входят в систему и выбирают подключения каналов из интуитивно понятного экранного меню, аналогичного цифровому ТВ. Пользователи также могут использовать предустановки для переключения каналов для нескольких экранов на нескольких приемниках.
Удаленное экранное меню
Удаленное экранное меню позволяет пользователю «передавать» видео и управлять им на другую станцию, на видеостену или проектор.
Избранное и переключение горячих клавиш
Каждый пользователь может выбрать свои любимые каналы в экранном меню и назначить горячую клавишу для быстрого переключения между каналами.
Выбор режимов подключения
Администраторы могут предоставить пользователям возможность подключаться в трех режимах: только просмотр, общий или эксклюзивный. Затем каждый разрешенный режим становится доступным в экранном меню.
Быстрое переключение видео и USB
Время переключения между компьютерами составляет менее 1 секунды, что обеспечивает удобство работы пользователей.
Многоадресная рассылка
Сетевая многоадресная рассылка позволяет системе передавать видео одновременно с одного передатчика на неограниченное количество приемников. Подходит для вывесок, мониторинга и совместного использования рабочих столов.
Совместное использование USB
Совместное использование USB позволяет нескольким пользователям одновременно подключаться к одному компьютеру и управлять им. Каждый передатчик может сообщать о 12 уникальных USB-устройствах (идентифицируемых кодами VID / PID), но объединяет устройства с одинаковым идентификатором, чтобы разрешить намного больше.
Каналы
Рассматриваемый как виртуальный передатчик, канал может объединять видео, аудио и USB от разных передатчиков как единый источник. Идеально подходит там, где требуются звуковые оповещения или смешанные источники видео.
Открытый API для сторонних систем управления
Adder Technology публикует простую структуру API, позволяющую легко интегрироваться с другими системами управления сторонних производителей, предоставляемыми такими компаниями, как AMX, Crestron, HRS или MediaLon на уровне HTTP.
Интеграция LDAP
Чтобы упростить настройку, система имеет интерфейс LDAP, позволяющий легко импортировать пользователей и пароли из других систем.
SNMP v3 get / walk
Внешние машины могут опрашивать AIM, чтобы узнать состояние сети и устройств AdderLink INFINITY. Реализована безопасность SNMP v3 с поддержкой транспорта AES / DES с аутентификацией MD5 / SHA.
Поддержка внешнего сервера NTP – NTPv4.2
Подключите до 3 серверов NTP с аутентифицированными соединениями, используя MD5 и Key ID, как определено в стандартах NTP. Все устройства AdderLink INFINITY в сети AIM теперь получают время с использованием аутентифицированного NTP от AIM
Резервные копии системы
Резервные копии базы данных могут быть сохранены внутри, снаружи или автоматически отправлены по электронной почте.Автоматические обновления могут быть запланированы ежечасно, ежедневно или еженедельно.
Централизованное обновление прошивки
Помимо управления собственным обновлением прошивки, AIM управляет обновлением каждого устройства в сети и может одновременно развертывать прошивку на сотнях устройств, то есть общесистемное обновление занимает всего несколько минут .
Простая настройка матрицы
При использовании сети с нулевой конфигурацией AIM автоматически получает MAC-адреса устройств расширения, когда они подключены к сети.Администратор выделяет IP-адреса, имена и местоположения, чтобы устройства было легко идентифицировать, настраивать и контролировать.
Устройство управления матрицей ADDERLink Infinity Manager AIM-24
A.I.M. сервер управления – это пакет управления, который преобразует Расширители AdderLink Infinity в цифровом матричном решении. С использованием стандартная IP-инфраструктура позволяет направить любую пользовательскую станцию на любой компьютер, подключенный к сети, без ущерба для видео качество или контроль.Это позволяет совместно использовать компьютеры и мультикастинг видео в любую точку.
• Интуитивно понятный многоязычный пользовательский интерфейс
• Несколько методов переключения
• Настраиваемые права доступа пользователей
• Полный контрольный журнал
• Простое централизованное управление
• Открытый API для стороннего контроля
Безопасный доступ и связь
Использование
TLS (безопасность транспортного уровня) и HTTPS, связь между
Модули AdderLink и A.I.M. и между А.I.M. и внешний мир
все в безопасности.
Работа с резервированием
Для круглосуточной надежности a
второй горячий A.I.M. могут быть добавлены для обеспечения постоянного времени безотказной работы и с двойным
Интерфейсы NIC на каждом устройстве AdderLink Infinity, системы могут быть легко
разработан для максимальной устойчивости.
Управление правами доступа пользователей и журнал аудита
Администраторы
может управлять правами доступа к каждому устройству в зависимости от пользователя, либо
вручную через веб-браузер или автоматически с помощью Active
Справочник.Отчеты, показывающие историю устройств, логинов пользователей и
подключения устройств можно просматривать и экспортировать в файл CSV или через
SYSLOG.
Простое централизованное управление
Доступ через Интернет
браузер, панель инструментов дает обзор системных подключений в режиме реального времени
и пользователи. Вкладки позволяют перемещаться между настройками и устройством или
подменю пользователя.
Подключение каналов управления и предустановок
A.I.M.
может использоваться для установления связи между отдельной парой
передающие и приемные устройства централизованно из системы управления
система.Использование предустановок, список предустановленных подключений, многоэкранный режим,
Настроить видеостену или вывески можно одним щелчком мыши.
Интернационализация
пользовательские столы могут выбирать различные конфигурации клавиатуры в соответствии с их
требований и в качестве глобальной настройки выберите язык экранного меню.
из более чем 14 языков на выбор.
ОСОБЕННОСТИ – интуитивно понятный пользовательский интерфейс
Экранное меню на каждой пользовательской станции
пользователей
войдите в систему и выберите подключения каналов из интуитивно понятного экранного меню, похожего на
что из цифрового телевидения.Пользователи также могут использовать пресеты для переключения каналов для
несколько экранов на нескольких приемниках.
Удаленное экранное меню
Удаленное экранное меню позволяет пользователю «передавать» видео и управлять им на другую станцию, на видеостену или проектор.
Избранное и переключение горячих клавиш
Каждый пользователь может выбрать свои любимые каналы в экранном меню и назначить горячую клавишу для быстрого переключения между каналами.
Выбор режима подключения
Администраторы
может предоставить пользователям возможность подключаться в трех режимах: Просмотр
только, общий или эксклюзивный.Затем становится доступным каждый разрешенный режим.
в экранном меню.
Быстрое переключение видео и USB
Время переключения между компьютерами составляет менее 1 секунды для обеспечения качественного взаимодействия с пользователем.
AIM-24 Менеджер конечных точек AdderLink Infinity 24
Открытый API для сторонних систем управления
Adder Technology публикует простую структуру API, позволяющую легко интегрироваться с другими системами управления сторонних производителей, предоставляемыми такими компаниями, как AMX, Crestron, HRS или MediaLon на уровне HTTP.
Интеграция с LDAP
Чтобы упростить настройку, система имеет интерфейс LDAP, поэтому пользователи и пароли из других систем могут быть легко импортированы.
SNMP v3 получение / прогулка
Внешние машины могут опрашивать A.I.M. чтобы узнать статус сети и устройств AdderLink Infinity. Реализована безопасность SNMP v3 с поддержкой транспорта AES / DES с аутентификацией MD5 / SHA.
Поддержка внешнего сервера NTP – NTPv4.2
Подключите до 3 серверов NTP с аутентифицированными соединениями с использованием MD5 и Key ID, как определено в стандартах NTP.Все блоки AdderLink Infinity в A.I.M. сеть теперь получает время с использованием аутентифицированного NTP от A.I.M.
Резервное копирование системы
Резервные копии базы данных могут быть сохранены внутри, снаружи или автоматически отправлены по электронной почте. Автоматические обновления можно планировать ежечасно, ежедневно или еженедельно.
Централизованное обновление прошивки
Помимо управления собственным обновлением прошивки, A.I.M. управляет обновлением каждого устройства в сети и может одновременно развертывать микропрограммное обеспечение на сотнях устройств, то есть общесистемное обновление занимает всего несколько минут.
Простая настройка матрицы
Используя сеть с нулевой конфигурацией, A.I.M. автоматически получает MAC-адреса устройств расширения, когда они подключены к сети. Администратор выделяет IP-адреса, имена и местоположения, чтобы устройства можно было легко идентифицировать, настраивать и контролировать.
Оборудование
Промышленный сервер с твердотельной памятью.
Программное обеспечение
Закрытая система под управлением Linux.
Физическая конструкция
19-дюймовый корпус высотой 1U в прочной металлической конструкции.432 мм / 17 дюймов (ширина), 44 мм / 1,73 дюйма (высота), 230 мм / 9 дюймов (глубина), 2,75 кг / 6 фунтов.
Мощность
Внешний блок ввода питания IEC, 100–240 В переменного тока, 50/60 Гц, 1,5 А, вход для адаптера питания. 12 В постоянного тока, выход 60 Вт.
Рабочая температура
от 0 до 40 ° C / от 32 до 104 ° F.
Сертификаты
CE, FCC
| 0
0 отзывов покупателей. Описание: Устройство AIM-192-US A.I.M. Сервер управления – это пакет управления, который превращает расширители AdderLink Infinity в решение с цифровой матрицей. Используя стандартную IP-инфраструктуру, можно направить любую пользовательскую станцию на любой компьютер, подключенный к сети, без какого-либо ущерба для качества видео или управления. AIM-192-US AdderLink Infinity Manager позволяет совместное использование компьютеров и многоадресную передачу видео в любое место назначения. Номер позиции: # AIM-192-US | ||||||||||||||||||||||||||||
Характеристики продукта
| |||||||||||||||||||||||||||||
Сопутствующие товары | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Сумматор INFINITY Manager | Административный пакет управления для ADDERLink
Сумматор INFINITY Manager | Административный пакет управления для ADDERLink
Дом А.Сервер управления I.M. – это пакет управления, который превращает расширители AdderLink Infinity в решение с цифровой матрицей. Используя стандартную IP-инфраструктуру, можно направить любую пользовательскую станцию на любой компьютер, подключенный к сети, без какого-либо ущерба для качества видео или управления. Это позволяет совместное использование компьютеров и многоадресную передачу видео в любое место.
- Интуитивно понятный многоязычный пользовательский интерфейс
- Несколько методов переключения
- Конфигурируемые права доступа пользователя
- Полный журнал аудита
- Простое централизованное управление
- Открытый API для стороннего контроля
ФУНКЦИИ 9075 – Системное администрирование
- Использование TLS (безопасность транспортного уровня) и HTTPS, связь между устройствами AdderLink и A.I.M. и между A.I.M. и внешний мир все в безопасности.
- Для надежности 24/7 второй горячий A.I.M. могут быть добавлены для обеспечения постоянного времени безотказной работы, а с двумя интерфейсами сетевых адаптеров на каждом модуле AdderLink Infinity можно легко спроектировать системы для обеспечения максимальной отказоустойчивости.
- Администраторы могут управлять правами доступа к каждому устройству для каждого пользователя вручную через веб-браузер или автоматически с помощью Active Directory.Отчеты, показывающие историю устройств, логинов пользователей и подключений устройств, можно просматривать и экспортировать в файл CSV или через SYSLOG.
- Информационная панель, доступная через веб-браузер, дает обзор подключений системы и пользователей в реальном времени. Вкладки позволяют перемещаться между настройками и подменю устройства или пользователя.
- A.I.M. может использоваться для централизованного установления соединений между отдельной парой передающих и приемных устройств из системы управления.Используя Presets, список предустановленных подключений, многоэкранных настроек, видеостен или вывесок можно принудительно запустить одним щелчком мыши.
- Пользовательские столы могут выбирать различные конфигурации клавиатуры в соответствии со своими требованиями и в качестве глобальной настройки выбирать язык для экранного меню из более чем 14 языков.
ОСОБЕННОСТИ – Пользовательский интерфейс
- Отображение на экране на каждой пользовательской станции
- Пользователи входят в систему и выбирают соединения каналов из интуитивно понятного экранного меню, аналогичного цифровому ТВ.Пользователи также могут использовать предустановки для переключения каналов для нескольких экранов на нескольких приемниках.
- Удаленное экранное меню
- Удаленное экранное меню позволяет пользователю «передавать» видео и управлять им на другую станцию, на видеостену или проектор.
- Избранное и переключение горячих клавиш
- Каждый пользователь может выбрать свои избранные каналы в экранном меню и назначить горячую клавишу для быстрого переключения между каналами.
- Выбор режимов подключения
- Администраторы могут предоставить пользователям возможность подключаться в трех режимах: только просмотр, общий или эксклюзивный.Затем каждый разрешенный режим становится доступным в экранном меню.
- Быстрое переключение видео и USB
- Время переключения между компьютерами составляет менее 1 секунды для обеспечения качественного взаимодействия с пользователем.
- Многоадресная рассылка
- Сетевая многоадресная рассылка позволяет системе одновременно передавать видео с одного передатчика на неограниченное количество приемников. Подходит для вывесок, мониторинга и совместного использования рабочих столов.
- Совместное использование USB
- Совместное использование USB позволяет нескольким пользователям одновременно подключаться к одному компьютеру и управлять им.Каждый передатчик может сообщать о 12 уникальных USB-устройствах (идентифицируемых кодами VID / PID), но объединяет устройства с одинаковым идентификатором, чтобы разрешить намного больше.
- Каналы
- Канал, рассматриваемый как виртуальный передатчик, может объединять видео, аудио и USB от разных передатчиков как один источник. Идеально подходит там, где требуются звуковые оповещения или смешанные источники видео.
- Открытый API для сторонних систем управления
- Adder Technology публикует простую структуру API, позволяющую легко интегрироваться с другими системами управления сторонних производителей, поставляемыми такими компаниями, как AMX, Crestron, HRS или MediaLon на уровне HTTP.
- Интеграция LDAP
- Чтобы упростить настройку, система имеет интерфейс LDAP, поэтому пользователи и пароли из других систем могут быть легко импортированы.
- Получение / обход SNMP v3
- Внешние машины могут опрашивать A.I.M. чтобы узнать статус сети и устройств AdderLink Infinity. Реализована безопасность SNMP v3 с поддержкой транспорта AES / DES с аутентификацией MD5 / SHA.
- Поддержка внешнего сервера NTP – NTPv4.2
- Подключите до 3 серверов NTP с аутентифицированными соединениями с использованием MD5 и идентификатора ключа, как определено в стандартах NTP.Все блоки AdderLink Infinity в A.I.M. сеть теперь получает время с использованием аутентифицированного NTP от A.I.M.
- Резервные копии системы
- Резервные копии базы данных могут быть сохранены внутри, снаружи или автоматически отправлены по электронной почте. Автоматические обновления могут быть запланированы ежечасно, ежедневно или еженедельно.
- Централизованное обновление прошивки
- Помимо управления собственным обновлением прошивки, A.I.M. управляет обновлением каждого устройства в сети и может одновременно развертывать микропрограммное обеспечение на сотнях устройств, то есть общесистемное обновление занимает всего несколько минут.
- Простая настройка матрицы
- Использование сети с нулевой конфигурацией, A.I.M. автоматически получает MAC-адреса устройств расширения, когда они подключены к сети. Администратор выделяет IP-адреса, имена и местоположения, чтобы устройства было легко идентифицировать, настраивать и контролировать.
- Спецификации
- Аппаратное обеспечение
- Сервер промышленных спецификаций с твердотельной памятью.
- Программное обеспечение
- Закрытая система под управлением Linux.
- Физическая конструкция
- 19-дюймовый корпус 1 RU, монтируемый в стойку, в прочной металлической конструкции. 432 мм / 17 дюймов (ширина), 44 мм / 1,73 дюйма (высота), 230 мм / 9 дюймов (глубина), 2,75 кг / 6 фунтов.
- Питание
- Внешний блок питания IEC, входной блок, 100–240 В переменного тока, 50/60 Гц, 1,5 А, вход для адаптера питания. 12 В постоянного тока, выход 60 Вт.
- Рабочая температура
- от 0 до 40ºC / от 32 до 104ºF.
- Допуски
Пожалуйста, смотрите вкладку «Технические характеристики» для получения дополнительной информации о Adder INFINITY Manager | Администратор Control Suite для ADDERLink.
Чтобы увидеть другие продукты Adder, доступные на веб-сайте служб интеграции вещания, щелкните или коснитесь здесь.
Технические характеристики: Сумматор INFINITY Manager | Административный пакет управления для ADDERLink
A.I.M. Сервер управления – это пакет управления, который превращает расширители AdderLink Infinity в решение с цифровой матрицей. Используя стандартную IP-инфраструктуру, можно направить любую пользовательскую станцию на любой компьютер, подключенный к сети, без какого-либо ущерба для качества видео или управления.Это позволяет совместное использование компьютеров и многоадресную передачу видео в любое место.
- Интуитивно понятный многоязычный пользовательский интерфейс
- Несколько методов переключения
- Конфигурируемые права доступа пользователя
- Полный журнал аудита
- Простое централизованное управление
- Открытый API для стороннего контроля
ФУНКЦИИ 9075 – Системное администрирование
- Использование TLS (безопасность транспортного уровня) и HTTPS, связь между устройствами AdderLink и A.I.M. и между A.I.M. и внешний мир все в безопасности.
- Для надежности 24/7 второй горячий A.I.M. могут быть добавлены для обеспечения постоянного времени безотказной работы, а с двумя интерфейсами сетевых адаптеров на каждом модуле AdderLink Infinity можно легко спроектировать системы для обеспечения максимальной отказоустойчивости.
- Администраторы могут управлять правами доступа к каждому устройству для каждого пользователя вручную через веб-браузер или автоматически с помощью Active Directory.Отчеты, показывающие историю устройств, логинов пользователей и подключений устройств, можно просматривать и экспортировать в файл CSV или через SYSLOG.
- Информационная панель, доступная через веб-браузер, дает обзор подключений системы и пользователей в реальном времени. Вкладки позволяют перемещаться между настройками и подменю устройства или пользователя.
- A.I.M. может использоваться для централизованного установления соединений между отдельной парой передающих и приемных устройств из системы управления.Используя Presets, список предустановленных подключений, многоэкранных настроек, видеостен или вывесок можно принудительно запустить одним щелчком мыши.
- Пользовательские столы могут выбирать различные конфигурации клавиатуры в соответствии со своими требованиями и в качестве глобальной настройки выбирать язык для экранного меню из более чем 14 языков.
ОСОБЕННОСТИ – Пользовательский интерфейс
- Отображение на экране на каждой пользовательской станции
- Пользователи входят в систему и выбирают соединения каналов из интуитивно понятного экранного меню, аналогичного цифровому ТВ.Пользователи также могут использовать предустановки для переключения каналов для нескольких экранов на нескольких приемниках.
- Удаленное экранное меню
- Удаленное экранное меню позволяет пользователю «передавать» видео и управлять им на другую станцию, на видеостену или проектор.
- Избранное и переключение горячих клавиш
- Каждый пользователь может выбрать свои избранные каналы в экранном меню и назначить горячую клавишу для быстрого переключения между каналами.
- Выбор режимов подключения
- Администраторы могут предоставить пользователям возможность подключаться в трех режимах: только просмотр, общий или эксклюзивный.Затем каждый разрешенный режим становится доступным в экранном меню.
- Быстрое переключение видео и USB
- Время переключения между компьютерами составляет менее 1 секунды для обеспечения качественного взаимодействия с пользователем.
- Многоадресная рассылка
- Сетевая многоадресная рассылка позволяет системе одновременно передавать видео с одного передатчика на неограниченное количество приемников. Подходит для вывесок, мониторинга и совместного использования рабочих столов.
- Совместное использование USB
- Совместное использование USB позволяет нескольким пользователям одновременно подключаться к одному компьютеру и управлять им.Каждый передатчик может сообщать о 12 уникальных USB-устройствах (идентифицируемых кодами VID / PID), но объединяет устройства с одинаковым идентификатором, чтобы разрешить намного больше.
- Каналы
- Канал, рассматриваемый как виртуальный передатчик, может объединять видео, аудио и USB от разных передатчиков как один источник. Идеально подходит там, где требуются звуковые оповещения или смешанные источники видео.
- Открытый API для сторонних систем управления
- Adder Technology публикует простую структуру API, позволяющую легко интегрироваться с другими системами управления сторонних производителей, поставляемыми такими компаниями, как AMX, Crestron, HRS или MediaLon на уровне HTTP.
- Интеграция LDAP
- Чтобы упростить настройку, система имеет интерфейс LDAP, поэтому пользователи и пароли из других систем могут быть легко импортированы.
- Получение / обход SNMP v3
- Внешние машины могут опрашивать A.I.M. чтобы узнать статус сети и устройств AdderLink Infinity. Реализована безопасность SNMP v3 с поддержкой транспорта AES / DES с аутентификацией MD5 / SHA.
- Поддержка внешнего сервера NTP – NTPv4.2
- Подключите до 3 серверов NTP с аутентифицированными соединениями с использованием MD5 и идентификатора ключа, как определено в стандартах NTP.Все блоки AdderLink Infinity в A.I.M. сеть теперь получает время с использованием аутентифицированного NTP от A.I.M.
- Резервные копии системы
- Резервные копии базы данных могут быть сохранены внутри, снаружи или автоматически отправлены по электронной почте. Автоматические обновления могут быть запланированы ежечасно, ежедневно или еженедельно.
- Централизованное обновление прошивки
- Помимо управления собственным обновлением прошивки, A.I.M. управляет обновлением каждого устройства в сети и может одновременно развертывать микропрограммное обеспечение на сотнях устройств, то есть общесистемное обновление занимает всего несколько минут.
- Простая настройка матрицы
- Использование сети с нулевой конфигурацией, A.I.M. автоматически получает MAC-адреса устройств расширения, когда они подключены к сети. Администратор выделяет IP-адреса, имена и местоположения, чтобы устройства было легко идентифицировать, настраивать и контролировать.
- Спецификации
- Аппаратное обеспечение
- Сервер промышленных спецификаций с твердотельной памятью.
- Программное обеспечение
- Закрытая система под управлением Linux.
- Физическая конструкция
- 19-дюймовый корпус 1 RU, монтируемый в стойку, в прочной металлической конструкции. 432 мм / 17 дюймов (ширина), 44 мм / 1,73 дюйма (высота), 230 мм / 9 дюймов (глубина), 2,75 кг / 6 фунтов.
- Питание
- Внешний блок питания IEC, входной блок, 100–240 В переменного тока, 50/60 Гц, 1,5 А, вход для адаптера питания. 12 В постоянного тока, выход 60 Вт.
- Рабочая температура
- от 0 до 40ºC / от 32 до 104ºF.
- Допуски
AIM-24-US Сумматор Устройство AdderLink Infinity Manager
PHAgc3R5bGU9InRleHQtYWxpZ246IGNlbnRlcjsiPjxzdHJvbmc + VGhpcyBsaXN0aW5nIGlzIGZvciBBSU0tMjQtVVMgb25seS4gVXNlIGRlc2NyaXB0aW9uIGJlbG93IGFzIGEgZ2VuZXJhbCByZWZlcmVuY2UuPC9zdHJvbmc + PC9wPg0KPHA + PHN0cm9uZz5TZWN1cmUgYWNjZXNzIGFuZCBjb21tdW5pY2F0aW9uczwvc3Ryb25nPjwvcD4gDQo8cD5Vc2luZyBUTFMgKHRyYW5zcG9ydCBsYXllciBzZWN1cml0eSkmbmJzcDthbmQgSFRUUFMsIGNvbW11bmljYXRpb25zIGJldHdlZW4mbmJzcDtBZGRlckxpbmsgdW5pdHMgYW5kIEEuSS5NLiBhbmQgYmV0d2VlbiZuYnNwO0EuSS5NLiBhbmQgdGhlIG91dHNpZGUgd29ybGQgYXJlIGFsbCBzZWN1cmUuPC9wPg0KPHA + PHN0cm9uZz5SZWR1bmRhbnQgb3BlcmF0aW9uPC9zdHJvbmc + PC9wPiANCjxwPkZvciAyNC83IHJlbGlhYmlsaXR5IGEgc2Vjb25kIGhvdCBBLkkuTS4mbmJzcDtjYW4gYmUgYWRkZWQgdG8gZW5zdXJlIGNvbnN0YW50IHVwdGltZSZuYnNwO2FuZCB3aXRoIGR1YWwgTklDIGludGVyZmFjZXMgb24gZXZlcnkmbmJzcDtBZGRlckxpbmsgSW5maW5pdHkgdW5pdCwgc3lzdGVtcyBjYW4gYmUmbmJzcDtlYXNpbHkgZGVzaWduZWQgZm9yIG1heGltdW0gcmVzaWxpZW5jZS48L3A + DQo8cD48c3Ryb25nPlVzZXIgYWNjZXNzIHJpZ2h0cyBtYW5hZ2VtZW50IGFuZCBhdWRpdCZuYnNwO3RyYWlsczwvc3Ryb25nPjwvcD4NCjxwPkFkbWluaXN0cmF0b3JzIGNhbiBtYW 5hZ2UgYWNjZXNzIHJpZ2h0cyZuYnNwO3RvIGVhY2ggZGV2aWNlIG9uIGEgdXNlciBieSB1c2VyIGJhc2lzJm5ic3A7ZWl0aGVyIG1hbnVhbGx5IHRocm91Z2ggdGhlIHdlYiBicm93c2VyJm5ic3A7b3IgYXV0b21hdGljYWxseSB1c2luZyBBY3RpdmUgRGlyZWN0b3J5LiZuYnNwO1JlcG9ydHMgc2hvd2luZyB0aGUgaGlzdG9yeSBvZiBkZXZpY2VzLCZuYnNwO3VzZXIgbG9naW5zIGFuZCBkZXZpY2UgY29ubmVjdGlvbnMgY2FuIGJlJm5ic3A7dmlld2VkIGFuZCBleHBvcnRlZCB0byBhIENTViBmaWxlIG9yIHZpYSZuYnNwO1NZU0xPRy48L3A + DQo8cD48c3Ryb25nPkVhc3kgY2VudHJhbGl6ZWQgbWFuYWdlbWVudDwvc3Ryb25nPjwvcD4NCjxwPkFjY2Vzc2VkIHZpYSBhIHdlYiBicm93c2VyLCB0aGUgZGFzaGJvYXJkJm5ic3A7Z2l2ZXMgYSByZWFsIHRpbWUgb3ZlcnZpZXcgb2Ygc3lzdGVtJm5ic3A7Y29ubmVjdGlvbnMgYW5kIHVzZXJzLiBUYWJzIGVuYWJsZSB5b3UgdG8mbmJzcDtuYXZpZ2F0ZSBiZXR3ZWVuIHNldHRpbmdzIGFuZCBkZXZpY2Ugb3ImbmJzcDt1c2VyIHN1Yi1tZW51cy48L3A + DQo8cD48c3Ryb25nPkNvbnRyb2wgQ2hhbm5lbCBhbmQgUHJlc2V0cyBjb25uZWN0aW9uczwvc3Ryb25nPjwvcD4NCjxwPkEuSS5NLiBjYW4gYmUgdXNlZCB0byBtYWtlIGNvbm5lY3Rpb25zJm5ic3A7YmV0d2VlbiBhbiBpbmRpdmlkdWFsIHBhaXIgb2YgdHJhbnNtaXR0ZXImbmJzcDthbmQgcmVjZWl2ZXIgZGV2aWNlcyBjZW 50cmFsbHkgZnJvbSB3aXRoaW4mbmJzcDt0aGUgbWFuYWdlbWVudCBzeXN0ZW0uIFVzaW5nIFByZXNldHMsJm5ic3A7YSBsaXN0IG9mIHByZS1kZWZpbmVkIGNvbm5lY3Rpb25zLCBtdWx0aXNjcmVlbiwmbmJzcDt2aWRlbyB3YWxsIG9yIHNpZ25hZ2Ugc2V0dXBzIGNhbiBiZSZuYnNwO2ZvcmNlZCB3aXRoIGEgc2luZ2xlIGNsaWNrLjwvcD4NCjxwPjxzdHJvbmc + SW50ZXJuYXRpb25hbGl6YXRpb248L3N0cm9uZz48L3A + DQo8cD5UaGUgdXNlciBkZXNrcyBjYW4gc2VsZWN0IGRpZmZlcmVudCZuYnNwO2tleWJvYXJkIGNvbmZpZ3VyYXRpb25zIHRvIHN1aXRlIHRoZWlyJm5ic3A7cmVxdWlyZW1lbnRzIGFuZCBhcyBhIGdsb2JhbCBzZXR0aW5nIHNlbGVjdCZuYnNwO3RoZSBsYW5ndWFnZSBmb3IgdGhlIE9TRCBmcm9tIGEgY2hvaWNlIG9mJm5ic3A7b3ZlciAxNCBsYW5ndWFnZXMuPC9wPg0KPHA + PHN0cm9uZz5GZWF0dXJlczwvc3Ryb25nPjwvcD4NCjxwPjxzdHJvbmc + T24gc2NyZWVuIGRpc3BsYXkgYXQgZWFjaCB1c2VyIHN0YXRpb248L3N0cm9uZz48L3A + DQo8cD5Vc2VycyBsb2dpbiBhbmQgY2hvb3NlIGNoYW5uZWwmbmJzcDtjb25uZWN0aW9ucyBmcm9tIGFuIGludHVpdGl2ZSBPU0Qgc2ltaWxhciZuYnNwO3RvIHRoYXQgb2YgYSBEaWdpdGFsIFRWLiBVc2VycyBjYW4gYWxzbyB1c2UmbmJzcDtQcmVzZXRzIHRvIGNoYW5nZSBjaGFubmVscyBmb3IgbXVsdGlwbGUmbmJzcDtzY3JlZW5zIGFjcm9zcyBtdWx0aXBsZS ByZWNlaXZlcnMuPC9wPg0KPHA + PHN0cm9uZz5SZW1vdGUgT1NEPC9zdHJvbmc + PC9wPg0KPHA + VGhlIHJlbW90ZSBPU0QgYWxsb3dzIHRoZSB1c2VyIHRvJm5ic3A7JmxkcXVvO3B1c2gmcmRxdW87IHZpZGVvIGFuZCBjb250cm9sIHRvIGFub3RoZXImbmJzcDtzdGF0aW9uIG9yIHRvIGEgdmlkZW8gd2FsbCBvciBwcm9qZWN0b3IuJm5ic3A7PC9wPg0KPHA + PHN0cm9uZz5GYXZvdXJpdGVzIGFuZCBob3RrZXkgc3dpdGNoaW5nPC9zdHJvbmc + PC9wPg0KPHA + RWFjaCB1c2VyIGNhbiBzZWxlY3QgdGhlaXIgZmF2b3VyaXRlJm5ic3A7Y2hhbm5lbHMgd2l0aGluIHRoZSBPU0QgYW5kIGFsbG9jYXRlIGEmbmJzcDtob3RrZXkgZm9yIGZhc3Qgc3dpdGNoaW5nIGJldHdlZW4gY2hhbm5lbHMuPC9wPg0KPHA + PHN0cm9uZz5DaG9pY2Ugb2YgY29ubmVjdGlvbiBtb2Rlczwvc3Ryb25nPjwvcD4NCjxwPkFkbWluaXN0cmF0b3JzIGNhbiBjaG9vc2UgdG8gZ2l2ZSB1c2VycyZuYnNwO3RoZSBhYmlsaXR5IHRvIGNvbm5lY3QgaW4gdGhyZWUgbW9kZXM6IFZpZXcmbmJzcDtvbmx5LCBTaGFyZWQgb3IgRXhjbHVzaXZlLiBFYWNoIHBlcm1pdHRlZCZuYnNwO21vZGUgaXMgdGhlbiBtYWRlIGF2YWlsYWJsZSB3aXRoaW4gdGhlJm5ic3A7T1NELjwvcD4NCjxwPjxzdHJvbmc + RmFzdCB2aWRlbyBhbmQgVVNCIHN3aXRjaGluZzwvc3Ryb25nPjwvcD4NCjxwPlRoZSBzd2l0Y2hpbmcgdGltZSBiZXR3ZWVuIGNvbXB1dGVycyBpcyZuYnNwO2xlc3 MgdGhhbiAxIHNlY29uZCB0byBwcm92aWRlIGEgcXVhbGl0eSB1c2VyJm5ic3A7ZXhwZXJpZW5jZS48L3A + DQo8cD48c3Ryb25nPlNwZWNpZmljYXRpb25zOjwvc3Ryb25nPjwvcD4NCjxwPjxzdHJvbmc + T3BlbiBBUEkgZm9yIDNyZCBwYXJ0eSBjb250cm9sIHN5c3RlbXM8L3N0cm9uZz48L3A + DQo8cD5BZGRlciBUZWNobm9sb2d5IHB1Ymxpc2hlcyBhIHNpbXBsZSBBUEkmbmJzcDtzdHJ1Y3R1cmUgdG8gYWxsb3cgZWFzeSBpbnRlZ3JhdGlvbiB3aXRoJm5ic3A7b3RoZXIgM3JkIFBhcnR5IGNvbnRyb2wgc3lzdGVtcyBzdXBwbGllZCZuYnNwO2J5IGNvbXBhbmllcyBsaWtlIEFNWCwgQ3Jlc3Ryb24gLCBIUlMgb3ImbmJzcDtNZWRpYUxvbiBhdCBhIEhUVFAgbGV2ZWwuPC9wPg0KPHA + PHN0cm9uZz5MREFQIGludGVncmF0aW9uPC9zdHJvbmc + PC9wPg0KPHA + VG8gaGVscCBlYXNlIHNldHVwLCB0aGUgc3lzdGVtIGhhcyBhbiZuYnNwO0xEQVAgaW50ZXJmYWNlIHNvIHVzZXJzIGFuZCBwYXNzd29yZHMmbmJzcDtmcm9tIG90aGVyIHN5c3RlbXMgY2FuIGVhc2lseSBiZSBpbXBvcnRlZC4mbmJzcDs8L3A + DQo8cD48c3Ryb25nPlNOTVAgdjMgZ2V0IC8gd2Fsazwvc3Ryb25nPjwvcD4NCjxwPkV4dGVybmFsIG1hY2hpbmVzIGNhbiBpbnRlcnJvZ2F0ZSBBLkkuTS4gdG8mbmJzcDtmaW5kIG91dCB0aGUgc3RhdHVzIG9mIHRoZSBBZGRlckxpbmsgSW5maW5pdHkmbmJzcDtuZXR3b3JrIGFuZCB1bml0cy4gU05NUCB2MyBzZWN1cm l0eSZuYnNwO2lzIGltcGxlbWVudGVkLCBzdXBwb3J0aW5nIEFFUy9ERVMmbmJzcDt0cmFuc3BvcnQgd2l0aCBNRDUvU0hBIGF1dGhlbnRpY2F0aW9uLiZuYnNwOzwvcD4NCjxwPjxzdHJvbmc + RXh0ZXJuYWwgTlRQIHNlcnZlciBzdXBwb3J0ICZuZGFzaDsgTlRQdjQuMiZuYnNwOzwvc3Ryb25nPjwvcD4NCjxwPkNvbm5lY3QgdXAgdG8gMyBOVFAgc2VydmVycyB3aXRoJm5ic3A7YXV0aGVudGljYXRlZCBjb25uZWN0aW9ucyB1c2luZyBNRDUgYW5kJm5ic3A7S2V5IElEIGFzIGRlZmluZWQgaW4gdGhlIE5UUCBzdGFuZGFyZHMuJm5ic3A7QWxsIEFkZGVyTGluayBJbmZpbml0eSB1bml0cyBpbiBhbiBBLkkuTS4mbmJzcDtuZXR3b3JrIG5vdyBnZXQgdGltZSB1c2luZyBhdXRoZW50aWNhdGVkJm5ic3A7TlRQIGZyb20gQS5JLk0uPC9wPg0KPHA + PHN0cm9uZz5TeXN0ZW0gYmFja3Vwczwvc3Ryb25nPjwvcD4NCjxwPkJhY2t1cHMgb2YgdGhlIGRhdGFiYXNlIGNhbiBiZSZuYnNwO3NhdmVkIGludGVybmFsbHksIGV4dGVybmFsbHkgb3IgZW1haWxlZCZuYnNwO2F1dG9tYXRpY2FsbHkuIEF1dG9tYXRpYyB1cGRhdGVzIGNhbiBiZSZuYnNwO3NjaGVkdWxlZCBvbiBhbiBob3VybHksIGRhaWx5IG9yIHdlZWtseSZuYnNwO2Jhc2lzLjwvcD4NCjxwPjxzdHJvbmc + Q2VudHJhbGl6ZWQgZmlybXdhcmUgdXBncmFkZXM8L3N0cm9uZz48L3A + DQo8cD5BcyB3ZWxsIGFzIG1hbmFnaW5nIGl0cyBvd24gZmlybXdhcmUmbmJzcDt1cGdyYW RlLCBBLkkuTS4gbWFuYWdlcyB0aGUgdXBncmFkZSBvZiZuYnNwO2VhY2ggZGV2aWNlIG9uIHRoZSBuZXR3b3JrIGFuZCBjYW4gZGVwbG95Jm5ic3A7ZmlybXdhcmUgdG8gaHVuZHJlZHMgb2YgZGV2aWNlcyBhdCB0aGUmbmJzcDtzYW1lIHRpbWUsIG1lYW5pbmcgYSBzeXN0ZW0td2lkZSB1cGdyYWRlJm5ic3A7dGFrZXMgb25seSBhIGZldyBtaW51dGVzLjwvcD4NCjxwPjxzdHJvbmc + RWFzeSBtYXRyaXggc2V0dXA8L3N0cm9uZz48L3A + DQo8cD5Vc2luZyBaZXJvIENvbmZpZ3VyYXRpb24gbmV0d29ya2luZywmbmJzcDtBLkkuTS4gYXV0b21hdGljYWxseSBvYnRhaW5zIHRoZSBNQUMmbmJzcDthZGRyZXNzZXMgb2YgZXh0ZW5kZXIgZGV2aWNlcyBhcyB0aGV5IGFyZSZuYnNwO2F0dGFjaGVkIHRvIHRoZSBuZXR3b3JrLiBUaGUgYWRtaW5pc3RyYXRvciZuYnNwO2FsbG9jYXRlcyBJUCBhZGRyZXNzZXMsIG5hbWVzIGFuZCBsb2NhdGlvbnMmbmJzcDtzbyB0aGF0IGRldmljZXMgYXJlIGVhc3kgdG8gaWRlbnRpZnksJm5ic3A7Y29uZmlndXJlIGFuZCBjb250cm9sLjwvcD4NCjxwPjxzdHJvbmc + SGFyZHdhcmU8L3N0cm9uZz48L3A + DQo8cD5JbmR1c3RyaWFsIHNwZWMgc2VydmVyIHdpdGggc29saWQgc3RhdGUmbmJzcDttZW1vcnkuPC9wPg0KPHA + PHN0cm9uZz5Tb2Z0d2FyZTwvc3Ryb25nPjwvcD4NCjxwPkNsb3NlZCBzeXN0ZW0gb3BlcmF0aW5nIExpbnV4LjwvcD4NCjxwPjxzdHJvbmc + UGh5c2ljYWwgZGVzaWduPC9zdH Jvbmc + PC9wPg0KPHA + MTkgaW5jaCAxVSByYWNrIG1vdW50YWJsZSBjaGFzc2lzIGluIGEmbmJzcDtyb2J1c3QgbWV0YWwgY29uc3RydWN0aW9uLiA0MzJtbS8xNyZyZHF1bzsmbmJzcDsodyksIDQ0bW0vMS43MyZyZHF1bzsgKGgpLCAyMzBtbS85JnJkcXVvOyAoZCksJm5ic3A7Mi43NWtnLzZsYnMuPC9wPg0KPHA + PHN0cm9uZz5Qb3dlcjwvc3Ryb25nPjwvcD4NCjxwPkV4dGVybmFsIHBvd2VyIElFQyBpbnB1dCB1bml0LCAxMDAtMjQwVkFDIDUwLzYwSHosIDEuNUEsIGlucHV0IHRvIHBvd2VyJm5ic3A7YWRhcHRlci4gMTJWREMsIDYwVyBvdXRwdXQuPC9wPg0KPHA + PHN0cm9uZz5PcGVyYXRpbmcgdGVtcGVyYXR1cmU8L3N0cm9uZz48L3A + DQo8cD4wIHRvIDQwJm9yZG07QyAvIDMyIHRvIDEwNCZvcmRtO0YuPC9wPg0KPHA + PHN0cm9uZz5BcHByb3ZhbHM8L3N0cm9uZz48L3A + DQo8cD5DRSwgRkNDLjwvcD4 =
AIM-24-US – это устройство AdderLink Infinity Manager, а его A.

 Стихия С.Ж. не материя и не энергия, а информация. Догадка о чьем либо С. ж. (в т. ч. о собственном) есть попытка понять скрытую форму правления души в теле, заключить о… … Современный философский словарь
Стихия С.Ж. не материя и не энергия, а информация. Догадка о чьем либо С. ж. (в т. ч. о собственном) есть попытка понять скрытую форму правления души в теле, заключить о… … Современный философский словарь Соотношение Клапейрона Клаузиуса не имеет смысл для фазовых превращений второго рода[1], так как и… … Википедия
Соотношение Клапейрона Клаузиуса не имеет смысл для фазовых превращений второго рода[1], так как и… … Википедия зап. 8 нояб.). Жизнь. Иоанн Дунс Скот. 1473… … Православная энциклопедия
зап. 8 нояб.). Жизнь. Иоанн Дунс Скот. 1473… … Православная энциклопедия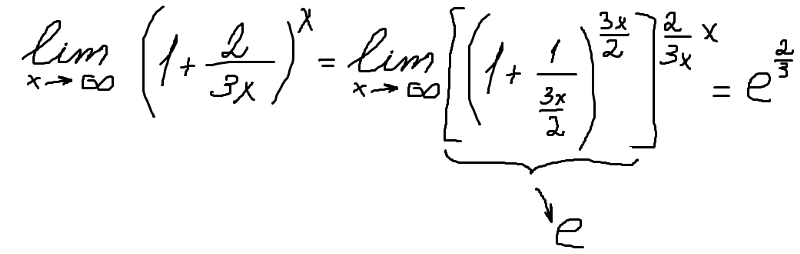 Европейского эротического искусство наиболее ярко выражено во французской гравюре этого времени. Стремление к запретному плоду в ней проявляется в полной мере.В эротике видят только забаву,… Подробнее Купить за 96 руб электронная книга
Европейского эротического искусство наиболее ярко выражено во французской гравюре этого времени. Стремление к запретному плоду в ней проявляется в полной мере.В эротике видят только забаву,… Подробнее Купить за 96 руб электронная книга 3 и выполним предельный переход
3 и выполним предельный переход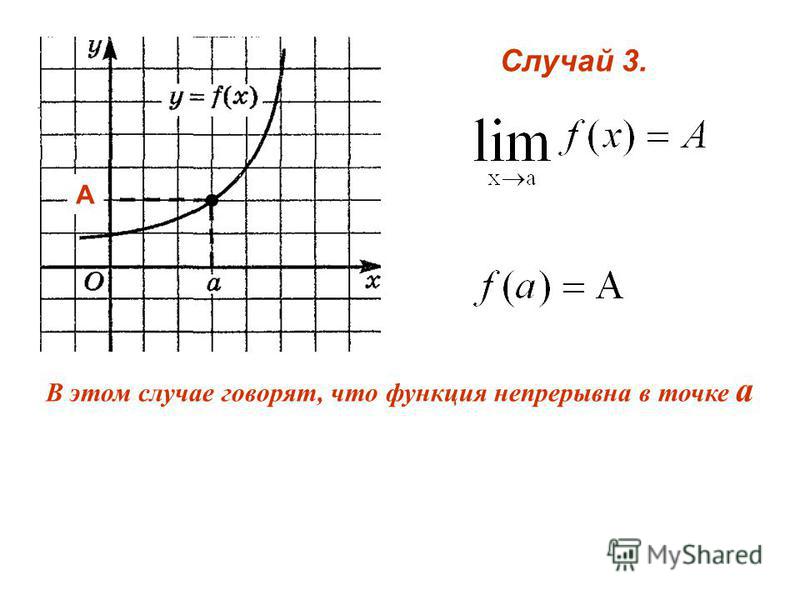 Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Дальнейшее вычисление сводится к вичислению предела степени экспоненты. 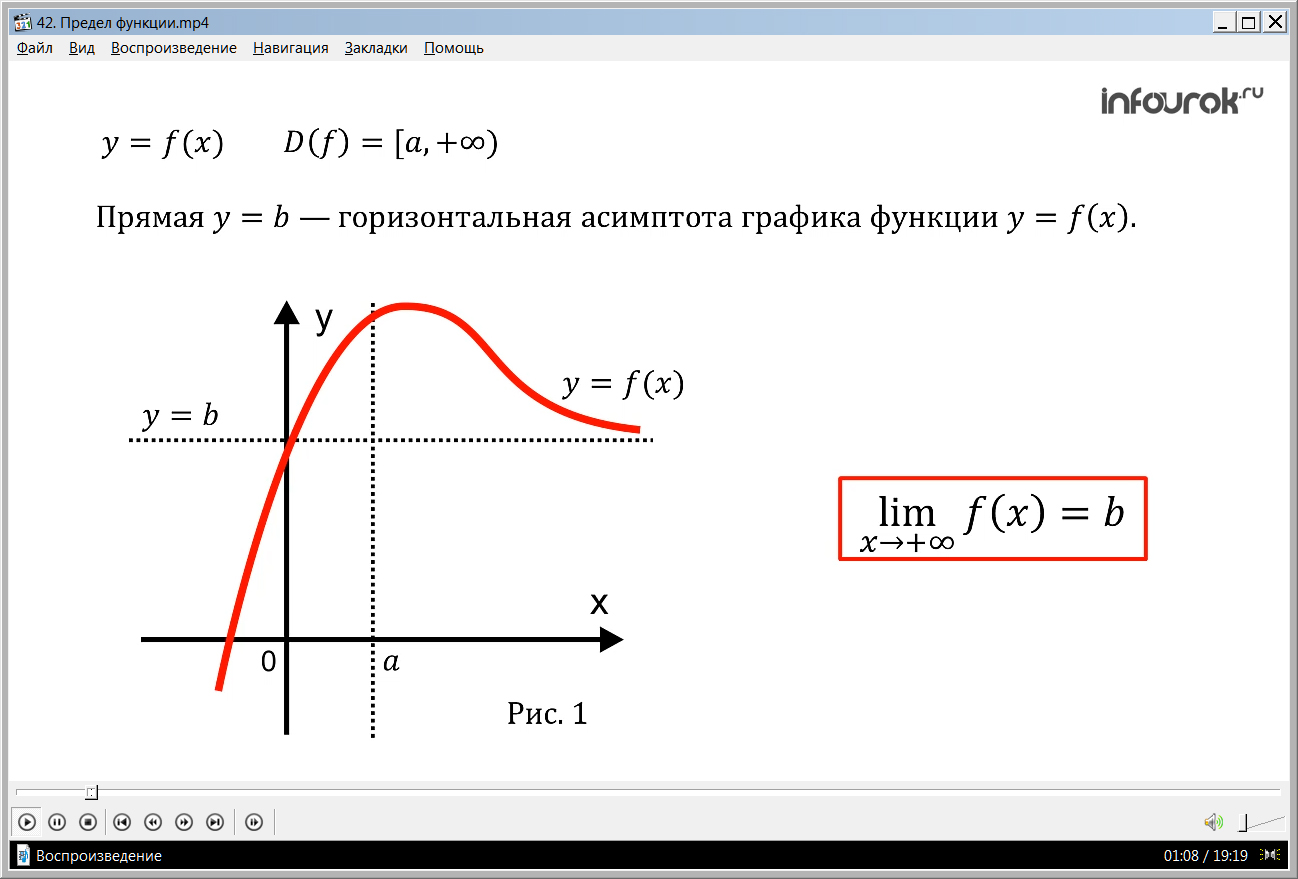 2
2