Стремится к нулю знак: Mathway | Популярные задачи

2

Метод интервалов – Умскул Учебник

На этой странице вы узнаете

• Как мы ежедневно расставляем знаки неравенства в жизни?
• Как быстро определить верное обозначение точки на прямой?
• Как правильно чередовать знаки на числовой прямой?

Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами. 

Метод интервалов

Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.

Для записи неравенств используют знаки > , < , ≥ , ≤ . 

При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства. 

Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.  

Как мы ежедневно расставляем знаки неравенства в жизни? Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства. Например, возьмем известную игру “Камень, ножницы, бумага”. Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится: Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше. И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.

Рассмотрим пример неравенства (х — 10)(х + 21) > 0.  

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем. 

Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается. 

Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств?  В таких случаях на помощь приходит метод интервалов.

Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.

Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами. 

Алгоритм решения неравенств методом интервалов 1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.   2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.  3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.  4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.

Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ. 

• Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми. 

Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.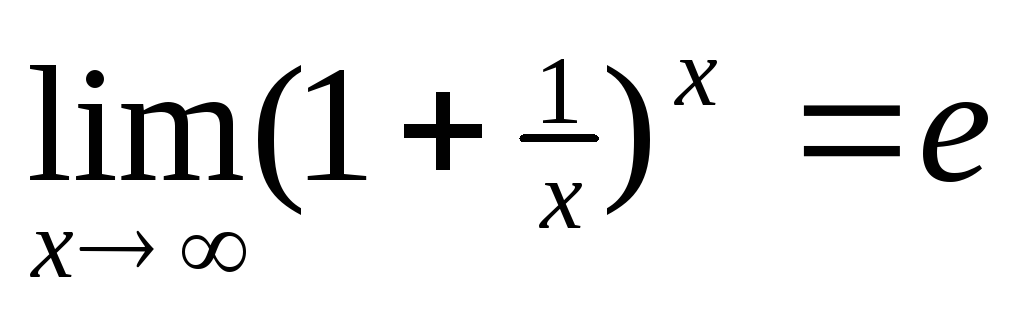  

• Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками. 

Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки. 

• Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим. 

Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками. 

Как быстро определить верное обозначение точки на прямой? В случае сомнений мы всегда можем проверить себя по простой схеме. Вывод: — если знак неравенства строгий, то все точки будут выколотыми; — если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).

Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции. 

При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой. 

Правила чередования знаков: 

• Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.

• Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется. 

Как правильно чередовать знаки на числовой прямой? Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и  убедиться в правильности расстановки знаков на прямой.   Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.

Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.  

Пример 1. Решить неравенство x² + 8x — 33 > 0. 

1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x² + 8x — 33 = 0. 

2. Находим корни уравнения, получаем х = 3 и х = -11. 

3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x² + 8x — 33. Получаем: 

(-12)² + 8*(-12) — 33 = 144 — 96 — 33 = 15. 

Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются. 2 ((-3) + 2)} = \frac{9 + 3 — 2}{9 * (-1)} = \frac{10}{-9}\)

Промежуток отрицательный. 

4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х² четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет. 

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2]. 

Фактчек

• Метод интервалов позволяет упростить решение любого  неравенства, а также экономит время, которое ограничено на экзамене. 
• Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала. 
• Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.  
• Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию. 
• Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется. 

Проверь себя

Задание 1. 
Какие знаки неравенства существуют?

1. Строгие
2. Нестрогие
3. Строгие и нестрогие 
4. Больше и меньше

Задание 2. 
Какой знак неравенства может встретиться в методе интервалов?

1. Только больше или меньше. 
2. Только “больше или равно” или “меньше или равно”. 
3. Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
4. Любой. 

Задание 3. 
Какое утверждение верное?

1. Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
2. Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
3. Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
4. Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты. 

Задание 4. 
Какое утверждение верное? 

1. При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
2. Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
3. Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
4. Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.

Задание 5. 
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе? 

1. Круглые
2. Квадратные
3. И круглые, и квадратные
4. Ни один из перечисленных вариантов 

Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1 

исчисление – разница между стремлением к нулю и близким к нулю

спросил 5 лет, 9 месяцев назад

Изменено 2 года, 9 месяцев назад

Просмотрено 5к раз

$\begingroup$

В исчислении нас учат, что производная функции $y$ по $x$ определяется как “величина, к которой стремится $\dfrac{\bigtriangleup{y}}{\bigtriangleup{x}}$, когда $ \bigtriangleup{x}$ стремится к нулю” 92 {\delta} = 2x + \delta\ne 2x$.

Итак, нет, это другой ответ. Вы не можете сказать, что $\Delta x$ не равно нулю в начале, а затем сказать: «Ну, $\Delta x$ очень близко к $0$, поэтому мы можем игнорировать это» в конце.

$\endgroup$

$\begingroup$

Вы можете рассматривать производную как тень отношения $\frac{\Delta y}{\Delta x}$, когда $\Delta x$ бесконечно мала. В качестве альтернативы вы можете использовать отношение, которое имел в виду Лейбниц, то есть отношение бесконечной близости. Лейбниц писал в своих статьях, что, когда он говорит о равенстве, он имеет в виду не строгое равенство, а равенство до ничтожного члена.

Лейбниц не различал в обозначениях строгое равенство и равенство с точностью до бесконечно малого, но он использовал альтернативное обозначение ${}_{\ulcorner\!\urcorner}\,$ для такого отношения, поэтому оно может быть поучительным выразить эту мысль следующим образом.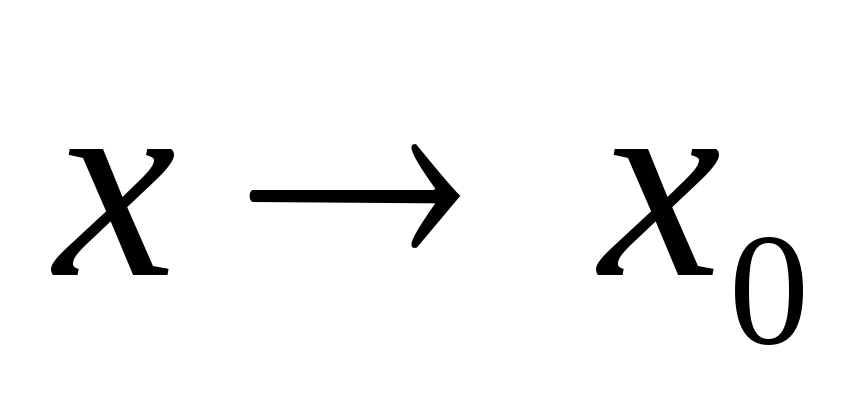

Если $y=f(x)$, то можно написать, что $f'(x)\;{}_{\ulcorner\!\urcorner}\,\frac{\Delta y}{\Delta x}$, понимая что $f'(x)$ должно быть реальным (или, как сказал бы Лейбниц, «присваиваемым»).

Тень такая же, как и у стандартной детали.

Между прочим, замечания Лейбница о понятии равенства «с точностью до незначительного члена» показывают, что критика исчисления со стороны епископа Беркли не имела оснований; подробности см. в этой статье.

$\endgroup$

4

$\begingroup$

Стремление к нулю просто означает, что с “изменением X” вы можете приближаться к нулю, как хотите, соответственно значение (изменение Y/ изменение X) будет все ближе и ближе к некоторому числу. Но если вы подставите значение ноль или любое другое значение, близкое к нулю, вы можете получить не то число, к которому мы двигались. Так что движение здесь важнее всего.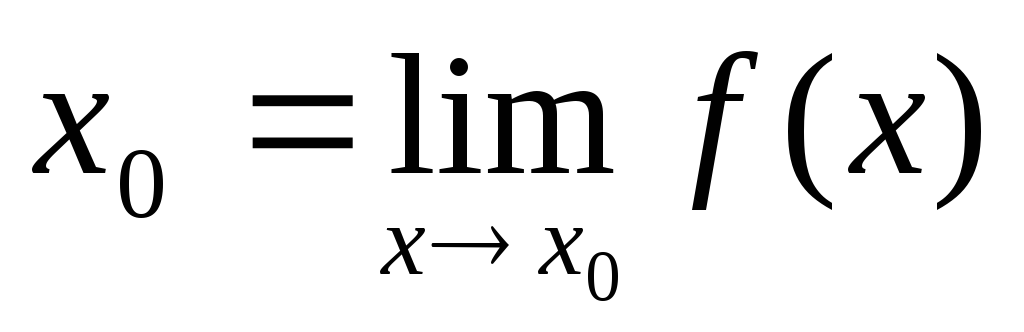 Это похоже на то, что функция косвенно сообщает нам свое значение, приближаясь все ближе и ближе к этому числу. В книге, которую я использовал, упоминалось, что это значение можно увидеть только после удаления общего множителя между числителем и знаменателем, иначе оба будут двигаться к нулю.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

исчисление – Значение ‘Tends’ $\rightarrow$

спросил 7 лет, 3 месяца назад

Изменено 7 лет, 3 месяца назад

Просмотрено 2к раз

$\begingroup$

Значение ‘Tends’ $\rightarrow$.

Я нашел определение тенденции в книге «Высшая алгебра» Барнарда и Чайлда, и я туплю.

“Определение: сказать, что x стремится к нулю, значит сказать, что x изменяется таким образом, что его числовое значение становится и остается меньше любого положительного числа, которое мы можем выбрать, каким бы малым оно ни было.”

Прокомментируйте данное определение и объясните факт.

• исчисление
• реальный анализ
• мягкий вопрос

$\endgroup$

4

$\begingroup$

Нет нужды останавливаться на «определении» отдельного значения символа, особенно в математике.

Символ $dx$, встречающийся в интеграле, сам по себе не имеет смысла, если только не говорить о дифференциальных формах. В том же знаке, символ “$\to$” определяется контекстом, то есть написание “$\to$” само по себе ничего конкретного не говорит. Чтобы проиллюстрировать это, просто вспомните, что мы используем «$\to$» как в контексте определения функций, так и в контексте ограничений.

На мой взгляд, лучший способ «определить» фразу «$x \to a$» в контексте, включающем пределы, — это сказать, что это просто наводящая на размышления мнемоническая аббревиатура строгого аналитического языка. Например, мы говорим «$f(x) \to l$ как $x \to a$», что означает «для каждого $\varepsilon > 0, \cdots$ $|f(x) – l| < \varepsilon \ cdots $

$\endgroup$

$\begingroup$

Прежде чем перейти к формальному определению стремления и предела, мы можем попытаться посмотреть, что происходит, когда мы приближаем x к произвольно близкому значению a, т.