Как найти сумму и разность матриц: правило, свойства, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Сложение и вычитание матриц
В данной публикации мы рассмотрим, как можно сложить две матрицы или вычесть одну из другой. Также приведем примеры для лучшего понимания изложенного материала.
- Сумма матриц
- Свойства сложения матриц
- Разность матриц
- Примеры задач
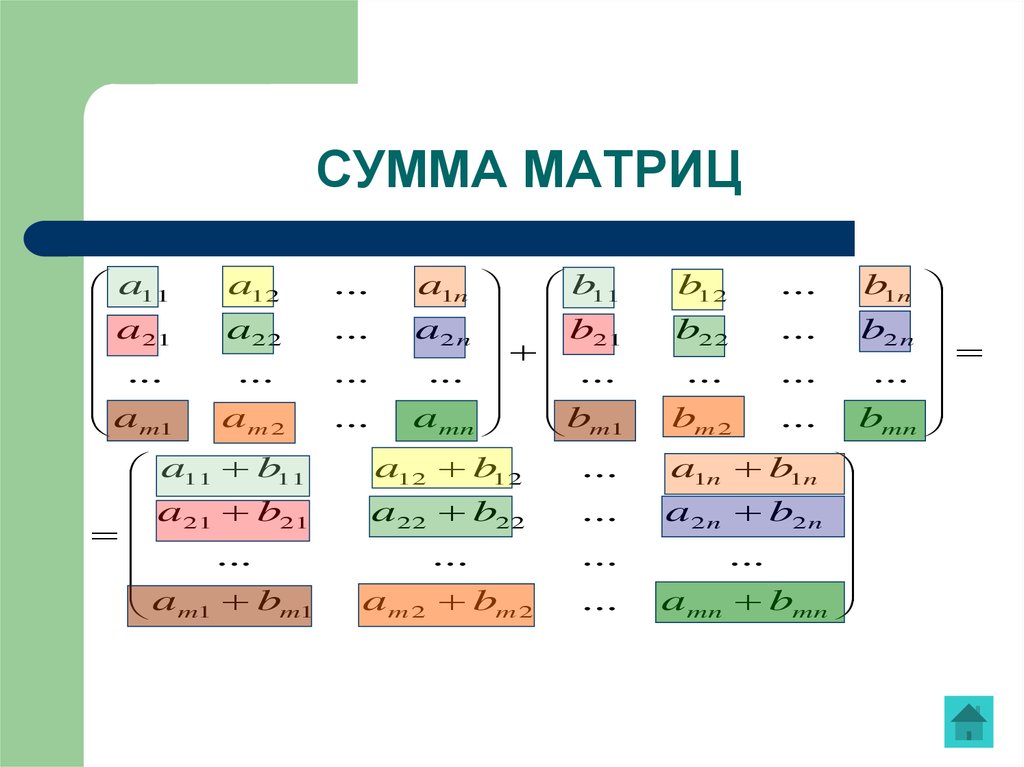
Сумма матриц
Если сложить матрицы A и B одинакового размера, то получится матрица C того же размера, элементы которой равны сумме соответствующих элементов исходных матриц.
Am x n + Bm x n = Cm x n
Примечание: найти можно только сумму матриц одинакового размера.
Свойства сложения матриц
1. Переместительный закон
A + B = B + A
2. Асоциативный закон
Асоциативный закон
(A + B) + C = A + (B + C)
3. Если к матрице прибавить нулевую матрицу, она не изменится.
A + Θ = A, где Θ – нулевая матрица.
4. Если из матрицы вычесть ее же, получится нулевая матрица.
A – A = Θ
Разность матриц
Разность матриц можно представить в виде сложения или умножения матрицы на число.
С = A – B = A + (-B) = A + (-1) ⋅ B
На деле это означает, что мы просто находим разность соответствующих элементов матриц.
Примечание: вычитать также, как и складывать, можно только матрицы одинакового размера.
Примеры задач
Задание 1
Найдем сумму матриц A и B, представленных ниже.
Решение:
Задание 2
Вычислим разность матриц A и B.
Решение:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Сумма (разность) матриц — Мегаобучалка
Сумма матриц – действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой.
– Такое действие не определено для этих матриц!
Определение: Для того чтобы получить матрицу, равную сумме (разности) двух исходных матриц, необходимо сложить (вычесть) их соответствующие элементы:
Пример:
Сложить матрицы и
В соответствии с определением, запишем:
.
Для разности матриц, аналогично, находим разность соответствующих элементов:
Пример:
Найти разность матриц и .
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу H:
Примечание: В теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
Умножение матриц.
Скажем сразу, правило умножения матриц (есть в любом учебнике по алгебре) выглядит очень странно для неподготовленного слушателя, но мы объясним это на конкретных примерах. Прежде всего: «Какие матрицы можно умножать?»
Следствие (из строгого определения): Для умножения матрицы K на матрицу L слева необходимо, чтобы число столбцов матрицыKравнялось числу строк матрицыL.
Пример:
Можно ли умножить матрицу
на матрицу ?
, значит, умножать данные матрицы можно.
А вот если, в данном случае, матрицы переставить местами, то умножение уже невозможно!
, значит, выполнить умножение нельзя, и, вообще, такая запись не имеет смысла:
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так, но с разным результатом, т. к. в общем случае KL ¹ LK. Например, для матриц
и существует как произведение , так и .
Как умножать матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Пример:
Умножить матрицу на матрицу
Мы будем сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность. Поэтому:
Пример сложнее:
Умножить матрицу на матрицу
Формула: . В таком случае произведение:
.
В результате мы получили так называемую нулевую матрицу.
Попробуйте самостоятельно выполнить умножение . Правильный ответ – .
Обратите внимание, что! Это почти всегда так!
Таким образом, переставлять матрицы в произведении нельзя!Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Ни в коем случае не наоборот.
Примеры с матрицами третьего порядка:
Умножить матрицу на матрицу .
Формула умножения очень похожа на предыдущие формулы:
.
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу на матрицу .
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
.
линейная алгебра – Выражение определителя суммы двух матриц?
спросил
Изменено 20 дней назад
Просмотрено 95 тысяч раз
$\begingroup$
Можно ли выразить $\det(A + B)$ через $\det(A), \det(B), n$
где $A,B$ — матрицы $n\times n$? 9{-1})\}\\
&+\дет Б. \end{split}
\end{split}
$\endgroup$
10
$\begingroup$
При $n\ge2$ ответ отрицательный. Для иллюстрации рассмотрим $$ A=I_n,\quad B_1=\pmatrix{1&1\\ 0&0}\oplus0,\quad B_2=\pmatrix{1&1\\ 1&1}\oplus0. $$ Если $\det(A+B)=f\left(\det(A),\det(B),n\right)$ для некоторой функции $f$, то должно получиться $\det(A+B_1)= f(1,0,n)=\det(A+B_2)$. Но на самом деле $\det(A+B_1)=2\ne3=\det(A+B_2)$ над любым полем. 9{s(\alpha) + s(\beta)} \det(A[\alpha | \beta]) \det(B(\alpha | \beta))$$ где $r$ перебирает целые числа из $0,\dots,n$; тогда внутренняя сумма пробегает все строго возрастающие последовательности $\alpha$ и $\beta$ длины $r$, выбранные из $1,\dots,n$.
$A[\alpha|\beta]$ — это квадратная подматрица размером $r$ на $r$ матрицы $A$, расположенная в строках $\alpha$ и столбцах $\beta$.
$B(\alpha|\beta)$ $(n-r)$-квадратная подматрица матрицы $B$, содержащая строки, дополнительные к $\alpha$, и столбцы, дополнительные к $\beta$.
$\endgroup$
$\begingroup$
Чтобы добавить к прекрасному ответу Дрейка Маркиза, еще одна формула для случая n = 2:
det(A + B) = det(A) + det(B) + tr(A)tr(B) – tr (АБ).
Доказательство дается следующим образом:
det(A + B) = (A 11 + B 11 )(A 22 + B 22 ) – (A 10 + B 9012 )(A 21 + B 21 )
, который расширяется до
(A 11 A 22 – A 12 A 21 ) + (B 11 B 22 – B 12 B 21 ) + A 11 B 22 + B 11 A 22 – A 12 B 21 – B 12 A 10 9.
Это можно записано
DET (A) + DET (B) + A 11 B 22 + B 11 A 22 – A 12 B 21 – B 12 A 21 .
Теперь нам просто нужно проверить кросс-члены. Теперь
TR (A) TR (B) = (A 11 + A 22 ) (B 11 + B 22 )
, который расширяется до
A 11 B 11 +. A 11 B 22 + A 22 B 11 + A 22 B 22
и
TR (AB) = A 11 B 11 + A 12 B 11 + A 12 9 12 9 12 9 9 9. 21 + А 21 В 12 + А 22 В 22 .
Следовательно, разность tr(A)tr(B) – tr(AB) является перекрестным членом, что завершает доказательство.
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
линейная алгебра – обратная сумма матриц
спросил
Изменено 16 дней назад
Просмотрено 334 тысячи раз
У меня есть две квадратные матрицы: $A$ и $B$. {-1}$.
{-1}$.
- линейная алгебра
- матрицы
- обратная
$\endgroup$
3
$\begingroup$
Вообще говоря, $A+B$ не обязательно обратимы, даже если $A$ и $B$ обратимы. Но кто-то может спросить, можно ли получить формулу при дополнительном предположении, что $A+B$ является обратимым.
Как заметил Адриан Баркеро, есть статья Кена Миллера, опубликованная в 9{-1}.$$
Из этой леммы мы можем взять общую $A+B$, которая является обратимой, и записать ее как $A+B = A + B_1+B_2+\cdots+B_r$, где $B_i$ каждый имеет ранг $1$ и такой, что каждый $A+B_1+\cdots+B_k$ обратим (такое разложение всегда существует, если $A+B$ обратимо и $\mathrm{rank}(B)=r$). Тогда вы получите:
Теорема. Пусть $A$ и $A+B$ — невырожденные матрицы, и пусть $B$ имеет ранг $r\gt 0$. Пусть $B=B_1+\cdots+B_r$, где каждое $B_i$ имеет ранг $1$, а каждое $C_{k+1} = A+B_1+\cdots+B_k$ неособо.
Этот результат хорош, потому что он требует только, чтобы $A$ и $A+B$ были несингулярными. Для сравнения, идентичность SMW или статья Кена Миллера (как упоминалось в других ответах) требуют некоторых несингулярных или ранговых условий $B$.
$\endgroup$
3 9{-1}\| < 1$ (здесь $\|\cdot\|$ означает норму). Это просто разложение Тейлора функции инверсии вместе с базовой информацией о сходимости.
(опубликовано одновременно с mjqxxx)
$\endgroup$
$\begingroup$
Удивительно, что никто не понимает, что это частный случай известной обратной леммы матрицы или [матрица Вудбери тождества] , там сказано,
$ \left(A+UCV \right)^{ -1} = A^{-1} – A^{-1}U \left(C^{-1}+VA^{-1}U \right)^{-1} VA^{-1}$ , 9{-1} – .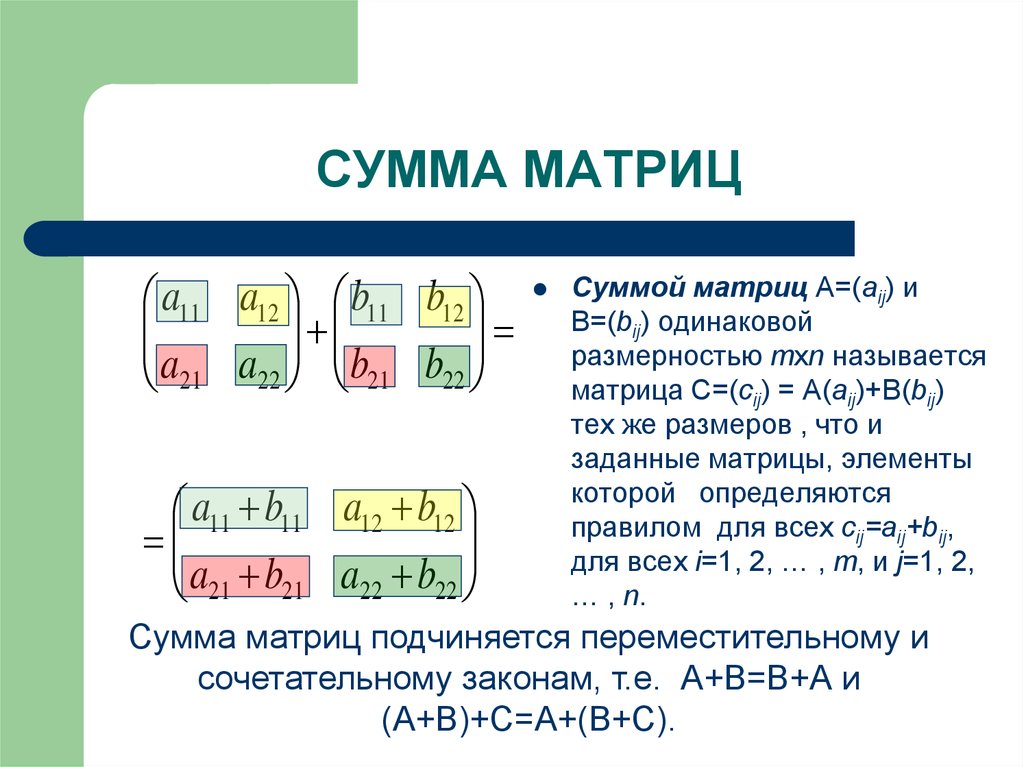 ..
\end{эквнаррай}
$$
При соответствующих условиях на собственные значения $A$ и $B$ (такие, что $A$ достаточно “большой” по сравнению с $B$), это будет сходиться к правильному результату при $\epsilon=1$.
..
\end{эквнаррай}
$$
При соответствующих условиях на собственные значения $A$ и $B$ (такие, что $A$ достаточно “большой” по сравнению с $B$), это будет сходиться к правильному результату при $\epsilon=1$.
$\endgroup$
3
$\begingroup$
Предполагая, что все хорошо обратимо, вы, вероятно, ищете идентичность SMW (которая, я думаю, также может быть обобщена до псевдоинверсий, если это необходимо) 9{-1} \тег{3}\метка{eq3} \end{уравнение} Это проще, чем \eqref{eq1}, и очень похоже на скалярное тождество: \begin{уравнение} \frac{1}{a+b}=\frac{1}{\left(1+\frac{b}{a}\right)a} \tag{4}\label{eq4} \end{equation}
Этот метод полезен при вычислениях, потому что, если значения в A и B могут сильно различаться по размеру, то вычисление $\frac{1}{A+B}$ по \eqref{eq3} дает более точный результат с плавающей запятой, чем при суммировании двух матриц.