§21.Момент инерции.
Определение: Моментом инерции материальной точки относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также, где- угловая скорость тела относительно данной оси.
Определение: Моментом инерции системы материальных точек относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой системы при вращательном движении и, равная алгебраической сумме произведений масс всех материальных точек системы на квадрат их расстояний до оси, т.е. .
Момент инерции определен только относительно оси.
В случае непрерывного распределения
масс с плотностью сумма заменится
на интеграл по всему объему тела:
(Интегрирование производится по всему
объёму; пределы интегрирования
устанавливаются исходя из конфигурации
тела и его размеров).
Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему, т.е. .
1. Момент инерции обручаотносительно оси, перпендикулярной к его плоскости и проходящей через его центр.
Обруч считается бесконечно тонким, т.е. толщиной обода можно пренебречь по сравнению с радиусом R.. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R2можно вынести из-под знака интеграла:, где
2. Момент инерции
дискаотносительно оси, перпендикулярной
его плоскости и проходящей через центр.
Диск считается бесконечно тонким, т.е.
его толщина много меньше радиуса R.Момент инерции,
согласно определению, величина аддитивная:
момент инерции целого тела равен сумме
моментов инерции его частей. Разобьем
диск на бесконечно тонкие обручи радиусомsи толщинойds (См.рис.).
Разобьем
диск на бесконечно тонкие обручи радиусомsи толщинойds (См.рис.).
Момент инерции диска относительно перпендикулярной оси, проходящей через центр.
.
Момент инерции обруча мы уже знаем: . Осталось просуммировать моменты инерции всех таких обручей:.
Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси.
3. Момент инерции шараотносительно его диаметра. Поступим аналогичным образом: “нарежем” шар на бесконечно тонкие диски толщинойdz.находящиеся на расстоянии
Момент инерции шара относительно
диаметра.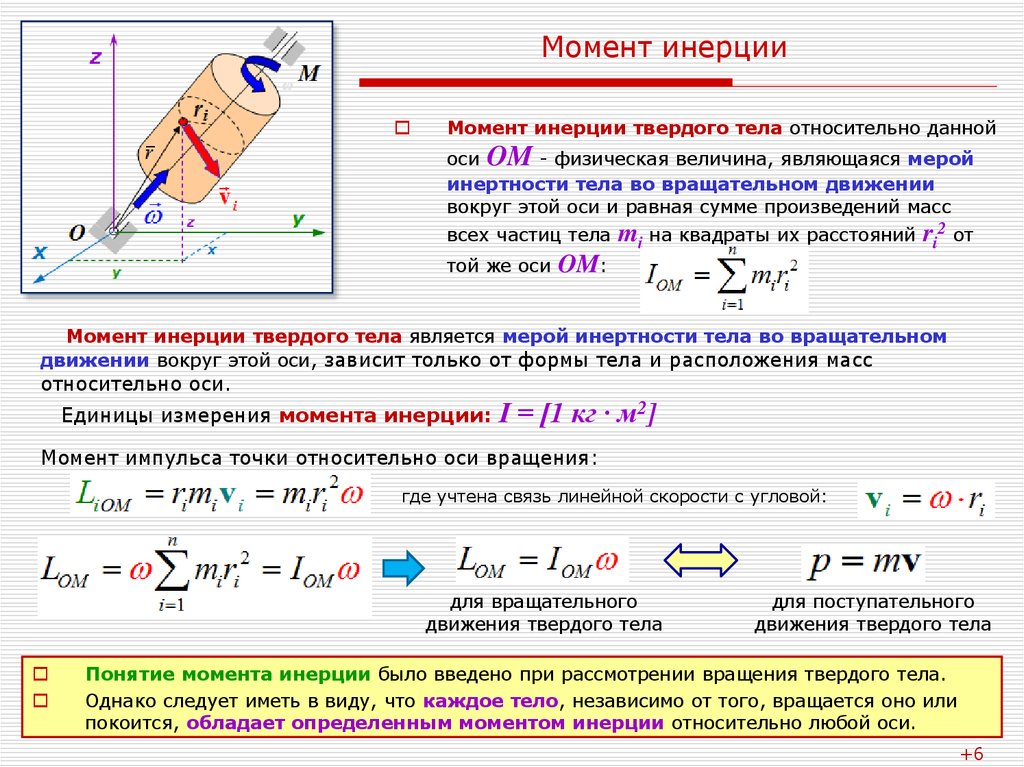
Радиус такого диска равен . Объем дискаdVz равен произведению его площади на толщину:
. Массу дискаdmнаходим, разделив массу шаратна его объем, умножив на объем диска:
.
Момент инерции диска был найден выше. В применении к данному случаю, он равен:
.
Момент инерции шара находится интегрированием по всем таким дискам:
4.Момент инерции тонкого стержня
Пусть стержень имеет длину ℓ.Направим осьxвдоль стержня. Начало координат по условию находится в центре стрежня. Возьмем элемент стержня длинойdx.находящийся на расстоянииxот оси вращения. Его масса равна
dm = (m/ℓ) dx,а момент инерцииdJ=(m/ℓ) x2 dx.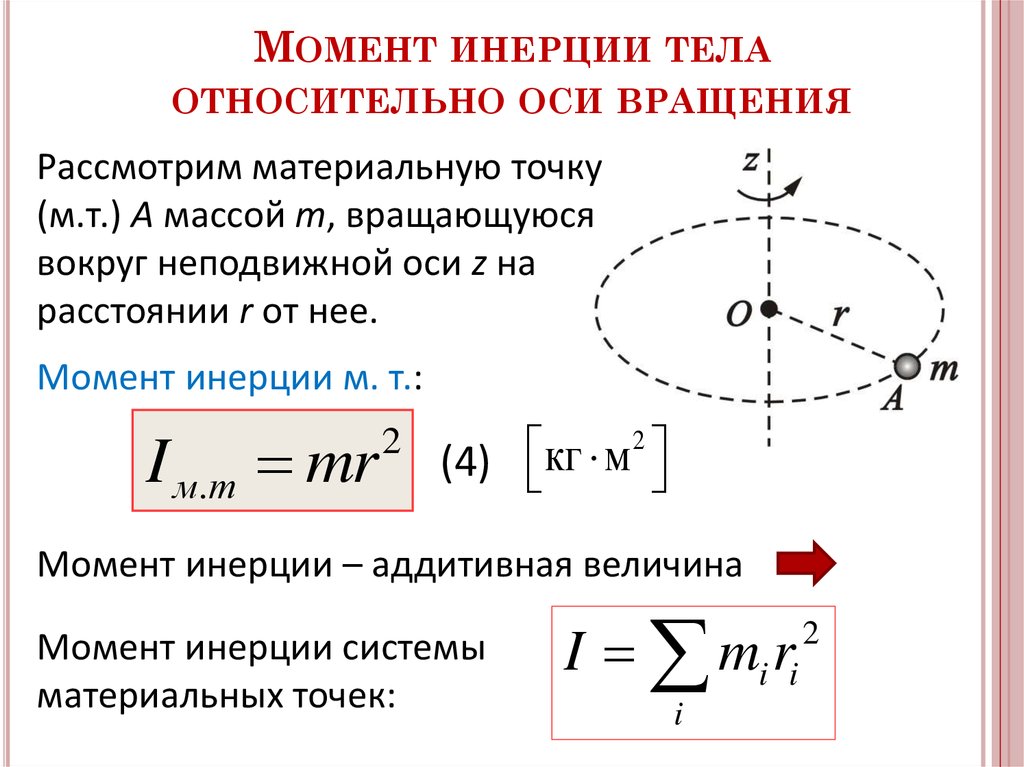 Отсюда находим момент инерции стрежня:
Отсюда находим момент инерции стрежня:
(*).
Момент инерции величина аддитивная, т.е. суммарный момент инерции системы тел относительно какой-либо оси, равен сумме моментов инерции каждого из тел данной системы относительно той же оси:
Физический смысл момента инерции:Инерционные свойства при поступательном движении характеризуются только массой тела, т.е. зависит только от массы. Инерционные свойства при вращательном движении характеризуются моментом инерции, т.е. зависят от его массы, расстояния до оси вращения и расположению теда по отношению к этой оси. Последнее означает, что относительно двух разных осей инерционные свойства вращательного движения одного и того же движения тела будут разными. Пример.
момент инерции | это… Что такое момент инерции?
ТолкованиеПеревод
- момент инерции
3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси.

Источник: ГОСТ Р 52776-2007: Машины электрические вращающиеся. Номинальные данные и характеристики оригинал документа
2.25. Момент инерции – момент инерции (динамический) тела относительно оси, представляющий собой сумму (интегральную) произведений масс его отдельных частей на квадраты их расстояний от оси.
Примечание. Эта величина обозначается буквенным символом I и выражается в кг · м2.
Источник: ГОСТ 28173-89: Машины электрические вращающиеся. Номинальные данные и рабочие характеристики оригинал документа
Смотри также родственные термины:
3.18 момент инерции (динамический момент инерции) ротора: Сумма произведений масс всех частиц ротора на квадраты расстояний от оси его вращения.
Определения термина из разных документов: момент инерции (динамический момент инерции) ротора
Источник: СТО 17330282.27.140.019-2008: Гидрогенераторы. Условия поставки. Нормы и требования
27. Момент инерции лопасти несущего винта относительно горизонтального и вертикального шарниров
Момент инерции лопасти
Момент инерции массы лопасти несущего винта и других агрегатов, совершающих вместе с лопастью маховое движение:
Определения термина из разных документов: Момент инерции лопасти несущего винта относительно горизонтального и вертикального шарниров
Источник: ГОСТ 22499-77: Аппараты винтокрылые.
 Механика полета в атмосфере. Термины, определения и буквенные обозначения оригинал документа
Механика полета в атмосфере. Термины, определения и буквенные обозначения оригинал документа3.8 момент инерции механизма : Приведенный к валу электродвигателя момент инерции сочлененного с ним механизма.
Определения термина из разных документов: момент инерции механизма
Источник: СТО 70238424.29.160.30.002-2009: Электродвигатели. Организация эксплуатации и технического обслуживания. Нормы и требования
28. Момент инерции несущего винта
Jω
Суммарный момент инерции массы лопастей и всех кинематически связанных с ним агрегатов, приведенный к оси вращения несущего винта.
Примечание. Кинематически связанные с несущим винтом агрегаты определяются в каждом конкретном случае
Определения термина из разных документов: Момент инерции несущего винта
Источник: ГОСТ 22499-77: Аппараты винтокрылые. Механика полета в атмосфере. Термины, определения и буквенные обозначения оригинал документа
Момент инерции поперечного сечения распорного кольца, мм4 (см4)
Iк
Определения термина из разных документов: Момент инерции поперечного сечения распорного кольца, мм4 (см4)
Источник: ГОСТ 25859-83: Сосуды и аппараты стальные.
 Нормы и методы расчета на прочность при малоцикловых нагрузках оригинал документа
Нормы и методы расчета на прочность при малоцикловых нагрузках оригинал документа74 момент инерции электропривода: Сумма моментов инерции всех движущихся масс электропривода при приведении их к скорости элемента приведения электропривода
Определения термина из разных документов: момент инерции электропривода
Источник: ГОСТ Р 50369-92: Электроприводы. Термины и определения оригинал документа
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
Игры ⚽ Поможем написать реферат
- момент затяжки М
- момент инерции (динамический момент инерции) ротора
Полезное
Момент инерции
Момент инерции Масса m помещена на стержень длины r и имеет пренебрежимо малую массу и вынуждена вращаться вокруг неподвижной оси. Если масса освобождается от горизонтальной ориентации, это можно описать либо с точки зрения силы и ускорения с помощью второго закона Ньютона для линейного движения, либо как чистое вращение вокруг оси с помощью второго закона Ньютона для вращения. | Индекс Moment of Inertia Concepts Moment of Inertia Примеры | ||
| R Nave |
Для однородного стержня незначительной толщины момент инерции около его центр масс равен
Момент инерции относительно конца стержня можно рассчитать напрямую или получить из выражения центра масс с помощью теоремы о параллельных осях.
Если толщина не пренебрежимо мала, то можно использовать выражение для I цилиндра около его конца. | Индекс Понятия момента инерции | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

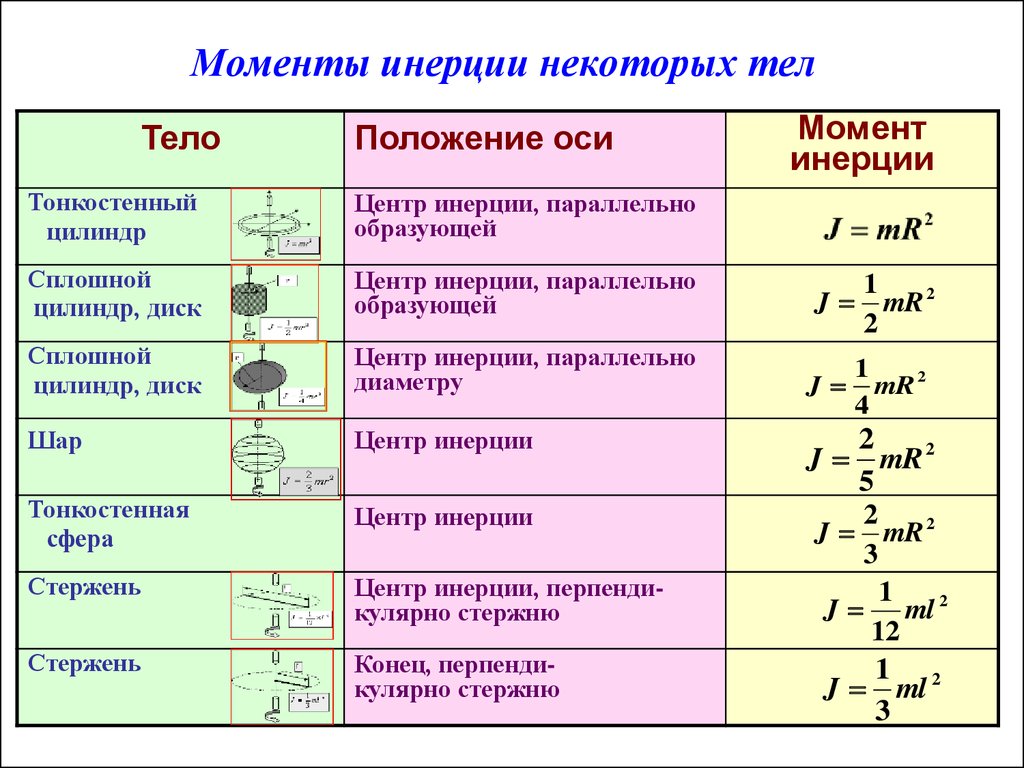
 Чтобы выполнить интеграл, необходимо выразить все в интеграле через одну переменную, в данном случае переменную длины r. Так как общая
длина L имеет массу M, тогда M/L
отношение массы к длине и масса
элемент может быть выражен, как показано.
Интегрируя от -L/2 до +L/2 от
центр включает в себя весь стержень. Интеграл
имеет полиномиальный тип:
Чтобы выполнить интеграл, необходимо выразить все в интеграле через одну переменную, в данном случае переменную длины r. Так как общая
длина L имеет массу M, тогда M/L
отношение массы к длине и масса
элемент может быть выражен, как показано.
Интегрируя от -L/2 до +L/2 от
центр включает в себя весь стержень. Интеграл
имеет полиномиальный тип:

 Подход включает в себя нахождение выражения для тонкого диска на расстоянии z от оси и суммирование по всем таким дискам.
Подход включает в себя нахождение выражения для тонкого диска на расстоянии z от оси и суммирование по всем таким дискам.