Дистанционный репетитор – онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376209 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
“
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
“
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
“
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
“
Алина Крякина
Надежда Васильевна Токарева
“
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
“
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
“
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
“
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
RU
- Class
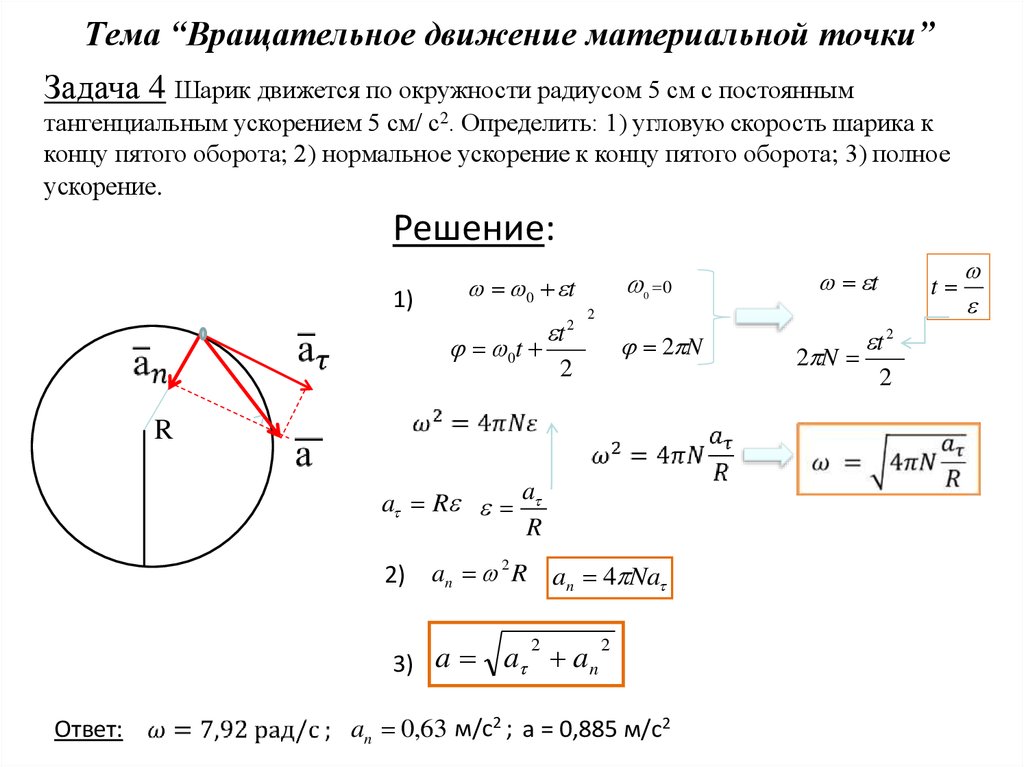
Скорость и ускорение точки. Частные случаи движения точки
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. КИНЕМАТИКА (основные понятия)
Дудко Ольга НиколаевнаЛидский колледж ГрГУ им.Я.Купалы
2. Вопросы на рассмотрение:
3.Скорость точки.4.Ускорение точки.
5.Частные случаи движения точки.
Дудко Ольга Николаевна
2
3.
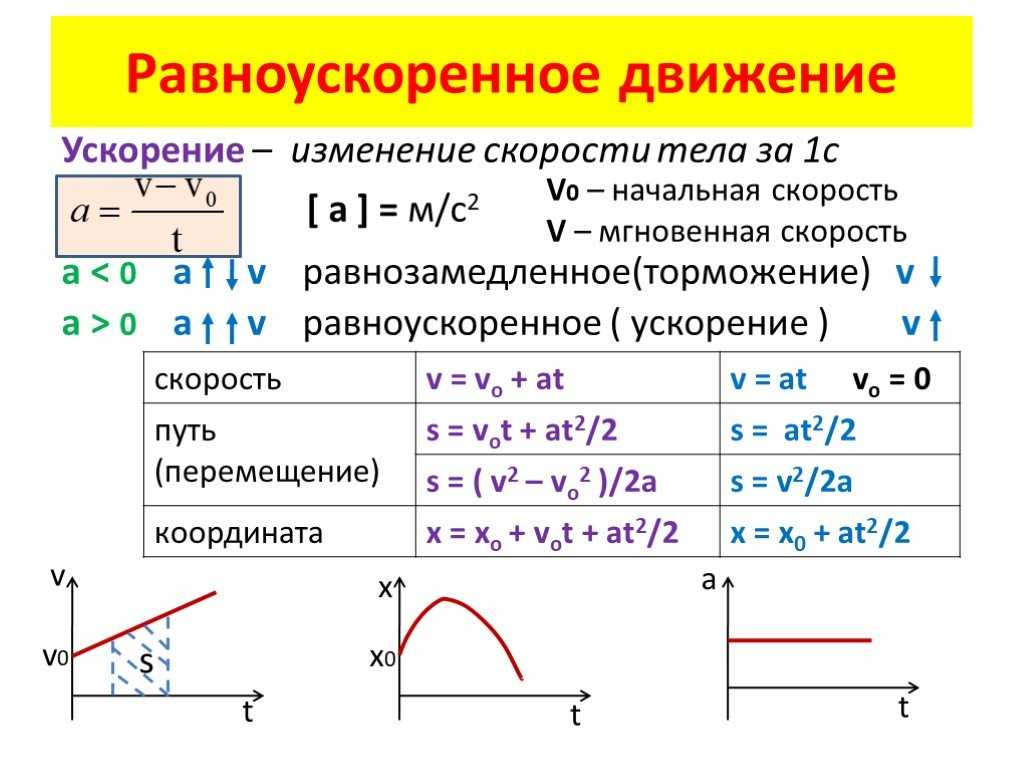3. Скорость точки.Скорость:векторная величина которая показывает
направление и быстроту движения точки.
Скорость показывает, какое перемещение тело
совершает в единицу времени.
Движение, при котором тело за любые равные промежутки времени проходит
равные отрезки пути, называют ПРЯМОЛИНЕЙНЫМ РАВНОМЕРНЫМ.
скорость равномерного движения –
s
v
t
[м/с]
Движение, при котором за равные промежутки времени тело проходит неравные
отрезки пути, называют неравномерным
скорость неравномерного движения:
или переменным.
ds
v
dt
[м/с]
Направление скорости при:
v2
прямолинейном движении –
неизменно
криволинейном движении – по
касательной к траектории в
данной точке
Дудко Ольга Николаевна
v1
v
v3
vv
4
4
равномерное
движение, при котором тело за любые
равные промежутки времени проходит
равные пути.
равномерное
S1
S2
S3
S4
t1
t2
t3
t4
неравномерное
неравномерное
движение, при котором тело за равные
промежутки времени проходит разные пути.
S1
S2
S3
S4
t1
t2
t3
t4
механическое движение
равномерное
неравномерное
движение,при котором тело за любые равные
промежутки времени проходит равные пути.
движение,при которм тело за равные
промежутки времени проходит разные пути.
S1
S2
S3
S4
S1
S2
S3
S4
t1
t2
t3
t4
t1
t2
t3
t4
20. Если известны проекции скорости на оси координат, то можно определить числовое значение скорости и ее направление по формуле:
Решение: найдемпервую производную от
скорости по времени, а
затем в полученное
выражение подставим
время равное 2 секунды.
Пример: определить
скорость точки в момент
времени 2 секунды от
начала движения, если
уравнения движения
точки S=2t3 + t – 1.
S′ = 2∙3∙t2 +1 =
(6t2 + 1)2=
6∙4+1=25 м/с.
Ответ: v= 25 м/с.
Дудко Ольга Николаевна
20
21. 4. ускорение точки.
Ускорение векторная величина, характеризующаябыстроту изменения направления и
числового значения скорости в единицу
времени .
Средним ускорением неравномерного
движения в интервале от t до t + ∆t
называется векторная величина, равная
отношению изменения скорости ∆v к
интервалу времени ∆t:
При свободном падении вблизи поверхности Земли
a g
g 9,8 м
Дудко Ольга Николаевна
с
Δv
a
Δt
, где
2
22
Переходя к пределу при Δt→0 найдем истинное
значение ускорения.
Ускорение точки, совершающей неравномерное
движение, равно первой производной от
скорости по времени либо второй производной
от пути по времени.
Дудко Ольга Николаевна
23
Вектор полного ускорения раскладывается на две
составляющие: касательную (тангенциальную) и
центростремительную(нормальную).
Дудко Ольга Николаевна
24
Касательная составляющая
направлена по касательной
к траектории и совпадает по
направлению со скоростью.
Эта составляющая
характеризует изменение
значения скорости.
Нормальная составляющая
перпендикулярна к
направлению скорости
точки.
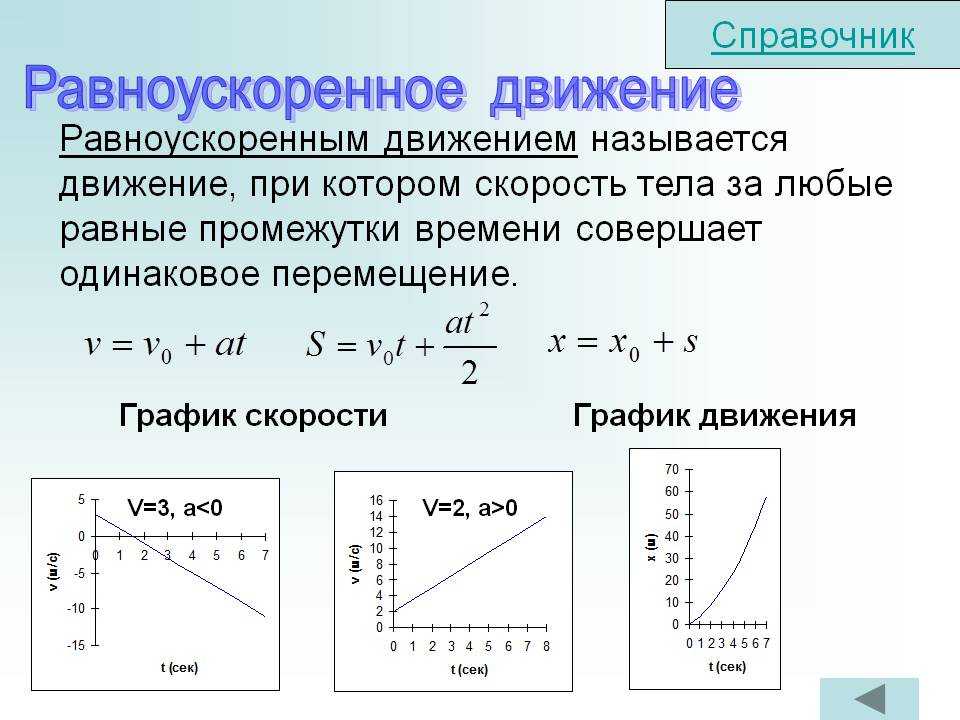Эта составляющаяхарактеризует изменение
направления вектора
скорости.
Дудко Ольга Николаевна
25
Модуль вектора ускорения можно найти по
формуле:
Дудко Ольга Николаевна
26
27. Составляющая аƮ вектора ускорения, направленная вдоль касательной к траектории в данной точке, называется тангенциальным
аб
Дудко Ольга Николаевна
27
Тангенциальная составляющая
ускорения аƮ равна первой
производной по времени от модуля
скорости, определяя тем самым
быстроту изменения скорости по
модулю:
Вторая составляющая ускорения,
равная:
называется нормальной составляющей
ускорения и направлена по нормали к
траектории к центру ее кривизны
(поэтому ее называют так же
центростремительным ускорением).
Полное ускорение есть геометрическая
сумма тангенциальной и нормальной
составляющих:
Дудко Ольга Николаевна
28
29. Пример: определить ускорение точки в момент времени 2 секунды от начала движения, если уравнения движения точки S=2t3 + t – 1.
Решение: найдем первую производную от скорости повремени, а затем в полученное выражение
подставим время равное 2 секунды.
S′ = 2∙3∙t2 +1 = 6t2 + 1
Для определения уравнения ускорения необходимо
взять производную от полученного уравнения
скорости.
A= (6t2 +1), = 6∙2∙t = 12t
В полученное уравнение подставляем время 2 секунды,
получаем а = 24м/с2.
Ответ: а= 24 м/с2.
Дудко Ольга Николаевна
29
30. 5. Частные случаи движения точки.
Касательное ускорение служит характеристикойнеравномерности движения по любой
траектории, а центростремительное ускорение –
характеристикой криволинейности движения.
Рассмотрим частные случаи движения точки.
Дудко Ольга Николаевна
31
32. Частные случаи движения в зависимости от ускорения
Дудко Ольга Николаевна32
33. 1.Равномерное прямолинейное движение.
v= constat = 0
an =0
Дудко Ольга Николаевна
33
34. 2.Равномерное криволинейное движение.
v= constat = 0
Дудко Ольга Николаевна
34
35. 3. Неравномерное прямолинейное движение.
ЧИСЛЕННОЕ ЗНАЧЕНИЕ СКОРОСТИ ИЗМЕНЯЕТСЯ, АНАПРАВЛЕНИЕ НЕ МЕНЯЕТСЯ.
v≠const
an=0
Дудко Ольга Николаевна
35
36. 4. Неравномерное криволинейное движение.
v≠constДудко Ольга Николаевна
36
37. 5. Равнопеременное движение.
А) РАВНОМЕРНОУСКОРЕННОЕat≠0=const >0
Б) РАВНОМЕРНОЗАМЕДЛЕННОЕ
at≠0 = const < 0
Дудко Ольга Николаевна
37
38. ЗАКРЕПЛЕНИЕ МАТЕРИАЛА
Дудко Ольга Николаевна38
39. Домашнее задание:
[1] стр.129-136 ,рабочая тетрадь стр. 16-19,
доклад учащегося по вопросу «Вращательное
движение тела»
Дудко Ольга Николаевна
39
40. CПИСОК ЛИТЕРАТУРЫ
1 Аркуша, А.И. Техническая механика [Текст]: Учебное пособие длятехникумов/ А.И. Аркуша, М.И. Фролов. ─ М.: Высш. шк., 2005. – 446 с.: ил.
2. Мовнин М.С., Израелит А.Б., Рубашкин А.Г. Основы технической
механики.
– Л.: Мащиностроение, 19903. Никитин Е.М. Теоретическая механика для техникумов.
http://files.school-collection.edu.ru/dlrstore/669bc789-e921-11dc-95ff0800200c9a66/1_1.swf
http://gannalv.narod.ru/img/p0002.gif
ttp://gannalv.narod.ru/img/p0005.gif
http://gannalv.narod.ru/img/p0012.gif
English Русский Правила
Ускорение и скорость: взаимосвязь | StudySmarter
Вы когда-нибудь задумывались о физике и механике прыжков с парашютом? Когда вы падаете, ваше ускорение изменяется вместе со скоростью, с которой вы падаете, а затем выравнивается в определенный момент — почему это так? Ответ — конечная скорость, потому что ваше ускорение будет зависеть от вашей скорости.
Это означает, что увеличение скорости при падении регулируется функцией ускорения, которая зависит от вашей изменяющейся скорости, и в определенный момент вы достигнете своей конечной скорости — скорости вашего падения, которую вы не можете превысить.
.
Подробнее об этом принципе читайте далее.
Сначала мы начнем с отношения между ускорением и скоростью.
Соотношение ускорения и скорости
Один большой вопрос относительно ускорение это как оно связано со скоростью ? Ответ на этот вопрос состоит в том, что ускорение есть производная от скорости, а это означает, что ускорение есть скорость изменения скорости.
И наоборот, если вы проинтегрируете выражение для ускорения, вы получите выражение для скорости.
Ускорение и скорость являются векторными величинами. Это означает, что они имеют размер и направление. Это означает, что при рассмотрении значений ускорения и скорости к ним прикреплены знаковые значения, указывающие направление.
Например, если у вас было отрицательное значение ускорения, объект, который вы исследуете, замедляется до уменьшения скорости.
Но в чем тогда разница между ускорением и скоростью?
Различия в ускорении и скорости
Хотя мы рассмотрели взаимосвязь и сходство между скоростью и ускорением , факт остается фактом: это разные переменные, и поэтому возникает вопрос, чем они отличаются.
Ускорение отслеживает изменение скорости ; как таковые, они будут иметь разные значения, но также могут иметь разные знаки.
Например, если вы изучаете ускорение автомобиля, замедляющегося , ускорение будет отрицательным для замедления , поскольку автомобиль замедляется, но скорость v по-прежнему будет положительной, поскольку он движется вперед, только с убывающей скоростью.
Теперь, когда мы знаем, как связаны ускорение и скорость и чем они различаются, мы переходим к производным ускорения и скорости.
Производные ускорения и скорости
Мы знаем, что ускорение — это скорость изменения скорости , но у нас также есть связь между скоростью и перемещением: скорость – скорость изменения смещения . Это означает, что ускорение является второй производной смещения .
Это соотношение работает и в обратном направлении: если у вас есть выражение для ускорения и его интегрирование, у вас будет выражение для скорости, а если у вас есть выражение для скорости и его интегрирование, у вас будет выражение для смещения .
На приведенном ниже рисунке показаны эти отношения.
График, показывающий взаимосвязь между перемещением, скоростью и ускорением — StudySmarter Originals 92}.\]Это производные отношения, которые мы используем для оценки скорости и ускорения. Как видно из рисунка выше, если бы мы хотели работать в другом направлении, мы бы просто интегрировали,\[v=\int a\quad dt\]\[r=\int v\quad dt.\]
Мы перейдем теперь к интерпретации графиков ускорения и скорости.
График ускорения и скорости
Теперь мы увидели, как смещение, скорость и ускорение связаны друг с другом, мы можем дополнительно визуализировать это, изучив графики скорости/ускорения во времени.
График, показывающий графики зависимости ускорения и скорости от времени для сравнения – StudySmarter Originals
Опираясь на то, что мы видели ранее с взаимосвязью между скоростью и ускорением, мы можем визуализировать это на графиках выше.
Когда мы дифференцируем, мы находим градиент линии скорости.
Изучив рисунок выше, вы можете увидеть это – посмотрите между \(4\) и \(5\) секундами на верхнем графике, и вы увидите, что скорость возрастает от \(1 м/с\) до \(4 м/с). \) более одной секунды. Это дает градиент \(3\), который вы можете увидеть в соответствующей точке на графике времени ускорения.
И наоборот, если мы посмотрим между \(0\) и \(1\) секундами на графике времени ускорения и вычислим площадь, очерченную линией, мы вернем наш профиль скорости. Это метод интегрирования — если мы интегрируем ускорение (в данном случае область над линией), мы получим скорость. Ответ интеграла равен \(-3\), так как он находится на нижней стороне осей, и если мы посмотрим на график скорости, мы увидим, что за этот период времени скорость уменьшилась на \(3 м/с.\)
Эти отношения должны помочь вам понять, как мы можем различать и интегрировать смещение, скорость и ускорение, как вы видели ранее.
Формула ускорения и скорости
При рассмотрении ускорения, которое зависит от скорости, нам обычно дают выражение, использующее функцию скорости.
Мы знаем, что наша формула для ускорения и скорости задается выражением \[a=\frac{dv}{dt},\], и если бы нам дали решить функцию скорости, у нас был бы вопрос в форме, \ [\frac{dv}{dt}=f(v).\] Этот тип вопроса утверждает, что ускорение для вопроса определяется функцией скорости. Так как бы мы решили это?
В вопросе есть член \(f(v)\), который равен нашему ускорению \((a)\). Следовательно, мы можем ожидать решения этой проблемы с помощью метода разделения переменных. Это означает, что мы собираем одинаковые члены по обе стороны от знака равенства, интегрируем и затем находим \(v\), чтобы получить выражение для скорости \((v)\) через время \((t)\) и любое константы. Давайте посмотрим на логику этого.
Мы знаем, что ускорение есть скорость изменения скорости,\[\поэтому a=\frac{dv}{dt}.\]Мы также знаем, что у нас есть функция \(f(v)\), равная к ускорению. Это приводит к выражению \[\frac{dv}{dt}=f(v).\]Отсюда мы собирали бы \(v\) термины с термином \(dv\) и собирали любые \( t\) с нашим \(dt\) термином по другую сторону от знака равенства.
Например, если \(f(v)=\frac{t}{v}\), где \(t\) – переменная времени, наше разделение переменных будет выглядеть так: \[\begin{align}a&= f(v)\\ \frac{dv}{dt}&=\frac{t}{v} \\ v dv&= tdt. \end{align}\] Отсюда мы можем проинтегрировать и получить выражение того, как скорость меняется со временем, из выражения для ускорения. Давайте посмотрим, как это может выглядеть на примере.
Ускорение частицы зависит от ее скорости и определяется уравнением \[a=3v-4.\]Найдите скорость частицы через 0,5 секунды, если частица движется со скоростью \(20 м/с\) при \(t=0.\)
Решение
Шаг 1. Разделение переменных
\[\begin{align} a&=3v-4\\ \frac{dv}{dt}&=3v-4\\ \frac{1 }{3v-4}dv&=1dt\end{align}\]
Шаг 2. Интеграция
\[\begin{align} \int \frac{1}{3v-4}dv&=\int 1dt \\ \frac{ln(|3v-4|)}{3}&=t+C\end{align}\]
Шаг 3. Перестановка для \(v\)
\[\begin{ align} \frac{ln(|3v-4|)}{3}&=t+C \\ ln(|3v-4|) &= 3t+C\\ 3v-4&= e^{3t+C} \\ v&=\frac{ e^{3t+C} +4}{3}\end{align}\] 9{3(0.
5)+ln(56)} +4}{3}\\ &= 84,99 м/с \end{align}\]
Конечная или предельная скорость
Мы также можем рассчитать конечную скорость объект, использующий тот же формат выражения, что и выше.
Если принять конечную скорость за максимальную скорость, которой может достичь объект, это означает, что скорость изменения скорости будет равна 0. Объект достиг своей максимальной скорости, поэтому скорость больше не может увеличиваться.
Примером этого может быть объект в свободном падении. В какой-то момент вес объекта ограничит скорость, с которой он падает, и эту скорость нельзя будет превысить. У нас по-прежнему будет ускорение \(a\), выраженное как функция скорости \(v\), что приводит к общему виду, \[\frac{dv}{dt}=f(v)\]\[0= f(v).\]Если мы затем переставим функцию для \(v\), мы получим 92&=237\\ v&=\sqrt{\frac{237}{6}} \\&=6,28 м/с\end{align}\]
Уравнения ускорения и скорости
У нас также есть другая методология, которую мы можем использовать при отслеживании ускорения с различной скоростью.
2+2as\\&(5)\quad v=u+at\end{align}\] 92\) через \(10\) секунд от начала.
Ускорение и скорость — ключевые выводы
- Вы можете перемещаться между смещением, скоростью и ускорением, дифференцируя в этом порядке или интегрируя в обратном порядке.
- Графики ускорения и скорости связаны между собой тем, что градиент графика скорости дает значение вашего ускорения, а область под графиком ускорения за временной интервал показывает изменение скорости.
- Если у вас есть уравнение, которое дает ускорение как функцию скорости, вы можете использовать метод разделения переменных и интегрирование, чтобы получить выражение для скорости.
- Конечную скорость объекта можно рассчитать, установив скорость изменения скорости как \(0\) и найдя \(v.\). Это принимает общий вид \(0=f(v).\)
Чтобы использовать приведенный выше калькулятор:
Существует математическая связь между частотой, смещением, скоростью и ускорением для синусоидального движения при рассмотрении их пиковых значений. Связь такова, что если известны любые две из четырех переменных, можно вычислить две другие. Приведенные ниже уравнения обеспечивают все необходимые комбинации. G в этих формулах — это , а не ускорение свободного падения. Это константа для расчета в различных системах. Поскольку движение является синусоидальным, перемещение, скорость и ускорение изменяются синусоидально. Однако они не совпадают по фазе. Фазовое соотношение между перемещением, скоростью и ускорением таково, что скорость равна 90° не совпадает по фазе с ускорением, а смещение составляет 180° не по фазе при ускорении. Другими словами, когда перемещение максимально, скорость минимальна, а ускорение максимально. Синусоидальное движение 20 Гц Еще одним применением этого калькулятора является определение максимальных частотных характеристик датчиков положения SpaceAge Control. Для этого обратитесь к таблицам данных, расположенным в нашем (Литературном зале), и обратите внимание на максимальное ускорение для данной модели. Затем используйте этот калькулятор, чтобы определить максимальную частоту модели для заданного смещения и соответствующей информации. Уравнения, графики и информация любезно предоставлены Ричардом Бейкером, который разработал VIBKIT, комплексный набор инструментов для испытаний на вибрацию, для которого доступна демонстрационная версия. Примечание: 1 gn = 9,80665 м/с² = 32,174 фута/с² = 386,0886 дюйма/с². Другие калькуляторы:
Отсутствие гарантий: Этот калькулятор и информация предоставляются «как есть» без каких-либо гарантий, условий или заявлений любого рода, явных или подразумеваемых, включая, помимо прочего, любые гарантии в отношении ненарушения прав, а также подразумеваемые гарантии условия товарной пригодности и пригодности для конкретной цели. | ||||||||||||||||||||||||||||||||||||||||
Выберите столбец для известных вам переменных. ->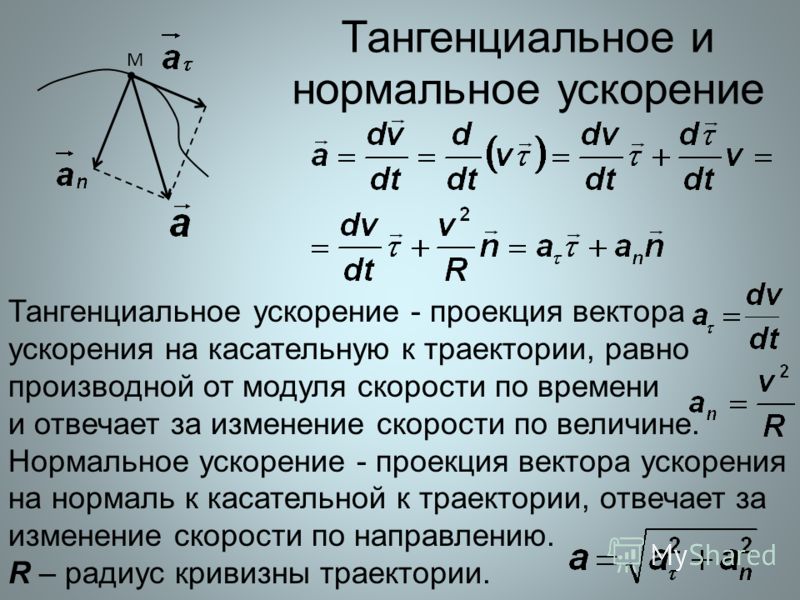 
Выберите свою систему измерения ниже. 
Для метрической системы G составляет 9,80665 м/с². Для Британских единиц G равно 386,0885827 дюймов/с² Для СИ G равно 1 м/с² 
