Kinetic Energy | Protocol (Translated to Russian)
7.4: Кинетическая энергия
Кинетическая энергия – это способность объекта в движении выполнять работу или производить изменения. Он может принимать различные формы. Например, вода, стекающая по водопаду, имеет кинетическую энергию. В биологических системах частицы света путешествуют и поглощаются растениями для создания химической энергии. Звери потребляют химическую энергию и высасывая молекулы, которые несут их запах по воздуху. Они также генерируют кинетическую энергию, когда убегают от хищников. Целые системы также обладают кинетической энергией, как и Солнечная система, где происходит движение целых планет и звезд.
Кинетическая энергия
Кинетическая энергия – это энергия объектов в движении. Например, в то время как вода за плотиной имеет потенциальную энергию, вода, быстро стекающая вниз по водопаду, имеет кинетическую энергию. Если бы на дне водопада вода перестала двигаться и объединиться, ее энергия снова была бы преобразована в потенциальную энергию.
В биологических системах кинетическая энергия приобретает различные формы по мере того, как объекты движутся по-разному. Например, частицы света-фотоны, которые растения поглощают, чтобы расти и делать пищу, двигаться очень быстро, изменить форму, и используются для работать- они используются, чтобы сделать химическую энергию в виде углеводов.
Кинетическая энергия позволяет молекулам, которые несут запах животных, отойти и привлечь близлежащего хищника. Химическая энергия растений, потребляемая животными, позволяет животным убегать от хищника, что также является формой кинетической энергии.
Кинетическая энергия также может передается от одного объекта к другому. Например, человек, играющий в бильярд, может ударить биток и его кинетическая энергия затем попадает в другой шар и приводит его в движение. Целые системы также могут обладать кинетической энергией – движение всех планет и звезд в нашей Солнечной системе – это кинетическая энергия.
Литература для дополнительного чтения
Kohn, Kathryn P. , Sonia M. Underwood, and Melanie M. Cooper. “Energy Connections and Misconnections across Chemistry and Biology.” CBE Life Sciences Education
, Sonia M. Underwood, and Melanie M. Cooper. “Energy Connections and Misconnections across Chemistry and Biology.” CBE Life Sciences Education
Кинетическая и потенциальная энергия. Закон сохранения энергии
Понятие энергии
Энергия – скалярная величина. В системе СИ единицей измерения энергии является Джоуль.
Кинетическая и потенциальная энергия
Различают два вида энергии – кинетическую и потенциальную.
Потенциальная энергия в поле тяготения Земли – это энергия, обусловленная гравитационным взаимодействием тела с Землей. Она определяется положением тела относительно Земли и равна работе силы тяжести по перемещению тела из данного положения на нулевой уровень:
Потенциальная энергия упруго деформированного тела – энергия, обусловленная взаимодействием частей тела друг с другом. Она равна работе внешних сил по растяжению (сжатию) недеформированной пружины на величину :
Тело может одновременно обладать и кинетической, и потенциальной энергией.
Полная механическая энергия тела или системы тел равна сумме кинетической и потенциальной энергий тела (системы тел):
Закон сохранения энергии
Для замкнутой системы тел справедлив закон сохранения энергии:
- полная механическая энергия замкнутой системы тел есть величина постоянная:
В случае, когда на тело (или систему тел) действуют внешние силы, например, сила трения, закон сохранения механической энергии не выполняется. В этом случае изменение полной механической энергии тела (системы тел) равно работе внешних сил:
Закон сохранения энергии позволяет установить количественную связь между различными формами движения материи. Так же, как и закон сохранения импульса, он справедлив не только для механических движений, но и для всех явлений природы. Закон сохранения энергии говорит о том, что в энергию в природе нельзя уничтожить так же, как и создать из ничего.
В наиболее общем виде закон сохранения энергии можно сформулировать так:
- энергия в природе не исчезает и не создается вновь, а только превращается из одного вида в другой.

Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Кинетическая энергия – это… Что такое Кинетическая энергия?
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.
Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
История
Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»
Лейбница, посвященных понятию «живой силы»
Физический смысл
Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:
— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:
Если система замкнута, то есть , то , а величина
остаётся постоянной. Эта величина называется
Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
где:
— масса тела
— скорость центра масс тела
— момент инерции тела
— угловая скорость тела.
Физический смысл работы
Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:
Релятивизм
При скоростях, близких к скорости света, кинетическая энергия любого объекта равна
где:
— масса объекта;
— скорость движения объекта в инерциальной системе отсчета;
— скорость света в вакууме ( — энергия покоя).
Данную формулу можно переписать в следующем виде:
При малых скоростях () последнее соотношение переходит в обычную формулу .
Соотношение кинетической и внутренней энергии
Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.
То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.
См. также
Преобразователь кинетической энергии в электрическую – Энергетика и промышленность России – № 3 (43) март 2004 года – WWW.
 EPRUSSIA.RU
EPRUSSIA.RUГазета “Энергетика и промышленность России” | № 3 (43) март 2004 года
Известный российский ученый А.О. Шахинов сказал о нем: “Это изобретение очень актуально для нашего XXI века. Так в свое время, когда была изобретена гидроэлектростанция, случился переворот, можно было получать энергию, не затрачивая на это ресурсов и так уже истощившегося запаса полезных ископаемых земного шара”.Это не гидроэлектростанция, для которой обязательно требуется река.
Это не приливно/отливная станция, для которой обязательно требуется море или озеро. И это не ветряные электростанции, которые работают только в том случае, если есть ветер. Наш преобразователь энергии действует в любом современном городе и не зависит от воды, ветра, прилива или отлива.
Суть изобретения: специальные встраиваемые панели в дороги города.
При совершении наезда любым видом транспорта на такую панель вырабатывается энергия. Причем вырабатывается очень большое количество энергии. Обратите внимание на то, что если поставить такую панель на оживленном шоссе, то энергия будет поступать бесконечно.
По подсчетам наших специалистов, два таких устройства смогут питать круглые сутки большой 9-этажный 108-квартирный дом! Заметьте, что никаких затрат, кроме первоначальной покупки и установки преобразователя, не требуется. Такой дом не будет зависеть ни от каких электростанций, кроме своей собственной – локальной.
При постройке новых домов можно добавлять в проект наш преобразователь. И спрос на такое жилье будет поистине большим. Ведь кому хочется покупать квартиру, за электроэнергию в которой постоянно надо платить, – если можно купить жилье, в котором можно жить и не переживать за повышение цен на электроэнергию. Энергия в таких домах будет совершенно бесплатна.
Но не только жилые дома могут черпать энергию из преобразователя. Ведь везде существуют предприятия, которые нуждаются в постоянном источнике электропитания.
Ведь везде существуют предприятия, которые нуждаются в постоянном источнике электропитания.
Вот один из вариантов. Если в аэропорту поставить пару преобразователей, то аэропорт не будет нуждаться в подводке проводов от других электростанций, которые расположены, как всегда, совсем не рядом. Помимо того, что не будет лишних затрат на километры проводов, не будет и надобности оплачивать бесконечное количество счетов от электростанций, которые отнимают значительную часть прибыли. Такой аэропорт сможет забыть про квитанции об оплате электроэнергии. В них отпадет надобность.
Возьмем город в целом. Если вдоль главной трассы поставить 100 таких устройств, то такая дорога будет питать весь город. Значительно улучшатся экологические показатели. А громоздкие сооружения в виде страшных дымящих труб исчезнут.
То есть это – экологически чистый, безопасный и бесплатный способ выработки энергии.
Преобразователь представляет собой редуктор с накопителем энергии – маховиком, который раскручивается за счет поступательного движения толкателя и поворота зубчатого сектора привода. Толкатель вертикально утапливается шарнирным соединением двух металлических площадок на всю ширину проезжей части, имеющих оптимальную длину по 20 метров в обе стороны от шарнира, причем верхняя точка шарнира от плоскости дорожного покрытия находится на высоте 0,5 метра.
Толкатель вертикально утапливается шарнирным соединением двух металлических площадок на всю ширину проезжей части, имеющих оптимальную длину по 20 метров в обе стороны от шарнира, причем верхняя точка шарнира от плоскости дорожного покрытия находится на высоте 0,5 метра.
Транспортное средство, двигаясь по площадкам, утапливает толкатель через шарнир, раскручивая маховик – накопитель энергии.
После прохождения транспортного средства по площадкам последние возвращаются в исходное положение простейшим механизмом возврата.
Таким образом преобразователь использует вторичный источник энергии, первичный (нефть, газ, уголь) уже затрачен на движение транспортного средства, при этом электрические транспортные средства можно перевести на непосредственное питание от преобразователей, установленных на маршрутах движения.
Проект готов к реализации, причем организация проекта осуществляется на базе любого машиностроительного предприятия и не изменяет принципиально и по существу действующую на нем организацию производства.
Преобразователь содержит силовой блок, включающий кинематически связанные между собой грузовой и уравнивающий механизмы и вал потребителя энергии. Грузовой механизм выполнен в виде двух подвижных шарнирно-соединенных между собой платформ. Платформы установлены своими опорными сторонами с возможностью возвратно-поступательного движения опорных сторон по направлению продольной оси дороги. Платформы являются частью проезжей части дороги. Ось шарнирного соединения платформ ориентирована параллельно опорным сторонам платформ и перпендикулярно продольной оси дороги.
Уравновешивающий механизм выполнен в виде механизма возврата, который содержит по меньшей мере два кронштейна, размещенных по обе стороны дороги, по меньшей мере два блока, размещенных на кронштейнах, по меньшей мере два груза и по меньшей мере два троса, каждый из которых одним своим концом через блок соединен с одним из грузов, а вторым – с грузовым механизмом непосредственно у шарнирного соединения. Кинематическая связь грузового механизма с валом потребителя энергии осуществляется посредством силового привода.
Силовой привод содержит толкатель, шатун, зубчатый сектор, храповой механизм с ведущей и ведомой шестернями, ведущую шестерню вала потребителя энергии и ведомую шестерню вала потребителя энергии, жестко соединенную с этим валом.
В 1998 году его для нас оценила оценочная компания (опытный образец) – 48 тыс. дол. Но это без вмонтирования устройства в дорогу.
С вмонтированием оного в дорогу получится примерно вдвое больше, т.е. около 100 тыс. дол.
Период окупаемости проекта – 1 год.
7 декабря пройдут встречи кандидатов на должность ректора с сотрудниками и студентами университета 7 декабря 2021 года (вторник) пройдут встречи кандидатов на должность ректора Новосибирского государственного архитектурно-строительного университета (Сибстрин) с сотрудниками и студентами. Встреча Косолаповой Ирины Анатольевны: в 12. 00 в ауд. 362
Встреча Сколубовича Юрия Леонидовича: в 14.00 в ауд. 239
Напоминаем, что 10 декабря 2021 года (пятница) состоится конференция научно-педагогических работников, представителей других категорий работников и обучающихся НГАСУ (Сибстрин) по выборам ректора университета.
Начало регистрации: в 13.30
Начало конференции: в 14.00 00 в ауд. 362
Встреча Сколубовича Юрия Леонидовича: в 14.00 в ауд. 239
Напоминаем, что 10 декабря 2021 года (пятница) состоится конференция научно-педагогических работников, представителей других категорий работников и обучающихся НГАСУ (Сибстрин) по выборам ректора университета.
Начало регистрации: в 13.30
Начало конференции: в 14.00 |
Сибстрин поддержал игру «Сделай шаг», способствующую профессиональному самоопределению школьников Новосибирской области В рабочем поселке Линево Искитимского района состоялась профильная игра «Сделай шаг». Ее организатором выступила средняя общеобразовательная школа №4 р.п. Линево и Центр детского научно-технического творчества «Спутник» Искитимского района Новосибирской области. На игру было заявлено десять команд школ Искитимского района. Школьникам и их кураторам были озвучены задачи инженерно-технологической направленности, подготовленные партнерами конкурса. Ими стали представители нескольких производственных предприятий, совет депутатов р.п. Линево и образовательные учреждения, в число которых вошел НГАСУ (Сибстрин).
Особенность игры заключалась в том, что участникам профильной смены предстояло найти решение задач в реальных условиях… Ими стали представители нескольких производственных предприятий, совет депутатов р.п. Линево и образовательные учреждения, в число которых вошел НГАСУ (Сибстрин).
Особенность игры заключалась в том, что участникам профильной смены предстояло найти решение задач в реальных условиях… |
Стартовала регистрация на пятый сезон Всероссийской олимпиады студентов «Я – профессионал» Стартовал пятый, юбилейный сезон, Всероссийской студенческой олимпиады «Я – профессионал» – одного из флагманских проектов президентской платформы «Россия – страна возможностей»! Олимпиада проводится для студентов российских вузов, которые учатся по программам бакалавриата, специалитета или магистратуры. Каждый участник сможет попробовать свои силы в одном или нескольких из 72 направлений. «Я — профессионал» — это практико-ориентированные состязания. Задания для участников составляют эксперты ведущих университетов и научно-исследовательских институтов совместно с опытными специалистами-практиками — представителями компаний-партнеров олимпиады. |
Кинетическая энергия и теорема об энергии работы
Далее: Гравитационная потенциальная энергия Up: Работа и энергия Пред .: Работа
Идея: Сила – вектор, работа и энергия – скаляры. Таким образом, это часто проще решать проблемы, используя соображения энергии вместо того, чтобы использовать Ньютона законы (т.е. со скалярами работать легче, чем с векторами).
Определение: Кинетическая энергия ( KE ) объекта массой м что
движется со скоростью v составляет:
| KE = мВ 2 . | (1) |
- Кинетическая энергия – скаляр.

- Единицы такие же, как и для работы (т. Е. Джоуль, Дж).
Связь между KE и W : Работа, выполняемая над объектом с помощью чистой силы равно изменение кинетической энергии объекта:
| W = KE f – KE i . | (2) |
Proof (для параллельного):
- 1.
- Вт = Fs Вт = ( мА ) с (по второму закону Ньютона).
- 2.
- Из третьего уравнения движения: как = ( v 2 – v 0 2 ) / 2 W = 1/2 м ( v 2 – v 0 2 ) = KE f – KE i .

Примечание:
- Если скорость объекта увеличивается ( v f > v i ) W> 0.
- Если W <0, то объект выполняет работу с агентом, прикладывая чистую силу.
- Интерпретация уравнения (5.2): Мы можем рассматривать KE как работу объект может прийти в состояние покоя.
Далее: Гравитационная потенциальная энергия Up: Работа и энергия Пред .: Работа www-admin @ theory.uwinnipeg.ca
09.10.1997
7.2 Кинетическая энергия и теорема об энергии работы – College Physics
Работа передает энергию
Что происходит с работой, выполняемой в системе? Энергия передается в систему, но в какой форме? Он останется в системе или продвинется дальше? Ответы зависят от ситуации. Например, если газонокосилку на рис. 7.2 (а) толкать достаточно сильно, чтобы она продолжала работать с постоянной скоростью, то энергия, вложенная в газонокосилку человеком, непрерывно удаляется за счет трения и, в конечном итоге, покидает систему в виде теплопередачи. Напротив, работа, проделанная с портфелем человеком, несущим его по лестнице на рис. 7.2 (d), хранится в системе «портфель-Земля» и может быть восстановлена в любое время, как показано на рис. 7.2 (e). Фактически, строительство пирамид в Древнем Египте является примером хранения энергии в системе путем выполнения работы с системой. Некоторая часть энергии, передаваемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и имеет потенциал для выполнения работы.
Напротив, работа, проделанная с портфелем человеком, несущим его по лестнице на рис. 7.2 (d), хранится в системе «портфель-Земля» и может быть восстановлена в любое время, как показано на рис. 7.2 (e). Фактически, строительство пирамид в Древнем Египте является примером хранения энергии в системе путем выполнения работы с системой. Некоторая часть энергии, передаваемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и имеет потенциал для выполнения работы.
В этом разделе мы начинаем изучение различных видов работы и форм энергии.Мы обнаружим, что некоторые виды работы, например, оставляют энергию системы постоянной, тогда как другие каким-то образом изменяют систему, например заставляют ее двигаться. Мы также разработаем определения важных форм энергии, таких как энергия движения.
Чистая работа и теорема работы-энергии
Мы знаем из изучения законов Ньютона в динамике: сила и законы движения Ньютона, что результирующая сила вызывает ускорение. В этом разделе мы увидим, что работа, совершаемая чистой силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.
В этом разделе мы увидим, что работа, совершаемая чистой силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.
Давайте начнем с рассмотрения общей, или чистой, работы, проделанной в системе. Сетевая работа определяется как сумма работы над объектом. Чистую работу можно записать в терминах чистой силы, действующей на объект. Размер FnetFnet 12 {F rSub {размер 8 {“net”}}} {}. В форме уравнения это Wnet = FnetdcosθWnet = Fnetdcosθ size 12 {W rSub {size 8 {“net”}} = F rSub {size 8 {“net”}} d “cos” θ} {}, где θθ size 12 { θ} {} – угол между вектором силы и вектором смещения.
На рис. 7.3 (a) показан график зависимости силы от смещения для составляющей силы в направлении смещения, то есть для FcosθFcosθ размером 12 {F “cos” θ} {} отdd размер 12 {d} {} график. В этом случае FcosθFcosθ size 12 {F “cos” θ} {} является постоянным. Вы можете видеть, что область под графиком соответствует FdcosθFdcosθ размером 12 {F “cos” θ} {} или проделанной работе.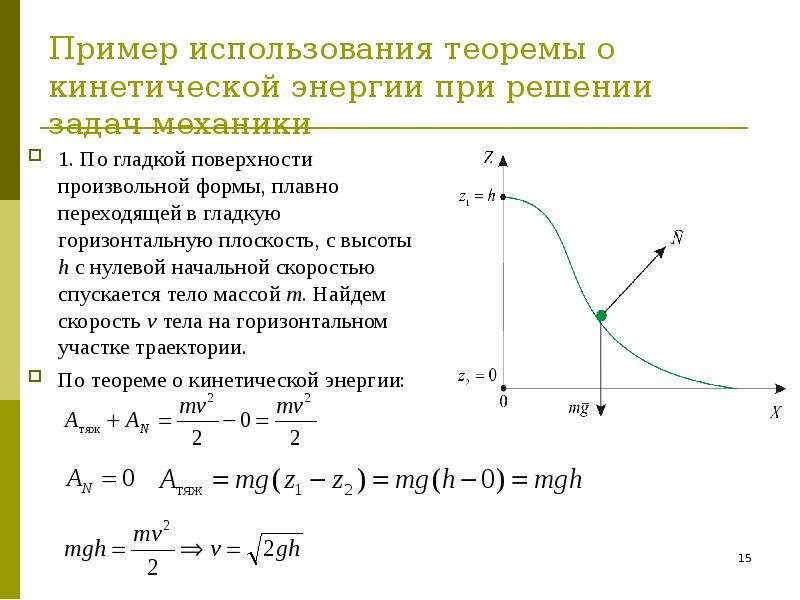 На рис. 7.3 (b) показан более общий процесс изменения силы. Площадь под кривой разделена на полосы, каждая из которых имеет среднюю силу (Fcosθ) i (ave) (Fcosθ) i (ave) размер 12 {\ (F “cos” θ \) rSub {size 8 {i \ (” пр. “\)}}} {}. Проделанная работа (Fcosθ) i (ave) di (Fcosθ) i (ave) di size 12 {\ (F “cos” θ \) rSub {size 8 {i \ (“ave” \)}} d rSub { размер 8 {i}}} {} для каждой полосы, а общая проделанная работа равна сумме размера WiWi 12 {W rSub {size 8 {i}}} {}.Таким образом, общая проделанная работа – это общая площадь под кривой, полезное свойство, о котором мы поговорим позже.
На рис. 7.3 (b) показан более общий процесс изменения силы. Площадь под кривой разделена на полосы, каждая из которых имеет среднюю силу (Fcosθ) i (ave) (Fcosθ) i (ave) размер 12 {\ (F “cos” θ \) rSub {size 8 {i \ (” пр. “\)}}} {}. Проделанная работа (Fcosθ) i (ave) di (Fcosθ) i (ave) di size 12 {\ (F “cos” θ \) rSub {size 8 {i \ (“ave” \)}} d rSub { размер 8 {i}}} {} для каждой полосы, а общая проделанная работа равна сумме размера WiWi 12 {W rSub {size 8 {i}}} {}.Таким образом, общая проделанная работа – это общая площадь под кривой, полезное свойство, о котором мы поговорим позже.
Чистую работу будет проще исследовать, если мы рассмотрим одномерную ситуацию, когда сила используется для ускорения объекта в направлении, параллельном его начальной скорости. Такая ситуация возникает для упаковки на ленточном роликовом конвейере, показанном на Рисунке 7.4.
Рис. 7.4 Пакет на роликовой ленте продвигается горизонтально на расстояние dd.Сила тяжести и нормальная сила, действующая на упаковку, перпендикулярны перемещению и не работают.Более того, они также равны по величине и противоположны по направлению, поэтому они сокращаются при вычислении чистой силы. Чистая сила возникает исключительно из приложенной горизонтальной силы FappFapp и горизонтальной силы трения ff. Таким образом, как и ожидалось, чистая сила параллельна смещению, так что θ = 0ºθ = 0º и cosθ = 1cosθ = 1 размер 12 {“cos” q = 1} {}, а чистая работа определяется как
Wnet = Fnetd.Wnet = Fnetd. size 12 {W rSub {size 8 {“net”}} = F rSub {size 8 {“net”}} d} {}7,7
Влияние чистой силы FnetFnet размер 12 {F rSub {size 8 { “net”}}} {} предназначен для ускорения пакета с v0v0 размера 12 {v rSub {size 8 {0}}} {} до vv размера 12 {v} {}.Кинетическая энергия пакета увеличивается, указывая на то, что чистая работа, выполняемая в системе, является положительной. (См. Пример 7.2.) Используя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Подстановка Fnet = maFnet = ma size 12 {F rSub {size 8 {“net”}} = ital “ma”} {} из второго закона Ньютона дает
Wnet = mad.Wnet = mad. размер 12 {W rSub {size 8 {“net”}} = ital “mad”} {}7,8
Чтобы получить взаимосвязь между работой сети и скоростью, придаваемой системе действующей на нее чистой силой, возьмем d = x − x0d = x − x0 размер 12 {d = x – x rSub {размер 8 {0}} } {} и используйте уравнение, изученное в уравнениях движения для постоянного ускорения в одном измерении, для изменения скорости на расстоянии dd, если ускорение имеет постоянное значение аа; а именно, v2 = v02 + 2adv2 = v02 + 2ad (обратите внимание, что aa появляется в выражении для сети).Решение для ускорения дает а = v2 − v022da = v2 − v022d. Когда aa подставляется в предыдущее выражение для WnetWnet, получаем
Wnet = mv2 − v022dd.Wnet = mv2 − v022dd.7.9
Размер dd 12 {d} {} отменяется, и мы изменяем это так, чтобы получить
Wnet = 12mv2−12mv0 2.Wnet = 12mv2−12mv0 2. Размер 12 {w “” lSub {size 8 {ital “net “}} = {{1} больше {2}} ital” mv “rSup {size 8 {2}} – {{1} over {2}} ital” mv “” “lSub {size 8 {0}}” “lSup {размер 8 {2}}”. ” } {}7,10
Это выражение называется теоремой работы-энергии, и оно фактически применяет в общем случае (даже для сил, которые меняются по направлению и величине), хотя мы вывели его для частного случая постоянной силы, параллельной смещению.Теорема подразумевает, что сетевая работа в системе равна изменению количества 12mv212mv2 размера 12 {{{1} по сравнению с {2}} курсивом “mv” rSup {size 8 {2}}} {}. Эта величина – наш первый пример формы энергии.
Теорема работы-энергии
Чистая работа в системе равна изменению количества 12mv212mv2 размером 12 {{{size 8 {1}} по сравнению с {размером 8 {2}}} ital “mv” rSup {size 8 {2}}} {}.
Wnet = 12mv2−12mv0 2Wnet = 12mv2−12mv0 2 размер 12 {w “” lSub {size 8 {ital “net”}} = {{1} over {2}} ital “mv” rSup {size 8 {2}} – {{1} больше {2}} ital “mv” “” lSub {size 8 {0}} “” lSup {size 8 {2}} “.”} {}7,11
Величина 12mv212mv2 размер 12 {{{1} больше {2}} ital “mv” rSup {size 8 {2}}} {} в теореме о работе-энергии определяется как поступательная кинетическая энергия (KE) масса мм размер 12 {м} {} движется со скоростью vv размером 12 {v} {}. ( Поступательная кинетическая энергия отличается от вращательной кинетической энергии , которая будет рассмотрена позже.) В форме уравнения поступательная кинетическая энергия,
KE = 12mv2, KE = 12mv2, размер 12 {“KE” = {{1} over {2}} ital “mv” rSup {size 8 {2}},} {}7.12
– энергия, связанная с поступательным движением. Кинетическая энергия – это форма энергии, связанная с движением частицы, отдельного тела или системы объектов, движущихся вместе.
Мы знаем, что требуется энергия, чтобы довести объект, например автомобиль или пакет на рис. 7.4, до скорости, но может быть немного удивительно, что кинетическая энергия пропорциональна квадрату скорости. Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км / ч, имеет в четыре раза большую кинетическую энергию, чем при 50 км / ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны.Теперь мы рассмотрим серию примеров, чтобы проиллюстрировать различные аспекты работы и энергии.
Пример 7.2
Расчет кинетической энергии упаковки
Предположим, что пакет весом 30,0 кг на роликовой ленточной конвейерной системе, показанной на рис. 7.4, движется со скоростью 0,500 м / с. Какова его кинетическая энергия?
Стратегия
Поскольку даны масса, мм и скорость vv, кинетическая энергия может быть рассчитана на основе ее определения, приведенного в уравнении KE = 12mv2KE = 12mv2 размер 12 {“KE” = {{1} over {2}} ital “mv” rSup {размер 8 {2}}} {}.
Раствор
Кинетическая энергия определяется как
KE = 12 мв2. KE = 12 мв2. размер 12 {“KE” = {{1} больше {2}} ital “mv” rSup {size 8 {2}} “.” } {}7,13
Ввод известных значений дает
KE = 0,5 (30,0 кг) (0,500 м / с) 2, KE = 0,5 (30,0 кг) (0,500 м / с) 2, размер 12 {“KE” = 0 “.” 5 \ (“30” “.” 0 “кг” \) \ (0 “.” “500” “м / с” \) rSup {size 8 {2}},} {}7.14
, что дает
KE = 3,75 кг⋅м2 / с2 = 3,75 J.KE = 3,75 кг⋅м2 / с2 = 3,75 J. размер 12 {“KE” = 3 “.” “75” `” кг “cdot m rSup {size 8 {2}}” / s “rSup {size 8 {2}} = 3″.”” 75 “` J “.”} {}7.15
Обсуждение
Обратите внимание, что единицей кинетической энергии является джоуль, то же самое, что и единица работы, как упоминалось при первом определении работы. Также интересно то, что, хотя это довольно массивный пакет, его кинетическая энергия невелика при такой относительно низкой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать пакеты таким образом, не изнуряя себя.
Пример 7.3
Определение работы по ускорению пакета
Предположим, вы нажимаете 30.Упаковка 0 кг на рис. 7.4 с постоянной силой 120 Н на расстоянии 0,800 м и средней противодействующей силой трения 5,00 Н.
(a) Рассчитайте чистую работу, проделанную с упаковкой. (b) Решите ту же задачу, что и в части (a), на этот раз определив работу, выполняемую каждой силой, которая вносит вклад в результирующую силу.
Стратегия и концепция для (a)
Это задача движения в одном измерении, потому что направленная вниз сила (от веса упаковки) и нормальная сила имеют равную величину и противоположное направление, так что они сводятся к нулю при вычислении чистая сила, в то время как приложенная сила, трение и смещение являются горизонтальными.(См. Рисунок 7.4.) Как и ожидалось, чистая работа – это чистая сила, умноженная на расстояние.
Решение для (a)
Чистая сила – это сила толчка за вычетом трения, или Fnet = 120 N – 5,00 N = 115 NFnet = 120 N – 5,00 N = 115 N размер 12 {F rSub {size 8 {“net “}}” = 120 N – 5 “”. ” “00 N = 115 N”} {}. Таким образом, чистая работа равна
Wnet = Fnetd = 115 N0,800 м = 92,0 Н⋅м = 92,0 J.Wnet = Fnetd = 115 N0,800 м = 92,0 Н⋅м = 92,0 J.alignl {stack { размер 12 {W rSub {размер 8 {“net”}} = F rSub {размер 8 {“net”}} d = left (“115″ `N right) left (0″.”” 800 “` м вправо)} {} # “” = “92” “.” 0`N cdot m = “92” “.” 0`J “.” {} }} {}7.16
Обсуждение для (a)
Это значение представляет собой чистую работу, проделанную над пакетом. Человек на самом деле выполняет больше работы, потому что трение препятствует движению. Трение совершает негативную работу и удаляет часть энергии, которую человек тратит, и преобразует ее в тепловую энергию. Чистая работа равна сумме работы, проделанной каждой отдельной силой.
Стратегия и концепция (b)
К силам, действующим на упаковку, относятся сила тяжести, нормальная сила, сила трения и приложенная сила.Нормальная сила и сила тяжести перпендикулярны перемещению и поэтому не работают.
Решение для (b)
Приложенная сила работает.
Wapp = Fappdcos0º = Fappd = 120 N0,800 м = 96,0 JWapp = Fappdcos0º = Fappd = 120 N0,800 м = 96,0 Jalignl {stack { размер 12 {W rSub {размер 8 {“app”}} = F rSub {размер 8 {“app”}} d “cos” влево (0 ° вправо) = F rSub {размер 8 {“app”}} d} {} # “” = left (“120 N” справа) left (0 “.” “800” “m” right) {} # “” = “96” “.”” 0 J “”. “{} }} {}7.17
Сила трения и смещение имеют противоположные направления, так что θ = 180ºθ = 180º размер 12 {θ = “180” °} {}, а работа, выполняемая трением, равна
Wfr = Ffrdcos180º = −Ffrd = −5,00 N0,800 м = −4,00 J.Wfr = Ffrdcos180º = −Ffrd = −5,00 N0,800 м = −4,00 J.alignl {stack { размер 12 {W rSub {размер 8 {“fr”}} = F rSub {размер 8 {“fr”}} d “cos” влево (“180” ° вправо) = – F rSub {размер 8 {“fr”} } d} {} # “” = – left (5 “.” “00 N” right) left (0 “.” “800” “m” right) {} # ital “” = – 4 “.”” 00 “J”. “{} }} {}7,18
Таким образом, количество работы, выполняемой гравитацией, нормальной силой, приложенной силой и трением, составляет, соответственно,
Wgr = 0, WN = 0, Wapp = 96,0 Дж, Wfr = −4,00 J.Wgr = 0, WN = 0, Wapp = 96,0 Дж, Wfr = −4,00 J.alignl {stack { размер 12 {W rSub {size 8 {“gr”}} = 0,} {} # W rSub {size 8 {N}} = 0, {} # W rSub {size 8 {“app”}} = “96” “.” 0 “J” {} # W rSub {size 8 {“fr”}} = – 4 “.” “00” “J” “.” {} }} {}7,19
Общая проделанная работа, как сумма работы, выполненной каждой силой, тогда составляет
Wtotal = Wgr + WN + Wapp + Wfr = 92.0 J.Wtotal = Wgr + WN + Wapp + Wfr = 92,0 J. размер 12 {W rSub {размер 8 {“total”}} = W rSub {размер 8 {“gr”}} + W rSub {размер 8 {N }} + W rSub {размер 8 {“app”}} + W rSub {размер 8 {“fr”}} = “92” “.” 0 “J”} {}7.20
Обсуждение для (b)
Расчетная общая работа WtotalWtotal size 12 {W rSub {size 8 {“total”}}} {} как сумма работы каждой группы согласовывается , как и ожидалось, с работой WnetWnet размером 12 {W rSub {size 8 {“net”}}} {} выполняется чистая сила. Работа, выполняемая совокупностью сил, действующих на объект, может быть рассчитана любым подходом.
Пример 7.4
Определение скорости по работе и энергии
Найдите скорость пакета на рис. 7.4 в конце проталкивания, используя концепции работы и энергии.
Стратегия
Здесь можно использовать теорему работы-энергии, потому что мы только что вычислили чистую работу, размер WnetWnet 12 {W rSub {size 8 {“net”}}} {} и начальную кинетическую энергию, 12mv0212mv02 размер 12 {{{1} больше {2}} ital “mv” rSub {size 8 {0} rSup {size 8 {2}}}} {}.Эти расчеты позволяют нам найти окончательную кинетическую энергию, 12 мв212 мв2, размер 12 {{{1} сверх {2}} ital “mv” rSup {size 8 {2}}} {}, и, таким образом, конечную скорость vv размер 12 {v } {}.
Решение
Теорема работы-энергии в форме уравнения:
Wnet = 12mv2−12mv02.Wnet = 12mv2−12mv02. размер 12 {W rSub {size 8 {“net”}} = {{1} over {2}} ital “mv” rSup {size 8 {2}} – {{1} over {2}} ital “mv” rSub {размер 8 {0} rSup {размер 8 {2}}} “.” } {}7.21
Решение для 12mv212mv2 размера 12 {{{1} over {2}} ital “mv” rSup {size 8 {2}}} {} дает
12mv2 = Wnet + 12mv02.12mv2 = Wnet + 12mv02. размер 12 {{{1} over {2}} ital “mv” “” lSup {size 8 {2}} = w rSub {size 8 {ital “net”}} + {{1} over {2}} ital “mv” “” lSub {size 8 {0}} “” lSup {size 8 {2}} “.” } {}7.22
Таким образом,
12mv2 = 92.0 J + 3.75 J = 95.75 J.12mv2 = 92.0 J + 3.75 J = 95.75 J. размер 12 {{{1} больше {2}} ital “mv” rSup {size 8 {2}} = “92” “.” 0`J + 3 “.” “75” `J =” 95 “”. ” “75” `J} {}7.23
Определение конечной скорости в соответствии с запросом и ввод известных значений дает
v = 2 (95.75 Дж) м = 191,5 кг⋅м2 / с 230,0 кг = 2,53 м / с. V = 2 (95,75 Дж) м = 191,5 кг⋅м2 / с 230,0 кг = 2,53 м / с.7.24
Обсуждение
Используя работу и энергию, мы не только приходим к ответу, мы видим, что конечная кинетическая энергия – это сумма начальной кинетической энергии и чистой работы, проделанной с упаковкой. Это означает, что работа действительно увеличивает энергию упаковки.
Пример 7.5
Работа и энергия могут определить расстояние, тоже
Как далеко уходит посылка на Рисунке 7.4 выбег после толчка, если трение остается постоянным? Используйте соображения работы и энергии.
Стратегия
Мы знаем, что как только человек перестанет толкать, трение остановит упаковку. Что касается энергии, трение выполняет отрицательную работу до тех пор, пока не убирает всю кинетическую энергию упаковки. Работа, совершаемая трением, – это сила трения, умноженная на пройденное расстояние, умноженное на косинус угла между силой трения и смещением; следовательно, это дает нам способ определить расстояние, пройденное после того, как человек прекратил толкать.
Решение
Нормальная сила и сила тяжести отменяются при вычислении чистой силы. Горизонтальная сила трения тогда представляет собой результирующую силу, и она действует противоположно смещению, поэтому θ = 180ºθ = 180º. Чтобы уменьшить кинетическую энергию пакета до нуля, работа WfrWfr за счет трения должна быть минус кинетическая энергия, с которой пакет начал, плюс то, что пакет накопил из-за толкания. Таким образом, Wfr = -95,75 JWfr = -95,75 J. Кроме того, Wfr = fd′cosθ = –fd′Wfr = fd′cosθ = –fd ′, где d′d ′ – расстояние, необходимое для остановки.Таким образом,
d ′ = – Wfrf = −− 95,75 J5,00 N, d ′ = – Wfrf = −− 95,75 J5,00 N, размер 12 {{{d}} sup {‘} = – {{W rSub { размер 8 {“fr”}}} больше {f}} = – {{- “95” “.” “75” `J} больше {5″. ” “00 N”}}} {}7.25
и т. Д.
d ′ = 19,2 м. d ′ = 19,2 м. размер 12 {{{d}} sup {‘} = “19” “.” 2 “м”} {}7.26
Обсуждение
Это разумное расстояние, на котором упаковка может двигаться по инерции на конвейерной системе с относительно низким уровнем трения. Обратите внимание, что работа, совершаемая трением, отрицательна (сила направлена в противоположном направлении движения), поэтому она снимает кинетическую энергию.
Некоторые примеры в этом разделе могут быть решены без учета энергии, но за счет упущения понимания того, какая работа и энергия делают в этой ситуации. В целом решения, использующие энергию, обычно короче и проще, чем решения, использующие только кинематику и динамику.
Теорема об энергии работы – Энергетическое образование
Теорема об энергии работы объясняет идею о том, что чистая работа – общая работа, выполненная всеми объединенными силами – проделанная над объектом, равна изменению кинетической энергии объект.После того, как чистая сила снимается (работа больше не выполняется), общая энергия объекта изменяется в результате проделанной работы.
Эта идея выражается в следующем уравнении: [1]
[математика] W_ {net} = \ Delta K = K_ {f} – K_ {i} [/ math]- [math] W [/ math] – общий объем проделанной работы.
- [math] \ Delta K [/ math] – изменение кинетической энергии.
- [math] K_ {f} [/ math] – окончательная кинетическая энергия
- [math] K_ {i} [/ math] – начальная кинетическая энергия
Для получения дополнительной информации об этой и других концепциях, связанных с работой и энергией, см. Гиперфизика.
Рис. 1. На верхнем изображении выполняется положительная работа, когда сила прикладывается в направлении движения, что приводит к увеличению скорости и кинетической энергии. На нижнем изображении выполняется негативная работа, поскольку сила действует против направления движения, что приводит к уменьшению скорости и кинетической энергии. [2]Пример
Чтобы лучше понять теорему работы-энергии, можно рассмотреть пример. Представьте себе лыжника, движущегося с постоянной скоростью по плоской поверхности без трения.Если кто-то подходит к нему сзади и толкает их на расстояние – по сути, выполняя работу с лыжником, – они ускоряются в результате увеличения их кинетической энергии. Этот тип работы известен как позитивная работа , поскольку сила прикладывалась при движении лыжника. Однако, если человек толкается в противоположную сторону от движения лыжника, лыжник замедляется из-за уменьшения его кинетической энергии. Этот вид работы известен как отрицательная работа . На изображении выше показан пример такой ситуации, когда лыжник заменен блоком.
Поскольку на самом деле поверхностей без трения нет, необходимо учитывать силу трения, препятствующую движению лыжников, и поэтому уравнение содержит член W net , так как это сумма всех действующих сил. на расстоянии. [3]
Список литературы
РАБОЧАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
РАБОЧАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯВ этом разделе мы познакомим вас с концепциями работы и кинетическая энергия.
Рисунок 1.Сила F, действующая на тело. Результирующий смещение обозначается вектором d.
Предположим, что на тело действует постоянная сила F, в то время как объект перемещается на расстояние d. И сила F, и смещение d – векторы, которые не обязательно указывают в одном направлении (см. рисунок 7.1). Работа, совершаемая силой F над объектом как он претерпевает смещение d определяется как
Единица работы – Джоуль (J). Работа, проделанная силой F равно нулю, если:
- d = 0: смещение равно нулю
- [фи] = 90 градусов.: сила, перпендикулярная перемещению
Рис. 2. Положительная или отрицательная работа.
Работа, совершаемая силой F, может быть положительной или отрицательной, в зависимости от на [фи]. Например, предположим, что у нас есть объект, движущийся с постоянной скорость. В момент времени t = 0 с прикладывается сила F. Если F – единственный сила, действующая на тело, объект будет либо увеличиваться, либо уменьшаться его скорость зависит от того, являются ли скорость v и сила F указывают в том же направлении (см. Рисунок 7.2). Если сила и скорость объекта указывают на одно и то же направление, скорость объекта увеличится и работа сделанное силой на объект будет положительным. Если сила и скорость объекта указывают в противоположном направлении, скорость объекта уменьшится, и работа, выполненная сила на объект будет отрицательной.
Наблюдение за движением объекта с определенной скоростью. указывает на то, что когда-то в прошлом работа должна была быть выполнена в теме.Получается, что работа, совершаемая силой, равна изменение величины, называемой кинетической энергией K. Кинетическая энергия K определяется как
где m – масса объекта, а v – его скорость. В единицей кинетической энергии является джоуль (Дж).
Если кинетическая энергия частицы изменяется от некоторой начальной значение Ki до некоторого окончательного значения Kf объем работы, выполненной на частица задается
W = Kf – Ki
Это указывает на то, что изменение кинетической энергии частицы равна полной работе, совершенной над этой частицей всеми силами которые действуют на это.2) / (2 д)
Делаем несколько выводов:
- Чем короче расстояние d, тем сильнее сила столкновения Fcol. Зоны крошения на автомобилях предназначены для увеличения остановки расстояние d и тем самым уменьшить силу столкновения Fcol.
- Для фиксированного тормозного пути d, чем выше начальная скорость, тем выше сила столкновения Fcol. Если начальная скорость удваивается, сила столкновения увеличивается в четыре раза.
Эксперименты
- Работа – Энергетическая теорема
- Сохранение механической энергии
- Простой Гармоническое движение – Масса на пружине
Присылайте комментарии, вопросы и / или предложения по электронной почте на адрес wolfs @ nsrl.rochester.edu и / или посетите домашняя страница Фрэнк Вольфс.
13.6: Теорема работы-кинетической энергии – Physics LibreTexts
Существует прямая связь между работой, выполняемой над точечным объектом, и изменением кинетической энергии, которому подвергается точечный объект. Если работа, выполняемая над объектом, не равна нулю, это означает, что на объект действует неуравновешенная сила, и объект подвергнется ускорению. Для объекта, совершающего одномерное движение, левая часть уравнения (13.{2} = K_ {f} -K_ {i} = \ Delta K \]
Когда работа, выполняемая с объектом, является положительной, объект увеличивает свою скорость, а отрицательная работа, выполняемая с объектом, вызывает снижение скорости. Когда проделанная работа равна нулю, объект будет поддерживать постоянную скорость. Фактически, соотношение работы и энергии довольно точное; работа, совершаемая силой, приложенной к объекту, идентично изменению кинетической энергии объекта.
Пример \ (\ PageIndex {1} \): гравитация и теорема работы-энергии
Предположим шар массы \ (m = 0.{-1} \]
Для падающего шара в постоянном гравитационном поле положительная работа силы гравитации на теле соответствует увеличению кинетической энергии и скорости. Для поднимающегося тела в том же поле кинетическая энергия и, следовательно, скорость уменьшаются, поскольку проделанная работа отрицательна.
Пример \ (\ PageIndex {2} \): Конечная кинетическая энергия движущейся чашки
Человек толкает чашку массой 0,2 кг по горизонтальному столу с силой 2,0 Н под углом \ (30 ^ {\ circ} \) по отношению к горизонтали на расстояние 0. {a} – \ mu_ {k} N \ right) \ left (x_ { f} -x_ {i} \ right) \\
& = \ left (1.{-1} \]
7: Работа и кинетическая энергия
- Последнее обновление
- Сохранить как PDF
- Соавторы и атрибуция
Применение законов Ньютона обычно требует решения дифференциальных уравнений, которые связывают силы, действующие на объект, с создаваемыми ими ускорениями.Часто аналитическое решение трудноразрешимо или невозможно, требуя длительных численных решений или моделирования для получения приблизительных результатов. В таких ситуациях более общие соотношения, такие как теорема работы-энергии (или закон сохранения энергии), по-прежнему могут дать полезные ответы на многие вопросы и потребовать более скромных математических вычислений. В частности, вы увидите, как теорема работы-энергии полезна для установления связи между скоростями частицы в разных точках ее траектории и силами, действующими на нее, даже если в противном случае траектория слишком сложна, чтобы иметь дело с ней.Таким образом, некоторые аспекты движения можно решить с помощью меньшего количества уравнений и без векторной декомпозиции.
- 7.1: Прелюдия к работе и кинетическая энергия
- В этой главе мы обсуждаем некоторые основные физические концепции, связанные с каждым физическим движением во Вселенной, выходя за рамки концепций силы и изменения движения. Эти понятия – работа, кинетическая энергия и мощность. Мы объясняем, как эти величины связаны друг с другом, что приведет нас к фундаментальной зависимости, называемой теоремой работы-энергии.В следующей главе мы обобщим эту идею на более широкий принцип сохранения энергии.
- 7.2: Работа
- В физике работа представляет собой вид энергии. Работа выполняется, когда сила действует на что-то, что перемещается из одного положения в другое. Силы могут варьироваться в зависимости от положения, а смещения могут происходить по разным путям между двумя точками. Сначала мы определяем приращение работы dW, совершаемой силой, действующей через бесконечно малое смещение, как скалярное произведение этих двух векторов.Затем мы можем сложить вклады для бесконечно малых смещений вдоль пути между двумя точками зрения
- 7.3: Кинетическая энергия
- Кинетическая энергия, связанная с силами, действующими на тело, и называлась «энергией движения. . » Кинетическая энергия частицы равна половине произведения массы частицы m и квадрата ее скорости v. частица равна изменению кинетической энергии частицы.Согласно этой теореме, когда объект замедляется, его конечная кинетическая энергия меньше, чем его начальная кинетическая энергия, изменение его кинетической энергии отрицательно, как и чистая работа, выполняемая над ним. Если объект ускоряется, чистая работа, проделанная с ним, положительна.
- 7.5: Мощность
- Понятие работы включает силу и смещение; Теорема работы-энергии связывает чистую работу, проделанную над телом, с разницей в его кинетической энергии, рассчитанной между двумя точками на его траектории.Ни одна из этих величин или соотношений не включает время явно, но мы знаем, что время, доступное для выполнения определенного объема работы, часто так же важно для нас, как и сама сумма.
- 7.E: Работа и кинетическая энергия (упражнения)
- 7.S: Работа и кинетическая энергия (сводка)
Миниатюра: Одной из форм энергии является механическая работа , энергия, необходимая для перемещения объекта массы \ (m \) на расстояние d, когда ему противодействует сила \ (F \), такая как гравитация.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Связь между работой и энергией
Энергия должна передаваться объекту, чтобы помочь ему двигаться, и энергия может передаваться в форме силы.Энергия, передаваемая силой для перемещения любого объекта, называется работой или выполненной работой. Следовательно, работа и энергия имеют прямую связь. Разница в кинетической энергии объекта называется работой, совершаемой объектом. Работа и энергия – общие термины в физике, и их можно рассматривать как две стороны медали. Эта статья необходима для установления взаимосвязи между работой и энергией.
Работа –
Работа выполняется при приложении силы для перемещения объекта. Работу также можно описать как деятельность, которая включает движение и силу в направлении силы.
Единица измерения в системе СИ – джоуль (Дж), что означает ньютон-метр.
Например, когда вы пинаете мяч ногой, вы прикладываете внешнюю силу, называемую F, заставляя его перемещаться на определенное расстояние. Это изменение положения мяча с A на B называется смещением (d). Работа рассчитывается путем умножения силы, приложенной к объекту, на движение объекта. W = F * d.
Энергия –
Энергия – это способность выполнять работу. Формула для потенциальной энергии: mgh, где m – масса объекта, g – сила тяжести, а h – высота, которую покрыл объект.Ниже вы можете найти соотношение между работой и потенциальной энергией / кинетической энергией.
Энергия не может быть создана или уничтожена. Энергия может передаваться только из одной формы в другую. Существуют различные типы энергии, и все они либо кинетические, либо потенциальные. Энергия в движении называется кинетической энергией, а энергия, хранящаяся в объекте, называется потенциальной энергией.
Существуют и другие виды энергии, в том числе:
Механическая энергия
Химическая энергия
Механическая волновая энергия
Электрическая энергия
Лучистая энергия
Магнитная энергия
Ядерная энергия
Упругая энергия
Тепловая энергия
Гравитационная энергия
Энергия ионизации
Тепловая энергия
Единица измерения энергии в системе СИ – Джоулз, названная в честь Джоуля Джоуля .
Какая связь между работой и энергией?
[Изображение будет скоро загружено]
Связь между работой и энергией можно описать с помощью коэффициента пропорциональности; оба прямо пропорциональны друг другу.
Соотношение между работой и энергией выглядит следующим образом:
W = ½ mvf2 – ½ mvi2.
Здесь
W – работа, выполняемая объектом, измеряется в джоулях.
M – масса рассматриваемого объекта, измеряется в кг.
Vf – конечная скорость рассматриваемого объекта, измеряемая в м / с.
vi – начальная скорость рассматриваемого объекта, измеряемая в м / с.
Следовательно, соотношение между работой и энергией (теорема работы-энергии) гласит:
Сеть, которую сила воздействует на объект, равна изменению его кинетической энергии.



