T это в физике: Дана формула: “a=v2-v1/t” Подскажите правильно решение. Как найти время? Расшифровка формулы: “Ускорение равняется разности последней…

Физика | Методические указания

Физика | Методические указания

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Молекулярная физика занимается изучением тепловой формы движения материи, рассматривает явления, происходящие внутри макроскопических тел. Молекулярная физика неразрывно связана с теорией строения вещества и характером движения и взаимодействия частиц составляющих вещество (молекул, атомов).

Теория, базирующаяся на положениях, что: все вещества состоят из молекул и атомов; между молекулами (атомами) существуют силы взаимодействия; молекулы и атомы находятся в непрерывном движении – называется молекулярно-кинетической. Она ставит себе целью истолковать те свойства тел, которые непосредственно наблюдаются на опыте, как суммарный результат действия большой совокупности молекул. При этом указанная теория пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь такими средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое ее название – статистическая физика. Молекулярная физика рассматривает движение и взаимодействие большого количества микрообъектов, составляющих макросистему; применяя законы классической механики к большому количеству микрочастиц, можно вычислить такие величины, как плотность, давление, температура, теплота, энтропия, внутренняя энергия и другие, которые являются характеристиками макросистемы.

Раздел физики, в котором изучаются соотношения между этими величинами, называется термодинамикой. Термодинамика изучает макроскопические свойства тел и явления природы, “не интересуясь” их микроскопической картиной. В основе термодинамики лежат экспериментально установленные законы, которые называют первым и вторым началами термодинамики. С помощью этих законов можно, не делая никаких предположений о молекулярном строении, изучаемых тел, получить многие сведения о свойствах тел в различных условиях.

Совокупность рассматриваемых тел, обменивающихся энергией как между собой, так и с другими (внешними) телами, называется термодинамической системой (ТДС). Состояние термодинамической системы определяется совокупностью значений всех величин, характеризующих физические свойства системы и называемых ее термодинамическими параметрами. Равновесное состояние ТДС можно задать с помощью ограниченного числа ее термодинамических параметров, которые называются параметрами системы. Между основными параметрами системы существует связь, называемая уравнением состояния.

Уравнение состояния (уравнение Менделеева-Клапейрона) идеального газа имеет вид

pV = (m/m)RT = nRT,

где m– масса газа; m –молярная масса газа; p– давление газа; V—объем газа; R—универсальная газовая постоянная; n – число молей газа; T—температура по шкале Кельвина.

Подходя к рассмотрению изменений состояния вещества с различных точек зрения, термодинамика и молекулярно-кинетическая теория взаимно дополняют друг друга, образуя, по существу, одно целое.

Как уже отмечалось, состояние системы описывается уравнением состояния.

Параметры состояния системы могут изменяться, тогда говорят, что система совершает термодинамический процесс. Для термодинамических процессов установлены опытные газовые законы:

а) для изотермического процесса (T = const, m = const) – закон Бойля- Мариотта

pV = const;

б) для изобарического процесса (P = const, m = const) – закон Гей-Люссака

V/T = const,

или, используя шкалу температур Цельсия,

V = V₀ (1+ ),

где = (1/273)(⁰С)^-1

;

в) для изохорического процесса (V = const, m = const) – закон Шарля

p/T = const,

или, используя шкалу температур Цельсия,

p = p₀ (1+t ),

где _{= (1/273)(⁰С)^-1 ;}

г) в случае изменения трех термодинамических параметров при неизменной массе газа (m = const) – объединенный газовый закон (уравнение Клапейрона)

pV/T = const.

Закон Дальтона, определяющий давление смеси газов.

p = p₁ + p₂ + p₃ + … + p

i +… + p_n,

где p_i – парциональное давление компонентов смеси; n – число компонентов смеси.

Молярная масса смеси газов

где m_i – масса i-го компонента смеси; n _i = m_i/m _i – количество вещества i-го компонента смеси; n – число компонентов смеси.

Концентрация молекул

n = N/V = ,

где N – число молекул, содержащихся в данной системе; N_A – число Авогадро; V – объем системы.

Основное уравнение кинетической теории газов

p = (2/3) n <E>,

здесь <E> – средняя кинетическая энергия поступательного движения молекул, равная (3/2) kT, где k – постоянная Больцмана.

Закон равномерного распределения энергии по степеням свободы

<E> = kT/2

и средняя полная кинетическая энергия молекулы

<E> = (i/2)kT,

где i – число степеней свободы молекулы.

Зависимость давления газа от его концентрации и температуры

p = nkT.

Распределение молекул по скоростям (распределение Максвелла)

,

где m – масса молекулы, v – ее скорость.

Средняя квадратичная скорость молекул

Средняя арифметическая скорость молекул

Наиболее вероятная скорость молекул

Распределение молекул по координатам (распределение Больцмана)

,

где U – потенциальная энергия молекулы, n – концентрация молекул.

Барометрическая формула

.

Здесь p – давление.

Первое начало термодинамики

где – теплота, сообщенная газу; – изменение внутренней энергии газа; – работа, совершаемая газом, против внешних сил.

Работа, совершаемая газом при его расширении,

A = P(V₂ – V₁) – при изобарическом процессе;

A = (m/m)RT ln(V₂/V₁) – при изотермическом процессе;

A = – DU = – (m/m)C_VDT или A = ((RT)/(g-1))(m/m)[1- (V₁/V₂)g^-1] – при адиабатном процессе.

КПД идеальной тепловой машины

, или

где Q₁ – теплота, полученная рабочим телом от нагревателя, Q₂ – теплота, переданная рабочим телом холодильнику, T₁

и T₂ – температуры нагревателя и холодильника.

Связь между удельной (с) и молярной (С) теплоемоемкостями

c = C/m

Уравнение Майера

C_P – C_V = R ,

где C_P – молярная теплоемкость при постоянном давлении и C_V – молярная теплоемкость при постоянном объеме.

Удельные теплоемкости газа при постоянном объеме (c_V) и постоянном давлении (c_P)

c_V = (i/2)(R/m),       c_P = ((i+2)/2)(R/m)

Уравнение Пуассона (уравнение адиабаты)(m = const, DQ = 0)

pV^g = const,

где g = c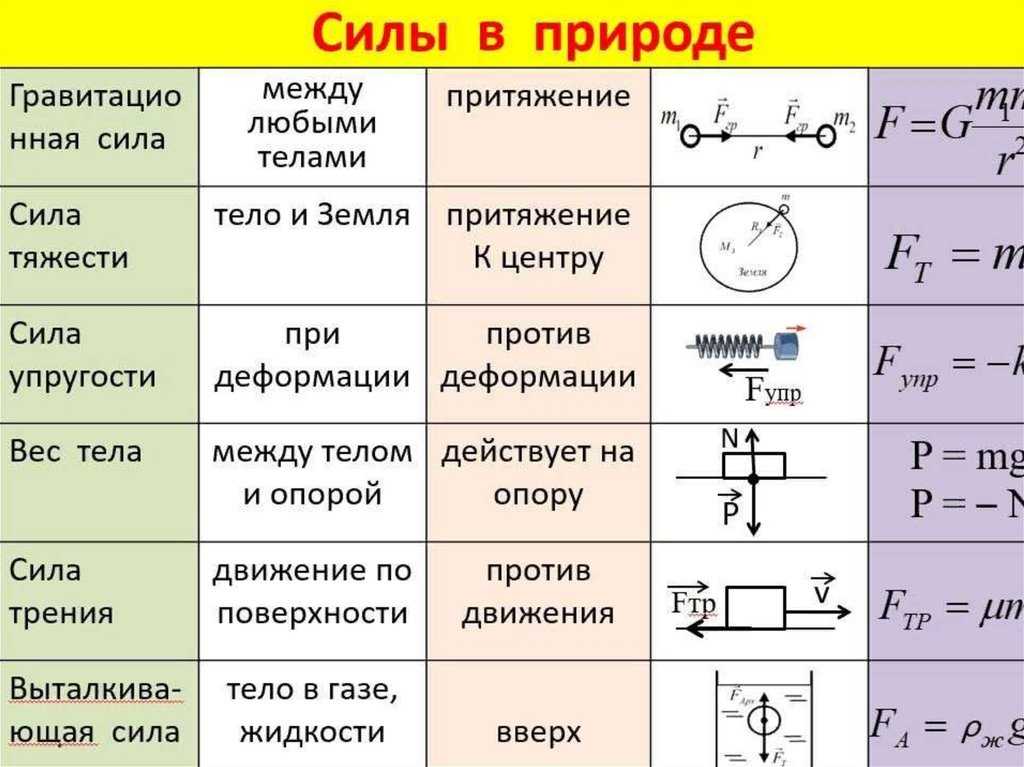

Р/c_V – показатель адиабаты.

Внутренняя энергия идеального газа

U = (m/m)(i/2)RT = (m/m)C_VT.

Задание 10 ЕГЭ по физике 2023: теория и практика

Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература

Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 Задание 22 Задание 23 Задание 24 Задание 25 Задание 26 Задание 27 Задание 28 Задание 29 Задание 30

За это задание ты можешь получить 2 балла. Уровень сложности: повышенный.
Средний процент выполнения: 59.5%
Ответом к заданию 10 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.

Разбор сложных заданий в тг-канале

Посмотреть

Задачи для практики

Задача 1

Поршень вставили в цилиндр на наибольший объём и закрепили. Цилиндр поместили в сосуд с горячей водой. Из приведённого ниже списка выберите два правильных утверждения, характеризующих этот процесс.

1. В сосуде будет происходить изохорный процесс.
2. Концентрация молекул в этом процессе увеличивается.
3. Концентрация молекул в этом процессе уменьшается.
4. В сосуде будет происходить изобарный процесс.
5. Концентрация молекул в этом процессе остаётся постоянной.

Решение

1) В сосуде будет происходить изохорный пройесс, т.к. объем сосуда меняеться не будет, поскольку его закрепили.

5) Концентрация молекул $n={N}/{V}$, где $N$ – число молекул, $V$ – объем цилиндра, т.к. $N=const$ и $V=const$, то концентрация молекул в этом процессе остается постоянной.

Ответ: 15

Показать решение

Бесплатный интенсив

Задача 2

В цилиндре с некоторым газом находится легкоподвижный поршень. Цилиндр помещают в сосуд с горячей водой. Из приведённого ниже списка на основании анализа этого процесса выберите все верные утверждения.

1. В сосуде будет происходить изохорный процесс.
2. Концентрация молекул в этом процессе увеличивается.
3. Концентрация молекул в этом процессе уменьшается.
4. В сосуде будет происходить изобарный процесс.
5. Концентрация молекул в этом процессе остаётся постоянной.

Решение

При помещении цилиндра в сосуд с горячей водой, температура газа в цилиндре будет увеличиваться и согласно уравнению Менделеева-Клайперона, будет увеличиваться объем цилиндра: $p·∆V={m}/{μ}R∆T$. Значит в сосуде будет происходить изобарный процесс, а концентрация молекул в цилиндре $n={N}/{V}$ уменьшится из-за увеличения объема, здесь $N$ – количество молекул газа под поршнем цилиндра.

Ответ: 34

Показать решение

Бесплатный интенсив

Задача 3

Легкоподвижный поршень вставлен в цилиндр на максимальный объём. Газ начинают медленно сжимать. Из приведённого ниже списка на основании опытных данных выберите все верные утверждения.

1. Масса газа увеличивается.
2. Масса газа не изменяется.
3. Внутренняя энергия газа увеличивается.
4. Внутренняя энергия газа уменьшается.
5. Внутренняя энергия газа остаётся неизменной.

Решение

2) При сжатии газа, число молекул в цилиндре остается постоянным, следовательно, масса газа не изменяется.

5) Поскольку газ сжимают медленно, его температура остается постоянной, следовательно, внутренняя энергия газа остается неизменной, т. к. внутренняя энергия есть функция температуры $U={i}/{2}υRT$, где $T$ – температура.

Ответ: 25

Показать решение

Бесплатный интенсив

Задача 4

На рисунке изображён циклический процесс, во время которого масса газа оставалась постоянной. Выберите из приведённого ниже списка все утверждения, которые соответствуют рисунку.

1. В процессе 1 → 2 к газу тепло подводится.
2. В процессе 1 → 2 тепло выделяется.
3. В процессе 2 → 3 к газу тепло подводится.
4. В процессе 2 → 3 тепло выделяется.
5. В процессе 3 → 4 к газу тепло подводится.

Решение

1) В процессе 1-2 к газу тепло подводится, т.к. $T_2 > T_1$, поскольку ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒V_1·T_2=V_2·T_1$, т.к. $p_1=p_2=const$, а $V_2 > V_1$, то, чтобы сохранилось равенство $T_2$ должна быть больше $T_1$.

4) Процесс 2-3 изохорный, тогда ${p_2}/{T_2}={p_3}/{T_3}⇒p_2T_3=p_3T_2⇒$, т. к. $p_2 > p_3$, то $T_3

Ответ: 14

Показать решение

Бесплатный интенсив

Задача 5

В результате эксперимента по изучению циклического процесса, проводившегося с некоторым постоянным количеством одноатомного газа, который в условиях опыта можно было считать идеальным, получилась зависимость объёма V от температуры T. Выберите два утверждения, соответствующих результатам этого эксперимента.

1. На участке 1–2 газ отдавал тепло.
2. Давление газа в точке 1 равно давлению в точке 2.
3. Изменение внутренней энергии газа на участке 2–3 отрицательно.
4. Работа, совершённая газом за весь цикл, отрицательна.
5. На участке 3–1 газ совершал положительную работу.

Решение

Решение:

Исходя из теории термодинамики и графика, давление в точке 1 и точке 2 равны, т.к. 1-2 изобара, а работа совершенная за цикл отрицательна так как $A_{31}=0; A_{23} 0 $, а $|A_{23}| > |A_{12}|$.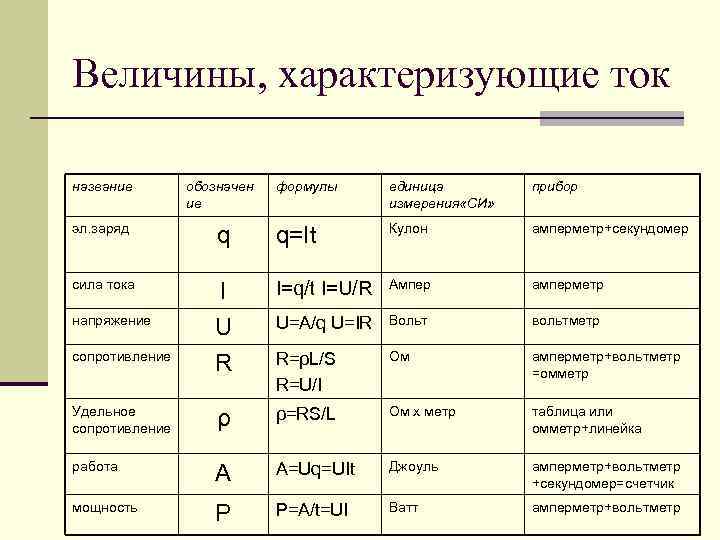 Тогда работа за весь цикл: $A = A_{23} + A_{12}

Понять, какая из работ больше или меньше очень легко, если нарисовать данный процесс в координатах pV и просто посмотреть на площади под графиком. Там же можно сразу определить знак работы за весь цикл по направлению цикла: если по часовой стрелке, то работа положительна, если против часовой – отрицательна.

Ответ: 24

Показать решение

Бесплатный интенсив

Задача 6

В результате эксперимента по изучению циклического процесса, проводившегося с некоторым постоянным количеством одноатомного газа, который в условиях опыта можно было считать идеальным, получилась зависимость объёма V от температуры T. Из приведённого ниже списка выберите два утверждения, соответствующих результатам этого эксперимента:

1. На участке 1–2 газ отдавал тепло.
2. Давление газа в точке 2 равно давлению в точке 3.
3. На участке 3–1 газ совершал отрицательную работу.
4. Изменение внутренней энергии газа на участке 3–1 положительно.
5. Работа, совершённая газом за весь цикл, отрицательна.

Решение

1) 1 закон термодинамики для процесса 12: $Q_{12}=∆U_{12}+A_{12}$. Т.к. объём не меняется $A_{12}=0$, т.к. температура растёт $∆U_{12}>0$, значит и $Q_{12}>0$, т.е. газ получает тепло, а не отдаёт (1 – неверно)

2) Давление в точке 2 равно точке 3, т.к. процесс изобарный (2 – верно)

3) На участке 3–1 газ совершал положительную работу, т.к. объём увеличивался (3 – неверно)

4) Т.к. температура не меняется $∆U_{31}=0$ (4 – неверно)

5) Работа за весь цикл отрицательная, т.к. $A_{12}=0; |A_{2-3}| > |A_{3-1}|; A_{23}

Понять, какая из работ больше или меньше очень легко, если нарисовать данный процесс в координатах pV и просто посмотреть на площади под графиком. Там же можно сразу определить знак работы за весь цикл по направлению цикла: если по часовой стрелке, то работа положительна, если против часовой – отрицательна.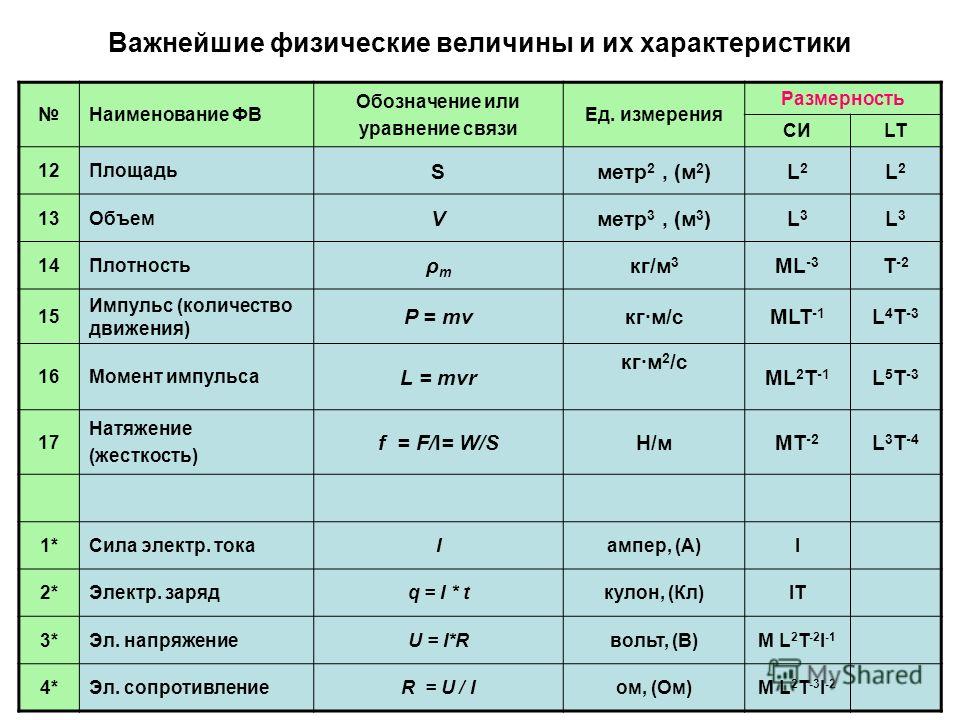

Ответ: 25

Показать решение

Бесплатный интенсив

Задача 7

При переходе идеального газа из состояния 1 в состояние 2 получили линейную зависимость концентрации молекул n от давления p. Масса газа в процессе остаётся постоянной. Из приведённого ниже списка выберите все правильные утверждения, характеризующих процесс 1–2.

1. Средняя кинетическая энергия теплового движения молекул газа остаётся неизменной.
2. Плотность газа уменьшается.
3. Газ получает тепло.
4. Происходит изотермическое сжатие газа.
5. Среднеквадратичная скорость теплового движения молекул газа уменьшается.

Решение

$m=const$, т.к. $p$, $n$ увеличиваются пропорционально, происходит изотермическое сжатие. Средняя кинетическая энергия молекул газа зависит от температуры, значит она тоже остается неизменной. В процессе изотермического сжатия изменения внутренней энергии газа равно нулю, а совершаемая им работа A

Ответ: 14

Показать решение

Бесплатный интенсив

Задача 8

Два вещества одинаковой массы, первоначально находившиеся в твёрдом состоянии при температуре 20◦C, равномерно нагревают на плитках одинаковой мощности в сосудах с пренебрежимо малой теплоёмкостью. На рисунке представлены полученные экспериментально графики зависимости температуры от времени нагревания. Используя данные графика, выберите из приведённого ниже списка все верные утверждения.

1. Температура плавления первого вещества 20◦C.
2. Удельная теплота плавления второго вещества равна удельной теплоте плавления первого вещества.
3. На нагревание первого и второго веществ до температуры плавления потребовалось одинаковое количество теплоты.
4. Удельная теплоёмкость первого вещества в жидком состоянии больше удельной теплоёмкости второго вещества в жидком состоянии.
5. В момент времени t = 9 мин оба вещества находились в жидком состоянии.

Решение

Из теории о теплообмене по графику очевидно, что удельная теплота плавления 2 и 1 вещества равны (за одно и то же время), а при $t=9$ мин оба вещества в жидких состояниях находились.

Ответ: 25

Показать решение

Бесплатный интенсив

Задача 9

На рисунке приведён график зависимости температуры воды t от времени процесса τ при нормальном атмосферном давлении. На основании анализа этого графика выберите все верные утверждения.

1. В процессе, соответствующем участку CD, внутренняя энергия пара уменьшается.
2. Участок AB соответствует процессу нагревания воды.
3. Точка D соответствует газообразному состоянию воды.
4. В процессе, соответствующем участку EF, внутренняя энергия системы «вода – пар» увеличивается.
5. В точке K вода находится в твёрдом состоянии (лёд).

Решение

1) Температура на участке CD растёт, значит внутренняя энергия увеличивается. 1 – неверно.

2) Так как изначально нам была дана вода (в жидком состоянии), то участок АВ соответствует нагреву воды (температура растёт). 2 – верно.

3) В процессе BC вода превратилась в пар, поэтому любая точка участков CD и DE, в том числе и точка D, соответствуют газообразному состоянию воды. 3 – верно.

4) Процесс EF – конденсация. В процессе конденсации внутренняя энергия вещества уменьшается. 4 – неверно

5) Точка K – это то же состояние, что и точка A, это жидкое состояние. 5 – неверно

Ответ: 23

Показать решение

Бесплатный интенсив

Задача 10

Смешали холодную и горячую воду. На рисунке приведён график зависимости температуры t◦ воды от времени τ . Теплообмен с окружающей средой пренебрежимо мал. Используя данные графика, выберите из приведённого ниже списка два верных утверждения.

1. Количество теплоты, отданное горячей водой, больше количества теплоты, полученного холодной водой.
2. Масса горячей воды больше массы холодной воды.
3. Изменение температуры холодной воды меньше, чем изменение температуры горячей воды.
4. Удельная теплоёмкость горячей воды меньше, чем холодной.
5. Температура t1 соответствует состоянию теплового равновесия.

Решение

По данному графику, очевидно, что масса горячей воды больше холодной, т.к. изменение температуры равновесия меньше, чем холодной воды до равновесия.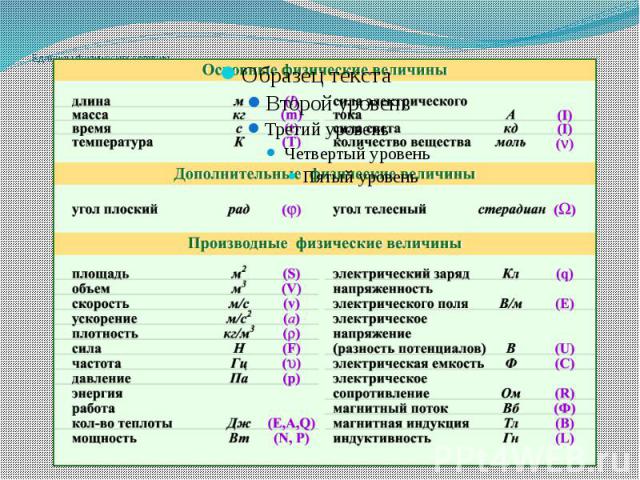 А при $t_1$ наступает тепловая равновесия.

Ответ: 25

Показать решение

Бесплатный интенсив

Задача 11

В результате эксперимента по изучению циклического процесса, проводившегося с некоторым постоянным количеством одноатомного газа, который в условиях опыта можно было считать идеальным, получилась зависимость давления p от объёма V , показанная на графике. Из приведённого ниже списка выберите все утверждения, соответствующих результатам этого эксперимента.

1. В процессе 2–3 объём газа увеличивался, а температура уменьшалась.
2. В процессе 1–2 газ не совершал работу.
3. В процессе 3–1 объём газа уменьшался, а давление увеличивалось.
4. В процессах 1–2 и 2–3 газ получал тепло.
5. В процессах 2–3 и 3–1 газ отдавал тепло.

Решение

В процессе 12 объём не меняется, поэтому работа не совершается, внутренняя энергия увеличивается (т. е. увеличивается произведение pV), значит газ получает тепло

Процесс 23 – изобарное расширение, при этом внутренняя энергия растёт (нагревание), значит Q=A+ΔU >0, газ получает тепло

В процессе 31 давление и объём уменьшаются, значит внутренняя энергия уменьшается, а работа отрицательная. Q=A+ΔU

Подходят только утверждения 2 и 4

Ответ: 24

Показать решение

Бесплатный интенсив

Задача 12

На рисунке приведён экспериментально полученный график зависимости температуры от времени при нагревании некоторого вещества. Первоначально вещество находилось в жидком состоянии. Выберите из приведённого ниже списка два утверждения, соответствующих результатам опыта.

1. Температура кипения равна 100◦C.
2. Теплоёмкости в жидком и газообразном состоянии одинаковы.
3. Наибольшей внутренней энергией вещество обладает в точке D.
4. Наименьшей внутренней энергией вещество обладает в точке D.
5. В точке D вещество находится в газообразном состоянии.

Решение

1) Температура кипения определяется по графику, она равна 80 (1-неверно)
2) Теплоёмкости в жидком и газообразном состоянии отличаются, так как наклон графиков нагревания жидкости и нагревания газа разный
3), 4) Наибольшая внутренняя энергия будет при наибольшей температуре (3 – верно, 4 – неверно)
5) Т.к. изначально вещество находилось в жидком состоянии, то АВ – это нагревание жидкости, ВС – парообразование (кипение), а СD – нагревание газа, значит в точке D вещество в газообразном состоянии (5-верно)

Ответ: 35

Показать решение

Бесплатный интенсив

Задача 13

Графики зависимости температуры двух тел A и B равной массы от времени приведены на рисунке. Первоначально они находились в жидком состоянии. Из приведённого ниже списка на основании анализа графиков выберите два верных утверждения.

1. Удельная теплоёмкость тела A в жидком состоянии больше удельной теплоёмкости тела B в жидком состоянии.
2. Удельная теплоёмкость тела A в жидком состоянии меньше удельной теплоёмкости тела B в жидком состоянии.
3. При кристаллизации тела A выделится больше энергии, чем тела при кристаллизации B.
4. При кристаллизации тела A выделится меньше энергии, чем тела при кристаллизации B.
5. Температура кристаллизации тела A меньше, чем тела B.

Решение

Удельная теплоемкость тела А в жидком состоянии больше удельной теплоемкости тела В в жидком состоянии, т.к. за одинаковый промежуток времени от 0 до С температура тела А изменилась меньше, чем тела В (1- верно).

При кристаллизации тела А выделится больше энергии, чем при кристаллизации тела В, т.к. кристаллизация тела А идет больше по времени, чем кристаллизация тела В (3-верно).

Ответ: 13

Показать решение

Бесплатный интенсив

Задача 14

На диаграмме pV показан процесс перехода одноатомного идеального газа из состояния 1 в состояние 3. Из приведённого ниже списка на основании анализа этого процесса выберите все верные утверждения.

1. В процессе 2–3 температура газа повышается.
2. В процессе 2–3 газ совершает положительную работу.
3. В процессе 1–2 внутренняя энергия газа понижается.
4. В процессе 2–3 газ отдаёт тепло.
5. Количество теплоты, полученное газом в процессе 1–2, идёт только на совершение работы.

Решение

1) В процессе 2-3 температура повышается, поскольку ${p_2V_2}/{T_2}={p_3V_3}/{T_3}⇒p_0·4V_0·T_3=4p_0·4V_0·T_2, T_3=4T_2,$ т.е. $T_3 > T_2$ (подходит).

2) Процесс 2-3 изохорный, т.е. $∆V=0$ и работа газа $A=p·V∆=0$ (не подходит).

3) Процесс 1-2 изотермический, значит, внутренняя энергия не меняется (не подходит).

4) В процессе 2-3 газ получает тепло, т.к. $T_3 > T_2$ (не подходит).

5) $Q=A+∆U, ∆U=0$, т.к. $∆T=0$, поскольку процесс 1-2 изотермический, то $Q=A$, т.е. количество теплоты, полученное газом в процессе 1-2 идет только на совершение работы (подходит).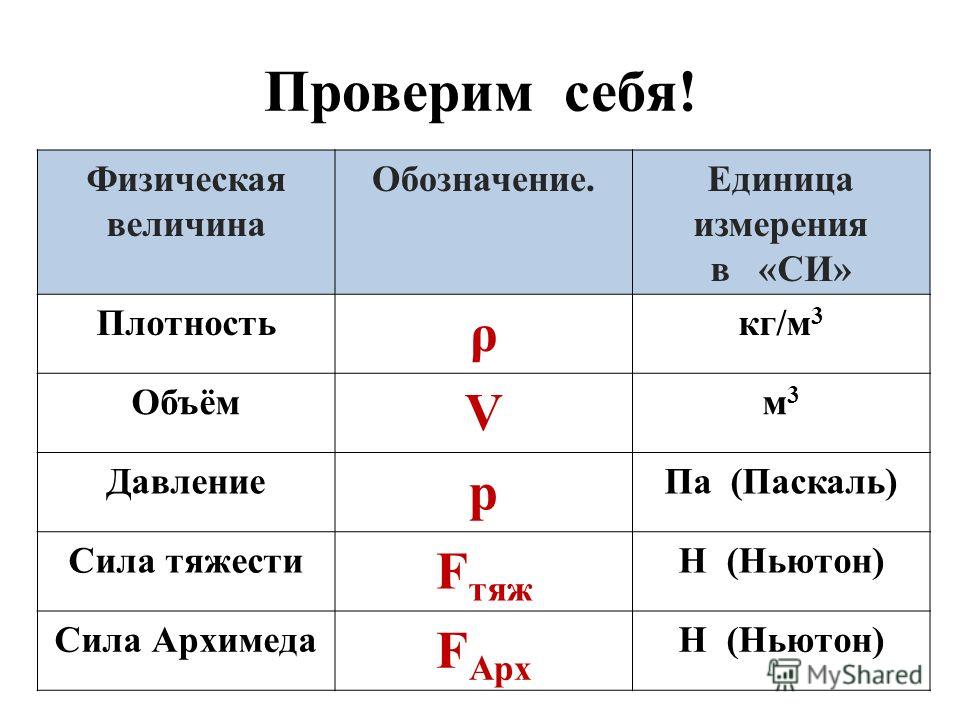

Ответ: 15

Показать решение

Бесплатный интенсив

Задача 15

Постоянную массу идеального газа переводят из состояния 1 в состояние 3, как показано на рисунке. В состоянии 1 температура газа была равна 327◦C. Из приведённого ниже списка на основании анализа графика этого процесса выберите все верные утверждения.

1. В процессе 1–2 температура газа повышается.
2. В процессе 1–2 газ совершает положительную работу.
3. Работа, совершённая над газом в процессе 2–3, положительна.
4. На участке 2–3 газ получает тепло.
5. В состоянии 3 температура газа равна 100 К.

Решение

1) В процессе 1-2 температура газа понижается: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒{2_{p_0}·3V_0}/{327+273}={p_03V_0}/{T_2}⇒T_2={600K}/{2}=300K$, т.к. $T_2=300K

2) В процессе 1-2 работа газа равна нулю (не подходит).

3) Работа, совершенная над газом в процессе 2-3 положительна, т. к. объем газа уменьшается $V_3

4) На участке 2-3 газ отдает тепло, т.к. над газом совершается работа (не подходит).

5) ${p_3V_3}/{T_3}={p_2V_2}/{T_2}⇒{p_0·V_0}/{T_3}={p_03V_0}/{300K}⇒3T_3=300K⇒T_3=100K$ (подходит).

Ответ: 35

Показать решение

Бесплатный интенсив

Задача 16

На рисунке показана зависимость давления от объёма идеального газа в циклическом процессе. Из приведённого ниже списка на основании анализа этого циклического процесса выберите два верных утверждения.

1. В процессе B–C температура газа уменьшается.
2. Наибольшую работу газ совершает в процессе A–B.
3. В процессе C–D внутренняя энергия газа не меняется.
4. В процессе A–B температура газа растёт.
5. В процессе A–D работа газа равна нулю.

Решение

1) В процессе В-С температура газа возрастает (не подходит).

2) В процессе А-В работа газа равна нулю, т.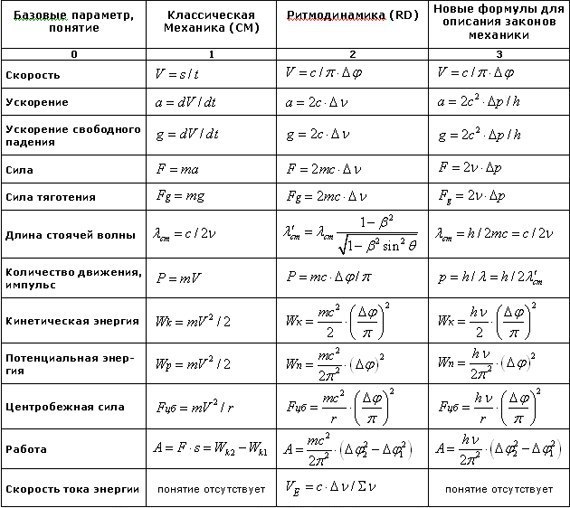 к. процесс изохорный $V_A=V_B$ (не подходит).

3) Процессе C-D изотермический, значит, внутренняя энергия газа не меняется, т.к. внутренняя энергия есть функция температуры $U={i}/{2}υRT$ (подходит).

4) В процессе А-В температура газа возрастает, т.к. ${p_A}/{T_A}={p_B}/{T_B}⇒p_A·T_B=p_B·T_A⇒T_B > T_A$ (подходит).

5) В процессе A-D объём газа меняется, а значит работа отлична от нуля (не подходит)

Ответ: 34

Показать решение

Бесплатный интенсив

Задача 17

На рисунке показана зависимость давления от температуры идеального газа в циклическом процессе. Из приведённого ниже списка на основании анализа этого циклического процесса выберите два верных утверждения.

1. Объём газа наибольший в состоянии 4.
2. Процесс 3–4 изохорный.
3. В процессе 1–2 внутренняя энергия газа не изменяется.
4. В процессе 4–1 объём газа уменьшается.
5. В процессе 2–3 газ отдаёт теплоту.

Решение

Воспользуемся методом исключения.

2) Процесс 3-4 не является изохорным, т.к. изохора в координатах p-T или ее продолжение, должна проходить через точку О (не подходит).

3) В процессе 1-2 внутренняя энергия газа повышается, т.к. температура увеличивается ($T_2 > T_1$), а внутренняя энергия есть функция температуры: $U={i}/{2}υRT$ (не подходит).

5) В процессе 2-3 газ получает теплоту, т.к. температура газа в данном процессе увеличивается $T_3 > T_2$ (не подходит).

Ответ: 14

Показать решение

Бесплатный интенсив

Задача 18

На рисунке показана зависимость объёма от температуры идеального газа в циклическом процессе. Из приведённого ниже списка на основании анализа этого циклического процесса выберите два верных утверждения.

1. Наибольшее давление на стенки сосуда газ оказывает в состоянии 4.
2. Наибольшую работу газ совершает в процессе 1–2.
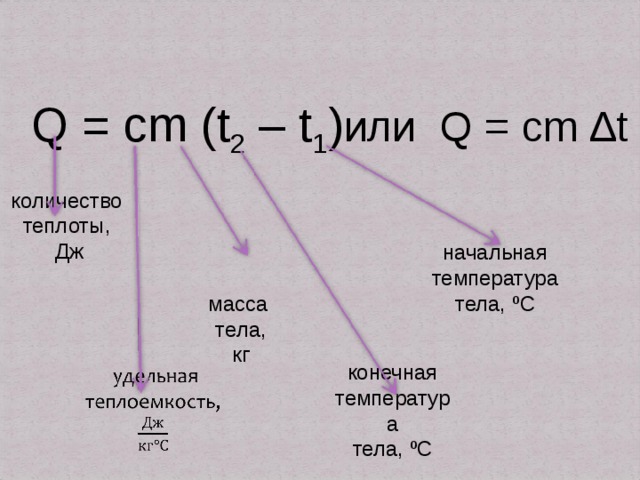
3. В процессе 1–2 работа газа равна нулю.
4. В процессе 2–3 объём газа уменьшается.
5. В процессе 4–1 температура газа растёт.

Решение

Воспользуемся методом исключения.

3) В процессе 1-2 работа газа не равна нулю, т.к. $A=p·∆V, ∆V≠0$, а значит, $A≠0$ (не подходит).

4) В процессе 2-3 объем газа не изменяется, т.к. $V_2=V_3$ (не подходит).

5) В процессе 4-1 температура газа уменьшается, т.к. $T_4 > T_1$ (не подходит).

Ответ: 12

Показать решение

Бесплатный интенсив

Задача 19

На рисунке показана зависимость давления от температуры идеального газа в циклическом процессе. Из приведённого ниже списка на основании анализа этого циклического процесса выберите два верных утверждения и укажите их номера.

1. В процессе B–C температура газа уменьшается.
2. Наименьшую работу газ совершает в процессе A–B.
3. В процессе C–A внутренняя энергия газа не изменяется.
4. В процессе A–B объём газа остаётся постоянным.
5. В процессе A–C температура газа растёт.

Решение

1. По графику видно, что температура $T_c

Процесс А-В изобарный $p_A=p_В=const$, а значит, в процессе А-В газ совершает наибольшую работу (не верно).

Процесс А-С изотермический $T_A=T_C=const$, а поскольку внутренняя энергия есть функция температуры, то в процессе С-А внутренняя энергия газа не изменяется (верно).

Ответ: 13

Показать решение

Бесплатный интенсив

Задача 20

На рисунке показана зависимость давления от температуры идеального газа в циклическом процессе. На основании анализа этого циклического процесса выберите два верных утверждения.

1. В процессе B–C объём газа остаётся постоянным.
2. Наибольшую работу газ совершает в процессе A–B.
3. В процессе C–A работа газа равна нулю.
4. В процессе A–B объём газа уменьшается.
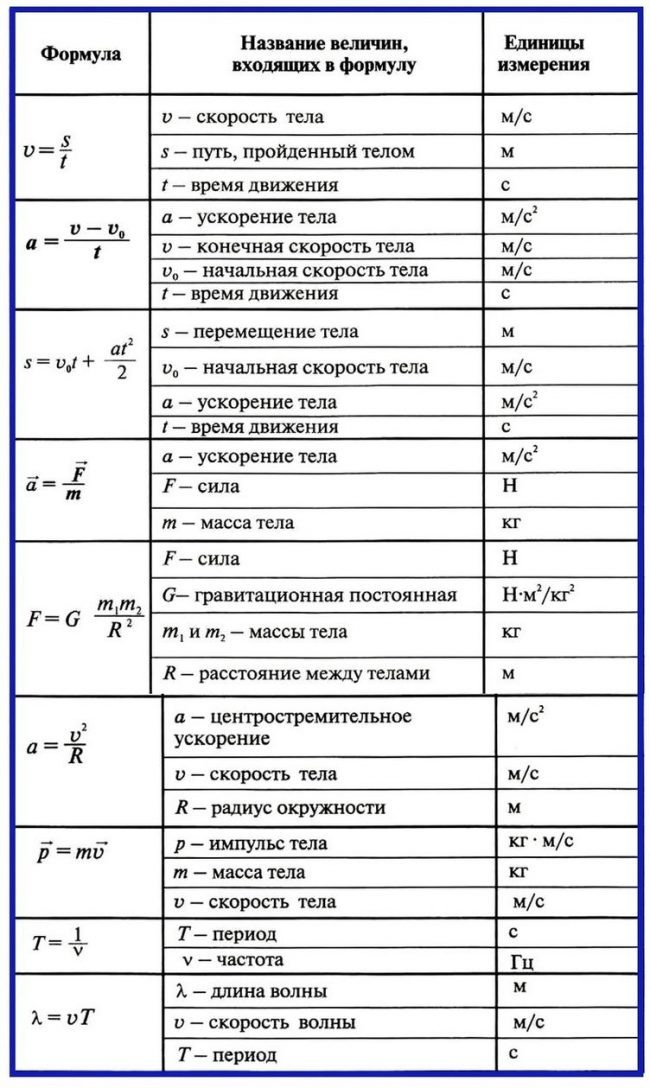
5. В процессе B–C температура газа растёт.

Решение

Поскольку ${р_в}/{Т_в}={p_c}/{T_c}=const$, то $V_в=V_c$, значит, в процессе В-С объем газа остается постоянным.

Поскольку $р_А=p_В=const$, то процесс А-В изобарный, значит, наибольшую работу газ совершает в процессе А-В.

Ответ: 12

Показать решение

Бесплатный интенсив

Показать еще

Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.

Включить уведомления

Бесплатный интенсив по физике

3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.

Курс стартует 23 января. Бесплатный интенсив

Искусственный интеллект сводит задачу квантовой физики из 100 000 уравнений всего к четырем уравнениям — ScienceDaily

С помощью искусственного интеллекта физики сжали сложную квантовую задачу, которая до сих пор требовала 100 000 уравнений, в краткую задачу, состоящую всего из четырех уравнений. – все без ущерба для точности. Работа, опубликованная 23 сентября в журнале Physical Review Letters , может произвести революцию в том, как ученые исследуют системы, содержащие много взаимодействующих электронов. Более того, если его можно масштабировать для решения других задач, этот подход потенциально может помочь в разработке материалов с востребованными свойствами, такими как сверхпроводимость или полезность для производства чистой энергии.

«Мы начинаем с этого огромного объекта, состоящего из всех этих связанных друг с другом дифференциальных уравнений; затем мы используем машинное обучение, чтобы превратить его в нечто настолько маленькое, что его можно пересчитать по пальцам», — говорит ведущий автор исследования Доменико Ди Санте, приглашенный научный сотрудник Центра вычислительной квантовой физики (CCQ) Института Флэтайрона в Нью-Йорке и доцент Болонского университета в Италии.

Огромная проблема касается того, как ведут себя электроны, когда они движутся по решетчатой ​​решетке. Когда два электрона занимают одно и то же место в решетке, они взаимодействуют. Эта установка, известная как модель Хаббарда, представляет собой идеализацию нескольких важных классов материалов и позволяет ученым узнать, как поведение электронов приводит к возникновению искомых фаз материи, таких как сверхпроводимость, при которой электроны проходят через материал без сопротивления. Модель также служит испытательным полигоном для новых методов, прежде чем они будут применены к более сложным квантовым системам.

Однако модель Хаббарда обманчиво проста. Даже для скромного числа электронов и передовых вычислительных подходов проблема требует серьезной вычислительной мощности. Это связано с тем, что когда электроны взаимодействуют, их судьбы могут стать квантово-механически запутанными: даже если они находятся далеко друг от друга в разных узлах решетки, два электрона нельзя рассматривать по отдельности, поэтому физики должны иметь дело со всеми электронами одновременно, а не с одним из них. время. Чем больше электронов, тем больше запутанностей возникает, что экспоненциально усложняет вычислительную задачу.

Одним из способов изучения квантовой системы является использование так называемой ренормализационной группы. Это математический аппарат, который физики используют, чтобы посмотреть, как поведение системы — такой как модель Хаббарда — меняется, когда ученые изменяют такие свойства, как температура, или рассматривают свойства в разных масштабах. К сожалению, ренормализационная группа, которая отслеживает все возможные связи между электронами и ничем не жертвует, может содержать десятки тысяч, сотни тысяч или даже миллионы отдельных уравнений, которые необходимо решить. Вдобавок ко всему, уравнения сложны: каждое представляет пару взаимодействующих электронов.

Ди Санте и его коллеги задались вопросом, могут ли они использовать инструмент машинного обучения, известный как нейронная сеть, чтобы сделать группу ренормализации более управляемой. Нейронная сеть похожа на нечто среднее между обезумевшим оператором коммутатора и эволюцией выживания наиболее приспособленных. Во-первых, программа машинного обучения создает соединения внутри полноразмерной группы перенормировки. Затем нейронная сеть настраивает сильные стороны этих связей, пока не найдет небольшой набор уравнений, который генерирует то же решение, что и исходная ренормгруппа гигантского размера. Выходные данные программы отражают физику модели Хаббарда даже с помощью всего четырех уравнений.

«По сути, это машина, способная обнаруживать скрытые закономерности, — говорит Ди Санте. «Когда мы увидели результат, мы сказали: «Вау, это больше, чем мы ожидали». Мы действительно смогли уловить соответствующую физику».

Обучение программы машинного обучения требовало больших вычислительных мощностей, и программа работала целые недели. Хорошая новость, по словам Ди Санте, заключается в том, что теперь, когда они тренируют свою программу, они могут адаптировать ее для работы над другими проблемами без необходимости начинать с нуля. Он и его сотрудники также изучают, что именно машинное обучение на самом деле «узнает» о системе, что может дать дополнительную информацию, которую в противном случае физикам было бы трудно расшифровать.

В конечном счете, самый большой открытый вопрос заключается в том, насколько хорошо новый подход работает с более сложными квантовыми системами, такими как материалы, в которых электроны взаимодействуют на больших расстояниях. Кроме того, существуют захватывающие возможности для использования этой техники в других областях, связанных с ренормализационными группами, таких как космология и нейробиология.

Ди Санте стал соавтором нового исследования вместе с приглашенным исследователем CCQ Матией Медвидович (аспиранткой Колумбийского университета), Алессандро Тоски из TU Wien в Вене, Джорджио Санджованни из Вюрцбургского университета в Германии, Чезаре Франчини из Болонского университета в Италии старший научный сотрудник CCQ и Центра вычислительной математики Анирван М. Сенгупта и содиректор CCQ Энди Миллис. Работа Ди Санте в CCQ была поддержана Международной стипендией Марии Кюри, которая поощряет транснациональное научное сотрудничество.

черных дыр – Почему физике не нравится бесконечность (или нравится)?

спросил 1 год, 10 месяцев назад

Изменено 9 месяцев назад

Просмотрено 5к раз

$\begingroup$

Недавно мне сказали, что в физике, если ваше уравнение содержит бесконечность, это обычно предполагает, что что-то не так. Например, бесконечность вокруг черных дыр (также) говорит нам о том, что общая теория относительности не дает полной картины гравитации. Насколько это верно? И какая логика лежит в основе этой методики проверки теории?

Отредактируйте, чтобы было достаточно этого поста Ответы, похоже, не объясняют почему ; нет никакого аналитического или эмпирического обоснования того, почему «пределы не подходят».

• черные дыры
• сингулярности
• приближения
• модели

$\endgroup$

8

$\begingroup$

Нет правила против бесконечности, есть только правило против эмпирической ошибки. Исторически бесконечность намекала, что мы что-то упускаем, но есть и множество других вещей. Давайте обсудим некоторые исторические примеры. 94{15}$. Чему пропорциональна выходная мощность светящегося объекта (черного или серого)? Если бы это было первое, наши источники энергии не могли бы сделать ничего достаточно горячим, чтобы светиться. {-1/2}$. Мы могли бы обойти это, установив $\epsilon_0=0$, чтобы $\rho=\epsilon_0\nabla\cdot E=0$, то есть электрические заряды не могли существовать, или $\mu_0=0$, чтобы токи не могли генерировать $\ nabla\times B$, но и они эмпирически неверны.

Ньютон был недоволен бесконечной скоростью действия на расстоянии в своей собственной теории гравитации, но он и многие его последователи приняли ее как грубый факт о Вселенной, и казалось, что так будет всегда. Эйнштейн потратил несколько лет на то, чтобы понять, как будет работать гравитация со скоростью $c$, не потому, что ничто не может быть бесконечным, а потому, что следствия специальной теории относительности казались очень далеко идущими. В конце концов, общая теория относительности была не только теоретически приемлемой, но и эмпирически подтвержденной. Но ОТО породила другой источник бесконечных величин: сингулярности. По сей день мы точно не знаем, как гравитационная физика после ОТО опровергнет это (но см. также здесь). 92$ нет. Но это неплохая идея в теории , поэтому аналогичные идеи могут быть более успешными. См. здесь для обсуждения таких методов.

По причине, обсуждаемой в приведенной выше ссылке (хотя это можно объяснить и по-другому), гравитационная версия этих проблем оказалась сложнее. Квантовая гравитация не поддается перенормировке (применяются T и C, следовательно, их множественные подходы или перекрытия для массирования бесконечностей, которые мы получаем на этот раз). Но вопросы перенормировки, независимо от того, в какое десятилетие они решаются, приводят к другому, более тонкому вопросу «бесконечно ли это и имеет ли это значение?» вопрос: сколько степеней свободы нужно, чтобы утвердить вашу теорию? Хотя бесконечно многие из них действительно представляют проблему (см., например, раздел 7.1 здесь), не все полезные теории перенормируемы, потому что первые несколько параметров могут выполнять большую часть работы по объяснению или предсказанию эмпирической реальности.

Что касается примеров, когда конечных величин слишком велики или слишком малы теоретически, чтобы соответствовать данным, мы могли бы быть здесь с ними весь день.

$\endgroup$

1

$\begingroup$

Бесконечность — это сокращение от неограниченного. Когда мы говорим, что $\frac 1 x$ стремится к бесконечности, когда $x$ приближается к $0$, мы на самом деле имеем в виду, что мы можем сделать $\frac 1 x$ сколь угодно большим, используя значение $x$, которое достаточно близко к $0$. Фактическое значение $\frac 1 x$ при $x=0$ не определено. Если ограничиться действительными числами, то бесконечности не существует.

Но действительные числа (а иногда и комплексные числа, но комплексное число — это пара действительных чисел) — это то, что мы используем в физике для моделирования всех аспектов реальности. Все, что мы измеряем в физике, будь то масса, длина, температура, плотность и т. д. и т. д., является действительным числом.

Итак, если модель реальности дает бесконечный (или, говоря более формально, неограниченный) результат в конкретном сценарии, то мы знаем, что модель должна разрушиться в этом сценарии. Таким образом, появление «бесконечностей» в модели говорит нам о том, что модель неполна. 92$ и так далее, у которых бесконечности в разных местах. Когда $x=\infty$, $y=0$. Когда $x=3$, $z=\infty$ и так далее. Таким образом, нахождение конкретной величины $x$ в уравнении, являющейся бесконечной, может просто означать, что более уместно говорить о $1/x$.

В физике черных дыр есть особенно известный пример: сингулярность Шварцшильда на горизонте событий. Когда Шварцшильд впервые решил уравнение Эйнштейна, чтобы найти гравитационное поле точечной массы в вакууме, существовал радиус, при котором выражение стремилось к бесконечности. 92}$.

Долгое время люди думали, что это означает, что физика становится бессмысленной и недействительной на горизонте событий. Однако позже выяснилось, что это всего лишь артефакт используемой системы координат. Это похоже на то, как сходят с ума координаты широты и долготы на северном и южном полюсах. Там на самом деле ничего странного или нефизического не происходит — сфера выглядит на северном полюсе так же, как и везде. Просто система координат там не работает. Точно так же, как есть другие системы координат, в которых северный полюс Земли выглядит нормально, существуют системы координат, в которых горизонт событий черной дыры выглядит нормальным и ничем не примечательным.

Однако сингулярность в центре черной дыры не может быть устранена никаким изменением координат. Пространство-время «формирует острие» там, как будто вдавливает в резиновый лист острым карандашом. Если вы посмотрите на любую другую часть пространства-времени и достаточно ее увеличите, она всегда будет выглядеть как крошечный микроскопический участок плоского пространства, в котором мы можем использовать физику плоского пространства, чтобы предсказать, что произойдет. Поверхности с этим свойством повсеместно называются «многообразиями». Однако, если вы увеличите пространство вокруг остроконечной сингулярности, оно никогда не выровняется — оно выглядит остроконечным в любом масштабе. Пространство-время больше не является многообразием, как предполагает общая теория относительности. Это означает, что мы никогда не сможем применить нашу хорошо известную физику плоского пространства. 9\circ$ вокруг точки на субатомной физике? Если частица вращается, то вращается ли она быстрее, или пытается перекрыть себя, или что? Поскольку мы не знаем, как работают элементарные частицы в таком масштабе, мы не можем даже догадываться.

(Конечно, я сильно упрощаю. Я просто пытаюсь дать смутное интуитивное представление о том, какую проблему она ставит.) избегать разговоров о реальных проблемах. Кривизна, стремящаяся к бесконечности, просто означает, что 1/кривизна стремится к нулю, и если вы можете объяснить свою физику, используя вместо этого 1/кривизну, возможно, ничего не пойдет не так. В случае с центральной сингулярностью черной дыры Шварцшильда проблема заключается в том, что вся материя упаковывается во все меньшее пространство, плотность энергии возрастает безгранично, и мы просто не знаем, что происходит при энергиях, намного превышающих те, которые у нас есть. исследованы экспериментально. {1,000,000}$ раз больше, это по-прежнему крошечные по сравнению с бесконечностью!) Применяются ли до сих пор известные законы физики? Почти наверняка нет, но никто не знает, чем их заменить.

$\endgroup$

10

$\begingroup$

Бесконечные значения хороши в контекстах, где они имеют смысл (скажем, в бесконечной вселенной), но проблематичны там, где их нет. Итак, если в теории появляется бессмысленная бесконечность, она логически неверна.

Пространство может быть бесконечным, поскольку нет никаких известных причин, по которым Вселенная должна быть ограничена. Точно так же полная энергия или количество частиц во Вселенной также может быть бесконечным. Но в любом конечном объеме должно быть конечное число частиц, иначе у нас была бы бесконечная масса с бесконечной плотностью, которая произвела бы черную дыру с бесконечным радиусом. Обратите внимание, что мы не получаем эту проблему с бесконечным числом частиц в бесконечном объеме, поскольку плотность все еще может быть конечной и ниже порога образования черной дыры.

Сверхпроводник может иметь бесконечную проводимость, но все это означает, что на нем нет падения напряжения (вспомним закон Ома: V = IR, где R — величина, обратная проводимости). Вы не можете получить бесконечный ток, проходящий через сверхпроводник, потому что этот проводник имеет только конечное число электронов, которые могут двигаться только с конечной скоростью.

Строго говоря, никто не может исключить сингулярности в черных дырах. Однако из квантовой механики мы знаем, что связанные частицы имеют более высокие нулевые энергии. Таким образом, сингулярность с нулевым радиусом будет иметь бесконечную энергию нулевой точки, что не является разумным решением. Без теории квантовой гравитации трудно сказать, что все это значит, но, учитывая, как квантовая механика имеет тенденцию распространять обычные частицы, такие как электроны, кажется разумным предположить, что сингулярности также могут быть распространены, полностью избегая проблемы.

Итак, да, физики, как правило, не любят бесконечности, появляющиеся там, где они не имеют смысла, но никто не возражает против их существования в контекстах, где они имеют смысл.

Быстрое дополнение: Чтобы ответить на ваше замечание о том, что общая теория относительности неполна, мы знаем это, потому что она не включает квантовую механику, и были значительные теоретические трудности, объединяющие их. Итак, мы знаем, что он неполный, потому что в квантовом мире есть много вещей, которые он не объясняет. Наше понимание физики черных дыр здесь не нужно.

$\endgroup$

9

$\begingroup$

Насколько верно то, что ядро ​​черной дыры имеет бесконечную кривизну, без каких-либо экспериментальных данных сказать невозможно. Я думаю, что то, что вы назвали метадологией, есть не что иное, как ожидание людей, что бесконечности нефизичны, потому что мы не встречались с ними в реальности. 2}\vec{e}_r$ сила колумба, $\epsilon$ диэлектрическая проницаемость вакуума (https://en .wikipedia.org/wiki/Vacuum_permittivity) и $e$ — элементарный заряд электрона. Вы видите, что для нулевого радиуса энергия расходится. Но это предполагает, что весь электрон может находиться в одной точке, и поэтому электрическое поле электрона имеет бесконечную плотность энергии в месте расположения электрона. Я не могу сделать расчет, но я ожидаю, как и люди выше для квантовой гравитации, что сингулярность в энергии должна исчезнуть в квантовой механике, потому что там электрон не был бы в одном месте, а «разбросан» и что мы вычисляем классически, это не вся картина, потому что мы не включаем квантовую механику электрона.

$\endgroup$

2

$\begingroup$

Сверхпроводимость — пример бесконечной измеримой величины в физике.

$\endgroup$

$\begingroup$

Почему бы не сказать, что уравнения, которые не содержат (или приводят к) бесконечности, должны быть оставлены? Почему Природа не должна любить бесконечности, говоря антропоморфно? Кто знает?
Это зависит от теории и того, что нам нравится. Например, в квантовой теории поля перенормировка вводится, чтобы избежать бесконечной массы. Нам не нравятся бесконечные массы (хотя разница между двумя бесконечными массами может быть конечной), поэтому теория перенормируется с целью получения конечных масс.
Совершенно нормально вводить бесконечную потенциальную яму. Соответствует ли это реальной бесконечности? Конечно. Бесконечные потенциальные стены действительно существуют (удержание кварков).
Когда вы приближаетесь к точечному электрическому заряду, сила, которую вы чувствуете, возрастает до бесконечности. Дойдет ли до бесконечности? Да, почему бы и нет? Является ли это признаком того, что классическая электродинамика неверна? Нет. Вы можете считать это даже признаком того, что CED идет по верному пути.
Однако согласно квантовой теории поля даже не имеет смысла говорить о силах и частицах. Но в КТП встречаются бесконечные массы и константы связи, которые подделываются какой-то бесконечной процедурой, чтобы соответствовать нашим ожиданиям конечности масс и констант связи.