Тангенциальное и нормальное ускорение формулы: Тангенциальное и нормальное ускорение — урок. Физика, 10 класс.

Понятие об ускорении. Ускорение тангенциальное, нормальное и полное. Формулы

Каждый, кто знаком с техникой и физикой, знает о понятии ускорения. Тем не менее мало кто знает о том, что эта физическая величина имеет две составляющие: ускорение тангенциальное и ускорение нормальное. Рассмотрим подробнее каждое из них в статье.

В физике ускорением называют величину, которая описывает быстроту изменения скорости. Причем под этим изменением понимают не только абсолютное значение скорости, но и ее направление. Математически это определение записывают так:

a¯ = dv¯/dt.

Заметим, что речь идет о производной изменения вектора скорости, а не только ее модуля.

В отличие от скорости, ускорение может принимать как положительные, так и отрицательные значения. Если скорость направлена всегда вдоль касательной к траектории перемещения тел, то ускорение направлено в сторону действующей на тело силы, что следует из второго закона Ньютона:

F¯ = m*a¯.

Ускорение измеряется в метрах в секунду квадратную. Так, 1 м/с² означает, что скорость на 1 м/с увеличивается за каждую секунду перемещения.

Прямолинейная и криволинейная траектории движения и ускорение

Окружающие нас объекты могут двигаться либо по прямой линии, либо по кривой траектории, например, по окружности.

В случае движения по прямой скорость тела изменяет только свой модуль, но сохраняет направление. Это означает, что полное ускорение может быть вычислено так:

a = dv/dt.

Отметим, что мы опустили значки вектора над скоростью и ускорением. Поскольку полное ускорение направлено по касательной к прямолинейной траектории, то оно называется тангенциальным или касательным. Эта составляющая ускорения описывает исключительно изменение абсолютной величины скорости.

Теперь предположим, что тело совершает движение по криволинейной траектории. В этом случае его скорость можно представить в виде:

v¯ = v*u¯.

Где u¯ – единичный вектор скорости, направленный вдоль касательной к кривой траектории. Тогда полное ускорение можно записать в такой форме:

a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.

Это и есть исходная формула нормального, тангенциального и полного ускорения. Как видно, равенство в правой части состоит из двух слагаемых. Второе из них отлично от нуля только при криволинейном перемещении.

Формула для касательной компоненты полного ускорения уже была приведена выше, запишем ее еще раз:

a_t¯ = dv/dt*u¯.

Формула показывает, что тангенциальное ускорение не зависит от того, куда направлен вектор скорости, и меняется ли он во времени. Оно определяется исключительно изменением абсолютного значения v.

Теперь запишем вторую компоненту – ускорение нормальное a_n¯:

a_n¯ = v*du¯/dt.

Несложно показать геометрически, что эта формула может быть упрощена до такого вида:

a_n¯ = v²/r*r_e¯.

Здесь r – кривизна траектории (в случае окружности – это ее радиус), r_e¯ – элементарный вектор, направленный к центру кривизны. Мы получили интересный результат: от тангенциальной нормальная составляющая ускорения отличается тем, что она совершенно не зависит от изменения модуля скорости. Так, в случае отсутствия этого изменения, касательного ускорения не будет, а нормальное примет некоторое значение.

Нормальное ускорение направлено к центру кривизны траектории, поэтому его называют центростремительным. Причиной его возникновения являются центральные силы в системе, которые изменяют траекторию. Например, это сила гравитации при вращении планет вокруг звезд или сила натяжения веревки при вращении камня, привязанного к ней.

Полное ускорение при вращении по окружности

Разобравшись с понятиями и формулами тангенциального ускорения и нормального ускорения, можно теперь переходить к вычислению полного ускорения. Решим эту задачу на примере вращения тела по окружности вокруг некоторой оси.

Рассмотренные две компоненты ускорения направлены под углом 90^o друг к другу (по касательной и к центру кривизны). Этот факт, а также свойство суммы векторов можно использовать, чтобы рассчитать ускорение полное. Получаем:

a = √(a_t² + a_n²).

Из формулы полного, нормального и тангенциального ускорений (ускорения a_n и a_t) следует два важных вывода:

• В случае прямолинейного перемещения тел полное ускорение совпадает с тангенциальным.
• Для равномерного вращения по окружности полное ускорение имеет только нормальную компоненту.

Во время движения по окружности центростремительная сила, сообщающая телу ускорение a_n, удерживает его на круговой орбите, препятствуя тем самым фиктивной центробежной силе.

Тангенциальное и нормальное ускорение. Касательное и нормальное ускорение

Изучение физики начинают с рассмотрения механического движения.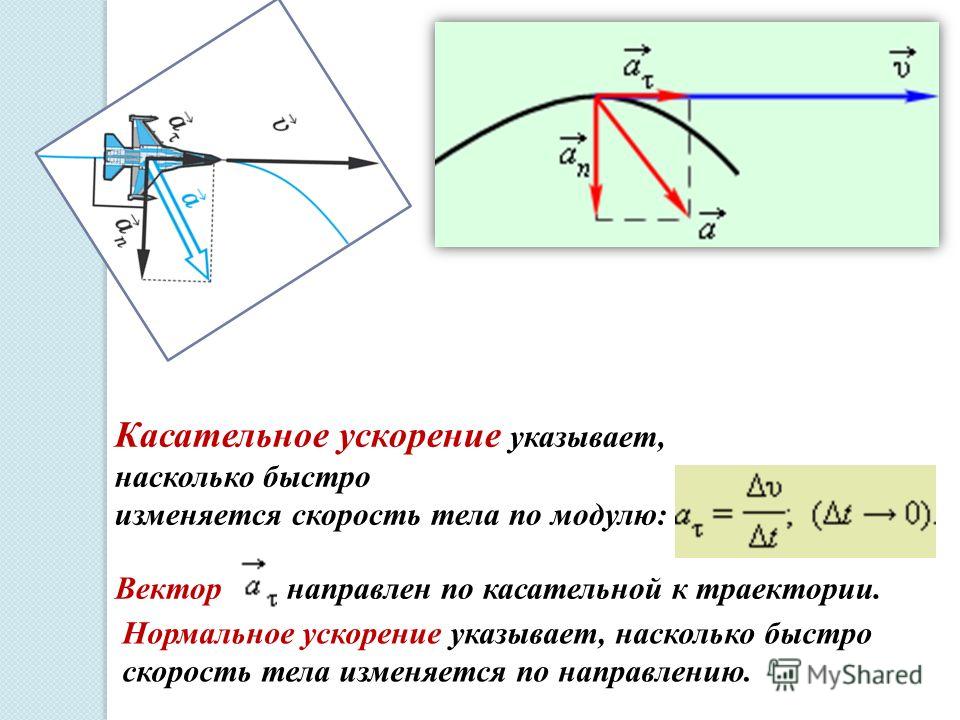 В общем случае тела движутся по кривым траекториям с переменными скоростями. Для их описания используют понятие ускорения. В данной статье рассмотрим, что такое тангенциальное и нормальное ускорение.

Кинематические величины. Скорость и ускорение в физике

Кинематика механического движения – это раздел физики, который занимается изучением и описанием перемещения тел в пространстве. Кинематика оперирует тремя главными величинами:

• пройденный путь;
• скорость;
• ускорение.

В случае движения по окружности используют аналогичные кинематические характеристики, которые приведены к центральному углу окружности.

С понятием скорости знаком каждый. Она показывает быстроту изменения координат тел, находящихся в движении. Скорость всегда направлена по касательной к линии, вдоль которой тело перемещается (траектории). Далее линейную скорость будем обозначать v¯, а угловую скорость – ω¯.

Ускорение – это скорость изменения величин v¯ и ω¯. Ускорение – это тоже векторная величина, однако ее направление совершенно не зависит от вектора скорости. Ускорение всегда направлено в сторону действующей на тело силы, которая вызывает изменение вектора скорости. Ускорение для любого типа движения можно рассчитать по формуле:

a¯ = dv¯ / dt

Чем сильнее изменится скорость за интервал времени dt, тем больше будет ускорение.

Для понимания изложенной дальше информации необходимо помнить, что ускорение появляется в результате любого изменения скорости, включая изменения как ее модуля, так и ее направления.

Касательное и нормальное ускорение

Предположим, что материальная точка движется по некоторой кривой линии. Известно, что в некоторый момент времени t ее скорость была равна v¯. Поскольку скорость – это касательный к траектории вектор, ее можно представить в следующем виде:

v¯ = v × u_t¯

Здесь v – длина вектора v¯, а u_t¯ – единичный вектор скорости.

Чтобы вычислить вектор полного ускорения в момент времени t, необходимо найти производную скорости по времени. Имеем:

a¯ = dv¯ / dt = d (v × u_t¯) / dt

Поскольку модуль скорости и единичный вектор изменяются со временем, то, пользуясь правилом нахождения производной от произведения функций, получаем:

a¯ = dv / dt × u_t¯ + d (u_t¯) / dt × v

Первое слагаемое в формуле называется тангенциальной, или касательной компонентой ускорения, второе слагаемое – это нормальное ускорение.

Касательное ускорение

Еще раз запишем формулу для вычисления касательного ускорения:

a_t¯ = dv / dt × u_t¯

Это равенство означает, что тангенциальное (касательное) ускорение направлено так же, как вектор скорости в любой точке траектории. Оно численно определяет изменение модуля скорости. Например, в случае прямолинейного движения полное ускорение состоит только из касательной составляющей. Нормальное ускорение при таком типе перемещения равно нулю.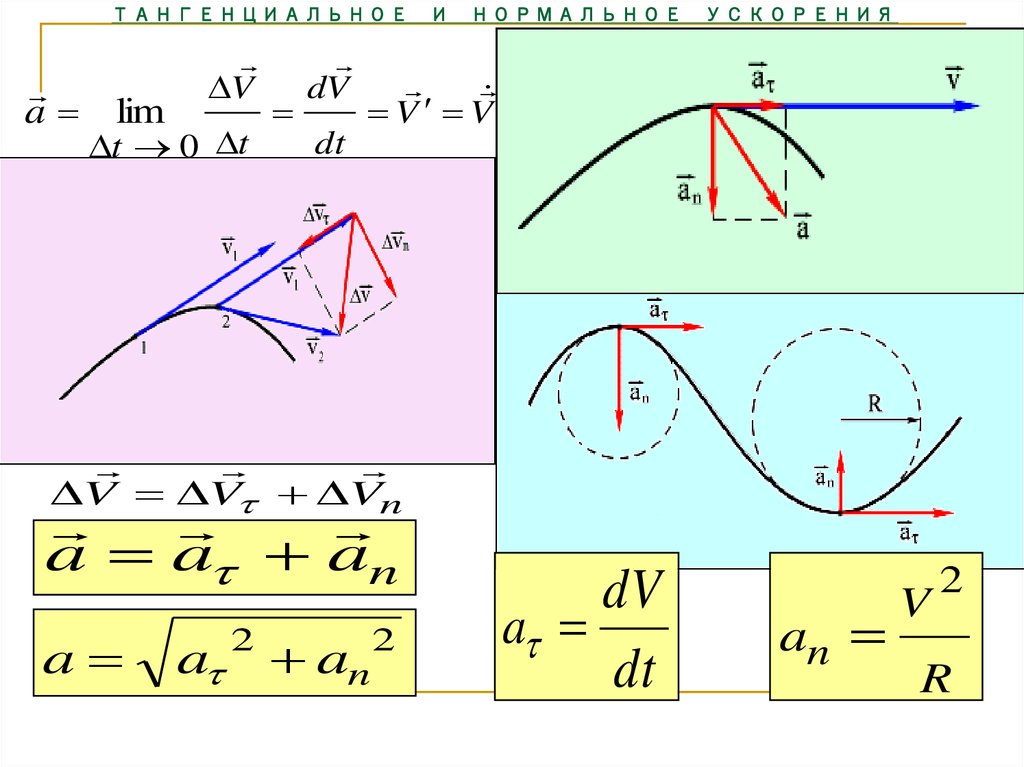

Причиной появления величины a_t¯ является воздействие внешней силы на движущееся тело.

В случае вращения с постоянным угловым ускорением α тангенциальная составляющая ускорения может быть вычислена по следующей формуле:

a_t = α × r

Здесь r – это радиус вращения рассматриваемой материальной точки, для которой вычисляется величина a_t.

Нормальное или центростремительное ускорение

Теперь выпишем еще раз вторую компоненту полного ускорения:

a_c¯ = d (u_t¯) / dt × v

Из геометрических соображений можно показать, что производная единичного касательного к траектории вектора по времени равна отношению модуля скорости v к радиусу r в момент времени t. Тогда выражение выше запишется так:

a_c = v² / r

Эта формула нормального ускорения свидетельствует, что оно, в отличие от касательной компоненты, не зависит от изменения скорости, а определяется квадратом модуля самой скорости. Также a_c возрастает с уменьшением радиуса вращения при постоянной величине v.

Нормальное ускорение называют центростремительным потому, что оно направлено от центра масс вращающегося тела к оси вращения.

Причиной появления этого ускорения является центральная компонента воздействующей на тело силы. Например, в случае вращения планет вокруг нашего Солнца центростремительной силой является гравитационное притяжение.

Нормальное ускорение тела изменяет только направление скорости. Оно не способно изменить ее модуль. Этот факт является важным его отличием от касательной компоненты полного ускорения.

Поскольку центростремительное ускорение возникает всегда, когда вектор скорости поворачивается, то оно существует также в случае равномерного вращения по окружности, при котором тангенциальное ускорение равно нулю.

На практике ощутить на себе влияние нормального ускорения можно, если находиться в машине, когда она совершает затяжной поворот. В этом случае пассажиров прижимает к противоположной направлению поворота двери автомобиля.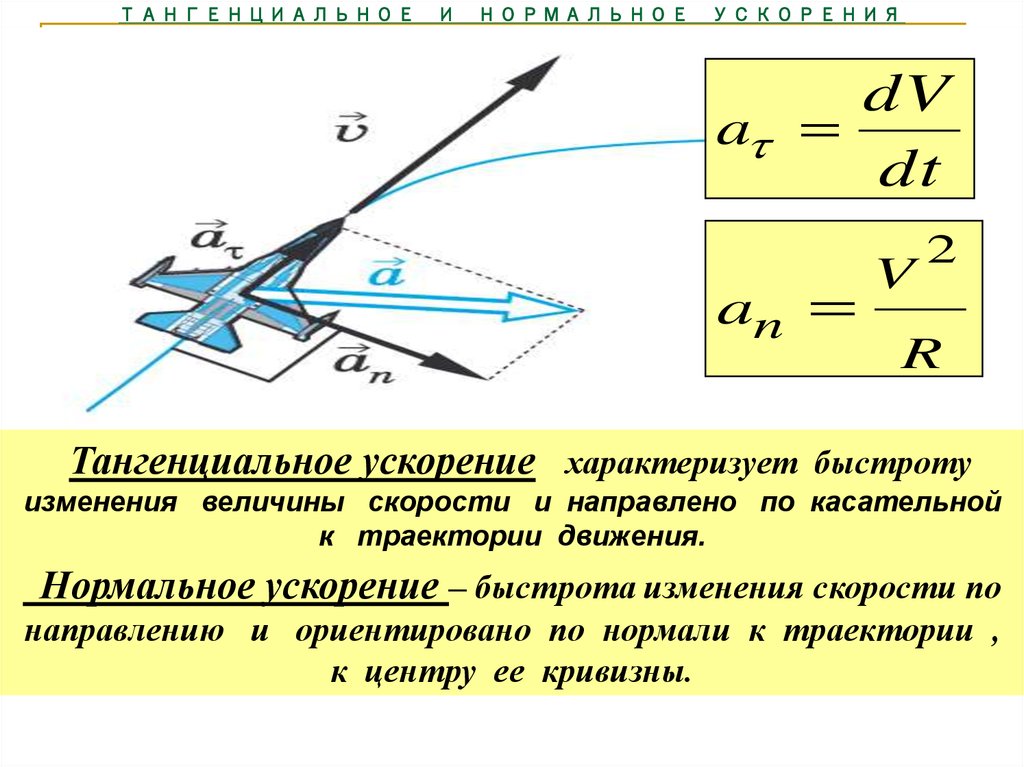 Это явление – результат действия двух сил: центробежной (смещение пассажиров со своих мест) и центростремительной (давление на пассажиров со стороны двери автомобиля).

Модуль и направление полного ускорения

Итак, мы выяснили, что тангенциальная компонента рассматриваемой физической величины направлена по касательной к траектории движения. В свою очередь, нормальная компонента перпендикулярна траектории в данной точке. Это означает, что две компоненты ускорения перпендикулярны друг другу. Их векторное сложение дает вектор полного ускорения. Вычислить его модуль можно по следующей формуле:

a = √(a_t² + a_c²)

Направление вектора a¯ можно определить как относительно вектора a_t¯, так и относительно a_c¯. Для этого следует использовать соответствующую тригонометрическую функцию. Например, угол между полным и нормальным ускорениями равен:

φ = arccos(a_c / a)

Решение задачи на определение центростремительного ускорения

Колесо, которое имеет радиус 20 см, раскручивается с угловым ускорением 5 рад/с² в течение 10 секунд.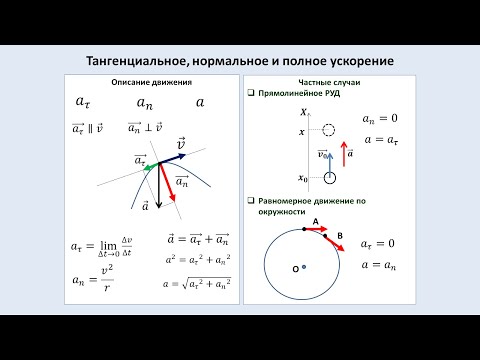 Необходимо определить нормальное ускорение точек, находящихся на периферии колеса, через указанное время.

Для решения задачи воспользуемся формулой связи между тангенциальным и угловым ускорениями. Получаем:

a_t = α × r

Поскольку равноускоренное движение длилось в течение времени t = 10 секунд, то приобретенная за это время линейная скорость была равна:

v = a_t × t = α × r × t

Полученную формулу подставляем в соответствующее выражение для нормального ускорения:

a_c = v² / r = α² × t² × r

Остается подставить известные значения в это равенство и записать ответ: a_c = 500 м/с².

Тангенциальные и нормальные компоненты вектора ускорения — Криста Кинг Математика

Что такое тангенциальная и нормальная составляющие вектора?

В любой заданной точке кривой мы можем найти вектор ускорения ???a??? что представляет собой ускорение в этой точке.

Если мы найдем единичный касательный вектор ???T??? и единичный вектор нормали ???N??? в той же точке, то тангенциальная составляющая ускорения ???a_T??? а нормальная составляющая ускорения ???a_N??? показаны на диаграмме ниже.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Тангенциальная составляющая ускорения

???a_T=\frac{r'(t)\cdot{r”(t)}}{\left|r'(t)\right|}???

Нормальная составляющая ускорения

???a_N=\frac{\left|r'(t)\times{r”(t)}\right|}{\left|r'(t)\right| }???

В этих формулах для тангенциальной и нормальной составляющих

???r(t)??? вектор положения, ???r(t)=r(t)_1\bold i+r(t)_2\bold j+r(t)_3\bold k???

???р'(т)??? является его первой производной, ???r'(t)=r'(t)_1\bold i+r'(t)_2\bold j+r'(t)_3\bold k???

???r”(t)??? является его второй производной, ???r”(t)=r”(t)_1\bold i+r”(t)_2\bold j+r”(t)_3\bold k???

???r'(t)\cdot{r”(t)}??? является точечным произведением первой и второй производных, ???r'(t)\cdot{r”(t)}=r'(t)_1r”(t)_1+r'(t)_2r’ ‘(т)_2+р'(т)_3р”(т)_3???

???\влево|r'(t)\вправо|??? – величина первой производной, ???\left|r'(t)\right|=\sqrt{\left[r'(t)_1\right]^2+\left[r'(t)_2 \right]^2+\left[r'(t)_3\right]^2}???

???\влево|r'(t)\times{r”(t)}\вправо|??? является величиной перекрестного произведения первой и второй производных, где перекрестное произведение ???r'(t)\times{r”(t)}=\begin{vmatrix}\bold i & \bold j & \жирный k\\ r'(t)_1 & r'(t)_2 & r'(t)_3\\ r”(t)_1 & r”(t)_2 & r”(t) _3\конец{vmatrix}???

Начнем с нахождения каждой из частей в списке выше, а затем подставим их в формулы для тангенциальной и нормальной составляющих вектора ускорения.

Как найти тангенциальную и нормальную составляющие вектора ускорения

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Учить больше

Нахождение тангенциальной составляющей и нормальной составляющей векторной функции

Пример

92+16}???

Если мы найдем единичный касательный вектор T и единичный вектор нормали N в одной и той же точке, то мы можем определить тангенциальную составляющую ускорения и нормальную составляющую ускорения.

Наконец, мы получим векторное произведение первой и второй производных, а затем найдем его величину.

???r'(t)\times{r”(t)}=\begin{vmatrix}\bold i & \bold j & \bold k\\ r'(t)_1 & r'(t )_2 & r'(t)_3\\ r”(t)_1 & r”(t)_2 & r”(t)_3\end{vmatrix}??? 92+16}}???

Это тангенциальная и нормальная составляющие вектора ускорения.

Получите доступ к полному курсу Calculus 3

Начать

Изучайте математикуКриста Кинг 25 ноября 2020 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление iii, исчисление iii, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, векторное исчисление, векторное исчисление , векторы ускорения, тангенциальная составляющая ускорения, нормальная составляющая ускорения, тангенциальная и нормальная составляющие, единичный касательный вектор, единичный вектор нормали, векторные произведения, исчисление, исчисление три

0 лайков

многомерное исчисление – Найдите тангенциальную и нормальную составляющие вектора ускорения для кривой

Задавать вопрос

спросил 5 лет, 5 месяцев назад

Изменено 5 лет, 5 месяцев назад

Просмотрено 4к раз 92}=2t+1/t $$

Единичный вектор в направлении скорости равен $$ \vec и(т) = \ гидроразрыва {\ vec v (т)} { v (т)} знак равно \фракция{1}{2т+1/т} < 2,2т,1/т>

$$

Касательная составляющая ускорения $a_T(t)$ находится по формуле $a_T(t) = \vec a(t) \cdot \vec u (t)$

Нормальная составляющая ускорения, Затем $\vec a_N$ можно найти, используя $\vec a(t) = a_T (t) \vec u_T(t) + a_N (t) \vec u_N(t)$.