Техника быстрого счета на пальцах: Ментальная Арифметика на Пальцах

Ментальная арифметика на пальцах | Сложение и вычитание

Каждый родитель мечтает, чтобы его ребенок рос умным, здоровым, успешным. Но как мы развиваем своих детей? Или надеемся только на занятия в детском саду и школе? Для гармоничного развития, укрепления памяти и уверенности в себе, стимулирования внимания детсадовских занятий мало! Здесь на помощь приходит ментальная арифметика. С этой методикой каждый ребенок полюбит математику, разовьет навыки концентрации внимания, быстрого устного счета, зрительной и слухоречевой памяти, гибкости ума, нестандартного мышления. Что это за система, ее плюсы, назначение и особенности – читайте ниже!

Ментальная арифметика. Что это такое

Это система обучения детей быстрому устному счету: сложению и вычитанию, умножению и делению. Мини-занятия можно начинать с детства, особенно эффективно обучаются дети 4-12 лет. Если ваш ребенок старше этого возраста, учиться тоже можно, но времени и усилий потребуется больше. В основе обучения ментальной математике (менар) лежит практика счета на абакусе – специальном инструменте, который имеет давнюю историю.

Где и когда можно заниматься

Методика ментальной арифметики пошаговая, состоящая из 10 уровней, из которых 5 уровней образуют базовую программу детского развития. Каждый уровень длится 4-6 месяцев, а все обучение базовой программы занимает 2-2,5 года.

Заниматься можно не только в специальных группах с педагогом, но и в домашних условиях с родителями. В группах мини-уроки обычно проходят 1-2 раза еженедельно по 30-45 мин. Дома можно упражняться через день по 15-20 мин.

На начальном уровне достигаются следующие цели:

• знакомство и навык работы с абакусом – специальными счетами;
• тренировка памяти, мелкой моторики;
• освоение ментальных карт, их визуализация;
• развитие логического, пространственного мышления.

Навык визуализации является значимым и переходным на следующий уровень. Если ребенок хорошо разовьет навык визуализации, то в дальнейшем быстро и самостоятельно сможет считать без счет в уме (ментально).

На начальном этапе для облегчения процесса используются специальные флеш-карточки, рабочие тетради, упражнения и игровые примеры. Их цели – стимулировать память, навык обращения с числами, запомнить простейшие действия и примеры, чтобы затем выполнять их в уме.

Счеты для ментальной арифметики. Какие и зачем

Потребность человека в количественном измерении, подсчете и математических расчетах появилась задолго до появления чисел. Первым расчетным инструментом, который природа предоставила в распоряжение человека, была его собственная рука/пальцы. Потом считать стали на ракушках, веточках, камешках и так далее.

Позднее, в Римской Империи, Древней Азии и других частях света, человек изобрел простые и быстрые способы счета и вычисления. Счеты или абакус – это древний азиатский вычислительный инструмент, который и в наше время помогает детям овладеть основными математическими навыками. Существует множество различных типов счетов, и во всем мире используются различные терминологии. Так, в Японии абакус широко распространен под названием японский соробан.

Эти счеты состоят из нескольких частей:

• деревянной или пластиковой рамы;
• горизонтальной линейки-разделителя;
• верхней и нижней части со стержнями, на которые нанизаны косточки/бусины.

Японский соборан или абакус напоминает наши, отечественные счеты, которые перевернули на бок.

Как быстро считать на абакусе. Общие правила

В счетах соробан имеет значение каждый элемент! Так:

• на 1-ой спице у нас единицы;
• на 2-ой – десятки;
• на 3-ей – сотни;
• на 4-ой – тысячи и т. д.

На верхних спицах располагаются «небесные» косточки/бусины, на нижних спицах – «земные». Одна «небесная» косточка = 5 «земных». В примерах это звучит так: если на 3-ей спице верхнего ряда отложена одна бусина к линейке, это 500. Если ни одна бусина не касается расчетной разделительной линейки, это ноль.

Чтобы освоить быстрый счет на абакусе удобно пользоваться двумя пальцами: большим и указательным. Нижние бусины поднимаются большим пальцем, а указательным – опускаются вниз. Верхние бусины опускаются и поднимаются указательным пальцем. Процесс со временем доводится до автоматического, и счет становится очень быстрым и правильным.

Существует история, что в конце 1946 года японский почтовый чиновник, весьма искусный в использовании абакуса, вступил в соревнование с иностранным солдатом, который для счета использовал самый современный калькулятор. В четырех из пяти состязаний японский чиновник со счетами оказался быстрее, уступив лишь в сложных задачах.

Сложение и вычитание на абакусе

Прежде всего, нужно научиться откладывать числа на счетах. Например:

• Если нужно 5, на 1ой верхней спице отпускаем 1-ну бусину.
• Если нужно 7, на 1ой верхней спице отпускаем 1-ну бусину, в это же время на нижней спице поднимаем 2-е вверх.
• Если нужно 73, на 2ой верхней спице опускаем бусину, на 2ой нижней – поднимаем 2-е бусины. Получается 70. Из первой нижней поднимаем три бусины. Образуется 73.

После того как дошкольник освоил цифры на абакусе, практику откладывания чисел, можно переходить к примерам простого сложения. Пошагово это происходит так:

Пример 14+25.

Откладываем число: на 2ой нижней спице поднимаем 1-ну бусину, на 1ой нижней – 4. Затем прибавляем 25: на 2ой нижней спице прибавляем 2, на 1ой спице – верхнюю бусину. Получаем результат 39.

Решение примеров вычитания начинается с наибольшего разряда числа (в трехзначных – с сотен, в двузначных – с десятков). Обязательно задействуется верхний блок косточек.

Пример 23 – 11.

С верхней 2ой спицы опускаем 2 бусины, с 1ой нижней поднимаем 3.

На 2ой и 1ой спицах возвращаем по 1-ной бусине.

Уроки ментальной арифметики по набору чисел, сложению/вычитанию можно предварительно смотреть в видео и сразу повторять с ребенком. Это особенно полезно, если занимаетесь сами, дома.

Умножение и деление на абакусе

После освоения сложения и вычитания можно приступать к действиям посложнее – умножению и делению. Важно не забывать, что подсчет производится двумя пальцами – большим и указательным.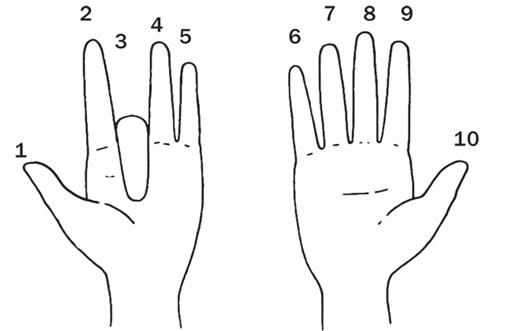

Пример 12 * 21.

Работаем с десятками: с нижней 3ей спицы поднимаем вверх 2-е бусины, 10 * 20 = 200.

Поднимаем на 2ой нижней спице вверх 4-е бусины, умножаем единицы первого числа на десятки, 2 * 20 = 40.

Опускаем на 2ой спице одну верхнюю бусину и все нижние, умножаем десятки первого числа на единицы второго, 10 * 1 = 10.

Поднимаем на 1ой нижней спице вверх 2-е бусины, умножаем единицы первого и второго числа, 2 * 1 = 2.

В результате: 12 * 21 = 252.

По мере тренировки и решения примеров приходит понимание действий, подсчет доводится до автоматизма.

После того, как хорошо усвоено умножение, можно приступать к примерам деления.

Пример 62 : 2.

Выставляем в правой половине счет 62, левая пустая, для ответа.

Делим 6 на 2, получаем 3 и откладываем его на крайней левой спице.

В первой половине на 2ой спице отнимается 6-ть бусин остается 2.

На второй слева спице откладывается 1, которая получилась, когда 2 : 2.

Решение примера получается: 62 : 2 = 31.

Как перейти от абакуса к счету на пальцах

Специальные счеты абакус не всегда будут в ходу. Цель дальнейших этапов – научить ребенка быстро и правильно считать без них, ментально. С помощью методов визуализации ребенок постепенно учится представлять счеты в своем уме, при этом помогая пальцами благодаря мышечной памяти.

Для того, чтобы в последующих уроках начать представлять бусинки, желательно проделывать различные задания, развивающие образное мышление. Например, нахождение различий на картинках, пересказ содержимого в картинке и ответ на вопросы по рисунку, определение фигур на ощупь.

Как правило, обучение ментальной арифметике завершается тем, что ребенок без специальных счет, в уме, быстро решает любые примеры, хорошо запоминает действия, имеет развитое логическое и математическое мышление.

Плюсы и минусы ментальной арифметики

Один из главных плюсов – гармоничное развитие левого и правого полушарий мозга.

Как мы все знаем, наш мозг имеет две части: правое полушарие и левое полушарие Левое управляет логическими, числовыми, аналитическими, последовательными фактами и памятью, в то время как правое отвечает за цвет, музыку, воображение, чувства, рифму, мечтательность и общее мышление. Левое полушарие управляет правыми конечностями, а правое – левыми. И наоборот, действие конечностей также оказывает влияние на развитие мозга.

С помощью магнитно-резонансного теста (МРТ) исследователи доказали, что большинство людей (90%) в мире используют в основном левую сторону мозга для своей повседневной деятельности, включая регулярные школьные занятия. При этом правое полушарие мозга развивается недостаточно, поэтому воображение, фантазия, креативность, гибкость мышления развиты недостаточно.

Таким образом, чтобы повысить общий интеллект головного мозга необходимо межполушарное взаимодействие. Чтобы достичь полного развития мозга, мы и используем ментальную арифметику как средство и счеты как инструмент.

Другие плюсы:

• Обучение ментальной арифметике помогает глубже раскрыть заложенный в детях потенциал, что в дальнейшем станет залогом успешной учебы, творческого развития и счастливого будущего.
• Доказано, что у детей существенно увеличивается качество и скорость усвоения информации и как следствие растет школьная успеваемость, уверенность в собственных силах, самооценка.
• Улучшается усидчивость и концентрация внимания.
• Появляются способности быстро решать задачи.
• Улучшается память.
• Ускоряется понимание других предметов школьной программы и навыки слушания.
• Улучшаются навыки визуализации, воображения.
• Развиваются творческие способности.

Уроки ментальной арифметики разрешены всем, независимо от пола, физической формы, они не имеют медицинских ограничений. Заниматься можно в группе и одному, дома, с родителями. Малыши с 4-х лет уже могут осваивать интересные счеты абакус и заниматься с игровым раздаточным материалом.

Есть ли минусы у ментальной математики? Многие педагоги подчеркивают важность правильного расписания занятий. Не перегрузить, чтобы не спровоцировать утомление и ухудшение результатов запоминания!

Еще один нюанс состоит в том, чтобы заниматься по плану, не перескакивая с темы на тему. В этом случае можно гарантировать стойкий результат и гармоничное развитие ребенка.

В школу с удовольствием

Подготовьте своего дошкольника к занятиям, используя методику ментальной арифметики. Он научится быстро считать, решать примеры и будет уверенно чувствовать себя на уроках. Учителя наверняка отметят гибкость его мышления, тягу к знаниям, которые вы развили с помощью менара!

Рейтинг: 4.5/5 – 2 голосов

Приемы устного счета

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Смирнов Ф. А. 1

---

1МОУ Кременкульская СОШ

Грязнова Т.А. 1

---

1МОУ Кременкульская СОШ

Автор работы награжден дипломом победителя II степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Устный счет – гимнастика для ума. Способы сложения, вычитания, умножения, деления, для производства которых, достаточно устного счета. Мотивацией для выбора темы послужило умения быстро и чётко находить результат математических действий. Говорят, если хотите уметь решать задачи, то должны начать их решать. Научиться считать быстро, считать в уме можно только при большом желании и систематической тренировке в решении задач.

Приёмы устного счёта известны давно. Великолепные способности к устному счёту таких блестящих математиков, как Гаусс, фон Нейман, Эйлер или Валлис, у многих вызывают настоящий восторг. Об этом много написано. Мы хотим рассказать и показать некоторые известные вычислительные секреты. И тогда перед вами откроется совсем другая математика. Живая, полезная и понятная.

Для того чтобы понять, какую роль в нашей жизни играют цифры, поставьте простой эксперимент. Попробуйте некоторое время обойтись без них. Без цифр, без вычислений, без измерений… Вы окажетесь в странном мире, где почувствуете себя абсолютно беспомощным, связанным по рукам и ногам. Как успеть на встречу вовремя? Отличить один автобус от другого? Позвонить по телефону? Купить хлеб, колбасу, чай? Сварить суп или картошку? Без чисел, а значит, без счета жизнь невозможна. Но как тяжело иногда дается эта наука! Попробуйте быстро перемножить 65 на 23? Не получается? Рука сама тянется за мобильником с калькулятором. А, между тем, полуграмотные русские крестьяне 200 лет назад спокойно делали это, пользуясь лишь первым столбиком таблицы умножения – умножением на два. Не верите? А зря.

Это – реальность.

«Компьютер» каменного века

Даже не зная чисел, люди уже пытались считать. Если нашим предкам, обитавшим в пещерах и носившим шкуры, нужно было поменяться чем-либо с соседним племенем, они поступали просто: расчищали площадку и выкладывали, например, наконечник стрелы. Рядом ложилась рыба или горсть орехов. И так до тех пор, пока не заканчивался один из обменных товаров, или глава “торговой миссии” не решал, что уже хватит. Примитивно, но по-своему очень удобно: и не запутаешься, и не обманут.

С освоением скотоводства задачи усложнились. Большое стадо нужно было как-то считать, чтобы знать, все ли козы или коровы на месте. “Счетной машиной” неграмотных, но умных пастухов стала долбленая тыква с камешками. Как только животное покидало загон, пастух клал в тыкву камешек. Вечером стадо возвращалось, и пастух вынимал по камешку с каждым входившим в загон животным. Если тыква пустела, он знал, что со стадом все в порядке.

Если оставались камешки – шел искать потерю.

Когда появились цифры, дело пошло веселее. Хотя еще долго у наших предков в ходу было лишь три числительных: “один”, “пара” и “много”.

Можно ли считать быстрее компьютера? Обогнать устройство, выполняющее сотни миллионов операций в секунду? Невозможно… Но тот, кто говорит так, жестоко лукавит, или просто кое-что умышленно упускает из вида. Компьютер – это лишь набор микросхем в пластике, он не считает сам по себе.

Поставим вопрос по-другому: может ли человек, считая в уме, обогнать того, кто выполняет вычисления на компьютере? И здесь ответ – да. Ведь, чтобы получить ответ от “черного чемоданчика”, данные в него необходимо сначала ввести. Это будет делать человек при помощи пальцев или голосом. А все эти действия имеют ограничения по времени. Непреодолимые ограничения. Сама природа поставила их человеческому телу. Всему – кроме одного органа.

Мозга!

Калькулятор умеет выполнять лишь две операции: сложение и вычитание. Умножение для него – это множественное сложение, а деление – множественное вычитание.

Наш мозг поступает по-другому. Класс, где учился будущий король математики, Карл Гаусс, как-то получил задание: сложить все числа от 1 до 100. Карл написал на своей доске абсолютно правильный ответ, как только учитель закончил объяснять задание. Он не стал прилежно складывать числа по порядку, как поступил бы любой уважающий себя компьютер. Он применил открытую им самим формулу: 101 х 50 = 5050. И это далеко не единственный прием, ускоряющий вычисления в уме.

Актуальность:

Данная тема является одной из самых актуальных. Выработка навыков устного счёта занимает особое место в  школе и является одной из главных задач обучения математике на этом этапе. Именно в первые годы обучения закладываются основные приёмы устных вычислений, которые активизируют мыслительную деятельность учеников, развивают память, речь, способность воспринимать на слух сказанное, повышают внимание и быстроту реакции.

Объект исследования: Математика.

Предмет исследования: Устный счет

Цель:

Узнать о способах и приемах устного счета.

Задачи:

Изучить теорию.

Составить историческую справку по данной теме

Рассмотреть все возможные элементы и приемы устного счета.

Доказать, что эти приемы действительно помогают.

Методы:

Теоретический.

Аналитический.

Гипотеза:

В жизни существует много различных способов и приемов устного счета.

Теоретическая часть

У́стный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т.  п.) и приспособлений (ручка, карандаш, бумага и т. п.).

Процесс устного счёта можно рассматривать как технологию счёта, объединяющую представления и навыки человека о числах, математические алгоритмы арифметики.

Имеются три вида технологии устного счёта, которые используют различные физические возможности человека:

счёт «на пальцах»;

аудиомоторная технология счёта;

визуальная технология счёта.

Характерной особенностью аудиомоторного устного счёта является сопровождение каждого действия и каждого числа словесной фразой типа «дважды два — четыре». Традиционная система счёта является именно аудиомоторной технологией. Недостатками аудиомоторного способа ведения расчётов являются:

отсутствие в запоминаемой фразе взаимосвязей с соседними результатами,

невозможность выделить во фразах о таблице умножения отдельно десятки и единицы произведения без повторения всей фразы;

невозможность обратить фразу вспять от ответа к множителям, что важно для выполнения деления с остатком;

медленная скорость воспроизведения словесной фразы.

Супервычислители, демонстрируя высокие скорости мышления, используют свои визуальные способности и отличную зрительную память. Люди, которые владеют скоростными вычислениями, не используют слов в процессе решения арифметического примера в уме. Они демонстрируют реальность 

визуальной технологии устного счёта, лишённой главного недостатка — замедленной скорости выполнения элементарных действий с числами.

Приемы устного счета

Умножение на 9.

Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9х3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9х3 – это 2), затем посчитайте после загнутого пальца (в нашем случае это 7).

Ответ: 27.

Умножение чисел от 10 до 20.

Можно очень просто умножать такие числа!

К одному из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел.

Например: 11*13=(11+3)*10+1*3=143

Умножение на 11.

Все мы знаем, что при умножении на 10 к числу добавляется 0, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:

Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.

Например: 21*11=231

Вычитание из 1000.

(Представьте, что вы пришли в магазин с крупной купюрой)

Чтобы выполнить вычитание из 1000 и быстро рассчитать сдачу, можете пользоваться этим простым правилом:

– Отнимите от 9 все цифры, кроме последней.

– А последнюю цифру отнимите от 10!

Например: 1000-254

9-2=7

9-5=4

10-4=6

Быстрое возведение в квадрат.

Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и все!

Пример: 252= (2 ∙ (2+1)) добавляем 25

2 ∙ 3 = 6. В ответе получаем 625

Умножение на 101.

Для умножения двузначного числа на 101 надо просто записать число два раза. 34 х 101 = 3434.

Для умножения числа на 4 нужно два раза умножить его на 2. Для деления – дважды разделить на 2.

Умножать на 5 удобнее так: сначала умножить на 10, а потом разделить на 2 посередине сумму (N+A).

При умножении на 1,5 умножаемое нужно разделить пополам и прибавить к умножаемому, например 48×1,5= 48/2+48=72. Можно применить при умножении на 15 48×1,5×10 = 720.

Большинство приемов быстрого счета похоже на фокусы. Много остроумных и, главное, быстрых приемов помогают возводить число в степень, извлекать квадратный корень. Знаменитые “30 приемов Перельмана” для математически мыслящих людей будут покруче шоу Коперфильда, потому что они еще и ПОНИМАЮТ что происходит, и как оно происходит. Ну а остальные могут просто наслаждаться красивым фокусом. Например, нужно перемножить 45 на 37. Напишем числа на листе и разделим их вертикальной чертой. Левое число делим на 2, отбрасывая остаток, пока не получим единицу. Правое – умножаем до тех пор, пока число строчек в столбике не сравняется. Затем вычеркиваем из ПРАВОГО столбика все те числа, напротив которых в ЛЕВОМ столбике получился четный результат. Оставшиеся числа из правого столбика складываем. Получится 1665. Перемножьте числа привычным способом. Ответ сойдется.

1.2 Соревнования по устному счёту

В настоящее время в прибалтийских странах,  Словении  и  Украине  проводятся соревнования по устному счёту среди школьников под названием Пранглимине (эст. Pranglimine). Начиная с 2004 года проводятся международные соревнования среди школьников и взрослых. В 2016 году соревнования прошли в Мурска-Собота (Словения).

Начиная с 2004 года, один раз в два года проводится Мировой чемпионат по вычислениям в уме. Соревнования проводятся по решению таких задач, как сложение десяти 10-значных чисел (по правилам 2016 года даётся 7 минут на это задание), умножение двух 8-значных чисел за 10 минут, расчёт дня недели по григорианскому календарю по заданной дате с 1600 по 2100 годы (1 минута), корень квадратный из 6-значного числа за 10 минут (результат должен быть представлен с точностью до 8 знаков после запятой). Также определяется победитель в категории «Лучший универсальный счётчик» по итогам решения шести неизвестных «задач с сюрпризом». К заявке на участие прикладываются результаты в интеллектуальных видах спорта и результат в программах Memoriad, подтверждёные кем-то (например, учителем математики). Ограничения по возрасту нет, не делается также различий между полами. Участник начинает выполнение каждого задания с команды «Нейроны готовсь, пошли» (Neurons: On the ready, go). Чемпионат в 2018 году прошёл 28—30 сентября 2018 года в Научном центре Phæno в Вольфсбурге, Германия по таким правилам.

Memoriad (MEntal math + meMORy + olimpIAD) — международная олимпиада по устному счёту, запоминанию и скорочтению, проводится раз в 4 года (совпадает по годам с летними Олимпийскими играми). Среди заданий по устному счёту: умножение 5-, 8- и 20-значных чисел, деление 10-значных чисел на 5-значные, извлечение квадратного корня из 6-, 8- и 10-значного числа, сложение 250 двухзначных чисел с показом каждого числа 0,6 секунды. Среди других заданий: запоминание бинарных чисел, десятичных чисел за определённое время (от 1 минуты до 1 часа).

1.3 Устный счёт в искусстве

В России хорошо известна картина русского художника Николая Богданова-Бельского  «Устный счёт в народной школе С. А. Рачинского» (рис.7), написанная в 1895 году. Приведённая на доске задача, над которой размышляют ученики, требует достаточно высоких навыков устного счёта и смекалки.

Феномен быстрого счёта больного аутизмом раскрывается в фильме «Человек дождя» (рис. 5) Барри Левинсона и в фильме «Пи» (рис. 3) Даррена Аронофски. Барри Левинсон (рис. 4) (англ. Barry Levinson; род. 6 апреля 1942) — американский кинорежиссёр, сценарист и продюсер. Лауреат премии «Оскар» 1989 года.

Да́ррен Ароно́фски (англ. Darren Aronofsky; род. 12 февраля 1969, Бруклин, Нью-Йорк, США) — американский кинорежиссёр, сценарист и продюсер (рис. 6).

Заключение

Приемы быстрого счета способны здорово облегчить жизнь и ребенку в школе, и маме в магазине или на кухне, и папе на производстве или в офисе. Самый простой способ тренировки и, одновременно, разминки мозга: устный счет вслух (обязательно!) через число до ста и обратно. Утром, стоя под душем, или готовя завтрак, посчитайте: 2.. 4.. 6.. 100… 98.. 96. Можно считать через три, через восемь – главное, делать это вслух. Всего через пару недель регулярных занятий вы удивитесь, насколько ПРОЩЕ станет обращаться с числами. Знания математики нужны всем – и ученикам, и учителям. Способ устного выполнения математических действий влияет на качество (наличие или отсутствие ошибок при вычислении). Также способ выполнения влияет на время проведения расчетов: знание определенных трюков для быстрого вычисления, конечно же, сокращает время выполнения задания.

Источники

http://www.calculator888.ru/blog/matematika/ustnyi-schet.html

https://xn--j1ahfl.xn--p1ai/library/nestandartnie_priemi_ustnogo_scheta_111544.html

https://4brain.ru/schitat-v-ume/

https://ru.wikipedia.org/wiki/%D0%A3%D1%81%D1%82%D0%BD%D1%8B%D0%B9_%D1%81%D1%87%D1%91%D1%82

Приложение 1

Рис. 1 Рис.2

Рис. 3 Рис. 4 Рис. 5

Рис. 6 Рис. 7

Просмотров работы: 4427

Приемы быстрого счета без калькулятора

18 мая, 2013

Автор: Maksim

Хоть и считается, что математика наводит ужас на значительную часть населения, но деньги считать умеют все. И вот как раз влет это умеют делать люди, далекие от математики.

Помнится, бабушка моего мужа показывала ему на пальцах таблицу умножения на 9. Никакого образования, только огромная практика торговли редиской и клубникой на рынке!

Так вот сегодня я предлагаю вам несколько интересненьких приемов устного счета. Ведь сколько бы замечательных гаджетов (телефоны, смартфоны, айподы и айпады, ай, да чего там…) своя голова она всегда лучше.

Содержание

• 1 Устный счет — приемы
  • 1.1 1. Умножение на 11
  • 1.2 2. Быстрое возведение в квадрат
  • 1.3 3. Умножение на 5
  • 1.4 4. Умножение на 9
  • 1.5 5. Умножение на 4
  • 1.6 6. Подсчет чаевых
  • 1.7 7. Сложное умножение
  • 1.8 8. Деление на 5
  • 1.9 9. Вычитание из 1000
  • 1.10 Интересные результаты:
  • 1.11 Любимая цифра.
  • 1.12 Угадать возраст.
  • 1.13 Всегда девятка

Итак, читаем, тут же проверяем и запоминаем приемы вычисления в уме.

1. Умножение на 11

Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:

53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583

59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649

2. Быстрое возведение в квадрат

Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.

85 х 85 = 7225
Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
Шаг 2 — Дописываем к получившемуся результату 25: 7225

45 x 45 = 2025
Шаг 1 — 4 х (4 + 1) = 20
Шаг 2 — 2025

3.

Умножение на 5

Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.

Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.

Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435

4. Умножение на 9

Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

5. Умножение на 4

Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58×4 = (58×2) + (58×2) = (116) + (116) = 232

6. Подсчет чаевых

Если вам нужно оставить 15% чаевых, есть простой способ сделать это.

Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75

И, как следствие):  чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину. Например,

34*1,5 = 34+17=51

125*1,5= 125+62,5=187,5

7. Сложное умножение

Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 все равно, что:
16×250 все равно, что:
8×500 все равно, что:
4×1000 = 4,000

8. Деление на 5

На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956
Шаг2: 595,6

9. Вычитание из 1000

Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:

1000-648

Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352

И, напоследок, несколько математических трюков:

Интересные результаты:

1 х 1 = 1
11 х 11 = 121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 = 123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321

1 х 9 + 2 = 11
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
123456789 х 9 + 10 = 1111111111

9 х 9 + 7 = 88
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888

1 х 8 + 1 = 9
12 х 8 + 2 = 98
123 х 8 + 3 = 987
1234 х 8 + 4 = 9876
12345 х 8 + 5 = 98765
123456 х 8 + 6 = 987654
1234567 х 8 + 7 = 9876543
12345678 х 8 + 8 = 98765432
123456789 х 8 + 9 = 987654321

Любимая цифра.

Предложите  задумать свою любимую цифру. А теперь выполните умножение (на калькуляторе) числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то умножить нужно на 35. Получится произведение, записанное только любимой цифрой.

Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45.

Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.

Угадать возраст.

Умножаем число своих лет на 10, затем любое однозначное число умножить на 9,  из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.

Всегда девятка

Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке. Затем вычесть меньшее из большего. Когда зритель это сделает, скажите ему, что в середине числа стоит девятка.

Секрет фокуса: Вы будете правы, потому что девятка всегда будет в середине независимо от того, какие цифры написаны.

Глава 5

Цели

К концу этого урока вы сможете…

1. решать задачи на счет, используя правило умножения
2. решить задачи на подсчет, используя перестановки
3. решать задачи на счет, используя комбинации
4. решать задачи на подсчет, связанные с перестановками с неразличимыми элементами
5. вычислить вероятности с участием перестановок и комбинаций

Для быстрого ознакомления с этим разделом посмотрите этот короткий видеоролик:

Помните классический метод расчета вероятностей из раздела 5. 1?

P(E) =	количество способов появления E	=	С(В)
	общее количество возможных исходов		Н(С)

Что ж, иногда подсчет «количества случаев, когда E может произойти» или «общее количество возможных исходов» может быть довольно сложным. В этом разделе мы изучим несколько методов подсчета, которые помогут нам рассчитать некоторые из более сложных вероятностей.

Правило счета умножения

Предположим, вы готовитесь к свадьбе и вам нужно выбрать смокинги для жениха. На складе мужских смокингов есть функция Build-A-Tux, которая позволяет вам просматривать определенные комбинации и создавать свой смокинг онлайн. Предположим, у вас есть компоненты, сузившиеся до двух жакетов, двух комбинаций жилета и галстука и трех цветов рубашки. Сколько всего комбинаций может быть?

Хорошим способом помочь понять ситуацию такого типа является так называемая древовидная диаграмма . Мы начинаем с выбора жакета, а затем каждый жакет «разветвляется» на две комбинации жилета и галстука, а затем каждая из них «разветвляется» на три комбинации рубашки. Это может выглядеть примерно так:

Всего у нас есть 12 возможных комбинаций курток, жилетов и рубашек. (Конечно, некоторые могут не соответствовать вашему вкусу, но это уже другой вопрос…)

Нет ли более простого способа сделать это? Почему да, есть! Подумайте об этом так: для каждого варианта куртки есть два варианта жилета и галстука. Это дает нам 4 комбинации пиджака и жилета/галстука. Затем для каждого из этих есть три варианта выбора рубашки, что дает нам в общей сложности 12.

В общем, мы умножаем количество способов сделать каждый выбор, так что…

общее количество нарядов = (количество курток)•(количество жилетов/галстуков)•(количество рубашек)

Это приводит нас к правилу подсчета умножения:

Правилу подсчета умножения

Если задача состоит из последовательности вариантов выбора, в которой есть p способов сделать первый выбор, q способов сделать второй второй и т. д., то задание можно выполнить

p•q•r• …

разными способами.

Давайте попробуем несколько примеров.

Пример 1

Сколько 7-значных номерных знаков возможно, если первые три символа должны быть буквами, а последние четыре должны быть цифрами от 0 до 9, а повторяющиеся символы разрешены?

[ раскрыть ответ ]

Общее количество номерных знаков будет:

(# вариантов для 1-го символа)• (# вариантов для 2-го символа) • и т. д..

= 26•26•26•10• 10•10•10 = 175 760 000

Пример 2

Источник: Sears

У многих гаражных ворот снаружи есть клавиатура удаленного доступа. Предположим, вор подходит к определенному гаражу и замечает, что четыре конкретных числа используются хорошо. Если предположить, что код использует все четыре числа ровно один раз, сколько 4-значных кодов должен попробовать вор?

[ раскрыть ответ ]

Не очень много!

общее количество кодов = (# вариантов для 1-й цифры)•(# для 2-й цифры) • и т. д.

= 4•3•2•1 = 24

Обратите внимание, что количество вариантов уменьшилось на единицу для каждой цифры, поскольку четыре числа использовались только один раз. Вы часто будете видеть, что это описывается либо как число, выбранное «без замены», либо как «повторение не разрешено».

 

Пример 2 из предыдущего раздела является примером особой техники подсчета, называемой перестановка . Вместо того, чтобы давать вам формулы и примеры, я хотел бы еще раз сослаться на некоторые материалы с одного из моих любимых веб-сайтов BetterExplained. Вот что пишет о перестановках автор Калид Азад:

Перестановки: волосатые подробности

Начнем с перестановок, или всех возможных способов что-то сделать. Мы используем модный термин «перестановка», поэтому позаботимся о каждой детали, включая порядок элементов. Допустим, у нас есть 8 человек:

1. Алиса
2. Боб
3. Чарли
4. Дэвид
5. Ева
6. Фрэнк
7. Джордж
8. Горацио

Сколькими способами мы можем получить золотую, серебряную и бронзовую медаль для «Лучшего друга в мире»?

Мы собираемся использовать перестановки, так как порядок, в котором мы раздаем эти медали, имеет значение.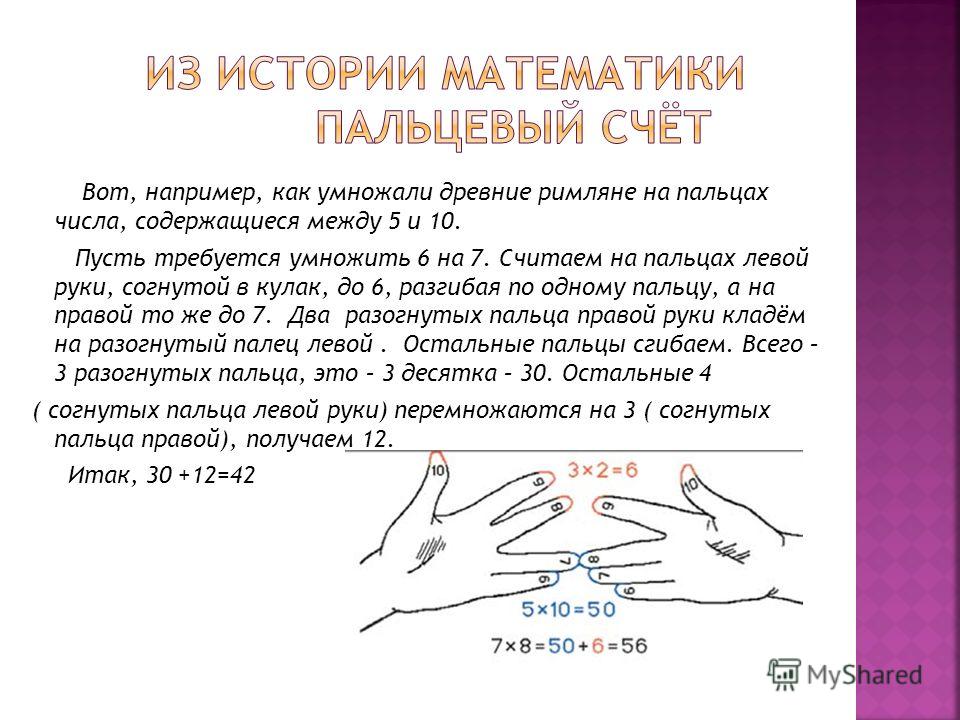 Вот как это происходит:

• Золотая медаль: 8 вариантов: A B C D E F G H (Умно, как я сопоставил имена с буквами, а?). Допустим, А выигрывает золото.
• Серебряная медаль: 7 вариантов: B C D E F G H. Допустим, B выиграет серебро.
• Бронзовая медаль: 6 вариантов: C D E F G H. Скажем… C выигрывает бронзу.

Мы выбрали определенных людей, чтобы выиграть, но детали не имеют значения: у нас было сначала 8 вариантов, затем 7, затем 6. Всего вариантов было 8 * 7 * 6 = 336.

Давайте посмотрим на детали. Пришлось заказывать 3 человека из 8. Для этого мы начинали со всех вариантов (8) потом забирали их по одному (7, потом 6) пока не кончились медали.

Мы знаем, что факториал равен:

К сожалению, это слишком много! Нам нужно только 8 * 7 * 6. Как мы можем «остановить» факториал на 5?

Вот где перестановки становятся крутыми: обратите внимание, как мы хотим избавиться от 5*4*3*2*1. Какое другое название для этого? 5 факториал!

Итак, если мы сделаем 8!/5! получаем:

А почему мы использовали цифру 5? Потому что она осталась после того, как мы взяли 3 медали из 8. Таким образом, лучше записать это так:

, где 8!/(8-3)! — это просто причудливый способ сказать: «Используйте первые 3 числа из 8!». Если у нас всего n предметов и мы хотим выбрать k в определенном порядке, мы получим:

просто означает «Используйте первые k чисел из n!»

А вот и причудливая формула перестановки: у вас есть n элементов, и вы хотите найти число способов k позиции можно заказать:

Источник: BetterExplained, Калид Азад
Артикул: Легкие перестановки и комбинации
Используется с разрешения.

Кстати, в вашем тексте используется обозначение _n P _k , а не P(n,k) Калида. Я видел, как используются оба, хотя последний, как правило, более распространен на уроках математики более высокого уровня. Мы будем придерживаться версии учебника, просто чтобы быть последовательными.

Перестановки

n различных объектов, взятых r одновременно

Количество комбинаций r объектов, выбранных из n объектов в котором

1. n объектов различны,
2. повторы не допускаются,
3. порядок имеет значение,

находится по формуле .

Хорошо, попробуем пару.

Пример 3

Предположим, организация избирает своих должностных лиц из попечительского совета. Если есть 30 попечителей, сколькими способами правление может избрать президента, вице-президента, секретаря и казначея?

[ раскрыть ответ ]

В этом примере у нас есть 30 «предметов» (доверенных лиц), из которых мы выбираем 4. Используя обозначения из вашего текста, мы хотим вычислить ₃₀ P ₄ , или

30 P 4 =	30!	=	30!	= 30•29•28•27 = 657 720
	(30-4)!		26!

Пример 4

Предположим, вам дан список из 100 десертов и вас попросили оценить ваши 3 лучших. Сколько существует возможных списков «3 лучших»?

[ раскрыть ответ ]

100 P 3 =	100!	=	100!	= 100•99•98 = 970 200
	(100-3)!		97!

На предыдущей странице мы говорили о количестве способов выбрать k предметов из n , если порядок имел значение – например, вручение медалей, избрание офицеров или маринование любимых десертов. Что, если порядок не имеет значения, как выбор членов комитета?

Опять же, я позволю Калиду Азаду объяснить.

Комбинации, Хо!

Комбинации легки. Порядок не имеет значения. Вы можете смешать это, и это будет выглядеть так же. Допустим, я скряга и не могу позволить себе отдельные золотые, серебряные и бронзовые медали. На самом деле, я могу позволить себе только пустые жестяные банки.

Сколькими способами я могу раздать 3 консервные банки 8 людям?

Ну, в данном случае порядок, в котором мы выбираем людей, не имеет значения. Если я даю банку Алисе, Бобу, а затем Чарли, это то же самое, что дать Чарли, Алисе, а затем Бобу. В любом случае, они будут одинаково разочарованы.

Это поднимает и интересный момент — у нас здесь есть некоторые излишества. Элис Боб Чарли = Чарли Боб Элис. На минутку давайте просто выясним, сколькими способами мы можем переставить 3 человек.

Итак, у нас есть 3 варианта для первого человека, 2 для второго и только 1 для последнего. Итак, у нас есть 3*2*1 способа переставить 3 человека.

Минуточку… это немного похоже на перестановку! Ты обманул меня!

Действительно. Если у вас есть N человек, и вы хотите знать, сколько аранжировок существует для всех из них, это просто N факториал или N!

Итак, если у нас есть 3 жестяных банки для раздачи, их будет 3! или 6 вариантов для каждого выбора, который мы выбираем. Если мы хотим выяснить, сколько комбинаций у нас есть, мы просто создаем все перестановки и делим на все избыточности . В нашем случае мы получаем 336 перестановок (сверху), делим на 6 избыточностей для каждой перестановки и получаем 336/6 = 56,9.0005

Общая формула:

, что означает «Найдите все способы выбрать k людей из n и разделите на k! варианты». Записав это, мы получим нашу формулу комбинации , или количество способов объединить k элементов из набора n:

Источник: BetterExplained, Калид Азад
Артикул: Легкие перестановки и комбинации
Используется с разрешения.

Кстати, в вашем тексте используется обозначение _n C _k , а не C(n,k) Калида. Как и в случае с перестановками, мы будем придерживаться версии из учебника, просто чтобы быть последовательными.

Комбинации

N отдельные объекты, взятые R за время

Количество объектов N с использованием R ≤ N из них, в которых

1. N объекта, в которых
   1. ,
   2. повторы не допускаются,
   3. порядок не имеет значения,

   находится по формуле .

   Хорошо, давайте попробуем этот новый.

   Пример 5

   Рассмотрим снова попечительский совет из 30 членов. Сколькими способами правление может избрать четырех членов финансового комитета?

   [ раскрыть ответ ]

   В этом примере у нас есть 30 «элементов» (доверенных лиц), из которых мы выбираем 4. В отличие от примера 3, в этом примере порядок не имеет значения, поэтому мы рассматриваем комбинация, а не перестановка.

   30 C 4 =	30!	=	30!	=	30•29•28•27	= 27 405
   	(30-4)!•4!		26!4!		4•3•2•1

   Вы можете заметить, что это число немного меньше, чем в примере 3. Причина в том, что сейчас нас не волнует порядок, поэтому выбор попечителей A, B, C и D для комитета ничем не отличается от избрание попечителей B, C, A и D. Это отличается от примера 3, где мы избирали их на определенные должности.

   Пример 6

   Источник: stock.xchng

   Предположим, вы организатор волейбольного турнира. На турнир зарегистрировалось 10 команд, и кажется хорошей идеей, чтобы каждая команда сыграла с каждой командой по круговой системе, прежде чем выйти в плей-офф. Сколько игр возможно, если каждая команда сыграет с каждой другой командой один раз?

   [ раскрыть ответ ]

   Сначала это может показаться не комбинацией, но давайте посмотрим поближе. У нас есть 10 «предметов» (команд), из которых мы выбираем 2. Порядок нам не важен, так как команда А играет с командой Б так же, как команда Б играет с командой А. Это именно комбинация!

   10 C 2 =	10!	=	10!	=	10•9	= 45
   	(10-2)!•2!		8!2!		2•1

   Ух ты, сколько игр! Вот почему большинство турниров имеют структуру «пула» и разбивают турнир на два «пула» по 5 игроков. 0005

   Подробнее о круговой системе турниров можно узнать в Википедии.

   Второй тип встречается реже. Что, если мы хотим узнать, сколько способов упорядочить n объектов, но не все они различны? Вот пример для иллюстрации:

   Пример 7

   Сколькими способами можно переставить буквы в слове СТАТИСТИКА?

   Ответ немного сложен. Думайте о переставленных словах как о местах для букв. Что-то вроде этого:

   В СТАТИСТИКЕ у нас есть следующие буквы:

   3 S
   3 T
   2 я
   1 А
   1 C

   На самом деле мы не можем сказать, что есть 4 варианта выбора для первой буквы и исходить оттуда, так как количество вариантов для второй буквы зависит от того, какая буква была выбрана для первой.

   Вместо этого мы выбираем точки для каждой из букв. Сначала выберите 3 из 10 мест для буквы S. Мы можем сделать это в ₁₀ C ₃ способов. Затем выберите 3 места для 3 Т. Мы можем сделать это ₇ C ₃ способами. Точно так же мы можем выбрать места для букв I, A и C способами ₄ C ₂ , ₂ C ₁ и ₁ C ₁ соответственно. Итого, значит переставляем буквы так:

   ₁₀ C ₃ • ₇ C ₃ • ₄ C _{2 90} • _{0 09 1} C ₁ способы

   Это может быть только я, это действительно грязный. Как ни странно, выписывание комбинаций показывает хороший способ их упростить:

   10!	•	7!	•	4!	•	2!	•	1!	=	10!
   7!•3!		4!•3!		2!•2!		1!•1!		1!•0!		3!•3!•2!•1!•1!

   Перестановки с неразличимыми элементами

   Количество перестановок n объектов, где имеется n1 объектов 1-го типа, n2 объектов 2-го типа и т. д., равно

   Один быстрый пример:

   Пример 8

   Сколькими способами можно переставить слово ПЕРЕСТРОЙКА?

   [ раскрыть ответ ]

   Кстати говоря, это то же самое, что и в предыдущем примере. В этом случае у нас есть 3 R, 2 A, 2 E, 1 N и 1 G. Таким образом, общее количество перестановок:

   9!	= 15 120
   3!•2!•2!•1!•1!

    

   Как быстро считать деньги – счетные машины с гвоздиками

   • 07, 20 декабря
   • 0 комментариев

   Содержание

   • Как считать купюры
   • Как считать монеты
   • Подсчет денег вручную и использование счетных машин
   • Советы по быстрому подсчету денег
   • Заключение

   Умение быстро считать деньги является важным навыком, если вы имеете дело с большими суммами наличных денег каждый день. Существует множество методов подсчета денег, которые можно использовать для обеспечения максимальной производительности. Для быстрого подсчета денег можно использовать ручные или автоматические методы, и эти методы будут рассмотрены в следующей статье.

   Существует множество методов, которые можно использовать при ручном пересчете денег. Однако они различаются в зависимости от того, какие деньги пересчитываются – монеты или купюры.

   • Разбивка стопок по номиналу. Разделение стопок на 1-долларовые, 5-долларовые, 10-долларовые купюры и т. д. помогает обеспечить быстрый подсчет.
   • Убедитесь, что долларовые купюры обращены лицевой стороной вверх — это может быть сделано, когда вы разбиваете стопки на разные номиналы. Это не только упрощает подсчет денег, но и упорядочивает ваши заметки в процессе.
   • Подсчитайте отдельные купюры, передавая их из рук в руки – возьмите стопку купюр и держите их в неосновной руке. Используйте свой указательный палец и основной большой палец, чтобы держать верхнюю часть купюры, чтобы убедиться, что вы держите только одну купюру. Считая каждую купюру, кладите ее на ровную поверхность, считая в соответствии с достоинством стопки.
   • Разделите пересчитанные купюры на стопки по 50 – используйте резиновую ленту, чтобы закрепить каждую стопку одного номинала. Перед этим шагом будет полезно сначала рассчитать, какой будет денежная стоимость, если она составляет 50 каждого номинала.
   • Сложите все стопки и все остатки. Сложите все стопки вместе, а затем все оставшиеся купюры. Может быть удобнее использовать калькулятор при сложении стеков вместе.
   • Разбивайте монеты по номиналу – Разделяйте монеты на стопки одного номинала.
   • Выберите сумму в долларах для подсчета ваших монет. Выберите сумму в долларах, которую будет легко сложить после того, как все ваши стопки будут созданы. Сумма в долларах будет меняться в зависимости от номинала каждой монеты.
   • Создавайте одинаковые стопки — создавайте одинаковые стопки каждого номинала, используя исходную стопку в качестве ориентира. Денежная стоимость каждого стека не имеет значения. Важно, чтобы в каждой стопке было одинаковое количество монет. Любые лишние монеты могут быть организованы в отдельную стопку, которую вы можете отложить.
   • Подсчитать общее количество стопок и дополнительных монет. Здесь вы будете подсчитывать денежную стоимость стопки каждого номинала. После этого подсчитайте количество дополнительных монет.
   • Добавить все стопки номиналов — сложите вместе все суммы из стопок каждого номинала. Будет проще всего сложить общую стоимость ваших монет, используя калькулятор и отслеживая стоимость каждой стопки, записывая ее на листе бумаги.

   Машины для подсчета денег — это самый быстрый способ подсчета денег, который можно использовать в различных условиях, связанных с обработкой больших сумм наличных денег. Сюда входят банки, розничные магазины и кинотеатры. По мере развития технологий появились машины для подсчета денег, которые теперь более портативны и совместимы с малым бизнесом, а также полезны для частных лиц. Они позволяют вам сортировать купюры разных номиналов с предельной точностью и скоростью в различных условиях. Ручной счет никогда не будет таким быстрым и точным, как машина для счета денег, поскольку всегда возможна человеческая ошибка. Тем не менее, техники и советы по быстрому пересчету денег, упомянутые в этой статье, всегда полезно знать тем, кто работает с наличными каждый день и может не иметь доступа к машинам для счета денег

   • Сосчитайте пальцами группами по пять штук. Сложите стопку купюр одного номинала вертикально, убедившись, что все 4 угла купюры обращены вниз. Затяните сложенную стопку указательным и большим пальцами с обеих сторон. Когда вы начнете считать, вращайте каждую купюру большим и указательным пальцами другой руки, чтобы прижать сложенную стопку и распутать каждую купюру по одной. Повторяйте эти действия, пока не распутаете и не сосчитаете всю стопку.
   • Потяните каждую купюру, используя противоположный большой палец. Большим пальцем держите стопку вертикально сложенных купюр одного номинала, убедившись, что их углы обращены вверх. Закрепите стопку, удерживая противоположный указательный палец на задней части стопки. Большим пальцем той же руки вытащите первую купюру из захвата другого большого пальца. Это можно сделать, проведя пальцем сбоку. Когда вы проводите по каждой купюре, не забудьте их пересчитать.
   • Обмен купюрами с резиновой лентой между руками – Наденьте резинку на середину стопки купюр одного номинала. Опустите стопку горизонтально на стол перед собой. Левую руку нужно положить на левую сторону стопки, следя за тем, чтобы были вытянуты только указательный и средний пальцы. Держите правый угол стопки правой рукой. Переместите большой палец правой руки влево от купюры, чтобы передать одну купюру. Переключайтесь между использованием левого указательного пальца и левого среднего пальца, чтобы держать каждую банкноту. Убедитесь, что считаете точно, когда вы делаете это.

   В этой статье показаны различные существующие способы быстрого подсчета денег. Некоторые методы ручного подсчета денег поначалу могут показаться сложными, но как только вы освоите их, это станет очень полезным жизненным навыком. Существует также большое разнообразие зарекомендовавших себя и технологически продвинутых машин для подсчета денег, которые можно использовать, если вы ищете простой способ подсчета денег, который также удобен и надежен. Деньги всегда нужно будет считать; это сводится к личным предпочтениям, какой метод вы выберете для выполнения работы.

   Поделиться :

   Старый пост Новое сообщение

   jsprice jsprice

   FROM_JS

   FROM_JS

   5.3a. Методы подсчета | Конечная математика |

   Подсчет? Вы уже умеете считать, иначе вы бы не посещали уроки математики в колледже, верно? Ну да, но что мы действительно будем исследовать здесь, так это способы подсчета 9.0005

   эффективно . Когда мы перейдем к вероятностным ситуациям чуть позже в этой главе, нам нужно будет подсчитать около очень больших чисел, например количество возможных выигрышных лотерейных билетов. Один из способов сделать это — записать все возможные наборы чисел, которые могут появиться на лотерейном билете, но поверьте мне: вы не хотите этого делать.

   Мы начнем, однако, с некоторых более разумных задач на счет, чтобы развить идеи, которые нам скоро понадобятся.

   Пример 1

   Предположим, в каком-то ресторане у вас есть три варианта аперитива (суп, салат или хлебные палочки) и пять вариантов основного блюда (гамбургер, бутерброд, пирог с заварным кремом, фахита или пицца). Если вам разрешено выбирать ровно по одному продукту из каждой категории для вашего обеда, сколько различных вариантов еды у вас есть?

   Решение 1

   Одним из способов решения этой проблемы будет систематический список всех возможных приемов пищи:

   суп + гамбургер	суп + бутерброд	суп + пирог с заварным кремом
   суп + фахита	суп + пицца	салат + гамбургер
   салат + бутерброд	салат + пирог с заварным кремом	салат + фахита
   салат + пицца	хлебные палочки + гамбургер	хлебные палочки + бутерброд
   хлебные палочки + пирог с заварным кремом	хлебные палочки + фахита	хлебные палочки + пицца

   Если предположить, что мы делали это систематически и что мы не упустили ни одной возможности и не указали ни одной возможности более одного раза, ответ будет 15. Таким образом, вы можете ходить в ресторан 15 ночей подряд и каждый вечер есть разные блюда.

   Решение 2

   Другим способом решения этой проблемы является перечисление всех возможных вариантов в таблице:

   	гамбургер	сэндвич	пирог с заварным кремом	фахита	пицца
   суп	суп+бургер
   салат	салат+бургер
   хлеб	и т. д.

   В каждой из ячеек таблицы мы могли бы указать соответствующий прием пищи: суп + гамбургер в левом верхнем углу, салат + гамбургер под ним и т. д. Но если бы нам было все равно

   сколько возможных приемов пищи, только сколько возможных приемов пищи, мы могли бы просто подсчитать количество клеток и получить ответ 15, который соответствует нашему ответу из первого решения. (Всегда хорошо, когда вы решаете проблему двумя разными способами и получаете один и тот же ответ!)

   Решение 3

   У нас уже есть два совершенно хороших решения. Зачем нам третий? Первый метод был не очень систематичен, и мы легко могли упустить его. Второй способ был лучше, но предположим, что помимо закуски и основного блюда мы еще больше усложнили задачу, добавив в меню десерты: мы использовали строки таблицы для закусок и столбцы для основных блюд — куда денутся десерты? Нам понадобится третье измерение, а поскольку рисовать трехмерные таблицы на двухмерной странице или на экране компьютера не так уж и просто, нам нужен лучший способ, если у нас есть три категории для выбора формы вместо двух.

   Итак, вернемся к проблеме в примере. Что еще мы можем сделать? Давайте нарисуем

   древовидную диаграмму :

   Это называется диаграммой «дерево», потому что на каждом этапе мы разветвляемся, как ветви на дереве. В этом случае мы сначала нарисовали пять веток (по одной на каждое основное блюдо), а затем на каждую из этих веток нарисовали еще три ветки (по одной на каждую закуску). Считаем количество ветвей на финальном уровне и получаем (сюрприз, сюрприз!) 15.

   Если бы мы хотели, то могли бы вместо этого на первом этапе нарисовать три ветки для трех закусок, а затем пять ветвей (по одной на каждое основное блюдо ), ответвляясь от каждой из этих трех ветвей.

   Итак, теперь мы знаем, как считать возможности с помощью таблиц и древовидных диаграмм. Эти методы по-прежнему будут полезны в некоторых случаях, но представьте себе игру, в которой у вас есть две колоды карт (по 52 карты в каждой) и вы выбираете по одной карте из каждой колоды. Вы действительно хотите нарисовать таблицу или древовидную диаграмму, чтобы определить количество исходов этой игры?

   Вернемся к предыдущему примеру, в котором нужно было выбрать блюдо из трех закусок и пяти основных блюд, и посмотрим на второе решение, в котором использовалась таблица. Обратите внимание, что один из способов подсчитать количество возможных приемов пищи — просто пронумеровать каждую из соответствующих ячеек в таблице, как мы сделали выше. Но другим способом подсчета количества ячеек в таблице было бы умножение количества строк (3) на количество столбцов (5), чтобы получить 15. Обратите внимание, что мы могли бы получить тот же результат, вообще не создавая таблицу. просто умножив количество вариантов закуски (3) на количество вариантов основного блюда (5). Мы обобщаем эту технику как

   Основное правило счета :

   Основное правило счета

   Если нас попросят выбрать по одному элементу из каждой из двух отдельных категорий, где имеется 90 005 90 004 90 703 m 90 704 предметов в первой категории и 90 703 n 90 704 предметов во второй категории, то общее количество доступных вариантов равно 90 703 m × 90 704 90 703 п .

   Это иногда называют правилом умножения вероятностей.

   Пример

   В списке для чтения на курсе английского языка в колледже 21 роман и 18 сборников стихов. Сколькими способами студент может выбрать один роман и один сборник стихов для чтения в течение четверти?

   Имеется 21 вариант выбора из первой категории и 18 из второй, поэтому 21 × 18 = 378 вариантов.

   Основное правило подсчета можно расширить, если категорий больше двух, применяя его повторно, как мы видим в следующем примере.

   Пример

   Предположим, в каком-то ресторане у вас есть три варианта аперитива (суп, салат или хлебные палочки), пять вариантов основного блюда (гамбургер, бутерброд, пирог с заварным кремом, фахита или паста) и два варианта десерта (пирог или мороженое). Если вам разрешено выбирать ровно по одному продукту из каждой категории для вашего обеда, сколько различных вариантов еды у вас есть?

   Есть 3 варианта закуски, 5 основных блюд и 2 десерта, поэтому

   3 × 5 × 2 = 30 вариантов.

   Пример 4

   Викторина состоит из 3 вопросов, на которые можно ответить верно или неверно. Сколькими способами ученик может ответить на тест?

   Есть 3 вопроса. Каждый вопрос имеет 2 возможных ответа (верно или неверно), поэтому на викторину можно ответить в виде

   2 × 2 × 2 = 8 разных способов. Напомним, что другой способ записать 2 × 2 × 2 — это 2 ³ , что намного компактнее.

   Попробуйте сейчас 1

   Предположим, в каком-то ресторане у вас есть восемь вариантов закусок, одиннадцать вариантов основного блюда и пять вариантов десерта. Если вам разрешено выбирать ровно по одному продукту из каждой категории для вашего обеда, сколько различных вариантов еды у вас есть?

   Показать ответ

   8 × 11 × 5 = 440 комбинаций меню

   В этом разделе мы разработаем еще более быстрый способ решения некоторых проблем, которые мы уже научились решать другими средствами. Начнем с пары примеров.

   Пример 5

   Сколькими способами можно переставить буквы в слове MATH, чтобы получилось четырехбуквенное кодовое слово?

   Эта проблема немного отличается. Вместо того, чтобы выбирать по одному элементу из каждой из нескольких разных категорий, мы многократно выбираем элементы из

   та же категория (категория: буквы слова МАТЕМАТИКА), и каждый раз, когда мы выбираем элемент, мы не заменяем его , поэтому на следующем этапе на один выбор меньше: у нас есть 4 варианта для первая буква (скажем, мы выбираем A), затем 3 варианта выбора для второго (M, T и H; допустим, мы выбираем H), затем 2 варианта выбора для следующей буквы (M и T; допустим, мы выбираем M) и только один выбор в последний этап (Т). Таким образом, имеется 4 × 3 × 2 × 1 = 24 способа написания кода с буквами MATH.

   В этом примере нам нужно было вычислить

   n⋅(n−1)⋅(n−2)⋅⋅⋅3⋅2⋅1\displaystyle{n}\cdot{\left({n}-{1 }\right)}\cdot{\left({n}-{2}\right)}\cdot\cdot\cdot{3}\cdot{2}\cdot{1}n⋅(n−1)⋅( n−2)⋅⋅⋅3⋅2⋅1

   . Это вычисление часто встречается в математике и называется факториалом и обозначается как n !

   Факториал

   n!=n⋅(n−1)⋅(n−2)⋅⋅⋅3⋅2⋅1\displaystyle{n}!={n}\cdot{\left({n}-{ 1}\right)}\cdot{\left({n}-{2}\right)}\cdot\cdot\cdot{3}\cdot{2}\cdot{1}n!=n⋅(n− 1)⋅(n−2)⋅⋅⋅3⋅2⋅1

   Пример 6

   Сколькими способами пять разных призов можно распределить между пятью людьми?

   Есть 5 вариантов приза для первого человека, 4 варианта для второго и так далее. Количество способов распределения призов составит

   5! = 5 × 4 × 3 × 2 × 1 = 120 способов.

   Теперь рассмотрим немного другие примеры.

   Пример 7

   В благотворительной акции принимают участие 25 человек, а в качестве призов разыгрываются три подарочных сертификата: один подарочный сертификат на сумму 100 долларов, второй на 25 долларов и третий на 10 долларов. Предполагая, что ни один человек не получает более одного приза, сколькими способами можно получить три подарочных сертификата?

   Согласно основному правилу подсчета, у человека, получившего 100-долларовый сертификат, есть 25 вариантов выбора, 24 оставшихся варианта для 25-долларового сертификата и 23 варианта для 10-долларового сертификата, поэтому существует

   25 × 24 × 23 = 13 800 способов. в котором могут быть вручены призы.

   Пример 8

   Восемь спринтеров вышли в финал Олимпийских игр в беге на 100 метров. Сколькими способами можно вручить золотые, серебряные и бронзовые медали?

   Согласно основному правилу подсчета, есть 8 вариантов для обладателя золотой медали, 7 оставшихся вариантов для серебряного и 6 для бронзового, то есть 8 × 7 × 6 = 336 способов присудить три медали 8 бегунам.

   Обратите внимание, что в этих предыдущих примерах подарочные сертификаты и олимпийские медали были выданы

   без замены ; то есть после того, как мы выбрали победителя первого приза или золотой медали, он не имеет права на получение других призов. Таким образом, на каждом последующем этапе решения на один выбор меньше (25, затем 24, затем 23 в первом примере; 8, затем 7, затем 6 во втором). Сравните это с ситуацией теста с множественным выбором, где может быть пять возможных ответов — A, B, C, D или E — на каждый вопрос теста.

   Обратите также внимание, что  порядок выбора был важен в каждом примере: для призов с тремя дверями выбор первым означает, что вы получаете значительно больше денег; в примере с Олимпийскими играми первое место означает, что вы получаете золотую медаль, а не серебряную или бронзовую. В каждом случае, если бы мы выбрали одних и тех же трех человек в другом порядке, приз в 100 долларов мог бы получить другой человек или другой золотой медалист. (Сравните это с ситуацией, когда мы можем вытащить три имени из шляпы, чтобы каждое из них получило подарочный сертификат на 10 долларов; в этом случае порядок выбора , а не важно, так как каждый из трех человек получает один и тот же приз. Ситуации, когда важен порядок , а не , будут обсуждаться в следующем разделе.)

   Мы можем обобщить ситуацию в двух приведенных выше примерах на любую задачу без замены , где порядок выбора важен . Если мы располагаем по порядку r предметов из n возможностей (вместо 3 из 25 или 3 из 8, как в предыдущих примерах), количество возможных расположений будет равно 9.0005

   n⋅(n−1)⋅(n−2)⋅⋅⋅(n−r+1)\displaystyle{n}\cdot{\left({n}-{1}\right)}\cdot{ \left({n}-{2}\right)}\cdot\cdot\cdot{\left({n}-{r}+{1}\right)}n⋅(n−1)⋅(n− 2)⋅⋅⋅(n−r+1)

   Если вы не понимаете, почему ( n – r + 1) правильное число для последнего фактора, просто вспомните первый пример. в этом разделе, где мы вычислили 25 × 24 × 23, чтобы получить 13 800. В этом случае n = 25 и r = 3, поэтому n – r + 1 = 25 – 3 + 1 = 23, что является правильным числом для конечного множителя.

   Итак, зачем нам использовать эту сложную формулу, если на самом деле проще использовать основное правило счета, как мы делали в первых двух примерах? Ну, на самом деле мы не будем использовать эту формулу так часто, мы только разработали ее, чтобы мы могли придать особое обозначение и специальное определение той ситуации, когда мы выбираем

   r предметов из n возможностей без замены и где важен порядок выбора . В этой ситуации мы пишем:

   Перестановки

    nPr=n⋅(n−1)⋅(n−2)⋯(n−r+1)\displaystyle{}_{{\ {n}}}{ P} _ {{r}} = {n} \ cdot {\ left ({n} – {1} \ right)} \ cdot {\ left ({n} – {2} \ right)} \ cdots {\ left({n}-{r}+{1}\right)} n​Pr​=n⋅(n−1)⋅(n−2)⋯(n−r+1)

   Мы говорим, что есть

   _n P _r перестановки размера r который может быть выбран из n вариантов без замены когда порядок имеет значение .

   Оказывается, этот результат можно выразить проще, используя факториалы.

    nPr=n!(n−r)!\displaystyle{}_{{\ {n}}}{P}_{{r}}=\frac{{{n}!}}{{{\left ({n}-{r}\right)}!}} n​Pr​=(n−r)!n!​

   На практике мы обычно используем технологию, а не факториалы или повторное умножение для вычисления перестановок.

   Пример 9

   У меня девять картин, и у меня есть место, чтобы разместить на стене только четыре из них одновременно. Сколькими разными способами я мог бы это сделать?

   Так как мы выбираем 4 картины из 9 без замены где важен порядок выбора есть ₉ P ₄ = 9 × 8 × 7 × 6 = 3024 перестановки.

   Пример 10

   Сколькими способами можно выбрать исполнительный комитет в составе четырех человек (президент, вице-президент, секретарь, казначей) из 16 членов совета директоров некоммерческой организации?

   Хотим выбрать 4 человека из 16 без замены и где важен порядок выбора. Таким образом, ответ   ₁₆ P ₄ = 16 × 15 × 14 × 13 = 43 680.

   Попробуйте сейчас 2

   Сколько 5-символьных паролей можно составить, используя буквы от A до Z

   1. , если разрешены повторы
   2. , если повторы не разрешены

   Показать ответ 1

   Всего 26 символов. 26 ⁵ = 11 881 376.

   Показать ответ 2

   Всего 26 символов. ₂₆ П ₅ = 2625242322 = 7 893 600

   В предыдущем разделе мы рассмотрели ситуацию, когда мы выбрали r элементов из n возможностей без замены и где порядок выбора был важен . Теперь рассмотрим аналогичную ситуацию, в которой важен порядок выбора 90 703, а не 90 704.

   Пример 11

   В благотворительной акции принимают участие 25 человек, на которых в качестве призов разыгрываются три подарочных сертификата на 50 долларов. Предполагая, что ни один человек не получает более одного приза, сколько различных способов вручения подарочных сертификатов?

   Согласно основному правилу подсчета, есть 25 вариантов для первого человека, 24 оставшихся варианта для второго человека и 23 для третьего, поэтому существует 25 24 23 = 13 800 способов выбрать трех человек. Предположим на мгновение, что Эйб выбирается первым, Беа — вторым, а Синди — третьим; это один из 13 800 возможных исходов. Другой способ присуждения призов – выбрать Эйба первым, Синди вторым и Беа третьим; это еще один из 13 800 возможных исходов. Но в любом случае Эйб, Беа и Синди получают по 50 долларов каждый, поэтому порядок, в котором мы их выбираем, не имеет большого значения. В скольких различных порядках можно выбрать Эйба, Беа и Синди? Оказывается есть 6:

   ABC ACB BAC BCA CAB CBA

   Как мы можем быть уверены, что посчитали их все? На самом деле мы просто выбираем 3 человека из 3, поэтому есть 3 × 2 × 1 = 6 способов сделать это; нам действительно не нужно перечислять их все, мы можем просто использовать перестановки!

   Итак, из 13 800 способов выбрать 3 человека из 25, шесть из них связаны с Эйбом, Беа и Синди. Тот же аргумент работает для любой другой группы из трех человек (скажем, Эйба, Би и Дэвида или Фрэнка, Глории и Хильди), поэтому каждая группа из трех человек считается 9.0703 шесть раз . Таким образом, цифра 13 800 в шесть раз больше. Количество различных групп из трех человек будет 13 800/6 = 2300.

   Мы можем обобщить ситуацию в этом примере выше на любую задачу выбора набора элементов

   без замены , где порядок выбора равен не важно . Если мы выбираем 90 703 r 90 704 элементов из 90 703 n 90 704 возможностей (вместо 3 из 25, как в предыдущих примерах), количество возможных вариантов будет дано , и мы можем использовать эту формулу для вычислений. Однако эта ситуация возникает так часто, что мы придаем специальное обозначение и специальное определение той ситуации, когда мы выбираем 9.0703 r позиции из n возможности без замены где порядок выбора не важный .

   Комбинации

   nCr=nPrrPr\displaystyle{}_{{n}}{C}_{{r}}=\frac{{{}_{{n}}{P}_{{r}}} }{{{}_{{r}}{P}_{{r}}}}n​Cr​=r​Pr​n​Pr​​

   Мы говорим, что есть  _n C _r комбинации размера r , которые можно выбрать из n вариантов без замены где порядок не имеет значения .

   Мы также можем записать формулу комбинаций в терминах факториалов:

   nCr=n!(n−r)!r!\displaystyle{}_{{n}}{C}_{{r}}=\frac {{{n}!}}{{{\left({n}-{r}\right)}!{r}!}}n​Cr​=(n−r)!r!n!​

   Пример 12

   Группа из четырех студентов должна быть выбрана из класса из 35 человек, чтобы представлять класс в студенческом совете. Сколькими способами это можно сделать?

   Поскольку мы выбираем 4 человека из 35  без замены где порядок выбора не важный есть

   35C4=35⋅34⋅33⋅324⋅3⋅2⋅1=combinations\displaystyle{}_{{35}}{C} _{{4}}=\frac{{{35}\cdot{34}\cdot{33}\cdot{32}}}{{{4}\cdot{3}\cdot{2}\cdot{1 }}}=\text{комбинации}35​C4​=4⋅3⋅2⋅135⋅34⋅33⋅32​=комбинации

   .

   Попробуйте сейчас 3

   Комитет Сената США по ассигнованиям состоит из 29 членов; Подкомитет по обороне Комитета по ассигнованиям состоит из 19члены. Независимо от партийной принадлежности или каких-либо специальных мест в подкомитете, сколько различных подкомитетов из 19 членов может быть выбрано из числа 29 сенаторов в комитете по ассигнованиям?

   Показать ответ

   Порядок не имеет значения. ₂₉ C ₁₉ = 20 030 010 возможных подкомитетов

   В предыдущей задаче «Попробуй сейчас» мы предполагали, что 19 членов Подкомитета защиты были выбраны без учета партийной принадлежности. На самом деле этого никогда не произойдет: если республиканцы будут в большинстве, они никогда не позволят большинству демократов заседать (и, таким образом, контролировать) какой-либо подкомитет. (Конечно, то же самое было бы верно, если бы демократы были у власти.) Итак, давайте снова рассмотрим проблему, но в несколько более сложной форме:

   Пример 13

   Комитет Сената США по ассигнованиям состоит из 29 членов, 15 республиканцев и 14 демократов. Подкомитет по обороне состоит из 19 членов, 10 республиканцев и 9 демократов. Сколькими способами можно выбрать членов подкомитета по обороне из числа 29 сенаторов комитета по ассигнованиям?

   В данном случае нам нужно выбрать 10 из 15 республиканцев и 9 из 14 демократов. Есть

   ₁₅ С ₁₀ = 3003 способа выбрать 10 республиканцев и ₁₄ C ₉ = 2002 способа выбрать 9 демократов.