Закон архимеда на тело погруженное в жидкость. Закон Архимеда: определение и формула
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа) . Сила называется силой Архимеда :
где – плотностьжидкости (газа), – ускорение свободного падения, а – объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена кцентру тяжестиэтого объёма.
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Следует
заметить, что тело должно быть полностью
окружено жидкостью (либо пересекаться
с поверхностью жидкости). Так, например,
закон Архимеда нельзя применить к
кубику, который лежит на дне резервуара,
герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.
где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.
18. Равновесие тела в покоящейся жидкости
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела. P выт = ρ ж gV погр
Для однородного тела плавающего на поверхности справедливо соотношение
где: V –
объем плавающего тела; ρ m –
плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K”L”M” , наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d”
 Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) если
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.
Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду.
Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.
Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы
Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.
Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.
Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела.Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
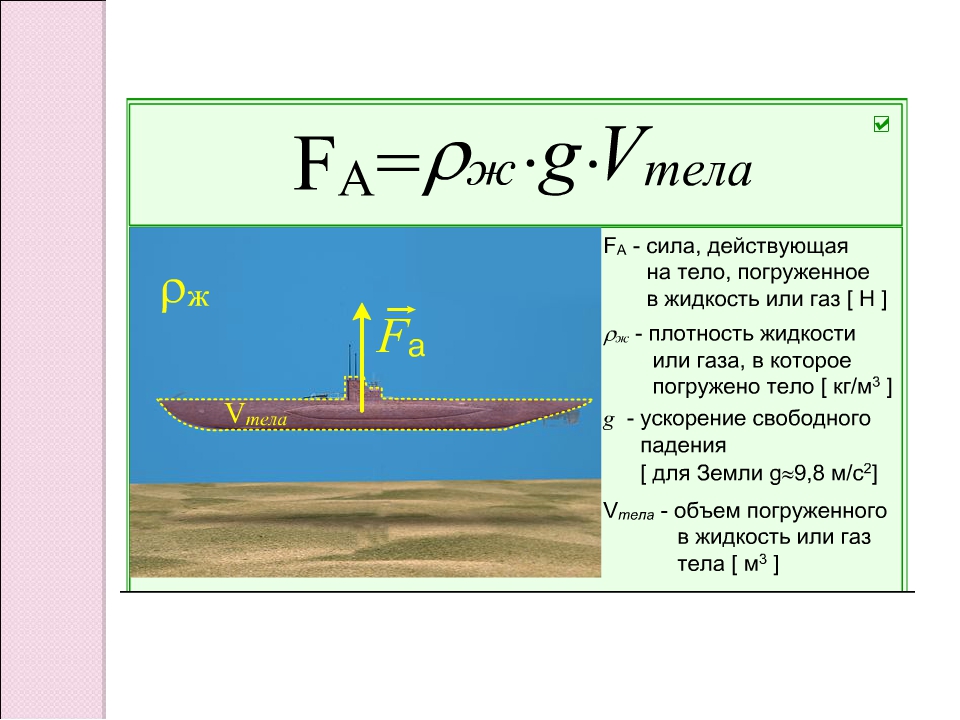
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Продолжим изучение архимедовой силы. Проделаем опыты. К коромыслу весов подвесим два одинаковых шара. Их вес одинаков, поэтому коромысло находится в равновесии (рис. «а»). Подставим под правый шар пустой стакан. От этого вес шаров не изменится, поэтому равновесие сохранится (рис. «б»).
Их вес одинаков, поэтому коромысло находится в равновесии (рис. «а»). Подставим под правый шар пустой стакан. От этого вес шаров не изменится, поэтому равновесие сохранится (рис. «б»).
Второй опыт. Подвесим к динамометру большую картофелину. Вы видите, что её вес равен 3,5 Н. Погрузим картофелину в воду. Мы обнаружим, что её вес уменьшился и стал равен 0,5 Н.
Вычислим изменение веса картофеля:
DW = 3,5 Н – 0,5 Н = 3 Н
Почему же вес картофеля уменьшился именно на 3 Н? Очевидно потому, что в воде на картофель подействовала выталкивающая сила такой же величины. Другими словами, сила Архимеда равна изменению веса т ела:
Эта формула выражает способ измерения архимедовой силы: нужно дважды измерить вес тела и вычислить его изменение. Полученное значение равно силе Архимеда.
Для вывода следующей формулы проделаем опыт с прибором «ведёрко Архимеда». Основные его части следующие: пружина со стрелкой 1, ведёрко 2, тело 3, отливной сосуд 4, стаканчик 5.
Сначала пружину, ведёрко и тело подвешивают к штативу (рис. «а») и отмечают положение стрелки жёлтой меткой. Затем тело помещают в отливной сосуд. По мере погружения тело вытесняет некоторый объём воды , который сливается в стаканчик (рис. «б»). Вес тела становится меньше, пружина сжимается, и стрелка поднимается выше жёлтой метки.
Перельём воду, вытесненную телом, из стаканчика в ведёрко (рис. «в»). Самое удивительное в том, что когда вода будет перелита (рис «г»), стрелка не просто опустится вниз, а укажет точно на жёлтую метку! Значит, вес влитой в ведёрко воды уравновесил архимедову силу . В виде формулы этот вывод запишется так:
Обобщая результаты двух опытов, получим закон Архимеда : выталкивающая сила, действующая на тело в жидкости (или газе), равна весу жидкости (газа), взятой в объёме этого тела и направлена противоположно вектору веса.
В § 3-б мы указали, что сила Архимеда обычно направлена вверх. Поскольку она противонаправлена вектору веса, а он не всегда направлен вниз, архимедова сила также не всегда действует вверх.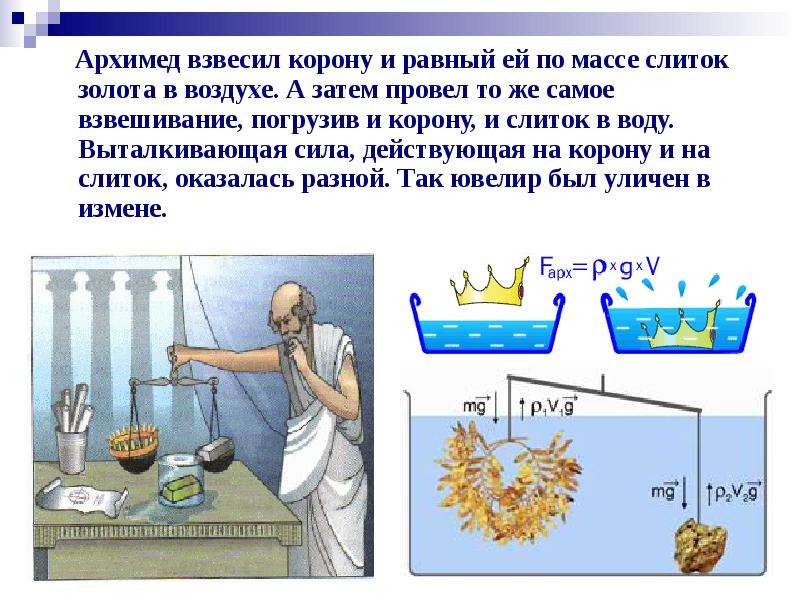 Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут всплывать не вверх, а отклоняясь к оси вращения.
Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут всплывать не вверх, а отклоняясь к оси вращения.
Закон Архимеда
Несомненно, Архимед (около 287—212 до н.э.) — самый гениальный учёный Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времён. Его труды посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью.
Сын астронома Фидия, написавшего сочинение о диаметрах Солнца и Луны, Архимед родился и жил в греческом городе Сиракузы на Сицилии. Он был приближён ко двору царя Гиерона II и его сына-наследника.
Хорошо известен рассказ о жертвенном венце Гиерона. Архимеду поручили проверить честность ювелира и определить, сделан венец из чистого золота или с примесями других металлов и нет ли внутри него пустот. Однажды, размышляя об этом, Архимед погрузился в ванну, и заметил, что вытесненная его телом вода пролилась через край.
 Гениального учёного тут же осенила яркая идея, и с криком
“Эврика, эврика!” он, как был нагой, бросился проводить эксперимент.
Гениального учёного тут же осенила яркая идея, и с криком
“Эврика, эврика!” он, как был нагой, бросился проводить эксперимент.Идея Архимеда очень проста. Тело, погружённое в воду, вытесняет столько жидкости, каков объём самого тела. Поместив венец в цилиндрический сосуд с водой, можно определить, какое количество жидкости он вытеснит, т.е. узнать его объём. А, зная объём и взвесив венец, легко вычислить удельную массу. Это и даст возможность установить истину: ведь золото — очень тяжёлый металл, а более лёгкие примеси, и тем более пустоты, уменьшают удельную массу изделия.
Но Архимед на этом не остановился. В труде “О плавающих телах” он сформулировал закон, который гласит: “Тело, погружённое в жидкость, теряет в своём весе столько, каков вес вытесненной жидкости” . Закон Архимеда является (наряду с другими, позже открытыми фактами) основой гидравлики — науки, изучающей законы движения и равновесия жидкостей. Именно этот закон объясняет, почему стальной шар (без пустот) тонет в воде, тогда как деревянное тело всплывает.
 В первом случае вес вытесненной воды меньше веса самого шара, т.е.
архимедова “выталкивающая” сила недостаточна для того, чтобы удержать его на
поверхности. А тяжело гружёный корабль, корпус которого сделан из металла, не
тонет, погружаясь только до так называемой ватерлинии. Поскольку внутри корпуса
корабля много пространства, заполненного воздухом, средняя удельная масса судна
меньше плотности воды и выталкивающая сила удерживает его на плаву. Закон
Архимеда объясняет также, почему воздушный шар, заполненный тёплым воздухом или
газом, который легче воздуха (водородом, гелием) , улетает ввысь.
В первом случае вес вытесненной воды меньше веса самого шара, т.е.
архимедова “выталкивающая” сила недостаточна для того, чтобы удержать его на
поверхности. А тяжело гружёный корабль, корпус которого сделан из металла, не
тонет, погружаясь только до так называемой ватерлинии. Поскольку внутри корпуса
корабля много пространства, заполненного воздухом, средняя удельная масса судна
меньше плотности воды и выталкивающая сила удерживает его на плаву. Закон
Архимеда объясняет также, почему воздушный шар, заполненный тёплым воздухом или
газом, который легче воздуха (водородом, гелием) , улетает ввысь.Знание гидравлики позволило Архимеду изобрести винтовой насос для выкачивания воды. Такой насос (кохля) до недавнего времени применялся на испанских и мексиканских серебряных рудниках.
ЗАКОН АРХИМЕДА – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.

Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме. Величина Архимедовой силы определяется по закону Архимеда.
9туальность выбранной темы
С помощью Закона Архимеда появилась новая отрасль физике, Например, гидростатика, с помощью этого людям легко удается изучать физику в практике.
Задачи
Шарик был опущен в воду, Какова сила Архимеда если объем шарика составляет 2 м3?
Алгоритм решение задач
F=pVg
F=1000*2*9.8=20 000
1)1000*2=2000
2)2000*9.8=19600
Действие выталкивающей силы на тело, погружённое в жидкость
Издавна люди наблюдали за природными явлениями и пытались их объяснить. Учёные пытались объяснить это научным путём.
Например: Архимед открыл, что на все тела, погружённые в жидкость и в газ, действует выталкивающая сила. Её назвали силой Архимеда.
Её назвали силой Архимеда.
Простейшая модель подводной лодки висит между поверхностью и дном. Но ни всплыть, ни погрузится глубже – она не может. А ведь настоящую лодку никто не будет вынимать из воды, чтобы смотать или домотать кусочек проволоки. Как же маневрирует подводная лодка? Как она всплывает, как ложится на дно? Простейшим примером такого «маневрирующего» подводного судна служит виноградинка в газированной воде! Мы знаем, что газированная вода, а также все фруктовые и минеральные воды, которые продаются в бутылках, насыщены газом под давлением. Но вот бутылка открыта, вода налита в стакан. Газ выходит в пене и брызгах. Но часть его ещё осталась. Эта часть продолжает постепенно выделяться, оседая пузырьками на стенках стакана. В стакан со свеженалитой водой бросим виноградину. Она чуть тяжелее воды и опустится на дно. Но на нее тут же начнут садиться пузырьки газа. Словно маленькие воздушные шарики! Скоро их станет так много, что виноградинка всплывёт. Но на поверхности пузырьки полопались, и газ улетел.
Отяжелевшая виноградинка вновь опустилась на дно. Здесь она снова «обросла» пузырьками газа и снова всплыла. Так повторялось несколько раз, пока вода не «выдохлась».
Подобным образом ведёт себя подводная лодка, она всплывает и погружается очень похожим способом. Только у лодки пузырьки газа не снаружи. Она ведь не в газировке плавает! У лодки есть внутри специальные цистерны. Называются они балластными, потому что в них набирают балласт – груз, который тянет лодку вниз. Этим грузом служит забортная вода.
Командир приказывает погрузиться. Цистерны открывают, и в них устремляется вода. Она вытесняет воздух. Спешат, бурлят воздушные пузыри. Они расстаются с лодкой, как пузырьки газа со всплывшей виноградиной. И лодка, словно виноградина, теряет плавучесть и опускается в глубину.
Надо снова всплыть. «Продуть балластные!» – приказывает командир. И цистерны снова открываются, но теперь в них устремляется сжатый воздух из специальных баллонов. Он вытесняет, выгоняет воду, он сам заполняет цистерны. Внутри лодки словно образуются большие воздушные пузырьки. И облегченная лодка всплывает.
Внутри лодки словно образуются большие воздушные пузырьки. И облегченная лодка всплывает.
Я решил пронаблюдать за поведением пузырька воздуха, находящегося в стакане с водой.
Оборудование : стакан с водой, линейка, таблица плотностей жидкости.
Выполнение наблюдений:
1. Налил воду из-под крана в стакан.
2. Убедился в наличии воздушных пузырьков на дне.
3. Пронаблюдал за поведением одного из них: пузырёк, увеличиваясь в объёме, по мере подъёма к поверхности воды, лопнул на поверхности воды, из-за разности давлений; атмосферного и внутри расширенного пузырька.
4. Расчитал изменение объёма пузырька в зависимости от высоты.
1) Объём пузырька на дне стакана
Vg=1мм. куб.
2) Высота водяного столба в стакане h=90мм=0,09м.
3) Давление на поверхности воды – атмосферное
Pа=100000Па
4) Давление на дне стакана
Рg=Pa+Ph , где Ph-давление водяного столба.
Ph=gph; где p – плотность воды =10000 кг/куб. м.
м.
Рh=10 н/кг 1000 кг/куб. м. 0,09=900 Па
Pg=100000+900+100900(Па)
Отношение Рg = 100900
– =1,009 двух давлений Pa 100000
5) Объём пузырька воздуха на поверхности стакана
Vn=Vg 1,009 =1мм. куб 1,009 =1,009 мм. куб.
Из расчётов видно, что объём пузырька воздуха увеличился.
6)Рассчитаем, как меняется объём пузырька воздуха поднимающегося со дна любого водоёма на поверхность воды:
Высота водоёма h =50м
Объём пузырька на дне Vg=3мм. куб.
Плотность воды Pв=1000кг/куб. м
Атмосферное давление Ра=100000Па
Найти объём пузырьков на поверхности Vп-?
Решение:
Р = Ра + Рв – давление на дне
Р воды = gph
Р воды=10 н/кг 100кг/куб. м 50м = 500000Па=500кПа
Р = 100000 + 500000 = 600000(Па)
Р/Ра=600000/100000=6(раз)
Vn=vg6 ; Vn=3 6=18(мм. куб. )
Герой книги Ж. Кусто и Ф. Дюма «В мире безмолвия» рассказывает: «На глубине шести футов (1,83 м- М. Т. ) уже было тихо и спокойно, но катящиеся наверху волны давали о себе знать до глубины в двадцать футов ритмичным усилием давления на барабанные перепонки». Это происходит так как давление внутри жидкости пропорционально глубине погружения. При наличии волн толщина слоя воды периодически изменяется. Это приводит к изменению давления ,что и ощущают барабанные перепонки.
Это происходит так как давление внутри жидкости пропорционально глубине погружения. При наличии волн толщина слоя воды периодически изменяется. Это приводит к изменению давления ,что и ощущают барабанные перепонки.
В ходе своих исследований я убедился, что увеличивающиеся воздушные пузырьки в опыте с виноградинкой помогают виноградинке всплыть.
На этих явлениях конструируются и работают подводные лодки. Ещё раз можно убедиться, что «живая природа» помогает человечеству в научно – техническом прогрессе.
история открытия и суть явления для чайников
Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере.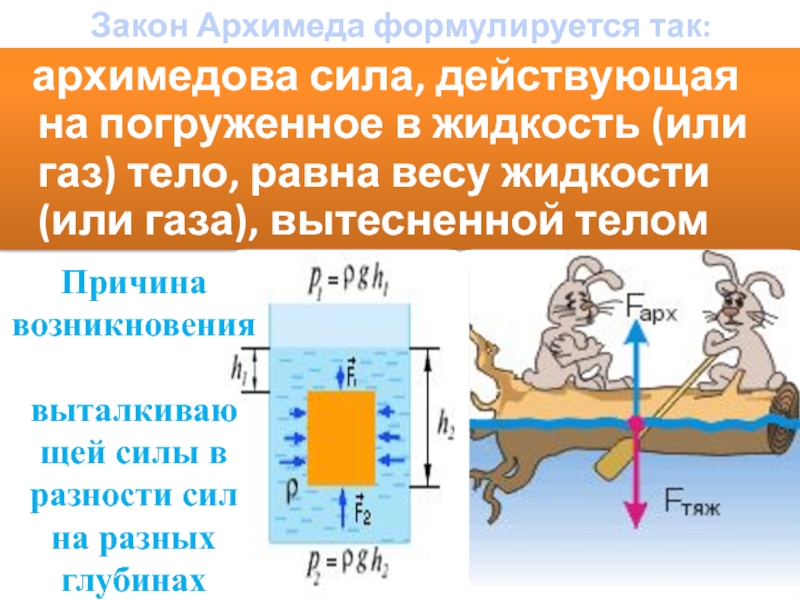 Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Чивилев В.И. Закон Архимеда //Квант. – 1987. – № 1. – С. 29-30.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
«…Удар сжатого воздуха хлопнул в трубах, вода в цистерне зажурчала, и глубомер пополз вверх. Лодка всплыла на ровном киле, и глубомер показал, что рубка уже вышла из воды»,- так описывается всплытие подводной лодки в книге Л. Соболева «Морская душа».
Соболева «Морская душа».
Причина всплытия – сила Архимеда, называемая еще выталкивающей силой, которая после продувки цистерн с водой сжатым воздухом превысила по модулю силу тяжести лодки. Когда же и в каком случае возникает сила Архимеда? Со стороны чего она действует? Куда приложена, как направлена и чему равна?
Выталкивающая сила – это сумма всех сил давления, действующих со стороны жидкости или газа на поверхность погруженного в нее тела (рис. 1). Истинная причина появления выталкивающей силы – наличие различного гидростатического давления на разных уровнях жидкости.
Для нахождения силы Архимеда мысленно заменим погруженное тело жидкостью в объеме этого тела (рис. 2).
На нее со стороны окружающей жидкости будет действовать такая же выталкивающая сила, как и на погруженное тело. По третьему закону Ньютона выделенная в объеме тела жидкость (вытесненная жидкость) будет действовать на окружающую жидкость с той же самой по модулю, но противоположно направленной силой. Это – вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета (необязательно инерциальной), называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.
Это – вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета (необязательно инерциальной), называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.
Итак, выталкивающая сила, действующая на погруженное в жидкость тело, равна по модулю и противоположна по направлению весу вытесненной жидкости. Это и есть закон Архимеда. Заметим, что в формулировке закона говорится именно о весе вытесненной жидкости, а не о силе тяжести. И это весьма существенно, так как вес тела (по модулю) не всегда совпадает с силой тяжести. Например, ящик массой m в кабине поднимающегося с ускорением а лифта давит на пол с силой m (g + a ). Это значит, что вес ящика равен Р = m (g + a ), в то время как сила тяжести, действующая на ящик, равна mg . Когда же кабина лифта опускается с тем же ускорением, вес ящика оказывается равным Р = m (g – a ).
Из последнего выражения ясно, что выталкивающая сила появляется тогда, когда нет состояния невесомости, то есть любое тело (в том числе и жидкость) имеет вес. Если сосуд с жидкостью свободно падает, то жидкость находится в состоянии невесомости и на погруженное в нее тело сила Архимеда не действует. Не действует эта сила и в космическом корабле, движущемся с выключенными двигателями.
При доказательстве закона Архимеда мы считали, что тело полностью погружено в жидкость и вся его поверхность соприкасается с жидкостью. Если же часть поверхности тела плотно прилегает к стенке или дну сосуда, так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Яркой иллюстрацией сказанного служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Брусок не всплывает, так как со стороны воды на него действует сила, не выталкивающая его вверх, а прижимающая ко дну (рис. 3).
Приведенная формулировка закона Архимеда остается справедливой и в случае, когда тело лишь частично опущено в жидкость, но не соприкасается со стенками сосуда. (Доказательство аналогично случаю полностью погруженного в жидкость тела.)
(Доказательство аналогично случаю полностью погруженного в жидкость тела.)
Нам осталось научиться находить вес вытесненной жидкости и линию действия выталкивающей силы. В общем случае (например, когда тело погружено в жидкость, вращающуюся вместе с сосудом) это не так легко сделать.
Рассмотрим наиболее простой и часто встречающийся на практике случай. Пусть сосуд с жидкостью неподвижен в некоторой инерциальной системе отсчета. Тогда, как известно, вес любого неподвижного тела равен силе тяжести, действующей на тело. Поэтому и выталкивающая сила равна по модулю силе тяжести, действующей на вытесненную жидкость, и противоположно ей направлена. Линия действия выталкивающей силы будет проходить через центр тяжести вытесненного объема жидкости. Покажем это.
На вытесненный объем жидкости массой m (рис. 4) действуют две силы – сила тяжести \(~m \vec g\), приложенная в центре тяжести этого объема, и выталкивающая сила \(~\vec F_B\). Так как жидкость находится в равновесии, то по правилу рычага (см. § 62 «Физики 6-7» или § 47 «Физики 8») действующие на нее силы обратно пропорциональны плечам этих сил. Плечо силы тяжести относительно оси, проходящей через центр тяжести, равно нулю. Значит, и плечо выталкивающей силы тоже равно нулю, т. е. линия действия выталкивающей силы проходит через центр тяжести «вытесненного» объема жидкости.
§ 62 «Физики 6-7» или § 47 «Физики 8») действующие на нее силы обратно пропорциональны плечам этих сил. Плечо силы тяжести относительно оси, проходящей через центр тяжести, равно нулю. Значит, и плечо выталкивающей силы тоже равно нулю, т. е. линия действия выталкивающей силы проходит через центр тяжести «вытесненного» объема жидкости.
Поскольку точку приложения силы можно переносить вдоль линии ее действия, обычно выталкивающую силу помещают в центр тяжести вытесненной жидкости и называют эту точку также центром давлений.
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием
умений анализировать свойства и явления на
основе знаний, выделять главную причину,
влияющую на результат. Развивать
коммуникативные умения. На этапе выдвижения
гипотез развивать устную речь. Проверить уровень
самостоятельности мышления школьника по
применению учащимися знаний в различных
ситуациях.
Проверить уровень
самостоятельности мышления школьника по
применению учащимися знаний в различных
ситуациях.
Архимед – выдающийся ученый Древней Греции, родился в 287 году до н.э. в портовом и судостроительном г. Сиракузы на острове Сицилия. Архимед получил блестящее образование у своего отца, астронома и математика Фидия, родственника сиракузского тирана Гиерона, покровительствовавшего Архимеду. В юности провёл несколько лет в крупнейшем культурном центре в Александрии, где у него сложились дружеские отношения с астрономом Кононом и географом-математиком Эратосфеном. Это послужило толчком к развитию его выдающихся способностей. В Сицилию вернулся уже зрелым ученым. Он прославился многочисленными научными трудами главным образом в области физики и геометрии.
Последние годы жизни Архимед был в
Сиракузах, осажденных римским флотом и войском.
Шла 2-я Пуническая война. И великий ученый, не
жалея сил, организовывает инженерную оборону
родного города. Он построил множество
удивительных боевых машин, топивших вражеские
корабли, разносивших их в щепы, уничтожавших
солдат. Однако слишком маленьким было войско
защитников города по сравнению с огромным
римским войском. И в 212 г. до н.э. Сиракузы были
взяты.
Однако слишком маленьким было войско
защитников города по сравнению с огромным
римским войском. И в 212 г. до н.э. Сиракузы были
взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал закон, впоследствии названный законом Архимеда. Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну, с возгласом “Эврика!” он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину. Суть этой истины и предстоит выяснить, нужно убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под
действием выталкивающей силы оно будет
всплывать из более глубоких слоев в менее
глубокие. Выведем формулу для определения силы
Архимеда для прямоугольного параллелепипеда.
Выведем формулу для определения силы
Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые
грани равна нулю, поэтому в расчетах не
участвует.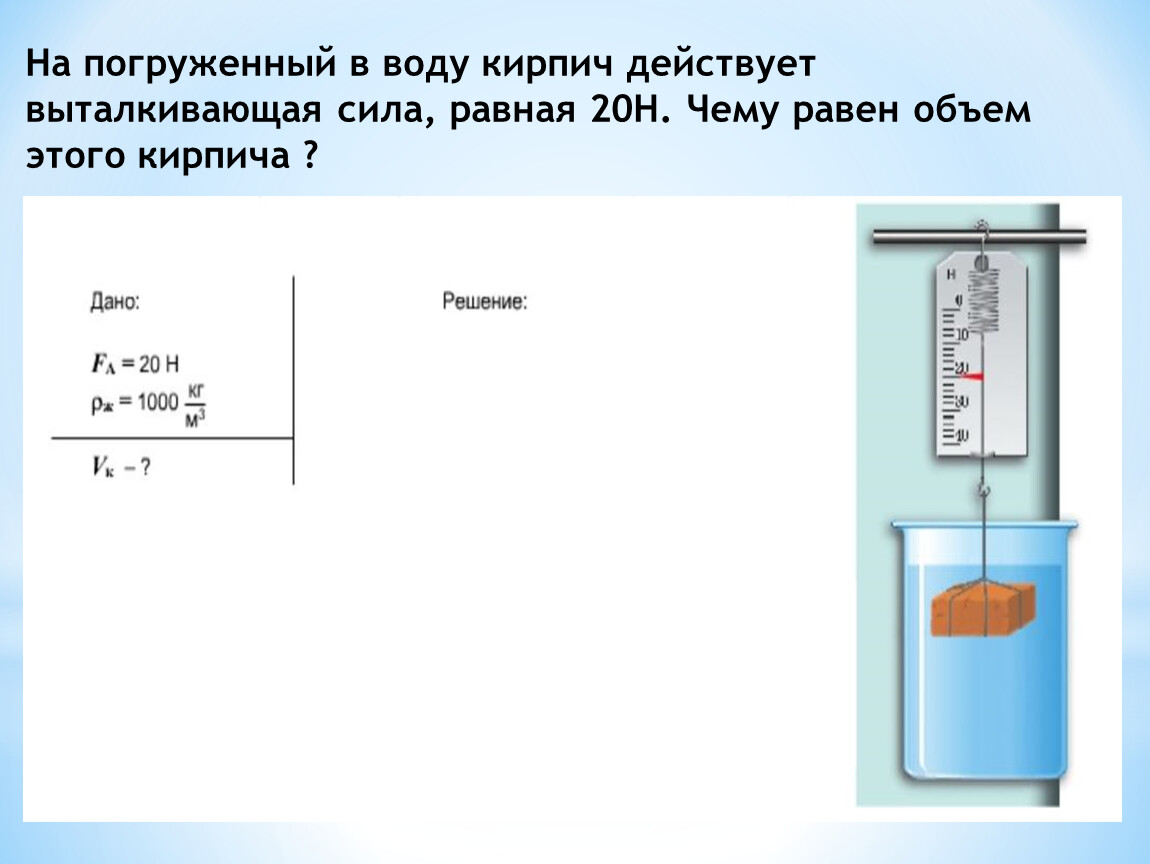
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом в трактате “О плавающих телах”. Архимед писал: “тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
P А = m т g – m ж g = g (m т – m ж)
Таким образам, если тело погружено в жидкость
(или газ), то оно теряет в своём весе столько,
сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны
жидкости, направлена по вертикали вверх,
приложена к центру тяжести вытесненного объема
жидкости.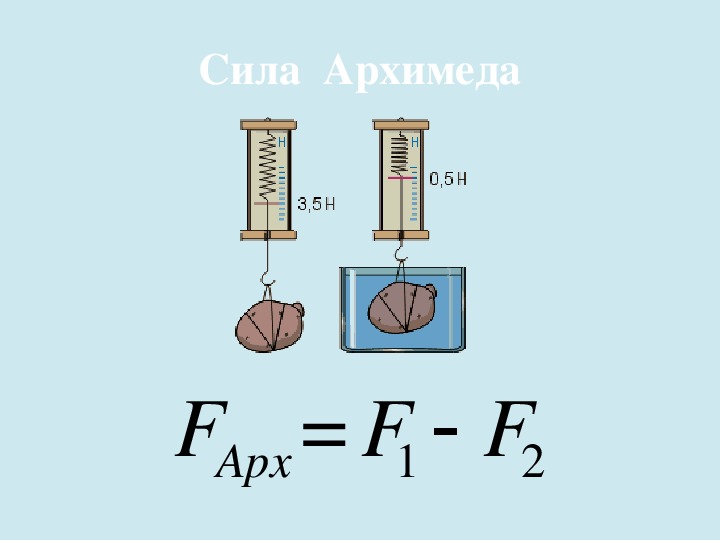 Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:
- F т > F A – тело тонет;
- F т = F A – тело плавает в жидкости или газе;
- F т
Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):
- P t > P s – тело тонет;
- P t = P s – тело плавает в жидкости или газе;
- P t
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то
сила Архимеда равна нулю.
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили
огромный бумажный шар, под которым поместили
чашку с горящим спиртом. Шар наполнился горячим
воздухом и начал подниматься, достигнув высоты
2000 метров.
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа) . Сила называется силой Архимеда :
где
– плотностьжидкости (газа),
– ускорение
свободного падения, а
– объём погружённого тела (или часть
объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется
вверх или вниз, то выталкивающая сила
(называемая также архимедовой силой)
равна по модулю (и противоположна по
направлению) силе тяжести, действовавшей
на вытесненный телом объём жидкости
(газа), и приложена кцентру
тяжестиэтого объёма.
Если тело плаваетна поверхности или равномерно движется
вверх или вниз, то выталкивающая сила
(называемая также архимедовой силой)
равна по модулю (и противоположна по
направлению) силе тяжести, действовавшей
на вытесненный телом объём жидкости
(газа), и приложена кцентру
тяжестиэтого объёма.
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.
где P A ,
P B – давления в точках A и B ,
ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного
сечения тела, V – объём погружённой части тела.
18. Равновесие тела в покоящейся жидкости
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела. P выт = ρ ж gV погр
Для однородного тела плавающего на поверхности справедливо соотношение
где: V – объем плавающего тела; ρ m – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность
плавающего тела, выведенного из состояния
равновесия, вновь возвращаться в это
состояние называется остойчивостью .
Вес жидкости, взятой в объеме погруженной
части судна называют водоизмещением ,
а точку приложения равнодействующей
давления (т.е. центр давления) – центром
водоизмещения .
При нормальном положении судна центр
тяжести С и
центр водоизмещения d лежат
на одной вертикальной прямой O”-O” ,
представляющей ось симметрии судна и
называемой осью плавания (рис. 2.5).
2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K”L”M” , наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d” . Приложим к точке d” подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O”-O” . Полученная точка m называется метацентром , а отрезок mC = h называется метацентрической высотой . Будем считать h положительным, если точка m лежит выше точки C , и отрицательным – в противном случае.
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) если h
Следовательно,
чем ниже расположен центр тяжести и,
чем больше метацентрическая высота,
тем больше будет остойчивость судна.
Как рассчитать вес тела в воде. Выталкивающая сила. Основные теоретические сведения
Жидкостей и газов, согласно которому на всякое тело, пог-руженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.
Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.
Ниже приведены выводы, следующие из закона Архимеда .
Действие жидкости и газа на погруженное в них тело.
Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?
На тело, погруженное в воду, со всех сторон действуют силы давления воды (рис. а ). В каж-дой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростати-ческое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих иа тело сверху.
Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростати-ческое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих иа тело сверху.
Если заменить все силы давления , приложенные к погруженному в воду телу, одной (резуль-тирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке б она обозначена как F A .
Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глу-бинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.
Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном про-странстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.
Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).
Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен P 0 , то его вес в воздухе равен:
,
где F´ A — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что P возд. =P 0 =mg .
Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе P возд. =P 0 , то вес тела в жидкости равен P жидк = Р 0 — F A . Здесь F A — архимедова сила, действующая в жидкости. Отсюда следует, что
Отсюда следует, что
Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.
Другими словами, учитывая формулу (1.32), можно сказать:
Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.
Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем пра-во это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила F A будет уравновешена действующей вниз силой тяжести m ж g (где m ж — масса жидкости в объеме данного тела):
Но сила тяжести равна весу вытесненной жидкости Р ж .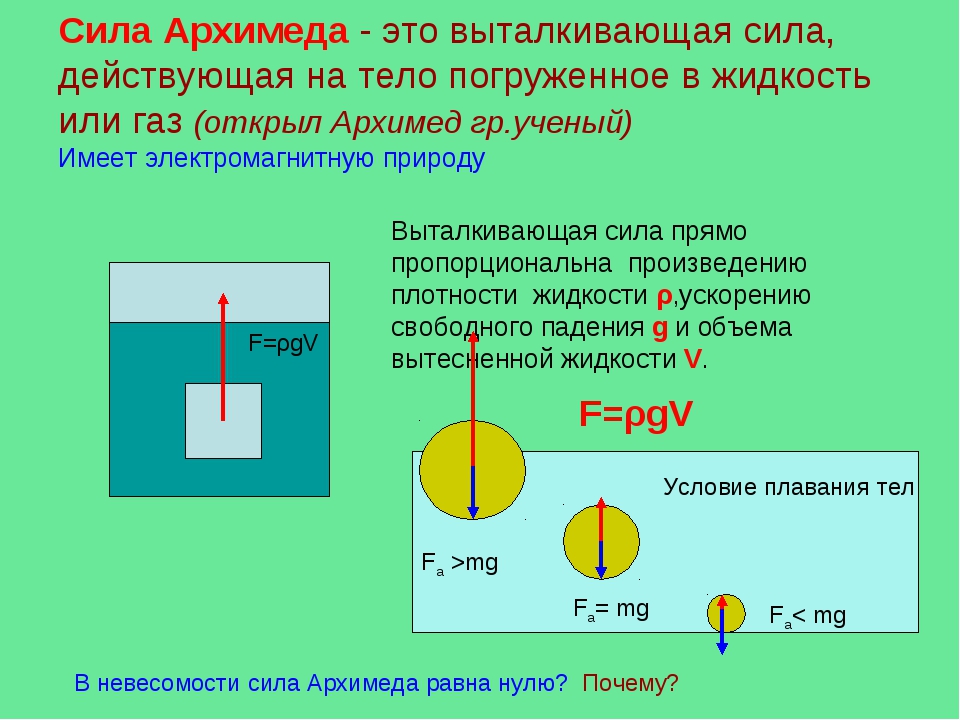 Таким образом.
Таким образом.
Учитывая, что масса жидкости равна произведению ее плотности ρ ж на объем, формулу (1.33) можно записать в виде:
где V ж — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погру-жена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом V всего тела; если же тело погружено в жидкость частично, то объем V ж вытесненной жидкости меньше объема V тела (рис. 1.39).
Формула (1.33) справедлива и для архимедовой силы, действующей в газе. Только в этом слу-чае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.
С учетом вышеизложенного закон Архимеда можно сформулировать так:
На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или га-за), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).
Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.

Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:
где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости.
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемоезаконом Архимеда , справедливо для тел любой формы.
При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg , а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:
Если принять, что вес покоящегося тела в воздухе равен mg , а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:
Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρ т больше плотности жидкости (или газа) ρ (или по–другому mg > F A), тело будет опускаться на дно. Если же ρ т ρ
(или по–другому mg F
A), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Плавание тел
Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:
где: V погр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел.
Основные теоретические сведения
Импульс тела
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р . Импульс тела равен произведению массы тела на его скорость, т. е. он рассчитывается по формуле:
е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Общий импульс системы тел равен векторной сумме импульсов всех тел системы:
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: p н – импульс тела в начальный момент времени, p к – в конечный. Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
При этом угол падения равен углу отражения.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой .
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называетсязаконом сохранения импульса (ЗСИ) . Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Плавучесть – это выталкивающая сила, действующая на тело, погруженное в жидкость (или газ), и направленная противоположно силе тяжести. В общих случаях выталкивающая сила может быть вычислена по формуле: F b = V s × D × g, где F b – выталкивающая сила; V s – объем части тела, погруженной в жидкость; D – плотность жидкости, в которую погружают тело; g – сила тяжести.
Шаги
Вычисление по формуле
Найдите объем части тела, погруженной в жидкость (погруженный объем). Выталкивающая сила прямо пропорциональна объему части тела, погруженной в жидкость. Другими словами, чем больше погружается тело, тем больше выталкивающая сила. Это означает, что даже на тонущие тела действует выталкивающая сила. Погруженный объем должен измеряться в м 3 .
Другими словами, чем больше погружается тело, тем больше выталкивающая сила. Это означает, что даже на тонущие тела действует выталкивающая сила. Погруженный объем должен измеряться в м 3 .
- У тел, которые полностью погружены в жидкость, погруженный объем равен объему тела. У тел, плавающих в жидкости, погруженный объем равен объему части тела, скрытой под поверхностью жидкости.
- В качестве примера рассмотрим шар, плавающий в воде. Если диаметр шара равен 1 м, а поверхность воды доходит до середины шара (то есть он погружен в воду наполовину), то погруженный объем шара равен его объему, деленному на 2. Объем шара вычисляется по формуле V = (4/3)π(радиус) 3 = (4/3)π(0,5) 3 = 0,524 м 3 . Погруженный объем: 0,524/2 = 0,262 м 3 .
Найдите плотность жидкости (в кг/м 3), в которую погружается тело. Плотность – это отношение массы тела к занимаемому этим телом объему. Если у двух тел одинаковый объем, то масса тела с большей плотностью будет больше. Как правило, чем больше плотность жидкости, в которую погружается тело, тем больше выталкивающая сила. Плотность жидкости можно найти в интернете или в различных справочниках.
Как правило, чем больше плотность жидкости, в которую погружается тело, тем больше выталкивающая сила. Плотность жидкости можно найти в интернете или в различных справочниках.
- В нашем примере шар плавает в воде. Плотность воды приблизительно равна 1000 кг/м 3 .
- Плотности многих других жидкостей можно найти .
Найдите силу тяжести (или любую другую силу, действующую на тело вертикально вниз). Не важно, плавает ли тело или тонет, на него всегда действует сила тяжести. В естественных условиях сила тяжести (а точнее сила тяжести, действующая на тело массой 1 кг) приблизительно равна 9,81 Н/кг. Тем не менее, если на тело действуют и другие силы, например, центробежная сила, такие силы необходимо учесть и вычислить результирующую силу, направленную вертикально вниз.
- В нашем примере мы имеем дело с обычной стационарной системой, поэтому на шар действует только сила тяжести, равная 9,81 Н/кг.
- Однако если шар плавает в емкости с водой, которая вращается вокруг некоторой точки, то на шар будет действовать центробежная сила, которая не позволяет шару и воде выплескиваться наружу и которую необходимо учесть в расчетах.

Если у вас есть значения погруженного объема тела (в м 3), плотность жидкости (в кг/м 3) и сила тяжести (или любая другая сила, направленная вертикально вниз), то вы можете вычислить выталкивающую силу. Для этого просто перемножьте указанные выше значения, и вы найдете выталкивающую силу (в Н).
- В нашем примере: F b = V s × D × g. F b = 0,262 м 3 × 1000 кг/м 3 × 9,81 Н/кг = 2570 Н.
Выясните, будет ли тело плавать или тонуть. По приведенной выше формуле можно вычислить выталкивающую силу. Но, выполнив дополнительные расчеты, вы можете определить, будет ли тело плавать или тонуть. Для этого найдите выталкивающую силу для всего тела (то есть в вычислениях используйте весь объем тела, а не погруженный объем), а затем найдите силу тяжести по формуле G = (масса тела)*(9,81 м/с 2). Если выталкивающая сила больше силы тяжести, то тело будет плавать; если же сила тяжести больше выталкивающей силы, то тело будет тонуть. Если силы равны, то тело обладает «нейтральной плавучестью».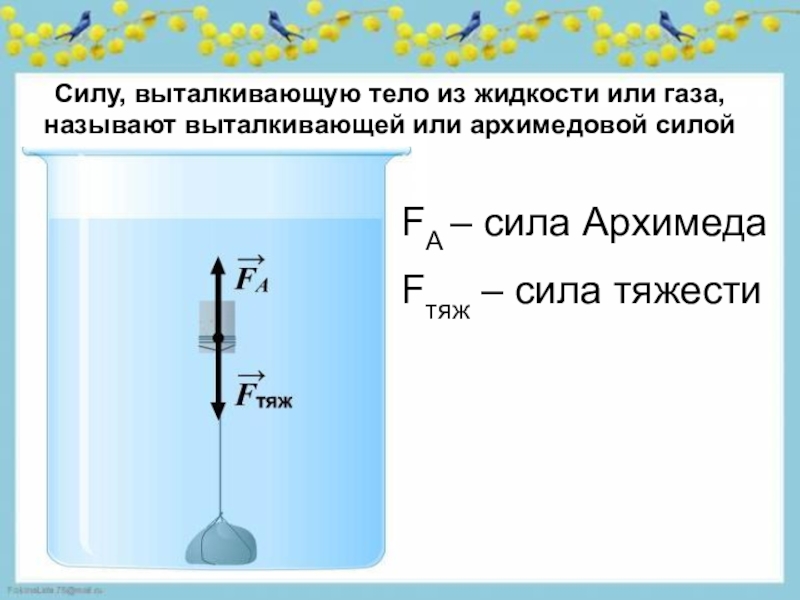
- Например, рассмотрим 20 килограммовое бревно (цилиндрической формы) с диаметром 0,75 м и высотой 1,25 м, погруженное в воду.
- Найдите объем бревна (в нашем примере объем цилиндра) по формуле V = π(радиус) 2 (высота) = π(0,375) 2 (1,25) = 0,55 м 3 .
- Далее вычислите выталкивающую силу: F b = 0,55 м 3 × 1000 кг/м 3 × 9,81 Н/кг = 5395,5 Н.
- Теперь найдите силу тяжести: G = (20 кг)(9,81 м/с 2) = 196,2 Н. Это значение намного меньше значения выталкивающей силы, поэтому бревно будет плавать.
Используйте описанные выше вычисления для тела, погруженного в газ. Помните, что тела могут плавать не только в жидкостях, но и в газах, которые вполне могут выталкивать некоторые тела, несмотря на очень небольшую плотность газов (вспомните про шар, наполненный гелием; плотность гелия меньше плотности воздуха, поэтому шар с гелием летает (плавает) в воздухе).
Постановка эксперимента
Поместите небольшую чашку в ведро.
 В этом простом эксперименте мы покажем, что на тело, погруженное в жидкость, действует выталкивающая сила, так как тело выталкивает объем жидкости, равный погруженному объему тела. Мы также продемонстрируем, как найти выталкивающую силу при помощи эксперимента. Для начала поместите небольшую чашку в ведро (или кастрюлю).
В этом простом эксперименте мы покажем, что на тело, погруженное в жидкость, действует выталкивающая сила, так как тело выталкивает объем жидкости, равный погруженному объему тела. Мы также продемонстрируем, как найти выталкивающую силу при помощи эксперимента. Для начала поместите небольшую чашку в ведро (или кастрюлю).Наполните чашку водой (до краев). Будьте осторожны! Если вода из чашки вылилась в ведро, вылейте воду и начните заново.
- Для эксперимента предположим, что плотность воды равна 1000 кг/м 3 (только если вы не используете соленую воду или другую жидкость).
- Для наполнения чашки до краев используйте пипетку.
Возьмите небольшой предмет, который поместится в чашке и не будет поврежден водой. Найдите массу этого тела (в килограммах; для этого взвесьте тело на весах и конвертируйте значение в граммах в килограммы). Затем медленно опустите предмет в чашку с водой (то есть погрузите тело в воду, но при этом не погружайте пальцы).
 Вы увидите, что некоторое количество воды вылилось из чашки в ведро.
Вы увидите, что некоторое количество воды вылилось из чашки в ведро.- В этом эксперименте мы опустим в чашку с водой игрушечный автомобиль массой 0,05 кг. Объем этого автомобиля нам не нужен, чтобы вычислить выталкивающую силу.
- ), а затем умножьте объем вытесненной воды на плотность воды (1000 кг/м 3).
- В нашем примере игрушечный автомобиль утонул, вытеснив около двух столовых ложек воды (0,00003 м 3). Вычислим массу вытесненной воды: 1000 кг/м 3 × 0,00003 м 3 = 0,03 кг.
Сравните массу вытесненной воды с массой погруженного тела. Если масса погруженного тела больше массы вытесненной воды, то тело утонет. Если масса вытесненной воды больше массы тела, то оно плавает. Поэтому для того, чтобы тело плавало, оно должно вытеснять количество воды с массой, превышающей массу самого тела.
- Таким образом, тела, имеющие небольшую массу, но большой объем, обладают наилучшей плавучестью. Эти два параметра характерны для полых тел.
 Вспомните лодку – она обладает превосходной плавучестью, потому что она полая и вытесняет много воды при небольшой массе самой лодки. Если бы лодка не была полой, она бы вообще не плавала (а тонула).
Вспомните лодку – она обладает превосходной плавучестью, потому что она полая и вытесняет много воды при небольшой массе самой лодки. Если бы лодка не была полой, она бы вообще не плавала (а тонула). - В нашем примере масса автомобиля (0,05 кг) больше массы вытесненной воды (0,03 кг). Поэтому автомобиль и утонул.
- Таким образом, тела, имеющие небольшую массу, но большой объем, обладают наилучшей плавучестью. Эти два параметра характерны для полых тел.
- Используйте весы, показания которых можно сбросить до 0 перед каждым новым взвешиванием. В этом случае вы получите точные результаты.
Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу вытесненной им жидкости.
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.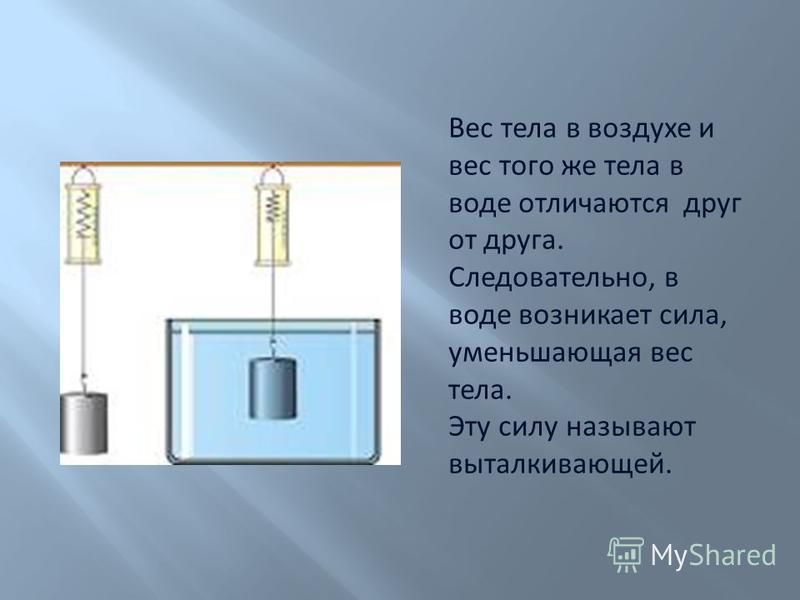
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести . Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории . В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
В каком случае сила архимеда. Вычисление силы архимеда. то тело плавает
Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.
Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела.Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.
В интегральной форме
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.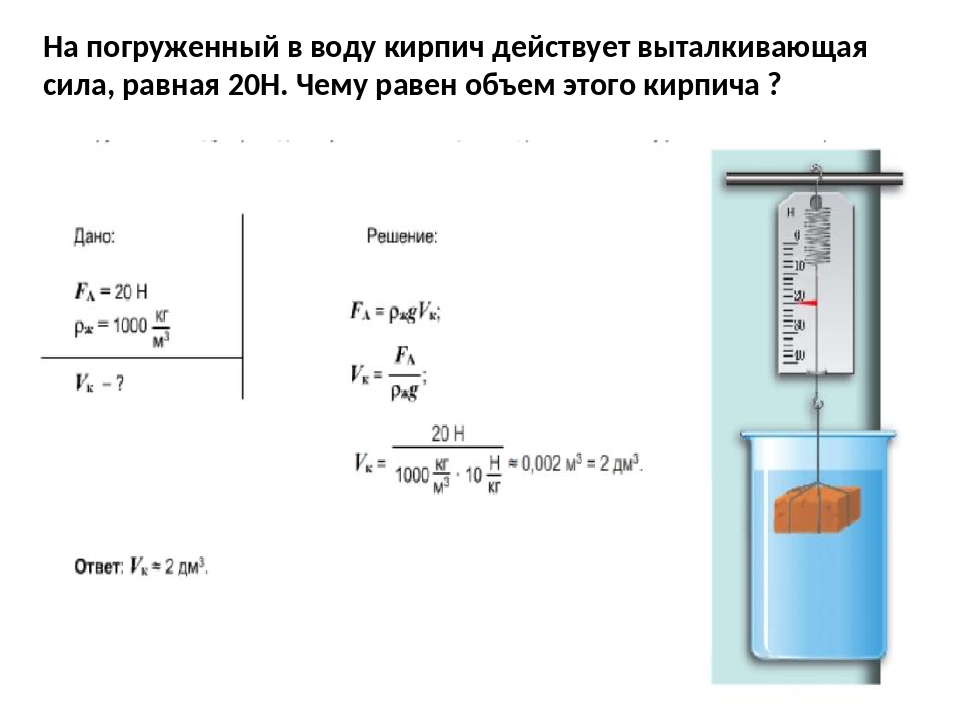
В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами
В формуле мы использовали:
Сила Архимеда
Плотность жидкости
Эмпирически еще в древней Греции было получено, что тело, погруженное в жидкость, весит меньше, чем находящееся в воздухе. На тело в жидкости со всех сторон она оказывает давление. Силы давления направлены перпендикулярно поверхности тела в каждой его точке. В том случае, если все силы, действующие на тело, были бы равны по модулю, то это тело испытывало только всестороннее сжатие. Мы знаем, что при увеличении глубины гидростатическое давление увеличивается, следовательно, силы давления, которые приложены к нижним частям тела больше, чем силы, которые действуют на тело вверху.
Если заменить все силы давления, которые приложены к телу, находящемуся в жидкости, одной результирующей силой, то эта сила будет направлена вверх. В этой связи ее назвали выталкивающей силой. По-другому ее называют силой Архимеда (${\overline{F}}_A$). Именно Архимед отметил факт ее существования и определил, как ее вычислить.
Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.
Величина силы Архимеда
Сила Архимеда, оказывающая действие на тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), в объеме вытесненной (вытесненным) этим телом.
Рассмотрим тело в виде прямоугольного параллелепипеда полностью находящееся в жидкости рис.1. Предположим, что верхнее и нижнее основания располагаются параллельно горизонту.
Силы давления, действующие на боковые грани параллелепипеда, попарно уравновешены (например, ${\overline{F}}_{12}$=$-{\overline{F}}_{21}$). Они только сжимают параллелепипед. Силы, которые действуют на верхнюю и нижнюю грани параллелепипеда не равны между собой. Сила ($F_1$), действия столба жидкости на верхнюю грань, будет равна:
Силы, которые действуют на верхнюю и нижнюю грани параллелепипеда не равны между собой. Сила ($F_1$), действия столба жидкости на верхнюю грань, будет равна:
где $\rho $ – плотность жидкости; $S$ – площадь основания; $h_1$ – высота столба жидкости над верхним основанием параллелепипеда.$\ p_0-$ давление атмосферы на поверхность жидкости.
Сила давления жидкости на нижнее основание параллелепипеда:
где $h_2$ – высота столба жидкости над нижним основанием. Так как $h_2>h_1$, значит $F_2>F_1$. Модуль результирующей силы, действующей на тело со стороны жидкости:
Если обозначить высоту параллелепипеда как $h=h_2-h_1$, получим:
где $V$ – объем параллелепипеда. При нахождении тела в жидкости (газе) частично, то под V понимают объем погруженный в вещество (жидкость, газ). Правую часть выражения (4) еще называют весом жидкости, которую вытесняет тело, погруженное в нее.
На тело, находящееся в жидкости или газе, действует сила Архимеда, величина которой равна весу вещества (жидкости или газа) в объеме погруженной части тела. Сила Архимеда направлена вертикально вверх.
Сила Архимеда направлена вертикально вверх.
Закон Архимеда (4) выполняется для тел любой формы.
Сила Архимеда дает возможность плавать разного рода кораблям, несмотря на то, что плотность материала, из которого изготовлен корпус транспортного средства в несколько раз больше, чем плотность воды. Необходимо только чтобы вес воды, которую вытесняет подводная часть судна, был равен силе тяжести, которая действует на судно. Средняя же плотность корабля меньше плотности воды.
Сила Архимеда действует на тела находящиеся в воздухе. Но так как плотность воздуха мала, действием этой силы часто пренебрегают. В состоянии невесомости сила Архимеда равна нулю. В состоянии невесомости нет гидростатического давления.
Следует учесть, рассуждая о действии силы Архимеда, мы имеем в виду, что тело окружено жидкостью (газом), может быть за исключением своей верхней части. Если тело примыкаем ко дну сосуда или его стенке, то равнодействующая сил гидростатического давления станет прижимать тело ко дну или стенке. {-2}$Н
{-2}$Н
Пример 2
Задание. Чему равна сила натяжения каната (N), при помощи которого из пресного водоема равномерно двигая, поднимают тело плотностью $\rho $ и объемом V? Плотность воды считайте известной (${\rho }_g$). Движение рассмотрите в жидкости.
Решение. Рассмотрим силы, действующие на тело, поднимаемое из воды (рис.2).
В соответствии со вторым законом Ньютона равнодействующая всех сил, приложенных к телу равна нулю, так как тело поднимают равномерно:
\[\overline{N}+m\overline{g}+{\overline{F}}_A=0\ \left(2.1\right).\]
В проекции на ось Y инерциальной системы отсчета, которую мы связали с Землей, уравнение (2.1) даст нам следующее скалярное выражение:
Масса поднимаемого тела может быть найдена как:
Силу Архимеда определим как:
Подставим правые части выражений (2.3) и (2.4) в формулу (2.2) вместо соответствующих величин, выразим силу натяжения каната:
Ответ. $N=\left(\rho -{\rho }_g\right)Vg$
F A = ρ g V , {\displaystyle F_{A}=\rho gV,}Описание
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести , прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление
p
{\displaystyle p} на глубине
h
{\displaystyle h} , оказываемое жидкостью плотностью
ρ
{\displaystyle \rho } на тело, есть
p
=
ρ
g
h
{\displaystyle p=\rho gh}
. Пусть плотность жидкости (
ρ
{\displaystyle \rho } ) и напряжённость гравитационного поля (
g
{\displaystyle g} ) – постоянные величины, а
h
{\displaystyle h} – параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. {**}grad(h)=\nabla h={\vec {e}}_{z}.}
{**}grad(h)=\nabla h={\vec {e}}_{z}.}
Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Замечание . Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погруженного тела на жидкость, приводит к изменению ее потенциальной энергии:
A = F Δ h = m ж g Δ h = Δ E p {\displaystyle \ A=F\Delta h=m_{\text{ж}}g\Delta h=\Delta E_{p}}
где m ж − {\displaystyle m_{\text{ж}}-} масса вытесненной части жидкости, Δ h {\displaystyle \Delta h} – перемещение ее центра масс. Отсюда модуль вытесняющей силы:
F = m ж g {\displaystyle \ F=m_{\text{ж}}g}
Инструкция
Архимедова сила возникает из-за разности давлений воды на уровне верхнего и нижнего срезов тела. На верхнюю часть давит столб воды высотой h2 с силой, равной весу этого . На нижнюю часть действует сила, равная весу столба высотой h3. Эта высота определяется сложением h2 и высотой самого тела. Согласно закону Паскаля, давление в жидкости или газе распределяется равномерно во все стороны. В том числе и вверх.
Эта высота определяется сложением h2 и высотой самого тела. Согласно закону Паскаля, давление в жидкости или газе распределяется равномерно во все стороны. В том числе и вверх.
Очевидно, что сила, действующая вверх, превышает силу, действующую вниз. Но, следует учесть, что принимается во внимание только воздействие столба жидкости. От собственного веса тела выталкивающая сила не зависит. Ни материал, из которого сделано тело, ни его иные качества, кроме размеров при вычислениях не используются. Расчет архимедовой силы базируется только на плотности жидкости и геометрических размерах погруженной части.
Существует два способа, архимедову силу, действующую на тело, погруженное в жидкость. Первый состоит в измерении объема тела и вычислении веса жидкости, занимающей аналогичный объем. Для этого необходимо, чтобы тело обладало правильной геометрической формой, то есть, было кубом, параллелепипедом, шаром, полусферой, конусом. Объем твердого тела более сложной формы рассчитать очень трудно, поэтому для определения силы Архимеда в этом случае существует более практичный способ № 2. Но о нем несколько позже.
Но о нем несколько позже.
Определив объем погружаемого тела, умножаем его на плотность жидкости и находим величину выталкивающей силы, действующей на это тело в однородной среде заданной плотности и на ускорение свободного падения g (9,8 м/с2). Формула для определения силы Архимеда выглядит так:
F=ρgV
ρ – удельная плотность жидкости;
g – ускорение свободного падения;
V – объем вытесненной жидкости.
Как и любая сила, она измеряется в Ньютонах (Н).
Второй способ базируется на измерении объема вытесненной жидкости. Он наиболее соответствует тому опыту, который и привел Архимеда к открытию своего закона. Этот способ очень удобен и при вычислении архимедовой силы при частичном погружении тела. Для получения необходимых данных исследуемое тело подвешивают на нитке и медленно опускают в жидкость.
Достаточно замерить уровень жидкости в сосуде до погружения тела и после, умножить разницу уровней на площадь поверхности и найти объем вытесненной жидкости. Как и в первом случае, умножаем этот объем на плотность жидкости и g. Полученная величина и является силой Архимеда. Чтобы единицей измерения силы стал Ньютон, следует объем измерять в м3, а плотность – в кг/м3.
Полученная величина и является силой Архимеда. Чтобы единицей измерения силы стал Ньютон, следует объем измерять в м3, а плотность – в кг/м3.
Закон архимеда простыми словами. Выталкивающая сила
Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.

Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Продолжим изучение архимедовой силы. Проделаем опыты. К коромыслу весов подвесим два одинаковых шара. Их вес одинаков, поэтому коромысло находится в равновесии (рис. «а»). Подставим под правый шар пустой стакан. От этого вес шаров не изменится, поэтому равновесие сохранится (рис. «б»).
Второй опыт. Подвесим к динамометру большую картофелину. Вы видите, что её вес равен 3,5 Н. Погрузим картофелину в воду. Мы обнаружим, что её вес уменьшился и стал равен 0,5 Н.
Вычислим изменение веса картофеля:
DW = 3,5 Н – 0,5 Н = 3 Н
Почему же вес картофеля уменьшился именно на 3 Н? Очевидно потому, что в воде на картофель подействовала выталкивающая сила такой же величины.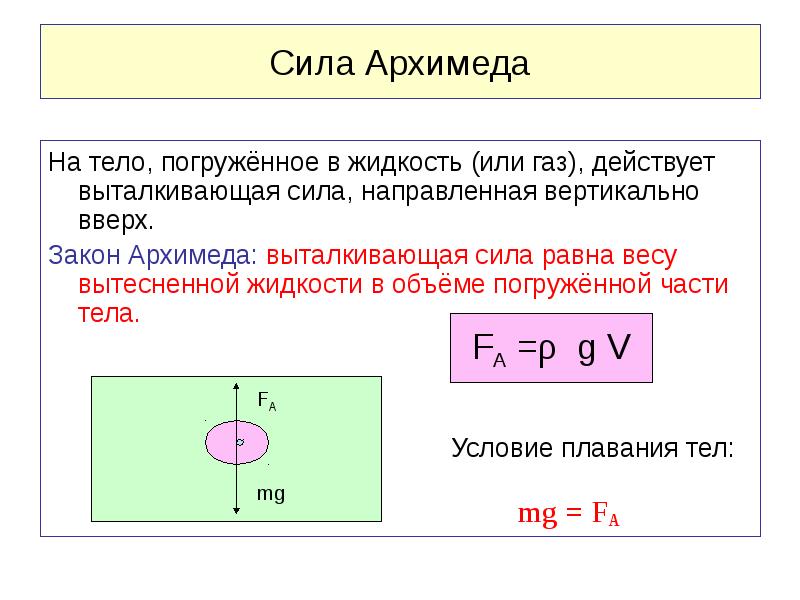 Другими словами, сила Архимеда равна изменению веса т ела:
Другими словами, сила Архимеда равна изменению веса т ела:
Эта формула выражает способ измерения архимедовой силы: нужно дважды измерить вес тела и вычислить его изменение. Полученное значение равно силе Архимеда.
Для вывода следующей формулы проделаем опыт с прибором «ведёрко Архимеда». Основные его части следующие: пружина со стрелкой 1, ведёрко 2, тело 3, отливной сосуд 4, стаканчик 5.
Сначала пружину, ведёрко и тело подвешивают к штативу (рис. «а») и отмечают положение стрелки жёлтой меткой. Затем тело помещают в отливной сосуд. По мере погружения тело вытесняет некоторый объём воды , который сливается в стаканчик (рис. «б»). Вес тела становится меньше, пружина сжимается, и стрелка поднимается выше жёлтой метки.
Перельём воду, вытесненную телом, из стаканчика в ведёрко (рис. «в»). Самое удивительное в том, что когда вода будет перелита (рис «г»), стрелка не просто опустится вниз, а укажет точно на жёлтую метку! Значит, вес влитой в ведёрко воды уравновесил архимедову силу . В виде формулы этот вывод запишется так:
В виде формулы этот вывод запишется так:
Обобщая результаты двух опытов, получим закон Архимеда : выталкивающая сила, действующая на тело в жидкости (или газе), равна весу жидкости (газа), взятой в объёме этого тела и направлена противоположно вектору веса.
В § 3-б мы указали, что сила Архимеда обычно направлена вверх. Поскольку она противонаправлена вектору веса, а он не всегда направлен вниз, архимедова сила также не всегда действует вверх. Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут всплывать не вверх, а отклоняясь к оси вращения.
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.
В интегральной форме
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами
В формуле мы использовали:
Сила Архимеда
Плотность жидкости
Несмотря на явные различия свойств жидкостей и газов, во многих случаях их поведение определяется одними и теми же параметрами и уравнениями, что позволяет использовать единый подход к изучению свойств этих веществ.
В механике газы и жидкости рассматривают как сплошные среды. Предполагается, что молекулы вещества распределены непрерывно в занимаемой ими части пространства. При этом плотность газа значительно зависит от давления, в то время как для жидкости ситуация иная. Обычно при решении задач этим фактом пренебрегают, используя обобщенное понятие несжимаемой жидкости, плотность которой равномерна и постоянна.
Определение 1
Давление определяется как нормальная сила $F$, действующая со стороны жидкости на единицу площади $S$.
$ρ = \frac{\Delta P}{\Delta S}$.
Замечание 1
Давление измеряется в паскалях. Один Па равен силе в 1 Н, действующей на единицу площади 1 кв. м.
В состояние равновесия давление жидкости или газа описывается законом Паскаля, согласно которому давление на поверхность жидкости, производимое внешними силами, передается жидкостью одинаково во всех направлениях.
При механическом равновесии, давление жидкости по горизонтали всегда одинаково; следовательно, свободная поверхность статичной жидкости всегда горизонтальна (кроме случаев соприкосновения со стенками сосуда). Если принять во внимание условие несжимаемости жидкости, то плотность рассматриваемой среды не зависит от давления.
Если принять во внимание условие несжимаемости жидкости, то плотность рассматриваемой среды не зависит от давления.
Представим некоторый объем жидкости, ограниченный вертикальным цилиндром. Поперечное сечение столба жидкости обозначим $S$, его высоту $h$, плотность жидкости $ρ$, вес $P=ρgSh$. Тогда справедливо следующее:
$p = \frac{P}{S} = \frac{ρgSh}{S} = ρgh$,
где $p$ – давление на дно сосуда.
Отсюда следует, что давление меняется линейно, в зависимости от высоты. При этом $ρgh$ – гидростатическое давление, изменением которого и объясняется возникновение силы Архимеда.
Формулировка закона Архимеда
Закон Архимеда, один из основных законов гидростатики и аэростатики, гласит: на тело, погруженное в жидкость или газ, действует выталкивающая или подъемная сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Замечание 2
Возникновение Архимедовой силы связано с тем, что среда – жидкость или газ – стремится занять пространство, отнятое погруженным в нее телом; при этом тело выталкивается из среды.
Отсюда и второе название для этого явление – выталкивающая или гидростатическая подъемная сила.
Выталкивающая сила не зависит от формы тела, также как и от состава тела и прочих его характеристик.
Возникновение Архимедовой силы обусловлено разностью давления среды на разных глубинах. Например, давление на нижние слои воды всегда больше, чем на верхние слои.
Проявление силы Архимеда возможно лишь при наличии тяжести. Так, например, на Луне выталкивающая сила будет в шесть раз меньше, чем на Земле для тел равных объемов.
Возникновение Силы Архимеда
Представим себе любую жидкую среду, например, обычную воду. Мысленно выделим произвольный объем воды замкнутой поверхностью $S$. Поскольку вся жидкость по условию находится в механическом равновесии, выделенный нами объем также статичен. Это означает, что равнодействующая и момент внешних сил, воздействующих на этот ограниченный объем, принимают нулевые значения. Внешние силы в данном случае – вес ограниченного объема воды и давление окружающей жидкости на внешнюю поверхность $S$. При этом получается, что равнодействующая $F$ сил гидростатического давления, испытываемого поверхностью $S$, равна весу того объема жидкости, который был ограничен поверхностью $S$. Для того чтобы полный момент внешних сил обратился в нуль, равнодействующая $F$ должна быть направлена вверх и проходить через центр масс выделенного объема жидкости.
При этом получается, что равнодействующая $F$ сил гидростатического давления, испытываемого поверхностью $S$, равна весу того объема жидкости, который был ограничен поверхностью $S$. Для того чтобы полный момент внешних сил обратился в нуль, равнодействующая $F$ должна быть направлена вверх и проходить через центр масс выделенного объема жидкости.
Теперь обозначим, что вместо этой условного ограниченной жидкости в среду было помещено любое твердое тело соответствующего объема. Если соблюдается условие механического равновесия, то со стороны окружающей среды никаких изменений не произойдет, в том числе останется прежним давление, действующее на поверхность $S$. Таким образом мы можем дать более точную формулировку закона Архимеда:
Замечание 3
Если тело, погруженное в жидкость, находится в механическом равновесии, то со стороны окружающей его среды на него действует выталкивающая сила гидростатического давления, численно равная весу среды в объеме, вытесненным телом. 2$.
2$.
Выталкивающая сила, действующая на тело, противоположна по направлению силе тяжести, поэтому поведение погруженного тела в среде зависит от соотношения модулей силы тяжести $F_T$ и Архимедовой силы $F_A$. Здесь возможны три случая:
- $F_T$ > $F_A$. Сила тяжести превышает выталкивающую силу, следовательно, тело тонет/падает;
- $F_T$ = $F_A$. Сила тяжести уравнивается с выталкивающей силой, поэтому тело «зависает» в жидкости;
- $F_T$
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы / или иначе силы Архимеда /, действующей на любое тело, погруженное в жидкость или газ.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Величина Архимедовой силы определяется по закону Архимеда.
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки. Скорее всего вы уже знаете легенду о том, как Архимед открыл свой закон: “Вызвал его однажды сиракузский царь Гиерон и говорит…. А что было дальше? …
Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
ВЕС ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ (ИЛИ ГАЗ)
Вес тела в вакууме Pо=mg .
Если тело погружено в жидкость или газ,
то P = Pо – Fа = Ро – Pж
Вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело.
Или иначе:
Тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость.
КНИЖНАЯ ПОЛКА
ОКАЗЫВАЕТСЯ
Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся.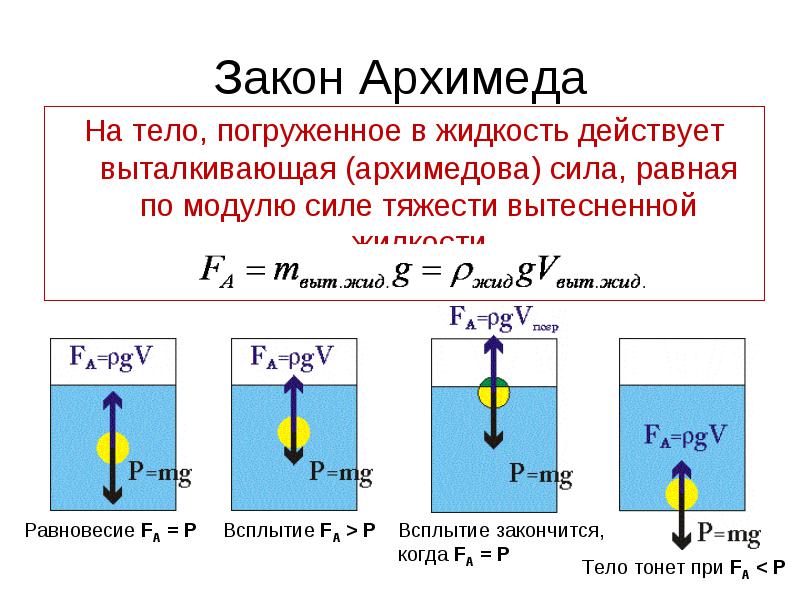 После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.
Поделитесь статьей с друзьями:
Похожие статьи
Пожалуйста, дважды проверьте веб-адрес или воспользуйтесь функцией поиска на этой странице, чтобы найти то, что вы ищете. Если вы уверены, что у вас правильный веб-адрес, но столкнулись с ошибкой, пожалуйста, свяжитесь с администрацией сайта. Спасибо. Возможно, вы искали…
|
Когда объект погружен в воду, он вытесняет 20 кг класса 11 по физике JEE_Main
Подсказка: Греческий ученый по имени Архимед обнаружил, что когда тело погружено в жидкость, частично или полностью погруженное, жидкость будет оказывать давление вверх. Эта направленная вверх тяга, действующая на тело, называется выталкивающей силой. Архимед установил, что выталкивающая сила, действующая на тело, равна весу жидкости, вытесняемой им при погружении в него. Здесь жидкостью является вода.
Эта направленная вверх тяга, действующая на тело, называется выталкивающей силой. Архимед установил, что выталкивающая сила, действующая на тело, равна весу жидкости, вытесняемой им при погружении в него. Здесь жидкостью является вода. Используемые формулы:
Вес тела определяется по формуле $W = mg$, где $m$ — масса тела, а $g$ — ускорение свободного падения.
Выталкивающая сила, действующая на тело, определяется выражением ${F_b} = \rho gV$, где $\rho $ – плотность жидкости, $g$ – ускорение свободного падения, а $V$ – объем вода вытеснена.{ – 2}}$ в уравнении (1) получаем, $W = 20 \times 10 = 200{\text{N}}$
Таким образом, вес воды, вытесненной при погружении в нее объекта, получается равным $W = 200{\text{N}}$ .
Основываясь на законе Архимеда, определите выталкивающую силу, действующую на объект.
Пусть ${F_b}$ — выталкивающая сила, действующая на тело, когда оно погружено в воду.
По закону Архимеда эта выталкивающая сила равна весу воды, вытесненной при погружении в нее предмета.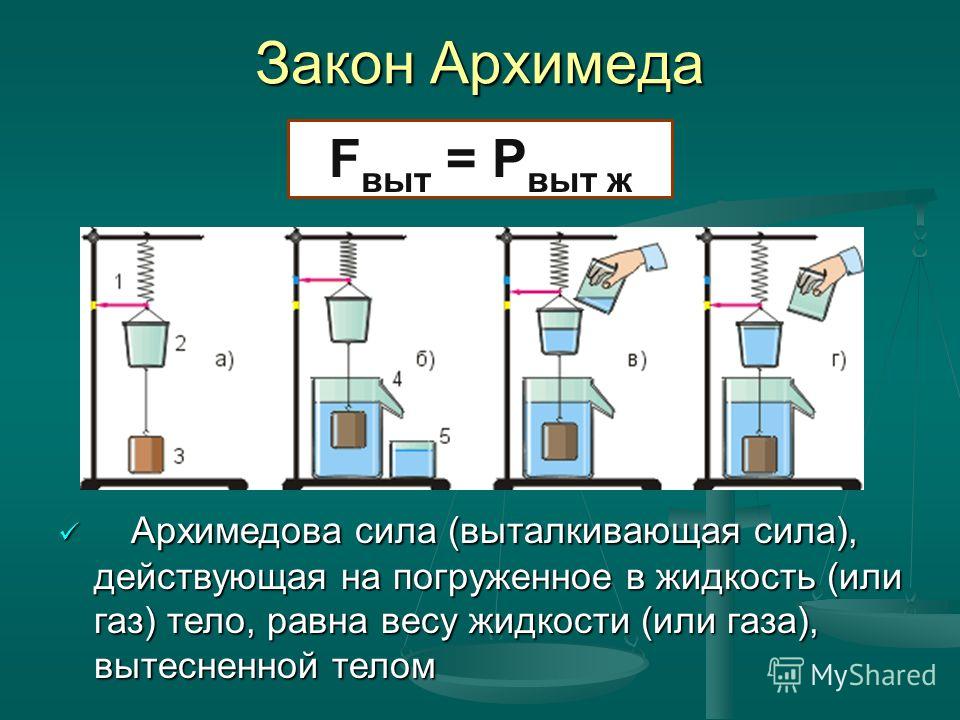 { – 2}}$ в уравнении (А) получаем, ${F_b} = 1000 \times 10 \times 0,02 = 200{\text{N}}$
{ – 2}}$ в уравнении (А) получаем, ${F_b} = 1000 \times 10 \times 0,02 = 200{\text{N}}$
$\следовательно $ получается выталкивающая сила, действующая на объект быть ${F_b} = 200{\text{N}}$.
11.7 Принцип Архимеда – Колледж физики: OpenStax
Резюме
- Определение выталкивающей силы.
- Государственный закон Архимеда.
- Поймите, почему объекты плавают или тонут.
- Поймите взаимосвязь между плотностью и принципом Архимеда.
Когда вы встаете после безделья в теплой ванне, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. рис. 1.)
Рис. 1. (а) Даже объекты, которые тонут, как этот якорь, частично поддерживаются водой, когда они погружены в воду. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Crystl)
(b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Crystl)Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Существует чистая направленная вверх или выталкивающая сила на любой объект в любой жидкости.(См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
ВЫПУСКНАЯ СИЛА
Выталкивающая сила – это чистая направленная вверх сила, действующая на любой объект в любой жидкости.
Рис. 2. Давление из-за веса жидкости увеличивается с глубиной, так как P=hρg . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие – выталкивающая сила F B . (Горизонтальные силы компенсируются.)
Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке 3.
Рис. 3. (a) На объект, погруженный в жидкость, действует выталкивающая сила F B . Если F B больше веса объекта, объект поднимется. Если F B меньше веса объекта, объект утонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес w fl . Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости.То есть F B = w fl , утверждение принципа Архимеда.
Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости.То есть F B = w fl , утверждение принципа Архимеда.Пространство, которое он занимает, заполнено жидкостью, имеющей вес [латекс]\boldsymbol{w _{\textbf{fl}}}.[/latex]Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна быть равна[латексу] ]\boldsymbol{w_{\textbf{fl}}},[/latex]вес жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н.C.), что он сформулировал этот принцип задолго до того, как прочно утвердились понятия силы. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
.[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/латекс]
, где [латекс]\boldsymbol{F_{\textbf{B}}}[/latex]является выталкивающей силой, а[латекс]\boldsymbol{w_{\textbf{fl}}}[/latex]является весом жидкость, вытесненная объектом. Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.
Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.
ПРИНЦИП АРХИМЕДА
В соответствии с этим принципом выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
.[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/латекс]
, где [латекс]\boldsymbol{F_{\textbf{B}}}[/latex]является выталкивающей силой, а[латекс]\boldsymbol{w_{\textbf{fl}}}[/latex]является весом жидкость, вытесненная объектом.
Humm … Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны давать никакого преимущества в плавучести. Как вы думаете, можно ли проверить это правило?
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ДОМАШНЕЕ РАССЛЕДОВАНИЕ
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?
Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?
Бросьте кусок глины в воду.3}[/latex]воды?
Стратегия для (а)
Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, приведенные в таблице 1. Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Раствор для (а)
Сначала мы используем определение плотности[латекс]\жирныйсимвол{\rho=\frac{m}{V}}[/латекс], чтобы найти объем стали, а затем подставляем значения для массы и плотности.7\textbf{ N}},[/latex]что намного больше, чем выталкивающая сила, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами.
Стратегия для (б)
Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка.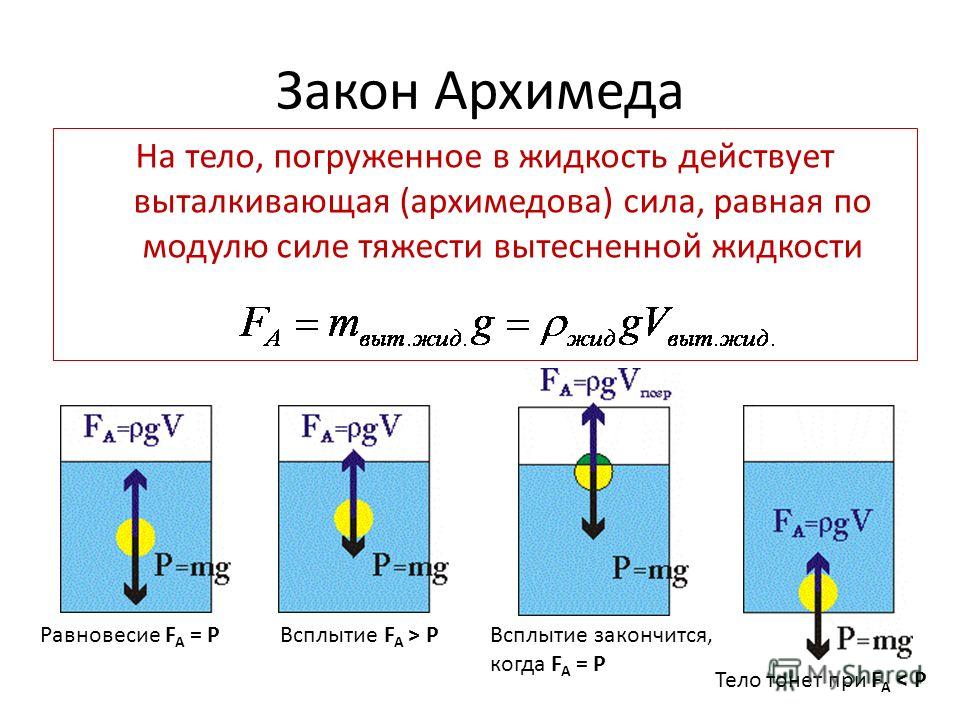 Выталкивающая сила равна весу этого объема воды.
Выталкивающая сила равна весу этого объема воды.
Раствор для (б)
Масса вытесненной воды определяется по ее отношению к плотности и объему, оба из которых известны.8\textbf{ N.}} \end{массив}[/latex]
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, и не утонуть.
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ДОМАШНЕЕ РАССЛЕДОВАНИЕ
Кусок бытовой алюминиевой фольги толщиной 0,016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз.
Плотность играет решающую роль в законе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке 4, например, незагруженный корабль имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным кораблем. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
. [латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{V _{\textbf{sub}}}{V _{\textbf{obj}}}} [/latex][латекс]\boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{V _{\textbf{fl}}}{V _{\textbf{obj}}}}.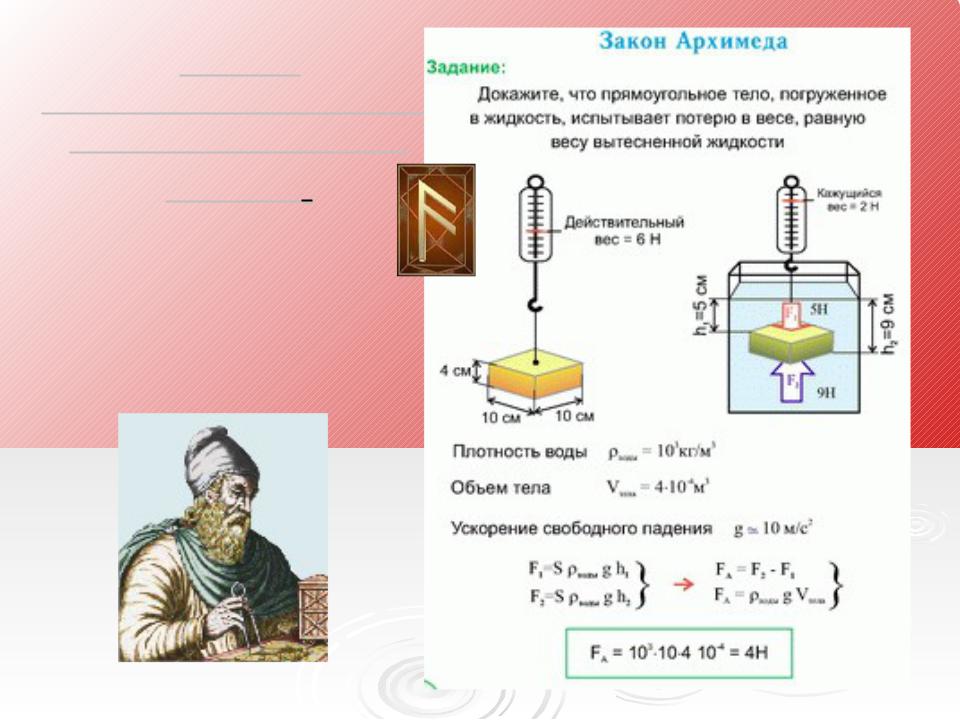 [/латекс]
[/латекс]
Погруженный объем равен объему вытесненной жидкости, который мы называем [латекс]\boldsymbol{V_{\textbf{fl}}}.[/latex]Теперь мы можем получить соотношение между плотностями, подставив [латекс]\жирныйсимвол {\rho=\frac{m}{V}}[/latex]в выражение. Это дает
[латекс]\boldsymbol{\frac{V _{\textbf{fl}}}{V_{\textbf{obj}}}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\ жирный символ {\ гидроразрыва {m _ {\ textbf {fl}}/\ rho _ {\ textbf {fl}}} {m _ {\ textbf {obj}}/\ bar {\ rho} _ {\ textbf {obj}}}} ,[/латекс]
, где [латекс]\boldsymbol{\bar{\rho}_{\textbf{obj}}}[/latex] — средняя плотность объекта, а [латекс]\boldsymbol{\rho _{\textbf{fl}} }[/latex] — плотность жидкости.Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}_{\textbf{obj}}}{\rho_{\ textbf{fl}}}}.[/latex]
Рисунок 4.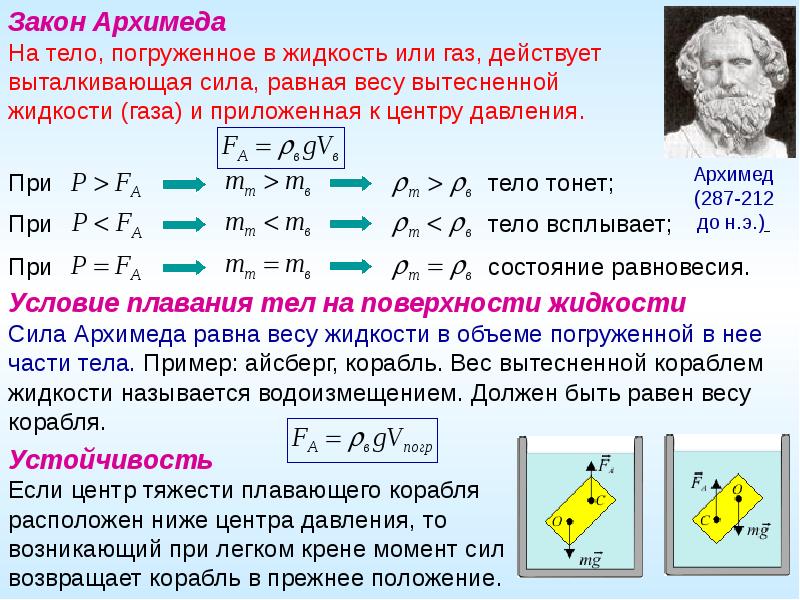 Незагруженный корабль (а) плавает выше в воде, чем загруженный корабль (б).
Незагруженный корабль (а) плавает выше в воде, чем загруженный корабль (б).Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра.Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес :
.[латекс]\boldsymbol{\textbf{удельный вес}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}}{\rho _{\textbf{w}}}}, [/латекс]
, где[латекс]\boldsymbol{\bar{\rho}}[/латекс]является средней плотностью объекта или вещества, а[латекс]\boldsymbol{\rho _{\textbf{w}}}[/латекс]является плотность воды при 4,00°С. Удельный вес безразмерен и не зависит от единиц измерения [латекс]\жирныйсимвол{\ро}.[/latex]Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния.Один прибор для измерения удельного веса показан на рисунке 5.
Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния.Один прибор для измерения удельного веса показан на рисунке 5.
УДЕЛЬНЫЙ ВЕС
Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Рисунок 5. Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.
Пример 2: расчет средней плотности: плавающая женщина
Предположим, что женщина весом 60,0 кг плавает в пресной воде, и [латекс]\жирныйсимвол{97,0\%}[/латекс] ее объема находится под водой, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность женщины, решив уравнение
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}_{\textbf{obj}}}{\rho_{\ textbf{fl}}}}[/latex]
для плотности объекта. 3}}.[/латекс]
3}}.[/латекс]
Обсуждение
Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. рис. 6.)
Рисунок 6. Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, что является частью определения плотности тела. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть.Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.
Существует много очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе». назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними.Даже кажущаяся твердой Земля обладает жидкими характеристиками.
назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними.Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Один из наиболее распространенных методов определения плотности показан на рисунке 7.
Рис. 7. (а) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости.Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты. Все эти расчеты основаны на законе Архимеда.
Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости.В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. Это
Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости.В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. Это
[латекс]\boldsymbol{\textbf{очевидная потеря веса}=\textbf{вес вытесненной жидкости}}[/латекс]
или
[латекс]\boldsymbol{\textbf{кажущаяся потеря массы}=\textbf{масса вытесненной жидкости.}}[/латекс]
Следующий пример иллюстрирует использование этой техники.
Пример 3: Расчет плотности: является ли монета подлинной?
Масса древнегреческой монеты определена в воздухе как 8.3}[/latex] и что эффекты, вызванные проволокой, подвешивающей монету, незначительны.
Стратегия
Чтобы вычислить плотность монеты, нам нужны ее масса (которая задана) и объем. Объем монеты равен объему вытесненной воды. Объем вытесненной воды[латекс]\boldsymbol{V_{\textbf{w}}}[/latex]можно найти, решив уравнение плотности[латекс]\boldsymbol{\rho=\frac{m}{V} }[/латекс]для[латекс]\boldsymbol{V}.[/латекс]
Объем монеты равен объему вытесненной воды. Объем вытесненной воды[латекс]\boldsymbol{V_{\textbf{w}}}[/latex]можно найти, решив уравнение плотности[латекс]\boldsymbol{\rho=\frac{m}{V} }[/латекс]для[латекс]\boldsymbol{V}.[/латекс]
Раствор
Объем воды [латекс]\boldsymbol{V _{\textbf{w}}=\frac{m _{\textbf{w}}}{\rho _{\textbf{w}}}}[/latex]где [латекс]\boldsymbol{m _{\textbf{w}}}[/latex] — масса вытесненной воды.3}.[/латекс]
Обсуждение
Из Таблицы 1 видно, что эта плотность очень близка к плотности чистого серебра, подходящего для этого типа древних монет. Большинство современных подделок не являются чистым серебром.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы. Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
ИССЛЕДОВАНИЯ PHET: ПЛАВУЧОСТЬ
Когда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками.Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Рисунок 8. Плавучесть- Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет.
 Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости. - Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
- Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Концептуальные вопросы
1: Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
2: Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом челноке? Поясните свой ответ.
3: Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ.
4: Мрамор упал в частично заполненную раковину ванны на дно. 3}?[/ латекс]
3}?[/ латекс]
2: Иногда бревна плавают вертикально в озере, потому что один конец стал заболоченным и более плотным, чем другой.3}?[/латекс]
5: В костях птиц есть воздушные карманы, чтобы уменьшить их вес — это также дает им среднюю плотность, значительно меньшую, чем у костей других животных. Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и находит, что ее масса равна[latex]\boldsymbol{45.0\textbf{g}}[/latex], а кажущаяся масса в погруженном состоянии составляет[latex]\boldsymbol{3.60\textbf {g}}[/latex](кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?
6: Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду.а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
7: Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
8: При иммерсионном измерении плотности женщины установлено, что она имеет массу 62,0 кг в воздухе и кажущуюся массу 0,0850 кг при полном погружении с пустыми легкими. а) Какую массу воды она вытесняет? б) Каков ее объем? (c) Рассчитайте ее плотность. (d) Если объем ее легких составляет 1,75 л, может ли она плавать, не топчась на месте, с легкими, наполненными воздухом?
9: Плотность некоторых рыб немного меньше плотности воды, и они должны прилагать усилия (плавать), чтобы оставаться под водой.3}?[/латекс]
10: (a) Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
11: (a) Какова плотность женщины, которая плавает в пресной воде с [латексом]\жирным символом{4,00\%}[/латекс] ее объема над поверхностью? Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой (кратковременно).3}[/latex](за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
13: Простой компас можно сделать, поместив небольшой стержневой магнит на плавающую в воде пробку. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
14: Какая часть веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
15: Известны случаи, когда подлые мошенники выдавали позолоченные вольфрамовые слитки за чистое золото и продавали их жадным по ценам намного ниже стоимости золота, но заслуженно намного выше стоимости вольфрама. С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
16: Двуспальный надувной матрас для кемпинга имеет размеры 100 см на 200 см на 15 см в надутом состоянии. Вес матраса 2 кг. Насколько тяжелый человек может выдержать надувной матрас, если его поместить в пресную воду?
17: По рисунку 3 докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда).Можно предположить, что выталкивающая сила равна[латекс]\boldsymbol{F_2-F_1}[/latex]и что концы цилиндра имеют одинаковую площадь[латекс]\boldsymbol{A}.[/latex]Обратите внимание, что объем цилиндр (и вытесняемая им жидкость) равен[латекс]\boldsymbol{(h_2-h_1)A}.[/latex]
18: (a) Мужчина массой 75,0 кг плавает в пресной воде, [латекс]\boldsymbol{3,00\%}[/latex] его объема над водой, когда его легкие пусты, и[латекс]\boldsymbol{5,00 \%}[/latex] его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Глоссарий
- Принцип Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, действующая на любой объект в любой жидкости
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
Решения
Задачи и упражнения
1:
[латекс]\boldsymbol{91.3}[/латекс]
(б)[латекс]\boldsymbol{6.34\%}[/латекс]
Она действительно больше плавает в морской воде.
13:
(а)[латекс]\boldsymbol{0.24}[/латекс]
(b)[латекс]\boldsymbol{0,68}[/латекс]
(c) Да, пробка будет плавать, потому что [латекс]\boldsymbol{\rho _{\textbf{obj}}\:
15:
Разница [латекс]\жирныйсимвол{0,006\%}. [/латекс]
[/латекс]
17:
[латекс]\begin{array}{lcl} \boldsymbol{F_{\textbf{net}}} & \boldsymbol{=} & \boldsymbol{F_2-F_1=P_2A-P_1A=(P_2-P_1)A} \ \ {} & \boldsymbol{=} & \boldsymbol{(h_2\rho _{\textbf{fl}}g-h_1\rho _{\textbf{fl}}g)A} \\ {} & \boldsymbol{=} & \boldsymbol{(h_2-h_1)\rho_{\textbf{fl}}gA} \end{массив}[/latex]
, где[латекс]\жирныйсимвол{\rho_{\textbf{fl}}}[/латекс]= плотность жидкости.Следовательно,
[латекс] \boldsymbol {F _ {\ textbf {net}} = (h_2-h_1) A \ rho _ {\ textbf {fl}} g = V _ {\ textbf {fl}} \ rho _ {\ textbf {fl}} г = м _ {\ textbf {фл}} г = ш _ {\ textbf {фл}}} [/латекс]
, где [латекс]\жирныйсимвол{w_{\textbf{fl}}}[/латекс]вес вытесненной жидкости.
27.6: Принцип Архимеда – Выталкивающая сила
Когда мы помещаем кусок твердого дерева в воду, он всплывает на поверхность. Плотность большинства деревьев меньше плотности воды, поэтому тот факт, что древесина плавает, не кажется таким уж удивительным. {B}\) обозначает результирующую силу, называемую выталкивающей силой, на поверхности элемента объема из-за давления жидкости.{B}=\rho_{f} V g \hat{\mathbf{k}}\] Выталкивающая сила зависит от плотности жидкости, гравитационной постоянной и объема элемента жидкости. Это макроскопическое описание выталкивающей силы, возникающей в результате очень большого числа столкновений молекул жидкости, называется принципом Архимеда .
{B}\) обозначает результирующую силу, называемую выталкивающей силой, на поверхности элемента объема из-за давления жидкости.{B}=\rho_{f} V g \hat{\mathbf{k}}\] Выталкивающая сила зависит от плотности жидкости, гравитационной постоянной и объема элемента жидкости. Это макроскопическое описание выталкивающей силы, возникающей в результате очень большого числа столкновений молекул жидкости, называется принципом Архимеда .
Теперь мы можем понять, почему, когда мы помещаем камень в воду, он тонет. Плотность камня больше плотности воды, поэтому выталкивающая сила на камне меньше силы тяжести на камне, и поэтому он ускоряется вниз.
Поместите однородный объект объема V и массы M с плотностью \(\rho_{o}=M / V\) в жидкость. Если плотность объекта меньше плотности жидкости, ρ , объект будет \(\rho_{o}<\rho_{f}\) плавать на поверхности жидкости. Часть объекта, находящаяся под поверхностью, вытесняет объем \(V_{1}\) жидкости. Часть объекта, находящаяся над поверхностью, вытесняет объем \(V_{2}=V-V_{1}\) воздуха (рис. 27.8).
27.8).
Поскольку плотность воздуха намного меньше плотности жидкости, выталкивающей силой воздуха на объект можно пренебречь.{g} = \ rho_ {f} V_ {1} g \ hat {\ mathbf {k}} – \ rho_ {o} V g \ hat {\ mathbf {k}} = \ rho_ {f} V_ {1} g \hat{\mathbf{k}}-\rho_{o}\left(V_{1}+V_{2}\right) g \hat{\mathbf{k}}\] Поэтому отношение объема открытые и погруженные части объекта должны удовлетворять \[\rho_{f} V_{1}=\rho_{o}\left(V_{1}+V_{2}\right)\] Мы можем решить уравнение. (27.6.4) и определить отношение объемов открытой и погруженной частей объекта \[\frac{V_{2}}{V_{1}}=\frac{\left(\rho_{f}- \rho_{o}\right)}{\rho_{o}}\] Теперь мы также можем понять, почему корабль массы M плавает.{B}=\rho_{f}\left(V_{s}+V_{w}\right) g \hat{\mathbf{k}}\] Если эта сила по модулю равна Mg , корабль будет плавать.
Пример 27.4 Закон Архимеда: плавающее дерево
Рассмотрим стакан с однородной площадью поперечного сечения A , наполненный водой с плотностью \(\rho_{w}\). Когда в стакан помещается прямоугольный деревянный брусок с площадью поперечного сечения \(A_{2}\), высотой и массой \(M_{b}\), дно бруска находится на неизвестной глубине z ниже уровня воды. поверхность воды.а) Насколько ниже поверхности z находится дно блока? б) Насколько увеличился уровень воды в стакане, когда в него поместили брусок?
Когда в стакан помещается прямоугольный деревянный брусок с площадью поперечного сечения \(A_{2}\), высотой и массой \(M_{b}\), дно бруска находится на неизвестной глубине z ниже уровня воды. поверхность воды.а) Насколько ниже поверхности z находится дно блока? б) Насколько увеличился уровень воды в стакане, когда в него поместили брусок?
Раствор
Мы пренебрегаем выталкивающей силой из-за вытесненного воздуха, потому что она пренебрежимо мала по сравнению с выталкивающей силой из-за воды. Стакан с плавающим деревянным бруском показан на рис. 27.10.
Рис. 27.10. Деревянный брусок, плавающий в стакане с водой. (a) Плотность деревянного бруска равна \(\rho_{b}=M_{b} / V_{b}=M_{b} / A_{b} h\) Объем погруженной части дерево равно \(V_{1}=A_{b} z\).Объем блока над поверхностью определяется выражением \(V_{2}=A_{b}(h-z)\). Мы можем применить уравнение (27.6.5) и определите, что \[\frac{V_{2}}{V_{1}}=\frac{A_{b}(hz)}{A_{b} z}=\frac{(hz )}{z}=\frac{\left(\rho_{w}-\rho_{b}\right)}{\rho_{b}}\] Теперь мы можем решить уравнение. (27.6.7) для глубины z дна блока \[z=\frac{\rho_{b}}{\rho_{w}} h=\frac{\left(M_{b} / A_{ b} h\right)}{\rho_{w}} h=\frac{M_{b}}{\rho_{w} A_{b}}\]
(27.6.7) для глубины z дна блока \[z=\frac{\rho_{b}}{\rho_{w}} h=\frac{\left(M_{b} / A_{ b} h\right)}{\rho_{w}} h=\frac{M_{b}}{\rho_{w} A_{b}}\]
(b) До помещения бруска в стакан объем воды в стакане был равен \(V_{w}=A s_{i}\), где \(s_{i}\) – начальная высота стакана. вода в стакане.Когда древесина плавает в стакане, объем воды в стакане равен \(V_{w}=A s_{f}-A_{b} z\), где \(s_{f}\) конечная высота воды в стакане и \(A_{b} z\) – объем погруженной части блока. Поскольку объем воды не изменился \[A s_{i}=A s_{f}-A_{b} z\] Мы можем решить уравнение. (27.6.9) для изменения высоты воды \(\Delta s=s_{f}-s_{i}\), через i – глубины z дна блока, \[\Delta s =s_{f}-s_{i}=\frac{A_{b}}{A} z\] Теперь подставим уравнение.(27.6.8) в уравнение. (27.6.10) и определить изменение высоты воды \[\Delta s=s_{f}-s_{i}=\frac{M_{b}}{\rho_{w} A}\]
Пример 27.5 Камень внутри плавающей салатницы
Камень массой mr и плотностью \(m_{r}\) помещен в салатник массой \(m_{b}\). Салатница и камень плавают в стакане с водой плотностью \(\rho_{w}\). Стакан имеет площадь поперечного сечения A. Затем камень вынимают из стакана и дают ему опуститься на дно стакана. Уровень воды поднимается или падает, когда камень бросают в воду?
Стакан имеет площадь поперечного сечения A. Затем камень вынимают из стакана и дают ему опуститься на дно стакана. Уровень воды поднимается или падает, когда камень бросают в воду?
 Поэтому уровень воды падает, когда камень падает в воду из салатницы.
Поэтому уровень воды падает, когда камень падает в воду из салатницы.Пример 27.6 Блок, плавающий между маслом и водой
Деревянный брусок кубической формы, каждая сторона которого имеет длину l = 10 см, плавает на границе раздела воздуха и воды.{-3}\).
б) Какова плотность деревянного бруска?
Раствор
(а) Выталкивающая сила равна силе тяжести, действующей на брусок. Следовательно, \[\rho_{b} g V=\rho_{\mathrm{w}} g V_{1}+\rho_{a} g\left(V-V_{1}\right)\], где \(V_ {1}\) — объем воды, вытесняемой блоком, \(V_{2}=V-V_{1}\) — объем воздуха, вытесняемый блоком, V — объем блока, \(\ rho_{b}\) — плотность деревянного бруска, а \(\rho_{a}\) — плотность воздуха (рис. 27.{-3}
\конец{массив}\]
Поскольку \(\rho_{b}>\rho_{o}\), приведенный выше анализ верен.
Узнайте о выталкивающей силе и законе Архимеда
Рассмотрим объект, например банку, погруженную в жидкость. Выталкивающая сила, действующая на банка задается разницей между направленной вверх и вниз силой как:
Поскольку давление связано с силой и площадью как P = F/A, перестановкой мы получаем F = PA. Восходящая сила возникает из-за давления на дно и наоборот, таким образом:
Восходящая сила возникает из-за давления на дно и наоборот, таким образом:
Fплавучесть=Pнижняя часть A−Pверхняя часть A{F_{плавучая}} = {P_{нижняя часть}}A – {P_{верхняя часть}}{\rm{ } }AFплавучесть=Pниз A−Pверх A
Давление также определяется как ρgh:
Fплавучесть=(ρghbottom)A−(ρghtop)A{F_{плавучесть}} = \left( {\rho g{h_ {bottom}}} \right)A – \left( {\rho g{h_{top}}} \right){\rm{}}AFbuoyant=(ρghbottom)A−(ρghtop)A
Fплавучесть =ρgA(hвнизу−верху){F_{плавучесть}} = \rho gA\left( {{{\rm{h}}_{низ – }}_{верхнее}{\rm{}}} \right)Fплавучесть =ρgA(hbottom−top)
Поскольку разница между дном банки (hbottomh_{bottom}hbottom) и верхом (htoph_{top}htop) равна высоте банки, уравнение может быть записано как:
Fbuoyant=ρgAhcan{F_{плавучесть}} = \rho gA{h_{can}}Fbuoyant=ρgAhcan
Поскольку площадь, умноженная на высоту, дает объем цилиндра, термин AhcanAh_ {can}Ahcan заменен на V. Это объем жидкости, вытесненной банкой, поэтому он записывается как VfV_fVf.
Это объем жидкости, вытесненной банкой, поэтому он записывается как VfV_fVf.
Fплавучесть=ρgVf{F_{плавучесть}} = \rho g{V_f}Fплавучесть=ρgVf
Плотность (ρ) может быть записана как масса, деленная на объем. Таким образом, плотность, умноженная на объем (ρVf\rho V_fρVf) — это масса жидкость, mfm_fmf:
Fbuoyant=mfg{F_{плавучесть}} = {m_f}gFbuoyant=mfg
Масса жидкости, умноженная на силу тяжести, дает вес вытесненной жидкости, WfW_fWf
Fbuoyant=Wf {F_{плавучесть}} = {W_f}Fплавучесть=Wf
Это математическое уравнение для принципа Архимеда
Набор вопросов 8
Набор вопросов 8Вопросы с несколькими вариантами ответов
1) Давление воды наибольшее по сравнению с
а.вершина подводного объекта.
б . дно подводного объекта.
в. сторон подводного объекта.
д. одинакова для всех поверхностей.
Рассуждение: Нижняя часть объекта на большей глубине. Поскольку давление зависит от глубины, дно будет действует более высокое давление. См. стр. 247.
2) Плотина в нижней части толще, чем в верхней частично потому что
а.вода плотнее на более глубоких уровнях.
б . давление воды увеличивается с увеличением глубины.
в. поверхностное натяжение существует только на поверхности жидкостей.
д. это выглядит лучше.
3) Давление в жидкости зависит от жидкости
а. плотность.
б. глубина.
с . Оба из них.
д. ни один из них.
4) Давление на дно кувшина, наполненного водой НЕ зависит от
а.ускорение из-за силы тяжести.
б. плотность воды.
в.высота жидкости.
д. площадь поверхности воды.
5) Один литр воды имеет массу
а. 1 килограмм.
б. 1 ньютон.
в. Оба из них.
д. ни один из них.
Обоснование: Один литр означает 1000 см3 вода.Плотность воды 1 г/см3. Таким образом, 1000 см3 воды имеет массу: (1000 см3)х(1 г/см3) = 1000 г = 1 кг.
6) Масса кубометра воды
а. 1 кг.
б. 10 кг.
в. 100 кг.
д . 1000 кг.
7) Пемза — плавучая вулканическая порода. Его плотность
а. меньше плотности воды.
б. равна плотности воды.
в. больше плотности воды.
Рассуждение: Чтобы плавать, плотность объекта должна быть меньше плотности жидкости.
8) Причина того, что выталкивающая сила действует вверх на подводное объект в том, что
а.
он действует в направлении противодействия гравитации.
б. если бы он действовал вниз, ничего бы не всплыло.
в.вес вытесненной жидкости реагирует восходящей силой.
д . восходящее давление на дно больше, чем нисходящее давление против верхней части затопленного объекта.
Обоснование: Этот вопрос обсуждается в компьютерный урок плавучести.
9) Полностью погруженный объект всегда смещает собственный
а. объем жидкости.
б.вес жидкости.
в. плотность жидкости.
д. все из этого.
10) Рыба обычно вытесняет свою собственную
и . объем воды.
б. вес воды.
с . Оба из них.
д. ни один из них.
Обоснование: Подробнее см. на стр. 254.
Плотность рыбы близка к плотности воды. Таким образом, вытесненный объем
воды имеет тот же вес, что и рыба.
11) Когда судно переходит из пресной воды в соленую, оно поплавок
а. ниже в воде.
б. выше в воде.
в. при том же уровне воды.
Обоснование: В соленой воде плотность вода выше. Таким образом, для создания той же плавучести требуется меньший объем воды. усилие. См. стр. 255.
12) Какова выталкивающая сила, действующая на 10-тонное судно, плавающее в океан?
а.менее 10 тонн
б. 10 тонн
в. более 10 тонн
д. зависит от плотности морской воды
13) Каков вес воды, вытесненной 100-тонным плавучий корабль?
а. менее 100 тонн
б. 100 тонн
в. более 100 тонн
д. 100 куб.м
14) Когда объект частично или полностью погружен в жидкий, буйный
а.силой, равной его собственному весу.
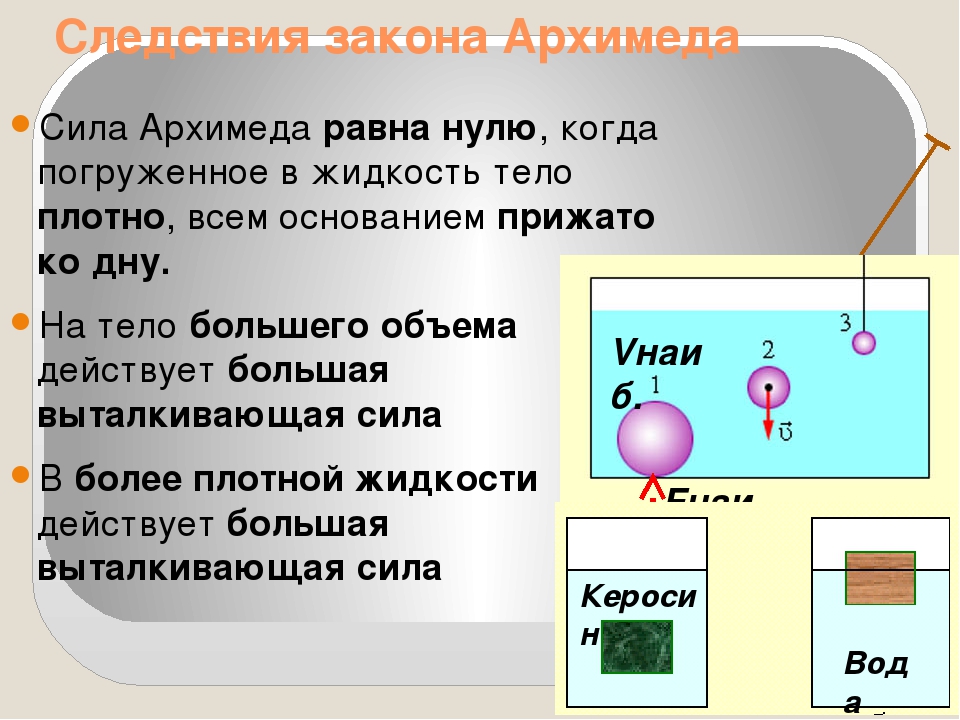
б . силой, равной весу вытесненной жидкости.
в. и плавает из-за закона Архимеда.
д. но тем не менее тонет.
15) Выталкивающая сила на предмет наименьшая, когда объект
а. частично погружен в воду.
б. погружается недалеко от поверхности.
в. погружается почти на дно.
д.ни один из них.
16) Выталкивающая сила на камне минимальна, когда камень находится под водой
а. возле поверхности.
б. на полпути ко дну.
в. возле дна.
д. все вышеперечисленное.
эл. ничего из вышеперечисленного
Обоснование: Выталкивающая сила останется то же самое, пока объект полностью погружен. Это потому, что плавучесть сила – это вес вытесненной воды.По мере того, как объект погружается глубже, вытесненная вода остается такой же, как и выталкивающая сила.
17) Причина, по которой спасательный жилет помогает вам плавать,
а.
куртка делает вас меньше весить.
б. куртка имеет ту же плотность, что и средний человек.
в. куртка отталкивает воду.
д. если вы утонете, куртка утонет.
и . плотность как у вас, так и у куртки вместе меньше, чем у вас плотность одна.
18) Артериальное давление обычно выше у вашего
а. уши.
б. футов.
в. одинаково в каждом.
19) В водонапорной башне просверлены три отверстия, которые заполнен водой в показанных местах. Вода будет бить наибольшее горизонтальное расстояние от отверстия
а. А.
б. Б.
в. С.
д. Горизонтальное расстояние будет одинаковым для всех трех отверстий.
20) Омары живут на дне океана. Плотность омара
а. больше, чем плотность морской воды.
б. равна плотности морской воды.
в.меньше плотности морской воды.
21) Омар заползает на напольные весы под водой на дне океана.По сравнению с его весом над поверхностью, Омар будет иметь кажущийся вес под водой, равный
.а. больше.
б . меньше.
в. то же.
22) Два спасательных жилета имеют одинаковый объем, но один заполнен пенополистиролом, а другой заполнен песком. Когда два спасательных круга полностью погружены в воду, плавучий сила больше на той, что заполнена
а.пенопласт.
б. песок.
в. одинаково на каждом, если их объемы одинаковы.
23) Когда кубик льда в стакане воды тает, уровень воды
а. поднимается.
б. падает.
в. остается прежним.
24) Камень, подвешенный на весах, весит 5 Н над водой и 3 Н при погружении в воду. Чему равна выталкивающая сила камня?
а.
8 Н
б. 5 Н
в. 3 N
д . 2 Н
25) Яйцо кладут на дно миски, наполненной с водой. В воду медленно добавляют соль, пока яйцо не поднимется. и плавает. Из этого эксперимента можно сделать
выводов.а. кальций в яичной скорлупе отталкивается хлоридом натрия.
б . плотность соленой воды превышает плотность яйца.
в. выталкивающая сила не всегда действует вверх.
д. соль опускается на дно.
Обучение физике | Почему мертвое тело плавает в воде?
Возможно, вы видели в фильмах мертвые тела, плавающие по воде. Человеческое тело не должно плавать на воде, учитывая его вес. Правильно! В противном случае нам не нужно учиться плавать, чтобы оставаться на плаву в воде. Этот вопрос о том, почему мертвое тело плавает, мог прийти вам на ум. Почему бы не задать этот вопрос на уроке физики? Итак, давайте сегодня ответим на этот вопрос на уроке физики.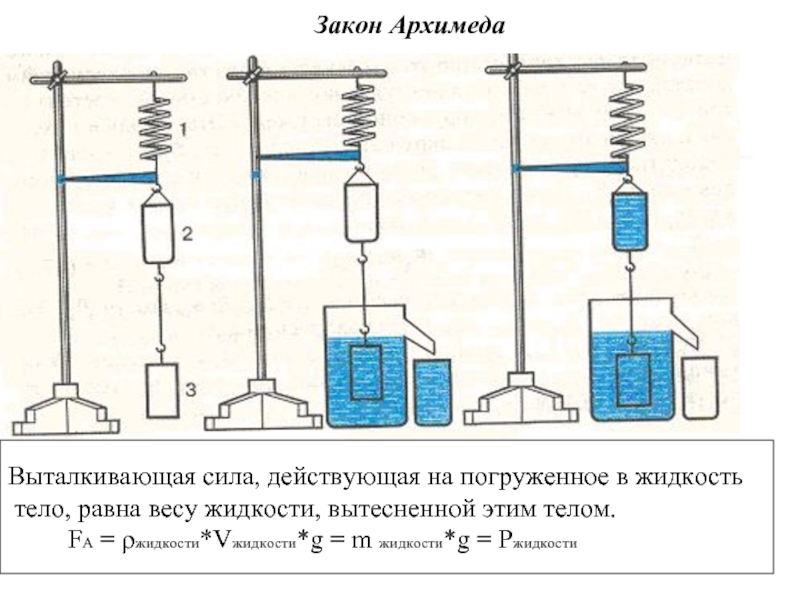 Если человек не умеет плавать, он, скорее всего, утонет в воде. А мертвое тело, наоборот, плавает по воде. Вы знаете, почему это так?
Если человек не умеет плавать, он, скорее всего, утонет в воде. А мертвое тело, наоборот, плавает по воде. Вы знаете, почему это так?
Согласно закону Архимеда, когда тело частично или полностью погружено в воду, оно вытесняет воду, равную его объему. Тело плавает в воде, если его вес меньше веса такого же объема воды. Если его вес равен весу такого же объема воды, он останется на плаву. Например, дерево или пробка плавают на воде, потому что их плотность меньше плотности воды.Тела, плотность которых больше плотности воды, тонут в воде.
Плотность человеческого тела меньше плотности воды. Поэтому, когда труп человека падает в воду, он несколько секунд плавает в ней. Но когда вода попадает в тело, его плотность становится больше, и он тонет. Но когда его тело начинает расширяться из-за дальнейшего добавления воды, объем всего тела увеличивается, что приводит к снова уменьшению его плотности. Другими словами, вес воды, вытесненной его телом, становится больше веса тела.В результате он начинает плавать.



 , 20:18
, 20:18