Лекция для СПО по математике по теме “Матрицы” для 2 курса
ФИНАНСЫ Лекция 1
Раздел 1. Основы линейной алгебры
Тема 1.1. Матрицы и операции над матрицами. Определители и их свойства
Цель: приобретение базовых знаний в области фундаментального раздела математики – линейной алгебры. Изучить понятие матрицы, её видов, операции над матрицами, определителей и их свойств.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Вид занятия: Комбинированное занятие, включающее в себя ознакомление с новым материалом, применение знаний и умений на практике, закрепление изученного.
Ход занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
Изучить теоретический материал по теме «Матрицы. Выполнение операций над матрицами. Определители и их свойства».
Рассмотреть примеры решения типовых заданий.
Ответить на контрольные вопросы.
Организационный момент.
Приветствует обучающихся. Проверяет подготовленность к учебному занятию, организует внимание обучающихся. Обеспечивает благоприятный настрой.
Создание проблемной ситуации при постановке темы, цели и задач лекции.
В школьном курсе алгебры 7 – 9 классов рассматриваются различные способы решения систем линейных уравнений: метод подстановки, метод сложения, метод двойного сложения, графический метод, метод сравнения. Возникает вопрос, а существуют ли какие-либо другие способы решения данных систем. Действительно, кроме методов, изучаемых в школе, существуют и другие, доступные для учащихся старших классов методы решения систем линейных уравнений: метод Крамера, метод Гаусса, матричный метод. Эти методы способствуют развитию внимания, памяти. При применении этих методов встречаются новые понятия: «матрица», «определитель», «минор», «дополнение». Возникает необходимость уметь вычислять определители, миноры, дополнения.
Возникает вопрос, а существуют ли какие-либо другие способы решения данных систем. Действительно, кроме методов, изучаемых в школе, существуют и другие, доступные для учащихся старших классов методы решения систем линейных уравнений: метод Крамера, метод Гаусса, матричный метод. Эти методы способствуют развитию внимания, памяти. При применении этих методов встречаются новые понятия: «матрица», «определитель», «минор», «дополнение». Возникает необходимость уметь вычислять определители, миноры, дополнения.
При решении систем линейных уравнений методом Гаусса также нужно уметь выполнять преобразования над строками матриц.
Что же такое матрица, какие действия с ними можно выполнять?
Изучение нового материала.
Определение матрицы.
Совокупность чисел, расположенных в виде прямоугольной таблицы, состоящей из строк и столбцов, называют матрицей порядка ( на ) и обозначают символом .
.
Числа называют элементами матрицы. Каждый элемент имеет два индекса: первый показывает номер строки, в которой стоит этот элемент, а второй – номер столбца. Размерность матрицы указывать не обязательно. При матрицу называют матрицей-строкой, а при – матрицей-столбцом.
Матрицу, все элементы которой, равны нулю, называют нулевой матрицей и обычно обозначают .
Таким образом, .
Если число строк матрицы совпадает с числом ее столбцов, т.е. , то матрицу называют
.
Ее называют единичной матрицей. Все элементы ее главной диагонали равны единице, а все остальные элементы – нули.
Квадратную матрицу называют треугольной, если все ее элементы, стоящие ниже или выше элементов главной диагонали, равны нулю. Например, матрицы и треугольные, причем матрицу называют верхнетреугольной, а матрицу – нижнетреугольной.
Например, матрицы и треугольные, причем матрицу называют верхнетреугольной, а матрицу – нижнетреугольной.
Определение. Две матрицы одинакового порядка и называют
равными и пишут = , если все элементы с одинаковыми
индексами обеих матриц совпадают.
Матрицей размером тп называется прямоугольная таблица, составленная из тп чисел и имеющая т строк и п столбцов. Числа ij, составляющие матрицу, называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй – номер столбца, в котором расположен этот элемент.
Для изображения матрицы употребляют круглые скобки и часто обозначают ее одной буквой, например,
А=(ij)= (1)
Первый индекс i (i = 1, 2, …m) обозначает номер строки, второй j (j = 1, 2, …n) – столбец матрицы. Матрицу принято обозначать заглавными буквами, например А, В, С и т.д.
Матрицу принято обозначать заглавными буквами, например А, В, С и т.д.
Горизонтальный ряд чисел называется строкой, а вертикальный – столбцом.
Определение. Если т = п
Определение. Если же m n, то матрица называется прямоугольной матрицей.
Определение. Две матрицы считаются равными, если они имеют одинаковые размеры и их соответствующие элементы равны. Пусть А = (ij) размером т п, В = (ij) размером pq. A = B, если m = p, n = q и ij
Определение. Последовательность элементов квадратной матрицы с одинаковыми индексами (i = j) называется главной диагональю матрицы (11, 22, 33,…,nn)/
Определение. Если в квадратной матрице все недиагональные элементы равны нулю (ij= 0, при
А =
Определение. Квадратная диагональная матрица, у которой элементы главной диагонали равны единице, называется единичной матрицей Е.
А =
Определение. Матрица, все элементы которой равны нулю, называется нуль-матрицей.
Определение. Матрица, состоящая только из одной строки, называется матрицей-строкой.
Определение.
Определение. Матрицу Аt называют транспонированной по отношению к матрице А ,если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками.
Например, пусть А – матрица размеров т п:
транспонированная ей матрица:
Можно сказать, что транспонированная матрица получается переворачиванием матрицы вокруг главной диагонали.
Переход от матрицы
Перечислим свойства операции транспонирования:
(At)t = A,
(A + B)t = At + Bt,
(A)t = At,
(AB)t = BtAt.

2. Операции над матрицами.
Определение. Суммой двух матриц А = (ij) и В = (ij) одинаковых размеров т п называется матрица С того же размера, элементы которых равны сумме соответствующих элементов матриц А и В. С=А + В = (ij + ij) для i = 1, 2, …, m, j = 1, 2, …, n. Ясно, что сложение матриц сводится к сложению всех пар соответствующих элементов. Для матриц разных размеров сумма не определена.
Сложение матриц подчиняется законам:
А + В = В + А (переместительный закон)
(А + В) + С = А + (В + С) (сочетательный закон)
А + О = О + А = А.

Для любой матрицы А размеров т п существует матрица В тех же размеров такая, что А + В = В + А = О. При этом если А = (ij) и В = (ij), то ij = – ij. Матрица В называется матрицей, противоположной матрице А и обозначается – А.
Определение. Произведением матрицы А = (ij) размером т п на число называется матрица (ij) тех же размеров, которая обозначается А.
Свойства умножения матрицы на число:
1. (А) = ()А.
( + )А = А + А.

(А + В) = А + В.
1А = А.
Разность двух матриц А и В одинаковых размеров определяется равенствами:
А – В = А + (- В) = А + (-1)В.
Определение. Произведением матрицы А = (ij) размеров т п на матрицу В = (ij) размеров nk называется матрица С = (сij) размеров mk, каждый элемент сij которой вычисляется по формуле
сij = i11j + i22j + … + innj , i = 1,2,…,m; j = 1,2,…,n. (2)
(2)
Другими словами, элемент сij равняется сумме произведений элементов строки с номером i матрицы А на соответствующие элементы столбца с номером j матрицы В. Произведение матрицы А на матрицу В обозначается АВ.
Замечание: Операция умножения двух матриц выполнима лишь в том случае, когда число столбцов первой матрицы – сомножителя А должно равняться числу строк второй матрицы сомножителя В. Если это условие не выполнено, произведение не существует.
Для запоминания формулы (2) пользуются мнемоническим правилом: «умножение i-той строки матрицы А на j-тый столбец матрицы В».
Приведем примеры умножения матриц.
Вычислить произведение АВ, где
Число столбцов в первой матрице совпадает с числом строк во второй матрице, поэтому произведение АВ существует. Положим С = АВ. В матрице С столько же строк, сколько в матрице А, и столько же столбцов, сколько в матрице В, т.е. матрица С размеров 23. Пусть С = (сij), тогда по формуле (2) получаем
Положим С = АВ. В матрице С столько же строк, сколько в матрице А, и столько же столбцов, сколько в матрице В, т.е. матрица С размеров 23. Пусть С = (сij), тогда по формуле (2) получаем
с11 = 2(-1) + 32 = 4, с12 = 22 + 31 = 7, с13 = 20 + 3(-1) = – 3,
с21 =(-1)(-1) + 42 = 9, с22 =(-1)2 + 41 = 2, с23 = (-1)0 + 4(-1) =-4.
Записав эти числа в матрицу, получим
Заметим, что произведение ВА не существует, поскольку число столбцов в матрице В не равно числу строк в матрице А.
2.
3.
4.
5.
Свойства умножения матриц:
Умножение матриц в некоторых отношениях похоже на умножение чисел, а в других отношениях отличается от умножения чисел.
Для чисел = . Для матриц из существования произведения АВ даже не следует существование произведения ВА (см. пример 1 из предыдущего пункта). Если оба произведения АВ и ВА существуют, то это могут быть матрицы разных размеров (см. примеры 4 и 5 из предыдущего пункта). Даже если матрицы АВ и ВА существуют и имеют одинаковые размеры, в общем случае АВ ВА. Например,
Если для чисел = 0, то один из сомножителей равен нулю. Но для матриц, как видно из приведенного примера, равенство АВ = О может выполняться и в случае, когда А О и В О.
Умножение матриц, подобно умножению чисел, подчиняется ассоциативному закону:
(АВ)С = А(ВС).
Известно, что сложение и умножение чисел связаны дистрибутивным законом.
 Свойство дистрибутивности умножения относительно сложения для матриц выражается двумя равенствами:
Свойство дистрибутивности умножения относительно сложения для матриц выражается двумя равенствами:
(А + В)С = АС + ВС,
А(В + С) = АВ + АС.
(АВ) = (А)В = А(В).
Рассмотрим теперь операцию умножения матрицы на матрицу. Пусть имеем матрицу
и матрицу
.
Сразу же обратим внимание на размерность матриц: число столбцов матрицы равно числу строк матрицы . Это условие является необходимым для того, чтобы можно было матрицу умножить на матрицу .
Будем рассматривать элементы каждой строки матрицы как координаты мерных векторов:
;
;
…………………….
.
Аналогично элементы каждого столбца матрицы также будем рассматривать как координаты мерных векторов:
;
;
;
……………………
Произведением матрицы на матрицу назовем матрицу .
Как видим, элементами матрицы являются скалярные произведения векторов , где на векторы , где .
Рассмотрим свойства операции умножения матриц. Из определения операции умножения матрицы на матрицу вовсе не следует, что можно умножить матрицу на матрицу . Это осуществимо только при условии, что . В противном случае произведение просто не существует. Следовательно, бессмысленно говорить о коммутативности операции умножения матриц. Однако имеют место свойства ассоциативности: и дистрибутивности: ; , которые легко проверяются.
Очевидно, что если и квадратные матрицы одного порядка, то существуют произведения и , но нельзя утверждать, что . Если же матрицы и таковы, что , то их называют перестановочными.
Особую роль при умножении квадратных матриц играет единичная матрица . Легко показать, что для любой квадратной матрицы имеет место равенство , т.е во множестве квадратных матриц порядка матрица является аналогом числа 1 во множестве действительных чисел.
Пусть имеем матрицу . Если в ней поменять местами строки и столбцы, сохранив их порядок, то получим матрицу , которую называют транспонированной для .
Легко заметить следующие два свойства операции транспонирования матрицы:
1°. Если матрицу транспонировать дважды, то в результате получим исходную матрицу : .
2°. При транспонировании квадратной матрицы элементы главной диагонали не меняются.
Определение 4. Если квадратная матрица совпадает со своей
транспонированной матрицей , то ее называют
симметрической.
Из определения симметрической матрицы видно, что ее элементы должны быть симметричны относительно главной диагонали. Например, матрица является симметрической, а матрица – нет.
Определители и их свойства.
Рассмотрим квадратную матрицу второго порядка . Определителем этой матрицы называют число, обозначаемое , или , или , полученное из элементов матрицы по следующему правилу: . Например, если , то .
Например, если , то .
Рассмотрим теперь квадратную матрицу третьего порядка . Определителем этой матрицы назовем число .
= , или
(1)
Равенство (1) называют разложением определителя по элементам первой строки.
Выражения ; и называют алгебраическими дополнениями элементов , и соответственно. Таким образом, разложение определителя третьего порядка по элементам первой строки может быть записано в виде: .
Нетрудно заметить, что аналогичным образом определитель третьего порядка может быть разложен по элементам второй и третьей строк, а также по элементам первого, второго или третьего столбца.
Рассмотрим теперь квадратную матрицу го порядка . Определителем такой матрицы, разложенным по ой строке, назовем число
, где – элементы ой строки, а – их алгебраические дополнения.
Рассмотрим основные свойства определителей.
1). При умножении всех элементов любой строки матрицы на некоторое число определитель исходной матрицы умножается на это число.
2). Определитель матрицы, содержащей нулевую строку, равен нулю.
3). При перестановке местами любых двух строк матрицы без изменения остальных строк определитель меняет знак.
4). Определитель матрицы, содержащей две одинаковые строки, равен нулю.
5). Определитель матрицы не изменится, если к любой строке матрицы прибавить любую другую строку, умноженную на некоторое число.
6). Определитель произведения двух квадратных матриц одинакового порядка равен произведению определителей этих матриц.
7). При транспонировании квадратной матрицы ее определитель не меняется.
Квадратную матрицу называют вырожденной
(невырожденной), если .
Число называют собственным числом матрицы , если оно является корнем уравнения .
Закрепление нового материала.
Пример 1: Найти сумму матриц: А = и В = .
Решение: С = А + В С =
Чтобы вычесть из матрицы А матрицу В, надо к матрице А прибавить матрицу, противоположную матрице В.
А – В = А + (-В)
Пример 2: Найти разность матриц А – В: А = и В = .
Решение: С = А – В -В = С =
Пример 3: Дана матрица А =. Найти матрицу С = 2А.
Решение: С = 2А =
Пример 4: Даны матрицы: А = и В = .
Найти произведение матриц А и В.
Решение: С = АВ С = С =
Задания для решения:
1.Вычислить произведение матриц:
.
Решение. Первая матрица имеет размеры 2´3, а вторая размеры 3´3, поэтому произведение существует. В результате умножения получится матрица С = (cij) размеров 2´3. Вычислим ее элементы.
с11 = (-2)×3 + 3×1 + 1×4 = 1, с12 = (-2)×(-1) + 3×1 + 1×6 = 11,
с13 = (-2)×2+3×0+1×8 = 4, с21 = 0×3 + 5×1 + 6×4 = 29,
с22 = 0×(-1) + 5×1 + 6×6 = 41, с23 = 0×2+5×0+6×8 = 48.
Ответ: .
2.Вычислить произведение матриц:
.
Решение. Первая матрица имеет размеры 3´3, а вторая размеры 2´3. Число столбцов в первой матрице (3) не совпадает с числом строк во второй матрице (2), поэтому произведение не существует,
Ответ: произведение не существует.
3.Вычислить произведение матриц:
.
Ответ: .
4.Вычислить произведение матриц:
.
5.Вычислить произведение матриц:
.
6.Вычислить произведение матриц:
.
7.Вычислить произведение матриц:
.
8.Вычислить произведение матриц:
.
9.Вычислить степень матрицы:
.
10. Вычислить степень матрицы:
.
11. Вычислить значение многочлена f(x) = 2x2 + x – 3 от матрицы .
Указание. f(А) = 2А2 + А – 3Е, где Е – единичная матрица размеров 2´2. Далее использовать определения операций умножения матриц, умножения матрицы на число и сложения матриц.
Ответ: .
12. Вычислить значение многочлена f(x) = x3 – x2 + x + 2 от матрицы
.
Ответ: .
Итоги занятия.
Вопросы и задания для самооценки:
ЧТО НАЗЫВАЕТСЯ:
– матрицей, квадратной, единичной, диагональной, транспонированной матрицей;
– обратной матрицей, рангом матрицы, базисным минором;
– определителем, минором, алгебраическим дополнением;
ПЕРЕЧИСЛИТЬ СВОЙСТВА:
– суммы матриц, произведения матрицы на скаляр, произведения матриц;
– определителей.
ЗАПИСАТЬ ФОРМУЛЫ:
– для вычисления определителей второго и n-го порядка, для нахождения обратной матрицы.
СФОРМУЛИРОВАТЬ
– существования и единственности обратной матрицы; теорему о базисном миноре.
Домашнее задание. Учить определения, составить опорную схему конспекта. Выполнить упражнения:
1.Найти , если .
2.Даны матрицы .
Найти: а) б)
3.Найти матрицу , если
а)
б)
Рефлексия.
Продолжи фразу
1. Я повторил …
2. Я узнал …
3. Я научился…
4. Я могу…
БГУ, 2017. – 53 с.
Please use this identifier to cite or link to this item:
https://elib. bsu.by/handle/123456789/176724
bsu.by/handle/123456789/176724
| Title: | Матрицы и определители : учебно-методическая разработка для студентов физического факультета и факультета радиофизики и компьютерных технологий / Л. Л. Березкина [и др.] ; БГУ, Физический фак., Каф. высшей математики и математической физики. – Минск : БГУ, 2017. – 53 с. |
| Authors: | Березкина, Лариса Лукинична Егоров, Андрей Александрович Глецевич, Марина Александровна Чехменок, Татьяна Александровна |
| Keywords: | ЭБ БГУ::ЕСТЕСТВЕННЫЕ И ТОЧНЫЕ НАУКИ::Математика |
| Issue Date: | 10-Jul-2017 |
| Abstract: | Учебно-методическая разработка включает в себя темы «Матрицы и линейные операции над ними», «Умножение матриц», «Транспонирование матриц», «Определители», «Обратная матрица», входящие в курс «Аналитическая геометрия и линейная алгебра» на физическом факультете и факультете радиофизики и компьютерных технологий БГУ. В кратком виде изложена теория, необходимая для успешного усвоения данных тем и для решения практических задач по ним. Разобрано большое количество примеров различного уровня сложности, а также приведены задачи для самостоятельного решения с ответами. Содержание и структура учебно-методической разработки позволяет студентам использовать ее для самостоятельной работы над данными темами. В кратком виде изложена теория, необходимая для успешного усвоения данных тем и для решения практических задач по ним. Разобрано большое количество примеров различного уровня сложности, а также приведены задачи для самостоятельного решения с ответами. Содержание и структура учебно-методической разработки позволяет студентам использовать ее для самостоятельной работы над данными темами. |
| URI: | http://elib.bsu.by/handle/123456789/176724 |
| Registration number: | Деп. в БГУ 07.07.2017, №005107072017 |
| Appears in Collections: | Учебная литература. 2017 Учебники и другие пособия физического факультета |
Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.
План-конспект занятия по дисциплине «Прикладная математика», тема: «Матрицы. Определители»
Омский летнотехнический колледж гражданской авиации имени А. В. Ляпидевского
филиал федерального государственного бюджетного образовательного учреждения
«Ульяновский институт гражданской авиации имени Главного маршала авиации Б.П.
высшего образования
Бугаева»
(ОЛТК ГА – филиал ФГБОУ ВО УИ ГА)
Планконспект занятия
по дисциплине «Прикладная математика»
2 курс
Тема: «Матрицы. Определители»
Разработала:
Пищагина Елена Станиславна Омск 2018
Тема урока. Матрицы. Определители.
Дата проведения: 13 сентября 2018 г.
Тип занятия: Комбинированный урок
Вид занятия: Получение, систематизация и закрепление знаний
Цели занятия:
Обучающие:
– Формировать навыки выполнения операций над матрицами: сложение, вычитание,
умножение матрицы на число, произведение матриц;
– Формировать умения находить определители матриц.
Развивающие:
– Формирование умения пользоваться математическими инструментами,
– Формирование умения применять свои знания при решении математических задач по
данной теме;
– Углубление знаний, умений и навыков; развитие творческой деятельности:
интуиции, пространственного воображения, смекалки;
– Развитие мыслительных операций посредством конкретизации, развитие зрительной
памяти, потребности к самообразованию, способствовать развитию познавательных
процессов.
В. Ляпидевского
филиал федерального государственного бюджетного образовательного учреждения
«Ульяновский институт гражданской авиации имени Главного маршала авиации Б.П.
высшего образования
Бугаева»
(ОЛТК ГА – филиал ФГБОУ ВО УИ ГА)
Планконспект занятия
по дисциплине «Прикладная математика»
2 курс
Тема: «Матрицы. Определители»
Разработала:
Пищагина Елена Станиславна Омск 2018
Тема урока. Матрицы. Определители.
Дата проведения: 13 сентября 2018 г.
Тип занятия: Комбинированный урок
Вид занятия: Получение, систематизация и закрепление знаний
Цели занятия:
Обучающие:
– Формировать навыки выполнения операций над матрицами: сложение, вычитание,
умножение матрицы на число, произведение матриц;
– Формировать умения находить определители матриц.
Развивающие:
– Формирование умения пользоваться математическими инструментами,
– Формирование умения применять свои знания при решении математических задач по
данной теме;
– Углубление знаний, умений и навыков; развитие творческой деятельности:
интуиции, пространственного воображения, смекалки;
– Развитие мыслительных операций посредством конкретизации, развитие зрительной
памяти, потребности к самообразованию, способствовать развитию познавательных
процессов. Воспитательные:
– Повторить правила выполнения операций с матрицами;
– Познакомиться с понятиями минор элемента матрицы и алгебраическое дополнение;
– Сформулировать правило вычисления определителей любого порядка
Используемые технологии: Дифференцированного обучения, коммуникативного общения,
Междисциплинарные связи: Электротехника, теория электрических цепей, информатика,
вычислительная техника
развивающее обучение
Планируемые образовательные результаты.
Обучающийся знает:
– Понятие матрицы и ее элементы
– Основные виды матриц
– Понятие, минора и определителя матрицы. Виды определителей и их свойства
– Применение и значение матриц в практической деятельности
Умеет:
– Определять вид матрицы
– Выполнять основные действия с матрицами (сложение, вычитание, умножение матрицы на
2
– Воспитание устойчивого интереса к математике,
– Воспитание математической культуры,
– Развитие самоорганизации обучающихся
Задачи: число, умножение матрицы на матрицу)
– Вычислять определитель матрицы, миноры и алгебраические дополнения
– Транспонировать матрицы
– Грамотно формулировать свои мысли по поставленному вопросу, анализировать, делать
выводы.
Воспитательные:
– Повторить правила выполнения операций с матрицами;
– Познакомиться с понятиями минор элемента матрицы и алгебраическое дополнение;
– Сформулировать правило вычисления определителей любого порядка
Используемые технологии: Дифференцированного обучения, коммуникативного общения,
Междисциплинарные связи: Электротехника, теория электрических цепей, информатика,
вычислительная техника
развивающее обучение
Планируемые образовательные результаты.
Обучающийся знает:
– Понятие матрицы и ее элементы
– Основные виды матриц
– Понятие, минора и определителя матрицы. Виды определителей и их свойства
– Применение и значение матриц в практической деятельности
Умеет:
– Определять вид матрицы
– Выполнять основные действия с матрицами (сложение, вычитание, умножение матрицы на
2
– Воспитание устойчивого интереса к математике,
– Воспитание математической культуры,
– Развитие самоорганизации обучающихся
Задачи: число, умножение матрицы на матрицу)
– Вычислять определитель матрицы, миноры и алгебраические дополнения
– Транспонировать матрицы
– Грамотно формулировать свои мысли по поставленному вопросу, анализировать, делать
выводы. Основные термины, понятия: матрица, определитель матрицы, минор, алгебраическое
дополнение.
Оборудование: доска, мел.
План урока:
1) Организационный этап. (2 мин.)
2) Постановка цели и задач занятия. Мотивация учебной деятельности обучающихся.
(5 мин.)
3) Актуализация опорных знаний (10 мин)
4) Закрепление умений (15 мин)
5) Первичное усвоение новых знаний. (25 мин.)
6) Первичное закрепление и систематизация изученного материала (23 мин.)
5) Подведение итогов занятия (5 мин.)
6) Информация о домашнем задании, инструктаж по его выполнению. (3 мин.)
7) Рефлексия (2 мин.)
Ход урока:
1. Организационный этап.
Приветствие курсантов. Проверка готовности курсантов к занятию.
2. Постановка цели урока. Мотивация учебной деятельности обучающихся.
Цель занятия изучение теоретического материала и формирование практических навыков
при решении задач по теме: Матрицы.
Основные термины, понятия: матрица, определитель матрицы, минор, алгебраическое
дополнение.
Оборудование: доска, мел.
План урока:
1) Организационный этап. (2 мин.)
2) Постановка цели и задач занятия. Мотивация учебной деятельности обучающихся.
(5 мин.)
3) Актуализация опорных знаний (10 мин)
4) Закрепление умений (15 мин)
5) Первичное усвоение новых знаний. (25 мин.)
6) Первичное закрепление и систематизация изученного материала (23 мин.)
5) Подведение итогов занятия (5 мин.)
6) Информация о домашнем задании, инструктаж по его выполнению. (3 мин.)
7) Рефлексия (2 мин.)
Ход урока:
1. Организационный этап.
Приветствие курсантов. Проверка готовности курсантов к занятию.
2. Постановка цели урока. Мотивация учебной деятельности обучающихся.
Цель занятия изучение теоретического материала и формирование практических навыков
при решении задач по теме: Матрицы. Операции с матрицами. Определитель.
Матричная алгебра широко применяется в различных отраслях знания – в математике,
физике, информатике, экономике, электронике. Например, матрицы используется для решения
систем алгебраических и дифференциальных уравнений, нахождения значений физических величин
в квантовой теории, шифрования сообщений в Интернете.
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным
квадратом». Основным применением матриц было решение линейных уравнений.
При решении систем линейных уравнений используют такие методы как: Метод Гаусса,
Метод Крамера, Матричный метод. Данные методы связаны с понятием матрицы и определителя
матрицы.
3 3. Актуализация опорных знаний
Вопросы по теме предыдущего занятия:
1. Что называется прямоугольной матрицей?
2. Какая матрица называется квадратной?
3. Какую диагональ квадратной матрицы называют главной?
4. Какая матрица называется нулевой?
5.
Какая матрица называется единичной?
6.
Операции с матрицами. Определитель.
Матричная алгебра широко применяется в различных отраслях знания – в математике,
физике, информатике, экономике, электронике. Например, матрицы используется для решения
систем алгебраических и дифференциальных уравнений, нахождения значений физических величин
в квантовой теории, шифрования сообщений в Интернете.
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным
квадратом». Основным применением матриц было решение линейных уравнений.
При решении систем линейных уравнений используют такие методы как: Метод Гаусса,
Метод Крамера, Матричный метод. Данные методы связаны с понятием матрицы и определителя
матрицы.
3 3. Актуализация опорных знаний
Вопросы по теме предыдущего занятия:
1. Что называется прямоугольной матрицей?
2. Какая матрица называется квадратной?
3. Какую диагональ квадратной матрицы называют главной?
4. Какая матрица называется нулевой?
5.
Какая матрица называется единичной?
6. Какая матрица называется треугольной?
7. Какая матрица называется диагональной
8. Какие матрицы называются равными?
9. Что называется суммой двух матриц?
10. Перечислите свойства сложения матриц.
11. Как умножить матрицу на число?
12. Какие две матрицы можно перемножить?
13. Перечислите свойства умножения матриц.
14. Какая матрица называется транспонированной?
15. Какая матрица называется матрицастрока?
16. Какая матрица называется матрицастолбец?
17. Какое уравнение называется матричным?
18. Что такое след матрицы?
4. Закрепление умений
Пример 1. Определить размеры матриц
Решение. Матрица
имеет размеры
, а матрица
Пример 2. Вычислить след матрицы
А =
2
1
1
0
1
2
4
2
3
Решение: Чтобы вычислить след исходной матрицы, нужно сложить элементы на главной
диагонали:
Sp( A ) = 2 1 + 3 = 4
Ответ: След матрицы A равен 4
4 Пример 3. Вычислить
A
1
1
2
4
3
3
А + В =
А – В =
1
1
1
1
2
4
2
4
3
3
3
3
+
0
1
–
0
1
B
0
1
1
3
5
3
.
Какая матрица называется треугольной?
7. Какая матрица называется диагональной
8. Какие матрицы называются равными?
9. Что называется суммой двух матриц?
10. Перечислите свойства сложения матриц.
11. Как умножить матрицу на число?
12. Какие две матрицы можно перемножить?
13. Перечислите свойства умножения матриц.
14. Какая матрица называется транспонированной?
15. Какая матрица называется матрицастрока?
16. Какая матрица называется матрицастолбец?
17. Какое уравнение называется матричным?
18. Что такое след матрицы?
4. Закрепление умений
Пример 1. Определить размеры матриц
Решение. Матрица
имеет размеры
, а матрица
Пример 2. Вычислить след матрицы
А =
2
1
1
0
1
2
4
2
3
Решение: Чтобы вычислить след исходной матрицы, нужно сложить элементы на главной
диагонали:
Sp( A ) = 2 1 + 3 = 4
Ответ: След матрицы A равен 4
4 Пример 3. Вычислить
A
1
1
2
4
3
3
А + В =
А – В =
1
1
1
1
2
4
2
4
3
3
3
3
+
0
1
–
0
1
B
0
1
1
3
5
3
.
5
3
5
3
=
3
1
1
2
2
0
=
1
0
8
1
6 7
.
,
1
3
1
3
Пример 4. Найти сумму матриц
,
Решение: Матрицы складывать нельзя.
Пример 5. Умножить матрицу на число 2.
Матрица
Число k=2.
Решение: Для того чтобы умножить матрицу A на число k нужно каждый элемент
матрицы A умножить на это число.
Таким образом, произведение матрицы A на число k есть новая матрица:
5 Ответ:
Пример 6. Транспонировать матрицу
.
Решение: Транспонирование матрицы А заключается в замене строк этой матрицы ее столбцами с
сохранением их номеров. Полученная матрица обозначается через AT
Пример 7. Найти число строк и столбцов матрицы C, которая является произведением двух
матриц A и B следующих размерностей:
а) 2 Х 10 и 10 Х 5;
б) 10 Х 2 и 2 Х 5;
в) 4 Х 4 и 4 Х 10.
Решение: а) 2 Х 5;
б) 10 Х 5;
в) 4 Х 10.
Пример 8. Найти произведение матриц A и B, если:
.
5
3
5
3
=
3
1
1
2
2
0
=
1
0
8
1
6 7
.
,
1
3
1
3
Пример 4. Найти сумму матриц
,
Решение: Матрицы складывать нельзя.
Пример 5. Умножить матрицу на число 2.
Матрица
Число k=2.
Решение: Для того чтобы умножить матрицу A на число k нужно каждый элемент
матрицы A умножить на это число.
Таким образом, произведение матрицы A на число k есть новая матрица:
5 Ответ:
Пример 6. Транспонировать матрицу
.
Решение: Транспонирование матрицы А заключается в замене строк этой матрицы ее столбцами с
сохранением их номеров. Полученная матрица обозначается через AT
Пример 7. Найти число строк и столбцов матрицы C, которая является произведением двух
матриц A и B следующих размерностей:
а) 2 Х 10 и 10 Х 5;
б) 10 Х 2 и 2 Х 5;
в) 4 Х 4 и 4 Х 10.
Решение: а) 2 Х 5;
б) 10 Х 5;
в) 4 Х 10.
Пример 8. Найти произведение матриц A и B, если:
. Решение. Число строк в матрице A 2, число столбцов в матрице B 2. Следовательно, размерность
матрицы C = AB 2 X 2.
Вычисляем элементы матрицы C = AB.
6 Найденное произведение матриц:
.
Пример 9. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A 2, число столбцов в матрице B 1. Следовательно, размерность
матрицы C = AB 2 X 1.
Вычисляем элементы матрицы C = AB.
Произведение матриц запишется в виде матрицыстолбца:
.
Пример 10. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A 3, число столбцов в матрице B 3. Следовательно, размерность
матрицы C = AB 3 X 3.
Вычисляем элементы матрицы C = AB.
7 Найденное произведение матриц:
.
Пример 11. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A 1, число столбцов в матрице B 1. Следовательно, размерность
матрицы C = AB 1 X 1.
Вычисляем элемент матрицы C = AB.
Произведение матриц является матрицей из одного элемента:
.
Пример 12. Дана матрица
. Найти A² и A³.
Решение. Число строк в матрице A 2, число столбцов в матрице B 2. Следовательно, размерность
матрицы C = AB 2 X 2.
Вычисляем элементы матрицы C = AB.
6 Найденное произведение матриц:
.
Пример 9. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A 2, число столбцов в матрице B 1. Следовательно, размерность
матрицы C = AB 2 X 1.
Вычисляем элементы матрицы C = AB.
Произведение матриц запишется в виде матрицыстолбца:
.
Пример 10. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A 3, число столбцов в матрице B 3. Следовательно, размерность
матрицы C = AB 3 X 3.
Вычисляем элементы матрицы C = AB.
7 Найденное произведение матриц:
.
Пример 11. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A 1, число столбцов в матрице B 1. Следовательно, размерность
матрицы C = AB 1 X 1.
Вычисляем элемент матрицы C = AB.
Произведение матриц является матрицей из одного элемента:
.
Пример 12. Дана матрица
. Найти A² и A³. Решение:
5. Первичное усвоение новых знаний.
Определитель матрицы
С
каждой
число
называется определителем матрицы. Определитель вычисляется по особым правилам и
обозначается |A|, det A, ΔA.
связывают число.
матрицей
квадратной
Это
Число строк (столбцов) определителя называется его порядком.
8 Определитель первого порядка матрицы
равен элементу a11: |A|=a11
Пример:
Не путать определитель первого порядка с модулем.
Вычисление определителя второго порядка
Дана
A
a
11
a
21
a
12
a
22
квадратная матрицы второго порядка.
Определителем второго порядка матрицы A называется число
A
a
11
a
21
a
12
a
22
a
a
11
22
a
21
a
12
Из произведения элементов главной диагонали вычитаем произведение элементов побочной
диагонали.
Пример.
Вычислить определитель второго порядка.
A
2
1
3
5
152
13
3
Вычисление определитель третьего порядка (метод треугольников)
Дана
A
a
11
a
a
21
31
a
12
a
a
22
32
a
13
a
a
23
33
квадратная матрицы третьего порядка
Определитель третьего порядка – Метод треугольников
Для начала перемножаем элементы главной диагонали и описываем два треугольника вокруг
диагонали следующим образом:
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
Элементы, стоящие на вершинах треугольника, перемножаем.
Решение:
5. Первичное усвоение новых знаний.
Определитель матрицы
С
каждой
число
называется определителем матрицы. Определитель вычисляется по особым правилам и
обозначается |A|, det A, ΔA.
связывают число.
матрицей
квадратной
Это
Число строк (столбцов) определителя называется его порядком.
8 Определитель первого порядка матрицы
равен элементу a11: |A|=a11
Пример:
Не путать определитель первого порядка с модулем.
Вычисление определителя второго порядка
Дана
A
a
11
a
21
a
12
a
22
квадратная матрицы второго порядка.
Определителем второго порядка матрицы A называется число
A
a
11
a
21
a
12
a
22
a
a
11
22
a
21
a
12
Из произведения элементов главной диагонали вычитаем произведение элементов побочной
диагонали.
Пример.
Вычислить определитель второго порядка.
A
2
1
3
5
152
13
3
Вычисление определитель третьего порядка (метод треугольников)
Дана
A
a
11
a
a
21
31
a
12
a
a
22
32
a
13
a
a
23
33
квадратная матрицы третьего порядка
Определитель третьего порядка – Метод треугольников
Для начала перемножаем элементы главной диагонали и описываем два треугольника вокруг
диагонали следующим образом:
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
Элементы, стоящие на вершинах треугольника, перемножаем.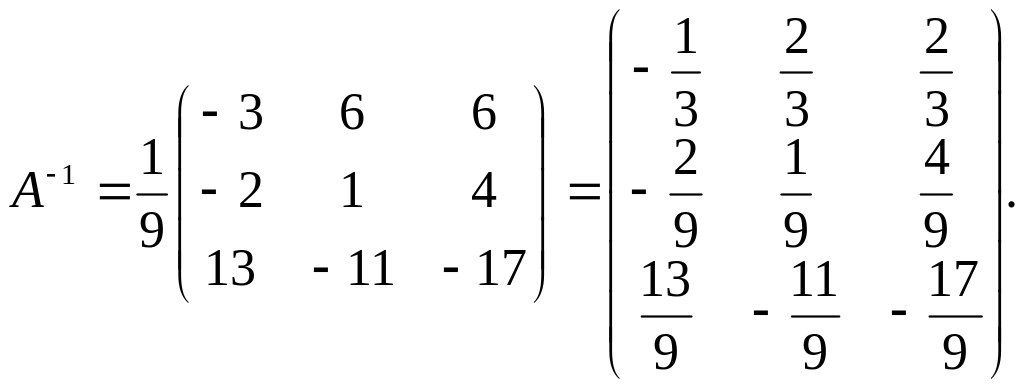 Затем ставим минус, перемножаем элементы побочной диагонали и описываем два
треугольника вокруг побочной диагонали:
9 A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
aA
a
11
a
33
a
12
a
23
a
31
a
21
a
32
a
13
22
a
a
22
a
13
a
21
a
a
12
33
a
32
a
23
31
11
a
Пример. Вычислить определитель третьего порядка методом треугольников.
10342
53
A
2
1
12
3
5
3
0
4
411
32
3
502
15
3
2
Определитель третьего порядка Правило Саррюса.
Пример: Найдем по упрощенной схеме определитель матрицы (4).
2
1
3
1
1
2
1
4
1
3)4(1)1(211)1(2
)11122)4(3)1()1((
4
.
!!! Все, что мы будем далее говорить для этой матрицы, справедливо и для квадратной матрицы
любого порядка. Определение определителя матрицы содержит два новых понятия. Оказывается,
для каждого элемента матрицы (а их 9) можно посчитать 2 числа, которые называются минором и
алгебраическим дополнением этого элемента.
Затем ставим минус, перемножаем элементы побочной диагонали и описываем два
треугольника вокруг побочной диагонали:
9 A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
A
a
a
a
11
21
31
a
a
a
12
22
32
a
13
a
a
23
33
aA
a
11
a
33
a
12
a
23
a
31
a
21
a
32
a
13
22
a
a
22
a
13
a
21
a
a
12
33
a
32
a
23
31
11
a
Пример. Вычислить определитель третьего порядка методом треугольников.
10342
53
A
2
1
12
3
5
3
0
4
411
32
3
502
15
3
2
Определитель третьего порядка Правило Саррюса.
Пример: Найдем по упрощенной схеме определитель матрицы (4).
2
1
3
1
1
2
1
4
1
3)4(1)1(211)1(2
)11122)4(3)1()1((
4
.
!!! Все, что мы будем далее говорить для этой матрицы, справедливо и для квадратной матрицы
любого порядка. Определение определителя матрицы содержит два новых понятия. Оказывается,
для каждого элемента матрицы (а их 9) можно посчитать 2 числа, которые называются минором и
алгебраическим дополнением этого элемента. Минором элемента матрицы
aij (обозначается Мij) называется значение определителя
матрицы, получающейся из данной матрицы вычеркиванием строки и столбца, на пересечении
которых стоит данный элемент (т.е. вычеркиванием iой строки и jго столбца).
Алгебраическим дополнением элемента матрицы
aij (обозначается Аij) называется число,
определяемое по формуле
(3) Аij = (–1)i+j Мij .
Поскольку (–1) в целой степени принимает всего два значения ( 1 – если показатель степени
есть четное число и (–1) – если нечетное), то алгебраическое дополнение элемента матрицы либо
10 ничем не отличается от минора этого элемента (если сумма его нижних индексов – т.е. сумма
номеров строки и столбца – есть четное число) или отличается от минора только знаком (если
сумма нижних индексов нечетна).
Пример. Найти миноры и алгебраические дополнения всех элементов матрицы
(4) А =
2
1
3
1
1
2
1
4
1
.
Минором элемента матрицы
aij (обозначается Мij) называется значение определителя
матрицы, получающейся из данной матрицы вычеркиванием строки и столбца, на пересечении
которых стоит данный элемент (т.е. вычеркиванием iой строки и jго столбца).
Алгебраическим дополнением элемента матрицы
aij (обозначается Аij) называется число,
определяемое по формуле
(3) Аij = (–1)i+j Мij .
Поскольку (–1) в целой степени принимает всего два значения ( 1 – если показатель степени
есть четное число и (–1) – если нечетное), то алгебраическое дополнение элемента матрицы либо
10 ничем не отличается от минора этого элемента (если сумма его нижних индексов – т.е. сумма
номеров строки и столбца – есть четное число) или отличается от минора только знаком (если
сумма нижних индексов нечетна).
Пример. Найти миноры и алгебраические дополнения всех элементов матрицы
(4) А =
2
1
3
1
1
2
1
4
1
. Сначала ищем миноры всех элементов.
М11=
1
2
4
1
7
, М12=
1
3
4
1
13
, М13=
1
3
1
2
5
,
М21=
1
2
1
1
3
, М22=
2
3
1
1
5
, М23=
12
23
,
1
М31=
1
1
1
4
5
, М32=
2
1
1
4
7
, М33=
2
1
1
1
3
.
Учитывая формулу (3) и приведенные ниже пояснения для этой формулы, получаем
следующие алгебраические дополнения
А11=7, А12= –13, А13=5, А21= –3, А22=5, А23= –1, А31= –5, А32=7, А33= –3
Для матрицы (4) для каждой строки (и столбца) проделаем: составим сумму попарных
произведений ее (его) элементов на их алгебраические дополнения. Например, для второго столбца
:
(1
)13
725)1(
4
. Взяв любой другой столбец (или строку), получим то же самое
число (для данной матрицы (– 4) ). Это общее свойство всех квадратных матриц − результат таких
вычислений не зависит от того, какую строчку или столбец матрицы мы выбрали. Поэтому
корректно следующее определение.
Сначала ищем миноры всех элементов.
М11=
1
2
4
1
7
, М12=
1
3
4
1
13
, М13=
1
3
1
2
5
,
М21=
1
2
1
1
3
, М22=
2
3
1
1
5
, М23=
12
23
,
1
М31=
1
1
1
4
5
, М32=
2
1
1
4
7
, М33=
2
1
1
1
3
.
Учитывая формулу (3) и приведенные ниже пояснения для этой формулы, получаем
следующие алгебраические дополнения
А11=7, А12= –13, А13=5, А21= –3, А22=5, А23= –1, А31= –5, А32=7, А33= –3
Для матрицы (4) для каждой строки (и столбца) проделаем: составим сумму попарных
произведений ее (его) элементов на их алгебраические дополнения. Например, для второго столбца
:
(1
)13
725)1(
4
. Взяв любой другой столбец (или строку), получим то же самое
число (для данной матрицы (– 4) ). Это общее свойство всех квадратных матриц − результат таких
вычислений не зависит от того, какую строчку или столбец матрицы мы выбрали. Поэтому
корректно следующее определение. Определителем квадратной матрицы (любого порядка!) называется число, равное сумме
попарных произведений элементов любой строки (столбца) на их алгебраические
дополнения.
Поэтому для матрицы (4) по определению: =
2
1
3
1
1
2
1
4
1
4
.
11
Для вычисления определителей матриц более высокого (чем третьего) порядка
упрощенной схемы нет, поэтому используется только метод, данный в определении: выбирается
строка или столбец матрицы и вычисляется сумма попарных произведений соответствующих
элементов матрицы на их алгебраические дополнения. При этом вычисление алгебраических
дополнений – самый трудоёмкий этап. Но поскольку строку (или столбец) можно выбирать
произвольно (результат от этого не зависит), то проще выбрать ту, среди элементов которой как
можно больше нулевых. При этом алгебраические дополнения нулевых элементов можно не
считать, так как при составлении упомянутой выше суммы попарных произведений
соответствующие слагаемые все равно обратятся в ноль.
Определителем квадратной матрицы (любого порядка!) называется число, равное сумме
попарных произведений элементов любой строки (столбца) на их алгебраические
дополнения.
Поэтому для матрицы (4) по определению: =
2
1
3
1
1
2
1
4
1
4
.
11
Для вычисления определителей матриц более высокого (чем третьего) порядка
упрощенной схемы нет, поэтому используется только метод, данный в определении: выбирается
строка или столбец матрицы и вычисляется сумма попарных произведений соответствующих
элементов матрицы на их алгебраические дополнения. При этом вычисление алгебраических
дополнений – самый трудоёмкий этап. Но поскольку строку (или столбец) можно выбирать
произвольно (результат от этого не зависит), то проще выбрать ту, среди элементов которой как
можно больше нулевых. При этом алгебраические дополнения нулевых элементов можно не
считать, так как при составлении упомянутой выше суммы попарных произведений
соответствующие слагаемые все равно обратятся в ноль. : Вычислить определитель 3го порядка: =.
Пример 1
Решение
:
Вычислим определитель, применяя правило (2) и учитывая принятые обозначения:
=
=
+
+
–
–
–
,
или:
: Вычислить определитель 3го порядка: =.
Ответ: d = 100.
Пример 2
Решение
:
Вычислим определитель, применяя правило (2) и учитывая
обозначения:
+
+
–
–
=
=
=100.
принятые
, или:
=1.
–
Ответ: d = 1.
6. Первичное закрепление и систематизация изученного материала
I. Курсанты выходят к доске и с помощью преподавателя решают задания.
Пример 1: Вычислить определитель второго порядка.
A
02
51
0152
10
Пример 2: Вычислить определитель третьего порядка методом треугольника
A
7
5
4
07
3
1
2
20
2
0
1
8
17
1
03
4
225
5214
3
1
702
15
6
0
12 Пример 3: Вычислить определитель разложением по элементам, какой либо строки или
столбца.
Воспользуемся свойствами определителя и обнулим все элементы, стоящие в первом
столбце кроме первого.
: Вычислить определитель 3го порядка: =.
Пример 1
Решение
:
Вычислим определитель, применяя правило (2) и учитывая принятые обозначения:
=
=
+
+
–
–
–
,
или:
: Вычислить определитель 3го порядка: =.
Ответ: d = 100.
Пример 2
Решение
:
Вычислим определитель, применяя правило (2) и учитывая
обозначения:
+
+
–
–
=
=
=100.
принятые
, или:
=1.
–
Ответ: d = 1.
6. Первичное закрепление и систематизация изученного материала
I. Курсанты выходят к доске и с помощью преподавателя решают задания.
Пример 1: Вычислить определитель второго порядка.
A
02
51
0152
10
Пример 2: Вычислить определитель третьего порядка методом треугольника
A
7
5
4
07
3
1
2
20
2
0
1
8
17
1
03
4
225
5214
3
1
702
15
6
0
12 Пример 3: Вычислить определитель разложением по элементам, какой либо строки или
столбца.
Воспользуемся свойствами определителя и обнулим все элементы, стоящие в первом
столбце кроме первого. Для этого: каждый элемент первой строки умножим на 2 и прибавим к ним
строки умножим на (5) и
соответствующий элемент второй строки; каждый элемент первой
прибавим к ним соответствующие элементы третьей строки.
A
2
1
12
3
5
42
53
3
0
4
I
2
II
5
I
1
0
0
2
5
7
3
6
19
III
1
A
11
0
A
21
A
1
0
31
11
1
5
7
6
19
95
II. Курсантам предлагается самостоятельно на оценку выполнить задания (по вариантам)
См. приложение 1.
7. Информация о домашнем задании, инструктаж по его выполнению.
1. Выучить теоретический материал;
2. Вычислить определитель матрицы второго порядка
3. Вычислить определитель матрицы третьего порядка методом диагоналей или
треугольников
A
1
4
2
02
5
2
3
7
4. Вычислить определитель матрицы третьего порядка методом разложения
8. Задание ученикам по рефлексии их деятельности.
Итак, сегодня мы с вами продолжили изучать тему: «Матрица и определитель».
Для этого: каждый элемент первой строки умножим на 2 и прибавим к ним
строки умножим на (5) и
соответствующий элемент второй строки; каждый элемент первой
прибавим к ним соответствующие элементы третьей строки.
A
2
1
12
3
5
42
53
3
0
4
I
2
II
5
I
1
0
0
2
5
7
3
6
19
III
1
A
11
0
A
21
A
1
0
31
11
1
5
7
6
19
95
II. Курсантам предлагается самостоятельно на оценку выполнить задания (по вариантам)
См. приложение 1.
7. Информация о домашнем задании, инструктаж по его выполнению.
1. Выучить теоретический материал;
2. Вычислить определитель матрицы второго порядка
3. Вычислить определитель матрицы третьего порядка методом диагоналей или
треугольников
A
1
4
2
02
5
2
3
7
4. Вычислить определитель матрицы третьего порядка методом разложения
8. Задание ученикам по рефлексии их деятельности.
Итак, сегодня мы с вами продолжили изучать тему: «Матрица и определитель». Давайте
повторим основные понятия данной темы: матрица, виды матриц, определитель, минор,
алгебраическое дополнение. Какие действия мы можем выполнять с матрицей?( сложение,
вычитание, умножение на число, перемножения матриц).
13 Также мы научились: вычислять определитель второго порядка, третьего порядка методом
треугольников, методом диагоналей, применять метод вычисления определителя с помощью
разложения по элементам строки и столбца.
Список использованной литературы
1. Омельченко В.П., Курбатова Э.В. Математика: Учебное пособие для среднего
профессионального образования. – РостовнаДону: Феникс, 2014.
2. Дадаян А.А. Математика: Учебник для среднего профессионального образования. – М.: Форум,
2008.
3.
Лисичкин В.Т., Соловейчик И.Л. Математика: Учебное пособие для техникумов. М.:
Высшая школа, 1991.
4. Дадаян А.А. Сборник задач по математике: Учебное пособие. – М.: Форум, 2008.
Варианты заданий для самостоятельной работы
Приложение 1.
Давайте
повторим основные понятия данной темы: матрица, виды матриц, определитель, минор,
алгебраическое дополнение. Какие действия мы можем выполнять с матрицей?( сложение,
вычитание, умножение на число, перемножения матриц).
13 Также мы научились: вычислять определитель второго порядка, третьего порядка методом
треугольников, методом диагоналей, применять метод вычисления определителя с помощью
разложения по элементам строки и столбца.
Список использованной литературы
1. Омельченко В.П., Курбатова Э.В. Математика: Учебное пособие для среднего
профессионального образования. – РостовнаДону: Феникс, 2014.
2. Дадаян А.А. Математика: Учебник для среднего профессионального образования. – М.: Форум,
2008.
3.
Лисичкин В.Т., Соловейчик И.Л. Математика: Учебное пособие для техникумов. М.:
Высшая школа, 1991.
4. Дадаян А.А. Сборник задач по математике: Учебное пособие. – М.: Форум, 2008.
Варианты заданий для самостоятельной работы
Приложение 1. 14 1 вариант
2 вариант
№1. Вычислить определитель по первой строке
№1. Вычислить определитель по второй строке
4
2
7
1
63
5
24
1
4
5
3
1
2
6
7
8
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
6
2
5
68
4
7
93
3
2
9
6
5
4
9
5
8
3 вариант
4 вариант
№1. Вычислить определитель по третьему
столбцу
№1. Вычислить определитель по первому столбцу
9
3
6
5
1
4
1
5
2
3
2
6
61
5
3
26
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
5
6
8
3
6
9
9
6
1
9
5
9
7
8
6
9
6
4
15 5 вариант
6 вариант
№1. Вычислить определитель по правилу
треугольника (диагоналей)
№1. Вычислить определитель по правилу
треугольника (диагоналей)
1
7
5
3
2
7
9
6
1
6
2
5
62
4
1
7
9
№2. Вычислить определитель по второй строке
№2. Вычислить определитель по второму
столбцу
6
9
6
8
4
7
2
7
5
8
6
7
7
9
8
11
5
7
7 вариант
8 вариант
№1.
14 1 вариант
2 вариант
№1. Вычислить определитель по первой строке
№1. Вычислить определитель по второй строке
4
2
7
1
63
5
24
1
4
5
3
1
2
6
7
8
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
6
2
5
68
4
7
93
3
2
9
6
5
4
9
5
8
3 вариант
4 вариант
№1. Вычислить определитель по третьему
столбцу
№1. Вычислить определитель по первому столбцу
9
3
6
5
1
4
1
5
2
3
2
6
61
5
3
26
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
5
6
8
3
6
9
9
6
1
9
5
9
7
8
6
9
6
4
15 5 вариант
6 вариант
№1. Вычислить определитель по правилу
треугольника (диагоналей)
№1. Вычислить определитель по правилу
треугольника (диагоналей)
1
7
5
3
2
7
9
6
1
6
2
5
62
4
1
7
9
№2. Вычислить определитель по второй строке
№2. Вычислить определитель по второму
столбцу
6
9
6
8
4
7
2
7
5
8
6
7
7
9
8
11
5
7
7 вариант
8 вариант
№1.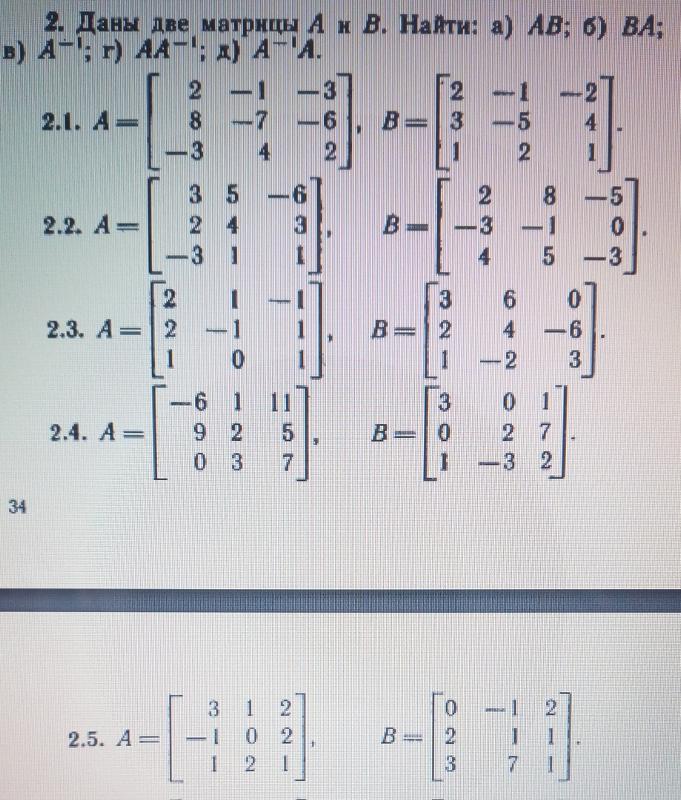 Вычислить определитель по третьей строке
№1. Вычислить определитель по третьему
столбцу
5
4
2
3
3
7
9
6
1
1
8
7
3
6
7
9
4
5
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
8
7
4
8
6
9
9
3
6
9
5
2
2
8
7
9
5
6
16 9 вариант
10 вариант
№1. Вычислить определитель по первой строке
№1. Вычислить определитель по второму
столбцу
3
2
6
61
3
5
26
1
7
5
3
2
7
9
6
1
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
6
2
5
62
1
4
7
9
9
3
6
5
1
4
1
5
2
17 Самоанализ урока
1. Внешние связи урока.
Занятие проводился в группе 202 первого курса очного отделения специальности 11.02.06
«Техническая эксплуатация транспортного радиоэлектронного оборудования».
Данный урок пятый в изучаемой теме «Матрицы и определители» в соответствии с
тематическим планированием.
Вычислить определитель по третьей строке
№1. Вычислить определитель по третьему
столбцу
5
4
2
3
3
7
9
6
1
1
8
7
3
6
7
9
4
5
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
8
7
4
8
6
9
9
3
6
9
5
2
2
8
7
9
5
6
16 9 вариант
10 вариант
№1. Вычислить определитель по первой строке
№1. Вычислить определитель по второму
столбцу
3
2
6
61
3
5
26
1
7
5
3
2
7
9
6
1
№2. Вычислить определитель по правилу
треугольника (диагоналей)
№2. Вычислить определитель по правилу
треугольника (диагоналей)
6
2
5
62
1
4
7
9
9
3
6
5
1
4
1
5
2
17 Самоанализ урока
1. Внешние связи урока.
Занятие проводился в группе 202 первого курса очного отделения специальности 11.02.06
«Техническая эксплуатация транспортного радиоэлектронного оборудования».
Данный урок пятый в изучаемой теме «Матрицы и определители» в соответствии с
тематическим планированием. В дальнейшем полученные знания будут применяться в следующих
темах раздела «Элементы линейной алгебры» (обратная матрица, решение СЛУ различными
методами).
2. Характеристика единой цели урока с опорой на характеристику группы.
Цель урока: отработать теоретический материал по теме: Матрицы. Операции с матрицами.
Определитель. Сформировать навыки выполнения операций над матрицами, вычисления
определителя матрицы.
3. Характеристика замысла урока. Характеристика этапов занятия.
1. Последовательность и распределение этапов занятия по времени.
I. Общая организация занятия
1) Организационный этап. (2 мин.)
2) Постановка цели и задач занятия. Мотивация учебной деятельности
обучающихся. (5 мин.)
3) Актуализация опорных знаний (10 мин)
4) Закрепление умений (15 мин)
5) Первичное усвоение новых знаний. (25 мин.)
6) Первичное закрепление и систематизация изученного материала (23 мин.)
5) Подведение итогов занятия (5 мин.)
6) Информация о домашнем задании, инструктаж по его выполнению.
В дальнейшем полученные знания будут применяться в следующих
темах раздела «Элементы линейной алгебры» (обратная матрица, решение СЛУ различными
методами).
2. Характеристика единой цели урока с опорой на характеристику группы.
Цель урока: отработать теоретический материал по теме: Матрицы. Операции с матрицами.
Определитель. Сформировать навыки выполнения операций над матрицами, вычисления
определителя матрицы.
3. Характеристика замысла урока. Характеристика этапов занятия.
1. Последовательность и распределение этапов занятия по времени.
I. Общая организация занятия
1) Организационный этап. (2 мин.)
2) Постановка цели и задач занятия. Мотивация учебной деятельности
обучающихся. (5 мин.)
3) Актуализация опорных знаний (10 мин)
4) Закрепление умений (15 мин)
5) Первичное усвоение новых знаний. (25 мин.)
6) Первичное закрепление и систематизация изученного материала (23 мин.)
5) Подведение итогов занятия (5 мин.)
6) Информация о домашнем задании, инструктаж по его выполнению. (3 мин.)
7) Рефлексия (2 мин.)
2. Организация познавательной деятельности на занятии (сочетание
фронтальной,
групповой, индивидуальной работы).
Курсанты выполняли практические задания у доски, с обсуждением предлагаемых методов
решения с группой, под руководством преподавателя. Так же курсантам предлагалось
самостоятельно выполнить ряд заданий.
3. Соблюдение охранительного режима.
Перед проведением занятий учебная аудитория была хорошо проветрена. На протяжении
всего занятия происходила смена видов деятельности курсантов.
18 4. Подведение итога занятия.
В результате проведения занятия были выполнены поставленные цели. Активность группы
при выполнении заданий у доски и самостоятельных заданий говорит о хорошем уровне
усвоения материала и наличия интереса к теме урока.
1. Научная, воспитательная и развивающая направленность урока.
II. Содержание урока
Обучающие:
– Формировать навыки выполнения операций над матрицами: сложение, вычитание,
умножение матрицы на число, произведение матриц;
– Формировать умения находить определители матриц.
(3 мин.)
7) Рефлексия (2 мин.)
2. Организация познавательной деятельности на занятии (сочетание
фронтальной,
групповой, индивидуальной работы).
Курсанты выполняли практические задания у доски, с обсуждением предлагаемых методов
решения с группой, под руководством преподавателя. Так же курсантам предлагалось
самостоятельно выполнить ряд заданий.
3. Соблюдение охранительного режима.
Перед проведением занятий учебная аудитория была хорошо проветрена. На протяжении
всего занятия происходила смена видов деятельности курсантов.
18 4. Подведение итога занятия.
В результате проведения занятия были выполнены поставленные цели. Активность группы
при выполнении заданий у доски и самостоятельных заданий говорит о хорошем уровне
усвоения материала и наличия интереса к теме урока.
1. Научная, воспитательная и развивающая направленность урока.
II. Содержание урока
Обучающие:
– Формировать навыки выполнения операций над матрицами: сложение, вычитание,
умножение матрицы на число, произведение матриц;
– Формировать умения находить определители матриц. Развивающие:
– Формирование умения пользоваться математическими инструментами,
– Формирование умения применять свои знания при решении математических задач по
данной теме;
– Углубление знаний, умений и навыков; развитие творческой деятельности:
интуиции, пространственного воображения, смекалки;
– Развитие мыслительных операций посредством конкретизации, развитие зрительной
памяти, потребности к самообразованию, способствовать развитию познавательных
процессов.
Воспитательные:
– Воспитание устойчивого интереса к математике,
– Воспитание математической культуры,
– Развитие самоорганизации обучающихся
2. Уровень знаний, умений, навыков обучающихся.
Курсанты понимают содержание учебного материала, применяют полученные знания для
решения практических задач.
III. Методическая сторона занятия и его оборудование
1. Качество методов и приемов обучения, их адекватность задачам занятия и уровню
развития познавательных возможностей курсантов.
При изложении и закреплении материала использовались Объяснительноиллюстративный и
репродуктивный методы обучения.
Развивающие:
– Формирование умения пользоваться математическими инструментами,
– Формирование умения применять свои знания при решении математических задач по
данной теме;
– Углубление знаний, умений и навыков; развитие творческой деятельности:
интуиции, пространственного воображения, смекалки;
– Развитие мыслительных операций посредством конкретизации, развитие зрительной
памяти, потребности к самообразованию, способствовать развитию познавательных
процессов.
Воспитательные:
– Воспитание устойчивого интереса к математике,
– Воспитание математической культуры,
– Развитие самоорганизации обучающихся
2. Уровень знаний, умений, навыков обучающихся.
Курсанты понимают содержание учебного материала, применяют полученные знания для
решения практических задач.
III. Методическая сторона занятия и его оборудование
1. Качество методов и приемов обучения, их адекватность задачам занятия и уровню
развития познавательных возможностей курсантов.
При изложении и закреплении материала использовались Объяснительноиллюстративный и
репродуктивный методы обучения. Курсантам был выдан теоретический материал под диктовку. На доске были рассмотрены
примеры решения задач преподавателем и студентами. Для закрепления материала курсантам было
предложено выполнить задания самостоятельно, на оценку. На этапе рефлексии курсанты подвели
итоги занятия.
2. Методы опроса. Правильность ответа обучающихся.
19 Занятие подразумевало работу курсантов у доски под наблюдением преподавателя. Была
проведена фронтальная работа. Курсанты самостоятельно решали практические задания.
4. Функциональный анализ урока.
Все структурные элементы занятия были выдержаны. Прослеживается взаимосвязь этапов
заняти. Структура занятия подчинена поставленным целям. На этапе «Первичное усвоение новых
знаний» курсанты познакомились с основным теоретическим материалом. На этапе первичной
проверки понимания курсанты развивали свои умения анализировать и логически мыслить. При
первичном закреплении курсанты показали свое умение применять теоретические знания к
решению практических задач.
Курсантам был выдан теоретический материал под диктовку. На доске были рассмотрены
примеры решения задач преподавателем и студентами. Для закрепления материала курсантам было
предложено выполнить задания самостоятельно, на оценку. На этапе рефлексии курсанты подвели
итоги занятия.
2. Методы опроса. Правильность ответа обучающихся.
19 Занятие подразумевало работу курсантов у доски под наблюдением преподавателя. Была
проведена фронтальная работа. Курсанты самостоятельно решали практические задания.
4. Функциональный анализ урока.
Все структурные элементы занятия были выдержаны. Прослеживается взаимосвязь этапов
заняти. Структура занятия подчинена поставленным целям. На этапе «Первичное усвоение новых
знаний» курсанты познакомились с основным теоретическим материалом. На этапе первичной
проверки понимания курсанты развивали свои умения анализировать и логически мыслить. При
первичном закреплении курсанты показали свое умение применять теоретические знания к
решению практических задач. На этапе рефлексии курсанты подводили итоги занятия.
5. Оценка конечного результата занятия.
Цели занятия были реализованы. Курсанты освоили новую тему и сформировали навыки
вычислений в рамках изученного материала.
20
На этапе рефлексии курсанты подводили итоги занятия.
5. Оценка конечного результата занятия.
Цели занятия были реализованы. Курсанты освоили новую тему и сформировали навыки
вычислений в рамках изученного материала.
20
Презентация по математике на тему “Морфологические матрицы”
Морфологический анализ
Морфологические
матрицы
Матрица — прямоугольная таблица, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы (морфологические свойства рассматриваемого объекта).
Морфологический анализ позволяет создавать конструкции новых устройств, обладающих требуемым и качествами. В наиболее простом случае для этого составляется двумерная (содержащая две оси или два главных показателя) матрица. По обеим осям записываются все возможные варианты решения задачи для заданных показателей (характеристик). Затем рассматриваются все возможные сочетания вариантов по каждой оси.
Затем рассматриваются все возможные сочетания вариантов по каждой оси.
ПАРАМЕТР
Наказание
РЕАЛИЗАЦИЯ
Поощрение
Плохая отметка
Распростра- нение опыта
Выставить с урока
Купить и наградить пирожками
Сообщить в стенгазету
Оставить после уроков
Выявление черт характера
Поставить хорошую отметку
Вывесить тетрадь на обозрение
Наградить 1 кг соли
Вызвать родителей
Гениальность
Похвалить на будущее
Издать информ. листок
Авантюр-ность
Организовать обмен опытом
Нахальство
Самостоя-тельность
Этапы решения задачи
- Выделить все значимые для каждого из вариантов решения задачи параметры.
- Оценить ранг и шкалу для каждого из параметров (факторов).
- Экспертно оценить в баллах значимость каждого из факторов в пределах выбранной шкалы.
- Сложить экспертные оценки по всем параметрам и по суммам определить, какой из вариантой надо выбрать
Правила составления матрицы
- Четко сформулировать цель задачи.
 Указать ограничения, область применения, требуемые характеристики
Указать ограничения, область применения, требуемые характеристики - Выявить основные параметры, характеризующие объект (или функции, которые объект должен выполнять). Записать эти параметры в левый столбец матрицы
- Для каждого из параметров (функций) выявить устройства, вещества или поля (электрическое, магнитное, тепловое, механическое и т.д. ), реализующие этот параметр. Записать их в строках правого столбца матрицы
- Синтезировать новые технические решения путем поочередного составления комбинаций из элементов каждой строки матрицы
- Проанализировать все полученные решения и выбрать те, которые отвечают условиям задачи
Применение метода:
- для составления списка всех возможных вариантов решения задачи,
- для сравнения или выбора одного из многих возможных решений технических, организационных и пр. задач
Пример 1:
двухмерная матрица на объект “наручные часы”
Требуется придумать оригинальную конструкцию корпуса электронных часов. В качестве главных осей выберем: форма корпуса и материал циферблата часов. Составим двухмерную матрицу на объект “часы”.
В качестве главных осей выберем: форма корпуса и материал циферблата часов. Составим двухмерную матрицу на объект “часы”.
Прямоу-гольная
Оргстекло
Кварц
Круглая
Цветное
Оваль-ная
Металл
Шарооб-разная
Кольце-вая
Стекло
В виде предмета (авторучка, сигарета)
Пластилин
Слой воздуха
Тонкая плёнка
Форма корпуса
Материал циферблата
При заполнении строк и столбцов матрицы необходимо вводить не только известные исполнения элементов осей, но и новые, неожиданные, несуществующие (пока).
требуется получить из матрицы оригинальную конструкцию
Поиск решения:
Выберем 1-й элемент столбца – оргстекло. Поочередно соединив его с элементами строки, получим:
прямоугольный корпус с циферблатом из оргстекла – известная конструкция;
круглый, овальный – то же самое;
шарообразный корпус с циферблатом из оргстекла.
Это могут быть бусы-часы, клипсы-часы, часы типа луковицы, часы-перстень и т.д.;
кольцевые часы с циферблатом из оргстекла – известные часы-браслет.
Форма корпуса
Оргстекло
Прямоу-гольная
Круглая
Кварц
+
Цветное
Оваль-ная
+
Металл
Шарооб-разная
+
+
Стекло
Кольце-вая
Пластилин
В виде предмета (авторучка, сигарета)
+
Слой воздуха
Тонкая плёнка
+
+
Материал циферблата
требуется получить из матрицы оригинальную конструкцию
Поиск решения:
Рассмотрев все варианты циферблата из оргстекла, переходим к кварцу, стеклу и т.д. Рассмотрев все возможные сочетания циферблатов с вариантами корпусов часов, оцениваем варианты. Из рассмотренной двухмерной матрицы можно получить
7х7=49 вариантов корпусов часов!
Форма корпуса
Прямоу-гольная
Оргстекло
Круглая
Кварц
+
Цветное
Оваль-ная
+
+
Металл
Шарооб-разная
+
+
+
+
+
Стекло
+
Кольце-вая
+
Пластилин
+
В виде предмета (авторучка, сигарета)
+
+
+
+
+
Тонкая плёнка
+
Слой воздуха
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Материал циферблата
Оценка вариантов и выбор наиболее оригинального производится экспертно.
организационная задача “Как отметить ученика, плохо ведущего тетрадь”
Пример 2:
Можно поставить двойку, но это мало улучшит дело. Поищем более эффективный способ борьбы с лентяем.
Цель: найти комплексный метод воздействия на ученика, плохо оформляющего тетрадь.
1. Основными направлениями воздействия (параметрами) выберем: наказание, поощрение, распространение опыта, выявление черт характера .
2. Составим морфологическую матрицу.
ПАРАМЕТР
Наказание
РЕАЛИЗАЦИЯ
Поощрение
Плохая отметка
Распростра- нение опыта
Выставить с урока
Купить и наградить пирожками
Выявление черт характера
Сообщить в стенгазету
Оставить после уроков
Поставить хорошую отметку
Наградить 1 кг соли
Вывесить тетрадь на обозрение
Вызвать родителей
Гениаль-ность
Похвалить на будущее
Издать информ. листок
Авантюр-ность
Организовать обмен опытом
Нахаль-ство
Самостоя-тельность
организационная задача “Как отметить ученика, плохо ведущего тетрадь”
Пример 2:
3. Синтезируем новые варианты действий:
Синтезируем новые варианты действий:
купить пирожков и сообщить в стенгазете о появлении гениальной личности;
купить пирожков, вывесить тетрадь на видное место и сообщить о появлении гения и т.д.
ПАРАМЕТР
РЕАЛИЗАЦИЯ
Наказание
Поощрение
Плохая отметка
Купить и наградить пирожками
Выставить с урока
Распростра- нение опыта
Оставить после уроков
Поставить хорошую отметку
Сообщить в стенгазету
Выявление черт характера
Гениальность
Наградить 1 кг соли
Вызвать родителей
Вывесить тетрадь на обозрение
Похвалить на будущее
Издать информ. листок
Авантюр-ность
Нахальство
Организовать обмен опытом
Самостоя-тельность
Таких вариантов будет (4 + 3) 4 5 = 140 вариантов!
Пересмотр на уроке всех 140 вариантов вряд ли возможен, поэтому выбор целесообразно производить, определив в каждой строке по одному, наиболее привлекательному.
организационная задача “Как отметить ученика, плохо ведущего тетрадь”
Пример 2:
4. Коллективным обсуждением выбираем самое интересное сочетание параметров, например: наградить килограммом соли, выпустить молнию (информационный листок) с информацией о появлении чересчур самостоятельной личности.
Выбор варианта в классе производится путем коллективного обсуждения.
ПАРАМЕТР
РЕАЛИЗАЦИЯ
Наказание
Поощрение
Плохая отметка
Купить и наградить пирожками
Распростра- нение опыта
Выставить с урока
Поставить хорошую отметку
Оставить после уроков
Сообщить в стенгазету
Выявление черт характера
Гениаль-ность
Наградить 1 кг соли
Вызвать родителей
Вывесить тетрадь на обозрение
Похвалить на будущее
Издать информ. листок
Авантюр-ность
Нахаль-ство
Организовать обмен опытом
Самостоя-тельность
техническая задача задача “Создания транспортного средства – снегохода”
Пример 3:
1. Определяем параметры – морфологические признаки, от которых зависит решение; составляем их список: А, Б, В, Г, Д.
Определяем параметры – морфологические признаки, от которых зависит решение; составляем их список: А, Б, В, Г, Д.
2. По каждому признаку возможны варианты: А1 (двигатель внутреннего сгорания), А2, А3, А4 и т.д.; Б1, Б2, Б3, Б4 и т.д.; В1, В2 – на двигатель, В3 и т.д.
техническая задача задача “Создания транспортного средства – снегохода”
Пример 3:
3. Сочетание одного из возможных вариантов морфологического признака с другим от каждого признака дает одно из возможных технических решений. На основе списка строим матрицу: А1, А2, А3, А4; Б1, Б2, Б3, Б4; В1, В2, В3; ….
ПАРАМЕТР
РЕАЛИЗАЦИЯ
Двигатель
Движитель
1
А
2
Б
Опора кабины
Двигатель внутреннего сгорания
3
Газовая турбина
Воздушный винт
Управление
В
Г
Гусеницы
4
Задний ход
Электро-двигатель
Опора на снег
. ..
..
Д
Опора на двигатель
Лыжи
Реактивный двигатель
Снегомёт
…
Опора на движитель
…
…
Опора на лыжи
…
…
…
…
Эта матрица – символическая форма описания возможных решений. Каждый вариант конструкции определяется набором элементов из разных строк.
Так, вариант А1 Б2 В2 Г2 будет снегоходом с ДВС, на гусеничном ходу, с опорой кабины на двигатель.
техническая задача задача “Создания транспортного средства – снегохода”
Пример 3:
Число всех возможных вариантов = произведению количества элементов в каждой из строк:
N = 4 4 3
ПАРАМЕТР
РЕАЛИЗАЦИЯ
Двигатель
1
Движитель
А
Б
2
Опора кабины
Двигатель внутреннего сгорания
Газовая турбина
Управление
В
Воздушный винт
3
Гусеницы
Г
4
Задний ход
Электро-двигатель
Опора на снег
Д
. ..
..
Лыжи
Реактивный двигатель
Опора на двигатель
Снегомёт
…
Опора на движитель
…
Опора на лыжи
…
…
…
…
…
5. Приступаем к определению функциональной ценности вариантов решений. Это трудоемкая и ответственная задача. Анализ вариантов решений позволяет выбрать наиболее рациональные, приемлемые в конкретных условиях.
Пример 4:
Пусть ученика интересуют 3 профессии: 1) экономист, 2) наладчик ЭВМ, 3) повар. В каждой профессии есть свои плюсы и минусы. Какую из них выбрать? Выделим наиболее значимые для ученика факторы важности, престижности и т.д. профессии. Запишем их в 1-ю колонку. В примере мы выбрали 5 параметров, их число может быть намного больше.
Значимые параметры
Значение шкалы, балл
Варианты профессий
1. Зарплата
1
2. Престижность
2
3. Возможность зани-маться самостоя-тельной творческой деятельностью
3
4. Режим работы
Режим работы
5. Возможность смены мест, путешествий
ИТОГО
решение задачи выбора профессии методом морфологического анализа
Пример 4:
Во второй колонке запишем шкалу, по которой будем оценивать параметры. Пусть в нашем примере наиболее значимый параметр – величина зарплаты (100 баллов), затем престижность и возможность заниматься творческой работой (90 баллов). Остальные факторы оцениваются более низко.
Значимые параметры
Значение шкалы, балл
Варианты профессий
1. Зарплата
1
2. Престижность
2
3. Возможность зани-маться самостоя-тельной творческой деятельностью
4. Режим работы
3
5. Возможность смены мест, путешествий
ИТОГО
100
90
90
80
50
решение задачи выбора профессии методом морфологического анализа
Пример 4:
Далее в пределах выбранных шкал экспертно оцениваются все три профессии. В результате сложения сумм экспертных оценок по всем параметрам ( строка “ИТОГО” ) мы определяем: наиболее предпочтительная – профессия экономиста.
В результате сложения сумм экспертных оценок по всем параметрам ( строка “ИТОГО” ) мы определяем: наиболее предпочтительная – профессия экономиста.
Значимые параметры
Значение шкалы, балл
Варианты профессий
1. Зарплата
100
1
2. Престижность
90
2
80
3. Возможность зани-маться самостоя-тельной творческой деятельностью
90
95
85
4. Режим работы
3
100
90
80
5. Возможность смены мест, путешествий
80
70
50
60
ИТОГО
60
30
60
20
30
80
355
335
50
320
Каждый из приведенных здесь параметров имеет разную значимость для разных людей. Поэтому при заполнении учащимися таблицы значения шкал будут разными.
Недостатки метода:
- обилие вариантов. Из такого количества трудно выбрать наилучший.

- не дает возможности определить, все ли возможные варианты отмечены.
Вместе с тем, поиск более систематичен и задача охватывается почти во всем многообразии решений.
Спасибо за внимание
Матричная и линейная алгебра – МАТЕМАТИКА 410
Матричная и линейная алгебра – МАТЕМАТИКА 410
CG • Раздел 8WK • 01.07.2018 – 31.12.2199 • Изменено 27.07.2021
Разработка курса3 Описание
4 понимание векторных пространств, систем линейных уравнений, матричной алгебры и линейных преобразований.
Информацию о предварительных требованиях для этого курса см. в Академическом каталоге курсов.
Обоснование
Этот курс представляет собой введение в конечномерную линейную алгебру.После успешного завершения этого курса студент должен уметь вычислять и объяснять все основные теоремы и результаты стандартной студенческой линейной алгебры.
Рассматриваемые темы включают матрицы, линейные преобразования, замену базиса, собственные значения, канонические формы, квадратичные формы и приложения. Это должно подготовить как преподавателей, так и студентов к дальнейшему изучению или обучению линейной алгебре.
Измеримые результаты обучения
После успешного завершения этого курса студент сможет:
- Вычислять сокращения строк и объяснять, как алгоритм Гаусса-Жордана используется для решения линейных систем,
- Вычислить и объяснить основы матричной алгебры, включая умножение и определители,
- Вычислить и объяснить линейную независимость подмножеств в векторных пространствах,
- Расчет и объяснение остовных множеств в линейной алгебре,
- Объясните, когда преобразование является линейным и как найти его матрицу относительно базиса,
- Расчет и объяснение систем координат и изменение векторов и линейных преобразований,
- Вычислить и объяснить длины и углы в векторном пространстве по норме или скалярному произведению,
- Расчет и объяснение ортогональных проекций и применение метода наименьших квадратов,
- Вычисление собственных значений и собственных векторов и соответствующих канонических форм,
- Общайтесь на языке линейной алгебры и применяйте теоремы линейной алгебры для решения реальных задач.

Назначение курса
7 Чтение учебников
Контрольный список требований
После прочтения курса Syllabus и ожидания студентов, студент завершит связанный сопутствующий контрольный список, найденный в модуле / неделях 1.
Домашние задания (15 )
Учащийся будет выполнять задания в WebAssign. Студенту дается 6 попыток ответить на каждый вопрос. Чтобы перейти к следующему заданию, викторине или тесту на этой неделе, необходимо набрать 70 % баллов.
Тесты WebAssign (4)
Каждый тест будет охватывать материалы для чтения и изучения для назначенных модулей/недель. Каждый тест будет представлять собой открытые заметки/открытую книгу и выполняться в WebAssign. У студента будет 2 попытки на каждый тест.
Тесты WebAssign (3)
Учащийся будет проходить тесты в течение модулей/недель 2, 4 и 6. Каждый тест будет длиться 2 часа, открытые заметки/открытая книга и охватит 2 модуля/недели материала. Тесты будут проходить в WebAssign.Письменные работы для тестов должны быть отправлены в Blackboard сразу после завершения теста в WebAssign и до установленной даты/времени. Тесты, представленные без сопроводительной письменной работы, не принимаются. Есть только одна попытка для тестов.
Тесты будут проходить в WebAssign.Письменные работы для тестов должны быть отправлены в Blackboard сразу после завершения теста в WebAssign и до установленной даты/времени. Тесты, представленные без сопроводительной письменной работы, не принимаются. Есть только одна попытка для тестов.
Заключительный экзамен
Совокупный выпускной экзамен будет выполнен с использованием программного обеспечения WebAssign. Экзамен будет длиться 2 часа 30 минут, открытые заметки/открытая книга и должен быть завершен за один присест. Письменная работа для итогового экзамена должна быть отправлена в Blackboard сразу после прохождения теста в WebAssign.Есть только одна попытка сдать выпускной экзамен.
Матрицы и определители: формулы, темы, примечания, вопросы
Матрицы и определители:
В математике одной из интересных, простых и важных тем являются матрицы и определители. Каждый год вы будете получать по крайней мере 1-3 вопроса на основном и других экзаменах JEE, прямо или косвенно, концепция этой главы будет задействована во многих других главах, таких как интегральное и дифференциальное исчисление. Концепция этой главы будет использоваться для концепции трансформации осей. Эта глава совершенно новая с точки зрения студента, так как вы увидите эту главу непосредственно в 12-й главе. Таким образом, некоторые учащиеся могут счесть Матрицы и Определитель немного сложными для понимания и решения задач на начальном этапе. Но по мере того, как вы будете решать все больше и больше задач в этой главе, вы будете знакомиться с концепциями и главой в целом, а затем обнаружите, что это одна из самых простых глав. После этого вопросы покажутся вам легкими.Часть «Матрицы» может показаться немного более сложной, чем «Определитель», но, в конце концов, вы обнаружите, что и то, и другое легко понять,
Концепция этой главы будет использоваться для концепции трансформации осей. Эта глава совершенно новая с точки зрения студента, так как вы увидите эту главу непосредственно в 12-й главе. Таким образом, некоторые учащиеся могут счесть Матрицы и Определитель немного сложными для понимания и решения задач на начальном этапе. Но по мере того, как вы будете решать все больше и больше задач в этой главе, вы будете знакомиться с концепциями и главой в целом, а затем обнаружите, что это одна из самых простых глав. После этого вопросы покажутся вам легкими.Часть «Матрицы» может показаться немного более сложной, чем «Определитель», но, в конце концов, вы обнаружите, что и то, и другое легко понять,
и определитель находят широкое применение в реальных задачах, например, в программном обеспечении Adobe Photoshop матрицы используются для обработки линейного преобразования для рендеринга изображений. Квадратная матрица используется для представления линейного преобразования геометрического объекта. В компьютерном программировании матрицы и их обратные используются для шифрования сообщений, для хранения данных, выполнения запросов и используются в качестве структуры данных для решения алгоритмических задач и т. д.В робототехнике движение робота программируется с помощью расчета на основе матриц.
Квадратная матрица используется для представления линейного преобразования геометрического объекта. В компьютерном программировании матрицы и их обратные используются для шифрования сообщений, для хранения данных, выполнения запросов и используются в качестве структуры данных для решения алгоритмических задач и т. д.В робототехнике движение робота программируется с помощью расчета на основе матриц.
После изучения этой главы:
1. Вам будет легко понять концепцию массива в информатике (если вы сдали информатику на уровне +2).
2. Это поможет вам решить задачу, связанную с одновременным уравнением с таким же количеством неизвестных переменных, как и уравнений.
3.Определитель поможет вам решить задачи, связанные с площадями и объемом, такие как площадь треугольника и объем тетраэдра.
Онлайн-подготовка к JEE Main/NEETCrack JEE 2021 с онлайн-программой подготовки к JEE/NEET
Начинай сейчас 4. Это поможет вам лучше организовать свою работу в виде матриц и, следовательно, поможет вам сохранять ясность ума в повседневной жизни.
Это поможет вам лучше организовать свою работу в виде матриц и, следовательно, поможет вам сохранять ясность ума в повседневной жизни.
5. И, очевидно, сама глава поможет вам получить некоторые оценки на экзамене, так как она имеет около 7% веса на джи-мейн и примерно такой же вес на других экзаменах.
Матрица и операции с матрицами
Типы матриц
Транспонирование матрицы, симметричной и кососимметричной матрицы
Сопряжение матрицы, эрмитовой и косоэрмитовой матрицы
Определитель матрицы
Минор и кофактор элемента матрицы/детерминанта
Сопряженная и обратная матрицы
Элементарные операции со строками и их использование для нахождения обратной матрицы
Система линейных уравнений и правило Крамера
Система однородных линейных уравнений
Обзор матрицы и определителя:
Матрица: Набор чисел или объектов или символов, представленных в виде прямоугольного массива, называется матрицей. Порядок матрицы определяется количеством строк и количеством столбцов, присутствующих в прямоугольном массиве представления. Например
Порядок матрицы определяется количеством строк и количеством столбцов, присутствующих в прямоугольном массиве представления. Например
Матрица состоит из 2 строк и 3 столбцов, поэтому говорят, что ее порядок равен 2 × 3.
Любой общий элемент матрицы представлен , где представляет элементы i-й строки и j-го столбца.
Операции с матрицами: Алгебраические операции с матрицами, такие как сложение, вычитание, умножение и деление, будут изучаться последовательно в подробной главе, и мы обнаружим, что их очень легко понять.
Транспонирование матрицы: если A — матрица, то матрица, полученная путем замены столбцов матрицы строками или строк столбцами, называется транспонированием матрицы.
Например:
Сопряженная матрица: Если матрица A имеет в качестве элемента комплексное число, то матрица, полученная заменой этих комплексных чисел на сопряженную, называется сопряженной матрицы A и обозначается .
Определитель матрицы: число, которое вычисляется из матрицы.Чтобы определитель существовал, матрица A должна быть квадратной матрицей. Определитель матрицы обозначается det A или |A|.
Минор и сомножитель элемента в матрице/детерминанте: Минор любого элемента, где i – количество строк, j – количество столбцов, это det матрицы, оставшийся после удаления i-й строки и j-го столбец.
Сопряжение матрицы: транспонирование кофактора элемента матрицы известно как сопряжение матрицы.
Обратная матрица: неособая квадратная матрица «А» называется обратимой, если существует невырожденная квадратная матрица В такая, что АВ = I=ВА, а матрица В называется обратной матрице А
Матрицы и определитель – это тема, полезная при преобразовании координат и некоторых понятиях дифференциального уравнения, а также в биномиальной теореме, вы должны пройти эту главу, а также помочь некоторым из этих понятий, а также это поможет вам набрать некоторые баллы. легкие оценки на основных экзаменах.
легкие оценки на основных экзаменах.
1. Начните с понимания основных понятий, таких как определение матрицы, алгебра матрицы, транспонирование матрицы и т. д.
2. Затем перейдите к сложному понятию, такому как сопряженная матрица и обратная матрица,
А затем система уравнений, определитель, правила Крамера и однородные уравнения.
3. После изучения этих концепций просмотрите решенные примеры, а затем перейдите к MCQ и попрактикуйтесь в решении задачи, чтобы убедиться, что вы поняли тему.
4. Решите вопросы из книг, за которыми вы следите, а затем перейдите к работам предыдущего года.
5. Вы можете сначала изучить матрицу, а затем определитель или сначала определитель, а затем матрицу. В разных книгах соблюдается разный порядок, вы можете выбрать свой собственный порядок или порядок коучинга или материала, которому вы следуете.
6. При изучении концепции убедитесь, что вы понимаете вывод формул, и попробуйте вывести их самостоятельно, так как часто вам не понадобится точная формула, но некоторые шаги вывода будут очень полезны для решения проблемы, если вы понимаете его вывод повысит вашу скорость решения проблем.
7. Так как эта тема в значительной степени связана с вычислениями, практикуйтесь как можно больше и при этом помните об общем весе, который она имеет (7%).
8. В конце главы постарайтесь сделать свои собственные краткие заметки для быстрого повторения, составьте список формул для быстрого повторения перед экзаменами или в любое время, когда вам потребуется пересмотреть главу, это сэкономит вам много времени.
Лучшие книги для подготовки к комплексным числам и квадратным уравнениям:
Во-первых, закончите все понятия, примеры и вопросы, данные в Книге по математике NCERT.Вы должны тщательно изучить теорию NCERT. Затем вы можете обратиться к книге «Алгебра, Арихант» доктора С.К. Гояла или Р.Д. Шармы или Cengage Mathematics Algebra, но убедитесь, что вы следуете любой из них, а не всем. Матрица и определитель очень хорошо объясняются в этих книгах, и есть достаточное количество вопросов с кристально ясными понятиями. Выбор справочника зависит от человека к человеку, найдите книгу, которая подходит вам лучше всего, в зависимости от того, насколько хорошо вы понимаете концепции и сложность вопросов, которые вам нужны.
Выбор справочника зависит от человека к человеку, найдите книгу, которая подходит вам лучше всего, в зависимости от того, насколько хорошо вы понимаете концепции и сложность вопросов, которые вам нужны.
Что такое матрица? – План урока
Продолжительность
45–60 минут
Стандарты учебной программы
- CCSS.MATH.CONTENT.HSA.REI.C.8
Представьте систему линейных уравнений в виде одного матричного уравнения с векторной переменной.
- CCSS.MATH.CONTENT.HSA.REI.C.5
Докажите, что для данной системы двух уравнений с двумя переменными замена одного уравнения суммой этого уравнения и произведением другого дает систему с теми же решениями.
- CCSS.MATH.CONTENT.HSA.SSE.B.3
Выберите и создайте эквивалентную форму выражения, чтобы раскрыть и объяснить свойства величины, представленной выражением.
Материалы
- Распечатка видеоурока Что такое матрица? и печатные экземпляры викторины урока
- Аудиовизуальное оборудование
- Игральные карты (или учетные карточки)
Разминка
- Начните урок с написания на доске сложной системы уравнений, подобной той, что предлагается в видеоуроке: x + y +2 z + a -2 b -3 c =8 и -2 x +2 y -4 z -2 w + a -3 b +1=10.
- Спросите, знает ли кто-нибудь, как решить эту систему.
- Позвольте учащимся подойти к доске и попробовать любые идеи, которые у них есть.
- Спросите, кто знает, что такое матрица. Если кто-то из учащихся скажет «да», спросите, думают ли они, что матрица поможет решить систему.
- Скажите своим ученикам, что на этом уроке вы познакомитесь с понятием математической матрицы и с тем, как использовать матрицы.
Инструкции
- Скажите учащимся, что вы собираетесь показать им короткое видео о матрицах, но затем вы будете медленно просматривать видео, повторяя основные понятия.
 Попросите учащихся воздержаться от заметок при первом просмотре видео и просто сосредоточиться на концепциях.
Попросите учащихся воздержаться от заметок при первом просмотре видео и просто сосредоточиться на концепциях. - Просмотреть видеоурок Что такое матрица?.
- Обсудить:
- Что такое матрица?
- Для чего он используется?
- Какие операции можно производить с матрицами?
- Что представляют строки? Колонны?
- Кто думает, что они могут перевести простое уравнение в маленькую матрицу?
- Напишите на доске трехчленное выражение (например, 3 x + 2 z – 4 y ) и позвольте добровольцу нарисовать и заполнить соответствующую матрицу.
- Разрешить другим добровольцам добавлять в матрицу свои собственные выражения из трех терминов.
- Скажите своим ученикам, что теперь вы будете работать с видео небольшими шагами и практиковать каждую часть по мере ее поступления. Раздайте стенограммы видео, поощряя студентов читать вместе, если это необходимо.
- Перезапустить видеоурок.

- Пауза на отметке времени 2:05. Попросите добровольца нарисовать матрицу и заполнить первую строку соответствующими коэффициентами.
- Разрешить другому добровольцу заполнить вторую строку.
- Продолжите видео, сделав паузу на отметке 2:11, чтобы проверить правильность работы учащихся на доске.
- Обратите внимание, что иногда в матрице используется прямая линия для обозначения знака равенства в уравнении. Проведите прямую линию вниз по матрице перед числами 16 и 10 на доске.
- Продолжить видео. Сделайте паузу на отметке времени 2:48 для первого занятия.
Задание 1
- Раздайте каждому учащемуся по одной игральной карте.
- Скажите учащимся, что каждый из них является термином в выражении. Их карта дает им коэффициент в их термине, а первый инициал их имени является переменной термина.
- Красные карточки отрицательные, а черные карточки положительные.
- Карты с картинками оцениваются в возрастающем порядке J=11, Q=12 и K=13.

- Попросите учеников пройтись по комнате, пока вы не подаст сигнал.
- По сигналу ученики должны сгруппироваться (пятеро в группе).
- Группы должны записать выражение, которое они образуют с терминами, представленными каждым учащимся.
- Затем каждая группа должна перевести свое выражение в соответствующую матрицу.
- Наконец, каждая группа должна перевести выражение другой группы в свою собственную матрицу.
- Все группы должны иметь матрицу с двумя строками по пять столбцов в каждой.
- Продолжить паузу видео на отметке времени 3:47 для второго действия.
Второе занятие
- Попросите учащихся вернуться в свои предыдущие группы.
- Напомните им, что у каждой группы должна быть матрица 2×5.
- Попросите каждую группу соединиться с другой группой.
- Сообщите наборам групп, чтобы они складывали и вычитали соответствующие матрицы. Теперь в каждой группе должно быть по три матрицы (исходная 2×5, сумма и разность).

- Попросите добровольцев продемонстрировать работу своей группы на доске.
- Попросите учеников вернуться на свои места, чтобы продолжить видео.
- Пауза на отметке времени 5:05.
- Нарисуйте на доске аналогичную пару матриц (как в видео) и проработайте ее шаг за шагом, позволяя учащимся давать ответы на каждый шаг.
- Пауза для третьего действия
Третье занятие
- Попросите учащихся вернуться в свои первоначальные группы.
- Пусть они используют игральные карты, чтобы создать свою собственную пару матриц для умножения.
- После того, как группы найдут свои продукты, предложите им подойти к доске, чтобы поделиться своей работой с остальным классом.
- Закончите видео.
- Дайте время для заключительного обсуждения, чтобы ответить на любые оставшиеся вопросы, которые могут возникнуть у учащихся по концепции.
- Раздайте тест на урок. Просмотрите каждый вопрос и ответ после того, как учащиеся завершат тест.

Как решать обратные матрицы
Квадратная матрица: определение и концепция
Изучение матричной математики с онлайн-курсами, классами и уроками
Что такое умножение матриц?
Умножение матриц — это функция линейной алгебры, позволяющая составить из двух матриц матрицу, представляющую собой композицию.Вычисление матричных произведений является центральной частью вычислительных приложений. Он позволяет упростить линейные уравнения, создавать ходы в таких приложениях, как теория игр, или улучшать визуализацию изображений, несмотря на небольшие сложности. Умножение матриц — дело непростое, но с помощью программ, которые сделают всю тяжелую работу за вас, вы сможете применить его к своим вычислениям без лишней работы. Изучив этот процесс, вы создадите свой набор инструментов для выполнения высокоуровневых команд программирования и откроете множество творческих программных решений.
Изучение умножения матриц в программировании
Умножение матриц — это всего лишь один из методов работы с алгоритмами. Это сложнее, чем скалярное умножение, основанное на скалярном произведении для умножения комбинаций различных столбцов и строк. В скалярных или векторных операциях вы применяете скаляр к каждому элементу в матрице. Для умножения матриц требуется больше ловкости. Эти операции являются неотъемлемой частью программирования нейронных сетей в рамках машинного обучения. Вы должны уметь строить операции, учитывающие различные решения в матрице, и каждая новая матрица — это возможность еще больше расширить алгоритм.
Это сложнее, чем скалярное умножение, основанное на скалярном произведении для умножения комбинаций различных столбцов и строк. В скалярных или векторных операциях вы применяете скаляр к каждому элементу в матрице. Для умножения матриц требуется больше ловкости. Эти операции являются неотъемлемой частью программирования нейронных сетей в рамках машинного обучения. Вы должны уметь строить операции, учитывающие различные решения в матрице, и каждая новая матрица — это возможность еще больше расширить алгоритм.
Matrix Math Courses
Если вы не понимаете, как это применимо к программированию, вам может помочь edX. В партнерстве с ведущими учебными заведениями, включая Гарвард и IT Bombay, вы сможете изучить основы программирования алгоритмов и то, как умножение матриц вписывается в систему алгоритмов. Например, вы можете получить исчерпывающий обзор алгоритмов с помощью IT Bombay и узнать, как использовать умножение матриц в сети алгоритмов других типов для создания высокоуровневых приложений. Гарвардская серия программ по программированию также затрагивает умножение матриц. Вы получите представление об основных понятиях, начиная с самой первой матрицы и заканчивая фундаментальными свойствами матричной алгебры. Вы будете работать с реальными числами и создавать ноу-хау для различных операций.
Гарвардская серия программ по программированию также затрагивает умножение матриц. Вы получите представление об основных понятиях, начиная с самой первой матрицы и заканчивая фундаментальными свойствами матричной алгебры. Вы будете работать с реальными числами и создавать ноу-хау для различных операций.
Создайте свой набор инструментов для программирования с помощью матричной математики
Вам необходимо знать операции матричной математики и то, как она вписывается в экосистему алгоритмов программирования. Вы сможете анализировать количество столбцов и строк, разбираться в матричной алгебре, строить отчеты и работать со сложными матричными операциями.У матричной математики есть приложения для искусственного интеллекта, игр, рендеринга изображений и других областей, поэтому наращивайте свои навыки программирования с четким пониманием. Ваше резюме по программированию будет вам благодарно.
Матричное преобразование приложения — приложения Win32
- Статья
- 7 минут на чтение
Пожалуйста, оцените свой опыт
да Нет
Любая дополнительная обратная связь?
Отзыв будет отправлен в Microsoft: при нажатии кнопки отправки ваш отзыв будет использован для улучшения продуктов и услуг Microsoft.Политика конфиденциальности.
Представлять на рассмотрение
Спасибо.
В этой статье
В этом разделе представлен математический обзор матричных преобразований для двумерной графики. Однако вам не нужно знать математику матриц, чтобы использовать преобразования в Direct2D. Прочтите эту тему, если вам интересна математика; в противном случае не стесняйтесь пропустить эту тему.
Введение в матрицы
Матрица представляет собой прямоугольный массив действительных чисел.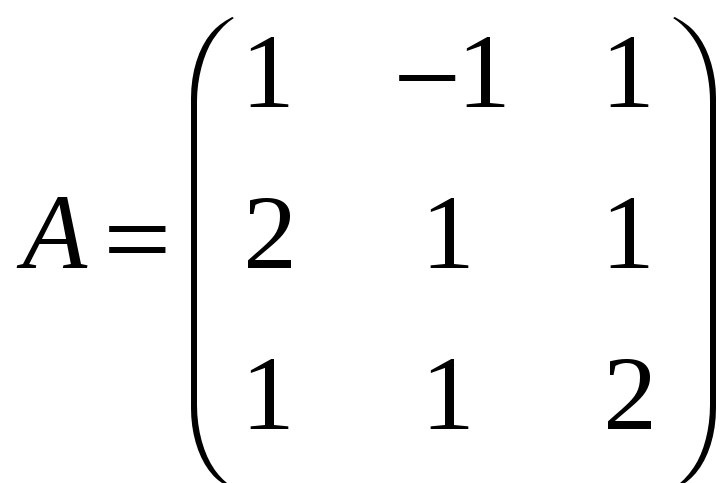 порядок матрицы – это количество строк и столбцов. Например, если матрица имеет 3 строки и 2 столбца, порядок будет 3 × 2. Матрицы обычно отображаются с элементами матрицы, заключенными в квадратные скобки:
порядок матрицы – это количество строк и столбцов. Например, если матрица имеет 3 строки и 2 столбца, порядок будет 3 × 2. Матрицы обычно отображаются с элементами матрицы, заключенными в квадратные скобки:
Обозначение: Матрица обозначается заглавной буквой. Элементы обозначаются строчными буквами. Нижние индексы указывают номер строки и столбца элемента. Например, a ij — это элемент в i-й строке и j-м столбце матрицы A.
На следующей диаграмме показана матрица размера i × j с отдельными элементами в каждой ячейке матрицы.
Операции с матрицами
В этом разделе описаны основные операции, определенные над матрицами.
Дополнение . Сумма A + B двух матриц получается сложением соответствующих элементов A и B:
- A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]
Скалярное умножение . Эта операция умножает матрицу на действительное число.Учитывая действительное число k , скалярное произведение kA получается путем умножения каждого элемента A на k .
- кА = k\[ a*ij* \] = \[ k × a*ij* \]
Умножение матриц . Для двух матриц A и B порядка (m × n) и (n × p) произведение C = A × B представляет собой матрицу порядка (m × p), определяемую следующим образом:
или эквивалентно:
- c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + … + a*in* + b*nj*
То есть для вычисления каждого элемента c ij выполните следующие действия:
- Возьмите i-ю строку A и j-й столбец B.
- Умножьте каждую пару элементов в строке и столбце: элемент первой строки на элемент первого столбца, элемент второй строки на элемент второго столбца и т. д.
- Суммировать результат.
Вот пример умножения матрицы (2 × 2) на матрицу (2 × 3).
Умножение матриц не является коммутативным. То есть A × B ≠ B × A. Также из определения следует, что не всякую пару матриц можно перемножать. Количество столбцов в левой матрице должно быть равно количеству строк в правой матрице. В противном случае оператор × не определен.
В противном случае оператор × не определен.
Определить матрицу . Единичная матрица, обозначенная I, представляет собой квадратную матрицу, определяемую следующим образом:
- I*ij* = 1, если *i* = *j*, или 0 в противном случае.
Другими словами, единичная матрица содержит 1 для каждого элемента, где номер строки равен номеру столбца, и ноль для всех остальных элементов. Например, вот единичная матрица 3 × 3.
Следующие равенства выполняются для любой матрицы M.
- М х Я = М
Я х М = М
Аффинные преобразования
Аффинное преобразование — это математическая операция, которая отображает одно координатное пространство в другое.Другими словами, он отображает один набор точек в другой набор точек. Аффинные преобразования имеют некоторые особенности, которые делают их полезными в компьютерной графике.
- Аффинные преобразования сохраняют коллинеарность . Если три или более точек попадают на линию, они все равно образуют линию после преобразования.
 Прямые линии остаются прямыми.
Прямые линии остаются прямыми. - Композиция двух аффинных преобразований является аффинным преобразованием.
Аффинные преобразования для двумерного пространства имеют следующий вид.
Если вы примените определение умножения матриц, данное ранее, вы можете показать, что произведение двух аффинных преобразований является другим аффинным преобразованием. Чтобы преобразовать 2D-точку с помощью аффинного преобразования, точка представляется в виде матрицы 1 × 3.
- Р = \| х у 1 \|
Первые два элемента содержат координаты x и y точки. 1 помещается в третий элемент, чтобы математика работала правильно. Чтобы применить преобразование, умножьте две матрицы следующим образом.
- П’ = П × М
Это расширяется до следующего.
где
- х’ = ах + су + е
у’ = Ьх + dy + f
Чтобы получить преобразованную точку, возьмите первые два элемента матрицы P’.
- p = (x’, y’) = (ax + cy + e, bx + dy + f)
Примечание
Матрица 1 × n называется вектором-строкой .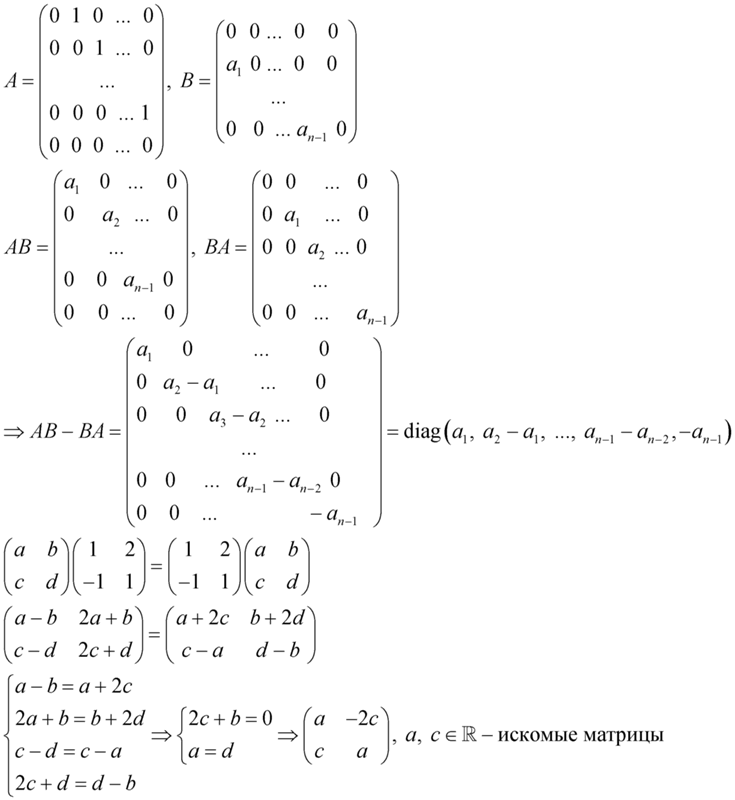 И Direct2D, и Direct3D используют векторы-строки для представления точек в 2D- или 3D-пространстве. Вы можете получить эквивалентный результат, используя вектор-столбец ( n × 1) и транспонируя матрицу преобразования.В большинстве графических текстов используется форма вектора-столбца. В этом разделе представлена форма вектора-строки для совместимости с Direct2D и Direct3D.
И Direct2D, и Direct3D используют векторы-строки для представления точек в 2D- или 3D-пространстве. Вы можете получить эквивалентный результат, используя вектор-столбец ( n × 1) и транспонируя матрицу преобразования.В большинстве графических текстов используется форма вектора-столбца. В этом разделе представлена форма вектора-строки для совместимости с Direct2D и Direct3D.
Следующие несколько разделов выводят базовые преобразования.
Преобразование перевода
Матрица преобразования перевода имеет следующий вид.
Подстановка точки P в это уравнение дает:
- P’ = (*x* + *dx*, *y* + *dy*)
, что соответствует точке (x, y), сдвинутой на dx по оси X и dy по оси Y.
Масштабирование преобразования
Матрица преобразования масштабирования имеет следующий вид.
Подстановка точки P в это уравнение дает:
- P’ = (*x* ∙ *dx*, *y* ∙ *dy*)
, что соответствует точке (x,y), масштабированной с помощью dx и dy .
Вращение вокруг начала координат
Матрица для поворота точки вокруг начала координат имеет следующий вид.
Преобразованная точка:
- P’ = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)
Доказательство.Чтобы показать, что P’ представляет собой вращение, рассмотрим следующую диаграмму.
Дано:
Р = (х, у)
Исходная точка для преобразования.
Ф
Угол, образованный линией (0,0) к пар.
Θ
Угол поворота (x,y) относительно исходной точки.
Р’ = (х’, у’)
Преобразованная точка.
Р
Длина линии (0,0) до P. Также радиус окружности вращения.
Примечание
На этой диаграмме используется стандартная система координат, используемая в геометрии, где положительная ось Y направлена вверх. Direct2D использует систему координат Windows, где положительная ось Y направлена вниз.
Угол между осью x и линией (0,0) к P’ равен Φ + Θ. Имеются следующие тождества:
- х = R cosΦ
у = R sinΦ
х’ = R cos (Ф + Θ)
у’ = Rsin(Φ+ Θ)
Теперь решите x’ и y’ через Θ.По формулам тригонометрического сложения:
- x’ = R(cosΦcosΘ – sinΦsinΘ) = RcosΦcosΘ – RsinΦsinΘ
y’ = R(sinΦcosΘ + cosΦsinΘ) = RsinΦcosΘ + RcosΦsinΘ
Подставляя, получаем:
- х’ = xcosΘ – ysinΘ
у’ = xsinΘ + ycosΘ
, что соответствует показанной ранее преобразованной точке P’.
Вращение вокруг произвольной точки
Для вращения вокруг точки (x,y), отличной от начала координат, используется следующая матрица.
Вы можете получить эту матрицу, приняв точку (x,y) за начало координат.
Пусть (x1, y1) будет точкой, полученной в результате вращения точки (x0, y0) вокруг точки (x,y). Мы можем получить x1 следующим образом.
- x1 = (x0 – x)cosΘ– (y0 – y)sinΘ + x
x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]
Теперь подставьте это уравнение обратно в матрицу преобразования, используя формулу x1 = ax0 + cy0 + e из предыдущей. Используйте ту же процедуру для получения y1.
Используйте ту же процедуру для получения y1.
Преобразование с наклоном
Косое преобразование определяется четырьмя параметрами:
- Θ: Величина перекоса по оси x, измеренная как угол от оси y.
- Φ: Величина перекоса по оси Y, измеренная как угол от оси X.
- ( px , py ): координаты x и y точки, относительно которой выполняется наклон.
Косое преобразование использует следующую матрицу.
Преобразованная точка:
- P’ = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΦ) – *py*tanΦ
или эквивалент:
- P’ = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΦ)
Чтобы увидеть, как работает это преобразование, рассмотрим каждый компонент по отдельности.Параметр Θ перемещает каждую точку в направлении x на величину, равную tanΘ. На следующей диаграмме показана связь между Θ и перекосом оси x.
Вот тот же наклон, примененный к прямоугольнику:
Параметр Φ имеет тот же эффект, но по оси Y:
На следующей диаграмме показан наклон по оси Y, примененный к прямоугольнику.
Наконец, параметры px и py смещают центральную точку перекоса по осям x и y.
Представление преобразований в Direct2D
Все преобразования Direct2D являются аффинными преобразованиями. Direct2D не поддерживает неаффинные преобразования. Преобразования представлены структурой D2D1_MATRIX_3X2_F . Эта структура определяет матрицу 3 × 2. Поскольку третий столбец аффинного преобразования всегда один и тот же ([0, 0, 1]), а Direct2D не поддерживает неаффинные преобразования, нет необходимости указывать всю матрицу 3 × 3. Внутри Direct2D использует матрицы 3 × 3 для вычисления преобразований.
Элементы D2D1_MATRIX_3X2_F названы в соответствии с их положением в индексе: элемент _11 является элементом (1,1), элемент _12 является элементом (1,2) и так далее. Хотя вы можете инициализировать элементы структуры напрямую, рекомендуется использовать класс D2D1::Matrix3x2F . Этот класс наследует D2D1_MATRIX_3X2_F и предоставляет вспомогательные методы для создания любых основных аффинных преобразований. Класс также определяет operator*() для составления двух или более преобразований, как описано в разделе Применение преобразований в Direct2D.
Этот класс наследует D2D1_MATRIX_3X2_F и предоставляет вспомогательные методы для создания любых основных аффинных преобразований. Класс также определяет operator*() для составления двух или более преобразований, как описано в разделе Применение преобразований в Direct2D.
Следующий
Модуль 4. Пользовательский ввод
Что такое матрица в математике? (Введение, типы и операции с матрицами)
Матрица — важная тема в математике. В этом посте мы обсудим эти моменты.
В 1858 году английский математик Артур Кэли впервые разработал «Теория матриц». Артур Кейли также был организатором Современной британской школы чистой математики.
В детстве он любил решать сложные математические задачи для удовольствия и блистал во французском, немецком, итальянском, греческом и математике в Тринити-колледже Кембриджа.
Что такое Матрица?
Как правило, представляет собой набор информации, хранящейся в упорядоченном виде. Математически это набор чисел, переменных или функций, расположенных в строках и столбцах. Матрицы представлены заглавными буквами английского алфавита, такими как A, B, C…… и т. д.
Математически это набор чисел, переменных или функций, расположенных в строках и столбцах. Матрицы представлены заглавными буквами английского алфавита, такими как A, B, C…… и т. д.
Например,
В приведенном выше примере матрица A имеет 3 строки и 3 столбца.
Применение матриц
Матрицы используются в различных отраслях науки, некоторые из его приложений:
- Кому решить систему линейных уравнений
- Компьютер Графика
- Физика
- Криптография
- График Теория
Порядок матрицы
Определяется количеством строк и столбцов в матрице.
Порядок матрицы = количество строк × количество столбцов
В выше пример, количество строк равно 3, а количество столбцов также равно 3, следовательно,
Порядок матрицы A равен 3 × 3.
Типы матриц
1. Матрица строк
Если
матрица имеет только одну строку, тогда она называется матрицей-строкой. Например,
Например,
Это представляет собой матрицу-строку порядка 1 на 3.
2. Матрица столбцов
Если матрица имеет только один столбец, она называется матрицей-столбцом.Например,
Это столбцовая матрица порядка 3 на 1.
3. Нулевая или нулевая матрица
Если все элементы матрицы равны нулю, то она называется Null или нулевая матрица. Например,
Это нулевая матрица порядка 2 на 2. Нулевая или нулевая матрица обозначается «O».
4. Квадратная матрица
В матрице, если количество строк равно количеству столбцов, она называется квадратной матрицей.Например, если матрица имеет 2 строки и 2 столбца, то она называется квадратной матрицей, как указано ниже
.5. Прямоугольная матрица
В матрице, если количество строк не равно количеству столбцов, она называется прямоугольной матрицей. Например, если матрица имеет 2 строки и 3 столбца, то она называется прямоугольной матрицей, как указано ниже.
6. Диагональная матрица
Если все элементы квадратной матрицы равны нулю, кроме элементов главной диагонали, то такая матрица называется диагональной.Однако некоторые элементы главной диагонали могут быть нулевыми, но не все элементы. Например,
7. Скалярная матрица
Если все диагональные элементы диагональной матрицы одинаковы, то она называется скалярной матрицей. Например,
8. Единица измерения или матрица идентичности
Если каждый диагональный элемент диагональной матрицы равен 1, то она называется единичной или единичной матрицей. Например,
9.Негатив матрицы
Отрицательная матрица получается заменой знаков всех ее элементов. Рассмотрим матрицу A и изменим ее на отрицательную матрицу –A as,
если
, затем
10. Транспонирование матрицы
Транспонирование матрицы получается путем замены всех ее строк на столбцы или столбцов на строки. Обозначается
Обозначается
Если
, затем
11.Симметричная матрица
Квадратная матрица называется симметричной, если она равна своей транспонированной. Например,
Если
, затем
Следовательно, A симметрична.
Если
тоСледовательно, B несимметричен.
12. Кососимметричная матрица
Квадратная матрица называется кососимметричной, если ее транспонирование равно отрицательному значению этой матрицы, т.е.
. Например,Если
, затем
Следовательно, матрица A кососимметрична.
Операции с матрицами
Добавление матриц:
Сложение двух матриц A и B приведет к быть возможным, если они имеют одинаковые заказы. Сложение двух матриц A и B равно обозначается A + B. Например,
Если
иЗатем
Вычитание матриц:
Вычитание одной матрицы из другой
матрицы будут возможны, если они имеют одинаковые порядки. Вычитание двух
матрицы A и B обозначаются через A – B.Например,
Вычитание двух
матрицы A и B обозначаются через A – B.Например,
Если
иЗатем
Произведение матриц:
Произведение двух матриц A и B будет возможно, если количество столбцов матрицы A равно количеству строк другой матрицы B. Например,
Если
иЗатем
Brilliant Math & Science Wiki
Наконец, есть более сложная операция умножения матриц .Произведение двух матриц определяется только , когда количество столбцов первой матрицы равно количеству строк второй; другими словами, возможно только умножение матриц размера m×nm \times nm×n и n×pn \times pn×p. Причина этого становится понятной при определении продукта:
Произведение PPP матрицы AAA размера m×nm \times nm×n и матрицы BBB размера n×pn \times pn×p удовлетворяет
Pi,j=Ai,∗⋅B∗,jP_{i,j} = A_{i,*} \cdot B_{*,j}Pi,j=Ai,∗⋅B∗,j
для всех i, ji, ji, j в пределах размера матриц.
\text{th}j-й столбец BBB, который также является вектором. Таким образом, точка (⋅)(\cdot)(⋅) в этом смысле относится к умножению векторов, определяемых скалярным произведением. Обратите внимание, что iii и jjj определены на 1≤i≤m1 \leq i \leq m1≤i≤m и 1≤j≤p1 \leq j \leq p1≤j≤p, поэтому произведение PPP будет m×pm \times pm×p матрица.
Это правило кажется довольно произвольным, поэтому его лучше всего проиллюстрировать на примере:
Что такое
(123456)(123456)?\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}\begin{pmatrix}1&2\\3&4\\5&6\end{pmatrix}?(142536)⎝⎛ 135246⎠⎞?
Во-первых, обратите внимание, что первая матрица имеет размер 2×32 х 32 х 3, а вторая 3 х 23 х 23 х 2, поэтому их произведение действительно определено и будет матрицей 2 х 22 х 22 х 2. .\text{st}1-й столбец второй матрицы, т.е.
(P1,1P1,2P2,1P2,2)=(123456)(123456)P1,1=(1,2,3)⋅(1,3,5)=1 ⋅ 1 + 2 ⋅ 3 + 3 ⋅ 5 =22.\begin{выровнено} \begin{pmatrix}\color{#20A900}{P_{1,1}} & P_{1,2}\\P_{2,1}&P_{2,2}\end{pmatrix} &= \begin{ pmatrix}\color{#D61F06}{1}&\color{#D61F06}{2}&\color{#D61F06}{3}\\4&5&6\end{pmatrix}\begin{pmatrix}\color{#3D99F6} {1}&2\\\color{#3D99F6}{3}&4\\\color{#3D99F6}{5}&6\end{pmatrix}\\\\ \color{#20A900}{P_{1,1}} &= (\color{#D61F06}{1, 2, 3}\color{#333333}{) \cdot (}\color{#3D99F6}{1 , 3, 5}\color{#333333}{)} \\ &= \color{#D61F06}{1~}\color{#333333}{\cdot}\color{#3D99F6}{~1~}\color{#333333}{+}\color{#D61F06}{~ 2~}\color{#333333}{\cdot}\color{#3D99F6}{~3~}\color{#333333}{+}\color{#D61F06}{~3~}\color{#333333} {\cdot}\color{#3D99F6}{~5}\\ &=22.
\end{выровнено}(P1,1P2,1P1,2P2,2)P1,1=(142536)⎝⎛135246⎠⎞= (1,2,3)⋅(1,3,5)=1 ⋅ 1 + 2 ⋅ 3 + 3 ⋅ 5=22.
Таким образом, верхний левый элемент результата равен 22. Остальная часть матрицы может быть заполнена таким же образом; например,
(P1,1P1,2P2,1P2,2)=(123456)(123456).\begin{pmatrix}P_{1,1} & \color{#20A900}{P_{1,2}}\\P_{ 2,1}&P_{2,2}\end{pmatrix} = \begin{pmatrix}\color{#D61F06}{1}&\color{#D61F06}{2}&\color{#D61F06}{3} \\4&5&6\end{pmatrix}\begin{pmatrix}1&\color{#3D99F6}2\\3&\color{#3D99F6}{4}\\5&\color{#3D99F6}{6}\end{pmatrix} .(P1,1P2,1P1,2P2,2)=(142536)⎝⎛135246⎠⎞.
Окончательный результат
Р=(22284964). □P = \begin{pmatrix}22&28\\49&64\end{pmatrix}.\ _\squareP=(22492864). □
Если A=(1−2323−1−312)A = \begin{pmatrix} 1 & -2 & 3 \\ 2 & 3 & -1 \\ -3 & 1 & 2 \end{pmatrix} A=⎝⎛ 12−3−2313−12⎠⎞ и B=(102012120),B = \begin{pmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end {pmatrix},B=⎝⎛101012220⎠⎞, затем найдите ABABAB и BABABA.
Какой вывод можно сделать из последних двух матриц?
И ААА, и ВВВ являются квадратными матрицами порядка 3×33 х 33×3. Следовательно, и ABABAB, и BABABA корректно определены и являются матрицами одного порядка 3 × 33 \× 33 × 3.
AB=(1−2323−1−312)⋅(102012120)=(1⋅1+(−2)⋅0+3⋅11⋅0+(−2)⋅1+3⋅21⋅2+(− 2)⋅2+3⋅02⋅1+3⋅0+(−1)⋅12⋅0+3⋅1+(−1)⋅22⋅2+3⋅2+(−1)⋅0(−3 )⋅1+1⋅0+2⋅1−3⋅0+1⋅1+2⋅2−3⋅2+1⋅2+2⋅0)=(44−21110−15−4)BA=(102012120 )⋅(1−2323−1−312)=(−507−453541).\begin{aligned} AB & = \begin{pmatrix} 1 & -2 & 3 \\ 2 & 3 & -1 \\ -3 & 1 & 2 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{pmatrix} \\ & = \begin{pmatrix} 1 \cdot 1 + (-2) \cdot 0 + 3 \cdot 1 и 1 \cdot 0 + (-2) \cdot 1 + 3 \cdot 2 и 1 \cdot 2 + (-2) \cdot 2 + 3 \ cdot 0 \\ 2 \cdot 1 + 3 \cdot 0 + (-1) \cdot 1 и 2 \cdot 0 + 3 \cdot 1 + (-1) \cdot 2 и 2 \cdot 2 + 3 \cdot 2 + (-1) \cdot 0 \\ (-3) \cdot 1 + 1 \cdot 0 + 2 \cdot 1 и -3 \cdot 0 + 1 \cdot 1 + 2 \cdot 2 & -3 \cdot 2 + 1 \cdot 2 + 2 \cdot 0 \end{pmatrix} \\ & = \begin{pmatrix} 4 & 4 & -2 \\ 1 & 1 & 10 \\ -1 & 5 & -4 \end{pmatrix} \ \\\ BA & = \begin{pmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{pmatrix} \cdot \begin{pmatrix} 1 & -2 & 3 \\ 2 & 3 & -1 \\ -3 & 1 & 2 \end{pmatrix} \ \ & = \begin{pmatrix} -5 & 0 & 7 \\ -4 & 5 & 3 \\ 5 & 4 & 1 \end{pmatrix}.
\end{align}ABBA=⎝⎛12−3−2313−12⎠⎞⋅⎝⎛101012220⎠⎞=⎝⎛1⋅1+(−2) ⋅0+3⋅12⋅1+3⋅0+(−1)⋅1(−3)⋅1+1⋅0+2⋅11⋅0+(−2)⋅1+3⋅22⋅0 +3⋅1+(−1)⋅2−3⋅0+1⋅1+2⋅21⋅2+(−2)⋅2+3⋅02⋅2+3⋅2+(−1)⋅ 0−3⋅2+1⋅2+2⋅0⎠⎞=⎝⎛41−1415−210−4⎠⎞=⎝⎛101012220⎠⎞⋅⎝ ⎛12−3−2313−12⎠⎞=⎝⎛−5−45054731⎠⎞.
Как видно, AB≠BAAB \neq BAAB=BA. Таким образом, мы можем заключить, что умножение матриц не обязательно должно быть коммутативным . □_\квадрат□
Отправьте свой ответ
Предположим, что xxx и yyy удовлетворяют следующему уравнению:
(xy21)(x0yx)=2(106−x30)+(52x4x).\left(\begin{array}{cc}x& y \\2&1 \end{массив}\right)\left(\begin{array}{cc}x&0 \\y& x \end{массив}\right)=2 \left(\begin{array}{cc}10&6-x \\3&0 \end{массив}\right)+\left(\begin{array}{cc}5&2x \\4& x \end{массив}\right) .
(x2y1)(xy0x)=2(1036−x0)+(542xx).
Оценить x+y.x+y.x+y.
До сих пор, по общему признанию, неясно, почему умножение матриц определяется таким образом. Одна из основных причин заключается в использовании систем линейных уравнений.Коэффициенты каждого уравнения могут быть объединены в матрицу коэффициентов из , а переменные могут быть организованы в вектор-столбец. Произведение матрицы коэффициентов и вектора-столбца само по себе будет вектором-столбцом, значениями каждого уравнения. Например, система уравнений
{x+2y+3z=93x+y+4z=122x+4y-z=4\влево\lbrace \begin{выровнено} х + 2у + 3з &= 9 \\ 3х + у + 4з &= 12 \\ 2x + 4y – z &= 4 \end{выровнено} \правильно. ⎩⎪⎨⎪⎧x+2y+3z3x+y+4z2x+4y−z=9=12=4
можно более лаконично записать в виде
(12331424−1)(xyz)=(9124).\begin{pmatrix}1&2&3\\3&1&4\\2&4&-1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}9\\12\\4\ end{pmatrix}.
⎝⎛13221434−1⎠⎞⎝⎛xyz⎠⎞=⎝⎛9124⎠⎞.
Это очень полезная трансформация помимо экономии места; в частности, если бы можно было «разделить» матрицы, было бы легко узнать, что такое x, y, zx, y, zx, y, z, путем деления матрицы коэффициентов. К сожалению, определение деления требует дополнительных усилий, поэтому его дальнейшее объяснение оставлено в следующем разделе.
В качестве предупреждения о матричном умножении крайне важно понимать следующее:
Умножение матриц — это , а не , коммутативное. Другими словами, , а не в целом верно, что AB=BAAB = BAAB=BA.
Простейший способ убедиться в этом состоит в том, что умножение матриц определено только для матриц размера m×nm \times nm×n и n×pn \times pn×p; изменение их порядка дает произведение матрицы n×pn \times pn×p и матрицы m×nm \times nm×n, и ppp не обязательно равен mmm.Даже в таком случае (например, квадратные матрицы) умножение обычно не является коммутативным.
Матрицы A, BA, BA, B, которые действительно удовлетворяют AB=BAAB = BAAB=BA, (соответственно) называются коммутирующими матрицами .
Сделайте две матрицы (1100)\begin{pmatrix}1&1\\0&0\end{pmatrix}(1010) и (2011)\begin{pmatrix}2&0\\1&1\end{pmatrix}(2101 ) добираться?
Нет, с
(1100)(2011)=(3100)\begin{pmatrix}1&1\\0&0\end{pmatrix}\begin{pmatrix}2&0\\1&1\end{pmatrix} = \begin{pmatrix}3&1\\0&0\ конец{pmatrix}(1010)(2101)=(3010)
но
(2011)(1100)=(2211).□\begin{pmatrix}2&0\\1&1\end{pmatrix}\begin{pmatrix}1&1\\0&0\end{pmatrix} = \begin{pmatrix}2&2\\1&1\end{pmatrix}.\ _\square( 2101)(1010)=(2121). □
Наконец, стоит отметить специальную матрицу: тождественная матрица
In=(100…0010…0001…0⋮⋮⋮⋱⋮000…1),I_n = \begin{pmatrix}1&0&0&\ldots&0\\0&1&0&\ldots&0\\0&0&1&\ldots&0\\\vdots&\vdots&\vdots&\ ddots&\vdots\\0&0&0&\ldots&1\end{pmatrix},In=⎝⎜⎜⎜⎜⎜⎛100⋮0010⋮0001⋮0………⋱…000⋮1⎠⎟⎟ ⎟⎟⎟⎞,
, которая представляет собой матрицу размера n × nn \times nn × n, которая равна нулю везде, кроме главной диагонали, которая содержит все единицы.





 Свойство дистрибутивности умножения относительно сложения для матриц выражается двумя равенствами:
Свойство дистрибутивности умножения относительно сложения для матриц выражается двумя равенствами: Указать ограничения, область применения, требуемые характеристики
Указать ограничения, область применения, требуемые характеристики
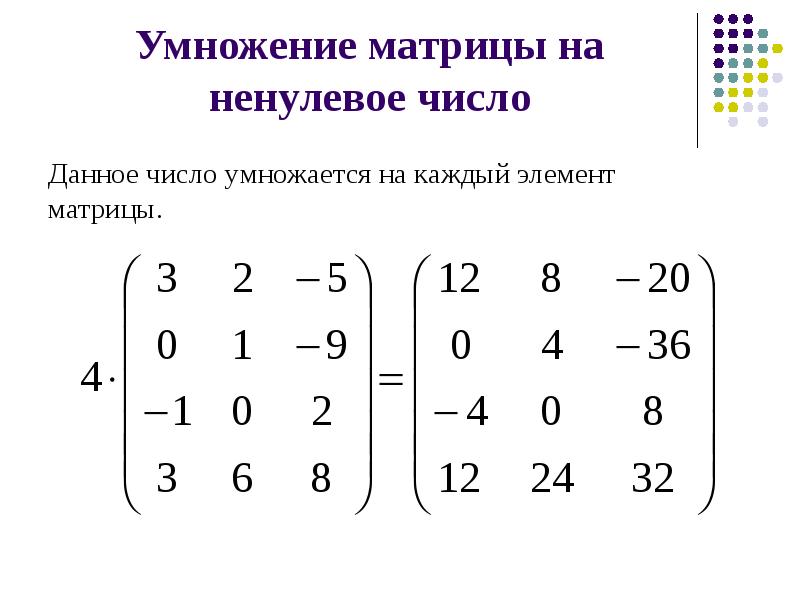
 Попросите учащихся воздержаться от заметок при первом просмотре видео и просто сосредоточиться на концепциях.
Попросите учащихся воздержаться от заметок при первом просмотре видео и просто сосредоточиться на концепциях.



 Прямые линии остаются прямыми.
Прямые линии остаются прямыми. \text{th}j-й столбец BBB, который также является вектором. Таким образом, точка (⋅)(\cdot)(⋅) в этом смысле относится к умножению векторов, определяемых скалярным произведением. Обратите внимание, что iii и jjj определены на 1≤i≤m1 \leq i \leq m1≤i≤m и 1≤j≤p1 \leq j \leq p1≤j≤p, поэтому произведение PPP будет m×pm \times pm×p матрица.
\text{th}j-й столбец BBB, который также является вектором. Таким образом, точка (⋅)(\cdot)(⋅) в этом смысле относится к умножению векторов, определяемых скалярным произведением. Обратите внимание, что iii и jjj определены на 1≤i≤m1 \leq i \leq m1≤i≤m и 1≤j≤p1 \leq j \leq p1≤j≤p, поэтому произведение PPP будет m×pm \times pm×p матрица. \end{выровнено}(P1,1P2,1P1,2P2,2)P1,1=(142536)⎝⎛135246⎠⎞= (1,2,3)⋅(1,3,5)=1 ⋅ 1 + 2 ⋅ 3 + 3 ⋅ 5=22.
\end{выровнено}(P1,1P2,1P1,2P2,2)P1,1=(142536)⎝⎛135246⎠⎞= (1,2,3)⋅(1,3,5)=1 ⋅ 1 + 2 ⋅ 3 + 3 ⋅ 5=22. Какой вывод можно сделать из последних двух матриц?
Какой вывод можно сделать из последних двух матриц? \end{align}ABBA=⎝⎛12−3−2313−12⎠⎞⋅⎝⎛101012220⎠⎞=⎝⎛1⋅1+(−2) ⋅0+3⋅12⋅1+3⋅0+(−1)⋅1(−3)⋅1+1⋅0+2⋅11⋅0+(−2)⋅1+3⋅22⋅0 +3⋅1+(−1)⋅2−3⋅0+1⋅1+2⋅21⋅2+(−2)⋅2+3⋅02⋅2+3⋅2+(−1)⋅ 0−3⋅2+1⋅2+2⋅0⎠⎞=⎝⎛41−1415−210−4⎠⎞=⎝⎛101012220⎠⎞⋅⎝ ⎛12−3−2313−12⎠⎞=⎝⎛−5−45054731⎠⎞.
\end{align}ABBA=⎝⎛12−3−2313−12⎠⎞⋅⎝⎛101012220⎠⎞=⎝⎛1⋅1+(−2) ⋅0+3⋅12⋅1+3⋅0+(−1)⋅1(−3)⋅1+1⋅0+2⋅11⋅0+(−2)⋅1+3⋅22⋅0 +3⋅1+(−1)⋅2−3⋅0+1⋅1+2⋅21⋅2+(−2)⋅2+3⋅02⋅2+3⋅2+(−1)⋅ 0−3⋅2+1⋅2+2⋅0⎠⎞=⎝⎛41−1415−210−4⎠⎞=⎝⎛101012220⎠⎞⋅⎝ ⎛12−3−2313−12⎠⎞=⎝⎛−5−45054731⎠⎞. (x2y1)(xy0x)=2(1036−x0)+(542xx).
(x2y1)(xy0x)=2(1036−x0)+(542xx). ⎝⎛13221434−1⎠⎞⎝⎛xyz⎠⎞=⎝⎛9124⎠⎞.
⎝⎛13221434−1⎠⎞⎝⎛xyz⎠⎞=⎝⎛9124⎠⎞. Матрицы A, BA, BA, B, которые действительно удовлетворяют AB=BAAB = BAAB=BA, (соответственно) называются коммутирующими матрицами .
Матрицы A, BA, BA, B, которые действительно удовлетворяют AB=BAAB = BAAB=BA, (соответственно) называются коммутирующими матрицами .