Теория цепей для чайников: Теория электрических цепей для чайников – Tokzamer

Основы теории цепей

Основы теории цепей

Основы теории цепей. Учебник для вузов. Изд.4-е, переработанное. М., «Энергия», 1975. – 752 с. В книге излагаются общие методы анализа и синтеза и описание свойств линейных электрических цепей с сосредоточенными и распределенными параметрами при постоянных, переменных, периодических и переходных токах и напряжениях Рассматриваются свойства и методы расчета установившихся и переходных процессов в нелинейных электрических и магнитных цепях постоянного и переменного тока Все положения теории иллюстрируются практическими примерами. Третье издание книги выпущено в 1965 г. Книга является учебником для студентов электротехнических специальностей вузов. Оглавление ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ ВВЕДЕНИЕ Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ 1-1. Элементы электрических цепей и электрических схем 1-2. Эквивалентные схемы для источников энергии 1-3. Закон Ома для участка цепи с э. д. с. 1-4. Распределение потенциала вдоль неразветвленной электрической цепи 1-5. Баланс мощностей для простейшей неразветвленной цепи 1-6. Применение законов Кирхгофа для расчета разветвленных цепей 1-7. Метод узловых потенциалов 1-8. Метод контурных токов 1-9. Уравнения состояния цепи в матричной форме 1-10. Преобразование линейных электрических схем Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 2-2. Свойство взаимности 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов 2-4. Применение топологических методов для расчета цепей 2-5. Топологические формулы и правила для определения передачи электрической цепи 2-6. Теорема о компенсации 2-7. Линейные соотношения между напряжениями и токами 2-8. Теорема о взаимных приращениях токов и напряжений 2-9. Общие замечания о двухполюсниках 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей 2-11. Передача энергии от активного двухполюсника к пассивному Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА 3-2. Понятие о генераторах переменного тока 3-3. Синусоидальный ток 3-4. Действующие ток, э. д. с. и напряжение 3-5. Изображение синусоидальных функций времени векторами и комплексными числами 3-6. Сложение синусоидальных функций времени 3-7. Электрическая цепь и ее схема 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости 3-9. Сопротивления 3-10. Разность фаз напряжения и тока 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости 3-12. Проводимости 3-13. Пассивный двухполюсник 3-14. Мощности 3-15. 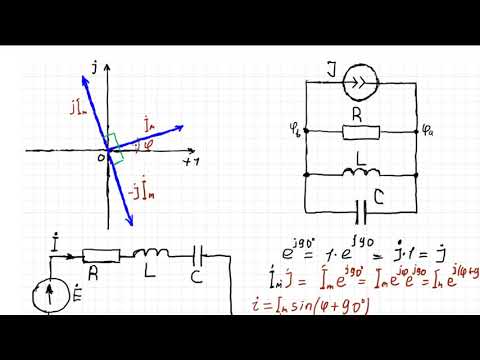Мощности в сопротивлении, индуктивности и емкости 3-16. Баланс мощностей 3-17. Знаки мощностей и направление передачи энергии 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра 3-19. Условия передачи максимальной мощности от источника энергии к приемнику 3-20. Понятие о поверхностном эффекте и эффекте близости 3-21. Параметры и эквивалентные схемы конденсаторов 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока 4-2. Последовательное соединение приемников 4-3. Параллельное соединение приемников 4-4. Смешанное соединение приемников 4-5. Сложные разветвленные цепи 4-6. Топографические диаграммы 4-7. Дуальность электрических цепей 4-8. Сигнальные графы и их применение для расчета цепей Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ 5-2. Частотные характеристики неразветвленной цепи 5-3. Резонанс в цепи с двумя параллельными ветвями 5-4. Частотные характеристики параллельного контура 5-5. Понятие о резонансе в сложных цепях Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ 6-2. Электродвижущая сила взаимной индукции 6-3. Последовательное соединение индуктивно связанных элементов цепи 6-4. Параллельное соединение индуктивно связанных элементов цепи 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности 6-6. Эквивалентная замена индуктивных связей 6-7. Передача энергии между индуктивно связанными элементами цепи 6-8. Трансформатор без стального сердечника (воздушный трансформатор) Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ 7-1. Комплексные уравнения прямой и окружности 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника 7-3. Круговые диаграммы для любой разветвленной цепи Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ 8-1. Четырехполюсники и их основные уравнения 8-2. Определение коэффициентов четырехполюсников 8-3. Режим четырехполюсника при нагрузке 8-4. Эквивалентные схемы четырехполюсников 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника 8-6. Идеальный трансформатор как четырехполюсник 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом 8-9. Расчеты электрических цепей с трансформаторами 8-10. Графы пассивных четырехполюсников и их простейшие соединения Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ 9-2. Эквивалентные схемы лампового триода 9-3. Транзисторы (полупроводниковые триоды) 9-4. Эквивалентные схемы транзисторов 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ 10-2. Соединения звездой и многоугольником 10-3. Симметричный режим трехфазной цепи 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений 10-5. Расчет симметричных режимов трехфазных цепей 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой 10-7. Напряжения на фазах приемника в некоторых частных случаях 10-8. Эквивалентные схемы трехфазных линий 10-9. Измерение мощности в трехфазных цепях 10-10. Вращающееся магнитное поле 10-11. Принципы действия асинхронного и синхронного двигателей Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей 11-4. Определение токов в симметричной цепи 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи 11-6. Расчет цепи с несимметричной нагрузкой 11-7. Расчет цепи с несимметричным участком в линии Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых 12-5. Несинусоидальные кривые с периодической огибающей 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами 12-8. Резонанс при несинусоидальных э. д. с. и токах 12-9. Мощность периодических несинусоидальных токов 12-10. Высшие гармоники в трехфазных цепях Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 13-2. Переходный, принужденный и свободный процессы 13-3. Короткое замыкание цепи r, L 13-4. Включение цепи r, L на постоянное напряжение 13-5. Включение цепи r, L на синусоидальное напряжение 13-6. Короткое замыкание цепи r, С 13-7. Включение цепи r, С на постоянное напряжение 13-8. Включение цепи r, С на синусоидальное напряжение 13-9. Переходные процессы в неразветвленной цепи r, С 13-10. Апериодический разряд конденсатора 13-11. Предельный случай апериодического разряда конденсатора 13-12. Периодический (колебательный) разряд конденсатора 13-13. Включение цепи r, С на постоянное напряжение 13-14. Общий случай расчета переходных процессов классическим методом 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля) 13-16. Включение пассивного двухполюсника на напряжение любой формы 13-17. Временная и импульсная переходные характеристики 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 14-2. Законы Ома и Кирхгофа в операторной форме 14-3. Эквивалентные операторные схемы 14-4. Переходные процессы в цепях с взаимной индуктивностью 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям 14-6. Определение свободных токов по их изображениям 14-7. Формулы включения 14-8. Расчет переходных процессов методом переменных состояния 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций) 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника 16-3. Вносимая и рабочая постоянные передачи 16-4. Цепные схемы 16-5. Частотные электрические фильтры 16-6. Низкочастотные фильтры 16-8. Полосные фильтры 16-11. Г-образный фильтр как пример несимметричного фильтра 16-12. Безындукционные (или r, C) фильтры Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы 17-3. Входные функции цепей. Положительные вещественные функции 17-4. Реактивные двухполюсники 17-5. Частотные характеристики реактивных двухполюсников 17-6. Синтез реактивных двухполюсников. Метод Фостера 17-7. Синтез реактивных двухполюсников. Метод Кауэра 17-8. Синтез двухполюсников с потерями. Метод Фостера 17-9. Синтез двухполюсников с потерями. Метод Кауэра 17-10. Понятие о синтезе четырехполюсников Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 18-2. Уравнения однородной линии 18-3. Установившийся режим в однородной линии 18-4. Уравнения однородной линии с гиперболическими функциями 18-5. Характеристики однородной линии 18-6. Входное сопротивление линии 18-7. Коэффициент отражения волны 18-8. Согласованная нагрузка линии 18-9. Линия без искажений 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями 18-11. Линии без потерь 18-12. Стоячие волны 18-13. Линия как четырехполюсник Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 19-2. Общее решение уравнений однородной линии 19-3. Возникновение волн с прямоугольным фронтом 19-4. Общие случаи нахождения волн, возникающих при переключениях 19-5. Отражение волны с прямоугольным фронтом от конца линии 19-6. Общий метод определения отраженных волн 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления 19-9. Блуждающие волны Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений) Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ 21-2. Расчет неразветвленных магнитных цепей 21-3. Расчет разветвленных магнитных цепей 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников 22-3. Явления в нелинейных цепях переменного тока 22-4. Методы расчета нелинейных цепей переменного тока Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ 23-2. Форма кривой тока в цепи с вентилями 23-3. Простейшие выпрямители 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями 23-5. Утроители частоты 23-6. Формы кривых тока и напряжения в цепях с терморезисторами 23-7. Замена реальных нелинейных элементов условно-нелинейными 23-8. Учет реальных свойств стальных магнитопроводов 23-9. Расчет тока в катушке со стальным магнитопроводом 23-10. Понятие о расчете условно-нелинейных магнитных цепей 23-11. Явление феррорезонанса 23-12. Стабилизаторы напряжения Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот 24-2. Вентили в цепях с постоянными и переменными э. д. с. 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с. 24-5. Удвоитель частоты 24-6. Метод гармонического баланса 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли 24-8. Принцип получения модулированных колебаний 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями 24-10. Магнитные усилители мощности Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями 25-5. Понятие о простейших запоминающих устройствах 25-6. Изображение переходных процессов на фазовой плоскости 25-7. Колебательный разряд емкости через нелинейную индуктивность Глава двадцать шестая. АВТОКОЛЕБАНИЯ 26-1. Нелинейные резисторы со спадающим участком характеристики 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний 26-7. Определение амплитуды автоколебаний методом гармонического баланса Приложение 1. Разложение периодических функций в тригонометрический ряд Приложение 2. Таблица оригиналов и изображений (по Лапласу) Приложение 3. Таблица функций и их частных спектров Приложение 4. Таблица функций для трапеций СПИСОК ЛИТЕРАТУРЫ

Лекции по Теоретическим основам электротехники (ТОЭ)

Лекции по ТОЭ

Введение

1. Элементы электрических цепей.
2. Топология электрических цепей.
3. Переменный ток. Изображение синусоидальных переменных.
4. Элементы цепи синусоидального тока, векторные диаграммы и комплексные соотношения для них.
5. Основы символического метода расчета. Методы контурных токов и узловых потенциалов.
6. Основы матричных методов расчета электрических цепей.
7. Мощность в электрических цепях.
8. Резонансные явления в цепях синусоидального тока.
9. Векторные и топографические диаграммы. Преобразование линейных электрических цепей.
10. Анализ цепей с индуктивно связанными элементами.
11. Особенности составления матричных уравнений при наличии индуктивных связей и ветвей с идеальными источниками.
12. Методы расчета, основанные на свойствах линейных цепей.
13. Метод эквивалентного генератора. Теорема вариаций.
14. Пассивные четырехполюсники.
15. Электрические фильтры.
16. Трехфазные электрические цепи: основные понятия и схемы соединения.
17. Расчет трехфазных цепей.
18. Применение векторных диаграмм для анализа несимметричных режимов. Мощность в трехфазных цепях.
19. Метод симметричных составляющих.
20. Теорема об активном двухполюснике для симметричных составляющих.
21. Вращающееся магнитное поле. Принцип действия асинхронного и синхронного двигателей.
22. Линейные электрические цепи при несинусоидальных периодических токах.
23. Резонансные явления в цепях несинусоидального тока. Высшие гармоники в трехфазных цепях.
24. Переходные процессы в линейных электрических цепях. Классический метод расчета переходных процессов.
25. Методика и примеры расчета переходных процессов классическим методом.
26. Определение постоянной времени. Переходные процессы в R-L-C-цепи.
27. Операторный метод расчета переходных процессов.
28. Последовательность расчета переходных процессов операторным методом. Формулы включения. Переходные проводимость и функция по напряжению.
29. Интеграл Дюамеля. Метод переменных состояния.
30. Нелинейные цепи постоянного тока. Графические методы расчета.
31. Расчет нелинейных цепей методом эквивалентного генератора. Аналитические и итерационные методы расчета цепей постоянного тока.
32. Нелинейные магнитные цепи при постоянных потоках.
33. Общая характеристика задач и методов расчета магнитных цепей.
34. Особенности нелинейных цепей переменного тока. Графический метод расчета с использованием характеристик для мгновенных значений.
35. Графические методы расчета с использованием характеристик по первым гармоникам и действующим значениям. Феррорезонанс. Аналитические методы расчета.
36. Метод кусочно-линейной аппроксимации. Метод гармонического баланса.
37. Понятие об эквивалентном эллипсе, заменяющем петлю гистерезиса. Потери в стали. Катушка и трансформатор с ферромагнитными сердечниками.
38. Переходные процессы в нелинейных цепях. Аналитические методы расчета.
39. Понятие о графических методах анализа переходных процессов в нелинейных цепях. Методы переменных состояния и дискретных моделей.
40. Цепи с распределенными параметрами в стационарных режимах: основные понятия и определения.
41. Линия без искажений. Уравнения линии конечной длины. Определение параметров длинной линии. Линия без потерь. Стоячие волны.
42. Входное сопротивление длинной линии. Переходные процессы в цепях с распределенными параметрами.
43. Сведение расчета переходных процессов в цепях с распределенными параметрами к нулевым начальным условиям. Правило удвоения волны.

Анализ схемы для чат-шпаргалки DUMMIES

BY: John Santiago и

Обновлено: 01-26-2022

Из книги: Анализ схемы для Dummies

Анализ схемы для Dummies

Explor На Amazon

При анализе цепей вам необходимо знать некоторые основные законы, электрические величины, взаимосвязи и теоремы.

Закон Ома является ключевым уравнением устройства, которое связывает ток, напряжение и сопротивление. Используя законы Кирхгофа, вы можете упростить сеть резисторов, используя один эквивалентный резистор. Вы также можете выполнить такой же расчет, чтобы получить эквивалентную емкость и индуктивность для сети конденсаторов или катушек индуктивности.

Для более сложных схем пригодятся методы анализа узловых напряжений и тока сетки. А если вы хотите попробовать разные нагрузки для конкретной схемы источника, вы можете использовать эквивалент Тевенина или Нортона.

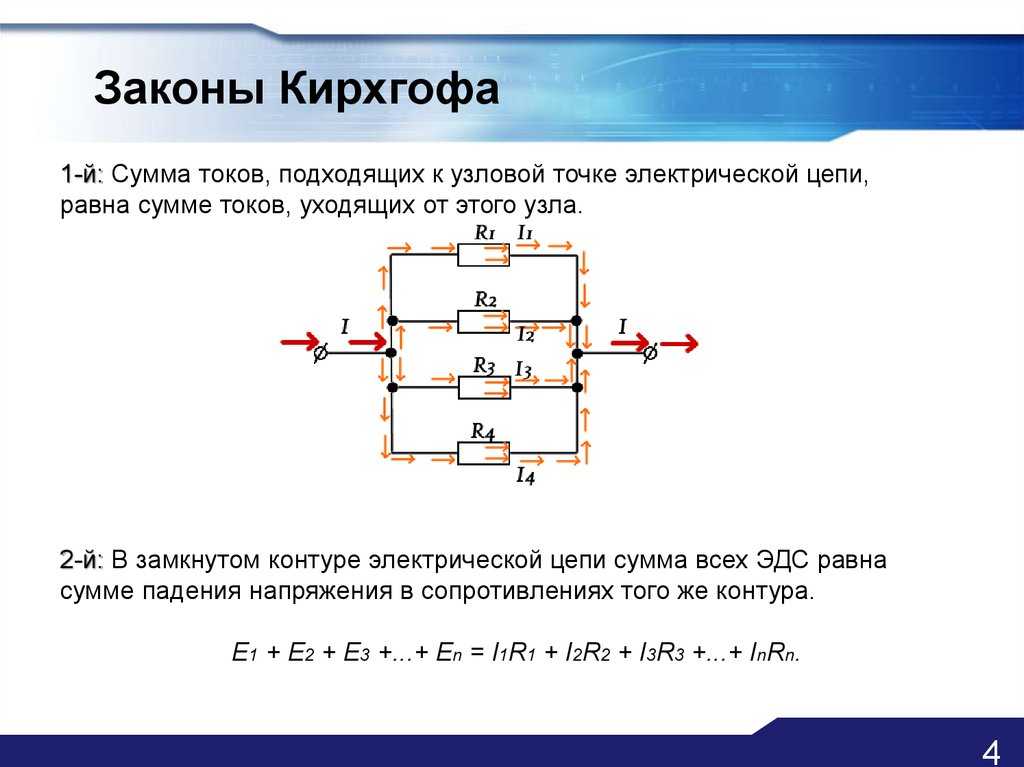
Три основных закона работы со схемами

На самом базовом уровне анализ схем включает в себя расчет тока и напряжения для конкретного устройства. Вот тут-то и появляются уравнения устройства и соединения. Уравнения устройства описывают взаимосвязь между напряжением и током для конкретного устройства.

Одним из наиболее важных уравнений устройства является закон Ома, который связывает ток (I) и напряжение (В) с использованием сопротивления (R) , , где R равно константе.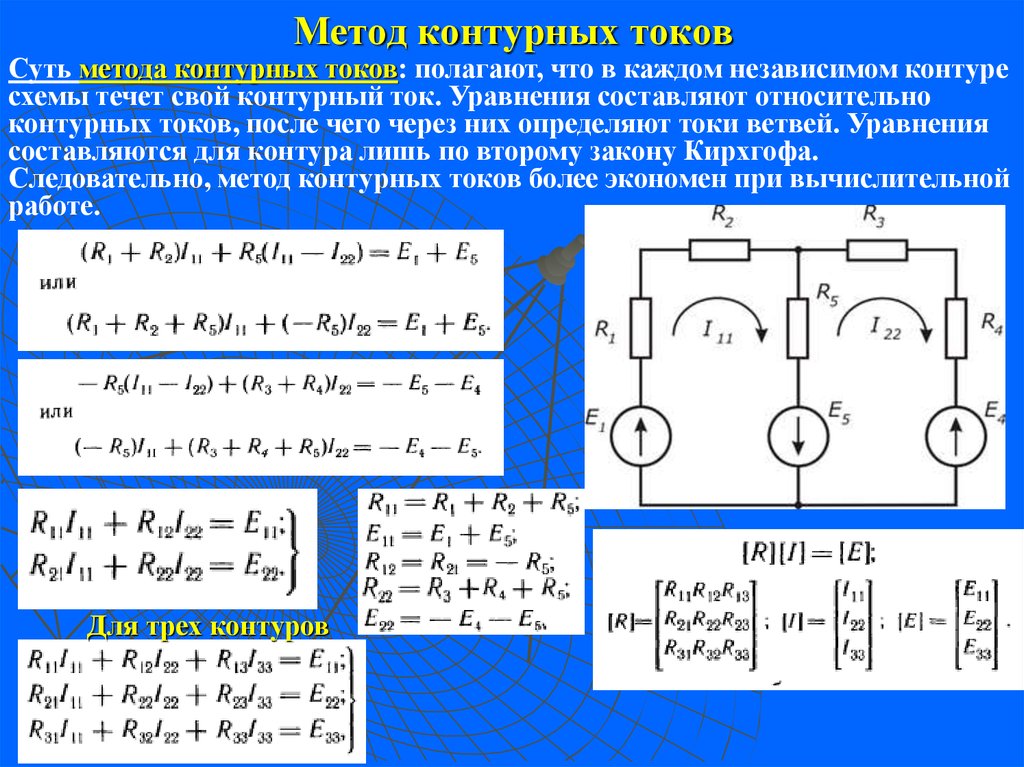 V = IR или I = V/R или R = V/I .

Вам необходимо знать два уравнения связи: закон Кирхгофа для тока (KCL) и закон Кирхгофа для напряжения (KVL):

Электрические величины и единицы измерения

Определенные электрические величины, отношения и электрические единицы необходимо знать при анализе и характеристике поведения схемы. Следующая таблица поможет вам сохранить эту информацию в чистоте.

Эквивалентное сопротивление, емкость и индуктивность

При анализе цепей можно упростить сети, состоящие только из резисторов, конденсаторов или катушек индуктивности, заменив их одним эквивалентным устройством. Следующие уравнения показывают эквивалентные последовательные и параллельные соединения для комбинаций только резистора, только конденсатора и только катушки индуктивности.

Методы анализа сложных цепей

При работе со сложными цепями, такими как схемы с большим количеством петель и узлов, вы можете использовать несколько приемов для упрощения анализа. Следующие методы анализа цепей пригодятся, когда вы хотите найти напряжение или ток для определенного устройства. Они также полезны, когда у вас есть много устройств, подключенных параллельно или последовательно, устройства, образующие петли, или несколько устройств, подключенных к определенному узлу.

• Анализ напряжения узла: Узлы — это определенные точки в цепи. Когда к определенной точке подключено много устройств, вы можете сделать этот узел опорным узлом и думать о нем как о имеющем напряжение 0 В. Затем вы используете его в качестве опорной точки для измерения напряжения для определенного узла.

  С помощью анализа узловых напряжений вы находите неизвестные узловые напряжения в цепи с помощью токового закона Кирхгофа. После нахождения узловых напряжений вы используете ток-напряжение ( i-v ) отношения, такие как закон Ома, для определения токов устройств и использование узловых напряжений для определения напряжений устройств.

• Текущий анализ сетки: Сетка представляет собой петлю без устройств, заключенных в петлю, где границы сетки — это те устройства, которые образуют петлю. Анализ тока сетки позволяет находить неизвестные токи сетки в цепи с помощью закона напряжения Кирхгофа (KVL). Уравнения сетки представляют собой уравнения КВЛ с неизвестными токами сетки в качестве переменных. После нахождения токов сетки вы используете 9Отношения 0027 i – v для определения напряжения устройства.

• Суперпозиция: Для линейных цепей с независимыми источниками вы можете использовать суперпозицию, чтобы найти выходное напряжение и ток для конкретного устройства. Суперпозиция включает в себя включение источников по одному при выключении других источников. Вы отключаете источник тока, заменяя его разомкнутой цепью, и вы отключаете источник напряжения, заменяя его коротким замыканием. Чтобы получить общий результат, вы вычисляете алгебраическую сумму индивидуальных вкладов каждого источника.

• Эквиваленты Thévenin/Norton: Анализ цепи может стать утомительным, если вы пробуете разные нагрузки с одной и той же цепью источника. Чтобы избавить себя от работы, замените схему источника эквивалентами Тевенина и Нортона. Теорема Тевенина говорит, что вы можете заменить линейную сеть источников и резисторов между двумя терминалами одним независимым источником напряжения (V _T ) последовательно с одним резистором (R _T ) , and Norton’s theorem says you can replace the linear network of sources and resistors with one independent current source (I _N ) in parallel с одним резистором (R _N ) — см. следующий рисунок . Эквивалентные схемы будут работать для всех нагрузок (включая нагрузки с разомкнутой цепью и короткозамкнутыми), если они имеют одинаковые отношения напряжения и тока на клеммах.

  Finding the Thévenin or Norton equivalent requires calculating the following variables: V _T = V _OC , I _N = I _SC , and R _T = R _N = V _OC /I _SC (где T означает Thévenin, OC означает нагрузку холостого хода, N означает нагрузку Norton и

  8 SC означает нагрузку короткого замыкания).

  Если вы хотите проанализировать различные нагрузки, подключенные последовательно к цепи источника, полезен эквивалент Тевенина; когда нагрузки подключены параллельно цепи источника, лучшим выбором будет аналог Norton. Два эквивалента связаны друг с другом преобразованием источника.

Об этой статье

Эта статья из книги:

• Анализ схем для чайников,

Об авторе книги:

Джон М. Сантьяго-младший, доктор наук, служил в ВВС США (USAF). ) в течение 26 лет. В течение этого времени он занимал различные руководящие должности в области управления техническими программами, разработки приобретений и поддержки исследований в области эксплуатации. Находясь в Европе, он руководил более чем 40 международными научными и инженерными конференциями/семинарами.

Эту статью можно найти в категории:

• Схема ,

Анализ цепей и уравнения тока сетки

Анализ тока сетки ( Анализ тока петли ) вы можете помочь уменьшить количество уравнений необходимо решить при анализе схемы. Анализ токов сетки — это просто закон напряжения Кирхольфа, адаптированный для цепей, в которых много устройств подключено в несколько контуров.

Анализ двухсетевых цепей

В этом разделе проводится анализ тока сетки, когда у вас есть два уравнения, одно для сетки A и одно для сетки B. В приведенной здесь примерной схеме обе сетки имеют ток по часовой стрелке.

Следующим шагом является применение KVL к сеткам A и B, чтобы получить следующие уравнения сетки:

Затем запишите токи устройства в терминах токов сетки. Затем выразите токи устройства через токи сетки, используя закон Ома:

Теперь вы можете подставить предыдущие значения напряжения в уравнения KVL, которые вы нашли ранее:

Если вы преобразуете предыдущие уравнения, чтобы привести их к стандартной форме, вы получите

Преобразование этих уравнений сетки в матричную форму приводит к

Предыдущее уравнение имеет вид Ax = b , где матрица A — коэффициенты резисторов, x — вектор неизвестных токов сетки, а b — вектор независимых источников напряжения.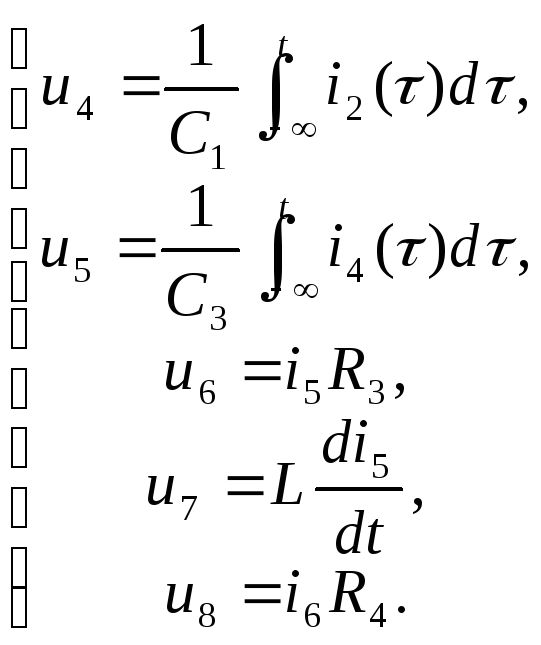

Вы можете использовать свой графический калькулятор или матричную программу, чтобы получить токи сетки:

С помощью этих рассчитанных токов сетки вы можете найти токи устройства:

я ₁ = i _А = 0,8 мА

i ₂ = i _A – i _B = 0,8 мА 9 – (–0,14 мА)

Для завершения анализа подставьте токи и сопротивления устройства в уравнения закона Ома. Вы найдете следующие напряжения устройства:

v ₁ = i ₁ R ₁ = (0,8 мА)(10 кОм) = 8 В

v ₂ = i ₂ R ₂ = (1,5 мА)(5 кОм) = 7 В

v ₃ = i ₃ R ₃ = (–0,6 мА)(5 кОм) = –3 В

Приведенные выше напряжения устройств имеют смысл, поскольку они удовлетворяют требованиям KVL для каждой сетки.

Анализ цепей с тремя и более сетками

Вы можете применить анализ тока сетки при работе со схемами, имеющими три или более ячеек. Процесс такой же, как и для цепей только с двумя токами сетки. Рассмотрим этот образец схемы, который показывает напряжения и токи для каждого из устройств, а также токи сетки i _A , i _B и i _C . Обратите внимание, что все токи сетки текут по часовой стрелке.

Уравнения KVL для сеток A, B и C равны

.

Теперь выразите токи устройства через токи сетки. Затем примените закон Ома, чтобы получить напряжения элементов с точки зрения токов сетки:

Когда вы подставляете предыдущие напряжения устройства в уравнения KVL, найденные ранее, вы получаете

Измените уравнения, чтобы привести их к стандартной форме. Вы можете вставить несколько нулей в качестве заполнителей, чтобы помочь вам настроить матрицы на следующем шаге:

И вы можете перевести эти стандартные уравнения в матричную форму, чтобы получить

Упростить элементы в матрице резисторов:

Обратите внимание, что в матрице резисторов все значения главной диагонали положительны, все значения вне диагонали отрицательные или нулевые, а значения вне диагонали симметричны. Для схемы с независимым источником эта симметрия относительно главной диагонали является хорошим признаком того, что вы правильно поставили задачу.

Вы можете использовать свой графический калькулятор или матричную программу, чтобы найти токи сетки:

Ток i _C = 0 имеет смысл из-за симметрии схемы. С помощью этих расчетных значений токов сетки вы найдете следующие токи устройства:

Чтобы завершить анализ, рассчитайте напряжения устройств, используя закон Ома, связывающий токи и напряжения устройств:

Предыдущие результаты имеют смысл, поскольку они удовлетворяют уравнениям KVL для трех сеток.

Об этой статье

Эта статья взята из книги:

• Анализ схем для чайников,

Об авторе книги:

Джон М.