Краткий курс теоретической механики
Краткий курс теоретической механики
ОглавлениеПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V.  ПЛОСКАЯ СИСТЕМА СИЛ§ 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ § 32. СИЛОВОЕ ПОЛЕ.  § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50.  РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ§ 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 64.  ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ§ 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Раздел третий. ДИНАМИКА ТОЧКИ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80.  ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ§ 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96.  ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНСГлава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110.  КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ§ 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ.  ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИГлава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX.  УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ§ 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ.  ЦЕНТР УДАРА |
Прикладная теория гироскопов Лукьянов Д.П., Распопов В.Я., Филатов Ю.В.
Каталог▲▼
Настоящий учебник посвящен основам теории гироскопов различного типа, являясь одним из первых изданий, в котором излагаются принципы построения большинства используемых в настоящее время гироскопов. Рассмотрены основные положения механики твердого тела, включающие уравнения Эйлера, Лагранжа и принцип Даламбера, используемые при составлении уравнений движения гироскопов.
Описываются концепции построения трех- и двухстепенных гироскопов в кардановом подвесе; гироскопов со сферическим шарикоподшипниковым и упругим подвесами, а также с неконтактными подвесами ротора (электростатические, газовые, жидкостные). Излагаются необходимые сведения по волновым твердотельным гироскопам с объемным и кольцевым резонаторами. Достаточное внимание уделено электронным контурам управления.
Рассмотрение микромеханических гироскопов проводится в основном на примере конструкций LL- и RR-типов, получивших наибольшее развитие.
Особое внимание уделено формированию выходных сигналов и оценке их погрешностей.
Основы лазерной гироскопии, использующей эффект Саньяка, опираются на метрику вращающейся системы отсчета и уравнения электродинамики в этой системе. Подробно рассматриваются методы линеаризации выходной характеристики лазерного гироскопа и невзаимные эффекты, используемые в лазерной гироскопии. Излагаются сведения по волоконно-оптическим гироскопам, их точностным характеристикам и особенностям конструкции. Анализируются возможности построения микрооптических гироскопов.
Материал по волновым твердотельным микромеханическим гироскопам содержит основы теории поверхностных акустических волн во вращающейся системе координат. С позиций молекулярной кинетики и 2-D технологий рассмотрены принципы построения гироскопов на поверхностных акустических волнах. Приводятся примеры их практической реализации.
Учебник предназначен для студентов, обучающихся по направлениям «Системы управления движением и навигация», «Приборостроение» и по соответствующим им профилям подготовки.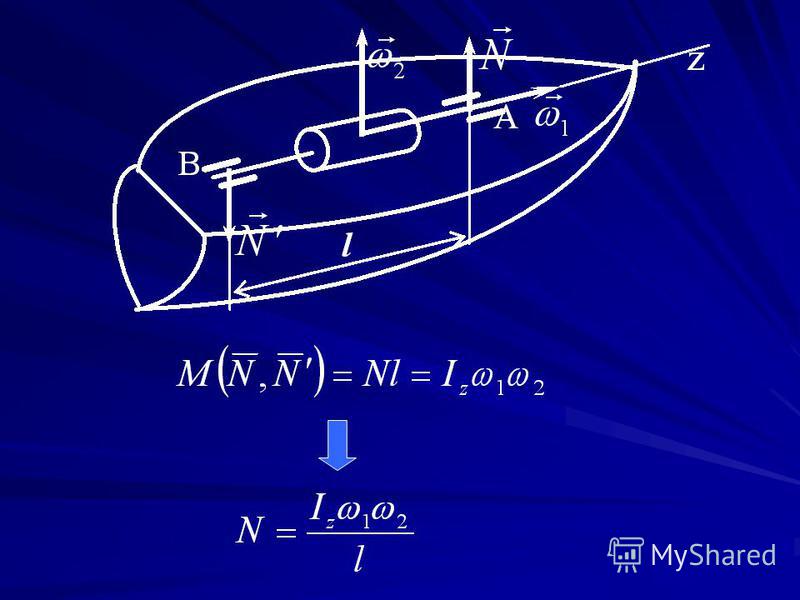
Он может быть использован студентами и аспирантами других направлений, профессиональная деятельность которых будет связана с созданием инерциальных систем навигации различного назначения. Учебник также будет полезен и специалистам промышленных предприятий, разрабатывающих образцы гироскопической техники.
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ. Гироскопы
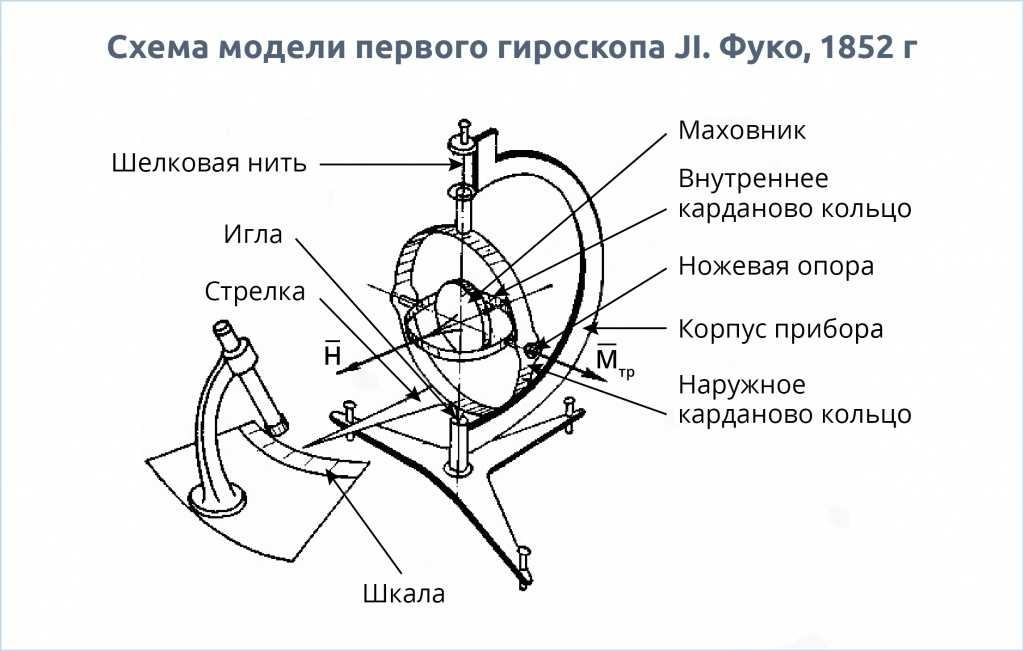
В.1. Волчок — детская игрушка с удивительными свойствами
В.2. От волчка к гироскопу
В.З. Основные типы гироскопов
В.4. От механики к оптике
В.5. Типы оптических гироскопов
В.6. Гироскопы на поверхностных акустических волнах
Литература к введению
Принятые сокращения
ГЛАВА 1. Некоторые положения механики твердого тела
1.1. Определение положения твердого тела с помощью углов Эйлера – Крылова
1.2. Угловые скорости твердого тела
1.3. Линейные скорости и ускорения точки твердого тела
1.4. Кинетическая энергия
1.5. Кинетический момент. Закон моментов
1.
6. Уравнения Эйлера вращательного движения твердого тела
1.7. Принцип Д’ Аламбера
1.8. Уравнения Лагранжа
1.9. Методы составления уравнений движения гироскопа
1.9.1. Применение обобщенных уравнений Эйлера
1.9.2. Применение уравнений Лагранжа второго рода
1.9.3. Применение принципа Д’ Аламбера (метод кинетостатики)
1.10. Прецессия и гироскопический момент
Литература к главе 1
Темы для самоконтроля
ГЛАВА 2. Роторные гироскопы
2.1. Трехстепенные гироскопы с кардановым подвесом
2.1.1. Устойчивость свободного гироскопа
2.1.2. Движение главной оси гироскопа под действием постоянных моментов
2.1.3. Физическая картина движения гироскопа под действием момента внешней силы
2.1.4. Структурные схемы и передаточные функции трехстепенного гироскопа
2.1.5. Сферы применения, конструктивные особенности, источники погрешностей свободных гироскопов
2.2. Гироприборы на базе трехстепенного гироскопа с кардановым подвесом
2.
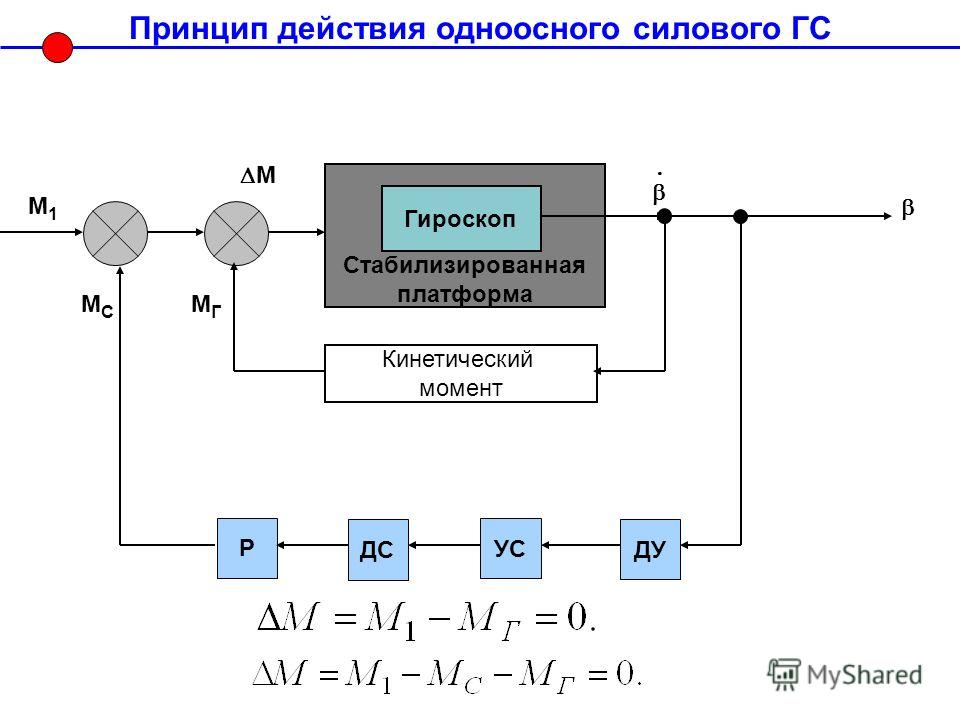2.1. Двухкомпонентный измеритель угловой скорости
2.2.2. Гироскопический интегратор линейных ускорений
2.3. Гироскопы с двумя степенями свободы
2.3.1. Принцип работы
2.3.2. Интегрирующий гироскоп
2.3.3. Датчик (измеритель) угловой скорости
2.3.4. Конструктивное исполнение поплавковых гироскопов
2.3.5. Гироскопы Фуко
2.4. Гироскопы со сферическим шарикоподшипниковым подвесом
2.4.1. Принципиальные схемы и причины возникновения возмущающих моментов
2.4.2. Динамика гироскопа
2.4.3. Конструктивные особенности
2.5. Гироскопы с упругим подвесом
2.5.1. Принципиальные схемы и выходной сигнал
2.5.2. Динамика двухстепенного гироскопа
2.5.3. Динамика трехстепенного гироскопа
2.5.4. Конструкция и сферы применения
2.6. Гироскопы с неконтактным подвесом ротора
2.6.1. Уравнения движения
2.6.2. Динамика гироскопа с неконтактным подвесом ротора
2.7. Гироскопы с электростатическим подвесом
2.7.1. Физические основы работы
2.
7.2. Статические и динамические характеристики подвеса
2.7.3. Конструктивные особенности
2.8. Гироскопы с газовым подвесом
2.8.1. Принципиальные схемы и классификационные признаки
2.8.2. Силовые и моментные реакции газового слоя
2.8.3. Конструктивные особенности
2.9. Гидродинамические гироскопы
2.9.1. Принципиальные схемы и физические основы работы
2.9.2. Математические модели и динамические характеристики
2.9.3. Конструктивные особенности
Литература к главе 2
Темы для самоконтроля
ГЛАВА 3. Волновые твердотельные гироскопы
3.1. Принцип работы
3.2. Гироскопы с объемным резонатором
3.2.1. Общая характеристика
3.2.2. Электронные контуры управления
3.2.3. Конструктивные особенности
3.3. Гироскопы с кольцевым резонатором
3.3.1. Общая характеристика
3.3.2. Электронные контуры управления
3.3.3. Модель формирования выходного сигнала
3.3.4. Конструктивные особенности
3.4. Источники погрешностей
Литература к главе 3
Темы для самоконтроля
ГЛАВА 4.
Микромеханические гироскопы
4.1. Определения и принципы работы
4.2. Гироскоп LL-типа
4.2.1. Математические модели
4.2.2. Динамические характеристики
4.3. Гироскоп RR -типа
4.3.1. Математическая модель
4.3.2. Динамические характеристики
4.4. Частотные характеристики
4.4.1. Гироскоп RR-типа
4.4.2. Гироскоп LL-типа
4.5. Погрешности
4.6. Конструктивные особенности
4.6.1. Классификационные признаки
4.6.2. Гироскопы LL-типа
4.6.3. Гироскопы RR-типа
Литература к главе 4
Темы для самоконтроля
ГЛАВА 5. Оптические гироскопы
5.1 Эффект Саньяка
5.2 Метрика вращающейся системы отсчета
5.3. Уравнения электродинамики во вращающейся системе отсчета
5.4. Пути построения оптического гироскопа
5.4.1. Интерферометр Саньяка
5.4.2. Кольцевой лазер
5.4.3. Пассивный кольцевой резонатор
5.5. Лазерный гироскоп
5.5.1. Расщепление собственных частот вращающегося кольцевого резонатора
5.
5.2. Масштабный коэффициент лазерного гироскопа
5.5.3. Сдвиг нуля выходной характеристики ЛГ
5.5.4. Синхронизация частот встречных волн
5.5.5. Линеаризация выходной характеристики ЛГ
5.5.6. Потенциальная точность лазерного гироскопа
5.5.7. Случайный дрейф, обусловленный виброподставкой
5.5.8. Особенности конструкций лазерных гироскопов
5.5.9. Характеристики современных лазерных гироскопов
5.6. Волоконно-оптический гироскоп
5.6.1. Принцип взаимности
5.6.2. Основные схемы построения ВОГ
5.6.3. Основные источники погрешностей
5.6.4. Классификация ВОГ
5.6.5. Характеристики современных ВОГ
5.6.6. Некоторые применения ВОГ
5.7. Микрооптические гироскопы
5.7.1 Основные направления миниатюризации оптических гироскопов
5.7.2 Оценка достижимой точности микрооптического гироскопа
Литература к главе 5
Темы для самоконтроля
ГЛАВА 6. Твердотельные микромеханические гироскопы на поверхностных акустических волнах
6.
1. Гироскопический эффект на бегущих поверхностных акустических волнах
6.2. Уравнение движения ПАВ во вращающейся системе координат
6.3. Чувствительность параметров ПАВ к угловой скорости
6.3.1. Измерение времени запаздывания ПАВ
6.3.2. Измерение фазового сдвига
6.3.3. Измерение приращения частоты автогенератора с JI3 в контуре положительной обратной связи
6.4. ТМГ на ПАВ с кольцевым резонатором и частотным методом измерения угловой скорости
6.5. ТМГ на ПАВ с двумя линиями задержки и частотным выходом
6.6. ТМГ на стоячих ПАВ
6.7. ТМГ на ПАВ с двойным преобразованием
Литература к главе 6
Темы для самоконтроля
ЗАКЛЮЧЕНИЕ
Базовая литература
Предметный указатель
Здесь Вы можете оставить свой отзыв
Чтобы оставить отзыв на товар Вам необходимо войти или зарегистрироватьсяSCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.
- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
| клиент@scirp. org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Подпишитесь на SCIRP
Свяжитесь с нами
| клиент@scirp. org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2023 Scientific Research Publishing Inc. Все права защищены.
ВершинаФизика «антигравитационного эффекта» гироскопа
На этой странице
АннотацияВведениеРезультаты и обсуждениеЗаключениеДоступность данныхКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме
Физика гироскопических эффектов более сложна, чем представлена в существующих математических моделях. Эффекты, представляемые этими моделями, не соответствуют реальным силам, действующим на гироскопические устройства. Новые исследования в этой области показали, что на гироскоп действует система инерционных моментов, создаваемых вращающейся массой вращающихся объектов. Действия системы сил инерции подтверждены практическими испытаниями движений гироскопа с одной боковой опорой. Действие момента внешней нагрузки на гироскоп с одной боковой опорой показывает, что движение гироскопа вверх ошибочно называют эффектом «антигравитации». Движение гироскопа вверх является результатом крутящего момента прецессии вокруг его горизонтальной оси. Новизна настоящей работы связана с математическими моделями движения гироскопов вверх и вниз под действием внешнего крутящего момента вокруг вертикальной оси. Это аналитическое исследование описывает физику восходящего движения гироскопов и подтверждает, что гироскопы не обладают свойством антигравитации.
1. Введение
Прикладная теория гироскопов возникла в основном в ХХ веке в связи с широким применением и интенсификацией вращения многочисленных вращающихся объектов в технике [1–4]. Свойства гироскопа используются во многих инженерных расчетах, связанных с вращающимися деталями в аэрокосмической, судостроительной и других отраслях промышленности, гироскопическим эффектам посвящено множество публикаций [5, 6]. Фундаментальные учебники и публикации по классической механике описывают гироскопические эффекты в эйлеровом члене изменения углового момента [7–9].]. Тем не менее предыдущие аналитические подходы основаны на нескольких предположениях и упрощениях, которые приводят к теоретической неопределенности в отношении гироскопических эффектов [10, 11]. Математические модели свойств гироскопов в публикациях не соответствуют практическим применениям гироскопических устройств [12–15]. Все вращающиеся объекты подвижных механизмов проявляют гироскопические эффекты, которые должны рассчитываться инженерными методами. Исходя из этого, исследователи придумали искусственные термины, такие как гироскопические эффекты и пары гироскопов, и установили неинерционные, негравитационные свойства, противоречащие принципам физики.
Физика гироскопических эффектов более сложна, чем представлено в литературе. Внешний вращающий момент, приложенный к гироскопу, создает систему восьми инерционных моментов, создаваемых центробежной, общей инерционной и кориолисовой силами, а также изменением углового момента вращающегося ротора. Действия системы инерционных моментов вокруг осей гироскопа взаимосвязаны и проявляют все необъяснимые ранее гироскопические свойства. На сегодняшний день физико-математические модели инерционных моментов гироскопов хорошо описаны и прошли валидацию [16–20]. Однако новый аналитический подход все еще имеет некоторые математические ошибки. В некоторых публикациях отмечается неточность математических моделей при рассмотрении моментов инерции, действующих на гироскоп [20]. В технике несколько моментов нагрузки гироскопических устройств могут действовать в разных направлениях вокруг их осей вращения. Взаимосвязанное действие внутренних и внешних моментов нагрузки на гироскоп представляет собой решаемую научно-техническую задачу. Новизна настоящей работы описывает точную математическую модель движения гироскопа вверх под действием внешнего крутящего момента и объясняет физику гироскопического эффекта, ошибочно названного свойством «антигравитации».
2. Методология
Недавние исследования физических принципов гироскопических эффектов привели к созданию математических моделей, которые можно использовать для оценки системы сил инерции, действующих на гироскоп. Новые математические модели внутренних крутящих моментов описали новые свойства гироскопа и поведение гироскопических устройств. Воздействие внешней нагрузки на гироскоп создает моменты сопротивления и прецессии, возникающие при вращении масс-элементов вращающегося ротора. Математические модели инерционных моментов, действующих на гироскоп, представлены в ряде публикаций [16–20]. В одной публикации приведены некорректные математические модели взаимосвязи внешних и внутренних моментов, действующих на гироскоп [20]. Следует внимательно рассмотреть действие системы взаимосвязанных инерционных моментов вокруг осей гироскопа. Анализ взаимозависимой последовательности действия внешнего и инерционного моментов позволяет сформулировать физические принципы движения гироскопа. Были рассмотрены действия системы крутящих моментов и их влияние на гироскопическую стойку, и соответствующие технические данные опубликованы [20]. Математические модели движения гироскопа представлены на двух примерах действия внешних и внутренних моментов на гироскоп с одной боковой опорой для его горизонтального расположения. Для простоты действия сил трения на опоры и шкворень не учитываются. Две математические модели движения гироскопа дают четкое представление о физике действующих внешних и внутренних моментов. Первая математическая модель рассматривает действие моментов внешней нагрузки, описываемых как момент, действующий на гироскоп вокруг оси, и момент веса гироскопа, действующий вокруг оси против часовой стрелки. Вторая математическая модель рассматривает внешние нагрузки, описываемые как действие момента по часовой стрелке вокруг оси и действие момента веса гироскопа против часовой стрелки вокруг оси. Эта конструктивная особенность стойки гироскопа создает уникальное сочетание действующих моментов инерции и различных движений.
2.1. Практический пример 1
Математическая модель движения гироскопа учитывает действие момента нагрузки вокруг оси в направлении против часовой стрелки и момента нагрузки, создаваемого весом гироскопа вокруг оси. В этих условиях действие момента внешней нагрузки порождает систему инерционных моментов, действующих вокруг осей гироскопа (рис. 1). Действие момента нагрузки создает следующие инерционные моменты:
(а) Момент сопротивления, создаваемый действием центробежных и кориолисовых сил вокруг оси по часовой стрелке (т. е. в направлении, противоположном действию момента нагрузки) (б) Процессный момент, создаваемый общими силами инерции и изменением в угловом моменте вращающегося ротора, возникающем на оси, но действующем вокруг оси по часовой стрелке (т.е. в направлении, противоположном действию веса гироскопа). Величина момента, создаваемого грузом гироскопа, меньше величины результирующих инерционных моментов, действующих вокруг оси. Последнее () вызывает движение гироскопа вверх (с) Процессный момент вокруг оси , в свою очередь, порождает момент сопротивления центробежной и Кориолисовой сил вокруг оси . Эти крутящие моменты движутся против часовой стрелки и усиливают действие веса 9 гироскопа.0003
Действие результирующего момента вокруг оси создает момент прецессии, создаваемый общими силами инерции, и изменение углового момента, возникающее на оси, но действующее вокруг оси и добавляемое к моменту сопротивления вокруг оси, что приводит к моменту сопротивления.
Действие нагрузок и изменение значений взаимосвязанных инерционных моментов, действующих вокруг двух осей. Действие внешнего момента порождает момент прецессии, который действует вокруг оси, противоположной действию веса гироскопа. Эта ситуация приводит к уменьшению величины результирующего момента инерции и момента прецессии, действующего вокруг оси . Изменения значений моментов инерции равны, поскольку они выражают внутреннюю кинетическую энергию. Это изменение выражается коэффициентом изменения инерционных моментов вокруг одной оси и объясняется следующим выражением:
где в уравнение (1) подставлены выражения инерционных моментов [16] и момента, создаваемого грузом гироскопа. Все компоненты указаны выше.
Коэффициент представляет уменьшение значения момента прецессии, действующего вокруг оси, при уменьшении значения момента инерции вокруг оси. Эта зависимость отражает взаимосвязь инерционных моментов, действующих вокруг двух осей. Анализ уравнения (1) приводит к следующим значениям коэффициента:
(i) Отсутствие момента нагрузки, действующей вокруг оси, означает, что коэффициент равен (т. е. нет изменения значения инерционных моментов, действующих вокруг двух осей) (ii) Действие момента нагрузки означает, что коэффициент равен (т. е. значения инерционных действующих моментов вокруг двух осей уменьшаются) (iii) Когда момент нагрузки равен моменту прецессии (), коэффициент равен (т. е. гироскоп не поворачивается вокруг оси, а вместо этого поворачивается вокруг оси под действием только действие веса гироскопа).
Эта особенность должна быть представлена в уравнениях движения гироскопа вокруг двух осей. Разработана математическая модель для оценки движений гироскопа, вызванных действием внешнего и внутреннего моментов. Эта модель включает поправки, основанные на взаимосвязанном действии инерционных моментов, и представлена следующими дифференциальными уравнениями Эйлера: где и – угловые скорости гироскопа вокруг осей и соответственно; , , , , , , , и – внутренние моменты, создаваемые центробежной, кориолисовой и общей силами инерции и изменением углового момента, действующего вокруг осей и , соответственно [16]. Знак (-) в уравнении (3) означает, что движение происходит по часовой стрелке. Все остальные компоненты указаны выше.
Уравнения инерционных моментов [16] и уравнение (1) подставляются в уравнения (2) и (3). Составляющие моментов, создаваемые центробежной и инерционной силами, имеющие одинаковое выражение, из уравнений (2) и (3) исключаются. Упрощение и модификация этих уравнений аналогичны решению, представленному в рукописях [17, 18], где этот процесс подробно обоснован. Модифицированные уравнения представлены следующей системой:
где уравнение (6) представляет собой зависимость угловых скоростей гироскопа вокруг осей, которые были добавлены к уравнениям (4) и (5). Это решение представлено в рукописях [17, 18], в которых используются аналогичные аналитические подходы. Все остальные параметры указаны выше.
Подстановка уравнения (6) в первое уравнение (3) и преобразование дает следующее уравнение: где все компоненты указаны выше.
2.1.1. Рабочий пример
Компоненты гироскопа с одной боковой опорой перемещаются под действием моментов нагрузки и , которые создаются весом гироскопа и действуют вокруг осей и соответственно . Значение первого крутящего момента составляет половину значения крутящего момента (т. е. ). Действия крутящих моментов и движений представлены на рисунке 1. Технические данные, относящиеся к гироскопу, представлены в рукописи ([20], таблица 1). Уравнение (7) представляет собой уравнение движения гироскопа вокруг оси . Отношение угловых скоростей вокруг двух осей рассчитывается с использованием уравнения (6). Угловая скорость вокруг оси определяется следующим решением. Подставляя исходные данные гироскопа [20] и данные, представленные выше, в уравнение (7), получаем следующее уравнение:
Уравнение (8) можно упростить следующим образом:
Уравнение (10) возникает путем разделения переменных для упрощения и преобразования уравнения (9):
Уравнение (11) является интегральной формой уравнения (10):
Левый интеграл уравнения (11) сведен в таблицу и представлен как интеграл . Правый интеграл прост. Решение интегралов дает следующее уравнение: тем самым приводя к следующему:
Уравнение (13) можно преобразовать в уравнение угловой скорости для гироскопа вокруг оси:
Правая часть уравнения (14) содержит выражение , имеющее малое значение высокого порядка, при котором угловая скорость вращающегося ротора составляет около . Следовательно, этой составляющей уравнения можно пренебречь. Решение уравнения (10) дает следующее уравнение:
где все компоненты указаны выше.
Угловая скорость гироскопа вокруг оси определяется скоростью вращения ротора . Подстановка в уравнения (15) и (6) дает угловые скорости гироскопа вокруг осей и : где знак (-) в уравнении (17) означает, что прецессия гироскопа вокруг оси происходит по часовой стрелке, т. е. гироскоп движется вверх.
Крутящий момент, действующий вокруг оси, приводит к медленному вращению против часовой стрелки вокруг оси и вызывает интенсивное прецессионное вращение гироскопа вокруг оси по часовой стрелке. Гироскоп движется вверх от своего горизонтального положения. Этот эффект служит практическим доказательством отсутствия свойства антигравитации.
2.2. Пример 2
Математическая модель движения гироскопа рассматривается для той же стойки гироскопа и технических параметров, представленных в Разделе 2.1, Пример 1. Отличие заключается в действии момента нагрузки по часовой стрелке вокруг оси . При этом условии действия внутренних крутящих моментов и движений гироскопа следующие:
(i) Момент нагрузки создает момент сопротивления, который действует против часовой стрелки вокруг оси, и момент прецессии, который действует вокруг оси против часовой стрелки. Это совпадает с действием крутящего момента нагрузки (ii) Действие крутящего момента, создаваемого весом гироскопа, создает моменты сопротивления и прецессии. Момент сопротивления действует по часовой стрелке вокруг оси. Момент прецессии действует против часовой стрелки вокруг оси как момент
Все действующие моменты и движения гироскопа с одной боковой опорой показаны на рисунке 2.
Уравнения моментов и движений гироскопа вокруг осей и представлены следующими выражениями: где знак (-) в уравнении (18) указывает на движение по часовой стрелке. Все остальные компоненты указаны выше.
Коэффициент представляет собой пропорциональное увеличение момента прецессии вокруг оси . Коэффициент выражается как отношение суммы моментов прецессии и нагрузки к моменту прецессии, действующему вокруг оси . Выражение получается аналогично уравнению (1) и представлено следующим уравнением:
где – коэффициент пропорционального увеличения величины момента прецессии, действующего вокруг оси . Все остальные параметры указаны выше.
Коэффициент обозначает увеличение момента прецессии вокруг оси oy , когда значение результирующего момента вокруг оси также увеличивается. Уравнение (20) демонстрирует следующие значения коэффициента : (i) Отсутствие момента нагрузки, действующей вокруг оси или , означает, что коэффициент (т. е. нет изменения значений инерционных моментов, действующих вокруг двух осей) (ii) Действие момента нагрузки означает, что коэффициент (т. е. увеличиваются значения инерционных моментов, действующих вокруг двух осей) (iii) При равенстве момента нагрузки веса гироскопа моменту прецессии () результирующий момент сопротивления, действующий вокруг оси )
Уравнения для инерционных моментов, то есть уравнения (17) и (20), подставляются в уравнения (18) и (19). Уравнения (21)–(23) упрощаются и преобразуются так же, как уравнения (4)–(6): где все параметры указаны выше.
При движении вокруг оси действующие моменты представлены совместным действием веса гироскопа с моментами прецессии и моментами сопротивления в противоположном направлении. Моменты, действующие вокруг оси, представлены действием момента нагрузки и комбинированных моментов сопротивления с моментами прецессии, действующими в противоположном направлении. Следующее решение для уравнений (21)–(23) такое же, как представлено в разделе 2.1, пример 1. Уравнение (21) можно решить, подставив определенное уравнение и используя преобразования, чтобы получить следующее уравнение:
где все компоненты указаны выше.
2.2.1. Рабочий пример
Движения гироскопа с одной боковой опорой выполняются под действием момента нагрузки вокруг оси по часовой стрелке. Схема действия моментов и движений представлена на рис. 2. Уравнение (24) представляет собой уравнение движения гироскопа вокруг оси . Должны быть определены угловые скорости прецессий вокруг двух осей. Подставив исходные данные гироскопа ([20], табл. 1) в уравнение (24) и проведя преобразования, получим следующее уравнение:
Уравнение (25) упрощено. Затем выполняются шаги решения, аналогичные шагам, представленным в Разделе 2. 1, Пример 1. Все комментарии, относящиеся к решениям уравнений, опущены.
где знак (-) указывает на движение по часовой стрелке.
Крутящий момент, действующий вокруг оси, вызывает медленное вращение вокруг оси по часовой стрелке и интенсивное вращение гироскопа вокруг оси против часовой стрелки. Эти вращения приводят к крутящему моменту против часовой стрелки вокруг оси.
3. Результаты и обсуждение
Математические модели гироскопических эффектов приводят к уравнениям движения гироскопа с одной боковой опорой для основного внешнего момента, действующего вокруг вертикальной оси. Модели движения гироскопа вокруг двух осей основаны на действии внешнего и внутреннего моментов, создаваемых центробежной, общей инерционной и кориолисовой силами. Они также основаны на изменении углового момента. Новый аналитический подход к задаче гироскопа демонстрирует, что действие момента внешней нагрузки вокруг вертикальной оси порождает моменты прецессии, которые поворачивают гироскоп вверх или вниз вокруг горизонтальной оси. Эти движения зависят от направления вращения вращающегося ротора. Математические модели движения гироскопа с одной боковой опорой, в которых действия внешних и внутренних моментов вокруг двух осей подтверждены наблюдениями, сделанными в ходе практических испытаний.
4. Заключение
Предыдущие математические модели гироскопических эффектов содержат много допущений и упрощений, не подтвержденных на практике. Это новое исследование гироскопических эффектов исследует действия системы инерционных моментов, создаваемых известными инерционными силами классической механики. Математические модели движения гироскопа с одной боковой опорой и действия моментов нагрузки против и по часовой стрелке вокруг вертикальной оси объясняют движение гироскопа вверх и вниз. Движение гироскопа вверх не является свойством антигравитации, как когда-то считалось, а является результатом действия момента прецессии, создаваемого моментом нагрузки. Величина момента прецессии больше, чем величина момента, создаваемого грузом гироскопа. Аналитические модели движения гироскопа вверх и вниз четко описывают физику таких гироскопических эффектов.
Номенклатура
| : | Ускорение свободного падения |
| : | Основание натурального логарифма |
| : | Индекс осей или |
| : | Момент инерции массы ротора диск |
| : | Момент инерции гироскопа вокруг оси |
| : | Расстояние между центром массы гироскопа и одной боковой опорой |
| : | Длина компонента гироскопа |
| : | Масса вращающихся компонентов |
| : | 900 98 Внешний радиус ротора|
| : | Радиус компонента гироскопа |
| : | Момент нагрузки, создаваемый грузом гироскопа |
| : | Момент нагрузки, приложенный к оси |
| : | Момент, создаваемый изменением углового момента, центробежный, кориолисовский , и силы инерции соответственно и действующие вокруг оси |
| : | Сопротивление и момент прецессии, соответственно, действующие вокруг оси |
| : | Время |
| : | 9 0098 Масса гироскопа|
| : | Угол наклона вращающейся оси |
| : | Коэффициент изменения значения внутренних крутящих моментов |
| : | Угловая скорость ротора |
| : | Угловая скорость прецессии вокруг оси . |
Доступность данных
Данные, использованные для поддержки результатов этого исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Автор заявляет об отсутствии конфликта интересов.
Благодарности
Работа выполнена при поддержке Кыргызского государственного технического университета им. И. Раззакова.
Каталожные номера
M.N.Armenise, C.Ciminelli, F.Dell’Olio, and V.M.N.Passaro, Advances in Gyroscope Technologies , Springer-Verlag Berlin and Heidelberg GmbH & Co. KG, Berlin, 2010.
RF Deimel, 9003 2 Механика of the Gyroscope , Dover Publications Inc, New York, 2003.
G. Greenhill, Report on Gyroscope Theory General Books LLC , Palala Press, London, 2016.
J. B. Скарборо, Теория гироскопа и приложения , Nabu Press, Лондон, 2011.
Дж. А. Феррари, «Прецессия гироскопа и принцип эквивалентности: ответ на Ø.
Grøn», Annalen der Physik , vol. 501, нет. 5, стр. 399-400, 1989.Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Вайнберг, Механические характеристики гироскопа: самый важный параметр , техническая статья MS-2158, Analog Devices, Норвуд, Массачусетс, США, 2011.
Дж. Р. Тейлор, Classical Mechanics , University Science Books, California, USA, 2005.
D. R. Gregory, Classical Mechanics , Cambridge University Press, New York, 2006.
M Д. Аардема, «Аналитическая динамика», в . Theory and Application , Academic/Plenum Publishers, New York, 2005.
Посмотреть по адресу:
Google Scholar
Д. Браун и М. Пек, «Энергетика гироскопов с управляющим моментом как совместных приводов», Journal of Guidance, Control and Dynamics , vol.
32, нет. 6, стр. 1871–1883, 2009.Посмотреть по адресу:
Сайт издателя | Google Scholar
В. К. Лян и С. К. Ли, «Завихренность, гироскопическая прецессия и сила кривизны вращения», Physical Review D , vol. 87, нет. 4, статья 044024, 2013.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Куросу, К. Кодама, М. Адачи и К. Камимура, «Анализ ошибок для системы измерения гироскопической силы», в Proceedings of International Measurement Confederation (IMEKO), Technical Committee 3 (TC3) International Conference , pp. 162–171, Istanbul, Turkey, 2001.
Посмотреть по адресу:
Google Scholar берг и А. Курепенис, «Источники ошибок в гироскопах MEMS с кремниевыми камертонами в плоскости», Journal of Microelectromechanical Systems , vol.
15, нет. 3, стр. 479–491, 2006 г.Посмотреть по адресу:
Сайт издателя | Академия Google
Дж. Э. Фаллер, У. Дж. Холландер, П. Г. Нельсон и М. П. МакХью, «Эксперимент по взвешиванию с помощью гироскопа с нулевым результатом», Physical Review Letters , vol. 64, нет. 8, стр. 825-826, 1990.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Уэйт, «Явление уменьшения веса прялки», Meccanica , vol. 42, стр. 359–364, 2007.
Посмотреть по адресу:
Сайт издателя | Академия Google
Р. Усубаматов, «Силы инерции, действующие на гироскоп», Journal of Mechanical Science and Technology , vol. 32, нет. 1, стр. 101–108, 2018 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р.