Теория пределов для чайников: Как решать пределы для чайников, примеры решений

Читать онлайн «Теория государства и права для чайников», Дмитрий Усольцев – ЛитРес

© Текст, Усольцев Д. А., 2017

© Оформление. ООО «Издательство «Эксмо», 2017

Глава 1

«Антитеория». О подходе к теме. О прокрустовом ложе теорий

Уверуй, что все было не зря: наши песни, наши сказки, наши неимоверной тяжести победы, наши страдания – не отдавай всего этого за понюх табаку… Мы умели жить. Помни это. Будь человеком.

Василий Шукшин

Осмотритесь. Видите? Что вы видите помимо стен, линий, границ, ограничений, пределов и препятствий? Каждый из нас живет в мире, обществе, государстве и наделен правами. И, конечно, чтобы в таком мире не просто выживать, прячась в свою нору, в свою соту в огромном высотном бараке со всеми удобствами, а по-настоящему жить, надо понимать этот мир, понимать общество, понимать государство, понимать право. Для того чтобы все это понять, в этом надо долго «вариться», долго изучать. Но есть более простой путь, который называется «вооружиться теорией». Поймете ли вы общество, государство и право, вооружившись современной теорией государства и права? Мой ответ: «Нет». И именно поэтому я пишу эту книгу, чтобы у вас была не только теория, но и антитеория, надтеория, т. е. некая мировоззренческая установка, помогающая оценивать и государство, и право, и теории о государстве и праве, и понимать их правильно.

Как принято изучать что-либо в современной системе образования? Есть мир. В мире есть человек. У человека есть тело. В теле есть печень. Есть люди, созданные для того, чтобы десятилетиями смотреть телевизор, лежа на диване, а есть люди, созданные для того, чтобы изучать медицину. Можно ли изучать печень в отрыве от человека? От его энергии, природы в отрыве от человека как части огромного мира? И нужно ли изучать печень, ничего не зная более? Нужно ли становиться «ученым человеком», важно изучающим пылинку, и зазубривать годами ворохи понятий на латинском языке? Стоит ли пытаться изучать государство и право как «вещь-в-се-бе»? Хорошо по этому поводу сказал выдающийся русский дореволюционный историк Василий Осипович Ключевский: «Детальное изучение отдельных органов отучает понимать жизнь всего организма».

Государство и право – это часть мира. В данной книге я описываю государство и право не так, как описывают муху, увиденную под микроскопом, а как часть мира. Ценность такого изучения государства и права заключается в том, что изучающий начинает лучше понимать и тетку из ЖКХ, и интервью бывшего сотрудника КГБ СССР, и лозунги на выборах губернатора, и логику поведения участкового, и рассуждения анастасиевца, горящего идеей создания родового поместья, и т. д. Лучше понимая мир, человек правильнее действует.

Надо учитывать еще одну загогулину: изучать государство и право, с одной стороны, и изучать теорию государства и права, с другой, – разные вещи. Есть государство и право. А есть кем-то созданный клубок теорий о них.

А что означает слово «теория»? Теория – это учение, идея, совокупность принципов и положений. Чье-то учение, чья-то идея, чья-то совокупность чьих-то принципов и положений. Знать их надо. Привносить их в свою картину мира нельзя (точнее, нельзя искажать ими свою картину мира).

Ценность данной книги заключается в том, что я не загоняю читающего в прокрустово ложе теории; я учу понимать теорию, но смотреть на нее извне; я учу не становиться ее рабом. Я не столько старался отвечать на вопросы, сколько задавать их, сколько подводить читателя к умственному и внеумственному пониманию темы. Как и предыдущие свои книги, я писал эту для того, чтобы она помогала именно понимать тему, а не заучивать позавчерашнюю заумную научную чепуху, обернутую в латинизмы. Надо почувствовать и понять, а не вызубрить интеллектуально-словесную ткань. Причем почувствовать надо, конечно же, как я уже сказал, внеумственно.

Вы спросите: «Ну… а что значит «внеумственно почувствовать»?» Для ответа на этот вопрос вместо ста страниц мировоззренческого текста приведу один пример из жизни. Однажды в результате некоторых авантюристических перипетий я попал в Зальцбург. Город на западе Австрии, на границе с Германией. И вот я иду по улице утром один-одинешенек без денег, без цели. И есть в городе только один человек, который мне нужен, а где он находится, я не знаю в принципе. Он русский, и мы виделись до этого всего один раз. Но он точно в Зальцбурге. Повторюсь: денег нет, есть нечего, пить нечего, изъясняюсь по-немецки хуже, чем «с трудом». Ну, да, я знаю по-немецки несколько стихотворений, песен, цитирую Гете, Ницше, Хайдеггера, Геббельса, но «быть культурным человеком» и «разговаривать с прохожими на улице» – разные вещи. И я иду. Карты нет, ориентируюсь по солнцу. Сентябрь, десять часов утра. И я принимаю самое ненормальное, странное и правильное решение: я решаю найти этого человека чутьем. Я отключаю ум и задаю себе вопросы: «Где он сейчас находится?», «О чем он думает?», «На улице ли он, можно ли его встретить?» и другие подобные. В итоге для того, чтобы натолкнуться на него (на входе в большой магазин), мне понадобилось сорок минут. То есть я спрашивал себя и просто бездумно шел. И медитировал. Шел, сосредоточившись на нем. Шел без ума. Веря в себя. И стараясь пребывать в ежесекундном сосредоточении, как боксер на ринге.

Теоретически я мог бы ходить по городу сутками и не встретить его. Один такой случай погоды не делает. Но таких случаев много. На Руси это умение называли «чутьем».

Есть и еще одна загогулина: все теории государства и права создавались в Европе. Европа прошла свой тягостный путь. В крови европейцев память о мытарствах, резне, чуме, кровопролитиях, голоде, холоде, одиночестве, неописуемых зверствах.

Теория редко и лишь в небольшой мере является следствием практики: с реальностью и самой Жизнью она связана слабо. Ну, вот, представьте: у Александра Сергеевича Пушкина были хорошие отношения с царем. Я, разумеется, имею в виду Николая I. Царь дает Александру Сергеевичу высочайшее указание-просьбу написать/ создать теорию государства и права. Александр Сергеевич Пушкин приезжает в Болдино, скидывает на слугу верхнюю одежду, садится за стол, отпивает чая из поднесенной чашки, слегка развязывает платок на шее, хватает перо, макает его в чернильницу и… откидывается на спинку кресла, а потом долго и вдумчиво смотрит на огонь в камине.

И в итоге наотрез отказывается писать такую книгу. Почему? А не его это – бюрократические теории писать. Он понимает и чувствует простые вещи: любая теория сужает и уродует мышление, любая теория помогает только теоретикам, любая теория нахлобучивает ящик на голову познающего, отупляет. Теория не становится врагом Жизни, если попадает к особым людям. Почему? Потому что любая теория – это всегда идеология.

Пушкин мог бы блестяще описать государство и право в художественном произведении. Но заниматься работой секретаря, писца, теоретизатора, идеолога, моралиста, работой современного ему западного философа – это не по нему.

Теория может быть полезна при отсутствии практики, полезна до практики, полезна для практики. И, как я сказал ранее, в целом она не есть следствие практики. Наоборот. После практики человек в нормальных естественных условиях либо отказывается от теории, либо сильно видоизменяет ее, либо создает другую и обязательно «зарубает себе на носу», что эта, уже усовершенствованная теория – слабая и малополезная тень того, что он уже познал на практике.

И теории ему в этом деле уже не нужны, он из них уже вырос.

Приведу пример того, что есть теория и какова ее роль. Предположим, что вы никогда не жили в глухом горном лесу в палатке. Что нужно для того, чтобы туда поехать и пожить там без стеснений, неурядиц, оплошностей, незадач и ошибок? Нужна теория. Для теории нужна осведомленность. Вы опрашиваете тех, кто уже имеет такой опыт, собираете информацию в Интернете. У вас в голове складывается представление, теория: ночью заметно холоднее, чем днем, поэтому нужна теплая одежда и/или спальник… Можно промокнуть под дождем, поэтому нужен навес, под ним – печь из камней, а между ними – веревка для сушки одежды. а для этого нужны скрепки-прищепки, потому что ветер уносит. А ночью (если это не лето) дрова частенько сыреют даже под навесом, значит, неприкосновенный запас дров лучше держать в изолированном полиэтиленовом пакете в палатке. Так. А комары?.. А освещение? А связь? А еноты, ворующие по ночам еду? А розжиг?.. А источники воды?.

. А рукомойник?.. и так далее. Мелочей – тысячи. Однозначно то, что теория жизни в лесу, создаваемая вами (или кем-нибудь) в голове и излагаемая на бумаге, ценна и полезна. И вот приходит день, вы оказываетесь в лесу, живете там какое-то время и в итоге возвращаетесь в город. О жизни в лесу вы теперь знаете. Теория сыграла роль, но – ценна ли теперь для вас та самая теория? До какой степени она вам теперь нужна? Информация уже внутри вас, а не вовне. Информация уже стала сведениями и почти знаниями. Поможет ли вам теперь та самая теория?

Подведем итог. Если вам надо вызубрить и забыть – не читайте эту книгу. Если же вы понимаете, что перед вами – долгий неизведанный жизненный путь, то эта книга для вас.

Итак, что такое «теория государства и права», мы разобрались.

Теперь перейдем к государству и праву как таковым.

Глава 2

Государство, право, люди, нелюди

Основные понятия темы

Эту небольшую подглаву я пишу для того, чтобы показать читателю общий путь нашего следования по смыслам данной книги.

Основные понятия теории государства и права: теория, общество, организованность, власть, государство, право, законодательство, общественные отношения, политика, идеология.

 

И есть еще одно слово, которое после 1917 года почти не употребляется, но которое незаменимо, ибо выражает существенную часть того, что мы изучаем. Это слово «порядок»: в этой книге я употребляю его в изначальном смысле – как «порядок вещей», «установившийся порядок», «общественный порядок».

Что такое общество? Что такое общество сейчас в России и что такое общество три тысячи лет назад здесь же, где-нибудь на Псковщине? Есть ли разница? Да, разница на самом деле непредставимо огромная. Когда-то общество было единым целым. Изгнание из общины, племени было равносильно смерти. Затем общество стало совокупностью людей, объединенных большим количеством уз – кровных, сословных, духовных, бытийных, метафизических и пр. В настоящее время общество – более разнообразное явление. В Индии общество одно, в Германии – другое. Общим признаком, однако, остается «совокупность людей, объединенных общим бэкграундом». Основное слово здесь – «объединенных». Общество – это не человек отдельно, общество – это объединение, т. е. единство, состоящее из множества личностей. Когда Фидель Кастро приехал в Советский Союз, он был удивлен, когда подарил мужчине из толпы сигару, и тот ее сразу же закурил и передал товарищу, и эта сигара разошлась дальше. Вот это было единство, единение. В других странах мира в таких ситуациях любой другой спрятал бы сигару поглубже в карман. Однако вернемся. Общество – это объединение людей. Важно следующее: людей объединяет некая постоянная и, возможно, бессознательное, т. е. это не очередная идеология, это не боление за футбольную команду, это не проживание на одной территории, это не общий язык; это вещи более серьезные: раса, кровь, верования, мировоззренческий код, культура, происхождение, религия. Общество – это нечто менее фундаментальное, нежели народ, это то, что выросло из народа, но не обрубило корни.

Постепенно, после возникновения в народе общества, в этом обществе (далеко не в каждом, а, скорее, как исключение) создается нечто, именуемое «государство». В данной книге я далее вкратце рассмотрю «алхимический» процесс формирования государства, на данном же этапе важно понимать, что в современном мире между обществом и государством нельзя ставить знак равенства. Государство находится вне общества, рядом с ним (и не путайте государство со страной).

Давайте изначально принципиально определимся со смыслами слова «государство».

Смыслов основных (общепринятых) три:

1) государство – это страна;

2) государство – это вид организации общества;

3) государство – это субъект власти и управления.

До какой степени эти определения правильны? Подробнее об этом мы поговорим далее.

Теперь «власть». Власть догосударственная – это одно, государственная – другое, послегосударственная – третье (государства ведь когда-то возникли и когда-нибудь исчезнут). При этом надо понимать, что если есть государство, это не значит, что в стране есть государственная власть и больше никакой ветви управления нет. Это не так. Государственная власть в стране не единственная. Догмы догмами, глупость глупостью, наука наукой, а действительность остается, и в ней все совсем не так, как в теории.

Возникновение государства сопровождалось возникновением права в современном смысле этого слова, как системы законодательства. Иными словами: рождение государства и законодательства – это процесс одновременный, можно сказать, что это один процесс. Возникающее и растущее государство нуждается в самоподдержке, самоохране, пресечении всего того, что эту государственность может разрушить… Иными словами, государство нуждается в строгой упорядоченности общественной жизни. И общественные системы самосохранения тут, разумеется, на государство почти не работают (они работают на общество), а между интересами общества и интересами государства возникает противоречие, поэтому появляется и развивается система самосохранения – законодательство. Не просто регулятор общественной жизни, это инструмент, существование и сила которого обеспечивается государством его же «руками».

Теперь о политике. Что это? Политика – это, прежде всего, деятельность. Это не вещь, не предмет, не субъект, не явление. Это глагол. Дело. Причем это деятельность общественная, государственная, межгосударственная, надгосударственная, надобщественная. Политика – это особый вид влияния кого-то на что-то. При этом это деятельность, имеющая отношение к власти и управлению – людьми, обществом, государством, страной, союзами. Политика – это вид воздействия, влияния, управления. В науке государства и права так и говорят: «политика как регулятор», «политика как инструмент».

Политика бывает явная и тайная, публичная и кулуарная, «сокрытая» (английское слово «secret» произошло от русского «скрыт»). Например, у католической церкви был отдельный «передовой отряд» – орден иезуитов. Его главным занятием была международная непубличная политика. Еще пример (политкорректный): долгое и сильное влияние итало-американской мафии на государственный аппарат США в середине XX века. При этом очевидно постоянное влияние сотен транснациональных корпораций (ТНК) на государственную политику стран мира. Или такой пример: влияние определенных сил из Центрального разведывательного управления США на управление наркокартелями Южной Америки. Еще пример. Пишет современный русский философ, политолог Александр Дугин: «22 ноября 1963 года в Далласе был убит президент США Джон Кеннеди. Убийца так до сих пор и не найден, подозреваемый Харви Ли Освальд сам был застрелен Джеком Руби. Тот был, в свою очередь, найден мертвым в своей камере, успев перед этим сказать, что серия убийств была хорошо подготовленной спецоперацией, за которой стояли лица из верхушки американского истеблишмента. При странных обстоятельствах погибли свидетели. Как показывает большинство соцопросов, почти все американцы считают, что убийство организовали противники Кеннеди из ЦРУ и его политические оппоненты. То есть был заговор с целью устранения американского президента, который нарушил интересы могущественных политических кланов, американского Болота начала 60-х годов».

Читать “Теория государства и права для чайников” – Усольцев Дмитрий Александрович – Страница 1

Дмитрий Дмитрий Теория государства и права для чайников © Текст, Усольцев Д. А., 2017 © Оформление. ООО «Издательство «Эксмо», 2017 Глава 1 «Антитеория». О подходе к теме. О прокрустовом ложе теорий Уверуй, что все было не зря: наши песни, наши сказки, наши неимоверной тяжести победы, наши страдания – не отдавай всего этого за понюх табаку… Мы умели жить. Помни это. Будь человеком. Василий Шукшин Осмотритесь. Видите? Что вы видите помимо стен, линий, границ, ограничений, пределов и препятствий? Каждый из нас живет в мире, обществе, государстве и наделен правами. И, конечно, чтобы в таком мире не просто выживать, прячась в свою нору, в свою соту в огромном высотном бараке со всеми удобствами, а по-настоящему жить, надо понимать этот мир, понимать общество, понимать государство, понимать право. Для того чтобы все это понять, в этом надо долго «вариться», долго изучать. Но есть более простой путь, который называется «вооружиться теорией». Поймете ли вы общество, государство и право, вооружившись современной теорией государства и права? Мой ответ: «Нет». И именно поэтому я пишу эту книгу, чтобы у вас была не только теория, но и антитеория, надтеория, т. е. некая мировоззренческая установка, помогающая оценивать и государство, и право, и теории о государстве и праве, и понимать их правильно. Как принято изучать что-либо в современной системе образования? Есть мир. В мире есть человек. У человека есть тело. В теле есть печень. Есть люди, созданные для того, чтобы десятилетиями смотреть телевизор, лежа на диване, а есть люди, созданные для того, чтобы изучать медицину. Можно ли изучать печень в отрыве от человека? От его энергии, природы в отрыве от человека как части огромного мира? И нужно ли изучать печень, ничего не зная более? Нужно ли становиться «ученым человеком», важно изучающим пылинку, и зазубривать годами ворохи понятий на латинском языке? Стоит ли пытаться изучать государство и право как «вещь-в-се-бе»? Хорошо по этому поводу сказал выдающийся русский дореволюционный историк Василий Осипович Ключевский: «Детальное изучение отдельных органов отучает понимать жизнь всего организма». Государство и право – это часть мира. В данной книге я описываю государство и право не так, как описывают муху, увиденную под микроскопом, а как часть мира. Ценность такого изучения государства и права заключается в том, что изучающий начинает лучше понимать и тетку из ЖКХ, и интервью бывшего сотрудника КГБ СССР, и лозунги на выборах губернатора, и логику поведения участкового, и рассуждения анастасиевца, горящего идеей создания родового поместья, и т. д. Лучше понимая мир, человек правильнее действует. Надо учитывать еще одну загогулину: изучать государство и право, с одной стороны, и изучать теорию государства и права, с другой, – разные вещи. Есть государство и право. А есть кем-то созданный клубок теорий о них. А что означает слово «теория»? Теория – это учение, идея, совокупность принципов и положений. Чье-то учение, чья-то идея, чья-то совокупность чьих-то принципов и положений. Знать их надо. Привносить их в свою картину мира нельзя (точнее, нельзя искажать ими свою картину мира). Ценность данной книги заключается в том, что я не загоняю читающего в прокрустово ложе теории; я учу понимать теорию, но смотреть на нее извне; я учу не становиться ее рабом. Я не столько старался отвечать на вопросы, сколько задавать их, сколько подводить читателя к умственному и внеумственному пониманию темы. Как и предыдущие свои книги, я писал эту для того, чтобы она помогала именно понимать тему, а не заучивать позавчерашнюю заумную научную чепуху, обернутую в латинизмы. Надо почувствовать и понять, а не вызубрить интеллектуально-словесную ткань. Причем почувствовать надо, конечно же, как я уже сказал, внеумственно. Вы спросите: «Ну… а что значит «внеумственно почувствовать»?» Для ответа на этот вопрос вместо ста страниц мировоззренческого текста приведу один пример из жизни. Однажды в результате некоторых авантюристических перипетий я попал в Зальцбург. Город на западе Австрии, на границе с Германией. И вот я иду по улице утром один-одинешенек без денег, без цели. И есть в городе только один человек, который мне нужен, а где он находится, я не знаю в принципе. Он русский, и мы виделись до этого всего один раз. Но он точно в Зальцбурге. Повторюсь: денег нет, есть нечего, пить нечего, изъясняюсь по-немецки хуже, чем «с трудом». Ну, да, я знаю по-немецки несколько стихотворений, песен, цитирую Гете, Ницше, Хайдеггера, Геббельса, но «быть культурным человеком» и «разговаривать с прохожими на улице» – разные вещи. И я иду. Карты нет, ориентируюсь по солнцу. Сентябрь, десять часов утра. И я принимаю самое ненормальное, странное и правильное решение: я решаю найти этого человека чутьем. Я отключаю ум и задаю себе вопросы: «Где он сейчас находится?», «О чем он думает?», «На улице ли он, можно ли его встретить?» и другие подобные. В итоге для того, чтобы натолкнуться на него (на входе в большой магазин), мне понадобилось сорок минут. То есть я спрашивал себя и просто бездумно шел. И медитировал. Шел, сосредоточившись на нем. Шел без ума. Веря в себя. И стараясь пребывать в ежесекундном сосредоточении, как боксер на ринге. Теоретически я мог бы ходить по городу сутками и не встретить его. Один такой случай погоды не делает. Но таких случаев много. На Руси это умение называли «чутьем». Есть и еще одна загогулина: все теории государства и права создавались в Европе. Европа прошла свой тягостный путь. В крови европейцев память о мытарствах, резне, чуме, кровопролитиях, голоде, холоде, одиночестве, неописуемых зверствах. Теория редко и лишь в небольшой мере является следствием практики: с реальностью и самой Жизнью она связана слабо. Ну, вот, представьте: у Александра Сергеевича Пушкина были хорошие отношения с царем. Я, разумеется, имею в виду Николая I. Царь дает Александру Сергеевичу высочайшее указание-просьбу написать/ создать теорию государства и права. Александр Сергеевич Пушкин приезжает в Болдино, скидывает на слугу верхнюю одежду, садится за стол, отпивает чая из поднесенной чашки, слегка развязывает платок на шее, хватает перо, макает его в чернильницу и… откидывается на спинку кресла, а потом долго и вдумчиво смотрит на огонь в камине. И в итоге наотрез отказывается писать такую книгу. Почему? А не его это – бюрократические теории писать. Он понимает и чувствует простые вещи: любая теория сужает и уродует мышление, любая теория помогает только теоретикам, любая теория нахлобучивает ящик на голову познающего, отупляет. Теория не становится врагом Жизни, если попадает к особым людям. Почему? Потому что любая теория – это всегда идеология. Пушкин мог бы блестяще описать государство и право в художественном произведении. Но заниматься работой секретаря, писца, теоретизатора, идеолога, моралиста, работой современного ему западного философа – это не по нему. Теория может быть полезна при отсутствии практики, полезна до практики, полезна для практики. И, как я сказал ранее, в целом она не есть следствие практики. Наоборот. После практики человек в нормальных естественных условиях либо отказывается от теории, либо сильно видоизменяет ее, либо создает другую и обязательно «зарубает себе на носу», что эта, уже усовершенствованная теория – слабая и малополезная тень того, что он уже познал на практике. И теории ему в этом деле уже не нужны, он из них уже вырос. Приведу пример того, что есть теория и какова ее роль. Предположим, что вы никогда не жили в глухом горном лесу в палатке. Что нужно для того, чтобы туда поехать и пожить там без стеснений, неурядиц, оплошностей, незадач и ошибок? Нужна теория. Для теории нужна осведомленность. Вы опрашиваете тех, кто уже имеет такой опыт, собираете информацию в Интернете. У вас в голове складывается представление, теория: ночью заметно холоднее, чем днем, поэтому нужна теплая одежда и/или спальник… Можно промокнуть под дождем, поэтому нужен навес, под ним – печь из камней, а между ними – веревка для сушки одежды. а для этого нужны скрепки-прищепки, потому что ветер уносит. А ночью (если это не лето) дрова частенько сыреют даже под навесом, значит, неприкосновенный запас дров лучше держать в изолированном полиэтиленовом пакете в палатке. Так. А комары?.. А освещение? А связь? А еноты, ворующие по ночам еду? А розжиг?.. А источники воды?. . А рукомойник?.. и так далее. Мелочей – тысячи. Однозначно то, что теория жизни в лесу, создаваемая вами (или кем-нибудь) в голове и излагаемая на бумаге, ценна и полезна. И вот приходит день, вы оказываетесь в лесу, живете там какое-то время и в итоге возвращаетесь в город. О жизни в лесу вы теперь знаете. Теория сыграла роль, но – ценна ли теперь для вас та самая теория? До какой степени она вам теперь нужна? Информация уже внутри вас, а не вовне. Информация уже стала сведениями и почти знаниями. Поможет ли вам теперь та самая теория?

Методические рекомендации по выполнению контрольной работы по дисциплине «Прикладная математика», тема “Теория пределов”

«Омский летно-технический колледж гражданской авиации
имени А.В. Ляпидевского» филиал Федерального государственного бюджетного
образовательного учреждения высшего профессионального образования
«Ульяновское высшее авиационное училище гражданской авиации (институт)»

(ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И))

КРАТКИЙ КУРС ЛЕКЦИЙ И

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

по дисциплине

«Математика»

Теория пределов

Омск – 2015

Рассмотрено

на заседании ЦМК ЕНД
от «_____»__________20__г.

Протокол №_________

Разработал: Пищагина Е.С., преподаватель математики

Краткий курс лекций и методические указания по выполнению контрольной работы по дисциплине «Математика», тема «Теория пределов»/ Е.С. Пищагина – ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И), 2015. – 27 с.

Краткий курс лекций и методические указания по выполнению контрольной работы по дисциплине «Математика» предназначены для подготовки специалистов со средним профессиональном образованием. Включает теоретические сведения, примеры решения заданий, примерные варианты контрольных заданий. Типовые задачи даются с подробным решением. Рекомендуется я самостоятельной проработки. Основное назначение – помочь курсанту самостоятельно, без помощи педагога закрепить знания по теме «Теория пределов» и подготовиться к контрольной работе.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Краткий курс лекций и методические рекомендации по выполнению контрольной работы по естественно – научной дисциплине «Математика» предназначены для курсантов 1-го курса специальностей:

25. 02.01 Техническая эксплуатация летательных аппаратов и двигателей;

25.02.03 Техническая эксплуатация электрифицированных и пилотажно-навигационных комплексов;

25.02.04 Летная эксплуатация летательных аппаратов.

Содержание раздела курса математики «Теория пределов» определяется федеральным государственным образовательным стандартом среднего профессионального образования (ФГОС СПО).

Пособие объединяет лекционный материал и примеры решения типовых задач, и может быть использовано для изучения и закрепления учебного материала.

Теория пределов.

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:

1. Понять, что такое предел.

2. Научиться решать основные типы пределов.    

Итак, что же такое предел?

Любой предел состоит из трех частей:

1) Всем известного значка предела . 

2) Записи под значком предела, в данном случае . Запись читается «икс стремится к единице». Чаще всего – именно , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ().

3) Функции под знаком предела, в данном случае .

Сама запись  читается так: «предел функции  при икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала , затем , , …, , …. 
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Готово.

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

Разбираемся, что такое ? Это тот случай, когда  неограниченно возрастает, то есть: сначала , потом , потом , затем  и так далее до бесконечности.

А что в это время происходит с функцией ? 
, , , …

Итак: если , то функция  стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию   бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать  до бесконечности, и смотрим на поведение функции:

Вывод: при  функция   неограниченно возрастает:

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, , , , , , , , , 
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.

В том случае, если , попробуйте построить последовательность  , , . Если , то  , , .

Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как , ,  и т.д.

Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.

Пределы с неопределенностью вида  и метод их решения

Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример:

Вычислить предел 

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим  в старшей степени:

Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим  в старшей степени:

Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на  в старшей степени.

Разделим числитель и знаменатель на 

Вот оно как, ответ , а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Пример 2

Найти предел 
Снова в числителе и знаменателе находим  в старшей степени:

Максимальная степень в числителе: 3

Максимальная степень в знаменателе: 4

Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности  делим числитель и знаменатель на .

Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на 

Пример 3

Найти предел 

Максимальная степень «икса» в числителе: 2

Максимальная степень «икса» в знаменателе: 1 ( можно записать как )

Для раскрытия неопределенности  необходимо разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:

Разделим числитель и знаменатель на 

Под записью  подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида  у нас может получиться конечное число, ноль или бесконечность.

Пределы с неопределенностью вида  и метод их решения

Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с материалом о бесконечно малых функциях.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Пример 4

Решить предел 

Сначала попробуем подставить -1 в дробь:

 
В данном случае получена так называемая неопределенность .

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, то ознакомьтесь с методическим материалом «Горячие формулы школьного курса математики». Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него: .

В случае если дискриминант большой, например 361,  используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни: 

Таким образом:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель  уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Разложим числитель на множители.

Пример 5

Вычислить предел 

Сначала «чистовой» вариант решения

Разложим числитель и знаменатель на множители.

Числитель: 
Знаменатель:



, 

Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.

Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

! Важно 

В ходе решения фрагмент типа  встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).

, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида 

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Пример 6

Найти предел 

Начинаем решать.

Сначала пробуем подставить 3 в выражение под знаком предела

Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

 

Получена неопределенность вида , которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности  используют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов: 
И смотрим на наш предел: 

Что можно сказать?  у нас в числителе уже есть. Теперь для применения формулы осталось организовать  (которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

Хорошо,  мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу :

Неопределенность  не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.

Готово.

Как должно выглядеть решение данного примера в чистовом варианте?

Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Пример 7

Найти предел 

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители:

Умножим числитель и знаменатель на сопряженное выражение

Четкое объяснение: мощная центральная предельная теорема | by Juhi Ramzai

Почему каждый инженер машинного обучения/специалист по данным ДОЛЖЕН знать об этом

На самом деле это одна из самых важных статистических теорем, читайте дальше, чтобы получить простое объяснение!

Источник: Giphy

Центральная предельная теорема (ЦПТ) — одна из фундаментальных теорем в статистике, и хорошая новость заключается в том, что это довольно простая концепция, что станет очевидным при дальнейшем чтении. Предварительная концепция, которую вы должны понять, прежде чем читать дальше — Нормальные дистрибутивы и почему они так чертовски важны! Прочтите мой пост о нормальном распределении, который служит прекрасным приквелом к ​​центральной предельной теореме.

Четкое объяснение: нормальное распределение и центральная предельная теорема

Что такого нормального или не очень нормального в этих концепциях?

в направлении datascience.com

Двигаемся дальше, стандартное определение:

Центральная предельная теорема (ЦПТ) утверждает, что при достаточно большом размере выборки выборочное распределение среднего значения переменной будет приближаться к нормальному распределению независимо от того, что распределение переменной в популяции.

Давайте сразу перейдем к некоторым примерам, и к тому времени, когда мы выйдем на другую сторону, CLT будет для нас кристально ясным.

Пример #1

Возьмем равномерное распределение (оно идет от 0 до 1 и называется равномерным распределением, поскольку существует одинаковая вероятность выбора значений между 0 и 1, таким образом, его функция плотности вероятности (PDF) равна прямая горизонтальная черная линия). Теперь предположим, что мы возьмем 20 случайных выборок из этого распределения (зеленые точки) и вычислим среднее значение этих выборок. В итоге мы получим одно значение, в данном случае 0,5, обозначенное черной пунктирной линией. Давайте нанесем это среднее значение на гистограмму. Поскольку на данный момент эта гистограмма имеет только одно среднее значение, она на самом деле ничего нам не говорит (левое изображение ниже). Продолжая извлекать больше случайных выборок из того же распределения, вычисляя соответствующие средние значения и снова отображая эти средние значения на гистограмме, мы начинаем получать интересный результат (правое изображение ниже)

Теперь, по мере того, как мы продолжаем брать все больше и больше случайных выборок из нашего равномерного распределения и продолжаем наносить средние значения выборки на гистограмму, в результате мы получаем следующее, и ЭТО ОКАЗЫВАЕТСЯ НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ (см. правую кривую ).

Вывод: Мы начали с равномерного распределения данных, но средние значения выборок, взятых из него, привели к нормальному распределению.

Пример № 2

Во втором примере давайте проделаем те же шаги, что и в примере № 1, с той лишь разницей, что на этот раз мы будем брать выборки из экспоненциального распределения.

Мы снова возьмем 20 случайных выборок, рассчитаем среднее значение выборки и нанесем его на гистограмму. Быстрая перемотка вперед к примерно 100 выборкам из этого экспоненциального распределения данных, гистограмма начинает выглядеть так, как показано ниже, и ее структура нас не удивляет. Да, вы правильно угадали, значит образцы привели к НОРМАЛЬНОЙ РАЗДАЧЕ!

Вывод: Мы начали с экспоненциального распределения данных, но средние значения выборок, взятых из него, привели к нормальному распределению.

Таким образом, в этот момент становится очень интуитивно понятно, что подразумевает CLT.

Центральная предельная теорема подразумевает, что даже если распределение данных НЕ НОРМАЛЬНО, распределение средних значений выборок, взятых из них, будет НОРМАЛЬНЫМ.

В мире аналитики мы ежедневно сталкиваемся с разнообразными данными, и распределение исходных данных нам не всегда известно, но, поскольку мы знаем о CLT, нам даже не нужно заботиться об этом. Дело в том, что средства всегда будут нормально распределены, и нам совершенно не нужно беспокоиться о распределении исходных данных.

(Примечание*. Чтобы CLT мог работать, мы должны быть в состоянии вычислить среднее значение ваших выборок. Существует распределение, известное как распределение Коши, которое не имеет выборочного среднего значения, и поэтому CLT не применяется. к нему, но, кроме Коши, я не встречал никаких других распределений, являющихся исключениями из CLT, поэтому в случае любого другого распределения вы можете быть уверены, что центральная предельная теорема применима к нему очень хорошо.)

Ниже приведены практические последствия знания того, что средства распределяются нормально:

1. Мы можем использовать нормальное распределение среднего, чтобы назначить доверительных интервалов .
2. Мы можем выполнить T-критерий (т. е. если есть разница между средними значениями двух выборок)
3. Мы можем выполнить ANOVA тест (т. е. если есть разница между средними значениями 3 или более выборок)
4. Мы можем выполнить любой статистический тест под солнцем, который использует среднее значение выборки.

И это подводит нас к концу этого поста! Этот пост охватывает всю теорию центральной предельной теоремы, которую мы должны знать при работе с данными и образцами.

Следите за новостями об аналитике, статистике и машинном обучении в этом разделе!!

Приятного обучения! 🙂

Центральная предельная теорема (ЦПТ): определение и основные характеристики

Что такое Центральная предельная теорема (ЦПТ)?

В теории вероятностей центральная предельная теорема (ЦПТ) утверждает, что распределение выборочной переменной приближается к нормальному распределению (т. фактической формы распределения населения.

Иными словами, CLT — это статистическая предпосылка, согласно которой при достаточно большом размере выборки из совокупности с конечным уровнем дисперсии среднее значение всех выборочных переменных из одной и той же совокупности будет приблизительно равно среднему значению всей совокупности. Кроме того, эти выборки аппроксимируют нормальное распределение, а их дисперсии примерно равны дисперсии генеральной совокупности по мере увеличения размера выборки в соответствии с законом больших чисел.

Хотя эта концепция была впервые разработана Абрахамом де Муавром в 1733 году, она не была формализована до 1930 года, когда известный венгерский математик Джордж Полиа назвал ее центральной предельной теоремой.

Ключевые выводы

• Центральная предельная теорема (ЦПТ) утверждает, что распределение выборочных средних приближается к нормальному распределению по мере увеличения размера выборки, независимо от распределения генеральной совокупности.
• Размеры выборки, равные или превышающие 30, часто считаются достаточными для выполнения CLT.
• Ключевым аспектом CLT является то, что среднее выборочных средних значений и стандартных отклонений будет равно среднему значению генеральной совокупности и стандартному отклонению.
• Достаточно большой размер выборки может более точно предсказать характеристики совокупности.
• CLT полезен в финансах при анализе большого набора ценных бумаг для оценки распределения портфеля и характеристик доходности, риска и корреляции.

Центральная предельная теорема

Понимание центральной предельной теоремы (ЦПТ)

Согласно центральной предельной теореме среднее значение выборки данных будет ближе к среднему значению всей рассматриваемой совокупности по мере увеличения размера выборки, независимо от фактического распределения данных. Другими словами, данные точны независимо от того, является ли распределение нормальным или аберрантным.

Как правило, размеры выборки около 30-50 считаются достаточными для выполнения CLT, а это означает, что распределение средних значений выборки является достаточно нормальным. Следовательно, чем больше выборок берется, тем больше графические результаты принимают форму нормального распределения. Обратите внимание, однако, что центральная предельная теорема по-прежнему будет аппроксимироваться во многих случаях для гораздо меньших размеров выборки, таких как n = 8 или n = 5.

Центральная предельная теорема часто используется в сочетании с законом больших чисел, который гласит, что среднее значение выборочных средних и стандартных отклонений будет приближаться к среднему значению генеральной совокупности и стандартному отклонению по мере роста размера выборки, что чрезвычайно полезно в точное предсказание характеристик популяций.

Инвестопедия / Сабрина Цзян

Ключевые компоненты центральной предельной теоремы

Центральная предельная теорема состоит из нескольких ключевых характеристик. Эти характеристики в значительной степени связаны с выборками, размерами выборок и совокупностью данных.

1. Отбор проб последовательный. Это означает, что некоторые единицы выборки являются общими с единицами выборки, выбранными ранее.
2. Выборка случайная. Все образцы должны быть выбраны случайным образом, чтобы они имели одинаковую статистическую вероятность быть выбранными.
3. Образцы должны быть независимыми. Выборки или результаты одной выборки не должны влиять на будущие выборки или другие результаты выборки.
4. Количество образцов должно быть ограничено. Часто упоминается, что выборка должна составлять не более 10% генеральной совокупности, если выборка проводится без замены. Как правило, большие размеры населения требуют использования больших размеров выборки.
5. Размер выборки увеличивается. Центральная предельная теорема актуальна при выборе большего количества выборок.

Центральная предельная теорема в финансах

CLT полезен при изучении доходности отдельных акций или более широких индексов, потому что анализ прост из-за относительной простоты получения необходимых финансовых данных. Следовательно, инвесторы всех типов полагаются на CLT для анализа доходности акций, построения портфелей и управления рисками.

Скажем, например, инвестор хочет проанализировать общую доходность фондового индекса, состоящего из 1000 акций. В этом сценарии этот инвестор может просто изучить случайную выборку акций, чтобы получить расчетную доходность общего индекса. Чтобы быть в безопасности, необходимо отобрать по крайней мере 30-50 случайно выбранных акций из различных секторов, чтобы центральная предельная теорема выполнялась. Кроме того, ранее выбранные акции должны быть заменены другими названиями, чтобы устранить предвзятость.

Чем полезна центральная предельная теорема?

Центральная предельная теорема полезна при анализе больших наборов данных, поскольку позволяет предположить, что выборочное распределение среднего значения в большинстве случаев будет нормально распределенным. Это позволяет упростить статистический анализ и выводы. Например, инвесторы могут использовать центральную предельную теорему для агрегирования данных об эффективности отдельных ценных бумаг и создания распределения выборочных средних, которые представляют большее распределение населения для доходности ценных бумаг за определенный период времени.

Почему центральная предельная теорема минимизирует размер выборки до 30?

Размер выборки, равный 30, довольно распространен в статистике. Размер выборки в 30 часто увеличивает доверительный интервал вашего набора данных о населении настолько, чтобы оправдать утверждения против ваших выводов. Чем больше размер вашей выборки, тем больше вероятность того, что она будет репрезентативной для вашего набора населения.

Что такое формула центральной предельной теоремы?

Центральная предельная теорема не имеет собственной формулы, но опирается на выборочное среднее и стандартное отклонение. По мере того, как средние значения выборки собираются из генеральной совокупности, стандартное отклонение используется для распределения данных по кривой распределения вероятностей.

Центральная предельная теорема – объяснение

Что такое центральная предельная теорема?

Автор Джейсон Гордон

Обновлено 16 апреля 2022 г.

• Маркетинг, реклама, продажи и PR

  Основы маркетинга Продажи Реклама Публичные отношения SEO, социальные сети, прямой маркетинг

• Бухгалтерский учет, налогообложение и отчетность

  Управленческий и финансовый учет и отчетность Налогообложение бизнеса

• Профессионализм и карьерный рост
• Право, сделки и управление рисками

  Правительство, правовая система, административное право и конституционное право Юридические споры – гражданское и уголовное право Агентское право HR, занятость, труд и дискриминация Субъекты бизнеса, корпоративное управление и собственность Деловые операции, антимонопольное право и право ценных бумаг Недвижимость, личная и интеллектуальная собственность Коммерческое право: договор, платежи, обеспечительные интересы и банкротство Защита потребителя Страхование и управление рисками Иммиграционное право Закон об охране окружающей среды Наследство, поместья и трасты

• Управление бизнесом и операции

  Управление операциями, проектами и цепочками поставок Стратегия, предпринимательство и инновации Деловая этика и социальная ответственность Глобальный бизнес, международное право и отношения Деловые коммуникации и переговоры Менеджмент, лидерство и организационное поведение

• Экономика, финансы и аналитика

  Экономический анализ и денежно-кредитная политика Исследования, количественный анализ и принятие решений Инвестиции, трейдинг и финансовые рынки Банковское дело, кредитование и кредитная индустрия Деловые финансы, личные финансы и принципы оценки

• Курсы

+ Еще

Содержание

Что такое центральная предельная теорема? Как используется центральная предельная теорема? Какие предположения лежат в основе CLT?Как работает центральная предельная теоремаФинансы и центральная предельная теоремаЗначение центральной предельной теоремыПрактическое применение центральной предельной теоремыАкадемические исследования центральной предельной теоремы

Центральная предельная теорема утверждает, что при допущении, что все выборки равны по размеру, пример шесть становится больше, распределение тех же средних значений приближается к нормальному распределению. Другими словами, CLT – это статистическая теория, которая утверждает, что при большом размере выборки из совокупности с конечным уровнем дисперсии средние значения всех выборок из одной и той же совокупности будут приблизительно равны среднему значению совокупности.

Назад к : ИССЛЕДОВАНИЕ, АНАЛИЗ И НАУКА ПРИНЯТИЯ РЕШЕНИЙ

Как используется центральная предельная теорема?

В центральной предельной теореме есть важный компонент, в котором средние значения ваших выборок также будут средними значениями генеральной совокупности. Это означает, что если вы добавите среднее значение для всей выборки, вы сможете найти среднее значение, которое также будет вашим реальным средним значением для всей совокупности. Точно так же, если в вашей выборке вы можете получить все стандартные отклонения, то вы сможете найти фактическое стандартное отклонение вашей совокупности. CLT — это ценное явление, которое может помочь вам правильно предсказать характеристики популяции.

Какие предположения лежат в основе CLT?

CLT, как метод, имеет различные допущения. Они следующие:

• Выборка данных должна быть выбрана случайным образом
• Собранные образцы должны быть независимы друг от друга в том смысле, что один образец не должен влиять на другие.
• Когда идет выборка выборок без замены, то все выборки не должны превышать десяти процентов совокупности.
• Размер выборки должен быть достаточно большим. Обратите внимание, что размер выборки будет зависеть от совокупности. Если генеральная совокупность симметрична, выборка из 30 может работать хорошо.

Как работает центральная предельная теорема

Пример Предположим, что на научном факультете университета имеется 15 секций, в каждой из которых обучается около 100 студентов. У вас есть задача рассчитать средний вес студентов на этом факультете естественных наук. В этом случае необходимо вычислить среднее значение. Ниже приведена процедура расчета среднего:

• Во-первых, вам нужно будет измерить вес всех студентов на естественном факультете 9.0070
• Во-вторых, вы складываете все веса
• Наконец, вы разделите общую сумму весов на общее количество студентов, чтобы получить среднее значение

Однако, если данные огромны, подход CLT вообще не имеет смысла. Причина в том, что измерение веса всех студентов будет утомительным и длительным процессом. Ниже приводится альтернативный подход к этому. Сначала вы создаете группы учащихся, выбранных случайным образом из класса. Возьмите это как образец. Затем вы сделаете несколько выборок по 30 студентов в каждой. Затем вы сделаете следующее:

• Рассчитать среднее значение этих выборок
• Вычислить среднее значение выборки
• Это значение даст вам примерный средний вес студентов на естественном факультете

Финансы и центральная предельная теорема  

CLT можно использовать для упрощения значительного числа аналитических процедур.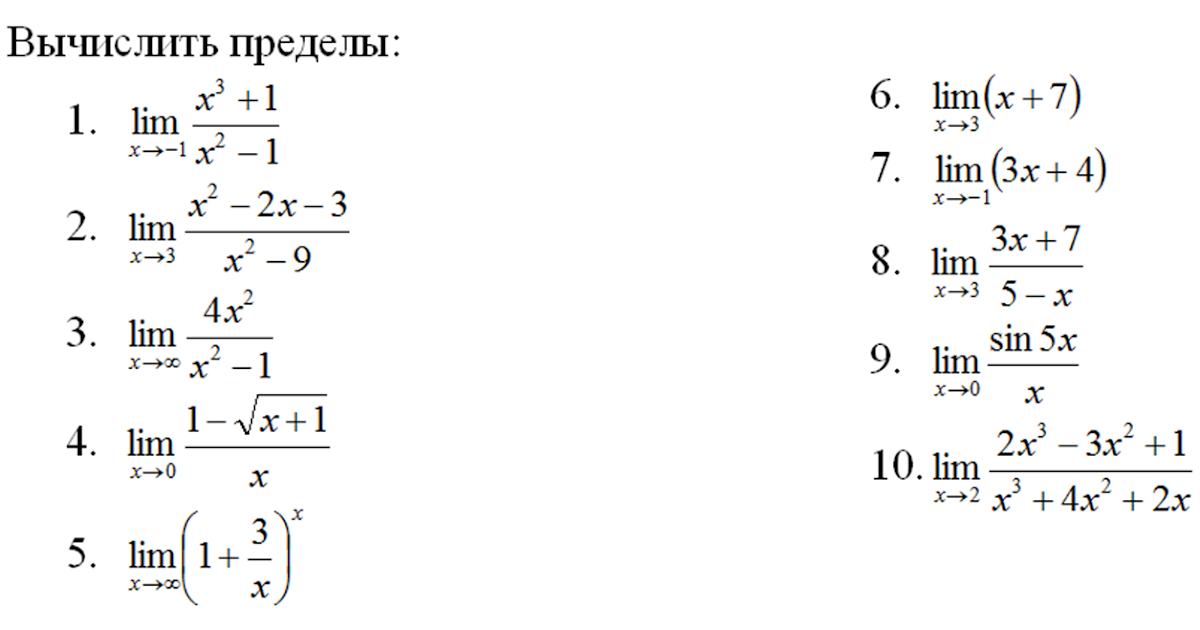 Например, все типы инвесторов могут использовать его для оценки доходности своих акций, управления рисками и создания портфелей. Обратите внимание, что в статистике статистики считают CLT основой для выборки. Это означает, что он держит основу для выборки, а также для статистического анализа в финансах. Пример Предположим, что Джон хочет проанализировать общую доходность своего фондового индекса, состоящего из 1000 акций. Он может взять случайные выборки акций из индекса, чтобы получить оценку общего прироста индексов. Для удержания CTL Джон решает случайным образом выбрать выборки и убедиться, что он оценивает не менее 30 акций в каждой выборке. Для того чтобы избежать систематической ошибки при выборе выборки, он гарантирует, что заменит ранее отобранные акции для выбора в других примерах. Как правило, средние доходы от выбранных выборок приближаются к доходам для всего индекса, включая нормальное распределение. Обратите внимание, что аппроксимация по-прежнему будет иметь место, даже если нет нормального распределения фактической доходности всех индексов.

Существует различная статистическая значимость и практическое применение центральной предельной теоремы. Статистическая значимость CLT Для анализа данных вам придется применять статистические методы, такие как проверка гипотез, а также построение доверительных интервалов. Согласно этому методу предполагается, что имеет место распределение популяции. Там, где имеются ненормальные распределения или неизвестные распределения, мы рассматриваем выборочное распределение как нормальное. Кроме того, выборка означает, что стандартное отклонение обязательно уменьшится, если вы увеличите выборки, взятые из совокупности. Благодаря этому вы сможете с большой точностью оценить среднее значение населения. Вы также можете использовать выборочное среднее, чтобы получить диапазон значений, называемый доверительным интервалом.

Практическое применение центральной предельной теоремы  

Политические аналитики могут применять CLT на выборах или политических опросах.