Главная
Термодинамические уравнения: Уравнение состояния системы. Уравнение состояния идеального газа.

Термодинамические уравнения: Уравнение состояния системы. Уравнение состояния идеального газа.

Уравнение состояния системы. Уравнение состояния идеального газа.

Уравнение состояния — уравнение, связывающее между собой термодинамические параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений. При этом реальные уравнения состояний реальных веществ могут быть крайне сложными.

Уравнение состояния системы не содержится в постулатах термодинамики и не может быть выведено из неё. Оно должно быть взято со стороны (из опыта или из модели, созданной в рамках статистической физики).

Заметим, что соотношения, задаваемые уравнением состояния, справедливы только для состояний термодинамического равновесия.

Виды уравнений состояния

Термическое уравнение состояния. Термическое уравнение состояния связывает макроскопические параметры системы.

Для системы с постоянным числом частиц его общий вид можно записать так: f(P,V,T)=0.

То есть, задать термическое уравнение состояния — значит конкретизировать вид функции f.

Калорическое уравнение состояния. Калорическое уравнение состояния показывает, как внутренняя энергия выражается через давление, объем и температуру. Для системы с постоянным числом частиц оно выглядит так: U=U(P,V,T) или, учитывая, что давление можно выразить из термического уравнения: U=U(V,T).

Каноническое уравнение состояния. Каноническое уравнение представляет собой выражение для одного из термодинамических потенциалов (внутренней энергии, энтальпии, свободной энергии или потенциала Гиббса) через независимые переменные, относительно которых записывается его полный дифференциал:

U=U(S,V) (для внутренней энергии),

H=H(S, P) (для энтальпии),

F=F(T,V) (для свободной энергии),

G=G(T,P) (для потенциала Гиббса).

Каноническое уравнение, независимо от того, в каком из этих четырех видов оно представлено, содержит полную информацию о термических и калорических свойствах термодинамической системы.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

p•VM = R•T,

где p — давление,VM — молярный объём,R — универсальная газовая постоянная,

T — абсолютная температура,К.

Так как VM=V

/ν, где υ — количество вещества, аυ=m/M, где m масса, M — молярная масса, уравнение состояния можно записать:

p•V = (m/M)•R•T,

p = n•k•T,  где n = N/V  – концентрация атомов, k = R/NA – постоянная Больцмана.

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную r, значение которой необходимо было измерять для каждого газа:

p•V = r•T

Менделеев же обнаружил, что r прямо пропорциональна υ, коэффициент пропорциональности R он назвал универсальной газовой постоянной.

Совокупность всех физических и химических свойств системы характеризует её термодинамическое состояние. Все величины, характеризующие какое-либо макроскопическое свойство рассматриваемой системы – это параметры состояния (температура, объем, давление, концентрация и т.д.). Всякое изменение термодинамического состояния системы (изменения хотя бы одного параметра состояния) есть

термодинамический процесс.

Изменение состояния системы может происходить при различных условиях, поэтому различают:

Равновесные процессы – это процессы, проходящие через непрерывный ряд равновесных состояний.

Неравновесные процессы – это процессы, после протекания которых систему нельзя вернуть в исходное состояние без того, чтобы в ней не осталось каких-либо изменений.

Процесс установления в термодинамической системе равновесного состояния называется релаксацией, а соответствующее время – временем релаксации.

Время релаксации – период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз (e — основание натурального логарифма), в основном обозначается греческой буквой τ.

Согласно принципу Ле Шателье – Брауна, при отклонении физической системы от состояния устойчивого равновесия возникают силы, которые пытаются вернуть систему к равновесному состоянию. Если в состоянии равновесия некоторая физическая величина 

f имеет значение , причём отклонение от равновесия, то в первом приближении можно считать, что эти силы пропорциональны отклонению. Кинетическое уравнение для величиныf запишется в виде

,

где λ — некоторый параметр, а знак минус указывает на то, что реакция системы на возмущение приводит к возвращению к равновесному состоянию.

Время релаксации

В таком случае величина f

будет изменяться по закону:

,

где – начальное возмущение.

Уравнение состояния | это… Что такое Уравнение состояния?

У этого термина существуют и другие значения, см. Уравнение состояния (космология).

Уравнение состояния
Статья является частью серии «Термодинамика».
Уравнение состояния идеального газа
Уравнение Ван-дер-Ваальса
Уравнение Дитеричи
Уравнение состояния Редлиха — Квонга
Уравнение состояния Барнера — Адлера
Уравнение состояния Суги — Лю
Уравнение состояния Бенедикта — Вебба — Рубина
Уравнение состояния Ли — Эрбара — Эдмистера
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править
См.
также «Физический портал»

Уравне́ние состоя́ния — уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений. При этом реальные уравнения состояний реальных веществ могут быть крайне сложными.

Уравнение состояния системы не содержится в постулатах термодинамики и не может быть выведено из неё. Оно должно быть взято со стороны (из опыта или из модели, созданной в рамках статистической физики). Термодинамика же не рассматривает вопросы внутреннего устройства вещества.

Заметим, что соотношения, задаваемые уравнением состояния, справедливы только для состояний термодинамического равновесия.

Содержание

  • 1 Виды уравнений состояния
    • 1.1 Термическое уравнение состояния
    • 1.2 Калорическое уравнение состояния
    • 1. 3 Каноническое уравнение состояния
  • 2 Примеры
  • 3 См. также
  • 4 Литература

Виды уравнений состояния

Термическое уравнение состояния

Термическое уравнение состояния связывает макроскопические параметры системы. Для системы с постоянным числом частиц его общий вид можно записать так:

Таким образом, задать термическое уравнение состояния значит конкретизировать вид функции

Калорическое уравнение состояния

Калорическое уравнение состояния показывает, как внутренняя энергия выражается через давление, объем и температуру. Для системы с постоянным числом частиц оно выглядит так:

или, учитывая, что давление можно выразить из термического уравнения:

Каноническое уравнение состояния

Основная статья: Термодинамические потенциалы.

Каноническое уравнение представляет собой выражение для одного из термодинамических потенциалов (внутренней энергии, энтальпии, свободной энергии или потенциала Гиббса) через независимые переменные, относительно которых записывается его полный дифференциал.

  • (для внутренней энергии),
  • (для энтальпии),
  • (для энергии Гельмгольца),
  • (для потенциала Гиббса).

Каноническое уравнение, независимо от того, в каком из этих четырех видов оно представлено, содержит полную информацию о термических и калорических свойствах термодинамической системы (предполагается, что известно и определение термодинамического потенциала, такое, как F = U − TS).

Примеры

  • Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона)
  • Уравнение Ван-дер-Ваальса (уравнение состояния реального газа)
  • Уравнение Дитеричи
  • Уравнение состояния Редлиха — Квонга
  • Уравнение состояния Барнера — Адлера
  • Уравнение состояния Суги — Лю
  • Уравнение состояния Бенедикта — Вебба — Рубина
  • Уравнение состояния Ли — Эрбара — Эдмистера

См. также

  • Термодинамическое равновесие
  • Закон соответственных состояний
  • Термодинамика, уравнение состояния, энтропия, потенциал взаимодействия (статьи, книги, лекции)

Литература

  • Базаров И.  П. Термодинамика. — М.: Высшая школа, 1991. — 376 с.
  • Базаров И. П. Заблуждения и ошибки в термодинамике. — Изд. 2-е, испр. — М.: Едиториал УРСС, 2003. — 120 с.
  • Квасников И. А. Термодинамика и статистическая физика. Т. 1: Теория равновесных систем: Термодинамика. Том 1. — Изд. 2-е, испр. и доп. — М.: УРСС, 2002. — 240 с.
  • Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.

1.1: Термодинамические переменные и уравнения состояния

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    398262
    • Серж Л. Смирнов и Джеймс Маккарти
    • Университет Западного Вашингтона

    Классическая термодинамика обеспечивает концептуальную основу, с помощью которой мы можем понять поведение молекулярных систем в биологических науках на количественном уровне. В этой главе вводятся некоторые понятия, относящиеся к свойствам системы и ее окружения, которые нам понадобятся для изучения классической термодинамики. Приложения к биологическим системам будут представлены в последующих главах. В этой главе мы сосредоточимся на том, как макроскопические свойства системы связаны и зависят от свойств составляющих ее атомов и молекул. В качестве примера мы обсудим уравнение идеального газа, диапазон его применимости и то, как его можно распространить на реальные газы или жидкости взаимодействующих молекул.

    Цели обучения
    • Построить точный словарь термодинамических определений, прежде чем применять их к биохимическим системам.
    • Понимать переменные состояния и то, как они математически связаны в уравнении состояния.
    • Уметь управлять уравнением состояния идеального газа.
    • Понять, как реальные газы отклоняются от идеальности и как реальные газы и жидкости можно моделировать с помощью вириального уравнения состояния, которое представляет собой выражение давления газа в виде полинома плотности.

    Основные определения

    Мы начнем обсуждение биохимической термодинамики с некоторых определений, которые позволят нам сделать общие утверждения о том, как энергия обменивается и преобразуется в различные формы.

    Система — это любая интересующая нас часть вселенной. Это может быть система Солнце-Земля-Луна, человеческое легкое, плодовая мушка, отдельная бактериальная клетка или лабораторный стакан на столешнице. Некоторые примеры систем показаны на рис. I.1.A: 9 .0051

    Рисунок I.1.A: Некоторые системы различной сложности включают систему солнце-земля-луна, легкое человека, плодовую мушку, отдельную бактериальную клетку или химический стакан

    Все остальное во Вселенной, которое не часть системы называется окружением . Система + окружение составляют вселенную .

    Мы можем разделить системы на 3 типа: открытые системы, закрытые системы или изолированные системы. Открытая система способна обмениваться с окружающей средой как веществом, так и теплом. А закрытая система не может обмениваться веществом с окружающей средой, но может обмениваться теплом с окружающей средой. Изолированная система не может обмениваться теплом или каким-либо веществом с окружающей средой. Эти три типа систем изображены на Рисунок I.1.B :

    Рисунок I.1.B: Открытая система может обмениваться веществом и теплом с окружающей средой. Замкнутая система не может обмениваться веществом с окружающей средой, но может обмениваться теплотой. Изолированная система не может обмениваться теплом или веществом с окружающей средой.

    Раздел науки под названием термодинамика интересуется отношениями между свойствами системы и тем, как свойства изменяются по мере изменения состояния системы. Свойство — это любой параметр системы, поддающийся математическому количественному определению. Некоторые свойства могут включать давление, температуру, плотность, показатель преломления и т.д.

    Мы можем различать два типа свойств: интенсивные и экстенсивные. Интенсивный свойств не зависит от измеряемой величины (количества вещества). Некоторые интенсивные свойства включают плотность, давление и температуру. С другой стороны, Обширные свойства зависят от измеряемой величины (суммы). Некоторыми экстенсивными свойствами являются масса, объем и число молей.

    Интенсивные свойства могут быть построены как соотношение между двумя экстенсивными свойствами. Например, плотность равна

    \[\text{density} = \frac{\text{mass}}{\text{volume}}\label{EQ:densitydef}\] 9{-3}\). В таблице I.1.i приведены некоторые распространенные единицы измерения давления.

    Таблица I.1.i: Некоторые распространенные единицы измерения давления

    1 Па = 1 Н·м -2
    1 бар = 100 кПа (10 5 Па)
    1 атм = 101,32 кПа
    1 торр (мм рт. ст.) = 1/760 атм

    Примечание: Энергия сама по себе (измеряется в джоулях или калориях) равна обширное свойство . Часто мы сообщаем энергии как молярное отношение в единицах Дж/моль или кал/моль, что является интенсивным свойством .

    Распространенным способом определения интенсивного свойства является определение молярной величины путем деления некоторой экстенсивной переменной на количество молей. Например, молярный объем определяется как:

    \[\bar{V} = \frac{V}{n}\label{EQ:molarV}\]

    Здесь \(\bf{n}\) — число молей, а \(\bf{\bar{V}}\) называется молярным объемом и является интенсивной величиной.

    Температура — еще один важный термодинамический параметр, который будет определяться разными способами в этом тексте. Сейчас мы определим температуру как меру движения атомов внутри системы. Это определение температуры подразумевает, что «термодинамическая» температура измеряется в градусах Кельвина, поскольку шкала Кельвина является шкалой абсолютной температуры. В пределе, когда Т=0 К (абсолютный нуль), движение атомов приближается к нулю. Мы можем преобразовать температуру в шкалах Кельвина и Цельсия, используя соотношение: 9{\circ}C) + 273,15\label{EQ:Temp}\]

    Осторожно

    Примечание. В термодинамических расчетах должны использоваться абсолютные температуры (в K).

    См. практические задачи 1 и 2.

    Термодинамические уравнения состояния

    Уравнение состояния представляет собой математическое выражение, полностью описывающее термодинамическое состояние системы в терминах набора физических свойств. Самый известный пример — закон идеального газа:

    \[PV=nRT\label{EQ:idealgas}\]

    или, вводя молярный объем (уравнение \ref{EQ:molarV}):

    \[P\bar{V} = RT\]

    где \(\bf{P}\) – давление, \ (\bf{V}\) — объем, \(\bf{n}\) — количество молей, \(\bf{T}\) — температура. \(\bf{R}\) – газовая постоянная, приведенная в Таблице I.1.ii . Уравнение \ref{EQ:idealgas} известно как уравнение состояния идеального газа . Уравнение состояния идеального газа (PV=nRT) позволяет нам увидеть, как связаны свойства идеального газа.

    Таблица I.1.ii: Общепринятые единицы измерения идеальной газовой постоянной R. 1 л атм = 101,34 Дж

    Уравнение состояния идеального газа будет для нас полезной моделью для работы при выводе термодинамических соотношений, поскольку оно интуитивно понятно и алгебраически легко манипулировать. Здесь уместно сделать несколько замечаний относительно уравнения состояния идеального газа:

    1. Уравнение состояния идеального газа можно вывести из первых принципов (кинетической теории газов).
    2. При достаточно высокой температуре и низком давлении все газы соответствуют закону идеального газа.
    3. Допущения, сделанные в законе идеального газа:
      • Молекулы газа сами по себе не занимают объема.
      • Между молекулами газа нет ни притяжения, ни отталкивания.
      • Все столкновения абсолютно упругие.

    См. практические задачи 3 и 4.

    Из-за этих предположений мы ожидаем, что все реальных газов будут отличаться от идеального поведения. Для количественной оценки этого мы определяем коэффициент сжимаемости , Z, как

    \[Z=\frac{P\bar{V}}{RT}\label{EQ:compress}\]

    Уведомление из уравнения \ref{ EQ:idealgas}, что для идеального газа \(Z=1.\) Все реальные газы будут отклоняться от этого идеального поведения. На рисунке I.1.C показан коэффициент сжимаемости \(Z\) как функция давления для N 2 газ при разных температурах. Идеальный идеальный газ имел бы \(Z=1\) для всех давлений и температур. Для газа N 2 мы видим, что при достаточно низком давлении \(Z \rightarrow 1\) и при более высокой температуре (фиолетовая кривая) газ ведет себя скорее как идеальный газ (пунктирная линия).

    Рисунок I. 1.C: Коэффициент сжимаемости газообразного азота в зависимости от давления при различных температурах. Предел идеального газа показан пунктирной линией при Z=1.

    Чтобы вывести уравнение состояния неидеального газа, мы можем рассмотреть разложение в ряд коэффициента сжимаемости \(\bf{Z}\) по степеням обратного молярного объема, \(\bf{ 1/\бар{V}}\): 93}+…\label{EQ:Virial}\]

    Уравнение \ref{EQ:Virial} называется вириальным уравнением состояния , а \(\bf{B_2}\) называется уравнением второй вириальный коэффициент , \(\bf{B_3}\) называется третьим вириальным коэффициентом и т.д…. Вириальные коэффициенты (\(B_2\), \(B_3\),…) обычно соответствуют экспериментальным данным и зависят от температуры. Обратите внимание, что для идеального идеального газа второй и более высокие вириальные коэффициенты равны нулю. Вириальное уравнение состояния хорошо работает для описания любого газа, но имеет недостаток, заключающийся в необходимости использования вириальных коэффициентов для подгонки к экспериментальным данным.

    Для газов с небольшими отклонениями от поведения идеального газа мы можем сократить уравнение \ref{EQ:Virial}, чтобы включить только второй вириальный коэффициент:

    \[Z \ приблизительно 1 + \frac{B_2}{\bar{ V}}\label{EQ:Virial2}\]

    Второй вирусный коэффициент, \(\bf{B_2}\) , связан с взаимодействиями между атомами, описываемыми функцией потенциальной энергии \(U(r)\ ), где \(r\) — расстояние между парами атомов. Для разбавленной системы неполярных молекул соотношение между вторым вириальным коэффициентом и потенциальной энергией равно 92 dr\label{EQ:Virial3}\]

    , где \(\bf{N_A}\) — число Авогадро, \(\bf{k_B}\) — постоянная Больцмана, а \(\bf {T}\) — температура. В большинстве случаев мы не можем аналитически решить интеграл в уравнении \ref{EQ:Virial3}. Обратите внимание, что в отсутствие взаимодействий \(U(r)=0\), то из уравнения \ref{EQ:Virial3}, \(B_2=0\) и газ ведет себя как идеальный газ, как мы и ожидали для невзаимодействующие молекулы газа.

    См. практические задачи 5-7.

    Примеры

    Пример \(\PageIndex{1}\)

    Классифицируйте каждую из следующих систем как открытую, закрытую или изолированную. (а) Эритроцит, (б) газ в поршне без клапанов, (в) кипящая вода в чайнике на плите, (г) Закрытый термос с горячим кофе (примерно).

    Раствор

    (а) открытый; (б) закрытый; (в) открытый; (d) изолированные

    Пример \(\PageIndex{2}\)

    Классифицируйте каждое из следующих свойств как интенсивное или экстенсивное: (a) молярная масса, (b) давление, (c) температура, (d) масса

    Раствор

    (а) интенсивный; б) интенсивный; в) интенсивный; (d) обширный

    Пример \(\PageIndex{3}\)

    Домашний пивовар из Беллингема собирает количество газа, выделяющегося в процессе ферментации. Позже пивовар измеряет объем газа 0,64 л при холодной температуре 12,3 ° C и 1 атм. Предполагая поведение идеального газа, каков был объем газа при температуре брожения 37,0 °С и 1 атм.

    Решение

    Мы используем уравнение идеального газа: PV=nRT, чтобы установить соотношение между низкотемпературной и высокотемпературной системой:

    \[ \frac{V_1}{V_2} = \frac{T_1}{T_2} \]

    \[ \frac{0,64 \ \text{L}}{V_2} = \frac{285,45 \\text{ K}}{310.15 \ \text{K}} \]

    \[ V_2 = 0,695 \ \text{L} \]

    Практические задачи

    Задача 1. Классифицируйте каждую из следующих систем как открытую, закрытые или изолированные. (а) идеально изолированный водонагреватель, (б) стеклянный термометр (в) вселенная (г) варка супа на плите (д) земля (е) автомобиль (ж) герметичная реакционная колба

    Задача 2. Классифицируйте каждое из следующих свойств как интенсивное или экстенсивное: (а) плотность, (б) сила, (в) молярный объем, (г) теплота.

    Задача 3. При каком из следующих наборов условий вы ожидаете, что реальный газ будет адекватно описан моделью идеального газа (a) низкое давление и низкая температура; (б) низкое давление и высокая температура, (в) высокое давление и высокая температура и (г) высокое давление и низкая температура.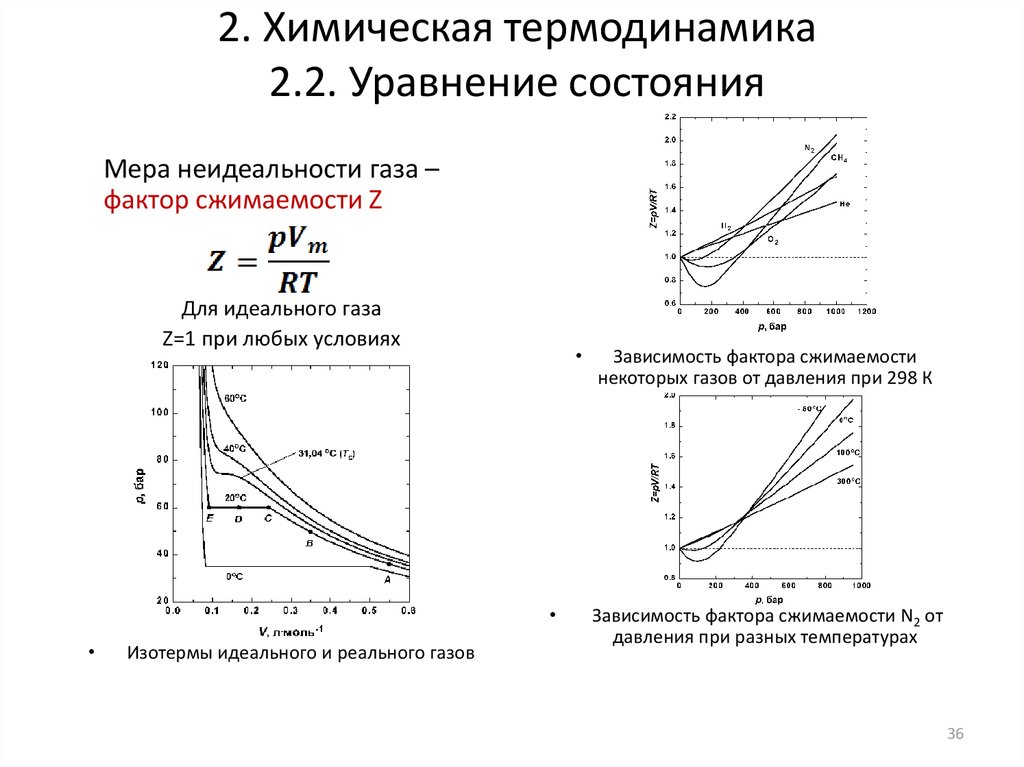

    Задача 4. Идеальный газ в поршне изначально находится при давлении 118,0 атм и температуре 85 °C. При расширении поршня его конечный объем, давление и температура составляли 3,5 л, 1,0 атм и 45 °С соответственно. Каков был первоначальный объем газа?

    Задача 5. При 300 К второй вириальный коэффициент (B 2 ) газа CO 2 равен -120,5 см 3 моль – 1 газ , второй вириальный коэффициент равен -41,9 см 3 моль -1 , а для газа N 2 второй вириальный коэффициент равен -4,2 см 3 моль – 1 . Расположите эти газы от наиболее идеального газа до наименее идеального газа при данной температуре? Объясните свои рассуждения.

    Задача 6. Рассчитайте давление метана при 398,15 К, если молярный объем равен 0,2 л моль -1 , учитывая, что второй вириальный коэффициент (B 2 ) метана равен -0,0163 л моль -1 . Сравните свои результаты с результатами, полученными с помощью уравнения идеального газа. Метан более или менее сжимаем, чем идеальный газ при этой температуре? (Предположим, что всеми остальными вириальными коэффициентами более высокого порядка можно пренебречь).

    Задача 7. Температура Бойля – это температура, при которой коэффициент B 2 равен нулю. Следовательно, реальный газ при этой температуре ведет себя как идеальный газ. (a) дать физическую интерпретацию этого поведения. (b) Рассчитайте температуру Бойля для газа, второй вириальный коэффициент которого имеет следующую форму: \(B_2 = a -\frac{b}{T}\) с экспериментально определенным вторым вириальным коэффициентом, измеренным при следующих температурах:

    Второй вириальный коэффициент (B 2 ) (л моль -1 ) Температура (К)
    -0,0237 292,95
    -0,0231 296,15
    -0,0228 298,15
    -0,0218 303,15
    -0,0201 313. 15
    -0,0185 323,15
    -0,0117 373,15
    -0,0065 423,15

    \(%А полимер в разбавленном растворе\)

    \(%Ленгмюровская пленка\)

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Серж Л. Смирнов и Джеймс Маккарти
        Лицензия
        CC BY-NC-SA
        Версия лицензии
        4,0
        Показать страницу TOC
        № на стр.
      2. Теги
          На этой странице нет тегов.

      Явление энтальпийно-энтропийной компенсации. Ограничения на использование некоторых основных термодинамических уравнений

      Обзор

      . 2018;19(11):1088-1091.

      дои: 10.2174/1389203719666180521092615.

      Сергей Храпунов 1

      принадлежность

      • 1 Кафедра биохимии, Медицинский колледж Альберта Эйнштейна, 1300 Morris Park Avenue, Bronx, NY 10461, США.
      • PMID: 29779476
      • PMCID: PMC6142176
      • DOI: 10. 2174/1389203719666180521092615

      Бесплатная статья ЧВК

      Отзыв

      Сергей Храпунов. Curr Protein Pept Sci. 2018.

      Бесплатная статья ЧВК

      . 2018;19(11):1088-1091.

      дои: 10.2174/1389203719666180521092615.

      Автор

      Сергей Храпунов 1

      принадлежность

      • 1 Кафедра биохимии, Медицинский колледж Альберта Эйнштейна, 1300 Morris Park Avenue, Bronx, NY 10461, США.
      • PMID: 29779476
      • PMCID: PMC6142176
      • DOI: 10. 2174/1389203719666180521092615

      Абстрактный

      Термодинамический анализ белков, комплексов белок-лиганд и белок-нуклеиновая кислота включает явление компенсации энтропии-энтальпии (S-H). Мы рассмотрели вопрос, является ли наблюдаемая компенсация искусственной или отражает что-то большее, чем известные законы статистической термодинамики (так называемая внетермодинамическая компенсация). Мы показали, что энтальпийно-энтропийная компенсация (ЭЭК) в основном является тривиальным следствием основных термодинамических законов и нет никаких экспериментальных доказательств существования внетермодинамической компенсации. В большинстве случаев ЭЭК, полученная в экспериментах посредством зависимости энтальпии (ΔH) и энтропии (TΔS) друг от друга, не имеет смысла из-за больших коррелированных ошибок в ΔH и TΔS, если не будут приняты специальные меры для минимизации, количественной оценки и распространения этих ошибок. Уравнение Вант-Гоффа можно использовать для расчета энтропии в ограниченных случаях, когда энтальпия измеряется в независимых экспериментах. Уравнение Эйринга ни в коем случае нельзя использовать для расчета энтропии, и оно должно быть исключено из научного использования. Оба уравнения, Вант-Гоффа и Эйринга, нельзя использовать для одновременного расчета значений энтальпии и энтропии с использованием одного набора данных. Все данные, полученные таким образом, следует признать ошибочными.

      Ключевые слова: Энтропийно-энтальпийная компенсация; доказательства; белковая термодинамика; термодинамические уравнения..

      Авторские права © Bentham Science Publishers; По любым вопросам пишите по адресу [email protected].

      Заявление о конфликте интересов

      Похожие статьи

      • Энтропийно-энтальпийная компенсация: факт или артефакт?

        Шарп К. Шарп К. Белковая наука. 2001 март; 10 (3): 661-7. doi: 10.1110/ps.37801. Белковая наука. 2001. PMID: 11344335 Бесплатная статья ЧВК.

      • Влияние соотношения фаз на анализ Вант-Гоффа в обращенно-фазовой жидкостной хроматографии и независимая от соотношения фаз оценка энтальпии переноса.

        Честер Т.Л., Койм Дж.В. Честер Т.Л. и др. J Chromatogr A. 2003 27 июня; 1003 (1-2): 101-11. дои: 10.1016/s0021-9673(03)00846-х. Дж Хроматогр А. 2003. PMID: 12899299

      • Поиск количественной энтропийно-энтальпийной компенсации среди вариантов белков.

        Бизли Дж. Р., Дойл Д. Ф., Чен Л., Коэн Д. С., Файн Б. Р., Пилак Г. Дж. Бизли Дж. Р. и соавт. Белки. 2002 15 ноября; 49 (3): 398-402. doi: 10.1002/прот.10189. Белки. 2002. PMID: 12360529

      • Могут ли термодинамические измерения связывания с рецепторами дать информацию о сродстве и эффективности лекарств?

        Бореа П.А., Далпиаз А., Варани К., Гилли П., Гилли Г. Бореа П.А. и др. Биохим Фармакол. 1 декабря 2000 г .; 60 (11): 1549-56. doi: 10.1016/s0006-2952(00)00368-3. Биохим Фармакол. 2000. PMID: 11077036 Обзор.

      • Кинетическая и термодинамическая компенсация. Текущий и практический обзор продуктов питания.

        Гарвин А., Ибарз Р., Ибарз А. Гарвин А. и др. Фуд Рез Инт. 2017 июнь; 96: 132-153. doi: 10.1016/j.foodres.2017.03.004. Epub 2017 6 марта. Фуд Рез Инт. 2017. PMID: 28528093 Обзор.

      Посмотреть все похожие статьи

      Цитируется

      • Структурная характеристика и характеристика ITC связывания пептида с белком: термодинамические последствия ограничений циклизации, тематическое исследование лигандов фактора роста эндотелия сосудов.

        Гоше Ж.Ф., Рейль-Серусси М., Брусси С. Гоше Дж. Ф. и соавт. Химия. 2022, 26 августа; 28(48):e202200465. doi: 10.1002/chem.202200465. Epub 2022 7 июля. Химия. 2022. PMID: 35665969 Бесплатная статья ЧВК.

      • Характеристика микросостояний протонирования белка с использованием выборки методом Монте-Карло.

        Хания У, Мао Дж., Вэй Р.Дж., Стрелок М.Р. Хания У и др. J Phys Chem B. 7 апреля 2022 г.; 126 (13): 2476-2485. дои: 10.1021/acs.jpcb.2c00139. Epub 2022 28 марта. J Phys Chem B. 2022. PMID: 35344367

      • В поисках решения: изучение роли гидратации белка в гелеобразовании шелка.

        Laity PR, Holland C. Laity PR и др. Молекулы. 2022 16 января; 27 (2): 551. doi: 10,3390/молекулы27020551.

      Оставить комментарий