Термодинамика формула: Ошибка: 404 Материал не найден

формулы и основные законы с пояснениями

Физическая дисциплина «Термодинамика», имеющая дословный перевод с греческого как θέρμη — «тепло», δύναμις — «сила», занимается изучением общих характеристик макросистем и обращения энергии внутри них. Эту науку относят к феноменологическому типу, хотя опирается она на факты, полученные опытным путем.

Термодинамическая система, рассматриваемая в данном ракурсе, имеет конкретные характеристики, не применимые к единичным атомам и молекулам. К ним относят температуру, энергию, объем, концентрацию растворов, давление.

Определение таких параметров происходит по формулам термодинамики.

Источник: en.ppt-online.org

Основные формулы термодинамики

Особенностью термодинамики является то, что ее постулаты не касаются взаимодействия отдельных единиц (атомов, молекул), как в молекулярной физике. Предметом изучения предстают общие взаимопревращения энергии, образование теплоты, теплопередача и совершение работы.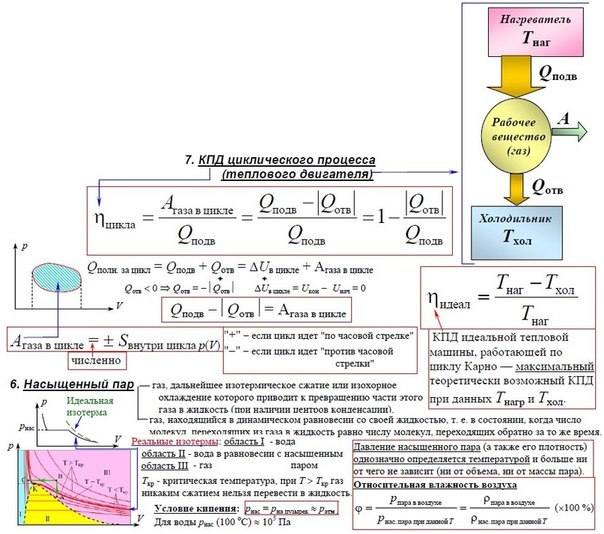

Исходя из этого, выделяют основные формулы термодинамики, к которым относятся:

1. Уравнение Менделеева-Клайперона: \(PV=(m/M)*RT\). Его смысл — в изменениях трех входящих величин, которые направлены на характеристику состояния идеального газа.
2. Количество вещества, обозначаемое буквой \(ν\). \(\nu=N/NA=m/\mu\)

   Величина, выражающая, сколько одинаковых структурных компонентов (единиц) находится в веществе.

3. Закон Дальтона: давление смеси газов на стенку сосуда равно сумме давлений каждого входящего в смесь элемента: \(p=p1+p2+…pn.\)
4. Главное уравнение МКТ (молекулярно-кинетической теории): \(p=2n/3<\varepsilon>n=N/V\). Выражает математическое соотношение таких параметров, как давление газа и микропараметров: массы молекул, их скорости движения, концентрации.
5. Средняя кинетическая энергия поступательного движения молекулы газа. Для обозначения применяется \(E_k\),  выражается через формулу: \(E_k=E_{моля}/NA=3/2\ast RT/NA\). Ее мерой является абсолютная температура идеального газа, поскольку потенциальная энергия (вследствие взаимодействия молекул друг с другом) равна нулю. Зная, что R/N_A=k, получается формула: \(E_k=3/2\ast kT\).
6. Давление идеального газа прямо пропорционально концентрации и его температуре: \(P=nkT.\)
7. Скорость молекул определяется по формулам:
   \(V=\surd(2kT/m_o)=\surd(2RT/\mu)\) — наиболее вероятная;
   \(<V>=\surd(8kT/\pi m_o)=\surd(8RT/\pi\mu)\) — среднеарифметическая;
   \(<Vкв>\surd(3kT/m_o)=\surd(3RT/\mu)\) — средняя квадратичная.
8. Сумма кинетических энергий всех молекул определяет внутреннюю энергию всего идеального газа. Математически выражение выглядит так: \(U=i/2\ast(m/\mu)\ast RT.\)
9. Формула для определения работы, которую совершает идеальный газ при расширении:\( A=P(V_2-V_1).\)
10. Формула первого закона термодинамики: \(Q=\Delta U+A.\)
11. Для определения удельной теплоемкости вещества применяется математическое выражение: \(С=\Delta Q/mdT. \)
12. Кроме удельной теплоемкости, существует понятие молярной теплоемкости. Для ее определения применяется формула: \(C=c\mu\). Для изохорного процесса правильная формула принимает вид: \(C_v=1/2\ast R\), для изобарного: \(C_p=((i+2)/2)\ast R\).

Первое начало термодинамики

Согласно первому закону термодинамики, \(Q\) (количество внутренней теплоты), которое получил газ извне, расходуется на совершение работы \(А\) и изменение внутренней энергии \(U\). Формула закона: \(Q=\Delta U+A\).

Источник: obrazovaka.ru

На практике газ может быть нагрет либо охлажден. Однако в данном случае рассматривается изотермический процесс, в котором один из характеризующих параметров остается неизменным.

Если процесс изотермичен, в химии включается закон Бойля-Мариота.

В нем говорится, что давление газа соотносится к изначальному объему, при стабильной температуре, обратно пропорционально.

\(Q=A\)

Когда процесс происходит при неизменном объеме, говорят об изохорности. Здесь вступает в действие закон Шарля. В обозначенных условиях то тепло, которое поступило к газу, расходуется на изменение внутренней энергии. Другими словами, \(P\) пропорционально \(T\).

\(Q=\Delta U\)

Протекание процессов в идеальном газе при неизменном давлении носит характер изобарного. Здесь действует закон Гей-Люссака, который выражается уравнением:

\(Q=\Delta U=p\Delta V\)

Полная формулировка закона гласит: полученное тепло при изобарном процессе расходуется на совершение работы газом, а также изменяет его внутреннюю энергию.

Часть процессов происходят изолированно от внешней среды. Газ не получает дополнительной энергии. Такая ситуация носит название адиабатной и математически записывается: \(Q=0\). Работа \(А\) в таком случае выражается: \(A=-\Delta U. \)

Уравнение идеального газа в термодинамике

Молекулы идеального газа постоянно движутся. От того насколько велика скорость их движения, зависит общее состояние газа, а также величина его воздействия, например, на стенки сосуда. Поэтому одним из основных уравнений термодинамики является Клайперона-Менделеева:

\(PV=(m/M)\ast RT\)

В уравнении \(m\) — единица массы газа, \(M\) — его молекулярная масса, \(R\) — универсальная величина, называемая газовой постоянной. Ее значение = 8,3144598. Измеряется в Дж/(моль*кг).

В основе термодинамики лежат и другие газовые постоянные, например, число Авогадро, постоянная Больцмана. Таким образом, \(R=kNA.\)

Из уравнения Клайперона-Менделеева можно также вычислить массу. Она будет равна произведению плотности на объем: \(m=\rho V\).

Основное уравнение молекулярно-кинетической теории (МКТ)

Решение части задач зависит от знания особенностей взаимосвязи между давлением газа и характеристикой кинетической энергии его молекул.

Математическое выражение такой зависимости носит название основного уравнения МКТ:

\(p=2/3\ast nE\)

В данном выражении кинетическая энергия обозначена буквой \(Е\), а концентрация молекул — \(n\). Каждую из этих величин физики можно найти исходя из соответствующих формул, после чего уравнение для молекулярно-кинетической теории (МКТ) приобретает вид:

\(p=nkT\)

Источник: encrypted-tbn0.gstatic.com

Формула теплоемкости и главная формула КПД в термодинамике

Когда теплообмен проявляется передачей телу определенного количества теплоты, его энергия, как и температура, меняются.

То количество теплоты, обозначаемое \(Q\), которое понадобится для того, чтобы 1 кг определенного вещества нагреется на 1 К, носит определение теплоемкости вещества и обозначается с.

Математическое выражение относительно переданного количества теплоты выглядит формулой:

\(Q=cm(t_2-t_1)=cm\Delta t\)

Измеряется величина в Дж/(кг∙К).

При t2〉t1, количество теплоты со знаком плюс, следовательно, вещество нагревается. Если наоборот, то Q — со знаком минус, и вещество остывает.

В физике, характеризуя свойства вещества, говорят о его теплоемкости. Это имеет значение, например, при выборе стройматериалов или сырья для изготовления нагревательных приборов. Теплоемкость равна произведению массы на удельную теплоемкость данного тела:

\(C=cm\)

Учитывая, что в величине теплоемкости уже отражена масса, то сокращенная формула для определения \(Q\) выглядит так:

 \(Q=C(t_2-t_1)\)

С другой стороны, то количество теплоты, которое отдает источник, можно высчитать по формуле: 

\(Q=Pt.\)

В выражении буквой \(P\) обозначается мощность нагревателя, а \(t\) — время их контакта.

Конструкция, состоящая из нагревателя, тела-реципиента теплоты и охладителя, носит название тепловой машины. В качестве примера рассматривается двигатель внутреннего сгорания. Как и любой механизм, она имеет такую характеристику, как КПД — коэффициент полезного действия.

Для его расчета применяется формула:

\(\eta=(Q_н-Q_x)/Q_н\)

Внутренняя энергия одноатомного и двухатомного идеального газа

Характерной особенностью идеального газа является отсутствие у его составляющих частей потенциальной энергии. Вся внутренняя энергия — это сумма кинетических энергий всех молекул. Она является величиной, прямо пропорциональной температуре идеального газа:

\(mw2/2=\alpha T\)

В этом уравнении:

\(\alpha T=3R\mu/2N\mu\)

Исходя из приведенных формул, величина кинетической энергии поступательного движения идеального газа должна определяться исходя из выражения:

\(mv2/2=(3R\mu/2N\mu)\ast T\)

Поступательное движение характеризуется тремя степенями свободы. На каждую из них приходится одна треть общей кинетической энергии.

Источник: cf.ppt-online.org

Двух- и более атомные молекулы газа характеризуются степенями свободы, касающимися вращательного движения.

Если обозначить число молекул в одном киломоле за \(Nμ\), то внутренняя энергия идеального газа будет измеряться по формуле:

\(U\mu=1/2(R\mu Ti)\)

В формуле \(i\) — число степеней свобод.

Если газ одноатомный, \(i=3\), двуатомный — 5, трех- и более — 6.

Источник: uslide.ru

Задачи на термодинамику характеризуют распространенные физические процессы, поэтому часть включаются в программы экзаменов. Если для их решения не хватает времени, можно обратиться за помощью в Феникс.Хелп. На профильном сайте вам помогут справиться с любой, даже запутанной задачей, экономя ваши время и силы.

Работа в термодинамике | Физика

Работа в механике и термодинамике. В механике работа определяется как произведение модулей силы и перемещения, умноженное на косинус угла между ними. Работа совершается при действии силы на движущееся тело и равна изменению кинетической энергии тела.

В термодинамике движение тела как целого не рассматривается и речь идет о перемещении частей макроскопического тела друг относительно друга. В результате меняется объем тела, а его скорость остается равной нулю. Следовательно, работа в термодинамике, определяемая так же, как и в механике, равна изменению не кинетической энергии тела, а его внутренней энергии.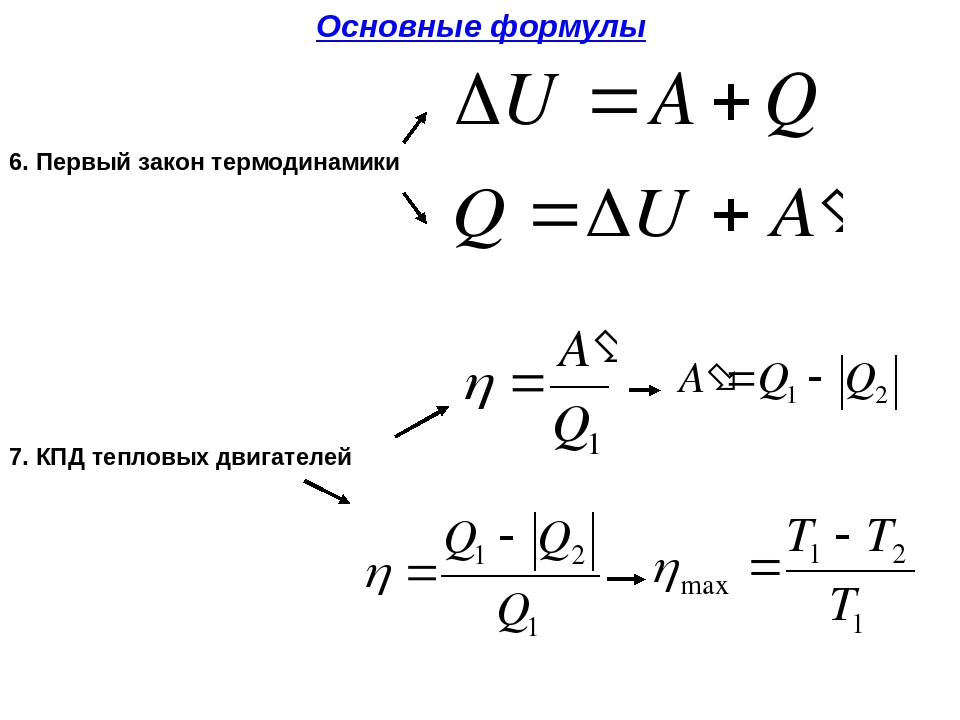

Изменение внутренней энергии при совершении работы. Почему при сжатии или расширении меняется внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?

Причина изменения температуры в процессе сжатия газа состоит в следующем: при упругих соударениях молекул с движущимся поршнем их кинетическая энергия изменяется. При движении навстречу молекулам поршень передает им во время столкновений часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги и сообщающему мячу скорость, значительно большую той, которой он обладал до удара.

Если газ, напротив, расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует футболист, для того чтобы уменьшить скорость летящего мяча или остановить его; нога футболиста движется от мяча, как бы уступая ему дорогу.

При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.

Вычисление работы. Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем (рис. 39). Проще всего вначале вычислить не работу силы F, действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя на поршень с силой F’. Согласно третьему закону Ньютона F’ = –F.

Модуль силы, действующей со стороны газа на поршень, равен: F’ = pS, где p – давление газа, а S – площадь поршня. Пусть газ расширяется и поршень смещается в направлении силы F’ на малое расстояние ∆h = h₂ – h₁. Если перемещение мало, то давление газа можно считать постоянным.

Работа газа равна:

A’ = F’∆h = pS(h₂ – h₁) = p(Sh₂ – Sh₁).     (4.2)

Эту работу можно выразить через изменение объема газа. Начальный объем V₁ = Sh₁, а конечный V₂ = Sh₂. Поэтому

A’ = p(V₂ – V₁) = p∆V,      (4.3)

где ∆V = V₂ – V₁ — изменение объема газа.

При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают. В процессе расширения газ передает энергию окружающим телам.

Если газ сжимается, то формула (4.3) для работы газа остается справедливой. Но теперь V₂1 и поэтому A’

Работа A, совершаемая внешними телами над газом, отличается от работы газа A’ только знаком: A = –A’, так как сила F, действующая на газ, направлена против силы F’, а перемещение остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:

A = –A’ = –p∆V     (4.4)

Знак минус указывает, что при сжатии газа, когда ∆V = V₂ – V₁ 0: при сжатии газа направления силы и перемещения совпадают. Совершая над газом положительную работу, внешние тела передают ему энергию. При расширении газа, наоборот, работа внешних тел отрицательна (A 2 – V₁ > 0. Теперь направления силы и перемещения противоположны.

Выражения (4.3) и (4.4) справедливы не только при сжатии или расширении газа в цилиндре, но и при малом изменении объема любой системы. Если процесс изобарный (p = const), то эти формулы можно применять и для больших изменений объема.

Геометрическое истолкование работы. Работе A’ газа для случая постоянного давления можно дать простое геометрическое истолкование.

Построим график зависимости давления газа от объема (рис. 41) . Здесь площадь прямоугольника abcd, ограниченная графиком p₁ = const, осью V и отрезками ab и cd, равными давлению газа, численно равна работе (4.3).

В общем случае при произвольном изменении объема газа давление не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (рис. 42). В этом случае для вычисления работы нужно разделить общее изменение объема на малые части, вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости p от V, осью V и отрезками ab и cd, равными давлениям p1, p2 в начальном и конечном состояниях.

1. От каких физических величин зависит внутренняя энергия тела? 2. Приведите примеры превращения механической энергии во внутреннюю и обратно в темнике и быту. 3. Чему равна внутренняя энергия идеального одноатомного газа? 4. Моль какого газа – водорода или гелия – имеет большую внутреннюю энергию при одинаковой температуре газов? 5. Почему газ при сжатии нагревается? 6. Чему равна работа, совершаемая внешними силами при сжатии и расширении тел?

Первый закон термодинамики – материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1).

Рис. 1.

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

(1)

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу .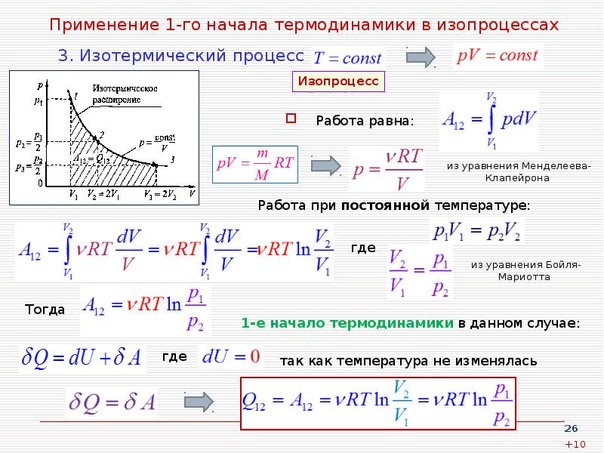 Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 \right )’ alt=’\left ( {A}’ > 0 \right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

(2)

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

(3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно.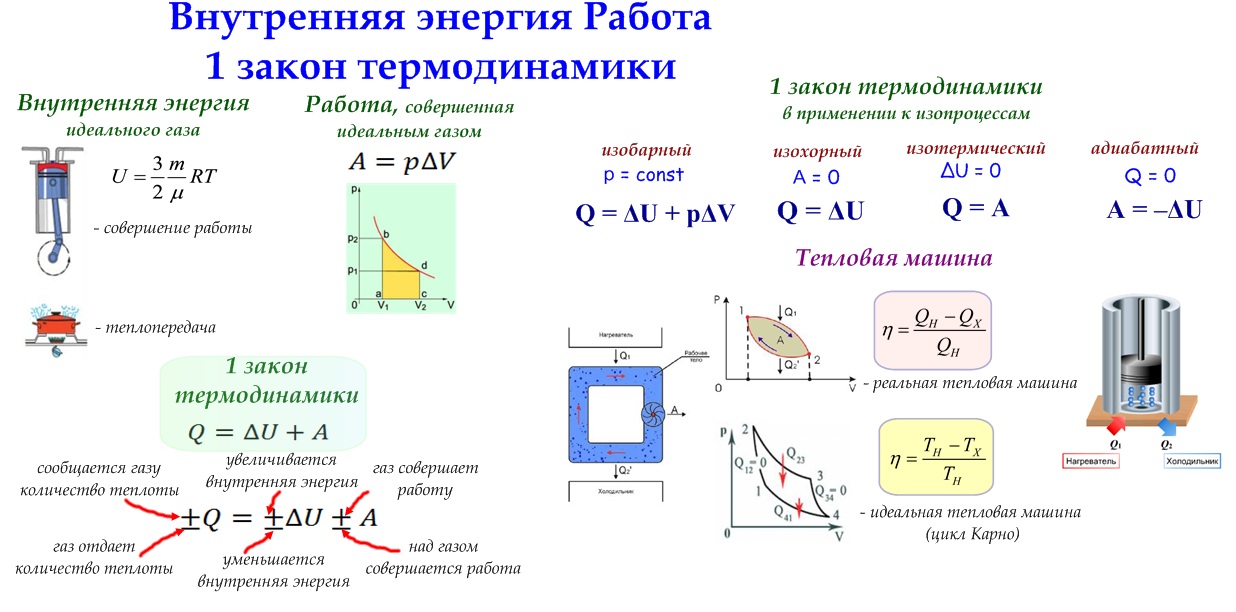 Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Работа в термодинамике | ЕГЭ по физике

Работа в термодинамике

В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.

Рассмотрим работу газа при изобарическом расширении.

Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:

$A’=F’∆h=pS∆h=p∆V$

Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V

Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:

$A=-A’=-p∆V$

Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.

На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.

Первый закон термодинамики

Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.

Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).

Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.

Первый закон термодинамики формулируется так:

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

$∆U=A+Q$

где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.

Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.

При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.

Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:

$Q=∆U+A’$

где $А’$ — работа, совершаемая системой ($А’=-А$).

Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.

Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.

Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.

Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.

Применение первого закона термодинамики к различным процессам

Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.

Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.

Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.

Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.

При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,

$∆U=Q$

т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.

Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q

Изотермический процесс графически изображается изотермой.

Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.

Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:

$Q=A’$

При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q

Изобарный процесс на термодинамической диаграмме изображается изобарой.

Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.

Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.

При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:

$Q=∆U+A’$

Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).

Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.

Адиабатический процесс

Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).

Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.

Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе

$∆U=A$

где $А$ — работа внешних сил.

При адиабатном расширении газа $А

Следовательно,

$∆U={i}/{2}·{m}/{M}R∆T

что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.

На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.

Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).

Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.

Принцип действия тепловых двигателей

Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.

Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.

Таким образом, основными элементами любого теплового двигателя являются:

1. рабочее тело (газ или пар), совершающее работу;
2. нагреватель, сообщающий энергию рабочему телу;
3. холодильник, поглощающий часть энергии от рабочего тела.

Коэффициент полезного действия теплового двигателя

Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:

$A’=|Q_1|-|Q_2|$

где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.

Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:

$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$

Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η

КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 – T_2=0$ двигатель не может работать.

Цикл Карно

Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.

Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».

Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.

Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.

Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.

На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:

$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:

$A_{23}=-∆U_{23}$

Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2

$A_{34}=Q_2,$

Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.

Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:

$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$

Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.

Первый закон термодинамики

На рисунке 3.9.1 условно проиллюстрированы энергетические потоки между выделенной термодинамической системой и окружающими телами. В случае, если тепловой поток направлен к термодинамической системе, то некоторая величина Q>0, если же система совершает положительную работу над окружающими ее объектами, то справедливо неравенство A>0.

Рисунок 3.9.1. Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Состояние системы меняется, когда происходит процесс ее обмена теплом с окружающими объектами, и она совершает положительную или отрицательную работу. Изменяются макроскопические параметры системы, такие как температура, объем и давление. По причине того, что внутренняя энергия U всецело определяется макроскопическими параметрами, которые характеризуют состояние системы, процессы совершения работы и теплообмена провоцируют изменения внутренней энергии данной системы ΔU.

Определение 1-го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

∆U=Q-A.

Определение 1

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.

Формула первого закона термодинамики, зачастую записывается в ином виде: 

Q=∆U+A.

Определение 2

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая ΔU своей внутренней энергии.

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

Определение 3

В изохорном процессе, то есть в условиях неизменного объема (V=const), газ не совершает работы, A=0.

В этом случае справедливой будет формула внутренней энергии газа:

Q=∆U=U(T2)-U(T1).

В данном выражении U(T1) и U(T2) представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло (Q>0), чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам (Q<0).

Определение 4

В изобарном процессе, предполагающем постоянность значения давления (p=const), работа, совершаемая газом, выражается в виде соотношения:

A=p(V2-V1)=p∆V.

Первый закон термодинамики для изобарного процесса дает: 

Q=U(T2)-U(T1)+p(V2-V1)=∆U+p∆V.

При изобарном расширении Q>0 тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии Q<0 тепло переходит внешним телам. В таком случае A<0. При изобарном сжатии уменьшаются температура газа T2<T1 и значение внутренней энергии ΔU<0.

Определение 5

В изотермическом процессе температура газа не меняет своей величины, следовательно, не изменяется и внутренняя энергия газа, ΔU=0.

Первый закон термодинамики для изотермического процесса выражается соотношением 

Q=A

Теплота Q, приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло.

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

Определение 6

Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Определение 7

Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими.

Рисунок 3.9.2. Модель адиабатического процесса.

Определение 8

В адиабатическом процессе Q=0. По данной причине первый закон термодинамики принимает вид: 

A=–ΔU.

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

Определение 9

Расширение или сжатие газа на плоскости p, V проиллюстрирована кривой, называемой адиабатой.

В процессе адиабатического расширения газом совершается положительная работа A>0, что является причиной понижения значения внутренней энергии ΔU<0. Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. 3.9.3).

Рисунок 3.9.3. Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.

В условиях координат (p, V) выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид: 

pVγ=const.

Данное выражение, в котором γ=CpCV – показатель адиабаты, Cp и CV – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом, называется уравнением Пуассона. В условиях одноатомного газа γ=53=1,67, двухатомного γ=75=1,4, многоатомного γ=1,33.

Работа газа в адиабатическом процессе выражается через температуры начального T1 и конечного T2 состояний и принимает вид: 

A=CV(T2-T1)

Адиабатический процесс относится к изопроцессам.

В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу ΔQT. Так как на каждом участке адиабатического процесса ΔQ=0, энтропия в нем не претерпевает изменений.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

Пример 1

Примером неквазистатического процесса, в котором промежуточные состояния не находятся в состоянии равновесия, служит расширение газа в пустоту. На рисунке 3.9.3 иллюстрируется жесткая адиабатическая оболочка, состоящая из двух разделенных вентилем K сообщающихся емкостей. В изначальном состоянии газом заполнен один из сосудов, в это же время во втором находится лишь вакуум. Открытие вентиля запускает процесс расширения газа. Он заполняет оба сосуда, и устанавливается новое равновесное состояние.

В таком процессе Q=0, по той причине, что исключен теплообмен с окружающими телами, и A=0, так как оболочка недеформируема. Первый закон термодинамики позволяет сказать, что ΔU=0, то есть внутренняя энергия газа не претерпела никаких изменений. Так как внутренняя энергия идеального газа зависит лишь от температуры, температура газа в начальном и конечном состояниях одинакова. Изображающие эти состояния точки на плоскости (p, V) лежат на одной изотерме. Все промежуточные состояния газа не являются равновесными и не могут быть изображены на диаграмме.

Пример 2

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.

Рисунок 3.9.4. Расширение газа в пустоту.

Открытое образование – Общая физика: механика, термодинамика и основы кинетической теории

• 12 weeks
• from 5 to 6 hours per week
• 3 credit points

Курс общей физики является базовой общенаучной дисциплиной в техническом образовании. Предлагаемый курс лекций включает основные темы разделов «Механика, термодинамика и основы кинетической теории», необходимые при изучении специальных дисциплин студентами инженерных направлений. В первой части курса обсуждаются основные физические законы, явления и понятия классической механики, во второй – рассматриваются основные вопросы молекулярно-кинетической теории вещества и термодинамики.

About

Онлайн-курс охватывает классический материал разделов общей физики: «Механика, термодинамика и основы молекулярно-кинетической теории». Курс читают преподаватели кафедры физики МИСиС и преподаватели других ВУЗов. Лекции содержат теоретический материал, демонстрации физических экспериментов, примеры решения задач, задания на понимание темы. Большое внимание уделено рассмотрению физического смысла и содержания основных понятий и законов. Показано применение изучаемых законов при решении конкретных задач. Полученные при изучении курса знания необходимы при освоении различных технических специальностей.

Format

В состав курса входят видео-лекции продолжительностью 6-13 минут, материалы для самостоятельного изучения пользователями, анимационные ролики с инфографикой, видеозаписи физических экспериментов. Разделы курса завершаются тестами на понимание материала (10-15 вопросов).

Information resources

1. Иродов И.Е. Механика. Основные законы / И.Е. Иродов. – Москва : Бином. Лаборатория знаний, 2014. – 309 с.
2. Иродов И.Е. Физика макросистем. Основные законы / И.Е. Иродов. – Москва : Бином. Лаборатория знаний, 2015. – 208 с.
3. Ландсберг Г.С. Элементарный учебник физики. В 3-х томах / Г.С. Ландсберг. – Москва : Физматлит, 2016.
4. Савельев И.В. Курс общей физики. В 3-х томах. Том 1. Механика. Молекулярная физика / И.В. Савельев. – Санкт-Петербург: Издательство «Лань», 2018. – 432 с.
5. Сивухин Д.В. Общий курс физики. В 5-и томах. Том 1. Механика / Д.В.Сивухин. – Москва : Физматлит, 2013. – 560 с.
6. Сивухин Д.В. Общий курс физики. В 5-и томах. Том 2. Термодинамика и молекулярная физика / Д.В. Сивухин – Москва : Физматлит, 2017. – 544 c.
7. Трофимова Т.И. Курс физики: учеб. пособие для вузов / Т.И. Трофимова. – Москва : Высшая школа, 2000. – 542 с.

Requirements

Для успешного освоения онлайн-курса слушателю желательно владеть основами математического анализа, знать основы теории вероятностей.

Course program

Курс состоит из 2 блоков, включающих 12 разделов, разбитых на уроки: 

Блок 1. Механика
Раздел 1. Кинематика 
Урок 1. Основные понятия кинематики. Механическое движение. Перемещение. Траектория
Урок 2. Скорость при равномерном движении материальной точки
Урок 3. Ускорение. Путь при равноускоренном движении
Урок 4. Движение в поле силы тяжести. Свободное падение. Движение тела, брошенного под углом к горизонту
Урок 5. Равномерное движение материальной точки по окружности
Урок 6. Равнопеременное движение материальной точки по окружности

Раздел 2. Динамика поступательного движения 
Урок 1. Динамика поступательного движения тел. Первый закон Ньютона. Масса 
Урок 2. Второй закон Ньютона. Понятие силы. Равнодействующая сил 
Урок 3. Третий закон Ньютона 
Урок 4. Фундаментальные взаимодействия 
Урок 5. Силы в механике. Центральные силы Гравитационное взаимодействие тел
Урок 6. Движение спутников
Урок 7. Силы упругости. Модуль Юнга. Модуль сдвига 
Урок 8. Силы трения. Силы сухого и вязкого трения 
Урок 9. Движение тела по наклонной плоскости 

Раздел 3. Динамика системы частиц 
Урок 1. Механическая система. Импульс системы. Внешние и внутренние силы. Импульс силы 
Урок 2. Центр масс системы. Уравнение движения центра масс 
Урок 3. Понятие замкнутой системы. Закон сохранения импульса 
Урок 4. Частные случаи сохранения импульса в незамкнутых системах
Урок 5. Примеры задач на закон сохранения импульса 
Урок 6. Момент импульса частицы. Момент силы. Закон сохранения момента импульса 
Урок 7. Закон сохранения момента импульса: 2-ой закон Кеплера 
Урок 8. Прибор Атвуда 

Раздел 4. Законы сохранения и превращения энергии при поступательном движении 
Урок 1. Работа постоянной и переменной силы. Понятие мощности 
Урок 2. Кинетическая энергия. Теорема об изменении кинетической энергии 
Урок 3. Консервативные и диссипативные силы. Потенциальная энергия 
Урок 4. Потенциальная энергия в поле тяготения 
Урок 5. Потенциальная энергия упругой деформации 
Урок 6. Закон сохранения и превращения энергии 
Урок 7. Соударения: абсолютно упругий и неупругий удар 
Урок 8. Абсолютно упругий нецентральный удар 
Урок 9. Неупругие соударения. Превращения энергии при неупругих соударениях 

Раздел 5. Динамика твердого тела 
Урок 1. Поступательное движение твердого тела. Центр масс твердого тела. Примеры определения положения центра масс. Центр тяжести 
Урок 2. Вращение твердого тела относительно неподвижной оси. Уравнение динамики вращательного движения твердого тела 
Урок 3. Момент инерции тела. Примеры вычисления моментов инерции тел. Теорема Гюйгенса- Штейнера 
Урок 4. Закон сохранения момента импульса 
Урок 5. Кинетическая энергия вращательного движения твердого тела. Работа внешних сил при вращении твердого тела 
Урок 6. Главные оси инерции твердого тела 
Урок 7. Главные оси инерции твердого тела 
Урок 8. Гироскоп. Гироскопический эффект и его применение 

Раздел 6. Движение в неинерциальных системах отсчета (НИСО). Элементы СТО 
Урок 1. Неинерциальные системы отсчета. Силы инерции при поступательном движении системы отсчета. Принцип эквивалентности сил инерции и сил тяготения 
Урок 2. Центробежные силы инерции. Проявление центробежной силы инерции на Земле (Часть 1) 
Урок 2. Центробежные силы инерции. Сила Кориолиса. Маятник Фуко (Часть 2)
Урок 3. Элементы специальной теории относительности (СТО). Относительность Галилея-Ньютона. Опыты Майкельсона-Морли. Постулаты Эйнштейна. Одновременность 
Урок 4. Преобразования Галилея и Лоренца. Некоторые следствия из преобразований Лоренца (парадокс близнецов, сокращение длины) 
Урок 5. Релятивистский импульс. Формула Эйнштейна 

Раздел 7. Механические колебания и волны 
Урок 1. Примеры колебательных движений в природе. Основные понятия – амплитуда, частота, период на примере колебаний груза на пружине 
Урок 2. Гармонические колебания. Уравнение движения гармонического осциллятора. Начальные условия. Энергия гармонического осциллятора. Связь гармонических колебаний с равномерным движением по окружности 
Урок 3. Сложение гармонических колебаний. Сложение колебаний одинакового направления (Часть 1) 
Урок 3. Сложение гармонических колебаний. Сложение взаимноперпендикулярных колебаний. Биения. Фигуры Лиссажу (Часть 2) 
Урок 4. Математический маятник. Период колебаний математического маятника. Физический маятник. Центр качания. Теорема Гюйгенса о центре качания 
Урок 5. Затухающие гармонические колебания. Логарифмический декремент затухания. Фазовая плоскость. Фазовые траектории маятника без затухания и с затуханием 
Урок 6. Вынужденные колебания. Резонанс. Резонансная частота.  Добротность 
Урок 7. Волновое движение. Характеристики волнового движения. Продольные и поперечные волны. Бегущая волна. Стоячая волна. Гармоники. Источники звука: колебания струны и столба воздуха 
Урок 8. Звук. Источники звука: колебания струны и столба воздуха. Эффект Доплера 

Блок 2. Основы молекулярно-кинетической теории и термодинамика 
Раздел 8. Молекулярно-кинетическая теория 
Урок 1. Основные положения МКТ и их опытные обоснования  
Урок 2. Масштабы физических величин в МКТ. Характерные значения масс молекул и атомов 
Урок 3. Основное уравнение МКТ. Макроскопическая система и ее параметры 
Урок 4. Уравнение состояния идеального газа. Закон Дальтона 
Урок 5. Изопроцессы в идеальном газа. Примеры изопроцессов в природе и технике 
Урок 6. Распределение молекул газа по скоростям: математическое введение. Основные понятия теории вероятности 
Урок 7. Распределение молекул газа по скоростям: распределение Максвелла 
Урок 8. Барометрическая формула. Распределение Больцмана. Влияние температуры, массы молекулы 
Урок 9. Газокинетические параметры. Средняя длина свободного пробега. Среднее время свободного пробега 

Раздел 9. Первое начало термодинамики 
Урок 1. Равновесные состояния и процессы 
Урок 2. Внутренняя энергия. Степени свободы молекул. Внутренняя энергия идеального газа 
Урок 3. Работа в термодинамике. Ее вычисление в различных процессах 
Урок 4. Первое начало и его применение к различным процессам. Количество теплоты. Первое начало и примеры его применения 
Урок 5. Адиабатный процесс. Равновесные и неравновесные адиабатные процессы. Уравнение Пуассона 
Урок 6. Теплоемкость газа. Теплоемкость в зависимости от процесса, теплоемкость смесей 
Урок 7. Политропические процессы. Вывод уравнения политропы, теплоемкость при политропических процессах 

Раздел 10. Второе и третье начала термодинамики 
Урок 1. Основной постулат второго начала термодинамики 
Урок 2. Круговые процессы. Тепловые машины 
Урок 3. Цикл Карно. КПД цикла Карно. Теоремы Карно. Термодинамическая температура 
Урок 4. Приведенная теплота. Энтропия как функция состояния. Неравенство Клаузиуса. Закон возрастания энтропии 
Урок 5. Энтропия в изопроцессах. Основное уравнение термодинамики 
Урок 6. Статистический смысл второго начала термодинамики. Формула Больцмана 
Урок 7. Границы применимости второго начала в классической термодинамике. Третье начало термодинамики 

Раздел 11. Реальные газы 
Урок 1. Отклонения от идеального газа. Газ Ван-дер-Ваальса как модель реального газа 
Урок 2. Изотермы газа Ван-дер-Ваальса. Уравнение состояния Ван-дер-Ваальса и его принципиальные особенности 
Урок 3. Критическая температура и критическое состояние. Критические параметры 
Урок 4. Стандартные и метастабильные состояния 
Урок 5. Фазовая диаграмма и границы раздела 
Урок 6. Фазовые переходы жидкость-газ, критическая температура. Перегретая жидкость и переохлаждённый пар 
Урок 7. Внутренняя энергия реального газа. Эффект Джоуля-Томсона 

Раздел 12. Конденсированное состояние вещества 
Урок 1. Жидкости. Переохлажденные жидкости, жидкие кристаллы. Межмолекулярные силы, Урок 2. Ближний порядок, средний и дальний порядок расположения атомов. Экспериментальные методы определения структуры 
Урок 3. Силы поверхностного натяжения. Границы раздела 
Урок 4. Пузыри и капли. Формула Лапласа. Смачивание. Капиллярные явления 
Урок 5. Фаза, фазовые диаграммы, правило фаз. Фазовые переходы 
Урок 6. Тройная точка. Уравнение Клапейрона-Клаузиуса 
 

Education results

В результате освоения курса студент:
– знает основные алгоритмы, принципы и критерии построения суждений при анализе информации для решения поставленной задачи;
– знает основные концепции и физические модели механики, молекулярной физики и термодинамики для описания  физических явлений;
– умеет применять алгоритмы решения типовых задач;
– умеет анализировать и описывать явления и процессы, используя физическую научную терминологию.

Formed competencies

ОПК-1: Способен решать задачи профессиональной деятельности, применяя методы моделирования, математического анализа, естественнонаучные и общеинженерные знания.

УК-1: Способен осуществлять поиск, критический анализ и синтез информации, применять системный подход для решения поставленных задач.

Первый закон термодинамики простыми словами

Определение первого закона термодинамики

Формула первого закона термодинамики

Процессы первого закона термодинамики

Первый закон термодинамики для изохорного процесса

Первый закон термодинамики для изобарного процесса

Применение первого закона термодинамики

Первый закон термодинамики, видео

Определение первого закона термодинамики

Простая формулировка первого закона термодинамики может звучать примерно так: изменение внутренней энергии той или иной системы возможно исключительно при внешнем воздействии. То есть другими словами, чтобы в системе произошли какие-то изменения необходимо приложить определенные усилия извне. В народной мудрости своеобразным выражением первого закона термодинамики могут служить пословицы – «под лежачий камень вода не течет», «без труда не вытащишь рыбку из пруда» и прочая. То есть на примере пословицы про рыбку и труд, можно представить, что рыбка и есть наша условно закрытая система, в ней не произойдет никаких изменений (рыбка сама себя не вытащит из пруда) без нашего внешнего воздействия и участия (труда).

Интересный факт: именно первый закон термодинамики устанавливает, почему потерпели неудачу все многочисленные попытки ученых, исследователей, изобретателей изобрести «вечный двигатель», ведь его существование является абсолютно невозможным согласно этому самому закону, почему, смотрите абзац выше.

В начале нашей статьи было максимального простое определение первого закона термодинамики, в действительности в академической науке существует целых четыре формулировки сути данного закона:

• Энергия ни откуда не появляется и ни куда не пропадает, она лишь переходит из одного вида в другой (закон сохранения энергии).
• Количество теплоты, полученной системой, идет на совершение ее работы против внешних сил и изменение внутренней энергии.
• Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданной системе, и не зависит от способа, которым осуществляется этот переход.
• Изменение внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты, переданной системе, и работой, совершенной системой над внешними силами.

Формула первого закона термодинамики

Формулу первого закона термодинамики можно записать таким образом:

Q = ΔU + A

Количество теплоты Q, передаваемое системе равно суме изменения ее внутренней энергии ΔU и работы A.

Процессы первого закона термодинамики

Также первый закон термодинамики имеет свои нюансы в зависимости от проходящих термодинамических процессов, которые могут быть изохронными и изобарными, и ниже мы детально опишем о каждом из них.

Первый закон термодинамики для изохорного процесса

Изохорным процессом в термодинамике называют процесс, происходящий при постоянном объеме. То есть, если будь-то в газе или жидкости нагреть вещество в сосуде, произойдет изохорный процесс, так как объем вещества останется неизменным. Это условие имеет влияние и на первый закон термодинамики, проходящий при изохорном процессе.

В изохорном процессе объем V является константой, следовательно, газ работы не совершает A = 0

Из этого выходит следующая формула:

Q = ΔU = U (T2) – U (T1).

Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

Первый закон термодинамики для изобарного процесса

Аналогично изобарным процессом называется термодинамический процесс, происходящий в системе при постоянном давлении и массе газа. Следовательно, в изобарном процессе (p = const) работа, совершаемая газом, выражается следующим уравнением первого закона термодинамики:

A = p (V2 – V1) = p ΔV.

Изобарный первый закон термодинамики дает:

Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.

Применение первого закона термодинамики

Первый закон термодинамике имеет практическое применение к различным процессам в физике, например, позволяет вычислить идеальные параметры газа при разнообразных тепловых и механических процессах. Помимо сугубо практичного применение можно этому закону найти применение и философское ведь что ни говорите, но первый закон термодинамики является выражением одного из самых общих законов природы – закона сохранения энергии. Еще Еклезиаст писал, что ничто ни откуда не появляется и никуда не уходит, все пребывает вечно, постоянно трансформируясь, в этом и кроется вся суть первого закона термодинамики.

Первый закон термодинамики, видео

И в завершение нашей статьи вашему вниманию образовательное видео о первом законе термодинамике и внутренней энергии.

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.

Эта статья доступна на английском – First Law of Thermodynamics.

Первый закон термодинамики

Цели обучения

К концу этого раздела вы сможете:

• Определите первый закон термодинамики.
• Опишите, как сохранение энергии соотносится с первым законом термодинамики.
• Выявить примеры первого закона термодинамики, работающие в повседневных ситуациях, включая биологический метаболизм.
• Рассчитать изменения внутренней энергии системы после учета теплопередачи и проделанной работы.

Рис. 1. Этот кипящий чайник представляет энергию в движении. Вода в чайнике превращается в водяной пар, потому что тепло передается от плиты к чайнику. По мере того, как вся система нагревается, работа выполняется – от испарения воды до свиста чайника. (кредит: Джина Гамильтон)

Если нас интересует, как теплопередача преобразуется в работу, тогда важен принцип сохранения энергии. Первый закон термодинамики применяет принцип сохранения энергии к системам, в которых передача тепла и выполнение работы являются методами передачи энергии в систему и из нее.Первый закон термодинамики гласит, что изменение внутренней энергии системы равно чистой теплопередаче в системе за вычетом чистой работы, выполненной системой. В форме уравнения первый закон термодинамики: Δ U = Q – W .

Здесь Δ U – это изменение внутренней энергии U системы. Q – это чистое тепло , , переданное в систему. , то есть Q – это сумма всей теплопередачи в систему и из нее. W – это чистая работа , выполненная системой , то есть W – это сумма всей работы, выполненной в системе или ею. Мы используем следующие условные обозначения: если значение Q положительное, значит, в системе имеется чистый теплообмен; если значение W положительное, значит, система выполняет чистую работу. Таким образом, положительный Q добавляет энергию в систему, а положительный W забирает энергию из системы. Таким образом Δ U = Q – Вт .Также обратите внимание, что если в систему передается больше тепла, чем проделанной работы, разница сохраняется как внутренняя энергия. Тепловые двигатели – хороший тому пример: в них происходит передача тепла, чтобы они могли выполнять свою работу. (См. Рисунок 2.) Теперь мы рассмотрим Q , W и Δ U далее.

Рис. 2. Первый закон термодинамики – это принцип сохранения энергии, установленный для системы, в которой тепло и работа являются методами передачи энергии для системы, находящейся в тепловом равновесии. Q представляет собой чистую теплопередачу – это сумма всех теплопередач в систему и из нее. Q положительно для чистой передачи тепла в систему. W – это общий объем работы, проделанной с системой. W положителен, когда система выполняет больше работы, чем над ней. Изменение внутренней энергии системы Δ U связано с теплом и работой по первому закону термодинамики Δ U = Q – Вт .

Установление связей: закон термодинамики и закон сохранения энергии

Первый закон термодинамики – это закон сохранения энергии, сформулированный в форме, наиболее полезной в термодинамике. Первый закон устанавливает связь между теплопередачей, проделанной работой и изменением внутренней энергии системы.

Нагрев

Q и рабочий Вт

Теплопередача ( Q ) и выполнение работы ( W ) – два повседневных средства подачи энергии в систему или вывода энергии из системы.Процессы совершенно разные. Теплообмен, менее организованный процесс, обусловлен разницей температур. Работа – это вполне организованный процесс, в котором действует макроскопическая сила, действующая на расстоянии. Тем не менее, тепло и работа могут дать одинаковые результаты, например, оба могут вызвать повышение температуры. Передача тепла в систему, например, когда Солнце нагревает воздух в шине велосипеда, может повысить ее температуру, и поэтому может работать над системой, например, когда велосипедист нагнетает воздух в шину.Как только произошло повышение температуры, невозможно сказать, было ли оно вызвано теплопередачей или работой. Эта неопределенность – важный момент. Теплообмен и работа – это энергия в пути, и ни одна из них не сохраняется как таковая в системе. Однако оба могут изменить внутреннюю энергию U системы. Внутренняя энергия – это форма энергии, полностью отличная от тепла или работы.

Внутренняя энергия

U

Мы можем думать о внутренней энергии системы двумя разными, но последовательными способами.Первый – это атомно-молекулярная точка зрения, которая исследует систему в атомном и молекулярном масштабе. Внутренняя энергия U системы – это сумма кинетической и потенциальной энергий ее атомов и молекул. Напомним, что кинетическая плюс потенциальная энергия называется механической энергией. Таким образом, внутренняя энергия – это сумма атомной и молекулярной механической энергии. Поскольку невозможно отследить все отдельные атомы и молекулы, мы должны иметь дело со средними значениями и распределениями.Второй способ взглянуть на внутреннюю энергию системы – с точки зрения ее макроскопических характеристик, которые очень похожи на средние атомные и молекулярные значения.

Макроскопически мы определяем изменение внутренней энергии Δ U как значение, определяемое первым законом термодинамики: Δ U = Q – Вт .

Многие детальные эксперименты подтвердили, что Δ U = Q – W , где Δ U – изменение полной кинетической и потенциальной энергии всех атомов и молекул в системе.Также экспериментально было определено, что внутренняя энергия U системы зависит только от состояния системы, а не от того, как она достигла этого состояния . Более конкретно, U оказывается функцией нескольких макроскопических величин (например, давления, объема и температуры), независимо от прошлой истории, такой как была ли передача тепла или проделанная работа. Эта независимость означает, что, зная состояние системы, мы можем рассчитать изменения ее внутренней энергии U на основе нескольких макроскопических переменных.

Установление соединений: макроскопическое и микроскопическое

В термодинамике мы часто используем макроскопическую картину при расчете поведения системы, в то время как атомная и молекулярная картина дает основные объяснения в терминах средних значений и распределений. Мы еще раз увидим это в следующих разделах этой главы. Например, в теме энтропии расчеты будут производиться с использованием атомно-молекулярного представления.

Чтобы лучше понять, как думать о внутренней энергии системы, давайте рассмотрим систему, переходящую из состояния 1 в состояние 2.Система имеет внутреннюю энергию U ₁ в Состоянии 1 и внутреннюю энергию U ₂ в Состоянии 2, независимо от того, как она попала в любое из состояний. Таким образом, изменение внутренней энергии Δ U = U ₂ – U ₁ не зависит от того, что вызвало изменение. Другими словами, Δ U не зависит от пути . Под путем мы подразумеваем способ добраться от начальной точки до конечной точки. Почему важна эта независимость? Обратите внимание, что Δ U = Q – W .И Q , и W зависят от пути , а Δ U – нет. Эта независимость от пути означает, что внутреннюю энергию U легче учитывать, чем теплопередачу или проделанную работу.

Пример 1. Расчет изменения внутренней энергии: одно и то же изменение в

U производится двумя разными процессами

1. Предположим, что теплопередача в систему составляет 40,00 Дж, в то время как система выполняет работу 10,00 Дж. Позже появляется теплоотдача 25.00 Дж из системы, в то время как в системе выполняется 4,00 Дж работы. Каково чистое изменение внутренней энергии системы?
2. Каково изменение внутренней энергии системы, когда в общей сложности 150,00 Дж теплопередачи происходит из (от) системы и 159,00 Дж работы выполняется в системе? (См. Рисунок 3).

Рисунок 3. Два разных процесса производят одно и то же изменение в системе. (a) Всего в системе происходит передача тепла 15,00 Дж, в то время как работа требует всего 6.00 Дж. Изменение внутренней энергии составляет ΔU = Q-W = 9,00 Дж. (B) При передаче тепла из системы удаляется 150,00 Дж, в то время как работа дает 159,00 Дж, что приводит к увеличению внутренней энергии на 9,00 Дж. Если система начинается в одном и том же состоянии в пунктах (а) и (б), она окажется в одном и том же конечном состоянии в любом случае – ее конечное состояние связано с внутренней энергией, а не с тем, как эта энергия была получена.

Стратегия

В части 1 мы должны сначала найти чистую теплопередачу и чистую работу, выполненную на основе данной информации.Тогда первый закон термодинамики (Δ U = Q – W ) может быть использован для определения изменения внутренней энергии. В части (b) приведены чистая теплопередача и проделанная работа, поэтому уравнение можно использовать напрямую.

Решение для Части 1

Чистая теплопередача – это теплопередача в систему за вычетом теплопередачи из системы, или

Q = 40,00 Дж – 25,00 Дж = 15,00 Дж

Аналогично, общая работа – это работа, выполненная системой за вычетом работы, выполненной в системе, или

Вт = 10.00 Дж – 4,00 Дж = 6,00 Дж.

Таким образом, изменение внутренней энергии определяется первым законом термодинамики:

Δ U = Q – W = 15,00 Дж – 6,00 Дж = 9,00 Дж

Мы также можем найти изменение внутренней энергии для каждого из двух шагов. Сначала рассмотрим 40,00 Дж теплопередачи на входе и 10,00 Дж на выходе, или Δ U ₁ = Q ₁ – W ₁ = 40,00 Дж – 10,00 Дж = 30,00 Дж.

Теперь рассмотрим 25,00 Дж теплоотдачи и 4,00 Дж работы на входе, или

Δ U ₂ = Q ₂ – W ₂ = –25,00 Дж – (- 4,00 Дж) = –21,00 Дж

Общее изменение – это сумма этих двух шагов, или Δ U = Δ U ₁ + Δ U ₂ = 30,00 Дж + (−21,00 Дж) = 9,00 Дж.

Обсуждение части 1

Неважно, смотрите ли вы на процесс в целом или разбиваете его на этапы, изменение внутренней энергии одинаково.

Решение для Части 2

Здесь чистая теплопередача и общая работа даны непосредственно как Q = –150,00 Дж и Вт = –159,00 Дж, так что

Δ U = Q – W = –150,00 Дж – (- 159,00 Дж) = 9,00 Дж.

Обсуждение части 2

Совершенно другой процесс в части 2 дает такое же изменение внутренней энергии на 9,00 Дж, что и в части 1. Обратите внимание, что изменение в системе в обеих частях связано с Δ U , а не с отдельным Q s или Вт с задействовано.Система оказывается в состоянии , одинаковое в обеих частях. Части 1 и 2 представляют два разных пути, которыми должна следовать система между одними и теми же начальными и конечными точками, и изменение внутренней энергии для каждой из них одинаково – оно не зависит от пути.

Метаболизм человека и первый закон термодинамики

Метаболизм человека – это преобразование пищи в теплообмен, работу и накопленный жир. Метаболизм – интересный пример действия первого закона термодинамики.Теперь мы еще раз посмотрим на эти темы с помощью первого закона термодинамики. Рассматривая тело как интересующую нас систему, мы можем использовать первый закон для изучения теплопередачи, выполнения работы и внутренней энергии в различных видах деятельности, от сна до тяжелых упражнений. Каковы некоторые из основных характеристик теплопередачи, выполнения работы и энергии в организме? Во-первых, температура тела обычно поддерживается постоянной за счет передачи тепла в окружающую среду. Это означает, что Q отрицательный. Другой факт: тело обычно работает с внешним миром.Это означает, что W положительный. В таких ситуациях тело теряет внутреннюю энергию, поскольку Δ U = Q – Вт отрицательно.

Теперь рассмотрим эффекты еды. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии (это неромантичный взгляд на хороший стейк). Тело метаболизирует всю пищу, которую мы потребляем. По сути, метаболизм – это процесс окисления, при котором высвобождается химическая потенциальная энергия пищи.Это означает, что питание осуществляется в форме работы. Энергия пищи указывается в специальной единице, известной как калория. Эта энергия измеряется сжиганием пищи в калориметре, как и определяются единицы.

В химии и биохимии одна калория (обозначается строчной c) определяется как энергия (или теплопередача), необходимая для повышения температуры одного грамма чистой воды на один градус Цельсия. Диетологи и любители веса склонны использовать диетических калорий, которые часто называют калориями (пишется с заглавной C).Одна еда Калория – это энергия, необходимая для повышения температуры одного килограмма воды на один градус Цельсия. Это означает, что одна диетическая калория для химика равна одной килокалории, и нужно быть осторожным, чтобы не путать их.

Опять же, рассмотрим внутреннюю энергию, потерянную телом. Эта внутренняя энергия может идти по трем направлениям – на передачу тепла, выполнение работы и накопленный жир (крошечная часть также идет на восстановление и рост клеток). Передача тепла и выполнение работы забирают внутреннюю энергию из тела, а пища возвращает ее.Если вы едите только нужное количество пищи, ваша средняя внутренняя энергия остается постоянной. Все, что вы теряете на теплопередачу и выполнение работы, заменяется едой, так что в конечном итоге Δ U = 0. Если вы постоянно переедаете, то Δ U всегда положительный, и ваше тело сохраняет эту дополнительную внутреннюю энергию в виде жира. Обратное верно, если вы едите слишком мало. Если Δ U будет отрицательным в течение нескольких дней, то организм усваивает собственный жир, чтобы поддерживать температуру тела и выполнять работу, отнимающую у тела энергию.Именно так соблюдение диеты способствует снижению веса.

Жизнь не всегда так проста, как знает любой человек, сидящий на диете. Тело накапливает жир или метаболизирует его только в том случае, если потребление энергии меняется в течение нескольких дней. После того, как вы сели на основную диету, следующая будет менее успешной, потому что ваше тело изменит способ реагирования на низкое потребление энергии. Ваша основная скорость метаболизма (BMR) – это скорость, с которой пища преобразуется в теплообмен и работу, выполняемую, когда организм находится в полном покое. Организм регулирует базальную скорость метаболизма, чтобы частично компенсировать переедание или недоедание.Организм будет снижать скорость метаболизма, а не устранять собственный жир, чтобы заменить потерянную еду. Вы легче простужаетесь и чувствуете себя менее энергичным в результате более низкой скорости метаболизма, и вы не будете терять вес так быстро, как раньше. Упражнения помогают похудеть, потому что они обеспечивают теплоотдачу от вашего тела и работы, а также повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя. Снижению веса также способствует довольно низкая эффективность тела в преобразовании внутренней энергии в работу, так что потеря внутренней энергии в результате выполнения работы намного больше, чем проделанная работа.Однако следует отметить, что живые системы не находятся в тепловом равновесии.

Тело дает нам отличный показатель того, что многие термодинамические процессы необратимы . Необратимый процесс может идти в одном направлении, но не в обратном, при заданном наборе условий. Например, хотя телесный жир может быть преобразован для выполнения работы и передачи тепла, работа, выполняемая телом, и передача тепла в него не могут быть преобразованы в телесный жир. В противном случае мы могли пропустить обед, загорая или спустившись по лестнице.Другой пример необратимого термодинамического процесса – фотосинтез. Этот процесс представляет собой поглощение растениями одной формы энергии – света – и ее преобразование в химическую потенциальную энергию. Оба применения первого закона термодинамики показаны на рисунке 4. Одно большое преимущество законов сохранения, таких как первый закон термодинамики, состоит в том, что они точно описывают начальную и конечную точки сложных процессов, таких как метаболизм и фотосинтез, без учета осложнения между ними.В таблице 1 представлена ​​сводка терминов, относящихся к первому закону термодинамики.

Рис. 4. (а) Первый закон термодинамики применительно к метаболизму. Тепло, передаваемое из тела (Q), и работа, выполняемая телом (W), удаляют внутреннюю энергию, в то время как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую организмом.) (Б) Растения преобразуют часть лучистой теплопередачи в солнечном свете в запасенную химическую энергию – процесс, называемый фотосинтезом.

Таблица 1.Краткое изложение терминов первого закона термодинамики, ΔU = Q – W
Срок	Определение
U	Внутренняя энергия – сумма кинетической и потенциальной энергий атомов и молекул системы. Можно разделить на множество подкатегорий, таких как тепловая и химическая энергия. Зависит только от состояния системы (например, P , V и T ), а не от того, как энергия поступает в систему.Изменение внутренней энергии не зависит от пути.
Q	Тепло – энергия, передаваемая из-за разницы температур. Характеризуется случайным движением молекул. Сильно зависит от пути. Q Вход в систему положительный.
Вт	Работа – энергия, передаваемая силой, перемещающейся на расстояние. Организованный, упорядоченный процесс. Зависит от пути. W , выполненный системой (либо против внешней силы, либо для увеличения объема системы), является положительным.

Сводка раздела

• Первый закон термодинамики задается как Δ U = Q – W , где Δ U – изменение внутренней энергии системы, Q – чистая теплопередача (сумма вся теплопередача в систему и из нее), а W – это чистая проделанная работа (сумма всей работы, проделанной в системе или ею).
• И Q , и W – энергия в пути; только Δ U представляет собой независимую величину, которую можно хранить.
• Внутренняя энергия U системы зависит только от состояния системы, а не от того, как она достигла этого состояния.
• Метаболизм живых организмов и фотосинтез растений – это особые виды передачи тепла, выполнения работы и внутренней энергии систем.

Концептуальные вопросы

1. Опишите фотографию чайника в начале этого раздела с точки зрения теплопередачи, проделанной работы и внутренней энергии. Как передается тепло? Какая работа и что делается? Как чайник поддерживает свою внутреннюю энергию?
2. Первый закон термодинамики и закон сохранения энергии, как обсуждалось в «Сохранении энергии», явно связаны.Чем они различаются по рассматриваемым видам энергии?
3. Теплопередача Q и выполненная работа Вт – это всегда энергия в пути, тогда как внутренняя энергия U – это энергия, запасенная в системе. Приведите пример каждого типа энергии и конкретно укажите, как он передается или находится в системе.
4. Чем отличаются теплопередача и внутренняя энергия? В частности, что можно сохранить как таковое в системе, а что нет?
5. Если вы сбежите по лестнице и остановитесь, что произойдет с вашей кинетической энергией и вашей начальной гравитационной потенциальной энергией?
6. Объясните, как пищевая энергия (калории) может рассматриваться как молекулярная потенциальная энергия (в соответствии с атомарным и молекулярным определением внутренней энергии).
7. Определите тип энергии, передаваемой вашему телу в каждом из следующих случаев: внутренняя энергия, теплопередача или выполнение работы: (а) купание в солнечном свете; (б) употребление пищи; (c) подъем на лифте на более высокий этаж.

Задачи и упражнения

1. Как изменится внутренняя энергия автомобиля, если в его бак залить 12 галлонов бензина? Энергетическая ценность бензина составляет 1,3 × 10 ⁸ Дж / галлон. Все остальные факторы, например температура в автомобиле, постоянны.
2. Сколько тепла происходит от системы, если ее внутренняя энергия уменьшилась на 150 Дж, пока она выполняла 30,0 Дж работы?
3. Система выполняет 1,80 × 10 ⁸ Дж работы, в то время как 7,50 × 10 ⁸ Дж теплопередачи происходит в окружающую среду. Каково изменение внутренней энергии системы при отсутствии других изменений (например, температуры или добавления топлива)?
4. Каково изменение внутренней энергии системы, которая выполняет 4,50 × 10 ⁵ Дж, пока 3.00 × 10 ⁶ Дж происходит теплопередача в системе, а 8.00 × 10 ⁶ Дж теплопередачи происходит в окружающую среду?
5. Предположим, что женщина выполняет 500 Дж работы, и 9500 Дж в процессе передачи тепла в окружающую среду. а) Как уменьшается ее внутренняя энергия, если не меняется температура или потребление пищи? (То есть другой передачи энергии нет.) Б) Какова ее эффективность?
6. (а) Сколько пищевой энергии человек усвоит в процессе усвоения 35.0 кДж работы при КПД 5,00%? б) Сколько тепла передается в окружающую среду, чтобы поддерживать постоянную температуру?
7. (а) Какова средняя скорость метаболизма в ваттах человека, который усваивает 10 500 кДж пищевой энергии за один день? (б) Какое максимальное количество работы в джоулях он может выполнить без расщепления жира, предполагая максимальную эффективность 20,0%? (c) Сравните его производительность с дневной мощностью двигателя 187 Вт (0,250 лошадиных сил).
8. (a) На сколько времени хватит энергии в стакане йогурта мощностью 1470 кДж (350 ккал) у женщины, выполняющей работу с мощностью 150 Вт с эффективностью 20?0% (например, при неспешном подъеме по лестнице)? (б) Означает ли время, указанное в части (а), легко потребить больше пищевой энергии, чем вы можете разумно ожидать, работая с упражнениями?
9. (a) Женщина, поднимающаяся на памятник Вашингтону, усваивает 6,00 × 10 ² кДж пищевой энергии. Если ее КПД составляет 18,0%, сколько тепла передается в окружающую среду, чтобы поддерживать ее температуру постоянной? (б) Обсудите величину теплопередачи, указанную в (а). Это согласуется с тем, что вы быстро разминаетесь во время тренировки?

Глоссарий

Первый закон термодинамики: утверждает, что изменение внутренней энергии системы равно чистой теплопередаче в систему за вычетом чистой работы, выполненной системой

внутренняя энергия: сумма кинетической и потенциальной энергий атомов и молекул системы

метаболизм человека: преобразование пищи в теплообмен, работу и накопленный жир

Избранные решения проблем и упражнения

1.1,6 × 10 ⁹ Дж

3. −9.30 × 10 ⁸ Дж

5. (а) -1,0 × 10 ⁴ Дж, или -2,39 ккал; (б) 5,00%

7. (а) 122 Вт; (б) 2,10 × 10 ⁶ Дж; (c) Работа двигателя составляет 1,61 × 10 ⁷ Дж; таким образом, двигатель производит в 7,67 раз больше работы, чем человек

9. (а) 492 кДж; (б) Такое количество тепла соответствует тому факту, что вы быстро согреваетесь во время тренировки. Поскольку организм неэффективен, выделяемое избыточное тепло должно рассеиваться через потоотделение, дыхание и т. Д.

1-й закон термодинамики – Chemistry LibreTexts

Чтобы понять и выполнить любой вид термодинамических расчетов, мы должны сначала понять фундаментальные законы и концепции термодинамики. Например, работа и тепло – понятия взаимосвязанные. Тепло – это передача тепловой энергии между двумя телами, находящимися при разных температурах, и не равная тепловой энергии. Работа – это сила, используемая для передачи энергии между системой и ее окружением и необходимая для создания тепла и передачи тепловой энергии.И работа, и тепло вместе позволяют системам обмениваться энергией. Взаимосвязь между двумя концепциями можно проанализировать с помощью темы термодинамики, которая представляет собой научное исследование взаимодействия тепла и других типов энергии.

Введение

Чтобы понять взаимосвязь между работой и теплом, нам нужно понять третий, связывающий фактор: изменение внутренней энергии. Энергия не может быть создана или уничтожена, но ее можно преобразовать или передать. Внутренняя энергия относится ко всей энергии в данной системе, включая кинетическую энергию молекул и энергию, хранящуюся во всех химических связях между молекулами.Благодаря взаимодействию тепла, работы и внутренней энергии происходит передача и преобразование энергии каждый раз, когда в системе вносятся изменения. Однако во время этих передач чистая энергия не создается и не теряется.

Закон термодинамики

Первый закон термодинамики гласит, что энергия может быть преобразована из одной формы в другую за счет взаимодействия тепла, работы и внутренней энергии, но она не может быть создана или разрушена ни при каких обстоятельствах. Математически это представлено как

\ [\ Delta U = q + w \ label {1} ​​\]

с

• \ (ΔU \) – полное изменение внутренней энергии системы,
• \ (q \) – теплообмен между системой и ее окружением, а
• \ (w \) – это работа, выполняемая системой или в ней.

Работа также равна отрицательному внешнему давлению в системе, умноженному на изменение объема:

\ [w = -p \ Delta V \ label {2} \]

где \ (P \) – внешнее давление на систему, а \ (ΔV \) – изменение объема. Это конкретно называется работой «давление-объем».

Внутренняя энергия системы уменьшится, если система будет выделять тепло или работать. Следовательно, внутренняя энергия системы увеличивается при увеличении тепла (это может быть сделано путем добавления тепла в систему).Внутренняя энергия также увеличилась бы, если бы работа выполнялась в системе. Любая работа или тепло, входящие в систему или выходящие из нее, изменяют внутреннюю энергию. Однако, поскольку энергия никогда не создается и не разрушается (таким образом, первый закон термодинамики), изменение внутренней энергии всегда равно нулю. Если энергия теряется системой, то она поглощается окружающей средой. Если энергия поглощается системой, то эта энергия была выпущена из окружающей среды:

\ [\ Delta U_ {system} = – \ Delta U_ {окружение} \]

, где ΔU _{система} – полная внутренняя энергия в системе, а ΔU _{окружающей среды} – полная энергия окружающей среды.

Таблица 1

Процесс	Знак тепла (q)	Знак работы (w)
Работа, выполненная системой	НЕТ	–
Работа над системой	НЕТ	+
Тепло, выделяемое системой – экзотермическое (поглощаемое окружающей средой)	–	НЕТ

Рисунок выше является наглядным примером Первого закона термодинамики.Синие кубы представляют систему, а желтые круги – окружение системы. Если энергия теряется системой кубов, то она приобретается окружением. Энергия никогда не создается и не уничтожается. Поскольку площадь куба-подсказки уменьшилась, визуальная область желтого круга увеличилась. Это символизирует то, как энергия, потерянная системой, приобретается окружающей средой. Воздействие различного окружения и изменения в системе помогают определить увеличение или уменьшение внутренней энергии, тепла и работы.

Таблица 2

Процесс	Изменение внутренней энергии	Теплопередача тепловой энергии (кв)	Работа (w = -PΔV)	Пример
q = 0 Адиабатический	+	0	+	Изолированная система, в которой тепло не проникает и не уходит, подобно пенополистиролу
ΔV = 0 Постоянный объем	+	+	0	Жесткая система с изолированным давлением, такая как калориметр бомбы
Постоянное давление	+ или –	энтальпия (ΔH)	-PΔV	Большинство процессов происходят при постоянном внешнем давлении
ΔT = 0 Изотермический	0	+	–	Нет изменений температуры, как в термостате

Пример \ (\ PageIndex {1} \)

Газ в системе имеет постоянное давление.Окружающая среда вокруг системы теряет 62 Дж тепла и выполняет 474 Дж работы с системой. Какова внутренняя энергия системы?

Раствор

Чтобы найти внутреннюю энергию ΔU, мы должны рассмотреть взаимосвязь между системой и окружающей средой. Поскольку Первый закон термодинамики гласит, что энергия не создается и не уничтожается, мы знаем, что все, что теряется в окружающей среде, приобретается системой. Окрестности теряют тепло и работают с системой.Следовательно, q и w положительны в уравнении ΔU = q + w, потому что система накапливает тепло и выполняет работу над собой.

\ [\ begin {align} ΔU & = (62 \, J) + (474 ​​\, J) \\ [4pt] & = 536 \, J \ end {align} \]

Пример \ (\ PageIndex {2} \)

Система имеет постоянный объем (ΔV = 0), а тепло вокруг системы увеличивается на 45 Дж.

1. Какой знак тепла (q) для системы?
2. Чему равно ΔU?
3. Какое значение внутренней энергии системы в Джоулях?

Раствор

Поскольку система имеет постоянный объем (ΔV = 0), член -PΔV = 0 и работа равна нулю.Таким образом, в уравнении ΔU = q + w w = 0 и ΔU = q. Внутренняя энергия равна теплу системы. Окружающее тепло увеличивается, поэтому тепло системы уменьшается, потому что тепло не создается и не разрушается. Таким образом, тепло отводится от системы, делая ее экзотермической и отрицательной. Значение внутренней энергии будет отрицательным значением тепла, поглощаемого окружающей средой.

1. отрицательный (q <0)
2. ΔU = q + (-PΔV) = q + 0 = q
3. ΔU = -45 Дж

Уравнения термодинамики

Химическая система будет иметь тенденцию переходить из одного состояния в другое любыми доступными средствами, так что универсальная энтропия увеличивается.Максимальное универсальное изменение энтропии будет совпадать с конечным состоянием, которое имеет тенденцию иметь наименьшую возможную полную свободную энергию из всех компонентов. Если это состояние достигается, то при таком точном составе все реагенты имеют точную полную свободную энергию, как и все продукты. Это также означает, что ∆ G = 0 в этой точке. Это точка, в которой было достигнуто равновесие. Нет больше никакой тенденции для реакции идти в чистом прямом направлении или чистом обратном направлении. Любой способ фактически увеличил бы свободную энергию системы.Состояние равновесия – это в основном то, чего «пытаются» достичь все реакции. «Стимул» к достижению этого положения / состояния – это изменение свободной энергии реакции ∆ G . Если это количество положительное, тогда реакция будет происходить в обратном направлении, чем написано на странице – несамопроизвольное прямое направление означает спонтанное обратное направление. Если величина отрицательная (-∆ G ), то реакция будет ускорена.

И последнее … по мере продвижения реакции количества реагентов и продуктов постоянно меняются. Количество реагентов уменьшается, а количество продуктов увеличивается. Осознайте, что свободная энергия связана с количеством вещества, а также с тем, что это за вещество. Когда соединение уменьшается, его свободная энергия также уменьшается, потому что ее становится все меньше и меньше. Если все это отреагирует, то свободная энергия этого вещества теперь равна нулю, потому что его больше нет. Конечно, по другую сторону стрелки – товары.Когда началась реакция, у них была нулевая свободная энергия (потому что там ничего не было), но затем начинают появляться продукты, и свободная энергия растет. Реакция фактически остановится, когда сумма всех свободных энергий реагентов сравняется с полной свободной энергией продуктов. Если свободные энергии совпадают, то ∆ G должно быть равно нулю, и система достигла равновесия.

Так что это значит? Что ж, независимо от того, какой у вас ∆ G для реакции – будь то положительное или отрицательное, абсолютное значение ∆ G будет уменьшаться и продолжать уменьшаться по мере того, как реакция продвигается вперед (или назад).Как только реакция достигает той точки, где ∆ G = 0, равновесие вступает в игру. Когда вы достигнете равновесия, большое значение приобретет множество замечательных отношений и уравнений. Все это “чудо” мы сохраняем для вас в Ch402.

Прочтите предыдущие абзацы снова и снова и ПОПРОБУЙТЕ, чтобы понять, о чем они говорят. Понимание этого – КЛЮЧ к хорошему пониманию того, что движет всем вокруг нас. Термодинамика управляет движущей силой всего.

Энергия, энтальпия и первый закон термодинамики

Энергия, энтальпия и первый закон Термодинамика

---

Химическая термодинамика

Термодинамика определяется как отрасль науки, которая занимается взаимосвязь между теплом и другими формами энергии, такими как работа. Часто бывает обобщены в виде трех законов, которые описывают ограничения на то, как различные формы энергии могут быть взаимопревращенными. Химическая термодинамика – это раздел термодинамики, относится к химическим реакциям.

Законы термодинамики

Первый закон: Энергия сохраняется; его нельзя ни создать, ни уничтожить.

Второй закон: В изолированной системе естественные процессы являются спонтанными, когда они приводят к увеличение беспорядка или энтропии.

Третий закон: энтропия идеального кристалла равна нулю, когда температура кристалл равен абсолютному нулю (0 К).

Было много попыток построить устройство, нарушающее законы термодинамика. Все потерпели неудачу. Термодинамика – одна из немногих областей науки в мире. для которых нет исключений.

---

Система и окружение

Одно из основных предположений термодинамики – это идея, что мы можем произвольно разделите Вселенную на систему и ее окружение .В граница между системой и ее окружением может быть такой же реальной, как стенки стакана который отделяет решение от остальной вселенной (как на рисунке ниже).

Или он может быть таким же воображаемым, как набор точек, которые просто разделяют воздух. над поверхностью металла от остальной атмосферы (как на рисунке ниже).

---

Внутренняя энергия

Одним из термодинамических свойств системы является ее внутренняя энергия , E , который представляет собой сумму кинетической и потенциальной энергий частиц, которые образуют систему.Внутреннюю энергию системы можно понять, исследуя простейшая из возможных систем: идеальный газ. Поскольку частицы в идеальном газе не взаимодействуют, эта система не имеет потенциальной энергии. Внутренняя энергия идеального газа равна следовательно, сумма кинетических энергий частиц в газе.

Кинетическая молекулярная теория предполагает, что температура газа равна прямо пропорциональна средней кинетической энергии его частиц, как показано на рисунок ниже.

Следовательно, внутренняя энергия идеального газа прямо пропорциональна температура газа.

E _sys = ³ / ₂ RT

В этом уравнении R – постоянная идеального газа в джоулях на моль. кельвин (Дж / моль-К), а T – температура в кельвинах.

Внутренняя энергия систем более сложных, чем идеальный газ нельзя измерить напрямую. Но внутренняя энергия системы по-прежнему пропорциональна его температура. Таким образом, мы можем отслеживать изменения внутренней энергии системы с помощью наблюдая, что происходит с температурой системы. Когда температура системы увеличивается, мы можем сделать вывод, что внутренняя энергия системы также выросла.

Предположим на время, что термометр, погруженный в стакан с водой на плите – 73.5 ^o C, как показано на рисунке ниже. Это измерение может описывать только состояние системы в данный момент времени. Он не может сказать нам, воду нагревали непосредственно от комнатной температуры до 73,5 ^o ° C или нагревали из комнаты температуру до 100- ^o ° C, а затем дают остыть.

Таким образом,

Температура является функцией состояния . Это зависит только от состояние системы в любой момент времени, а не путь, по которому система государственный.Поскольку внутренняя энергия системы пропорциональна ее температуре, внутренняя энергия также является функцией состояния. Любое изменение внутренней энергии системы равна разнице между его начальным и конечным значениями.

E _sys = E _f – E _i

---

Первый закон термодинамики

Первый закон термодинамики можно выразить в следующем уравнении: который утверждает, что энергия Вселенной постоянна.Энергию можно передавать от систему в ее окружение или наоборот, но она не может быть создана или уничтожена.

Первый закон термодинамики :

E унив = E sys + E surr = 0

Более полезная форма первого закона описывает, как сохраняется энергия.Это говорит, что изменение внутренней энергии системы равно сумме тепла полученные или утраченные системой, а также работа, выполненная системой или в ней.

Первый закон термодинамики :

E sys = q + w

Знаковое соглашение о соотношении внутренней энергии систему и тепло, получаемое или теряемое системой, можно понять, подумав о конкретный пример, такой как стакан с водой на горячей плите.Когда плита повернута при включении система получает тепло от окружающей среды. В результате и температура, и внутренняя энергия системы увеличивается, а E составляет положительных . Когда конфорка выключена, вода теряет тепло в окружающую среду при охлаждении до комнатной температуры, а E – отрицательное значение .

Взаимосвязь между внутренней энергией и работой можно понять с помощью Рассмотрим другой конкретный пример: вольфрамовая нить внутри лампочки.Когда работаешь осуществляется в этой системе путем пропускания электрического тока через вольфрамовую проволоку, система нагревается и E , следовательно, положительный . (В конце концов, проволока становится достаточно горячей светиться.) И наоборот, E отрицательное значение , когда система работает со своим окружением.

Условные обозначения для тепла, работы и внутренней энергии кратко изложены в рисунок ниже. Внутренняя энергия и температура системы уменьшаются ( E <0), когда система либо теряет тепло, либо работает со своим окружением.И наоборот, внутренняя энергия и повышение температуры ( E > 0), когда система получает тепло от окружающей среды или когда она работает в системе.

---

Система и работа

Система обычно определяется как химическая реакция, а граница контейнер, в котором протекает реакция.В ходе реакции тепло либо испускается или поглощается системой. Кроме того, система либо работает на нем. окружение или работа, проделанная с ним его окружением. Любое из этих взаимодействий может влияют на внутреннюю энергию системы.

E _sys = q + w

С химической реакцией обычно связаны два вида работы: электрическая работа и работа расширения .Химические реакции могут повлиять на их окружение, пропуская электрический ток по внешнему проводу. Реакции тоже делают работать с их окружением, когда объем системы увеличивается в течение реакция Количество работы расширения, совершаемой реакцией, равно произведению давление, против которого система расширяется, умноженное на изменение объема система.

w = – PV

Знаковое соглашение для этого уравнения отражает тот факт, что внутреннее энергия системы уменьшается, когда система действительно работает со своим окружением.

---

Энтальпия относительно внутренней энергии

Что произойдет, если мы создадим набор условий, при которых работа не будет что делает система в своем окружении или наоборот, во время химической реакции? Под В этих условиях тепло, выделяемое или поглощаемое реакцией, будет равно изменение внутренней энергии системы.

E _sys = q (тогда и только тогда, когда w = 0)

Самый простой способ достичь этих условий – запустить реакцию при постоянный объем, при котором работа расширения невозможна.При постоянном объеме тепло выделяется или поглощается реакцией, равно изменению внутренней энергии, которая происходит во время реакции.

E _sys = q _v (при постоянном объеме)

На рисунке ниже показан калориметр, в котором реакции могут проводиться при постоянный объем. Однако большинство реакций проводят в открытых колбах и лабораторных стаканах. Когда это сделано, объем системы не является постоянным, потому что газ может входить или выходить из контейнер во время реакции.Однако система находится под постоянным давлением, поскольку общее давление внутри контейнера всегда равно атмосферному давлению.

Если во время реакции из колбы выходит газ, система работать над его окрестностями. Если в результате реакции в колбу втягивается газ, окружающая среда работать над системой. Мы все еще можем измерить количество тепла, выделяемого или поглощаемого во время реакции, но она больше не равна изменению внутренней энергии система, потому что часть тепла была преобразована в работу.

E _sys = q + w

Мы можем обойти эту проблему, введя понятие энтальпии ( H ), который представляет собой сумму внутренней энергии системы плюс произведение давление газа в системе, умноженное на объем системы.

H _sys = E _sys + PV

Для простоты индекс “sys” будет опущен. символ внутренней энергии системы и энтальпии системы из сейчас на.Поэтому мы будем сокращать соотношение между энтальпией системы и внутренняя энергия системы следующим образом.

H = E + PV

Изменение энтальпии системы во время химической реакции равно равна изменению его внутренней энергии плюс изменение произведения давления раз больше объема системы.

H = E + ( PV )

Предположим, что реакция протекает в стакане из пенополистирола, как показано на рисунок ниже.

Поскольку реакция протекает при постоянном давлении, изменение энтальпия, возникающая во время реакции, равна изменению внутренней энергии система плюс произведение постоянного давления на изменение объема система.

H = E + PV (при постоянном давлении)

Подстановка первого закона термодинамики в это уравнение дает следующий результат.

H = ( q _p + w ) + PV

Предполагая, что единственная работа, совершаемая реакцией, – это работа расширения дает уравнение, в котором члены PV сокращаются.

H = ( q _p – PV ) + PV

Таким образом, тепло, выделяемое или поглощаемое во время химической реакции при постоянное давление равно изменению энтальпии системы.

H = q _p (при постоянном давлении)

Связь между изменением внутренней энергии системы во время химической реакции и энтальпию реакции можно резюмировать следующим образом.

1. Тепло, выделяемое или поглощаемое при протекании реакции при константе . объем равен изменению внутренней энергии системы.

E _sys = q _v

2.Тепло, выделяемое или поглощаемое при протекании реакции при константе давление равно изменению энтальпии системы.

H _sys = q _p

3. Изменение энтальпии системы во время химической реакции равно равна изменению внутренней энергии плюс изменение произведения давления количества газа в системе и его объема.

H _sys = E _sys + ( PV )

4.Разница между E и H для системы небольшая для реакций, в которых участвуют только жидкости и твердые вещества, потому что изменений практически нет в объеме системы во время реакции. Разница может быть относительно большой, однако для реакций, в которых участвуют газы, при изменении количества молей газ в процессе реакции.

Практическая задача 1: Какая из следующих процессы выполняются с постоянным объемом, а какие – при постоянном давлении? (а) кислотно-основное титрование (б) разложение CaCo 3 путем нагревания известняка в тигле с бунзеном. горелка (c) реакция между металлическим цинком и водным раствором ионов Cu 2+ до образуют металлическую медь и ионы Zn 2+ (d) измерение калорий в 1 унции.подача хлопьев для завтрака путем сжигания хлопьев в калориметре бомбы Нажмите здесь, чтобы проверить свой ответ на «Практика» Задача 1.

12.2 Первый закон термодинамики: тепловая энергия и работа

Биология: биологическая термодинамика

Мы часто думаем о термодинамике как о полезной для изобретения или тестирования оборудования, такого как двигатели или паровые турбины. Однако термодинамика также применима к живым системам, таким как наши собственные тела.Это составляет основу биологической термодинамики (рис. 12.7).

Рис. 12.7 (a) Первый закон термодинамики применим к метаболизму. Тепло, передаваемое из тела (Q), и работа, выполняемая телом (W), удаляют внутреннюю энергию, тогда как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую организмом.) (Б) Растения преобразуют часть лучистой энергии солнечного света в запасенную химическую энергию, процесс, называемый фотосинтез .

Сама жизнь зависит от биологической передачи энергии.Посредством фотосинтеза растения поглощают солнечную энергию и используют эту энергию для преобразования углекислого газа и воды в глюкозу и кислород. Фотосинтез принимает одну форму энергии – свет – и преобразует ее в другую форму – химическую потенциальную энергию (глюкозу и другие углеводы).

Человеческий метаболизм – это преобразование пищи в энергию, выделяемую теплом, работой, выполняемой клетками тела, и накопленным жиром. Метаболизм – интересный пример действия первого закона термодинамики.Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии; это неромантичный взгляд на хороший буррито.

Организм усваивает всю пищу, которую мы потребляем. По сути, метаболизм – это процесс окисления, при котором высвобождается химическая потенциальная энергия пищи. Это означает, что питание осуществляется в форме работы. Упражнения помогают вам похудеть, поскольку они обеспечивают передачу энергии от вашего тела как за счет тепла, так и за счет работы, и повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя.

Биологическая термодинамика также включает изучение трансдукции между клетками и живыми организмами. Трансдукция – это процесс, при котором генетический материал – ДНК – передается от одной клетки к другой. Это часто происходит во время вирусной инфекции (например, гриппа), и именно так вирус распространяется, а именно путем передачи своего генетического материала все большему количеству ранее здоровых клеток. Как только достаточное количество клеток заражается, вы начинаете ощущать воздействие вируса (симптомы гриппа – мышечная слабость, кашель и заложенность носа).

Энергия передается вместе с генетическим материалом и, таким образом, подчиняется первому закону термодинамики. Энергия передается – а не создается и не уничтожается – в процессе. Когда с элементом выполняется работа или тепло передает энергию ячейке, внутренняя энергия ячейки увеличивается. Когда клетка работает или теряет тепло, ее внутренняя энергия уменьшается. Если количество работы, выполняемой ячейкой, такое же, как количество энергии, передаваемой теплом, или количество работы, выполняемой ячейкой, совпадает с количеством энергии, передаваемой теплом, чистого изменения внутренней энергии не будет. .

Проверка захвата

Исходя из того, что вы знаете о теплопередаче и о первом законе термодинамики, нужно ли вам есть больше или меньше, чтобы поддерживать постоянный вес в холодную погоду? Объяснить, почему.

еще
1. ; поскольку в холодную погоду организм теряет больше энергии, потребность в еде увеличивается, чтобы поддерживать постоянный вес
Еще
2. ; употребление большего количества пищи означает накопление большего количества жира, что защитит организм от холодной погоды и уменьшит потерю энергии
На
3. меньше; поскольку в холодную погоду организм теряет меньше энергии, потребность в еде уменьшается, чтобы поддерживать постоянный вес
На
4. меньше; употребление меньшего количества пищи означает накопление меньшего количества жира, поэтому для сжигания жира потребуется меньше энергии, и в результате вес останется постоянным

Термодинамика | Физика для идиотов

Есть 4 закона термодинамики, и это одни из самых важных законов во всей физике.Законы следующие

• Нулевой закон термодинамики – Если две термодинамические системы каждая находится в тепловом равновесии с третьей, то они находятся в тепловом равновесии друг с другом.
• Первый закон термодинамики – Энергия не может быть ни создана, ни разрушена. Он может только менять формы. В любом процессе общая энергия Вселенной остается неизменной. Для термодинамического цикла чистое тепло, подаваемое в систему, равно чистой работе, выполненной системой.
• Второй закон термодинамики – Энтропия изолированной системы, не находящейся в равновесии, будет иметь тенденцию увеличиваться со временем, приближаясь к максимальному значению в состоянии равновесия.
• Третий закон термодинамики – Когда температура приближается к абсолютному нулю, энтропия системы приближается к постоянному минимуму.

Прежде чем я рассмотрю эти законы более подробно, будет проще, если я сначала расскажу об энтропии.

Энтропия – очень важная вещь в области термодинамики. Это основная идея второго и третьего законов, которая проявляется повсюду. По сути, энтропия – это мера беспорядка и случайности в системе. Вот 2 примера

• Допустим, у вас есть контейнер с молекулами газа.Если все молекулы находятся в одном углу, это будет состояние с низкой энтропией (высокоорганизованное). По мере того, как частица перемещается и заполняет остальную часть контейнера, энтропия (беспорядок) увеличивается.
• Если у вас есть мяч, летящий по воздуху, он начнет движение с организованной энергией, то есть кинетической энергией движения. Однако, когда он движется по воздуху, часть кинетической энергии распределяется между частицами воздуха, поэтому общая энтропия системы увеличивается (однако общая энергия сохраняется благодаря первому закону)

Чтобы получить более подробную картину энтропии, нам нужно взглянуть на концепцию фазового пространства.Некоторые концепции для этого могут быть немного запутанными, но потерпите меня, как только вы разберетесь с мыслями, все не так уж и плохо.

Фазовое пространство похоже на график, но точка на этом графике представляет все состояние системы. Приведем пример. Представьте, что у меня есть ящик с 4 частицами газа внутри. Каждая точка в фазовом пространстве этой системы сообщает вам, где находятся все 4 шара в коробке.

В нашем примере нас интересуют только положения 4 частиц, поэтому каждая точка в фазовом пространстве должна содержать координаты x, y и z для каждой частицы, чтобы наше фазовое пространство было 3N-мерным, где N – число частиц в системе.Итак, в нашем случае фазовое пространство 12-мерное, чтобы каждая точка могла описывать расположение 4 тел.

На всех диаграммах я буду изображать фазовое пространство как 2D, чтобы было легче передать то, что оно на самом деле представляет. Для наших целей нам не нужно рассматривать размеры.

Если мы представим, что каждая из частиц имеет разный цвет, мы сможем легче отслеживать их положение. Если мы представим случай, когда все частицы расположены в одном углу контейнера, то у нас будет ситуация

С точки зрения системы существует множество других комбинаций из 4 частиц, которые будут организованы так же, как и состояние выше

и так далее.Каждая из этих установок будет соответствовать разному положению в фазовом пространстве, поскольку все они представляют собой различные схемы системы из 4-х частиц. Если мы добавим их в фазовое пространство вместе с оригиналом, мы получим что-то вроде

.

Эти 5 макетов из 4 частиц вместе с 11 другими комбинациями составляют набор состояний, которые (помимо цветов) неразличимы. Итак, в фазовом пространстве мы могли бы поместить рамку вокруг 16 состояний, которая определяет все состояния внутри него как макроскопически неразличимые.

Общее фазовое пространство системы будет иметь множество областей разной формы и размера и может выглядеть следующим образом:

Но как все это абстрактное представление связано с энтропией? Энтропия, обозначенная в уравнениях как символ, определяется как

.

Где – постоянная Больцмана (), а – объем прямоугольника в фазовом пространстве. Все точки в области фазового пространства имеют одинаковую энтропию, и значение энтропии связано с логарифмом объема (изначально Больцман никогда не вставлял константу в формулу, поскольку его не интересовали единицы измерения.Буква k, по-видимому, впервые была введена Планком).

Энтропию также можно определить как изменение при передаче энергии при постоянной температуре

Где – изменение энтропии, – энергия или тепло, а T – постоянная температура.

Нулевой закон назван так, потому что он появился после остальных 3. Законы 1, 2 и 3 существовали некоторое время, прежде чем важность этого закона была полностью осознана. Оказалось, что этот закон был настолько важен и фундаментален, что он должен был пойти раньше остальных трех, и вместо того, чтобы переименовать уже известные три закона, они назвали новый закон Нулевым и поместили его в начале списка.

Но что это на самом деле означает? В законе указано

«Если две термодинамические системы каждая находится в тепловом равновесии с третьей, то они находятся в тепловом равновесии друг с другом».

В принципе, если A = B и C = B, то A = C. Это может показаться настолько очевидным, что об этом не нужно говорить, но без этого закона мы не смогли бы определить температуру и не смогли бы построить термометры.

Первый закон термодинамики в основном утверждает, что энергия сохраняется; его нельзя ни создать, ни уничтожить, просто поменять с одного на другое,

«Общее количество энергии в изолированной системе сохраняется.”

Энергия в системе может быть преобразована в тепло, работу или другие вещи, но у вас всегда будет та же сумма, с которой вы начали.

В качестве аналогии подумайте об энергии как о неразрушимых блоках. Если у вас есть 30 блоков, то что бы вы ни делали с блоками или с ними, у вас всегда будет 30 из них в конце. Вы не можете уничтожить их, только перемещайте их или разделяйте, но их всегда будет 30. Иногда вы можете потерять один или несколько, но их все равно нужно учитывать, потому что энергия сохраняется.

Фундаментальное термодинамическое соотношение

Из второго закона мы можем записать, что изменение внутренней энергии, системы, равно теплу, подводимому к системе, минус любая работа, выполняемая системой,,

(1)

Из определения энтропии, приведенного выше, мы можем заменить, и мы также можем сделать замену, дающую нам

(2)

Теперь, если у нас есть система различных частиц, мы можем получить протекающие химические реакции, поэтому нам нужно добавить еще один член, чтобы учесть это.

(3)

Это, пожалуй, самый известный (по крайней мере, среди ученых) и важный закон всей науки.Говорится;

«Энтропия Вселенной стремится к максимуму».

Другими словами, энтропия либо остается прежней, либо увеличивается, энтропия вселенной никогда не может снизиться.

Проблема в том, что этот грех не всегда так. Если вы возьмете наш пример с 4 атомами в коробке, то все они, находящиеся в одном углу, представляют собой высокоупорядоченную систему и, следовательно, будут иметь низкую энтропию, а затем со временем они будут двигаться, становясь более неупорядоченными и увеличивая энтропию.Но ничто не мешает им беспорядочно возвращаться в угол. Это невероятно маловероятно, но на самом деле возможно.

Если вы посмотрите на проблему с точки зрения фазового пространства, вы увидите, что со временем более вероятно, что вы переместитесь в более крупную коробку, что означает более высокую энтропию, но на самом деле нет никаких препятствий, мешающих вам вернуться в меньшую коробку.

Третий закон обеспечивает абсолютную точку отсчета для измерения энтропии, говоря, что

«Когда температура системы приближается к абсолютному нулю (−273.15 ° C, 0 K), то значение энтропии приближается к минимуму ».

Значение энтропии обычно равно 0 при 0K, однако бывают случаи, когда в системе все еще остается небольшое количество остаточной энтропии.

Когда вы нагреваете что-либо, в зависимости от того, из чего оно сделано, для нагрева требуется разное количество времени. Если предположить, что мощность, количество энергии, передаваемой за единицу времени, остается постоянной, это должно означать, что некоторым материалам требуется больше энергии для повышения их температуры на 1 К (1 К на самом деле то же самое, что 1 ° C, они просто начинаются в другом месте. .Для получения дополнительной информации щелкните здесь), чем другие. Если задуматься, в этом есть смысл. Деревянная ложка нагревается намного дольше, чем металлическая. Мы говорим, что металл является хорошим проводником тепла, а дерево – плохим проводником тепла. Энергия, необходимая для подъема 1 кг вещества на 1 К, называется удельной теплоемкостью. Формула, которую мы используем, чтобы найти, сколько энергии требуется, чтобы поднять 1 кг вещества на 1К, составляет:

где = энергия, = масса, = удельная теплоемкость и = изменение температуры.

1а. Лора готовит завтрак перед работой в воскресенье утром (пожалуйста, пришлите сюда свои сообщения сочувствия, что мне пришлось работать в воскресенье). Она больше не хочет мыть посуду, которая абсолютно необходима, поэтому решает помешать спагетти, которые готовит, вилкой, вместо того, чтобы мыть деревянной ложкой. Она оставляет вилку на сковороде, намазывает тост маргарином и натирает сыр. Плита выдает вилке 1000 Дж энергии за то время, пока она ее не трогает.Каким будет повышение температуры вилки, если предположить, что половина выделяемой энергии будет потеряна для окружающей среды, а начальная температура вилки составляла 20 ° C, а масса вилки составляет 50 г и изготовлена ​​из материала с особыми свойствами. тепловая мощность 460 Джкг-1К-1

Хотя я почти уверен, что где-то читал, что попытка проработать энергетические изменения в вилках первым делом утром была симптомом безумия, я время от времени делаю это. Для этого вопроса нам понадобится уравнение Q = mcΔT. Это уравнение, которое вам, вероятно, понадобится, так что стоит попытаться запомнить его.Это также возникает в химии. Прежде всего, нам нужно изменить уравнение, чтобы сделать ΔT объектом. После перестановки этого вопроса вы должны получить ΔT = Q / (mc). Подставляя данные нам значения в вопрос, вы получаете:

ΔT = 1000 / (50 x 10-3 x 460)
ΔT = 43K
Итак, поскольку начальная температура вилки была 20 ° C, конечная температура вилки будет 63 ° C.

• Внутренняя энергия:
• Бесплатная энергия Гельмгольца:
• Энтальпия:
• Свободная энергия Гиббса:

Отношения Максвелла

(4)

(5)

(6)

(7)

термодинамика | Законы, определения и уравнения

Термодинамика , наука о взаимосвязи между теплотой, работой, температурой и энергией.В широком смысле термодинамика занимается передачей энергии из одного места в другое и из одной формы в другую. Ключевое понятие заключается в том, что тепло – это форма энергии, соответствующая определенному количеству механической работы.

Популярные вопросы

Что такое термодинамика?

Термодинамика – это изучение отношений между теплотой, работой, температурой и энергией. Законы термодинамики описывают, как изменяется энергия в системе и может ли система выполнять полезную работу со своим окружением.

Является ли термодинамика физикой?

Да, термодинамика – это раздел физики, изучающий изменение энергии в системе. Ключевое понимание термодинамики состоит в том, что тепло – это форма энергии, которая соответствует механической работе (то есть приложению силы к объекту на расстоянии).

Тепло не было официально признано формой энергии примерно до 1798 года, когда граф Рамфорд (сэр Бенджамин Томпсон), британский военный инженер, заметил, что при сверлении стволов пушек может генерироваться безграничное количество тепла, а также Вырабатываемое тепло пропорционально работе, проделанной при токарной обработке тупого расточного инструмента.Наблюдение Рамфорда пропорциональности выделяемого тепла и проделанной работы лежит в основе термодинамики. Еще одним пионером был французский военный инженер Сади Карно, который в 1824 году представил концепцию цикла тепловой машины и принцип обратимости. высокотемпературная теплопередача как движущая сила. Позже в том же веке эти идеи были развиты Рудольфом Клаузиусом, немецким математиком и физиком, в первый и второй законы термодинамики соответственно.

Наиболее важные законы термодинамики:

• Нулевой закон термодинамики. Когда две системы находятся в тепловом равновесии с третьей системой, первые две системы находятся в тепловом равновесии друг с другом. Это свойство делает целесообразным использование термометров в качестве «третьей системы» и определения шкалы температур.
• Первый закон термодинамики или закон сохранения энергии. Изменение внутренней энергии системы равно разнице между теплом, добавляемым к системе из окружающей среды, и работой, выполняемой системой над своим окружением.
• Второй закон термодинамики. Тепло не перетекает самопроизвольно из более холодной области в более горячую, или, что то же самое, тепло при данной температуре не может быть полностью преобразовано в работу. Следовательно, энтропия замкнутой системы или тепловая энергия на единицу температуры со временем увеличивается до некоторого максимального значения. Таким образом, все закрытые системы стремятся к состоянию равновесия, в котором энтропия максимальна, а энергия недоступна для выполнения полезной работы.
• Третий закон термодинамики. Энтропия идеального кристалла элемента в его наиболее стабильной форме стремится к нулю, когда температура приближается к абсолютному нулю. Это позволяет установить абсолютную шкалу энтропии, которая со статистической точки зрения определяет степень случайности или беспорядка в системе.

Хотя термодинамика быстро развивалась в 19 веке в ответ на необходимость оптимизации работы паровых двигателей, широкая общность законов термодинамики делает их применимыми ко всем физическим и биологическим системам.В частности, законы термодинамики дают полное описание всех изменений энергетического состояния любой системы и ее способности выполнять полезную работу со своим окружением.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Эта статья посвящена классической термодинамике, которая не включает рассмотрение отдельных атомов или молекул. Такие проблемы находятся в центре внимания раздела термодинамики, известного как статистическая термодинамика или статистическая механика, которая выражает макроскопические термодинамические свойства в терминах поведения отдельных частиц и их взаимодействий.Его корни уходят в последнюю половину XIX века, когда атомные и молекулярные теории материи стали общепринятыми.

Основные концепции

Термодинамические состояния

Применение принципов термодинамики начинается с определения системы, которая в некотором смысле отличается от своего окружения. Например, система может быть образцом газа внутри цилиндра с подвижным поршнем, целым паровым двигателем, марафонцем, планетой Земля, нейтронной звездой, черной дырой или даже всей вселенной.В общем, системы могут свободно обмениваться теплом, работой и другими формами энергии со своим окружением.

Состояние системы в любой момент времени называется ее термодинамическим состоянием. Для газа в баллоне с подвижным поршнем состояние системы определяется температурой, давлением и объемом газа. Эти свойства являются характеристическими параметрами, которые имеют определенные значения в каждом состоянии и не зависят от способа, которым система пришла в это состояние. Другими словами, любое изменение значения свойства зависит только от начального и конечного состояний системы, а не от пути, пройденного системой от одного состояния к другому.Такие свойства называются функциями состояния. Напротив, работа, выполняемая при движении поршня и расширении газа, и тепло, которое газ поглощает из окружающей среды, зависят от того, каким образом происходит расширение.

Поведение сложной термодинамической системы, такой как атмосфера Земли, можно понять, сначала применив принципы состояний и свойств к ее составным частям – в данном случае к воде, водяному пару и различным газам, составляющим атмосферу.