Теория функций комплексного переменного | Открытые видеолекции учебных курсов МГУ
Курс «Теория функций комплексного переменного» читается студентам второго курса физического факультета МГУ имени М. В. Ломоносова в 3 семестре. На семинарских занятиях рассматриваются следующие темы:
Комплексные числа, функции комплексной переменной.
Непрерывность и дифференцируемость функции комплексной переменной. Понятие аналитической функции комплексной переменной.
Интеграл от функции комплексной переменной, Интеграл типа Коши. Свойства интегралов.
Ряды аналитических функций. Степенные ряды.
Ряд Лорана. Особые точки функций.
Вычеты. Основная теорема теории вычетов. Вычисление несобственных интегралов действительной переменной с помощью вычетов.
Основные понятия операционного исчисления.
Список всех тем лекций
Семинар 1. Действия с комплексными числами.
Действия с комплексными числами Примеры Экспонента с чисто мнимым показателем Формы записи комплексного числа Вычисление корня n-ной степени Возведение числа в целую степень Примеры (нахождение модуля и аргумента) Нахождение с помощью формулы Муавра тригонометрических функций кратных углов Множества на комплексной плоскости
Семинар 2. Понятие функции комплексной переменной. Элементарные функции.
Семинар 3. Аналитические функции. Условия Коши-Римана. Интеграл по кривой. Теорема и интегральная формула Коши.
Непрерывность, сходимость на комплексной плоскости
Условия Коши-Римана
Следствия условий Коши-Римана
Интеграл по кривой
Теорема Коши
Интегральная формула Коши
Семинар 4.
Радиус и круг сходимости
Семинар 5. Ряд Лорана.
Ряд Лорана
Семинар 6. Классификация особых точек. Однозначные и многозначные функции.
Особые точки однозначных функций
Точки ветвления
Семинар 7. Вычисление вычетов.
Вычисление вычетов
Вычисление вычетов разложением в ряд Лорана
Вычисление вычетов другими методами
Семинар 8. Вычисление интегралов с помощью вычетов. Часть 1.
Теорема теории вычетов
Пример 1
Пример 2
Вычисление интегралов функции вещественной переменной
Пример 3
Лемма
Пример 4
Пример 5
Семинар 9.
Лемма Жордана
Семинар 10. Операционное исчисление (преобразование Лапласа).
Свойства преобразования Лапласа
Изображения некоторых элементарных функций
Формула Меллина
Методические указания к решению задач по теории функций комплексного переменного для студентов радиофизического и физического факультетов
eKhNUIR >
Фізичний факультет >
Навчальні видання. Фізичний факультет >
Please use this identifier to cite or link to this item: |
| Название: | Методические указания к решению задач по теории функций комплексного переменного для студентов радиофизического и физического факультетов |
| Авторы: | Кондратьев, Б. В. В. |
| Ключевые слова: | комплексные числа функции комплексного переменного конформные отображения интегрирование ФКП степенные ряды ряды Лорана особые точки ФКП вычеты и их применения операционное исчисление специальные функции теория плоского электростатического поля |
| Issue Date: | 2010 |
| Издатель: | ХНУ имени В. Н. Каразина |
| Библиографическое описание: | Методические указания к решению задач по теории функций комплексного переменного для студентов радиофизического и физического факультетов / Сост. : Кондратьев Б.В. – Х. : ХНУ имени В. Н. Каразина, 2010. – 76 с. |
| Краткий осмотр (реферат): | Методические указания имеют целью оказать помощь студентам радиофизического и физического факультетов при подготовке к практическим занятиям по теории функций комплексного переменного и ее приложениям (свойства аналитических функций, их отображения, интегралы и вычеты, операционные методы, плоское электростатическое поле, асимптотические методы и др. |
| URI: | http://dspace.univer.kharkov.ua/handle/123456789/6192 |
| Appears in Collections: | Навчальні видання. Фізичний факультет Навчальні видання. Радіофізичний факультет |
Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.
ПРОГРАММА ДИСЦИПЛИНЫ 04 ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
(ТГПУ)
УТВЕРЖДАЮ
Проректор по учебной работе
(декан факультета)
_________________________
“___”____________200__ г.
ПРОГРАММА ДИСЦИПЛИНЫ
ДПП.Ф.04 ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО(050201.65 Математика)
Томск – 2008
Пояснительная записка
Теория функций комплексной переменной является одним из заключительных разделов общего курса высшей математики, изучаемой студентами физиками. Фундаментальные понятия теории функций комплексной переменной находят широкое применение в большинстве разделов современной математики и физики.
Теория
функций комплексной переменной связана
с изучением аналитических функций. В
данном курсе важнейшие понятия
математического анализа функций
действительной переменной, такие как
предел, непрерывность, дифференцируемость,
интегрируемость, ряд и его сходимость
формулируются для функций комплексной
переменной и изучаются их свойства. При
этом возникают новые интересные аспекты,
связанные с конформными отображениями
и методами вычисления определенных
интегралов от функций действительной
переменной на основе понятий теории
функций действительной переменной.
1. Цели и задачи дисциплины:
Курс теория функций комплексной переменной направлен на развитие методов исследования функций в комплексной области и применение этих методов к задачам математического анализа. Формулируются базовые понятия математического анализа, такие как предел, непрерывность, производная, интеграл и ряд для комплексных функций, зависящих от комплексной переменной. Материалы данного курса используются при изучении курсов методы математической физики, классическая механика, электродинамика, квантовая механика, а также спецкурсов по теоретической физике. Знание методов теории функций комплексной переменной является необходимым элементов математического образования современного ученого-физика.

Для достижения данной цели необходимо решить следующие задачи:
сформировать представления об аналитических функциях, конформном отображении, комплексном интеграле, аналитическом продолжении, римановой поверхности и особых точках функции, рядах аналитических функций, вычетах;
выработать умения и навыки дифференцирования функций комплексного переменного, построения конформных отображений простейших областей, вычисления комплексных интегралов, разложения функций в ряд Тейлора и ряд Лорана, а также вычисления вычетов функций;
научить применять методы комплексного анализа для вычисления определённых и несобственных интегралов и решения других задач алгебры и анализа;
познакомить с современными направлениями развития комплексного анализа.
2. Требования к уровню освоения содержания дисциплины:
В результате изучения дисциплины студент должен:
иметь представление об основных понятиях теории функций комплексного переменного;
знать и уметь доказывать основные теоремы курса;
уметь вычислять производные и интегралы функций комплексного переменного,
восстанавливать аналитическую функцию по её действительной или мнимой части;
уметь производить конформные отображения с помощью линейной и дробно-линейной функций, степенной и радикала, экспоненты и логарифма, а также тригонометрических функций;
уметь представлять элементарные функции комплексного переменного рядами Тейлора и Лорана, находить их области сходимости;
уметь применять теорию вычетов для вычисления комплексных и вещественных интегралов;
иметь представление о современных направлениях развития комплексного анализа и его приложениях.

3. Объем дисциплины и виды учебной работы:
Вид учебной работы | Всего часов | Семестры | |||
5 | 6 | 7 | 8 | ||
Общая трудоемкость дисциплины | 126 | 126 | |||
Аудиторные занятия | 54 | 54 | |||
Лекции | 36 | 36 | |||
Практические занятия (ПЗ) | 18 | 18 | |||
Семинары (С) | |||||
Лабораторные работы (ЛР) | |||||
И (или) др. | |||||
Самостоятельная работа (СР) | 72 | 72 | |||
Курсовые работы | |||||
Расчетно-графические работы | |||||
Рефераты | |||||
И (или) др. виды | |||||
Вид итогового контроля (зачет, экзамен) | Экз. | ||||
4. Содержание дисциплины:
4.1. Разделы дисциплины и виды занятий (Тематический план)
5 семестр
№ п/п | Разделы дисциплины | Лекции | Практ. занятия или семинары | Лаборат. Работы |
1 | Комплексные числа | 4 | 2 | |
2 | Аналитические функции и их свойства | 8 | 6 | |
3 | Интеграл по
комплексной переменной. | 8 | 6 | |
4 | Ряды аналитических функций | 6 | 2 | |
5 | Основные понятия теории конформных отображений | 6 | 2 | |
6 | Преобразование Лапласа | 4 | ||
Всего | 36 | 18 |
4. 2. Содержание разделов дисциплины:
2. Содержание разделов дисциплины:
Комплексные числа: определение и геометрическая интерпретация; арифметика комплексных чисел; алгебра комплексных чисел: Сфера Римана. Бесконечно удаленная точка. Области и их связность.
Аналитические функции и их свойства: определение функции комплексной переменной и ее геометрическое истолкование, выделение действительной и мнимой части. Последовательность комплексных чисел и ее предел. Предел функции комплексной переменной. Непрерывность. Понятия производной функции комплексной переменной. Дифференциал. Условие дифференцируемости функции комплексной переменной. Понятие аналитической функции. Гармонические функции. Восстановление аналитической функции по ее действительной (мнимой) части. Элементарные аналитические функции в комплексной области: Показательная и тригонометрическая функции в комплексной области и их свойства. Применение формул Эйлера. Логарифмы комплексных чисел.

Интеграл по комплексной переменной: понятие интеграла от функции комплексной переменной и его свойства. Интегральная теорема Коши для односвязной области, интегральная теорема для многосвязной области. Интегральная формула Коши и ее следствия. Аналитичность непрерывно дифференцируемой функции. Применение формулы Коши к вычислению определенных интегралов.
Ряды аналитических функций: степенные ряды в комплексной области; ряд Тейлора; теорема единственности аналитических функций; понятие об аналитическом продолжении функций. Ряд Лорана: теорема Лорана; изолированные особые точки; классификация изолированных особых точек. Устранимые особые точки, полюсы, существенно особые точки. Вычеты: определение и применение к вычислению определенных интегралов.
Основные понятия теории конформных отображений, отображение кривых и областей. Дифференцирование функций комплексной переменной и конформные отображения: геометрический смысл аргумента и модуля производной.
 Конформные отображения
I и II рода. Функция Жуковского, конформное
отображение
.
Гиперболические функции в конформной
области и их свойства.
Конформные отображения
I и II рода. Функция Жуковского, конформное
отображение
.
Гиперболические функции в конформной
области и их свойства.Преобразование Лапласа: определение и свойства; операционное исчисление; решение дифференциальных уравнений и систем дифференциальных уравнений с помощью преобразования Лапласа.
5. Лабораторный практикум, практические занятия (семинары)
“Арифметика” комплексных чисел; определение операций над комплексными числами и их выполнение. Решение задач.
Дифференцирование комплексных функций, аналитические функции, гармонические функции. Решение задач.
Интегрирование комплексных функций, теорема и формула Коши. Вычеты. Вычисление интегралов.
Ряды на множестве комплексных чисел: ряд Тейлора и ряд Лорана. Основные понятия теории.
Понятие о конформном отображение.
 Решение задач.
Решение задач.
6. Учебно-методическое обеспечение дисциплины:
6.1. Рекомендуемая литература:
а) основная литература:
Волковыский, Л.И. Сборник задач по теории функций комплексного переменного: учебное пособие для вузов/ Л.И. Волковыский, Г.Л. Лунц, И.Г. Араманович. – М.: Наука, 2006. – 312с.
Лунц, Г.Л. Функции комплексного переменного: учебник для вузов/ Г.Л. Лунц, Л.Э. Эльсгольц. – М.: Наука, 2002. – 296 с.
б) дополнительная литература:
Евграфов, М.А. Сборник задач по теории аналитических функций: учебное пособие для вузов/ М.А. Евграфов [и др.]. – М.: Наука, 1972. -187с.
Куваев, М.Р. Математический анализ: учебник для вузов. В 3 ч. Ч. 3/ М.Р. Куваев. – Томск: ТГУ, 1980. – 311с.
Лаврентьев, М.
 А. Методы теории функций комплексного
переменного: учебное пособие для вузов./
М.А. Лаврентьев, Б.В. Шабат. – М.: Наука,
1987. – 158с.
А. Методы теории функций комплексного
переменного: учебное пособие для вузов./
М.А. Лаврентьев, Б.В. Шабат. – М.: Наука,
1987. – 158с.Маркушевич, А.И. Краткий курс теории аналитических функций: учебное пособие для вузов/ А.И. Маркушевич. – М.: Наука. 1978. – 319с.
Маркушевич, А.И. Теория аналитических функций: учебное пособие для вузов/ А.И. Маркушевич. – М.: Наука. 1980. – 329с.
Привалов, И.И. Введение в теорию функций комплексной переменной: учебник для вузов/ И.И.Привалов. – М.: Наука. 1999. – 432с.
Шабат, М.И. Введение в теорию функций комплексной переменной: учебник для вузов/ М.И. Шабат. – М.: Наука. 1984. – 317с.
6.2. Средства обеспечения освоения дисциплины:
Рабочие программы по математическому анализу.
7. Материально-техническое обеспечение дисциплины
Не предусмотрено
8. Методические
рекомендации по организации изучения
дисциплины
Методические
рекомендации по организации изучения
дисциплины
8.1.Для преподавателей:
Необходимо сделать акцент на вопросах, ближе всего стоящих к профессиональным интересам студентов. Так на факультете экономики и управления следует уделить больше внимания решению математических задач экономического содержания.
Лекция – главное звено дидактического цикла обучения. Её цель – формирование у студентов ориентировочной основы для последующего усвоения материала методом самостоятельной работы. Содержание лекции должно отвечать следующим дидактическим требованиям:
изложение материала от простого к сложному, от известного к неизвестному;
логичность, четкость и ясность в изложении материала;
возможность проблемного изложения, дискуссии, диалога с целью активизации деятельности студентов;
тесная связь теоретических положений и выводов с практикой и будущей профессиональной деятельностью студентов.

Лекция по теме должна завершаться обобщающими выводами.
Цель практических занятий состоит в выработке устойчивых навыков решения основных примеров и задач дисциплины, на которых основана теория лекционного курса.
Практические занятия проводятся по узловым и наиболее сложным вопросам (темам, разделам) учебной программы. Они могут быть построены как на материале одной лекции, так и на содержании обзорной лекции, а также по определённой теме без чтения предварительной лекции. Главная и определяющая особенность любого практического занятия – наличие элементов дискуссии, проблемности, диалога между преподавателем и студентами и самими студентами.
В конце практического занятия рекомендуется дать оценку всей работы, обратив особое внимание на следующие аспекты:
качество подготовки;
степень усвоения знаний;
активность;
положительные стороны в работе студентов;
ценные и конструктивные предложения;
недостатки в работе студентов;
задачи и пути устранения недостатков.

По курсу практических занятий рекомендуется проведение контрольных работ и расчетно-графических домашних заданий, оценка которых осуществляется по пятибальной системе.
Организуя самостоятельную работу, необходимо постоянно обучать студентов методам такой работы.
При проведении итоговой аттестации студентов важно всегда помнить, что систематичность, объективность, аргументированность – главные принципы, на которых основаны контроль и оценка знаний студентов. Проверка, контроль и оценка знаний студента, требуют учета его индивидуального стиля в осуществлении учебной деятельности. Знание критериев оценки знаний обязательно для преподавателя и студента.
8.2 Для студентов:
Студентам предлагается использовать
указанную литературу и методические
рекомендации, разработанные сотрудниками
кафедры математического анализа ТГПУ
для более прочного усвоения учебного
материала, изложенного на лекциях, а
также для изучения материала,
запланированного для самостоятельной
работы. Студентам необходимо выполнить
индивидуальные задания по основным
темам курса. Задания, вынесенные на
самостоятельную работу, проверяются
преподавателем в течение семестра.
Оценки за индивидуальные задания и
самостоятельную работу учитываются
при выставлении оценок на экзаменах.
Студентам необходимо выполнить
индивидуальные задания по основным
темам курса. Задания, вынесенные на
самостоятельную работу, проверяются
преподавателем в течение семестра.
Оценки за индивидуальные задания и
самостоятельную работу учитываются
при выставлении оценок на экзаменах.
Целью самостоятельной работы, т.е. работы, выполняемой студентами во внеаудиторное время по заданию и руководству преподавателя является глубокое понимание и усвоение курса лекций и практических занятий, подготовка к выполнению контрольных работ, к выполнению семестрового задания, к сдаче зачета и (или) экзамена, овладение профессиональными умениями и навыками деятельности, опытом творческой, исследовательской деятельности.
Для успешной подготовки и сдачи зачета (экзамена) необходимо проделать следующую работу:
Изучить теоретический материал, относящийся к каждому из разделов.
Выработать устойчивые навыки в решении типовых практических заданий.

Выполнить контрольные работы, проводимые в течение семестра.
Перечень примерных контрольных вопросов и заданий для самостоятельной работы:
Определение комплексных чисел, алгебраическая и тригонометрическая формы комплексных чисел. Возведение в натуральную степень и извлечение корня из комплексных чисел. Операции над комплексными числами в тригонометрической форме. Определение показательной функции и логарифма комплексного числа.
Комплексные функции действительного аргумента. Геометрия на комплексной плоскости: геометрическая интерпретация комплексных чисел и операций над ними, кривые и множества на комплексной плоскости.
Комплексные числовые последовательности: определение, сходимость, свойства (теорема о сходимости, ограниченные последовательности, необходимое и достаточное условия сходимости числовых последовательностей, критерий сходимости Коши).

Множества и области на комплексной плоскости – основные понятия и терминология. Комплексные функции комплексного переменного: определение и геометрическая интерпретация. Кривые и области на комплексной плоскости.
Предел функции комплексного переменного: определение и геометрическая интерпретация. Свойства функций имеющих предел. Непрерывность функции комплексного переменного: определение и свойства.
Дифференцирование функции комплексного переменного: определение производной, дифференцируемые функции и их свойства. Условия Коши-Римана. Аналитические функции. Различные формы условий Коши-Римана. Свойства аналитических функций. Геометрический смысл производной комплексной функции (модуль и аргумент производной). Конформные отображения. Восстановление комплексной функции по ее действительной или мнимой части.
Интегрирование комплексной функции действительного аргумента.
 Интегрирование комплексной
функции комплексного аргумента, связь
комплексного интеграла с криволинейным
интегралом. Интегральная теорема Коши.
Формула Коши и ее следствия. Вычисление
интегралов с помощью интегральной
теоремы и формулы Коши.
Интегрирование комплексной
функции комплексного аргумента, связь
комплексного интеграла с криволинейным
интегралом. Интегральная теорема Коши.
Формула Коши и ее следствия. Вычисление
интегралов с помощью интегральной
теоремы и формулы Коши.Ряды числовые и функциональные на множестве комплексных чисел. Степенные ряды: определение, область и радиус сходимости, свойства. Ряды Тейлора: определение, теорема Тейлора, разложение в ряд Тейлора.
Ряд Лорана: правильные и особые точки аналитических функций, определение ряда Лорана, область сходимости ряда Лорана, Теорема Лорана. Особые изолированные точки аналитических функций: определение и классификация. Теоремы об особых точках.
Вычеты в особых изолированных точках. Основная теорема теории вычетов. Применение теории вычетов для вычисления интегралов. Логарифмический вычет и его применение.
Примерные темы рефератов, курсовых работ:
Темы рефератов
Формальные производные.
 Условия Коши – Римана в
полярных координатах.
Условия Коши – Римана в
полярных координатах.Конформные отображения I и II родов.
Функция Жуковского и ее свойства.
Интеграл типа Коши и его свойства.
Формулы Сохоцкого.
Интеграл Пуассона. Решение задачи Дирихле.
Целые и мероморфные функции. Примеры. Порядок и тип.
Бесконечные произведения с комплексными членами.
Конформные отображения круга на круг или на верхнюю полуплоскость.
Дробно – линейные функции и интерпретация геометрии Лобачевского.
Римановы поверхности радикала, логарифма и других функций.
Гармонические функции и их свойства. Задача Дирихле.
Плоское векторное поле и комплексный потенциал. Физические представления.

Краевая задача Римана.
Сингулярные интегральные уравнения.
Применение ТФКП в решении уравнений с частными производными.
Задачи гидродинамики и газовой динамики.
Разложения мероморфных функций на элементарные дроби.
Разложения функций в бесконечные произведения.
Нули аналитических функций и теория устойчивости.
Методы асимптотических оценок.
Темы курсовых работ
Формальные производные.
Конформные отображения II рода.
Функция Жуковского и ее свойства.
Интеграл типа Коши и его свойства.
Формулы Сохоцкого.
Интеграл Пуассона.
 Решение задачи Дирихле.
Решение задачи Дирихле.Целые и мероморфные функции.
Бесконечные произведения с комплексными членами.
Конформные отображения круга на круг или на верхнюю полуплоскость.
Теорема Пикара.
Дробно – линейные функции и интерпретация геометрии Лобачевского.
Римановы поверхности радикала, логарифма и других функций.
Гармонические функции и их свойства. Задача Дирихле.
Плоское векторное поле и комплексный потенциал. Физические представления.
Краевая задача Римана.
Сингулярные интегральные уравнения.
Применение ТФКП в решении уравнений с частными производными.
Задачи гидродинамики и газовой динамики.
Разложения мероморфных функций на элементарные дроби.

Разложения функций в бесконечные произведения.
Нули аналитических функций и теория устойчивости.
Методы асимптотических оценок.
Программа составлена в соответствии с Государственным образовательным стандартом высшего профессионального образования по специальности 050201.65 “Математика”.
Программу составил:
Голубенко Т.Я.____________
Доцент кафедры математического анализа ТГПУ
Программа дисциплины утверждена на заседании кафедры математического анализа
« » 2008 г.
Заведующий кафедрой
математического анализа. _________________ Лавров П.М.
Программа дисциплины одобрена методической комиссией физико-математического факультета ТГПУ
Председатель методической комиссии
ФМФ ТГПУ _____________ Шишковский В.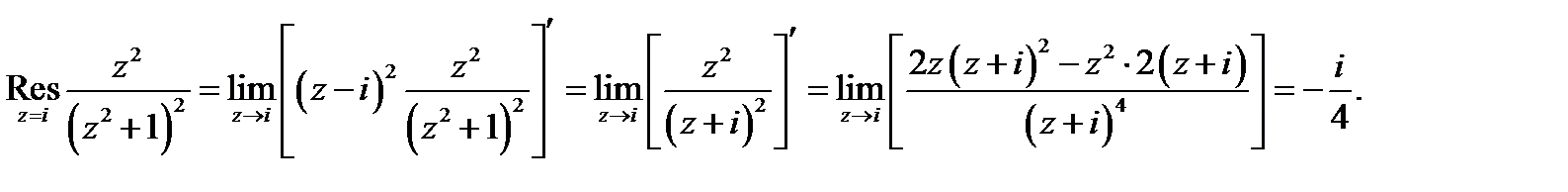 И.
И.
Согласовано:
Декан физико-математического факультета ТГПУ _ _______________ Макаренко А.Н.
Методическая разработка Решение задач по ТФКП Комплексные числа Операции над комплексными числами Комплексная плоскость – Методическая разработка
Вычисление вычетов.
Вычетом функции f(z) в конечной изолированной особой точке a называется число
,
где C-окружность достаточно малого радиуса с центром в точке a, пробегаемая против часовой стрелки. Вычет в бесконечности (-изолированная особая точка) определяется по формуле
,
где C– -окружность достаточно большого радиуса, пробегаемая по часовой стрелке. Вычет функции f(z) в конечной изолированной особой точке a равен коэффициенту с-1 в разложении функции f(z) в ряд Лорана при (z–a)-1
.
Вычет функции f(z) в изолированной особой точке равен коэффициенту –с-1 в разложении функции f(z) в ряд Лорана при z-1
.
Если у аналитической функции f(z) имеется лишь конечное чисто изолированных особых точек, то сумма вычетов в этих точках, включая вычет в равна нулю.
Если a – полюс порядка n функции f(z), то
.
В случае полюса первого порядка формула имеет вид
.
1. Найти вычет функции относительно всех изолированных особых точек (и.о.т.).
Решение. Функция имеет два полюса второго порядка в точках i и –i. В имеется устранимая особенность.
. Аналогично . Из формулы для суммы вычетов следует, что .
2. Найти вычет функции относительно всех изолированных особых точек.
Решение.
Функция имеет две и. о.т. 0 и .
Воспользуемся разложением экспоненты
в ряд Тейлора для получения разложения
исходной функции в ряд Лорана.
о.т. 0 и .
Воспользуемся разложением экспоненты
в ряд Тейлора для получения разложения
исходной функции в ряд Лорана.
Разложение имеет место в кольце 0<|z|<. Найдем коэффициент c-1этого разложения. Для получения этого слагаемого необходимо выполнение условия k–m=-1, откуда m=k+1. Учитывая это, получим
.
3. Найти вычет функций относительно всех изолированных особых точек.
Решение. Покажем вначале, что функции sin z и cos z в комплексной плоскости имеют нули только на вещественной оси. Действительно,
. Откуда следует, что sin z = 0 лишь в случае sin x = 0 и sh y = 0. Аналогично для функции cos z имеем: .
Откуда
следует, что cos z = 0 лишь в случае cos x = 0 и sh y = 0.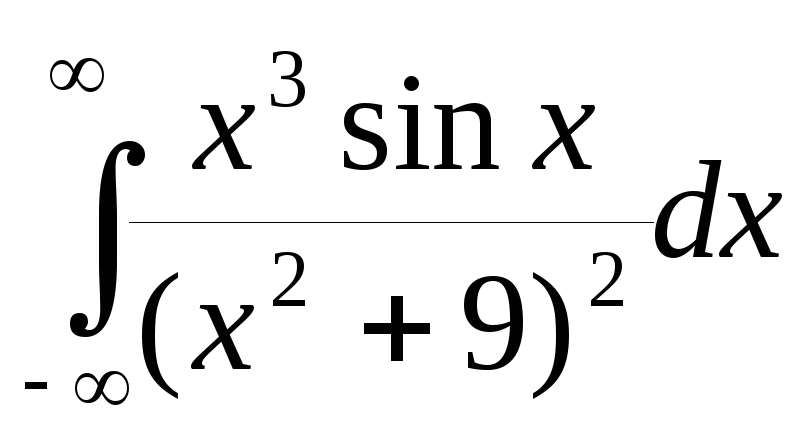 Таким образом, исходная
функция имеет только полюсы второго
порядка в нулях синуса, т.е. в точках k.
Так как
и
вычет единицы равен нулю, то вычеты
можно считать для функции
.
Имеем
Таким образом, исходная
функция имеет только полюсы второго
порядка в нулях синуса, т.е. в точках k.
Так как
и
вычет единицы равен нулю, то вычеты
можно считать для функции
.
Имеем
.
. Воспользовавшись первыми двумя членами разложений в ряд Тейлора функций sin и cos легко установить, что бесконечно малая sin u – u cos u в нуле имеет третий порядок малости. таким образом в последнем выражении числитель имеет четвертый порядок малости, в то время, как знаменатель имеет третий порядок малости, и указанный предел равен нулю. Все вычеты равны нулю.
4. Найти вычет функций относительно всех изолированных особых точек.
Решение. Функция имеет две и.о.т. 0 и . Воспользуемся разложением синуса в ряд Тейлора для получения разложения исходной функции в ряд Лорана.
. При перемножении общий член ряда Лорана будет иметь вид . Отсюда следует, что c-1=0. вычеты в нуле и бесконечности равны нулю.
5.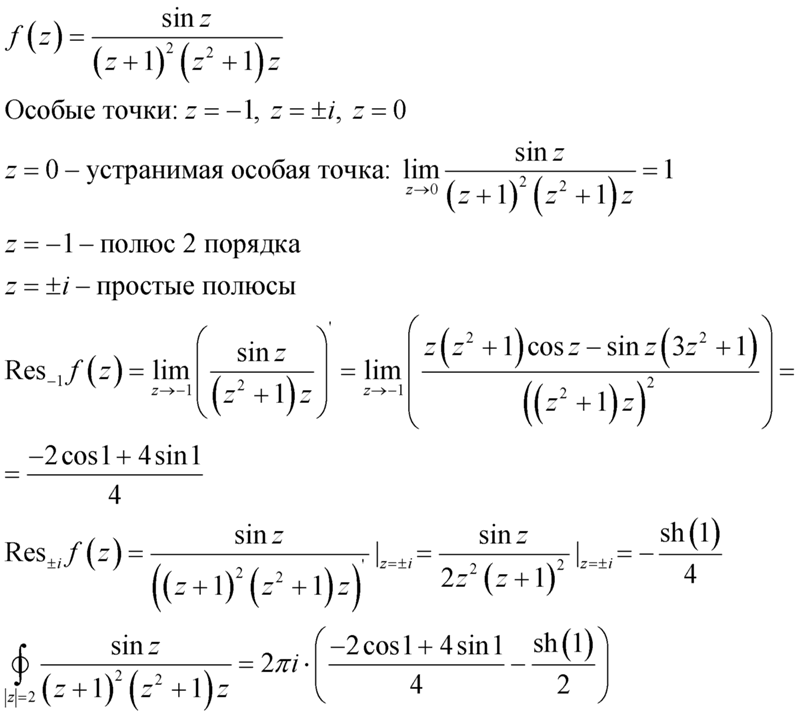 Найти вычет функций
относительно
всех изолированных особых точек.
Найти вычет функций
относительно
всех изолированных особых точек.
Решение. Функция имеет две и.о.т. 0 и . Воспользуемся разложением косинуса в ряд Тейлора для получения разложения исходной функции в ряд Лорана по степеням z-2.
Коэффициент c-1 будет складываться из двух значений, из первой суммы при k=2 и третьей сумма при k=1
. Вычет в будет равен 143/24.
6. Найти вычет функций относительно всех изолированных особых точек.
Решение. Функция имеет полюс второго порядка в 0, полюс первого порядка в 1 и устранимую и.о.т. в .
. Отсюда следует, что
.
Вычисление интегралов.
Если функция непрерывна вплоть до границы области D и аналитична внутри области, за исключением конечного число особых точек ak, то
.
1.
Вычислить интеграл
, С={x2 +y2 =2x}, проходимый в положительном направлении.
Решение. Контур представляет собой окружность радиуса 1 с центром в начале координат. Корни знаменателя подынтегральной функции лежат на единичной окружности и на биссектрисах первого-третьего и второго-четвертого углов. Внутрь контура C попадают два из них, лежащих в правой полуплоскости . Остальные два лежат вне области.
.
. Исходный интеграл будет равен .
2. Вычислить интеграл , проходимая в положительном направлении.
Решение. Внутри контура лежат пять особых точек, вне контура две: 3-полюс первого порядка, - устранимая особая точка. Вычет в точке три будем считать по формуле для полюсов, вычет в вычислим по ряду Лорана.
. Разложение в ряд Лорана подынтегральной функции в окрестности имеет вид
.
Ряд сходится в кольце 3<|z|<.
Коэффициент c-1 формируется из индексов,
удовлетворяющих условию 5m+k+6=1, так как таких индексов
нет, то c-1=0 и
,
поэтому
.
3. Вычислить интеграл , проходимая в положительном направлении.
Решение. Все особые точки подынтегральной функции лежат не окружности радиуса , и, таким образом, попадают внутрь контура интегрирования. Следовательно, интеграл будет равен
. Для вычисления вычета в воспользуемся разложением в ряд Лорана
, откуда c-1=0.5, следовательно Ответ i.
4. Вычислить интеграл где С – окружность |z|=r, проходимая в положительном направлении.
Решение. является изолированной особой точкой. Для вычисления вычета в бесконечности воспользуемся разложением в ряд Лорана.
.
Не нулевой коэффициент при –1 степени формируется из индексов, удовлетворяющих условию 2k+2m-2=1, k+m=3/2. Таких индексов нет, следовательно, интеграл равен нулю.
5. Вычислить интеграл где n- целое и С – окружность |z|=r, проходимая в положительном направлении.
Решение. Воспользуемся разложением в ряд Лорана.
Воспользуемся разложением в ряд Лорана.
. Равенство k-n=1 Будет выполнено при n -1. Для этих значений параметра . Для остальных значений параметра n интеграл I=0.
Вычисление интегралов. Продолжение.
Для вычисления интегралов вида используют следующие два вспомогательных утверждения
Лемма. Если f(z) аналитична в {Im z >= 0 } кроме конечного числа о.т. ak{Im z > 0} и , то
.
Здесь CR={Im z 0, |z|=R}.
Обобщённая лемма. Если f(z) аналитична в {Im z >= 0 } кроме конечного числа о.т. ak{Im z > 0}, на вещественной оси имеются только полюсы первого порядка bk и , то
Лемма
Жордана. Если f(z) непрерывна в { |z|R0,
Im z -a, a>0 } и Тогда для любого >0.
Следствие. Если для функции f(z) выполнены условия леммы, то, где сумма берется по всем вычетам подынтегральной функции из верхней полуплоскости.
Для решения задач этого раздела можно использовать следующие оценки для значений модуля многочлена на окружности радиуса R.
,
где m>0. Аналогично, . Таким образом, при оценках значения рациональной функции на окружности радиуса R следует смотреть лишь на старшие члены многочленов числителя и знаменателя
. Учитывая это, условие леммы для рациональной функции будет выполнены, если n–m+1-1, или n–m+1<0.
1. Вычислить интеграл
Решение. Для подынтегральной функции выполнено условие n–m+1=-1<0. Далее
.
2. Вычислить интеграл
Решение. Условие леммы выполнено n – m +1 = -2 < 0. Нули знаменателя
. В верхнюю полуплоскость попадает нуль
,
являющийся полюсом второго порядка для f(z).
В верхнюю полуплоскость попадает нуль
,
являющийся полюсом второго порядка для f(z).
. Откуда .
3. Вычислить интеграл
Решение. Условие леммы выполнено n – m +1 = -1 < 0. Нули знаменателя . В верхнюю полуплоскость попадает нуль , являющийся полюсом второго порядка для f(z).
. Откуда .
4. Вычислить интеграл
Решение. Условие леммы выполнено n – m +1 = -3 < 0. В верхнюю полуплоскость попадают нули знаменателя , являющиеся полюсами первого порядка для функции f(z). Поэтому
.
5. Вычислить интеграл
Решение. Условие леммы выполнено n – m +1 = -1 < 0. Корни знаменателя подынтегральной функции лежат на единичной окружности и на биссектрисах первого-третьего и второго-четвертого углов.
.
В
верхнюю полуплоскость попадают нули
.
. Отметим, что
поэтому
Исходный интеграл будет равен .
6. Вычислить интеграл
Решение. Рассмотрим функцию . Для функции f(z) выполнены условия леммы Жордана , поэтому
.
Операционное исчисление
Преобразование Лапласа. Комплекснозначная функция f(t), t(-,) называется оригиналом, если
f(t)=0 при t<0
в (a,b) есть лишь конечное число разрывов первого рода. Иногда, дополнительно будет требоваться выполнение условия Липшица
|f(t+h)-f(t)|A|h|, для всех h,|h|h0, 1 на интервалах непрерывности функции
M s t: |f(t)|Mest (*)
Число , S – множество тех s, для которых выполенно условие (*), называется показателем роста оригинала.
Пример. Функция Хевисайда
является оригиналом нулевого показателя роста.
Изображением функции оригинала f(t) ( по Лапласу ) называют функцию комплексного переменного p=s+i, определяемую равенством
Пишут F=L[f], F
f, f F.
Свойства преобразования Лапласа. Далее в этом разделе везде под f(t) понимается f(t)H(t).
Преобразования Лапласа простейших функций: ,
Свойство линейности f(t)+g(t)F(p)+G(p).
Свойство подобия. При 0
Свойство запаздывания. Для f(t-)e-pF(p).
Дифференцирование изображения F(n)(p)(-1)ntnf(t).
Дифференцирование оригинала f(t)pF(p)-f(0).
Следствие. f(n)(t)pnF(p)-pn-1f(0)-pn-2f(0)-…-f(n-1)(0)
Интегрирование изображения
Если f(t)F(p), Re p > s0 и – оригинал, то
Интегрирование оригинала.
Если f(t)F(p), Re p > s0, то
Свертка оригиналов и умножение изображений.
Свертка определяется по формуле . Отметим, что f*g=g*f. f*gF(p)G(p)
Отметим, что если f, g – оригиналы, то и f*g – оригинал.
Умножение оригиналов, свёртка изображений
Таблица основных свойств преобразования Лапласа
f(t)+g(t)F(p)+G(p) | ||
0 , | , f(t-)e-pF(p) | F(p-)etf(t) |
f’(t)pF(p)-f(0), | f(n)(t)pnF(p)-pn-1f(0)-…-f(n-1)(0) | |
Таблица некоторых преобразований Лапласа
Оригинал | Изображение | Оригинал | Изображение | ||
1 | t (>-1) | 11 | ch t | ||
2 | e–t | 12 | |||
3 | e–t t (>-1) | 13 | |||
4 | sin t | 14 | |||
5 | cos t | 15 | |||
6 | tn sin t | 16 | |||
7 | tn cos t | 17 | |||
8 | e–t sin (t+) | 18 | |||
9 | e–t cos (t+) | 19 | |||
10 | sh t | 20 |
Пример 1.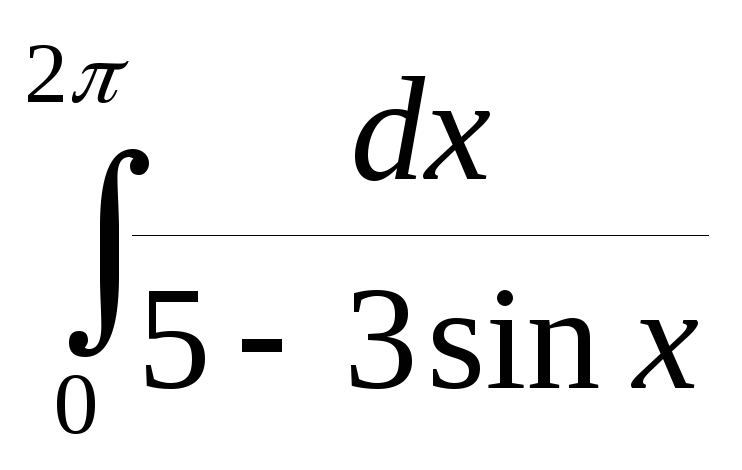 x+a2x=b
sin at, общие
начальные данные x0,
x1,
x+a2x=b
sin at, общие
начальные данные x0,
x1,
, поэтому
Согласно 5 из таблицы ,
согласно 4 из таблицы ,
согласно 6 из таблицы , отсюда, используя свойство интегрирования оригинала, получим , откуда
Окончательно
Пример 2. x+3x+3x+x=1, нулевые начальные условия.
(p+1)3X(p)=1/p,. Откуда
Пример 3. x+x=1, нулевые начальные условия.
Оригинал находим по второй теореме Хевисайда
Пример 3. x+x=1, нулевые начальные условия.
,
По второй теореме Хевисайда
Пример 4. , нулевые условия. Используя 4 из таблицы, получим . По второй теореме Хевисайда
=
Пример 5. x’’+2x=a[H(t)-H(t-b)], нулевые начальные условия.
, по второй теореме Хевисайда
Свойство запаздывания дает
Окончательно
Пример 6.
x+ax=f(t), нулевые условия
Остаток в положении 15 TCP-домена определяет связывание.
 ..
..Контекст 1
… основных областей TCP11 и других TCP-белков выявил наличие двух неконсервативных изменений, а именно Ser 11 вместо остатка глицина и Thr 15 вместо остатка аргинина в TCP11 (фиг. 5А). Предполагая, что эти остатки могут быть ответственны за различные ДНК-связывающие свойства TCP11, мы выполнили одиночные мутации, чтобы преобразовать положения 11 и 15 в остатки глицина и аргинина соответственно….
Контекст 2
… глицина в положении 11 не вызывал заметных изменений в ДНК-связывающем поведении TCP11, кроме снижения эффективности ДНК-связывания. Мутант T15R, в свою очередь, проявлял повышенную чувствительность к изменению в положении 3 BS и предпочтение C20 по отношению к аналогичной последовательности с парой A:T в положении 5 вместо положения 6 (рис. 5B и 5C). Мы также проанализировали противоположные изменения в TCP20. …
Контекст 3
… также проанализированы противоположные изменения в TCP20.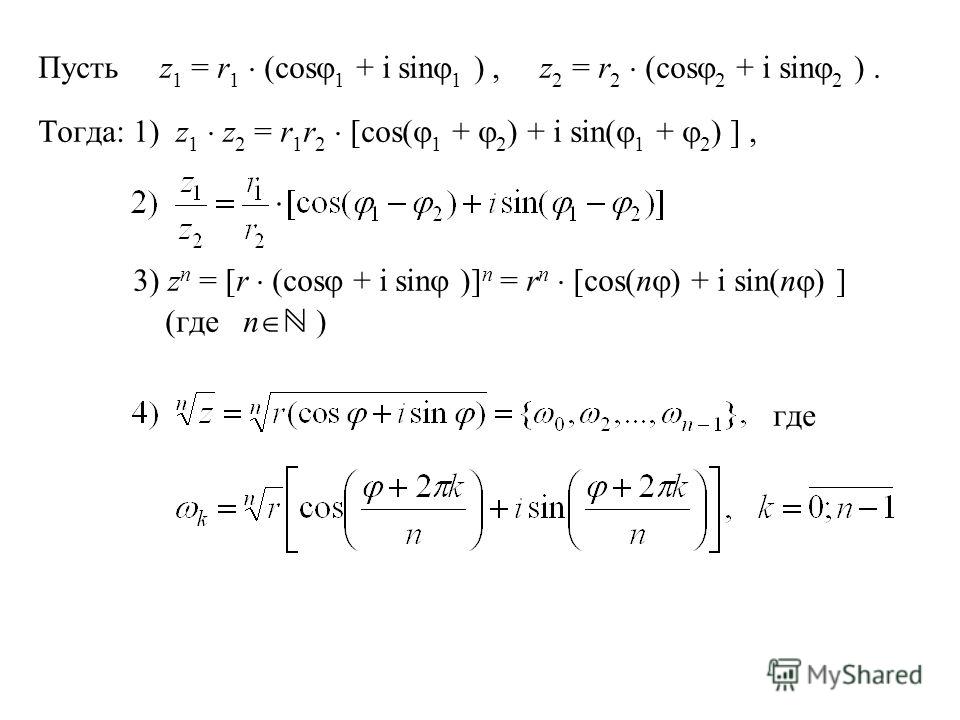 Введение остатка треонина в положение 15 TCP20 приводило к получению белка с пониженной чувствительностью к изменению положения 3 BS (фиг. 5B). Thr 15 -TCP20 также демонстрировал явное предпочтение BS и с большей эффективностью связывал последовательность с парой A:T в положении 5 по сравнению с последовательностью с парой A:T в положении 6 (рис. 5C). …
Введение остатка треонина в положение 15 TCP20 приводило к получению белка с пониженной чувствительностью к изменению положения 3 BS (фиг. 5B). Thr 15 -TCP20 также демонстрировал явное предпочтение BS и с большей эффективностью связывал последовательность с парой A:T в положении 5 по сравнению с последовательностью с парой A:T в положении 6 (рис. 5C). …
Контекст 4
… остатка треонина в положении 15 TCP20 продуцировал белок с пониженной чувствительностью к изменению в положении 3 BS (рис. 5В).Thr 15 -TCP20 также демонстрировал явное предпочтение BS и с большей эффективностью связывал последовательность с парой A:T в положении 5 по сравнению с последовательностью с парой A:T в положении 6 (рис. 5C). Результаты показывают, что наличие остатка треонина в положении 15 TCP-домена отвечает за различные свойства связывания ДНК, проявляемые TCP11. …
Контекст 5
… в дополнение к изменениям, описанным выше, природа остатка, присутствующего в положении 15, также влияет на эффективность связывания белка. Мутация Arg 15 на остаток треонина приводила к значительному снижению связывания TCP20 с BS, тогда как введение аргинина в положение 15 в TCP11 повышало эффективность связывания (фиг. 5D). Это свидетельствует о том, что остаток аргинина в этом положении устанавливает более энергичные контакты с ДНК. …
Мутация Arg 15 на остаток треонина приводила к значительному снижению связывания TCP20 с BS, тогда как введение аргинина в положение 15 в TCP11 повышало эффективность связывания (фиг. 5D). Это свидетельствует о том, что остаток аргинина в этом положении устанавливает более энергичные контакты с ДНК. …
Контекст 6
… предполагает, что остаток аргинина в этом положении устанавливает более энергичные контакты с ДНК. Мутация Thr 15 на остаток аланина в TCP11 полностью устранила взаимодействие с ДНК (рис. 5D), указывая на то, что этот остаток треонина также участвует в связывании ДНК….
Интеграции – Home Assistant
Все (1936) Избранное Добавлено: 2022.2 (16)
2021,9 (6)
2021,8 (9)
2021,7 (7)
2021,6 (10)
2021,5 (8)
2021,4 (3)
2021,3 (13)
2021,2 (6)
2021.12 (11)
2021.11 (2)
2021.10 (5)
2021.1 (1)
2020.12 (8)
0,118 (1)
0,117 (7)
0,116 (5)
0,115 (14)
0,114 (6)
0,113 (3)
0,112 (4)
0,111 (3)
0,110 (12)
0,109 (4)
0,108 (7)
0,107 (5)
0,106 (7)
0,105 (7)
0,104 (11)
0,103 (8)
0,102 (6)
0,101 (6)
0,100 (8)
0,99 (10)
0,98 (4)
0,97 (7)
0,96 (7)
0,95 (13)
0,94 (8)
0. 93 (7)
0,92 (9)
0,91 (2)
0,90 (5)
0,89 (8)
0,88 (10)
0,87 (15)
0,86 (3)
0,85 (19)
0,84 (6)
0,83 (12)
0,82 (7)
0,81 (18)
0,80 (3)
0,79 (7)
0,78 (6)
0,77 (2)
0,76 (6)
0,75 (7)
0,74 (3)
0,73 (4)
0,72 (10)
0,71 (5)
0,70 (4)
0,69 (5)
0,68 (8)
0,67 (7)
0,66 (7)
0,65 (10)
0,64 (8)
0,63 (5)
0,62 (5)
0,61 (11)
0,60 (9)
0,59 (5)
0,58 (7)
0,57 (15)
0,56 (13)
0,55 (9)
0,54 (9)
0,53 (9)
0,52 (5)
0,51 (9)
0,50 (11)
0,49 (12)
0,48 (11)
0,47 (14)
0,46 (2)
0,45 (6)
0,44 (15)
0,43 (10)
0,42 (9)
0,41 (4)
0,40 (10)
0.39 (16)
0,38 (12)
0,37 (14)
0,36 (19)
0,35 (11)
0,34 (12)
0,33 (5)
0,32 (15)
0,31 (12)
0,30 (7)
0,29 (7)
0,28 (5)
0,27 (13)
0,26 (8)
0,25 (8)
0,24 (3)
0,23 (8)
0,22 (4)
0,21 (5)
0,20 (8)
0,19 (8)
0,18 (8)
0,17 (5)
0,16 (4)
0,15 (3)
0,14 (10)
0,13 (16)
0,12 (6)
0,11 (7)
0,10 (9)
0,9 (6)
0,8 (8)
0,7,6 (7)
0,7,5 (2)
0,7,4 (5)
0,7,3 (6)
0,7,2 (2)
0,7 (77)
0,0 (1)
93 (7)
0,92 (9)
0,91 (2)
0,90 (5)
0,89 (8)
0,88 (10)
0,87 (15)
0,86 (3)
0,85 (19)
0,84 (6)
0,83 (12)
0,82 (7)
0,81 (18)
0,80 (3)
0,79 (7)
0,78 (6)
0,77 (2)
0,76 (6)
0,75 (7)
0,74 (3)
0,73 (4)
0,72 (10)
0,71 (5)
0,70 (4)
0,69 (5)
0,68 (8)
0,67 (7)
0,66 (7)
0,65 (10)
0,64 (8)
0,63 (5)
0,62 (5)
0,61 (11)
0,60 (9)
0,59 (5)
0,58 (7)
0,57 (15)
0,56 (13)
0,55 (9)
0,54 (9)
0,53 (9)
0,52 (5)
0,51 (9)
0,50 (11)
0,49 (12)
0,48 (11)
0,47 (14)
0,46 (2)
0,45 (6)
0,44 (15)
0,43 (10)
0,42 (9)
0,41 (4)
0,40 (10)
0.39 (16)
0,38 (12)
0,37 (14)
0,36 (19)
0,35 (11)
0,34 (12)
0,33 (5)
0,32 (15)
0,31 (12)
0,30 (7)
0,29 (7)
0,28 (5)
0,27 (13)
0,26 (8)
0,25 (8)
0,24 (3)
0,23 (8)
0,22 (4)
0,21 (5)
0,20 (8)
0,19 (8)
0,18 (8)
0,17 (5)
0,16 (4)
0,15 (3)
0,14 (10)
0,13 (16)
0,12 (6)
0,11 (7)
0,10 (9)
0,9 (6)
0,8 (8)
0,7,6 (7)
0,7,5 (2)
0,7,4 (5)
0,7,3 (6)
0,7,2 (2)
0,7 (77)
0,0 (1)
Интегрируйте это! – Интеграция SAP и MES.
 Пошаговое руководство
Пошаговое руководствоЦитата.
«В связи с возросшим масштабом и сложностью систем SAP и других компаний требуется, чтобы мы искали
способов упростить требования к системной интеграции»
Эта цитата из серии сообщений в блоге («Интегрируйте это…») об интеграции между различными системами SAP и не-SAP
Еще посты из этой серии (Список обновляется.)
О.
Системы управления производством (MES) — это компьютеризированные системы, используемые в производстве для отслеживания и документирования преобразования сырья в готовую продукцию. MES предоставляет информацию, которая помогает лицам, принимающим решения на производстве, понять, как можно оптимизировать текущие условия на заводе для повышения производительности. MES работает в режиме реального времени, позволяя контролировать несколько элементов производственного процесса (например, ресурсы, персонал, машины и службы поддержки).
MES может работать в нескольких функциональных областях, например, управление определениями продукта на протяжении жизненного цикла продукта, планирование ресурсов, выполнение заказов и отправка, анализ производства и управление простоями для общей эффективности оборудования (OEE), качества продукта или материалов. отслеживать и отслеживать.MES создает запись «как построено», фиксируя данные, процессы и результаты производственного процесса. Это может быть особенно важно в регулируемых отраслях, таких как производство продуктов питания и напитков или фармацевтика, где может потребоваться документация и подтверждение процессов, событий и действий.
Преимущества MES:
Сокращение количества отходов, переделок и брака, в том числе сокращение времени переналадки
Более точный сбор информации о затратах (например,г. рабочая сила, лом, время простоя и оснастка)
Увеличение времени безотказной работы
Включить безбумажный рабочий процесс
Отслеживание производственных операций
Сокращает время простоя и упрощает поиск неисправностей
Сокращение запасов за счет ликвидации запасов на всякий случай
Общие случаи использования, когда система MES интегрирована с системами SAP EWM и/или SAP ERP
MES-система использует основные данные (материалы, партии, контейнеры и т. д.) из ERP-системы
д.) из ERP-системы
Предпосылки.
Вы хотите узнать больше об интеграции SAP-MES с SAP PI/PO в общих чертах.
Разрешение.
Шаг 0. Введение
В этом сценарии интеграции:
SAP ERP — SAP S/4HANA
Шина сообщений (брокер интеграции) — SAP PO
Давайте сначала взглянем на схему сценария интеграции:
Шаг 1. Примеры потока сообщений
Материалы из ERP в MES
Пакеты из ERP в MES
Поставки из ERP в MES
- Ручки
от ERP до MES
Технологические заказы из ERP в MES
Материалы из MES в ERP
Шаг 2.Интеграция с точки зрения SAP PO
Шаг 2.1. С точки зрения корпоративного репозитория служб (ESR):
Опишите поток сообщений с шага 1
1. Название версии программного компонента
2.
Пространство имен
3. Объекты типов данных (DT)
Пример материального потока
Элементы: MaterialType, MaterialNumber, Brand и т. д.
4. Объекты MessageTypes (MT) будут созданы автоматически из DT
.5.Входящие/исходящие объекты сервисного интерфейса (SI)
Назначить роль запроса для созданного MT и роль ошибки для типа сообщения об ошибке
6. Действия по приему/отправке
Назначить действие приема с интерфейсом In Service
Назначить действие отправки с выходным сервисным интерфейсом
Шаг 2.2. С точки зрения Integration Builder (IB)
Для веб-сервиса (SOAP):
Маршрут в/из системы MES
Компонент конфигурации без участника — Бизнес-система — (например, BSYSTEM_MES_QAS)
Тип адаптера — SOAP
Канал связи отправителя SOAP
Канал связи приемника SOAP (целевой URL-адрес веб-службы MES с учетными данными и номером порта)
Компонент конфигурации без стороны — бизнес-система — (например, BSYSTEM_S4HANA_CLIENTXXX_QAS)
Тип адаптера — SOAP
Адаптер — Отправитель
Транспортный протокол — HTTP
Тип адресации — назначение HTTP
HTTP Destination — Имя HTTP Destination
Пример отправителя SOAP:
Маршрут в/из системы ERP
Конфигурационный компонент без стороны — Бизнес-система — (например, BSYSTEM_MES_QAS)
Тип адаптера — SOAP
Адаптер – приемник
Канал связи отправителя SOAP
Канал связи приемника SOAP (целевой URL-адрес веб-службы MES с учетными данными и номером порта))
Пример приемника SOAP:
Для интеграции IDoc:
Конфигурационный компонент без стороны — Бизнес-система —
Настройки канала связи:
Бизнес-система —
Тип адаптера — IDoc_AAE
Тип адаптера — приемник
Транспортный протокол — tRFC
Протокол обмена сообщениями — IDOC XML
Модуль адаптера — Центральный модуль адаптера
Пример отправителя IDoc:
Для интегрированной конфигурации (ICO) в ИБ:
Для сценария конфигурации в ИБ:
Например, сценарий конфигурации пакетной репликации.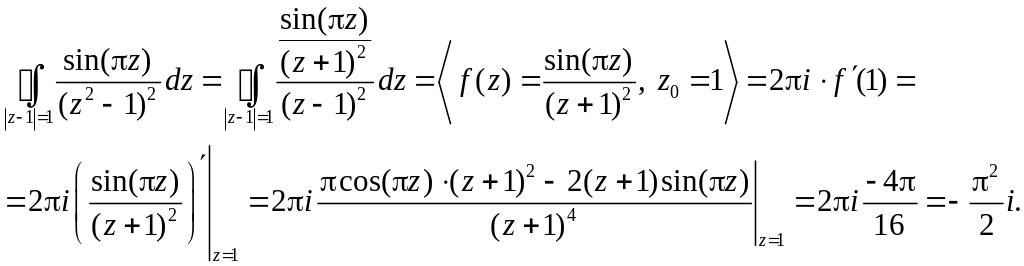
Примечание. Целевой системой для рабочего процесса основных данных может быть несколько систем
.Конфигурация модели:
Исходная система — SAP ERP
Целевые системы – MES, стороннее программное обеспечение для бизнес-аналитики и т. д.
Шаг 3. Интеграция с точки зрения ERP
Шаг 3.1. Интеграция IDOC
Примечание.
IDoc, сокращение от Intermediate Document, представляет собой формат документа SAP для передачи данных бизнес-транзакций.Сам IDoc представляет собой структурированный текстовый файл, что означает, что IDoc можно использовать на всех платформах, нет необходимости переводить двоичные данные
транзакции SAP:
Шаг 3.1.1. Настройки в СМ59
Транзакция SM59 — Конфигурация соединений RFC
Тип подключения — T (подключения TCP/IP)
Хост шлюза — Путь к SAP PI/PO
Идентификатор программы —
1) Канал отправителя RfcAdapter регистрируется с этим идентификатором программы в качестве RFC-сервера на шлюзе SAP. Отправляющая система использует тот же идентификатор программы для идентификации RFC-сервера на шлюзе SAP.
Отправляющая система использует тот же идентификатор программы для идентификации RFC-сервера на шлюзе SAP.
Когда система-отправитель отправляет несколько вызовов RFC, шлюз SAP будет искать в своем списке регистраций идентификатор программы, предоставленный системой-отправителем
2)Идентификатор программы чувствителен к регистру.
3) Тот же идентификатор программы должен быть указан в канале отправителя RFC.
Служба шлюза — sapgw
Шаг 3.1.2. Настройки в WE31
Транзакция — WE31 — Сегмент разработки IDoc
Привязки между сегментом IDoc и элементами данных
Например, тип сегмента E1BATMAS и поля в сегменте, такие как МАТЕРИАЛ
Шаг 3.1.3. Настройки в WE81
Транзакция — WE81 — Типы логических сообщений
Например:
Объект SAP — МАТЕРИАЛ имеет стандартный тип сообщения IDoc MATMAS. В транзакции WE81 мы можем создать собственный тип сообщения, например, ZMATMAS.
Шаг 3. 1.4. Настройки в SM30
1.4. Настройки в SM30 Транзакция — SM30 — Ведение табличного представления — V_TBDA2
Активировать указатель изменения для пользовательского типа сообщения
Шаг 3.1.5. Настройки в WE82
Транзакция — WE82 — Назначение сообщений для типа IDoc
Привязка между пользовательским типом сообщения и базовым типом сообщения.
Шаг 3.1.6. Настройки в BD61
Транзакция — BD61 — активировать указатели изменений в целом
Установить Указатели изменений активированы – обычно.
Шаг 3.1.7. Настройки в BD50
Транзакция — BD50 — активировать указатели изменений для типа сообщения
Активировать указатель изменений для нашего пользовательского типа сообщения
Шаг 3.1.8. Настройки в BD52
Транзакция — BD52 — Актив. Изменить указатель на документ chng
Привязки между элементами документа изменений и пользовательским типом сообщения
Например, привязка между типом сообщения ZXXX и
.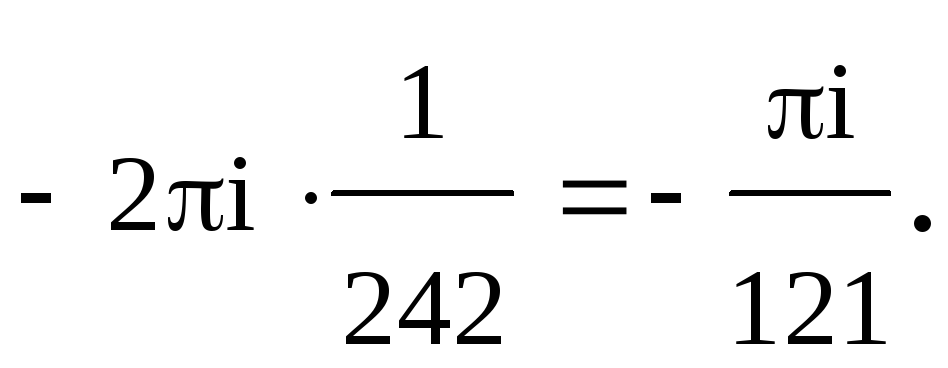
CHARGE_LM — мастер партии (с длинным номером материала)
MCHA – Партии (таблица)
LICHA – LICHA Номер партии поставщика (поле)
Шаг 3.1.9. Настройки в BD64
Транзакция — BD64 — Показать модель распределения
Мы можем добавить сообщение в модель Distributon.
1.Создать модель распространения
2. Добавить в модель распределения ERP и системы PI
3. Добавить в тип сообщения модели распространения. Например LOIPRO (Производственный заказ)
Шаг 3.1.10. Настройки в WE21
Транзакция — WE21 — Порты в обработке IDoc
Связывание порта IDoc с портом RFC, определенным на шаге 3.1.1
Шаг 3.1.11. Настройки в WE20
Транзакция — WE20 — Профили партнеров
Привязки между типом сообщения и портом получателя
Тип/роль партнера используется для идентификации партнеров в SAP-системах. Тип партнера — KU для клиента, LI для поставщика и LS для логической системы.
Шаг 3.2. Интеграция RFC
Шаг 3.2.1. СПРОКСИ
Транзакция — SPROXY — Браузер корпоративного репозитория
Использовать здесь объекты SAP PO ESR.
Связи между сгенерированной z-структурой из типа данных SAP PO и пользовательским кодом, который заполнил данные для этой z-структуры
Шаг 3.2.2. ABAP-разработка
Транзакция — SE80 — Навигатор объектов и другие средства разработки, такие как SM30 и SE38
(создание пакетов/подпакетов, структур, функциональных модулей, программ и т. д.)
Например, сгенерированная Z-структура прокси для материала
Шаг 3.2.3. Планирование
Транзакция — SM36 — Запланировать фоновое задание
Для IDOC:
SE38 -> Создать вариант для каждого типа сообщения, используемого в интеграции SAP-MES. Отчет RBDMIDOC -> Создать вариант
SM36 -> Создать фоновое задание для каждого варианта отчета RBDMIDOC
Периодическое время, например каждые 5 минут
Для RFC:
SM36 -> Создать фоновое задание для каждой пользовательской программы ABAP, которая отправляет данные в интеграцию
Шаг 4.
 Интеграция с точки зрения MES
Интеграция с точки зрения MESКраткий обзор сценария интеграции с точки зрения MES.
Например, система MES с частью интеграции на базе Apache Camel.
Небольшая цитата об архитектуре:
«Обмен данными ERP осуществляется в виде текстовых файлов XML, которые соответствуют выбранному набору SAPIDOC. IDOC из файловой системы преобразуются из XML в обычные бизнес-объекты и доставляются на FTPC через очереди сообщений JMS. Используя список событий, Shop Operations Server считывает сообщения из этой очереди и запускает определенный набор действий для обработки каждого сообщения.
Архитектура и конфигурация:
Конфигурация интеграции:
Поставщики службы сообщений Java:
- Входящая конфигурация
- Исходящая конфигурация
Шаг 5. Мониторинг
Мониторинг со стороны ERP:
Транзакция — WE02 (отображение IDoc)
Транзакция – WE05 (список IDoc)
Пример:
Сообщение 29 — Ошибка в службе ALE
Транзакция — BD87 — Монитор состояния для сообщений ALE
Монитор состояния для сообщений ALE, например, состояние для LOIPRO (производственный заказ)
Транзакция — SXMB_MONI (Мониторинг механизма интеграции)
Монитор обработанных сообщений XML
Транзакция SMQS — монитор TRFC
Мониторинг со стороны SAP PO:
SAP Netweaver -> Домашняя страница конфигурации и мониторинга
Механизм адаптера -> Монитор сообщений
Мониторинг со стороны MES:
Этот шаг зависит от типа системы MES.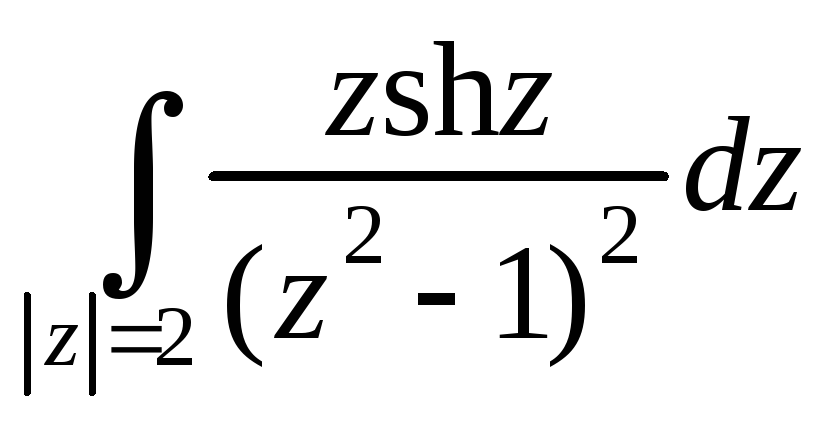 Для Rockwell Factory Talk это Inbound Events Monitor
Для Rockwell Factory Talk это Inbound Events Monitor
Устранение неполадок.
Транзакция SMQS — монитор TRFC
Проблема:
Ошибка в очереди “Не удалось разрешить ссылку на репозиторий @XI_IDOC_DE FAULT_DESTINATION”
Разрешение:
SAP PI — Администратор SAP Netweaver — Конфигурация — Направления
Проверить учетные данные, пинг и т. д. для пункта назначения XI_IDOC_DE FAULT_DESTINATION
Ссылки.
Статус ошибки Idoc «Запись в исходящей таблице не найдена»
Основы IDoc для функциональных консультантов
137412 — Создание партии — без указателя изменений для ALE
Заключение.
Интеграция SAP-MES с SAP PI/PO в общих чертах предоставлена
Системные требования мобильной печати| PaperCut
РУКОВОДСТВА ПО ПРОДУКЦИИ
Мобильность Печать руководства
РЕКОМЕНДУЕМАЯ ПРОДУКЦИЯ
Требования к серверу
| Аппаратные требования | |
|---|---|
| ЦП | Любой процессор x86-64 (Intel или AMD)** |
| Память | 2 ГБ или больше |
| Жесткий диск | 3 ГБ свободного места или более |
| Требования ОС | |
|---|---|
| Окна | Windows 8, 10/сервер 2012r2, 2012, 2016, 2019 |
| Mac | macOS 10. 12+ 12+ |
| Linux |
|
Дополнительные соображения
** Сообщалось, что эмуляция работает на новых компьютерах Mac с процессором m1, но это официально не тестировалось и не разрабатывалось.Другие устройства, поддерживающие архитектуру ARM, такие как Raspberry Pi, не поддерживаются.
- Системы класса Windows «Desktop», такие как Windows 7, 8 и 10, допускают только 10 одновременных подключений. Это означает, что эти системы следует использовать в качестве «сервера» для размещения очередей печати только в тех сетях, в которых ожидается обработка менее 10 одновременных заданий на печать.
- Требуется подключение к Интернету для автоматического обновления программного обеспечения при появлении новых версий.
 Дополнительные сведения см. в разделе Как обновить сервер Mobility Print? раздел часто задаваемых вопросов.
Дополнительные сведения см. в разделе Как обновить сервер Mobility Print? раздел часто задаваемых вопросов.
Требования к принтеру
Mobility Print работает с подавляющим большинством принтеров. Ключевым требованием является наличие у принтера драйвера печати для операционной системы хоста сервера (например, драйвер Windows).
Mobility Print поддерживает все принтеры с драйверами для современных операционных систем Windows , за исключением принтеров и плоттеров для этикеток . Это связано с тем, что драйверы для принтеров этикеток и плоттеров используют нестандартные размеры страниц. Если вы обнаружите какие-либо исключения или у вас возникнут проблемы, сообщите нам об этом.
Требования клиента
Предупреждение
У клиента должен быть включен IPP.- iOS 11.0+
- macOS X 10.12+ (Sierra), 64-разрядная версия
- Windows 7+
- Андроид 4.4+
- Chrome OS с версией Chrome 69+
Интеграция PaperCut NG/MF
Mobility Print интегрируется с PaperCut NG/MF версии 17. 0.3 или выше.
0.3 или выше.
Функция облачной печати интегрируется с PaperCut NG/MF версии 17.0,3 и выше.
Правила брандмауэра
Какие протоколы и порты настроить, зависит от метода обнаружения принтера, который вы собираетесь использовать.
Автоматическое обновление
Следующие конечные точки порта и URL-адреса должны быть доступны извне для автоматического обновления:
Использование mDNS
| Клиент | Клиентское ПО? | Протокол обнаружения принтера | Порт сервера (для обнаружения принтера) | Протокол доставки заданий | Порт сервера (для доставки заданий) |
|---|---|---|---|---|---|
| macOS | Нет | мДНС | Входящий: 5353 UDP Исходящий: 5353 UDP | IPPS/HTTPS | 9164 TCP |
| iOS | Нет | мДНС | Входящий: 5353 UDP Исходящий: 5353 UDP | IPPS/HTTPS | 9164 TCP |
| Андроид | Мобильное приложение для печати | mDNS HTTPS | Входящий: 5353 UDP Входящий: 9164 TCP Исходящий: 5353 UDP | HTTPS | 9164 TCP |
| Хром | Мобильное приложение для печати | mDNS HTTP | Входящий: 5353 UDP Входящий: 9163 TCP Исходящий: 5353 UDP | HTTP API (зашифрованная полезная нагрузка) | 9163 TCP |
| Окна | Установщик | mDNS HTTPS | Входящий: 5353 UDP Входящий: 9164 TCP Исходящий: 5353 UDP | IPP/HTTP | 9163 TCP |
Использование известного хоста
При настройке Mobility Print с известным хостом следующие конечные точки порта и URL-адреса должны быть доступны извне, чтобы можно было получить файлы настройки клиента:
| Клиент | Клиентское ПО? | Протокол обнаружения принтера | Порт сервера (для обнаружения принтера) | Протокол доставки заданий | Порт сервера (для доставки заданий) |
|---|---|---|---|---|---|
| macOS | Мобильное приложение для печати | HTTPS | Входящий: 9164 TCP Исходящий: н/д | IPPS/HTTPS | 9164 TCP |
| iOS | Профиль конфигурации | HTTPS | Входящий: 9164 TCP Исходящий: н/д | IPPS/HTTPS | 9164 TCP |
| Андроид | Мобильное приложение для печати | HTTPS | Входящий: 9164 TCP Исходящий: н/д | API HTTPS | 9164 TCP |
| Хром | Мобильное приложение для печати | HTTP | Входящий: 9163 TCP Исходящий: н/д | HTTP API (зашифрованная полезная нагрузка) | 9163 TCP |
| Окна | Установщик | HTTPS | Входящий: 9164 TCP Исходящий: н/д | IPP/HTTP | 9163 TCP |
Использование DNS
| Клиент | Клиентское ПО? | Протокол обнаружения принтера | Порт сервера (для обнаружения принтера) | Протокол доставки заданий | Порт сервера (для доставки заданий) |
|---|---|---|---|---|---|
| macOS | Нет | DNS | Входящий: 53 UDP Входящий: 53 TCP Исходящий: 53 UDP Исходящий: 53 TCP | IPPS/HTTPS | 9164 TCP |
| iOS | Нет | DNS | Входящий: 53 UDP Входящий: 53 TCP Исходящий: 53 UDP Исходящий: 53 TCP | IPPS/HTTPS | 9164 TCP |
| Андроид | Мобильное приложение для печати | DNS HTTPS | Входящий: 53 UDP Входящий: 9164 TCP Исходящий: 53 UDP | API HTTPS | 9164 TCP |
| Хром | Мобильное приложение для печати | DNS HTTPS | Входящий: 53 UDP Входящий: 9163 TCP Исходящий: 53 UDP | HTTP API (зашифрованная полезная нагрузка) | 9163 TCP |
| Окна | Установщик | DNS HTTPS | Входящий: 53 UDP Входящий: 9164 TCP Исходящий: 53 UDP | IPP/HTTP | 9163 TCP |
Виртуальный принтер
Локальный (тот же хост)
| Служба пользовательского контекста клиента | только внутреннее/локальное соединение |
|---|---|
| порт 9165 TCP | локальный хост (127. 0.0.1) 0.0.1) |
Входящий
Нет правил брандмауэра.
Исходящий
Предупреждение
Если ваш сервер Mobility Print использует прокси-сервер для исходящего интернет-соединения, тогда Cloud Print будет работать с , а не .| Для регистрации сервера и уведомления о поступающих заданиях | |
|---|---|
| порт 443 TCP | mp.cloud.papercut.com |
| порт 8883 TCP | кв.м.googleapis.com (служба уведомлений) |
| Для организации однорангового соединения | |
|---|---|
| порт 3478 TCP порт 3478 UDP | global.stun.twilio.com |
| порт 443 TCP порт 3478 UDP | global.turn.twilio.com |
Остатки линкера регулируют активность и стабильность гексокиназы 2, многообещающей противораковой мишени
https://doi. org/10.1074/jbc.RA120.015293Получить права и содержание
org/10.1074/jbc.RA120.015293Получить права и содержание Гексокиназа (HK) катализирует первый этап метаболизма глюкозы, что делает ее интересной мишенью для ингибирования возникновения и прогрессирования опухоли из-за их повышенного метаболизма глюкозы. Повышающая регуляция гексокиназы-2 (НК2) при многих видах рака и ее ограниченная экспрессия в нормальных тканях делают ее особенно привлекательной мишенью для селективного ингибирования роста рака и ликвидации опухолей с ограниченными побочными эффектами. Разработка такой безопасной и эффективной противоопухолевой терапии требует разработки специфичных для HK2 ингибиторов, которые не будут мешать другим изоферментам HK.Поскольку HK2 уникален среди HK наличием каталитически активного N-концевого домена (NTD), мы сосредоточили наше внимание на этой области. Ранее мы обнаружили, что на активность NTD влияет размер линкерной спирали-α 13 , которая соединяет N- и C-концевые домены HK2. Было обнаружено, что три остатка неактивного сайта (D447, S449 и K451) в начале линкерной спирали-α 13 регулируют NTD-активность HK2. Мутация этих остатков привела к увеличению динамики, как показано с помощью анализа водородно-дейтериевого обмена и молекулярно-динамического моделирования.D447A внес наибольший вклад в улучшенную динамику NTD при сниженной калориметрической энтальпии HK2. Подобные остатки существуют в С-концевом домене (CTD), но они не нужны для активности HK1 и HK2. Таким образом, мы постулируем, что эти остатки служат регуляторным сайтом для HK2 и могут дать новые направления для разработки противоопухолевых терапевтических средств, которые снижают скорость гликолиза при раке посредством специфического ингибирования HK2.
Мутация этих остатков привела к увеличению динамики, как показано с помощью анализа водородно-дейтериевого обмена и молекулярно-динамического моделирования.D447A внес наибольший вклад в улучшенную динамику NTD при сниженной калориметрической энтальпии HK2. Подобные остатки существуют в С-концевом домене (CTD), но они не нужны для активности HK1 и HK2. Таким образом, мы постулируем, что эти остатки служат регуляторным сайтом для HK2 и могут дать новые направления для разработки противоопухолевых терапевтических средств, которые снижают скорость гликолиза при раке посредством специфического ингибирования HK2.
Ключевые слова
гексокиназы
метаболизма рака
инактивации фермента
Варбург эффект
и противораковых терапевтических средств
Сокращения
CIDстолкновения индуцированной диссоциации
ДСКдифференциальной сканирующей калориметрии
DSFдифференциальной сканирующей флуориметрии
& delta; H + CALкалориметрическая энтальпия
HDX-MSводород / дейтериум обмен масс-спектрометрией
Hikтермоэтактивация кинетики
HKDC1домен гексокиназы, содержащий 1
K ATPMichaelis Constance для ATP
K GLUMichaelis константа для глюкозы
PCAанализ основных компонентов
RMSFсреднеквадратичные колебания
VDACпотенциалзависимый анионный канал
Рекомендуемые статьиСсылки на статьи (0)
© 2020 The Authors. Опубликовано Elsevier Inc от имени Американского общества биохимии и молекулярной биологии.
Опубликовано Elsevier Inc от имени Американского общества биохимии и молекулярной биологии.
Рекомендуемые статьи
Ссылки на статьи
IEA MD TCP Annex 17 — Технологический университет Граца
Основная цель проекта IEA IETS TCP Annex 17 состоит в том, чтобы обеспечить оптимальное использование лигноцеллюлозного материала в концепции биоперерабатывающего завода по энергопотреблению и стоимости -эффективное разделение
технологий. Целлюлозно-бумажная промышленность служит основой подхода биопереработки не только из-за использования древесины в качестве сырья, но и из-за больших объемов производства.В Австрии этот сектор промышленности относится к энергоемким отраслям; она занимает второе место в рейтинге конечного энергопотребления. Подход к биопереработке направлен на создание максимально возможной стоимости за счет использования сырья с пониженным циклом
. Мембранные процессы разделения сочетают в себе преимущество использования материалов компонентов частично селективными механизмами разделения с мерами энергоэффективности
. Большой интерес представляют новые мембранные процессы, такие как прямой осмос (FO), мембранная дистилляция (MD), первапорация (PV) и проницаемость через мембрану жидкости (LMP).В этом проекте особое внимание уделяется MD и LMP для обработки различных технологических потоков.
Большой интерес представляют новые мембранные процессы, такие как прямой осмос (FO), мембранная дистилляция (MD), первапорация (PV) и проницаемость через мембрану жидкости (LMP).В этом проекте особое внимание уделяется MD и LMP для обработки различных технологических потоков.
Предметом услуги НИОКР является сотрудничество с Приложением 17 и управление одной подзадачей. В дополнение к технологической цели, проект IEA IETS TCP Annex 17
укрепит сеть австрийского ландшафта исследований мембран и биоперерабатывающих заводов. Кроме того, благодаря обмену мнениями с международной командой из Приложения 17 оптимизируется использование материала, содержащего лигноцеллюлозу, на биоперерабатывающих заводах с помощью энергоэффективных и экономичных технологий разделения.В рамках подзадач A-F оцениваются, оптимизируются и интегрируются различные энергоэффективные мембранные процессы, а также разрабатываются стратегии утилизации компонентов биомассы. Технологическая цель состоит в том, чтобы достичь максимального содержания сухих веществ в обрабатываемых технологических потоках при минимизации загрязнения за счет оптимальной настройки параметров процесса, а также подходящей стратегии очистки. С использованием процессов мембранной сепарации и интеграции промышленного сбросного тепла должен быть продемонстрирован устойчивый путь утилизации отходов / потоков отходов и снижения потребности в воде.Австрийский вклад разрабатывает руководство по использованию новых технологий мембранной сепарации на биоперерабатывающих заводах на основе потоков сточных/технологических вод с целлюлозно-бумажной фабрики.
С использованием процессов мембранной сепарации и интеграции промышленного сбросного тепла должен быть продемонстрирован устойчивый путь утилизации отходов / потоков отходов и снижения потребности в воде.Австрийский вклад разрабатывает руководство по использованию новых технологий мембранной сепарации на биоперерабатывающих заводах на основе потоков сточных/технологических вод с целлюлозно-бумажной фабрики.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно.Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.

- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
.


 виды
аудиторных занятий
виды
аудиторных занятий
 Интеграл Коши
Интеграл Коши
 Конформные отображения
I и II рода. Функция Жуковского, конформное
отображение
.
Гиперболические функции в конформной
области и их свойства.
Конформные отображения
I и II рода. Функция Жуковского, конформное
отображение
.
Гиперболические функции в конформной
области и их свойства. Решение задач.
Решение задач. А. Методы теории функций комплексного
переменного: учебное пособие для вузов./
М.А. Лаврентьев, Б.В. Шабат. – М.: Наука,
1987. – 158с.
А. Методы теории функций комплексного
переменного: учебное пособие для вузов./
М.А. Лаврентьев, Б.В. Шабат. – М.: Наука,
1987. – 158с.

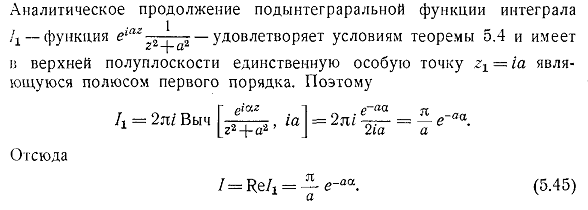

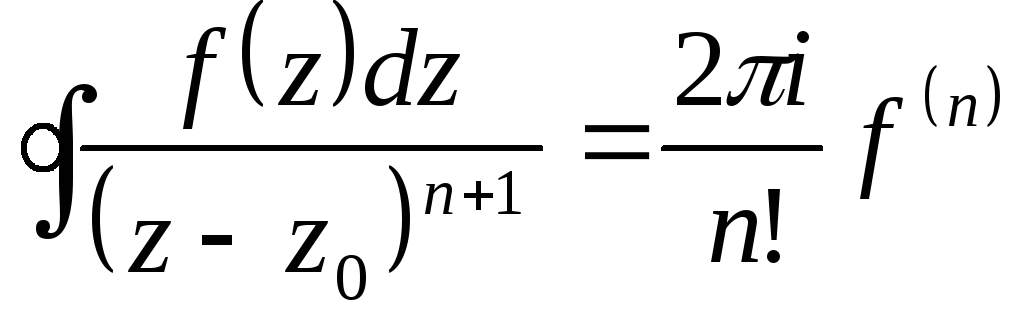 Интегрирование комплексной
функции комплексного аргумента, связь
комплексного интеграла с криволинейным
интегралом. Интегральная теорема Коши.
Формула Коши и ее следствия. Вычисление
интегралов с помощью интегральной
теоремы и формулы Коши.
Интегрирование комплексной
функции комплексного аргумента, связь
комплексного интеграла с криволинейным
интегралом. Интегральная теорема Коши.
Формула Коши и ее следствия. Вычисление
интегралов с помощью интегральной
теоремы и формулы Коши. Условия Коши – Римана в
полярных координатах.
Условия Коши – Римана в
полярных координатах.
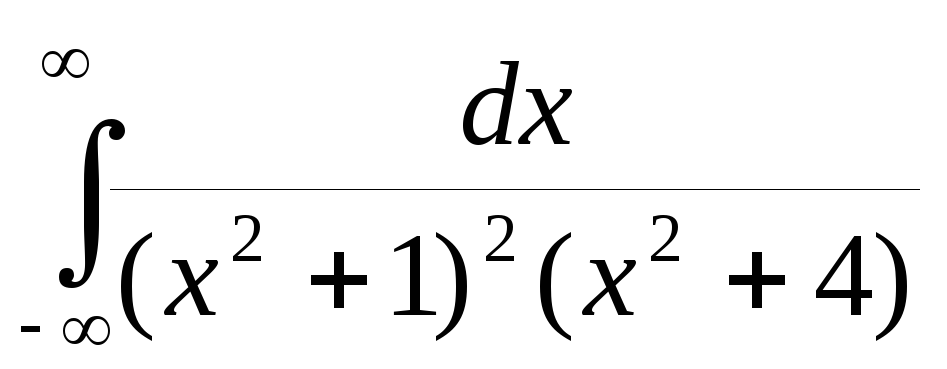 Решение задачи Дирихле.
Решение задачи Дирихле.
 Пространство имен
Пространство имен Дополнительные сведения см. в разделе Как обновить сервер Mobility Print? раздел часто задаваемых вопросов.
Дополнительные сведения см. в разделе Как обновить сервер Mobility Print? раздел часто задаваемых вопросов.