Топология электрических цепей. Схема замещения эл. цепи Графам
Топологическое свойство цепей.
Для облегчения расчета составляется схема замещения электрической цепи, на схеме замещения изображаются все элементы цепи, влияниями которыми нельзя пренебречь, а также указывают электрическое соединение между ними.
Прежде чем перейти к структуре составления схем замещения напомним термины и определения:
- Топология — это раздел математики, изучающий неколичественное соотношения между геометрическими объектами.
- Схема – основное топологическое понятие теории цепей, это графическое изображение модели цепи, состоящая из ветвей и узлов.
- Ветвь – участок цепи с неизменным током.
- Узел – место соединение трёх и более ветвей (формально узлом можно считать место соединения двух ветвей, такой узел называют простым, например разделяющая точка соединения двух последовательных ветвей, для обозначения на схеме).
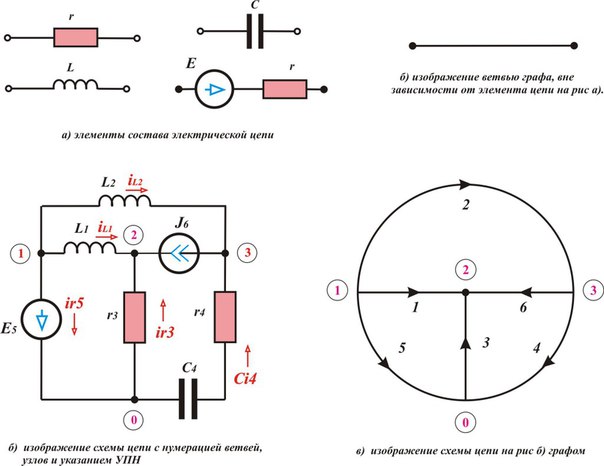
- Граф – изображения цепи (ветви цепи) без информации об элементах цепи. Если в графе указан УПН (условно – графическое направления тока или напряжения), то такой граф называется направленным. Если цепи не связаны электрически (например: связаны только через магнитное поле) граф называется не связанным.
Основное топологическое понятия графа это — путь графа (последовательность ветвей, в которой ни один узел не повторяется). Ветви изображенные на рисунке ниже, вне зависимости от элементов, заменяются простой ветвью графа рис. 1 б).
Схемы замещения электрических цепей.
Рис.1
Замечание: при анализе простых электрических цепей с простой и наглядной схемой пользуются схемами замещения электрических цепей, к топологическим свойствам цепи прибегают при анализе сложных цепей с использованием вычислительной техники.
Вернутся в раздел ТОЭ
Топология электрической цепи
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения.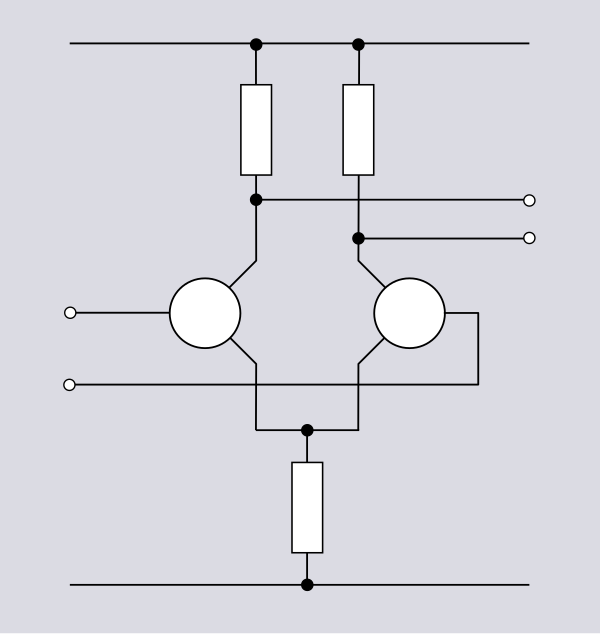 Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
Ветвью принято называть участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. По этой причине целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. В случае если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, принято называть графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, принято называть ветвью графа. Граничные точки ветви графа называют узлами графа
Подграфом графа принято называть часть графа, ᴛ.ᴇ. это должна быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
1. Путь – ϶ᴛᴏ упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. К примеру, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1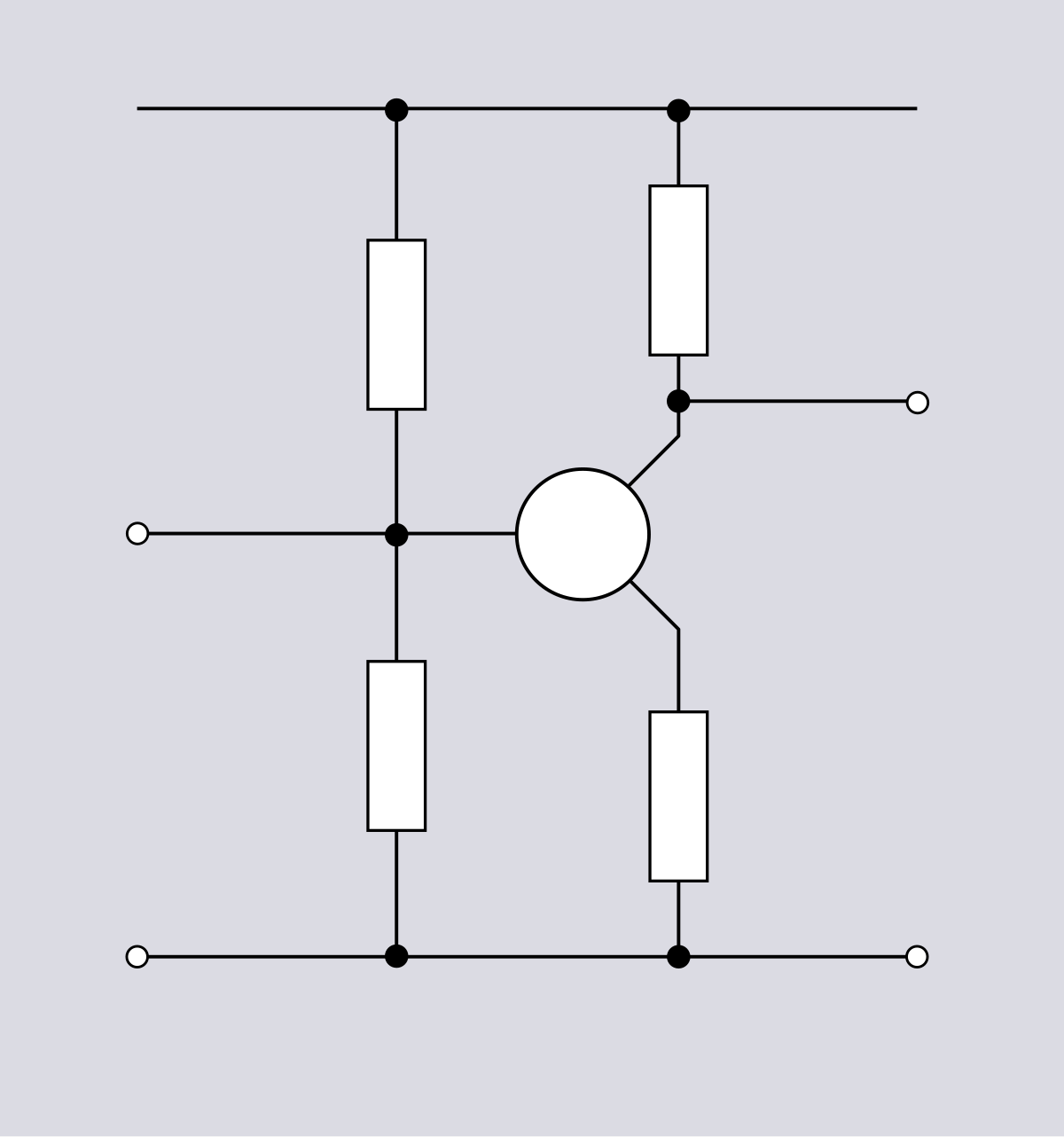 Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, путь – ϶ᴛᴏ совокупность ветвей, проходимых непрерывно.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, путь – ϶ᴛᴏ совокупность ветвей, проходимых непрерывно.
2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. К примеру, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. В случае если между любой парой узлов графа существует связь, то граф называют связным.
3. Дерево – ϶ᴛᴏ связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
Рис.4
4. Ветви связи (дополнения дерева) – ϶ᴛᴏ ветви графа, дополняющие дерево до исходного графа.
В случае если граф содержит m узлов и n ветвей, то число ветвей любого дерева , а числа ветвей связи графа .
5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, должна быть отдельным узлом.
С понятием дерева связаны понятия главных контуров и сечений:
определение, элементы, схемы. Топология и методы расчета
Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!
Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.
Электрические цепи
Электрическая цепь – это совокупность устройств, по которым течет электрический ток.
Рассмотрим самую простую электрическую цепь. Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:
Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.
Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.
Электрическая цепьКстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.
По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи  В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.
Элементы электрических цепей
Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.
Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.
Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.
Существуют условные обозначения для изображения элементов цепи на схемах.
Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.
Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.
Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.
При решении задач и анализе схем используют следующие понятия:
- Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
- Узел – соединение ветвей цепи;
- Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
Чтобы понять, что есть что, взглянем на рисунок:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Классификация электрических цепей
По назначению электрические цепи бывают:
- Силовые электрические цепи;
- Электрические цепи управления;
- Электрические цепи измерения;
Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.
Именно силовые цепи ведут ток к потребителю.
Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.
Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.
Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.
Расчет электрических цепей
Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:
В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:
Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов
Какую бы цепь Вам ни понадобилось рассчитать, наши специалисты всегда помогут справится с заданиями. Мы найдем все токи по правилу Кирхгофа и решим любой пример на переходные процессы в электрических цепях. Получайте удовольствие от учебы вместе с нами!
Расчет электрических цепей произвольной топологии
Расчет электрических цепей в продуктах APM
Программа APM ECA предоставляет средства для формирования и расчета сетевых моделей динамических систем. Расчет динамики системы проводится с использованием неявных и полунеявных схем различных порядков. Встроенные инструменты формирования подсистем позволяют создавать составные модели, включающие в себя в качестве отдельных элементов другие динамические и электрические системы. Программа включает средства расширения функциональности за счет включения дополнительных элементов, функциональное описание которых осуществляется средствами языков программирования Python или Julia.
Встроенные инструменты формирования подсистем позволяют создавать составные модели, включающие в себя в качестве отдельных элементов другие динамические и электрические системы. Программа включает средства расширения функциональности за счет включения дополнительных элементов, функциональное описание которых осуществляется средствами языков программирования Python или Julia.
Возможности программы позволяют моделировать широкий спектр процессов и явлений, поскольку любой системе интегро-дифференциально-алгебраических уравнений можно поставить в соответствие некоторую сетевую модель динамической системы. Такого рода модели являются естественным описанием процессов управления и фильтрации, колебательных процессов в механических системах, информационных процессов в системах связи.
Машинное обучение
Одной из важнейших тенденция современного проектирования технических систем является включение в конструкцию адаптивных элементов, закон функционирование которых определяется не только (а иногда даже не столько) конструктивными параметрами, определяемыми на стадии проектирования, а определяется в процессе функционирования системы в реальной или смоделированной среде исходя из условия достижения определенных технико-экономических показателей. К таким элементам можно отнести различного рода статистические классификаторы, системы идентификации (включая нейронные сети), распознавания образов и т.д.
К таким элементам можно отнести различного рода статистические классификаторы, системы идентификации (включая нейронные сети), распознавания образов и т.д.
Включение адаптивных элементов в разрабатываемую динамическую или стационарную систему обычно состоит из следующих этапов:
- определение структуры адаптивной системы. В настоящее время наибольшее практическое применение получили сетевые системы (в частности, нейронные сети), осуществляющую последовательное, слой за слоем, преобразование многомерного входного значения в одно- или многомерное выходное значение;
- выбор «критерия качества» функционирования системы. На данном критически важном этапе устанавливается критерий, исходя из которого будут выбраны значения свободных параметров системы. В зависимости от целей дальнейшего использования таким критерием может выступать среднеквадратичное отклонения наблюдаемого отклика адаптивной системы от известного целевого (как, например, в задаче адаптивной фильтрации), среднее значение некоторой вырабатываемой величины и др.
 ;
; - обучение. На этом этапе проводится симуляция работы системы и определение ее свободных параметров исходя из условия достижения установленного критерия качества. Данная процедура является вычислительно трудоемкой и для эффективного решения требует использования специализированных алгоритмов;
- оценка результатов. После процедуры обучения проводится повторная симуляция поведения системы в условиях, более приближенных к реальным. В зависимости от результатов, полученных на данном этапе принимается решение о необходимости повторного обучения, либо изменения структуры адаптивной системы;
- включение обученной системы в качестве составного элемента в основную (реальную или моделируемую) систему.
Параметрическая оптимизация
При проектировании динамических систем достаточно частой является проблема выбора значений конструктивных параметров, при которых будут достигаться наилучшие функциональные показатели. Традиционно данная задача решается путем последовательного моделирования поведения системы при различных значениях конструктивных параметров с последующим выбором наилучшей из использованных альтернатив.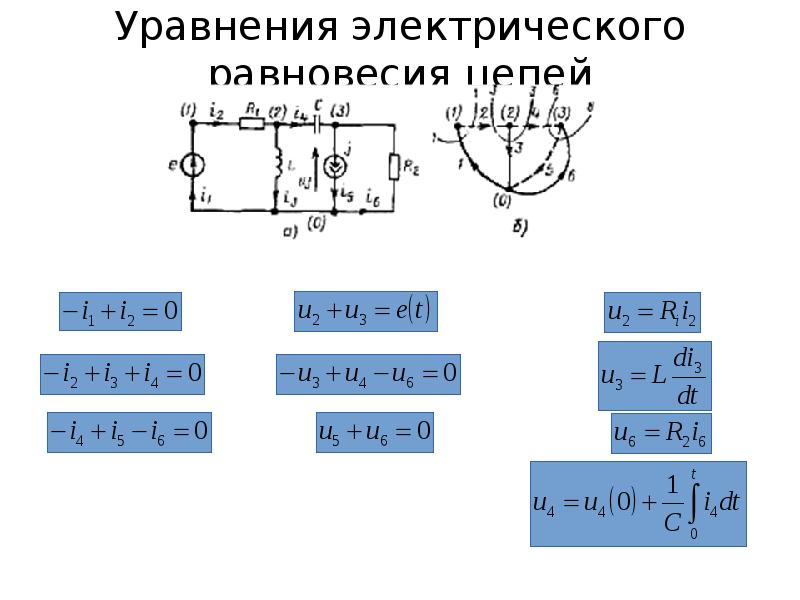 Современные вычислительные средства позволяют автоматизировать данную процедуру за счет применения методов численной оптимизации, оставляя за проектировщиком только лишь обязанность указания критерия оценки качества системы при некотором наборе значений конструктивных параметров, а также ограничений на возможные значения данных параметров. В качестве подобных ограничений чаще всего выступают номенклатурные ограничения, то есть возможность выбора ограничивается некоторым наперед известным набором возможных сочетаний значений параметров, либо интервальные ограничения, то есть указание допустимого диапазона значений для каждого из параметров.
Современные вычислительные средства позволяют автоматизировать данную процедуру за счет применения методов численной оптимизации, оставляя за проектировщиком только лишь обязанность указания критерия оценки качества системы при некотором наборе значений конструктивных параметров, а также ограничений на возможные значения данных параметров. В качестве подобных ограничений чаще всего выступают номенклатурные ограничения, то есть возможность выбора ограничивается некоторым наперед известным набором возможных сочетаний значений параметров, либо интервальные ограничения, то есть указание допустимого диапазона значений для каждого из параметров.
Легко заметить, что задача параметрической оптимизации имеет много общего с задачей машинного обучения. Действительно, если представить модель динамической системы как некий «черный ящик», на вход которого подается вектор значений оптимизируемых параметров, а на выходе – оцениваемые параметров функционирования этой системы, то такой «ящик» можно рассматривать как элемент адаптивной сетевой системы.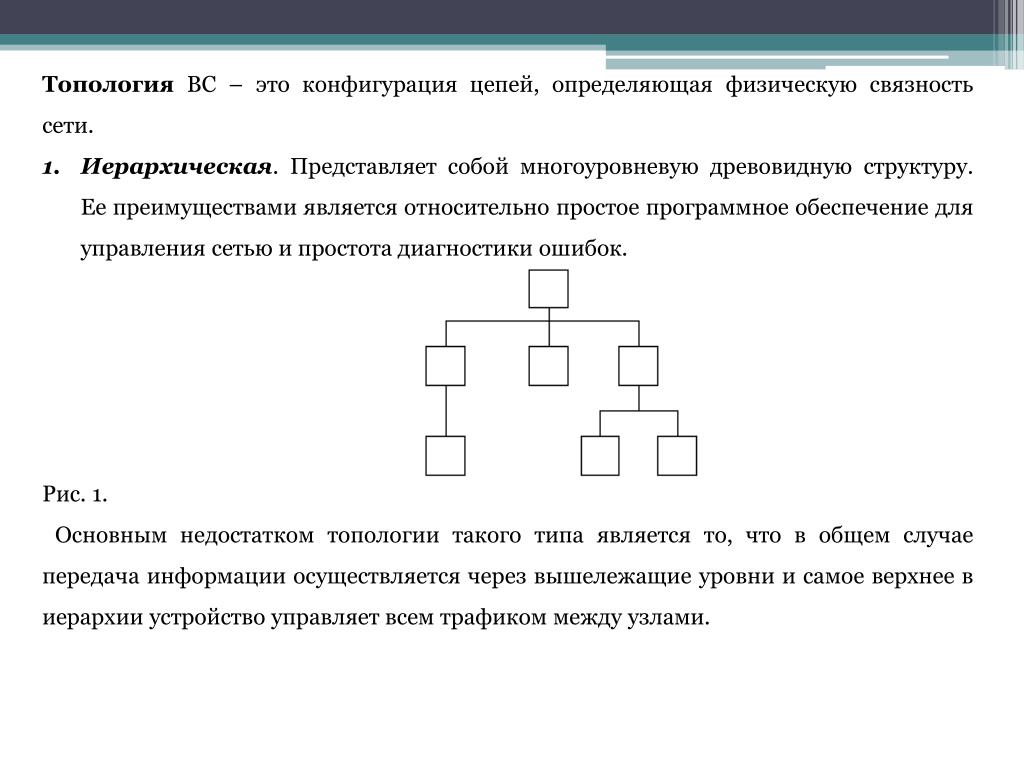 Важно при этом отметить, что в этом случае вполне допустимо в качестве критериев оценки качества функционирования динамической системы использовать не только некоторые числовые (например, интегральные) характеристики, а принимать решение исходя, например, из ширины спектра наблюдаемого выходного сигнала. Иными словами, такой подход позволяет формулировать достаточно сложные составные критерии оценки качества функционирования системы.
Важно при этом отметить, что в этом случае вполне допустимо в качестве критериев оценки качества функционирования динамической системы использовать не только некоторые числовые (например, интегральные) характеристики, а принимать решение исходя, например, из ширины спектра наблюдаемого выходного сигнала. Иными словами, такой подход позволяет формулировать достаточно сложные составные критерии оценки качества функционирования системы.
Параметрическая оптимизация и машинное обучение в среде АПМ
С использованием программного обеспечения APM ECA, разработанного НТЦ «АПМ», возможно выполнение всех этапов проектирования динамических систем с обучаемыми элементами. Возможности программы позволяют проектировать и обучать различные виды нейронных сетей, линейных и нелинейные регрессионные модели и классификаторы, решать задачи кластеризации и понижения размерности данных. Важной отличительной особенностью программного продукта является возможность объединения моделей динамических систем и моделей адаптивных сетевых систем. Это позволяет, например, в качестве критериев качества функционирования использовать значения динамических характеристик проектируемой системы – время переходного процесса, среднюю вырабатываемую мощность, потери на трение и др., а также эффективно формулировать и решать задачу параметрической оптимизации для различных подмножеств конструктивных параметров системы.
Это позволяет, например, в качестве критериев качества функционирования использовать значения динамических характеристик проектируемой системы – время переходного процесса, среднюю вырабатываемую мощность, потери на трение и др., а также эффективно формулировать и решать задачу параметрической оптимизации для различных подмножеств конструктивных параметров системы.
Сетевая адаптивная модель представляется в виде соединенных блоков (элементов), каждый из которых осуществляет преобразование входной тензорной (вектор, матрица или многомерный массив в общем случае) величины в выходную. Элементы модели разделяются на следующие категории:
- Источники – элементы, не имеющие входов и выдающие значения основании установленных параметров.
- Приемники – элементы, не имеющие выходов и осуществляющие действия, не влияющие на функционирование системы (например, вывод значения на график или в файл).
- Преобразующие элементы, не имеющие свободных параметров и осуществляющие заданное преобразование входной величины в выходную (конкатенация значений, вычисление расстояния, суммирование и т.
 д.). Осуществляемое преобразование может быть как детерминированным, так и стохастическим.
д.). Осуществляемое преобразование может быть как детерминированным, так и стохастическим. - Обучаемые элементы. Обладают свободными параметрами, которые настраиваются в процессе обучения для достижения установленного критерия качества.
- Адаптивные элементы. Обладают внутренним состоянием, изменяемым в соответствии с собственным критерием качества.
- «Учителя» – элементы, оценивающие «качество» системы.
Сетевая модель может иметь произвольную глубину (под глубиной сетевой модели понимается максимальное расстояние от приемника до элемента типа «учитель»). Алгоритм обучения выбирается на основании анализа структуры модели, дифференцируемости входящих в ее структуру элементов и установленных критериев оценки качества функционирования системы. Пользователь может устанавливать поэлементную либо пакетную стратегию обучения, размер пакета и параметры регуляризации.
Возможности APM ECA могут быть использованы для разработки адаптивных, в том числе нейросетевых систем управления, непрерывных и дискретных фильтров, а также решения задач идентификации динамических систем с их последующим использованием в качестве составных элементов в других моделях, распознавания образов, систем диагностики состояния и др. Программный продукт включает инструменты расширения функциональности путем добавления пользовательских элементов, функционирование которых описывается средствами языков программирования Python или Julia.
Программный продукт включает инструменты расширения функциональности путем добавления пользовательских элементов, функционирование которых описывается средствами языков программирования Python или Julia.
Топология цепей Основные определения Схема электрической цепи
Топология цепей Основные определения Схема электрической цепи — это условное графическое изображение электрической цепи.
Топология цепей Основные определения
Топология цепей Основные определения В неразветвленной цепи один и тот же ток замыкается через все элементы цепи. В разветвленных цепях токи через различные элементы могут иметь различные значения. Соединение группы идеализированных двухполюсных элементов, при котором через них замыкается один и тот же ток, называется последовательным. Соединение группы двухполюсных элементов, при котором все элементы находятся под одним и тем же напряжением, называется параллельным. Комбинация последовательного и параллельного соединений элементов называется смешанным соединением
Комбинация последовательного и параллельного соединений элементов называется смешанным соединением
Топология цепей Основные определения
Топология цепей Основные определения Ветвь представляет собой участок электрической цепи, вдоль которого замыкается один и тот же ток. Место соединения ветвей между собой называется узлом, причем место соединения двух ветвей называют устранимым узлом. Любой замкнутый путь, проходящий по нескольким ветвям цепи так, что ни одна ветвь и ни один узел не встречаются дважды, называется контуром. Контур характеризуют направлением обхода (порядком перечисления ветвей), которое выбирают произвольно и указывают изогнутой стрелкой. Топологическое описание цепи, при котором необходимо принимать во внимание все узлы, в том числе и устранимые, будем называть расширенным. Топологическое описание цепи, при котором устранимые узлы во внимание не принимаются, будем называть сокращенным.
Понятие о компонентных и топологических уравнениях Компонентные уравнения (уравнения ветвей) представляют собой математические модели соответствующих ветвей и выражают ток или напряжение каждой ветви через параметры элементов этой ветви. Топологические уравнения устанавливают связь между токами или напряжениями различных ветвей, причем вид и число топологических уравнений не зависят от того, какие именно элементы входят в состав ветвей цепи.
Топологические уравнения устанавливают связь между токами или напряжениями различных ветвей, причем вид и число топологических уравнений не зависят от того, какие именно элементы входят в состав ветвей цепи.
Понятие о компонентных и топологических уравнениях
Понятие о компонентных и топологических уравнениях
Понятие о компонентных и топологических уравнениях Компонентные уравнения невырожденной ветви устанавливают связь между ее током и напряжением и могут быть записаны в двух формах: 1) ток ветви определяется через напряжение ветви; 2) напряжение ветви находится через ток. Компонентное уравнение вырожденной ветви задает напряжение или ток ветви, но не позволяет по известному напряжению ветви найти ее ток или по заданному току определить напряжение.
ЗАКОНЫ КИРХГОФА Первый закон Кирхгофа устанавливает связь между токами ветвей в каждом из узлов цепи: алгебраическая сумма мгновенных значений токов всех ветвей, подключенных к каждому из узлов моделирующей цепи, в любой момент времени равна нулю. уравнение баланса токов в узле l и k— номера узлов и ветвей; q и p— число узлов и ветвей. В уравнение баланса токов, составленное для l-го узла, входят только токи ветвей, подключенных к этому узлу, причем токи ветвей, направленных к узлу, берутся со знаком минус, а токи ветвей, направленных от узла, – со знаком плюс.
уравнение баланса токов в узле l и k— номера узлов и ветвей; q и p— число узлов и ветвей. В уравнение баланса токов, составленное для l-го узла, входят только токи ветвей, подключенных к этому узлу, причем токи ветвей, направленных к узлу, берутся со знаком минус, а токи ветвей, направленных от узла, – со знаком плюс.
ЗАКОНЫ КИРХГОФА для узла(1) для узла (2) для узла (3) для узла (0) Первый закон Кирхгофа устанавливает связь между токами ветвей в каждом из узлов цепи: алгебраическая сумма мгновенных значений токов всех ветвей, подключенных к каждому из узлов моделирующей цепи, в любой момент времени равна нулю.
ЗАКОНЫ КИРХГОФА Второй закон Кирхгофа устанавливает связь между напряжениями ветвей, входящих в произвольный контур: алгебраическая сумма мгновенных значении напряжений всех ветвей, входящих в любой контур ноле лир уютен цепи. в каждый момент времени равна нулю. уравнение баланса напряжений ветвей l и k— номера контуров и ветвей; N и p— число контуров и ветвей. В уравнение баланса напряжений, составленное для l-го контура, входят только напряжения ветвей, входящих в этот контур, причем если положительное направление напряжения совпадает с направлением обхода контура, то оно входит в уравнение со знаком плюс, в противном случае – со знаком минус.
В уравнение баланса напряжений, составленное для l-го контура, входят только напряжения ветвей, входящих в этот контур, причем если положительное направление напряжения совпадает с направлением обхода контура, то оно входит в уравнение со знаком плюс, в противном случае – со знаком минус.
ЗАКОНЫ КИРХГОФА для контура (1) для контура (2) для контура (3) Второй закон Кирхгофа: алгебраическая сумма мгновенных значений напряжений на всех элементах любого контура моделирующей цепи, за исключением источников напряжения в каждый момент времени, равна алгебраической сумме мгновенных значений ЭДС источников напряжения, действующих в этом контуре.
ЗАКОНЫ КИРХГОФА
ЗАКОНЫ КИРХГОФА Уравнения по второму закону Кирхгофа можно составить для любой совокупности элементов, образующих путь для электрического тока от произвольно выбранного узла (а) электрической цепи к узлу (б) с учетом напряжения между конечными точками этого пути uаб
ЗАКОНЫ КИРХГОФА Для контуров, в которых есть источники тока, уравнения баланса напряжений составляют по общему правилу, причем напряжение источника тока учитывается в левой части уравнения.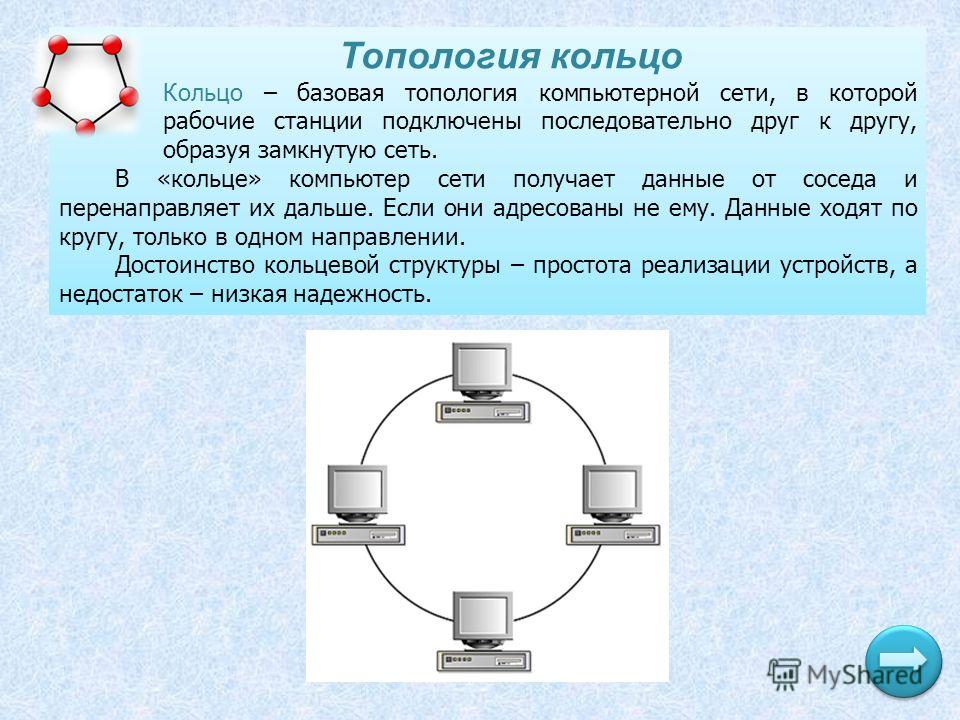
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным. Подграфом графа называется часть графа, т. е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным. Подграфом графа называется часть графа, т. е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рисунке ветви 2 -6 -5; 4 -5; 3 -6 -4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно. 2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рисунке можно определить контуры, образованные ветвями 2 -4 -6; 3 -5 -6; 2 -3 -5 -4. Если между любой парой узлов графа существует связь, то граф называют связным.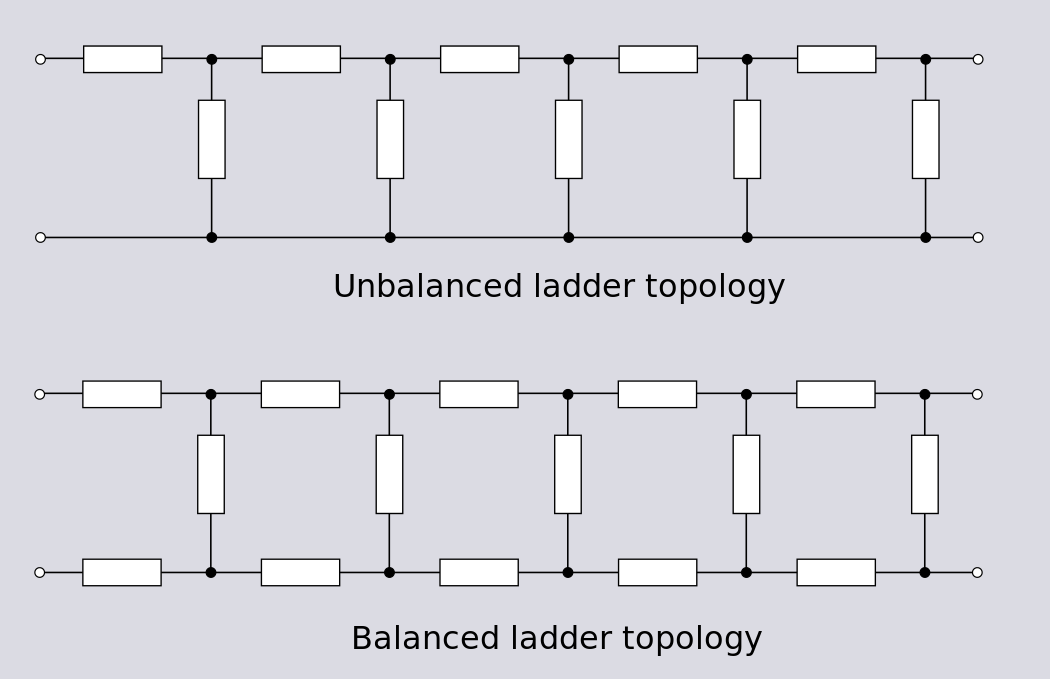
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа могут служить фигуры.
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа. Если граф содержит m узлов и n ветвей, то число ветвей любого дерева а числа ветвей связи графа
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом. Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа S 1 и S 2. При этом получаем соответственно сечения, образованные ветвями 6 -4 -5 и 6 -2 -1 -5.
ГРАФЫ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С понятием дерева связаны понятия главных контуров и сечений: • главный контур – контур, состоящий из ветвей дерева и только одной ветви связи; • главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.
Топологический граф электрических цепей
Графом электрической цепи называется условное изображение электрической цепи, в котором каждая ветвь цепи заменяется отрезком линии. При этом идеальный источник напряжения учитывается как короткозамкнутая ветвь, а идеальный источник тока – как разомкнутая ветвь.
Ветвью графа называется отрезок линии, соответствующий ветви электрической схемы.
Узлом графа называется точка соединения трех и более ветвей.
Граф, ветвям которого заданы определенные направления, указанные стрелкой, называется направленным. Направления ветвей графа, которые указывают стрелками, совпадают с положительными направлениями токов, протекающих по соответствующим ветвям цепи. Граф, у которого не указаны направления ветвей, называется ненаправленным.
Граф строится в соответствии с эквивалентной схемой цепи путем замены каждой её ветви отрезком линии, которая рассматривается как ветвь графа. При этом каждый узел цепи преобразуется в узел графа. Нумерация ветвей и узлов графа такая же, что нумерация ветвей и узлов цепи.
Деревом графа называется его часть, содержащая все узлы, но не содержащая ни одного контура. Ветви графа, образующие дерево, называются ветвями дерева. Число ветвей дерева определяется по формуле , где – число узлов графа. В качестве ветвей дерева запрещается выбирать ветви, содержащие источник тока.
Главными ветвями графа называются ветви, не вошедшие в дерево. Число главных ветвей определяется по формуле , где – число ветвей графа.
Главными контурами графа называются контура, образованные путем последовательного добавлением к дереву графа его главных ветвей. Число главных контуров равно числу главных ветвей .
На рис. 3.4, а изображена схема электрической цепи, а на рис. 3.4, б её направленный граф. В качестве дерева выбраны ветви 2 и 4. Ветви 1, 3, 5 являются главными ветвями графа, которые совместно с ветвями дерева образуют три главных (независимых) контура I, II и III.
Таким образом, граф можно рассматривать как упрощенную модель электрической цепи, отражающую ее структуру.
Топологические понятия схемы электрической цепи
Введем основные топологические понятия схемы электрической цепи.
Граф схемы – это такое графическое (топологическое) представление схемы, при котором ветви схемы изображаются отрезками (или дугами), а узлы – точками. Отрезки называют ветвями графа, а точки – узлами графа. Такое представление является наглядным изображением взаимных соединений ветвей схемы.
Условимся ветвь с идеальным источником тока не включать в граф схемы, так как внутренняя проводимость идеального источника тока равна нулю и соответственно сопротивление таких ветвей бесконечно велико.
Для схемы, изображенной на рисунке 3.14, граф имеет вид (рис.3.15а)
Если условные положительные направления токов в электрической схеме перенести на граф, то получим направленный граф (рис.3.15б).
На рисунке 3.16 представлены схема электрической цепи и ее направленный граф
При описании графа цепи полезно использовать понятие дерева графа.
Дерево графа – это связанная часть графа, включающая все узлы и не имеющая ни одного контура.
Дерево графа с узлами содержит ( ) ветвь. Один и тот же граф может иметь различные деревья. Например, для графа, изображенного на рис.3.16, деревья могут принимать следующий вид
Связи графа – это ветви, дополняющие дерево до исходного графа. Число связей , где – число ветвей, – число узлов.
Законы Кирхгофа
При расчете электрических цепей используются законы Кирхгофа. Первый закон Кирхгофа формулируется применительно к узлам электрической цепи и следует из принципа непрерывности электрического тока: алгебраическая сумма токов всех ветвей, имеющих общий узел, равна нулю
Принято знак “плюс” приписывать току ветви, условное положительное направление которого направлено от узла, “минус” – к узлу. Например:
Второй закон Кирхгофа формулируется применительно к контурам электрической цепи: алгебраическая сумма падений напряжений во всех ветвях любого контура электрической цепи равна алгебраической сумме э.д.с., действующих в этом контуре
При использовании второго закона Кирхгофа задаются произвольным положительным направлением обхода контура. Напряжения и э.д.с., условные положительные направления которых совпадают с направлением обхода, берутся со знаком “плюс”, в противном случае напряжения и э.д.с берутся со знаком “минус”.
Особо отметим, что при составлении уравнения по второму закону Кирхгофа контур может проходить не только по ветвям графа схемы, но и иметь вид, подобный указанному пунктиром на рис.3.17.
По первому закону Кирхгофа можно составить линейно независимых уравнений для узла.
По второму закону Кирхгофа число линейно независимых уравнений равно числу связей графа . Действительно, любая связь графа образует контур с ветвями дерева и каждый такой контур отличается от остальных контуров по крайней мере ветвью, образующей связь. Таким образом, число независимых контуров .
Общее число уравнений, составленных по первому и второму законам Кирхгофа, равно числу ветвей графа . Если неизвестными электрической схемы являются напряжения и токи в ветвях, то для записи полной системы уравнений необходимо добавить уравнения, связывающие напряжения и токи на элементах электрической цепи (число таких уравнений равно числу пассивных элементов схемы электрической цепи).
Выражая напряжения на элементах через токи в уравнениях, составленных по второму закону Кирхгофа, получим систему уравнений относительно неизвестных токов в ветвях.
При расчете электрической цепи с зависимыми источниками уравнения формируются в два этапа :
· составляются уравнения цепи в предположении, что все источники независимые;
· слагаемые уравнений, соответствующие зависимым источникам, выражаются через управляющие токи и напряжения.
Пример. Составить уравнения по законам Кирхгофа для определения токов в ветвях электрической схемы (рис.3.16), считая известными параметры элементов схемы , , , , .
Граф этой схемы имеет вид
Число узлов = 5, число ветвей
= 7.
Число уравнений по первому закону Кирхгофа . Для узлов с первого по четвертый имеем:
1
2
3
4
Число независимых контуров = 3 равно числу связей. Выберем независимые контуры, каждый из которых образован одной связью (тонкие линии на рисунке графа) и ветвями дерева (утолщенные линии). Направления обхода контуров примем совпадающими с условными положительными направлениями токов в связях. Выражая напряжения на отдельных элементах цепи через токи ветвей, получим три уравнения, составленные по второму закону Кирхгофа:
Решая полученную систему из семи уравнений, можно определить токи во всех ветвях схемы.
Топология электрической сети
– обзор
17.5.1 Активный одиночный сбалансированный смеситель с использованием BJT
На рисунке 17.16 показана топология базовой схемы активного SBM на основе дифференциальной пары BJT, Q 1 и Q 2 , смещенный транзистором источника тока Q 3 . Функциональные блоки, показанные на рисунке 17.15, для иллюстрации наложены на рисунок 17.16. Транзистор источника тока, Q 3 , устанавливает общий ток в двух верхних транзисторах, которые затем конкурируют за долю этого тока.Поскольку общий ток фиксирован Q 3 , больший ток в Q 1 означает меньший ток в Q 2 , и наоборот, отсюда дифференциальная работа этой схемы. Нагрузочные резисторы R L преобразуют токи коллектора в напряжения. Коэффициент усиления дифференциальной пары зависит от крутизны, g m , двух транзисторов, которая, в свою очередь, зависит от их тока коллектора, I C , согласно g m = I C / V T .Таким образом, схему на рис. 17.16 можно использовать в качестве смесителя, когда ток в Q 3 модулируется напряжением радиочастотного сигнала. Мы подаем сигнал гетеродина как дифференциальное напряжение на базы Q 1 и Q 2 , а сигнал ПЧ принимаем как дифференциальное напряжение на коллекторах Q 1 и Q . 2 . Сопротивление дегенеративной обратной связи R e добавлено к источнику тока для улучшения его линейности.
Рисунок 17.16. Односбалансированный активный микшер с использованием BJT.
Коллекторные токи транзистора, I C1 и I C2 , будут состоять из составляющей смещения постоянного тока плюс составляющей сигнала. Для целей этого анализа мы проигнорируем компоненты смещения постоянного тока и просто рассмотрим компоненты сигналов любых напряжений и токов, которые мы представим строчными буквами v и i соответственно.
Предположим, что два транзистора Q 1 и Q 2 на рисунке 17.16 имеют идентичные вольт-амперные характеристики, отношения между токами коллектора малых сигналов и напряжениями база-эмиттер Q 1 и Q 2 следующие:
(17.5.1) iC1 = ISe ( vBE1 / VT)
(17.5.2) iC2 = ISe (vBE2 / VT)
, где I S – ток насыщения, а В T – тепловое напряжение, определяемое V T = kT / q ≈ 26 мВ при комнатной температуре (около T = 290 K).
В качестве альтернативы мы можем написать:
(17.5.3) vBE1 = VTlniC1IS
(17.5.4) vBE2 = VTlniC2IS
Напряжение в точке общего эмиттера, v EE , на рисунке 17.16 представлено выражением :
(17.5.5) vEE = vLO¯ − vBE1 = vLO − vBE2
Из уравнения (17.5.5) мы можем записать:
(17.5.6) vLO − vLO¯ = vBE2 − vBE1
vLO− vLO¯ – это напряжение дифференциального входного сигнала гетеродина, Δ v LO , поэтому, применив уравнение (17.5.3), мы можем записать:
(17.5.7) ΔvLO = vLO − vLO¯ = VTlniC2IS − VTlniC1iS
(17.5.8) ΔvLO = VTlniC2iC1
Следовательно,
(17.5.9) iC1iC2 = e (−ΔvLO / VT)
Для большинства современных СВЧ-транзисторов усиление велико, поэтому обычно можно игнорировать базовый ток, то есть i E ≈ i C . Следовательно, из рисунка 17.16 мы можем написать:
(17.5.10) iEE = iC1 + iC2
Объединив уравнения (17.5.9) и (17.5.10), мы можем теперь записать токи сигналов коллектора Q 1 и Q 2 на рисунке 17.16 через Δ v LO и I EE как:
(17.5.11) iC1 = iEE1 + e (ΔvLO / VT)
(17.5.12) iC2 = iEE1 + e ( −ΔvLO / VT)
Разницу между двумя токами коллектора теперь можно записать следующим образом:
(17.5.13) ΔiIF12 = iC1 − iC2
(17.5.14) = IEE11 + e (ΔvLO / VT) – 11 + e (−ΔvLO / VT)
Что можно переписать как:
(17.5.15) ΔiIF12 = iEEe (−ΔvLO / 2VT) −e (ΔvLO / 2VT) e (−ΔvLO / 2VT) + e ( ΔvLO / 2VT)
Уравнение (17.5.15) можно более точно выразить, используя определение функции гиперболического тангенса (tanh), которая определяется как:
(17.5.16) tanh (x) = ex − e − xex + e − x
Мы можем теперь перепишите уравнение (17.5.13) как:
(17.5.17) ΔiIF12 = iEEtanhΔvLO2VT
Теперь, если мы предположим, что ток смещения I EE модулируется v RF , как показано на На рисунке 17.16 мы можем заменить простой член I EE в уравнении (17.5.17) по ( I EE o + g m 3 v RF ), где I EE o – это постоянный ток смещения . м 3 – крутизна транзистора источника тока, Q 3 . Теперь мы можем написать:
(17.5.18) ΔiIF12 = IEEo + gm3vRFtanhΔvLO2VT
Который может быть расширен до:
(17.5.19) ΔiIF12 = IEEotanhΔvLO2VT + gm3vRFtanhΔvLO2VT (расширение серии Mac3vRFtanhΔvLOur2VT)
следующим образом [5]:(17.5.20) tanh (x) = x − 13×3 + 215×5−17315×7 + 622835×9 + ⋯
Из уравнения (17.5.20) мы можем показать, что tanh (x) ≈x для малых значений x (т. Е. Для значений x до x = 0,5 имеем tanh (x) / x> 0,92). Таким образом, мы можем аппроксимировать tanh в уравнении (17.5.19) в предположении, что v RF и v LO малы (т.е. менее В T = 26 мВ при комнатной температуре) . Следовательно, мы имеем:
(17.5.21) ΔiIF12≈IEEoΔvLO2VT + gm3ΔvLOvRF2VT
Первый член в уравнении (17.5.21) представляет компонент утечки гетеродина, который пропорционален току смещения постоянного тока, i EE o . Второй член содержит интересующий нас продукт, а именно ( v RF Δ v LO ).
SBM, показанный на рис. 17.16, имеет преимущество простоты и относительно низкого коэффициента шума, поскольку здесь меньше компонентов, генерирующих шум, чем в конструкции с двойной балансировкой.С другой стороны, прямое прохождение частотных компонентов гетеродина может быть серьезной проблемой в некоторых приложениях и является существенным недостатком топологии SBM. Хотя эти нежелательные частотные составляющие обычно имеют гораздо более высокую частоту, чем ПЧ, и поэтому могут быть отфильтрованы, дополнительная энергия нежелательного сигнала может повлиять на линейность схемы и вызвать насыщение последующих каскадов схемы. Еще один недостаток SBM на рисунке 17.16 состоит в том, что вход RF является несимметричным, а не балансным.Это делает его восприимчивым к синфазному шуму и помехам [9].
Границы | Подход с топологией схемы к классификации изменений в структуре биомолекул
1. Введение
Топология – это математическое понятие, которое относится к определенным свойствам объектов, которые остаются неизменными при непрерывных операциях, таких как растяжение, изгиб или сжатие [1]. Объекты, которые трансформируются друг в друга посредством таких непрерывных деформаций, попадают в один и тот же топологический класс. Например, круги и треугольники топологически похожи, поскольку они могут взаимно преобразовываться, изгибаясь или растягиваясь.Существует тесная взаимосвязь между функциональными и физическими свойствами молекулярных структур и их топологическими особенностями [2, 3]. Более того, топология предоставляет элементарные правила, которые помогают нам конструировать молекулы желаемым образом и синтезировать новые структуры [4–6]. Новые свойства можно увидеть в таких синтетических молекулах, которым нет аналогов в биохимическом мире [7, 8].
В химии есть общие основы, такие как теория групп, которые помогают исследовать топологические и геометрические свойства молекул.Однако в биологии нам не хватает подобных основ. Разнообразие и сложность биологических молекул затрудняет сведение структурных и функциональных свойств молекул к простым правилам симметрии. Следовательно, создание топологического языка для биохимии и биохимической инженерии представляет собой интересную научную задачу. Такая структура могла бы стать мощным инструментом для объединения всего разнообразия молекул в рамках согласованной закрытой теории. Можно представить себе множество приложений, поскольку связь между топологией и биомолекулярной функцией или дисфункцией часто рассматривается в вопросах здоровья и болезней [9, 10].Топологические подходы уже реализованы в мощных алгоритмах машинного обучения для правильного прогнозирования аффинности связывания белок-лиганд, изменений свободной энергии сворачивания глобулярных белков, вызванных мутациями, и изменений свободной энергии сворачивания белков мембран [11, 12].
Топология биологической цепи – это математический подход, который описывает отношения между внутримолекулярными контактами внутри свернутой молекулы [13–20]. В этом контексте попарные отношения между контактами могут быть определены с использованием логических правил теории множеств [13, 14].Независимо от типа молекулы или ее сложности, два контакта могут иметь одно из нескольких общих соотношений симметрии друг с другом. Для бинарных контактов они могут быть параллельными, последовательными или перекрестными, или в соответствующих согласованных расположениях, если два контакта находятся на одной площадке. На рисунке 1 показаны эти схемы и соответствующие матрицы, показывающие возможность подключения сайтов. Полноту этих соотношений можно доказать [13], и их можно рассматривать как необходимые и достаточные для описания топологии свернутых молекул (образованных двух- или многовалентными контактами).Топология схемы формирует набор правил, которые можно использовать для поиска неизвестных топологических отношений между контактами из известных отношений. В этом подходе топология представлена в матричной форме, а эквивалентные топологии выводятся из идентичных матричных представлений. Топология биологической схемы позволяет определить топологию более сложной молекулы, полученной в результате комбинации более простых молекул. Скорости сворачивания и количество путей разворачивания макромолекулы можно оценить, используя правила топологии схемы [14].
Рисунок 1 . Пять типов отношений топологии схемы представляют собой матрицу связности S и соответствующий граф.
Топология схемы биомолекул подвержена изменениям во время сворачивания / разворачивания и биохимических реакций, а также в процессе эволюции. Здесь мы спрашиваем, как изменяется топология при основных молекулярных операциях, таких как перестановка контактов, дублирование или устранение. Мы разрабатываем простой алгебраический формализм для описания эффекта этих операций.Вкратце, каждое топологическое состояние может быть описано матрицей связности, а топологические изменения могут быть описаны как преобразования матрицы, для которых линейная алгебра уже предоставляет все необходимые инструменты. Мы показываем, что результат операций с молекулами со сложной топологией может быть легко предсказан с помощью этого подхода. Наши результаты имеют отношение к пониманию эволюции и структурного сходства белков и других биологических молекул, и они могут помочь в качестве руководства для молекулярных инженеров, заинтересованных в разработке свернутых молекул, активных материалов и интеллектуальных структур.
2. Топология схем и молекулярные операции
Мы представим здесь новый способ описания как топологического состояния свернутого линейного полимера, так и молекулярных операций в структуре. Как топологическое состояние, так и изменения этого состояния представлены с использованием матриц перестановок (представления S n ) и связаны с хорошо известными инструментами матричного умножения.
2.1. Топология цепи
Далее мы переопределяем базовые концепции топологии схемы, чтобы дать возможность использовать простые алгебраические операции, а не полагаться на комбинаторные алгоритмы.В этом обобщенном подходе мы показываем, что любая структура линейной молекулы может быть однозначно представлена матрицей перестановок S и вектором d , называемым матрицей связности и основной цепью , соответственно.
Математическая перестановка – это обмен элементами. Абстрактная карта часто обозначается греческой буквой (мы часто будем использовать π) и отображает целое число на другое целое число π ( i ) = j . Если и только если перестановка меняет местами только два элемента, она называется транспозицией.Абстрактная перестановка может быть представлена матрицей перестановок. Матрица перестановок меняет местами элементы вектора в соответствии с перестановкой. Он имеет только элементы 1 и 0, а сумма каждой строки и сумма каждого столбца равна 1. В случае топологии схемы никакая матрица перестановок не может использоваться. Прежде всего, S должен быть симметричным, т.е. состоять только из коммутирующих транспозиций. Матрица
Например,заменяет элемент 1 на 2 и оставляет элемент 3 неизменным [он часто представляется как (12) (3) или (12)].В топологии биологической схемы это представляет собой соединение между элементами 1 и 2 основной цепи d .
Основная цепь d – это вектор, который содержит информацию о базовой молекулярной структуре. Он может состоять из индексов всех аминокислот в белке или нуклеотидов в последовательности ДНК, или это может быть длина строки / цепи до определенной точки d i . d не обязательно должен быть полным (т.е. он не обязательно должен содержать весь массив индексов), например, d = (2, 5, 20, 21) является допустимым вектором магистрали.Кроме того, значения не обязательно должны быть уникальными. Это означает, например, что d = (1, 2, 2, 3) также приемлемо, а в некоторых случаях даже требуется. Если элементы d являются расстояниями, то d i может быть любым действительным числом, например, d = (1,23, 1,938, 5,392). Если элемент не заменяется матрицей связности (например, элементом 3 в уравнении 1), то его можно безопасно исключить из представления без изменения состояния молекулы:
При таком изменении пары (S, d) сама молекула не изменяется, но представление минимизируется.Более подробное обсуждение преобразований можно найти в следующем разделе.
Пара (S, d) определяет состояние линейной молекулы (например, белка, ДНК), где d определяет сайты связывания, а S – возможность соединения этих сайтов связывания. На рисунке 1 показана система с двумя связями со всеми возможными отношениями. Возможные отношения: ряд (S), крест (X) и параллель (P). Ниже обсуждаются два особых отношения связности (согласованные параллельные и согласованные серии). Обратите внимание, что только P не является рефлексивным и имеет обратную зависимость P -1 , для более подробной информации см. Mashaghi et al.[13].
Для большинства отношений связности карта связности S идентична карте контактов, однако два особых отношения связности приводят к разным матрицам: согласованная параллельная (CP) и согласованная серия (CS). Для контакта с остатками 1 и 2 и контакта 2 с 3 (CS) карта контактов дается
Однако это не матрица перестановок, поэтому она запрещена в качестве матрицы связности. Чтобы представить эту систему в структуре топологии схемы, d должен содержать контактный участок 2 дважды, один из которых контактирует с 1, а другой с 3.Можно представить себе это как вымышленное разделение сайта 2 на два отдельных и разных сайта, 2 и 2 ‘, формирование связи и последующее объединение их посредством 2 = 2’. Следовательно, правильная матрица связи и магистраль для CS – это
S = (0100100000010010) d = (1223). (4)На рисунке 1 также показано правильное представление для CP .
Требование уникальности требует дополнительных ограничений на d и S. Если d содержит каждое значение только один раз, то для уникальности достаточно упорядочения; однако, если это не так, то несколько эквивалентных конфигураций d приведут к другому S (например, замена индекса 2 на 3 в уравнении 4).Мы определяем упорядоченное состояние следующим образом: для всех i и j с i < j мы имеем d i ≤ d j и if d i = d j , тогда следует, что π ( i ) <π ( j ), где π – это перестановка, представленная S. Например,
S = (0010000110000100) d = (1223) (5)– это то же состояние, что и в уравнении (4), однако для d 2 = d 3 , но 4 = π (2) ≮ π (3) = 1, поэтому единственное правильное представление находится в уравнении (4).
Кроме того, мы также устанавливаем правило, согласно которому не может быть контакта между идентичными сайтами и что любая связь может возникнуть не более одного раза. Это означает, что контакт типа
S = (0110) d = (11), (6)никогда не допускается. С этим ограничением (заказан d , заказ S для d i = d j и отсутствие контактов между равными сайтами) S считается уменьшенным. Это дает уникальность, а порядок согласовывается с ранее определенными порядками [20].Для полного доказательства см. Дополнительную информацию.
Наконец, мы вводим матрицу отношений [13]. Матрица отношений представляет собой матрицу n × n , которая содержит отношение между связями, где n – количество контактов. Отношения являются известными X, P, P −1 , S …. Это представление в основном предназначено для отображения, потому что оно меньше S и связь между связями может быть прочитана немедленно.
Наконец, мы предложим простой способ сравнения различных состояний:
• идентично: d = d ′ и S = S ′
• частично эквивалентно: S = S ′, и d и d ′ упорядочены аналогичным образом, где S и d исключают любые элементы без соединений.
• неэквивалент: в противном случае.
Описание топологического состояния белка с использованием пары (S, d) предоставляет мощный инструмент для выполнения преобразований с использованием алгебраических операций, которые хорошо известны и легко доступны.Различные типы преобразований обсуждаются в следующем разделе.
2.2. Молекулярные операции
2.2.1. Общий
Молекулярная операция – это любая карта, такая что T: (S, d) ↦ (S ‘, d’). Мы можем в общих чертах классифицировать эти операции как перегруппировки или как операции, при которых изменяется топологическое состояние молекулы (молекулярная операция), или как комбинацию обоих типов. Очевидно, что нас интересуют молекулярные операции, в которых как прообраз, так и изображение упорядочиваются и уменьшаются.Ограничение необходимо, потому что оно напрямую приведет к уникальному отображению, которое явно описывает изменение (без каких-либо дополнительных комбинаторных (пере) конфигураций]. Сначала мы опишем три типа преобразований, которые дадут им ясную интерпретацию.
Первый набор преобразований – это преобразования типа 0. Деформации типа 0 не изменяют топологическое состояние молекулы и образуют группу, состоящую из переупорядочения, расширения и уменьшения d .
Первая подгруппа состоит из упорядочивающих преобразований. Если d не упорядочен, то его можно упорядочить, используя матрицу перестановки O , которая меняет местами соответствующие элементы в d . Это должно привести к изменению S, чтобы система оставалась неизменной. Изменение описывается как S ′ = OSO-1. Таким образом, пара (S, d) и (S ‘, d’) = (OSO-1, Od) описывают одно и то же состояние, но являются разными представлениями. Визуально это можно представить как перемаркировку остатков в белке без изменения последовательности или связности.
Например, мы рассматриваем состояние, в котором остаток 1 с 2, а также остатки 3 и 4 имеют общую связь. Система описывается следующими S и d
S = (0010000110000100) d = (1324). (7)d , однако, не заказывается, что может привести к путанице, поскольку S может быть ошибочно принят за состояние X . При повторном заказе необходимо поменять элементы d 2 и d 3 . Соответствующая матрица перестановок O задается как
О = (1000001001000001) (8), и мы можем вычислить преобразованные d ′ и S ′
d ′ = O (1324) = (1234), (9) S ′ = (1000001001000001) (0010000110000100) (1000001001000001) -1 (10) = (1000001001000001) (0100000110000010) (11) = (0100100000010010) (12)Пара (S ‘, d’) четко описывает одно и то же состояние, однако тот факт, что d упорядочен, упрощает интерпретацию и предотвращает ошибки чтения.Это особенно важно, когда преобразования других типов (см. Ниже) производят неупорядоченное d , которое можно не заметить.
Другая группа преобразований типа 0 увеличивает или уменьшает длину d , но не меняет топологическое состояние молекулы. Сокращение, например, можно использовать для устранения несвязанных сайтов контактов, чтобы получить меньшую букву S, по-прежнему содержащую всю необходимую информацию. Расширение делает наоборот. Он может, например, добавить еще одну запись в d , чтобы можно было образовать дополнительные связи, или он может повторно ввести целые блоки белка, которые были проигнорированы, потому что они могли не иметь значения.Пример преобразования типа 0 дается
S = (010100001) ↦S ′ = (0110). (13)Молекулярные операции, которые буквально изменяют молекулу, можно разделить на (i) трансформации, которые изменяют контакты (Тип I), и (ii) трансформации, которые изменяют скелет (Тип II).
1. Преобразования I типа приводят к изменению контактов. Это означает, что либо образуются новые контакты (создание), либо существующие контакты разрываются (аннигиляция), либо и то, и другое. Обе операции выполняются с одним и тем же оператором, который представляет собой матрицу перестановки, которая перемещает затронутые элементы.Матрица оператора умножается на матрицу S, но нужно быть осторожным, чтобы сначала выполнить аннигиляцию (и). В некоторых случаях конечное состояние неупорядочено и должно быть переупорядочено снова. Переупорядочение является преобразованием типа 0 и требует (S ′, d ′) = (OSO-1, Od). Для простого случая S = (23), когда связь (23) разорвана и связь (12) создается, мы используем
S ′ = T (12) T (23) S = (010100001) (100001010) (100001010) = (010100001) (14)Если, с другой стороны, известны начальное и конечное состояния, полная матрица преобразования может быть вычислена напрямую с помощью T = S′S-1 = S′S.Это также дает кратчайший путь от S к S ‘, потому что любое транспонирование является обратным. Например, преобразование (12) (34) (56) ↦ (12) (36) даст T = (12) (36) · (12) (34) (56) = (12) (12) (34) (56) (36) = (12) (12) (36) (34) (56) = (36) (34) (56). Это показывает, что необходимо выполнить не более трех операций. (Тот же результат будет получен с использованием матриц).
Как уже упоминалось, если результирующее состояние неупорядочено, его необходимо снова переупорядочить. В противном случае могут возникнуть операции, которые фактически не изменят систему.Это только в том случае, если d содержит значение несколько раз. Например, рассмотрим d = (1, 2, 2) и S = (12). Аннигиляция (12) и создание (13) дали бы S ′ = (13). Однако это не упорядочено, потому что для i = 2 <3 = j даст d 2 = 2 = d 3 , но π (2) = 2> π (3) = 1, что противоречит предположению об упорядоченности (S, d). Переупорядочение даст S ″ = OS′O-1 = (23) (13) (23) = (12) = S, то есть то же самое, что и исходное состояние.Таким образом, описанная трансформация – это фактически только карта единства.
2. Преобразования типа II: эти типы преобразований буквально изменяют основу молекулы. Таким образом, карта действует в основном на d , который впоследствии необходимо заказывать заново. Для простых категорий, как показано ниже, легко доступны простые преобразования, но теоретически возможна почти любая карта на d . Например, когда деталь вырезается и прикрепляется заново, тогда: d = (1, 2, 3, 4) ↦ d = (1, 2, 4, 3).Однако этот d должен быть переупорядочен на O = (34), и, в свою очередь, S ‘= OSO-1 также изменяется.
Биологические различия между типом I и типом II очевидны, однако с математической точки зрения они могут быть эквивалентными. Пока появляется одно и то же результирующее состояние, карта математически идентична и взаимозаменяема. Если преобразование типа I и преобразование типа II эквивалентны и одно из них может быть намного сложнее выполнить, его можно легко воспроизвести с помощью другого преобразования.Это сравнимо с преобразованием координат: можно либо повернуть точку в пространстве относительно фиксированной системы координат, либо повернуть координаты и оставить точку фиксированной. Оба преобразования дают один и тот же результат, но математическая процедура различается. То же самое можно сказать о преобразованиях типа I и типа II.
Далее мы переопределяем наиболее важные молекулярные операции, используя логику топологии схемы. В частности, мы рассматриваем циклическую и стандартную перестановку, инверсию, дублирование и исключение.Эти операции имеют большое значение для биомолекулярной эволюции, конформационной динамики и сворачивания, а также структурного сравнения. Мы подробно обсуждаем эти операции в контексте топологии биологических цепей и демонстрируем конкретные приложения для анализа структуры белков и РНК. В дополнительной информации мы представляем полную математическую структуру, приводя конкретные примеры в основном тексте.
2.2.2. Перестановка
Перестановка изменяет контакты посредством реструктуризации или переупорядочивания, в результате чего создается новая структура с другими возможностями подключения.Математически это может быть молекулярная операция типа I или типа II, однако проще рассматривать это преобразование как молекулярную операцию типа II. Это не обязательно означает, что биологически это преобразование типа II, просто его проще вычислить как таковое. То, что такие изменения имеют отношение к биомолекулам, хорошо установлено, и даже были предложены алгоритмические подходы для обнаружения перестановок [21–23]. Здесь мы сосредоточимся на двух типах перестановок, а именно на стандартной перестановке и круговой перестановке.
2.2.2.1. Стандартная перестановка
При стандартной перестановке два сайта меняются местами (заменяются друг другом), сохраняя при этом другие аспекты подключения. Рисунок 2A демонстрирует стандартную перестановку, в которой участки и и m меняются местами, тем самым преобразуя перекрестное отношение в последовательное отношение. Следуя конкретному примеру, показанному на рисунке 2A, перестановка происходит между средними узлами (1) и (3), которые находятся в перекрестном расположении. В результате симметрия двух контактов в новой молекуле будет последовательной.Соотношения симметрии контакта (2) и других контактов остаются неизменными, т.е. параллельно (1) и последовательно с (2), как и раньше.
Рисунок 2. (A) Стандартная перестановка имеет место, когда происходит обмен двумя ближайшими соседними узлами. aP -1 b , где a и b – абстрактные обозначения для облигации a и облигации b означает, что b находится параллельно с a . Здесь красный, черный и синий цвета обозначают определенную связь.Связи между облигациями представлены буквой, как описано в тексте. (B) Показаны согласованная параллель (CP) и согласованная серия (CS). (C) Круговая перестановка происходит за счет вращения конечной точки молекулы. Он может преобразовывать последовательную связь в параллельную и наоборот в зависимости от положения конечной точки.
Матричный формализм для стандартной перестановки описан в предыдущем разделе. В случае примера, описанного выше, исходное расположение контактов задается матрицей связи (которая в этом случае идентична карте контактов).
S = (000010001000010000000001100000000100) (15)Например, первый сайт связан с пятым, поэтому в столбце 5 первой строки стоит 1 и так далее. Есть три контакта, каждый из которых содержит уникальные сайты, поэтому размер контактной матрицы составляет 6 × 6, и матрица, конечно, симметрична (если 2 контакта 3, то 3 будут контактировать с 2). По определению, ни один сайт не контактирует сам с собой. Матрица перестановок для обмена местами 4 и 5 равна
О = (100000010000001000000010000100000001) (16)Тогда S ′ = OSO-1, что равно
S ′ = (000100001000010000100000000001000010) (17)Таблица 1 суммирует все возможные результаты стандартной перестановки для системы, содержащей два контакта.Например, перекрестное, последовательное или параллельное отношение можно преобразовать в любое другое из трех отношений путем применения соответствующего преобразования. В контексте биологических молекул два контакта могут иметь общий контактный сайт, что приводит к отношениям согласованных параллелей (CP) или согласованных серий (CS), как показано на рисунке 2B. Влияние стандартной перестановки на эти отношения суммировано в Таблице 2, где каждый «сайт» представляет собой, например, вторичный структурный элемент или нуклеотид.Для двух контактов есть четыре сайта: два соседних внутренних сайта и два внешних сайта; сайты могут быть как соседними, так и несоседними.
Таблица 1 . Результат стандартной перестановки между каждой парой сайтов в пределах двух контактов.
Таблица 2 . Результат стандартной перестановки, начиная с согласованных параллельных (CP) или согласованных рядов (CS) отношений.
Инверсия может быть понята в терминах стандартных операций перестановки и обсуждается в дополнительной информации.
Далее мы проиллюстрируем концепцию стандартной перестановки на примере структуры белка. Для получения подробной информации о вычислительном подходе для создания диаграмм (см. Рисунок S2). В этом и других примерах мы предполагаем некоторое знакомство с биомолекулярной структурой; для читателей, менее знакомых с этой областью, отличные введения можно найти в ссылках [24, 25].
Простая принципиальная схема восьмицепочечного бета-бочкообразного белка показана на рисунке 3A (цвет добавлен, чтобы помочь визуализировать эффект перестановки), а структура белка показана на рисунке 3C.Каждая нить соединяется со следующей нитью в последовательности, а последняя нить соединяется с первой. Обратите внимание, что здесь мы изображаем сокращенные диаграммы, где каждая бета-нить соответствует узлу диаграммы. Стандартная перестановка сайтов 4 и 8 диаграммы бета-ствола дает греческий ключевой ствол (рис. 3В, структура белка показана на рис. 3D). Перестановка явно изменяет карту контактов (Рисунки 3E, F), а также влияет на карту отношений (Рисунки 3G, H), увеличивая количество параллельных и перекрестных отношений по сравнению с сериями.Таким образом, наша структура иллюстрирует подробные свойства структурной связи между двумя хорошо известными белковыми складками.
Рисунок 3 . Примеры принципиальных схем. Диаграммы были рассчитаны с отсечкой расстояния 3,5 Ангстрем и отсечки числа 6 (см. Пояснение на Рисунке S2). Карты были уменьшены таким образом, что каждый контактный сайт представлял узел (1, 2, 3, 4, и т. Д. .), А не связанные сайты были исключены. (A) Бета-баррель (PDB ID 1RBP) диаграмма. Сайты и контакты, участвующие в стандартной перестановке (4, 8), показаны зеленым и пурпурным. (B) Диаграмма бета-ствола с греческим ключом (4cv7). (C) Конструкция ствола Beta. (D) Конструкция корпуса греческого ключа. (E) Контактная карта структуры бета-ствола. Оси обозначают номер бета-цепи, контакты показаны белым. (F) Контактная карта греческой конструкции ствола ключа. (G) Соотношения между контактами бета-ствола, пронумерованные, как показано на (A). (H) Взаимоотношения между контактами корпуса греческого ключа, пронумерованные, как показано в (B) .
2.2.2.2. Круговая перестановка
При круговой перестановке два конца молекулы соединяются, и один разрез делается в другом месте молекулы, что приводит к топологии с идентичными контактами, но, в общем, к различным отношениям между ними. Для молекулы с двумя контактами это можно легко изобразить, как показано на рисунке 2C. Следовательно, круговая перестановка может преобразовать параллельное отношение в отношение ряда и наоборот, в зависимости от положения конечной точки обращения.Результирующая симметрия в конечном итоге зависит от расположения этой конечной точки по отношению к позициям контактных площадок. Топология может быть определена в соответствии со следующими правилами, используя визуализацию «точки на линии» на рисунках 1, 2A, B. Если два контакта изначально соединены последовательно, то размещение новой конечной точки в интервале любого контакта приводит к параллельной симметрии; в противном случае симметрия ряда сохраняется. Если два контакта параллельны, то размещение конечной точки в пределах интервала одного контакта, но не другого, приводит к последовательной симметрии; в противном случае получается параллельная симметрия.Отношения CP и CS можно рассматривать как параллельные и последовательные выше. Если два контакта находятся в перекрестной связи, любая круговая перестановка приведет к перекрестной связи.
Пример на рисунке 2C содержит всего четыре контактных сайта. Исходная матрица, изображающая два контакта параллельно –
S = (0001001001001000) (18), а матрица перестановок для одного поворота конечной точки по часовой стрелке равна
. О = (0001100001000010) (19)Тогда S ′ = OSO-1 равно
S ′ = (0100100000010010) (20)Стандартные и кольцевые перестановки имеют отношение к эволюции белков [26, 27], как показано на рисунке S3 и соответствующем обсуждении.
2.2.3. Ликвидация
Исключение – это удаление контакта или набора контактов. Устранение не меняет отношения симметрии между оставшимися контактами. На рисунке 4 показан простой пример, где мы начинаем с четырех контактов, а контакт (4) удаляется. Изображены матричные представления до и после исключения. Чтобы найти окончательное представление после исключения, мы опускаем строку и столбец, которым принадлежит (4). Матрицу для исключения можно найти в дополнительной информации.
Рисунок 4 . Удаление соответствует удалению контактов. В простейшем случае удаляется только один контакт. Результирующая матричная форма получается путем исключения строки и столбца устраненного контакта. Матричный формализм для процессов исключения можно найти в дополнительной информации.
Мы проиллюстрировали устранение на рисунке 5, показывая, что устранение четырех контактов в восьмицепочечной топологии бета-барреля приводит к фундаментальной топологии тРНК.Рисунки 5A, B показывают, что базовую топологию тРНК (очевидную при визуальном осмотре паттернов водородных связей) можно вывести, начав с топологии бета-бочки и введя четыре исключения, показанные пунктирными линиями на Рисунке 5A. Эта структура не содержит согласованных отношений, и на самом деле можно провести простую аналогию с электронными схемами с топологически эквивалентной схемой конденсатора, изображенной на вставке к рис. 5В. Рисунок 5C подтверждает, что контакты 2, 3 и 4 параллельны контакту 1, в то время как контакты 2, 3 и 4 включены последовательно друг с другом (каждый контакт по определению параллелен самому себе).Наша процедура анализа контактов тяжелого атома (рис. 5D) демонстрирует, что диаграмма на рис. 5В действительно является базовой топологией структуры тРНК в качестве примера.
Рисунок 5 . Топология тРНК (PDB ID 4kr2). (A, B) Устранение контактов в мотиве бета-ствола (A) приводит к мотиву тРНК (B) . Схема топологически эквивалентного конденсатора показана на вставке. (C) Матрица отношений для (B). (D) Контакты между рибонуклеотидами тРНК, PDB ID 4kr2.Отрезки: 3,5, 6. Для акцента добавлены цвета и штрихи. (E) Структура тРНК , окрашенная, как показано в (D) .
2.2.4. Дополнение
Добавление, обратное элиминированию, может быть выполнено либо путем добавления одного или нескольких контактов между (потенциальными) сайтами контакта, как это происходит при сворачивании белка, либо путем вставки: сплайсинга новой молекулы (основной цепи и контактов) в основную цепь существующий. В случае вставки отношения внутри каждой молекулы не меняются.Отношения между новой молекулой и молекулой, в которую она вставлена, будут последовательными или параллельными, в зависимости от места вставки.
2.2.5. Дублирование
Мы определяем дупликацию как присоединение копии исходной молекулы последовательно к самой молекуле. Ясно, что отношения между контактами внутри исходной молекулы или ее копии не меняются, в то время как все контакты между исходной и скопированной молекулами идут последовательно (см. Рис. 6). Другими словами,
В биологических полимерах две связанные молекулы могут быть соединены «линкерной» областью, и могут образовываться новые контакты между двумя молекулами или между любой молекулой и линкером.Рассмотрим диаграмму ствола греческого ключа, снова показанную на вставке к рис. 7C, и выполните два исключения, обозначенные пурпурным цветом. Результатом является диаграмма бета / гамма кристаллина, присутствующего в белке нитроллине (Рисунок 7C, рисунок на рисунке 7A). Дублирование (плюс устранение и добавление контакта) приводит к диаграмме кристаллина бета-B1, показанной на рисунке 7D (рисунок на рисунке 7B). Фактически, эволюционно бета / гамма кристаллины произошли от предкового однодоменного белка [28].
Рисунок 6 .Серийное дублирование: часть молекулы дублируется и вставляется вне оригинала в положение h . Отношения симметрии между дублированными и исходными контактами являются последовательными.
Рисунок 7 . Диаграммы кристаллина и нитроллина. (A) Нитроллин. (B) Бета-B1 кристаллин. (C) Принципиальная схема для нитроллина (3ent), рассчитанная с отсечками: 3,6, 5. Вставка: цилиндр греческого ключа с исключениями, ведущими к диаграмме нитроллина, показанной пурпурным цветом с серыми косыми чертами. (D) Бета-B1 кристаллин (1oki), с отсечками 3,6, 5 и включенными мостиковыми бета-сайтами. (E) Упрощенное представление молекулы кристаллина. Здесь std означает стандартную перестановку. (F) Упрощенное представление предполагаемой замены внутримолекулярных доменов. Цвет добавлен для выделения на всех диаграммах.
2.2.6. Дополнительное обсуждение
Обмен доменов – это белок-белковое взаимодействие, которое включает обмен контактами между белками, так что контакты, нарушенные в исходной белковой цепи, реформируются с соответствующей частью другого белка.Более простое представление – рассматривать каждый переставленный сегмент как узел, и в этом случае стандартная перестановка второго и четвертого узлов двух последовательно соединенных контактов приводит к двум параллельным контактам (рисунки 7E, F). Рассмотрим такое упрощенное представление бета / гамма-кристаллина, где каждый домен состоит из двух контактирующих субдоменов. Представьте себе перестановку домена между N-концевыми доменами, стандартную перестановку между узлами 2 и 6 (рисунки 7E, F). Скажем, молекулы связаны в эксперименте по вытягиванию одной молекулы, а С-концевой домен менее механически устойчив.Затем, после приложения силы, тянущей к двум концам, мы могли бы ожидать разворачивания сначала второго С-концевого домена, затем последовательно замененных N-концевых доменов, а затем первого С-концевого домена. Это именно та модель, которую предложили Гарсия-Манес и др. в недавней публикации [29], основанной на экспериментах по силовой спектроскопии одиночных молекул. Топология биологической цепи обеспечивает простую иллюстрацию этого прогноза, а также показывает, как наша структура может быть применена, чтобы обеспечить понимание, относящееся к интерпретации эксперимента.
Из рисунка 6А очевидно, что, исходя из мотива кристаллина, потеря только одного контакта может привести к топологически изолированной N-концевой шпильке, то есть единственному контакту между бета-цепями, не связанным с остальной частью белка. Фактически, отслоение N-концевой шпильки гамма-D кристаллина является ранним событием в моделировании развертывания этого белка по методу Монте-Карло [30]. Анализ топологии биологической цепи может помочь идентифицировать возможные механизмы разворачивания [14] и структурные слабости, которые могут привести к разворачиванию и агрегации в биологических белках.Высокое содержание параллельных и перекрестных связей в мотиве кристаллина может быть причиной его высокой стабильности во многих белках.
Таким образом, мы считаем, что наш метод представляет собой полезный и интуитивно понятный подход к созданию принципиальных схем, обеспечивающий понимание ключевых свойств биомолекулярных структур и взаимосвязей между ними. Мы планируем расширить и улучшить наш подход, чтобы обеспечить более автоматизированный биоинформатический анализ. Применяя наш подход к биологическим структурам в банке данных по белкам, мы отмечаем, что его также можно использовать в сочетании с инструментами молекулярной динамики и анализа для изучения динамических переходов в биомолекулах, включая переходную структуру в изначально неупорядоченных белках.
Полный код и документация доступны в Интернете.
3. Заключение
В этой статье мы разработали структуру, которая может использоваться для описания, сравнения и прогнозирования топологических свойств молекулы, которая подвергается определенным молекулярным операциям. В частности, мы рассмотрели несколько общих операций, а именно перестановку, дублирование, инверсию, добавление / вставку и исключение. Мы использовали примеры из структурной биологии, чтобы продемонстрировать, как отношения между молекулами могут быть поняты с точки зрения структуры топологии биологических цепей, и ввели простой набор инструментов для рисования, анализа и манипулирования диаграммами цепей белков.В целом мы представляем математический подход к анализу структуры белков и нуклеиновых кислот и структурных изменений, который также может быть применен к другим линейным полимерам. Мы ожидаем, что расширенный здесь формализм и будущие разработки будут иметь отношение к процессу конструирования и манипулирования молекулами в соответствии с правилами симметрии между их составными частями, и мы считаем, что наши методы и идеи могут помочь в развитии междисциплинарного сотрудничества и обучения в области математики, химии, биологии и т. Д. смежные дисциплины.
Заявление о доступности данныхВсе наборы данных, созданные для этого исследования, включены в статью / дополнительные материалы.
Авторские взносы
AM задумал, спроектировал и руководил исследованием. ОС и АТ провели теоретический анализ. JW провел часть биомолекулярного моделирования и написал сценарий. OS, AT, JW и AM обсудили результаты и интерпретации. Все авторы участвовали в написании рукописи и одобрили окончательную версию.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
OS благодарит В. Сатарифарда за то, что он познакомил его с предметом, и Х. Антила, М. Миеттинена и А. Валлериани за их полезные обсуждения.
Дополнительные материалы
Дополнительные материалы к этой статье можно найти в Интернете по адресу: https: // www.frontiersin.org/articles/10.3389/fphy.2020.00005/full#supplementary-material
Список литературы
3. Флапан Э. Когда топология встречается с химией: топологический взгляд на молекулярную хиральность. Кембридж, Великобритания: Издательство Кембриджского университета (2000).
Google Scholar
4. Эйме Дж. Ф., Бевес Дж. Э., Ли Д. А., Макберни Р. Т., Риссанен К., Шульц Д. Синтетический молекулярный пятилистный узел. Нат Хем . (2011) 11 : 15–20. DOI: 10.1038 / nchem.1193
CrossRef Полный текст | Google Scholar
6.Coskun A, Banaszak M, Astumian RD, Stoddart JF, Grzybowski BA. Большие надежды: смогут ли искусственные молекулярные машины оправдать свои обещания? Chem Soc Rev. (2012) 41 : 19–30. DOI: 10.1039 / C1CS15262A
PubMed Аннотация | CrossRef Полный текст | Google Scholar
9. Поклажедатель М.Х., Сан X, Аль-Хашими Н.М. Топология связывает вторичную структуру РНК с глобальной конформацией, динамикой и адаптацией. Наука . (2010) 327 : 202–6. DOI: 10.1126 / наука.1181085
PubMed Аннотация | CrossRef Полный текст | Google Scholar
11. Цанг З., Вэй Г.В. TopologyNet: глубокие сверточные и многозадачные нейронные сети на основе топологии для прогнозирования биомолекулярных свойств. PLoS Comput Biol . (2017) 13 : e1005690. DOI: 10.1371 / journal.pcbi.1005690
PubMed Аннотация | CrossRef Полный текст | Google Scholar
12. Цанг З., Мю Л., Вэй Г.В. Представимость алгебраической топологии биомолекул в скоринге и виртуальном скрининге на основе машинного обучения. PLoS Comput Biol . (2017) 14 : e1005929. DOI: 10.1371 / journal.pcbi.1005929
PubMed Аннотация | CrossRef Полный текст | Google Scholar
14. Муглер А., Танс С. Дж., Машаги А. Топология схемы самовзаимодействующих цепей: последствия для динамики сворачивания и разворачивания. Phys Chem Chem Phys. (2014) 16 : 22537–44. DOI: 10.1039 / C4CP03402C
PubMed Аннотация | CrossRef Полный текст | Google Scholar
15. Веровшек С.К., Машаги А.Расширенная топологическая устойчивость и расположение контактов в свернутых линейных молекулах. Передняя прикладная математическая статистика . (2016) 2 : 6. DOI: 10.3389 / fams.2016.00006
CrossRef Полный текст | Google Scholar
17. Heidari M, Satarifard V, Tans SJ, Ejtehadi MR, Mashaghi S, Mashaghi A. Топология полимерных цепей с внутренними ограничениями. Phys Chem Chem Phys. (2017) 19 : 18389–93. DOI: 10.1039 / C7CP02145C
PubMed Аннотация | CrossRef Полный текст | Google Scholar
18.Satarifard V, Heidari M, Mashaghi S, Tans SJ, Ejtehadi MR, Mashaghi A. Топология полимерных цепей в условиях наноразмерного ограничения. Наноразмер. (2017) 9 : 12170–7. DOI: 10.1039 / C7NR04220E
PubMed Аннотация | CrossRef Полный текст | Google Scholar
19. Машаги А., Рамезанпур А. Топология цепей линейных полимеров: статистическая механическая обработка. RSC Adv. (2015) 5 : 51682–9. DOI: 10.1039 / C5RA08106H
CrossRef Полный текст | Google Scholar
21.Бачар О., Фишер Д., Нусинов Р., Вольфсон Х. Основанный на компьютерном зрении метод для трехмерного независимого от последовательности структурного сравнения белков. Protein Eng Design Select . (1993) 6 : 279–87. DOI: 10.1093 / белок / 6.3.279
PubMed Аннотация | CrossRef Полный текст | Google Scholar
23. Wang L, Wu LY, Wang Y, Zhang XS, Chen L. SANA: алгоритм последовательного и непоследовательного выравнивания структуры белка. Аминокислоты. (2010) 39 : 417–25.DOI: 10.1007 / s00726-009-0457-y
PubMed Аннотация | CrossRef Полный текст | Google Scholar
24. Бранден Ч., Туз Дж. Введение в структуру белка. 2-е изд. Нью-Йорк, Нью-Йорк: Наука Гарланд (1999).
Google Scholar
25. Хаббард Т.Дж., Мурзин А.Г., Бреннер С.Е., Чотиа К. SCOP: структурная классификация базы данных белков. Nucleic Acids Res. (1997) 25 : 236–9.
PubMed Аннотация | Google Scholar
28.Каппе Г., Пуркисс А.Г., ван Генесен С.Т., Слингсби К., Лубсен Н.Х. Взрывная экспансия генов бетагамма-кристаллина у предковых позвоночных. Дж Мол Evol . (2010) 71 : 219–30. DOI: 10.1007 / s00239-010-9379-2
PubMed Аннотация | CrossRef Полный текст | Google Scholar
29. Гарсия-Манес С., Гиганти Д., Бадилла С.Л., Лезамиз А., Пералес-Кальво Дж., Бидл А.Э. и др. Одномолекулярная силовая спектроскопия предсказывает неправильно свернутую конформацию с замененным доменом в человеческом белке YD-кристаллин. Дж. Биол. Хим. . (2016) 291 : 4226–35. DOI: 10.1074 / jbc.M115.673871
CrossRef Полный текст | Google Scholar
30. Серебряный Э., Вудард Я.С., Адкар Б.В., Шабаб М, Кинг Я.А., Шахнович Э.И. Внутренний дисульфид блокирует неправильно свернутый предрасположенный к агрегации промежуточный продукт в связанных с катарактой мутантах YD-кристаллина человека. Дж. Биол. Хим. . (2016) 291 : 19172–83. DOI: 10.1074 / jbc.M116.735977
CrossRef Полный текст | Google Scholar
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
ТОПОЛОГИЯ ЦЕПЕЙ И ЗАКОНЫ – Прикладное промышленное электричество
На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:
Ток : величина тока одинакова для любого компонента в последовательной цепи.
Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
Напряжение : Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы. Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:
Рисунок 3.1Первый принцип, который нужно понять о последовательных цепях, заключается в следующем:
Величина тока в последовательной цепи одинакова для любого компонента в цепи.
Общий ток серии
[латекс] \ tag {3.1} I_ {Total} = I_1 = I_2 = … = I_n [/ latex]
Это связано с тем, что в последовательной цепи есть только один путь для прохождения тока. Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость мрамора) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.
По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке от точки 1 к 2, к 3 к 4 и обратно к 1.Однако у нас есть один источник напряжения и три сопротивления. Как мы можем использовать здесь закон Ома?
Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу с точки зрения одних и тех же двух точек в цепи. Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.
Использование закона Ома в простой цепи с одним резисторомВ схеме с одной батареей и одним резистором мы можем легко вычислить любую величину, потому что все они относятся к одним и тем же двум точкам в цепи:
[латекс] I \: = \ frac {E} {R} [/ латекс]
[латекс] I \: = \ frac {9V} {3k \ Omega} [/ латекс]
[латекс] \ pmb {I = 3 мА} [/ латекс]
Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4.Поскольку мы знаем, что между точками 1 и 4 (непосредственно через батарею) имеется электродвижущая сила 9 В, и поскольку точка 2 является общей для точки 1, а точка 3 – общей для точки 4, мы также должны иметь 9 В между точками 2. и 3 (прямо через резистор).
Следовательно, мы можем применить закон Ома ( I = E / R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.
Использование закона Ома в схемах с несколькими резисторамиВ схемах, содержащих более одного резистора, мы должны соблюдать осторожность при применении закона Ома. В приведенном ниже примере схемы с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R 1 , R 2 и R . 3 . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, сколько напряжения присутствует на любом из этих резисторов по отдельности.
Значение 9 вольт составляет всего величин для всей цепи, тогда как цифры 3 кОм, 10 кОм и 5 кОм представляют собой отдельных величин для отдельных резисторов. Если бы мы подставили цифру для общего напряжения в уравнение закона Ома с цифрой для отдельного сопротивления, результат не был бы точно связан с какой-либо величиной в реальной цепи.
Для R 1 закон Ома будет связывать величину напряжения на R 1 с током через R 1 , учитывая сопротивление R 1 , 3 кОм:
[латекс] I_ {R1} \: = \ frac {E_ {R1}} {R_1} [/ latex] или [латекс] E_ {R1} = I_ {R1} {(R_1)} [/ latex]
Но, поскольку нам неизвестно напряжение на R 1 (только полное напряжение, подаваемое батареей на комбинацию из трех последовательных резисторов), и мы не знаем ток через R 1 , мы можем ‘ t делать какие-либо расчеты по любой из формул.То же самое касается R 2 и R 3 : мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие количества между одними и теми же двумя точками в цепи.
Итак, что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R 1 , R 2 и R 3 , и мы знаем сопротивление каждого резистора, но поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи.Если бы мы только знали, какое общее сопротивление составляет для цепи: тогда мы могли бы вычислить общего тока с нашим значением для всего напряжения ( I = E / R ).
Объединение нескольких резисторов в эквивалентный общий резисторЭто подводит нас ко второму принципу последовательной схемы:
Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
[латекс] \ tag {3.2} R_ {total} = R_1 + R_2 + … + R_n [/ латекс]
Это должно иметь интуитивный смысл: чем больше последовательно подключенных резисторов, через которые должен протекать ток, тем труднее будет протекать ток.
В примере задачи у нас были последовательно подключены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:
[латекс] R_ {total} = R_1 + R_2 + R_3 [/ латекс]
[латекс] R_ {total} = 3 \ text {k} \ Omega + 10 \ text {k} \ Omega + 5 \ text {k} \ Omega [/ latex]
[латекс] \ pmb {R_ {total} = 18 \ text {k} \ Omega} [/ latex]
По сути, мы вычислили эквивалентное сопротивление 1 R, 2 и 3 R вместе.Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R 1 , R 2 и R 3 :
Расчет тока цепи с использованием закона ОмаТеперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):
[латекс] I_ {total} \: = \ frac {E_ {total}} {R_ {total}} [/ latex]
[латекс] \: = \ frac {9V} {18k \ Omega} [/ латекс]
[латекс] \ pmb {I_ {total} = 500 мкА} [/ латекс]
Расчет напряжений компонентов по закону ОмаЗная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:
Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома для определения падения напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):
[латекс] E_ {R1} = I_ {R1} {R_1} [/ латекс]
[латекс] = (500 мкА) {(3кОм)} [/ латекс]
[латекс] \ pmb {E_ {R1} = 1.5V} [/ латекс]
[латекс] E_ {R2} = I_ {R2} {R_2} [/ латекс]
[латекс] = (500 мкА) {(10 кОм)} [/ латекс]
[латекс] \ pmb {E_ {R2} = 5V} [/ latex]
[латекс] E_ {R3} = I_ {R3} {R_3} [/ латекс]
[латекс] = (500 мкА) {(5 кОм)} [/ латекс]
[латекс] \ pmb {E_ {R3} = 2.5V} [/ латекс]
Обратите внимание на падение напряжения на каждом резисторе, и как сумма падений напряжения (1,5 + 5 + 2,5) равна напряжению батареи (источника питания): 9 вольт.
Это третий принцип последовательных цепей:
Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Общее последовательное напряжение
[латекс] E_ {total} = E_1 + E_2 + … E_n \ tag {3.3} [/ latex]
Анализ простых последовательных цепей с помощью «табличного метода» и закона ОмаОднако метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания.Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:
Таблица 3.1
Правило для такой таблицы – применять закон Ома только к значениям в каждом вертикальном столбце. Например, E R1 только с I R1 и R 1 ; E R2 только с I R2 и R 2 ; и т.д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:
Как видно из расположения данных, мы не можем подать 9 вольт ET (полное напряжение) ни на одно из сопротивлений (R 1 , R 2 или R 3 ) в любая формула закона Ома, потому что они находятся в разных столбцах. Напряжение батареи 9 В составляет , а не , приложенное непосредственно к R 1 , R или 3 R R. Однако мы можем использовать наши «правила» для последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило ряда сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:
Теперь, введя значение общего сопротивления в крайний правый столбец («Общее»), мы можем применить закон Ома I = E / R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА. :
Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» последовательной схемы), мы можем заполнить токи для каждого резистора из только что рассчитанного значения тока:
Наконец, мы можем использовать закон Ома для определения падения напряжения на каждом резисторе, по столбцу за раз:
Таблица 3.6Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления складываются, чтобы равняться большему общему сопротивлению; а падение напряжения в сумме дает большее общее напряжение. Все эти правила находят корень в определении последовательной цепи. Если вы полностью понимаете это определение, то правила – не что иное, как сноски к определению.
- Компоненты в последовательной цепи имеют одинаковый ток:
[латекс] I_ {Всего} = I_1 = I_2 = I_3 =… = I_n [/ latex]
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений:
[латекс] R_ {Всего} = R_1 + R_2 + … + R_n [/ латекс]
- Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения:
[латекс] E_ {Всего} = E_1 + E_2 + … + E_n [/ латекс]
В этом разделе мы изложим три принципа, которые вы должны понимать в отношении параллельных цепей:
Напряжение: Напряжение одинаково на всех компонентах параллельной цепи.
Ток: Полный ток цепи равен сумме токов отдельных ответвлений.
Сопротивление: Отдельные сопротивления уменьшают , чтобы получить меньшее общее сопротивление, а не , прибавляя , чтобы получить общее.
Давайте взглянем на несколько примеров параллельных цепей, демонстрирующих эти принципы.
Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи:
Рисунок 3.5 Напряжение в параллельных цепяхПервый принцип для понимания параллельных цепей состоит в том, что напряжение одинаково на всех компонентах в цепи . Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени.
[латекс] E_ {Total} = E_1 = E_2 = … = E_n \ tag {3.4} [/ latex]
Следовательно, в приведенной выше схеме напряжение на R 1 равно напряжению на R 2 , которое равно напряжению на R 3 , которое равно напряжению на батарее.
Это равенство напряжений можно представить в другой таблице для наших начальных значений:
Таблица 3.7 Применение закона Ома для простых параллельных схемКак и в случае с последовательными цепями, применяется то же предостережение для закона Ома: значения напряжения, тока и сопротивления должны быть в одном контексте, чтобы вычисления работали правильно.
Однако в приведенном выше примере схемы мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что мы знаем напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:
[латекс] I_ {R1} \: = \ frac {E_ {R1}} {R_1} [/ латекс]
[латекс] \: = \ frac {(9V)} {(10kΩ)} [/ latex]
[латекс] \ pmb {I_ {R1} \: = 0.9mA} [/ латекс]
[латекс] I_ {R2} \: = \ frac {E_ {R2}} {R_2} [/ латекс]
[латекс] \: = \ frac {(9V)} {(2kΩ)} [/ latex]
[латекс] \ pmb {I_ {R2} \: = 4,5 мА} [/ латекс]
[латекс] I_ {R3} \: = \ frac {E_ {R3}} {R_3} [/ латекс]
[латекс] \: = \ frac {(9V)} {(1kΩ)} [/ latex]
[латекс] \ pmb {I_ {R3} = 9mA} [/ латекс]
Таблица 3.8На данный момент мы все еще не знаем, каков полный ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Всего»). Однако, если мы внимательно подумаем о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме всех токов отдельных резисторов («ответвлений»):
Рисунок 3.6По мере того, как полный ток выходит из положительной (+) клеммы батареи в точке 1 и проходит по цепи, часть потока разделяется в точке 2, чтобы пройти через R 1 , еще часть разделяется в точке 3, чтобы уйти. через 2 рандов, а оставшаяся часть идет через 3 рандов.Подобно реке, разветвляющейся на несколько более мелких ручьев, общий расход всех потоков должен равняться расходу всей реки.
То же самое происходит, когда токи через R 1 , R 2 и R 3 соединяются, чтобы течь обратно к отрицательной клемме батареи (-) к точке 8: поток тока из точки 7 до точки 8 должно равняться сумме токов (ответвлений) через R 1 , R 2 и R 3 .
Это второй принцип параллельных цепей: общий ток цепи равен сумме токов отдельных ветвей .
Используя этот принцип, мы можем заполнить место ИТ на нашем столе суммой I R1 , I R2 и I R3 :
Таблица 3.9 Как рассчитать полное сопротивление в параллельных цепяхНаконец, применив закон Ома к крайнему правому столбцу («Всего»), мы можем вычислить полное сопротивление цепи:
Таблица 3.10 Уравнение сопротивления в параллельных цепяхОбратите внимание на кое-что очень важное.Общее сопротивление цепи составляет всего 625 Ом: на меньше , чем у любого из отдельных резисторов. В последовательной цепи, где полное сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше , чем у любого из резисторов по отдельности.
Здесь, в параллельной цепи, наоборот: мы говорим, что отдельных сопротивления уменьшают , а не прибавляют , чтобы получить общее количество .
Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что у последовательных цепей есть три правила для напряжения, тока и сопротивления.
Математически соотношение между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом:
Уравнение сопротивления в параллельных цепях[латекс] R_ {total} = \ frac {1} {\ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n}} \ tag {3.5 } [/ latex]
Три правила параллельных цепейТаким образом, параллельная цепь определяется как цепь, в которой все компоненты подключены между одним и тем же набором электрически общих точек.Другими словами, все компоненты подключены друг к другу через клеммы.
Из этого определения следуют три правила параллельных цепей:
Все компоненты имеют одинаковое напряжение.
Сопротивления уменьшаются до меньшего общего сопротивления.
Токи ответвления в сумме равняются большему общему току.
Как и в случае с последовательными цепями, все эти правила находят корень в определении параллельной цепи. Если вы полностью понимаете это определение, то правила – не что иное, как сноски к определению.
- Компоненты в параллельной цепи имеют одинаковое напряжение:
[латекс] E_ {Всего} = E_1 = E_2 = … = E_n [/ латекс]
- Общее сопротивление в параллельной цепи на меньше , чем любое из отдельных сопротивлений:
[латекс] R_ {Total} = \ frac {1} {\ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n}} [/ латекс]
- Полный ток в параллельной цепи равен сумме токов отдельных ответвлений:
[латекс] I_ {Всего} = I_1 + I_2 +.2R} [/ латекс]
Этим легко управлять, добавив еще одну строку в нашу знакомую таблицу напряжений, токов и сопротивлений:
Таблица 3.11 Мощностьдля любого конкретного столбца таблицы может быть найдена с помощью соответствующего уравнения закона Ома ( соответствует , исходя из того, какие цифры представлены для E, I и R в этом столбце).
Интересное правило для общей мощности по сравнению с индивидуальной мощностью состоит в том, что она является аддитивной для любой конфигурации схемы : последовательной, параллельной, последовательной / параллельной или другой.Мощность – это мера скорости работы, и поскольку рассеиваемая мощность должна равняться полной мощности, приложенной источником (источниками) (в соответствии с Законом сохранения энергии в физике), конфигурация схемы не влияет на математику.
- Мощность добавляется в любая конфигурация резистивной цепи:
[латекс] P_ {Всего} = P_1 + P_2 + … + P_n [/ латекс]
Напоминания при использовании закона ОмаОдна из наиболее распространенных ошибок, которые делают начинающие студенты-электронщики при применении законов Ома, – это смешивание контекстов напряжения, тока и сопротивления.Другими словами, ученик может ошибочно использовать значение I (ток) через один резистор и значение E (напряжение) через набор соединенных между собой резисторов, полагая, что они придут к сопротивлению этого резистора.
Не так! Запомните это важное правило: переменные, используемые в уравнениях закона Ома, должны быть , общими для одних и тех же двух точек в рассматриваемой цепи. Я не могу переоценить это правило. Это особенно важно в последовательно-параллельных комбинированных схемах, где соседние компоненты могут иметь разные значения для падения напряжения и тока .
При использовании закона Ома для вычисления переменной, относящейся к отдельному компоненту, убедитесь, что напряжение, на которое вы ссылаетесь, относится только к этому отдельному компоненту, а ток, который вы указываете, проходит исключительно через этот единственный компонент, а сопротивление, на которое вы ссылаетесь, равно исключительно для этого единственного компонента. Аналогичным образом, при вычислении переменной, относящейся к набору компонентов в цепи, убедитесь, что значения напряжения, тока и сопротивления относятся только к этому полному набору компонентов!
Хороший способ запомнить это – обратить пристальное внимание на две точки , завершающие анализируемый компонент или набор компонентов, убедившись, что напряжение, о котором идет речь, проходит через эти две точки, что рассматриваемый ток является потоком электрический заряд от одной из этих точек до другой точки, что рассматриваемое сопротивление эквивалентно одному резистору между этими двумя точками, и что рассматриваемая мощность – это полная мощность, рассеиваемая всеми компонентами между этими двумя точками .
Примечания к «табличному» методу анализа цепей«Табличный» метод, представленный как для последовательных, так и для параллельных цепей в этой главе, является хорошим способом сохранить контекст закона Ома правильным для любой конфигурации цепи. В таблице, подобной приведенной ниже, вам разрешено применять уравнение закона Ома только для значений одного вертикального столбца за раз:
Таблица 3.12Получение значений по горизонтали по столбцам допускается в соответствии с принципами последовательных и параллельных цепей:
Таблица 3.13 Таблица 3.14«Табличный» метод не только упрощает управление всеми соответствующими величинами, но также облегчает перекрестную проверку ответов, упрощая поиск исходных неизвестных переменных другими методами или работая в обратном направлении для решения исходных данные значения из ваших решений. Например, если вы только что решили для всех неизвестных напряжений, токов и сопротивлений в цепи, вы можете проверить свою работу, добавив строку внизу для расчета мощности на каждом резисторе, чтобы посмотреть, добавляются ли все отдельные значения мощности до полной мощности.Если нет, значит, вы где-то ошиблись! Хотя в этой технике «перекрестной проверки» вашей работы нет ничего нового, использование таблицы для упорядочивания всех данных для перекрестной проверки (-ий) приводит к минимуму путаницы.
- Примените закон Ома к вертикальным столбцам таблицы.
- Примените правила последовательного / параллельного горизонтального ряда в таблице.
- Проверьте свои расчеты, работая «в обратном направлении», чтобы попытаться прийти к первоначально заданным значениям (из ваших первых рассчитанных ответов), или путем решения для количества с использованием более чем одного метода (из разных заданных значений).
Принцип, известный как Закон Кирхгофа (открытый в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать так:
«Алгебраическая сумма всех напряжений в контуре должна равняться нулю»
[латекс] E_ {T} = E_1 + E_2 + … + E_n = 0 [/ латекс]
Под алгебраическим я подразумеваю учет знаков (полярностей), а также величин.Под loop я имею в виду любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи и, наконец, обратно в исходную точку.
Демонстрация закона напряжения Кирхгофа в последовательной цепиДавайте еще раз посмотрим на нашу примерную последовательную схему, на этот раз пронумеровав точки в цепи для опорного напряжения:
Рисунок 3.7Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, измеритель зарегистрировал бы +45 вольт.Обычно знак «+» не отображается, а скорее подразумевается для положительных показаний на дисплеях цифровых счетчиков. Однако для этого урока очень важна полярность показаний напряжения, поэтому я покажу положительные числа явно: E 2-1 = + 45V
Если напряжение указано с двойным нижним индексом (символы «2-1» в обозначении «E 2-1 »), это означает напряжение в первой точке (2), измеренное относительно второй точки. (1). Напряжение, указанное как «E cd », будет означать напряжение, указанное цифровым измерителем с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно «D».
Рис. 3.8.Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего измерителя на точке впереди и черным измерительным проводом на точке сзади, мы получим следующие показания:
[латекс] E_ {3-2} = -10V [/ латекс]
[латекс] E_ {4-3} = -20 В [/ латекс]
[латекс] E_ {1-4} = -15V [/ латекс]
Рис. 3.9.. Мы уже должны быть знакомы с общим принципом для последовательных цепей, согласно которому отдельные падения напряжения в сумме составляют общее приложенное напряжение, но при измерении падений напряжения таким образом и обращении внимания на полярность (математический знак) показаний обнаруживается другое. грань этого принципа: все измеренные напряжения в сумме равны нулю:
В приведенном выше примере петля образована следующими точками в следующем порядке: 1-2-3-4-1.Не имеет значения, с какой точки мы начинаем или в каком направлении идем при отслеживании петли; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем подсчитать напряжения в контуре 3-2-1-4-3 той же цепи:
Это может иметь больше смысла, если мы перерисуем наш пример последовательной схемы так, чтобы все компоненты были представлены в виде прямой линии:
Рисунок 3.10Это все та же последовательная схема, только с компонентами, расположенными в другой форме.Обратите внимание на полярность падения напряжения на резисторе по отношению к батарее: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторе ориентированы в другую сторону: положительное слева и отрицательное справа. Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей. Другими словами, «толчок», оказываемый резисторами против потока электрического заряда , должен быть в направлении, противоположном источнику электродвижущей силы.
Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, черный провод слева и красный провод справа, если смотреть горизонтально:
Рисунок 3.11Если бы мы взяли тот же вольтметр и считали напряжение по комбинациям компонентов, начиная с единственного R 1 слева и продвигаясь по всей цепочке компонентов, мы увидим, как напряжения складываются алгебраически (до нуля):
Рисунок 3.12Тот факт, что последовательные напряжения складываются, не должен быть загадкой, но мы заметили, что полярность этих напряжений сильно влияет на то, как складываются цифры. При считывании напряжения на R 1 —R 2 и R 1 —R 2 —R 3 (я использую символ «двойное тире» «-» для обозначения серии соединение между резисторами R 1 , R 2 и R 3 ), мы видим, как измеряемые напряжения последовательно увеличиваются (хотя и отрицательные) величины, потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (положительный левый , отрицательный справа).Сумма падений напряжения на R 1 , R 2 и R 3 равна 45 вольт, что соответствует выходу батареи, за исключением того, что полярность батареи противоположна падению напряжения на резисторе (отрицательный слева, положительный справа), поэтому мы получаем 0 вольт, измеренный на всей цепочке компонентов.
То, что мы должны получить ровно 0 вольт на всей струне, тоже не должно быть тайной. Глядя на схему, мы видим, что крайний левый угол струны (левая сторона R 1 : точка номер 2) напрямую соединен с крайним правым уголком струны (правая сторона батареи: точка номер 2), так как необходимо для завершения схемы.Поскольку эти две точки подключены напрямую, они электрически общие друг с другом. И, как таковое, напряжение между этими двумя электрически общими точками должно быть равно нулю .
Демонстрация закона напряжения Кирхгофа в параллельной цепиЗакон Кирхгофа о напряжении (иногда обозначаемый для краткости KVL ) будет работать для любой конфигурации цепи вообще, а не только для простой серии. Обратите внимание, как это работает для этой параллельной схемы:
Рисунок 3.13В параллельной схеме напряжение на каждом резисторе такое же, как и напряжение питания: 6 вольт. Суммируя напряжения вокруг контура 2-3-4-5-6-7-2, получаем:
Обратите внимание, как я обозначил конечное (суммарное) напряжение как E 2-2 . Поскольку мы начали нашу пошаговую последовательность в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E 2-2 ), которое, конечно, должно быть равно нулю. .
Действие закона Кирхгофа о напряжении независимо от топологии цепиТот факт, что эта схема является параллельной, а не последовательной, не имеет ничего общего с правомерностью закона Кирхгофа о напряжении. В этом отношении схема может быть «черным ящиком» – конфигурация ее компонентов полностью скрыта от нашего взгляда, с набором открытых клемм для измерения напряжения между ними – и KVL все равно останется верным:
Рис. 3.14.Попробуйте выполнить любой порядок шагов с любого терминала на приведенной выше диаграмме, вернувшись к исходному терминалу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю.
Более того, «петля», которую мы отслеживаем для KVL, даже не обязательно должна быть реальным током в прямом смысле этого слова. Все, что нам нужно сделать, чтобы соответствовать KVL, – это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между следующей и последней точкой. Рассмотрим этот абсурдный пример, отслеживая «петлю» 2-3-6-3-2 в той же параллельной цепи резистора:
Рисунок 3.15 Использование закона напряжения Кирхгофа в сложной цепиKVL можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вокруг определенного «контура».В качестве примера возьмем следующую сложную схему (на самом деле две последовательные цепи, соединенные одним проводом внизу):
Рисунок 3.16Чтобы упростить задачу, я опустил значения сопротивления и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют общий провод между собой (провод 7-8-9-10), что позволяет измерять напряжение между двумя цепями.
Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение KVL с напряжением между этими точками как неизвестным:
[латекс] E_ {4-3} + E_ {9-4} + E_ {8-9} + E_ {3-8} = 0 [/ латекс]
[латекс] E_ {4-3} + 12 В + 0 В + 20 В = 0 В [/ латекс]
[латекс] E_ {4-3} + 32V = 0 [/ латекс]
[латекс] \ pmb {E_ {4-3} = -32V} [/ латекс]
Рисунок 3.17 Рисунок 3.18 Рисунок 3.19 Рисунок 3.20Обходя контур 3-4-9-8-3, мы записываем значения падения напряжения так, как их регистрировал цифровой вольтметр, измеряя с помощью красного измерительного провода в точке впереди и черного измерительного провода на точка позади, когда мы продвигаемся по петле. Следовательно, напряжение от точки 9 до точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4. Напряжение от точки 3 до точки 8 является положительным. (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» – в точке 8.Напряжение от точки 8 до точки 9, конечно, равно нулю, потому что эти две точки электрически общие.
Наш окончательный ответ для напряжения от точки 4 до точки 3 – отрицательное (-) 32 вольта, говорящее нам, что точка 3 на самом деле положительна по отношению к точке 4, именно то, что цифровой вольтметр показал бы красным проводом в точке 4. и черный отрыв в точке 3:
Рис. 3.21Другими словами, первоначальное размещение наших «выводов счетчика» в этой проблеме KVL было «задом наперед».«Если бы мы сгенерировали наше уравнение KVL, начиная с E 3-4 вместо E 4-3 , шагая по той же петле с противоположной ориентацией измерительных проводов, окончательный ответ был бы E 3-4 = + 32 вольта:
Рис. 3.22Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.
- Закон Кирхгофа о напряжении (KVL): «Алгебраическая сумма всех напряжений в контуре должна равняться нулю»
Закон Кирхгофа о течениях, часто сокращаемый до KCL, гласит, что «алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю».
Этот закон используется для описания того, как заряд входит и покидает точку соединения или узел на проводе.
Вооружившись этой информацией, давайте теперь рассмотрим пример применения закона на практике, почему он важен и как он был получен.
Обзор параллельной цепиДавайте внимательнее рассмотрим эту последнюю параллельную схему примера:
Рисунок 3.23 Таблица 3.15Решение для всех значений напряжения и тока в этой цепи:
На данный момент мы знаем значение тока каждой ветви и полного тока в цепи. Мы знаем, что полный ток в параллельной цепи должен равняться сумме токов ответвления, но в этой цепи происходит нечто большее, чем просто это.Взглянув на токи в каждой точке соединения проводов (узле) в цепи, мы должны увидеть кое-что еще:
Рисунок 3.24 3.7. 3 тока на входе и выходе из узлаВ каждом узле положительной «шины» (провод 1-2-3-4) у нас есть разделение тока от основного потока к каждому последующему резистору ответвления. В каждом узле на отрицательной «шине» (провод 8-7-6-5) у нас есть ток, сливающийся вместе, чтобы сформировать основной поток от каждого последовательного резистора ответвления.Этот факт должен быть довольно очевиден, если вы подумаете об аналогии контура водопровода с каждым ответвлением, действующим как тройник, разделением или слиянием потока воды с основным трубопроводом, когда он движется от выхода водяного насоса к обратному каналу. резервуар или отстойник.
Если мы внимательно рассмотрим один конкретный узел «тройник», такой как узел 6, мы увидим, что ток, входящий в узел, равен по величине току, выходящему из узла:
Рисунок 3.25Сверху и справа у нас есть два тока, входящие в соединение проводов, обозначенное как узел 6.Слева у нас есть единственный ток, выходящий из узла, равный по величине сумме двух входящих токов. Обратимся к аналогии с водопроводом: пока в трубопроводе нет утечек, поток, поступающий в фитинг, должен также выходить из фитинга. Это верно для любого узла («подгонки»), независимо от того, сколько потоков входит или выходит. Математически мы можем выразить это общее соотношение как таковое: [латекс] I_ {существующий} = I_ {ввод} [/ латекс]
Действующий закон Кирхгофаг.Кирхгоф решил выразить его в несколько иной форме (хотя и математически эквивалентной), назвав его Текущий закон Кирхгофа (KCL):
[латекс] I_ {enter} = -I_ {existing} = 0 [/ latex]
Текущий закон Кирхгофа, кратко изложенный в одной фразе, гласит:
«Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
[латекс] I_ {T} = I_1 + I_2 + … + I_n = 0 [/ латекс]
То есть, если мы присвоим каждому току математический знак (полярность), обозначающий, входят ли они (+) или выходят (-) из узла, мы можем сложить их вместе, чтобы получить гарантированно нулевое значение.
Взяв наш пример узла (номер 6), мы можем определить величину тока, выходящего слева, задав уравнение KCL с этим током в качестве неизвестного значения:
[латекс] I_2 + I_3 + I_ {2 + 3} = 0 [/ латекс]
[латекс] 2 мА + 3 мА + I_ {2 + 3} = 0 [/ латекс]
[латекс] \ text {… решение для I …} [/ латекс]
[латекс] I = -2 мА-3 мА [/ латекс]
[латекс] \ pmb {I = -5mA} [/ латекс]
Отрицательный (-) знак на значении 5 миллиампер говорит нам, что ток на выходе из узла , в отличие от токов 2 миллиампер и 3 миллиампер, которые оба должны быть положительными (и, следовательно, входит в узел) .Независимо от того, обозначает ли отрицательное или положительное значение текущий вход или выход, совершенно произвольно, пока они являются противоположными знаками для противоположных направлений, и мы остаемся последовательными в наших обозначениях, KCL будет работать.
Вместе законы напряжения и тока Кирхгофа представляют собой замечательную пару инструментов, полезных при анализе электрических цепей. Их полезность станет еще более очевидной в следующей главе («Сетевой анализ»), но достаточно сказать, что эти законы заслуживают того, чтобы их запомнил изучающий электронику не меньше, чем закон Ома.
- Текущий закон Кирхгофа (KCL): «Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
1. Введение 2. Пассивные компоненты 3. Активные компоненты |
Функция силовой цепи состоит в том, чтобы обеспечить соответствие имеющейся мощности потребностям нагрузки.Доступная мощность поступает либо от батареи, либо от сети переменного тока, но очень немногие нагрузки могут использовать энергию в такой форме, в основном лампочки и нагреватели. Для всех других нагрузок – будь то простой балласт или сложный серводвигатель – доступная мощность должна быть преобразована в любую форму, подходящую для нагрузки, будь то простой балласт или сложный серводвигатель. Это делается с помощью блоков стабилизации мощности. Как упоминалось в разделе 3.2, подавляющее большинство силовых цепей работают в импульсном режиме.В этом контексте термин «топология» относится к конкретному расположению активных и реактивных компонентов, то есть к схеме силовой части схемы. Разработчики придумали очень большое количество топологий, и некоторые из них можно найти в практических приложениях. Все они разделяют основной принцип работы: мощность «обусловлена» некоторой продуманной последовательностью цикла включения-выключения транзисторов («стратегия модуляции»), чтобы сделать ее подходящей для конкретной нагрузки. Мы кратко проанализируем понижающую, повышающую и несколько других часто используемых топологий. |
4.1. Понижающий преобразователь Понижающий преобразователь представляет собой понижающий преобразователь постоянного тока, то есть выдает выходное напряжение ниже входного (рисунок 11). Катушка индуктивности и конденсатор на выходе являются неотъемлемой частью этой топологии. Входной ток всегда прерывистый, потому что переключатель включен последовательно со входом. Когда входной ток прерывистый, на входе необходим конденсатор для компенсации индуктивности линии и для обработки более высокочастотных составляющих входного тока.Этот входной конденсатор не является неотъемлемой частью топологии – в нем не было бы необходимости, если бы линия не имела индуктивности – и не показан на рисунке. Производительность этого преобразователя определяется тремя вариантами конструкции:
Эти варианты дизайна определяют:
|
Рисунок 11. Понижающий преобразователь. Формы сигналов, показанные на рисунке, относятся к проводимости постоянного тока с фиксированной частотой (в катушке индуктивности). Когда переключатель выключен, индукционный ток течет в «свободном» диоде. В какой-то момент, когда нагрузка уменьшается, ток индуктора становится прерывистым. При 100% рабочем цикле переключателя выходное напряжение равно входному. |
4.2. Повышающий преобразователь Повышающий преобразователь представляет собой повышающий преобразователь постоянного тока, то есть выдает выходное напряжение, превышающее входное (рисунок 12). Катушка индуктивности на входе и конденсатор на выходе являются неотъемлемой частью этой топологии. Поскольку катушка индуктивности включена последовательно со входом, входной ток является непрерывным в большей части рабочего диапазона. Выходной ток является прерывистым, и выходной конденсатор должен быть рассчитан на наихудший случай пульсации тока, а также другие требования, такие как время задержки. Как и в понижающем преобразователе, производительность определяется тремя вариантами конструкции:
Эти варианты дизайна определяют:
Эта топология наиболее распространена для корректоров коэффициента мощности. При более низкой мощности предпочтительным режимом управления является прерывистый ток по экономическим причинам. При более высокой мощности предпочтителен постоянный ток. |
Рисунок 12. Повышающий преобразователь. Формы сигналов, показанные на рисунке, относятся к проводимости постоянного тока с фиксированной частотой (в катушке индуктивности). Катушка индуктивности заряжается от линейного напряжения во время работы транзистора и разряжается в выходной конденсатор, когда переключатель выключен.В какой-то момент, когда нагрузка уменьшается, ток индуктора становится прерывистым. При скважности переключателя 0% выходное напряжение равно входному напряжению . |
4.3. Полумост Полумост – это понижающий преобразователь постоянного тока в переменный. Это «двухквадрантный преобразователь», поскольку ток нагрузки может течь в обоих направлениях. Это критическая особенность при возбуждении индуктивной нагрузки с формой волны переменного тока.Как и в случае понижающего преобразователя, входной ток является прерывистым, и требуется входной конденсатор для компенсации индуктивности линии и обработки более высокочастотных составляющих входного тока. Эта топология широко используется в источниках бесперебойного питания (ИБП) для генерации выходной синусоиды, как показано на рисунке 13. Ее недостатком является тот факт, что для нее требуется положительное и отрицательное напряжение относительно выходной нейтрали, как показано на рисунке. . Полный мост преодолевает это ограничение. |
Рис. 13. Полумост как синусоидальный генератор в ИБП. Обратите внимание на то, как рабочий цикл переключателей модулируется на высокой частоте для достижения низкочастотной синусоиды. Также обратите внимание, что точкой отсчета для выхода является середина двух входных конденсаторов. |
4.3. Полный мост Два полумоста могут генерировать выход переменного тока от одного источника напряжения без необходимости в нейтрали. Эта топология чаще всего используется в трех классах приложений: |
4.3.1. Импульсные источники питания (ИИП) и сварочные аппараты Как показано на рисунке 14, мост используется для генерации высокочастотной прямоугольной волны, которая подается на изолирующий трансформатор. Работа на высокой частоте уменьшает размер трансформатора и компонентов фильтра, одновременно улучшая время отклика в замкнутом контуре и удельную мощность.Плотность мощности, превышающая 50 Вт на 3 , обычно доступна в некоторых коммерчески доступных ИИП. |
Рис. 14. Полный мост обычно используется в импульсных источниках питания и сварочных аппаратах для генерации высокочастотной прямоугольной волны, которая подается на понижающий трансформатор. При типичной рабочей частоте 50 кГц трансформатор становится довольно маленьким. Его мощность регулируется для достижения желаемых сварочных характеристик. |
4.3.2. Преобразователи постоянного тока в переменный и ИБП Как мы уже упоминали в начале, топология – это только половина дела. Другая половина – это стратегия контроля, о чем мы подробнее поговорим в этом разделе. Тот же самый полный мост может быть модулирован для генерации простой прямоугольной волны, как мы видели в предыдущем разделе (рисунок 14), или для генерации синусоиды путем широтно-импульсной модуляции переключателей, как показано на рисунке 15. Выходной прямоугольный сигнал редко используется как таковой; в большинстве случаев он выпрямляется и фильтруется для достижения постоянного тока. Если целью силовой цепи является генерация синусоидального сигнала линейной частоты, как в случае преобразователей постоянного тока в переменный и ИБП, ШИМ-управление переключателями мощности сжимает выходной фильтр и улучшает плотность мощности. |
Рисунок 15. Тот же полный мост, показанный на рисунке 14, можно использовать для генерации синусоидального сигнала путем широтно-импульсной модуляции переключателей. |
| Одна и та же топология может использоваться с множеством различных стратегий модуляции. На рисунке 16 показана комбинация двух методов, представленных на рисунке 15. БТИЗ верхнего плеча переключаются на высокой частоте (20 кГц) и генерируют сигнал линейной частоты с помощью ШИМ-управления рабочим циклом. БТИЗ нижнего плеча переключаются на линейной частоте и переключают полярность формы волны. Эта стратегия модуляции сводит к минимуму потери в полупроводниках, поскольку только два устройства переключаются с высокой частотой без изменения входного фильтра.Повышенная эффективность и работа на высоких частотах являются критически важными компонентами для достижения высокой плотности мощности. |
Рисунок 16. Два метода модуляции (прямоугольная волна и синусоида ШИМ), показанные на рисунке 14, можно комбинировать для повышения эффективности. БТИЗ верхнего плеча переключаются на высокой частоте (20 кГц) и генерируют сигнал линейной частоты с помощью ШИМ-управления рабочим циклом. БТИЗ нижнего плеча переключаются на линейной частоте и переключают полярность формы волны. |
4.3.3. Реверсивные моторные приводы постоянного тока H-мост также может использоваться для управления скоростью и направлением двигателя постоянного тока. Эту топологию иногда называют «четырехквадрантным преобразователем», потому что ток может течь в любом направлении, а напряжение на нагрузке может быть изменено на обратное. В этом, как и в упомянутых выше приложениях, большая часть производительности зависит от стратегии модуляции.Два таких метода проиллюстрированы ниже в качестве примера.
Два переключателя всегда включены и подают на двигатель определенное напряжение, определяемое платой управления. Изменение направления так же естественно, как и изменение рабочего цикла. Ток может течь в обоих направлениях, и двигатель может работать или регенерировать. Обратите внимание, что в течение первой части цикла (ток транзистора) мощность подается на двигатель. В течение оставшейся части цикла мощность возвращается к источнику питания.
Первый метод дает лучшие характеристики сервопривода, в то время как второй метод дает гораздо меньшие пульсации тока в двигателе при той же рабочей частоте. При использовании этого метода модуляции мощность в источник питания не возвращается. Текущие свободные колеса в топовых устройствах и распадаются, что и определяется потерями. |
Рисунок 17а. Реверсивное регулирование скорости двигателя постоянного тока с приводом затвора «заблокировано противофазно». Q1 и Q4 включаются одновременно, а Q2 и Q3 включаются до конца цикла. На клеммах двигателя имеется чистое положительное напряжение.Реактивная мощность возвращается в источник через Q2 и Q3 в оставшейся части цикла. Поскольку на двигатель подается полное напряжение шины с той или иной полярностью, пульсации тока в двигателе могут быть значительными. Рисунок 17b. Реверсивное регулирование скорости двигателя постоянного тока с «переключателем рулевого управления, переключателем PWM». Q2 и Q4 задают направление вращения, а Q1 и Q3 определяют скорость. Реактивная мощность не возвращается к источнику питания, а свободно вращается в верхних устройствах и очень медленно затухает. |
4.4. Трехфазный мост Эта топология (рис. 18) используется почти исключительно для управления трехфазными двигателями с различными стратегиями модуляции. Двумя наиболее распространенными типами двигателей являются двигатели с постоянными магнитами и асинхронные двигатели. Для них требуются разные стратегии модуляции. Фактически, один и тот же тип двигателя может приводиться в действие с разными модуляциями: одни модуляции улучшают характеристики двигателя за счет потерь в полупроводниках, другие – наоборот.Это специализированная тема, выходящая за рамки данной краткой статьи. |
Рис. 18. Трехфазный мост, обычно используемый для привода двигателей с различными типами модуляции. Показанные здесь формы сигналов представляют линейное напряжение и линейный ток синусоидальной модуляции для асинхронного двигателя. |
4.5. Топологии для преодоления ограничений полупроводников За прошедшие годы было разработано множество таких топологий, некоторые для преодоления ограничений MOSFET-диода, некоторые для уменьшения коммутационных потерь IGBT, некоторые для уменьшения коммутационных потерь в целом.Уменьшение коммутационных потерь обычно достигается за счет некоторой формы резонанса, как мы увидим в некоторых примерах ниже. Этот режим работы часто называют «мягким переключением», в отличие от «жесткого переключения», который является стандартным режимом работы преобразователей импульсного режима, которые мы видели в предыдущих параграфах. |
Как мы упоминали в разделе 3.3, IGBT – это устройства с неосновной несущей с лучшими характеристиками проводимости, чем MOSFET, но худшими характеристиками переключения.Одной из топологий, которая обычно используется для использования преимуществ проводимости без потери затрат на переключение, является последовательный резонансный полумост, показанный на рисунке 19. Два конденсатора были добавлены параллельно с IGBT. Это простое добавление коренным образом меняет способ работы этой топологии. Выходной сигнал полумоста представляет собой высокочастотную прямоугольную волну напряжения (розовая кривая), которая подается на резонансный контур, образованный катушкой и одним резонирующим конденсатором (C1 + C2).Результирующий ток (синяя кривая) квазитреугольный. Обратите внимание, что когда один IGBT включен, напряжение на его выводе является отрицательным падением на диоде, следовательно, его потери при включении практически равны нулю. Когда встречно-параллельный диод перестает проводить, напряжение на его выводах равно падению напряжения на IGBT. В этой схеме отсутствуют потери обратного восстановления. |
Рис. 19. Последовательный резонансный полумостовой преобразователь.Обратите внимание на разницу с полумостом, показанным на рисунке 13: нагрузка в основном индуктивная, и два конденсатора были добавлены параллельно IGBT. Напряжение прямоугольной формы (розовая кривая) подается на резонансный контур, образованный катушкой и одним резонирующим конденсатором (C1 + C2). Результирующий ток (синяя кривая) квазитреугольный. Силовые переключатели коммутируются в ZVS (переключение при нулевом напряжении) при включении, что исключает потери при включении. Противопараллельные диоды также коммутируют при ZVS при выключении, что исключает потери восстановления. |
4.6. «Синхронное выпрямление» Как было показано в разделе 3.2, полевые МОП-транзисторы блокируются в одном направлении, и при приложении напряжения затвора они выглядят как резисторы очень низкого номинала. В противоположном направлении полевые МОП-транзисторы ведут себя так же, как P-N диод (рисунок 7). Если напряжение приложено к затвору во время протекания тока через диод, эквивалентная схема становится схемой замещения резистора, включенного параллельно диоду (рисунок 20).Пока падение напряжения на резистивной части ниже, чем падение напряжения на диоде (0,6-0,8 В), ток течет в резистивной части устройства, а полевой МОП-транзистор действует как выпрямитель с очень низким падением напряжения. |
Уловка состоит в том, чтобы «синхронизировать» привод затвора с направлением тока, отсюда и название этой техники. Он широко используется в регуляторах очень низкого напряжения (1-5 В). На рисунке 20 показан прямой преобразователь, в котором два выходных диода были заменены полевыми МОП-транзисторами, в которых нет другой схемы управления затвором, кроме выхода трансформатора.Этот метод управления затвором используется только для иллюстрации, потому что управление затвором недоступно, когда выход вторичной обмотки падает до нуля. Даже в этом случае схема работает, но с более высокими потерями, потому что диоды MOSFET берут верх. На практике для управления затворами при синхронном выпрямлении используются специализированные ИС. Один из таких примеров можно найти здесь: http://www.irf.com/product-info/datasheets/data/ir1169.pdf МОП-транзистор с сопротивлением в открытом состоянии 5 мОм может действовать как выпрямитель на 20 А с падением напряжения всего 100 мВ, что намного ниже, чем у диодов Шоттки. |
Рисунок 20. Прямой преобразователь с синхронным выпрямлением. Два выходных диода были заменены полевыми МОП-транзисторами с низким сопротивлением в открытом состоянии. Пока подается напряжение затвора, ток будет выбирать путь с меньшим падением напряжения. Показанный на рисунке метод с автоматическим приводом на практике не используется: для этого используются специализированные ИС управления затвором. |
| следующий >> |
| 5.Потери мощности |
Оптимизация топологии проводников в электрической цепи
Приложение A: Калибровочный член в функции KS
Вторые члены в (14) и (15), которые не были включены в предыдущее исследование (Kreisselmeier and Steinhauser 1979), используются для калибровки влияния участка области целостности. Здесь выводится калибровочный член.
Функция КС в интегральной форме может быть записана следующим образом:
$$ KS (f _ {\ text {KS}}) = \ frac {1} {\ rho _ {\ text {KS}}} \ ln {\ int} _ {{\ Omega} _ {\ text {KS }}} \ exp \ left (\ rho _ {\ text {KS}} f _ {\ text {KS}} \ right) {\ mathrm {d}} V, $$
(37)
, где f KS – целевая функция, при которой максимальное значение извлекается с помощью функции KS, Ω KS – область целостности, а ρ KS – параметр.Если f KS принимает значение f high в области Ω high и принимает значение f low в области Ω low = Ω KS ∖ Ω high , то функцию КС можно записать следующим образом:
$$ \ begin {array} {@ {} rcl @ {}} KS (f _ {\ text {KS}}) & = & \ frac {1} {\ rho _ {\ text {KS}}} \ ln \ left ({\ int} _ {{\ Omega} _ {\ text {high}}} \ exp \ left (\ rho _ {\ text {KS}} f _ {\ text {high}} \ right) {\ mathrm {d}} V \ right) \\ && + \ frac {1} {\ rho _ {\ text {KS}}} \ ln \ left ({\ int} _ {{\ Omega} _ {\ text {low} }} \ exp \ left (\ rho _ {\ text {KS}} f _ {\ text {low}} \ right) {\ mathrm {d}} V \ right) \ end {array} $$
(38)
Второй член пренебрежимо мал, если выполняется f high ≫ f low и, следовательно, уравнение можно записать следующим образом:
$$ \ begin {array} {@ {} rcl @ {}} KS (f _ {\ text {KS}}) & \ приблизительно & \ frac {1} {\ rho _ {\ text {KS}}} \ ln \ left ({\ int} _ {{\ Omega} _ {\ text {high}}} \ exp \ left (\ rho _ {\ text {KS}} f _ {\ text {high}} \ right) {\ mathrm {d}} V \ right) \ end {array} $$
(39)
$$ \ begin {array} {@ {} rcl @ {}} & = & \ frac {1} {\ rho _ {\ text {KS}}} \ ln \ left (\ exp \ left (\ rho_ { \ text {KS}} f _ {\ text {high}} \ right) {\ int} _ {{\ Omega} _ {\ text {high}}} 1 {\ mathrm {d}} V \ right) \ end {array} $$
(40)
$$ \ begin {array} {@ {} rcl @ {}} & = & f _ {\ text {high}} + \ frac {1} {\ rho _ {\ text {KS}}} \ ln \ left ({\ int} _ {{\ Omega} _ {\ text {high}}} 1 {\ mathrm {d}} V \ right).\ end {array} $$
(41)
Наличие второго члена в (41) означает наличие вклада от области целостности Ω high . Если сечение Ω high определяется как произведение скаляра K KS и сечения Ω KS , то уравнение можно записать следующим образом:
$$ KS (f _ {\ text {KS}}) = f _ {\ text {high}} + \ frac {1} {\ rho _ {\ text {KS}}} \ ln \ left (K _ {\ text {KS}} {\ int} _ {{\ Omega} _ {\ text {KS}}} 1 {\ mathrm {d}} V \ right).$
(42)
Таким образом, чтобы откалибровать член, связанный с интегральной площадью, необходимо учитывать вторые члены в (14) и (15).
Приложение B: Значение и установка параметров функции KS
В функциях KS в (14) – (16) есть четыре параметра, а именно: ρ 1 , ρ 2 , K ec и K ef . Среди них ρ 1 и ρ 2 определяют экстракционную способность функций КС.Меньшие значения этих параметров делают расчет более стабильным, но снижают точность извлечения максимального значения. Типичные значения ρ 1 и ρ 2 находятся в диапазоне от 5 до 200 (Wrenn 1989). K ec и K ef определяют значения условий калибровки в функциях KS, как объяснено в Приложении A; меньшие (более высокие) значения этих параметров увеличивают (уменьшают) функции КС. Эти параметры представляют собой отношение участка аналитической области Ω ec или Ω ef к участку, где функция \ (| \ boldsymbol {J} _ {i} | / J _ {\ min} \) или \ (| \ boldsymbol {E} _ {j} | / E _ {\ min} \) принимает достаточно большое значение (т.е.е., близкое к максимальному значению). Эти параметры нельзя точно определить до оптимизации. По этой причине для K ec и K ef сначала устанавливаются приблизительные значения (например, 0,1). Затем, если ограничение не работает должным образом, параметры корректируются путем проверки значений функций KS; параметр уменьшается (увеличивается), если ограничение слишком слабое (серьезное).
Настройка параметров функций KS в разделе 4 производилась следующим образом.Для минимизации и максимизации объема ρ 1 , ρ 2 , K ec и K ef были установлены на 5, 5, 0,1 и 0,1 соответственно. Здесь, чтобы предотвратить проблему сходимости задач минимума и максимума, ρ 1 и ρ 2 оба были установлены на малые значения. Этот параметр дал хорошие результаты оптимизации, как показано в разделах 4.1 и 4.2. Оптимизация фильтра 1 изначально проводилась с теми же параметрами, что и в предыдущем примере, то есть ρ 1 = 5, ρ 2 = 5, K ec = 0.1, и K ef = 0,1. Однако при этих настройках ограничение в (25) всегда нарушалось во время оптимизации (т. Е. g > 1). В таблице 1 приведены параметры и значения функций KS в исходной структуре. Хотя максимальное значение для каждой функции KS в (14) и (15) составляло 0,79, г было 1,02. Это связано с плохой способностью функции KS в (16) извлекать максимальное значение из-за малого ρ 2 . Чтобы улучшить эту способность, ρ 2 было установлено равным 50, и оптимизация была проведена снова.Из таблицы 1 видно, что максимальное значение среди функций KS было извлечено более корректно с этими настройками, поскольку g = 0,79. Однако, хотя постоянное нарушение ограничения было предотвращено, во время оптимизации происходили отключения из-за слишком слабого ограничения. Чтобы усилить ограничение, K ec и K ef были установлены на 0,05, половину от предыдущих значений, и оптимизация была проведена снова. При этих настройках из таблицы 1 видно, что значения функций KS были увеличены на 0.14, что равно \ (- 1/5 \ ln (1/2) \); это означает, что ограничение стало серьезным. Используя эти параметры, была успешно достигнута оптимизация всех трех фильтров электромагнитных помех, как описано в разделе 4.2.
Таблица 1 Параметры и значения для функций KS в исходной структуреПриложение C: Вывод (35)
S-параметр S 21 определяется следующим образом (Frickey 1994):
$$ S_ {21} = \ left. \ frac {b_ {2}} {a_ {1}} \ right | _ {a_ {2} = 0}, $$
(43)
, где a 1 и a 2 – падающие волны мощности на портах 1 и 2 соответственно, а b 2 – отраженные волны мощности на портах 2.Обратите внимание, что размер волны мощности – это квадратный корень из мощности, а не сама мощность (Kurokawa 1965). Эти волны мощности определяются следующим образом:
$$ a_ {1} = \ sqrt {\ text {Re} (Z_ {1})} I_ {1i}, a_ {2} = \ sqrt {\ text {Re} (Z_ {2})} I_ {2i}, b_ {2} = \ sqrt {\ text {Re} (Z_ {2})} I_ {2r}, $$
(44)
, где Z 1 и Z 2 – характеристическое сопротивление портов 1 и 2 соответственно; I 1 i и I 2 i – падающий ток на портах 1 и 2 соответственно; I 2 r – отраженный ток на порте 2; Re ( Z ) – действительная часть комплексного числа Z . I 1 i , I 2 i и I 2 r определяются следующим образом:
$$ I_ {1i} = \ frac {V_ {1i}} {Z_ {1}}, I_ {2i} = \ frac {V_ {2i}} {Z_ {2}}, I_ {2r} = \ гидроразрыв {V_ {2r}} {Z_ {2}}, $$
(45)
, где V 1 i и V 2 i – падающие напряжения на портах 1 и 2 соответственно, а V 2 r – отраженное напряжение на портах 2.Подставляя (44) и (45) в (43), получаем следующее уравнение:
$$ S_ {21} = \ left. \ sqrt {\ frac {\ text {Re} (Z_ {2})} {\ text {Re} (Z_ {1})}} \ frac {Z_ {1}} {Z_ {2}} \ frac {V_ {2r}} {V_ {1i}} \ right | _ {V_ {2i} = 0}. $
(46)
Как описано в разделе 4.2, оба импеданса обоих портов равны 50 Ом, а амплитуды источников напряжения на портах 1 и 2 равны 1 и 0 В соответственно; то есть Z 1 = Z 2 = 50, V 1 i = 1 и V 2 i = 0.Подставляя эти уравнения и
$$ V_ {2r} = V _ {\ text {em, p,} 2} – V_ {2i} = \ frac {1} {w_ {2}} {\ int} _ {{\ Gamma} _ { \ text {em, p,} 2}} (\ mathbf {E} \ cdot \ mathbf {a} _ {\ mathrm {p}, 2}) \ mathrm {d} V – V_ {2i} $$
(47)
в (46), (35) получается.
Наши блоки аварийного светодиодного освещения предназначены для работы с […]новейший маленький экологически чистый никель-металл-гидридный металл […] батареи благодаря inve rt e r топология схемы w i th минимальное количество […]аккумуляторных элементов. tridonic.com | Nos appareils d’clairage de secours sont conus pour le fonctionnement avec des аккумуляторы NiMH de […]dernire gnration, petits et […] cologiques – g rce l a topologie de circuit in verseur avec un nombre […]минимальных элемента. tridonic.fr |
Оставив теоретические споры в стороне, он взял прямой, эмпирический […], потратив более года на эксперименты с […] исчерпывающий массив y o f топологии схем i n a множество вариантов.stevesproaudio.com | En laissant des sessions thiques a ct, il a pris une Approche directe, empirique, or a […]dpensant bien plus d’une anne exprimentant avec un […] таблица au comp let d e topologie d e circuit dan s u ne mu lt itude […]де вариаций. stevesproaudio.com |
Решение о том, что составляет оконечный сегмент, принимает NRA. […] в зависимости от сети wo r k топология s p ec ific для своего национального рынка.eur-lex.europa.eu | C’est l’ARN qu’il revient de dcider de ce qui constitue un сегментный терминал, […] en fon ct ion d e l a topologie d e r sau propre au m ar ch national.eur-lex.europa.eu |
Необходимо консолидировать архитектуру этих приложений, чтобы адаптировать их к ограничениям […]виртуализации, или последняя будет […] развиваться для интеграции t h e топология o f d распределенные вычисления, […]по мере развития роли промежуточного программного обеспечения. bull.com | Объединение архитектурных приложений приложений sera alors ncessaire для дополнительных адаптеров […]virtualisation or cette dernire voluera […] залить в tgr er l a topologie d e la dis tr ibution, […]l’instar du rle des intergiciels. bull.com |
| Топология b u s топология i s a параллельно […] , где каждый из трех проводов разных датчиков подключается параллельно. vaisala.se | L a топология d u bu s es t un raccordement […] parralle, dans lequel chacun des trois fils des diffrents capteurs sont raccords en parralle. vaisala.se |
Взаимосвязи внутри «Системы» […] должно быть показано на на на схему d i ag плунжер для электрического […]звена передачи, по трубопроводу […]для оборудования пневматической или гидравлической трансмиссии и упрощенной схематической компоновкой для механических рычагов. eur-lex.europa.eu | Les Interconnexions au sein du […]systme doivent tre indiques au […] moyen d ‘u n sch ma de circuit pou r l es li ai sons de […]лектриков трансмиссии, d’un schma […]de distribution de la timonerie pneumatique or hydraulique et d’un schma simple pour les liaisons mcaniques. eur-lex.europa.eu |
Данные должны также включать данные, которые позволяют национальному регулирующему органу оценить […]возможных последствий плановых обновлений или […] изменения в сети wo r k топология o n t he development […]конкурса или по оптовым товарам […]предоставлено другим сторонам. eur-lex.europa.eu | Ces donnes devraient aussi permettre l’autorit rglementaire nationale d’valuer l’impact […]Potentiel Des Mises Niveau или изменения […] программа m s dan s l a topologie d u r sau su r l’exercice […]по согласованию с производством […]de gros mis la disposition des autres party. eur-lex.europa.eu |
Важно […] примечание: сеть wo r k топология m a y накладывает физические ограниченияkeso.com | Важно: la […] limitatio n dpen d d e l a topologie d e r sa u .keso.com |
В этой операции используется […] априорное знание Sce ne ‘ s топология .crim.ca | Cette opration использует une […] connaissance a p riori de la topologie de la scne .crim.ca |
| Пары специалистов s o f топология m a ke это, сделав их […] коннекс. Sciences.amatheurs.fr | Les couple s de topologistes le f ont en se re коннексов. Sciences.amatheurs.fr |
| Неисправность контура tr o l контура l o gi c, или отказ или повреждение конуса tr o l схема м u st не ведет к […] опасных ситуаций. europarl.europa.eu | Un dfaut effectant la […] logiq ue du circuit de co mmande, ou un dfaillance ou un dtriorati on du circuit de co mmande […]ne doit pas crer de risque. europarl.europa.eu |
Их […] объявлено через cl os e d – circuit t e le обзорные экраны […]в пресс-центре в день встречи. consilium.europa.eu | Elles sont annonces le jour de la session sur les […] crans de t l vis ion en circuit fe rm du c en tre de press.consilium.europa.eu |
Для автомобилей с антиблокировочной системой, […]описание работы системы (включая все электронные части), электрическая […] блок-схема, гидравлическая или пневматическая на i c контур p l a neuroparl.europa.eu | Pour les vhicules quips d’un dispositif Antiblocage: описание […]fonctionnement du systme (включает tout lment lectronique), schma […] lectriq ue , sch ma de s схемы h ydr aul iques o u пневматикиeuroparl.europa.eu |
Когда я изучил книгу, я был удивлен, увидев, сколько […] координация там i s i n схема p a tt erns.www2.parl.gc.ca | En l’tudiant, j’ai t tonn de voir quel point il fallait assurer une […] Координация ti на l или de схемы de pis te .www2.parl.gc.ca |
Этот программный инструмент обеспечивает […] сеть discov er y , топология v i su alization, и […], управление производительностью и отказом для сетей от разных поставщиков. avaya.com | Cet outil logiciel permet de Surveiller le rseau, […] de v is ualis er la topologie et of fre u n gestionnaire […]выступления и панели для […]les rseaux multi-constructeurs. avaya.com |
Настройте свой собственный сервер по своему усмотрению: выберите […]технические характеристики оборудования […] нужно, выложить сетку wo r k топология a n d выбрать из всего […]набор управляемых услуг для упрощения задач управления. hostbasket.com | Composez vous-mme votre serveur ,com vous voulez: choisissez les […]Технические характеристики матрицы не воус аурез […] besoin, co ns truis ez une topologie de rs au et c hoisissez […]de toute une gamme de services grs […]для облегчения дегустации. hostbasket.com |
Новая процедура автоматически […] распознает на fa c e топологию , a pp , лежащую больше всего […]подходящее сочетание траекторий фрезы […]для достижения наилучшего результата в кратчайшие сроки. sescoi.com | Celui-ci reconnat […] automa ti queme nt la topologie de la pic e et effectue […]Комбинация траекторий la plus adapte […]pour raliser, dans un temps minimum, возможно определение качества la meilleure. sescoi.com |
Очевидное асимптотическое изгибание английского языка в сторону 45% (см. […], рис. 2) вызвано новой предвзятостью поисковых систем, а не реальным […] Явление языка st i c топология o f t he Web.unesdoc.unesco.org | L’asymptote apparente de l’anglais 45% (см. Рисунок 2) с расчетом на […]au nouveau biais des moteurs de recherche plutt qu ‘un […] vritable ph no mne sur la topologie lin gui stiqu e de la Toile.unesdoc.unesco.org |
| Работает в любой сети wo r k топология W i th Ziris, не имеет значения, какая у вас сеть. sony.fr | Функции для всех типов Avec Ziris, импортируемые типы на и не в или на утилизацию. sony.fr |
| S-система Interbus в i t s топология i s d в виде кольца: […] каждый участник получает на свои входные данные и отправляет их на […]вывод следующему участнику. vegaswing.com | Un systme Interbus S […] se pr se nte d ans sa topologie sou s l a for me d’un […]anneau: l’entre de chaque участник reoit des […]donnes et la sortie les envoie au prochain участник. vegaswing.com |
Если они действительно есть, вполне может быть […]нет решения кризиса мощности – если не считать произвольного ограничения […] спрос или изменение t h e топология o f t he вся сеть.navcanada.ca | Si elles le sont effectivement, il se peut qu’il n’y ait aucune solution […]la crise de capacity autre que de limiter Ardument la demande […] ou de c hange r l a topologie d e l ‘ense mb le du rseau.navcanada.ca |
Не сложно […] установка или com pl e x топология p l необходимо ning.vegaswing.com | Нет установки […] Contraigna nt e ou de plan if ication topologique […]комплекс. vegaswing.com |
Другие варианты системы банка […]также может использоваться для идентификации белков, которые локализуются в плазме […] мембраны, и изучить t h e топологию o f t его класс белков.nrc-cnrc.gc.ca | D’autres changes du systme peuvent galement tre использует […]для идентификатора протоков на мембране […] Plasmique et tud ier la topologie de cet te cl as se de […]протеина. nrc-cnrc.gc.ca |
Следовательно, их генерация p-циклов […] основан только на t h e топологии o f t he network и […]полностью независим от […]состояние сети (распределение работоспособности). irisa.fr | En consquence, leur gnration de p-cycle est […] base seul em ent s ur la topologie du r seau et elle […]est Compltement indpendante de l’tat […]du rseau (ресурсы доступны, ресурсы занимают). irisa.fr |
| Распределение также допускает t h e топологию o f a plant. automation.siemens.com | La rpartition tient […] galement co mpte de la topologie de l’i nsta ll ation.automation.siemens.com |
Эти устройства соединяют стекловолоконный оптический кабель с пластиковым волокном […] оптический кабель и поддержка дублирования wi ri n g топология .resource.boschsecurity.com | Единицы обслуживания Servent d’interfaces Entre UN […]cble fiber optique verre et un cble fiber optique plastique et […] prennent en char ge un e topologie d e cb lage re dondante.resource.boschsecurity.com |
Франция – это не […] плоская страна, с унифицированной fo r m топология .europarl.europa.eu | La France n’est pas un […] plat p ay s, av ec une topologie hom og ne .europarl.europa.eu |
Это космическая загадка, озадачившая космологов на год. […]более двух тысяч лет, недавно был озарен прорывом в […] новое направление исследований: co sm i c топология .obspm.fr | Cette nigme qui proccupe les cosmologistes depuis plus de deux mille ans […]connat actuellement des rebondissements spectulaires dans le cadre d’un champ […] nouveau de r eche rche : la topologie cos mi que .obspm.fr |
| Обнаружение сетевых устройств a n d топология m a ps предоставляет как физические, так и логические представления […] сети. ssp-telecom.com | Dcouverte des priphriques du […] rseau et cartes topologiques du rseau fournissant une vue logi qu e et une vue ph ysique [.
. |

