Третий закон ньютона и второй закон ньютона: Второй и третий законы Ньютона.

§ 3. Сила, второй закон Ньютона — ЗФТШ, МФТИ

Сила является мерой взаимодействия (взаимного действия). Если действие велико (мало), то говорят о большой (малой) силе. Сила обозначается буквой `F` (первая буква слова force).

При взаимодействии чем больше сила, тем больше ускорение тела, на которое эта сила действует. Следовательно, ускорение прямо пропорционально действующей силе: `a~F`.

Но уже говорилось о том, что ускорение зависит от массы тела: `a~1/m`.

Обобщая эти зависимости получим:

Теперь рассмотрим свойства силы, устанавливаемые опытным путём:

Из приведённых свойств силы следует, как обобщение опытных фактов, второй закон Ньютона:

Данное выражение можно представить и в другой форме: так как  `veca=(vecv_”к”-vecv_0)/t`,  то второй закон Ньютона  примет вид: `sumvecF=m(vecv_”к”-vecv_0)/t`.

Произведение массы тела и его скорости называют импульсом тела: `vecp=mvecv`,

тогда получим новое выражение для второго закона Ньютона:  

Из второго закона в частности следует, что ускорение тела, подвергающегося действию нескольких сил, равно сумме ускорений, сообщаемых каждой силой:

Первая форма записи второго закона `(sumvecF=mveca)`  справедлива только  при малых  скоростях  по  сравнению   со   скоростью   света. И, разумеется, выполняется второй закон Ньютона только в инерциальных системах отсчёта. Также следует отметить, что второй закон Ньютона справедлив для тел неизменной массы, конечных размеров и движущихся поступательно.

Второе (импульсное) выражение имеет более общий характер и справедливо при любых скоростях.

Как правило, в школьном курсе физики сила со временем не меняется. Однако последняя импульсная форма записи позволяет учесть зависимость силы от времени, и тогда изменение импульса тела будет найдено с помощью определённого интеграла на исследуемом интервале времени. В более простых случаях (сила изменяется со временем по линейному закону) можно брать среднее значение силы.

Иногда очень полезно знать, что произведение `vecF*t` называют импульсом силы, и его значение `vecF*t=Deltavecp`  равно изменению импульса тела.

Для постоянной силы на графике зависимости силы от времени можем получить, что площадь фигуры под графиком равна изменению импульса (рис. 5).

 

Но даже если сила будет изменяться со временем, то и в этом случае, разбивая время на малые интервалы `Deltat` такие, что величина силы на этом интервале остаётся неизменной (рис. 6), а потом, суммируя полученные «столбики», получим:

В наблюдаемых природных явлениях сила, как правило, меняется со временем. Мы же часто, применяя простые модели процессов, считаем силы постоянными. Сама же возможность использования простых моделей появляется из возможности подсчёта средней силы, т. е. такой постоянной силы, у которой площадь под графиком от времени будет равна площади под графиком реальной силы.

Следует добавить ещё одно очень важное следствие второго закона Ньютона, связанное с равенством инертной и гравитационной масс.

Третий закон Ньютона

Силы взаимодействия тел

Замечание 1

Известно, что не бывает одностороннего действия одного тела на другое, тела всегда взаимодействуют друг с другом. Например, во время забивания гвоздя не только молоток действует на гвоздь, но и гвоздь, в свою очередь, действует на молоток, в результате чего молоток останавливается.

Выясним, с какими силами два тела действуют друг на друга. Для этого рассмотрим такие опыты.

Рисунок 1.

На рисунке 1 изображены два сцепленных друг с другом динамометра, один из которых прикреплен к вертикальной стойке С. Если потянуть за другой динамометр, то пружины обоих приборов растянутся и будут действовать друг на друга силами упругости $\overline{F}_{1} $~и $\overline{F}_{2} $, направленными в противоположные стороны. При этом показания динамометров будут одинаковы – значит, модули сил $F_{1} $, и $F_{2} $~равны.

Если за правый динамометр потянуть сильнее, то показания обоих динамометров возрастут на одну и ту же величину, т. е. опять будут равны друг другу. Значит, и в этом случае динамометры взаимодействуют с одинаковыми по модулю силами.

Тела действуют друг на друга с равными по модулю силами и в том случае, если взаимодействие происходит на расстоянии. Опыт, доказывающий это, изображен на рисунке 2.

На нем мы видим два демонстрационных динамометра на штативе.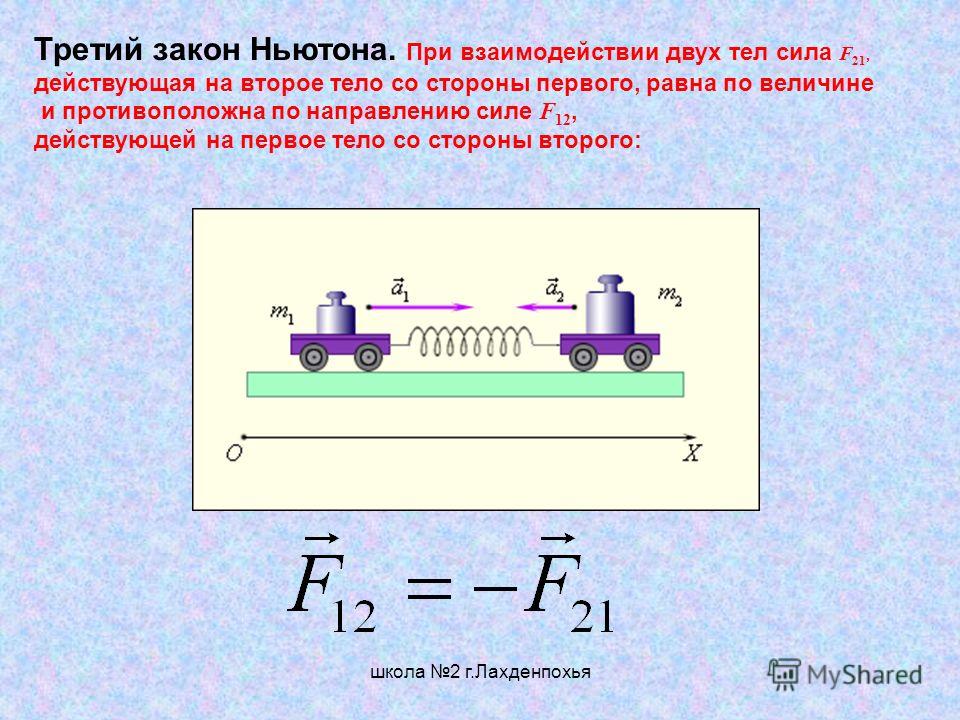 На стержни динамометров надеты круглые столики, к которым клейкой лентой прикреплены плоские керамические магниты. Магниты отталкиваются, поскольку обращены друг к другу одноименными полюсами. До начала опыта динамометры были разведены на такое расстояние, при котором силы взаимодействия магнитов были практически равны нулю и не регистрировались динамометрами.

Когда один из динамометров стали приближать к другому, их стрелки начали отклоняться от нуля в разные стороны. Это означает, что силы, с которыми магниты действуют друг на друга, противоположны по направлению.

Рисунок 2.

При сближении магнитов показания динамометров возрастают, но в каждый момент они равны друг другу — значит, магниты отталкиваются с равными по модулю силами.

Теперь рассмотрим опыт, в котором силы взаимодействия измеряются в процессе движения взаимодействующих тел. На рисунке 3 изображен самодвижущийся игрушечный трактор, который тянет на буксире металлическую коробку с грузом. В качестве буксирного троса использованы сцепленные друг с другом трубчатые динамометры, один из которых прикреплен к трактору, а второй – к коробке. Показания динамометров одинаковы, значит, движущиеся трактор и коробка действуют друг на друга с равными по модулю силами.

Рисунок 3.

Проделанные опыты свидетельствуют о том, что \textbf{силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.}

Этот закон был открыт Ньютоном и называется третьим законом Ньютона.

Третий закон Ньютона

Математическая запись третьего закона Ньютона имеет следующий вид:

Знак минус показывает, что векторы сил направлены в разные стороны.

Любое из наблюдаемых нами движений различных тел можно объяснить с помощью законов Ньютона. Например, идущий человек движется вперед благодаря тому, что он отталкивается ногами от земли, т. е. взаимодействует с ней. Человек и земля действуют друг на друга с одинаковыми по модулю и противоположно направленными силами и получают ускорения, обратно пропорциональные их массам. Поскольку масса Земли огромна по сравнению с массой человека, то ускорение Земли практически равно нулю, т. е. она не меняет свою скорость. Человек же приходит в движение относительно Земли.

Замечание 2

Следует отметить, что силы, возникающие в результате взаимодействия тел, являются силами одной и той же природы. Например, Земля и Луна взаимодействуют друг с другом посредством сил всемирного тяготения, стальной гвоздь и магнит притягиваются благодаря действию магнитных сил.

Примеры сил взаимодействия:

• сила гравитационного притяжения двух тел;
• силы притяжения и отталкивания двух магнитов;
• силы притяжения и отталкивания двух электрически заряженных тел;
• силы притяжения нуклонов в атомной ядре;
• силы, возникающие при упругой деформации;
• силы взаимодействия молекул.

Замечание 3

Следует помнить, что силы, о которых говорится в третьем законе Ньютона, никогда не уравновешивают друг друга, поскольку они приложены к разным телам.

2.$

Найти: $m$-?

Решение: Девочки, оттолкнувшись, приобрели ускорения, которые направлены по одной прямой в противоположные стороны и подействовали друг на друга с силами, которые имеют одинаковые модули и противоположные направления:

\[\overline{F}_{1} =-\overline{F}_{2} \]

Запишем второй закон Ньютона для движущихся девочек:

$F_{1} =m_{1} a_{1} $ – сила, с которой вторая девочка вместе с братом действуют на первую девочку.

$F_{2} =(m_{2} +m)a_{2} $ – сила, с которой первая девочка действует на вторую девочку.

Подставив выражения для сил в выражение для третьего закона Ньютона, найдем массу брата:

$m=\frac{m_{1} a_{1} -m_{2} a_{2} }{a_{2} } =28$кг

Ответ: $m=28$кг.

ньютоновской механики. Учитывая третий закон Ньютона, почему вещи способны двигаться?

Если бы я мог изменить только одну вещь в физическом образовании, это была бы формулировка третьего закона Ньютона. Согласно моей копии Magnificent Principia (автор Колин Паск, Prometheus Books, 2013), формулировка «Каждому действию всегда противостоит равное противодействие. 2}$$

Обратите внимание, что указаны две массы, но нет ни “исходной”, ни “целевой” массы. И есть только одна сила, произведенная этим уравнением. Теперь вы можете посмотреть на это как на две

различных силы: $m_1$, притягивающая $m_2$, и $m_2$, притягивающая $m_1$. Но это заблуждение. Создается впечатление, что силы каким-то образом существуют независимо. Но это не так. Они полностью, неразрывно связаны. Настолько, что я думаю, что это имеет гораздо больше смысла, чем 92}$$

Опять же, вы можете думать об этом как о двух разных силах. Но я думаю, что уравнение действительно намекает на единую силу притяжения (разные знаки заряда) или единую силу отталкивания (одинаковые знаки заряда) между двумя зарядами .

Именно это имел в виду Ньютон под своим третьим законом. $m_1$ не может притянуть $m_2$ без того, чтобы $m_1$ не был захвачен t

той же самой силой притяжения между двумя частицами. И $q_1$ не может притянуть или оттолкнуть $q_2$, пока $q_1$ не попадет в та самая сила .

Третий закон Ньютона традиционно преподается как пары сил . Думаю, имеет смысл представить его как единую силу , которая всегда должна действовать между парами тел , как следует из закона Кулона и уравнения всемирного тяготения.

Это труднее увидеть при контактных силах. Часть проблемы заключается в том, что человеческие мышцы должны постоянно расходовать энергию на молекулярном уровне, чтобы оставаться в сокращенном состоянии. Так что легко спутать

усилие с расходом энергии . А у людей есть познание и свобода действий. Таким образом, высказывание «Человек давит на спичечный коробок, а спичечный коробок давит на человека» кажется неправильным, потому что человек тратит энергию; спичечного коробка нет. У человека есть свобода воли, и он инициирует толчок; спичечный коробок неодушевленный.

Чтобы лучше понять третий закон Ньютона, вообразите себя в глубоком бассейне, где ваши ноги находятся над дном. Ты рядом со стеной. Теперь нажмите на стену. Что случается?

Ты отталкиваешься от стены . Традиционное объяснение состоит в том, что вы толкаете стену, а «стена давит на вас в ответ». И хотя технически это верно, это не имеет интуитивного смысла, потому что вы чертовски хорошо знаете, что толкаете именно вы.

На самом деле происходит то, что вы создаете отталкивающую силу между стеной и собой . Стена прикреплена к земле, а земля очень большая и ее трудно сдвинуть. Итак, сила отталкивания проявляется в том, что вы отталкиваетесь от стены.

Когда вы «толкаете спичечный коробок», вы создаете силу отталкивания между пальцем и спичечным коробком. (Конечно, на молекулярном уровне это всего лишь кулоновское отталкивание.) Но вы намного массивнее спичечного коробка. Ваш вес и трение между обувью и полом, по сути, привязывают вас к полу и делают вас неподвижным. Итак, сила отталкивания проявляется в движении спичечного коробка.

Многие физические проблемы формулируются как «А притягивает Б» или «А отталкивает Б». Такая формулировка в лучшем случае вводит в заблуждение. На самом деле происходит следующее: «А и В притягиваются друг к другу» или «А и В отталкиваются друг от друга». Всегда. Это 3-й закон Ньютона.

Наконец, при работе с силами, в которых одна масса (или один заряд) каким-то образом фиксирована или намного больше другой (например, яблоко, падающее на землю), очень часто игнорируется тот факт, что массы притягивают друг друга, и формулировать взаимодействие так, как будто это просто земля притягивает яблоко и ничего более. Это чрезмерное упрощение. Но это оправдано тем, что сила притяжения между двумя массами в подавляющем большинстве проявляется в движении яблока.

Фактически, Ньютон хорошо сформулировал эту часть в «Началах»,

“Изменения, производимые этими действиями, равны… если тела не сдерживается никакими другими препятствиями. . . изменения скоростей относительно общих частей обратно пропорциональны телам [массам].»

Видео-урок: Применение третьего закона движения Ньютона к столкновениям

Стенограмма видео

В этом видео мы рассмотрим, как применить третий закон движения Ньютона к сценариям, где два объекта столкновение. Мы рассмотрим, как найти силы, действующие на объекты во время столкновения, с учетом изменения импульса каждого из объектов, и мы увидим, как эти силы подчиняются третьему закону Ньютона. движение. Итак, начнем с того, что вспомним это закон.

Третий закон движения Ньютона говорит нам, что если объект — скажем, объект А — оказывает силу на другой объект, объект B, то объект B оказывает равную и противоположную силу на объект A. Другими словами, скажем, что это вот объект А, а это объект Б. Теперь эти два объекта сталкиваются друг с другом. Другими словами, объект А есть приложение силы вправо к объекту B. Предположим, что эта сила имеет величина 𝐹. Ну, по третьему закону Ньютона движение, объект B оказывает равную по величине силу. Таким образом, величина равна 𝐹, но противоположна в направлении, т.

е. влево на объект А.

А теперь давайте вспомним как мы сказали ранее, что мы будем рассматривать изменение импульса каждого из также этих объектов. А теперь, прежде всего, вспомним что импульс объекта 𝑝 определяется путем умножения его массы 𝑚 на его скорость 𝑣. Так что же должен делать импульс с силами, приложенными к объекту? Что ж, чтобы ответить на этот вопрос, мы нужно вспомнить еще один из законов движения Ньютона, а именно второй закон.

Теперь второй закон Ньютона. говорит нам, что результирующая сила, действующая на объект, равна скорости изменения импульс объекта. И мы можем записать это в символах как 𝐹 нижний индекс net, который представляет собой результирующую силу, действующую на объект, равную изменению импульс объекта, где эта греческая буква Δ представляет собой изменение, а 𝑝 импульс.

И мы разделяем это изменение на импульса на время, необходимое для того, чтобы это изменение импульса произошло, другими словами, интервал времени, в течение которого происходит это изменение импульса. Теперь мы видим, что изменение импульс равен изменению массы, умноженному на скорость тела потому что помните, что импульс объекта равен массе, умноженной на его скорость.

Допустим, мы рассматриваем объект при столкновении. И столкновение изолировано так единственные силы, действующие на объект, – это силы, вызванные столкновением. Ну, в таком случае чистая сила на объект просто сила из-за столкновения. И, следовательно, если мы знаем импульс тела до столкновения и импульса тела после столкновения. столкновения, мы можем вычислить изменение импульса. Кроме того, если мы знаем количество времени, за которое происходит столкновение, то мы знаем количество времени за которой происходит изменение импульса тела. И, следовательно, мы можем разработать эту сеть сила, действующая на объект, которая, как мы сказали, для изолированной системы оказывается силы из-за столкновения. Итак, это связь между импульс объекта или, точнее, изменение импульса объекта и сила, приложенная при изолированном столкновении.

Теперь обратите внимание, что мы говорим о изолированное столкновение, когда действуют только силы, вызванные столкновением сам. Причина, как мы уже говорили, потому что второй закон Ньютона имеет дело только с чистой силой, действующей на объект или другими словами, общая сила, действующая на объект. Однако, скажем, какой-нибудь другой силы должны были воздействовать на эти объекты. Скажем, например, что они находились в гравитационном поле Земли, поэтому их вес действовал на них как Что ж. Допустим, у них был вес 𝑊 один и 𝑊 два соответственно.

Ну, в таком случае, пока мы Имея информацию об этих весах, мы сможем вычислить результирующую силу, воздействующую на объекта, используя второй закон движения Ньютона, предполагая, что мы знали об изменении импульс одного из этих объектов. И, следовательно, мы могли бы работать из силы из-за столкновения. Или наоборот, если бы мы уже знали сила из-за столкновения, мы могли бы вычислить изменение объекта в импульс. Но что еще более важно, мы могли бы работать изменение импульса другого объекта, также участвовавшего в столкновении при этом зная информацию только о первом. Итак, что мы подразумеваем под этим?

Итак, давайте еще раз рассмотрим изолированное столкновение. Действуют только силы силы из-за столкновения. Теперь предположим, что мы знаем о изменение импульса одного из объектов, потому что, например, мы знаем массу объект и скорость объекта до и после столкновения. Кроме того, мы знаем время для которого произошло это столкновение. Ну, судя по всей этой информации, мы могли бы рассчитать изменение импульса и разделить его на время столкновение, чтобы дать нам чистую силу, действующую на этот объект, которая вызвала этот импульс изменить в первую очередь. Но тогда из-за третьего Ньютона закон движения, мы знали бы, что эта сила, которую мы только что нашли, равна величине силы, действующей на другой объект.

И еще, потому что в то время полученные при столкновении, одинаковы для обоих объектов, очевидно, потому что они столкнувшихся, мы также знали бы изменение импульса второго объект. Он должен быть таким же, как изменение импульса первого объекта. И это справедливо для изолированного системе, потому что если единственными действующими силами являются силы столкновения, то сеть сила на каждом из объектов одинакова; это сила столкновения. И время, в течение которого эта сила действия – это просто время столкновения, и это то же самое для обоих объектов, что и Что ж. Отсюда и изменение импульса обоих объектов будет одинаковым.

А также это, если бы мы знали массы этих объектов, предполагая, что эти массы не меняются в течение столкновения, мы могли бы затем вычислить новые скорости этих объектов. Таким образом, мы можем использовать третий закон Ньютона. закон движения в сочетании со вторым законом движения Ньютона, чтобы принять информация, которая у нас есть об одном объекте в столкновении, и выяснить, о чем другой объект в столкновении.

Теперь также стоит быстро отметить что, как мы уже видели, изменение импульса тела равно изменение массы, умноженное на скорость. Однако, если масса объекта остается постоянна в течение столкновения, то можно сказать, что изменение импульса объекта равен постоянной массе, умноженной только на изменение скорость. И тогда, когда мы возьмем это уравнение для Δ𝑝 и подставляя его во второй закон движения Ньютона, мы видим, что сеть сила, действующая на объект, равна массе объекта, которая, как мы уже говорили, постоянна в этом случае умножается на изменение скорости, деленное на время, затраченное на это произойти столкновение. Но потом мы понимаем, что изменение скорости тела, деленное на время, затраченное на это изменение возникающая скорость – это просто ускорение объекта.

Итак, в ситуации, когда масса объекта постоянна, второй закон Ньютона просто сводится к говорит нам, что результирующая сила, действующая на объект, равна массе, умноженной на ускорение объекта, известное уравнение 𝐹 равно 𝑚𝑎. И в этой ситуации мы не даже обязательно нужно иметь дело с изменением импульса объекта. Мы можем просто справиться с этой массой и ускорение. Теперь все хорошо и хорошо у нас обсуждение этой темы, но лучше всего это понять, попробовав несколько примеров. Итак, давайте сделаем это сейчас.

Два предмета А и В брошены в воздух и сталкиваются друг с другом, как показано на диаграмме. Объект А имеет вес 12 ньютонов. а объект B имеет вес 20 ньютонов. При столкновении объект А оказывает сила 24 ньютона на объект Б. Какая сила приложена к объекту А объектом Б во время столкновения? Какому объекту придается большее ускорение из-за столкновения?

Итак, в этом вопросе мы можем видите, что у нас есть два объекта: объект A синего цвета и объект B розового цвета. Теперь нам сказали, что они были подброшены в воздух и столкнулись друг с другом. И дополнительно во время этого при столкновении объект A действует на объект B с силой в 24 ньютона. И, наконец, мы также знаем массы этих предметов. Это пригодится в минута. Но первое, что нам нужно попытаться сделать, это выяснить, какая сила приложена к объекту A объектом B во время столкновение. Другими словами, мы знаем, что Объектом А к объекту Б приложена сила в 24 ньютона. противоположный сценарий.

Какая сила приложена к объекту B к объекту А? Чтобы ответить на этот вопрос, нам нужно Вспомним третий закон Ньютона. Теперь третий закон Ньютона говорит нам что если объект А действует на объект В, то объект В оказывает равную и противоположная сила на объект А. Другими словами, мы уже знаем сила, действующая со стороны А на В; это 24 ньютона вправо. И тогда по третьему закону Ньютона мы знаем, что сила, действующая со стороны В на А, будет иметь ту же величину, равная величина. Но это будет в противоположное направление. Иными словами, тогда сила оказываемое B на A, будет в этом направлении левее. И это также будет иметь магнитуда 24 ньютона.

Итак, возвращаясь к этому вопросу, мы видим, что на самом деле нам не нужно указывать направление силы. Но нас только что попросили найти приложенная сила. Таким образом, мы можем просто констатировать величина этой силы, которая составляет 24 ньютона. Итак, переходим к следующей части вопрос, то нам нужно найти, какой объект получает большее ускорение из-за столкновение, будь то объект A или объект B.

Теперь, чтобы ответить на этот вопрос, давайте сначала начнем с того, что вспомним еще один из законов движения Ньютона, второй закон Ньютона. особенно в ситуации, когда масса объекта, который мы применяем Второй закон Ньютона остается постоянным. Другими словами, масса объект не меняется. Что ж, в таком случае мы можем Напомним, что результирующая сила, действующая на объект, равна массе этого объекта. умножить на его ускорение. Теперь, поскольку нас просят найти ускорение на этих объектах именно из-за столкновения, мы только нужно думать о силе столкновения. Нам не нужно учитывать их веса, потому что помните, независимо от того, каковы их веса, эти веса всегда действовать в направлении вниз и производить ускорение 𝑔 или, другими словами, 9.8 метров в секунду в квадрате в каждом из этих объектов. И поэтому нам нужно беспокоиться только о ускорение, вызванное силами столкновения.

Теперь мы знаем, что столкновение силы равны по величине на оба эти тела. На объект действует сила в 24 ньютона A и силой в 24 ньютона на объект B. Поскольку нас просят найти какой из них имеет большее ускорение, нам не нужно беспокоиться о направлениях, только величина этого ускорения. Итак, прежде всего, думая о объект А, мы знаем, что сила, которую мы рассматриваем в данном случае, 24 ньютона силы. Это сила, обусловленная столкновение, вызывающее ускорение объекта. И тогда можно сказать, что это равна массе объекта, который мы будем называть индексом 𝑚 A, умноженной на его ускорение в нижнем регистре 𝑎 нижний индекс A. И мы можем сделать то же самое для B. Мы знаем, что сила на объект, который мы рассматриваем, составляет 24 ньютона. Это сила столкновения. А это равно массе индекс объекта 𝑚 B, умноженный на его ускорение.

Теперь, что мы пытаемся сделать в этот вопрос заключается в сравнении 𝑎 нижнего индекса A с 𝑎 нижним индексом B. Какое из ускорений объектов из-за столкновения больше? Итак, чтобы сделать это, нам нужно знать, каковы массы предметов. И здесь мы видим, почему мы были даны веса этих объектов в первую очередь. Если бы мы просто собирались игнорировать эти веса, то это было бы отвлекающим маневром. Но вот где они приходят удобно, потому что мы можем вспомнить, что вес объекта равен массе этого объекта, умноженное на ускорение свободного падения, 90,8 метра в секунду в квадрате.

Итак, для объекта А мы можем сказать что вес A — который мы будем называть индексом 𝑊 A — равен его массе, которая равна 𝑚 индекс A, умноженный на ускорение свободного падения, которое является константой. И мы можем сделать то же самое для B. Вес B равен масса B, умноженная на ускорение свободного падения. Теперь в этот момент мы можем видеть, что вес A меньше веса B. Другими словами, 𝑊 A меньше, чем 𝑊 B. Следовательно, масса A должна быть меньше массы B, потому что мы умножаем массу на постоянное значение в оба случая, чтобы дать нам вес. Итак, это означает, что меньший вес объекта А по сравнению с объектом В означает, что масса объекта А должна также быть меньше, чем масса объекта B. Мы можем записать это как массу A меньше массы B.

И тогда мы можем вернуться к этим два уравнения, которые мы составили здесь. Мы видим, что в обоих случаях сила, приложенная к этим объектам, одинакова; это 24 ньютона. Однако, как мы видели, массы этих объектов различны. И так, чтобы компенсировать это и чтобы дать нам одну и ту же левую часть в обоих случаях, значения этих двух ускорения должны быть разными. И так, если мы собираемся сказать, что сила в 24 ньютона, действующая на объект А, равна меньшей массе, умноженной на некоторое ускорение, то для того, чтобы дать нам значение 24 ньютона в качестве силы для того, чтобы чтобы компенсировать малую массу, ускорение объекта должно быть больше. И наоборот, можно сказать, что 24 ньютонов сила, действующая на объект B, равна большей массе B, умноженной на меньшее ускорение Б.

Итак, на данный момент мы нашли ответ на наш вопрос. Поскольку оба объекта имеют одинаковые сила, действовавшая на них при столкновении, но масса объекта А была меньше массы массы объекта B, это означает, что объект A получает большее ускорение из-за столкновение.

Итак, теперь, когда мы посмотрели на примере вопроса, давайте посмотрим на другой.

Пуля массой 10 грамм является летит со скоростью 450 метров в секунду и сталкивается с неподвижной игрушечной машинкой массой 400 грамм. Пуля останавливается 0,01 секунд после столкновения с автомобилем. Какая сила необходима, чтобы привести пуля отдыхает за 0,01 секунды? Каково ускорение автомобиля из-за отдачи от пули?

Итак, в этом вопросе, что нам сказали, что изначально у нас есть пуля массой 10 граммов, движущаяся в направлении автомобиль со скоростью 450 метров в секунду. И эта машина – игрушечная машинка, в которой есть масса 400 грамм и изначально он неподвижен. Теперь, в какой-то момент, пуля и автомобиль сталкивается, в результате чего пуля останавливается за 0,01 секунды. Теперь, в первой части вопрос, нас попросили попытаться определить силу, необходимую для этого, чтобы полностью остановить пулю за 0,01 секунды, если она изначально летела со скоростью 450 метров в секунду.

Теперь, чтобы ответить на этот вопрос, мы нужно вспомнить второй закон движения Ньютона. Этот закон говорит нам, что сеть сила на объекте 𝐹 нижняя сеть равна скорости изменения импульс или, другими словами, изменение импульса объекта, деленное на время принимается для того, чтобы произошло это изменение импульса. Теперь, в этом случае, мы знаем, что пуля изначально летела со скоростью 450 метров в секунду. А потом он останавливается, когда сталкивается с автомобилем. Итак, мы знаем, что пуля скорость меняется; оно уменьшается. И поскольку эта скорость меняется, мы знаем, что импульс пули меняется, потому что помните импульс тела равен произведению массы тела на его скорость. Итак, изменение импульса объект, который мы назовем Δ𝑝, будет равен изменению массы умножается на скорость объекта.

Теперь, в ситуации, когда масса объекта остается постоянной, как и у пули, мы знаем, что она остается на 10 грамм во время столкновения и после столкновения, в этом случае мы можем сказать, что изменение импульса объекта равно этой постоянной массе умножается на изменение скорости тела. Итак, приступим к поиску изменение импульса пули. Мы знаем, что он равен массе пули, которая составляет 10 граммов или в базовых единицах, это 0,01 килограмма. И тогда нам нужно умножить это массы за счет изменения скорости пули. А изменение скорости движения пуля – это конечная скорость минус начальная скорость.

Теперь мы знаем, что конечная скорость равна нулю метров в секунду, потому что пуля в конце неподвижна. И начальная скорость 450 метров в секунду, потому что это то, с чем он двигался раньше. А теперь обратите внимание, что мы сделали предположение, что начальная скорость пули вправо положительна и, следовательно, наше изменение скорости будет отрицательным, потому что пуля замедляется; теряет скорость. Но так или иначе, мы находим, что изменение импульса пули равно минус 4,50 кг м на второй.

Итак, теперь, когда мы вычислили это изменение импульса, мы можем рассчитать результирующую силу, действующую на пулю. сила, необходимая для остановки пули за 0,01 секунды. Для этого нам просто нужно сказать что результирующая сила, действующая на пулю 𝐹 нижняя сетка, равна изменению импульса который мы рассчитали как отрицательные 4,50 килограмма метров в секунду, деленные на время, в течение которого происходит столкновение, о котором нам сказали, составляет 0,01 секунды. И затем, поскольку мы работаем в базовые единицы — это килограммы-метры в секунду для импульса и секунды для времени. — мы знаем, что последней единицей этого вычисления будут килограммы-метры. на секунду в квадрате, что эквивалентно ньютону, единице силы.

Таким образом, когда мы оцениваем правую стороны этого уравнения, мы находим, что результирующая сила, действующая на пулю, отрицательна на 450 ньютоны. Теперь, потому что нас просто спросили чтобы найти требуемую силу, и их специально не просили беспокоиться о направлении, мы опустим знак минус в нашем ответе. Мы просто скажем, что величина силы, необходимой для замедления пули за 0,01 секунды до остальное 450 ньютонов. Итак, теперь, когда мы вычислили это, давайте посмотрим на следующую часть вопроса.

Каково ускорение автомобиля из-за отдачи от пули? Ну, чтобы ответить на это, мы можем вспомнить Третий закон Ньютона.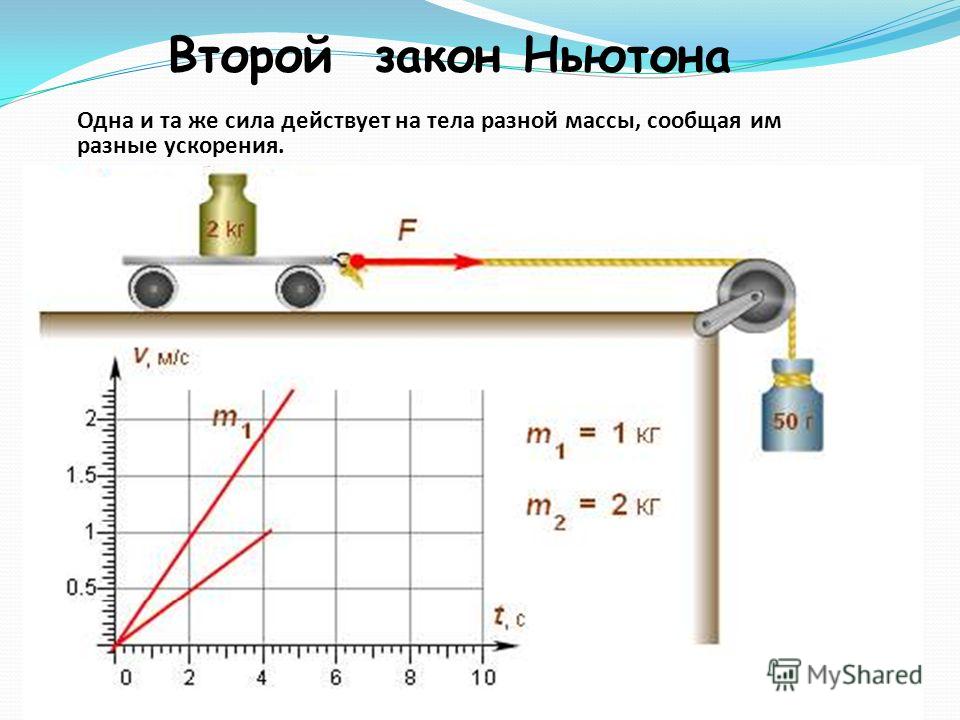 Третий закон Ньютона говорит нам, что если объект — скажем, объект А — оказывает силу на другой объект, объект В. Тогда В оказывает равную и сила, действующая на A. Теперь мы видим в этом столкновении что на пулю действует сила в 450 ньютонов для замедления Это. Ну, эта сила была бы оказанного автомобилем на пулю из-за столкновения, которое произошло между два объекта. Итак, по третьему закону Ньютона движение, мы можем видеть, что пуля будет оказывать силу в противоположном направлении на машина. И величина этой силы то же, 450 ньютонов.

И потом, мы можем вспомнить, что для объекта с постоянной массой, как мы уже видели, изменение импульса объект равен этой постоянной массе, умноженной на изменение скорости. Но тогда, если мы возьмем это уравнение для изменения импульса и подставить его обратно во второй закон Ньютона. движения, мы видим, что результирующая сила на объекте 𝐹 нижняя сетка равна массе умножить на изменение скорости, деленное на изменение времени или время, затраченное чтобы в этом случае произошло столкновение. И тогда мы можем заметить, что изменение скорости, деленное на изменение во времени, равно ускорению объект. Итак, в ситуации, когда масса объекта остается постоянной, второй закон Ньютона сводится к результирующей силе равно массе тела, умноженной на его ускорение.

Теперь мы уже знаем силу действующие на автомобиль; это 450 ньютонов. Итак, мы знаем чистую силу. А еще мы знаем массу автомобиль. Мы знаем, что это 400 граммов. Следовательно, мы можем разработать ускорение путем перестановки этого уравнения. Можно сказать, что ускорение автомобиля равна чистой силе, деленной на его массу. В итоге получается 450 ньютонов.