Третий закон ньютона определение и формула: определение, формула + рассуждения по теме

определение, формула + рассуждения по теме

 

В первом законе Ньютона говорится о поведении тела, изолированного от воздействия других тел. Второй закон говорит о прямо противоположной ситуации. В нем рассматриваются случаи, когда тело или несколько тел воздействуют на данное.

Оба эти закона описывают поведение одного конкретного тела. Но во взаимодействии всегда участвуют минимум два тела. Что будет происходить с обоими этими телами? Как описать их взаимодействие? Анализом этой ситуации и занялся Ньютон после формулировки своих первых двух законов. Займемся и мы такими же изысканиями.

Взаимодействие двух тел

Мы знаем, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы. Такое может происходить среди по-разному воспитанных людей, но никак не в природе.

Мы знаем, что если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не ощутимо.

Однако, если вы попробуете пнуть тяжелый железный мяч, то живо ощутите это ответное воздействие. Фактически, мы каждый день по многу раз пинаем очень и очень тяжелый мяч нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе.

Соотношение сил во взаимодействии между телами

Так что из этих рассуждений видно, что при взаимодействии двух тел, не только первое действует на второе с некоторой силой, но и второе в ответ действует на первое также с некоторой силой. Возникает вопрос: а как соотносятся эти силы? Какая из них больше, какая меньше?

Для этого необходимо проделать некоторые измерения. Потребуются два динамометра, но в домашних условиях их вполне могу заменить два безмена. Они измеряют вес, а вес это тоже сила, только выраженная в единицах массы в случае безмена. Поэтому, если у вас есть два безмена, то проделайте следующее.

Один из них оденьте колечком на что-то неподвижное, например, на гвоздь в стене, а второй соедините с первым крючками. И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен.

И хотя мы тянем только за один из них, окажется, что показания обоих, как на очной ставке, будут совпадать. Получается, что сила, с которой мы воздействуем вторым безменом на первый, равна силе, с которой первый безмен воздействует на второй.

Третий закон Ньютона: определение и формула

Сила действия равна силе противодействия. В этом и состоит суть третьего закона Ньютона. Определение его таково: силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению. Третий закон Ньютона можно записать в виде формулы:

F_1  = – F_2,

Где F_1 и F_2 силы действия друг на друга соответственно первого и второго тела.

Справедливость третьего закона Ньютона была подтверждена многочисленными экспериментами. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются.

Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.

Нужна помощь в учебе?

Предыдущая тема: Второй закон Ньютона: формула и определение + маленький опыт
Следующая тема:&nbsp&nbsp&nbspСвободное падение тел: суть, ускорение свободного падения, формулы

формулировка или определение закона в физике в 9 классе, что в нем описано и в чем состояло его уточнение

Например, книга, лежащая на столе, действует на стол с силой, прямо пропорциональной своей массе и направленной вертикально вниз. Согласно третьему закону Ньютона стол в это же время действует на книгу с абсолютно такой же по величине силой, но направленной не вниз, а вверх.

Когда яблоко падает с дерева, это Земля действует на яблоко силой своего гравитационного притяжения (вследствие чего яблоко равноускоренно движется к поверхности Земли), но при этом и яблоко притягивает к себе Землю с такой же силой.

Третий закон Ньютона

Взаимодействие двух тел — это всегда двухсторонний процесс.

Пример:

При забивании гвоздя не только молоток действует на гвоздь, но и гвоздь, в свою очередь, действует на молоток (сопротивляется ему), в результате чего молоток останавливается (рис. 1).

Рис. 1

Проведём опыт.

Сцепим два динамометра вместе крючками и потянем их в разные стороны. Показания динамометров будут одинаковы (рис. 2). Следовательно, динамометры взаимодействуют равными по модулю и противоположно направленными силами.

Рис. 2

Обрати внимание! Тела действуют друг на друга с равными по модулю силами и в том случае, если взаимодействие происходит на расстоянии.

К одному из динамометров прикрепим стальной брусок, а к другому — магнит (рис. 3).

Рис. 3

Сначала динамометры разведём на такое расстояние, при котором силы взаимодействия магнита и стального бруска практически равны нулю. При этом показания обоих динамометров будут равны нулю.

Если один из динамометров приближать к другому, их стрелки начнут отклоняться от нуля в разные стороны. Это означает, что силы, с которыми магнит и брусок действуют друг на друга, противоположны по направлению.

При сближении динамометров их показания возрастут, но в любой момент движения динамометров эти показания равны друг другу — значит, магнит и брусок взаимодействуют с равными по модулю силами.

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению, то есть:

F1=−F2.

Этот закон был открыт Ньютоном и называется третьим законом Ньютона.

Знак «минус» показывает, что векторы сил направлены в разные стороны.

С помощью законов Ньютона можно объяснить любое движение, наблюдаемое нами.

Пример:

Катящееся колесо движется вперёд благодаря тому, что оно отталкивается от Земли, т.е. взаимодействует с ней.

Колесо и Земля действуют друг на друга с одинаковыми по модулю и противоположно направленными силами и получают ускорения, обратно пропорциональные их массам.

Поскольку масса Земли огромна по сравнению с массой колеса, то ускорение Земли практически равно нулю, т. е. она не меняет свою скорость. Колесо же приходит в движение относительно Земли.

Обрати внимание! Силы, возникающие в результате взаимодействия тел, являются силами одной природы.

Так, стальной гвоздь и магнит, взаимодействие которых описано выше, притягиваются благодаря действию магнитных сил.

Пример:

Под действием притяжения к Земле предметы, лежащие на опоре, немного сжимаются сами и сжимают находящуюся под ними опору (обычно эти деформации так малы, что мы не замечаем их). В результате и в самих телах, и в опоре возникают силы упругости, посредством которых тело и опора взаимодействуют друг с другом (рис. 4).

Рис. 4

Силу, приложенную к опоре и направленную вертикально вниз, называют весом тела P→, а силу, приложенную к телу и направленную вертикально вверх, — силой реакции опоры N→. Обе эти силы являются силами упругости.

Обрати внимание! Силы, о которых говорится в третьем законе Ньютона, никогда не уравновешивают друг друга, поскольку они приложены к разным телам.

Источник: https://www.yaklass.ru/p/fizika/9-klass/zakony-vzaimodeistviia-i-dvizheniia-tel-osnovy-dinamiki-18748/tretii-zakon-niutona-253023/re-d8120d91-e1f7-47d4-aaf6-9c5577c934f3

Третий закон Ньютона

При взаимодействии тел силы, возникающие между ними, равны по модулю и направлены друг против друга. Так работает третий закон Ньютона, который важен не только в механике, но и в темах 10 класса – электричестве и магнетизме.

Исаак Ньютон в математических началах натуральной философии ввел принцип, известный теперь как третий закон Ньютона. Согласно этому принципу на всякое действие существует равное и противоположное противодействие. В современной физике его формулируют иначе: материальные точки действуют друг на друга с силами одной природы, абсолютные величины которых равны, а направления противоположны.

Наглядно описывает механизм третьего закона система двух тел, соединенных нитью. Если одно из тел тянуть, то возникнет сила натяжения нити. Она действует одинаково в двух противоположных направлениях.

Другой пример – это предмет, лежащий на любой поверхности. Сам предмет давит на поверхность с силой $vec P = m vec g$, называемой весом тела. С другой стороны, поверхность воздействует на предмет с силой $vec N = m vec g$, называемой силой нормальной реакции опоры.

Сила всемирного тяготения также действует обоюдно. Равно как Земля притягивает Луну, так и Луна притягивает Землю. Но поскольку ускорение свободного падения для Луны много больше, чем для Земли, то внешне всё выглядит так, будто падает только Луна.

Формула третьего закона Ньютона выглядит так:

$F_{1,2} = – F_{2,1}$, где знак минус указывает как направлены силы.

Он справедлив для инерциальных систем отсчета и сил любой природы. Так силы кулоновского взаимодействия между точечными зарядами равны по модулю и противоположны по направлению, а сам закон Кулона в математической записи выглядит аналогично закону всемирного тяготения.

В замкнутой системе силы взаимодействия между материальными точками возникают парами и уравновешивают друг друга, а сама система покоится. 2$. Найти силу, с которой бортик отталкивается от человека. Сопротивлением воды пренебречь.

Решение

По третьему закону Ньютона сила, с которой бортик воздействует на человека равна силе, с которой человек воздействует на бортик.

$F_{1,2} = – F_{2,1}$

$F_{1,2} = ma = 60 Н$

Тогда:

$F_{2,1} = – 60 Н$

В ходе урока было сформулировано определение третьего закона Ньютона, рассмотрены примеры, иллюстрирующие его, дана математическая запись закона и приведено важное дополнение, следующее из него – сохранение импульса замкнутой системы. В завершении урока разобраны задачи.

Источник: https://obrazovaka.ru/fizika/tretiy-zakon-nyutona-formula-opredelenie.html

Законы механики Ньютона

1) Первый закон Ньютона: Существуют такие системы отсчета, называемые инерциальными, относительно которых свободные тела движется равномерно и прямолинейно.

Первый закон механики, или закон инерции, как его часто называют, бал, по существу, установлен еще Галилеем, но общую формулировку ему дал Ньютон.

Свободным телом – называют тело, на которое не действуют какие – либо другие тела или поля. При решении некоторых задач тело можно считать свободным, если внешние воздействия уравновешены.

Системы отсчета, в которых свободная материальная точка покоится или движется прямолинейно и равномерно, называются инерциальными системами отсчета.

Прямолинейное и равномерное движение свободной материальной точки в инерциальной системе отсчета называется движением по инерции.

При таком движении вектор скорости материальной точки остается постоянным ( = const ). Покой точки является частным   случаем движения по  инерции ( =0).

В инерциальных системах отсчета покой или равномерное движение представляет собой естественное состояние, а динамика должна объяснить изменение этого состояния (т.е. появление уско­рения тела под действием сил).

Свободных тел, не подверженных воздействию со стороны других тел не существует.

Однако, благо­даря убыванию всех: известных взаимодействий с увеличением рас­стояния, такое тело можно реализовать с любой требуемой, точ­ностью.

Системы отсчета, в которых свободное тело не сохраняет ско­рость движения неизменной, называются неинерциальными. Неинерциальной является система отсчета, движущаяся с ускорением отно­сительно любой инерциальной системы отсчета. В неинерциальной системе отсчета даже свободное тело может двигаться с ускорением.

Равномерное и прямолинейное движение системы отсчета не влияет на ход механических явлений, протекающих в ней. Никакие механические опыты не позволяют отличить покой инерциальной системы отсчета от ее равномерного прямолинейного движения.

Для любых механических явлений все инициальные системы отсче­та оказываются равноправными. Эти утверждения выражают меха­нический принцип относительности (принцип относительности Галилея).

Принцип относительности является одним из наиболее об­щих законов природы, в специальной теории относительности он распространяется на электромагнитные и оптические явления.

2) Масса, плотность, сила.

Свойство тела сохранять свою скорость при отсутствии взаимодействия с другими телами называется инертностью. Физическая величина, являющаяся мерой инертности тела в поступательном движении, называется инертной массой.

Масса тела измеряется в килограммах: . Масса характеризует также  способность тела взаимодействовать с другими телами в соответствии с законом всемирного тяготения.

В этих случаях масса выступает как мера гравитации и ее называют гравитационной массой.

В современной физике с высокой степенью точности доказана тождественность значений инертной и гравитационной масс данно­го тела. Поэтому говорят просто о массе тела (m ).

• В механике Ньютона считается, что
• а) масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит;
• б)  для данной совокупности тел выполняется закон сохранения массы: при любых процессах, происходящих в системе тел, ее масса остается неизменной.

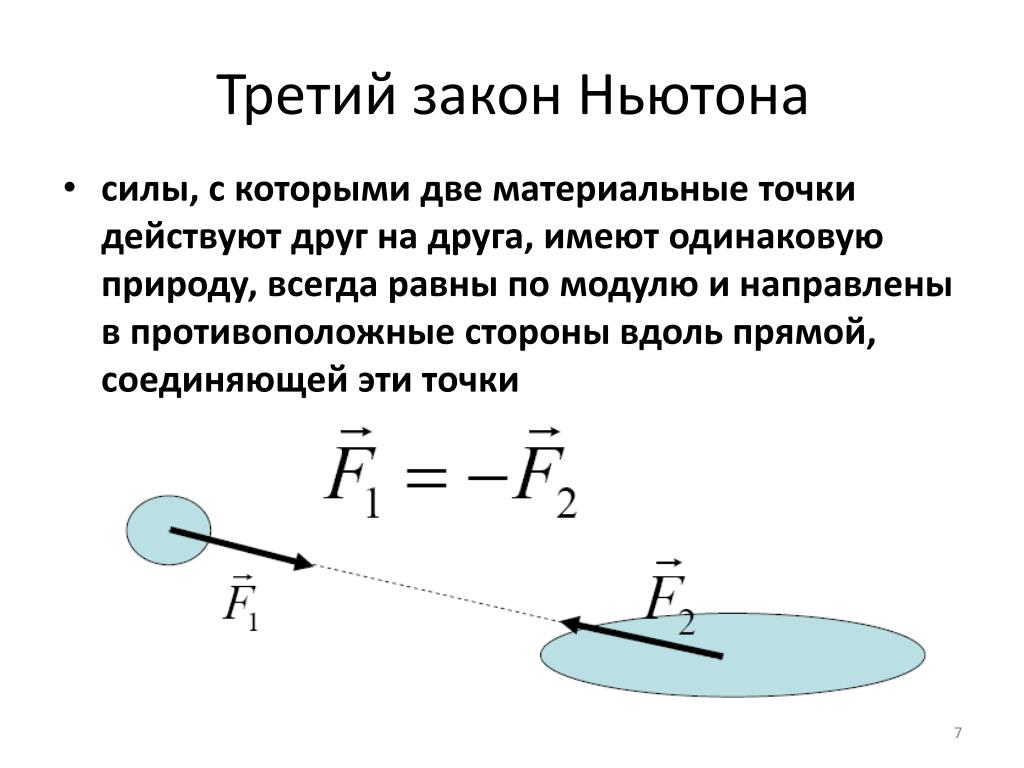
Плотность однородного тела равна . Единица плотности 1 кг/м3.

Силой называется векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей. Сила полностью определена, если заданы ее модуль, направление и точка приложения. Прямая,  вдоль которой направ­лена сила, называется линией действия силы.

В результате действия силы тело изменяет скорость движения (приобретает ускорение) или деформируется. На основании этих опытных фактов производится измерение сил.

Сила является причиной возникновения не скорости, а ускорения тела. С направлением силы совпадает во всех случаях направление ускорения, но не скорости.

В задачах механики учитываются гравитационные силы (силы тяготения) и две разновидности электромагнитных сил — силы упру­гости и силы трения.

3) Второй закон Ньютона

Второй закон Ньютона описывает движение частицы, вызванное влиянием окружающих тел, и устанавливает связь между ускорением частицы, ее массой и силой, с которой на нее действуют эти тела:

Если на частицу с массой т окружающие тела действуют с силой , то эта частица приобретает такое ускорение , что произведение ее массы на ускорение будет равно действующей силе.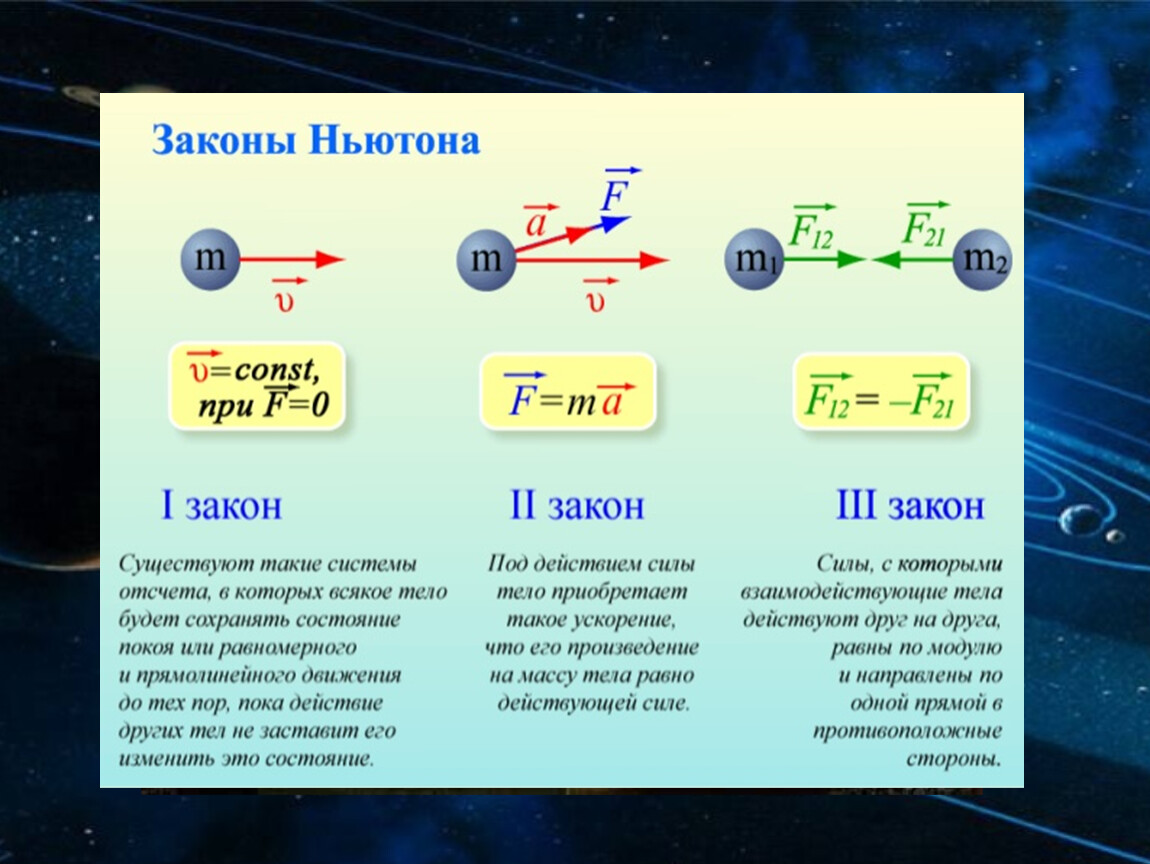 Математически второй закон Ньютона записывается в виде:

На основе этого закона устанавливается единица силы — 1 Н (нью­тон). 1 Н — это сила, с которой нужно действовать на тело массой 1 кг, чтобы сообщить ему ускорение 1 м/с2.

Если сила , с которой тела действуют на данную частицу, из­вестна, то записанное для этой частицы уравнение второго закона Ньютона называют ее уравнением движения.

Второй закон Ньютона часто называют основным законом дина­мики, так как именно в нем находит наиболее полное математическое выражение принцип причинности и именно он, наконец, позволяет решить основную задачу механики.

Для этого нужно выяснить, какие из окружающих частицу тел оказывают на нее существенное действие, и, выразив каждое из этих действий в виде соответствующей силы, следует составить уравнение движения данной частицы.

Из уравнения движения (при известной массе) находится ускорение частицы. Зная

же ускорение можно определить ее скорость, а после скорости — и положение данной частицы в любой момент времени.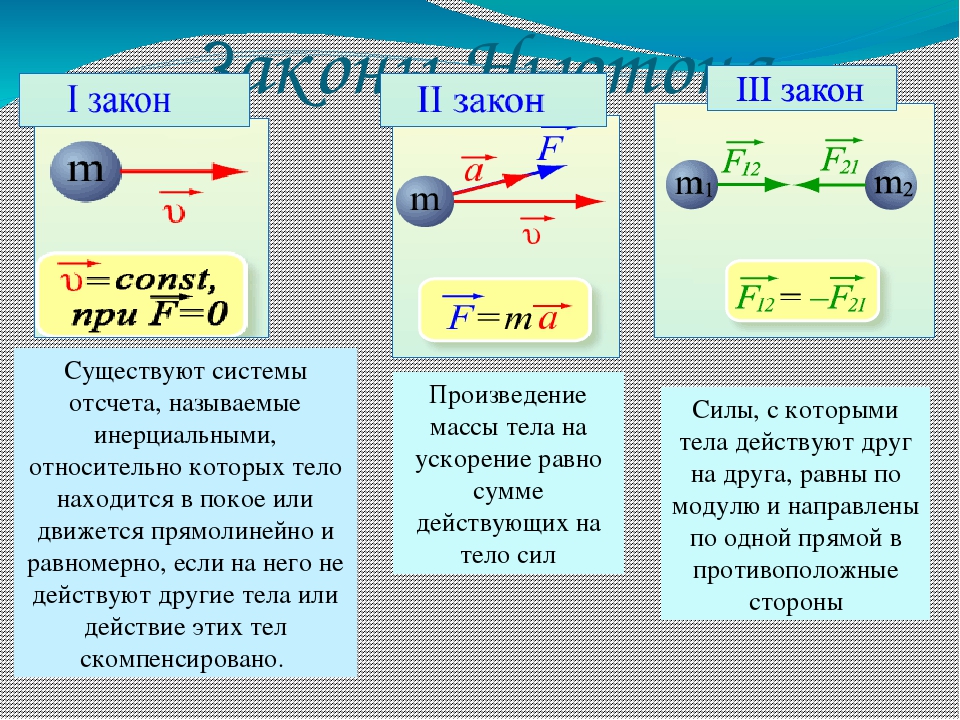

Практика показывает, что решение основной задачи механики с помощью второго закона Ньютона всегда приводит к правильным результатам. Это и является экспериментальным подтверждением справедливости вто­рого закона Ньютона.

4) Третий закон Ньютона.

Третий закон Ньютона: Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.

Это означает, что если на тело А со стороны тела В действует сила ,  то одновременно на тело В со стороны тела А будет действовать сила , причем используя второй закон Ньютона, можно  записать:

Отсюда следует, что т. е. отношение модулей ускорений  и взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил. Более массивное тело получает меньшее ускорение, а легкое — большее.

Важно понимать, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому они не могут уравновешивать друг друга.

5) Следствия из законов Ньютона

Законы Ньютона представляют собой систему взаимосвязанных законов, которые позволяют глубже понять сущность понятий силы и массы.  Следствия из законов:

1. Сила является мерой воздействия, оказываемого на данную частицу со стороны других тел, и с увеличением расстояния до них убывает, стремясь к нулю.

То, что сила является мерой воздействия со стороны окружающих частику тел, следует из того, что она зависит от состояния этих тел  и при этом определяет ускорение данной частицы: .

Убывания действующей силы до нуля при неогра­ниченном удалении от частицы окружающих ее тел  является следствием первого и второго законов Ньютона.

Так как, со­гласно первому закону Ньютона, бесконечно удаленная от всех тел

частица имеет нулевое ускорение . Согласно второму закону Нью­тона Поэтому при  и сила .

2. Сила, с которой сразу несколько тел действует на данную частицу, равна сумме сил, с которыми эти тела действуют на нее по отдельности:

Это утверждение  называется принципом  независимости  взаимодействий. С учетом этого принципа второй закон Ньютона записы­вается в виде:

Сумму сил, стоящую в правой части этого закона, называют равнодействующей силой.

Принцип независимости взаимодействий иначе называют принципом суперпозиции сил.

3. Сумма всех внутренних сил, действующих в любой сис­теме, всегда равна нулю.

Под внутренними понимают те силы, которые действуют между телами самой рассматриваемой системы.

Внутренние силы не способны привести в движение систему тел как целое. Действительно, для этого нужно было бы сообщить ускорение, а ускорение, как это следует из второго закона Ньютона, могут сообщить системе лишь те силы, сумма ко­торых отлична от нуля.

4. Отношение модулей ускорений, полученных двумя те­лами в результате взаимодействия друг с другом, равно обратному отношению их масс:

Источник: https://sfiz.ru/materials/mehanika/111

1 2 и 3 закон ньютона – Третий закон Ньютона определение.

Формула третьего закона Ньютона. Третий закон Ньютона, сила

Кратко и понятно о первом, втором и третьем законах Ньютона: формулировки, примеры и формулы

Три закона Ньютона — это основа классической механики. В 1867 году Ньютон опубликовал работу под названием «Математические начала натуральной философии». Там были все знания, накопленные до него другими учёными, а также новые, открытые самим Ньютоном. Его считают одним из самых первых основоположником современной физики. Благодаря систематизированным знаниям, которые были описаны в вышеуказанном труде, он открыл множество законов механики, Закон всемирного тяготения и многое другое.

Кратко о законах Ньютона

Первый закон Ньютона

1. Формулировка. В наше время встречаются несколько формулировок, вот одна из самых современных: «Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно». Этот закон иногда называют Законом инерции.
2. Трактовка. Если описать это утверждение простыми словами, то можно увидеть, что всё достаточно просто: если какое-то тело находится в покое относительно чего-либо, то оно и будет оставаться в покое до тех пор, пока на него не подействует какой-либо предмет. То же самое, если тело движется равномерно прямолинейно, то оно будет продолжать так двигаться, пока на него не подействует какая-либо сила. До Ньютона его открыл Галилео Галилей, но он не совсем точно его описал. Теперь осталось только разобраться, что такое инерциальные системы отсчёта. Проще говоря, это такая система, для которой выполняется Первый закон Ньютона.
3. Пример действия. Представьте себе парашютиста, который движется прямолинейно равномерно к Земле. Это будет продолжаться до тех пор, пока притяжение к поверхности Земли будет компенсироваться сопротивлением воздуха. Если же сопротивление станет меньше либо больше, то тогда на тело начнёт действовать сила притяжения, и оно станет двигаться прямолинейно равноускоренно.
4. История открытия. Существует легенда об открытии этого утверждения. Когда-то Ньютон сидел под деревом, и рядом с ним упало яблоко. Это подтолкнуло его на размышления о том, почему яблоко упало перпендикулярно земле, каковы были причины данного явления. По крайней мере, так описывал этот эпизод знаменитый биограф Уильям Стьюкли.
5. Формулы у него нет.

Это интересно: система отсчета в физике – определение и ее виды.

Второй закон Ньютона

Он описывает поведение тела при действии на него других объектов. Что с ним происходит, как он начинает двигаться и прочее.

1. Формулировка. «В инерциальных системах отсчёта ускорение тела с постоянной массой прямо пропорционально равнодействующей всех сил и обратно пропорционально его массе».
2. Формула. Математическое описание этого утверждения такое: а = F/m, где a — это ускорение, F — равнодействующая всех сил, приложенных к телу, m — масса тела.
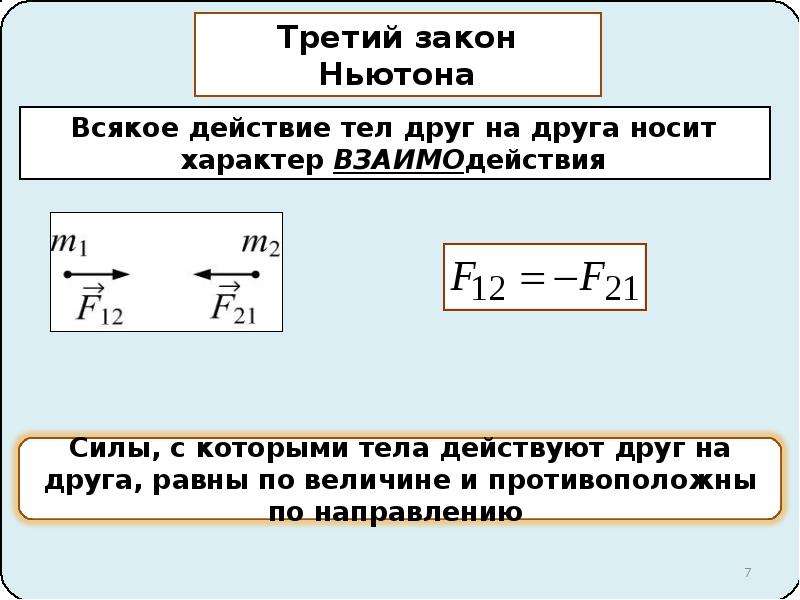
3. Трактовка. Из формулы мы видим, что ускорение тела зависит от силы, приложенной к этому телу, и массы. А также можно увидеть, что чем больше равнодействующая всех сил, то тем больше ускорение, и чем больше масса тела, тем ускорение меньше. Говоря простым языком, если равнодействующая всех сил не равна нулю и не меньше нуля, то выполняется данное утверждение. Можно сказать ещё проще, если на тело действует сила, то оно приобретает ускорение.
4. Пример действия. Возьмём бейсбольную биту и мяч. Если ударить битой по мячу, и удар будет сильнее действия всех других сил, то мяч приобретёт ускорение равное отношению равнодействующей всех сил к массе.

Это интересно: формула всемирного тяготения – определение закона.

Третий закон Ньютона

1. Формулировка. «Тела взаимодействуют друг на друга с силами одинаковой природы, направленными вдоль прямой, которая соединяет центры масс этих тел, а силы равны по модулю и разнонаправленны».
2. Трактовка. Это значит, что на каждое действие есть своё противодействие.
3. Пример действия. Более понятно это можно рассмотреть на таком примере: представьте пушку, из которой стреляют ядром. Ядро будет действовать на пушку с той же силой, с какой пушка вытолкала ядро. Поэтому при выстреле пушка откатится чуть-чуть назад, это происходит из-за того, что размеры пушки и ядра разные. Примерно то же самое происходит и при падении яблока на землю. Земля действует на яблоко с некой силой и яблоко тоже действует на Землю. Только из-за того, что масса Земли в миллионы раз больше яблока этого действия не видно. Еще один пример действия Третьего закона для закрепления усвоенного. Возьмём довольно сложный пример: притяжение планет. Луна вертится вокруг Земли благодаря тому, что она притягивается к Земле, но по Третьему закону Ньютона Луна тоже притягивает Землю к себе. Однако, из-за того, что их массы разные, Луна не может притянуть Землю, но у неё получается вызвать отливы и приливы в морях и океанах.
4. Формула. Математически это утверждение можно записать так: F1 = -F2, где F1 — это сила, с которой первое тело действует на второе, а F2 — сила, с которой второе тело действует на первое.

obrazovanie.guru

Законы ньютона 1 2 3 кратко определение

Они могут узнать его, пользуясь такой «цепочкой». Им известно начальное положение корабля на стартовой площадке и его начальная скорость. Им известны и силы, которые действуют на корабль в любой точке траектории. Пользуясь этими данными, они и решают задачу механики применительно к космическому полету. Но так как силы, действующие на корабль, все время изменяются, то вычисления настолько сложны, что приходится привлекать на помощь вычислительные машины. Мы все время говорили, что основная задача механики — определение положения движущегося тела в любой момент времени.

Он равномерно приближается к земле, когда действие силы тяжести компенсируется силой натяжения строп парашюта, которая в свою очередь обусловлена сопротивлением воздуха. 1 -ая формулировка — ускорение, приобретаемое телом в инерциальной системе отсчета прямо пропорционально действующей на него силе и обратно пропорциональна его массе a = F

1.2. Законы ньютона

1.2.1. Формулировка
законов

До сих
пор мы
пользовались статическим определением
силы, полученным на основе уравновешивания
сил, приложенных к телу, с помощью силы,
возникающей от динамометра. Опыт
показывает, что если сумма всех сил,
приложенных к телу, не равна нулю, то
тело придет в движение. Для изучения
динамических
свойств силы
мы должны обратиться к законам Ньютона.

Первый закон.
Всякое тело продолжает удерживаться в
своем состоянии покоя или равномерного
и прямолинейного движения, пока и
поскольку оно не вынуждается приложенными
силами изменить это состояние. Современную
формулировку этого закона следует
повторить
еще раз:

Существуют такие
системы отсчета, называемые инерциальными,
относительно которых свободное
тело находится
в состоянии покоя или равномерного и
прямолинейного движения.

Второй закон.
Изменение
количества движения пропорционально
приложенной движущей силе и происходит
по направлению той прямой, по которой
действует эта сила.

Третий закон.
Действию
всегда есть равное и противоположное
противодействие, иными словами,
взаимодействия двух тел равны между
собой и направлены в противоположные
стороны.

Определение.
Под
количеством
движения
понимается векторная
величина, равная произведению массы
тела на его скорость

(1.2.1)

где
— масса тела. Мы ввели новую физическую
величину – массу, которую пока точно
не определили. Это мы сделаем в следующем
разделе,
а здесь нам достаточно
обыденного понимания этого понятия.
Строгая формулировка второго закона
имеет следующий вид:

(1.2.2)

Из (1.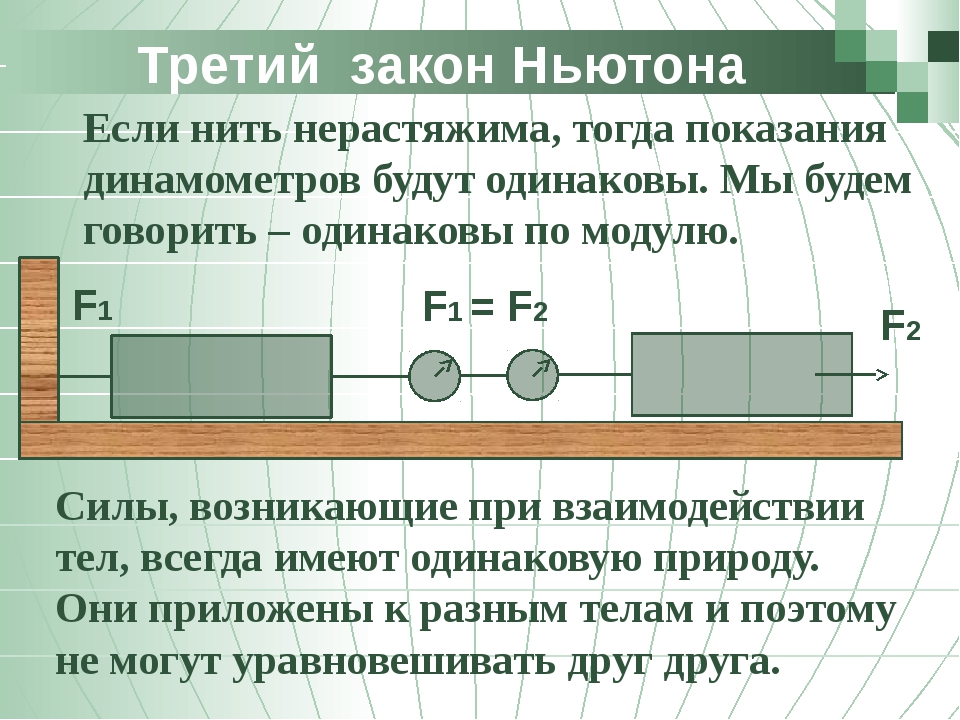 2.2) видно, что
при равенстве суммы сил нулю скорость
тела будет постоянной, т. е. мы приходим
к математической формулировке первого
закона. Однако ни в коей мере нельзя
полагать, что все физическое содержание
первого закона является тривиальным
следствием второго закона. Мы
воспользовались гелиоцентрической
системой отсчета, в которой всякая сила
— есть результат воздействия на данное
тело какого-то другого тела. Чтобы это
было очевидно, рассмотрим следующий
пример.

Пример.
Представьте
себе, что вы находитесь в закрытом вагоне
поезда, идущего плавно по рельсам. К
потолку вагона прикреплен с помощью
нити шарик (рис. 1.2.1). Другой шарик
находится на идеально гладком полу. Вы
наблюдаете, что нить расположена
вертикально относительно пола, другой
шарик покоится на полу. Сами вы чувствуете
себя спокойно. Вдруг вы замечаете, что
нить отклонилась от вертикали, шарик
на полу пришел в движение. Вы же сами
стали испытывать некоторые ощущения
и предпринимаете
определенные усилия, чтобы удержаться
в кресле. С вашей точки зрения (в системе
отсчета, связанной с вагоном) шарик на
полу пришел в движение. Задайте себе
вопрос: если сила, действующая на тело,
есть результат воздействия на это тело
какого-то другого тела, то какое тело
внутри вагона
заставляет шарик двигаться? Какое тело
внутри вагона заставляет шарик на нити
отклониться от вертикали? Сколько
бы ни искали, вы таких тел не найдете.

Рис.
1.2.1. Рассматриваемая экспериментальная
ситуация

В то же время с
точки зрения наблюдателя, находящегося
на платформе, все обстоит достаточно
просто. Он видит (измеряет), что вагон
движется с ускорением и, следовательно,
результирующая сила, действующая на
висящий шарик, должна быть направлена
в сторону ускорения вагона. Именно
поэтому нить и отклонится от положения
равновесия,
а шарик на идеально гладком
полу в этой системе остается неподвижным
относительно наблюдателя на платформе.

Вернемся ко второму
закону Ньютона. В школьном курсе физики
этот закон обычно дается в виде:

studfiles.net

Математические начала натуральной философии»

Ньютон был современником Петра 1 и Людовика XIV. Окончив университет, Ньютон получил ученое звание бакалавра, затем магистра. С 1669 года стал во главе кафедры физики и математики в Кембриджском университете. Внешне жизнь Ньютона протекала спокойно, мирно и однообразно.

Но ее заполняли непрестанный труд, математические изыскания, физические и химические опыты, вызывавшие восхищение его современников.

С высокой степенью точности инерциальной системой считается система отсчета, связанная с Солнцем (гелиоцентрическая). Если рассматриваемое время движения невелико, то инерциальной можно считать систему отсчета, связанную с Землей (геоцентрическая).

Пример. В качестве примера выполнения 1 закона Ньютона можно рассмотреть движение парашютиста (см. рис. 2). Он равномерно приближается

Он утверждает, что существуют такие системы отсчета, в которых любое тело, что не подверглось воздействию внешних сил, сохраняет состояние покоя или прямолинейного равномерного движения.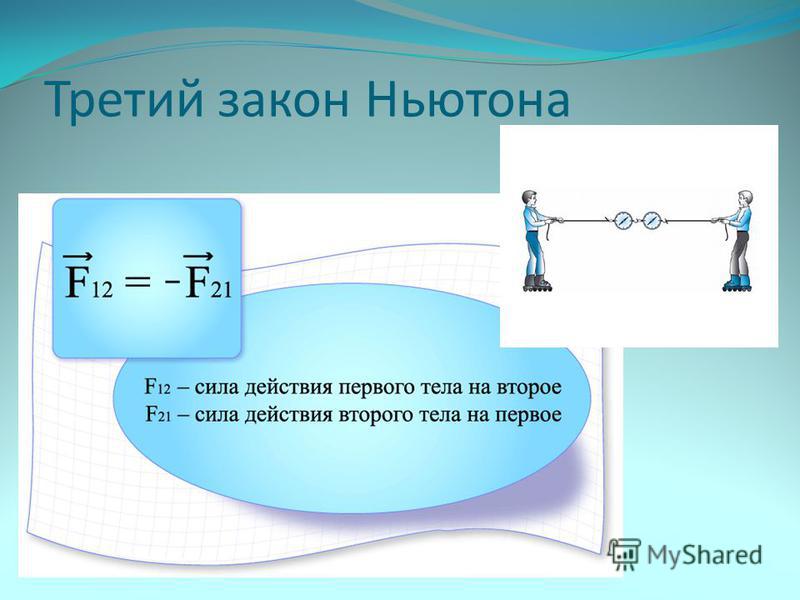 Закон говорит, что в этой же системе любые другие свободные тела должны вести себя абсолютно одинаково.

Состояние покоя или равномерного движения являются вполне равноправными и не требуют объяснения. Любая система, которая находится в поступательном движении, прямолинейно и равномерно по отношению к инерциальной также является инерциальной. Второй закон Ньютона говорит, что причиной изменения скорости тел, которые находятся в состоянии равномерного движения, может изменить свою скорость только при воздействии посторонних тел.

Второй и третий законы Ньютона

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: законы динамики, сила, принцип суперпозиции сил, второй закон Ньютона, третий закон Ньютона.

Взаимодействие тел можно описывать с помощью понятия силы. Сила – это векторная величина, являющаяся мерой воздействия одного тела на другое.

Будучи вектором, сила характеризуется модулем (абсолютной величиной) и направлением в пространстве. Кроме того, важна точка приложения силы: одна и та же по модулю и направлению сила, приложенная в разных точках тела, может оказывать различное воздействие. Так, если взяться за обод велосипедного колеса и потянуть по касательной к ободу, то колесо начнёт вращаться. Если же тянуть вдоль радиуса, никакого вращения не будет.

Принцип суперпозиции.

 

Опыт показывает, что если на данное тело действуют несколько других тел, то соответствующие силы складываются как векторы. Более точно, справедлив принцип суперпозиции.
Принцип суперпозиции сил. Пусть на тело действуют силы . Если заменить их одной силой то результат воздействия не изменится.

Сила называется равнодействующей сил .

Второй закон Ньютона.

 

Если равнодействующая сил, приложенных к телу, равна нулю (то есть воздействия других тел компенсируют друг друга), то в силу первого закона Ньютона найдутся такие системы отсчёта (называемые инерциальными), в которых движение тела будет равномерным и прямолинейным. Но если равнодействующая не обращается в нуль, то в инерциальной системе отсчёта у тела появится ускорение.
Количественную связь между ускорением и силой даёт второй закон Ньютона.

Второй закон Ньютона. Произведение массы тела на вектор ускорения есть равнодействующая всех сил, приложенных к телу: .

Подчеркнём, что второй закон Ньютона связывает векторы ускорения и силы. Это означает, что справедливы следующие утверждения.

1. , где – модуль ускорения, – модуль равнодействующей силы.

2. Вектор ускорения сонаправлен с вектором равнодействующей силы, так как масса тела положительна.

Например, если тело равномерно движется по окружности, то его ускорение направлено к центру окружности. Стало быть, к центру окружности направлена и равнодействующая всех сил, приложенных к телу. Второй закон Ньютона справедлив не в любой системе отсчёта. Вспомним шатающегося наблюдателя ( Первый закон Ньютона ): относительно него дом движется с ускорением, хотя равнодействующая всех сил, приложенных к дому, равна нулю. Второй закон Ньютона выполняется лишь в инерциальных системах отсчёта, факт существования которых устанавливается первым законом Ньютона.

Третий закон Ньютона.

 

Опыт показывает, что если тело А действует на тело В, то и тело В действует на тело А. Количественную связь между действиями тел друг на друга даёт третий закон Ньютона (“действие равно противодействию”).

Третий закон Ньютона. Два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.

Например, если карандаш действует на стол с силой , направленной вниз, то стол действует на карандаш с силой , направленной вверх (рис. 1). Эти силы равны по абсолютной величине.

Рис. 1.

 

Силы и , как видим, приложены к разным телам и поэтому не могут уравновешивать друг друга (нет смысла говорить об их равнодействующей).
Третий закон Ньютона, как и второй, справедлив только в инерциальных системах отсчёта.
Механика, основанная на законах Ньютона, называется классической механикой. Классическая механика, однако, имеет ограниченную область применимости. В рамках классической механики хорошо описывается движение не очень маленьких тел с не очень большими скоростями. При описании атомов и элементарных частиц на замену классической механике приходит квантовая механика. Движение объектов со скоростями, близкими к скорости света, происходит по законам теории относительности.

 

Сила. Три закона Ньютона | LAMPA

Три закона Ньютона

Три закона Ньютона определяют “правила жизни” в механике. Обычно в школе их излагают в прямой последовательности — от первого закона к третьему. Мы поступим по-другому. Мы изложим их в обратном порядке. Нам кажется, что так будет понятнее. Приступим.

Третий закон Ньютона. Попробуйте надавить рукой на стол. При этом ладонью своей руки вы почувствуете поверхность стола. И вы также почувствуете некоторое сопротивление со стороны стола. Будто и сам стол давит на вас. При этом, если бы вы не давили на стол, а держали руку неподвижно, а поверхность стола приближалась бы к вашей руке и сама давила на вашу руку, то ощущения были бы точно такими же.

Можно предположить, что когда тело А воздействует на другое тело — тело B (например, вы действуете на стол), — то и тело B действует на тело А.

Рассмотрим другой пример. Девочка А и девочка B стоят на коньках на льду. Девочка А начинает толкать девочку B. Наш жизненный опыт подсказывает нам, что девочка B будет двигаться в ту сторону, куда ее толкает девочка А. Но! Жизненный опыт нам подсказывает, что и девочка А начнет двигаться так, будто ее толкнула девочка B.

Это подтверждает нашу догадку, что когда тело А действует с некоторой силой на тело B, то и тело B действует на тело А.

Оказывается, что наше предположение — верное. Более того, силы, с которыми тела действуют друг на друга, одинаковые (!).

Итак, третий закон Ньютона звучит следующим образом:

Силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению: F⃗1→2=−F⃗2→1.\vec{F}_{1\to 2}=-\vec{F}_{2\to 1}{.}F⃗1→2​=−F⃗2→1​.

Второй закон Ньютона. Представьте себе ситуацию: на столе неподвижно стоит мячик. Мы толкаем его, то есть мы действуем силой. При этом мячик начинает двигаться. Значит, у него появилась скорость.

Итак, сначала мячик покоился и у него была нулевая скорость: V1=0V_1=0V1​=0. А затем мячик двигался, и его скорость была уже не нулевой: V2≠0V_2\neq 0V2​≠0. То есть скорость изменилась (!). У нас есть изменение скорости. А это значит, что есть ускорение.

Итак, можно сделать вывод, что сила придает телу ускорение, она “создает” ускорение тела. Логично будет предположить, что бОльшая сила даст мячику бОльшее ускорение: ускорение тела тем больше, чем больше сила. Но это еще не все.

Возьмем два мячика: легкий шарик для пинг-понга и тяжелый железный шарик из подшипника. Подействуем на них одинаковой силой. Оба они получат ускорение. Но ускорение будет разное. Это подсказывает нам жизненный опыт.

Более тяжелый (массивный, с большей массой) стальной шарик получит небольшую скорость; его ускорение будет небольшим.

Легкий (с меньшей массой) шарик для пинг-понга получит большую скорость; ускорение у него будет большим.

Само собой у нас получилось ввести некоторую величину — массу mmm. Получается, что масса показывает, насколько неохотно тело изменяет свою скорость. Если масса тела велика, то ускорение тела — мало. То есть, если величина силы неизменна (сила зафиксирована по величине), то чем больше масса — тем меньше ускорение, которое получает тело.

Взаимодействие тел — определение, характеристика, примеры

Масса, объем и плотность

Масса

Как ни странно, начнем мы с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.

В Международном бюро мер и весов в Париже есть цилиндр массой один килограмм. Материал этого цилиндра — сплав иридия и платины. Его масса равна одному килограмму, и этот цилиндр — эталон для всего мира.

Высота этого цилиндра приблизительно равна 4 см, но чтобы его поднять, нужно приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.

Второй закон Ньютона F — сила, действующая на тело (равнодействующая) [Н] m — масса [кг] a — ускорение [м/с2]

В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.

Закон Всемирного тяготения F = GMm/R2 F — сила [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне.

Откуда берется масса

Физики убеждены, что у элементарных частиц должна быть масса. Например, доказано, что у электронов масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.

А еще Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не было бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.

Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.

Источник: Википедия

Бозон Хиггса невозможно представить — это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.

Объем тела

Масса зависит от двух величин: плотности и объема. Начнем с известной нам из математики величины — с объема.

• Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Уметь соотносить объемы — важный навык. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.

А если вернуться к задачкам, то чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.

Вычисляем объем по формуле:

Формула объема параллелепипеда V = a*b*c V — объем [м^3] a — длина [м] b — ширина [м] c — высота [м]

А для цилиндра будет справедлива такая формула:

Формула объема цилиндра V = S*h V — объем [м^3] S — площадь основания [м^2] h — высота [м]

Плотность вещества

Плотность — скалярная физическая величина. 3]

Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.

Маленькое исключение С водой такая история не работает: плотность воды меньше плотности льда. Объяснение кроется в молекулярной структуре льда. Когда вода переходит из жидкого состояния в твердое, она изменяет молекулярную структуру так, что расстояние между молекулами увеличивается. Соответственно, плотность льда меньше плотности воды.

Ниже представлены значения плотностей для разных веществ — это поможет при решении задач по физике:

Твердое вещество	кг/м3	г/см3
Платина	21500	21,5
Золото	19300	19,3
Вольфрам	19000	19,0
Свинец	11400	11,4
Серебро	10500	10,5
Медь	8900	8,9
Никель	8800	8,8
Латунь	8500	8,5
Сталь, железо	7900	7,9
Олово	7300	7,3
Цинк	7100	7,1
Чугун	7000	7,0
Алмаз	3500	3,5
Алюминий	2700	2,7
Мрамор	2700	2,7
Гранит	2600	2,6
Стекло	2600	2,6
Бетон	2200	2,2
Графит	2200	2,2
Лёд	900	0,9
Парафин	900	0,9
Дуб (сухой)	700	0,7
Берёза (сухая)	650	0,65
Пробка	200	0,2
Платиноиридиевый сплав	21500	21,5

Жидкость	кг/м3	г/см3
Ртуть	13600	13,6
Мёд	1300	1,3
Глицерин	1260	1,26
Молоко	1036	1,036
Морская вода	1030	1,03
Вода	1000	1
Подсолнечное масло	920	0,92
Нефть	820	0,82
Спирт	800	0,8
Бензин	700	0,7

Газ	кг/м3
Хлор	3,22
Озон	2,14
Пропан	2,02
Диоксид углерода	1,98
Кислород	1,43
Воздух	1,29
Азот	1,25
Гелий	0,18
Водород	0,09

Где самая большая плотность? Самая большая плотность во Вселенной — в черной дыре. Плотность черной дыры составляет около 1014 кг/м3.

Средняя плотность

В школьном курсе чаще всего говорят о средней плотности тела. Дело в том, что если мы рассмотрим какое-нибудь неоднородное тело, то в одной его части будет, например, большая плотность, а в другой — меньшая.

Если вы когда-то делали ремонт, то знакомы с такой вещью, как цемент. Он состоит из двух веществ: клинкера и гипса. Чтобы найти плотность цемента, можно сделать так: отдельно найти плотность гипса, плотность клинкера по формуле выше, а потом найти среднее арифметическое двух плотностей.

А можно просто массу цемента разделить на объем цемента и мы получим ровно то же самое. Просто в данном случае мы берем не массу и объем вещества, а массу и объем тела.

Формула плотности тела р — плотность тела [кг/м^3] m — масса тела [кг] V — объем тела [м^3]

Инертность

Масса придает телу такое свойство, как инертность. Но не напрямую — у этого есть некая последовательность. Если посмотреть, как строитель толкает тачку или родитель везет ребенка на санках — можно заметить, что и тачка, и санки, изменяют свою скорость только при наличии нескомпенсированного действия — силы, которую прикладывают и строитель, и родитель.

Так как быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела.

Давайте вернемся к нашим строителям и родителям. Если строитель приложит к тачке ту же силу, что и родитель, то ускорение не обязательно будет одинаковым.

Чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело.

• Инертность — это свойство тела сохранять свою скорость постоянной. Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным.

Например, движущийся по дороге автомобиль не может мгновенно остановиться — для уменьшения скорости требуется некоторое время.

Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение. Эту закономерность описывает второй закон Ньютона.

Второй закон Ньютона

Мы уже упоминали его в начале статьи, давайте разберемся подробнее.

Второй закон Ньютона F — сила, действующая на тело (равнодействующая) [Н] m — масса [кг] a — ускорение [м/с2]

В этом законе есть такое понятие, как равнодействующая сила. Часто можно встретить, что она обозначается не буквой F, а буквой R. Равнодействующая является векторной суммой всех сил, приложенных к телу.

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина тому — сила.

• Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

А в чем разница между инертностью и инерцией? Инертность — это свойство тело, инерция — явление сохранения скорости тела.

Первый закон Ньютона

Понятие «инерция» сформулировали отдельно друг от друга Галилео Галилей и Исаак Ньютон:

	Галилео Галилей	Исаак Ньютон
Формулировка закона инерции	Когда тело движется по горизонтальной поверхности, не встречая никакого сопротивления движению, то его движение — равномерно, и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца.	Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние.
Определение инерции	Инерция — это физическое явление, при котором тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела.	Инерция – это физическое явление сохранения скорости тела постоянной, если на него не действуют другие тела или их действие скомпенсировано.

Варианты формулировки не противоречат друг другу и говорят, по сути, об одном и том же, просто разными словами — выбирайте ту, что вам нравится больше.

Ньютоновская формулировка закона инерции по-другому называется первым законом Ньютона:

Существуют такие системы отсчета, относительно которых тело сохраняет свою скорость постоянной, в том числе равной нулю, если действие на него других сил отсутствует или скомпенсировано.

Первый закон Ньютона -> R = 0, если v=const R — результирующая сила, сумма всех сил, действующих на тело [Н] v — скорость [м/с] const — постоянная величина

А вы небось уже подумали, что мы про первый закон Ньютона забыли и сразу перескочили ко второму. Все в порядке — первый тоже на месте.

В этом законе встречается такое словосочетание, как «система отсчета». Оно изучается в самом начале курса физики, но там это понятие читают в контексте «такие системы отсчета». Напрашивается вопрос: какие такие системы отсчета?

Системы отсчета: инерциальные и неинерциальные

Чтобы описать движение, нам нужны три штуки:

• тело отсчета, относительно которого определяем местоположение других тел;
• система координат: в школьном курсе мы используем прямоугольную декартову систему координат;
• часы, чтобы измерять время.

В совокупности эти три опции образуют систему отсчета:

• Инерциальная система отсчета — система отсчёта, в которой все тела движутся прямолинейно и равномерно, либо покоятся.
• Неинерциальная система отсчета — система отсчёта, движущаяся с ускорением.

Рассмотрим разницу между этими системами отсчета на примере задачи.

Аэростат — летательный аппарат на картиночке ниже — движется равномерно и прямолинейно параллельно горизонтальной дороге, по которой равноускоренно движется автомобиль.

Выберите правильное утверждение:

1) Система отсчёта, связанная с аэростатом, является инерциальной, а система отсчёта, связанная с автомобилем, инерциальной не является.

2) Система отсчёта, связанная с автомобилем, является инерциальной, а система отсчёта, связанная с аэростатом, инерциальной не является.

3) Система отсчёта, связанная с любым из этих тел, является инерциальной.

4) Система отсчёта, связанная с любым из этих тел, не является инерциальной.

Решение:

Система отсчёта, связанная с землёй, инерциальна. Да, планета движется и вращается, но для всех процессов вблизи планеты этим можно пренебречь. Во всех задачах систему отсчета, связанную с землей можно считать инерциальной.

Поскольку система отсчёта, связанная с землёй инерциальна, любая другая система, которая движется относительно земли равномерно и прямолинейно или покоится — по первому закону Ньютона тоже инерциальна.

Движение аэростата удовлетворяет этому условию, так как оно равномерное и прямолинейное, а равноускоренное движение автомобиля — нет. Аэростат — инерциальная система отсчёта, а автомобиль — неинерциальная.

Ответ: 1.

Третий закон Ньютона

Он честно-пречестно последний.

Третий закон Ньютона обобщает огромное количество опытных фактов, которые показывают, что силы — результат взаимодействия тел.

Он формулируется так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще: сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе — можно сказать и так: на каждую силу найдется другая сила 🙈

Третий закон Ньютона F1 = — F2 F1 — сила, с которой первое тело действует на второе [Н] F2 — сила, с которой второе тело действует на первое [Н]

Важный нюанс!

В первом и втором законах Ньютона мы имеем дело с одним телом, а в третьем — с двумя. Это важно учитывать при решении задач.

Законы Ньютона: определения, формулы и примеры из жизни

Законы Ньютона — это законы соотношения между силами, действующими на массивное тело, и движением тела, это их взаимодействие; всего их 3, и впервые их сформулировал английский физик и математик сэр Исаак Ньютон в 1686 году.

Законы Ньютона кратко:

1-й закон Ньютона: закон инерции — если на тело не действуют внешние силы, то покоящееся тело будет оставаться в покое, а движущееся тело останется в равномерном движении по прямой.

2-й закон Ньютона: основной закон динамики — существует связь между силой, которая действует на тело и ускорением (тело приобретает ускорение из-за действующей на него силы, т.е. F = m × a).

3-й закон Ньютона: закон равенства действия и противодействия — на каждое действие существует равное и противоположное противодействие.

Сила — это мера взаимодействия тел и измеряется в ньютонах (Н; единица измерения 1 Н = 1 кг·м/с²). Ньютон — это интенсивность силы, приложенная к частице массой 1 кг, вызывающая ускорение 1 метр в секунду в секунду, т.е. 1 м/с².

Первый закон Ньютона: закон инерции

Определение

Если на тело не действуют внешние силы, то покоящееся тело будет оставаться в покое, а движущееся тело останется в равномерном движении по прямой.

Этот закон также используется как определение инерции.

Если на объект не действует внешняя сила, то его скорость будет постоянной. Если скорость будет нулевой, то и объект не сдвинется с места. Если будет существовать внешняя сила, из-за этой силы его скорость изменится.

Имеется в виду, что вещи не останавливаются, не начинают двигаться сами по себе и не меняют направление без силы, которая действует на них извне, что и вызывает такие изменения их движений.

Например, при игре в футбол мяч полетит в ту сторону, куда игрок его пнёт. Так, объект, на который действует сила, может изменить свою скорость и направление. Когда мяч попадает в ворота, другая сила (сила сетки ворот) действует на него, останавливая.

Другое определение инерции:

Инерция — это свойство тел, заставляющее их сопротивляться изменениям скорости и/или направления.

Формулы первого закона Ньютона не существует.

Второй закон Ньютона: основной закон динамики

Определение

Существует связь между силой (F), которая действует на тело (массы m), и ускорением (a). Тело приобретает ускорение из-за действующей на него силы.

Пример:

Например, если взять два круглых предмета разной массы и ударить по ним битой (на картинке — бейсбольный мяч и шар для боулинга) с одинаковой силой, то результат будет разный.

Поскольку у них разная масса, то при ударе с одинаковой силой они будут перемещаться на разное расстояние и с разной скоростью. Если увеличится сила удара по тому же бейсбольному мячу, то результат тоже изменится — он улетит дальше.

Насколько объект ускоряется (a), зависит от массы тела (m) и силы, приложенной к нему (F).

Например, воздействие силы (F) 15 Н (Ньютонов) на бейсбольный мяч (массой m1) будет намного больше, чем та же самая сила, действующая на шар для боулинга (массой m2).

Формула

или

Где:

F — сила, приложенная к телу (в Н)

m — масса тела (в кг)

a — ускорение тела (в м/с²)

То есть ускорение (a) прямо пропорционально силе, приложенной к телу (F) и обратно пропорционально массе тела (m). F — это сила, возникающая в результате всех сил, действующих на тело.

Пример использования формулы

Сколько требуется силы для разгона автомобиля массой 1000 кг со скоростью 5 м/с²?

Записываем известные:

m = 1000 кг

a = 5 м/с²

Решение:

Используем эту формулу

F = 1000 кг × 5 м/с² = 5000 Н

Ответ: сила, необходимая для разгона автомобиля массой 1000 кг со скоростью 5 м/с², составляет 5000 Ньютонов.

Третий закон Ньютона: закон равенства действия и противодействия

Определение

На каждое действие существует равное и противоположное противодействие/реакция.

Имеется в виду, что на каждую силу действия, приложенную к телу, возникает другая сила противодействия в другом теле, и эта сила (реакции/противодействия) имеет ту же интенсивность, что и сила действия, но она действует в противоположном направлении. Так, парами, эти силы появляются и компенсируют друг друга.

Пример:

Действие — это сила стопы атлета на земле, а сила противодействия заключается в том, что земля отталкивает тело в противоположном направлении.
Таким образом, 3 закон Ньютона объясняет то, как мы можем бегать и ходить по земле. Другой пример: когда каратист ударяет по боксёрской груше, она “ударяет” каратиста с той же силой, и это понятно по тому, как у него болит от этого удара нога.

Формула

Для постоянной массы тела справедлива следующая формула:

Где:

F1 — сила действия первого тела на второе;

F2 — сила действия второго тела на первое.

Эта формула означает, что взаимодействие двух тел даёт пару сил F1 и F2, которые:

• взаимодействуют друг с другом;
• равняются по модулю;
• ориентированы в противоположные направления вдоль прямой, которая совмещает эти два тела.

Узнайте также про Закон сохранения энергии, Ускорение свободного падения и Силу Архимеда.

5.6: Третий закон Ньютона – Physics LibreTexts

Цели обучения

• Третий закон движения Ньютона
• Определение сил действия и противодействия в различных ситуациях
• Применять третий закон Ньютона для определения систем и решения проблем движения

До сих пор мы рассматривали силу как толчок или тягу; однако, если вы подумаете об этом, вы поймете, что никакие толчки или тяги никогда не возникают сами по себе. Когда вы толкаете стену, стена давит на вас.Это подводит нас к третьему закону Ньютона.

Третий закон движения Ньютона

Каждый раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает. Математически, если тело A оказывает силу \ (\ vec {F} \) на тело B, то B одновременно оказывает силу \ (- \ vec {F} \) на A, или в форме векторного уравнения,

\ [\ vec {F} _ {AB} = – \ vec {F} _ {BA} \ ldotp \ label {5.10} \]

Третий закон Ньютона представляет собой определенную симметрию в природе: силы всегда возникают парами, и одно тело не может воздействовать на другое, не испытав силы.Мы иногда в общих чертах называем этот закон «действием-противодействием», где приложенная сила – это действие, а сила, испытываемая как следствие, – это противодействие. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.

Мы легко можем увидеть в действии третий закон Ньютона, взглянув на то, как люди передвигаются. Представьте себе пловца, отталкивающегося от края бассейна (рисунок \ (\ PageIndex {1} \)). Она отталкивается ногами о стену бассейна и ускоряется в направлении, противоположном ее толчку.Стена оказала на пловца равную и противоположную силу. Вы можете подумать, что две равные и противоположные силы уравновешиваются, но они не равны , потому что они действуют на разные системы . В этом случае мы можем исследовать две системы: пловец и стенку. Если мы выберем пловца в качестве интересующей системы, как на рисунке, тогда стена F _{на стопах} является внешней силой для этой системы и влияет на ее движение. Пловец движется в направлении этой силы.Напротив, сила F _{футов на стене} действует на стену, а не на нашу интересующую систему. Таким образом, F _{футов на стене} не влияет напрямую на движение системы и не отменяет F _{на стене на ногах} . Пловец толкает в направлении, противоположном тому, в котором она хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении. В диаграмме свободного тела, такой как показанная на рисунке \ (\ PageIndex {1} \), мы никогда не включаем обе силы пары действие-противодействие; в этом случае мы используем только стену F _{на ножках} , а не F _{футов на стене} .

Рисунок \ (\ PageIndex {1} \): Когда пловец воздействует на стену, она ускоряется в противоположном направлении; Другими словами, чистая внешняя сила, действующая на нее, действует в направлении, противоположном F _{футов на стене} . Это противодействие возникает потому, что в соответствии с третьим законом Ньютона стена оказывает на пловца силу F _{wall на ступнях} , равную по величине, но в направлении, противоположном тому, которое она оказывает на нее. Линия вокруг пловца указывает на интересующую его систему.Таким образом, диаграмма свободного тела показывает только F _{, стенка} , _{на ступнях,} , w (сила тяжести) и BF, которая представляет собой выталкивающую силу воды, поддерживающую вес пловца. Вертикальные силы w и BF компенсируются, потому что нет вертикального ускорения.

Легко найти другие примеры третьего закона Ньютона:

• Когда профессор ходит перед доской, он прикладывает силу назад к полу. Пол оказывает на профессора противодействующую силу, которая заставляет его ускоряться.
• Автомобиль ускоряется вперед, потому что земля толкает ведущие колеса вперед в ответ на движение ведущих колес по земле. Вы можете увидеть свидетельство того, что колеса отталкиваются назад, когда шины вращаются на гравийной дороге и отбрасывают камни назад.
• Ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большое обратное усилие на газ в камере сгорания ракеты; следовательно, газ оказывает на ракету большую реактивную силу.Эта сила реакции, которая толкает тело вперед в ответ на силу, направленную назад, называется тягой и . Распространенное заблуждение, что ракеты движутся сами по себе, толкаясь о землю или воздух позади них. На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы.
• Вертолеты создают подъемную силу, выталкивая воздух вниз, тем самым испытывая восходящую силу реакции.
• Птицы и самолеты также летают, воздействуя на воздух силой в направлении, противоположном той силы, которая им нужна.Например, крылья птицы заставляют воздух двигаться вниз и назад, чтобы подняться и двигаться вперед.
• Осьминог движется по воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу.
• Когда человек тянет вниз по вертикальной веревке, веревка тянет человека вверх (рисунок \ (\ PageIndex {2} \)).

Рисунок \ (\ PageIndex {2} \): Когда альпинист тянет вниз веревку, веревка тянет вверх альпиниста.

Есть две важные особенности третьего закона Ньютона.Во-первых, прилагаемые силы (действие и противодействие) всегда равны по величине, но противоположны по направлению. Во-вторых, эти силы действуют на разные тела или системы: сила A действует на B, а сила B действует на A. Другими словами, эти две силы представляют собой разные силы, которые не действуют на одно и то же тело. Таким образом, они не отменяют друг друга.

Для ситуации, показанной на рисунке 5.2.5, третий закон указывает, что, поскольку стул толкает мальчика вверх с силой \ (\ vec {C} \), он толкает стул вниз с силой \ (- \ vec {C} \).Точно так же он толкает вниз с силами \ (- \ vec {F} \) и \ (- \ vec {T} \) на пол и стол, соответственно. Наконец, поскольку Земля тянет мальчика вниз с силой \ (\ vec {w} \), он тянет вверх на Землю с силой \ (- \ vec {w} \). Если бы этот ученик в отчаянии сердито ударил по столу, он быстро усвоил бы болезненный урок (которого можно избежать, изучая законы Ньютона), что стол не менее сильно ударяет по столу.

Человек, идущий или бегущий, инстинктивно применяет третий закон Ньютона.Например, бегун на Рисунке \ (\ PageIndex {3} \) толкает назад по земле так, что толкает его вперед.

Рисунок \ (\ PageIndex {3} \): бегун подчиняется третьему закону Ньютона. (а) Бегун прилагает силу к земле. (b) Сила реакции земли на бегуна толкает его вперед.

Пример 5.9: Силы на неподвижном объекте

Пакет на рисунке \ (\ PageIndex {4} \) находится на шкале. Силы на упаковке следующие: \ (\ vec {S} \), что связано с масштабом, и \ (- \ vec {w} \), что связано с гравитационным полем Земли.Силы реакции, которые оказывает пакет, равны \ (- \ vec {S} \) в масштабе и \ (\ vec {w} \) на Земле. Поскольку пакет не ускоряется, применение второго закона дает

\ [\ vec {S} – \ vec {w} = m \ vec {a} = \ vec {0}, \]

т.

\ [\ vec {S} = \ vec {w} \ ldotp \]

Таким образом, показания весов показывают величину веса упаковки. Однако весы не измеряют вес упаковки; он измеряет силу \ (- \ vec {S} \) на своей поверхности. Если система ускоряется, \ (\ vec {S} \) и \ (- \ vec {w} \) не будут равны, как объясняется в разделе «Применение законов Ньютона».

Рисунок \ (\ PageIndex {4} \): (a) Силы, действующие на пакет, лежащий на весах, вместе с их силами реакции. Сила \ (\ vec {w} \) – это вес упаковки (сила, вызванная гравитацией Земли), а \ (\ vec {S} \) – это сила весов на упаковке. (b) Изоляция системы «пакет-масштаб» и системы «пакет-Земля» делает ясными пары действия и реакции.

Пример 5.10: Быстрое освоение: выбор правильной системы

Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал (рис. \ (\ PageIndex {5} \)).Ее масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Вычислите ускорение, возникающее, когда профессор прикладывает к полу силу 150 Н. Все силы, противодействующие движению, такие как трение колес тележки и сопротивление воздуха, составляют 24,0 Н.

Рисунок \ (\ PageIndex {5} \): Профессор толкает тележку со своим демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (кроме \ (\ vec {f} \), потому что они слишком малы для масштабирования).Система 1 подходит для этого примера, потому что она запрашивает ускорение всей группы объектов. Только \ (\ vec {F} _ {floor} \) и \ (\ vec {f} \) являются внешними силами, действующими на Систему 1 вдоль линии движения. Все остальные силы либо отменяют, либо действуют во внешнем мире. Система 2 выбрана для следующего примера, так что \ (\ vec {F} _ {prof} \) является внешней силой и входит во второй закон Ньютона. Диаграммы свободного тела, которые служат основой второго закона Ньютона, меняются в зависимости от выбранной системы.

Стратегия

Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на рисунке \ (\ PageIndex {5} \). Профессор отталкивается назад с силой F _{, фут} , равной 150 Н. Согласно третьему закону Ньютона, пол оказывает прямое противодействие F _пол , равное 150 Н. Система 1. Поскольку все движения горизонтальны, мы можем предположить, что нет чистой силы в вертикальном направлении. Следовательно, задача одномерная по горизонтали.Как уже отмечалось, трение f противодействует движению и, таким образом, находится в противоположном направлении от пола F _{. Мы не включаем силы F prof или F cart , потому что это внутренние силы, и мы не включаем F foot , потому что они действуют на пол, а не на систему. Никаких других значительных сил, действующих на Систему 1. Если чистая внешняя сила может быть найдена из всей этой информации, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение. См. Диаграмму свободного тела на рисунке.}

Решение

Второй закон Ньютона дает

\ [a = \ frac {F_ {net}} {m} \ ldotp \]

Чистая внешняя сила в Системе 1 выводится из рисунка \ (\ PageIndex {5} \), а из предыдущего обсуждения –

.

\ [F_ {net} = F_ {floor} – f = 150 \; N – 24,0 \; N = 126 \; N \ ldotp \]

Масса Системы 1

\ [m = (65,0 + 12,0 + 7,0) \; кг = 84 \; кг \ лдотп \]

Эти значения F _net и m дают ускорение

.

\ [a = \ frac {F_ {net}} {m} = \ frac {126 \; N} {84 \; кг} = 1.{2} \ ldotp \]

Значение

Ни одно из сил между компонентами Системы 1, например, между руками профессора и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это состоит в том, что силы между компонентами системы отменяются. потому что они равны по величине и противоположны по направлению. Например, сила, прилагаемая профессором к тележке, приводит к тому, что на профессора действует равная и противоположная сила.В этом случае обе силы действуют на одну и ту же систему и, следовательно, отменяются. Таким образом, внутренние силы (между компонентами системы) отменяются. Выбор Системы 1 имел решающее значение для решения этой проблемы.

Пример 5.11: Принуждение тележки: выбор новой системы

Рассчитайте силу, которую профессор оказывает на тележку, показанную на рисунке \ (\ PageIndex {5} \), при необходимости используя данные из предыдущего примера.

Стратегия

Если мы определим интересующую систему как тележку плюс оборудование (Система 2 на рисунке \ (\ PageIndex {5} \)), то чистая внешняя сила в Системе 2 – это сила, которую профессор оказывает на тележку за вычетом трения.Сила, которую она оказывает на тележку, F _prof , является внешней силой, действующей на Систему 2. F _prof был внутренним по отношению к Системе 1, но внешним по отношению к Системе 2 и, таким образом, входит во второй закон Ньютона для этой системы.

Решение

Второй закон Ньютона можно использовать для нахождения F _prof . Начнем с

\ [a = \ frac {F_ {net}} {m} \ ldotp \]

Величина чистой внешней силы в Системе 2 составляет

.

\ [F_ {net} = F_ {prof} – f \ ldotp \]

Решаем для F _prof , желаемое количество:

\ [F_ {prof} = F_ {net} + f \ ldotp \]

Значение f дано, поэтому мы должны вычислить чистую F _чистую .{2}) = 29 \; N \ ldotp \]

Теперь мы можем найти желаемую силу:

\ [F_ {prof} = F_ {net} + f = 29 \; N + 24,0 \; N = 53 \; N \ ldotp \]

Значение

Эта сила значительно меньше, чем сила в 150 Н, которую профессор приложил к полу. Не вся сила 150 Н передается на тележку; кое-что ускоряет профессора. Выбор системы – важный аналитический шаг как в решении проблем, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).

Упражнение 5.7

Два блока покоятся и контактируют на поверхности без трения, как показано ниже, с m ₁ = 2,0 кг, m ₂ = 6,0 кг и приложенной силой 24 Н. (a) Найдите ускорение системы блоки. (б) Предположим, что блоки позже разделятся. Какая сила даст второму блоку массой 6,0 кг такое же ускорение, как и система блоков?

Примечание

Просмотрите это видео, чтобы увидеть примеры действий и противодействий.Посмотрите это видео, чтобы увидеть примеры законов Ньютона, а также внутренних и внешних сил.

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

4.4 Третий закон движения Ньютона – Физика

Задачи обучения раздела

К концу этого раздела вы сможете делать следующее:

• Опишите третий закон Ньютона, как словесно, так и математически
• Используйте третий закон Ньютона для решения задач

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:

• (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
  • (D) вычисляет влияние сил на объекты, включая закон инерции, взаимосвязь между силой и ускорением и характер пар сил между объектами.

Раздел Основные термины

Третий закон движения Ньютона

нормальная сила

напряжение

тяга

Описание третьего закона движения Ньютона

Поддержка учителей

Поддержка учителей

[BL] [OL] Просмотрите первый и второй законы Ньютона.

[AL] Начните обсуждение действия и реакции с примеров. Представьте концепции интересующих систем и систем. Объясните, как силы можно классифицировать как внутренние или внешние по отношению к интересующей системе. Приведите примеры систем. Спросите студентов, какие силы являются внутренними, а какие – внешними в каждом сценарии.

Если вы когда-либо наносили удар пальцем ноги, вы заметили, что, хотя палец ноги инициирует удар, поверхность, по которой вы наносите удар, оказывает на ваш палец силу обратно.Хотя первая мысль, которая приходит вам в голову, скорее всего, «ой, больно», а не «это прекрасный пример третьего закона Ньютона», оба утверждения верны.

Это именно то, что происходит всякий раз, когда один объект оказывает силу на другой – каждый объект испытывает силу той же силы, что и сила, действующая на другой объект, но действующая в противоположном направлении. Повседневные переживания, такие как удар пальцем ноги или бросок мяча, – все это прекрасные примеры действия третьего закона Ньютона.

Третий закон движения Ньютона гласит, что всякий раз, когда первый объект оказывает силу на второй объект, первый объект испытывает силу, равную по величине, но противоположную по направлению силе, которую он оказывает.

Третий закон движения Ньютона гласит, что силы всегда возникают парами, и один объект не может воздействовать на другой, не испытав взамен такой же силовой силы. Мы иногда называем эти пары сил парами действие-реакция , где прилагаемая сила – это действие, а сила, испытываемая в ответ, – это реакция (хотя это зависит от вашей точки зрения).

Третий закон Ньютона полезен для выяснения того, какие силы являются внешними по отношению к системе. Напомним, что определение внешних сил важно при постановке задачи, потому что внешние силы необходимо сложить вместе, чтобы найти результирующую силу.

Мы можем увидеть в действии третий закон Ньютона, посмотрев на то, как люди передвигаются. Представьте себе пловца, отталкивающегося от края бассейна, как показано на рис. 4.8. Она толкается ногами о стенку бассейна и ускоряется в направлении, противоположном ее толчку.Таким образом, стена оказывает на пловца силу равной величины, но в направлении, противоположном ее толчку. Вы можете подумать, что две силы равной величины, но действующие в противоположных направлениях, аннулируются, , но это не так, потому что они действуют на разные системы.

В этом случае есть две разные системы, которые мы можем выбрать для исследования: пловец или стена. Если мы выберем пловца в качестве интересующей нас системы, как показано на рисунке, тогда стена на ступнях является внешней силой для пловца и влияет на ее движения.Поскольку ускорение происходит в том же направлении, что и чистая внешняя сила, пловец движется в направлении стены на ногах. Поскольку пловец – это наша система (или объект интереса), а не стена, нам не нужно учитывать силу Ffeet на стенеFfeet на стене, потому что она исходит из от пловца , а не от , действующей на пловца. Следовательно, Ffeet on wallFfeet on wall не влияет напрямую на движение системы и не отменяет Fwall на ногах.Fwall на ногах. Обратите внимание, что пловчиха толкает в направлении, противоположном направлению, в котором она хочет двигаться.

Рис. 4.8. Когда пловец прикладывает силу Ffeet к стене Ffeet на стене на стене, он ускоряется в направлении, противоположном направлению ее толчка. Это означает, что чистая внешняя сила, действующая на нее, направлена ​​в направлении, противоположном Ffeet на стене. Ffeet на стене. Это противодействие является результатом третьего закона движения Ньютона, который гласит, что стена оказывает на пловца силу, равную по величине, но действующую в направлении, противоположном силе, которую пловец оказывает на стену. .

Легко найти другие примеры третьего закона Ньютона. Когда учитель шагает перед доской, он прикладывает силу к полу. Пол оказывает на учителя противодействующую силу в прямом направлении, которая заставляет его ускоряться вперед. Точно так же автомобиль ускоряется, потому что земля толкает колеса вперед в ответ на толчки колес автомобиля по земле. Вы можете видеть свидетельства того, что колеса отталкиваются назад, когда колеса вращаются на гравийной дороге и отбрасывают камни назад.

Другой пример – сила бейсбольного мяча при контакте с битой. Вертолеты создают подъемную силу, выталкивая воздух вниз, создавая восходящую силу реакции. Птицы летают, создавая силу в воздухе в направлении, противоположном тому, в котором они хотят лететь. Например, крылья птицы заставляют воздух двигаться вниз и назад, чтобы подняться и двигаться вперед. Осьминог движется вперед в воде, выбрасывая воду назад через воронку в своем теле, что похоже на то, как движется водный мотоцикл.В этих примерах осьминог или водный мотоцикл толкают воду назад, а вода, в свою очередь, толкает осьминога или водный мотоцикл вперед.

Применение третьего закона Ньютона

Поддержка учителя

Поддержка учителя

[BL] Просмотрите понятие веса как силы.

[OL] Спросите студентов, что происходит, когда объект падает с высоты. Почему он останавливается, когда ударяется о землю? Введем термин “нормальная сила”.

Демонстрация учителей

[BL] [OL] [AL] Продемонстрируйте концепцию напряжения, используя физические объекты.Подвесьте такой предмет, как ластик, на стержень с помощью резинки. Повесьте еще одну резинку рядом с первой, но без каких-либо предметов. Спросите студентов, в чем разница между ними. Какие силы действуют на первый стержень? Объясните, как резинка (т. Е. Соединитель) передает силу. Теперь спросите учащихся, в каком направлении действуют внешние силы, действующие на соединитель. Также поинтересуйтесь, какие внутренние силы действуют на разъем. Если удалить ластик, в каком направлении будет двигаться резинка? Это направление силы, приложенной резинкой к ластику.

Силы классифицируются и получают имена в зависимости от их источника, способа передачи или их воздействия. В предыдущих разделах мы обсуждали силы, называемые толчком , массой и трением . В этом разделе применение третьего закона движения Ньютона позволит нам исследовать еще три силы: нормальную силу, натяжение и тягу. Однако, поскольку мы еще не рассмотрели векторы подробно, в этой главе мы будем рассматривать только одномерные ситуации.В другой главе мы рассмотрим силы, действующие в двух измерениях.

Гравитационная сила (или вес) действует на объекты всегда и везде на Земле. Из второго закона Ньютона мы знаем, что чистая сила вызывает ускорение; Итак, почему все не находится в постоянном состоянии свободного падения к центру Земли? Ответ – нормальная сила. Нормальная сила – это сила, которую поверхность прилагает к объекту, чтобы выдержать вес этого объекта; он действует перпендикулярно поверхности, на которой лежит объект.Если объект на плоской поверхности не ускоряется, чистая внешняя сила равна нулю, а нормальная сила имеет ту же величину, что и вес системы, но действует в противоположном направлении. В форме уравнения запишем, что

Обратите внимание, что это уравнение верно только для горизонтальной поверхности.

Слово напряжение происходит от латинского слова, означающего , чтобы растянуть . Натяжение – это сила по длине гибкого соединителя, такого как веревка, веревка, цепь или кабель.Независимо от типа соединителя, прикрепленного к интересующему объекту, необходимо помнить, что соединитель может тянуть (или прикладывать натяжение ) только в направлении параллельно его длине. Натяжение – это натяжение, которое действует параллельно соединителю и действует в противоположных направлениях на двух концах соединителя. Это возможно, потому что гибкий соединитель представляет собой просто длинную серию сил действия-противодействия, за исключением двух концов, где внешние объекты обеспечивают один член сил действия-противодействия.

Представьте человека, держащего гирю на веревке, как показано на рис. 4.9.

Рис. 4.9. Когда идеально гибкий соединитель (не требующий силы для его сгибания), такой как веревка, передает силу T , эта сила должна быть параллельна длине веревки, как показано. Такой гибкий соединитель создает натяжение. Обратите внимание, что веревка тянется с одинаковой силой, но в противоположных направлениях по отношению к руке и массе (без учета веса веревки).Это пример третьего закона Ньютона. Веревка – это среда, которая передает силы одинаковой величины между двумя объектами, но действуют в противоположных направлениях.

Натяжение веревки должно равняться весу поддерживаемой массы, как мы можем доказать, используя второй закон Ньютона. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю, поэтому Fnet = 0. Fnet = 0. Единственными внешними силами, действующими на массу, являются ее вес W и натяжение T , создаваемое веревкой.Суммируя внешние силы, мы получаем суммарную силу

Fnet = T − W = 0, Fnet = T − W = 0,

4,18

, где T и W – величины натяжения и веса, соответственно, и их знаки указывают направление, причем верхнее положительное значение. Подставив м г на F _net и изменив уравнение, натяжение будет равно весу поддерживаемой массы, как и следовало ожидать

Для массы 5,00 кг (без учета массы веревки) мы видим, что

Т = мг = (5.00 кг) (9,80 м / с2) = 49,0 N.T = mg = (5,00 кг) (9,80 м / с2) = 49,0 N.

4,20

Другой пример действия третьего закона Ньютона – это толчок. Ракеты движутся вперед, выбрасывая газ назад с высокой скоростью. Это означает, что ракета прилагает большую силу назад к газу в камере сгорания ракеты, а газ, в свою очередь, в ответ оказывает большую силу вперед на ракету. Эта сила реакции называется , тяга .

Советы для успеха

Распространенное заблуждение состоит в том, что ракеты двигаются сами по себе, толкаясь о землю или воздух позади них.На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы.

Ссылки на физику

Математика: стратегия решения проблем для законов движения Ньютона

Основы решения проблем, представленные ранее в этом тексте, сопровождаются здесь конкретными стратегиями применения законов движения Ньютона. Эти методы также укрепляют концепции, которые полезны во многих других областях физики.

Во-первых, определите задействованные физические принципы.Если проблема связана с силами, то здесь задействованы законы движения Ньютона, и важно нарисовать тщательный набросок ситуации. Пример эскиза показан на рисунке 4.10. Затем, как показано на рисунке 4.10, используйте векторы для представления всех сил. Тщательно пометьте силы и убедитесь, что их длина пропорциональна величине сил, а стрелки указывают направление, в котором действуют силы.

Рис. 4.10 (а) Эскиз Тарзана, неподвижно свешивающегося на лозе.(b) Стрелки обозначают все силы. T – это напряжение, прилагаемое к Тарзану лозой, FTFT – это сила, приложенная к лозе Тарзаном, а W – это вес Тарзана (т. Е. Сила, действующая на Тарзана под действием силы тяжести Земли). Предполагается, что все другие силы, такие как легкий ветерок, незначительны. (c) Предположим, нам дали массу Тарзана и попросили найти напряжение в лозе. Мы определяем интересующую систему, как показано, и рисуем диаграмму свободного тела, как показано на (d).FTFT больше не отображается, потому что не влияет на интересующую систему; скорее FTFT действует во внешнем мире. (d) Диаграмма свободного тела показывает только внешние силы, действующие на Тарзана. Чтобы их сумма равнялась нулю, мы должны иметь T = W.T = W.

Затем составьте список известных и неизвестных и присвойте имена переменных количествам, указанным в задаче. Выясните, какие переменные необходимо вычислить; это неизвестные. Теперь тщательно определите систему: какие объекты представляют интерес для задачи.Это решение важно, потому что второй закон Ньютона включает только внешние силы. После идентификации системы можно увидеть, какие силы являются внешними, а какие – внутренними (см. Рисунок 4.10).

Если система воздействует на объект вне системы, то вы знаете, что внешний объект оказывает на систему силу равной величины, но в противоположном направлении.

Диаграмма, показывающая интересующую систему и все внешние силы, действующие на нее, называется диаграммой свободного тела.На диаграммах свободного тела показаны только внешние силы, а не ускорение или скорость. На рис. 4.10 показана диаграмма свободного тела для интересующей системы.

Изобразив диаграмму свободного тела, примените второй закон Ньютона для решения проблемы. Это показано на рис. 4.10 для случая, когда Тарзан висит на лозе. Когда внешние силы четко определены на диаграмме свободного тела, переведите силы в форму уравнения и решите для неизвестных. Обратите внимание, что силы, действующие в противоположных направлениях, имеют противоположные знаки.По соглашению силы, действующие вниз или влево, обычно отрицательны.

Захват

Если проблема имеет более одной интересующей системы, требуется более одной диаграммы свободного тела для описания внешних сил, действующих на разные системы.

1. Истинно
2. Ложь

Watch Physics

Третий закон движения Ньютона

Это видео объясняет третий закон движения Ньютона на примерах, включающих толчок, нормальную силу и тягу (силу, которая приводит в движение ракету или реактивный самолет).

Захват

Если космонавт на видео хотел двигаться вверх, в каком направлении он должен бросить объект? Почему?

1. Он должен бросить объект вверх, потому что, согласно третьему закону Ньютона, объект будет оказывать на него силу в том же направлении (т. Е. Вверх).
2. Он должен бросить объект вверх, потому что, согласно третьему закону Ньютона, объект будет оказывать на него силу в противоположном направлении (то есть вниз).
3. Он должен бросить объект вниз, потому что, согласно третьему закону Ньютона, объект будет оказывать на него силу в противоположном направлении (т. Е. Вверх).
4. Он должен бросить объект вниз, потому что, согласно третьему закону Ньютона, объект будет оказывать на него силу в том же направлении (т. Е. Вниз).

Рабочий пример

Тележка с ускоряющим оборудованием

Учитель физики толкает тележку с демонстрационным оборудованием в класс, как показано на рисунке 4.11. Масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Чтобы толкнуть тележку вперед, ступня учителя прикладывает к полу силу 150 Н в противоположном направлении (назад). Рассчитайте ускорение, произведенное учителем. Сила трения, противодействующая движению, составляет 24,0 Н.

Рисунок 4.11

Стратегия

Поскольку они ускоряются вместе, мы определяем систему как учитель, тележку и оборудование. Учитель отталкивается назад с силой FfootFfoot 150 Н.Согласно третьему закону Ньютона, пол воздействует на систему передним усилием FfloorFloor равным 150 Н. Поскольку все движения горизонтальны, мы можем предположить, что в вертикальном направлении не действует никакая результирующая сила, и проблема становится одномерной. Как показано на рисунке, трение f противодействует движению и, следовательно, действует в направлении, противоположном направлению Ffloor.Floor.

Мы не должны включать силы FteacherFteacher, FcartFcart или FfootFfoot, потому что они применяются системой , а не системой .Мы находим чистую внешнюю силу, складывая внешние силы, действующие на систему (см. Диаграмму свободного тела на рисунке), а затем используем второй закон Ньютона, чтобы найти ускорение.

Решение

Второй закон Ньютона –

Чистая внешняя сила, действующая на систему, является суммой внешних сил: силы пола, действующей на учителя, тележку и оборудование (в горизонтальном направлении), и силы трения. Поскольку трение действует в противоположном направлении, мы присваиваем ему отрицательное значение.Таким образом, для чистой силы получаем

Fnet = Ffloor − f = 150 N − 24,0 N = 126 N.Fnet = Ffloor − f = 150 N − 24,0 N = 126 N.

4,22

Масса системы складывается из массы учителя, тележки , и оборудование.

m = (65,0 + 12,0 + 7,0) кг = 84 кг · m = (65,0 + 12,0 + 7,0) кг = 84 кг

4,23

Вставьте эти значения нетто F и m во второй закон Ньютона, чтобы получить ускорение системы. .

a = Fnetma = 126 N84 кг = 1,5 м / с2a = Fnetma = 126 N84 кг = 1,5 м / с2

4.24

Обсуждение

Ни одна из сил между компонентами системы, например, между руками учителя и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к системе. Другой способ взглянуть на это – отметить, что силы между компонентами системы компенсируются, потому что они равны по величине и противоположны по направлению. Например, сила, прикладываемая учителем к тележке, имеет равную величину, но в противоположном направлении силы, прикладываемой тележкой к учителю.В этом случае обе силы действуют на одну и ту же систему, поэтому они нейтрализуются. Определение системы имело решающее значение для решения этой проблемы.

Практические задачи

14.

Каково уравнение нормальной силы для тела массой м , которое покоится на горизонтальной поверхности?

1. N = м
2. N = мг
3. N = мВ
4. N = г

15.

Объект массой м. покоится на полу.Какова величина и направление действующей на него нормальной силы?

1. N = мВ в направлении вверх
2. N = мг в направлении вверх
3. N = мВ в направлении вниз
4. N = мг в направлении вниз

Проверьте свое понимание

Поддержка учителей

Поддержка учителей

Используйте вопросы в разделе «Проверьте свое понимание», чтобы оценить, усвоили ли учащиеся учебные цели этого раздела.Если учащиеся не справляются с какой-либо конкретной целью, проверка «Проверьте свое понимание» поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.

16.

Что такое третий закон движения Ньютона?

1. Каждый раз, когда первое тело оказывает силу на второе тело, первое тело испытывает силу, которая в два раза больше, и действует в направлении приложенной силы.
2. Каждый раз, когда первое тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и действующую в направлении приложенной силы.
3. Каждый раз, когда первое тело оказывает силу на второе тело, первое тело испытывает силу, которая в два раза больше, но действует в направлении, противоположном направлению приложенной силы.
4. Каждый раз, когда первое тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине, но действующую в направлении, противоположном направлению приложенной силы.

17.

Учитывая третий закон Ньютона, почему две равные и противоположные силы не уравновешивают друг друга?

1. Поскольку две силы действуют в одном направлении
2. Потому что две силы имеют разную величину
3. Потому что две силы действуют на разные системы
4. Поскольку две силы действуют в перпендикулярных направлениях

5.5 Третий закон Ньютона | Университетская физика, том 1,

Цели обучения

К концу раздела вы сможете:

• Третий закон движения Ньютона
• Определение сил действия и противодействия в различных ситуациях
• Применять третий закон Ньютона для определения систем и решения проблем движения

До сих пор мы рассматривали силу как толчок или тягу; однако, если вы подумаете об этом, вы поймете, что никакие толчки или тяги никогда не возникают сами по себе.Когда вы толкаете стену, стена давит на вас. Это подводит нас к третьему закону Ньютона .

Третий закон движения Ньютона

Каждый раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает. Математически, если тело A прикладывает силу [латекс] \ overset {\ to} {F} [/ latex] к телу B , то B одновременно прикладывает силу [латекс] \ text {-} \ overset {\ to} {F} [/ latex] на A , или в форме векторного уравнения

[латекс] {\ overset {\ to} {F}} _ {\ text {AB}} = \ text {-} {\ overset {\ to} {F}} _ {\ text {BA}}.[/ латекс]

Третий закон Ньютона представляет собой определенную симметрию в природе: силы всегда возникают парами, и одно тело не может воздействовать на другое, не испытав силы. Мы иногда в общих чертах называем этот закон «действием-противодействием», где приложенная сила – это действие, а сила, испытываемая как следствие, – это противодействие. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.

Мы легко можем увидеть в действии третий закон Ньютона, взглянув на то, как люди передвигаются.Представьте, что пловец отталкивается от края бассейна ((Рисунок)). Она отталкивается ногами о стену бассейна и ускоряется в направлении, противоположном ее толчку. Стена оказала на пловца равную и противоположную силу. Вы можете подумать, что две равные и противоположные силы уравновешиваются, но это не , потому что они действуют на разные системы . В этом случае мы можем исследовать две системы: пловец и стенку. Если мы выберем пловца в качестве интересующей нас системы, как на рисунке, тогда [латекс] {F} _ {\ text {wall on feet}} [/ latex] является внешней силой в этой системе и влияет на ее движение.Пловец движется в направлении этой силы. Напротив, сила [латекс] {F} _ {\ text {feet on wall}} [/ latex] действует на стену, а не на интересующую нас систему. Таким образом, [латекс] {F} _ {\ text {ноги на стене}} [/ латекс] не влияет напрямую на движение системы и не отменяет [латекс] {F} _ {\ text {стена на ногах} }. [/ latex] Пловчиха толкает в направлении, противоположном тому, в котором она хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении. В диаграмме свободного тела, такой как показанная на рисунке, мы никогда не включаем обе силы пары действие-противодействие; в этом случае мы используем только [латекс] {F} _ {\ text {стена на ногах}} [/ латекс], а не [латекс] {F} _ {\ text {ноги на стене}} [/ латекс].

Рис. 5.16 Когда пловец воздействует на стену, она ускоряется в противоположном направлении; другими словами, чистая внешняя сила действует на нее в направлении, противоположном [латексу] {F} _ {\ text {ноги на стене}}. [/ latex] Это противодействие возникает из-за того, что в соответствии с третьим законом Ньютона стена оказывает на пловца силу [латекс] {F} _ {\ text {wall on feet}} [/ latex], равную по величине, но в направлении, противоположном тому, которое она оказывает на него. Линия вокруг пловца указывает на интересующую его систему.Таким образом, диаграмма свободного тела показывает только [латекс] {F} _ {\ text {wall on feet}}, [/ latex] w (гравитационная сила) и BF, которая является выталкивающей силой воды, поддерживающей вес пловца. Вертикальные силы w и BF компенсируются, потому что нет вертикального ускорения.

Легко найти другие примеры третьего закона Ньютона:

• Когда профессор ходит перед доской, он прикладывает силу назад к полу. Пол оказывает на профессора противодействующую силу, которая заставляет его ускоряться.
• Автомобиль ускоряется вперед, потому что земля толкает ведущие колеса вперед в ответ на движение ведущих колес по земле. Вы можете увидеть свидетельство того, что колеса отталкиваются назад, когда шины вращаются на гравийной дороге и отбрасывают камни назад.
• Ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большое обратное усилие на газ в камере сгорания ракеты; следовательно, газ оказывает на ракету большую реактивную силу.Эта сила реакции, которая толкает тело вперед в ответ на силу, направленную назад, называется тягой и . Распространенное заблуждение, что ракеты движутся сами по себе, толкаясь о землю или воздух позади них. На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы.
• Вертолеты создают подъемную силу, выталкивая воздух вниз, тем самым испытывая восходящую силу реакции.
• Птицы и самолеты также летают, воздействуя на воздух силой в направлении, противоположном той силы, которая им нужна.Например, крылья птицы заставляют воздух двигаться вниз и назад, чтобы подняться и двигаться вперед.
• Осьминог движется по воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу.
• Когда человек тянет вниз по вертикальной веревке, веревка тянет человека вверх ((Рисунок)).

Рисунок 5.17 Когда альпинист тянет веревку вниз, веревка тянет вверх альпиниста.

Есть две важные особенности третьего закона Ньютона.Во-первых, прилагаемые силы (действие и противодействие) всегда равны по величине, но противоположны по направлению. Во-вторых, эти силы действуют на разные тела или системы: сила A, действует на B, и сила B, действует на A, . Другими словами, две силы – это разные силы, которые не действуют на одно и то же тело. Таким образом, они не отменяют друг друга.

Для ситуации, показанной на (Рисунок), третий закон указывает, что, поскольку стул толкает мальчика вверх с силой [латекс] \ overset {\ to} {C}, [/ латекс] он толкает стул вниз. с силой [латекс] \ text {-} \ overset {\ to} {C}.[/ latex] Точно так же он толкает вниз силами [latex] \ text {-} \ overset {\ to} {F} [/ latex] и [latex] \ text {-} \ overset {\ to} {T } [/ latex] на полу и на столе соответственно. Наконец, поскольку Земля тянет мальчика вниз с силой [латекс] \ overset {\ to} {w}, [/ latex], он тянет вверх на Земле с силой [латекс] \ text {-} \ overset {\ to} { ш} [/ латекс]. Если бы этот ученик в отчаянии сердито ударил по столу, он быстро усвоил бы болезненный урок (которого можно избежать, изучая законы Ньютона), что стол не менее сильно ударяет по столу.

Человек, идущий или бегущий, инстинктивно применяет третий закон Ньютона. Например, бегун на (Рис.) Толкает назад землю так, что это толкает его вперед.

Рис. 5.18 Бегун подчиняется третьему закону Ньютона. (а) Бегун прилагает силу к земле. (b) Сила реакции земли на бегуна толкает его вперед.

Пример

Силы на стационарном объекте

Пакет на (Рис.) Стоит на весах.Силы, действующие на упаковку, следующие: [латекс] \ overset {\ to} {S}, [/ latex], что связано с масштабом, и [латекс] \ text {-} \ overset {\ to} {w}, [ / latex], который возникает из-за гравитационного поля Земли. Силы реакции, которые оказывает упаковка, следующие: [latex] \ text {-} \ overset {\ to} {S} [/ latex] на шкале и [latex] \ overset {\ to} {w} [/ latex] на Земля. Поскольку пакет не ускоряется, применение второго закона дает

[латекс] \ overset {\ to} {S} – \ overset {\ to} {w} = m \ overset {\ to} {a} = \ overset {\ to} {0}, [/ latex]

т.

[латекс] \ overset {\ to} {S} = \ overset {\ to} {w}.[/ латекс]

Таким образом, показания весов показывают величину веса упаковки. Однако весы не измеряют вес упаковки; он измеряет силу [латекс] \ text {-} \ overset {\ to} {S} [/ latex] на своей поверхности. Если система ускоряется, [latex] \ overset {\ to} {S} [/ latex] и [latex] \ text {-} \ overset {\ to} {w} [/ latex] не будут равны, поскольку объяснено в Приложениях законов Ньютона.

Рис. 5.19 (a) Силы, действующие на упаковку, лежащую на весах, вместе с их силами реакции.Сила [латекс] \ overset {\ to} {w} [/ latex] – это вес упаковки (сила земного притяжения), а [латекс] \ overset {\ to} {S} [/ latex] – сила весов на упаковке. (b) Изоляция системы «пакет-масштаб» и системы «пакет-Земля» делает ясными пары действия и реакции.

Пример

Начало работы: выбор правильной системы

Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал ((Рисунок)).Ее масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Вычислите ускорение, возникающее, когда профессор прикладывает к полу силу 150 Н. Все силы, противодействующие движению, такие как трение колес тележки и сопротивление воздуха, составляют 24,0 Н.

Рисунок 5.20 Профессор толкает тележку со своим демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (кроме [latex] \ overset {\ to} {f} \ text {,} [/ latex], потому что они слишком малы для масштабирования).Система 1 подходит для этого примера, потому что она запрашивает ускорение всей группы объектов. Только [латекс] {\ overset {\ to} {F}} _ {\ text {floor}} [/ latex] и [latex] \ overset {\ to} {f} [/ latex] являются внешними силами, действующими на систему 1 по линии движения. Все остальные силы либо отменяют, либо действуют во внешнем мире. Система 2 выбрана для следующего примера, так что [latex] {\ overset {\ to} {F}} _ {\ text {prof}} [/ latex] является внешней силой и входит во второй закон Ньютона. Диаграммы свободного тела, которые служат основой второго закона Ньютона, меняются в зависимости от выбранной системы.

Стратегия

Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на (Рисунок). Профессор толкает назад с силой [латекс] {F} _ {\ text {foot}} [/ latex] в 150 Н. Согласно третьему закону Ньютона, пол оказывает прямое противодействие [латекс] {F} _ { \ text {floor}} [/ latex] 150 Н в Системе 1. Поскольку все движения горизонтальны, мы можем предположить, что в вертикальном направлении нет результирующей силы. Следовательно, задача одномерная по горизонтали.Как уже отмечалось, трение f противодействует движению и, таким образом, имеет направление, противоположное [латексному] {F} _ {\ text {floor}}. [/ latex] Мы не включаем силы [латекс] {F} _ {\ text {prof}} [/ latex] или [latex] {F} _ {\ text {cart}} [/ latex], потому что они внутренние силы, и мы не включаем [латекс] {F} _ {\ text {foot}} [/ latex], потому что он действует на пол, а не на систему. Никаких других значительных сил, действующих на Систему 1. Если чистая внешняя сила может быть найдена из всей этой информации, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение.См. Диаграмму свободного тела на рисунке.

Решение

Второй закон Ньютона дает

[латекс] a = \ frac {{F} _ {\ text {net}}} {m}. [/ латекс]

Чистая внешняя сила в Системе 1 выводится из (Рисунок) и предыдущего обсуждения, чтобы быть

.

[латекс] {F} _ {\ text {net}} = {F} _ {\ text {floor}} – f = 150 \, \ text {N} -24.0 \, \ text {N} = 126 \ , \ text {N} \ text {.} [/ latex]

Масса Системы 1

[латекс] m = (65,0 + 12,0 + 7,0) \, \ text {кг} = 84 \, \ text {кг} \ text {.{2}. [/ латекс]

Значение

Ни одно из сил между компонентами Системы 1, например, между руками профессора и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это состоит в том, что силы между компонентами системы отменяются. потому что они равны по величине и противоположны по направлению. Например, сила, прилагаемая профессором к тележке, приводит к тому, что на профессора действует равная и противоположная сила. В этом случае обе силы действуют на одну и ту же систему и, следовательно, отменяются.Таким образом, внутренние силы (между компонентами системы) отменяются. Выбор Системы 1 имел решающее значение для решения этой проблемы.

Пример

Усилие на тележке: выбор новой системы

Рассчитайте силу, которую профессор оказывает на тележку (рисунок), используя при необходимости данные из предыдущего примера.

Стратегия

Если мы определим интересующую систему как тележку плюс оборудование (Система 2 на (Рисунок)), то чистая внешняя сила в Системе 2 – это сила, которую профессор оказывает на тележку за вычетом трения.Сила, которую она оказывает на тележку, [латекс] {F} _ {\ text {prof}} [/ latex], является внешней силой, действующей на Систему 2. [latex] {F} _ {\ text {prof}} [/ latex] был внутренним по отношению к Системе 1, но он был внешним по отношению к Системе 2 и, таким образом, входит во второй закон Ньютона для этой системы.

Решение

Второй закон Ньютона можно использовать, чтобы найти [латекс] {F} _ {\ text {prof}}. [/ latex] Начнем с

[латекс] a = \ frac {{F} _ {\ text {net}}} {m}. [/ латекс]

Величина чистой внешней силы в Системе 2 составляет

.

[латекс] {F} _ {\ text {net}} = {F} _ {\ text {prof}} – ф.[/ латекс]

Решаем за [латекс] {F} _ {\ text {prof}} [/ latex], желаемое количество:

[латекс] {F} _ {\ text {prof}} = {F} _ {\ text {net}} + f. [/ латекс]

Дано значение f , поэтому мы должны вычислить net [latex] {F} _ {\ text {net}}. [/ latex] Это можно сделать, потому что известны и ускорение, и масса Системы 2. Используя второй закон Ньютона, мы видим, что

[латекс] {F} _ {\ text {net}} = ma, [/ latex]

, где масса Системы 2 равна 19.{2}) = 29 \, \ text {N} \ text {.} [/ Latex]

Теперь мы можем найти желаемую силу:

[латекс] {F} _ {\ text {prof}} = {F} _ {\ text {net}} + f = 29 \, \ text {N} +24.0 \, \ text {N} = 53 \ , \ text {N} \ text {.} [/ latex]

Значение

Эта сила значительно меньше, чем сила в 150 Н, которую профессор приложил к полу. Не вся сила 150 Н передается на тележку; кое-что ускоряет профессора. Выбор системы – важный аналитический шаг как в решении проблем, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).

Проверьте свое понимание

Два блока находятся в покое и контактируют на поверхности без трения, как показано ниже, с [latex] {m} _ {1} = 2.0 \, \ text {kg}, [/ latex] [latex] {m} _ { 2} = 6.0 \, \ text {kg}, [/ latex] и приложенная сила 24 Н. (a) Найдите ускорение системы блоков. (б) Предположим, что блоки позже разделятся. Какая сила даст второму блоку массой 6,0 кг такое же ускорение, как и система блоков?

Показать решение

а.{2} [/ латекс]; б. 18 N

Сводка

• Третий закон движения Ньютона представляет собой основную симметрию в природе, с испытываемой силой, равной по величине и противоположной по направлению действующей силе.
• Две равные и противоположные силы не отменяются, потому что они действуют на разные системы.
• Пары действие-реакция включают пловца, отталкивающего стену, вертолеты, создающие подъемную силу, выталкивая воздух вниз, и осьминога, толкающего себя вперед, выбрасывая воду из своего тела.Ракеты, самолеты и автомобили толкаются вперед за счет силы реакции тяги.
• Выбор системы – важный аналитический шаг в понимании физики проблемы и ее решении.

Концептуальные вопросы

Определите силы действия и противодействия в следующих ситуациях: (а) Земля притягивает Луну, (б) мальчик бьет футбольный мяч, (в) ракета ускоряется вверх, (г) машина ускоряется вперед, (д) ​​высоко прыгун прыгает, и (е) из ружья выпускается пуля.

Показать решение

а. действие: Земля притягивает Луну, реакция: Луна притягивает Землю; б. действие: ступня прикладывает силу к мячу, реакция: мяч прикладывает силу к ступне; c. действие: ракета толкает газ, реакция: газ толкает ракету обратно; d. действие: автомобильные шины толкают назад по дороге, реакция: дорога толкает вперед шины; е. действие: парашютист толкает перемычку вниз, реакция: земля толкает перемычку; f. Действие: пистолет толкает пулю вперед, реакция: пуля толкает пистолет назад.

Предположим, вы держите в руке чашку кофе.Определите все силы на чашке и реакцию на каждую силу.

(a) Почему обычная винтовка дает отдачу (отдачу назад) при выстреле? (b) Ствол безоткатного ружья открыт с обоих концов. Опишите, как действует третий закон Ньютона при увольнении. (c) Можете ли вы безопасно стоять рядом с одним из них, когда из него стреляют?

Показать решение

а. Винтовка (снаряд, поддерживаемый винтовкой) прикладывает силу, чтобы выбить пулю; реакция на эту силу – это сила, которую пуля оказывает на винтовку (снаряд) в противоположном направлении.{2} [/ латекс]. (а) Какова сила трения между ногами проигравшего игрока и травой? (b) Какую силу прилагает выигравший игрок к земле, чтобы двигаться вперед, если его масса плюс снаряжение составляет 110,0 кг?

Книга по истории лежит на столе по физике, как показано ниже; также показана диаграмма свободного тела. Книги по истории и физике весят 14 Н и 18 Н соответственно. Обозначьте каждую силу, действующую на каждую книгу, с помощью двойного индекса (например, сила контакта книги истории, прижатой к книге физики, может быть описана как [латекс] {\ overset {\ to} {F}} _ {\ text {HP }} [/ latex]) и определите значение каждой из этих сил, объясняя используемый процесс.

Показать решение

Поскольку вес книги по истории – это сила, прилагаемая Землей к книге по истории, мы представляем ее как [латекс] {\ overset {\ to} {F}} _ {\ text {EH}} = – 14 \ hat {j} \, \ text {N} \ text {.} [/ latex] Помимо этого, книга истории взаимодействует только с книгой физики. Поскольку ускорение книги истории равно нулю, чистая сила, действующая на нее, равна нулю по второму закону Ньютона: [латекс] {\ overset {\ to} {F}} _ {\ text {PH}} + {\ overset {\ to} {F}} _ {\ text {EH}} = \ overset {\ to} {0}, [/ latex] где [latex] {\ overset {\ to} {F}} _ {\ text {PH }} [/ latex] – это сила, прилагаемая книгой по физике к учебнику истории.Таким образом, [латекс] {\ overset {\ to} {F}} _ {\ text {PH}} = \ text {-} {\ overset {\ to} {F}} _ {\ text {EH}} = \ text {-} (- 14 \ hat {j}) \, \ text {N} = 14 \ hat {j} \, \ text {N} \ text {.} [/ latex] Мы обнаруживаем, что книга по физике оказывает на книгу истории восходящую силу величиной 14 Н. На книгу по физике действуют три силы: [латекс] {\ overset {\ to} {F}} _ {\ text {EP}} [/ latex] из-за Земли, [латекс] {\ overset {\ to} {F}} _ {\ text {HP}} [/ latex] из-за книги по истории и [latex] {\ overset {\ to} {F}} _ {\ text {DP}} [/ latex] из-за на рабочий стол.Поскольку книга по физике весит 18 Н, [латекс] {\ overset {\ to} {F}} _ {\ text {EP}} = – 18 \ hat {j} \, \ text {N} \ text {.} [/ latex] Согласно третьему закону Ньютона, [latex] {\ overset {\ to} {F}} _ {\ text {HP}} = \ text {-} {\ overset {\ to} {F}} _ { \ text {PH}}, [/ latex] так [латекс] {\ overset {\ to} {F}} _ {\ text {HP}} = – 14 \ hat {j} \, \ text {N} \ text {.} [/ latex] Второй закон Ньютона, примененный к книге по физике, дает [latex] \ sum \ overset {\ to} {F} = \ overset {\ to} {0}, [/ latex] или [latex] {\ overset {\ to} {F}} _ {\ text {DP}} + {\ overset {\ to} {F}} _ {\ text {EP}} + {\ overset {\ to} {F} } _ {\ text {HP}} = \ overset {\ to} {0}, [/ latex] так [латекс] {\ overset {\ to} {F}} _ {\ text {DP}} = \ text {-} (- 18 \ hat {j}) – (- 14 \ hat {j}) = 32 \ hat {j} \, \ text {N} \ text {.{2} [/ латекс]. Найдите величину ускорения автомобиля.

Глоссарий

Третий закон движения Ньютона

всякий раз, когда одно тело прикладывает силу ко второму телу, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно прикладывает.

тяга

Сила реакции, которая толкает тело вперед в ответ на обратную силу

Третий закон движения Ньютона: симметрия сил

Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал, как показано на рисунке 2.Масса 65,0 кг, тележки 12,0 кг, снаряжения 7,0 кг. Вычислите ускорение, возникающее, когда профессор прикладывает к полу силу 150 Н. Все силы, противодействующие движению, такие как трение колес тележки и сопротивление воздуха, составляют 24,0 Н.

Рис. 2. Профессор толкает тележку с демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (за исключением f , поскольку он слишком мал для масштабирования).В каждом примере задаются разные вопросы; таким образом, интересующая система должна определяться по-разному для каждой из них. Система 1 подходит для примера 4.4, так как она запрашивает ускорение всей группы объектов. Только F _пол и f являются внешними силами, действующими на Систему 1 вдоль линии движения. Все остальные силы либо отменяют, либо действуют во внешнем мире. Система 2 выбрана для этого примера, так что F _prof будет внешней силой и будет соответствовать второму закону Ньютона.Обратите внимание, что диаграммы свободного тела, которые позволяют нам применять второй закон Ньютона, различаются в зависимости от выбранной системы.

Стратегия

Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на Рисунке 2. Профессор толкает назад с силой F _фут , равной 150 Н. Согласно третьему закону Ньютона, пол оказывает прямую противодействующую силу F _пол , равную 150 Н для Системы 1. Поскольку все движения горизонтально, мы можем предположить, что в вертикальном направлении нет результирующей силы.Таким образом, проблема одномерная в горизонтальном направлении. Как уже отмечалось, f противодействует движению и, таким образом, находится в противоположном направлении от пола F _{. Обратите внимание, что мы не включаем силы F prof или F cart , потому что это внутренние силы, и мы не включаем F foot , потому что они действуют на пол, а не на систему. Никаких других значительных сил, действующих на Систему 1. Если чистая внешняя сила может быть найдена из всей этой информации, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение.См. Диаграмму свободного тела на рисунке.}

Решение

Второй закон Ньютона дается формулой [latex] a = \ frac {{F} _ {\ text {net}}} {m} [/ latex].

(Единица измерения времени в системе СИ, секунд (сокращенно s), имеет долгую историю. В течение многих лет она определялась как 1/86400 среднего солнечного дня. Совсем недавно был принят новый стандарт для повышения точности и определить второе как неизменное или постоянное физическое явление (поскольку солнечный день удлиняется из-за очень постепенного замедления вращения Земли).Атомы цезия можно заставить колебаться очень устойчиво, и эти колебания можно легко наблюдать и подсчитывать. В 1967 году вторая была определена как время, необходимое для 9 192 631 770 таких колебаний. (См. Рис. 1.18.) Точность основных единиц важна, потому что все измерения в конечном итоге выражаются в единицах основных единиц и не могут быть более точными, чем сами основные единицы.

Чистая внешняя сила, действующая на Систему 1, выводится из Рисунка 2 и приведенного выше обсуждения как

.

F _чистая = F _пол – f = 150 N – 24.{2} [/ латекс]

Обсуждение

Ни одна из сил между компонентами Системы 1, например, между руками профессора и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это – отметить, что силы между компонентами система отменяет, потому что они равны по величине и противоположны по направлению. Например, сила, прилагаемая профессором к тележке, приводит к тому, что на нее действует равная и противоположная сила.В этом случае обе силы действуют на одну и ту же систему и, следовательно, отменяются. Таким образом внутренние силы (между компонентами системы) отменяются. Выбор Системы 1 имел решающее значение для решения этой проблемы.

Равные и противоположные реакции: третий закон движения Ньютона

Второй закон движения Исаака Ньютона описывает, что происходит, когда внешняя сила действует на массивное тело в состоянии покоя или в равномерном линейном движении. Что происходит с телом, к которому прилагается эта внешняя сила? Эта ситуация описывается третьим законом движения Ньютона.В нем говорится: «На каждое действие есть равное и противоположное противодействие».

Ньютон опубликовал свои законы движения в 1687 году в своей основополагающей работе «Philosophiæ Naturalis Principia Mathematica» (Математические принципы естественной философии), в которой он формализовал описание того, как массивные тела движутся под действием внешних сил.

Ньютон расширил более раннюю работу Галилео Галилея, который разработал первые точные законы движения масс, по словам Грега Ботуна, профессора физики в Университете Орегона.Эксперименты Галилея показали, что все тела ускоряются с одинаковой скоростью, независимо от размера и массы. Ньютон также раскритиковал и расширил работы Рене Декарта, который также опубликовал свод законов природы в 1644 году, через два года после рождения Ньютона. Законы Декарта очень похожи на первый закон движения Ньютона.

Возврат

Силы всегда возникают попарно; когда одно тело прижимается к другому, второе тело с такой же силой отталкивается. Например, когда вы толкаете тележку, тележка толкает вас назад; когда вы тянете за веревку, веревка тянется к вам; и когда сила тяжести прижимает вас к земле, земля толкает вас к вашим ногам.Упрощенная версия этого феномена была выражена так: «Вы не можете прикоснуться без прикосновения».

Если корпус A оказывает усилие F на корпус B , то корпус B оказывает равную и противоположную силу – F обратно на корпус A . Математическое выражение для этого: F AB = – F BA

Нижний индекс AB указывает, что A оказывает силу на B , а BA указывает, что B действует усилие на A .Знак минус указывает на то, что силы направлены в противоположные стороны. Часто F AB и F BA упоминаются как сила действия и сила реакции ; однако выбор which is совершенно произвольный.

Если один объект намного, намного массивнее другого, особенно в случае, когда первый объект привязан к Земле, практически все ускорение передается второму объекту, и ускорение первого объекта может быть безопасно игнорировать.Например, если бы вы поставили ноги и бросили бейсбольный мяч на запад, вам не нужно было бы учитывать, что вы фактически заставили вращение Земли немного ускориться, пока мяч находился в воздухе. Однако, если бы вы стояли на роликовых коньках и бросили шар для боулинга вперед, вы бы начали двигаться назад с заметной скоростью.

Кто-то может спросить: «Если две силы равны и противоположны, почему они не нейтрализуют друг друга?» Собственно, в некоторых случаях это так. Представьте книгу, лежащую на столе.Вес книги давит на стол с силой мг , в то время как стол толкает книгу вверх с равной и противоположной силой. В этом случае силы нейтрализуют друг друга, потому что книга не ускоряется. Причина этого в том, что обе силы действуют на одно и то же тело, а третий закон Ньютона описывает два разных тела, действующих друг на друга.

Рассмотрим лошадь и телегу. Лошадь тянет телегу, и телега тянет лошадь назад. Две силы равны и противоположны, так почему же тележка вообще движется? Причина в том, что лошадь также оказывает силу на землю, которая является внешней по отношению к системе телеги, а земля оказывает обратную силу на систему телеги, заставляя ее ускоряться.

Третий закон Ньютона в действии

Ракеты, путешествующие в космосе, охватывают все три закона движения Ньютона.

Когда двигатели запускают и толкают ракету вперед, это результат реакции. Двигатель сжигает топливо, которое ускоряется к задней части корабля. Это заставляет силу в противоположном направлении толкать ракету вперед. Двигатели также можно использовать по бокам ракеты, чтобы заставить ее изменить направление, или спереди, чтобы создать обратную силу, чтобы замедлить ракету.

И если во время работы снаружи ракеты у космонавта порвется веревка, и он отнесется от ракеты, он может использовать один из своих инструментов, например, чтобы изменить направление и вернуться к ракете. Астронавт может бросить свой молот в направлении, прямо противоположном тому, куда он хочет. Молот очень быстро улетит от ракеты, а космонавт очень медленно вернется к ракете. Вот почему Третий закон Ньютона считается фундаментальным принципом ракетостроения.

Дополнительный отчет подготовила Рэйчел Росс, участник Live Science.

См. Также:

Дедуктивное доказательство третьего закона Ньютона.

Дедуктивное доказательство третьего закона Ньютона Кен Эмис

1. Справочная информация

Каждый студент-физик изучает три закона движения Ньютона. Заманчиво считать, что это три отдельных и независимых закона. Это не так. И первый, и третий законы могут быть математически выведены из Второй закон, как мы покажем.

То, что первый закон может происходить из второго, известно давно. Второй закон, F _net = m a , говорит нам, что чистая (векторная сумма) всех сил, действующих на тело, равна равняется произведению массы тела на его векторное ускорение. Когда ускорение равно нулю, результирующая сила должна быть равна нулю. Это именно содержание первого закона.

2.Третий закон

Третий закон Ньютона часто считают «тривиальным», но он более тонкий, чем большинство студентов понимают. В нем утверждается, что «если тело A действует на тело B, то B оказывает на A. силу равной величины и противоположного направления ». F _AB = – F _BA . Пара сил в этом законе часто называется «парой действие-противодействие». О каждой силе говорят, что она является “реактивной” силой другой, хотя этот язык просто оформление витрины.Термины “действие” и “реакция” часто вводят в заблуждение. студентам, и их лучше избегать в этих обсуждениях, поскольку они не нужны.

Давайте сначала рассмотрим случай контакта двух тел. Каждый оказывает влияние на другой – на интерфейсе или в точке соприкосновения, где тела соприкасаются. Если эта точка или граница раздела рассматривается как “тело” нулевой массы, тогда второй закон Ньютона говорит нам, что F _net = 0 a , поэтому F _нетто = 0 .Таким образом, результирующая сила, действующая на тело нулевой массы, всегда равна нулю, какие бы силы ни действовали на него. Следовательно, если на тело нулевой массы действуют только две силы, они должны складываться в ноль и, следовательно, должны быть одинакового размера и противоположно направленными. Это устанавливает третий закон Ньютона.

Повторение этого может прояснить ситуацию. Любую силу можно разложить на две части. В этом случае чистую силу на интерфейсе можно считать суммой: (1) чистая сила из-за действия A на границу раздела, и (2) чистая сила сила из-за B, действующего на интерфейс.Два соприкасающихся тела эквивалентны двум телам с телом нулевой массы между ними в точке соприкосновения. Мы показали, что эти две силы складываются в ноль, поэтому они должны быть силами равной величины и противоположного направления. Q.E.D.

3. Взгляд внимательнее

Если это кажется вам слишком “банальным”, мы можем сделать аргументацию более строгой. Рассмотрим три шарика, контактирующих друг с другом, как показано на рис. 1A. Мы показываем только контактные силы двух больших шаров, действующих на меньший.Конечно, меньший оказывает равные и противоположно направленные силы и на большие. Теперь рассмотрим предельный случай, когда маленький шарик стал меньше, как на рис. 1B, и, наконец, на рис. 1C маленький шарик сжался до нулевого размера – точки. Показанные изначально неравные силы обязательно стали равными. Теперь они также коллинеарны и разнонаправлены.

Рис. 1. Три тела в контакте. Силы, действующие на меньшую середину один изначально неравный по размеру или направление.В пределе как средний размер и масса тела оба идут в ноль, эти два силы становятся равными, противоположные и коллинеарно в точке контакт.

Хотя на рис.1 показан случай сжатия в точке контакта, этот аргумент в равной степени применим к силам противоположного направления, например гравитационному притяжению.

4. Контактная поверхность

Когда тела соприкасаются по поверхности, мы можем подразделить поверхность на бесконечно малые части, которые можно рассматривать как точки.Аргумент раздела 2 может быть применен, заключая, что сила A, действующая на B, имеет равную величину и противоположное направление к силе B, действующей на A, и эти силы являются коллинеарными, поэтому они не производят крутящий момент. Теперь, интегрируя по всей поверхности контакта, находим, что чистая сила A, действующая на B, также имеет тот же размер и противоположный размер к чистой силе B, действующей на A, а чистый крутящий момент от всех сил равен нулю, что означает, что F _AB = – F _BA .Опять же, у нас есть установил третий закон Ньютона.

В качестве конкретной иллюстрации рассмотрим два соприкасающихся тела. Теперь поместите кусок бумаги, разделяющей их в точке соприкосновения. Тот факт, что в статье гораздо меньшая масса, чем у двух тел, гарантирует, что результирующая сила, действующая на бумагу очень мала, и силы, которые действуют на нее два тела, почти равны и наоборот. Этот пример может быть полезен при обучении студентов этой концепции.

5.Окончательное обобщение

До сих пор мы рассматривали только тела, находящиеся в контакте. А как насчет сил, которые действуют на расстояние, такое как гравитационные, электрические и магнитные силы? Вот где наш подход к этой проблеме позволяет сделать действительно глубокое понимание.

Рис. 2. Схематическое изображение двух отдельных тел A и B. взаимодействуя с пространством в соответствии с третьим законом Ньютона. Силы на этих телах показаны.

Если между двумя телами любой протяженности есть пространство, но с нулевой массой, тогда рассмотрение пространства как “третьего тела в середине” дает тот же результат, что и выше! Вы не ожидали, что это будет так просто, не так ли?

6. Новые идеи этого подхода

Рассмотрим последствия этого нового подхода. Если третий закон Ньютона верен во всех отношениях, он говорит нам, что пространство между объектами действительно должно иметь нулевую массу.Вспомните, сколько лет физики потратили на идею вещества, называемого «светоносный эфир», который «заполняет все пространство». [1] Если бы у них была только польза из доказательства, которое мы изложили выше, они бы поняли, что этот эфир должен иметь ровно нулевую массу. Тогда, если бы они действительно верили третьему закону Ньютона, у них не было бы беспокоило (теперь заброшенное) понятие эфира. Они бы поняли, что их эфир экспериментально неотличимы от ничего.[3]

Хотя идея светоносного эфира исчезла из учебников, редко оценив даже сноску, современная физика ввела более тонкие и более хитрые способы придать пространству структуру и содержание. У них есть фантазии такие названия, как «состояния вакуума». Если что-то из этого нового якобы “в” космосе имеет массу, или если само пространство имеет массу, то тщательные измерения сил между взаимодействующими телами должны выявить этот факт. Любое неравенство сил действия и противодействия на телах, взаимодействующих через промежуточное пространство, выявило бы массу пространства.

Критики такой интерпретации Третьего закона Ньютона могут возражать против рассмотрения пространство как «безмассовое тело». Почему это должно вызывать такую ​​тревогу? Физики развлекали еще более безумные концепции и даже включали их в свои теории. В ХХ веке физики вполне комфортно жили с понятием безмассовые нейтрино.

7. Почему Ньютон не рассказал нам об этом?

Этот анализ не фигурирует в трудах Ньютона, но он изобрел исчисление и наверняка имел некоторое представление о предельных процессах.[2] Почему он разделил свою революционную идею на три отдельные части? Может быть, он не понимал, что три закона действительно были одним? Мог ли он сдержать это важное понимание чтобы конкуренты не могли легко следовать его «стопам гиганта»?

8. Заключение

Пора перестать говорить о «трех законах Ньютона» и просто сослаться на к такой важной идее, как «закон механики Ньютона». Это на два меньше Студентам, изучающим законы, нужно будет ломиться перед экзаменами.Часто говорят, что можно пройдите элементарный курс физики, если вы знаете законы механики Ньютона и все их логические следствия. Эти последствия включают в себя законы сохранения энергии и импульса. Возможно, в этом что-то есть.

---

Примечания

1. Свенсон, Лойд С. Эфирный эфир, история Эксперименты Майкельсона-Морли-Миллера с дрейфом эфира. Техасский университет Press, 1972 г.

2. Ньютон, сэр Исаак. Математические основы естественной философии. 1729.

3. Физики теперь играют с понятиями темной материи и темной энергии, предположительно. заполняя все пространство, учитывая малозаметные данные о движении далеких звезд и галактики. Это никоим образом не отменяет приведенные здесь аргументы. Это просто делает расчеты сложнее.

---

© 2002 Кен Эмис и Дональд Э. Симанек. Разрешение на воспроизведение и использование всего этого документа разрешено образовательной некоммерческой только для целей.

Вернуться на первую страницу.
Перейти к новой теории гравитации Кена Эмиса.
Вернуться к началу этого документа.
Вернитесь к передовой науке.

Законы движения для детей

Пожалуйста, напишите или поделитесь этой статьей!

В 1600-х годах в Англии сэр Исаак Ньютон был занят, пытаясь объяснить то, что происходит на Земле и в природе. Он всегда спрашивал: «Почему?»

Он объяснил гравитацию, движение, движение планет, свет и цвет.

Он открыл так много вещей и смог показать, как они работают, с помощью экспериментов и математики. Настолько, что его часто называют «отцом современной науки».

На протяжении многих лет идеи Ньютона проверялись снова и снова. Теперь ученые согласны с идеями Ньютона о движении и назвали их тремя законами движения Ньютона.

Первый закон Ньютона:

Объект, который сидит в состоянии покоя, будет оставаться в состоянии покоя, а объект, который находится в движении, будет оставаться в движении, пока на него не действует сила.

Вот почему астронавты могут отпускать инструмент в космосе, и он будет оставаться на одном месте, пока они его не схватят. Если космонавт бросит инструмент, он полетит по прямой и никогда не остановится.

Таким образом, инструмент будет оставаться на одном месте или продолжать двигаться в одном направлении и с той же скоростью вечно, потому что в пространстве нет силы тяжести или воздуха, которые могли бы воздействовать на инструмент.

Второй закон Ньютона:

F = ma: Чем больше сила, тем больше ускорение.Чем больше масса, тем больше сила, необходимая для перемещения объекта.

Два объекта с разным весом (массой) будут нуждаться в разных силах для их перемещения, и уровни ускорения будут разными.

Формула, используемая для второго закона Ньютона: F = ma. Это Сила = масса, умноженная на ускорение. Вы можете найти ускорение, изменив формулу на a = F ÷ m.

В алгебре есть правило: «что бы ни было сделано с одной стороной уравнения, вы должны сделать то же самое с другой стороной».

Попробуйте найти формулу для определения массы. Вы правы, если придумали m = F ÷ a

Третий закон Ньютона:

На каждое действие есть равная и противоположная реакция. Силы всегда находятся в парах. Если силы равны в противоположных направлениях, объект не будет двигаться. Силы нейтрализуют друг друга, так что ускорение равно нулю.

Если одна сила, действующая в одном направлении, больше, чем сила, действующая в противоположном направлении, объект будет двигаться.

Например, если вы тянете за веревку, привязанную к грузу кирпичей, и кирпичи начинают двигаться, сила, которую вы используете, больше, чем кирпичи используют, чтобы оставаться на одном месте.

Ракеты, отправляемые в космос, используют три закона движения Ньютона.

Когда срабатывают двигатели, ракета поднимается вверх, преодолевая гравитацию Земли, и в то же время взрыв топлива создает силу в нижней части ракеты.

Сила вперед больше, чем сила назад, и ракета ускоряется вверх.

Вопросы:

1. Что такое первый закон движения Ньютона?
2. Что такое второй закон движения Ньютона?
3. Что такое третий закон движения Ньютона?
4. Почему в космосе молот космонавта остается в одном месте, когда он его роняет?
5. Какие две равные силы действуют при зажигании двигателей ракеты?

Ответы:

1. Первый закон движения Ньютона: покоящийся объект будет оставаться в покое, а движущийся объект будет оставаться в движении, если на него не действует сила.
2. Второй закон движения Ньютона: сила равна массе, умноженной на ускорение.
3. Третий закон движения Ньютона: на каждое действие существует противоположная реакция, и силы действуют парами.
4. Молот космонавта будет оставаться в одном месте, потому что на него не действуют сила тяжести и воздух.
5. Когда зажигаются двигатели ракеты, одна сила толкает ракету вверх в атмосферу, а другая толкает сгоревшее топливо из выхлопных газов на землю.