Богданов К.Ю. – учебник физики для 10 класса
§ 10. ТРЕТИЙ ЗАКОН НЬЮТОНА: ДЕЙСТВИЕ РАВНО ПРОТИВОДЕЙСТВИЮ
Два тела, взаимодействующие между собой, всегда действуют друг на друга с силами, векторы которых равны по модулю, противоположны по направлению и лежат на одной прямой.
В справедливости третьего закона Ньютона мы убеждаемся на каждом шагу. Действительно, делая шаг, мы действуем на землю с силой, направленной вниз. От действия нашей силы участок земли под ступнёй деформируется, и возникающие в результате этого упругие силы земли действуют на ступню вверх. Стоя на земле, мы давим на неё вниз с силой, равной силой тяжести, а она в ответ действует на нас с точно такой же силой, направленной вверх.
Попробуем использовать
третий закон Ньютона, чтобы найти силу, с которой мяч массой m действует на стену, отскакивая от
неё (см. рис.
Опыты показали, что третий закон Ньютона справедлив не только для сил упругости, которыми обмениваются взаимодействующие тела, но и для сил трения. Так, тело
 рис. 10б).
рис. 10б).
Наглядным примером, иллюстрирующим третий закон Ньютона, может служить плавание человека в воде, когда он движется вперёд, толкая назад воду руками и ногами. Каждый раз, когда он с силой толкает воду назад, такая же по величине сила действует на него вперёд со стороны воды.
Взаимодействующие тела действуют друг на друга с равными по величине силами не только при непосредственном контакте, но и на расстоянии. Земля с помощью сил гравитации притягивает Луну с точно такой же силой, с какой Луна притягивает Землю. Однако сила притяжения Луны для Земли очень мала, так масса Земли в 80 раз больше, чем у Луны. Поэтому Луна вращается вокруг Земли, а Земля вокруг Солнца, масса которого почти в миллион раз больше. Третий закон Ньютона справедлив также для электрических и магнитных сил.
Третий закон Ньютона,
казалось бы, делает бессмысленной известную игру «перетягивание каната», ведь,
на людей, тянущих за канат с обеих сторон, действуют одинаковая сила – упругая
сила растянутой верёвки (см.
Автомобиль не мог бы
сдвинуться с места без третьего закона Ньютона. Работа мотора заставляет
участок колеса, соприкасающийся с землёй, двигаться назад (см. рис. 10г).
Однако хорошее сцепление с дорогой препятствует этому движению, и колесо лишь
давит на землю с силой
рис. 10г).
Однако хорошее сцепление с дорогой препятствует этому движению, и колесо лишь
давит на землю с силой
Вопросы для повторения:
· Сформулируйте третий закон Ньютона?
· Для каких видов сил справедлив этот закон?
· Приведите несколько примеров, иллюстрирующих действие третьего закона Ньютона.
Рис. 10. Применение третьего закона Ньютона для (а) вычисления силы, действующей на стену со стороны отскакивающего мяча, (
Примеры 2 и 3 закона ньютона.
 Примеры применения третьего закона ньютона
Примеры применения третьего закона ньютонаТри закона сэра Исаака Ньютона описывают движение массивных тел и как они взаимодействуют.
В то время как законы Ньютона могут показаться очевидными для нас сегодня, более трех веков назад они считались революционными.
Содержание:
Ньютон, пожалуй, наиболее известен своей работой по изучению гравитации и движения планет. Призванный астрономом Эдмондом Галлеем после признания того, что за несколько лет до этого он потерял доказательство эллиптических орбит, Ньютон опубликовал свои законы в 1687 году в своей оригинальной работе «Philosophiæ Naturalis Principia Mathematica» (Математические принципы естественной философии), в которой он формализовал описание того, как массивные тела движутся под воздействием внешних сил.
Формулируя свои три закона, Ньютон упростил обращение к массивным телам, считая их математическими точками без размера или вращения. Это позволило ему игнорировать такие факторы, как трение, сопротивление воздуха, температура, свойства материала и т. д. и сосредоточиться на явлениях, которые могут быть описаны исключительно по массе, длине и времени. Следовательно, три закона не могут быть использованы для описания точности поведения больших жестких или деформируемых объектов. Однако во многих случаях они обеспечивают подходящие точные приближения.
д. и сосредоточиться на явлениях, которые могут быть описаны исключительно по массе, длине и времени. Следовательно, три закона не могут быть использованы для описания точности поведения больших жестких или деформируемых объектов. Однако во многих случаях они обеспечивают подходящие точные приближения.
Законы Ньютона
Законы Ньютона относятся к движению массивных тел в инерциальной системе отсчета, иногда называемой ньютоновской системой отсчета, хотя сам Ньютон никогда не описывал такую систему. Инерциальную систему отсчета можно описать как трехмерную систему координат, которая либо стационарна, либо равномерно линейна, т. е. Не ускоряется и не вращается. Он обнаружил, что движение в такой инерциальной системе отсчета может быть описано тремя простыми законами.
Первый закон движения Ньютона

Требуется сила, действующая на них извне, чтобы вызвать такое изменение. Это свойство массивных тел сопротивляться изменениям в их движении иногда называют инерцией.
В современной физике первый закон Ньютона принято формулировать в следующем виде:
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Второй закон движения Ньютона
Описывает, что происходит с массивным телом, когда на него воздействует внешняя сила. В нем говорится: Сила, действующая на объект, равна массе этого объекта своего ускорения. Это написано в математической форме как F = ma, где F — сила, m — масса, a — ускорение. Жирные буквы указывают, что сила и ускорение являются векторными величинами, что означает, что они имеют как величину, так и направление. Сила может быть одной силой, или это может быть векторная сумма более чем одной силы, которая является чистой силой после объединения всех сил.
Когда постоянная сила действует на массивное тело, она заставляет ее ускоряться, т. е. Изменять свою скорость с постоянной скоростью. В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация просматривается из движущейся системы отсчета, это тело может показаться ускоряющимся, замедляющим или изменяющим направление в зависимости от направления силы и направлений, в которых объект и система отсчета перемещается относительно друг друга.
В современной физике второй закон Ньютона принято формулировать в следующем виде:
В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
Третий закон движения Ньютона
Гласит: Для каждого действия существует равное противодействие. Этот закон описывает то, что происходит с телом, когда оно оказывает силу на другое тело. Силы всегда встречаются парами, поэтому, когда одно тело толкает другого, второе тело отталкивается так же сильно. Например, когда вы нажимаете тележку, тележка отталкивается от вас; когда вы тянете за веревку, веревка откидывается на вас; когда сила тяжести тянет вас к земле, земля подталкивает вас и когда ракета воспламеняет свое топливо за ним, расширяющийся выхлопной газ толкается на ракете, заставляя его ускоряться.
Этот закон описывает то, что происходит с телом, когда оно оказывает силу на другое тело. Силы всегда встречаются парами, поэтому, когда одно тело толкает другого, второе тело отталкивается так же сильно. Например, когда вы нажимаете тележку, тележка отталкивается от вас; когда вы тянете за веревку, веревка откидывается на вас; когда сила тяжести тянет вас к земле, земля подталкивает вас и когда ракета воспламеняет свое топливо за ним, расширяющийся выхлопной газ толкается на ракете, заставляя его ускоряться.
Если один объект намного, гораздо более массивный, чем другой, особенно в случае привязки первого объекта к Земле, практически все ускорение передается второму объекту, и ускорение первого объекта можно безопасно игнорировать, Например, если вы бросили мяч на запад, вам не нужно было бы считать, что вы на самом деле заставили вращаться Землю быстрее, пока мяч находился в воздухе. Однако, если вы стоите на роликовых коньках, и вы бросили мяч для боулинга, вы начнете двигаться назад с заметной скоростью.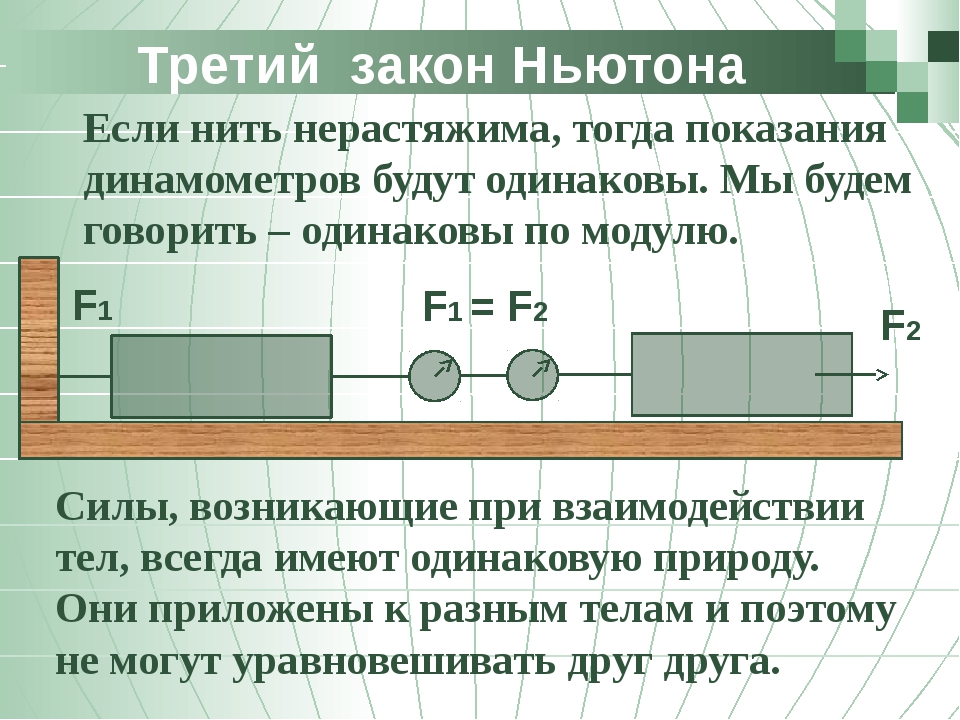
В современной физике третий закон Ньютона принято формулировать в следующем виде:
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Три закона были проверены бесчисленными экспериментами за последние три столетия, и до сих пор они широко используются для описания видов предметов и скоростей, с которыми мы сталкиваемся в повседневной жизни. Они составляют основу того, что сейчас известно как классическая механика, а именно изучение массивных объектов, которые больше, чем очень мелкие масштабы, рассматриваемые квантовой механикой, и которые движутся медленнее, чем очень высокие скорости, релятивистские механики.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой F2, с какой лошадь тянет сани вперед (сила F1)? Почему эти силы не уравновешиваются?
Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 9).
Сила F1 со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения f1полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней F2направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы f2, направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна; и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила f1 будет уравновешена силами f2 (первый закон Ньютона).
После того как лошадь сдвинула сани и установилось равномерное движение саней, сила f1 будет уравновешена силами f2 (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Третий закон Ньютона позволяет объяснить явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 10) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую.
ньютон третий движение отдача
Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Рис. 72. Лошадь сдвинет и повезет нагруженные сани, потому что со стороны дороги на ее копыта действуют большие силы трения, чем на скользкие полозья саней
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой
, с какой лошадь тянет сани вперед (сила
)? Почему эти силы не уравновешиваются? Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они, приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 72). Сила
со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения
полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней
, направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы
, направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила
будет уравновешена силами
(первый закон Ньютона).
72). Сила
со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения
полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней
, направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы
, направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила
будет уравновешена силами
(первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Рис. 73. При нагревании пробирки с водой пробка вылетает в одну сторону, а «пушка» катится в противоположную сторону
Третий закон Ньютона позволяет рассчитатьявление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 73) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую. Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей. Таким образом, ускорения, получаемые пушкой и снарядом, направлены противоположно, а по модулю обратно пропорциональны массам этих тел. В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении. Обозначим скорость, полученную снарядом, через
, а скорость, полученную пушкой, через
, а массы этих тел обозначим через
и
соответственно. Тогда
В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении. Обозначим скорость, полученную снарядом, через
, а скорость, полученную пушкой, через
, а массы этих тел обозначим через
и
соответственно. Тогда
Примеров взаимодействия тел можно привести сколь угодно много. Когда вы, находясь в одной лодке, начнете за веревку подтягивать другую, то и ваша лодка обязательно продвинется вперед (рис. 1). Действуя на вторую лодку, вы заставляете ее действовать на вашу лодку.
Если вы ударите ногой по футбольному мячу, то немедленно ощутите об-ратное действие на ногу. При соударении двух бильярдных шаров изменяют свою скорость, т. е. получают ускорения, оба шара. Когда при формировании железнодорожного состава вагоны наталкиваются друг на друга, буферные пружины сжимаются у обоих вагонов. Все это проявления общего закона взаимодействия тел.
Действия тел друг на друга носят характер взаимодействия не только при непосредственном контакте тел.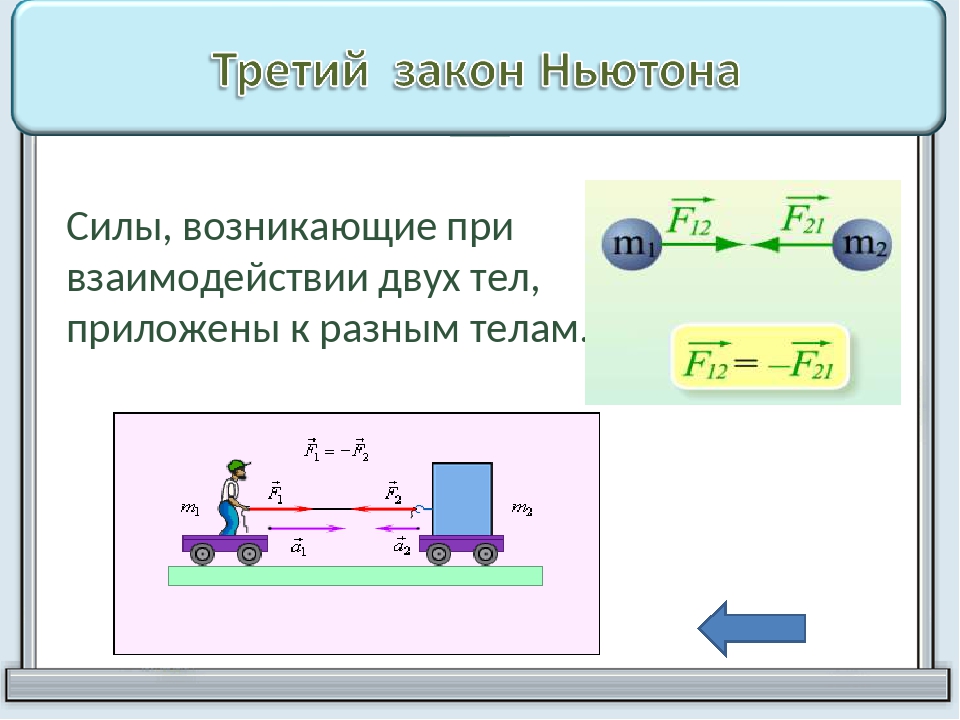 Положите, например, на гладкий стол два сильных магнита разноименными полюсами навстречу друг другу, и вы тут же обнаружите, что магниты начнут двигаться навстречу друг другу. Земля притягивает Луну (сила всемирного тяготения) и заставляет ее двигаться по криволинейной траектории; в свою очередь Луна также притягивает Землю (тоже сила всемирного тяготения). Хотя, естественно, в системе отсчета, связанной с Землей, ускорение Земли, вызываемое этой силой, нельзя обнаружить непосредственно (непосредственно нельзя обнаружить даже значительно большее ускорение, вызываемое притяжением Земли Солнцем), оно проявляется в виде приливов.
Положите, например, на гладкий стол два сильных магнита разноименными полюсами навстречу друг другу, и вы тут же обнаружите, что магниты начнут двигаться навстречу друг другу. Земля притягивает Луну (сила всемирного тяготения) и заставляет ее двигаться по криволинейной траектории; в свою очередь Луна также притягивает Землю (тоже сила всемирного тяготения). Хотя, естественно, в системе отсчета, связанной с Землей, ускорение Земли, вызываемое этой силой, нельзя обнаружить непосредственно (непосредственно нельзя обнаружить даже значительно большее ускорение, вызываемое притяжением Земли Солнцем), оно проявляется в виде приливов.
Заметные изменения скоростей обоих взаимодействующих тел наблюдаются, однако, лишь в тех случаях, когда массы этих тел не сильно отличаются друг от друга. Если же взаимодействующие тела значительно различаются по массе, заметное ускорение получает только то из них, которое имеет меньшую массу. Так, при падении камня Земля заметно ускоряет движение камня, но ускорение Земли (а ведь камень тоже притягивает Землю) практически обнаружить нельзя, так как оно очень мало.
Силы взаимодействия двух тел
Выясним с помощью опыта, как связаны между собой силы взаимодействия двух тел. Грубые измерения сил взаимодействия можно произвести на следующих опытах.
1 опыт . Возьмем два динамометра, зацепим друг за друга их крючки и, взявшись за кольца, будем растягивать их, следя за показаниями, обоих динамометров (рис. 2).
Мы увидим, что при любых растяжениях показания обоих динамометров будут совпадать; значит, сила, с которой первый динамометр действует на второй, равна силе, с которой второй динамометр действует на первый.
2 опыт . Возьмем достаточно сильный магнит и железный брусок и положим их на катки, чтобы уменьшить трение о стол (рис. 3). К магниту и бруску прикрепим одинаковые мягкие пружины, зацепленные другими концами на столе. Магнит и брусок притянутся друг к другу и растянут пружины.
Опыт показывает, что к моменту прекращения движения пружины оказываются растянутыми совершенно одинаково. Это означает, что на оба тела со стороны пружин действуют одинаковые по модулю и противоположные по направлению силы:
\(\vec F_1 = -\vec F_2 \qquad (1)\)
Так как магнит покоится, то сила \(\vec F_2\) равна по модулю и противоположна по направлению силе \(\vec F_4\), с которой на него действует брусок:
\(\vec F_1 = \vec F_4 \qquad (2)\)
Точно так же равны по модулю и противоположны по направлению силы, действующие на брусок со стороны магнита и пружины:
\(\vec F_3 = -\vec F_1 \qquad (3)\)
Из равенств (1), (2), (3) следует, что силы, с которыми взаимодействуют магнит и брусок, равны по модулю и противоположны по направлению:
\(\vec F_3 = -\vec F_4 \qquad (1)\)
Опыт показывает, что силы взаимодействия между двумя телами равны по модулю и противоположны по направлению и в тех случаях когда тела движутся.
3 опыт . На двух тележках, которые могут катиться по рельсам, стоят два человека А и В (рис. 4). Они держат в руках концы веревки. Легко обнаружить, что независимо от того, кто натягивает («выбирает») веревку, А или В или оба вместе, тележки всегда приходят в движение одновременно и притом в противоположных направлениях. Измеряя ускорения тележек, можно убедиться, что ускорения обратно пропорциональны массам каждой из тележек (вместе с человеком). Отсюда следует, что силы, действующие на тележки, равны по модулю.
Третий закон Ньютона
На основе этих и подобных опытов можно сформулировать третий закон Ньютона.
Силы, с которыми тела действуют друг на друга, равны по модулю и на-правлены вдоль одной прямой в противоположные стороны.
Это означает, что если на тело А со стороны тела В действует сила \(\vec F_A\) (рис. 5), то одновременно на тело В со стороны тела А действует сила \(\vec F_B\), причем
\(\vec F_A = -\vec F_B \qquad (5)\)
Используя второй закон Ньютона, можно равенство (5) записать так:
\(m_1 \cdot \vec a_1 = -m_2 \cdot \vec a_2 \qquad (6)\)
Отсюда следует, что
\(\frac{a_1}{a_2} = \frac{m_2}{m_1}= \mbox{const} \qquad (7)\)
Отношение модулей а 1 и а 2 ускорений взаимодействующих тел определяется обратным отношением их масс и совершенно не зависит от природы действующих между ними сил.
(Здесь имеется в виду, что никакие другие силы, кроме сил взаимодействия, на эти тела не действуют.)
В этом можно убедиться на следующем простом опыте. Поставим на гладкие рельсы две тележки одинаковой массы и на одной из них закрепим небольшой электрический двигатель, на вал которого может наматываться нить, привязанная к другой тележке, а на другую поставим гирю, масса которой равна массе двигателя (рис. 6). При работающем двигателе обе тележки устремляются с одинаковыми ускорениями навстречу друг другу и проходят одинаковые пути. Если массу одной из тележек сделать вдвое большей, то ее ускорение окажется в два раза меньше, чем другой, и за то же время она пройдет вдвое меньший путь.
Связь ускорений взаимодействующих тел с их массами можно установить и на таком опыте (рис. 7). На горизонтальную платформу помещают два катка разной массы, соединенные нитью.
Опыт покажет, что можно найти такое положение катков, когда они при вращении платформы не перемещаются по ней. Измерив радиусы обращения катков вокруг центра платформы, определим отношение центростремительных ускорений катков:
Измерив радиусы обращения катков вокруг центра платформы, определим отношение центростремительных ускорений катков:
\(\frac{a_1}{a_2} = \frac{\omega \cdot R_1}{\omega \cdot R_2}\) или \(\frac{a_1}{a_2} = \frac{R_1}{R_2}\).
Сравнив это отношение с обратным отношением масс тел \(\frac{m_2}{m_1}\), убеждаемся, что \(\frac{a_1}{a_2} = \frac{m_2}{m_1}\) при любых скоростях вращения платформы.
Примечание
Надо помнить, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому не могут уравновешивать друг друга.
Непонимание этого часто приводит к недоразумениям. Так, иногда с помощью третьего закона Ньютона пытаются объяснить, почему то или иное тело находится в покое. Например, утверждают, что мел на столе покоится якобы потому, что сила тяжести \(\vec F_t\), действующая на тело, согласно третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости \(\vec N\) (силе реакции опоры), действующей на него со стороны стола. На самом деле равенство \(\vec F_t + \vec N = 0\) является следствием второго закона Ньютона, а не третьего: ускорение равно нулю, поэтому и сумма сил, действующих на тело, равна нулю. Из третьего же закона Ньютона вытекает лишь, что сила реакции опоры \(\vec N\) равна по модулю силе \(\vec P\), с которой мел давит на стол (рис. 8). Эти силы приложены к разным телам и направлены в противоположные стороны.
На самом деле равенство \(\vec F_t + \vec N = 0\) является следствием второго закона Ньютона, а не третьего: ускорение равно нулю, поэтому и сумма сил, действующих на тело, равна нулю. Из третьего же закона Ньютона вытекает лишь, что сила реакции опоры \(\vec N\) равна по модулю силе \(\vec P\), с которой мел давит на стол (рис. 8). Эти силы приложены к разным телам и направлены в противоположные стороны.
Примеры применения третьего закона Ньютона.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой F 2 , с какой лошадь тянет сани вперед (сила F 1)? Почему эти силы не уравновешиваются?
Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 9).
Сила F 1 со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения f 1 полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней F 2 направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы f 2 , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна; и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила f 1 будет уравновешена силами f 2 (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Третий закон Ньютона позволяет объяснить явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 10) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую.
Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
О значении третьего закона Ньютона
Главное значение третьего закона Ньютона обнаруживается при исследовании движения системы материальных точек или системы тел. Этот закон позволяет доказать важные теоремы динамики и сильно упрощает изучение движения тел в тех случаях, когда их нельзя рассматривать как материальные точки.
Третий закон сформулирован для точечных тел (материальных точек). Его применение для реальных тел, имеющих конечные размеры, требует уточнения и обоснования. В данной формулировке нельзя применять этот закон и в неинерциальных системах отсчета.
Литература
- Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
- Элементарный учебник физики: Учебное пособие. В 3 т. / Под ред. Г.С. Ландсберга: Т. 1. Механика. Теплота. Молекулярная физика – М.: ФИЗМАТЛИТ, 2003. – 608с.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Рис. 72. Лошадь сдвинет и повезет нагруженные сани, потому что со стороны дороги на ее копыта действуют большие силы трения, чем на скользкие полозья саней
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой , с какой лошадь тянет сани вперед (сила )? Почему эти силы не уравновешиваются? Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они, приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 72). Сила со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней , направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила будет уравновешена силами (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Рис. 73. При нагревании пробирки с водой пробка вылетает в одну сторону, а «пушка» катится в противоположную сторону
Третий закон Ньютона позволяет рассчитать явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 73) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую. Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей. Таким образом, ускорения, получаемые пушкой и снарядом, направлены противоположно, а по модулю обратно пропорциональны массам этих тел. В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении. Обозначим скорость, полученную снарядом, через , а скорость, полученную пушкой, через , а массы этих тел обозначим через и соответственно. Тогда
Здесь и – модули скоростей.
Выстрел из всякого оружия сопровождается отдачей. Старинные пушки после выстрела откатывались назад. В современных орудиях ствол укрепляется на лафете не жестко, а при помощи приспособлений, которые позволяют стволу отходить назад; затем пружины снова возвращают его на место. В автоматическом огнестрельном оружии явление отдачи используется для того, чтобы перезарядить орудие. При выстреле отходит только затвор. Он выбрасывает использованную гильзу, а затем пружины, возвращая его на место, вводят в ствол новый патрон. Этот принцип используется не только в пулеметах и автоматических пистолетах, но и в скорострельных пушках.
Рекомендуем также
Третий закон Ньютона
Цели:
- Сформулировать третий закон Ньютона, следствия из этого закона.
- Продолжить формирование навыка решения задач на законы Ньютона.
Оборудование: Штатив, динамометры, шарики разной массы, брусок, грузы, мультимедиа-плеер. На уроке используется презентация. (Приложение 1).
Ход урока| Эпиграф: … Не знаю, чем я могу казаться миру, но самому себе кажусь я мальчиком, играющим у моря, которому удалось найти более красивый камешек, чем другим: но океан неизвестности лежит передо мной. Исаак Ньютон (1643–1727 гг.) |
1. Постановка проблемного вопроса.
| На слайде фрагмент мультфильма “Ну, погоди!”:
волк хочет догнать корабль с зайцем, садится в
парусную лодку и заставляет лодку двигаться, дуя
в парус. Учитель: Ребята попробуйте объяснить можно ли заставить двигаться лодку, как это сделал волк из мультфильма “Ну, погоди!”? Ответить на этот вопрос вы сможете, изучив тему сегодняшнего урока. Открываем тетради, записываем число, тему урока “Третий закон Ньютона”. |
2. Актуализация знаний
Фронтальный опрос:
– Что называется инерцией?
– Приведите примеры движения тел по инерции? (+
задачи подготовленные учениками).
– Продемонстрируйте явление инерции, используя
стакан, открытку и монету.
– Как читается 1-й закон Ньютона?
– Какие системы отсчета называются
инерциальными?
– Что такое сила?
– Назовите характеристики силы?
– Экспериментально обоснуйте утверждение:
ускорение тела прямо пропорционально
равнодействующей сил, приложенных к нему.
– Докажите экспериментально, что ускорение тела
обратно пропорционально массе тела.
– Сформулируйте второй закон Ньютона (пример
доказательства справедливости закона:
презентация ученика).
– Как математически записывается второй закон
Ньютона?
– Какие из величин: сила, скорость, ускорение,
перемещение – всегда совпадают по направлению?
Самостоятельная работа:
1. В каких из приведенных ниже случаев речь идет о движении тел по инерции?
А. Человек, поскользнувшись, падает назад;
Б. Всадник летит через голову споткнувшейся лошади;
В. Пузырек воздуха равномерно и прямолинейно движется в трубке с водой.
2. Ниже перечислены движения тел относительно Земли. Какую систему отсчета, связанную с одним из этих тел, нельзя считать инерциальной системой отсчета? Систему отсчета, связанную с Землей, примите за инерциальную.
А. Девочка бежит с постоянной скоростью.
Б. Поезд движется равноускоренно.
В. Хоккейная шайба равномерно скользит по гладкому льду.
3. Как движется шарик массой 500 г под действием постоянной силы 4 Н?
А. С ускорением 2 м/с2;
Б. С постоянной скоростью 0,125 м/с;
В. С постоянным ускорением 8 м/с2.
Ответы:
- А, Б, В.
- Б.
- В.
Решите задачу:
Автомобиль за 20с развивает скорость 36 км/ч.
Найдите силу, сообщающую ускорение, если масса
автомобиля 2 т? (Ответ: 1 кН).
3. Изучение нового материала
Учитель: Мы знаем, что не бывать одностороннего действия одного тела на другое, тела всегда взаимодействуют друг с другом.
Ударьте слегка ладошкой по столу. Что вы почувствовали? Ударьте сильнее по столу, что вы теперь ощущаете? Почему больно вам, если вы действовали на стол?
При взаимодействии друг с другом тела оказываются “равноправными”. Поскольку характеристикой взаимодействия является сила, то “равноправие” тел при взаимодействии выражается в равенстве сил, с которыми тела действуют друг на друга.
Демонстрация: Зацепим крючками два динамометра слегка и разведем их в стороны. Заметим показания обеих динамометров. Увеличим действие динамометров друг на друга. Заметим новые показания.
Равенство сил при взаимодействии тел или частиц отражает 3-й закон Ньютона.
Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.
Математическая запись закона:
Проиллюстрируем 3-й закон Ньютона:
Пример: Человек при ходьбе действует на почву силой F1. Почва с такой же силой F2 действует на человека вперед. Эта сила уравновешивает мышечное усилие, действующее на ступню назад. Нога остается на месте (не проскальзывает). Человек имеет возможность переступить на другую ногу.
| Реактивное движение. |
Реактивный двигатель действует на топливо с силой F1, направленной против предполагаемого движения ракеты. Топливо же действует на двигатель в противоположную сторону, приводя в движение ракету.
Мини-исследовательская работа: Изучение 3-го закона Ньютона (работа ученика).
Особенности 3-го закона Ньютона.
- Силы возникают при взаимодействии;
- Появляются парами;
- Одной природы;
- Не уравновешиваются;
- Приложены к разным темам.
Вернемся к фрагменту мультфильма. Скажите, соответствует ли эта ситуация тому, что мы изучили сегодня на уроке. По третьему закону Ньютона, выходящий из волка воздух действует на него с той же силой, с какой волк выдыхает. Но волк и лодка с парусом – единое целое. Силы приложены не к разным телам, а к одному. Эти силы равны по модулю и противоположны по направлению. По первому закону их равнодействующая равна нулю, следовательно, скорость в данном случае равна нулю.
4. Закрепление
- Два мальчика взялись за руки. Первый мальчик толкает второго с силой 105 Н. С какой силой толкает второй мальчик первого?
- Вопрос-шутка. Возможно ли? Вы получили удар в челюсть при боксерском поединке, и ушли в нокдаун. А когда вышли из него, сказали: “Ох, я ему и дал”.
- Оцените достоверность его рассказа.
Некий озорной барон
Был в болото погружен.
За косичку себя взял
И себя с конем поднял.
Это быть могло когда-то?
Как считаете, ребята?
- К железной тележке с помощью длинного стержня прилеплен магнит. Придет ли тележка в движение?
5. Домашнее задание
- § 12
- Упр. 12(3)
- Приведите примеры проявления законов Ньютона в быту и природе.
Примеры применения третьего закона ньютона. Законы Ньютона
Три закона сэра Исаака Ньютона описывают движение массивных тел и как они взаимодействуют.
В то время как законы Ньютона могут показаться очевидными для нас сегодня, более трех веков назад они считались революционными.
Содержание:
Ньютон, пожалуй, наиболее известен своей работой по изучению гравитации и движения планет. Призванный астрономом Эдмондом Галлеем после признания того, что за несколько лет до этого он потерял доказательство эллиптических орбит, Ньютон опубликовал свои законы в 1687 году в своей оригинальной работе «Philosophiæ Naturalis Principia Mathematica» (Математические принципы естественной философии), в которой он формализовал описание того, как массивные тела движутся под воздействием внешних сил.
Формулируя свои три закона, Ньютон упростил обращение к массивным телам, считая их математическими точками без размера или вращения. Это позволило ему игнорировать такие факторы, как трение, сопротивление воздуха, температура, свойства материала и т. д. и сосредоточиться на явлениях, которые могут быть описаны исключительно по массе, длине и времени. Следовательно, три закона не могут быть использованы для описания точности поведения больших жестких или деформируемых объектов. Однако во многих случаях они обеспечивают подходящие точные приближения.
Законы Ньютона
Законы Ньютона относятся к движению массивных тел в инерциальной системе отсчета, иногда называемой ньютоновской системой отсчета, хотя сам Ньютон никогда не описывал такую систему. Инерциальную систему отсчета можно описать как трехмерную систему координат, которая либо стационарна, либо равномерно линейна, т. е. Не ускоряется и не вращается. Он обнаружил, что движение в такой инерциальной системе отсчета может быть описано тремя простыми законами.
Первый закон движения Ньютона
Гласит: Если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения. Это просто означает, что вещи не могут начинать, останавливать или изменять направление самостоятельно.
Требуется сила, действующая на них извне, чтобы вызвать такое изменение. Это свойство массивных тел сопротивляться изменениям в их движении иногда называют инерцией.
В современной физике первый закон Ньютона принято формулировать в следующем виде:
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Второй закон движения Ньютона
Описывает, что происходит с массивным телом, когда на него воздействует внешняя сила. В нем говорится: Сила, действующая на объект, равна массе этого объекта своего ускорения. Это написано в математической форме как F = ma, где F — сила, m — масса, a — ускорение. Жирные буквы указывают, что сила и ускорение являются векторными величинами, что означает, что они имеют как величину, так и направление. Сила может быть одной силой, или это может быть векторная сумма более чем одной силы, которая является чистой силой после объединения всех сил.
Когда постоянная сила действует на массивное тело, она заставляет ее ускоряться, т. е. Изменять свою скорость с постоянной скоростью. В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация просматривается из движущейся системы отсчета, это тело может показаться ускоряющимся, замедляющим или изменяющим направление в зависимости от направления силы и направлений, в которых объект и система отсчета перемещается относительно друг друга.
В современной физике второй закон Ньютона принято формулировать в следующем виде:
В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
Третий закон движения Ньютона
Гласит: Для каждого действия существует равное противодействие. Этот закон описывает то, что происходит с телом, когда оно оказывает силу на другое тело. Силы всегда встречаются парами, поэтому, когда одно тело толкает другого, второе тело отталкивается так же сильно. Например, когда вы нажимаете тележку, тележка отталкивается от вас; когда вы тянете за веревку, веревка откидывается на вас; когда сила тяжести тянет вас к земле, земля подталкивает вас и когда ракета воспламеняет свое топливо за ним, расширяющийся выхлопной газ толкается на ракете, заставляя его ускоряться.
Если один объект намного, гораздо более массивный, чем другой, особенно в случае привязки первого объекта к Земле, практически все ускорение передается второму объекту, и ускорение первого объекта можно безопасно игнорировать, Например, если вы бросили мяч на запад, вам не нужно было бы считать, что вы на самом деле заставили вращаться Землю быстрее, пока мяч находился в воздухе. Однако, если вы стоите на роликовых коньках, и вы бросили мяч для боулинга, вы начнете двигаться назад с заметной скоростью.
В современной физике третий закон Ньютона принято формулировать в следующем виде:
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Три закона были проверены бесчисленными экспериментами за последние три столетия, и до сих пор они широко используются для описания видов предметов и скоростей, с которыми мы сталкиваемся в повседневной жизни. Они составляют основу того, что сейчас известно как классическая механика, а именно изучение массивных объектов, которые больше, чем очень мелкие масштабы, рассматриваемые квантовой механикой, и которые движутся медленнее, чем очень высокие скорости, релятивистские механики.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Рис. 72. Лошадь сдвинет и повезет нагруженные сани, потому что со стороны дороги на ее копыта действуют большие силы трения, чем на скользкие полозья саней
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой , с какой лошадь тянет сани вперед (сила )? Почему эти силы не уравновешиваются? Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они, приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 72). Сила со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней , направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила будет уравновешена силами (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Рис. 73. При нагревании пробирки с водой пробка вылетает в одну сторону, а «пушка» катится в противоположную сторону
Третий закон Ньютона позволяет рассчитать явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 73) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую. Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей. Таким образом, ускорения, получаемые пушкой и снарядом, направлены противоположно, а по модулю обратно пропорциональны массам этих тел. В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении. Обозначим скорость, полученную снарядом, через , а скорость, полученную пушкой, через , а массы этих тел обозначим через и соответственно. Тогда
Здесь и – модули скоростей.
Выстрел из всякого оружия сопровождается отдачей. Старинные пушки после выстрела откатывались назад. В современных орудиях ствол укрепляется на лафете не жестко, а при помощи приспособлений, которые позволяют стволу отходить назад; затем пружины снова возвращают его на место. В автоматическом огнестрельном оружии явление отдачи используется для того, чтобы перезарядить орудие. При выстреле отходит только затвор. Он выбрасывает использованную гильзу, а затем пружины, возвращая его на место, вводят в ствол новый патрон. Этот принцип используется не только в пулеметах и автоматических пистолетах, но и в скорострельных пушках.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику . А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу ! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g . Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона – это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона , действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона , сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы . Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.
Примеров взаимодействия тел можно привести сколь угодно много. Когда вы, находясь в одной лодке, начнете за веревку подтягивать другую, то и ваша лодка обязательно продвинется вперед (рис. 1). Действуя на вторую лодку, вы заставляете ее действовать на вашу лодку.
Если вы ударите ногой по футбольному мячу, то немедленно ощутите об-ратное действие на ногу. При соударении двух бильярдных шаров изменяют свою скорость, т. е. получают ускорения, оба шара. Когда при формировании железнодорожного состава вагоны наталкиваются друг на друга, буферные пружины сжимаются у обоих вагонов. Все это проявления общего закона взаимодействия тел.
Действия тел друг на друга носят характер взаимодействия не только при непосредственном контакте тел. Положите, например, на гладкий стол два сильных магнита разноименными полюсами навстречу друг другу, и вы тут же обнаружите, что магниты начнут двигаться навстречу друг другу. Земля притягивает Луну (сила всемирного тяготения) и заставляет ее двигаться по криволинейной траектории; в свою очередь Луна также притягивает Землю (тоже сила всемирного тяготения). Хотя, естественно, в системе отсчета, связанной с Землей, ускорение Земли, вызываемое этой силой, нельзя обнаружить непосредственно (непосредственно нельзя обнаружить даже значительно большее ускорение, вызываемое притяжением Земли Солнцем), оно проявляется в виде приливов.
Заметные изменения скоростей обоих взаимодействующих тел наблюдаются, однако, лишь в тех случаях, когда массы этих тел не сильно отличаются друг от друга. Если же взаимодействующие тела значительно различаются по массе, заметное ускорение получает только то из них, которое имеет меньшую массу. Так, при падении камня Земля заметно ускоряет движение камня, но ускорение Земли (а ведь камень тоже притягивает Землю) практически обнаружить нельзя, так как оно очень мало.
Силы взаимодействия двух тел
Выясним с помощью опыта, как связаны между собой силы взаимодействия двух тел. Грубые измерения сил взаимодействия можно произвести на следующих опытах.
1 опыт . Возьмем два динамометра, зацепим друг за друга их крючки и, взявшись за кольца, будем растягивать их, следя за показаниями, обоих динамометров (рис. 2).
Мы увидим, что при любых растяжениях показания обоих динамометров будут совпадать; значит, сила, с которой первый динамометр действует на второй, равна силе, с которой второй динамометр действует на первый.
2 опыт . Возьмем достаточно сильный магнит и железный брусок и положим их на катки, чтобы уменьшить трение о стол (рис. 3). К магниту и бруску прикрепим одинаковые мягкие пружины, зацепленные другими концами на столе. Магнит и брусок притянутся друг к другу и растянут пружины.
Опыт показывает, что к моменту прекращения движения пружины оказываются растянутыми совершенно одинаково. Это означает, что на оба тела со стороны пружин действуют одинаковые по модулю и противоположные по направлению силы:
\(\vec F_1 = -\vec F_2 \qquad (1)\)
Так как магнит покоится, то сила \(\vec F_2\) равна по модулю и противоположна по направлению силе \(\vec F_4\), с которой на него действует брусок:
\(\vec F_1 = \vec F_4 \qquad (2)\)
Точно так же равны по модулю и противоположны по направлению силы, действующие на брусок со стороны магнита и пружины:
\(\vec F_3 = -\vec F_1 \qquad (3)\)
Из равенств (1), (2), (3) следует, что силы, с которыми взаимодействуют магнит и брусок, равны по модулю и противоположны по направлению:
\(\vec F_3 = -\vec F_4 \qquad (1)\)
Опыт показывает, что силы взаимодействия между двумя телами равны по модулю и противоположны по направлению и в тех случаях когда тела движутся.
3 опыт . На двух тележках, которые могут катиться по рельсам, стоят два человека А и В (рис. 4). Они держат в руках концы веревки. Легко обнаружить, что независимо от того, кто натягивает («выбирает») веревку, А или В или оба вместе, тележки всегда приходят в движение одновременно и притом в противоположных направлениях. Измеряя ускорения тележек, можно убедиться, что ускорения обратно пропорциональны массам каждой из тележек (вместе с человеком). Отсюда следует, что силы, действующие на тележки, равны по модулю.
Третий закон Ньютона
На основе этих и подобных опытов можно сформулировать третий закон Ньютона.
Силы, с которыми тела действуют друг на друга, равны по модулю и на-правлены вдоль одной прямой в противоположные стороны.
Это означает, что если на тело А со стороны тела В действует сила \(\vec F_A\) (рис. 5), то одновременно на тело В со стороны тела А действует сила \(\vec F_B\), причем
\(\vec F_A = -\vec F_B \qquad (5)\)
Используя второй закон Ньютона, можно равенство (5) записать так:
\(m_1 \cdot \vec a_1 = -m_2 \cdot \vec a_2 \qquad (6)\)
Отсюда следует, что
\(\frac{a_1}{a_2} = \frac{m_2}{m_1}= \mbox{const} \qquad (7)\)
Отношение модулей а 1 и а 2 ускорений взаимодействующих тел определяется обратным отношением их масс и совершенно не зависит от природы действующих между ними сил.
(Здесь имеется в виду, что никакие другие силы, кроме сил взаимодействия, на эти тела не действуют.)
В этом можно убедиться на следующем простом опыте. Поставим на гладкие рельсы две тележки одинаковой массы и на одной из них закрепим небольшой электрический двигатель, на вал которого может наматываться нить, привязанная к другой тележке, а на другую поставим гирю, масса которой равна массе двигателя (рис. 6). При работающем двигателе обе тележки устремляются с одинаковыми ускорениями навстречу друг другу и проходят одинаковые пути. Если массу одной из тележек сделать вдвое большей, то ее ускорение окажется в два раза меньше, чем другой, и за то же время она пройдет вдвое меньший путь.
Связь ускорений взаимодействующих тел с их массами можно установить и на таком опыте (рис. 7). На горизонтальную платформу помещают два катка разной массы, соединенные нитью.
Опыт покажет, что можно найти такое положение катков, когда они при вращении платформы не перемещаются по ней. Измерив радиусы обращения катков вокруг центра платформы, определим отношение центростремительных ускорений катков:
\(\frac{a_1}{a_2} = \frac{\omega \cdot R_1}{\omega \cdot R_2}\) или \(\frac{a_1}{a_2} = \frac{R_1}{R_2}\).
Сравнив это отношение с обратным отношением масс тел \(\frac{m_2}{m_1}\), убеждаемся, что \(\frac{a_1}{a_2} = \frac{m_2}{m_1}\) при любых скоростях вращения платформы.
Примечание
Надо помнить, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому не могут уравновешивать друг друга.
Непонимание этого часто приводит к недоразумениям. Так, иногда с помощью третьего закона Ньютона пытаются объяснить, почему то или иное тело находится в покое. Например, утверждают, что мел на столе покоится якобы потому, что сила тяжести \(\vec F_t\), действующая на тело, согласно третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости \(\vec N\) (силе реакции опоры), действующей на него со стороны стола. На самом деле равенство \(\vec F_t + \vec N = 0\) является следствием второго закона Ньютона, а не третьего: ускорение равно нулю, поэтому и сумма сил, действующих на тело, равна нулю. Из третьего же закона Ньютона вытекает лишь, что сила реакции опоры \(\vec N\) равна по модулю силе \(\vec P\), с которой мел давит на стол (рис. 8). Эти силы приложены к разным телам и направлены в противоположные стороны.
Примеры применения третьего закона Ньютона.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой F 2 , с какой лошадь тянет сани вперед (сила F 1)? Почему эти силы не уравновешиваются?
Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 9).
Сила F 1 со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения f 1 полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней F 2 направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы f 2 , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна; и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила f 1 будет уравновешена силами f 2 (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Третий закон Ньютона позволяет объяснить явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 10) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую.
Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
О значении третьего закона Ньютона
Главное значение третьего закона Ньютона обнаруживается при исследовании движения системы материальных точек или системы тел. Этот закон позволяет доказать важные теоремы динамики и сильно упрощает изучение движения тел в тех случаях, когда их нельзя рассматривать как материальные точки.
Третий закон сформулирован для точечных тел (материальных точек). Его применение для реальных тел, имеющих конечные размеры, требует уточнения и обоснования. В данной формулировке нельзя применять этот закон и в неинерциальных системах отсчета.
Литература
- Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
- Элементарный учебник физики: Учебное пособие. В 3 т. / Под ред. Г.С. Ландсберга: Т. 1. Механика. Теплота. Молекулярная физика – М.: ФИЗМАТЛИТ, 2003. – 608с.
Движение всех окружающих нас макроскопических объектов описывается с помощью так называемых трех законов Ньютона. В данной статье не будем говорить ничего о первых двух из них, а рассмотрим подробно третий закон Ньютона и примеры его проявления в жизни.
Формулировка закона
Каждый из нас замечал, что при прыжке на какую-либо поверхность она будто бы “ударяет” по нашим ногам, или же если взяться за руль велосипеда, то он начинает давить на ладони. Все это примеры третьего закона Ньютона. В курсе физики в общеобразовательных школах он формулируется следующим образом: любое тело, оказывающее силовое воздействие на некоторое другое тело, испытывает аналогичное воздействие от последнего, направленное в противоположную сторону.
Математически этот закон может быть записан в следующем виде:
В левой части равенства записана сила, с которой первое тело действует на второе, в правой части стоит аналогичная по модулю сила, с которой второе тело воздействует на первое, но уже в противоположном направлении (поэтому появляется знак минуса).
Равенство модулей и противоположное направление рассмотренных сил привели к тому, что этот закон часто называют взаимодействием, или принципом воздействия-противодействия.
Действие на различные тела – ключевой момент рассматриваемого закона
Взглянув на представленную выше формулу, можно подумать, что раз уж силы по модулю равны, а по направлению противоположны, то зачем вообще их рассматривать, ведь они аннулируют друг друга. Это суждение является ошибочным. Доказательством этого является огромное количество примеров третьего закона Ньютона из жизни. Например, лошадь тянет телегу. Согласно рассматриваемому закону лошадь воздействует на телегу, но с такой же силой последняя действует на животное в противоположном направлении. Тем не менее вся система (лошадь и телега) не стоит на месте, а движется.
Приведенный пример показывает, что рассматриваемый принцип действия-противодействия не является таким простым, как это кажется на первый взгляд. Силы F 12 ¯ и -F 21 ¯ не аннулируются, поскольку приложены они к разным телам. Лошадь не стоит на месте, хотя телега и препятствует этому, только потому, что на ее копыта действует еще одна сила, которая и стремится сообщить ускорение животному – это воздействие поверхности земли (реакция опоры).
Таким образом, при решении задач на 3-й ньютоновский принцип следует всегда рассматривать силы, которые действуют на отдельные конкретные тела, а не на всю систему сразу.
Связь с законом сохранения количества движения
Третий ньютоновский закон по сути является причиной сохранения импульса системы. Действительно, рассмотрим один интересный пример третьего закона Ньютона – движение ракеты в космическом пространстве. Всем известно, что оно осуществляется за счет реактивной тяги. Но откуда берется эта тяга? Ракета несет на своем борту баки с топливом, например с керосином и кислородом. Во время сгорания топливо покидает ракету и вылетает с огромной скоростью в космическое пространство. Этот процесс характеризуется воздействием сгоревших газов на корпус ракеты, последний же оказывает воздействие на газы с аналогичной силой. Результат проявляется в ускорении газов в одну сторону, а ракеты – в другую.
Но ведь эту задачу можно рассмотреть и с точки зрения сохранения импульса. Если учесть знаки скоростей газа и ракеты, то суммарный импульс окажется равным нулю (он таким и был до сгорания топлива). Импульс сохраняется только потому, что действующие согласно принципу действия-противодействия силы являются внутренними, существующими между частями системы (ракетой и газами).
Как рассматриваемый принцип связан с ускорением всей системы?
Иными словами, как изменятся силы F 12 ¯ и -F 21 ¯, если система, в которой они возникают, будет двигаться ускоренно? Обратимся к примеру с лошадью и телегой. Допустим, вся система начала увеличивать свою скорость, однако силы F 12 ¯ и -F 21 ¯ останутся при этом неизменными. Ускорение возникает за счет увеличения силы, с которой поверхность земли действует на копыта животного, а не за счет уменьшения силы противодействия телеги -F 21 ¯.
Таким образом, взаимодействия внутри системы не зависят от ее внешнего состояния.
Некоторые примеры из жизни
“Приведите примеры третьего закона Ньютона” – это задание часто можно слышать от школьных учителей. Выше уже были приведены примеры с ракетой и лошадью. В списке ниже перечислим еще некоторые:
- отталкивание пловца от стенки бассейна: пловец получает ускорение, поскольку на него воздействует стена;
- полет птицы: толкая воздух вниз и назад при каждом взмахе крыла, птица получает толчок от воздуха вверх и вперед;
- отскок футбольного мяча от стены: проявление противодействия силы реакции стены;
- притяжение Земли: с какой силой наша планета притягивает нас вниз, с точно такой же мы воздействуем на нее вверх (для планеты это мизерная сила, она ее “не замечает”, а мы – да).
Все эти примеры приводят к важному выводу: любые силовые взаимодействия в природе всегда возникают в виде пары противодействующих сил. Невозможно оказать воздействие на объект, не испытав при этом его противодействие.
примеры, связь с ускорением системы и с ее импульсом. Примеры применения третьего закона ньютона Всегда ли действует третий закон ньютона
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику . А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу ! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g . Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона – это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона , действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона , сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы . Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой F 2 , с какой лошадь тянет сани вперед (сила F 1)? Почему эти силы не уравновешиваются?
Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 9).
Сила F 1 со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения f 1 полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней F 2 направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы f 2 , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна; и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила f 1 будет уравновешена силами f 2 (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Третий закон Ньютона позволяет объяснить явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 10) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую.
Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Рис. 72. Лошадь сдвинет и повезет нагруженные сани, потому что со стороны дороги на ее копыта действуют большие силы трения, чем на скользкие полозья саней
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой , с какой лошадь тянет сани вперед (сила )? Почему эти силы не уравновешиваются? Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они, приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 72). Сила со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней , направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила будет уравновешена силами (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Рис. 73. При нагревании пробирки с водой пробка вылетает в одну сторону, а «пушка» катится в противоположную сторону
Третий закон Ньютона позволяет рассчитатьявление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 73) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую. Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей. Таким образом, ускорения, получаемые пушкой и снарядом, направлены противоположно, а по модулю обратно пропорциональны массам этих тел. В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении. Обозначим скорость, полученную снарядом, через , а скорость, полученную пушкой, через , а массы этих тел обозначим через и соответственно. Тогда
ОПРЕДЕЛЕНИЕ
Формулировка третьего закона Ньютона . Два тела действуют друг на друга с , равными по модулю и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.
Описание третьего закона Ньютона
Например, книга, лежащая на столе, действует на стол с силой, прямо пропорциональной своей и направленной вертикально вниз. Согласно третьему закону Ньютона стол в это же время действует на книгу с абсолютно такой же по величине силой, но направленной не вниз, а вверх.
Когда яблоко падает с дерева, это Земля действует на яблоко силой своего гравитационного притяжения (вследствие чего яблоко равноускоренно движется к поверхности Земли), но при этом и яблоко притягивает к себе Землю с такой же силой. А то, что нам кажется, что это именно яблоко падает на Землю, а не наоборот, является следствием . Масса яблока по сравнению с массой Земли мала до несопоставимости, поэтому именно яблока заметно для глаз наблюдателя. Масса же Земли, по сравнению с массой яблока, огромна, поэтому ее ускорение практически незаметно.
Аналогично, если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не чувствуется. Однако если пнуть тяжелый железный мяч, ответное воздействие хорошо ощущается. Фактически, мы каждый день по многу раз «пинаем» очень и очень тяжелый мяч — нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе.
Таким образом, третий закон Ньютона утверждает, что силы как меры взаимодействия всегда возникают парами. Эти силы не уравновешиваются, так как всегда приложены к разным телам.
Третий закон Ньютона выполняется только в и справедлив для сил любой природы.
Примеры решения задач
ПРИМЕР 1
| Задание | На полу лифта стоит груз массой 20 кг. Лифт движется с ускорением м/с , направленным вверх. Определить силу, с которой груз будет действовать на пол лифта. |
| Решение | Сделаем рисунок На груз в лифте действуют сила тяжести и сила реакции опоры . По второму закону Ньютона: Направим координатную ось , как показано на рисунке и запишем это векторное равенство в проекциях на координатную ось: откуда сила реакции опоры: Груз будет действовать на пол лифта с силой, равной его весу. По третьему закону Ньютона, эта сила равна по модулю силе, с которой пол лифта действует на груз, т.е. силе реакции опоры: Ускорение свободного падения м/с Подставив в формулу численные значения физических величин, вычислим: |
| Ответ | Груз будет действовать на пол лифта с силой 236 Н. |
ПРИМЕР 2
| Задание | Сравнить модули ускорений двух шаров одинакового радиуса во время взаимодействия, если первый шар сделан из стали, а второй – из свинца. |
| Решение | Сделаем рисунок Сила удара, с которой второй шар действует на первый: а сила удара, с которой первый шар действует на второй: По третьему закону Ньютона, эти силы противоположны по направлению и равны по модулю, поэтому можно записать. Примеров взаимодействия тел можно привести сколь угодно много. Когда вы, находясь в одной лодке, начнете за веревку подтягивать другую, то и ваша лодка обязательно продвинется вперед (рис. 1). Действуя на вторую лодку, вы заставляете ее действовать на вашу лодку. Если вы ударите ногой по футбольному мячу, то немедленно ощутите об-ратное действие на ногу. При соударении двух бильярдных шаров изменяют свою скорость, т. е. получают ускорения, оба шара. Когда при формировании железнодорожного состава вагоны наталкиваются друг на друга, буферные пружины сжимаются у обоих вагонов. Все это проявления общего закона взаимодействия тел. Действия тел друг на друга носят характер взаимодействия не только при непосредственном контакте тел. Положите, например, на гладкий стол два сильных магнита разноименными полюсами навстречу друг другу, и вы тут же обнаружите, что магниты начнут двигаться навстречу друг другу. Земля притягивает Луну (сила всемирного тяготения) и заставляет ее двигаться по криволинейной траектории; в свою очередь Луна также притягивает Землю (тоже сила всемирного тяготения). Хотя, естественно, в системе отсчета, связанной с Землей, ускорение Земли, вызываемое этой силой, нельзя обнаружить непосредственно (непосредственно нельзя обнаружить даже значительно большее ускорение, вызываемое притяжением Земли Солнцем), оно проявляется в виде приливов. Заметные изменения скоростей обоих взаимодействующих тел наблюдаются, однако, лишь в тех случаях, когда массы этих тел не сильно отличаются друг от друга. Если же взаимодействующие тела значительно различаются по массе, заметное ускорение получает только то из них, которое имеет меньшую массу. Так, при падении камня Земля заметно ускоряет движение камня, но ускорение Земли (а ведь камень тоже притягивает Землю) практически обнаружить нельзя, так как оно очень мало. Силы взаимодействия двух телВыясним с помощью опыта, как связаны между собой силы взаимодействия двух тел. Грубые измерения сил взаимодействия можно произвести на следующих опытах. 1 опыт . Возьмем два динамометра, зацепим друг за друга их крючки и, взявшись за кольца, будем растягивать их, следя за показаниями, обоих динамометров (рис. 2). Мы увидим, что при любых растяжениях показания обоих динамометров будут совпадать; значит, сила, с которой первый динамометр действует на второй, равна силе, с которой второй динамометр действует на первый. 2 опыт . Возьмем достаточно сильный магнит и железный брусок и положим их на катки, чтобы уменьшить трение о стол (рис. 3). К магниту и бруску прикрепим одинаковые мягкие пружины, зацепленные другими концами на столе. Магнит и брусок притянутся друг к другу и растянут пружины. Опыт показывает, что к моменту прекращения движения пружины оказываются растянутыми совершенно одинаково. Это означает, что на оба тела со стороны пружин действуют одинаковые по модулю и противоположные по направлению силы: \(\vec F_1 = -\vec F_2 \qquad (1)\) Так как магнит покоится, то сила \(\vec F_2\) равна по модулю и противоположна по направлению силе \(\vec F_4\), с которой на него действует брусок: \(\vec F_1 = \vec F_4 \qquad (2)\) Точно так же равны по модулю и противоположны по направлению силы, действующие на брусок со стороны магнита и пружины: \(\vec F_3 = -\vec F_1 \qquad (3)\) Из равенств (1), (2), (3) следует, что силы, с которыми взаимодействуют магнит и брусок, равны по модулю и противоположны по направлению: \(\vec F_3 = -\vec F_4 \qquad (1)\) Опыт показывает, что силы взаимодействия между двумя телами равны по модулю и противоположны по направлению и в тех случаях когда тела движутся. 3 опыт . На двух тележках, которые могут катиться по рельсам, стоят два человека А и В (рис. 4). Они держат в руках концы веревки. Легко обнаружить, что независимо от того, кто натягивает («выбирает») веревку, А или В или оба вместе, тележки всегда приходят в движение одновременно и притом в противоположных направлениях. Измеряя ускорения тележек, можно убедиться, что ускорения обратно пропорциональны массам каждой из тележек (вместе с человеком). Отсюда следует, что силы, действующие на тележки, равны по модулю. Третий закон НьютонаНа основе этих и подобных опытов можно сформулировать третий закон Ньютона. Силы, с которыми тела действуют друг на друга, равны по модулю и на-правлены вдоль одной прямой в противоположные стороны. Это означает, что если на тело А со стороны тела В действует сила \(\vec F_A\) (рис. 5), то одновременно на тело В со стороны тела А действует сила \(\vec F_B\), причем \(\vec F_A = -\vec F_B \qquad (5)\) Используя второй закон Ньютона, можно равенство (5) записать так: \(m_1 \cdot \vec a_1 = -m_2 \cdot \vec a_2 \qquad (6)\) Отсюда следует, что \(\frac{a_1}{a_2} = \frac{m_2}{m_1}= \mbox{const} \qquad (7)\) Отношение модулей а 1 и а 2 ускорений взаимодействующих тел определяется обратным отношением их масс и совершенно не зависит от природы действующих между ними сил. (Здесь имеется в виду, что никакие другие силы, кроме сил взаимодействия, на эти тела не действуют.) В этом можно убедиться на следующем простом опыте. Поставим на гладкие рельсы две тележки одинаковой массы и на одной из них закрепим небольшой электрический двигатель, на вал которого может наматываться нить, привязанная к другой тележке, а на другую поставим гирю, масса которой равна массе двигателя (рис. 6). При работающем двигателе обе тележки устремляются с одинаковыми ускорениями навстречу друг другу и проходят одинаковые пути. Если массу одной из тележек сделать вдвое большей, то ее ускорение окажется в два раза меньше, чем другой, и за то же время она пройдет вдвое меньший путь. Связь ускорений взаимодействующих тел с их массами можно установить и на таком опыте (рис. 7). На горизонтальную платформу помещают два катка разной массы, соединенные нитью. Опыт покажет, что можно найти такое положение катков, когда они при вращении платформы не перемещаются по ней. Измерив радиусы обращения катков вокруг центра платформы, определим отношение центростремительных ускорений катков: \(\frac{a_1}{a_2} = \frac{\omega \cdot R_1}{\omega \cdot R_2}\) или \(\frac{a_1}{a_2} = \frac{R_1}{R_2}\). Сравнив это отношение с обратным отношением масс тел \(\frac{m_2}{m_1}\), убеждаемся, что \(\frac{a_1}{a_2} = \frac{m_2}{m_1}\) при любых скоростях вращения платформы. ПримечаниеНадо помнить, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому не могут уравновешивать друг друга. Непонимание этого часто приводит к недоразумениям. Так, иногда с помощью третьего закона Ньютона пытаются объяснить, почему то или иное тело находится в покое. Например, утверждают, что мел на столе покоится якобы потому, что сила тяжести \(\vec F_t\), действующая на тело, согласно третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости \(\vec N\) (силе реакции опоры), действующей на него со стороны стола. На самом деле равенство \(\vec F_t + \vec N = 0\) является следствием второго закона Ньютона, а не третьего: ускорение равно нулю, поэтому и сумма сил, действующих на тело, равна нулю. Из третьего же закона Ньютона вытекает лишь, что сила реакции опоры \(\vec N\) равна по модулю силе \(\vec P\), с которой мел давит на стол (рис. 8). Эти силы приложены к разным телам и направлены в противоположные стороны. Примеры применения третьего закона Ньютона.В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю. Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой F 2 , с какой лошадь тянет сани вперед (сила F 1)? Почему эти силы не уравновешиваются? Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 9). Сила F 1 со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения f 1 полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней F 2 направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы f 2 , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна; и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила f 1 будет уравновешена силами f 2 (первый закон Ньютона). Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места. Третий закон Ньютона позволяет объяснить явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 10) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую. Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей. О значении третьего закона НьютонаГлавное значение третьего закона Ньютона обнаруживается при исследовании движения системы материальных точек или системы тел. Этот закон позволяет доказать важные теоремы динамики и сильно упрощает изучение движения тел в тех случаях, когда их нельзя рассматривать как материальные точки. Третий закон сформулирован для точечных тел (материальных точек). Его применение для реальных тел, имеющих конечные размеры, требует уточнения и обоснования. В данной формулировке нельзя применять этот закон и в неинерциальных системах отсчета. Литература
Возможно вас заинтересует |
Третий закон Ньютона – AP Physics 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Ньютонов Третий закон – сила
Третий закон движения Ньютона гласит, что всякий раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает.
Третий закон движения Ньютона представляет собой определенную симметрию в природе: силы всегда возникают парами, и одно тело не может воздействовать на другое, не испытав силы. Всякий раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает. Математически, если тело A оказывает усилие F на тело B , то B одновременно оказывает усилие – F на A .В форме векторного уравнения:
F AB = −F BA
Мы иногда в общих чертах называем этот закон «действие-противодействие», где приложенная сила – это действие, а сила, испытываемая как следствие, – это противодействие. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.
Например, разгребите пловца, который отталкивается ногами от стены, чтобы набрать скорость. Чем больше силы она прикладывает к стене, тем сильнее она отталкивается.Это потому, что стена оказывает на нее ту же силу, что и она. Она толкает стену в направлении позади себя, поэтому стена будет оказывать на нее силу в направлении впереди нее и толкать ее вперед. Эта сила реакции, которая толкает тело вперед в ответ на силу, направленную назад, называется тягой и .
Есть две важные особенности третьего закона Ньютона. Во-первых, прилагаемые силы (действие и противодействие) всегда равны по величине, но противоположны по направлению.Во-вторых, эти силы действуют на разные тела или системы: сила A, действует на B, , а сила B действует на A . Другими словами, две силы – это разные силы, которые не действуют на одно и то же тело. Таким образом, они не отменяют друг друга.
Практические вопросы
Академия Хана
Силы по камню в почках
Травмы колена у спортсменов
Электростатика, медицина и металлические сферы
Официальная подготовка MCAT (AAMC)
Physics Question Pack Отрывок 17, вопрос 101
Ключевые точки
• Третий закон движения Ньютона представляет собой основную симметрию в природе, с испытываемой силой, равной по величине и противоположной по направлению действующей силе.
• Две равные и противоположные силы не отменяются, потому что они действуют на разные системы.
• Пары действие-реакция включают пловца, отталкивающего стену, вертолеты, создающие подъемную силу, выталкивая воздух вниз, и осьминога, толкающего себя вперед, выбрасывая воду из своего тела. Ракеты, самолеты и автомобили толкаются вперед за счет силы реакции тяги.
• Выбор системы – важный аналитический шаг в понимании физики проблемы и ее решении.
Ключевые термины
Третий закон движения Ньютона : Когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает.
Тяга : Сила реакции, которая толкает тело вперед в ответ на силу, направленную назад.
3-й закон Ньютона
3-й закон НьютонаДалее: Вес и масса Up: законы Ньютона Предыдущая: 2-й закон Ньютона
3-й закон Ньютона Второй закон Ньютона касается одного объекта, на который действует сила. проявил. Третий и последний закон движения, открытый Ньютоном, объясняет что происходит с объект, оказывающий силу.Третий закон можно резюмировать следующим образом: заявив, что:
Это говорит нам о том, что объект, оказывающий силу, испытывает “ реакцию ” силы той же величины, но в противоположном направлении от сила, которую он проявляет. Вот два примера этого закона. Представьте, что вы толкаете (твердую) стену с довольно большой силой, и предположим, что вы не сломаете через. Согласно Согласно третьему закону Ньютона стена оказывает равную и противоположную силу вернусь к вам. Как это согласуется со 2-м законом, который гласит, что сила вызывает ускорение? Ответ заключается в том, что когда вы толкаете стену, и стена давит на вас, трение между вашей обувью и полом также оказывает давление на вы, которого, если вам повезет, достаточно, чтобы вы не двигались назад от стены.Если вы толкнетесь в стену, стоя на лед, сила трения намного меньше, и вы действительно ускоряетесь назад подальше от стены.
Представьте себе немного другой сценарий. Предположим, вы совершаете космическую прогулку
рядом с космическим шаттлом, и ваш страховочный трос оборвется. Как бы ты вернулся
к шаттлу? Что нужно сделать, это взять один из инструментов из
пояс с инструментами и бросить его так тяжело, как вы можете, прямо подальше от волана.
Тогда с помощью второго и третьего законов Ньютона вы ускорите
обратно к шаттлу.Когда вы бросаете инструмент, вы толкаете его, вызывая
это ускорить. В то же время, согласно третьему закону Ньютона, инструмент подталкивает
спиной к вам в противоположном направлении, что заставляет вас ускоряться
обратно к шаттлу, если хотите.
Это принцип реактивного движения:
реактивная ракета быстро выбрасывает топливо, “ давя на него ”. Посредством
Третий закон: топливо оказывает равную и противоположную силу против
ракета, поэтому ракета ускоряется в направлении, противоположном направлению
выгнанное топливо идет.Другой пример 3-го закона – книга лжи.
на столе. Если бы стола не было, книга попала бы под
сила притяжения
между книгой и землей. Почему же тогда книга не съезжает со стола в соответствии с
2-й закон? Стол оказывает давление на книгу, которая просто
достаточно, чтобы отменить действие силы тяжести на книгу. По Ньютону
третий закон, книга также оказывает равную и противоположную силу на
стол, и поэтому стол чувствует вес книги.Если
книга была очень тяжелой, из-за ее веса стол
гнуться или даже сломаться. Это показано на следующем рисунке.
Далее: Вес и масса Up: законы Ньютона Предыдущая: 2-й закон Ньютона [email protected]
1999-09-29
Симметрия в силах – Колледж физики, главы 1-17
4 Динамика: сила и законы движения Ньютона
Сводка
- Поймите третий закон движения Ньютона.
- Применяйте третий закон Ньютона для определения систем и решения проблем движения.
В мюзикле Man of La Mancha есть отрывок, относящийся к третьему закону движения Ньютона. Санчо, описывая Дон Кихоту драку с женой, говорит: «Конечно, я нанес ей ответный удар, ваша светлость, но она намного сильнее меня, и вы знаете, что они говорят:« Попадает ли камень в кувшин или в кувшин ». ударится о камень, это будет плохо для питчера ». Это именно то, что происходит, когда одно тело воздействует на другое тело – первое также испытывает силу (равную по величине и противоположную по направлению).Многочисленные обычные переживания, такие как удар ногой или бросок мяча, подтверждают это. Это точно указано в третьем законе движения Ньютона .
ТРЕТИЙ ЗАКОН ДВИЖЕНИЯ НЬЮТОНА
Каждый раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает.
Этот закон представляет собой определенную симметрию в природе : Силы всегда возникают парами, и одно тело не может воздействовать на другое, не испытав силы.Мы иногда в общих чертах называем этот закон «действием-противодействием», где приложенная сила – это действие, а сила, испытываемая как следствие, – это противодействие. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.
Мы легко можем увидеть в действии третий закон Ньютона, взглянув на то, как люди передвигаются. Представьте себе пловца, отталкивающегося от края бассейна, как показано на рисунке 1. Она отталкивается ногами о стенку бассейна и ускоряется в направлении , противоположном направлению от ее толчка.Стена оказывает на пловца равную и противоположную силу. Вы можете подумать, что две равные и противоположные силы уравновешиваются, но они не , потому что они действуют на разные системы . В этом случае есть две системы, которые мы могли бы исследовать: пловец или стена. Если мы выберем пловца в качестве интересующей системы, как на рисунке, тогда [latex] \ textbf {F} _ {\ textbf {wall on feet}} [/ latex] является внешней силой для этой системы и влияет на ее движение. Пловец движется в направлении [латекса] \ textbf {F} _ {\ textbf {стены на ногах}}.[/ latex] Напротив, сила [latex] \ textbf {F} _ {\ textbf {feet on wall}} [/ latex] действует на стену, а не на интересующую нас систему. Таким образом, [latex] \ textbf {F} _ {\ textbf {feet on wall}} [/ latex] не влияет напрямую на движение системы и не отменяет [latex] \ textbf {F} _ {\ textbf {wall на ногах}}. [/ latex] Обратите внимание, что пловец толкает в направлении, противоположном тому, в котором она хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении.
Рис. 1. Когда пловец прикладывает силу F футов к стене на стене, она ускоряется в направлении, противоположном направлению ее толчка.Это означает, что чистая внешняя сила, действующая на нее, направлена в направлении, противоположном F футов на стене . Это противодействие возникает потому, что в соответствии с третьим законом движения Ньютона стена оказывает на нее силу F на ногах , равную по величине, но в направлении, противоположном тому, которое она оказывает на нее. Линия вокруг пловца указывает на интересующую его систему. Обратите внимание, что F футов на стене не действует на эту систему (пловца) и, таким образом, не отменяет F на стене на ногах .Таким образом, диаграмма свободного тела показывает только F стена на ногах , w , сила тяжести, и BF , подъемная сила воды, поддерживающая вес пловца. Вертикальные силы w и BF отменяются, поскольку нет вертикального движения.Легко найти другие примеры третьего закона Ньютона. Когда профессор шагает перед доской, она прикладывает силу к полу. Пол оказывает на профессора противодействующую силу, которая заставляет ее ускоряться вперед.Точно так же автомобиль ускоряется, потому что земля толкает ведущие колеса вперед в ответ на движение ведущих колес по земле. Вы можете видеть свидетельства того, что колеса отталкиваются назад, когда колеса вращаются на гравийной дороге и отбрасывают камни назад. В другом примере ракеты движутся вперед, выбрасывая газ назад с высокой скоростью. Это означает, что ракета оказывает большую обратную силу на газ в камере сгорания ракеты, и, следовательно, газ оказывает на ракету большую силу реакции вперед.Эта сила реакции называется тяги . Распространенное заблуждение, что ракеты двигаются сами по себе, толкаясь о землю или воздух позади них. На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы. Вертолеты также создают подъемную силу, выталкивая воздух вниз, тем самым испытывая восходящую силу реакции. Птицы и самолеты также летают, воздействуя на воздух в направлении, противоположном направлению силы, которая им нужна. Например, крылья птицы заставляют воздух двигаться вниз и назад, чтобы подняться и двигаться вперед.Осьминог движется в воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу. В ситуации, аналогичной ситуации с Санчо, профессиональные бойцы в клетках испытывают силу реакции при ударе, иногда ломая руку, ударившись о тело противника.
Пример 1: Приступая к работе: выбор правильной системы
Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал, как показано на рисунке 2. Ее масса составляет 65,0 кг, а масса тележки – 12 кг.0 кг, а оборудование – 7,0 кг. Вычислите ускорение, возникающее при приложении профессором к полу обратной силы 150 Н. Все силы, противодействующие движению, такие как трение колес тележки и сопротивление воздуха, составляют 24,0 Н.
Рисунок 2. Профессор толкает тележку с демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (за исключением f , поскольку он слишком мал для масштабирования). В каждом примере задаются разные вопросы; таким образом, интересующая система должна определяться по-разному для каждой из них.Система 1 подходит для примера 2, так как она запрашивает ускорение всей группы объектов. Только F пол и f являются внешними силами, действующими на Систему 1 вдоль линии движения. Все остальные силы либо отменяют, либо действуют во внешнем мире. Система 2 выбрана для этого примера, так что F prof будет внешней силой и будет соответствовать второму закону Ньютона. Обратите внимание, что диаграммы свободного тела, которые позволяют нам применять второй закон Ньютона, различаются в зависимости от выбранной системы.Стратегия
Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на рисунке 2. Профессор толкает назад с силой [латекс] \ textbf {F} _ {\ textbf {foot}} [/ latex] 150 Н. Согласно третьему закону Ньютона, пол движется вперед. сила реакции [latex] \ textbf {F} _ {\ textbf {floor}} [/ latex] 150 Н в Системе 1. Поскольку все движения горизонтальны, мы можем предположить, что в вертикальном направлении нет результирующей силы. Таким образом, проблема одномерная в горизонтальном направлении.Как уже отмечалось, [latex] \ textbf {f} [/ latex] препятствует движению и, таким образом, находится в противоположном направлении от [latex] \ textbf {F} _ {\ textbf {floor}}. [/ Latex] Обратите внимание, что мы не включайте силы [latex] \ textbf {F} _ {\ textbf {prof}} [/ latex] или [latex] \ textbf {F} _ {\ textbf {cart}} [/ latex], потому что они являются внутренними force, и мы не включаем [latex] \ textbf {F} _ {\ textbf {foot}} [/ latex], потому что он действует на пол, а не на систему. Никаких других значительных сил, действующих на Систему 1. Если чистая внешняя сила может быть найдена из всей этой информации, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение.См. Диаграмму свободного тела на рисунке.
Решение
Второй закон Ньютона дает
[латекс] \ boldsymbol {a \: =} [/ latex] [латекс] \ boldsymbol {\ frac {F _ {\ textbf {net}}} {m}.} [/ Latex]
Чистая внешняя сила, действующая на Систему 1, выводится из Рисунка 2 и приведенного выше обсуждения как
.[латекс] \ boldsymbol {\ textbf {F} _ {\ textbf {net}} = \ textbf {F} _ {\ textbf {floor}} – \ textbf {f} = 150 \ textbf {N} -24,0 \ textbf {N} = 126 \ textbf {N}.} [/ latex]
Масса Системы 1
[латекс] \ boldsymbol {m = (65.2} \ end {array} [/ latex]
Обсуждение
Ни одна из сил между компонентами Системы 1, например, между руками профессора и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это – отметить, что силы между компонентами система отменяет, потому что они равны по величине и противоположны по направлению. Например, сила, прилагаемая профессором к тележке, приводит к тому, что на нее действует равная и противоположная сила.В этом случае обе силы действуют на одну и ту же систему и, следовательно, отменяются. Таким образом внутренние силы (между компонентами системы) отменяются. Выбор Системы 1 имел решающее значение для решения этой проблемы.
Пример 2: Усилие тележки – выбор новой системы
Вычислите силу, которую профессор оказывает на тележку, показанную на рис. 2, при необходимости, используя данные из предыдущего примера.
Стратегия
Если мы теперь определим интересующую систему как тележку плюс оборудование (Система 2 на рисунке 2), то чистая внешняя сила в Системе 2 – это сила, которую профессор оказывает на тележку за вычетом трения.Сила, которую она оказывает на тележку, [latex] \ textbf {F} _ {\ textbf {prof}}, [/ latex] – это внешняя сила, действующая на Систему 2. [latex] \ textbf {F} _ {\ textbf {prof}} [/ latex] был внутренним по отношению к Системе 1, но он был внешним по отношению к Системе 2 и войдет во второй закон Ньютона для Системы 2.
Решение
Второй закон Ньютона можно использовать для поиска [latex] \ textbf {F} _ {\ textbf {prof}}. [/ Latex] Начиная с
[латекс] \ boldsymbol {a \: =} [/ latex] [латекс] \ boldsymbol {\ frac {F _ {\ textbf {net}}} {m}} [/ latex]
и отметив, что величина чистой внешней силы в Системе 2 составляет
[латекс] \ boldsymbol {F _ {\ textbf {net}} = F _ {\ textbf {prof}} – f,} [/ latex]
решаем для [latex] \ boldsymbol {F _ {\ textbf {prof}}}, [/ latex] желаемое количество:
[латекс] \ boldsymbol {F _ {\ textbf {prof}} = F _ {\ textbf {net}} + f.2) = 29 \ textbf {N}.} [/ Latex]
Теперь мы можем найти желаемую силу:
[латекс] \ boldsymbol {F _ {\ textbf {prof}} = F _ {\ textbf {net}} + f,} [/ latex]
[латекс] \ boldsymbol {F _ {\ textbf {prof}} = 29 \ textbf {N} +24.0 \ textbf {N} = 53 \ textbf {N}.} [/ Latex]
Обсуждение
Интересно, что эта сила значительно меньше, чем сила в 150 Н, которую профессор приложил к полу назад. Не вся сила 150 Н передается на тележку; кое-что ускоряет профессора.
Выбор системы – важный аналитический шаг как в решении проблем, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).
PHET EXPLORATIONS: GRAVITY FORCE LAB
Визуализируйте гравитационную силу, которую два объекта действуют друг на друга. Измените свойства объектов, чтобы увидеть, как изменяется сила тяжести.
Рисунок 3. Лаборатория силы тяжести- Третий закон движения Ньютона представляет собой основную симметрию в природе.Он гласит: всякий раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оказывает первое тело.
- Тяга – это сила реакции, которая толкает тело вперед в ответ на силу, направленную назад. Ракеты, самолеты и автомобили толкаются вперед за счет силы реакции тяги.
Концептуальные вопросы
1: Когда вы взлетаете на реактивном самолете, возникает ощущение, что вас толкают обратно в сиденье.Объясните, почему вы двигаетесь назад в сиденье – действительно ли на вас действует сила, направленная назад? (Те же рассуждения объясняют хлыстовые травмы, при которых голова явно запрокинута назад.)
2: Баллистокардиограф, используемый с 1940-х годов для измерения ударов или отдачи тела из-за ударов сердца. Какие физические принципы используются здесь для измерения силы сердечного сокращения? Как мы можем построить такое устройство?
3: Опишите ситуацию, в которой одна система воздействует на другую силу и, как следствие, испытывает силу, равную по величине и противоположную по направлению.Какие из законов движения Ньютона применимы?
4: Почему обычная винтовка дает отдачу (отдачу назад) при выстреле? Ствол у безоткатного ружья открыт с обоих концов. Опишите, как действует третий закон Ньютона при увольнении. Сможете ли вы безопасно стоять рядом с одним из них, когда из него стреляют?
5: Линейный судья американского футбола считает, что бессмысленно пытаться оттолкнуть соперника, поскольку независимо от того, насколько сильно он толкает, он будет испытывать равную и противоположную силу со стороны другого игрока.Воспользуйтесь законами Ньютона и нарисуйте диаграмму свободного тела соответствующей системы, чтобы объяснить, как он может все же опередить оппозицию, если он достаточно силен.
6: Третий закон движения Ньютона гласит, что силы всегда возникают парами равной и противоположной величины. Объясните, как выбор «интересующей системы» влияет на отмену одной такой пары сил.
Задачи и упражнения
1: Какая чистая внешняя сила действует на артиллерийский снаряд массой 1100 кг, выпущенный с линкора, если снаряд ускоряется в [латекс] \ boldsymbol {2.2} [/ latex] задом наперед. (а) Какова сила трения между ногами проигравшего игрока и травой? (b) Какую силу прилагает выигравший игрок к земле, чтобы двигаться вперед, если его масса плюс снаряжение составляет 110 кг? (c) Нарисуйте набросок ситуации, показывающий интересующую систему, используемую для решения каждой части. В этой ситуации нарисуйте диаграмму свободного тела и напишите уравнение чистой силы.
Глоссарий
- Третий закон движения Ньютона
- всякий раз, когда одно тело прикладывает силу ко второму телу, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую прикладывает первое тело
- тяга
- сила реакции, которая толкает тело вперед в ответ на силу, направленную назад; ракеты, самолеты и автомобили толкаются вперед силой реакции тяги
Решения
Задачи и упражнения
1:
Усилие на оболочке: [латекс] \ boldsymbol {2.7 \ textbf {N}}, [/ latex] по третьему закону Ньютона
4,4 Третий закон движения Ньютона
Применение третьего закона Ньютона
Силы классифицируются и получают имена в зависимости от их источника, способа передачи или их воздействия. В предыдущих разделах мы обсуждали силы, называемые толчком , массой и трением . В этом разделе применение третьего закона движения Ньютона позволит нам изучить еще три силы: нормальную силу, натяжение и тягу.Однако, поскольку мы еще не рассмотрели векторы подробно, в этой главе мы будем рассматривать только одномерные ситуации. В другой главе мы рассмотрим силы, действующие в двух измерениях.
Гравитационная сила (или вес) действует на объекты всегда и везде на Земле. Из второго закона Ньютона мы знаем, что чистая сила вызывает ускорение; Итак, почему все не находится в постоянном состоянии свободного падения к центру Земли? Ответ – нормальная сила. Нормальная сила – это сила, которую поверхность прилагает к объекту, чтобы выдержать вес этого объекта; он действует перпендикулярно поверхности, на которой лежит объект.Если объект на плоской поверхности не ускоряется, чистая внешняя сила равна нулю, а нормальная сила имеет ту же величину, что и вес системы, но действует в противоположном направлении. В форме уравнения запишем, что
Обратите внимание, что это уравнение верно только для горизонтальной поверхности.
Слово напряжение происходит от латинского слова, означающего для растяжения . Натяжение – это сила по длине гибкого соединителя, такого как веревка, веревка, цепь или кабель.Независимо от типа соединителя, прикрепленного к интересующему объекту, необходимо помнить, что соединитель может тянуть (или прикладывать напряжение ) только в направлении параллельно к его длине. Натяжение – это натяжение, которое действует параллельно соединителю и действует в противоположных направлениях на двух концах соединителя. Это возможно, потому что гибкий соединитель представляет собой просто длинную серию сил действия-противодействия, за исключением двух концов, где внешние объекты обеспечивают один член сил действия-противодействия.
Представьте человека, держащего гирю на веревке, как показано на рис. 4.10.
Рис. 4.10 Когда идеально гибкий соединитель (не требующий силы для его сгибания), такой как веревка, передает силу T , эта сила должна быть параллельна длине веревки, как показано. Такой гибкий соединитель создает натяжение. Обратите внимание, что веревка тянется с одинаковой силой, но в противоположных направлениях по отношению к руке и массе (без учета веса веревки).Это пример третьего закона Ньютона. Веревка – это среда, которая передает силы одинаковой величины между двумя объектами, но действуют в противоположных направлениях.
Натяжение веревки должно равняться весу поддерживаемой массы, как мы можем доказать, используя второй закон Ньютона. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю, поэтому Fnet = 0. Fnet = 0. Единственными внешними силами, действующими на массу, являются ее вес W и натяжение T , создаваемое веревкой.Суммируя внешние силы, мы получаем суммарную силу
4.18 Fnet = T − W = 0, Fnet = T − W = 0,, где T и W – величины натяжения и веса, соответственно, и их знаки указывают направление, где верх положительный. Подставив м г на F net и изменив уравнение, натяжение будет равно весу поддерживаемой массы, как и следовало ожидать
Для массы 5,00 кг (без учета массы веревки) мы видим, что
4.20T = мг = (5,00 кг) (9,80 м / с2) = 49,0 Н.Т = мг = (5,00 кг) (9,80 м / с2) = 49,0 Н.Другой пример действия третьего закона Ньютона – это толчок. Ракеты движутся вперед, выбрасывая газ назад с высокой скоростью. Это означает, что ракета прилагает большую силу назад к газу в камере сгорания ракеты, а газ, в свою очередь, в ответ оказывает большую силу вперед на ракету. Эта сила реакции называется тяги .
Советы для успеха
Распространенное заблуждение состоит в том, что ракеты двигаются сами по себе, ударяясь о землю или воздух позади них.На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы.
Ссылки на физику
Математика: стратегия решения проблем для законов движения Ньютона
Основы решения проблем, представленные ранее в этом тексте, сопровождаются здесь конкретными стратегиями применения законов движения Ньютона. Эти методы также укрепляют концепции, которые полезны во многих других областях физики.
Во-первых, определите задействованные физические принципы.Если проблема связана с силами, то здесь задействованы законы движения Ньютона, и важно нарисовать тщательный набросок ситуации. Пример эскиза показан на рисунке 4.11. Затем, как показано на рисунке 4.11, используйте векторы для представления всех сил. Тщательно пометьте силы и убедитесь, что их длина пропорциональна величине сил, а стрелки указывают направление, в котором действуют силы.
Рис. 4.11 (а) Эскиз Тарзана, неподвижно свешивающегося на лозе.(b) Стрелки обозначают все силы. T – это напряжение, прилагаемое к Тарзану лозой, FTFT – это сила, приложенная к лозе со стороны Тарзана, а W – вес Тарзана (т. Е. Сила, действующая на Тарзана под действием силы тяжести Земли). Предполагается, что все остальные силы, такие как легкий ветерок, незначительны. (c) Предположим, нам дали массу Тарзана и попросили найти напряжение в лозе. Мы определяем интересующую систему, как показано, и рисуем диаграмму свободного тела, как показано на (d). FT FT больше не отображается, потому что не влияет на интересующую систему; скорее FT FT действует во внешнем мире.(d) Диаграмма свободного тела показывает только внешние силы, действующие на Тарзана. Чтобы их сумма равнялась нулю, мы должны иметь T = W. Т = Ш.Затем составьте список известных и неизвестных и присвойте имена переменным количествам, указанным в задаче. Выясните, какие переменные необходимо вычислить; это неизвестные. Теперь тщательно определите систему: какие объекты представляют интерес для задачи. Это решение важно, потому что второй закон Ньютона включает только внешние силы. После того, как система идентифицирована, можно увидеть, какие силы являются внешними, а какие – внутренними (см. Рисунок 4.11).
Если система воздействует на объект вне системы, то вы знаете, что внешний объект оказывает на систему силу равной величины, но в противоположном направлении.
Диаграмма, показывающая интересующую систему и все внешние силы, действующие на нее, называется диаграммой свободного тела. На диаграммах свободного тела показаны только внешние силы, а не ускорение или скорость. На рис. 4.11 показана диаграмма свободного тела для интересующей системы.
Изобразив диаграмму свободного тела, примените второй закон Ньютона для решения проблемы.Это показано на рисунке 4.11 для случая, когда Тарзан висит на лозе. Когда внешние силы четко определены на диаграмме свободного тела, переведите силы в форму уравнения и решите для неизвестных. Обратите внимание, что силы, действующие в противоположных направлениях, имеют противоположные знаки. По соглашению силы, действующие вниз или влево, обычно отрицательны.
Проверка захвата
Если проблема имеет более одной интересующей системы, требуется более одной диаграммы свободного тела для описания внешних сил, действующих на разные системы.
- Истинно
- Ложь
Watch Physics
Третий закон движения Ньютона
Это видео объясняет третий закон движения Ньютона на примерах, включающих толчок, нормальную силу и тягу (силу, которая приводит в движение ракету или реактивный самолет).
Проверка захвата
Если космонавт на видео хотел двигаться вверх, в каком направлении он должен бросить объект? Почему?
- Он должен бросить объект вверх, потому что, согласно третьему закону Ньютона, объект будет воздействовать на него силой в том же направлении (т.е., вверх).
- Он должен бросить объект вверх, потому что, согласно третьему закону Ньютона, объект будет оказывать на него силу в противоположном направлении (то есть вниз).
- Он должен бросить объект вниз, потому что, согласно третьему закону Ньютона, объект будет оказывать на него силу в противоположном направлении (т. Е. Вверх).
- Он должен бросить объект вниз, потому что, согласно третьему закону Ньютона, объект будет оказывать на него силу в том же направлении (т.е., вниз).
Рабочий пример
Ускоряющийся поезд метро
Учитель физики толкает тележку с демонстрационным оборудованием в класс, как показано на рис. 4.12. Ее масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Чтобы толкнуть тележку вперед, ступня учителя прикладывает к полу силу 150 Н в противоположном направлении (назад). Рассчитайте ускорение, произведенное учителем. Сила трения, препятствующая движению, равна 24.0 Н.
Стратегия
Поскольку они ускоряются вместе, мы определяем систему как учитель, тележку и оборудование. Учитель отталкивается назад с силой Ffoot Ffoot, равной 150 Н. Согласно третьему закону Ньютона, пол оказывает на систему прямую силу Ffloor Ffloor, равную 150 Н. Поскольку все движения горизонтальны, мы можем предположить, что в вертикальном направлении не действует никакая результирующая сила, и проблема становится одномерной. Как показано на рисунке, трение f противодействует движению и, следовательно, действует против направления Ffloor.Этаж.
Мы не должны включать силы Fteacher Fteacher, FcartFcart или Ffoot Ffoot, потому что они применяются системой , а не системой . Мы находим чистую внешнюю силу, складывая внешние силы, действующие на систему (см. Диаграмму свободного тела на рисунке), а затем используем второй закон Ньютона, чтобы найти ускорение.
Решение
Второй закон Ньютона –
Чистая внешняя сила, действующая на систему, представляет собой сумму внешних сил: силы пола, действующей на учителя, тележку и оборудование (в горизонтальном направлении), и силы трения.Поскольку трение действует в противоположном направлении, мы присваиваем ему отрицательное значение. Таким образом, для чистой силы получаем
4.22Fnet = Ffloor − f = 150 N − 24.0 N = 126 N.Fnet = Ffloor − f = 150 N − 24.0 N = 126 N.Масса системы складывается из массы учителя, тележки и оборудование.
4,23 м = (65,0 + 12,0 + 7,0) кг = 84 кгм = (65,0 + 12,0 + 7,0) кг = 84 кгВставьте эти значения нетто F и м во второй закон Ньютона, чтобы получить ускорение системы.
4,24 a = Fnetma = 126 N84 кг = 1.5 м / с2a = Fnetma = 126 N84 кг = 1,5 м / с2Обсуждение
Ни одна из сил между компонентами системы, например, между руками учителя и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к системе. Другой способ взглянуть на это – отметить, что силы между компонентами системы компенсируются, потому что они равны по величине и противоположны по направлению. Например, сила, прикладываемая учителем к тележке, имеет равную величину, но в противоположном направлении силы, прикладываемой тележкой к учителю.В этом случае обе силы действуют на одну и ту же систему, поэтому они нейтрализуются. Определение системы имело решающее значение для решения этой проблемы.
Перейти к основному содержанию ПоискПоиск
- Где угодно
Поиск Поиск
Расширенный поиск- Войти | регистр
- Подписка / продление
- Учреждения
- Индивидуальные подписки
- Индивидуальные продления
- Библиотекари
- Полные платежи, тарифы Чикагский пакет
- Полный охват и охват содержимого
- Файлы KBART и RSS-каналы
- Разрешения и перепечатки
- Инициатива развивающихся стран Чикаго
- Даты отправки и претензии
- Часто задаваемые вопросы библиотекарей
- Расценки, заказы
- и платежи
- О нас
- Публикуйте у нас
- Новые журналы tners
- Подпишитесь на уведомления eTOC
- Пресс-релизы
- СМИ
- Книги издательства Чикагского университета
- Распределительный центр в Чикаго
- Чикагский университет
- Положения и условия
- Заявление об издательской этике
- Уведомление о конфиденциальности
- Доступность Chicago Journals
- Доступность университета
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
- Свяжитесь с нами
- Запросы СМИ и рекламы
- Открытый доступ в Чикаго
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
Объяснитель урока: Третий закон движения Ньютона
В этом объяснителе мы узнаем, как применять третий закон движения Ньютона для анализа систем сил.
Представьте себе теннисиста, размахивающего ракеткой и ударяющего по теннисному мячу. Мы знаем, что ракетка оказывает давление на мяч. Однако верно и то, что мяч оказывает на ракетку силу, которая заметна для игрока. Фактически сила, которую мяч оказывает на ракетку, равна по величине и противоположна по направлению силе, которую ракетка оказывает на мяч, как показано ниже.
Это взаимное приложение силы является примером третьего закона движения Ньютона.
Определение: Третий закон движения Ньютона
Для пары взаимодействующих объектов третий закон движения Ньютона гласит, что сила, оказываемая первым объектом на второй, равна по величине и противоположна по направлению силе, оказываемой вторым. объект по первому.
В отличие от первых двух законов движения, третий закон Ньютона фокусируется на парах взаимодействующих объектов. Это может быть столкновение двух бильярдных шаров, запуск ракетного корабля или даже луна, вращающаяся вокруг планеты. Третий закон движения Ньютона описывает силы, участвующие в этих взаимодействиях.
Иногда этот закон движения формулируется так: «На каждое действие есть равное и противоположное противодействие».
Здесь «действие» и «противодействие» относятся к силам, возникающим при взаимодействии двух объектов.Рассматривая перечисленные выше случаи, мы можем сказать, что эти силы могут быть контактными (как при столкновении бильярдных шаров, ракеты и выхлопа) или неконтактными силами (как в случае гравитационного притяжения). Пары равных и противоположных сил в каждом сценарии показаны ниже.
Обратите внимание: какая сила считается «действием», а какая – «противодействием» – это произвольно. Например, нет особой причины называть силу на левом бильярдном шаре силой «действия», а силу на правом шаре – силой «реакции» или наоборот.Точно так же и с ракетой, и с выхлопом, и в целом.
Важным моментом является то, что эти силы действуют на разные объекты в противоположных направлениях с одинаковой силой.
Еще одна пара взаимодействующих объектов, которую мы могли бы рассмотреть, – это книга, покоящаяся на земле. Задействованы две пары сил.
Во-первых, это гравитационная сила, действующая на книгу из-за Земли, и гравитационная сила книги на Земле, как показано ниже. В соответствии с третьим законом движения Ньютона эти силы равны и противоположны.
Аналогично, нормальная сила реакции книги на Земле и нормальная сила реакции Земли на книгу равны и противоположны, как показано ниже.
Обратите внимание, что в контексте третьего закона Ньютона мы можем использовать слово «реакция» для обозначения самых разных вещей.
Одно из значений состоит в том, что сила реакции – это одна из сил в паре сил любого вида между двумя взаимодействующими объектами.
Другое значение – это сила контакта, действующая на твердые объекты и препятствующая их прохождению друг через друга, которую мы часто называем нормальной силой реакции.
Третий закон движения Ньютона выполняется даже тогда, когда массы двух взаимодействующих объектов сильно различаются. Теннисная ракетка примерно в 6 раз массивнее теннисного мяча, но когда они сталкиваются, мяч оказывает на ракетку такое же усилие, как и ракетка на мяч.
Несмотря на то, что силы равны по величине, ускорение, испытываемое ракеткой и мячом, неодинаково. Мы можем убедиться в этом, рассмотрев второй закон движения Ньютона: 𝐹 = 𝑚𝑎.
При определенной силе приложенной силы, чем меньше масса объекта, тем больше он будет ускоряться в ответ на силу.Таким образом, для ракетки, столкнувшейся с теннисным мячом, мяч будет ускоряться примерно в 6 раз сильнее, чем ракетка.
Объединение третьего и второго законов движения Ньютона может привести к удивительным результатам.
Представьте, что вместо того, чтобы взаимодействовать с теннисной ракеткой, наш мяч взаимодействует с Землей посредством гравитации, как показано ниже.
Если мяч подброшен в воздух, в любой момент Земля тянет за шар, а шар тянет за Землю – и третий закон движения Ньютона гласит, что эти тяги равны по силе.
Поскольку сила, действующая на теннисный мяч, пропорциональна его массе, второй закон движения Ньютона говорит нам, что мяч будет ускоряться достаточно, чтобы мы заметили – мы увидим, как он упадет обратно на Землю.
А как насчет Земли? На него действует такая же сила, но он во много раз массивнее теннисного мяча. Если мы разделим силу силы на массу Земли, мы получим ускорение настолько мало, что для всех практических целей оно равно нулю.
Однако математически это не совсем ноль.В этой ситуации Земля очень незначительно ускоряется по направлению к летящему мячу!
Чтобы убедиться, что это действительно так, представьте, что наш теннисный мяч увеличился в массе до тех пор, пока его масса не сравнялась с массой Земли, как показано ниже.
Эти равные массы будут одинаково притягиваться друг к другу и вызывать одинаковое ускорение у другой. Осознание того, что Земля будет ускоряться из-за притяжения сопоставимой массы, показывает, что даже если бы эта масса была несопоставимой, оба объекта, включая Землю, ускорялись бы под действием силы тяжести.
Чтобы лучше понять третий закон движения Ньютона, давайте теперь рассмотрим некоторые возможные описания этого закона.
Пример 1: Третий закон движения Ньютона
Какое из следующих утверждений наиболее правильно описывает третий закон движения Ньютона?
- Когда к объекту прикладывается сила, объект оказывает силу равной величины в направлении, противоположном приложенной силе.
- Когда к объекту прикладывается сила, объект оказывает силу равного размера в направлении приложенной силы.
- Когда к объекту прикладывается сила, объект оказывает силу в направлении, противоположном приложенной силе, которая пропорциональна массе объекта, который применяет силу.
- Когда к объекту прикладывается сила, объект оказывает силу в направлении, противоположном приложенной силе, которая пропорциональна массе объекта, к которому эта сила применяется.
Ответ
Давайте вспомним определение третьего закона движения Ньютона: для пары взаимодействующих объектов сила, прикладываемая первым объектом ко второму, равна силе, прикладываемой вторым объектом к первому, и противоположна ей.
Оба варианта D и C утверждают, что сила противодействия в паре сила действия-противодействия зависит от массы – либо массы одного объекта, либо массы другого.
Строго говоря, приложенная сила может каким-то образом быть связана с массой объекта, который ее прикладывает. Например, если приложенная сила является гравитационной, то эта сила пропорциональна массе объекта, который ее генерирует.
Следовательно, сила, действующая в ответ, которая, согласно третьему закону движения Ньютона, равна по величине приложенной силе, может косвенно зависеть от массы объекта, применяющего силу.
Однако, как правило, это не так, особенно для приложенных сил, которые не зависят от массы объекта.
Тогда мы могли бы сказать, что вариант C более вероятен, чем вариант B, но ни один из них не является в целом точным описанием третьего закона движения Ньютона.
Вариант B утверждает, что две силы действуют в одном направлении. Однако мы знаем, что на самом деле силы в паре действуют в противоположных направлениях.
Вариант A описывает равные силы, действующие в противоположных направлениях, без учета каких-либо свойств объекта, таких как масса.Это правильный ответ.
Теперь давайте посмотрим, как третий закон движения Ньютона может помочь нам понять систему взаимодействующих объектов в состоянии покоя.
Пример 2: Третий закон движения Ньютона
К веревке прикреплен объект с весом = 20N. Другой конец веревки прикреплен к пружине, как показано на схеме. Пружина растягивается до упора.
- Какая сила, направленная вниз по вертикали, приложена к пружине?
- Какое усилие, направленное вверх по вертикали, прикладывает пружина к струне?
- Какая сила, направленная вверх по вертикали, приложена к объекту?
Ответ
Часть 1
Мы видим, что объект 20 N находится в равновесии.Это означает, что сила 20 Н, действующая вверх на груз, противодействует его силе в 20 Н. Струна обеспечивает эту силу, как показано ниже.
Если мы рассмотрим силы, действующие на струну (а не на вес), мы поймем, что существует направленная вниз сила 20 Н, которая должна действовать на струну из-за веса объекта.
Как и объект, струна находится в равновесии. Следовательно, пружина должна оказывать на струну направленное вверх усилие в 20 Н, как показано ниже.
Наконец, учитывая силы, действующие на пружину, мы видим, что струна должна прилагать направленную вниз силу 20 Н. Поскольку пружина находится в состоянии покоя, поверхность, к которой она прикреплена, должна оказывать на нее равную и противоположную силу. Силы, действующие на пружину, показаны ниже.
Используя эту диаграмму, мы можем ответить на заданный вопрос. Нисходящая сила, которую струна прикладывает к пружине, составляет 20 Н.
Часть 2
Мы вернемся к диаграмме, показывающей силы, которые конкретно действуют на струну.Эта диаграмма выглядит следующим образом.
Мы видим, что пружина воздействует на струну с вертикально направленной вверх силой 20 Н.
Часть 3
Сила струны на объект изображена на следующей диаграмме, показывающей силы, действующие на только объект.
На этом рисунке мы видим, что струна оказывает направленное вверх усилие в 20 Н на объект.
Пример 3: Третий закон движения Ньютона
Два шара одинаковой массы сталкиваются друг с другом, как показано на диаграмме.Шарики движутся со скоростью 𝑉 и 𝑣 соответственно, где 𝑉 больше.
Какая из следующих диаграмм правильно представляет силы реакции, которые будут действовать, когда шары сталкиваются, игнорируя любые объекты, кроме двух шаров?
Ответ
Третий закон движения Ньютона гласит, что всякий раз, когда пара объектов взаимодействует, сила первого объекта на второй равна по величине и противоположна по направлению силе второго на первый.Это верно независимо от того, имеют ли объекты одинаковую массу или движутся с одинаковой скоростью.
Мы можем ожидать, что сила серого шара на зеленом шаре будет равна и противоположна силе зеленого шара на сером шаре. Просматривая наши варианты ответов, мы видим только один вариант (E), в котором утверждается, что две силы имеют равную величину. Эта опция также показывает силы, действующие в противоположных направлениях, как мы знаем, что они должны. Тогда наш ответ – вариант E.
Давайте подведем итог тому, что мы узнали в этом объяснении.
Ключевые моменты
- Третий закон движения Ньютона применяется к взаимодействиям между парами объектов, а не отдельными объектами по отдельности.
- Для двух объектов A и B третий закон Ньютона гласит, что любая сила, которую объект B оказывает на объект A, равна по величине и противоположна по направлению любой силе, которую объект A оказывает на объект B.
- Силы, действующие на пары объектов это взаимодействие может быть как привлекательным, так и отталкивающим.
- Силы, действующие на пары взаимодействующих объектов, могут быть как контактными (силы реакции из-за столкновения, так и силы между телами в состоянии покоя), либо они могут быть силами, действующими на любом расстоянии (например, гравитацией).
