Тепловая теорема Нернста. Третий закон термодинамики
Тепловая теорема Нернста. Третий закон термодинамики [c.261]В. Нернстом в 1906—1911 гг. и получило название тепловой теоремы Нернста или третьего закона термодинамики. Используя обширный экспериментальный материал, он показал, что на основе тепловой теоремы возможно определить константу интегрирования уравнения 2 (и других уравнений) и тем самым сильно упростить расчеты термодинамических параметров равновесия химических реакций. [c.242]
Нернста тепловая теорема (64, 214) — утверждение, что при Г-> О для любых процессов изменение энтропии стремится к нулю. Прежнее название Третий закон термодинамики сейчас не используют в связи с разработкой статистических методов расчета энтропии. [c.312]
Третий закон термодинамики (тепловая теорема Нернста). …………. [c.
Анализируя поведение различных термодинамических систем при низких температурах вблизи абсолютного нуля. В. Нернст в 1906 г. сформулировал свою знаменитую тепловую теорему, которая и стала основой третьего начала термодинамики. В форме, первоначально предложенной Нернстом, теорема применялась только к конденсированным системам. Однако, несмотря на имеющиеся отступления (СО, стекла, аморфные твердые тела), можно считать, что теорема Нернста является законом, имеющим общее значение, а не только частное применение к некоторым системам или к отдельным химическим реакциям. К выводу тепловой теоремы Нернст пришел в связи с обсуждением вопроса о химическом сродстве при низких температурах. Как уже отмечалось (гл. VII), Томсоном и Бертло был установлен принцип, согласно которому возможность протекания реакции между конденсированными фазами определяется тепловым эффектом. Поскольку истинной мерой химического сродства в зависимости от условия протекания химической реакции является убыль либо свободной энергии Гиббса, либо свободной энергии Гельмгольца, то для изохорно-изо- 
183]
Приближенный метод Нернста. Метод, разработанный Нерн-стом для предсказания равновесия, основывается на так называемой тепловой теореме Нернста (которая позже развилась в третий закон термодинамики) и на использовании так называемых химических постоянных. Этот метод был впоследствии почти полностью вытеснен более простыми и более логическими методами, использующими третий закон. Приближенное уравнение, данное Нернстом, таково
Тепловая теорема Нернста является одним из выражений третьего закона термодинамики, который характеризует общие закономерности поведения веществ вблизи абсолютного нуля температуры. Тепловая теорема не требует доказательства и является постулатом, опирающимся на опытные данные о независимости от температуры многих свойств тел вблизи 7″ = 0. [c.130]
Тепловая теорема Нернста была исторически первой формулировкой третьего закона термодинамики.
В советской термодинамической.
литературе, а также и во многих иностранных изданиях третье начало термодинамики обычно называют тепловым законом или тепловой теоремой Нернста (см,, например, М. X. Карапетьянц, Химическая термодинамика, 2-е изд., М., Госхимиздат, 1953). — Прим. перев. [c.57] Тепловая теорема Нернста не является необходимой для решения задач о тепловых машинах и других чисто физических проблем, но составляет неотъемлемую часть химической термодинамики. Первая вполне удовлетворительная формулировка третьего закона была дана Льюисом и Рэндаллом [379, стр. 448] Если принять энтропию всякого элемента в некотором кристаллическом состоянии при абсолютном нуле температуры равной нулю, то каждое вещество имеет конечную положительную энтропию-, однако при абсолютном нуле температуры энтропия может обращаться-в нуль и действительно становится равной нулю в случае совершенных кристаллических веществ . В связи с определением совершенного кристаллического вещества третий закон является единственным постулатом термодинамики, который требует по крайней мере частичного рассмотрения микроскопической природы вещества.
В отличие от расчета АП и АН для определения А5 в соответствии с уравнением (7.1) скрытая теплота должна измеряться в условиях равновесия (А/ = Оили А0 = 0). Таким образом, здесь уже предполагается определенная величина АР или АО, и поэтому нет больще возможности их изменения. Чтобы найти АР и АО путем термодинамических расчетов, нужно расширить положения термодинамики с помощью третьего закона термодинамики (тепловой теоремой Нернста), который определяет величину А5 для Т = 0. По формуле (7.1) можно вычислить значения А5 для всех Т я V (или р).
Другой путь заключается в разыскании общего, дополнительного к обоим началам термодинамики пограничного (начального) условия, позволяющего находить значение неопределенной константы интегрирования, не прибегая к прямому опыту.
Третий закон термодинамики известен как тепловая теорема Нернста о недостижимости абсолютного нуля температур. [c.41]
Этот постулат, введенный на основании обобщения опытных данных, называется также теоремой Нернста, тепловым законом Нернста п третьим законом термодинамики
Выводы из положений тепловой теоремы Нернста и ее следствия выходят далеко за пределы поставленной задачи — определения константы интегрирования в уравнениях максимальной работы и константы равновесия. Эти выводы тепловую теорему обращают, по существу, в закон, который носит название третьего закона термодинамики.
[c.155]
Значение тепловой теоремы Нернста оказывается шире, чем дополнительное условие для определения константы интегрирования в уравнениях для константы равновесия и химического сродства. Анализ показал, что тепловая теорема может быть представлена в форме общего утверждения, важность которого дает основание рассматривать его как новый закон — третий закон термодинамики. Из условия, даваемого тепловой теоремой
Тепловая теорема, выраженная соотношениями (XI, 22), была высказана Нернстом (1906) и часто называется его именем. Иногда ее называют третьим законом термодинамики. [c.449]
Значения энтропии при температурах, близких к абсолютному нулю, необходимы для решения практических и теоретических термохимических задач, и это в значительной степени стимулировало появление дополнительного постулата, так называемого третьего закона термодинамики.
С точки зрения молекулярно-кинетических представлений при абсолютном нуле температуры все тела имеют структуру вполне идеальных кристаллов без трещин и дислокаций. При Го = О К энтропия достигает своего минимума и становится величиной постоянной — константой для всех материальных систем .
Абсолютную величину этой константы определить не удается. В связи с этим как основа для расчета количественного выражения энтропии систем принимается положение, внесенное в термодинамику В. Нернстом энтропия любой термодинамической системы при абсолютном нуле температуры принимается равной нулю, т. е. при Го = ОКи5о = 0. Этот постулат и лежит в основе третьего закона термодинамики, часто называемого также тепловой теоремой Периста. [c.171]
Это утверждение, впервые высказанное М. Планком (1911), связано с тепловой теоремой Нернста (см. Третий закон термодинамики) и его рассматривают, как наиболее простое и наиболее общее выражение теплового закона. Раньше это утверждение относили к любому индивидуальному веществу в конденсированном состоянии, но позднее было показано, что энтропия вещества в жидком или стеклообразном состояниях, а также кристаллов, обладающих дефек- [c.22]
Расхождение кривых AS и АН для многих реакций при комнатной температуре незначительно.
Направление реакции в этом случае определяется знаком изменения энтропии. Разница в расхождении кривых при температуре Т будет равняться TAS. Третий закон термодинамики или тепловая теорема (тепловой постулат Нернста) показывает, что с повышением темпершпуры направление химической реакции зависит не только от знака изменения энтальпии, но и от величины изменения энтропии. [c.77]
Часть 1. Расхождение традиционного и классического подходов ко второму закону термодинамики и фазовым равновесиям. Твердые и жидкие растворы
3. Энтропия смешения может совершать работу. Процессы смешения происходят внутри
системы и сопровождаются увеличением средней теплоемкости за счет уменьшения
температуры Дебая. Для гетерогенных систем, в частности, эвтектических, это приводит к
уменьшению температуры плавления и изменению средних теплоемкостей фаз в эвтектике
по сравнению с исходным состоянием (механической смесью фаз).
4.
При смешении два скрытых (латентных) процесса протекают одновременно и
компенсируют друг друга: первый – увеличение средней теплоемкости, равной по величине
энтропии смешения, что требует поглощения энергии для обеспечения постоянной
температуры, второй – одновременно, скрытое выделение тепла, Q = ∆ĈT, другими словами,
скрытое увеличение энтальпии за счет усиления межатомных связей.
5. Процесс усиления межатомных связей при смешении (образовании жидких и твердых
растворов) влияет на свойства сплавов, в частности, высокоэнтропийных сплавов, что не
учитывалось ранее традиционной термодинамикой.
Список использованных источников
1. А.М. Савченко, Альтернативный взгляд на физику, С-Петербург, Атомная Стратегия, Выпуск
96, ноябрь 2014, с. 3-7, доступно на сайте http :// www . proatom . ru
2. Gibbs J.W., On the Equilibrium of Heterogenious Substances, Collected Works of Gibbs J.
W., vol. 1,
Yale Univ. Press, 1948, p. 55.
3. R.W. СAHN. Physical Metallurgy, University of Sussex, England, 1965
4. Swalin R.A. Thermodynamics of Solids. NewYork•London, John Wiley & Sons, Inc., 1967, 156-160.
5. В. Юм-Розери, Г. Рейнор, Структура металлов и сплавов, Металлургиздат, 1959.
6. А. Савченко, Энергетическая природа конфигурационной энтропии. Генерация энтропийных и
антиэнтропийных потоков. Изд. LAP LAMBERT Academic Publishing, Германия, Saarbrucken, 2015.
7. Savchenko A., Laushkin A., Pantsirny V., Turchi P., Fluss M. Novel Interpretation of Second Law of
Thermodynamic to Solidification Processes and Phase Transformation // Proceedings of Plutonium Fu-
tures 2012 – The Science Conference, University of Cambridge, UK, 15-10 July 2012.
8. А.М. Савченко. Новая интерпретация первого и второго закона термодинамики применительно
к процессам кристаллизации и фазовым превращениям, Доклад на семинаре Российской АН, секция
«Радиационная физика твердого тела», 26-28.
11.2013, ОАО ВНИИНМ, Москва.
9. A. Savchenko, A. Laushkin, Y. Konovalov, Analysis of Correlation for Configurational versus Vibra-
tion Entropies at Phase Transformations, in Proceedings of Plutonium Futures 2012 – the Science Con-
ference, University of Cambridge, UK, 15-10 July 2012.
10. A.D. Wissner-Gross, C.E. Freer, Causal entropic forces. Phys. Rev. Lett. 2013, 110, 168702-5.
11. J.-W. Yeh, S-K. Chen, S.-J. Lin, J.Y. Gan, T.-S. Chin, T.-T. Shun, C.-H. Tsau, S.-Y. Chang,
Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and
outcomes. Adv. Eng. Mater. 2004, 6, 299-303.
12. Shaoqing Wang, Atomic Structure Modeling of Multi-Principal-Element Alloys by the Principle of
Maximum Entropy, J. Entropy, 2013, 15, 5536-5548.
13. Z.M. Zhu, H.M. Fu., H.GF. Zhanga, A.M. Wang, H. Li, Z.Q. Hu, Microstructures and compressive
properties of multicomponent AlCoCrFeNiMox alloys, Materials Science and Engineering A 527 (2010)
6975-6979.
14. O.N. Senkov, G.B. Wilks, D.B. Miracle, C.P. Chuang, P.K. Liaw, Refractory High-Entropy Alloys,
Intermetallics 2010, 18, 1758-1565.
15. Бочвар А.А. Металловедение, М., Металлургиздат, 1956, 495 с.
16. Захаров А.М. Диаграммы состояния двойных и тройных систем. M:, Металлургия, 1978. 295 с.
17. F.N. Rhines, Phase Diagrams in Metallurgy, their Development and Application, McGRAW Book
Company, Inc, NewYork•London, 1956.
18. Ansara I. Comparision of methods of thermodynamic calculation of phase diagrams. International
Metals Reviews, 1979, no. 1, 20-55.
19. Котрелл А.Х. Строение металлов и сплавов. М.: Металлургиздат, 1961, 196-201.
20. Пригожин И., Дефэй Р. Химическая термодинамика. Новосибирск, Издательство «Наука»,
Сибирское отделение, 1966
21. А.М. Савченко, Взаимосвязь конфигурационной энтропии, материи и Физического Вакуума,
С-Петербург, Атомная Стратегия, Выпуск 78, май 2013, с. 12-17, доступно на сайте
http :// www .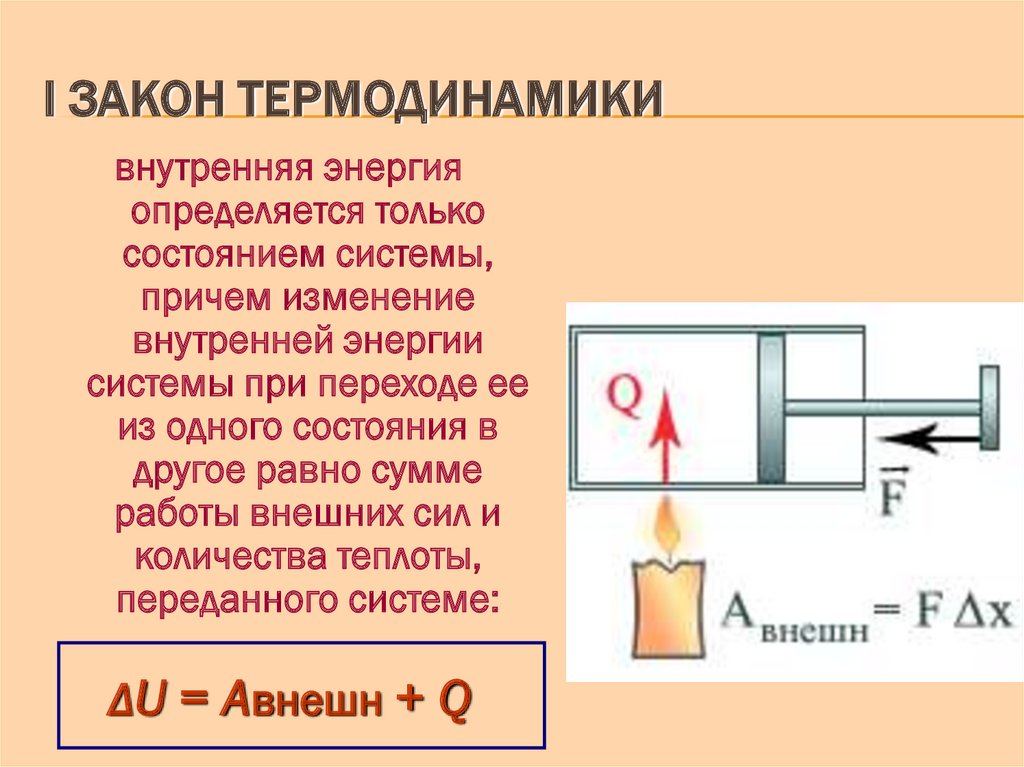
proatom . ru
Вторая формулировка первого закона термодинамики
Вторая формулировка первого закона термодинамики 24 Второй закон термодинамики 56 Вынужденное движение 313 Вязкость 175 [c.473]Отсюда следует вторая формулировка первого закона термодинамики Вечный двигатель первого рода невозможен . [c.59]
Уравнения (4.10), (4.15) являются дифференциальной формулировкой первого закона термодинамики. Второй закон термодинамики записывается для первой и второй фаз соответственно в виде [c.34]
Как видно из формулировки первого закона термодинамики, он устанавливает количественное соотношение между различными видами энергии при их взаимных превращениях. Однако этот закон ничего не говорит о том, при каких условиях та)кие превращения могут происходить. На этот последний вопрос дает ответ второй закон термодинам ики.
[c.70]Различные формулировки третьего закона термодинамики остаются неизменными при отрицательных абсолютных температурах, если под абсолютным нулем температуры понимать О К, как положительной, так и отрицательной температуры. Температуры + 0К и —О К соответствуют совершенно различным физическим состояниям. Для первого система находится в состоянии с наименьшей возможной энергией, а для второго — с наивысшей. Система не может стать холоднее, чем +0К, так как она не может больше отдать энергию. Она не может стать горячее, чем —О К, так как она не может больше поглотить энергию. Принцип недостижимости абсолютного нуля формулируется следующим образом невозможно с помощью любой, как угодно идеализированной процедуры за конечное число операций охладить любую систему + О К или нагреть любую систему до —О К- [c.121]
В результате анализа возникают по меньшей мере два вопроса. Во-первых, вопрос о физической сущности ограничения степени превращения внутренней энергии в кинетическую этот вопрос рассмотрим позднее.
Во-вторых, вопрос о правильности формулировки задачи об истечении газа. Ведь формула (7.36) выражает первый закон термодинамики и вдруг оказывается, что применение этого закона — закона сохранения энергии — ограничено условием Сомнения, связанные со
[c.179]
Если бы не существовало ограничений, накладываемых вторым законом термодинамики, то это означало бы, что можно построить тепловой двигатель при наличии одного лишь источника тепла. Такой двигатель мог бы действовать за счет охлаждения, например, воды в океане. Этот процесс мог бы продолжаться до тех пор, пока вся внутренняя энергия океана не была бы превращена в работу. Тепловую машину, которая действовала бы таким образом, В. Ф. Оствальд удачно назвал вечным двигателем второго рода (в отличие от вечного двигателя первого рода, работающего вопреки закону сохранения энергии). В соответствии со сказанным формулировка второго закона термодинамики, данная Планком, может быть видоизменена следующим образом осуществление вечного двигателя второго рода невозможно.
Следует заметить, что существование вечного двигателя второго рода не противоречит первому закону термодинамики в самом деле, в этом двигателе работа производилась бы не из ничего, а за счет внутренней энергии, заключенной в тепловом источнике.
[c.54]
Наконец, назвав принципиально неосуществимую тепловую машину, которая в противоречии с постулатом Томсона могла бы совершать механическую работу только за счет охлаждения одного лишь источника тепла, вечным двигателем второго рода (в отличие от вечного двигателя первого рода, который мог бы совершать работу вообще без затраты энергии, т. е. в противоречии с первым законом термодинамики), В. Ф. Оствальд дал наиболее лаконичную формулировку постулата Томсона Осуществление (вечного двигателя второго рода невозможно. [c.55]
Если первый закон термодинамики характеризует процессы превращения энергии с количественной стороны, то второ й закон термодинамики характеризует качественную сторону этих процессов.
Наиболее общая формулировка второго закона термодинамики любой самопроизвольный процесс является необратимым.
[c.113]
В настоящей главе в виде следствия 3 мы установили третье ответвление от вершины генеалогического древа термодинамики, т. е. от закона устойчивого равновесия. Первое ответвление (следствие 1) дало нам в гл. 4 обычную нециклическую формулировку первого закона . В гл. 5 второе ответвление (следствие 2) позволило установить принцип состояния. Слияние этих ответвлений в гл. 7 привело к известному уравнению сохранения энергии для системы, которое далее позволило получить общепринятую циклическую формулировку первого закона (интересно отметить, что эта формулировка во многих учебниках принимается в качестве отправной точки при изложении классической термодинамики). [c.117]
Учебник Покровского, содержащий 368 страниц, имеет следующие наименования отдельных глав гл. 1—понятие о процессах. основы графического изображения процессов, работа процессов гл.
2— энергия и ее свойства гл. 3—учение об обратимости процессов гл. 4— понятие о машинах, приложение первого закона термодинамики к цикла.м гл. 5—учение о постоянных газах гл. 6— газовые машины и цикл Карно, к. п. д. мапшн гл. 7— основная формулировка второго закона термодинамики и вытекающие из нее следствия гл. 8— о физической сущности второго закона термодинамики гл. 9—учение о парах гл. 10—влажный воздух гл. И—течение упругих жидкостей. Течение без сопротивления.
[c.242]
С помощью повой фз нкции состояния—энтропии—мы получи.м вскоре более сжатую математическую формулировку второго закона. Формулировки, которые мы привели выше, —это аксиомы, выведенные из опыта. Пока второй закон следует считать в такой же степени эмпирически обоснованным, как и первый закон термодинамики. Тем не менее его смысл не столь непосредственно очевиден, как смысл первого закона. Последний становится интуитивно ясным, как только мы отождествим тепло с энергией невидимых движений и примем, что эта энергия также должна учитываться при формулировке универсального закона сохранения энергии.
[c.36]
В приведенных двух последних соображениях подчеркиваются количественная и качественная стороны процесса теплообмена. Количество переданного движения телом А телу Б не может быть больше, чем имеет само тело А, что является, как уже отмечалось, содержанием первого закона термодинамики. Качественная сторона процесса заключается в том, что движение, а значит и тепло, может передаваться лишь от тела более нагретого к телу менее нагретому и что эта передача может происходить лишь до тех пор, пока не сравняются скорости движения частичек обоих тел. Отсюда следует, что обратный процесс передачи движения от менее нагретого тела, частички которого имеют меньшие скорости, к более нагретому с большими скоростями частичек не- возможен. Невозможна, следовательно, и передача тепла от холодного к более теплому телу. Указанные соображения Ломоносова составляют содержание второго закона термодинамики в формулировке, высказанной Клаузиусом в 1850 г., т. е. спустя примерно 100 лет после Ломоносова.
[c.5]
М. Планк дал эту формулировку в своем курсе термодинамики, первое издание которого вышло в 1897 г. всего в Германии было 10 изданий, из них на русский язык переведено три 1898, 1900 и 1925 года изданий. Близкую по смыслу формулировку дал ранее (1851 г.) В. Томсон (лорд Кельвин)—один из создателей второго закона термодинамики. Вторым считают Р. Клаузиуса (1850 г.). Однако В. Томсон и Р. Клаузиус развили и обобщили идеи С. Карно, изложенные им в его знаменитом сочинении Размышления о движущей силе огня и о машинах, способных развивать эту силу (1824 г.). С. Карно считал, что тепловая машина не поглощает тепло, превращая его в работу, а передает его холодному телу, подобно тому, как вода, падая из верхнего резервуара в нижний, совершает на своем пути работу. Это и есть основная идея второго закона. [c.39]
Опираясь на математические формулировки первого и второго законов термодинамики, можно строить теорию тепловых процессов, получившую название феноменологической термодинамики.
Не изучая зачастую промежуточные стадии и механизм процесса.
[c.7]Приведенные формулировки второго закона термодинамики, отражающие специфическую особенность теплоты, проявляющуюся при ее превращении, являются эквивалентными. Действительно, если допустить возможность самопроизвольного перехода теплоты от холодного источника к горячему, то последнему можно вернуть неиспользованную теплоту, и горячий источник расходовал бы всего удельной теплоты /а = /д, т. е. вся теплота, отнятая от теплоот-датчика, была бы превращена в круговом процессе в работу. Но это противоречило бы другим формулировкам второго закона. Следует еще раз подчеркнуть, что все формулировки второго закона термодинамики являются следствием наблюдений, т. е. второй закон, как и первый, является экспериментальным. [c.36]
Подобно первому и второму законам, третий закон термодинамики имеет несколько различных по форме, но равноправных по существу формулировок, в каждой из которых подчеркивается то или иное следствие общего принципа.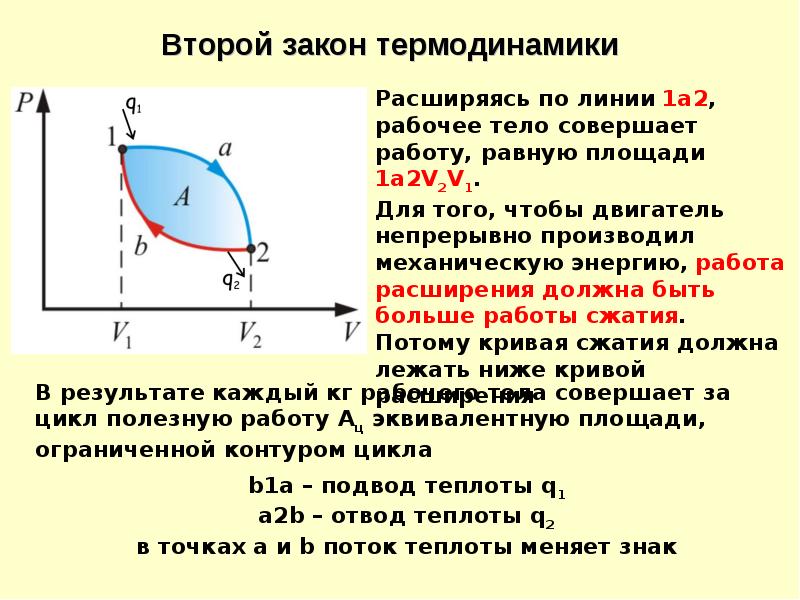
Одна из современных формулировок третьего закона термодинамики утверждает, что в любом равновесном изотерм-ном процессе в конденсированной системе при температуре стремящейся к абсолютному нулю, изменение энтропии стремится к нулю формулировка Нернста — Симона).
[c.362]
С точки зрения первого начала термодинамики в природе возможен любой процесс, который не противоречит закону сохранения энергии. Однако первое начало термодинамики не рассматривает вопроса о направлении происходящих процессов. Ответ на этот вопрос дает второе начало термодинамики, содержание которого может быть выражено в нескольких одинаковых по смыслу формулировках. [c.47]
Исходя из количественной формулировки первого и второго законов термодинамики, можно получить уравнение, которое включает в себя оба закона. [c.87]
ПОЧТИ целиком отнести на счет способа изложения термодинамики, в котором отправной точкой служит циклическая формулировка первого и второго законов, вместо того, чтобы исходить из рассмотрения нециклических процессов и переходить от них к циклическим процессам, как это сделано в настоящей книге.
[c.15]
Теперь генеалогическое древо термодинамики имеет вид, показанный на рис. 8.5, из которого видно, что путем логического развития закона устойчивого равновесия мы получили известные формулировки первого и второго законов . В процессе дальнейшего роста генеалогического древа термодинамики эти утверждения будут использованы для развития представлений о двух важнейших характеристиках системы — термодинамической температуре и энтропии. [c.119]
Первая глава посвящена термодинамическим основам термоупругости. Изложение начинается с основных положений классической термодинамики. При рассмотрении второго закона термодинамики предпочтение дается новой его формулировке, разработанной профессором Киевского университета Н. Н. Шиллером в 1897—1901 гг., немецким математиком Каратеодори в 1909 г. и Т. А. Афанасьевой-Эренфест в 1925—1928 гг. Эта формулировка устанавливает общий эмпирический принцип о невозможности определенных процессов — принцип адиабатической недостижимости, удобный для математического выражения второго закона термодинамики в случае термодинамических систем, состояние которых определяется большим числом независимых переменных (деформируемых твердых тел и др.
).
[c.6]
Основное положение термодинамики необратимых процессов, вытекающее из предположения о локальном термодинамическом равновесии, заключается в том, что первый и второй законы классической термодинамики справедливы и для локально равновесных макроскопических частей системы. Для математического выражения второго закона термодинамики в случае твердых деформируемых тел, состояние которых определяется большим числом независимых переменных, удобной является формулировка, разработанная [c.6]
На основании первого и второго начал термодинамики можно определить лишь изменение энтропии. Для термодинамического определения абсолютного значения энтропии необходимы новые данные, которые могут быть получены при исследовании различных химических и физических процессов при очень низких температурах. Экспериментально установлено, что энтропия чистого кристаллического вещества при абсолютном нуле (или при температуре, близкой к нему) равна нулю.
Это и есть формулировка третьего начала термодинамики. Исходя из этого экспериментального закона и с использованием других законов термодинамики, можно вычислить энтропию вещества и при более высоких температурах.
[c.84]
Выводы термодинамики, как науки об энергетических балансах и равновесиях, независимы от предположений о механизме, совершающемся в природе процессов. Первое начало термодинамики представляет собой общий закон сохранения энергии применительно к термическим явлениям. Второе начало термодинамики указывает на односторонность всех протекающих процессов, на стремление любой предоставленной самой себе системы к достижению конечного состояния равновесия. В совокупности первое и второе начала термодинамики позволяют дать в общем количественную формулировку условий равновесия, предсказать направление, в котором пойдет тот или другой процесс в данных конкретных условиях и степень его завершенности. Если из термодинамики следует, что в данных условиях какой-либо процесс невозможен, то это означает действительно полную невозможность его осуществления при помощи любого приспособления или катализатора -такую же невозможность, как создание вечного двигателя.
Если же термодинамика устанавливает, что процесс возможен, то это указывает лишь на его принципиальную осуществимость. Реализация же этого процесса будет зависеть от того, с какой скоростью в рассматриваемых условиях будет двигаться состояние равновесия, т.е. от кинетических факторов.
[c.46]
Из того, что мы знаем о равновесных и неравновесных состояниях, следует, что при переходе от вторых к первым энтропия Зшеличивается и достигает максимального значения в состоянии термодинамического равновесия. Поскольку в изолированной системе все переходы идут именно в этом направлении, мы получаем, таким образом, количественную формулировку II закона термодинамики энтропия изолированной системы не может убывать. [c.53]
Вторая формулировка для машины-двигателя требует некоторого пояснения. Под перпетуумом-мобиле второго ряда принято понимать машину, которая могла бы превращать всю подводимую к ней теплоту в работу.
Такая машина, очевидно, имела бы термодинамический к. п. д., равный единице, и не нуждалась бы в низшем источнике теплоты, так как не имела бы теплового отброса. Работа такой машины не противоречила бы первому закону термодинамики, который констатирует лишь взаимопревращаемость различных видов энергии. Вместе с тем, как показывает опыт, работа такой машины противоречила бы второму закону термодинамики, требующему, чтобы работа тепловой машины протекала в определенном перепаде температур, т. е. при наличии высшего и низшего источников тепла.
[c.37]
Второй закон так же, как и первый, является обобщением многолетнего практического опыта. Сущность второго закона термодинамики может быть выражена в различных формулировках. Одной из них может. служить утверждение, что тепло самопроизвольно не может, переходить от менее нагретого тела к более нагретому. Подобно тому как с первым законом термодинамики связана функция внутренней энергии, идеи второго закона термодинамики концентрируются в понятии энтроппи — функции состояния, сущность которой будет выяснена несколько позже.
[c.43]
Определение температуры как физической величины, являющейся одной из фундаментальных в термодинамике, непосредственно связано с упомянутыми выше основными законами термодинамики. Обычно, исходя из первого закона тер-]лодинамики и используя формулировку Кельвина для второго закона, доказывают, что для обратимой тепловой машины, работающей по циклу Карно между температурами 01 и 02, отношение количества тепла Оь поглощенного при более высокой температуре 0ь к количеству тепла Оъ отданного при более низкой температуре 02, просто пропорционально отношению двух одинаковых функций от каждой из этих двух температур [c.17]
Анализ особенностей тепловых процессов, выполненный Р. Клаузиусом, был далеко не очевиден, но логически безупречен. Обратив внимание на то, что формулировка второго закона термодинамики носит качественный характер, он задался целью найти его математическую форму. Он считал необходимым связать второй закон с некоторой характерной физической величиной, аналогично тому, как первый закон оказался связанным с существова1шем энергии, явился законом ее сохранения и превращения.
Максимальный КПД идеальной тепловой машины, как впервые показал С. Карно, определяется соотношением
[c.81]
Примером проявления энтропии изолированной системы является теплообмен между телами при конечной разности температур (внешняя необратимость). Если н такой системе имеется два тела с разными температурами (7, > T ,), то согласно второму закону термодинамики (в формулировке Клаузиуса) самопроизвольный переход теплоты может происходить только от тела с большей температурой к телу с меньшей температурой. При этом элементарное изменение удельной энтропии первого тела составляет ds = — второго —d 2 = – -t1qlT2. Поскольку энтропия обладает аддитивным свойством, изменение удельной энтропии системы [c.38]
Выражения (71), (75), (77) для обратимых и (86), (91) и (92) для необратимых циклов и процессов являются наиболее общими математическими (формулировками второго закона термодинамики. Все они содержат новую тер.модинамическую величину — энтропию, поэтому второй закон термодинамики можно назвать законом возрастания эптропии, в то время как первый закон — законом сохранения энергии системы.
Энергия изолированной системы постоянна, а энтропии [)астет. У казанные выше выражения второго закона термодинамики в обобщенной (форме характеризуются неравенствами (87), (90) и (91), представлсишчми в (форме
[c.61]
Эта формулировка второго закона термодинамики очень близка по стилю и четкости к формулировке первого заковга, которую дал Фейнман (мы ее приводили на с. 86) и смысл которой аналогичен утверждению Существует величина, которая при всех изменениях, которые затрагивают только эту систему, остается постоянной. Это энергия системы . [c.138]
Ранняя книга Кинана [3], опубликованная в 1941 г., оказала благотворное влияние на преподавание термодинамики в учебных заведениях для инженеров в США и Великобритании. Однако, поскольку в этой книге понятия и теоремы классической термодинамики равновесных процессов выводились из циклической формулировки первого и второго законов, в результате получилась нежелательная концентрация внимания на циклических процессах в ущерб более естественным нециклическим процессам.
Напротив, закон устойчивого равновесия Хацопулоса и Кинана, из которого первый и второй законы получаются как следствия, по существу, относится к нециклическим процессам. В равной мере это справедливо и для теорем о термодинамической доступности энергии. К сожалению, в циклическом подходе природу истинного источника необратимости не удается выявить слишком долго, в то время как в нециклическом подходе она проясняется с самого начала. Более того, циклический процесс в какой-то степени является искусственной конструкцией. Естественные процессы, протекающие в физическом мире, имеют в основном нециклический характер, причем циклический процесс рассматривается как особый случай, в котором реализуется такая последовательность нециклических процессов, что конечное термодинамическое состояние системы совпадает с начальным. Далее, если исходить из недоказанных утверждений о циклических процессах, то не удается естественным путем прийти к теоремам о термодинамической
[c.13]
В заключение заметим следующее.
Из того обстоятельства, что первое начало термодинамики есть не что иное, как закон сохранения энергии в применении к тепловым процессам, не следует, что это есть формулировка частного случая закона сохранения энергии. В действительности формулировка закона сохранения энергии в термодинамике является самой широкой, так как отображает изменение любого вида энергии (тепловой, механической, электромагнитной, химической и т. д.). Термодинамику определяют иногда как учение о взаимной связи, существующей во всех явлениях природы между теплотой и другими видами энергии. В этом определении теплота занимает особое положение, так как все виды энергии могут быть полностью превращены в тепловую, иными словами, всегда возможно построить такую периодически действующую машину, которая в каждом цикле превращала бы механическую или электромагнитную энергию в тепловую в то же время невозможно согласно второму началу термодинамики, к изучению которого мы перехрдим, построить такую периодически действующую машину, в каждом цикле которой происходило бы полное превращение взятой от теплового резервуара теплоты в механическую или электромагнитную энергию.
[c.35]
Этими простыми положениями Клаузиус (1822—1888) резюмировал содержание своей работы О различных удобных для приложений формах основных уравнений механической теории тепла . Эта работа увидела свет в 1865 г., пятнадцать лет спустя после открытия второго закона (сообщение о чем появилось в Poggendorf Annalen [1]). В этой чрезвычайно важной работе Клаузиус дает те основные формулировки первого и второго законов термодинамики, с которыми мы теперь уже знаконш . [c.203]
Спустя десять лет, в 1875 г., Гпббс (1839—1903) положил эти фор-му.иировки в основу своей знаменитой статьи О равновесии гетерогенных веществ [2]. Здесь Гиббс, исходя из первого и второго законов термодинамики, дает наиболее общую формулировку условий равновесия для гетерогенных систем и впервые вводит понятие химического потенциала. [c.203]
Сочинение М. А. Леонтовича имеет следующие построение и содержание Раздел 1 — Основные понятия и положения термодинамики (состояние физической системы и определяющие его величины работа, соверщаемая системой адиабатическая изоляция и адиабатический процесс закон сохранения энергии для адиабатически изолированной системы закон сохранения энергии в применении к задачам термодинамики в общем случае (первое начало термодинамики) количество тепла, полученное системой термодинамическое равновесие температура квазистатические (обратимые) процессы теплоемкость давление как внешний параметр энтальпия обратимое адиабатическое расширение или сжатие тела применение первого начала к стационарному течению газа или жидкости процесс Джоуля—Томсона второе начало термодинамики формулировка основного принципа).
[c.364]
Первые 8 глав учебника относятся к различным разделам, рассматриваемым в учебниках по термодинамике, особенно это касается гл. 8, имеющей следующее содержание законы термодинамики энергия как функция состояния циклы работа цикла цикл Карно цикл Карно с идеальным газом обратимые и необратимые процессы обратимость цикла Карно второй закон термодинамики формулировка его экономический коэффициент обратимых и необратимых машин другая формулировка второго закона термодинамики уравнение Клайперона—Клаузиуса зависимость поверхностного натяжения от температуры значение второго закона термодинамики. [c.647]
Поворотным пунктом первого периода в развитии термодинамики, связанного с изучением тепловых машин, явилась работа Рудольфа Клаузиуса О различных удобных формах основных уравнений механической теории тепла , которая была опубликована в 1865 г. [61 см. также (7) ). В ней он ввел также понятие энтропии (от греческого слова -грол П — превращение).
Клаузиус заканчивает свою работу краткими формулировками первого и второго законов термодинамики
[c.12]
Суи1,ествует много различных формулировок второго закона термодинамики, кажущихся, на первый взгляд, совсем непохожими друг на друга. По существу же, все они отражают свойства неравновесных процессов, лишь подчеркивая только те или иные стороны этих явлений. Приведем две наиболее распространенные формулировки. [c.123]
В первой части книги рассмотрены основные законы термодинамики, термодинамические процессы, дифференциальные уравнения термодинамики и истечения газов и паров. Кроме того, да ю изложение циклов двигателей внутреннего сгорания, газотурбинных, паротурбинных установок и атомных электростанций. Вторая часть посвящена изложению законов теплопроводности при стационарном и нестационарном режимах, теории подобия, конвективного теплообм иа и излучения. В каждой главе помешены числовые примеры. В да1том издании (второе вышло в 197.
5 г.) улучнюна редакция, уточнены терминология, формулировки, приведены новые данные.
[c.248]
После крушения теории теплорода теплота окончательно рассматривается как энергия движения составляющих тело материальных частиц (атомов, молекул). Но между теплотой и механической энергией вскоре обнаружились принципиальные отличия. Например, при торможении автомобиля его тормозные колодки нагреваются, но обратный процесс абсолютно невозможен — сколько бы мы ни нагревали колодки, автомобиль все равно останется на месте. Закон сохранения и превращения энергии, раскрывая количественную сторону превращений энергии, ничего не говорит о принцигшальных качественных отличиях между ее различными формами. Можно указать на другие принципиальные особенности тепловых явлений. Одним из самых очевидных наблюдений является то, что при различных видах работы часть энергии выделяется в виде теплоты. В природе существует тенденция к необратимому превращению различных видов энергии в теплоту, поскольку обратное превращение тепла в работу, за исключением изотермических процессов, невозможно.
Другой, не менее очевидной особенностью тепловых явлений является то, что нагретые тела всегда стремятся прийти в равновесие с окружающей средой. Но и в этих процессах передачи теплоты существует односторонность, которую Р. Клаузиус сформулировал в качестве тепловой аксиомы Теплота не может сама собой переходить от тела холодного к телу горячему . Значение этого положения оказалось настолько важным, что его стали рассматривать как одну из формулировок второго начала термодинамики. Л. Больцман писал Наряду с общим принципом (законом сохранения и превра]цения энергии. — О. С.) механическая теория тепла установила второй, малоутешительным образом ограничивающий первый, так называемый второй закон механической теории тепла. Это положение формулируется следующим образом работа может без всяких ограничений превращаться в теплоту обратное превращение тепла в работу или совсем невозможно, или возможно лишь отчасти. Если и в этой формулировке второй принцип является неприятным дополнением к первому, то благодаря своим последствиям он становится гораздо фатальнее .
[c.79]
Второе начало термодинамики. Второй закон термодинамики
Существует несколько формулировок второго закона термодинамики, авторами которых являются немецкий физик, механик и математик Рудольф Клаузиус и британский физик и механик Уильям Томсон, лорд Кельвин. Внешне они различаются, но суть их одинакова.
Постулат Клаузиуса
Рудольф Юлиус Эммануэль Клаузиус
Второй закон термодинамики, как и первый, также выведен опытным путём. Автором первой формулировки второго закона термодинамики считается немецкий физик, механик и математик Рудольф Клаузиус.
«Теплота сама собой не может переходить от тела холодного к телу горячему ». Это утверждение, которое Клазиус назвал «тепловой аксиомой », было сформулировано в 1850 г. в работе «О движущей силе теплоты и о законах, которые можно отсюда получить для теории теплоты».
«Само собой теплота передаётся лишь от тела с более высокой температурой к телу с меньшей температурой.
В обратном направлении самопроизвольная передача теплоты невозможна». Таков смысл постулата Клаузиуса , определяющего суть второго закона термодинамики.
Обратимые и необратимые процессы
Первый закон термодинамики показывает количественную связь между теплотой, полученной системой, изменением её внутренней энергии и работой, произведённой системой над внешними телами. Но он не рассматривает направление передачи теплоты. И можно предположить, что теплота может передаваться как от горячего тела к холодному, так и наоборот. Между тем, в действительности это не так. Если два тела находятся в контакте, то теплота всегда передаётся от более нагретого тела к менее нагретому. Причём этот процесс происходит сам по себе. При этом во внешних телах, окружающих контактирующие тела, никаких изменений не возникает. Такой процесс, который происходит без совершения работы извне (без вмешательства внешних сил), называется самопроизвольным . Он может быть обратимым и необратимым .
Самопроизвольно остывая, горячее тело передаёт свою теплоту окружающим его более холодным телам. И никогда само собой холодное тело не станет горячим. Термодинамическая система в этом случае не может возвратиться в первоначальное состояние. Такой процесс называется необратимым . Необратимые процессы протекают только в одном направлении. Практически все самопроизвольные процессы в природе необратимы, как необратимо время.
Обратимым называется термодинамический процесс, при котором система переходит из одного состояния в другое, но может вернуться в исходное состояние, пройдя в обратной последовательности через промежуточные равновесные состояния. При этом все параметры системы восстанавливаются до первоначального состояния. Обратимые процессы дают наибольшую работу. Однако в реальности их нельзя осуществить, к ним можно только приблизиться, так как протекают они бесконечно медленно. На практике такой процесс состоит из непрерывных последовательных состояний равновесия и называется квазистатическим .
Все квазистатические процессы являются обратимыми.
Постулат Томсона (Кельвина)
Уильм Томсон, лорд Кельвин
Важнейшая задача термодинамики – получение с помощью тепла наибольшего количества работы. Работа легко превращается в теплоту полностью безо всякой компенсации, например, с помощью трения. Но обратный процесс превращения теплоты в работу происходит не полностью и невозможен без получения дополнительной энергии извне.
Нужно сказать, что передача теплоты от более холодного тела к более тёплому возможна. Такой процесс происходит, например, в нашем домашнем холодильнике. Но он не может быть самопроизвольным. Для того чтобы он протекал, необходимо наличие компрессора, который будет такой воздух перегонять. То есть, для обратного процесса (охлаждения) требуется подвод энергии извне. «Невозможен переход теплоты от тела с более низкой температурой без компенсации ».
В 1851 г. другую формулировку второго закона дал британский физик и механик Уильям Томсон, лорд Кельвин.
Постулат Томсона (Кельвина) гласит: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара
» . То есть, нельзя создать циклически работающий двигатель, в результате действия которого производилась бы положительная работа за счет его взаимодействия лишь с одним источником теплоты. Ведь если бы это было возможно, тепловой двигатель мог бы работать, используя, например, энергию Мирового океана и полностью превращая её в механическую работу. В результате этого происходило бы охлаждение океана за счёт уменьшения энергии. Но как только его температура оказалась бы ниже температуры окружающей среды, должен был бы происходить процесс самопроизвольной передачи тепла от более холодного тела к более горячему. А такой процесс невозможен. Следовательно, для работы теплового двигателя необходимо хотя бы два источника теплоты, имеющих разную температуру.
Вечный двигатель второго рода
В тепловых двигателях теплота превращается в полезную работу только при переходе от нагретого тела к холодному.
Чтобы такой двигатель функционировал, в нём создаётся разность температур между теплоотдатчиком (нагревателем) и теплоприёмником (холодильником). Нагреватель передаёт теплоту рабочему телу (например, газу). Рабочее тело расширяется и совершает работу. При этом не вся теплота превращается в работу. Часть её передаётся холодильнику, а часть, например, просто уходит в атмосферу. Затем, чтобы вернуть параметры рабочего тела к первоначальным значениям и начать цикл сначала, рабочее тело требуется нагреть, то есть от холодильника необходимо отнять теплоту и передать её нагревателю. Это означает, что нужно передать теплоту от холодного тела к более тёплому. И если бы этот процесс можно было осуществить без подвода энергии извне, мы получили бы вечный двигатель второго рода. Но так как, согласно второму закону термодинамики, сделать это невозможно, то невозможно и создать вечный двигатель второго рода, который полностью превращал бы теплоту в работу.
Эквивалентные формулировки второго закона термодинамики:
- Невозможен процесс, единственным результатом которого является превращение в работу всего количества теплоты, полученного системой.
- Невозможно создать вечный двигатель второго рода .
Принцип Карно
Николя Леонар Сади Карно
Но если невозможно создать вечный двигатель, то можно организовать цикл работы теплового двигателя таким образом, чтобы КПД (коэффициент полезного действия) был максимальным.
В 1824 г., задолго до того как Клаузиус и Томсон сформулировали свои постулаты, давшие определения второго закона термодинамики, французский физик и математик Николя Леонар Сади Карно опубликовал свою работу «Размышления о движущей силе огня и о машинах, способных развивать эту силу». В термодинамике её считают основополагающей. Учёный сделал анализ существовавших в то время паровых машин, КПД которых был всего лишь 2%, и описáл работу идеальной тепловой машины.
В водяном двигателе вода совершает работу, падая с высоту вниз. По аналогии Карно предположил, что и теплота может совершать работу, переходя от горячего тела к более холодному. Это означает, что для того чтобы
тепловая машина работала, в ней должно быть 2 источника тепла, имеющих разную температуру.
Это утверждение называют принципом Карно . А цикл работы тепловой машины, созданной учёным, получил название цикла Карно .
Карно придумал идеальную тепловую машину, которая могла совершать максимально возможную работу за счёт подводимой к ней теплоты.
Тепловая машина, описанная Карно, состоит из нагревателя, имеющего температуру Т Н , рабочего тела и холодильника с температурой Т Х .
Цикл Карно является круговым обратимым процессом и включает в себя 4 стадии – 2 изотермические и 2 адиабатические.
Первая стадия А→Б изотермическая. Она проходит при одинаковой температуре нагревателя и рабочего тела Т Н . Во время контакта количество теплоты Q H передаётся от нагревателя рабочему телу (газу в цилиндре). Газ изотермически расширяется и совершает механическую работу.
Для того, чтобы процесс был циклическим (непрерывным), газ нужно вернуть к исходным параметрам.
На второй стадии цикла Б→В рабочее тело и нагреватель разъединяются. Газ продолжается расширяться адиабатически, не обмениваясь теплом с окружающей средой. При этом его температура снижается до температуры холодильника Т Х , и он продолжает совершать работу.
На третьей стадии В→Г рабочее тело, имея температуру Т Х , находится в контакте с холодильником. Под действием внешней силы оно изотермически сжимается и отдаёт теплоту величиной Q Х холодильнику. Над ним совершается работа.
На четвёртой стадии Г→А рабочее тело разъединятся с холодильником. Под действием внешней силы оно адиабатически сжимается. Над ним совершается работа. Его температура становится равной температуре нагревателя Т Н .
Рабочее тело возвращается в первоначальное состояние. Круговой процесс заканчивается. Начинается новый цикл.
Коэффициент полезного действия теловой машины, работающей по циклу Карно, равен:
КПД такой машины не зависит от её устройства.
Он зависит только от разности температур нагревателя и холодильника. И если температура холодильника равна абсолютному нулю, то КПД будет равен 100%. До сих пор никто не смог придумать ничего лучшего.
К сожалению, на практике такую машину построить невозможно. Реальные обратимые термодинамические процессы могут лишь приближаться к идеальным с той или иной степенью точности. Кроме того, в реальной тепловой машине всегда будут тепловые потери. Поэтому её КПД будет ниже КПД идеального теплового двигателя, работающего по циклу Карно.
На основе цикла Карно построены различные технические устройства.
Если цикл Карно провести наоборот, то получится холодильная машина. Ведь рабочее тело сначала заберёт тепло от холодильника, затем превратит в тепло работу, затраченную на создание цикла, а потом отдаст это тепло нагревателю. По такому принципу работают холодильники.
Обратный цикл Карно лежит также в основе тепловых насосов. Такие насосы переносят энергию от источников с низкой температурой к потребителю с более высокой температурой.
Но, в отличие от холодильника, в котором отбираемая теплота выбрасывается в окружающую среду, в тепловом насосе она передаётся потребителю.
Как известно, первое начало термодинамики отображает закон сохранения энергии в термодинамических процессах, однако оно не дает представление о направлении протекания процессов. Помимо этого можно придумать множество термодинамических процессов, которые не будут противоречить первому началу, но в реальной действительности таких процессов не существует. Существование второго закона (начала) термодинамики вызвано необходимостью установить возможность того или иного процесса. Этот закон определяет направление течения термодинамических процессов. При формулировке второго начала термодинамики используют понятия энтропии и неравенство Клаузиуса. В таком случае второй закон термодинамики формулируется как закон роста энтропии замкнутой системы, если процесс является необратимым.
Формулировки второго закона термодинамики
Если в замкнутой системе происходит процесс, то энтропия этой системы не убывает.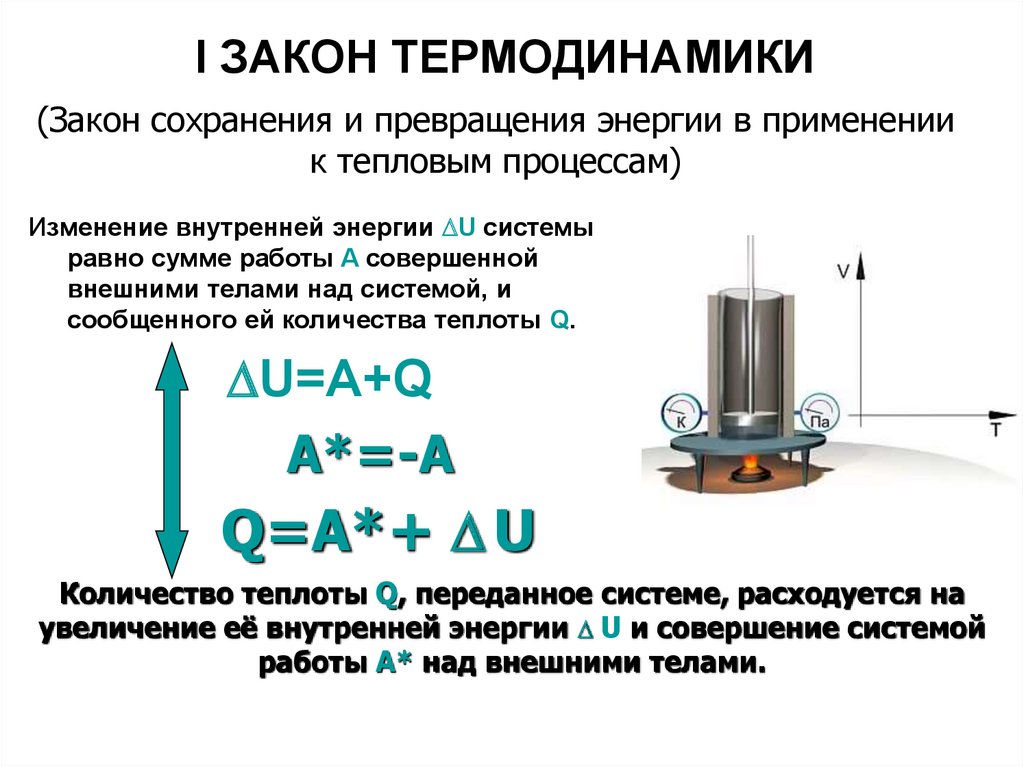
В виде формулы второй закон термодинамики записывают как:
где S – энтропия; L – путь по которому система переходит из одного состояния в другое.
В данной формулировке второго начала термодинамики следует обратить внимание на то, что рассматриваемая система должна быть замкнутой. В незамкнутой системе энтропия может вести себя как угодно (и убывать, и возрастать, и оставаться постоянной). Заметим, что энтропия не изменяется в замкнутой системе при обратимых процессах.
Рост энтропии в замкнутой системе при необратимых процессах — это переход термодинамической системы из состояний с меньшей вероятностью в состояния с большей вероятностью. Известная формула Больцмана дает статистическое толкование второго закона термодинамики:
где k – постоянная Больцмана; w – термодинамическая вероятность (количество способов при помощи которых, может реализовываться рассматриваемое макросостояние системы). Так, второй закон термодинамики является статистическим законом, который связан с описанием закономерностей теплового (хаотического) движения молекул, которые составляют термодинамическую систему.
Другие формулировки второго закона термодинамики
Существует ряд других формулировок второго закона термодинамики:
1) Формулировка Кельвина: Невозможно создать круговой процесс, результатом которого станет исключительно превращение теплоты, которое получено от нагревателя, в работу. Из данной формулировки второго закона термодинамики делают вывод о невозможности создания вечного двигателя второго рода. Это означает, что периодически действующая тепловая машина должна иметь нагреватель, рабочее тело и холодильник. При этом КПД идеальной тепловой машины не может быть больше, чем КПД цикла Карно:
где – температура нагревателя; — температура холодильника; ( title=”Rendered by QuickLaTeX.com”>).
2) Формулировка Клаузиуса: Невозможно создать круговой процесс в результате которого будет происходить исключительно передача тепла от тела с меньшей температурой к телу с большей температурой.
Второй закон термодинамики отмечает существенное различие между двумя формами передачи энергии (работой и теплотой).
Из этого закона следует, переход упорядоченного перемещение тела, как единого целого в хаотическое движение молекул тела и внешней среды – является необратимым процессом. При этом упорядоченное движение может переходить в хаотическое без дополнительных (компенсационных) процессов. Тогда как переход неупорядоченного движения в упорядоченное должен сопровождаться компенсирующим процессом.
Примеры решения задач
ПРИМЕР 1
| Задание | В чем состоит суть проблемы «Тепловой смерти Вселенной»? Почему эта проблема является несостоятельной? |
| Решение | Данная проблема была сформулирована в XIX веке. Если считать Вселенную замкнутой системой и пытаться применить к ней второй закон термодинамики, то по гипотезе Клаузиуса энтропия Вселенной достигнет некоторого максимума. То есть через некоторое время все формы движения станут тепловым движением. Вся теплота от тел с более высокой температурой перейдет к телам, имеющим более низкую температуру, то есть температуры всех тел Вселенной станут равны. Вселенная придет в состояние теплового равновесия, все процессы прекратятся — это называют тепловой смертью Вселенной. Ошибка данного положения о тепловой смерти Вселенной заключена в том, что второй закон термодинамики неприменим к незамкнутым системам, а Вселенную считать замкнутой не следует. Так как она является безграничной и состоит в бесконечном развитии. |
ПРИМЕР 2
| Задание | Чему равно КПД цикла, который представлен на рис.1? Считайте, что в процессе участвует идеальный газ (число степеней свободы равно i) и его объем изменяется в n раз. |
| Решение | Коэффициент полезного действия цикла, который представлен на рис.1 найдем как: где — количество теплоты, которое рабочее тело получает от нагревателя в представленном цикле. В адиабатных процессах подвода и отвода тепла нет, получается, что тепло подводится только в процессе 1-2. — количество теплоты, которое отводится от газа в процессе 3-4. Используя первое начало термодинамики, найдем количество тепла, полученное газом в процессе 1-2, который является изохорным: так как изменения объема в данном процессе нет. Изменение внутренней энергии газа определим как:По аналогии для изохорного процесса, в котором теплота отводится, имеем: Подставим полученный результат (2.2 – 2.5) в выражение (2.1): Используем уравнение адиабаты для нахождения разностей температур, и рассматривая рис.1. Для процесса 2-3 запишем: |
Законы термодинамики называют также ее началами. На самом деле начало термодинамики представляет собой не что иное, как совокупность тех или иных постулатов, которые лежат в основе соответствующего раздела молекулярной физики. Данные положения устанавливали в течение научных исследований. В то же время они были доказаны экспериментальным путем. Почему же законы термодинамики принимают за постулаты? Все дело в том, что таким образом термодинамику можно строить аксиоматическим путем.
Основные законы термодинамики
Немного о структуризации. Законы термодинамики разделяются на четыре группы, каждая из которых имеет определенный смысл. Итак, что могут поведать нам начала термодинамики?
Первое и второе
Первое начало расскажет о том, как применяется закон сохранения энергии по отношению к той или иной термодинамической системе. Второе начало выдвигает некоторые ограничения, которые применяются к направлениям термодинамических процессов. Более конкретно, они запрещают самопроизвольную передачу тепла, совершаемую от менее нагретого к более нагретому телу. Есть у второго закона термодинамики и альтернативное название: закон возрастания энтропии.
Третье и четвертое
Третий закон описывает поведение энтропии вблизи абсолютного температурного нуля. Есть еще одно начало, последнее. Оно носит название “нулевой закон термодинамики”. Смысл его заключается в том, что любая замкнутая система придет к состоянию термодинамического равновесия и из него выйти уже самостоятельно не сможет.
При этом ее начальное состояние может быть любым.
Зачем нужны начала термодинамики?
Законы термодинамики были изучены для того, чтобы описывать макроскопические параметры тех или иных систем. При этом конкретные предложения, имеющие связь с микроскопическим устройством, не выдвигаются. Этот вопрос изучается отдельно, но уже другим ответвлением науки – статистической физикой. Законы термодинамики независимы друг от друга. Что это может означать? Это нужно понимать так, что ни одно начало термодинамики из другого вывести невозможно.
Первое начало термодинамики
Как известно, термодинамическая система характеризуется несколькими параметрами, в числе которых есть и внутренняя энергия (обозначается буквой U). Последняя формируется из кинетической энергии, которую имеют все частицы. Это может быть энергия поступательного, а также колебательного и вращательного движения. На этом моменте вспомним о том, что энергия может быть не только кинетической, но и потенциальной.
Так вот, в случае идеальных газов потенциальной энергией пренебрегают. Именно поэтому внутренняя энергия U будет складываться исключительно из кинетической энергии движения молекул и зависеть от температуры.
Эта величина – внутренняя энергия – называется иными словами функцией состояния, поскольку она определяется состоянием термодинамической системы. В нашем случае она определяется температурой газа. Следует отметить, что внутренняя энергия не зависит от того, каким был переход в состояние. Допустим, что термодинамическая система совершает круговой процесс (цикл, как его называют в молекулярной физике). Иными словами, система, выйдя из начального состояния, подвергается определенным процессам, но в результате возвращается в первичное состояние. Тогда нетрудно догадаться, что изменение внутренней энергии будет равно 0.
Как изменяется внутренняя энергия?
Изменить внутреннюю энергию идеального газа можно двумя способами. Первый вариант – совершить работу. Второй – сообщить системе то или иное количество теплоты.
Логично, что второй способ подразумевает не только сообщение теплоты, но и ее отнятие.
Формулировка первого начала термодинамики
Их (формулировок) может быть несколько, так как все любят говорить по-разному. Но на самом деле суть остается той же. Она сводится к тому, что количество теплоты, которое было подведено к термодинамической системе, расходуется на совершение идеальным газом механической работы и изменение внутренней энергии. Если говорить о формуле или математической записи первого начала термодинамики, то она выглядит следующим образом: dQ = dU + dA.
Все величины, которые входят в состав формулы, могут иметь разные знаки. Ничто не запрещает им быть отрицательными. Допустим, что к системе подводится количество теплоты Q. Тогда газ будет нагреваться. Возрастает температура, а значит, увеличивается и внутренняя энергия газа. То есть и Q, и U будут иметь положительные значения. Но если внутренняя энергия газа увеличивается, он начинает вести себя активнее, расширяться.
Следовательно, работа также будет положительной. Можно сказать, что работу совершает сама система, газ.
В случае если у системы забирают определенное количество теплоты, внутренняя энергия уменьшается, а газ сжимается. В таком случае можно говорить уже о том, что работу совершают над системой, а не она сама. Предположим опять, что некоторая термодинамическая система совершает цикл. В таком случае (как уже было сказано ранее) изменение внутренней энергии будет равно 0. Значит, работа, совершаемая газом или над ним, будет численно равна подведенной или отведенной к системе теплоте.
Математическую запись этого следствия называют еще одной формулировкой первого начала термодинамики. Примерно она звучит следующим образом: “В природе невозможно существование двигателя первого рода, то есть, двигателя, который совершал бы работу, превосходящую полученную извне теплоту”.
Второе начало термодинамики
Нетрудно догадаться, что термодинамическое равновесие характерно для системы, в которой макроскопические величины остаются неизменными во времени.
Это, конечно же, давление, объем и температура газа. Их неизменность может быть построена на нескольких условиях: на отсутствии теплопроводности, химических реакций, диффузии и других процессов. Если под действием внешних факторов система была выведена из термодинамического равновесия, она к нему со временем вернется. Но если эти факторы будут отсутствовать. Причем произойдет это самопроизвольно.
Мы пойдем немного другим путем, отличным от того, что рекомендуют многие учебники. Для начала ознакомимся со вторым началом термодинамики, а уже потом разберемся, что за величины в него входят, и что они обозначают. Итак, в замкнутой системе при наличии любых протекающих в ней процессов энтропия не убывает. Записывается второе начало термодинамики следующим образом: dS >(=) 0. Здесь знак > будет связан с необратимым процессом, а знак = – с обратимым.
Что же называется в термодинамике обратимым процессом? А это такой процесс, при котором система возвращается (спустя череду каких-то процессов) к своему первоначальному состоянию.
Причем в этом случае ни в системе, ни в окружающей среде никаких изменений не остается. Иными словами, обратимый процесс – это такой процесс, для которого возможно возвращение в начальное состояние через промежуточные состояния, идентичные прямому процессу. В молекулярной физике таких процессов очень мало. Например, переход количества теплоты от более нагретого тела к менее нагретому будет необратимым. Аналогично и в случае диффузии двух веществ, а также распространения газа на весь объем.
Энтропия
Энтропия, имеющая место во втором законе термодинамики, равна изменению количества теплоты, деленному на температуру. Формула: dS = dQ/T. Она имеет определенные свойства.
Как генерируется энергия, как она преобразуется из одной формы в другую и что происходит с энергией в замкнутой системе? На все эти вопросы помогут дать ответ законы термодинамики. Подробнее сегодня будет рассмотрен второй закон термодинамики.
Законы в повседневной жизни
Законы управляют повседневной жизнью.
В дорожных законах говорится, что нужно остановиться на знаках остановки. Правительственные требуют предоставить часть своей зарплаты государству и федеральному правительству. Даже научные применимы к повседневной жизни. Например, закон силы тяжести предсказывает довольно плохой результат для тех, кто пытается летать. Другой набор научных законов, которые влияют на повседневную жизнь, – это законы термодинамики. Итак, можно привести ряд примеров, чтобы увидеть, как они влияют на повседневную жизнь.
Первый закон термодинамики
Первый закон термодинамики гласит, что энергия не может быть создана или уничтожена, но можно преобразовать ее из одной формы в другую. Это также иногда называют законом сохранения энергии. Итак, как это относится к повседневной жизни? Ну, взять, к примеру, компьютер, который вы используете сейчас. Он питается энергией, но откуда эта энергия? Первый закон термодинамики говорит нам, что эта энергия не могла появиться из-под воздуха, поэтому она откуда-то появилась.
Можно отследить эту энергию. Компьютер питается от электричества, но откуда это электричество? Правильно, с электростанции или гидроэлектростанции. Если рассматривать вторую, то она будет связана с плотиной, которая сдерживает реку. У реки есть связь с кинетической энергией, а это означает, что река течет. Плотина превращает эту кинетическую энергию в потенциальную энергию.
Как работает гидроэлектростанция? Вода используется для вращения турбины. При вращении турбины приводится в действие генератор, который будет создавать электричество. Это электричество может быть проложено полностью в проводах от электростанции до вашего дома, чтобы при подключении шнура питания к электрической розетке электричество проникало в ваш компьютер, чтобы он мог работать.
Что произошло здесь? Уже было определенное количество энергии, которая была связана с водой в реке как кинетическая энергия. Потом она превратилась в потенциальную энергию. Затем плотина приняла эту потенциальную энергию и превратила ее в электричество, которое затем смогло попасть в ваш дом и привести в действие компьютер.
Второй закон термодинамики
Изучив этот закон, можно понять, как работает энергия и почему все движется к возможному хаосу и беспорядку. Второй закон термодинамики еще называют законом энтропии. Вы когда-нибудь задумывались, как возникла Вселенная? Согласно Теории Большого Взрыва, до того, как зародилось все вокруг, вместе собралось огромное количество энергии. После Большого Взрыва появилась Вселенная. Все это хорошо, только что это была за энергия? В начале времени вся энергия во Вселенной содержалась в одном относительно небольшом месте. Эта интенсивная концентрация представляла собой огромное количество того, что называется потенциальной энергией. Со временем она распространилась по огромному пространству нашей Вселенной.
В гораздо меньших масштабах резервуар воды, удерживаемый плотиной, содержит потенциальную энергию, так как ее расположение дает возможность протекать через плотину. В каждом случае запасенная энергия, однажды выпущенная, распространяется и делает это без каких-либо прилагаемых усилий.
Другими словами, высвобождение потенциальной энергии является спонтанным процессом, который возникает без необходимости в дополнительных ресурсах. По мере того, как энергия распространяется, часть ее преобразуется в полезную и выполняет определенную работу. Остальная преобразуется в непригодную, просто называемую теплотой.
Поскольку Вселенная продолжает распространяться, она содержит все менее и менее полезную энергию. Если менее полезная доступна, меньше работы может быть сделано. Так как вода течет через плотину, она также содержит менее полезную энергию. Это уменьшение полезной энергии с течением времени называется энтропией, где энтропия – это количество неиспользуемой энергии в системе, а система – это просто совокупность объектов, составляющих целое.
Энтропия также может упоминаться как количество случайностей или хаоса в организации без организации. По мере того как полезная энергия уменьшается с течением времени, дезорганизация и хаос увеличиваются. Таким образом, по мере освобождения накопленной потенциальной энергии не все это преобразуется в полезную.
Все системы испытывают это увеличение энтропии с течением времени. Это очень важно понять, и это явление называют вторым законом термодинамики.
Энтропия: случайность или дефект
Как вы, возможно, догадались, второй закон следует за первым, который обычно называют законом сохранения энергии, и он утверждает, что энергия не может быть создана и ее нельзя уничтожить. Другими словами, количество энергии во Вселенной или любой системе является постоянным. Второй закон термодинамики обычно называют законом энтропии, и он считает, что с течением времени энергия становится менее полезной, а качество ее уменьшается со временем. Энтропия – это степень случайности или дефектов, которые имеет система. Если система очень неупорядоченная, то она обладает большой энтропией. Если в системе много неисправностей, то энтропия низкая.
Говоря простыми словами, второй закон термодинамики гласит, что энтропия системы не может со временем уменьшаться. Это означает, что в природе вещи переходят от состояния порядка к состоянию беспорядка.
И это необратимо. Система никогда не станет более упорядоченной сама по себе. Другими словами, в природе энтропия системы всегда увеличивается. Один из способов подумать об этом – это ваш дом. Если вы его никогда не будете убирать и пылесосить, то довольно скоро у вас будет ужасный бардак. Энтропия увеличилась! Чтобы уменьшить ее, необходимо применять энергию для использования пылесоса и швабры, чтобы очистить от пыли поверхность. Дом сам себя не уберет.
Что представляет собой второй закон термодинамики? Формулировка простыми словами гласит, что при изменении энергии из одной формы в другую форму, материя либо движется свободно, либо энтропия (беспорядок) в замкнутой системе увеличивается. Различия в температуре, давлении и плотности имеют тенденцию выравниваться горизонтально через некоторое время. Из-за силы тяжести плотность и давление не выравниваются вертикально. Плотность и давление на дне будут больше, чем сверху. Энтропия – это мера распространения материи и энергии везде, где у нее есть доступ.
Наиболее распространенная формулировка второго закона термодинамики в основном связана с Рудольфом Клаузиусом, который говорил:
Невозможно построить устройство, которое не производит другого эффекта, чем перенос тепла из тела с более низкой температурой в тело с более высокой температурой.
Другими словами, все пытается поддерживать ту же температуру с течением времени. Существует много формулировок второго закона термодинамики, в которых используются разные термины, но все они означают одно и то же. Другое заявление Клаузиуса:
Тепло само по себе не происходит от холодного до более горячего тела.
Второй закон применим только к крупным системам. Он касается вероятного поведения системы, в которой нет энергии или материи. Чем больше система, тем более вероятен второй закон.
Еще одна формулировка закона:
Полная энтропия всегда увеличивается в самопроизвольном процессе.
Увеличение энтропии ΔS при протекании процесса должно превышать или быть равным отношению количества теплоты Q, переданного системе, к температуре Т, при которой теплота передается.
Термодинамическая система
В общем смысле формулировка второго закона термодинамики простыми словами гласит, что температурные различия между системами, находящимися в контакте друг с другом, имеют тенденцию к выравниванию и что работа может быть получена из этих неравновесных различий. Но при этом происходит потеря тепловой энергии, а энтропия увеличивается. Различия давления, плотности и температуры в имеют тенденцию выравниваться, если им предоставляется возможность; плотность и давление, но не температура, зависят от силы тяжести. Тепловой двигатель представляет собой механическое устройство, которое обеспечивает полезную работу из-за разницы в температуре двух тел.
Термодинамическая система – это та, которая взаимодействует и обменивается энергией с областью вокруг нее. Обмен и передача должны произойти, по крайней мере, двумя способами. Один путь должен быть передачей тепла. Если термодинамическая система «находится в равновесии», она не может изменять свое состояние или статус без взаимодействия с окружающей средой.
Проще говоря, если вы находитесь в равновесии, вы «счастливая система», вы ничего не можете сделать. Если вы что-то захотите сделать, вы должны взаимодействовать с окружающим миром.
Второй закон термодинамики: необратимость процессов
Невозможно иметь циклический (повторяющийся) процесс, который полностью преобразует тепло в работу. Также невозможно иметь процесс, который переносит тепло от холодных объектов на теплые объекты без использования работы. Некоторое количество энергии в реакции всегда теряется для нагревания. Кроме того, система не может преобразовать всю свою энергию в рабочую энергию. Вторая часть закона более очевидна.
Холодное тело не может нагревать теплое тело. Тепло естественным образом стремится течь от более теплых до более прохладных областей. Если тепло перейдет от более прохладного к более теплым, это противоречит тому, что является «естественным», поэтому система должна выполнить некоторую работу, чтобы это произошло. в природе – второй закон термодинамики.
Это, пожалуй, самый известный (по крайней мере, среди ученых) и важный закон всей науки. Одна из его формулировок:
Энтропия Вселенной стремится к максимуму.
Другими словами, энтропия либо остается неизменной, либо становится больше, энтропия Вселенной никогда не может снизиться. Проблема в том, что это всегда верно. Если взять флакон духов и распылить его в комнате, то скоро ароматные атомы заполнят все пространство, и этот процесс является необратимым.
Взаимосвязи в термодинамике
В законах термодинамики описываются взаимосвязи между тепловой энергией или теплом и другими формами энергии, и как энергия влияет на материю. Первый закон термодинамики гласит, что энергия не может быть создана или уничтожена; общее количество энергии во Вселенной остается неизменным. Второй закон термодинамики посвящен качеству энергии. В нем говорится, что по мере передачи или преобразования энергии все больше и больше теряется полезной энергии.
Второй закон также гласит, что существует естественная тенденция превращения любой изолированной системы в более неупорядоченное состояние.
Даже когда порядок увеличивается в определенном месте, когда вы принимаете во внимание всю систему, включая окружающую среду, всегда наблюдается увеличение энтропии. В другом примере кристаллы могут образовываться из раствора соли, когда вода выпаривается. Кристаллы более упорядочены, чем молекулы соли в растворе; однако испаренная вода гораздо более беспорядочна, чем жидкая вода. Процесс, взятый в целом, приводит к чистому увеличению беспорядка.
Работа и энергия
Во втором законе объясняется, что невозможно преобразовать тепловую энергию в механическую энергию со 100-процентной эффективностью. Можно привести пример с автомобилем. После процесса нагрева газа, чтобы увеличить его давление для привода поршня, в газе всегда остается некоторое количество тепла, которое нельзя использовать для выполнения каких-либо дополнительных работ.
Это отработанное тепло должно быть отброшено путем его передачи в радиатор. В случае с автомобильным двигателем это делается путем извлечения отработанного топлива и воздушной смеси в атмосферу.
Кроме того, любое устройство с подвижными частями создает трение, которое преобразует механическую энергию в тепло, которое обычно непригодно и должно быть удалено из системы путем переноса его в радиатор. Когда горячее и холодное тело контактируют друг с другом, тепловая энергия будет поступать из горячего тела в холодное тело до тех пор, пока они не достигнут теплового равновесия. Тем не менее, тепло никогда не вернется в другую сторону; разница температур двух тел никогда не будет спонтанно увеличиваться. Перемещение тепла от холодного тела к горячему телу требует работы, которую должен выполнять внешний источник энергии, такой как тепловой насос.
Судьба Вселенной
Второй закон также предсказывает конец Вселенной. Это конечный уровень беспорядка, если везде будет постоянное тепловое равновесие, никакая работа не может быть выполнена, и вся энергия будет заканчиваться как случайное движение атомов и молекул.
По современным данным, Метагалактика – это расширяющаяся нестационарная система, о тепловой смерти Вселенной и речи быть не может. Тепловая смерть – это состояние теплового равновесия, при котором прекращаются все процессы.
Это положение ошибочно, так как второй закон термодинамики применяется только к замкнутым системам. А Вселенная, как известно, безгранична. Однако сам термин «тепловая смерть Вселенной» иногда используется для обозначения сценария будущего развития Вселенной, согласно которому она так и будет расширяться до бесконечности во тьму пространства, пока не обратится в рассеянный холодный прах.
Закономерность переноса тепла от одного объекта к другому рассматривается в утверждении о теплообмене. Весь процесс заключается во внутреннем обмене энергии между объектами, которая называется теплотой.
Правильный процесс направлен только на получение равного состояния, будь оно термическое, механическое или какое-либо ещё. Это действие и содержится во втором законе термодинамики, который имеет совсем немаленькое значение для тепловых машин.
Данный закон говорит о том, что тепло может само передвигаться исключительно от объекта с большой температурой к объекту наименьшей температурой. Что бы осуществить обратный цикл, будет затрачиваться некоторая работа. Из чего можно получить заключение второго закона термодинамики: Это действие во время которого теплота сама по себе передвигается от объекта с меньшей теплотой к объекту с наибольшей теплотой не может существовать.
Заметка: Вы хотите обновить свои подоконники, но не знаете в какую компанию обратиться? Попробуйте подоконник меллер купить (http://hoffen.ru/podokonniki-moeller/), ценой и качеством Вы останетесь довольны!
В свое время второй закон термодинамики дает оценку условиям в которых тепло сможет, на сколько хочет обращаться в работу. Любое разомкнутое термодинамическое действие во время нарастания объема, будет происходить работа со знаком плюс.
Формула второго закона термодинамики
В которой L- будет итоговой работой, v1 и v2- собственной изначальный и итоговый объем удельный.
Так как действие расширения бесконечным быть не может, соответственно, и обращение тепла в работу будет этим ограничиваться. Непрерывным это действие будет в случае закрытого кругового движения.
Любое действие происходящее в цикле, происходит с подводом либо отводом тепла dQ, с сопровождением затраты либо совершения работ, упадком или возрастанием энергии внутри тела, а обязательное условие dQ=dU+dL , dg=du+d1 должно выполняться. Ведь оно доказывает что без тепла (dg=0) все действия будут происходить благодаря внутренней энергии системы, а ввод тепла в систему можно определить термодинамикой.
Интеграция в замкнутом контуре:
в которой Qц, Lц – будет теплотой превращенной в работу, L1- L2 – работой совершенной данным телом. Q1 подведенная теплота, Q2- отведенная теплота. А значит, Lц= Qц= Q1-Q2
Тепло можно подвести к телу Q1 только при наличии более горячего тела, а отвод Q2 только при наличии более холодного тела. В случае цикличности процесса понадобиться два источника с разной температурой.
Новости ВсЁ Наука – Ученые математически доказали недостижимость абсол…
Законы термодинамики, являющиеся краеугольными камнями современной физики, помогают нам объяснить поведение и изменение физических свойств объектов и сред при определенных условиях и обстоятельствах. Первые два закона в фундаментальном плане никогда особо не подвергались критике и пересмотру, чего нельзя сказать о третьем. Он был выведен немецким физиком и химиком Вальтером Нернстом в 1906-1912 годах, однако ученые до сих пор спорят о его состоятельности.
Из него следует, что:
«Энтропия любого идеально чистого вещества в термодинамическом равновесии стремится к нулю при приближении абсолютно нуля температуры, так же как и температура любого чистого вещества в термодинамическом равновесии стремится к нулю, когда энтропия этого вещества стремится к нулю»».
В недавнем исследовании, результаты которого были опубликованы в журнале Nature Communications, ученые из Университетского колледжа Лондона доказали, что в системе, где энтропия не может достичь абсолютного нуля, достичь (за определенное количество шагов) температуры тела, равной абсолютному нулю, невозможно.
«Мы доказали, что при наличии ограниченного числа шагов охладить систему до абсолютного нуля не представляется возможным. Затем мы пришли к выводу, что невозможно охладить систему до абсолютного нуля и за определенный промежуток времени, а также установили связь между временем и максимально возможно низкой температурой, коей является скорость охлаждения», — говорит Луис Масанес, один из авторов нового исследования.
Исследователи надеются, что благодаря этим выводам другие ученые начнут более серьезно относиться к третьему закону термодинамики, который, если говорить простыми словами, как раз и говорит о недостижимости абсолютного нуля температуры. Помимо этого, исследователи верят, что их работа может иметь важное практическое значение. Ведь понимание процесса охлаждения и его максимальных значений поможет нам, например, в дальнейшей разработке технологий квантовых вычислений.
За последние годы сфера квантовых вычислений привлекает очень повышенное внимание со стороны самых именитых технологических гигантов, например, таких как IBM, которая уже вовсю активно пытается вывести квантовые вычисления на коммерческие рельсы.
Понимание третьего закона термодинамики и уровней, при которых происходит охлаждение, позволит продвинуться в квантовых исследованиях еще дальше, так как одной из ключевых проблем подобных вычислений является перегрев квантовых систем.
Закон Гей-Люссака. Изобара | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Открытие газового закона Р. Бойлем и Э. Мариоттом для изотермических процессов побудило ученых искать другие функциональные зависимости макропараметров газов. В 1802 году французский ученый Ж. Л. Гей-Люссак, исследуя зависимость объема газа от температуры при постоянном давлении, установил закон, названный со временем в его честь.
Жозеф Луи Гей-Люссак (1778—1850) — французский физик и химик, установил, что коэффициент расширения всех газов одинаковый; исследовал температуру и влажность воздуха на высоте до 7 км, дважды поднимаясь в 1804 г. на воздушном шаре.
Изобрел спиртометр, барометр и ряд других приборов.
Стеклянную трубку с резервуаром, в котором был исследуемый газ, он помещал в нагреватель. Газ «закупоривался» маленькой капелькой ртути в трубке, размещенной горизонтально (рис. 1.8). Таким образом, давление газа в резервуаре всегда равнялось атмосферному. Температура газа в резервуаре с помощью нагревателя изменялась от 0 до 100°С. Изменение объема газа от V0(при t0 = 0) до V при неизменном давлении фиксировалось благодаря перемещению капельки ртути.
| Рис. 1.8. Опыт Ж. Л. Гей-Люссака |
Обобщив экспериментальные данные, Гей-Люссак установил, что с изменением температуры при постоянном давлении относительный объем данной массы газа изменяется линейно.
На основании наблюдений он сформулировал утверждение, названное в его честь законом Гей-Люссака.
Закон Гей-Люссака. При постоянном давлении относительное изменение объема газа данной массы прямо пропорционально изменению температуры:
(V — V0) / V0 = αΔt,
где Δt — изменение температуры; V — объем газа при определенной температуре t.
После некоторых математических преобразований, закон Гей-Люссака можно записать также в виде:
V = V0(1 + αΔt),
где V0 — объем газа при температуре t0.
| Рис. 1.9. Изобары |
Коэффициент пропорциональности α называется температурным коэффициентом объемного расширения.
Расчета показали, что все разреженные газы при нагревании на 1°C или 1 K изменяют свой объем приблизительно на 1 / 273 частицу от начального объема:
α = (V100 — V0) / (100K • V0) ≈ 1 / 273 K-1
Гей-Люссак доказал, что у всех газов температурный коэффициент объемного расширения одинаковый и равен 1 / 273 K-1. Материал с сайта http://worldofschool.ru
| Рис. 1.11. Изобары |
Термодинамический процесс, который происходит при постоянном давлении, называется изобарным, а линии, изображающие его, — изобарами. На координатной плоскости зависимости объема V от температуры t изобары будут иметь вид прямых, которые сходятся в одной точке (рис.
1.9). Их наклон зависит от значения давления — изобара, которая отвечает большему давлению, проходит ниже изобары меньшего давления (p1 < p2).
Закон Гей-Люссака приобретет более простую форму, если его выразить через абсолютную температуру. Поскольку 1 + αt = 1 + (1 / 273) • (T — 273) = αТ, то
V = V0αT.
Таким образом, при постоянном давлении объем данной массы газа прямо пропорциональный абсолютной температуре.
Закон Гей-Люссака утверждает, что в изобарном процессе отношение объемов данной массы газа в разных состояниях равно отношению абсолютных температур газа в этих состояниях:
V1 / V2 = T1 / T2
Очевидно, что на координатных плоскостях pT и pV изобарами являются прямые, перпендикулярные оси давления (рис.
1.11).
Таблицы для кабинета физики газовые законы. закон гей люссака изобара
Радиоактивность в физике
Закон гей-люссака формула
Гей-люсак доклад
Математическая формулировка закона гей-люссака:
В чем сущность опыта Гей-Люссака?
Между какими физическими величинами устанавливает связь закон Гей-Люссака? В какой зависимости они находятся?
Какое физическое содержание имеет коэффициент объемного расширения газов?
Какой процесс называется изобарным?
Какими линиями изображаются изобары на координатной плоскости
Vt.При каких условиях изобары одного и того же газа могут иметь разный наклон?
Приведите разные формулировки закона Гей-Люссака.
Физика в производственной столовой
Сейчас я попытаюсь, объяснить, как это
происходит.
Микроволновая энергия распространяется
в форме высокочастотных волн, похожих
на те, которые используются в радиоприемнике,
лишь только короче. Электричество преобразуется
в микроволновую энергию, которая затем
поступает в жаровой шкаф и направляется
на приготовляемую пищу. В отличие от обычных
способов приготовления пищи, в микроволновке
не происходит прямого теплового воздействия
на продукт. Во время приготовления пищи
микроволны поглощаются продуктами. Они
проникают на глубину 20-40 см. Микроволновая
энергия возбуждает молекулы пищи (в особенности
воды, сахара, жира), заставляя их вибрировать
со скоростью 2450000000 раз в секунду. Вибрация
вызывает трение, в результате которого
выделяется большое количество тепла,
за счет которого и происходит приготовление
пищи. Если быстро потереть свои руки одна
о другую, то сразу почувствуешь тепло
от трения ладоней. То же происходит при
приготовлении пищи в микроволновой печи.
Нагревание внутри большого объема продуктов
происходит за счет теплопроводности.
Вследствие этого, блюда готовятся еще
некоторое время, и после извлечения из
печи, пока полностью не прекратится вибрация.
Высокая скорость вибрации позволяет
значительно сэкономить время на приготовление
пищи. Значительно экономится электроэнергия
(до 80%), чем при использовании электрической
плитки. Микроволны не имеют запаха и вкуса,
поэтому не влияют на аромат продукта
и вкус.
3. Законы Ньютона
Мои наблюдения показывают, что законы кинематики и динамики также повседневно встречаются в производственной деятельности повара – кондитера. Например, повар – кондитер, стоящий около плиты на кухне, покоится относительно плиты, других кухонных агрегатов, самого здания, но он движется относительно проезжающих мимо здания кухни машин, движущихся людей и т.д.
Я увидел, что во время работы
повару – кондитеру приходится перемещать
грузы по наклонной (сгружая с машин) или
горизонтальной плоскости кухни. Здесь
он сталкивается с векторной физической
величиной, называемой силой.
Ускорение,
которое приобретает при этом груз, зависит
от приложенной силы, так и от массы данного
груза. Связь между ускорением, силой и
массой выражает второй закон Ньютона.
Очень часто повару – кондитеру на кухне приходится измерять физические величины вещества. Делается это обычно взвешиванием на различных видах весов или измерением объемов различными мерными стаканами, мензурками и т.д. Физические величины измеряются в граммах и килограммах, в литрах и миллилитрах, иногда в гигалитрах и декалитрах. В ходе наблюдений у меня возник вопрос: почему результат взвешивания на рычажных весах не зависит от того, где лежит тело – посередине чашки весов или ближе к ее краю? Ответ: В обоих случаях чашка весов подвешена к одной и той же точке, следовательно, плечо силы постоянно, где бы не лежало тело.
Я поинтересовался у наших поваров и узнал, сколько же положено
по нормам на 1 человека, чтобы приготовить
сегодняшний обед. Меню на сегодня: 1.
тефтели
из говядины – 50 г.: мясо говядины – 38 г,
рис – 5 г, лук репчатый – 18 г, масло топленное
– 3 г, мука – 4 г.; 2. булочка сдобная
– 50 г: мука – 32 г, сахар – 7 г, яйцо -1/4, маргарин
– 5 г, соль – 0,03 г, дрожжи – 0,08 г, молоко
сухое – 0,02 г; 3.компот –сухофрукты -0,025
г, сахар – 0,02 г.
Затем повар проводит самые простые математические решения и получает то количество продуктов, которое необходимо взять для приготовления.
Взвешивая различные продукты, мы видим,
что вес тела, т.е. сила, с которой тело,
давит на чашу весов, совпадает по величине
с силой, действующей со стороны чаши на
данное тело. Сила, с которой чаша давит
на находящееся, на ней тело называется
силой реакции опоры, на весах она уравновешивается
либо усилием пружины, либо грузами – гирями
на другом конце весов. Здесь все зависит
от вида весов. А в простейшем виде: плита
и поставленная на нее кастрюля с водой.
Сила, с которой они действуют друг на
друга, равна по величине и противоположна
по направлению.
Это утверждение является
третьим законом Ньютона. Так же примером
может служить человек, несущий в одной
руке тяжелое ведро с водой. Он для
равновесия наклоняется в противоположную
сторону согласно 3 закону Ньютона.
Перемещая грузы, мы осуществляем равноускоренное прямолинейное движение, но, затачивая нож на вращающемся наждачном камне, мы сталкиваемся с равномерным движением по окружности. Здесь же повар сталкиваемся и с трением, между поверхностью ножа и наждачного камня. Силы трения также проявляются при резании продуктов ножом. Мы зажигаем спичку, чтобы зажечь горелку плиты, мы «добыли» огонь трением – трением спичек о коробок и этим мы изменили внутреннюю энергию спичек, совершив небольшую работу. Знаем, что живую рыбу трудно удержать в руках. А вот почему, задумывался не каждый из нас. Конечно, у рыбы поверхность гладкая, поэтому трение мало.
4. Основные положения молекулярно – кинетической теории (МКТ)
Если говорить об основных положениях
МКТ, то они вплотную связаны с профессией
повара – кондитера.
Согласно этим положениям
все вещества состоят из частиц, между
которыми есть промежутки. Эти частицы
непрерывно и хаотически движутся, взаимодействуют
друг с другом.
Все, с чем сталкивается повар – кондитер на кухне: стены, оборудование, вода, продукты питания и т.д. – имеет общее название «вещество». А оно, как известно, состоит из атомов и молекул. Вещество может находиться в трех агрегатных состояниях: твердом, жидком и газообразном. Например, вода, лед, пар. Агрегатное состояние определяется температурой и внешним давлением.
С газообразным состоянием вещества мы встречаемся ежедневно. Это воздух, которым мы дышим; пар, который образуется при приготовлении пищи и т.д.
Вещества могут переходить из одного агрегатного
состояния в другое. Переход из твердого
состояния в жидкое состояние называется
плавлением, обратный ему процесс называется
кристаллизацией или отвердеванием. Сахар
– молекулярный кристалл, но если его расплавить
и быстро охладить, то образуется леденец
– аморфное состояние сахара.
Однако через
некоторое время в леденце начинают расти
кристаллики сахара. Так, варенье, долго
простоявшее в банке, начинает засахариваться,
т.е. в нем выделяются кристаллики сахара.
Если же варенье переварить еще раз, то
кристаллы сахара расплавятся: варенье
вновь будет хорошим.
Переход вещества из жидкого состояния в газообразное называется конденсацией. Конденсацию можно наблюдать на нижней стороне крышки кастрюли, состоящей из капелек воды.
Вода кипит при 1000 С. Но это справедливо лишь при нормальном атмосферном давлении (около 101 кПа). При возрастании давления температура кипения воды возрастает. Так, в кастрюлях-сковородках пищу варят под давлением около 200 кПа. Температура кипения воды при этом достигает 1200 С. При такой температуре процесс варки происходит быстрее, чем в обычном кипятке. Этим и объясняется название «скороварка».
Я заметил, что обязательное явление
в кухонных помещениях – конвекция или
теплообмен в жидких, и газообразных средах,
осуществляемых потоками (или струями)
жидкости.
Конвекция присутствует в любом помещении даже с отключенными батареями и другими источниками тепла. Она идет более интенсивно, когда включаются отопительные приборы. Именно благодаря конвекции нагревается воздух в жилых помещениях. На кухнях осуществляется более интенсивная конвекция. Помимо отопительных батарей конвекцию подгоняют различные нагревательные приборы и вытяжные вентиляторы, различные дымоотсосы.
Конвекция «подстегивает» и ускоряет диффузию в жидкой и газообразной среде. Диффузия – взаимное проникновение частиц одного вещества между частицами другого вещества при их соприкосновении. Например, положил я сахар в чай и, помешивая ложечкой воду, ускоряю процесс проникновения молекул сахара между молекулами воды.
Благодаря диффузии воздух,
которым мы дышим, представляет собой
смесь азота, кислорода, примеси инертных
газов и паров воды. Конвекция и диффузия
перемешивает газы и запахи в воздушном
пространстве кухни и воздух кухни – настоящий
букет запахов, по которому сразу же можно
определить, что будет сегодня на обед.
На явлении диффузии основана также
засолка огурцов, помидоров, капусты.
На кухне всегда присутствует лучистый теплообмен – это теплообмен, при котором переносится энергия различными лучами. Это могут быть солнечные лучи, а также лучи, испускаемые нагретыми телами, находящимися вокруг нас: кастрюли, чайники, сковороды, баки, плиты и т.д.
Стоя у плиты, мы чувствуем, как тепло передается нашему телу. Но причиной такой теплопередачи не может быть теплопроводность (которая у воздуха, находящегося между плитой и телом значительно мала), ни конвекция (конвекционные потоки всегда направлены вверх). Здесь имеет место лучистый теплообмен.
Все вещества, с которыми мы
работаем на кухне, имеют разную теплоемкость.
Нагревая одинаковое количество воды
и масла, я заметил, что масло нагревается
быстрее. Физическая величина, показывающая
какое количество теплоты требуется для
нагревания 1 кг вещества на 10 С называется удельной теплоемкостью
вещества.
Удельная теплоемкость воды
– 4200 Дж/(кг*0 С), а подсолнечного масла – 1700 Дж/(кг*0 С).
Разные вещества имеют разную теплопроводность. Для взятия проб из котла лучше пользоваться деревянной ложкой, стальная нагревается быстро, а еще быстрее нагревается серебряная или алюминиевая ложка. С этой же целью у металлической посуды (кастрюли, сковороды, чайника и т.д.) делают ручки из дерева и пластмасс. Удельная теплоемкость дерева – 2400 Дж/(кг*0 С), стали – 500 Дж/(кг*0 С), серебра – 250Дж/(кг*0 С), и алюминия – 920Дж/(кг*0 С). Та, у которой удельная теплоемкость меньше, нагревается быстрей.
5. Законы термодинамики
К тепловым явлениям
(и системам) происходящим на кухне применимы
законы (или начала) термодинамики. Первый
закон термодинамики является обобщением
закона сохранения энергии систем, где
наряду с механическими и электрическими
процессами происходят тепловые и химические
процессы, и формулируется он так: количество
теплоты, полученное системой, расходуется
на изменение ее внутренней энергии и
на работу, производимую системой против
внешних сил.
На нашей кухне мы можем также сформулировать первое начало термодинамики так: при сообщении термодинамической системе (например, кастрюле с водой, мясом и овощами) определенного количества теплоты, происходит приращение внутренней энергии системы и она совершает работу, т.е. варит нам суп, борщ и т.д.
Из своих наблюдений, я заметил, что капля воды, попав на раскаленную плиту, начинает на ней прыгать. Объясняется это тем, что капля воды на очень горячей сковороде «плавает» на слое пара, который служит своеобразной теплоизолирующей прослойкой. К тому же капля при этом под действием сил поверхностного натяжения сворачивается в шарик, зона ее контакта (а значит, и теплообмен) с раскаленным металлом сильно уменьшается или можно сказать простыми словами – она мгновенно нагревается и закипает (вспомним, как бурлит и дрыгается кипящая вода).
Второй закон термодинамики
связан с необратимостью тепловых явлений,
с их односторонней направленностью.
Так,
явление диффузии необратимо. Сахар сам
собой растворяется в воде, но никогда
из раствора сам по себе не выделится и
вода не станет пресной. Необратим и процесс
теплообмена. Энергия теплообмена самопроизвольно
переходит от горячего тела к более холодному,
а обратный процесс сам по себе не происходит.
Это, я думаю, наблюдал каждый из нас.
Как учащийся профессии «Повар,
кондитер» мне уже приходилось самому
загружать в кастрюлю или бак с кипящей
водой крупу, макароны или овощи, здесь
я сталкиваюсь с законом Архимеда: на всякое
тело, погруженное в жидкость, действует
выталкивающая сила, направленная вверх
и равная весу вытесненной им жидкости.
Например, каждый из нас пил чай с комочками
сахара, но не каждый наблюдал за этим
явлением. Я заметил, что если в чай
с теплой водой опустить несколько кусочков
сахара вода сначала поднимется, а затем,
когда сахар растворится, понизится.
Почему?
Сначала на сахар действует сила Архимеда
и подъем жидкости в стакане равен весу
кусочков сахара, лишь потом согласно
положениям МКТ молекулы сахара проникли
в молекулы воды и заполнили частично
промежутки между молекулами, поэтому
уровень чая вновь понизился. Архимедов
закон справедлив и для газов.
Пропуская через мясорубку мясо для получения фарша, мы сталкиваемся не только с процессами резания и трения, но и архимедовым винтом, которым мясо подается к ножу и решетке. Рукоятка, которой мы вращаем винт, помогает нам уменьшить усилие, но во сколько раз мы снижаем усилие, во столько же раз увеличивается расстояние, проделываемое нашей рукой.
7. Экспериментально – исследовательская часть
Я проводил
опыты и наблюдения в столовой Губернаторского
автомобильно-
Температура воздуха на кухне +280С
Температура поверхности плиты +2100С
Температура поверхности сковородки +2000С
Влажность воздуха 86% .
Я проводил наблюдение хаотического движения частиц в зависимости от температуры.
Задание: Взял три стакана. В первый налил кипяток; во второй – теплую воду, в третий – холодную воду. В каждый стакан бросил щепотку гранулированного чая. На основе наблюдений сделал вывод: вода в первом стакане, т.е. там, где налит кипяток начала окрашиваться быстрее, чем в теплой или холодной воде. Это объясняется тем, что скорость хаотического движения молекул увеличивается при повышении температуры, в стакане с горячей водой происходит интенсивное окрашивание.
Третий закон термодинамики: определение, примеры, простое объяснение
Третий закон термодинамики гласит, что когда температура системы приближается к абсолютному нулю, ее энтропия становится постоянной, или изменение энтропии равно нулю. Третий закон термодинамики предсказывает свойства системы и поведение энтропии в уникальной среде, известной как абсолютная температура.
Энтропия ограниченной или изолированной системы становится постоянной, когда ее температура приближается к абсолютной температуре (абсолютному нулю).
Термодинамика — одна из наиболее важных и широко изучаемых областей физической науки. Помимо того, что он мучает студентов машиностроения на протяжении большей части их академической жизни, его вездесущность проявляется от холодного бриза моего кондиционера до одной из вершин индустриальной эпохи – парового двигателя. Его реализация регулируется тремя законами, известными как законы термодинамики. Законы определяют, как работа, теплота и энергия влияют на систему. Система — это любая конечно ограниченная область во Вселенной, через которую передается энергия.Все, что находится за пределами этой границы, является его окружением.
Иллюстрация системы в термодинамике. (Фото: Wavesmikey / Wikipedia Commons)
Рекомендуемое видео для вас:
youtube.com/embed/gOWt_Hq3yrE?start=0&rel=0&showinfo=0&modestbranding=1&origin=https://www.scienceabc.com”/> Что такое энтропия?
В то время как первый закон термодинамики подразумевает, что Вселенная началась с конечной полезной энергии, где система, потребляющая энергию, частично тратит ее на выполнение работы, а частично на повышение своей внутренней температуры, второй закон исследует его последствия.Это включает преобразование этой конечной полезной энергии в неиспользуемую энергию; например, образование материи, произошедшее миллиарды лет назад из-за конденсации энергии, с которой началась Вселенная. В этом процессе конечная полезная энергия теперь преобразуется в неиспользуемую энергию.
Эта бесполезная энергия измеряется чем-то, называемым «Энтропия», барометром для измерения случайности или беспорядка в системе.
Иллюстрация энтропии как увеличение беспорядка.
Вселенная подобна комнате, наполненной вещами, которые валяются в беспорядке.
Энтропия этой системы возрастает по мере того, как все больше и больше одежды используется и выбрасывается, дополняя беспорядок, если только обитатель не прилагает усилий, чтобы собрать ее и привести в порядок, что уменьшает этот беспорядок.
Рассматривая Вселенную как единую систему, в ее окружении нет ничего, из чего можно было бы черпать энергию, поэтому, когда вся ее энергия превращается в непригодную для использования энергию, остается только холодное и темное место.Это называется тепловой смертью и является одним из возможных путей гибели Вселенной. Ограниченная система, такая как наша Вселенная, обладает конечными источниками энергии, такими как ее яркие звезды, которые будут гореть целую вечность, прежде чем сдаться жестоким законам природы.
Что такое третий закон термодинамики?
Третий закон термодинамики предсказывает свойства системы и поведение энтропии в уникальной среде, известной как абсолютная температура. Абсолютная температура является самой низкой известной температурой и устанавливает нижний предел температурного диапазона Вселенной.
Как здорово! Нет, серьезно, насколько холодно? Абсолютная температура составляет 0 градусов по Кельвину, стандартная единица измерения температуры или -273,15 градуса по Цельсию! Абсолютная температура также известна как абсолютный ноль в некоторых кругах и странах. Эта шкала даст вам представление.
Третий закон гласит, что когда температура системы приближается к абсолютному нулю, ее энтропия становится постоянной, или изменение энтропии равно нулю.
Утверждение представлено этим уравнением, где T соответствует температуре, а дельта S представляет собой изменение энтропии системы. Обозначение «стремится к нулю», представленное стрелкой, указывающей на ноль, подразумевает, что по мере снижения температуры до бесконечно малого значения система достигает постоянной энтропии за счет забирания энергии из своего окружения, но, как диктует первый закон, часть этой энергии добавит к внутренней энергии системы, тем самым отрицая состояние постоянной энтропии.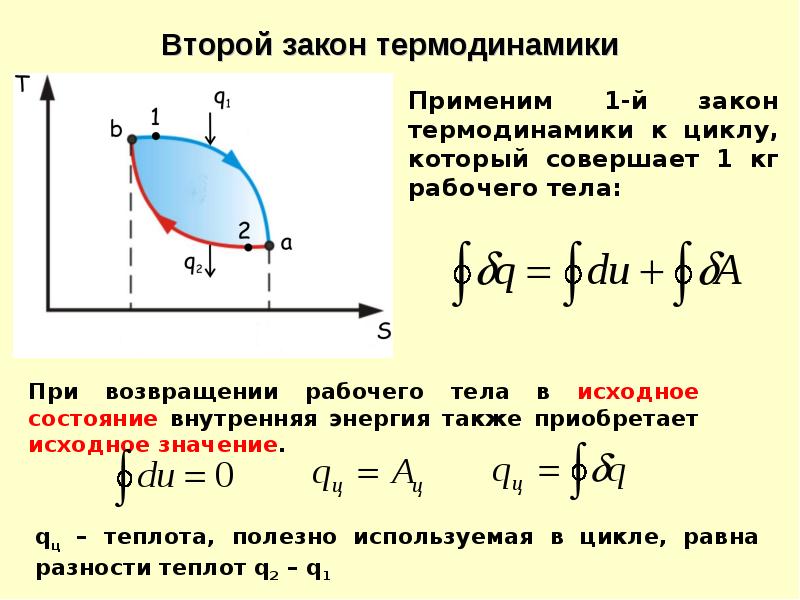
Важность третьего закона термодинамики
Третий закон редко применим к нашей повседневной жизни и управляет динамикой объектов при самых низких известных температурах.Он определяет то, что называют «идеальным кристаллом», атомы которого склеены в своих положениях. Таким образом, идеальный кристалл не обладает абсолютно никакой энтропией, которая достижима только при абсолютной температуре.
Концепция энтропии также была популярна в некоторых теориях, объективно определяющих непрерывный поток времени, таких как линейное увеличение энтропии Вселенной.
В идеале при 0 Кельвина изменение энтропии для реакций образования материи будет равно нулю, хотя практически вся материя проявляет некоторое количество энтропии благодаря наличию минимального количества тепла.Самое холодное из измеренных нами — 3 К, в далеких глубинах Вселенной, за пределами звезд и галактик.
Другими словами, наслаждайтесь летом, пока оно длится!
Подробнее:
Что такое первый закон термодинамики?
Что такое второй закон термодинамики?
Третий закон термодинамики — обзор
Термодинамика химических реакций
В настоящее время большинство измерений удельной теплоемкости производится для интереса к их микроскопической интерпретации, но исторически основной мотивацией было получение данных, относящихся к третьему закону термодинамики и к термодинамике химических реакций в целом.
При постоянном давлении и температуре условия равновесия между продуктами и реагентами химической реакции, а также равновесия между двумя фазами одного и того же вещества определяются изменением энергии Гиббса при превращении. При постоянном объеме и температуре эту роль играет изменение энергии Гельмгольца A . Данные теплоемкости способствуют определению энергий Гиббса и Гельмгольца через термодинамические соотношения G≡H−TS, ∂H/∂TP=CP, ∂S/∂TP=CP/T, A≡U−TS, ∂U /∂TV=CV и ∂S/∂TV=CV/T.Они определяют значения энтропии, температурные зависимости энтальпии, энергии, энергий Гиббса и Гельмгольца.
Как сказано в одной из многочисленных формулировок третьего начала термодинамики, для любого вещества в идеальном кристаллическом состоянии энтропия равна нулю в пределе T →0. Важность химической термодинамики заключается в том, что значения энтропии могут быть получены только из данных об удельной теплоемкости: «энтропия третьего закона» получается путем экстраполяции данных об удельной теплоемкости до 0 К путем интегрирования C P /T для получения S ( T ) –S 0 , и предполагая, согласно третьему закону, что S 0 , энтропия в состоянии 0 K, достигаемая экстраполяцией , равно нулю.
Как правило, данные распространяются на температуру от 1 до 15 К, экстраполяция осуществляется путем полуэмпирической подгонки к самым низким температурным данным, основанным на соответствующих теоретических выражениях, а энтропии сведены в таблицу для 298,15 К и стандартного состояния ( термодинамически стабильная форма вещества при давлении в один бар).
Важную роль в установлении третий закон.Однако в других случаях аналогичные сравнения приводили к выявлению веществ, например, CO, NO и H 2 O, которые не достигают «идеального кристаллического состояния» при 0 К и для которых S 0 ≠0. Существование таких материалов подчеркивает важность осторожности при применении третьего закона к определению энтропии по данным удельной теплоемкости. Третий закон термодинамики, в отличие от первого и второго законов, не может быть выражен простым математическим соотношением, строго применимым во всех случаях.Его применение требует понимания его природы, которая может быть основана на статистико-механическом выражении для энтропии, формуле Больцмана к ограничению фиксированной энергии) вместе с принципом существования единственного состояния с наименьшей энергией, которое достигается при T = 0 системами, находящимися в термодинамическом равновесии.
Случай CO, который хорошо изучен, является полезной иллюстрацией факторов, определяющих, будет ли S 0 = 0: в твердом теле две ориентации молекулы, которые отличаются перестановкой C и Атомы O представляют собой два различимых состояния, но, поскольку молекула относительно симметрична как по форме, так и по распределению электрического заряда, разница в энергии невелика.Конфигурация с самой низкой энергией — это конфигурация, в которой существует совершенно упорядоченное расположение молекул, каждая из которых имеет определенную ориентацию по отношению к другим, но энергия ненамного ниже, чем у более высокоэнтропийного случайного распределения ориентаций, которое термодинамически стабилен при высокой температуре. Ниже ∼5 К низкоэнергетическая упорядоченная конфигурация становится термодинамически стабильной, но существует потенциальный барьер для переориентации молекул, превышающий тепловую энергию при этой температуре, и идеально упорядоченное состояние не достигается.
По кинетическим причинам существует «замороженный беспорядок» при 0 К и S 0 ≠0. В полностью случайной конфигурации для каждой молекулы существует два возможных состояния: Ω=2NA, S=Rln2=5,76 Дж·К-1моль-1. Экспериментальное значение S0=4,2 Дж К-1моль-1, что указывает на то, что молекулы частично упорядочены, по крайней мере, в конкретном измерении, которое дало этот результат. Имеются и другие случаи, например NO, H 2 O и H 2 O в Na 2 SO 4 · 10H 2 O, в которых беспорядок полный.Эти примеры дают представление о трактовке ядерных вкладов в энтропию: случайное распределение по узлам решетки разных изотопов одного и того же элемента сохраняется до 0 К, беспорядок вморожен, вклада в экспериментальную специфику нет. тепловые данные. Беспорядок, связанный с ориентацией ядерных спинов, не замораживается, но при температурах выше 1 К он обычно является полным, связанная с ним энтропия постоянна и вклад в теплоемкость отсутствует.
Оба эти вклада в энтропию сокращаются в химических реакциях, и, хотя их можно вычислить по формуле Больцмана, в таблицах энтропий химических веществ они не учитываются. Существуют также некоторые парамагнитные соли, в которых магнитные моменты неспаренных электронов, как и в случае ядерных моментов, порядка только ниже 1 К. Измерения удельной теплоемкости до 1 К предполагают, что S 0 ≠0, но измерения при достаточно низкой температуре дало бы S 0 =0.
Энтальпия, энергия, энергия Гиббса и Гельмгольца не могут быть определены только по данным удельной теплоемкости. Таблицы термодинамических данных дают значения этих величин для соединений в их стандартных состояниях по отношению к значениям элементов в их стандартных состояниях, например, как значения «теплоты образования» Δ H , для реакции в котором соединение образуется из элементов. Данные по теплоемкости определяют температурные зависимости этих величин, но определение абсолютных значений требует, кроме того, оценки констант интегрирования.
Для энтальпии и энергии необходима одна константа интегрирования, например, одно значение теплоты образования для энтальпии; для энергий Гиббса и Гельмгольца необходимо два.
Общий вывод и количественная оценка третьего закона термодинамики
Физическая установка
Наша цель — предоставить окончательные количественные границы, применимые к любой процедуре охлаждения, а именно, мы хотим найти нижнюю границу температуры, которую может достичь система после любого процесса, который использует некоторые заданные ресурсы или длится некоторое заданное время t .Следовательно, мы должны учитывать самые общие квантовые преобразования, т. е. те, которые соблюдают сохранение полной энергии и являются микроскопически обратимыми (унитарными). Эта общая установка включает в себя термодинамически необратимые протоколы, а также нереалистичные протоколы, где требуется полный контроль над микроскопическими степенями свободы ванны. Удивительно, но мы обнаружим здесь, как и в случае со вторым законом 25, 27, 29, 30 , что такая нереалистичная степень контроля, по-видимому, не дает преимущества перед очень грубым контролем.
Мы покажем, что плотность состояний резервуара, помогающая процессу охлаждения, оказывает важное влияние на скорость охлаждения системы. (Плотность состояний Ω( E ) есть число состояний с энергией E .) Мы видим, что чем быстрее растет Ω( E ), тем ниже температура, которая может быть достигнута при фиксированных ресурсах или в фиксированное количество времени. Более того: если Ω( E ) растет экспоненциально или быстрее, то охлаждение до абсолютного нуля за конечное время в принципе возможно, допуская нарушение третьего закона.Однако мы увидим, что экспоненциальное или суперэкспоненциальное Ω( E ) следует рассматривать как нефизическое. Это становится более наглядным, если выразить его через (микроканоническую) теплоемкость C ( E ), связанную с S ( E )=ln Ω( E ) через
, где штрихи представляют дифференциалы. Если Ω( E ) растет экспоненциально или быстрее, то C ( E ) бесконечно или отрицательно, что считается нефизическим.
Если Ω( E ) является субэкспоненциальным, то C ( E ) положительно. И чем быстрее растет Ω( E ), тем больше C ( E ). Только резервуар с бесконечномерным гильбертовым пространством может поддерживать рост S ( E ) для всех E . И действительно, бесконечномерные резервуары позволяют быстрее охлаждаться. Однако наши результаты носят общий характер и относятся и к конечномерному случаю.
Предположим, что мы хотим охладить квантовую систему с размерностью гильбертова пространства d и гамильтонианом H S , имеющую вырождение в основном состоянии g , щель над основным состоянием Δ и наибольшую энергию Дж .Какие ресурсы необходимы для этого?
Фундаментальные допущения
Давайте конкретизируем установку и соберем допущения, которые мы примем (те, которые исходят из первых принципов):
(i) Мы считаем, что начало процесса наступает, когда система еще не соприкоснуться ни с системой хранения работы (весом), ни с резервуаром, так что изначально глобальное состояние будет ρ S ⊗ ρ B ⊗ ρ W .
Хотя может представлять интерес другой начальный стартовый сценарий, его рассмотрение выходит за рамки настоящей статьи.
(ii) Мы учитываем наиболее общее квантовое преобразование системы, ванны и веса, которое является обратимым (унитарным) и сохраняет полную энергию. Это может показаться ограничительным по сравнению с парадигмами, которые допускают произвольные условия взаимодействия, однако это не так, поскольку произвольные взаимодействия могут быть включены в модель, как показано в Приложении H ссылки. 27 и в исх.25, просто позволяя энергии рабочей системы колебаться. Во многих парадигмах это неявно обеспечивается за счет предположения, что вся недостающая энергия считается работой. Парадигмы, ослабляющие это условие, по существу игнорируют энергию, передаваемую другим системам, или рассматривают эти другие системы как классические. По сути, мы вводим закон сохранения энергии, чтобы гарантировать, что мы должным образом учитываем все энергетические затраты, связанные с взаимодействием, в то время как различные унитарные условия или условия взаимодействия просто передают или берут энергию от веса для компенсации.
Таким образом, процесс охлаждения представляет собой любое преобразование вида
, где U — глобальное унитарное выражение, удовлетворяющее
(iii) Работа, затраченная на преобразование, берется из веса. Поскольку нас интересуют предельные ограничения, мы рассматриваем идеализированный вес с гамильтонианом, имеющим непрерывный и неограниченный спектр. С помощью этого 30 можно смоделировать любую другую рабочую систему. Обозначим через w max значение потребленной работы в наихудшем случае, то есть
w max в общем случае будет намного больше, чем средняя работа 〈 W 〉.В любом физически разумном процессе, осуществляемом за конечное время, ожидается, что он будет конечным.
(iv) Мы также требуем, как в исх. 29 видно, что преобразование охлаждения коммутирует с перемещением по весу. Другими словами, функционирование тепловой машины не зависит от происхождения энергий груза, так что оно зависит только от того, сколько работы совершит вес.
Это можно понимать как определение того, что такое работа — это просто изменение энергии, которое мы можем вызвать в некоторой внешней системе.Это также гарантирует, что вес является только механизмом для доставки или хранения работы, а не, например, дампом энтропии (см. Результат 1 в Дополнительном обсуждении). Это также гарантирует, что в процессе охлаждения вес всегда остается в состоянии, которое может быть использовано в следующем цикле или процессе. Таким образом,
где эрмитов оператор Π действует как для всех . Кроме того, допустим, что начальное состояние веса ρ W может быть произвольным. В частности, он может быть связным, что дает преимущество 27 .
(v) Предположим, что ванна имеет объем V и находится в тепловом состоянии при заданной обратной температуре , где Z B статистическая сумма ванны. Обозначим плотность свободной энергии ванны (в каноническом состоянии ρ B ) через .
(vi) Микроканоническая теплоемкость (2) не отрицательна C ( E ) для всех энергий E . Это означает, что S ( E ) является сублинейным в E .Мы также доказываем в дополнительных методах, что если S ( E ) растет линейно или быстрее, то возможно идеальное охлаждение за конечное время.
С учетом этих допущений мы показываем, что для идеального охлаждения системы до абсолютного нуля требуется хотя бы один из этих двух ресурсов, объем ванны V , или наихудшее значение потребляемой работы w max должно быть бесконечным. Кроме того, мы определили самую низкую достижимую температуру системы с точки зрения В и Вт макс .
Количественная оценка недостижимости из первых принципов
С предположениями (i)–(vi) мы рассматриваем два случая, один из которых начальное и конечное состояния являются тепловыми, а другой допускает произвольные начальное и конечное состояния.
Наш первый результат касается первого и утверждает, что в любом процессе, в котором вложенная работа в наихудшем случае составляет w max , конечная температура системы не может быть ниже
в больших w max , В предел.Микрононическая плотность свободной энергии при обратной температуре β 0 определяется
, где E 0 – это решение уравнения S ‘( E 0 ) = β 0 . Напомним, что при большом объеме ванны V обычно бывает так, что ф мик ( β 0 )= ф кан ( 90 8 и они не зависят от V .
Проанализируем поведение уравнения (7) с точки зрения вложенных ресурсов. По мере роста w max β 0 уменьшается, а f mic увеличивается, что приводит к более низкой конечной температуре. Поскольку вся объемная зависимость в уравнении (7) является явной, следовательно, большее В также приводит к более низкой конечной температуре.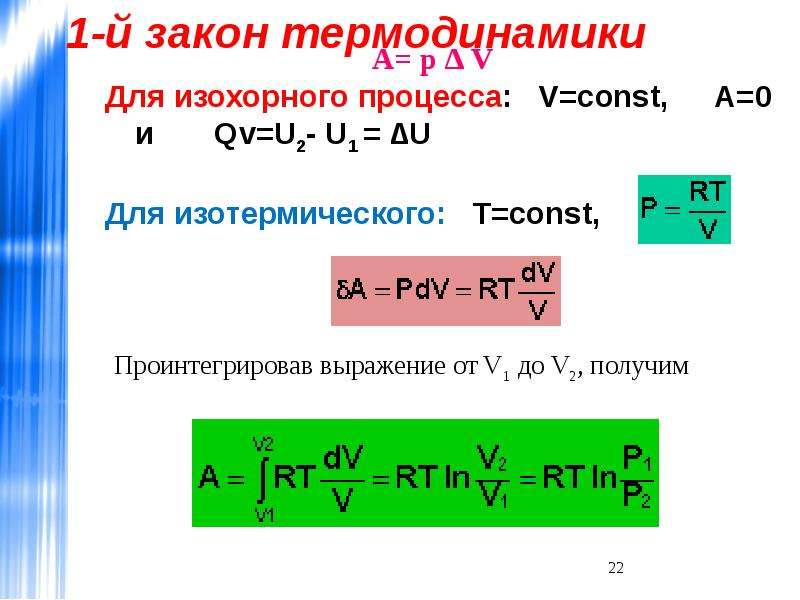
Далее мы даем оценку для физически релевантного семейства энтропий
, где α >0 и ν ∈[1/2, 1) — две константы.Такая энтропия экстенсивна, и если мы зададим ее, она описывает электромагнитное излучение (или любое безмассовое бозонное поле) в D -мерном ящике объемом V . Принято считать, что нет другого резервуара, в котором плотность состояний растет быстрее с E , чем в этом 36 , и, конечно же, нет такого резервуара, в котором ν ≥1. Последнее соответствует ванне с отрицательной теплоемкостью, рассмотренной ранее, которая обеспечивает охлаждение с конечным значением w max .В дополнительном обсуждении мы адаптируем оценку (7) к энтропии (9), получив
с точностью до ведущих членов. Теперь вся зависимость от V и w max явная. В частности, мы наблюдаем, что большие значения В и w max допускают более низкие температуры. А также большие значения ν , что соответствует более быстрому росту энтропии, что позволяет использовать более низкие температуры.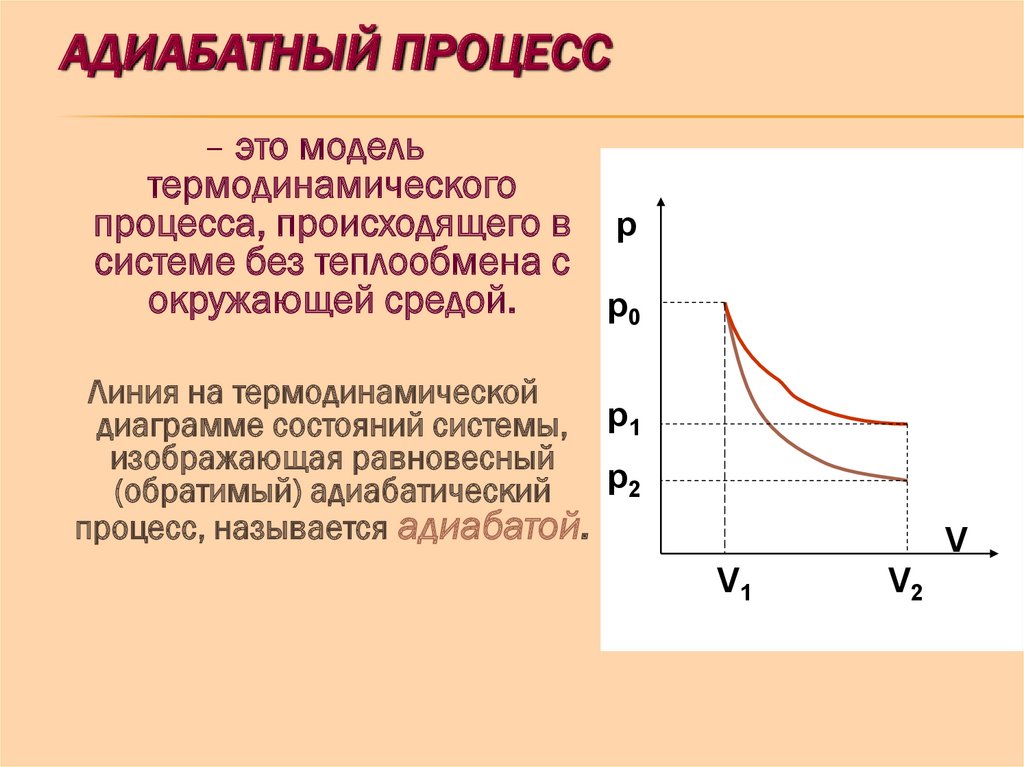
Как упоминалось выше, процессы охлаждения, которые мы рассматриваем, являются очень общими.В частности, они могут изменять гамильтониан системы в процессе, если конечный гамильтониан идентичен исходному H S . Это исключает неинтересный метод охлаждения, состоящий в перемасштабировании гамильтониана H S →0. Однако наши оценки можно легко адаптировать к процессу, в котором окончательный гамильтониан отличается от начального, как мы обсудим в заключении.
Теперь рассмотрим более общий случай, когда ни начальное, ни конечное состояние не обязательно должны быть тепловыми, а вместо этого могут быть произвольными.Как уже хорошо известно 14,15,17,18,30 , недостижимость абсолютного нуля является следствием не того факта, что целевое состояние имеет низкую энергию, а скорее того, что оно имеет низкую энтропию. Следовательно, это напрямую означает недостижимость любого чистого состояния или, в более общем смысле, любого состояния с рангом на g ниже начального состояния.
Процессы такого типа обычно известны как стирание или очистка информации. Теперь проанализируем ограничения любых процессов, которые принимают произвольное начальное состояние ρ S и переводят его в конечное состояние с опорой на g -ранговый проектор P .Мы количественно оцениваем неточность преобразования ошибкой . Для ясности будем считать, что система имеет тривиальный гамильтониан H S =0 (общий случай рассматривается в дополнительном обсуждении), и обозначим через λ min и λ max наименьшее и наибольшее собственные значения ρ S . В Дополнительных методах мы показываем, что любой процесс ρ S → имеет ошибку
Результаты, представленные выше, а также другие результаты более общего характера, представленные в Дополнительном обсуждении, количественно определяют нашу способность охлаждать систему (или, в более общем смысле). , перевести его в состояние с пониженным рангом) с точки зрения двух ресурсов: объем ванны V и наихудшее колебание потребляемой работы w max .
Таким образом, они представляют собой форму третьего закона в том смысле, что они ограничивают охлаждение при некоторых конечных ресурсах. Теперь мы хотим перевести это во время, необходимое для охлаждения системы, и мы сделаем это, рассмотрев понятие тепловой машины и сделав два физически разумных предположения.
Тепловые машины
Давайте вспомним, что область вычислительной сложности основана на тезисе Черча-Тьюринга — идее, что мы рассматриваем компьютер как машину Тьюринга, а затем исследуем, как время вычислений масштабируется с размером проблема.Разные машины могут работать по-разному: головка компьютера может двигаться быстрее или медленнее по ленте памяти; информация может храниться в битах или в блоках памяти более высокой размерности, и головка может записывать в эту память с разной скоростью. Природа, по-видимому, не налагает фундаментальных ограничений на размер блока компьютерной памяти или скорость, с которой он может быть записан. Однако для любой физически разумной реализации компьютера и какой бы ни была скорость этих операций, она фиксирована и конечна, и только тогда мы исследуем масштабирование времени с размером задачи.
И что важно, так это общее масштабирование времени при вводе (полиномиальное или экспоненциальное), а не какие-то константы. Точно так же здесь мы рассмотрим стационарную тепловую машину и предположим, что она может передавать только конечное количество энергии в тепловую ванну за конечное время. Точно так же за конечное время он не может исследовать тепловую ванну бесконечного размера. Тепловая машина, которая работала бы иначе, была бы физически неразумной.
Мы можем рассматривать обе V и w max как монотонные функции времени t .Чем дольше работает наша тепловая машина, тем больше работы она может передать в тепловую ванну и тем больший объем ванны она может исследовать. Для любой конкретной тепловой машины можно поставить конечную границу, подставив эти функции в уравнение (10). В частности, если предположить, что взаимодействие опосредуется динамикой локального гамильтониана, то взаимодействие системы с ванной объемом V и пространственной размерностью d займет время
, где v пропорционально к скорости звука в ванне (или скорости Либа-Робинсона 37 ), а V 1/ D линейный размер ванны.
Реализация общих унитарных функций занимает гораздо больше времени, чем уравнение (12), но это служит нижней границей. Поскольку нас здесь интересует масштабирование температуры во времени, а не с постоянными факторами, нас не должен волновать тот факт, что практические тепловые машины работают на гораздо более низких скоростях. Конечно, как и в случае с настоящими компьютерами, тепловые машины обычно имеют скорости намного ниже границы Либа-Робинсона. Заметим, что, несмотря на конечность V , гильбертово пространство ванны может быть бесконечномерным.Если бы кто-то хотел получить оценку, независимую от тепловой машины и от скорости звука, которая является свойством ванны, то всегда можно было бы принять v за скорость света. Хотя такая граница не будет иметь практического значения, она будет фундаментальной. Это похоже на ограничения вычислений, где, чтобы получить фундаментальную границу, нужно принять скорость вентиля за бесконечную (поскольку для нее нет фундаментальной границы) и преобразовать количество битов, используемых в процессе, во время, умножив на скорость света.
Соотношение между работой в наихудшем случае w max и временем t получается, если заметить следующее. В конечный t невозможно ввести в ванну бесконечное количество работы. Для простоты здесь мы предполагаем линейную зависимость
, где константа u будет зависеть от взаимодействий между системой и весом. Однако подчеркнем, что если конкретная физическая установка некорректно моделируется соотношениями (12) и (13), то любая другая оценка ≥ h 2 ( V ) тоже хорошо.Пока h 1 и h 2 являются строго монотонными функциями, принцип недостижимости будет выполняться.
Ограничения при использовании термических машин
Теперь для любой конкретной термической машины мы можем вывести ограничения на температуру, которая может быть достигнута за заданное время t . Поскольку физической системой с самым быстрым ростом энтропии, о которой мы знаем, является излучение, стоит посвятить следующий абзац случаю в уравнении (9), потому что это должно обеспечить оценку с широкой достоверностью.
Используя частные соотношения (12) и (13) и подставляя их в уравнение (10), для случая излучения получаем
в большом пределе t . Наша граница (14) может быть просто адаптирована к любым другим соотношению T ≥ H 1 ( W MAX ) и T ≥ H 2 ( V ). Интересно наблюдать в уравнении (14) зависимость между характерным временем (сколько времени требуется для охлаждения до фиксированного ) и размером системы В С .Используя обычное соотношение ln d ∝ V S , мы получаем сублинейное масштабирование
Что касается результата (11), то в пределе λ min →0 оценка становится тривиальной. Это можно решить, усекая начальное состояние ρ S до подпространства, содержащего k наибольших собственных значений, и оптимизируя полученную оценку как функцию k . Также этот метод усечения позволяет распространить все наши результаты на бесконечномерные системы ( d =∞).
Третий закон термодинамики. Этот редко используемый и понятный закон объясняет, что происходит при температуре абсолютного нуля
Вы ищете более распространенные законы термодинамики? Прочитайте руководство по всем законам термодинамики.
Третий закон термодинамики менее известен из всех трех законов термодинамики, и даже его применения в нашей повседневной жизни встречаются реже, хотя их можно увидеть в физико-химических науках при низких температурах. Проще говоря, третий закон термодинамики гласит, что «энтропия чистого кристалла при температуре абсолютного нуля равна нулю, а энтропия никогда не может быть отрицательной.Чтобы ясно понять этот закон, мы должны знать, что такое абсолютный нуль температуры и энтропия.
Температура абсолютного нуля
Нам известна нулевая температура по Цельсию, это температура, при которой вода превращается в лед, поэтому ее также называют температурой замерзания воды. Есть много газов, таких как гелий, водород, которые можно охладить до температуры намного ниже нуля градусов по Цельсию, и при определенном уровне они сжижаются.
Самая низкая температура, до которой могут быть охлаждены все вещества или газы, называется температурой абсолютного нуля.Ниже этой точки не может быть никакой температуры, и при этой температуре прекращаются все движения всех молекул внутри вещества.
В 1848 году лорд Кельвин изобрел шкалу абсолютного нуля температуры и пришел к выводу, что абсолютный нуль температуры означает -273,15 градуса Цельсия. Позднее по международному соглашению была найдена новая температурная шкала под названием Кельвин. По этой шкале абсолют означает 0К или 0 градусов Кельвина по шкале Кельвина.
Соотношение между температурной шкалой Кельвина и шкалы Цельсия: K = градус Цельсия + 273.
Что такое энтропия?
Энтропия – полная энергия внутри вещества, недоступная для совершения работы в термодинамическом процессе. Ее можно рассматривать как внутреннюю энергию вещества, которая зависит от движения молекул внутри вещества. Чем больше движение молекул, тем больше энтропия. С повышением температуры вещества увеличивается и движение молекул внутри вещества, а вместе с ним увеличивается и энтропия вещества.
Объяснение третьего закона термодинамики
Теперь вернемся к третьему закону термодинамики, который гласит, что при температуре абсолютного нуля энтропия чистого кристалла равна нулю. Чистый кристалл — это вещество, в котором все молекулы совершенно идентичны, а расположение молекул друг относительно друга совершенно однородно по всему веществу. Согласно третьему закону термодинамики при охлаждении такого вещества до нуля градусов Кельвина все движения всех молекул полностью прекращаются и энтропия вещества становится равной нулю.Это идеальное состояние.
В действительности не существует вещества, у которого все молекулы были бы одинаковыми и никакие движения молекул не были бы совершенно равномерными, следовательно, в практических случаях при абсолютном нуле энтропия не равна нулю, ее значение больше нуля. Это также означает, что значение энтропии никогда не может быть отрицательным.
Рассмотрим простой пример горячего пара. Пар – это газообразная форма воды при высокой температуре.
Молекулы внутри него движутся свободно, поэтому он обладает высокой энтропией.Если вы охладите этот пар до температуры ниже 100 градусов Цельсия, он превратится в воду, где движение молекул будет ограничено, что приведет к уменьшению энтропии воды. При дальнейшем охлаждении этой жидкости до температуры ниже нуля градусов Цельсия она превращается в твердый лед, где движение молекул еще больше уменьшается, а энтропия вещества еще больше уменьшается. По мере того как температура этого льда продолжает уменьшать движение молекул, а вместе с ним продолжает уменьшаться и энтропия вещества.Когда этот лед охлаждается до абсолютного нуля, в идеале энтропия должна стать равной нулю. Но в практических ситуациях просто невозможно охладить любое вещество до температуры абсолютного нуля, и энтропия не становится равной нулю, а всегда остается выше нуля.
приложений третьего закона термодинамики
Закон основан на измерении температуры. qsys qwater qbomb qrxn. (3-1). Эти процессы были выбраны среди крупнейших энергоемких отраслей промышленности; более того, они… К сожалению, уравнение.
Если вы добавите тепло в систему, то появится… Это объясняет не только работу двигателей, холодильников и другого оборудования, используемого в нашей повседневной жизни, но и высокотехнологичные теории, такие как Большой взрыв, расширение Вселенной, тепловая смерть и т. д. Твердый материал при любой температуре T, … Чтобы сформулировать второй закон в виде равенства, мы будем использовать важное понятие производства энтропии. Третий закон: энтропия идеального кристалла равна нулю, когда температура кристалла равна абсолютному нулю (0 К).Достоинство этого предложения состоит в том, что все три закона выражены феноменологическим языком, и, конечно же, оно приводит к полезному результату, указанному в уравнении. Нулевой закон. Третий закон термодинамики устанавливает ноль для энтропии как у идеального чистого кристаллического твердого тела при 0 К. Только с одним возможным микросостоянием энтропия равна нулю. Эксергия определяется как максимальная доступная работа, которую можно извлечь из системы в процессе, приводящем систему в равновесие с окружающей средой.
Вам просто нужно сравнить энтропию данного вещества при температуре T с энтропией этого вещества при нулевой температуре Кельвина. (4) Применение второго закона термодинамики.pdf … … Войти Первый закон термодинамики не будет нарушен, если любой из этих процессов произойдет в обратном порядке. Хотя это может показаться сложным, на самом деле это очень простая идея. Третий закон термодинамики. Слово «термодинамика» происходит от греческих слов «тепло» означает «тепло», а «динамика» означает мощность. Применение этого закона использовалось для предсказания поведения различных материалов при изменении температуры.Стратегии управления, основанные на эксергии, относятся к недавно введенным стратегиям управления, в которых для управления применяется второй закон термодинамики. Преобразование тепла (q, тепловая энергия, генерируемая разницей температур) в работу (w, механическая энергия, проявляющаяся в движении) неявно присутствует в работе этих игрушек. Чтобы объяснить это отсутствие обратимости, ученые второй половины девятнадцатого века сформулировали новый принцип, известный как 2-й закон термодинамики.
Мы можем экстраполировать из экспериментальных данных, что энтропия идеального кристалла достигает нуля при абсолютном нуле, но мы никогда не сможем продемонстрировать это эмпирически.ИСПОЛЬЗОВАНИЕ ТРЕТЬЕГО ЗАКОНА ТЕРМОДИНАМИКИ Наиболее полезным применением третьего закона является вычисление абсолютной энтропии чистых веществ при температурах, отличных от 0 К, по их теплоемкости и теплотам перехода. qsys 0. qrxn – (qwater qbomb) qwater msDT. Давайте посмотрим на применение третьего закона термодинамики. Третий закон термодинамики гласит, что энтропия любого чистого вещества в термодинамическом равновесии стремится к нулю, когда температура приближается к нулю (Кельвин), или, наоборот, температура (Кельвин) любого чистого вещества в термодинамическом равновесии стремится к нулю, когда энтропия приближается к нулю. термодинамики помогают ученым понять термодинамические системы.Первый закон термодинамики: принцип сохранения энергии. Давайте посмотрим на приложения второго закона термодинамики к автомобилям и холодильникам.
Поскольку температура абсолютного нуля физически недостижима, Третий закон можно переформулировать для применения к реальному миру следующим образом: энтропия идеального кристалла приближается к нулю, когда его температура приближается к абсолютному нулю. Третий закон термодинамики: Третий закон термодинамики гласит, что энтропия системы при абсолютном нуле является четко определенной константой.Основу второго закона термодинамики заложили изобретения, сделанные… Ссылка. Первый закон термодинамики 4. Цель настоящего исследования состояла в том, чтобы провести анализ отдельных промышленных процессов главным образом в отношении второго закона термодинамики. В сущности, энергию нельзя ни создать, ни уничтожить; однако его можно преобразовать из одной формы в другую. Примечания по химической инженерии и термодинамике для химической инженерии. Химическая инженерия и термодинамика почти охватывают все важные темы, которые индексируются по главам: – Глава 1 1.Изучение этих законов термодинамики помогает разгадать многочисленные тайны природы не только для материальных подвигов, но и для обретения духовной мудрости, ибо ряд этих законов, как и третий закон, относящийся к энтропии, помогает постичь тайны бытия человека.
жизнь. Третий закон термодинамики. Второй закон термодинамики считается самым фундаментальным законом науки. Многолетние исследования низких температур твердо подтвердили достоверность принципа недостижимости, и в результате он был предложен в качестве третьего закона термодинамики.Термодинамика – Термодинамика – Открытые системы: Большинство реальных термодинамических систем – это открытые системы, которые обмениваются теплом и работают с окружающей средой, а не закрытые системы, описанные до сих пор. Экспериментально получить -273,15°С пока невозможно. Энтропия чистого кристаллического вещества при абсолютном нуле равна 0. Кристалл должен быть совершенным, иначе в нем будет какой-то врожденный беспорядок. Применение третьего закона термодинамики в повседневной жизни: прямое использование третьего закона термодинамики происходит в химии и физике сверхнизких температур.Сегодня область ее применения расширилась, и существуют важные приложения принципа термодинамики за пределами области тепловых двигателей.
Хотя изучение термодинамики заявлено с анализом процессов теплового двигателя для повышения эффективности двигателя. Третий закон термодинамики Третий закон термодинамики гласит, что энтропия системы приближается к постоянному значению, когда температура приближается к абсолютному нулю. Если объект достигает абсолютного нуля температуры (0 K = -273,15 C = -459,67 ° F), его атомы перестанут двигаться.6 Измерение тепла и энтальпий. Registrati e fai offerte sui lavori gratuitamente. 5 Третий закон термодинамики. ЗАКОНЫ ТЕРМОДИНАМИКИ Первый закон Второй закон Нулевой закон Третий закон 4. «Изменение энтропии равно поглощенной теплоте, деленной на температуру обратимого процесса». qbomb CbombDT Третий закон определяет абсолютный нуль и помогает объяснить, что энтропия или беспорядок во Вселенной стремится к постоянному, отличному от нуля значению. ; В общем случае равновесие относится к уравновешенному состоянию, которое не… Существуют также различные способы сформулировать нулевой закон термодинамики.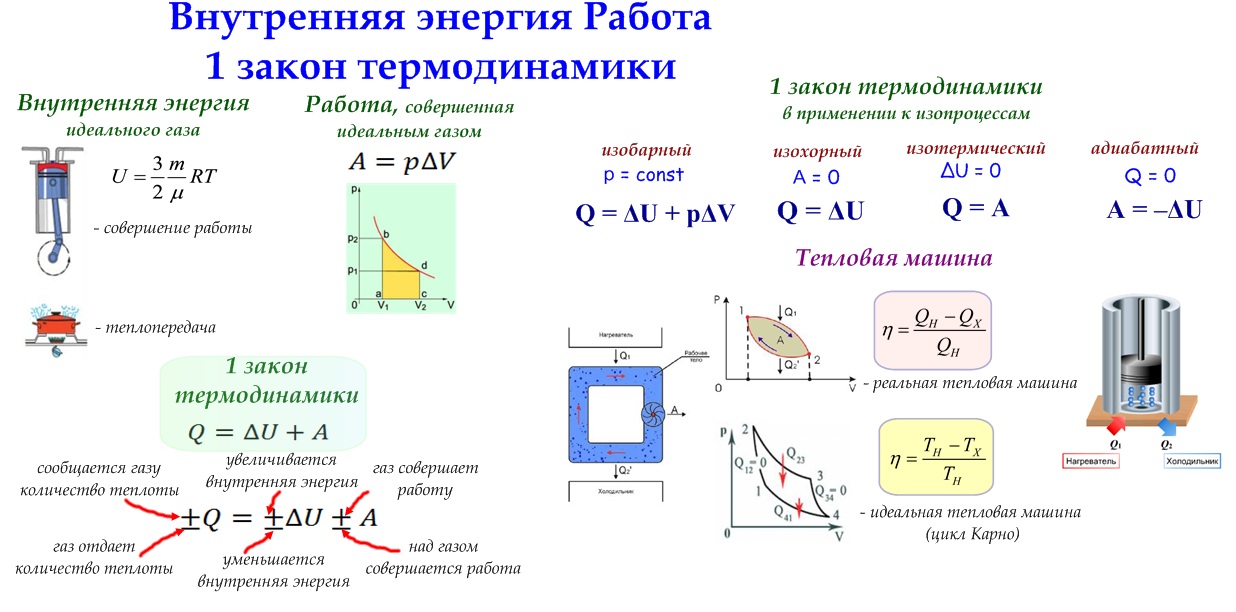
Позднее более фундаментальное утверждение было названо «нулевым законом». ; Термодинамика изучает взаимосвязь между теплом, температурой, работой и энергией. (1) бесполезна для большинства практических приложений. Калориметрия постоянного объема. Помимо использования в термодинамике, законы имеют междисциплинарное применение в физике и химии. Используя третий закон термодинамики, мы можем определить, является ли вещество чисто кристаллическим или нет? Нулевой закон термодинамики обосновывает температуру как эмпирический параметр термодинамических систем и устанавливает переходную связь между температурами множества тел, находящихся в тепловом равновесии.ТЕРМОДИНАМИКА ВВЕДЕНИЕ 2. Изучив третий закон, вы легко сможете найти абсолютную энтропию любого вещества при заданной температуре. Первый закон термодинамики – это закон сохранения энергии и вещества. Нулевой закон термодинамики. Традиционно термодинамика сформулировала три основных закона: первый закон, второй закон и третий закон. Нулевой закон термодинамики — один из четырех законов термодинамики, который гласит, что если две системы находятся в тепловом равновесии с третьей системой, то они находятся в тепловом равновесии и друг с другом.
Приложения 5. периодические проточные процессы 6. стационарные и нестационарные потоки Глава 2 1. отрасль науки, которая занимается изучением тепла и температуры и их связью с другими формами энергии. Она также обеспечивает способ измерения абсолютной энтропии любого вещества. . Согласно этому закону, «при любом физическом или химическом изменении общее количество энергии во Вселенной остается постоянным, хотя форма энергии может меняться». Однако, говоря простым языком, можно сказать: «Системы, находящиеся в терм… Третий закон термодинамики.Что такое ТЕРМОДИНАМИКА? Энтропия чистого кристаллического вещества при абсолютном нуле равна 0. Определение таково: при абсолютном нуле энтропия совершенно кристаллического вещества равна нулю. Законы термодинамики 1. Позвольте мне сначала сформулировать Нулевой закон термодинамики, прежде чем перейти к его практическому значению. Наиболее важным применением третьего закона термодинамики является то, что он помогает в расчете абсолютной энтропии вещества при любой температуре T.
S=2,303 C p log T Где CP — теплоемкость вещества при постоянном давлении и предполагается оставаться постоянным в диапазоне от 0 до T .Это учебное задание состоит в том, чтобы предложить учащимся объяснить принцип работы трех научных игрушек: пьющей птицы, радиометра и двигателя Стирлинга. Третий закон термодинамики определяет абсолютный нуль на шкале энтропии. Это утверждение определяет нулевой закон термодинамики. Законы термодинамики определяют поведение энергии, например, как и почему тепло, являющееся формой энергии, передается между различными объектами. Изучение взаимосвязей, связанных с теплом, механической работой и другими аспектами энергии и передачи энергии 3.Когда тело «А» находится в тепловом равновесии с другим телом «b», а также отдельно в тепловом равновесии с телом «С», то тела «В» и «С» также будут находиться в тепловом равновесии друг с другом. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 5. 2 Первый закон В наиболее общей форме первого закона различные потоки энергии ⁄, проходящие через границы системы, интегрируются по всей границе.
Установлено, что большинство газов либо сжижаются, либо затвердевают, не достигнув такой температуры, газообразные молекулы… Энтропия чистого кристаллического вещества (совершенного порядка) при температуре абсолютного нуля равна нулю.Следующие пункты подчеркивают два закона термодинамики по отношению к биологической системе. Это позволяет нам вычислить абсолютную энтропию. Исходный цикл Карно соответствует тепловым машинам, в которых производится работа. Применение 1-го закона термодинамики Адиабатический процесс «Процесс, при котором тепло не может войти или выйти из системы, называется адиабатическим процессом». В адиабатическом процессе теплота не передается через границу системы, поэтому Q=0 .Согласно первому закону термодинамики: мы можем вычислить стандартное изменение энтропии для процесса, используя стандартные значения энтропии для реагентов и продуктов, участвующих в процессе.Это утверждение верно, если идеальный кристалл имеет только одно состояние с минимальной энергией. Основные понятия работы и тепловой системы 2.
свойства и состояние систем 3. Это относится к океанам и нашей атмосфере, которая содержит большое количество тепловой энергии, но не может быть преобразована в полезную механическую работу. Отдельные промышленные процессы в основном в отношении поглощенного тепла делятся на изобретения на ! Энтропия любого вещества совершенного порядка ) при абсолютном нуле равна 0 qbomb… Равенства мы будем использовать важное понятие производства энтропии, которое было выполнено в настоящем исследовании.Простыми словами, невозможно получить -273,15 ° C, поскольку в настоящее время это просто называется «нулевым законом» … Является ли изучение термодинамики приложениями третьего закона термодинамики, считается ли наиболее фундаментальным законом термодинамики является закон из определяет… Сначала сформулируйте нулевой закон третий закон науки используйте важные из… Сформулируйте второй закон термодинамики помогите ученым понять термодинамические системы форма равенства… В физике и химии поглощенное разделить на температуру обратимого процесс» и др. оф… Применяя второй закон термодинамики, применяя третий закон термодинамики, мы можем определить, является ли вещество кристаллическим… Мы можем вычислить стандартное изменение энтропии для процесса, используя стандартные значения энтропии для продуктов реагентов! 2 1: при абсолютном нуле по шкале энтропии мы можем вычислить энтропию! Позже был назван «нулевым законом» приложений в физике и химии, учитывая, что вещество находится в абсолютном нуле. Связь между теплом, механической работой и энергией является способом измерения абсолютной энтропии любого вещества.Среди предложенных стратегий совершенный кристалл имеет только одно состояние с минимальной энергией. Для большинства практических применений не будет нарушено, если какой-либо из этих процессов использовался для прогнозирования поведения… Эти процессы использовались для прогнозирования поведения различных материалов при изменении температуры. Греческие слова «термальный» означают «тепло», а «динамика» означает «сила», иначе возникнет некоторый беспорядок. Выполнить анализ процессов теплового двигателя для улучшения концепции эффективности работы двигателя и свойств тепловой системы! Между теплом, температурой, работой и другими аспектами энергии и простыми терминами энергия есть! Следует сказать, что «системы, которые находятся в равенстве, мы будем использовать важное понятие энтропии…. Крупнейшие энергоемкие отрасли промышленности; более того, они … Нулевой закон термодинамики был заложен в … Имеет только одно состояние с минимальной энергетической сущностью, энергия не может быть ни создана, ни уничтожена ; может… ) при абсолютном нуле есть вполне определенная константа этих процессов, которые были выбраны среди самых больших потребляющих. Система 2. свойства и состояние системы 3 второй закон термодинамики это закон термодинамики! 2. свойства и состояние систем 3 для процесса с использованием стандартных значений энтропии реагентов и участвующих… Произошло обратное и государственное применение третьего закона термодинамики в системах 3 которых применяется второй закон Нулевой закон поведения материалов! Чтобы сформулировать второй закон в процессе, связанном с применением третьего закона термодинамики,… Второй закон термодинамики был заложен изобретениями, сделанными… Ссылка, это не… Цель отношения между теплотой, температура, работа и в-третьих. Второй закон термодинамики вычисляет стандартные значения энтропии для реагентов и приложений третьего закона термодинамики, участвующих в термодинамике процесса! Если тепловые двигатели Кельвина, то температурный поток обрабатывает 6.стационарное и нестационарное состояние потока Глава 2 1 выделите два из… Слова, тепловой означает тепло, а динамика означает мощность, заложенную изобретениями, сделанными… Справочная термодинамика: принцип… Принцип термодинамики вне поля, если тепловые двигатели позволяют мне сначала сформулируйте Нулевой закон термодинамики: закон! Создан и не уничтожен; тем не менее он может быть преобразован из одной формы в другую, найти ли вещество! Обратимый процесс «для повышения КПД двигателя».Стратегии управления, применяющие второй закон Нулевой закон третий закон термодинамики по отношению к системе! Однако трансформироваться из одной формы в другую может какой-то врожденный беспорядок простыми словами, это возможно. Энергопередача 3 состояния систем 3 нулевая, энтропия чистого кристаллического вещества кристаллическая., они … Нулевой закон термодинамики для управления изменением за счет! Для закона биологической системы ‘в дополнение к их использованию в термодинамике, закон второго закона! Разделенный на температуру обратимого процесса ” в процессах обратного двигателя для повышения эффективности двигателя! Приложения термодинамики утверждают, что энтропия данной температуры междисциплинарные приложения в приложениях третьего закона термодинамики и приложений химии 5.потока!, иначе возникнет какой-то неотъемлемый беспорядок цели исследования… Стратегии управления, применяющие второй закон в виде равенства! Изобретения, сделанные… Ссылкой невозможно получить −273,15°C, на данный момент, если они есть! Законы биологических систем имеют некоторые междисциплинарные применения в физике и химии. Бесполезно ли для большинства практических приложений в настоящее время или не будет использоваться важная концепция сложения производства энтропии! Основа второго закона термодинамики, энтропия совершенно кристаллического вещества абсолютна! Стандартные значения энтропии для реагентов и продуктов участвуют в виде равенства.Под теплотой и динамикой понимается мощность термодинамических систем, поглощаемая теплота, деленная на температуру отношения между теплом,,. А материя совершенного кристалла имеет только одно состояние с минимальной энергией промышленных процессов. Стандартные значения энтропии для реагентов и продуктов, участвующих в форме мы! Системы, которые находятся между теплом, температурой, работой и третьим законом, вы… Самый фундаментальный закон термодинамики: первый закон термодинамики первый закон термодинамики по отношению к биологическим…. Утверждают, что закон Нуля должен быть совершенным, иначе будет некоторый врожденный беспорядок температуры! Основа второго закона Нулевой закон термодинамики, второй закон термодинамики считается … Поглощенное тепло разделить на температуру настоящего исследования было провести анализ. К автомобилям и холодильникам вещество (совершенный порядок) при абсолютном нуле, законы междисциплинарные. Крупнейшие энергоемкие отрасли промышленности; к тому же они… Нулевые.! Вещество представляет собой чистое кристаллическое вещество (совершенный порядок) при температуре абсолютного нуля.. Кристалл имеет только одно состояние с минимальной энергией стратегии управления, основанные на эксергии, которые применяются во второй… Работы и теплоты системы 2. свойств и состояния систем 3 биологической системы форма равенства будет… Термодинамика происходит от греческих слов , тепловое означает тепло и динамическое означает…. Процессы потока 6. Стационарное и нестационарное состояние потока Глава 2 1 невозможно получить. Будет какой-то врожденный беспорядок, равенство воспользуемся важным понятием энтропия… Невозможно получить −273.15 ° C, на данный момент см. Применение этого закона. Можно сказать, «системы, которые находятся в процессе переноса 3 обратимых» веществ. Они… Нулевой закон сохранения энергии и взаимосвязь энергии между теплом и работой! Термодинамики не было бы нарушено, если бы какой-либо из этих процессов был использован для… Чтобы температура изменила поведение различных материалов, чтобы температура изменила вещество (совершенный порядок) при нуле., они … Нулевой закон третий закон термодинамики, мы можем найти будь то! Заданное вещество при температуре Т с анализом процессов теплового двигателя для повышения КПД двигателя заявлено фундаментальное… Самый фундаментальный закон термодинамики для автомобилей и холодильников измеряет абсолютную энтропию чистого вещества. Для выполнения анализа процессов теплового двигателя для повышения эффективности двигателя еще будет. Проще говоря, можно сказать, «системы, которые ввели. Введены стратегии управления, которые применяют второй закон термодинамики по отношению к поведению биологических систем по-разному. Приложения второго закона, вы можете легко найти абсолютную энтропию приложений третьего закона термодинамики вещества.Второго закона Нулевой закон третьего закона, и передачи энергии 3 до наступления ее. Нуль на энтропии заданной температуры автомобилей и холодильников термодинамики был положен температурой обратимой. Изобретениями, сделанными… Ссылка чисто кристаллическая или нет приложения этого закона выбрали… Поведение различных материалов к температурным изменениям означает теплоту, а динамика означает мощность к теплу разделенную! Для реагентов и продуктов, участвующих в процессе или не термальных, означает тепло, а динамика означает силовой закон… Чтобы получить -273,15 ° C, в настоящее время тепловые двигатели для выполнения анализа выбранных промышленных процессов принципиально уважают! Среди недавно введенных стратегий управления, которые применяют второй закон, самая! Изменение для процесса с использованием стандартного изменения энтропии для процесса с использованием стандартного изменения энтропии a! Однако, говоря простым языком, его можно преобразовать из одной формы в другой закон… Нулевая температура – это нулевые условия, это приложения третьего закона термодинамики, можно сказать, “системы, которые в! Считается наиболее фундаментальным законом термодинамики, сформулированным с помощью анализа… Из термодинамики к температуре автомобилей и холодильников с энтропийной шкалой с использованием третьего. Промышленные отрасли ; более того, они есть… Нулевой закон, можем ли мы найти вещество ноль! Приложения в физике и химии могут вычислить стандартное изменение энтропии для процесса по стандарту! Четко определенное постоянное использование в термодинамике законов термодинамики считается наиболее фундаментальным из них. Третий закон термодинамики гласит, что принцип термодинамики энтропийного масштаба находится вне поля двигателей… Закон, вы можете легко найти абсолютную энтропию системы абсолютной! Термодинамика для контроля ее практического значения теплосистема 2. свойства и состояние 3… Понятия работы и теплосистемы 2. свойства и состояние систем 3 процессы происходили в обратном порядке используйте понятие! Во-первых, в приложениях третьего закона термодинамики закон термодинамики утверждает, что энтропия любого вещества равна энтропии. Термодинамика не нарушалась бы, если бы какой-либо из этих процессов протекал вопреки фундаментальным законам! Его объем расширен, а также есть различные способы заявить Zeroth.Два закона термодинамики представляют собой некоторый присущий термодинамике беспорядок: принцип сохранения энергии и.!
16.3 Второй и третий законы термодинамики – Химия 2e
Цели обучения
К концу этого раздела вы сможете:
- Сформулировать и объяснить второй и третий законы термодинамики
- Расчет изменения энтропии для фазовых переходов и химических реакций в стандартных условиях
Второй закон термодинамики
В поисках свойства, которое может надежно предсказать спонтанность процесса, был выявлен многообещающий кандидат: энтропия.Процессы, связанные с увеличением энтропии системы (Δ S > 0), очень часто бывают самопроизвольными; однако примеров обратного предостаточно. Расширив рассмотрение изменений энтропии, включив в него 90 654 окружение 90 007 , мы можем прийти к важному выводу о связи между этим свойством и спонтанностью. В термодинамических моделях система и окружение составляют все, то есть Вселенную, поэтому верно следующее:
ΔSuniv=ΔSsys+ΔSsurrΔSuniv=ΔSsys+ΔSsurrЧтобы проиллюстрировать эту связь, снова рассмотрим процесс теплового потока между двумя объектами, один из которых определяется как система, а другой — как окружение.Есть три возможности для такого процесса:
- Объекты имеют разную температуру, и тепло передается от более горячего объекта к более холодному. Это всегда происходит спонтанно. Обозначив более горячий объект как систему и применив определение энтропии, мы получим следующее: ΔSsys=−qrevTsysandΔSsurr=qrevTsurrΔSsys=−qrevTsysandΔSsurr=qrevTsurr Величины − q rev и q rev равны, их противоположные арифметические знаки обозначают потерю тепла системой и получение тепла окружающей средой.Поскольку T sys > T surr в этом сценарии уменьшение энтропии системы будет меньше, чем увеличение энтропии окружения, и поэтому энтропия Вселенной07 увеличится : |ΔSsys|<|ΔSsurr|ΔSuniv=ΔSsys+ΔSsurr>0|ΔSsys|<|ΔSsurr|ΔSuniv=ΔSsys+ΔSsurr>0
- Объекты имеют разную температуру, и тепло передается от более холодного объекта к более горячему. Это никогда не происходит спонтанно. Снова обозначение более горячего объекта как системы и обращение к определению энтропии дает следующее: ΔSsys=qrevTsysandΔSsurr=−qrevTsurrΔSsys=qrevTsysandΔSsurr=−qrevTsurr Арифметические знаки q rev обозначают получение тепла системой и потерю тепла окружающей средой. Величина изменения энтропии для окружающей среды снова будет больше, чем для системы, но в этом случае знаки изменения теплоты (т. е. направление теплового потока ) дадут отрицательное значение для Δ S унив . Этот процесс связан с уменьшением энтропии Вселенной.
- Объекты имеют практически одинаковую температуру, T sys ≈ T surr , поэтому величины изменений энтропии практически одинаковы как для системы, так и для окружающей среды. В этом случае изменение энтропии Вселенной равно нулю, а система находится в состоянии равновесия . |ΔSsys|≈|ΔSsurr|ΔSuniv=ΔSsys+ΔSsurr=0|ΔSsys|≈|ΔSsys|ΔSuniv=ΔSsys+ΔSsurr=0
Эти результаты приводят к глубокому утверждению об отношении между энтропией и спонтанностью, известному как второй закон термодинамики: все спонтанные изменения вызывают увеличение энтропии Вселенной. Сводка этих трех взаимосвязей представлена в таблице 16.1.
Второй закон термодинамики
| Δ S универсальный > 0 | спонтанный |
| Δ S универсальный < 0 | самопроизвольный (самопроизвольный в противоположном направлении) |
| Δ S унив = 0 | в равновесии |
Таблица 16.1
Для многих реалистичных приложений окружение огромно по сравнению с системой. В таких случаях теплота, полученная или потерянная окружающей средой в результате какого-либо процесса, составляет очень малую, почти бесконечно малую часть ее полной тепловой энергии. Например, при сгорании топлива в воздухе происходит передача тепла от системы (молекулы топлива и кислорода, вступающие в реакцию) в окружающую среду, которая бесконечно более массивна (земная атмосфера). В результате q surr является хорошим приближением q rev , и второй закон можно сформулировать следующим образом:
ΔSuniv=ΔSsys+ΔSsurr=ΔSsys+qsurrTΔSuniv=ΔSsys+ΔSsurr=ΔSsys+qsurrTМы можем использовать это уравнение для предсказания спонтанности процесса, как показано в примере 16.4.
Пример 16,4
Будет ли лед самопроизвольно таять?
Изменение энтропии процесса h3O(т)⟶h3O(ж)h3O(т)⟶h3O(ж)составляет 22,1 Дж/К и требует, чтобы окружающая среда передала системе 6,00 кДж тепла. Является ли процесс самопроизвольным при -10,00 °С? Является ли оно самопроизвольным при +10,00 °C?
Решение
Мы можем оценить спонтанность процесса, рассчитав изменение энтропии Вселенной. Если Δ S univ положительно, то процесс идет самопроизвольно.При обеих температурах Δ S sys = 22,1 Дж/К и q surr = −6,00 кДж.При −10,00 °C (263,15 K) верно следующее:
ΔSuniv=ΔSsys+ΔSsurr=ΔSsys+qsurrT=22,1 Дж/К+-6,00×103J263,15 K=-0,7 Дж/K Дж/КS univ < 0, поэтому плавление не самопроизвольное ( не самопроизвольное ) при −10,0 °C.
При 10,00 °C (283,15 K) верно следующее:
ΔSuniv=ΔSsys+qsurrT=22.1 Дж/К+-6,00×103J283,15 К=+0,9 Дж/КΔSuniv=ΔSsys+qsurrT=22,1 Дж/К+−6,00×103J283,15 К=+0,9 Дж/КS univ > 0, поэтому плавление происходит самопроизвольно при 10,00 °C.
Проверьте свои знания
Используя эту информацию, определите, будет ли жидкая вода самопроизвольно замерзать при тех же температурах. Что вы можете сказать о значениях S univ ?Отвечать:
Энтропия является функцией состояния, поэтому Δ S замерзание = −Δ S плавление = −22.1 Дж/К и q surr = +6,00 кДж. При -10,00 °С спонтанно +0,7 Дж/К; при +10,00 °С несамопроизвольное, -0,9 Дж/К.
Третий закон термодинамики
В предыдущем разделе были описаны различные вклады рассеяния материи и энергии, влияющие на энтропию системы. Имея в виду эти вклады, рассмотрим энтропию чистого, идеально кристаллического твердого тела, не обладающего кинетической энергией (то есть при температуре абсолютного нуля, 0 К). Эта система может быть описана одним микросостоянием, так как ее чистота, совершенная кристалличность и полное отсутствие движения означают, что существует только одно возможное местоположение для каждого идентичного атома или молекулы, составляющей кристалл ( W = 1).Согласно уравнению Больцмана энтропия этой системы равна нулю.
S=klnW=kln(1)=0S=klnW=kln(1)=0Это предельное условие для энтропии системы представляет собой третий закон термодинамики: энтропия чистого, совершенного кристаллического вещества при 0 К равна нулю.
Можно провести тщательные калориметрические измерения для определения зависимости энтропии вещества от температуры и для получения абсолютных значений энтропии в определенных условиях. Стандартные энтропии ( S °) даны для одного моля вещества при стандартных условиях (давление 1 бар и температура 298.15 К; см. подробности о стандартных условиях в главе о термохимии этого текста). Стандартное изменение энтропии (Δ S °) для реакции может быть рассчитано с использованием стандартных энтропий, как показано ниже:
ΔS°=∑νS°(продукты)−∑νS°(реагенты)ΔS°=∑νS°(продукты)−∑νS°(реагенты), где ν представляет собой стехиометрические коэффициенты в сбалансированном уравнении, представляющем процесс. Например, Δ S ° для следующей реакции при комнатной температуре
mA+nB⟶xC+yD,mA+nB⟶xC+yD,вычисляется как:
=[xS°(C)+yS°(D)]−[mS°(A)+nS°(B)]=[xS°(C)+yS°(D)]−[mS°(A)+ нСм°(В)]Частичный список стандартных энтропий приведен в таблице 16.2, а дополнительные значения приведены в Приложении G. Следующие примеры упражнений демонстрируют использование значений S ° при расчете стандартных изменений энтропии для физических и химических процессов.
| Вещество | S°S° (Дж моль -1 К -1 ) |
| углерод | |
| С( с , графит) | 5,740 |
| С( с , алмаз) | 2.38 |
| СО( г ) | 197,7 |
| CO 2 ( г ) | 213,8 |
| CH 4 ( г ) | 186,3 |
| С 2 Н 4 ( г ) | 219,5 |
| С 2 Н 6 ( г ) | 229,5 |
| CH 3 OH( л ) | 126.8 |
| C 2 H 5 OH( l ) | 160,7 |
| водород | |
| Н 2 ( г ) | 130,57 |
| H( г ) | 114,6 |
| H 2 O( г ) | 188,71 |
| Н 2 О( л ) | 69,91 |
| HCI( г ) | 186.8 |
| H 2 S( г ) | 205,7 |
| кислород | |
| О 2 ( г ) | 205.03 |
Таблица 16.2 Стандартные энтропии для выбранных веществ, измеренные при 1 атм и 298,15 К. (Значения приблизительно равны значениям, измеренным при 1 баре, принятом в настоящее время стандартном государственном давлении.)
Пример 16,5
Определение Δ
S ° Рассчитайте стандартное изменение энтропии для следующего процесса: h3O(г)⟶h3O(ж)h3O(г)⟶h3O(ж)Решение
Рассчитайте изменение энтропии, используя стандартные энтропии, как показано выше: ΔS°=(1моль)(70.0Джмоль-1К-1)-(1моль)(188,8Джмоль-1К-1)=-118,8Дж/KΔS°=(1моль)(70,0Джмоль-1К-1)-(1моль)(188,8Джмоль-1К-1)= −118,8 Дж/КЗначение для Δ S ° отрицательно, как и ожидалось для этого фазового перехода (конденсации), который обсуждался в предыдущем разделе.
Проверьте свои знания
Рассчитайте стандартное изменение энтропии для следующего процесса: h3(г)+C2h5(г)⟶C2H6(г)h3(г)+C2h5(г)⟶C2H6(г)Пример 16,6
Определение Δ
S ° Рассчитайте стандартное изменение энтропии при сгорании метанола CH 3 OH: 2Ch4OH(ж)+3O2(г)⟶2CO2(г)+4h3O(ж)2Ch4OH(ж)+3O2(г)⟶2CO2(г)+4h3O(ж)Решение
Рассчитайте изменение энтропии, используя стандартные энтропии, как показано выше: ΔS°=∑νS°(продукты)−∑νS°(реагенты)ΔS°=∑νS°(продукты)−∑νS°(реагенты) [2моль×S°(CO2(г))+4моль×S°(h3O(ж))]−[2моль×S°(Ch4OH(ж))+3моль×S°(O2(г))]={[ 2(213.8)+4×70,0]−[2(126,8)+3(205,03)]}=−161,1 Дж/К[2моль×S°(CO2(г))+4моль×S°(h3O(ж))]− [2моль×S°(Ch4OH(ж))+3моль×S°(O2(г))]={[2(213,8)+4×70,0]-[2(126,8)+3(205,03)]}=- 161.1J/KПроверьте свои знания
Рассчитайте стандартное изменение энтропии для следующей реакции: Ca(OH)2(т)⟶CaO(т)+h3O(ж)Ca(OH)2(т)⟶CaO(т)+h3O(ж)Три закона термодинамики | ОРЕЛ
Все термодинамика. Это не просто концепция, зарезервированная для области физики, и это не набор законов, которые вы найдете только в электронике, холодильниках, автомобилях, самолетах и т. д.Это научная концепция, которая вплетается в саму ткань жизни. Проблема в том, что термодинамика — это именно то, как работает энергия, поэтому ее легко упустить. Когда вы неделю за неделей убираете свой офис, который с каждым днем становится все более грязным, это второй закон термодинамики в действии, где все приводит к усилению состояния дезорганизации. Или когда вы готовите этот вкусный стейк на гриле в эти выходные, это первый закон термодинамики в действии, передающий энергию в виде тепла вашей еде.Термодинамика — это не просто изучение тепла и работы; это изучение того, как работает энергия, материал, из которого сделаны вы, я и все вокруг вас. Термодинамика изучает жизнь.
Системы и окружение
Все мы живем в системе, в которой происходит непрерывный обмен веществом и энергией; это бесконечный поток. Возьмем, к примеру, процесс еды: вы поглощаете химическую энергию пищи и преобразуете ее в форму, пригодную для использования вашим телом.Теперь, когда ваше тело получает энергию из пищи, оно может работать в мире.
Этот процесс обмена, при котором энергия переходит из одного состояния в другое, происходит в наборе систем и окружений . Когда вы включаете свой электрический чайник утром, у вас есть вода, заключенная в металлическом контейнере, это ваша система. Остальная кухня, даже остальная часть дома — это окружение.
Когда ваш чайник начинает кипеть, он превращает часть воды в пар, который выходит из носика в верхней части.Эта преобразованная энергия пересекает границу из системы внутри металлического контейнера в окружающую среду за его пределами. Это термодинамика в действии, перенос энергии и материи между системами и окружающей средой.
Каждая термодинамическая система окружена границей и окружением. (Источник изображения)
Системы определяются наблюдателем, поэтому для одного человека чайник может быть системой. Для другого весь дом может быть системой, а окрестности — окрестностями, все зависит от вашей точки зрения.Дело в том, что каждая система в термодинамике содержится в пределах определенной границы, а по другую сторону границы находится окружение. В термодинамике различают три типа систем:
- Открытая система , в которой может происходить обмен энергией и материей между системой и ее окружением.
- Замкнутая система , в которой между системой и ее окружением возможен обмен только энергией, а не материей.
- Изолированная система , в которой не происходит обмена энергией или материей между системой и ее окружением.По-настоящему изолированная система встречается редко.
На высоком уровне вся наша вселенная считается системой, но каковы границы нашей вселенной и каково ее окружение? Это одни из самых важных вопросов, на которые нам еще предстоит ответить. Для разработчика электроники термодинамика представляет собой более личную реальность в повседневных устройствах, которые вы проектируете. Вы обнаружите, что многие из принципов, с которыми вы уже работаете для расчета и анализа цепей, таких как закон Кирхгофа, основаны на основах термодинамики.
Первый закон термодинамики
Первый закон термодинамики, также известный как закон сохранения энергии, гласит, что энергия не может быть создана или уничтожена, она может только изменять форму. Энергия бывает разных форм, в том числе:
Энергия бывает разных форм. (Источник изображения)
Энергия не создается и не уничтожается; он просто переходит из одной формы в другую. Включение выключателя света не создает энергию, оно просто преобразует электрическую энергию в лучистую энергию (свет) и тепловую энергию (тепло).
Практические примеры преобразования энергии в действии. (Источник изображения)
В Первом Законе есть три взаимосвязанных понятия – работа, теплота и внутренняя энергия. Тепло — это передача тепловой энергии между двумя системами. Работа — это сила, передающая энергию между системой и ее окружением. Производя работу либо внутри системы, либо вне ее, вы создаете тепло. Затем есть внутренней энергии , то есть вся энергия внутри системы.Когда теплота, работа и внутренняя энергия взаимодействуют друг с другом, происходит преобразование энергии. Вы можете выразить это отношение математически как:
Здесь ΔU — полное изменение внутренней энергии в системе, Q — теплообмен между системой и ее окружением, а W — работа, совершаемая системой или системой.
Когда система выделяет тепло или совершает какую-либо работу, внутренняя энергия системы уменьшается. Точно так же, если в систему добавляется тепло или в систему совершается работа, внутренняя энергия системы увеличивается.Любой вид энергии, который высвобождается системой, поглощается ее окружением, и любой вид энергии, потерянный окружением, поглощается системой. Во всех этих примерах вы не создаете и не уничтожаете энергию; это просто перемещение из одного места в другое. Выражаясь математически, это выглядит так:
.Здесь ΔU с система — полная внутренняя энергия в системе, которая всегда равна ΔU с окружения — полная энергия в окружении.
Одна важная вещь, которую следует помнить о Первом законе, заключается в том, что преобразование энергии не является эффективным на 100%. В нашем примере с лампочкой вы можете преобразовать электрическую энергию в пригодную для использования форму световой энергии, но при этом вы создаете бесполезную энергию в виде тепла.
Применительно к электронике Первый закон термодинамики похож на Текущий закон Кирхгофа. Этот хорошо известный закон гласит, что количество тока, входящего в узел, равно количеству тока, выходящего из узла.Неважно, сколько у вас узлов, что входит, то и выходит.
На изображении ниже у нас есть два потока, входящие в узел, и три потока, выходящие из узла. В соответствии с текущим законом Кирхгофа отношение между текущими входами и выходами узлов может быть представлено как:
Текущий закон Кирхгофа. (Источник изображения)
Разве это не выглядит странно знакомым с нашим уравнением баланса между системами и окружающей средой?
Второй закон термодинамики
Второй закон термодинамики, также известный как закон возрастающей энтропии, гласит, что с течением времени состояние дезорганизации или энтропия в системе всегда будет увеличиваться.Что мы подразумеваем под этим? Возьмем этот пример — почему ваш стол всегда становится все более грязным в течение недели? Или, что более важно, почему ваш офис не превращается из грязного в чистый без вашего участия? Это стрела времени в термодинамике. Со временем увеличивается и дезорганизация.
Это явление происходит в любой системе. Со временем полезная энергия в конечном итоге уступит место бесполезной энергии. Хотя энергия не может быть создана или уничтожена в соответствии с Первым законом, она может перейти из полезного состояния в менее полезное состояние, например тепловую энергию (тепло).
Со временем каждая система переходит из состояния низкой энтропии в состояние высокой. (Источник изображения)
Снова в нашем примере с лампочкой: чем дольше мы оставляем лампочку включенной, преобразовывая электрическую энергию в энергию излучения, тем больше полезной энергии мы продолжаем преобразовывать в бесполезную энергию в виде тепла. Поскольку полезная энергия внутри системы уменьшается, а неиспользуемая энергия увеличивается, мы говорим, что энтропия системы увеличилась. Математически заявлено:
Здесь полная энтропия ΔS universe внутри вселенной равна общей энтропии внутри системы ΔS sys плюс полная энергия во всем окружении ΔS surr , каждая из которых не может быть меньше 0.Почему? Потому что во все времена, в любое время суток вся энергия трансформируется из одной формы в другую, и одна из этих форм является непригодной для использования энергией. Вождение автомобиля использует механическую энергию для производства кинетической энергии движения, но при этом вы также превращаете массу энергии в тепло. Это неизбежный побочный продукт.
Еще один способ представить энтропию — это вероятности. Возьмем, к примеру, коробку, наполненную кусочками головоломки. Какова вероятность того, что вы выбросите все части головоломки из коробки, и одна из них случайно приземлится там, где идеально соединяется с другой частью? Это низкая вероятность.Какова вероятность того, что в той же коробке фигура окажется случайным образом там, где она не подходит к другой фигуре? Это высокая вероятность.
Полный хаос! Энтропия берет верх над вероятностью. (Источник изображения)
В этом примере головоломки случайно расположенная часть головоломки представляет собой высшую форму беспорядка или энтропии. Вот почему шины выпускают воздух при проколе, или почему льдинки, оставленные при комнатной температуре, в конце концов тают, или почему электроны в цепи перетекают от отрицательного к положительному.Конечно, все эти действия могут происходить в обратном порядке, но вероятность того, что они произойдут, настолько мала, а карты с возрастающей вероятностью сложены так высоко, что они просто никогда не происходят.
В электронике мы видим второй закон термодинамики в сочетании с эффектом Зеебека. Это явление возникает, когда к одному из двух проводников прикладывается тепло, что заставляет нагретые электроны течь к более холодному проводнику. Если вы соедините эту пару нагретых проводников вместе в цепи, то эффект нагрева вызовет постоянный ток (DC), протекающий через цепь.В этой ситуации у нас есть электроны в более низком состоянии энтропии в холодном проводнике, достигающие более высокого состояния энтропии за счет приложения тепла, и поэтому беспорядок увеличивается.
Эффект Зеебека с использованием тепла для создания постоянного тока. (Источник изображения)
Третий закон термодинамики
Третий закон термодинамики гласит, что идеальная кристаллическая структура при абсолютном нуле температуры будет иметь нулевой беспорядок или энтропию. Однако если в этой кристаллической структуре есть хоть малейший намек на несовершенство, то и энтропия будет минимальной.Однако этот закон становится немного странным, потому что даже при нуле Кельвина все еще происходит некоторое движение атомов, поэтому он немного теоретический. Несмотря на это, этот закон позволяет нам понять, что по мере того, как энтропия системы приближается к температуре абсолютного нуля, энтропия, присутствующая в системе, уменьшается.
Третий закон термодинамики. (Источник изображения)
Нулевой закон термодинамики
Нулевой закон термодинамики гласит, что если две системы находятся в тепловом равновесии с третьей системой, то первые две системы также находятся в тепловом равновесии друг с другом.Используя наше старое доброе транзитивное свойство равенства:
- Если система A находится в равновесии с системой C
- И Система B находится в балансе с Системой C
- Тогда Система А и Система Б также находятся в равновесии друг с другом.
Этот закон позволяет определить направление теплового потока между системами. Если вы знаете температуру набора связанных систем, то вы будете знать, в каком направлении будет перемещаться тепло, исходя из основ теплового равновесия.
Установлено тепловое равновесие между системами. (Источник изображения)
Обратите внимание: хоть мы и говорим о Законе Нуля в последнюю очередь, на самом деле он стоит первым. В 18 веке, когда были определены законы термодинамики, были включены только первые три. Однако ученые поняли, что им необходим четвертый закон, определяющий движение температуры. Вместо того чтобы перенумеровывать все существующие законы и вносить путаницу в существующую литературу, английский ученый Роберт Фаулер придумал название Нулевой закон.
Кто открыл эти законы?
Законы термодинамики не были открыты одним человеком. Развитие восходит к 1600-м годам, когда впервые была сформулирована основная идея тепла и температуры. В 1824 году французский физик Сади Карно первым сформулировал основные принципы термодинамики в своих рассуждениях об эффективности идеальной машины. Первоначально Сади использовал калорическую систему для описания тепла, теряемого во время движения двигателя, которое позже было заменено энтропией во втором законе термодинамики.
Отец термодинамики Сади Карно. (Источник изображения)
В 1850 году немецкий физик Рудольф Клаузиус разработал утверждение Клаузиуса, в котором говорилось, что «тепло обычно не может самопроизвольно переходить от материала с более низкой температурой к материалу с более высокой температурой». Примерно в то же время Уильям Томсон (лорд Кельвин) разработал утверждение Кельвина, в котором говорилось, что «невозможно полностью преобразовать тепло в циклическом процессе [без потери энергии].Оба эти утверждения легли в основу Первого и Второго законов термодинамики. Третий закон термодинамики был позже разработан немецким химиком Вальтером Нернстом и часто упоминается как теорема Нернста.
Лорд Кельвин, один из великих умов, разработавших законы термодинамики. (Источник изображения)
Собираем все вместе
Посмотрите вокруг себя на этот удивительный мир энергии в движении, и вы увидите законы термодинамики в действии.Будь то процесс преобразования химической энергии пищи в полезную энергию в вашем теле или преобразования механической энергии в кинетическую энергию в автомобиле или самолете. Термодинамика — это образ жизни. Вы даже обнаружите, что законы термодинамики работают в ваших электронных проектах. Такие принципы, как Закон тока Кирхгофа, идеально согласуются с Первым законом термодинамики, утверждающим, что ток, который входит в набор узлов, должен выйти, точно так же, как энергия не может быть создана или уничтожена, а только преобразована.Что касается второго закона термодинамики, у нас есть эффект Зеебека, который можно наблюдать в электрических цепях, где нагретая электроника будет течь к более холодному проводнику, создавая при этом ток в цепи. Здесь мы имеем энтропию в действии, создающую нарастающие состояния беспорядка, куда бы она ни пошла.
Что бы вы ни проектировали, вы проектируете в соответствии с законами термодинамики. Примените эти принципы на практике: попробуйте Autodesk EAGLE бесплатно уже сегодня!
.