Третий закон: Третий закон Ньютона — урок. Физика, 9 класс.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

смысл, формулировка, свойства и применение

Предмет, лежащий на полке, действует на нее с определенной силой. В ответ на это полка противодействует этой силе с аналогичной силой. Однако аналогичным является лишь значение, направление же противоположно. Такое взаимодействие отражено в третьем законе Ньютона.

Закон Ньютона

Классическая механика опирается на три закона, сформулированные Ньютоном в конце XVII века.

Пальма первенства первого закона принадлежит основоположнику экспериментальной физики Галилео Галилею. Он носит название закона инерции и был включен Ньютоном в систему законов классической механики.

Определение 1

Закон инерции: когда на тело отсутствует воздействие других тел, оно пребывает в состоянии покоя или осуществляет прямолинейное равномерное движение.

К примеру, по дороге движется машина. Если компенсировать действие силы тяги двигателя, а также силы трения поверхности дороги, то машина будет двигаться равномерно.

В физике говорят, что в такой ситуации тело движется по инерции.

Таким образом, понятно, что тело будет находиться в покое, если воздействие на него других тел компенсируется.

Второй закон Ньютона направлен на установление зависимости ускорения тела, взаимодействующего с другим телом, от его массы и силы, воздействующей на него. Из опытов следует, что более интенсивная сила вызывает большее ускорение.

Например, водитель автобуса, нажимая на педаль тормоза, регулирует скорость остановки. В то же время ускорение будет зависеть от массы тел. Так, грузовой автомобиль имеет больший тормозной путь с выключенным двигателем.

Определение 2

Второй закон Ньютона: ускорение тела прямо пропорционально силе, действующей на тело и обратно пропорционально его массе.

Третий закон Ньютона выражает особенности ситуации возникновения силы в опоре либо теле, подвергшемся действию силы. Такие ситуации окружают человека повсюду, в окружающей природе и в быту. Например, толкая мяч, человек испытывает ответное давление на ногу со стороны мяча.

Чувствовать его интенсивность не получается, поскольку масса мяча значительно меньше, чем человека. В то же время, если пнуть металлический шар, ноге станет больно. Проекцией данной ситуации в крупном масштабе является ходьба людей по земному шару. Каждый шаг — это «пинок», в ответ на который земля отталкивает ногу.

Указанные примеры отражают факт, что при взаимодействии тел силы в природе существуют парами. Однако их уравновешивание будет нарушаться, если точки приложения принадлежат разным телам.  

Когда тела действуют друг на друга, каждое из них приобретает ускорение. Так, груз, который подвесили на нити, воздействует на нее. Вектор этой силы направлен вниз, поэтому характеризуется свойством растягивать нить, которая также воздействует на груз. Однако вектор этой силы направлен вверх. По модулю значения этих двух сил равны, однако их направления противоположны.

Пояснения к третьему закону Ньютона

Объяснение третьего закона Ньютона можно дать следующим образом:

Источник: formulki.ru

Из рассмотренного выше следует:

Единицей измерения силы является Ньютон.

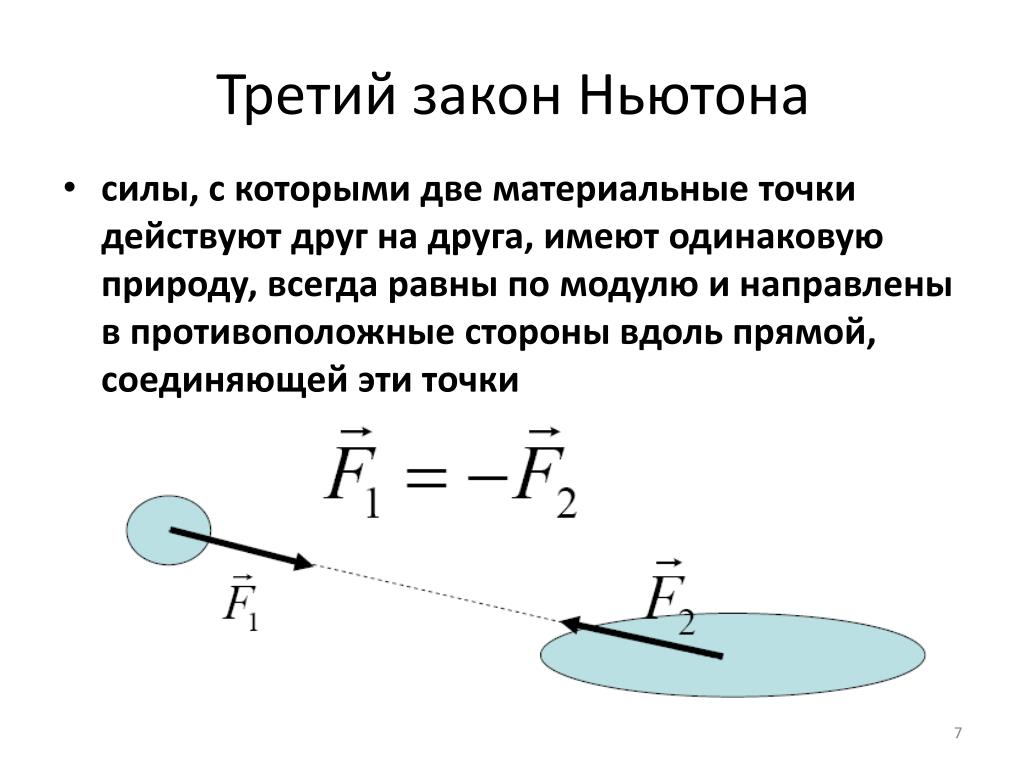
Красный и черный векторы равны, при этом перед одним из них стоит знак «минус». Благодаря такому обозначению мы понимаем, что векторы имеют противоположные направления. Поэтому формулу правильно записать так:

Знак равенства между векторами подчеркивает особенность, что по модулю векторы равны.

Проявлениями третьего закона Ньютона являются следующие характеристики:

1. Когда тела взаимодействуют, силы действуют как на одно, так и на другое тело.
2. По модулю силы, действующие на оба тела, равны.
3. Действующие на оба тела силы имеют противоположное направление.

Мы подошли к формулировке третьего закона Ньютона.

Формулировка третьего закона Ньютона, формула

Определение 3

Взаимодействие тел происходит с силами, значения по модулю которых равны, а направления противоположны. Действия сил происходят вдоль прямой, соединяющей эти материальные точки (тела).

Так звучит третий закон Ньютона. Его просто выразить с помощью формулы:

Источник: nauka. club

Смысл закона заключается в том, что силы между взаимодействующими телами возникают парами. При этом одна из них носит название «сила действия», а вторая — «сила противодействия». Принимая во внимание, что силы действуют на разные тела, складывать их нельзя, как и утверждать, что они могут уравновешивать друг друга.

Примечание 

Все три закона Ньютона являются справедливыми при условии инерциальных систем отсчета.

Источник: nauka.club

В отличие от первого и второго законов Ньютона, в третьем речь идет не об одном, а о двух телах. Силы взаимодействия, возникающие между ними, приложены к разным телам, однако они одинаковы по модулю и направлены в противоположные стороны.

Примеры применения третьего закона Ньютона

Применение третьего закона Ньютона в жизни человека встречается часто. Без него не обходится строительство зданий, мостов, с учетом его действия не тонут корабли, да и сами люди не проваливаются под землю. Причина этому — присутствие сил взаимодействия с другими телами. Любой из названых предметов имеет опору (земля, подставка, стол, вода, воздух и т.д.). Простыми словами, силу, которая тянет физические тела к центру Земли, компенсирует ответное действие опоры.

Границы действия закона необходимо учитывать в таких ситуациях, как, например, выпрыгивание из лодки. В момент прыжка лодка отплывет назад, поскольку на нее будет действовать сила с направлением, противоположным направлению прыжка. Прыгающий на берег человек упадет в воду, не рассчитав возникшее дополнительное расстояние.

Таких ситуаций в жизни много. Изменить их проявление можно с помощью дополнительных опор.

Пароходы, лодки и катера могут двигаться вперед за счет взаимодействия с водой. Такие технические плавсредства, как и водоплавающие животные, в результате работы винтов (с помощью лапок, хвостов, плавников) отталкивают воду назад и, испытывая ответное действие воды, плывут вперед.

Аналогичная ситуация с самолетами, вертолетами, птицами и прочими летающими живыми существами. Их движение становится в воздухе реальным по причине взаимодействия с воздухом. Отталкивая воздух назад, с учетом ответного действия, они совершают движение вперед.

Человек использует такие природные закономерности в своей профессиональной деятельности. Так, электромонтеры (связисты), которым необходимо подниматься на столбы, пользуются «кошками» — специальными приспособлениями, представляющими собой две железные дуги, имеющие острые зубцы, и опоры для ног.

Работник охватывает «кошкой» столб, ее шипы впиваются в дерево (бетон). Перенося центр тяжести своего тела на эту «кошку», он закрепляет вторую ногу. Так, поочередно «шагая» вверх, он поднимается на нужную высоту. Если предположить, что со столбом отсутствует взаимодействие, такого результата рабочий достичь бы не смог.

4.4 Третий закон движения Ньютона: симметрия сил – College Physics 2e

Цели обучения

К концу этого раздела вы сможете:

• Поймите третий закон движения Ньютона.
• Применить третий закон Ньютона для определения систем и решения задач движения.

Бейсбольный питчер Мариано Ривера пользовался таким уважением, что в год его выхода на пенсию команды соперников устраивали прощальные презентации, когда он играл на их стадионах. Миннесотские близнецы преподнесли уникальный подарок: стул из сломанных летучих мышей. Любая подача может сломать биту, но с фирменной подачей Риверы, известной как каттер, мяч и бита часто сталкивались в точке, которая разбивала твердую древесину. Как правило, мы думаем о нападающем в бейсболе или софтболе, оказывающем силу на входящий мяч, а бейсбольные аналитики сосредотачиваются на результирующей «скорости выхода» как на ключевой статистике. Но сила мяча может нанести ущерб. Именно это и происходит всякий раз, когда одно тело действует с силой на другое — на первое тоже действует сила (равная по величине и противоположная по направлению). Многочисленные распространенные переживания, такие как ушиб пальца ноги или отталкивание от пола во время прыжка, подтверждают это.

Это точно сформулировано в третьем законе движения Ньютона.

Третий закон Ньютона

Всякий раз, когда одно тело воздействует на другое тело, на первое тело действует сила, равная по величине и противоположная по направлению силе, которую оно оказывает.

Этот закон представляет определенную симметрию в природе : Силы всегда возникают парами, и одно тело не может воздействовать силой на другое, не испытывая на себе силы. Иногда мы в общих чертах называем этот закон «действием-противодействием», где прилагаемая сила является действием, а сила, воспринимаемая как следствие, является противодействием. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.

Мы легко можем увидеть третий закон Ньютона в действии, взглянув на то, как люди передвигаются. Рассмотрим пловца, отталкивающегося от края бассейна, как показано на рис. 4.9. Она упирается ногами в стенку бассейна и ускоряется в направлении , противоположном направлению ее толчка в направлении . Стена воздействовала на пловца равной и противоположной силой. Вы можете подумать, что две равные и противоположные силы нейтрализуют друг друга, но это не так , потому что они действуют на разные системы

. В этом случае есть две системы, которые мы могли бы исследовать: пловец или стена. Если в качестве интересующей системы выбрать пловца, как на рисунке, то Fстенка на ногах Fстенка на ногах является внешней силой, действующей на эту систему и влияющей на ее движение. Пловец движется в направлении Fстен на ногах Fстен на ногах. Напротив, сила Ffeet on wallFfeet on wall действует на стену, а не на нашу интересующую систему. Таким образом, Fноги на стенеFноги на стене не влияют непосредственно на движение системы и не отменяют Fстену на ногахFстену на ногах. Обратите внимание, что пловец отталкивается в направлении, противоположном тому, в котором он хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении.

Рисунок 4.9 Когда пловец прикладывает силу F ног к стене, F ног к стене на стене, он ускоряется в направлении, противоположном направлению его толчка. Это означает, что результирующая внешняя сила, действующая на нее, направлена ​​в направлении, противоположном Ffeet on wallFfeet on wall. Это противодействие возникает потому, что в соответствии с третьим законом движения Ньютона стена действует на нее с силой Fстена на ногиFстена на ноги, равной по величине, но в направлении, противоположном тому, которое она прикладывает к ней. Линия вокруг пловца указывает интересующую систему. Заметим, что Fноги на стенеFноги на стене не действуют на эту систему (пловца) и, таким образом, не отменяют Fстену на ногахFстену на ногах. Таким образом, на диаграмме свободного тела показаны только Fwall на ногах Fwall на ногах, ww — сила тяжести и BFBF — выталкивающая сила воды, поддерживающая вес пловца. Вертикальные силы ww и BFBF сокращаются, так как нет вертикального движения.

Другие примеры третьего закона Ньютона найти несложно. Когда профессор идет перед доской, она оказывает давление на пол назад. Пол оказывает на профессора реактивную силу, которая заставляет ее двигаться вперед с ускорением. Точно так же автомобиль ускоряется, потому что земля давит на ведущие колеса вперед в ответ на то, что ведущие колеса толкают землю назад. Вы можете увидеть следы отталкивания колес назад, когда шины пробуксовывают на гравийной дороге и отбрасывают камни назад. В другом примере ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большую обратную силу на газ в камере сгорания ракеты, и поэтому газ оказывает большую реактивную силу на ракету вперед. Эта сила реакции называется тягой. Это распространенное заблуждение, что ракеты движутся сами по себе, отталкиваясь от земли или воздуха позади себя. На самом деле они лучше работают в вакууме, где они легче удаляют выхлопные газы. Точно так же вертолеты создают подъемную силу, толкая воздух вниз, тем самым испытывая восходящую силу реакции.

Птицы и самолеты также летают, воздействуя на воздух в направлении, противоположном тому, в котором они нуждаются. Например, крылья птицы толкают воздух вниз и назад, чтобы подняться и двигаться вперед. Осьминог передвигается в воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу. Боксеры и бойцы других единоборств испытывают силы реакции, когда наносят удары, иногда ломая себе руку, ударяя по телу соперника.

Пример 4.3

Приступая к работе: выбор правильной системы

Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал, как показано на рис. 4.10. Ее масса 65,0 кг, тележки 12,0 кг, оборудования 7,0 кг. Вычислите ускорение, возникающее, когда профессор прикладывает к полу обратную силу 150 Н. Все силы, противодействующие движению, такие как трение о колеса тележки и сопротивление воздуха, составляют в сумме 24,0 Н.

Рисунок 4.10 Профессор толкает тележку с демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (за исключением ff, так как он слишком мал, чтобы рисовать в масштабе). В каждом примере задаются разные вопросы; таким образом, система интересов должна быть определена по-разному для каждого. Система 1 подходит для этого примера, так как она запрашивает ускорение всей группы объектов. Только FfloorFfloor и ff являются внешними силами, действующими на Систему 1 вдоль линии движения. Все остальные силы либо отменяют, либо воздействуют на внешний мир. Система 2 выбрана для примера 4.4 так, чтобы FprofFprof была внешней силой и входила во второй закон Ньютона. Обратите внимание, что диаграммы свободного тела, которые позволяют нам применить второй закон Ньютона, зависят от выбранной системы.

Стратегия

Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на рис. 4.10. Профессор толкает назад с силой FfootFfoot, равной 150 Н. Согласно третьему закону Ньютона, пол оказывает на Систему 1 поступательную силу реакции FfloorFfloor, равную 150 Н. направление. Таким образом, задача является одномерной в горизонтальном направлении. Как уже отмечалось, ff противостоит движению и, таким образом, находится в направлении, противоположном FfloorFfloor. Обратите внимание, что мы не включаем силы FprofFprof или FcartFcart, потому что это внутренние силы, и мы не включаем FfootFfoot, потому что они действуют на пол, а не на систему. На Систему 1 не действуют другие значительные силы. Если из всей этой информации можно найти результирующую внешнюю силу, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение. См. диаграмму свободного тела на рисунке.

Решение

Второй закон Ньютона определяется выражением

a=Fnetm.a=Fnetm.

4.18

Суммарная внешняя сила, действующая на Систему 1, выведена из рис. 4.10 и приведенных выше рассуждений:

N=126 N.

4,19

Масса Системы 1 равна

m=(65,0 + 12,0 + 7,0) кг = 84 кг. m=(65,0 + 12,0 + 7,0) кг = 84 кг.

4,20

Эти значения FnetFnet и mm дают ускорение

a=Fnetm,a=126 N84 кг= 1,5 м/с2. a=Fnetm,a=126 N84 кг= 1,5 м/с2.

4.21

Обсуждение

Ни одна из сил между компонентами Системы 1, например, между руками профессора и тележкой, не вносит вклад в результирующую внешнюю силу, поскольку они являются внутренними по отношению к Системе 1. обратите внимание, что силы между компонентами системы сокращаются, потому что они равны по величине и противоположны по направлению. Например, сила, приложенная профессором к тележке, приводит к тому, что на нее действует равная и противоположная сила. В этом случае обе силы действуют на одну и ту же систему и, следовательно, сокращаются. При этом внутренние силы (между компонентами системы) сокращаются. Выбор Системы 1 имел решающее значение для решения этой проблемы.

Пример 4.4

Сила, действующая на тележку — выбор новой системы

Рассчитайте силу, которую профессор оказывает на тележку на рис. 4.10, используя при необходимости данные из предыдущего примера.

Стратегия

Если теперь мы определим интересующую нас систему как тележку плюс оборудование (Система 2 на рис. 4.10), то результирующая внешняя сила на Систему 2 будет равна силе, которую профессор оказывает на тележку за вычетом трения. Сила, которую она прикладывает к тележке, FprofFprof — это внешняя сила, действующая на Систему 2. FprofFprof является внутренней по отношению к Системе 1, но является внешней по отношению к Системе 2 и входит во второй закон Ньютона для Системы 2.

Решение

Второй закон Ньютона можно использовать для нахождения FprofFprof. Начиная с

a=Fnetma=Fnetm

4,22

и учитывая, что величина чистой внешней силы в Системе 2 равна

Fnet=Fprof-f,Fnet=Fprof-f,

4,23

9 0004 решаем для FprofFprof, требуемое количество:

Fprof=Fnet+f.Fprof=Fnet+f.

4,24

Значение ff задано, поэтому мы должны вычислить чистый FnetFnet. Это можно сделать, поскольку известны и ускорение, и масса Системы 2. Используя второй закон Ньютона, мы видим, что

Fnet=ma,Fnet=ma,

4,25

где масса Системы 2 равна 19,0 кг (mm= 12,0 кг + 7,0 кг) и ее ускорение равно a=1,5 м/с2a=1,5 м/ s2 в предыдущем примере. Таким образом,

Fnet=ma,Fnet=ma,

4,26

Fnet=(19,0 кг)(1,5 м/с2)=29 N.Fnet=(19,0 кг)(1,5 м/с2)=29 N.

4.27

Теперь мы можем найти искомую силу:

Fprof=Fnet+f,Fprof=Fnet+f,

4.28

Fprof=29 N+24.0 N=53 N.Fprof=29N+24,0 N=53 Н.

4,29

Обсуждение

Интересно, что эта сила значительно меньше силы в 150 Н, которую профессор приложил назад к полу. Не вся эта сила в 150 Н передается на тележку; часть из них ускоряет профессора.

Выбор системы — важный аналитический шаг как в решении задач, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).

Исследования ФЕТ

Лаборатория силы гравитации

Визуализируйте гравитационную силу, с которой два объекта действуют друг на друга. Меняйте свойства объектов, чтобы увидеть, как меняется сила гравитации.

Что такое третий закон термодинамики?

Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот как это работает.

Температурные шкалы. При 0 К энтропия останавливается. Это называется абсолютным нулем, и теоретически это невозможно. (Изображение предоставлено: ttsz через Getty Images)

Третий закон термодинамики касается поведения систем при приближении температуры к абсолютному нулю. Он связывает теплоту и энтропию при этой конечной самой низкой температуре для кристаллов, которые относятся к любому твердому материалу, состоящему из атомов, расположенных в определенном симметричном порядке, согласно Британнике. Третий закон термодинамики гласит: «энтропия идеального кристалла равна нулю, когда температура кристалла равна абсолютному нулю (0 К)». Согласно Университету Пердью, «кристалл должен быть совершенным, иначе будет какой-то врожденный беспорядок. Он также должен быть при 0 К; иначе внутри кристалла будет тепловое движение, которое приведет к беспорядку».

Сиабал Митра, профессор физики Университета штата Миссури, предлагает еще одно следствие этого закона.

«Одна из версий третьего закона гласит, что для достижения абсолютного нуля потребуется бесконечное количество шагов, а это означает, что вы никогда не доберетесь туда», — сказал Митра Live Science. Если бы вы могли достичь абсолютного нуля, это нарушило бы второй закон, потому что если бы у вас был радиатор на абсолютном нуле, вы могли бы построить машину со стопроцентной эффективностью».

Теоретически можно было бы расти совершенный кристалл, в котором все пространства решетки заняты одинаковыми атома . Однако принято считать, что достичь температуры абсолютного нуля невозможно. Следовательно, вся материя содержит по крайней мере некоторую энтропию благодаря наличию некоторой тепловой энергии.

История третьего закона термодинамики

Третий закон термодинамики был впервые сформулирован немецким химиком и физиком Вальтером Нернстом в 1906 году согласно Britannica . В своей книге «Обзор термодинамики» (Американский институт физики, 1994), Мартин Бейлин цитирует утверждение Нернста о третьем законе: «Ни одна процедура не может привести к изотерме T = 0 за конечное число шагов». Это, по сути, устанавливает, что температура абсолютного нуля недостижима примерно так же, как скорость света c в вакууме никогда не может быть превышена. Теоретические положения и эксперименты показали, что независимо от того, насколько быстро что-то движется, его всегда можно заставить двигаться быстрее, но оно никогда не может достичь скорость света , по данным Университета Морнингсайд . Точно так же, независимо от того, насколько холодна система, ее всегда можно сделать еще холоднее, но она никогда не достигнет абсолютного нуля.

В своей книге «История физики» (Arcturus, 2012) Энн Руни написала: «Третий закон термодинамики требует концепции минимальной температуры, ниже которой никакая температура не может опускаться — известной как абсолютный ноль». Она продолжила: «Роберт Бойль впервые обсудил концепцию минимально возможной температуры в 1665 году в «Новых экспериментах и ​​наблюдениях, касающихся холода» [Crook Publishing], в которой он назвал эту идею первый холодный. ”

Считается, что абсолютный ноль был впервые рассчитан с достаточной точностью в 1779 году Иоганном Генрихом Ламбертом, согласно Хайме Висняку из Университета Бен-Гуриона в Негеве в Израиле . Ламберт основывал этот расчет на линейной зависимости между давление и температура газа. Когда газ нагревается в замкнутом пространстве, его давление увеличивается. Это происходит потому, что температура газа является мерой средней скорости молекул в газе. Чем он горячее становится тем быстрее движутся молекулы и тем большее давление они оказывают при столкновении со стенками сосуда Ламберт имел право предположить, что если бы температуру газа можно было довести до абсолютного нуля, движение молекулы газа можно было полностью остановить, чтобы они больше не оказывали никакого давления на стенки камеры.  

Если бы можно было построить зависимость температуры и давления газа на графике с температурой по оси x (горизонтальная) и давлением по оси y (вертикальная), точки образовали бы прямую с наклоном вверх линия, указывающая на линейную зависимость между температурой и давлением, согласно Университета штата Флорида . Таким образом, должно быть довольно просто протянуть линию назад и считать температуру, где линия пересекает x , т. е. где y = 0, что указывает на нулевое давление. Используя эту технику, Ламберт вычислил абсолютный ноль как минус 270 градусов по Цельсию (минус 454 по Фаренгейту), что было очень близко к современному принятому значению минус 273,15 C (минус 459,67 F), согласно Britannica .

Температурная шкала Кельвина

Фотография Уильяма Томсона, 1-го барона Кельвина. Шкала Кельвина названа в его честь. (Изображение предоставлено Беттманном / автором Getty Images)

Человек, больше всего связанный с концепцией абсолютного нуля, — Уильям Томсон, 1-й барон Кельвин. Единица измерения температуры, носящая его имя, кельвин (К), наиболее часто используется учеными во всем мире. Температурные приращения по шкале Кельвина имеют тот же размер, что и по шкале Цельсия, но поскольку они начинаются с абсолютного нуля, а не с точки замерзания воды, их можно использовать непосредственно в математических расчетах, особенно при умножении и делении. Например, 100 К на самом деле вдвое горячее, чем 50 К, согласно Техасский университет . Образец замкнутого газа при температуре 100 К также содержит в два раза больше тепловой энергии и давление в два раза выше, чем при 50 К. Такие расчеты нельзя выполнить с использованием шкал Цельсия или Фаренгейта, т. е. 100 °С — это , а не .

Последствия третьего закона

Поскольку температура абсолютного нуля физически недостижима, третий закон может быть переформулирован для применения к реальному миру как : энтропия идеального кристалла приближается к нулю, когда его температура приближается к абсолютному нулю. Мы можем экстраполировать из экспериментальных данных, что энтропия идеального кристалла достигает нуля при абсолютном нуле, но мы никогда не сможем продемонстрировать это эмпирически. 9−12 K)», — сказал Дэвид Макки, профессор физики Южного государственного университета штата Миссури.

Микрогравитация (ZARM) в Бременском университете в Германии.Они поймали облако примерно из 100 000 атомов рубидия в магнитном поле внутри вакуумной камеры и бросили камеру в падающую башню, чтобы позволить атомам плавать без сдерживания тяжести и замедлить их молекулярное движение. Облако достигло рекордных 38 пикокельвинов, или 38 триллионных долей Кельвина.

Хотя температуры абсолютного нуля в природе не существует, и ученые не могут получить ее в лаборатории, концепция абсолютного нуля имеет решающее значение для расчетов, связанных с температурой и энтропией. Многие измерения подразумевают связь с некоторой отправной точкой. Когда кто-то указывает расстояние, они должны спросить, расстояние от чего? Когда они дают время, они должны спросить, время с какого момента? Определение нулевого значения на температурной шкале придает смысл положительным значениям на этой шкале. Когда температура указывается как 100 К, это означает, что температура на 100 К выше абсолютного нуля, что в два раза выше абсолютного нуля, чем 50 К, и в два раза выше, чем 200 К. 

При первом чтении третий закон кажется довольно простым и очевидным. Однако он служит заключительным периодом в конце длинного и последовательного рассказа, полностью описывающего природу тепла и тепловой энергии.

Эта статья была обновлена ​​2 февраля 2022 г. участником Live Science Эшли Хамер.

Дополнительные ресурсы

• На веб-сайте Energy Education Университета Калгари объясняется концепция абсолютного нуля.
• В этом видео от StarTalk Нил де Грасс Тайсон объясняет, почему нельзя достичь абсолютного нуля.
• Политехнический институт Ренсселера имеет другое объяснение третьего закона термодинамики , дополненное тремя различными формулировками закона.

Библиография

Университет Пердью, «Энтропия и 2-й и 3-й законы термодинамики». http://chemed.chem.purdue.edu/genchem/topicreview/bp/ch31/entropy.php  

Нобелевская премия, «Вальтер Нернст: биографический». 1966. https://www.nobelprize.org/prizes/chemistry/1920/nernst/biographical/  

Мартин Бейлин, «Обзор термодинамики», Американский институт физики, 1994

Университет Морнингсайд, «Предел скорости». https://webs.morningside.edu/slaven/Physics/relativity/relativity10.html  

Энн Руни, «История физики», Arcturus, 2012

Роберт Бойл, «Новые эксперименты и наблюдения, касающиеся холода», Крук, 1665

Хайме Висняк, «Развитие концепции абсолютной нулевой температуры», Educación Química, январь 2005 г. https://www.researchgate.net/publication/236235474_Development_of_the_Concept_of_Absolute_Zero_Temperature  

Ill Государственный университет Инойса, “MAT 312: Вероятность и статистика для Учителя средних школ», https://math.illinoisstate.edu/day/courses/old/312/notes/twovar/twovar02. html  

Университет штата Флорида, «Законы о газе». https://www.chem.fsu.edu/chemlab/chm1045/gas_laws.html

Britannica, «Абсолютный ноль», 9 апреля 2021 г. https://www.britannica.com/science/absolute-zero

Центр медицинских наук Техасского университета в Хьюстоне, «Биостатистика для клинициста. ” https://www.uth.tmc.edu/uth_orgs/educ_dev/oser/L1_2.HTM  

Бременский университет, «Чрезвычайно долго и невероятно холодно», 27 августа 2021 г. https://www.zarm .uni-bremen.de/en/press/single-view/article/extremely-long-and-incredably-cold.html  

Будьте в курсе последних научных новостей, подписавшись на нашу рассылку Essentials.

Свяжитесь со мной, чтобы сообщить о новостях и предложениях от других брендов Future. Получайте электронные письма от нас от имени наших надежных партнеров или спонсоров.

Джим Лукас — автор статей для Live Science. Он охватывает физику, астрономию и инженерное дело. Джим окончил Университет штата Миссури, где получил степень бакалавра наук в области физики, а также астрономию и техническое письмо.