Тяготения силы: Сила тяготения

Урок 8. гравитационные силы – Физика – 10 класс

Физика, 10 класс

Урок 8. Гравитационные силы

Перечень вопросов, рассматриваемых на уроке:

1)познакомиться с явлением всемирного тяготения и сформулировать закон всемирного тяготения.

2) понять физический смысл гравитационной постоянной;

3) проанализировать некоторые физические явления на основе знаний закона всемирного тяготения;

Глоссарий по теме:

Закон всемирного тяготения – все материальные тела притягивают друг друга с силами прямо пропорциональными их массам и обратно пропорциональными квадрату расстояния между ними.

Тяготение – свойство материи, которое состоит в том, что между любыми двумя частицами существуют силы притяжения.

Масса тела – основная механическая величина, определяющая величину ускорения, сообщаемого телу данной силой.

Сила тяжести – векторная величина, определяющая силу притяжения к Земле любого тела.

Первая космическая скорость – наименьшая скорость, которую нужно сообщить телу на поверхности Земли, чтобы оно стало двигаться вокруг Земли по круговой орбите над её поверхностью только под действием силы гравитационного притяжения Земли

Вес – сила, с которой любое тело вследствие притяжения Земли действует на опору или подвес.

Невесомость – состояние, при котором вес тела равен нулю.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 89 – 106.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.:Дрофа,2009.

Открытые электронные ресурсы

:

http://kvant.mccme.ru/1987/11/zakon_vsemirnogo_tyagoteniya.htm

Теоретический материал для самостоятельного изучения

В механике обычно имеют дело с тремя видами сил – силами тяготения, упругости и трения.

Силу, с которой Земля действует на тело, называют силой тяжести.

Ньютон является первым учёным, который открыл закон всемирного тяготения. Он строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Эта сила всемирного тяготения, действующая между любыми телами Вселенной.

Ньютон после долгих наблюдений сделал вывод, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы с определённой скоростью, могла бы стать такой, что он никогда не достиг бы поверхности Земли, а двигался бы подобно тому, как планеты вокруг Солнца.

Исаак Ньютон сделал выводы:

1) ускорение и сила притяжения тел к Земле обратно пропорциональны квадрату расстояния до центра Земли:

2) Солнце сообщает всем планетам ускорение, обратно пропорциональное квадрату расстояния от планет до Солнца.

Ньютон нашёл причину множества явлений: от падения брошенного камня на землю до движения огромных космических тел. И причину этих явлений он выразил одной формулой – законом всемирного тяготения.

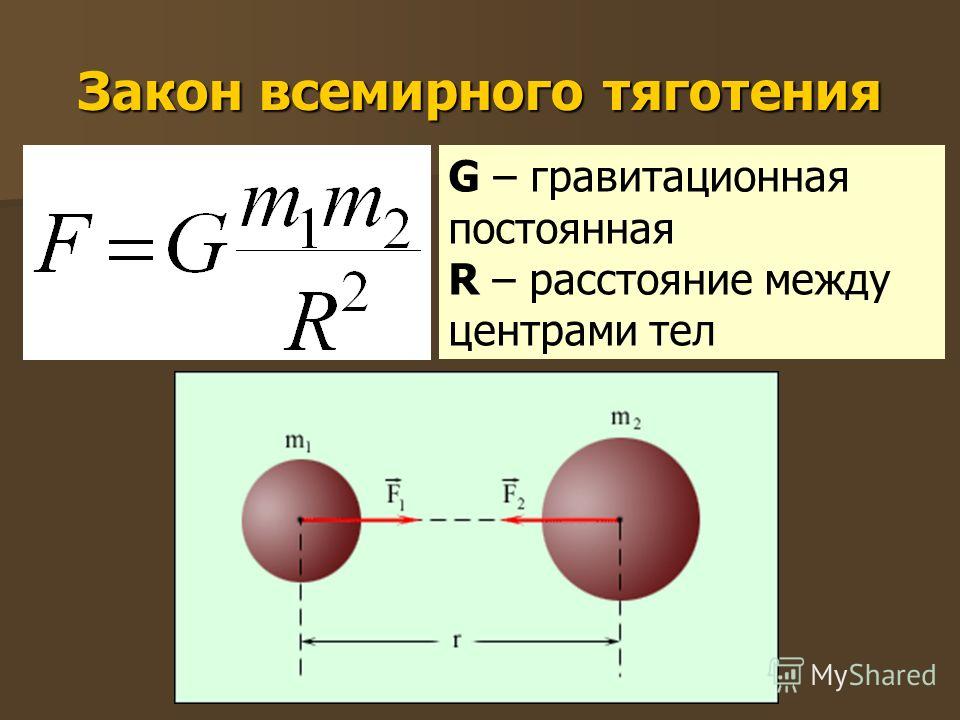
Закон всемирного тяготения

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:

F – модуль вектора силы гравитационного притяжения между телами с массами , находящимися на расстоянии r друг от друга.

G – это коэффициент, который называется гравитационной постоянной

Измерения показывают, что

Первая космическая скорость – минимальная скорость, которую надо сообщить телу на поверхности Земли, чтобы оно стало спутником Земли, движущимся по орбите.

Примеры и разбор решения заданий

1.На столе несколько гвоздиков, кнопка, ластик, карандаш. На какие из этих тел действует одинаковые силы тяжести?

1) на ластик и карандаш;

2) на гвозди;

3) на кнопку и карандаш;

4) на все эти тела.

Правильный ответ: на гвозди.

2. Чему равна сила тяжести, действующая на мяч массой 100 г, если он находится на космическом корабле? Космический корабль движется на высоте 1600 км над поверхностью Земли. Радиус Земли 6400 км. Масса Земли равна

Решение:

Ответ: F = 0,63 Н.

Сила тяготения

Любые два тела притягиваются друг к другу — по той лишь одной причине, что они имеют массу. Эта сила притяжения называется силой тяготения или гравитационной силой.

Закон всемирного тяготения

Гравитационное взаимодействие любых двух тел во Вселенной подчиняется достаточно простому закону. Закон всемирного тяготения. Две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

(1)  

Коэффициент пропорциональности называется гравитационной постоянной. Это фундаментальная константа, и её численное значение было определено на основе эксперимента Генри Кавендиша:

= 6,67 · 10⁻¹¹ (Н · м²)/кг².

Порядок величины гравитационной постоянной объясняет, почему мы не замечаем взаимного притяжения окружающих нас предметов: гравитационные силы оказываются слишком малыми при небольших массах тел. Мы наблюдаем лишь притяжение предметов к Земле, масса которой грандиозна и равна примерно 6 · 10²⁴ кг.

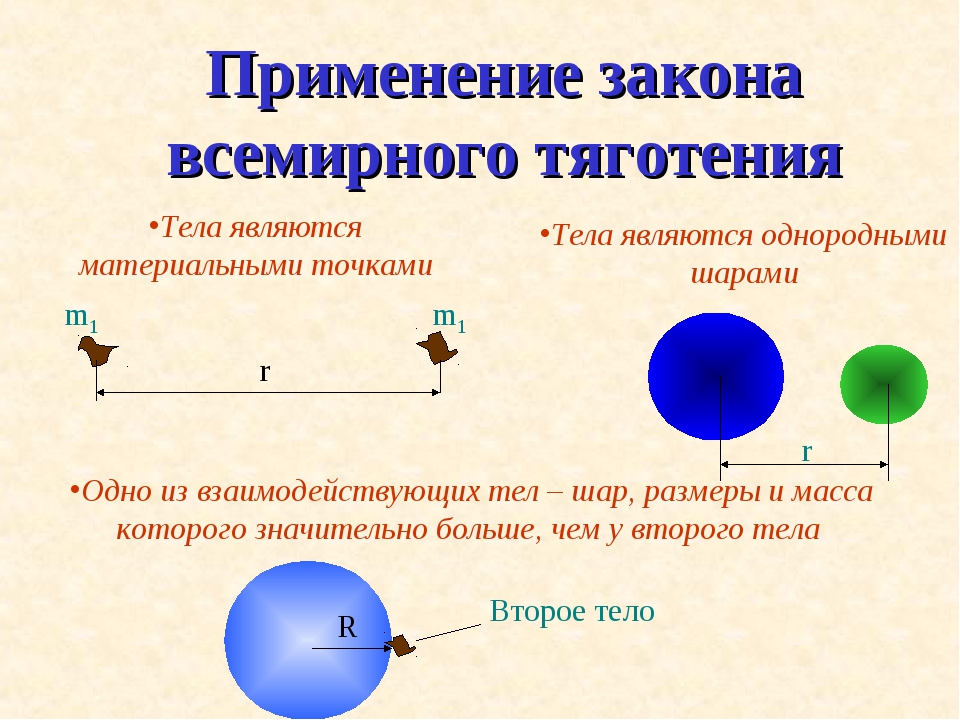
Формула (1), будучи справедливой для материальных точек, перестаёт быть верной, если размерами тел пренебречь нельзя. Имеются, однако, два важных для практики исключения.

1. Формула (1) справедлива, если тела являются однородными шарами. Тогда — расстояние между их центрами. Сила притяжения направлена вдоль прямой, соединяющей центры шаров.
2. Формула (1) справедлива, если одно из тел — однородный шар, а другое — материальная точка, находящаяся вне шара. Тогда r — расстояние от точки до центра шара. Сила притяжения направлена вдоль прямой, соединяющей точку с центром шара.

Второй случай особенно важен, так как позволяет применять формулу (1) для силы притяжения тела (например, искусственного спутника) к планете.

Сила тяжести

Предположим, что тело находится вблизи некоторой планеты. Сила тяжести — это сила гравитационного притяжения, действующая на тело со стороны планеты.

В подавляющем большинстве случаев сила тяжести — это сила притяжения к Земле. Пусть тело массы лежит на поверхности Земли. На тело действует сила тяжести , где
— ускорение свободного падения вблизи поверхности Земли. С другой стороны, считая Землю
однородным шаром, можно выразить силу тяжести по закону всемирного тяготения:

   

где — масса Земли, ≈ 6400 км — радиус Земли. Отсюда получаем формулу для ускорения свободного падения на поверхности Земли:

(2)  

Эта же формула, разумеется, позволяет найти ускорение свободного падения на поверхности любой планеты массы и радиуса .

Если тело находится на высоте над поверхностью планеты, то для силы тяжести получаем:

   

Здесь — ускорение свободного падения на высоте :

   

В последнем равенстве мы воспользовались соотношением которое следует из формулы (2).

Вес тела. Невесомость

Рассмотрим тело, находящееся в поле силы тяжести. Предположим, что есть опора или подвес, препятствующие свободному падению тела. Вес тела — это сила, с которой тело действует на опору или подвес. Подчеркнём, что вес приложен не к телу, а к опоре (подвесу).

На рисунку изображено тело на опоре. Со стороны Земли на тело действует сила тяжести (в случае однородного тела простой формы сила тяжести приложена в центре симметрии тела). Со стороны опоры на тело действует сила упругости (так называемая реакция опоры). На опору со стороны тела действует сила — вес тела. По третьему закону Ньютона силы и равны по модулю и противоположны по направлению.

Предположим, что тело покоится. Тогда равнодействующая сил, приложенных к телу, равна нулю. Имеем:

   

С учётом равенства получаем . Стало быть, если тело покоится, то его вес равен по модулю силе тяжести.

Силы тяготения. История познания :: Класс!ная физика

СИЛЫ ТЯГОТЕНИЯ

ИСТОРИЯ ПОЗНАНИЯ

История познания сил Всемирного Тяготения началась давно. Во времена Аристотеля уже считали, что все тела стремятся к центру мира – к центру Земли.

Галилео Галилей своими опытами показал, что все тела падают с одинаковым ускорением.

Исаак Ньютон вывел закон Всемирного Тяготения. Но относительно природы тяготения он сказал: «Мне еще не удалось вывести основу свойств тяжести, а гипотез я не придумываю и придумывать не хочу».

Ломоносов создал прибор, который реагировал на изменения силы тяжести.

Ученые Кавендиш, Этвеш и Рихарц провели опыты по сравнению двух масс – гравитационной и инертной. Они измерили силу, с которой массы тяготеют друг к другу. Результаты опытов показали, что инертная масса равна гравитационной. (Гравитационная масса – это масса, вызывающая притяжение тел.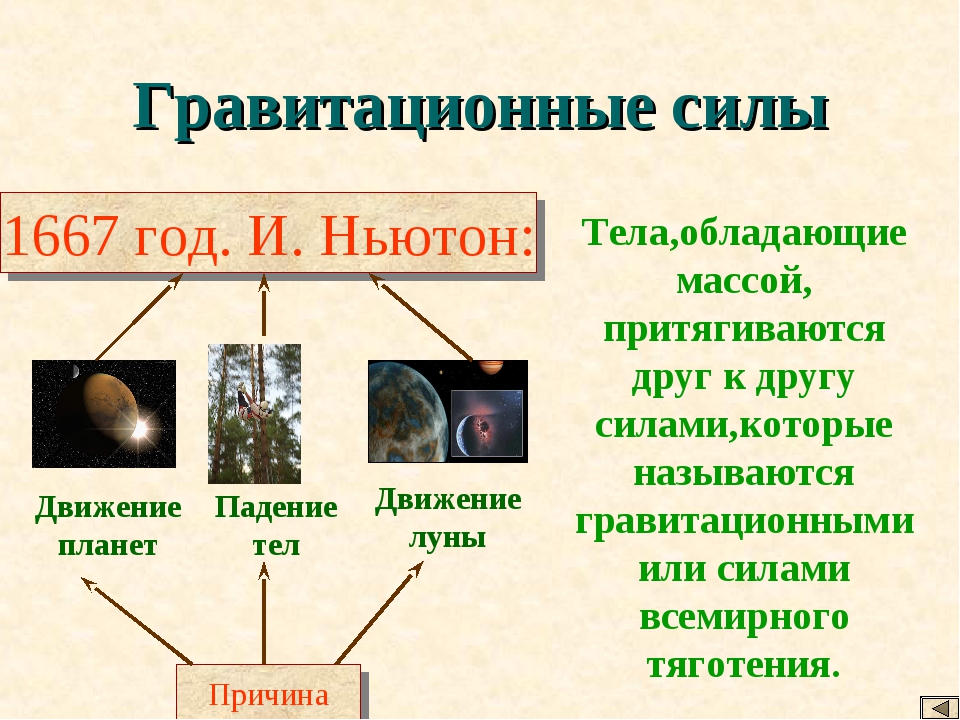 Инертная масса – масса, препятствующая ускорению тел.)

Теория дальнодействия утверждала, что тяготеющие тела действуют друг на друга мгновенно через абсолютную пустоту. Эта теория «объясняла» причины тяготения тем, что оно якобы «врожденное свойство материи».

Теория эфира считала, что силы тяготения, возникают и передаются вследствие  движений и натяжений особой,  всепроникающей упругой среды – мирового эфира.

Теория относительности Альберта Эйнштейна – это теория природы тяготения, она установила общность между силами тяготения и силами инерции. Предмет может  стремиться к дну ракеты  вследствие притяжения к земле. Однако предмет может падать и тогда,  когда  сил  тяготения нет, но ракета, движется с ускорением. В теории относительности взаимодействия между телами распространяются с определенной скоростью, равной скорости света в пустоте. Теория  относительности утверждает, что поле тяготения возникает вследствие «искривления  пространства».

Гравитационная теория считает, что силы тяготения переносятся особыми частицами тяготения – гравитонами. И вот тут-то начинаются и не заканчиваются пока еще вопросы и споры! Существуют ли все-таки гравитоны?

Мы знаем, как заслониться от электрического, магнитного и электромагнитного полей и как управлять ими.
Но можно  ли экранироваться от поля тяготения, управлять им и создавать его?

Разгадка природы сил тяготения все еще продолжается!

Явление Всемирного тяготения. Приведите примеры проявления силы тяготения

Когда учитель проводит урок физики в школе, то он часто дает следующее задание ученикам: “Приведите примеры проявления силы тяготения”. В данной статье рассмотрим, что собой представляет явление универсальной гравитации, а также покажем на примерах результат ее проявления.

Исаак Ньютон и его закон

Каждый школьник знаком с тремя законами Ньютона, которые используются для описания механического взаимодействия между телами и для изучения их движения. В данной же статье речь пойдет о законе гравитации, который также был открыт Исааком Ньютоном в конце XVII века. Не следует думать, что великий англичанин смог самостоятельно решить проблему вселенского масштаба. В действительности многие его предшественники догадывались о математической зависимости для определения силы взаимодействия между массивными телами. Заслуга же Ньютона состоит в систематизации и детальном анализе накопленного научного опыта, которые привели к появлению закона Всемирного тяготения. Соответствующая формула имеет следующий вид:

F = G*m₁*m₂/r².

Словесное ее описание следующее: сила F притяжения между телами с массами m₁и m₂прямо пропорциональна произведению их масс и обратно пропорциональна расстоянию r между ними. Величина G – это гравитационная постоянная.

Рассматривая явление тяготения и силу тяготения, следует запомнить, что она действует между абсолютно любыми телами во Вселенной, которые обладают конечной массой.

Земное притяжение

Если старшеклассник слышит слова “сила тяготения Земли”, то у него в памяти всплывает следующая формула:

F = m*g,

где g – ускорение свободного падения. Однако немногие знают, откуда берется эта формула. Получается она непосредственно из записанного выше выражения для силы F. Действительно, в случае нашей планеты следует рассматривать тело массой m и Землю массой M. Расстояние между ними приблизительно равно радиусу Земли R, тогда:

F = G*m*M /R² = m*g, где g = G*M/R².

Если в равенство для g подставить массу и радиус планеты, то получается g = 9,81 м/с².

Значение g не является постоянной величиной на Земле. В данной местности оно зависит от особенностей рельефа и наличия в земной коре полезных ископаемых и пустот. Тем не менее эти изменения составляют доли процента. С увеличением высоты g уменьшается, но даже на высоте 300-400 км оно изменяется всего на 5 %.

Примеры силы тяготения

Когда просят: “Приведите примеры проявления тяготения силы в земных условиях и в быту”, то первое, что следует назвать, – это падение любых тел вниз. Независимо от того, бросают ли вверх тело, является ли оно тяжелым или легким, отпускают ли его на некоторой высоте, оно всегда падает на землю. Траектории падения могут быть параболическими или прямолинейными, что зависит от направления начальной скорости тела.

Другой класс примеров действия силы тяжести на Земле – это появление веса у всех тел, находящихся на опоре или подвешенных на нити, пружине и так далее. Например, стакан с водой, находящийся на столе, испытывает действие силы тяжести, с которой он давит на поверхность стола. Последняя реагирует, генерируя силу, направленную вверх, которая уравновешивает силу тяжести.

Примеры силы тяготения в космосе

Если учитель просит: “Приведите примеры проявления тяготения силы в космическом пространстве”, то первым делом нужно назвать вращение нашей и других планет вокруг Солнца. Сила притяжения между звездой и ее планетами играет роль центростремительной силы, которая заставляет нашу Землю, Венеру, Марс и другие тела вращаться по некоторым замкнутым орбитам.

Сила притяжения проявляет себя также в том, что многие планеты имеют спутники, что галактики существуют как единые скопления и не рассыпаются на отдельные звезды.

Выполняя задание с формулировкой “приведите примеры проявления силы тяготения”, следует упомянуть также об отклонении от прямолинейной траектории электромагнитных волн, когда они распространяются вблизи массивных космических объектов.

1.2.6 Закон всемирного тяготения. Сила тяжести. Зависимость силы тяжести от высоты над поверхностью планеты

Видеоурок: Закон всемирного тяготения

Лекция: Закон всемирного тяготения.  Сила тяжести. Зависимость силы тяжести от высоты над поверхностью планеты

Закон гравитационного взаимодействия

До некоторого времени Ньютон не задумывался о том, что его предположения справедливы для всех тех, находящихся во Вселенной. Спустя некоторое время им были изучены законы Кеплера, а также законы, которых придерживаются тела, что свободно падают на поверхность Земли. Данные мысли не были зафиксированы на бумаге, а только остались заметки про яблоко, упавшее на Землю, а также о Луне, которая вращается вокруг планеты. Он считал, что

• все тела рано или поздно упадут на Землю;

• они падают с одинаковым ускорением;

• Луна двигается по окружности с постоянным периодом;

• размеры Луны практически в 60 раз меньше, чем у Земли.

В результате всего это был сделан вывод, что все тела притягиваются друг к другу. При этом, чем больше масса тела, тем с большей силой оно притягивает к себе окружающие объекты.

В результате этого был открыт закон всемирного притяжения:

Любые материальные точки притягиваются друг к другу с силой, увеличивающейся в зависимости от роста их масс, но при этом уменьшается в квадратной пропорциональности в зависимости от расстояния между этими телами.

F – сила гравитационного притяжения
m₁, m₂​ – массы взаимодействующих тел, кг
r – расстояние между телами (центрами масс тел), м
G – коэффициент (гравитационная постоянная) ≈ 6,67*10^-11 Нм²/кг²​​​

Данный закон справедлив в том случае, когда тела можно принять за материальные точки, а вся их масса сконцентрирована в центре.

Коэффициент пропорциональности из закона всемирного тяготения был определен экспериментальным путем ученым Г.Кавендишем. Гравитационная постоянная равна силе, с которой притягиваются килограммовые тела на расстоянии одного метра:

G = 6,67*10^-11 Нм²/кг²

Взаимное притяжение тел объясняется гравитационным полем, подобным электрическому, которое находится вокруг всех тел.

Сила тяжести

Вокруг Земли также существует такое поле, его еще называют полем земного притяжения. Все тела, что находятся в местах его действия, притягиваются к Земле.

Сила тяжести – это равнодействующая гравитационной силы, а также центростремительной силы, направленной по оси вращения.

Именно с такой силой все планеты притягивают к себе другие тела.

Характеристика силы тяжести:

1. Точка приложения: центр масс тела.

2. Направление: к центру Земли.

3. Модуль силы определяется по формуле:

F_тяж = gm
g = 9,8 м/с² – ускорение свободного падения
m – масса тела

Так как сила тяжести – это частный случай закона гравитационного взаимодействия, то ускорение свободного падения определяется по формуле:

g – ускорение свободного падения, м/с2
G – гравитационная постоянная, Нм²/кг²​​​
M₃ – масса Земли, кг
R₃ – радиус Земли

Из этого можно сделать вывод: 

• чем больше масса космического объекта, тем больше ускорение свободного падения; 

• чем больше расстояние до космического объекта, тем меньше ускорение свободного падения.  

Более того, на данную величину влияет и период вращения планеты вокруг оси.

Если тело находится на некотором расстоянии от поверхности Земли, то определить ускорение можно по следующей формуле:

Если же с увеличением высоты уменьшается ускорение, то можно сделать вывод, что сила тяжести так же уменьшается.

Сила тяжести: формула, единицы измерения, особенности

Сила тяжести и ее источник: Freepick

Разбираетесь с такой физической категорией, как сила тяжести? Формула, ее составляющие и единицы измерения укажут, что сильнее притянет Земля — яблоко или поезд. Отличается ли сила тяжести от силы тяготения? Объясним, как не перепутать эти две величины.

Что такое сила тяжести

Каждый день наблюдаем, как тела вокруг деформируются (меняют форму или размеры), ускоряются или тормозят, падают. В реальной жизни с различными телами происходят самые разнообразные вещи. Причина всех действий и взаимодействий кроется в некой силе. О чем идет речь?

Понятие силы

Силой называют физическую векторную величину, которая оказывает воздействие на тело, а ее источниками становятся другие тела. Что означает понятие векторной величины? Это говорит о том, что сила наделена направлением. В зависимости от того, куда она направлена, можно получить разные результаты.

Это как если стоять на вершине горы на сноуборде, то от направления толчка будет зависеть дальнейшее движение. Таков результат приложения силы в этом случае. Силы, которые изучают ученые-физики, разнообразны и очень важны для нашей повседневной жизни.

Определение и значение силы тяжести

Одна из них носит название сила тяжести. Физика предлагает следующее определение: сила тяжести — это величина, которая показывает, насколько сильно Земля притягивает тело, которое расположено на ее поверхности или рядом с ней. Таким образом, направление этой силы — центр нашей планеты.

Сила тяжести на Земле крайне важна по следующим причинам:

• Наша планета притягивает все, что попадает в сферу действия этой силы, будь то твердое тело, жидкость или газ.
• Благодаря ее существованию стало возможным создание атмосферы (молекулы газов, которые ее составляют, не улетают в космические просторы), появились и остаются на своих местах моря и океаны.
• Любой предмет, который приподнимаем и роняем, обязательно упадет вниз по направлению к Земле.

Кстати, именно из-за воздействия этой силы люди не могут летать. Самостоятельно развить скорость, на которой полет становится возможным (так называемую первую космическую) человек не способен, а потому в обычной жизни всегда твердо стоит ногами на Земле.

Сила тяжести и сила тяготения: отличия

Падение перьев как пример силы тяжести: Freepick

Сила тяжести, определение которой дали выше, схожа с силой тяготения. Оба варианта связывает сила притяжения.

Однако эти две силы не одно и то же, хоть их и часто путают. Давайте разберемся, в чем тут дело.

Еще в 1682 году Исаак Ньютон открыл закон о всемирном тяготении. Сформулирован он был так: тела притягивают друг друга, а сила этого тяготения — величина, прямо пропорциональная произведению их масс и обратно пропорциональна расстоянию, возведенному в квадрат.

Математически силу тяготения записывают так: F = G×M×m/R², где:

• F — сила тяготения, Н;
• M — масса первого тела (часто планеты), кг;
• m — масса второго тела, кг;
• R — дистанция между ними, м;
• G — постоянная величина (G = 6,67×10⁻¹¹ м³×кг⁻¹×с⁻²).

Продемонстрировать эту силу легко — достаточно встать на весы. Стрелка сразу же отклонится, показывая вес тела. Так происходит из-за очень большой массы Земли, благодаря которой мы придавлены к ней. На Луне, масса которой меньше, вес человека меньше в несколько раз.

Итак, закон о всемирном тяготении и соответствующая сила необходимы для вычисления силы взаимодействий между разнообразными телами. При этом их размеры должны быть меньше, чем расстояние между ними.

Теперь вернемся к нашей теме и рассмотрим подробно, что же такое сила тяжести, обозначение которой дали выше, и как она связана с силой тяготения.

Сила тяжести: формула, единицы измерения

Напомним, что когда говорим о силе тяжести, то имеем в виду силу, с которой осуществляет притяжение наша планета.

Формула силы тяжести такова: F = m×g, где:

• F — сила тяжести, Н;
• m — масса тела, кг;
• g — ускорение свободного падения, м/с².

В этой формуле видим новую величину — ускорение свободного падения. Так называют ускорение, которое приобретает тело рядом с Землей во время свободного и беспрепятственного падения. Рядом с поверхностью Земли значение этой величины примерно равняется 9,81 м/с², а в приблизительных расчетах используют округленное значение 10 м/с².

По этой формуле рассчитывается сила тяжести, единица измерения которой — Ньютоны (в честь Исаака Ньютона).

Капл дождя падают на Землю благодаря силе тяжести: Freepick

Чему равна сила тяжести? Глядя на эту формулу, можно сказать, что сила тяжести схожа с весом тела. В покое на Земле эта величина и вес будут идентичны. Но это не одно и то же. Почему? Объяснение не сложное:

• Силой, с которой на тела действует Земля, называют силу тяжести.
• Вес тоже сила, с которой тела действуют на опору.
• То есть у них отличаются точки действия: первая направлена на центр массы тел, а вес направлен на опору.

Кроме того, на величину силы тяжести влияет масса и планета, на которой проводятся измерения. Вес определяется также ускорением, с которым происходит движение тела и опоры.

К примеру, вес тела в лифте определяется тем, в каком направлении и как быстро происходит движение тела. Сила тяжести не учитывает, куда и что движется: эти внешние факторы на нее не влияют.

Итак, с весом разобрались. А что же с силой тяготения, которую упоминали выше? Можем ли две эти силы приравнять? На этот раз ответ будет утвердительным. Но только, когда мы говорим о Земле и теле, которое к ней притягивается. В этом случае обе силы будут равны.

Выразим это математически:

• F = m×g.
• F = G×M×m/R².
• m×g = G×M×m/R².

Если обе части полученного уравнения разделить на массу, то получим такую формулу: g = G×M/R².

Величина g (ускорение свободного падения) уникальна для каждой планеты:

1. На нашей Земле свободно падающее тело с каждой секундой ускоряется примерно на 9,81 метр (м/с²).
2. Ускорение свободного падения рядом с Луной имеет величину всего 1,62 м/с².
3. На Юпитере это значение достигает 26,2 м/с². Человек, который весит 60 кг, на этой планете почувствует себя так, будто бы поправился на 100 кг.

Как изменится величина, если тело будет падать 4 секунды? Попробуем подсчитать:

• Скорость падения в начальной точке составит 0 м/с².
• В течение первой секунды она увеличится до 9,81 м/с².
• За вторую секунду величина вырастет вдвое и составит 19,62 м/с².
• Третья секунда добавить еще одну величину ускорения и получится 29,43 м/с².
• В четвертую секунду скорость движения тела достигнет 39,24 м/с², что равняется приблизительно 141 км/ч.

Отметим, что яблоко и кирпич будут падать с равной скоростью. Только очень легкие предметы во время падения замедляет воздух, оказывая им ощутимое сопротивление. Так, птичье перышко будет совершать падение очень медленно и плавно.

Задумываемся об этом или нет, на каждого из нас оказывает воздействие сила тяжести. Формула ее расчета состоит из массы, умноженной на величину ускорения свободного падения. Эта сила показывает воздействие планет на тела, которые находятся рядом с их поверхностями. Поэтому ее величина отличается на Земле и на Луне.

Оригинал статьи: https://www.nur.kz/family/school/1909020-sila-tyazhesti-formula-edinitsy-izmereniya-osobennosti/

Урок физики по теме “Сила. Явление тяготения. Сила тяжести”

Цель: ввести силу, как меру взаимодействия тел.

Задачи: ввести формулу нахождения силы тяжести; учить решать задачи на нахождение силы тяжести; продолжать работу с кратными и дольными единицами; совершенствовать умения познавательной деятельности – умение наблюдать и объяснять результаты экспериментов; расширить кругозор учащихся.

Оборудование: компьютер, мультимедиапроектор, презентация, экран, брусок, 3 шара разного объема; шарик, подвешенный на нити; брусок; спички; Лукашик «Сборник задач по физике 7-9 кл», листы по теме «Сила».

Демонстрации: опыт с неподвижным бруском, опыт с шарами, взаимодействие шаров при столкновении, демонстрация падения шарика после пережигания нити.

Ход урока

Этап урока	Время	Деятельность педагога	Деятельность учащихся
Организационный момент.	2 мин.	Приветствие, проверка готовности учащихся к уроку.	Приветствие, запись даты, темы урока.
Анализ итогов контрольной работы №1.	5 мин.	Анализ контрольной работы (указывает типичные ошибки при решении задач).	Выполняют работу над ошибками.
Актуализация.	4 мин.	Постановка проблемы, демонстрация опытов.	Наблюдают за проведением опыта, составляют отчет, формулируют вывод.
Новый материал.	20 мин.	Объяснение нового материала; демонстрация опытов.	Внимательно слушают, делают записи по ходу объяснения; наблюдают за проведением опыта, формулируют вывод.
Закрепление. Решение задач.	7 мин.	Фронтальный опрос; Объясняет решение задач по теме.	Работа с учебной литературой; решают задачи на нахождение массы и силы тяжести.
Итог урока. Домашнее задание.	2 мин.	Рефлексия. Итог урока. Домашнее задание.	Заполняют лист рефлексии. Записывают домашнее задание.

I. Организационный момент.

Здравствуйте, ребята! Открываем тетради и записываем в тетради дату и тему урока. (Слайд 1)

II. Анализ контрольной работы.

– Как рассчитать массу тела?

– Как рассчитать плотность?

Решение задач №3.16, №3.20.

III. Актуализация.

(Слайд 2)

Однажды М. Фарадей произнес: «Как это удивительно обнаружить, что все явления природы управляются столь небольшим числом сил!».

Сегодня, мы познакомимся с понятием силы и познакомимся с явлением тяготения.

Как вы считаете, при каком условии тело будет неподвижным?
– Если на него не действуют другие тела.

Опыт 1. Опыт с неподвижным бруском.

Задание учащимся: внимательно наблюдать за проведением опыта. Составить отчет по данному опыту. Схема отчета представлена на слайде. (Слайд 3)

Вывод: если на неподвижный брусок, лежащий, на опоре, не действуют другие тела, кроме Земли и опоры, он не изменит своего положения.

Определим, при каком условии тело изменит свою скорость?

Опыт 2. Опыт с шарами. Взаимодействие шаров при столкновении.

Вывод: если скорость тела изменяется, мы всегда обнаруживаем действие на него другого тела.

Под действием силы, которая действует на тело, тело может изменить форму и размер.

Любое изменение формы и размера тела называется деформацией. (Слайд 4)

Рассмотрим виды деформаций: кручение, изгиб, сжатие, растяжение, сдвиг и срез.

IV. Изучение нового материала.

Дадим определение силы и запишем его в тетради:

Сила – векторная величина, мера взаимодействия тел между собой.

– Как вы считаете, почему сила векторная величина? (Сила имеет направление)

Обычно направление силы указывают стрелкой. Силу принято обозначать F. Сила приложена к определенной точке тела. (Слайд 5)

Сила характеризуется:

1. числовым значением;
2. направлением в пространстве;
3. точкой приложения.

(Слайд 6)

За единицу силы в системе СИ принят 1 Н – в честь великого английского ученого Исаака Ньютона.

Сила в 1Н – такая сила, которая за 1 с изменяет скорость на 1 м/с.

Кратными и дольными приставками единицы силы являются:
1 кН = 1000 Н
1мН = 0,001 Н
1 МН = 1000000Н

Камень падает на Землю потому, что его притягивает Земля. Камень тоже притягивает Землю. Силы взаимодействия между камнем и Землей – это силы всемирного тяготения. Приведите примеры силы всемирного тяготения. (Земля притягивает Луну, в свою очередь Луна притягивает Землю и т.д.)

Все тела, которые находятся на Земле, либо у ее поверхности, всегда испытывают действие хотя бы одной силы, о природе которой мы будем вести разговор после демонстрации опыта.

Опыт 3. Демонстрация падения шарика после пережигания нити.

Все тела на Земле или у ее поверхности испытывают влияние земного притяжения. С явлением тяготения каждый знаком с раннего детства.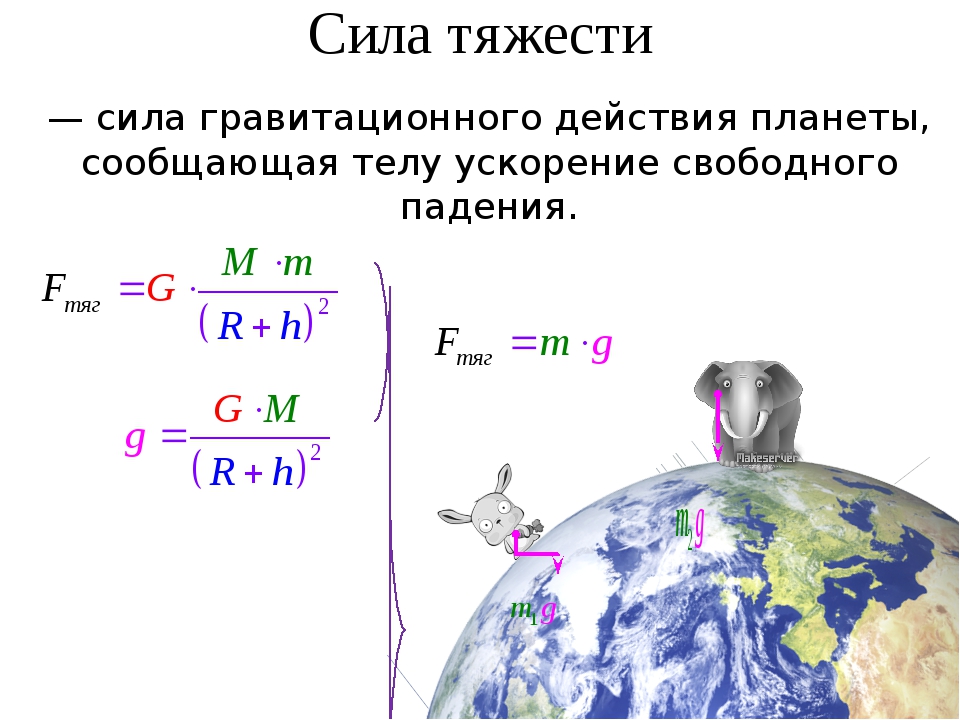 Например, падение капель дождя, падение мяча. Приведите свои примеры.

(Слайд 7)

Та сила, с которой Земля притягивает к себе тело, называется силой тяжести. Она обозначается F_т.

Силу земного притяжения можно найти по формуле:
F_т = mg, где g – ускорение свободного падения;
g = F_т/m     [g] = [Н/кг]
на экваторе – 9,78 Н/кг;
на полюсе – 9,83 Н/кг.

При решении задач ускорение свободного падения можно принимать 10 Н/кг. Сила тяжести всегда направлена вниз.

V. Закрепление. Решение задач.

(Слайд 8, 9)

Найдите ответы на поставленные вопросы в учебнике.

1. Что такое сила?
2. Что называют всемирным тяготением?
3. Какая сила называется силой тяжести?
4. Запишите формулу силы тяжести.
5. Запишите формулу для нахождения массы тела.
6. 5 кН = ?Н; 6,7 кН = ? Н; 5,4 МН = ? Н; 3 мН = ? Н; 8000 Н = ? кН; 5600 Н = ? кН.

Открываем сборник задач по физике на стр. 44, №348.
Прочитайте задачу. Что известно? Что надо найти?

Дано:
F_т = 392 Н
g = 10 Н/Кг
m = ?
Решение:
m = F_т/g
m = 392 Н / 10 Н/кг = 39,2 кг
Ответ: 39,2 кг.

(Слайд 10) Решите задачу №336.

– Что вы знаете об этих животных?

Зайцы – семейство млекопитающих отряда зайцеобразных. Ок. 50 видов, в т. ч. беляк, русак, кролик. Детеныши зайцев появляются на свет на голой земле, зрячие, покрытие шерстью. Уже в возрасте нескольких дней могут самостоятельно передвигаться. Кролики живут в норах колониями. Детеныши рождаются голыми, слепыми, беспомощными.

Волк – род хищных млекопитающих семейства волчьих. 7 видов: волк, шакал, койот, рыжий волк, домашняя собака. На территории России 2 вида — волк и шакал. Волки – санитары леса.

Медведь – семейство млекопитающих отряда хищных, самые крупные из современных хищных зверей; включает 8 видов, в том числе бурый медведь, губач, белый медведь, белогрудый медведь, барибал, малайский медведь, очковый медведь. Длина тела современных медведей 110–300 см, высота в холке до 135 см, масса до 700 кг. Тело мощное.

Носорог – семейство млекопитающих отряда непарнокопытных, включает четыре рода, в которые входят пять видов — белый, черный, яванский, суматранский и индийский носороги. Длина их тела около 2-4 м, хвоста 60-76 см, высота в холке 1-2 м, вес до 3,6 т.

Слон – Самые крупные современные наземные млекопитающие. Длина тела до 7,5 м, высота до 4-4,5 м, масса до 7,5 т. На коротких дистанциях могут развивать скорость до 40 км/ч. Хорошо развиты обоняние, слух и звуковая коммуникация. Продолжительность жизни 50-60 лет.

VI. Итог урока. Домашнее задание. (Слайд 11)

Сегодня на уроке я узнал (а)__________________________
Хотел (а) бы узнать о________________________________

Д/з. § 23,24; лист «Сила» В. 1,2.;
Практическая часть упр.9 (1, 3).

Что такое гравитационная сила? – Вселенная сегодня

Закон всемирного тяготения Ньютона используется для объяснения силы тяготения. Этот закон гласит, что каждая массивная частица во Вселенной притягивает каждую другую массивную частицу с силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Этот общий физический закон был выведен из наблюдений, сделанных методом индукции. Другой способ, более современный способ сформулировать закон: «Каждая точечная масса притягивает каждую другую точечную массу силой, направленной вдоль линии, пересекающей обе точки.Сила пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния между точечными массами.

Нас окружает гравитационная сила. Это то, что определяет, сколько мы весим и как далеко баскетбольный мяч пролетит, когда его бросят, прежде чем он вернется на поверхность. Сила гравитации на Земле равна силе, которую Земля оказывает на вас. В состоянии покоя, на поверхности Земли или вблизи нее, сила тяжести равна вашему весу. На другом астрономическом теле, таком как Венера или Луна, ускорение свободного падения отличается от земного, поэтому, если вы встанете на весы, это покажет вам, что вы весите другое количество, чем на Земле.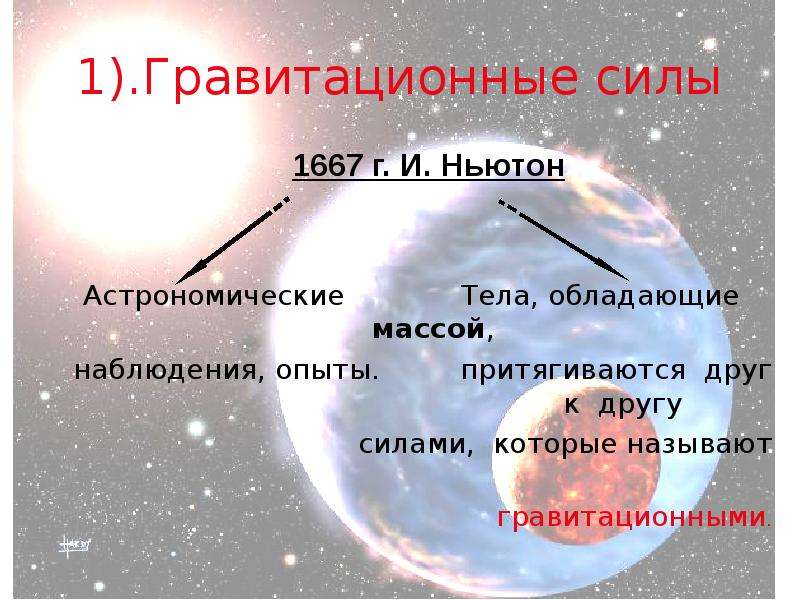

Когда два объекта гравитационно заблокированы, их сила тяжести сосредоточена в области, которая находится не в центре любого объекта, а в барицентре системы. Принцип похож на качели. Если два человека с очень разным весом сидят по разные стороны от точки равновесия, более тяжелый должен сидеть ближе к точке равновесия, чтобы они могли уравнять массу друг друга. Например, если более тяжелый человек весит вдвое больше, чем более легкий, он должен сидеть только на половине расстояния от точки опоры.Точка баланса – это центр масс качелей, так же как центр тяжести – это точка баланса системы Земля-Луна. Эта точка фактически движется вокруг Солнца по орбите Земли, в то время как Земля и Луна движутся по своим орбитам вокруг барицентра.

Каждая система в галактике и, предположительно, во Вселенной имеет барицентр. Толчок и притяжение гравитационной силы объектов – это то, что удерживает все в космосе от столкновения друг с другом.

Мы написали много статей о силе тяготения для Вселенной сегодня. Вот статья о гравитации в космосе, а вот статья об открытии гравитации.

Если вам нужна дополнительная информация о гравитации, ознакомьтесь с «Постоянное притяжение гравитации: как это работает?», А вот ссылка на статью «Гравитация на Земле и гравитация в космосе: в чем разница?».

Мы также записали целый эпизод Astronomy Cast, посвященный гравитации. Послушайте, Эпизод 102: Гравитация.

Как это:

Нравится Загрузка …

Сила тяжести – обзор

10.3.4.2 Методы упругих элементов

Помимо гравитационных сил, создаваемых калиброванными массами, следующей наиболее интуитивно понятной и распространенной технологией, используемой для создания калиброванных сил, является упругий элемент с известной жесткостью пружины. Элемент, например консольная или винтовая пружина, отклоняется испытательной силой. Отклонение измеряется либо внешней системой, такой как интерферометр, либо бортовым устройством микроэлектромеханической системы (MEMS), например пьезоэлектрическим элементом. С помощью жесткости пружины, предварительно определенной с помощью отслеживаемого прибора, такого как баланс электростатических сил, можно рассчитать величину испытательного усилия.Таким образом передается калибровка силы.

В нескольких примерах упругих элементов используются модифицированные кантилеверы AFM, поскольку они имеют соответствующий размер и эластичность, имеют более простую геометрию, чем нестандартные конструкции, и, следовательно, моделируются более надежно и, как правило, хорошо понимаются специалистами в отрасли. Очень тонкие кантилеверы, производство которых сейчас возможно, имеют достаточно низкую жесткость пружины, чтобы, в принципе, можно было измерять силу на уровне наноньютонов.

Калибровка жесткости пружины кантилевера AFM обсуждается в разделе 7.3.6. Здесь будут описаны другие методы упругих элементов, которые не обязательно зависят от АСМ. Чтобы обеспечить подходящую производительность в рабочем диапазоне, обычно одной жесткости пружины недостаточно.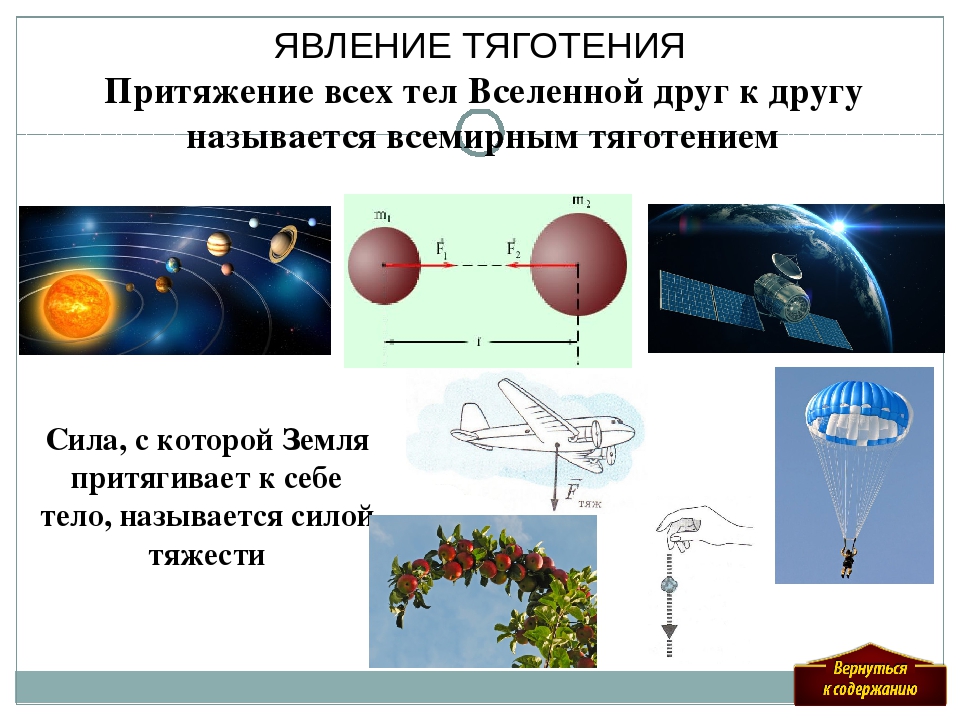 Обычно конструируют устройства, содержащие элементы с диапазоном жесткости пружины. Это может быть достигнуто двумя способами с помощью консольных устройств. Используется либо массив кантилеверов с прикрепленными зондами или отдельными точками зондирования, либо один консоль с несколькими определенными точками зондирования.Пример первого, названный «массив эталонных кантилеверов», был разработан в NIST [44] и показан на рисунке 10.5. Массивы, изготовленные из монокристаллического кремния, содержат консоли с расчетными номинальными значениями жесткости пружины в диапазоне 0,02–0,2 Н · м ^–1 . Изменения резонансной частоты менее 1% сообщаются для одних и тех же кантилеверов в изготовленных партиях как показатель однородности. Константы пружины были проверены на балансе электростатических сил NIST.Для неследящей калибровки АСМ коммерчески доступны консольные решетки. Однако их путь к отслеживанию значительно снижает их точность и указанные неопределенности.

Рисунок 10.5. Экспериментальный образец эталонного консольного массива – вид сверху.

Поскольку простые устройства, описанные в этом разделе, являются пассивными, они потребуют вдавливания в LFB с помощью исполнительной системы и некоторых внешних средств измерения отклонения. Это второе требование важно, поскольку оно зависит от метрологии смещения целевого прибора.Погрешность работы этих устройств выше, чем у кантилеверов активного типа, и их можно лучше калибровать с помощью такого артефакта активного типа.

Альтернативой массивам высококачественных пассивных консолей, рассмотренным выше, является одиночный консоль со встроенной метрологией отклонения. Их можно использовать для калибровки целевых инструментов или более дешевых одноразовых артефактов с низкой точностью. Один из первых примеров зонда АСМ со встроенным пьезорезистивным датчиком отклонения обсуждается в [4].[45]. Устройство было изготовлено как единый пьезорезистивный деформационный элемент с остроконечной кантилеверной геометрией. Исследователи заявляют о вертикальном разрешении 0,01 нм, что эквивалентно 1 нН с жесткостью пружины 10 Н · м ^-1 для этого экспериментального устройства.

Ряд пьезорезистивных кантилеверов был разработан несколькими НМИ. NPL разработала консольную сборную матрицу эталонных пружин (C-MARS) как часть набора микроизготовленных устройств с упругими элементами, предназначенных для прослеживаемой калибровки АСМ [46].Относительно большой кантилевер (ширина 150 мкм × длина 1600 мкм) помечен реперными точками, которые в принципе позволяют точно выровнять точку контакта для калибровки кантилевера по кантилеверу. На размер реперных точек влияет поле зрения 100 мкм × 100 мкм типичных АСМ. Поверхностные пьезорезисторы рядом с основанием кантилевера позволяют при необходимости контролировать смещение и колебания кантилевера. Деталь устройства представлена ​​на рисунке 10.6. Константы пружины указаны для взаимодействия для каждого реперного знака, обеспечивая диапазон 25–0.03 Н · м ⁻¹ . NIST также разработал консольное устройство с тонкими ножками у корня, чтобы сконцентрировать изгибы в этой области корня и реперные отметки по его длине [47].

Рисунок 10.6. Изображения устройства NPL C-MARS с деталями его реперных отметок; оксидные квадраты размером 10 мкм образуют двоичную систему нумерации вдоль оси симметрии.

Исследователи из PTB создали пьезорезистивный кантилевер немного большего размера, шириной 1 мм и длиной несколько миллиметров, для использования в наноиндентировании и работе с текстурой поверхности [48].Компания PTB также создала пример сферического зонда с двумя ножками и пример зонда с одним наконечником. Прототипы, изготовленные с использованием стандартной технологии объемной микрообработки кремния, имеют диапазон жесткости 0,66–7,7 Н · м ^–1 . Сообщалось о весьма линейной зависимости между выходным напряжением датчика и силой зондирования в диапазоне микроньютонов.

В режиме непрерывного сканирования измерительный наконечник пьезорезистивного кантилевера, такого как устройство NIST, можно медленно перемещать по балке кантилевера с регулярной регистрацией значений отклонения луча и внешней силы. Насечки с четко определенными положениями проявляются как разрывы на записанной кривой «сила-смещение» и действуют как шкала для точного определения положения наконечника зонда по данным. Результатом является функция, которая описывает жесткость пружины артефакта передачи после измерения с помощью LFB. Для взаимодействия с балансом электростатических сил, работающим в режиме с нулевым положением, такое устройство необходимо вставить в наконечник баланса.

Физики все же измеряют гравитационную силу между самыми маленькими массами

Физик Маркус Аспельмейер хорошо помнит тот день, почти десять лет назад, когда посетитель его лаборатории заявил, что гравитационное притяжение его офисного кресла слишком мало для измерения.Измеримая или нет, эта сила, безусловно, должна существовать. Еще со времен работы Исаака Ньютона в 1687 году физики поняли, что гравитация универсальна: каждый объект оказывает на все вокруг гравитационную силу, пропорциональную своей массе. Комментарий посетителя был призван вернуть на Землю все более причудливую беседу, но Аспельмейер, профессор Венского университета, воспринял это как вызов. «Мое решение было:« Хорошо, я собираюсь не только измерить гравитационное поле этого стула, но и мы будем маленькими, маленькими, маленькими! »- вспоминает он.

Исследование, начатое в тот день, принесло первый результат: измерение силы тяжести между двумя крошечными золотыми сферами, каждая размером с кунжутное семя и весящей не меньше четырех зерен риса – наименьших масс, сила тяжести которых был измерен на сегодняшний день. Результаты, опубликованные сегодня в журнале Nature № , на один шаг приближают физиков к далекой цели – примирить гравитацию с квантовой механикой, теорией, лежащей в основе всей негравитационной физики.

Точность силы тяжести

Трудно представить, насколько необычайно слабая гравитация для таких малых масс. Гравитационное притяжение одной сферы («исходная масса») на другую («пробная масса») в нескольких миллиметрах от нас более чем в 10 миллионов раз меньше, чем сила падающей снежинки. Основная задача, стоящая перед командой Аспельмейера, заключалась в разработке детектора, чрезвычайно чувствительного к этой гравитационной силе, но совершенно нечувствительного к гораздо большим фоновым силам, толкающим и тянущим испытательную массу со всех сторон.

Исследователи достигли этой чувствительности с помощью детектора, называемого торсионным маятником, который выглядит как миниатюрная версия мобильного телефона, висящего над детской кроваткой. Сфера с пробной массой прикреплена к одному концу тонкого стержня, который подвешен в середине на кварцевом волокне толщиной четыре микрона. Аналогичная сфера на другом конце стержня действует как противовес. Сила, действующая на испытательную массу, заставляет маятник кручения вращаться до тех пор, пока он не уравновесится возвращающей силой от скручивания волокна.Такое тонкое волокно чрезвычайно податливо, поэтому даже очень слабая сила приводит к относительно большому вращению. Что особенно важно, торсионный маятник очень нечувствителен к силам от удаленных объектов, которые вместе тянут испытательную массу и противовес и, таким образом, не вызывают вращения.

Гравитацию можно понять как возникшую в результате искривления пространства-времени, что показано на снимке этого художника. Предоставлено: Arkitek Scientific

. Но даже эта продуманная конструкция торсионного маятника не полностью изолировала испытательную массу от оживленной городской среды дневной Вены.«Сладкие места всегда с полуночи до 5 утра, когда на улице нет людей», – объясняет Аспельмейер. «[Но] этого не было в пятницу или субботу».

Чтобы измерить гравитационную силу массы источника, исследователи не просто поместили его рядом с исследуемой массой. Вместо этого они непрерывно перемещали его вперед и назад со средним расстоянием в несколько миллиметров. Этот метод, называемый модуляцией, неявно используется в конструкции сигналов поворота и мигающих велосипедных огней: регулярные периодические сигналы гораздо более заметны на фоне постоянно присутствующего фонового шума, чем постоянные.Разумеется, ученые наблюдали колебательную силу именно с нужной частотой. Затем они повторили этот процесс много раз, изменяя среднее расстояние между массами и измеряя силы всего 10 фемтоньютон на расстоянии от 2,5 до 5,5 миллиметров.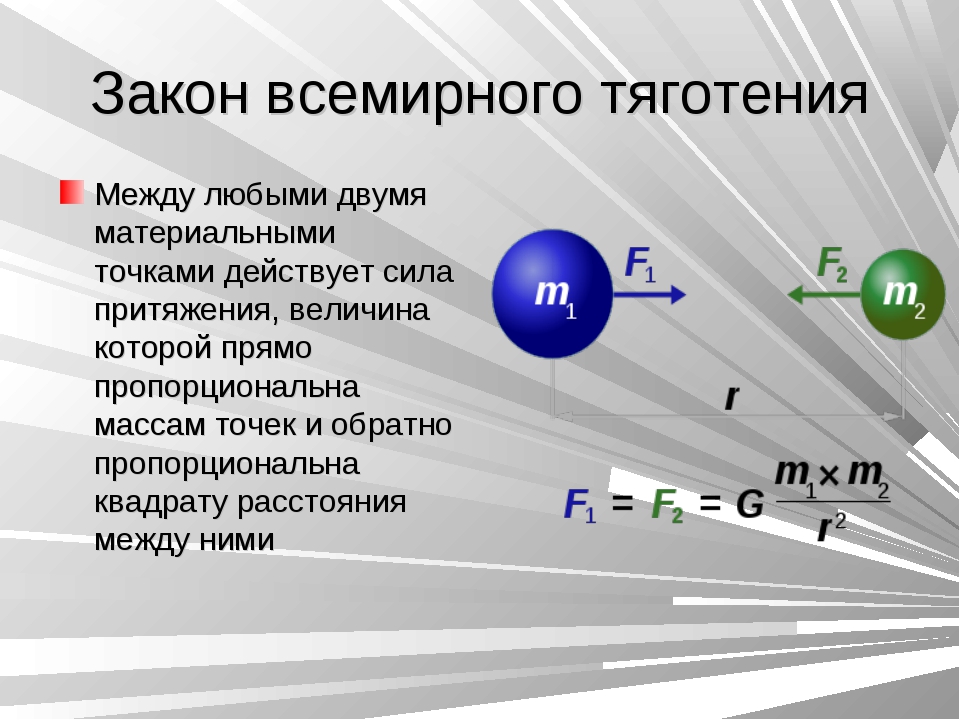 Команда сравнила эти измерения со знаменитым законом обратных квадратов Ньютона, который описывает, как сила тяготения между двумя объектами зависит от их разделения: данные соответствовали закону Ньютона с точностью до 10 процентов.

«[То, что] вы можете измерить эти действительно, действительно, очень крошечные силы – я думаю, это довольно удивительно», – говорит Стефан Шламмингер, физик из Национального института стандартов и технологий, который изучает гравитацию, но не принимал участия в работе. .

Но Аспельмейер и его коллеги еще не могли объявить о победе: им все же пришлось исключить возможность того, что модуляция массы источника порождает другие силы на испытательной массе, которые будут колебаться с точно такой же частотой.Периодическое раскачивание стола, поддерживающего экспериментальный прибор, вызванное отдачей от едва видимого движения массы источника, было лишь одним из множества факторов, мешающих исследованию, которые исследователи должны были тщательно определить количественно.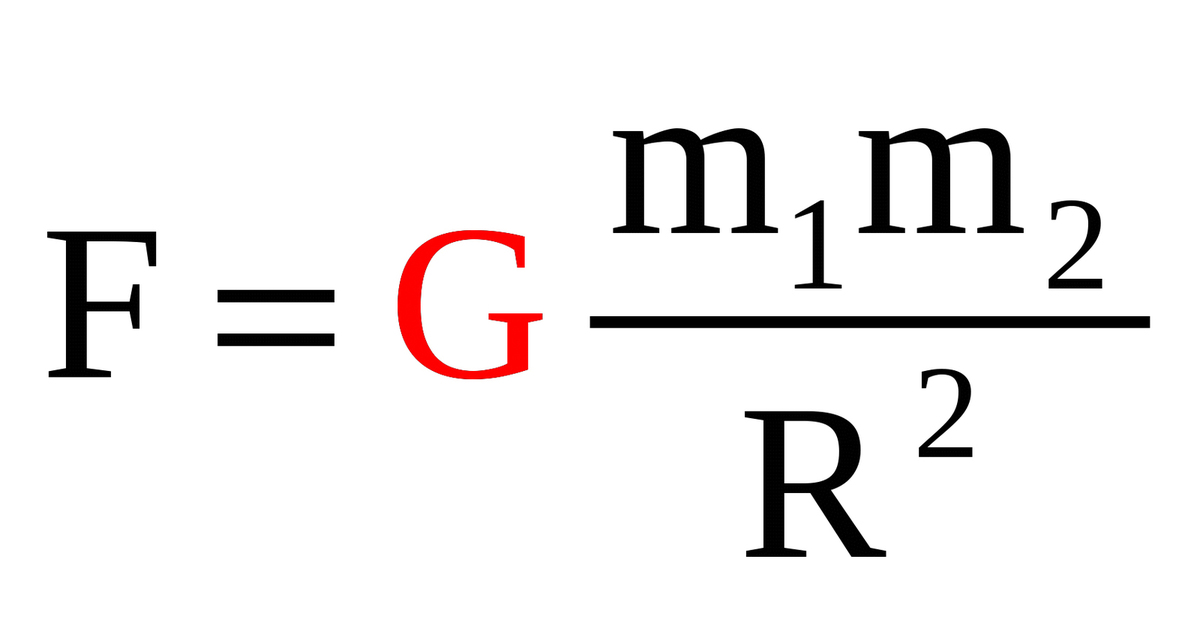 В конце концов они обнаружили, что все известные негравитационные силы будут как минимум в 10 раз меньше, чем гравитационное взаимодействие.

Достижение квантовых масштабов

Аспельмейер считает, что усовершенствованный торсионный маятник будет чувствителен к гравитации масс, которые в 5000 раз меньше – легче, чем одна ресница.Его конечная цель – экспериментально проверить квантовую природу гравитации – вопрос, который ставит физиков в тупик почти столетие. Квантовая механика – одна из самых успешных и точно проверенных теорий во всей науке: она описывает все, от поведения субатомных частиц до физики полупроводников, которая делает возможными современные вычисления. Но попытки разработать квантовую теорию гравитации неоднократно блокировались противоречивыми и бессмысленными предсказаниями.

Частицы, описываемые квантовой механикой, ведут себя удивительно нелогичным образом.Один из самых странных видов квантового поведения – это особая форма корреляции, называемая сцеплением: когда две частицы запутываются, их судьбы становятся неразрывно связанными, и их невозможно описать по отдельности. Запутанность и другие квантовые эффекты наиболее заметны в очень маленьких и хорошо изолированных системах, таких как атомы и молекулы, и они становятся все более хрупкими в больших масштабах, где важна гравитация. До недавнего времени казалось, что проверка квантовой гравитации выходит за рамки лабораторных экспериментов.

Но за последние несколько лет мы стали свидетелями заметного экспериментального прогресса в обнаружении тонких квантовых эффектов во все более крупных системах. В конце 2017 года две группы физиков-теоретиков независимо друг от друга предложили амбициозный, но, возможно, осуществимый эксперимент, который мог бы сделать окончательное утверждение о квантовой природе гравитации. Эти усилия позволят измерить, может ли гравитация запутать две квантовые частицы. Если это так, то «никуда не деться от того факта, что это должно быть в некотором смысле неклассическим», – говорит Кьяра Марлетто, физик-теоретик из Оксфордского университета, соавтором одного из предложений со своим оксфордским коллегой Влатко Ведралом. .

Наблюдение гравитационного запутывания было бы новаторским. Но для убедительной демонстрации того, что гравитация является квантово-механической, потребуется доказать, что две частицы взаимодействовали только посредством гравитации. Попытки Аспельмейера изолировать гравитационные силы между постепенно уменьшающимися массами – важный шаг к такому окончательному испытанию. «Поскольку квант движется от малого к большему, есть шанс, что гравитация и квант встретятся где-то посередине», – говорит Сугато Бозе, физик-теоретик из Университетского колледжа Лондона, который вместе с девятью соавторами написал другое предложение.

«Вопрос о том, является ли гравитация принципиально квантовой, является экспериментальным вопросом», – говорит Аспельмейер. «Нам не терпится пройти все девять ярдов и посмотреть, как все обернется».

Документ без названия

Гравитационная сила

Обычно называют гравитацией, важно поощрять использование правильного термина, гравитационная сила. В отчете исследования SPACE Силы (Рассел и др., 1998) определяют этапы развития детей. понимание гравитационной силы и связанных с ней явлений.Это дает полезную основу для рассмотрения и разработки собственных идеи.

Сила гравитации удерживает предметы на земле и останавливает их уплывает

На самом простом уровне это утверждение описывает наиболее очевидные явление, связанное с силой тяжести. Фильм космонавтов в невесомости или ситуации с низкой гравитацией ясно показывают, что происходит, когда сила тяжести не тянет с той силой, которая нам знакома

Гравитационная сила – это свойство Земли и, следовательно, притяжение снизу

Притяжение силы тяжести направлено к центру Земли

В обоих случаях важно слово «тянуть», так как оно начинает увести детей от распространенного заблуждения о том, что сила тяжести действует как клей.

Второе утверждение явно основано на первом и проиллюстрировано детским рисунком Земли в разрезе со стрелками, указывающими направление действия гравитационной силы, которое украшает недавний Национальный Цели учебной программы (стр. 22). Восприятие нашим обществом географических Север над географическим югом приносит пользу как детям, так и взрослым. неспособность избавиться от интуитивного представления о том, что жители Австралии должны отвалится!

Величина силы тяжести зависит от массы объект, притягиваемый Землей

Размер этой силы равен весу объекта

Эти связанные утверждения являются корнем большей части трудностей. что люди связывают с пониманием силы тяжести.Дети и взрослым, столкнувшимся с этим утверждением, трудно понять, как гравитационная сила Земли знает, что она должна тянуть большую массу с большая сила, чем меньшая масса.

Чтобы прояснить это, возьмем простую модель частиц. материя, которая визуализирует, что все объекты состоят из разного количества единиц массы (т.е. каждая единица массы одинакова). Логично, что гравитационный сила будет притягивать каждую единицу массы с одинаковой степенью силы.Следует что объект, состоящий из двух единиц массы, будет тянуться вдвое сильнее, чем объект состоит только из одной единицы массы.

Эта же модель помогает преодолеть трудность понимания почему, если это так, объекты разной массы ускоряются в направлении Земля с такой же скоростью (при условии, что эффекты сопротивления воздуха не учитываются). Этот противоречит широко распространенному заблуждению о том, что тяжелые предметы падают быстрее легких (даже во время экспериментов, роняющих такие предметы, как испорченные бумажные шарики и стальные килограммовые массы доказывают обратное).Гравитационный сила тянет на каждую единицу массы с постоянной силой, что приводит к постоянному ускорение (увеличение скорости примерно на 10 метров в секунду каждую секунду). Независимо от того, притягивает ли он одну единицу массы или тысячу единиц массы, это постоянство ускорения остается прежним.

[Эти две идеи о больших гравитационных силах на больших массах объекты и постоянство ускорения из-за притяжения силы тяжести независимо от массы запутались, конечно, из-за воздействия сопротивление воздуха падающим предметам.Об этом пойдет речь в разделе, посвященном трение и сопротивление воздуха.]

Понятие единицы массы как постоянной величины независимо от силы тяжести действует или нет, также помогает нам различать массу и вес. Объекты масса определяется количеством составляющих ее единиц массы. Его вес определяется степенью действия на него гравитационной силы. На земле объект массой 100 грамм притягивается к центру планеты с силой 1 Ньютон.Говорят, что это вес объекта (т. Е. нисходящая сила, которую он оказывает, потому что на него действует гравитационная сила). В пространство, где есть пренебрежимо малая гравитация, сила, действующая на объект, практически nil, поэтому объект, сохранив массу 100 грамм, теперь невесом.

Сила притяжения на Луне меньше, чем на Земле

Луна – это меньший по размеру объект, чем Земля, и меньшая масса.Как следствие, его гравитационное поле тянет только с силой около пятая часть земного. Объект массой 100 грамм и весом 1 Ньютон. на Земле будет весить всего 0,2 Ньютона на Луне (примечание: масса остается неизменной. на 100 грамм).

Величина силы тяжести определяется массой объекта и массы Земли или Луны

Между любыми двумя объектами существует сила тяжести

Дети и взрослые признают, что невидимое гравитационные силы, которые они испытывают, связаны с невообразимо большие массы планет и других небесных тел.Идея о том, что маленькие массовые такие объекты, как они сами, также обладают силой тяготения – тоже часто ступенька далеко в плане доверчивости! Однако принимая, что это последнее утверждение верно, тогда гравитационная сила между двумя объектами является суммой обоих.

Размер этой гравитационной силы зависит не только от от их массы, но также и от расстояния между этими объектами

Хотя это утверждение идет вверх по порядку прогрессии связаны с пониманием гравитационных сил, для многих детей и взрослым это более очевидно, чем некоторые другие идеи, с которыми нужно справляться с участием.Казалось бы, влияние силы будет меньше, чем дальше он действовал, это можно просто продемонстрировать с помощью магнитного силы например. Единственная проблема с упоминанием магнетизма в контексте гравитационной силы заключается в том, что она не рассматривается как просто аналог, дети могут думать о магнетизме как о , как о как о гравитации.

Что такое гравитация и где она самая сильная в США? | Ребята из науки

Что такое гравитация и где она самая сильная в США?

Январь 2003 г.

Из четырех фундаментальных сил – гравитации, электромагнитной, сильной ядерной и слабой ядерной – гравитация наиболее знакома людям.Исааку Ньютону приписывают «открытие гравитации». На самом деле он дал нам аналитическую интерпретацию гравитации, то есть описал величины, которые определяют силу гравитации на объекте.

Согласно Ньютону, любые два объекта обладают силой притяжения, пытающейся сблизить их. Величина этой силы зависит от массы каждого объекта и расстояния между центрами двух объектов. Математически мы говорим, что сила тяжести напрямую зависит от масс объектов и обратно пропорционально расстоянию между объектами в квадрате.[F = G M1 M2 / D2] G в соотношении – это постоянная, которая называется универсальной гравитационной постоянной.

Для повседневных предметов, таких как люди, автомобили, шары и самолеты, сила тяжести между любыми двумя из этих объектов настолько мала, что несущественна. Однако, когда один из объектов очень массивен, например, Земля, сила тяжести становится значительной. На самом деле ваш вес – это просто сила тяжести между массой вашего тела и массой Земли. Мы чувствуем, как Земля притягивает нас с силой, которую мы называем гравитацией.

«Сила тяжести» часто выражается в единицах ускорения, которое гравитационная сила придает объекту при падении. Это ускорение свободного падения записывается в виде малого g и используется для описания силы тяжести в разных местах на Земле, а также на других планетах.

В целом, чем ближе центры двух объектов, тем больше становится сила тяжести. Следовательно, можно ожидать, что гравитация в Соединенных Штатах будет сильнее там, где вы ближе всего к центру Земли.Самая низкая точка в США – это Долина Смерти, поэтому можно ожидать, что гравитация там (где вы ближе всего к центру Земли) будет сильнее. Однако Земля не является однородным материалом по всей своей внутренней части, и сила тяжести зависит от того, какая именно масса находится между вами и центром Земли.

Таким образом, когда вы перемещаетесь по США, ускорение свободного падения (g) варьируется от 9,79 до 9,81 метра в секунду в квадрате. Среднее значение Земли составляет 9,80 м / с2 (32 фута / с2), что обычно обозначается как ускорение свободного падения на Земле.Это означает, что упавший объект будет увеличивать скорость 32 фута / с каждую секунду при отсутствии сопротивления воздуха. Для сравнения, ускорение свободного падения на Луне составляет всего 1,63 м / с2 из-за ее состава и меньших размеров.

Объяснение гравитации Ньютоном подходит для повседневной жизни. Однако, чтобы понять самые сложные детали гравитации, нужно включить гравитационную теорию Эйнштейна, которая математически сложна.

орбит и гравитация

орбит и гравитация

Астрономия 1101: от планет к космосу

Ключевые идеи:

Закон падающих тел (Галилей)

• Все падающие тела испытывают одинаковое гравитационное ускорение

Закон всемирного тяготения (Ньютон)

• Гравитация – это сила притяжения между всеми парами массивные объекты
• Сила тяжести пропорциональна массам, и обратно пропорционально квадрату расстояния между ними.

Ньютон обобщил законы Кеплера применительно к любым двум тела, вращающиеся вокруг друг друга

• Первый закон: Орбиты – это конических сечения с центром масс двух тел в фокусе.
• Второй закон: сохранение углового момента.
• Обобщенный третий закон, зависящий от масс двух тел.

Орбитальная скорость определяет форму орбиты:

• круговая скорость
• Escape Speed ​​(Скорость побега)

---

ПРИМЕЧАНИЕ:
Эта и следующие лекции, вероятно, самые математические из всех. лекции, которые будут прочитаны в этом классе.Я призываю вас всех прочтите эти заметки заранее и постарайтесь следовать приведенным в них аргументам. В облегчит чтение лекции. [rwp]

---

Закон падающих тел

До своей телескопической работы Галилей выполнил фундаментальные исследования движения.

Изучал скорость падения тел, сбрасывая различные гирь, или скольжение по наклонным плоскостям.

Закон падающих тел

• При отсутствии воздуха, тяжелых и легких предметов падение с той же постоянной скоростью ускорения.

---

Универсальная взаимная гравитация

Исаак Ньютон в своем труде Principia сформулировал закон Универсальная взаимная гравитация:

Гравитация – это Привлекательная сила :

Он сближает массивные объекты

Гравитация – это Универсальная сила :

Он действует повсюду во Вселенной.

Гравитация – это Взаимная сила :

Работает между парами массивных объектов.

---

Сила тяжести

Сила гравитации между любыми двумя объектами зависит только от:

массирует двух объектов:

• Более массивные объекты оказывают на более сильную гравитационную силу.

Расстояние между ними:

• Сила усиливается на по мере приближения двух объектов друг к другу.
• Сила ослабевает по мере того, как два объекта отдаляются друг от друга.

Это не зависит от формы, цвета или состава объекты.

---

Сила гравитационного притяжения между любыми двумя массивные тела пропорциональны их массам и обратно пропорционально пропорционально квадрату расстояния между ними центры.

Сила гравитации является примером силы закона обратных квадратов

Выражаясь математически, сила тяжести между двумя массивными тела это:

Где:

F = сила тяжести.

M ₁ = масса первого тела

M ₂ = масса второго корпуса

d = расстояние между их центрами.

G = Постоянная гравитационной силы

---

Постоянная гравитационной силы

Силовая постоянная G – это число, определяющее размер гравитационная связь между двумя массивными объектами.

G очень мало, в метрических единицах:

G = 6.7х10 ^-11 Ньютон-метр ² / килограмм ²

Ньютон – метрическая единица измерения силы:

4,41 Ньютона = 1 фунт

G должен быть измерен экспериментально. [ПРИМЕЧАНИЕ: G – это «константа гравитационного взаимодействия», которая устанавливает величину силы между двумя массивными объектами, разделенными заданным расстоянием. Поскольку гравитация – самая слабая из четырех фундаментальных сил природы, G трудно измерить экспериментально с какой-либо точностью.Ньютон не знал значения G, но он мог ставить свои проблемы таким образом, чтобы G выпадала математически, поэтому для него это была просто константа пропорциональности. Первое экспериментальное измерение G было выполнено британским физиком Генри Кавендишем в экспериментах, проведенных между 1797 и 1798 годами, с использованием торсионных весов для измерения силы тяжести между двумя грузами в лаборатории. Однако явной целью Кавендиша для этого эксперимента было точное измерение плотности – и, следовательно, Массы – Земли, и он ни разу не упомянул G в своей работе или явно не получил для нее значения.Подобно Ньютону, Кавендиш ставил свои задачи так, что G математически отменял. Мы сделаем то же самое в этом классе, поэтому вам никогда не понадобится знать G на экзаменах или при выполнении домашних заданий. Только намного позже (почти 75 лет спустя) его экспериментальные данные были использованы другими для получения значения G. Лишь в конце XIX века астрономам понадобилось знать G, чтобы они могли, среди прочего, вещи, вычислите плотности небесных тел, таких как Луна и Солнце.]

---

Падение яблока.

Встаньте на Землю и уроните яблоко.

Какова сила Земли на яблоке?

F = GM _земля M _яблоко / R _земля ²

Каково ускорение яблока (2-й закон движения Ньютона):

a _яблоко = F / M _яблоко = GM _земля / R _земля ² = 9,8 м / с ²

Обратите внимание, что масса яблока (M _apple ) была разделена на уравнение.Это означает, что ускорение свободного падения равно независимо от массы яблока , как показал Галилей. ранее.

---

Равные и противоположные реакции

Но третий закон движения Ньютона утверждает, что все силы входят в равных, но противоположных пар

Какую силу яблоко прикладывает к Земле взамен?

F = GM _земля M _яблоко / R _земля ²

Насколько Земля ускоряется по направлению к яблоку?

a _земля = F / M _земля = GM _яблоко / R _земля ²

Это можно переписать, чтобы выразить ускорение Земли в терминах ускорения яблока к Земле как

a _земля = _яблоко x (M _яблоко / M _земля )

где _яблоко = 9.8 м / сек ² , а соотношение От Массы яблока к Массе Земли очень мало. Для типичного 200-граммового яблока это составляет примерно 10 ^-25 м / сек ² , очень маленькое ускорение.

---

Масса Земли

Мы можем напрямую измерить ускорение свободного падения на поверхности Землю, бросая объекты и рассчитывая время их падения (например, как это было сделано Галилео). Мы нашли

a = 9,8 м / сек ²

Мы также можем измерить радиус Земли, используя геометрию (Эратосфен):

R _Земля = 6378 километров = 6 378 000 метров

Объединив их вместе, используя формулу Ньютона для гравитационного Сила позволяет нам оценить массу Земли следующим образом:

Это пример одного из важных выводов Ньютоновского Закон всемирного тяготения: он дает нам возможность использовать движение объектов под влияние их взаимного тяготения для измерения масс планеты, звезды, галактики и т. д.

---

Орбита Луны

Падающие яблоки – это одно, а что насчет Луны?

Что удерживает Луну на орбите вокруг Земли?

Закон инерции (закон Ньютона Первый закон движения) предсказывает:

Если бы между Луна и Земля, Луна будет двигаться по прямой линии на постоянной скорости .

Но, конечно, Луна действительно движется по кривой траектории:

Отклоняется от прямой из-за сила тяжести .

Это приводит к тому, что Луна немного опускается к Земле в то же время. время у него сдвигается в сторону.

---

Падение Луны

Как далеко Луна опускается вокруг Земли за 1 секунду? Как далеко яблоко падает на Землю за первую секунду? Ньютон также знал, что:

• Луна удалена от Земли примерно на 60 радиусов Земли.

Суммируя цифры:

Луна:

• Расстояние, на которое Луна падает по направлению к Земле за 1 секунду: x _Луна = 0.00136 метров
• Расстояние Луны от центра Земли: d _Луна = 60 R _Земля
• Ускорение Луны: a _луна = GM _земля / d _луна ² = GM _{заземление} / (60R _{заземление} ) ²

Apple :

• Расстояние, на которое яблоко падает на Землю за 1 секунду: x _яблоко = 4.9 метров
• Расстояние яблока от центра Земли: d _яблоко = 1 R _земля
• Разгон Apple: a _яблоко = GM _земля / d _яблоко ² = GM _земля / R _земля ²

Соотношение отклонений Яблока и Луны за 1 секунду – отношение их ускорений:

Собирая всю информацию, которая у нас есть, мы получаем следующее:

Это предсказывает, что отклонение Луны за 1 секунду необходимо для удерживать его на орбите вокруг Земли нужно 1/3600 ^-го -го отклонение яблока в первую секунду его падения на Землю.

Наблюдения против прогноза

Это правильно?

Ранее мы обнаружили из наблюдений, что прогиб Луна и яблоко за 1 секунду – это:

• x _луна = 0,00136 метра
• x _яблоко = 4,9 метра

Гравитация предсказывает, что

• x _яблоко /3600 = 4,9 метра / 3600 = 0,00136 метра !!

Соглашение по сути идеальное!

Это показывает, что один и тот же закон всемирного тяготения применим как к яблоко и луна! Оба ощущают притяжение Земли в виде сила, которая становится слабее как квадрат расстояния от центра земли.

---

Итак, почему Луна

вращается вокруг Земли? Если Луна немного падает к Земле, как яблоко упал на поверхность, почему Луна движется вокруг Земли в орбите вместо того, чтобы на нее упасть?

Чтобы ответить на этот вопрос, сначала подумайте, что происходит, если не действовала гравитация:

Вопрос :

Как далеко пролетит Луна по прямой в 1 секунду, если бы не действовала гравитация?

Ответ :

Около 1000 метров.

В то же время движение Луны по прямолинейной траектории также заставит его переместиться на дальше от Земли.

Вопрос :

Как далеко от Земли переместится Луна за 1? во-вторых, если бы не действовала гравитация?

Ответ :

Около 0,00136 метра!

Круглые числа показывают, насколько Луна падает на Землю из-за гравитации достаточно, чтобы компенсировать прямолинейный путь, который потребуется, если гравитация не действовала, чтобы отклонить его.Этот баланс эффективно закрывает петля.

Таким образом, мы пришли к поразительному выводу:

Луна действительно постоянно падает вокруг Земли!

Это совершенно другой взгляд на “орбиту” под влияние гравитации.

Хотя на первый взгляд падение яблока и орбита Луны кажутся двумя совершенно разными явлениями, рассматриваемыми в свете Законы движения Ньютона, на самом деле они являются разными проявлениями тоже самое! Падение Луны вокруг Земли такое же движения, как падение яблока на Землю.Оба описаны те же три закона движения, и оба чувствуют силу тяжести описывается тем же универсальным законом силы.

---

Вселенская гравитация

Закон всемирного тяготения Универсальный :

• Управляет падением яблока на Землю.
• Управляет падением Луны вокруг Земли.
• Управляет падением системы Земля / Луна вокруг Солнца.
• Управляет падением Солнца вокруг центра Млечный путь.
• Управляет падением Млечного Пути и галактик Андромеды. на их взаимной орбите …

и так далее по всей Вселенной.

---

Возвращение к законам Кеплера

Законы движения планет Кеплера заключаются в следующем:

Первый закон:

Планеты вращаются по эллипсам с Солнцем в одном фокусе.

Второй закон:

Планета сметает равные площади за равное время.

Третий закон:

Квадрат периода пропорционален размеру Большая полуось в кубе.

Математически выражается как: P ² = a ³ , для P в годах и a в AU.

---

Обобщение Ньютона

Ньютон показал, что законы Кеплера могут быть получены из

• Три закона движения
• Закон всемирного тяготения.

Далее, Ньютон обобщил законы, применимые к любым два тела движутся под действием их взаимного тяготения. Для Например, эти законы в равной степени применяются к

• Луна на орбите Земли.
• Космический зонд на орбите Луны.
• Две звезды, вращающиеся вокруг друг друга.

и так далее…

---

Форма орбиты – коническое сечение с центр масс в одном фокусе.

Формулировка Ньютоном Первого закона Кеплера состоит из двух частей:

Формы орбит представляют собой конические сечения:

• Кривые, полученные при разрезании конуса плоскостью.
• Круги, эллипсы, параболы и гиперболы

Центр масс в фокусе:

• Строго говоря, это не только Земля, вращающаяся вокруг Солнца.Земля и Солнце на обращаются друг к другу на орбите вокруг их взаимный центр масс.

Поскольку Земля намного меньше Солнца, их общий центр массы находится внутри Солнца, поэтому разница не сразу заметна.

---

Кривые конического сечения

Это кривые, образованные пересечением конуса и плоскости. разрезая его под разными углами.

Конические кривые бывают двух семейств:

замкнутые кривые:

• Эллипсы
• Окружности , которые являются частным случаем эллипса с e = 0
• Эти орбиты связаны с : объекты будут вращаться по орбите вечно вокруг родительского тела.

Открытые кривые:

• Гиперболы
• Параболы , которые являются частным случаем гиперболы
• Эти орбиты несвязаны : объекты будут проходить мимо родительского тела только один раз, а затем вырваться из-под тяготения родительского тела.

На какой из этих орбит вы попадете, определяется вашей орбитой . скорость . Особый интерес представляют две особые скорости …

---

Скорость, необходимая для поддержания круговой орбиты с заданным радиусом r около массивное тело, М:

• Если ваша скорость меньше v _C на вашем текущем расстоянии, ваша орбита будет иметь форму эллипса на меньше на , чем круговая орбита.
• Если ваша скорость немного больше v _C при вашей текущей расстояние, ваша орбита будет иметь форму эллипса на больше , чем круговая орбита
• Однако в какой-то момент ваша скорость может стать настолько большой, что вы вырваться на свободу и сбежать …

Эта формула строго верна только в том случае, если вращающийся объект намного менее массивен, чем центральное массивное тело. Например, для спутника или космонавта это правильно, но не для Луны.

---

Это минимальная скорость, необходимая для выхода из-под гравитации тела масса M, начиная с расстояния r от нее:

Как и в случае с круговой скоростью, эта формула строго верна только в том случае, если движущийся объект намного менее массивен, чем центральное массивное тело, из которого он «убегает». Кроме того, строго говоря, объект никогда не «убегает» или «вырывается» из-под гравитации другого объекта, он просто становится несвязанным и находится на траектории, которая никогда не повернется к большему объекту, как замкнутая или «связанная» орбита.

На поверхности Земли:

• v _C = 7,9 км / сек (28400 км / ч)
• v _E = 11,2 км / сек (40300 км / ч)

Семейства Орбит

С помощью этих двух скоростей (круговой и аварийной) мы можем увидеть, как различные типы замкнутых и открытых орбит конического сечения вокруг большого центрального возникает массивное тело. Все показанные ниже орбиты начинаются с общая точка P, отмеченная справа (где пересекаются все 5 кривых), но с разными скоростями:

[Щелкните изображение, чтобы просмотреть его полноразмерную версию (9 КБ GIF)] (Графика Р.Погге)

Какую орбиту имеет объект, определяется орбитальной скоростью на в этой точке относительно круговой и аварийной скорости в этой точке:

• Если орбитальная скорость точно равна круговой скорости в точке P (V _C ), орбита будет Circle проходит через точку P, с центром на центральном теле (красная кривая).
• Если орбитальная скорость на меньше , чем V _C в точке P, орбита будет на эллипса меньше круга, который проходит через P , с центральным телом в дальнем фокусе (синяя кривая).
• Если орбитальная скорость на выше , чем V _C в точке P, но меньше, чем скорость убегания в точке P (V _E ), тогда орбита будет эллипсом на больше, чем круговая орбита, проходящая через точку P, с центральное тело в ближнем фокусе (зеленая кривая).
• Если орбитальная скорость в точности соответствует скорости ухода в точке P (V _E ), орбита будет открытой. Парабола (пурпурная кривая).
• Если орбитальная скорость на больше, чем скорость ухода от точки P, орбита будет представлять собой гиперболу (черная кривая).Чем больше скорость, более “плоская” (более открытая) гиперболическая орбита.

---

Центр масс

Два объекта вращаются вокруг своего центра масс :

• Точка равновесия между двумя массами

[Щелкните изображение, чтобы просмотреть полноразмерную версию (5 КБ)] (Рисунок Р. Погге)

• Большая полуось: a = a ₁ + a ₂
• Взаимное расположение: a ₂ / a ₁ = M ₁ / M ₂

Пример: Земля и Солнце

M _солнце = 2 x 10 ³⁰ кг

M _земля = 6 x 10 ²⁴ кг

Из соотношения баланса расстояния Солнца и Земли от их взаимный центр масс связан с размером большой полуавтоматики. оси орбиты Земли (а) и соотношением масс:

a _солнце + _земля = 1 AU = 1.5 x 10 ⁸ км

a _солнце / a _земля = M _земля / M _солнце = 3 x 10 ^-6

После некоторой простой алгебры (сделайте это!), Мы находим:

a _Солнце = 450 км

Поскольку радиус Солнца составляет 700 000 км, это означает, что центр масс системы Земля-Солнце находится на глубине внутри Солнце.

---

Орбитальные движения сохраняют угловой момент.

Это не похоже на «равные площади в равное время», но на самом деле это одно и то же.

Угловой момент:

L = mvr = постоянная

Где:

м = масса,

v = скорость,

r = расстояние от центра масс.

Эта формула является упрощением для случая круговой орбиты, но она иллюстрирует основной эффект. В общем, угловой момент – это вектор, равный массе, умноженной на векторное произведение радиального вектора и вектора скорости в 3-х измерениях.

---

Угловой момент и равные площади

Угловой момент сохраняется , что означает, что L является постоянная .

При изменении расстояния скорость должна измениться на компенсировать так, чтобы L оставалось постоянным:

Рядом с перигелием:

• Планета на ближе к Солнцу, поэтому r на меньше .
• Скорость v должна быть пропорционально быстрее для компенсации.

Рядом с Афелием:

• Планета находится на дальше от Солнца на , поэтому r на больше .
• Скорость v должна быть пропорционально медленнее для компенсации.

Знакомый пример того же принципа в работе – фигурист. делает вращение. В “вертикальном вращении” фигурист стоит на одной ноге с руки вытянуты и вращаются вокруг оси вверх / вниз. Спин ускоряется фигуристом, тянущим на руках. Рисуя в его / ее руки, они перемещают массу ближе к центру своего тела, а сохранение углового момента требует, чтобы они вращались быстрее.

---

Ньютоновское обобщение Кеплера 3 ^rd Закон:

Где:

P = период орбиты

a = большая полуось орбиты

M ₁ = масса первого тела

M ₂ = масса второго тела

---

Третий закон для каждого тела

Пропорциональность между квадратом периода и куб большой полуоси теперь зависит от масс два тела.

Для планет, вращающихся вокруг Солнца, M _sun намного больше любого планеты (даже Юпитер, на 1/1000 ^-й M _солнце ), что мы восстановить версию Третьего закона Кеплера из более общей теории Ньютона. форма:

Обратите внимание, что коэффициент пропорциональности одинаков для всех планет. (с хорошим приближением, конечно, в пределах данных Кеплера от Тихо).

В версии Кеплера коэффициент пропорциональности равен 1.0 если мы используем единицы лет для P и AU для большой полуоси, a. В то время как вычислительно удобный, он скрывает основную зависимость от массы Солнца из поля зрения. Проблема с эмпирическими законами, подобными законам Кеплера. формулировка, заключается в том, что они показывают только поверхность, а не важные детали лежащие в их основе.

---

Измерительные массы

Обобщенная форма Ньютона 3-го закона Кеплера дает нам способ измерить массы по орбитальному движению!

Например, мы можем получить массу Солнца, используя период и размер орбиты Земли:

P _земля = 1 год = 3.156 x 10 ⁷ секунд

a _земля = 1 AU = 1,496 x 10 ¹¹ метров

Использование формы Ньютона 3-го закона Кеплера для солнечной системы выше, мы видим, что если мы знаем P и a (G и pi – константы), единственное, что неизвестно – это масса Солнца, которую можно решить для легко после небольшой легкой алгебры:

(Вы можете проверить цифры самостоятельно, используя G = 6,67 x 10 ^-11 Ньютон м ² / кг ² , а значения P и a для Земли, указанные выше в секундах и метрах.Сделай это!).

---

Универсальный метод измерения масс

Обобщенная форма Третьего закона Кеплера дает нам мощный инструмент для измерения масс объектов путем измерения периодов и размеры их орбит. Например:

Мы можем измерить массу Юпитера по орбитам Галилеевы спутники, начиная с M _Юпитер >> M _{спутников}

• Найдите M _Юпитер = 300 M _Земля

Мы можем измерить общую массу системы Земля и Луна.

• Земля всего в ~ 81 раз массивнее Луны, так что вы необходимо использовать полную формулу.
• Получите массу Земли независимо (например, наша эксперимент с падающими телами из вчерашней лекции).

Мы можем измерить массы двойных звезд, используя полную формулу и наблюдая за параметрами их орбиты (вы увидите это сделано в Астрономии 162).

---

The

Почему планетарных движений

Законы Кеплера – это описания движения:

• Получено методом проб и ошибок с некоторыми неопределенными представлениями о небесных гармониях
• Описывать только движения, не объясняя, почему они двигайся туда.

Ньютон дает объяснение:

• Законы Кеплера являются естественным следствием трех законов Ньютона. Движение и его закон всемирного тяготения.

Обращаясь к вопросу «почему», Ньютон придал своим законам предсказательную силу, которая позволяет использовать их в качестве инструментов для исследования Вселенной, как образно, так и буквально. Мы можем предсказывать новые явления или понимать странности в движения (эти законы дают нам основу для интерпретации данных), и мы можем буквально использовать их, чтобы летать на космических кораблях через Солнечную систему.

---

---

Обновлено: 2014 г., Тодд А. Томпсон,
Авторские права Ричард В. Погге, Все права защищены.

Tide Formation — Гравитационное притяжение | manoa.hawaii.edu/ExploringOurFluidEarth

Гравитация

Гравитация – сила притяжения между любыми двумя объектами. Гравитация прямо пропорциональна массе объектов и обратно пропорциональна квадрату расстояния между ними. Это означает, что объект, который имеет большую массу, может оказывать большую гравитационную силу на другой объект, и чем ближе два объекта друг к другу, тем больше сила притяжения между ними.Эта связь может быть выражена следующим уравнением:

F _g – сила тяжести, G – гравитационная постоянная, m ₁ и m ₂ – массы двух объектов, а r – расстояние между центрами масс объектов. Хотя между всеми массивными объектами существуют гравитационные силы, гравитационная сила между Землей и объектами на ее поверхности намного больше, чем гравитационные силы между любыми из этих объектов, из-за огромных размеров Земли.Гравитация – причина того, что у Земли есть атмосфера. Гравитация также является причиной того, почему люди остаются на поверхности земли и почему предметы падают на землю при падении.

Гравитационное притяжение Луны

---

Гравитация также является причиной приливов. Гравитация Земли удерживает воду на поверхности планеты. Однако Луна достаточно велика и расположена достаточно близко, чтобы ее гравитационная сила оказывала заметное влияние на большие водоемы на Земле.Вода на Земле в области непосредственно под Луной притягивается силой тяжести к Луне (рис. 6.5), создавая выпуклость на поверхности океана. На противоположной стороне Земли также есть выпуклость, вызванная разницей в гравитационной силе Луны, действующей на Землю. Выпуклости океана на обеих сторонах Земли, обращенных к Луне, и на стороне, противоположной Луне, называются приливными выпуклостями . Поверхность суши Земли также выпуклая, как и Луна, хотя и не в такой степени, как океан.

Приливные выпуклости очень малы – кажутся незначительно маленькими – по сравнению с радиусом Земли. Приливные выпуклости в цифрах в этом блоке сильно преувеличены. Высота приливной выпуклости в открытом океане в большинстве районов менее метра. Однако, поскольку океан настолько обширен, приливные волны могут поднимать огромное количество воды. Прилив, вызванный гравитационным притяжением Луны, называется лунным приливом .

Луна каждый день очень мало движется вокруг Земли.За один день Земля совершает полный оборот вокруг своей оси, в то время как Луне требуется почти месяц, чтобы облететь вокруг Земли. На рис. 6.6 мы видим, что это означает, что Земля вращается через приливные выступы. В полночь человек, стоящий на берегу океана недалеко от экватора, увидел бы прилив, вызванный гравитационной силой Луны (рис. 6.6 A). Если бы этот человек оставался в том же месте в течение целого дня, пока Земля вращалась, он переместился бы в область отлива в 6:13 a.м. Это потому, что место на Земле, где она стоит, превратилось бы в желоб между двумя приливными выступами (рис. 6.6 B). В 12:25 будет еще один прилив, вызванный внешней силой вращения Земли. Рис. 6.6 C). В 18:38 будет еще один отлив (рис. 6.6 D), а в 12:50 – еще один прилив (рис. 6.6 E).

---

Поскольку Луна движется по своей орбите вокруг Земли примерно на 12 градусов (˚) за каждый 24-часовой период, и поскольку она вращается в том же направлении, что и Земля, Луна не будет находиться прямо над наблюдателем снова, пока она не завершится. один оборот и снова полный.Это объясняет, почему для любого наблюдателя на поверхности Земли Луна кажется восходящей примерно на 50 минут позже каждый день и почему время прилива и отлива наступает примерно на 50 минут позже каждый день. Это также объясняет, почему вымышленный человек, описанный в предыдущем абзаце на рис. 6.6, наблюдал приливы и отливы с разницей в шесть часов и 12,6 минут.

Гравитационное притяжение Солнца

Солнце также оказывает на Землю гравитационную силу, создавая солнечный прилив .Как и в случае с Землей и Луной, вода на Земле прямо на линии Солнца притягивается гравитационной силой к Солнцу, создавая водную выпуклость. На противоположной от Солнца стороне Земли также есть выпуклость. Подобно лунному приливу, когда Земля вращается через выпуклость воды, создаваемую Солнцем, уровень прилива меняется с высокого на низкий и обратно. Поскольку Земля вращается каждые 24 часа, солнечные приливные изменения происходят по 24-часовому графику.

Взаимодействие гравитационных сил Луны и Солнца

Хотя масса солнца намного больше массы луны, луна имеет большее влияние на приливы, чем солнце.Это связано с тем, что Солнце находится намного дальше от Земли, поэтому его приливная сила составляет лишь половину от силы Луны. Сила гравитации зависит как от массы объектов, так и от расстояния между ними.

Поскольку Луна перемещается немного дальше каждый день в своем орбитальном путешествии вокруг Земли, приливы, вызванные гравитацией Луны, происходят на 50 минут позже, чем приливы, вызванные гравитацией Солнца. Чтобы совершить полный оборот вокруг Земли, Луне требуется около 29,5 дней.Этот период называется лунным месяцем года. Луна и Солнце вызывают предсказуемые периодические изменения в диапазоне приливов и отливов в течение лунного месяца. Поэтому лунный месяц также называют приливным месяцем .

Когда Земля, Луна и Солнце выстраиваются в линию, лунные и солнечные приливы происходят почти в одно и то же время и создают самые большие приливные интервалы в течение лунного месяца. Они происходят во время новолуния года, года, когда Луна находится между Землей и Солнцем, или полнолуния, года, когда Земля находится между Луной и Солнцем (рис.6.7). В это время случаются сверхвысокие и сверхмалые приливы. Их называют весенними приливами , потому что они «подпрыгивают» или «подпрыгивают». Когда Солнце и Луна находятся под прямым углом (90˚) друг к другу, Луна находится либо в своей первой четверти , либо в ее третьей четверти . В этом положении солнечный и лунный приливы имеют тенденцию нейтрализовать друг друга, и возникает уменьшенный прилив, называемый приливом (рис. 6.7). В приливном месяце бывает два весенних прилива и два восходящих прилива.

Деятельность

Изобразите комбинированный эффект приливных изменений, вызванных солнцем и луной во время весеннего и морского приливов.

.