U в физике обозначение
Главная Новости сайта Вспомни физику: 7 класс 8 класс 9 класс класс задачи кл. Его величество Музеи науки Викторина по физике Физика в кадре Учителю Читатели пишут Физика 8 класс.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Основные законы и формулы по математике и физике: Справочник
- Формулы по Электродинамике
- Формула внутренней энергии
- Решение задач на тему: “Электрическое сопротивление. Закон Ома”
- Основные законы и формулы по математике и физике: Справочник
Формула ЭДС - Мощность электрического тока
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Обозначение намерений
youtube.com/embed/WQFwkaiVcBU” frameborder=”0″ allowfullscreen=””/>Основные законы и формулы по математике и физике: Справочник
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились.
То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения. Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи или на отдельных участках цепи.
Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой ЭДС , действующей в цепи или на участке цепи.
Если напряженность поля сторонних сил не равна нулю только в части цепи, например, на отрезке , тогда интегрирование в выражении 2 можно вести только по данному участку. Соответственно, ЭДС, действующая на участке цепи определяется как:. Участок цепи, на котором действуют сторонние силы, называют неоднородным.
Для него выполняется равенство:. Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в направлении тока ток течет от минуса к плюсу источника. Размерность ЭДС совпадает с размерностью потенциала. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А.
Металлический диск, имеющий радиус a, вращается с угловой скоростью , включен в электрическую цепь при помощи скользящих контактов, которые касаются оси диска и его окружности рис. Какой будет ЭДС, которая появится между осью диска и его наружным краем? В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила F которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:. Fдействует на заряженную частицу электрон , следовательноучитывая 2. Читать дальше: Формулы по физике. Копирование материалов с сайта возможно только с разрешения администрации портала и при наличие активной ссылки на источник. Образовательные онлайн-сервисы Меню. Решение задач онлайн. Отправить задания. Главная Справочник Формулы по физике Формула ЭДС Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились.
Определение и формула ЭДС Определение Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой ЭДС , действующей в цепи или на участке цепи. Математически определение ЭДС запишем как: где A — работа сторонних сил, q — заряд, над которым производится работа.
Пример Задание. В качество основы для решения задачи используем формулу для вычисления ЭДС: Заряд, который проходит в рассматриваемой цепи за 1 мин. Формулу для вычисления центробежной силы запишем как: где m — масса электрона, r — расстояние от оси диска.
В соответствии с формулой, определяющей ЭДС участка цепи, получаем: Ответ. Вы поняли, как решать? Помощь с решением. Рассчитайте цену решения ваших задач. Узнать точную цену. Сервисы Онлайн калькуляторы Справочник Примеры решений Образовательный форум. Услуги Контрольные на заказ Курсовые на заказ Дипломы на заказ Рефераты на заказ.
Webmath О проекте Новости Контакты Политика конфиденциальности.
Формулы по Электродинамике
Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул. Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений например для энергии , скорости , длины и других , чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Формулы по физике 8 класс. прямо пропорциональна напряжению (U) на концах этого участка и обратно пропорциональна его сопротивлению (R).
Формула внутренней энергии
На этой страничке кратко излагаются основные величины электрического тока.
Решение задач на тему: “Электрическое сопротивление. Закон Ома”
Адсорбция — изменение концентрации вещества на границе раздела фаз по сравнению с объемом. Адсорбция физическая — адсорбция, обусловленная силами межмолекулярного взаимодействия; как правило – обратима. Хемосорбция — поглощение газов, паров или растворенных веществ твердыми или жидкими поглотителями, сопровождающееся образованием химических соединений. Если поверхность энергетически неоднородна , используют эмпирическое уравнение Френдлиха :. Аккумулятор — вторичный гальванический элемент , в отличие от первичного г.
Главная Новости Обучение Лекции Тестирование.
Основные законы и формулы по математике и физике: Справочник
У вас уже есть абонемент? На уроке будут рассмотрены задачи, связанные с применением закона Ома и формулой для расчета сопротивления проводника. Будут разобраны примеры решения задач, а также возможное их применение на практике. На предыдущих уроках мы говорили, что сила тока зависит от напряжения и сопротивления проводника. Также мы выяснили, что сопротивление проводника зависит от его геометрических размеров и материала, из которого он сделан.
Формула ЭДС
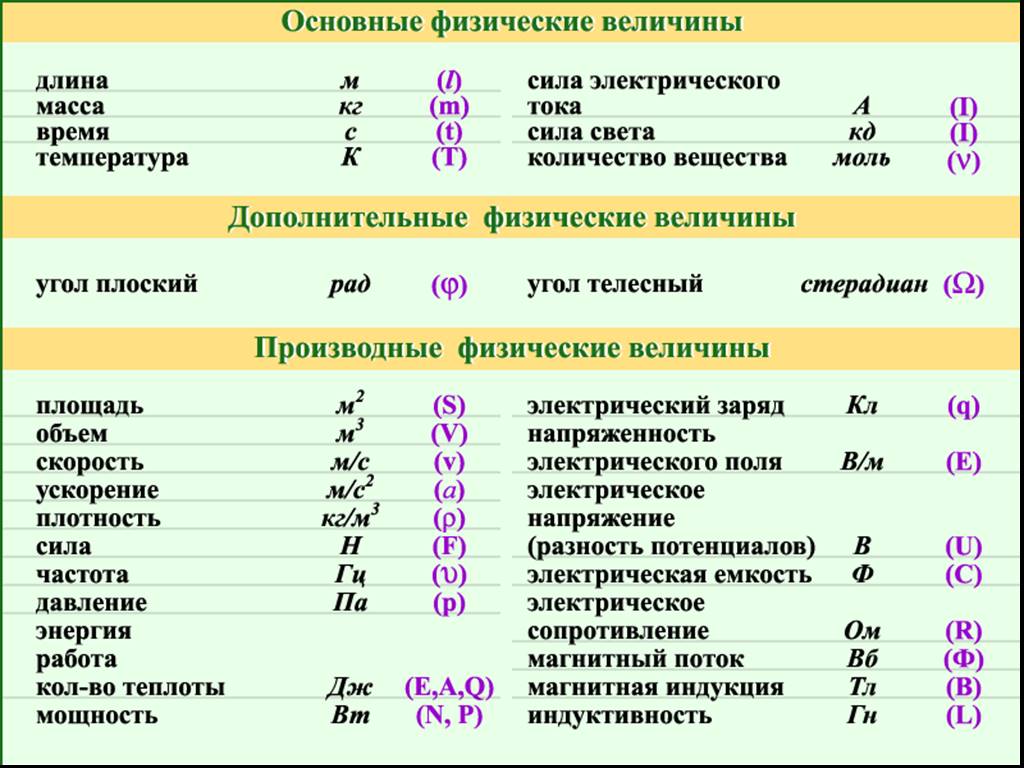
Рекордом R. D, d — диаметр : на основе латинского diametrus — диаметр. L, l — длина : на основе английского length — длина. R, r — радиус : на основе позднелатинского radius — радиус. S — площадь : на основе английского square — площадь. V — объём : на основе английского volume — объем.
Сила тока измеряется в Амперах (I=[А]), напряжение – в Вольтах (U=[В]), сопротивление – в Омах (R=[Ом]).
Мощность электрического тока
Постоянный ток — электрический ток, не изменяющийся по времени и по направлению. За направление тока принимают направление движения положительно заряженных частиц. В том случае, если ток образован движением отрицательно заряженных частиц, направление его считают противоположным направлению движения частиц.
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения. Такие силы именуются сторонними.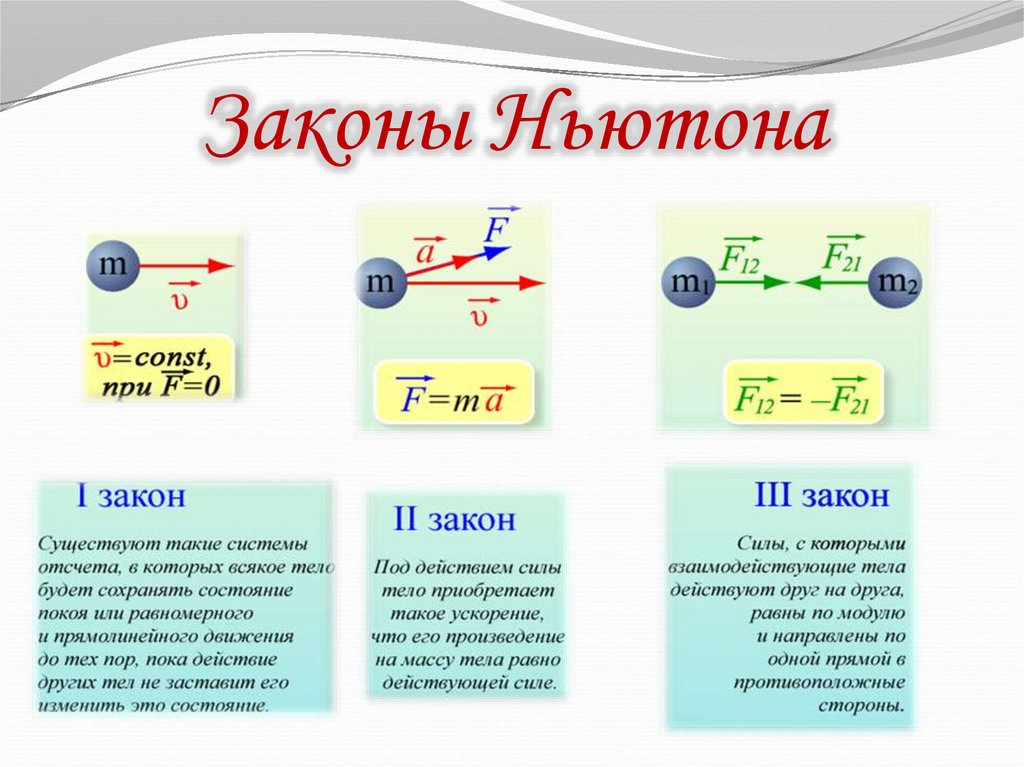 Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи или на отдельных участках цепи.
Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи или на отдельных участках цепи.
Доброго дня уважаемые радиолюбители!
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб! Внутренняя энергия зависит от массы, температуры тела, рода вещества и от того, в каком агрегатном состоянии находится тело — твердом, жидком или газообразном. Внутренняя энергия идеального газа равна кинетической энергии теплового движения его атомов или молекул. Существует формула для внутренней энергии одного моля идеального газа, молекулы которого совершают только поступательное движение:.
Время полета, дальность полета и максимальная высота при движении тела, брошенного под углом к горизонту. Импульс, работа, энергия. Законы сохранения в механике.
Ядерная физика. Том 84, Номер 1/, 2021
- На главную
- Электронные версии
- Ядерная физика
Содержание
Том 84, Номер 1/, 2021
ЯДРА
Эксперимент
- Измерение отношения кумулятивных спектров бета-частиц от продуктов деления 235U и 239Pu для решения задач физики реакторных антинейтрино
В. И. Копейкин, Ю.Н. Панин, А.А. Сабельников
И. Копейкин, Ю.Н. Панин, А.А. СабельниковИнформация о статьеПолный текст (PDF)
- 3-11
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ
Теория
- Обобщение теоремы Левинсона об асимптотическом значении фазы амплитуды рассеяния
М.И. Криворученко, К.С. ТыринИнформация о статьеПолный текст (PDF)
- 12-16
Материалы Сессии-конференции Секции ядерной физики ОФН РАН,
10–12 марта 2020 г., Новосибирск∗
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ
- Физика тяжелых ионов на установке “Компактный мюонный соленоид” (CMS) на Большом адронном коллайдере (LHC)
С.В. ПетрушанкоИнформация о статьеПолный текст (PDF)
- 17-19
- Физика электрослабых взаимодействий в эксперименте CMS на LHC
В.В. Шалаев, С.В. ШматовИнформация о статьеПолный текст (PDF)
- 20-25
- Система сбора данных для калориметра детектора Belle II
В.В. Жуланов, А.С. Кузьмин, Д.В. Матвиенко, M. А. Ремнев, Ю.В. Усов
А. Ремнев, Ю.В. УсовИнформация о статьеПолный текст (PDF)
- 26-29
- Изучение процесса e+e− → KSK±π∓ с детектором КМД-3
А.А. Усков, Г.В. Федотович, В.Л. Иванов, Д.Н. ШемякинИнформация о статьеПолный текст (PDF)
- 30-36
- Эксперимент T2K: последние результаты и перспективы
М.М. ХабибуллинИнформация о статьеПолный текст (PDF)
- 37-39
- Измерение сечения процесса e+e− → ωπ0 → π+π−π0π0 на детекторе СНД
М.Н. Ачасов, А.А. Байков, А.Ю. Барняков, K.И. Белобородов, А.В. Бердюгин, А.Г. Богданчиков, А.А. Ботов, В.Б. Голубев, Т.В. Димова, В.П. Дружинин, В.Н. Жабин, В.В. Жуланов, Л.В. Кардапольцев, Д.П. Коврижин, А.А. Король, А.С. Купич, К.А. Мартин, Н.А. Мельникова, Н.Ю. Мучной, А.Е. Oбразовский, Е.В. Пахтусова, К.В. Пугачев, Я.C. Савченко, С.И. Середняков, З.К. Силагадзе, И.К. Сурин, Ю.В. Усов, А.Г. Харламов, Д.А. Штоль
Пахтусова, К.В. Пугачев, Я.C. Савченко, С.И. Середняков, З.К. Силагадзе, И.К. Сурин, Ю.В. Усов, А.Г. Харламов, Д.А. ШтольИнформация о статьеПолный текст (PDF)
- 40-43
- Измерение сечения процесса e+e− → K+K−π0 на детекторе СНД при энергии в системе центра масс √s = 1.3−2.0 ГэВ
М.Н. Ачасов, А.Ю. Барняков, М.Ю. Барняков, К.И. Белобородов, А.В. Бердюгин, А.Г. Богданчиков, А.А. Ботов, А.Р. Бузыкаев, В.Б. Голубев, Т.В. Димова, В.П. Дружинин, Л.В. Кардапольцев, Д.П. Коврижин, А.А. Король, Е.А. Кравченко, А.С. Купич, К.А. Мартин, Н.А. Мельникова, А.Е. Образовский, А.П. Онучин, Е.В. Пахтусова, К.В. Пугачев, С.И. Середняков, З.К. Силагадзе, И.К. Сурин, Ю.В. Усов, А.Г. Харламов, Д.А.ШтольИнформация о статьеПолный текст (PDF)
- 44-47
- Изучение нейтринных осцилляций в эксперименте NOvA
Л.Д. Колупаева, О.Б. СамойловИнформация о статьеПолный текст (PDF)
- 48-52
- Проект DERICA и стратегия развития ядерной физики низких энергий
Л. В. Григоренко, Г.Н. Кропачев, Т.В. Кулевой, И.Н. Мешков, С.М. Полозов, А.С. Фомичев, Б.Ю. Шарков, П.Ю. Шатунов, М.И. Явор
В. Григоренко, Г.Н. Кропачев, Т.В. Кулевой, И.Н. Мешков, С.М. Полозов, А.С. Фомичев, Б.Ю. Шарков, П.Ю. Шатунов, М.И. ЯворИнформация о статьеПолный текст (PDF)
- 53-66
- Разработка детектора ионов на основе время-проекционной камеры низкого давления для ускорительной масс-спектрометрии
А.Е. Бондарь, А.Ф. Бузулуцков, В.В. Пархомчук, А.В. Петрожицкий, А.В. Соколов, Е.А. Фролов, Т.М. ШакироваИнформация о статьеПолный текст (PDF)
- 67-72
- Дифракционное рассеяние виртуальных фотонов на ядрах и его интерференция с процессом тормозного излучения мюонов
A. Сандрок, Э.В. Бугаев, Р.П. Кокоулин, А.А. ПетрухинИнформация о статьеПолный текст (PDF)
- 73-76
- Мюонная загадка в космических лучах и возможности ее решения
А.А. ПетрухинИнформация о статьеПолный текст (PDF)
- 77-84
- Треxреджеонные разрезы в амплитудах КХД
В.С. ФадинИнформация о статьеПолный текст (PDF)
- 85-89
- Преобразование Ландау–Халатникова–Фрадкина и четные ζ-функции
А. В. Котиков, С. Тебер
В. Котиков, С. ТеберИнформация о статьеПолный текст (PDF)
- 90-92
Информация о выпуске
Всего статей
16Страницы
3-92
Ядерная физика
Архивы выпусков Информация о журнале Отправить рукопись в журнал
10.1 Вращательные переменные — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Описать физический смысл переменных вращения применительно к вращению с фиксированной осью
- Объясните, как угловая скорость связана с тангенциальной скоростью
- Рассчитать мгновенную угловую скорость с учетом функции углового положения
- Найти угловую скорость и угловое ускорение во вращающейся системе
- Рассчитать среднее угловое ускорение при изменении угловой скорости
- Рассчитать мгновенное угловое ускорение по функции угловой скорости
До сих пор в этом тексте мы в основном изучали поступательное движение, включая описывающие его переменные: смещение, скорость и ускорение. Теперь мы расширим наше описание движения до вращения, точнее, вращательного движения вокруг фиксированной оси. Мы обнаружим, что вращательное движение описывается набором связанных переменных, подобных тем, которые мы использовали в поступательном движении.
Теперь мы расширим наше описание движения до вращения, точнее, вращательного движения вокруг фиксированной оси. Мы обнаружим, что вращательное движение описывается набором связанных переменных, подобных тем, которые мы использовали в поступательном движении.
Угловая скорость
Равномерное круговое движение (обсуждавшееся ранее в разделе «Движение в двух и трех измерениях») — это движение по окружности с постоянной скоростью. Хотя это простейший случай вращательного движения, он очень полезен во многих ситуациях, и мы используем его здесь, чтобы ввести вращательные переменные.
На рис. 10.2 мы показываем частицу, движущуюся по кругу. Система координат фиксирована и служит в качестве системы отсчета для определения положения частицы. Его вектор положения от начала окружности к частице заметает угол θθ, который увеличивается в направлении против часовой стрелки по мере того, как частица движется по круговой траектории. Угол θθ называется угловым положением частицы.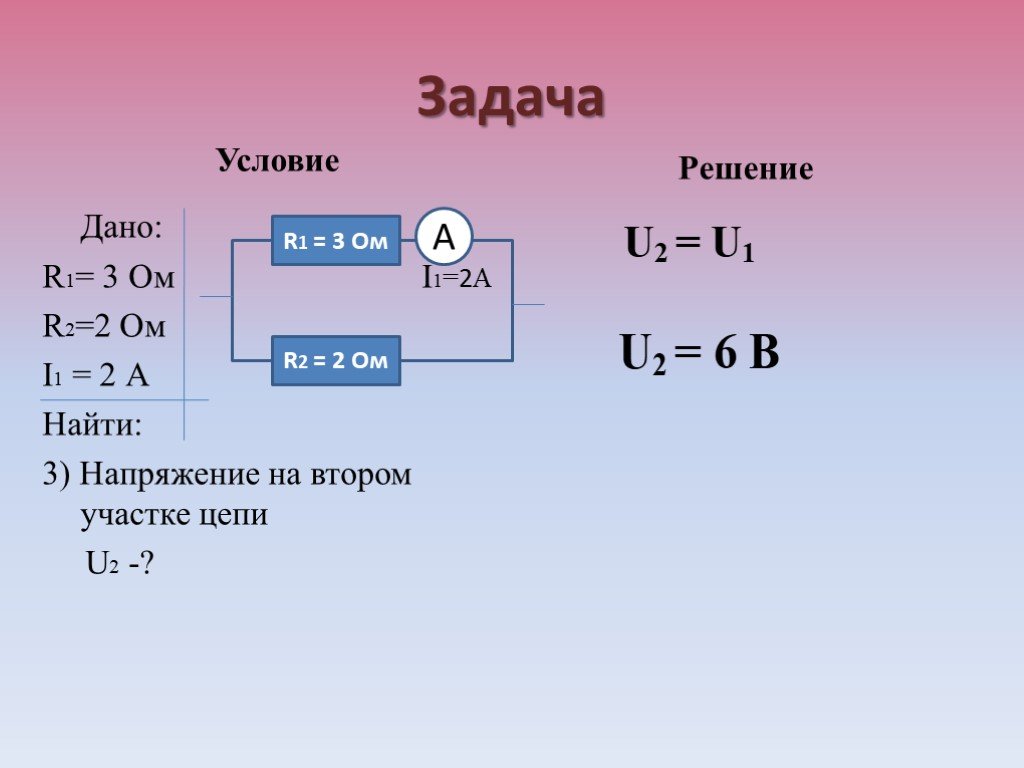 Поскольку частица движется по круговой траектории, она также описывает дугу длиной с .
Поскольку частица движется по круговой траектории, она также описывает дугу длиной с .
Рисунок 10.2 Частица движется по круговой траектории. Когда он движется против часовой стрелки, он образует положительный угол θθ по отношению к оси x- и описывает дугу длиной s .
Угол связан с радиусом окружности и длиной дуги как
θ=ср.θ=ср.
10,1
Угол θθ, угловое положение частицы на ее пути, измеряется в радианах (рад). В 360°.360° содержится 2π2π радиан. Обратите внимание, что мера радиана представляет собой отношение измерений длины и, следовательно, является безразмерной величиной. При движении частицы по круговой траектории ее угловое положение изменяется, и она испытывает угловые смещения Δθ.Δθ.
Мы можем присвоить векторы величинам в уравнении 10.1. Угол θ→θ→ — это вектор вне страницы на рис. 10. 2. Вектор углового положения r→r→ и длина дуги s→s→ лежат в плоскости страницы. Эти три вектора связаны друг с другом на
2. Вектор углового положения r→r→ и длина дуги s→s→ лежат в плоскости страницы. Эти три вектора связаны друг с другом на
с→=θ→×r→.s→=θ→×r→.
10,2
То есть длина дуги представляет собой векторное произведение вектора угла и вектора положения, как показано на рис. 10.3.
Рисунок 10.3 Вектор угла указывает на ось z-, а также вектор положения и вектор длины дуги лежат в плоскости xy . Мы видим, что s→=θ→×r→s→=θ→×r→. Все три вектора перпендикулярны друг другу.
Величина угловой скорости, обозначаемая ωω, представляет собой временную скорость изменения угла θθ по мере того, как частица движется по круговой траектории. Мгновенная угловая скорость определяется как предел, при котором Δt→0Δt→0 в средней угловой скорости ω–=ΔθΔtω–=ΔθΔt:
ω=limΔt→0ΔθΔt=dθdt,ω=limΔt→0ΔθΔt=dθdt,
10,3
, где θθ — угол поворота (рис. 10.2). Единицами угловой скорости являются радианы в секунду (рад/с). Угловую скорость также можно назвать скоростью вращения в радианах в секунду. Во многих ситуациях нам дают скорость вращения в оборотах/с или циклах/с. Чтобы найти угловую скорость, мы должны умножить количество оборотов/с на 2π2π, поскольку в одном полном обороте содержится 2π2π радиан. Поскольку направление положительного угла в окружности направлено против часовой стрелки, мы принимаем вращение против часовой стрелки как положительное, а вращение по часовой стрелке как отрицательное.
10.2). Единицами угловой скорости являются радианы в секунду (рад/с). Угловую скорость также можно назвать скоростью вращения в радианах в секунду. Во многих ситуациях нам дают скорость вращения в оборотах/с или циклах/с. Чтобы найти угловую скорость, мы должны умножить количество оборотов/с на 2π2π, поскольку в одном полном обороте содержится 2π2π радиан. Поскольку направление положительного угла в окружности направлено против часовой стрелки, мы принимаем вращение против часовой стрелки как положительное, а вращение по часовой стрелке как отрицательное.
Мы можем увидеть, как угловая скорость связана с тангенциальной скоростью частицы, продифференцировав уравнение 10.1 по времени. Мы перепишем уравнение 10.1 как
.с=rθ.s=rθ.
Взяв производную по времени и учитывая, что радиус r есть константа, имеем
dsdt=ddt(rθ)=θdrdt+rdθdt=rdθdtdsdt=ddt(rθ)=θdrdt+rdθdt=rdθdt
, где θdrdt=0θdrdt=0. Здесь dsdtdsdt — это просто тангенциальная скорость vtvt частицы на рис. 10.2. Таким образом, используя уравнение 10.3, мы получаем
10.2. Таким образом, используя уравнение 10.3, мы получаем
vt=rω.vt=rω.
10,4
То есть тангенциальная скорость частицы равна ее угловой скорости, умноженной на радиус окружности. Из уравнения 10.4 мы видим, что тангенциальная скорость частицы увеличивается с расстоянием от оси вращения при постоянной угловой скорости. Этот эффект показан на рис. 10.4. Две частицы размещены на разных радиусах на вращающемся с постоянной угловой скоростью диске. При вращении диска тангенциальная скорость увеличивается линейно с радиусом от оси вращения. На рис. 10.4 мы видим, что v1=r1ω1v1=r1ω1 и v2=r2ω2v2=r2ω2. Но диск имеет постоянную угловую скорость, поэтому ω1=ω2ω1=ω2. Это означает v1r1=v2r2v1r1=v2r2 или v2=(r2r1)v1v2=(r2r1)v1. Таким образом, поскольку r2>r1r2>r1, v2>v1v2>v1.
Рисунок 10.4 Две частицы на вращающемся диске имеют разные тангенциальные скорости в зависимости от их расстояния до оси вращения.
До сих пор мы обсуждали величину угловой скорости ω=dθ/dt, ω=dθ/dt, которая является скалярной величиной — изменением углового положения по отношению ко времени. Вектор ω→ω→ — это вектор, связанный с угловой скоростью и направленный вдоль оси вращения. Это полезно, потому что, когда твердое тело вращается, мы хотим знать как ось вращения, так и направление, в котором тело вращается вокруг оси, по часовой стрелке или против часовой стрелки. Угловая скорость ω→ω→ дает нам эту информацию. Угловая скорость ω→ω→ имеет направление, определяемое так называемым правилом правой руки. Правило правой руки состоит в том, что если пальцы правой руки обернутся против часовой стрелки от 9Если отклонить ось 0027 x (направление увеличения θθ) к оси y-, большой палец указывает в направлении положительной оси z (рис. 10.5). Таким образом, угловая скорость ω→ω→, направленная вдоль положительной оси z , соответствует вращению против часовой стрелки, тогда как угловая скорость ω→ω→, направленная вдоль отрицательной оси z , соответствует вращению по часовой стрелке.
Вектор ω→ω→ — это вектор, связанный с угловой скоростью и направленный вдоль оси вращения. Это полезно, потому что, когда твердое тело вращается, мы хотим знать как ось вращения, так и направление, в котором тело вращается вокруг оси, по часовой стрелке или против часовой стрелки. Угловая скорость ω→ω→ дает нам эту информацию. Угловая скорость ω→ω→ имеет направление, определяемое так называемым правилом правой руки. Правило правой руки состоит в том, что если пальцы правой руки обернутся против часовой стрелки от 9Если отклонить ось 0027 x (направление увеличения θθ) к оси y-, большой палец указывает в направлении положительной оси z (рис. 10.5). Таким образом, угловая скорость ω→ω→, направленная вдоль положительной оси z , соответствует вращению против часовой стрелки, тогда как угловая скорость ω→ω→, направленная вдоль отрицательной оси z , соответствует вращению по часовой стрелке.
Рисунок 10,5 Для вращения против часовой стрелки в показанной системе координат угловая скорость указывает на положительные z- направление по правилу правой руки.
Подобно уравнению 10.2, можно установить отношение перекрестного произведения к вектору тангенциальной скорости, как указано в уравнении 10.4. Следовательно, имеем
v→=ω→×r→.v→=ω→×r→.
10,5
То есть тангенциальная скорость представляет собой векторное произведение угловой скорости и вектора положения, как показано на рис. 10.6. Из части (а) этого рисунка видно, что при угловой скорости в положительном z -направление, вращение в плоскости xy против часовой стрелки. В части (b) угловая скорость находится в отрицательном направлении z-, что дает вращение по часовой стрелке в плоскости xy-.
Рисунок 10,6 Показанные векторы представляют собой угловую скорость, положение и тангенциальную скорость. (a) Угловая скорость указывает в положительном направлении z-, что дает вращение против часовой стрелки в плоскости xy-. (b) Угловая скорость указывает на отрицательную z -направление, дающее вращение по часовой стрелке.
Пример 10.1
Вращение маховика
Маховик вращается так, что образует угол со скоростью θ=ωt=(45,0 рад/с)tθ=ωt=(45,0рад/с)t радиан. Колесо вращается против часовой стрелки, если смотреть в плоскости страницы. а) Чему равна угловая скорость маховика? б) Куда направлена угловая скорость? в) Сколько радиан совершает оборот маховика за 30 с? г) Какова тангенциальная скорость точки маховика на расстоянии 10 см от оси вращения?
Стратегия
Функциональная форма углового положения маховика задается в задаче как θ(t)=ωtθ(t)=ωt, поэтому, взяв производную по времени, можно найти угловую скорость. Воспользуемся правилом правой руки, чтобы найти угловую скорость. Чтобы найти угловое смещение маховика за 30 с, ищем угловое смещение ΔθΔθ, где изменение углового положения находится в пределах от 0 до 30 с. Чтобы найти тангенциальную скорость точки на расстоянии от оси вращения, мы умножаем ее расстояние на угловую скорость маховика.
Воспользуемся правилом правой руки, чтобы найти угловую скорость. Чтобы найти угловое смещение маховика за 30 с, ищем угловое смещение ΔθΔθ, где изменение углового положения находится в пределах от 0 до 30 с. Чтобы найти тангенциальную скорость точки на расстоянии от оси вращения, мы умножаем ее расстояние на угловую скорость маховика.
Раствор
- ω=dθdt=45рад/sω=dθdt=45рад/с. Мы видим, что угловая скорость постоянна.
- По правилу правой руки сгибаем пальцы в направлении вращения, то есть против часовой стрелки в плоскости страницы, а большой палец указывает в направлении угловой скорости, которая вне страницы.
- Δθ=θ(30 с)−θ(0 с)=45,0(30,0 с)−45,0(0 с)=1350,0 рад .
- vt=rω=(0,1 м)(45,0 рад/с)=4,5 м/свт=rω=(0,1 м)(45,0 рад/с)=4,5 м/с.
Значение
За 30 с маховик сделал довольно много оборотов, около 215, если разделить угловое перемещение на 2π2π. Таким образом можно использовать массивный маховик для накопления энергии, если потери на трение минимальны. В недавних исследованиях рассматривались сверхпроводящие подшипники, на которые опирается маховик, с нулевыми потерями энергии из-за трения.
Таким образом можно использовать массивный маховик для накопления энергии, если потери на трение минимальны. В недавних исследованиях рассматривались сверхпроводящие подшипники, на которые опирается маховик, с нулевыми потерями энергии из-за трения.
Угловое ускорение
Мы только что обсудили угловую скорость для равномерного кругового движения, но не всякое движение является равномерным. Представьте фигуриста, вращающегося с вытянутыми руками — когда он тянет руки внутрь, его угловая скорость увеличивается. Или подумайте о жестком диске компьютера, который останавливается при уменьшении угловой скорости. Мы рассмотрим эти ситуации позже, но мы уже видим необходимость определения углового ускорения для описания ситуаций, когда изменяется ωω. Чем быстрее изменение ωω, тем больше угловое ускорение. Определим мгновенное угловое ускорение αα как производную угловой скорости по времени:
α=limΔt→0ΔωΔt=dωdt=d2θdt2,α=limΔt→0ΔωΔt=dωdt=d2θdt2,
10,6
, где мы приняли предел среднего углового ускорения α–=ΔωΔtα–=ΔωΔt при Δt→0Δt→0.
Единицы углового ускорения: (рад/с)/с или рад/с2рад/с2.
Таким же образом, как мы определили вектор, связанный с угловой скоростью ω→ω→, мы можем определить α→α→, вектор, связанный с угловым ускорением (рис. 10.7). Если угловая скорость вдоль положительной z- , как на рис. 10.5, и dωdtdωdt положительно, то угловое ускорение α→α→ положительно и направлено вдоль оси +z-+z-. Точно так же, если угловая скорость ω→ω→ направлена вдоль положительной оси z-, а dωdtdωdt отрицательно, то угловое ускорение отрицательно и направлено вдоль оси -z–z-.
Рисунок 10,7 Вращение против часовой стрелки как в (а), так и в (б) с угловой скоростью в том же направлении. (а) Угловое ускорение имеет то же направление, что и угловая скорость, что увеличивает скорость вращения. (b) Угловое ускорение противоположно угловой скорости, что уменьшает скорость вращения.
Мы можем выразить вектор тангенциального ускорения как векторное произведение углового ускорения и вектора положения. Это выражение можно найти, взяв производную по времени от v→=ω→×r→v→=ω→×r→ и оставить в качестве упражнения:
Это выражение можно найти, взяв производную по времени от v→=ω→×r→v→=ω→×r→ и оставить в качестве упражнения:
а→=α→×r→.a→=α→×r→.
10,7
Векторные соотношения для углового ускорения и тангенциального ускорения показаны на рис. 10.8.
Рисунок 10,8 а) Угловое ускорение равно положительному z -направление и создает тангенциальное ускорение против часовой стрелки. (b) Угловое ускорение направлено в отрицательном направлении z и создает тангенциальное ускорение по часовой стрелке.
Мы можем связать тангенциальное ускорение точки на вращающемся теле на расстоянии от оси вращения так же, как мы связали тангенциальную скорость с угловой скоростью. Если мы продифференцируем уравнение 10.4 по времени, отметив, что радиус r константа, получаем
at=rα.at=rα.
10,8
Таким образом, тангенциальное ускорение atat равно произведению радиуса на угловое ускорение. Уравнение 10.4 и уравнение 10.8 важны для обсуждения качения (см. Угловой момент).
Уравнение 10.4 и уравнение 10.8 важны для обсуждения качения (см. Угловой момент).
Давайте применим эти идеи к анализу нескольких простых сценариев вращения с фиксированной осью. Прежде чем сделать это, мы представляем стратегию решения проблем, которая может быть применена к вращательной кинематике: описание вращательного движения.
Стратегия решения проблем
Вращательная кинематика
- Изучите ситуацию, чтобы определить, задействована ли вращательная кинематика (вращательное движение).
- Точно определите, что нужно определить в задаче (идентифицируйте неизвестные). Набросок ситуации полезен.
- Составьте полный список того, что дано или может быть выведено из заявленной проблемы (укажите известное).
- Решите соответствующее уравнение или уравнения для определяемой величины (неизвестной). Может быть полезно подумать в терминах поступательного аналога, потому что теперь вы знакомы с уравнениями поступательного движения.

- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численное решение с единицами измерения. Обязательно используйте радианы для углов.
- Проверьте свой ответ, чтобы убедиться, что он разумен: Имеет ли ваш ответ смысл?
Теперь давайте применим эту стратегию решения проблем к нескольким конкретным примерам.
Пример 10.2
Вращающееся велосипедное колесо
Веломеханик устанавливает велосипед на ремонтный стенд и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об/мин за 5,00 с. (a) Рассчитайте среднее угловое ускорение в рад/с2 рад/с2. (b) Если теперь она нажмет на тормоз, вызывая угловое ускорение −87,3 рад/с2рад/с2, сколько времени понадобится колесу, чтобы остановиться?
Стратегия
Среднее угловое ускорение можно найти непосредственно из его определения α–=ΔωΔtα–=ΔωΔt, поскольку заданы конечная угловая скорость и время. Мы видим, что Δω=ωконечная-ωначальная=250 об/мин, Δω=ωконечная-ωначальная=250 об/мин, а ΔtΔt составляет 5,00 с. Для части (b) мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение среднего углового ускорения и решив ΔtΔt, что дает
Мы видим, что Δω=ωконечная-ωначальная=250 об/мин, Δω=ωконечная-ωначальная=250 об/мин, а ΔtΔt составляет 5,00 с. Для части (b) мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение среднего углового ускорения и решив ΔtΔt, что дает
Δt=Δωα.Δt=Δωα.
Решение
- Вводя известные сведения в определение углового ускорения, получаем
α–=ΔωΔt=250 об/мин5,00 с.α–=ΔωΔt=250 об/мин5,00 с.
Поскольку ΔωΔω выражается в оборотах в минуту (об/мин), а для углового ускорения нам нужны стандартные единицы рад/с2рад/с2, нам нужно преобразовать об/мин в рад/с:Δω=250об/мин·2πрадоб·1мин60с=26,2рад. Δω=250обмин·2πрадоб·1мин60с=26,2рад.
Подставляя эту величину в выражение для αα, получаемα=ΔωΔt=26,2рад/с5,00с=5,24рад/с2.α=ΔωΔt=26,2рад/с5,00с=5,24рад/с2.
- Здесь угловая скорость уменьшается с 26,2 рад/с (250 об/мин) до нуля, так что ΔωΔω составляет −26,2 рад/с, а αα принимается равной –87,3 рад/с2рад/с2.
 Таким образом,
Таким образом,Δt=-26,2рад/с-87,3рад/с2=0,300с. Δt=-26,2рад/с-87,3рад/с2=0,300с.
Значение
Обратите внимание, что угловое ускорение, когда механик вращает колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю.
Проверьте свое понимание 10.1
Лопасти вентилятора турбовентиляторного реактивного двигателя (показанного ниже) разгоняются из состояния покоя до скорости вращения 40,0 об/с за 20 с. Увеличение угловой скорости вентилятора постоянно во времени. (Турбовентиляторный двигатель GE90-110B1, установленный на Boeing 777, как показано, в настоящее время является самым большим турбовентиляторным двигателем в мире, способным развивать тягу 330–510 кН.)
(a) Каково среднее угловое ускорение?
(b) Чему равно мгновенное угловое ускорение в любой момент времени в течение первых 20 с?
Рисунок 10,9 (кредит: «Bubinator»/Wikimedia Commons)
Пример 10.
 3
3Ветряная турбина
Ветряная турбина (рис. 10.10) на ветряной электростанции останавливается на техническое обслуживание. Турбине требуется 30 с для перехода от рабочей угловой скорости до полной остановки, при которой функция угловой скорости имеет вид ω(t)=[(ts−1−30,0)2/100,0]рад/sω(t)=[ (тс-1-30,0)2/100,0] рад/с. Если турбина вращается против часовой стрелки, глядя в страницу, а) каковы направления векторов угловой скорости и ускорения? б) Чему равно среднее угловое ускорение? (c) Каково мгновенное угловое ускорение при t=0,0,15,0,30,0 с?t=0,0,15,0,30,0 с?
Рисунок 10.10 Ветряная турбина, вращающаяся против часовой стрелки, если смотреть сверху.
Стратегия
- Нам дано направление вращения турбины, то есть против часовой стрелки в плоскости страницы. Используя правило правой руки (рис. 10.5), мы можем установить направления векторов угловой скорости и ускорения.

- Рассчитаем начальную и конечную угловые скорости, чтобы получить среднее угловое ускорение. Мы устанавливаем знак углового ускорения из результатов в (а).
- Нам дана функциональная форма угловой скорости, поэтому мы можем найти функциональную форму функции углового ускорения, взяв ее производную по времени.
Решение
- Поскольку турбина вращается против часовой стрелки, угловая скорость ω→ω→ направлена за пределы страницы. Но поскольку угловая скорость уменьшается, угловое ускорение α→α→ указывает на страницу, в противоположном угловой скорости направлении.
- Начальная угловая скорость турбины, настройка t=0,isω=9.0рад/ст=0,isω=9.0рад/с. Конечная угловая скорость равна нулю, поэтому среднее угловое ускорение равно 90 004 =-0,3 рад/с2.
- Взятие производной угловой скорости по времени дает α=dωdt=(t−30,0)/50,0рад/с2α=dωdt=(t−30,0)/50,0рад/с2
α(0,0с)=−0,6рад /с2, α(15,0 с)=-0,3 рад/с2 и α(30,0 с)=0 рад/с.
 α(0,0 с)=-0,6 рад/с2,α(15,0 с)=-0,3 рад/с2 и (30,0 с)=0 рад/с.
α(0,0 с)=-0,6 рад/с2,α(15,0 с)=-0,3 рад/с2 и (30,0 с)=0 рад/с.
Значение
Из расчетов (а) и (б) мы обнаружили, что угловое ускорение αα и среднее угловое ускорение α–α– отрицательны. Турбина имеет угловое ускорение, противоположное ее угловой скорости.
Теперь у нас есть базовый словарь для обсуждения кинематики вращения с фиксированной осью и взаимосвязей между переменными вращения. Мы обсудим больше определений и связей в следующем разделе.
градусов по физике | Колледж науки и техники
Рекомендуемые навигационные ссылки
Программы обучения
Результаты обучения
Новости и события
Студенческие ресурсы
Преподаватели и сотрудники
ФИЗИКА — ФУНДАМЕНТАЛЬНАЯ НАУКА
Физика является фундаментальной наукой, на которой строятся все другие естественные науки и большинство инженерных наук. Это делает физику самой разнообразной и применимой технической специальностью, которую вы можете получить. Физики работают над тем, чтобы глубоко понять самые маленькие вещи, самые большие вещи, самые старые вещи, новейшие вещи и все, что между ними. Люди со степенями физики или работавшие физиками изобрели такие важные инновации, как электроэнергия, электрическая батарея, электродвигатель, радио, рентгеновское изображение, масс-спектрометр, электронный цифровой компьютер, ЯМР и МРТ, ПЭТ-сканирование, ядерная энергия. реактор, транзистор, интегральная схема, лазер, первая видеоигра, беспроводная локальная сеть и всемирная паутина.
Это делает физику самой разнообразной и применимой технической специальностью, которую вы можете получить. Физики работают над тем, чтобы глубоко понять самые маленькие вещи, самые большие вещи, самые старые вещи, новейшие вещи и все, что между ними. Люди со степенями физики или работавшие физиками изобрели такие важные инновации, как электроэнергия, электрическая батарея, электродвигатель, радио, рентгеновское изображение, масс-спектрометр, электронный цифровой компьютер, ЯМР и МРТ, ПЭТ-сканирование, ядерная энергия. реактор, транзистор, интегральная схема, лазер, первая видеоигра, беспроводная локальная сеть и всемирная паутина.
ВАРИАНТЫ СТЕПЕНИ ПО ФИЗИКЕ
Программа Университета Сиэтла по физике предлагает два направления для студентов, желающих получить диплом по физике.
Степень бакалавра наук по физике предназначена для студентов, планирующих поступать в магистратуру по физике, прикладной физике, астрофизике, астрономии, инженерии или другим программам для выпускников или профессионалам.
Степень бакалавра гуманитарных наук по физике предназначена для специалистов по физике, которые ищут больше места в своем расписании, чтобы удвоить специальность или разрешить различные факультативные курсы из других факультетов.
Узнайте больше здесь: Программы обучения
МАЛЕНЬКИЙ КЛАСС, Внимательный преподавательский состав, сложная учебная программаФизический факультет Сиэтлского университета предлагает небольшие классы и индивидуальный подход к обучению студентов, специализирующихся в области физики. Активные исследования нашего факультета вносят свой вклад в знания, оживляют классы и предоставляют мотивированным студентам возможность участвовать в текущих исследовательских проектах. Зачем идти в огромный университет с гигантскими обезличенными классами, которые ведут аспиранты? В Сиэтлском университете вас обучают заботливые, преданные своему делу и очень способные профессора.
В центре внимания выпускников
Роуз Мари учится в Орегонском университете, где изучает оптические материалы и устройства в рамках магистерской программы промышленной стажировки, в рамках которой студенты проходят два семестра интенсивной курсовой работы, за которой следует трехсеместровая стажировка.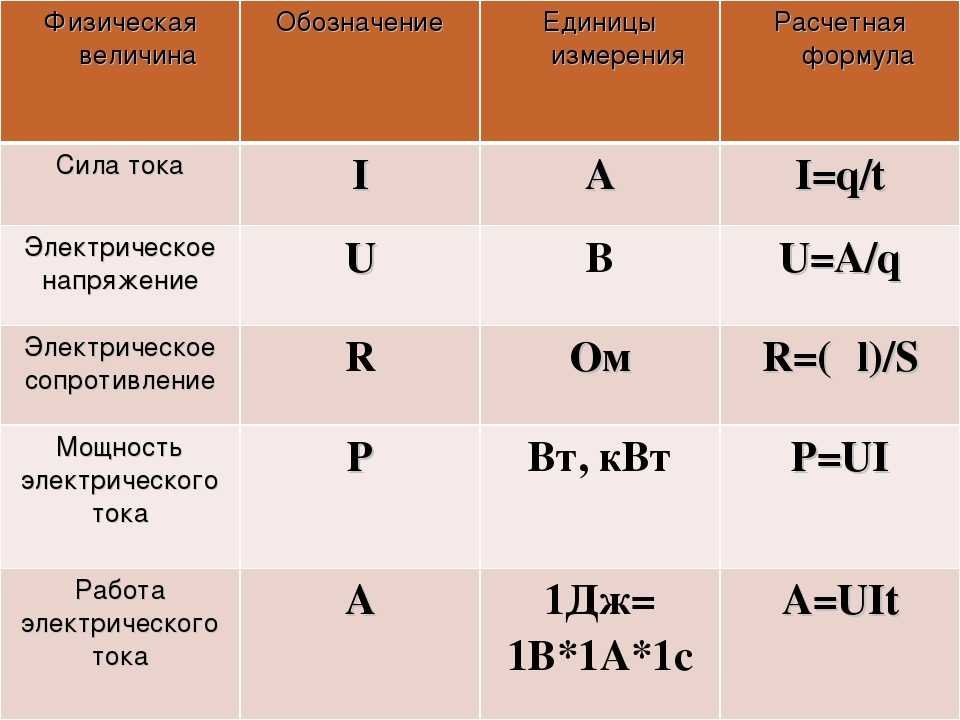 В январе она начнет свою стажировку в компании Thermo Fisher Scientific в Хиллсборо, штат Орегон, где войдет в состав группы инженеров по разработке приложений для электронных микроскопов и сфокусированных ионных пучков.
В январе она начнет свою стажировку в компании Thermo Fisher Scientific в Хиллсборо, штат Орегон, где войдет в состав группы инженеров по разработке приложений для электронных микроскопов и сфокусированных ионных пучков.
Роуз Мари Хейнс ’17
РАЗЛИЧНЫЕ ПРОФЕССИОНАЛЬНЫЕ РАБОТЫ ДЛЯ ВЫПУСКНИКОВ ФИЗИКИ
Выпускники нашего физического факультета нашли интересную техническую работу или продолжили обучение в аспирантуре в области физики, астрономии, геофизики, машиностроения, электротехники и биомедицины. У нас есть выпускники, которые летают на переоборудованных самолетах-шпионах для НАСА, работают инженерами и физиками в частных корпорациях, государственных лабораториях и университетах, программируют компьютеры или управляют компьютерными сетями.
В последние годы мы направили выпускников факультета физики SU на докторские программы по физике, машиностроению, планетарным наукам, электротехнике, аэрокосмической технике и математике в Стэнфорде, Калифорнийском университете в Сан-Диего, Аризоне, штате Огайо, Калифорнийском университете в Санта-Барбаре, Мичиган, Орегон, Вандербильт, штат Пенсильвания, штат Висконсин, штат Техас A&M, штат Пердью и Сан-Диего.

 И. Копейкин, Ю.Н. Панин, А.А. Сабельников
И. Копейкин, Ю.Н. Панин, А.А. Сабельников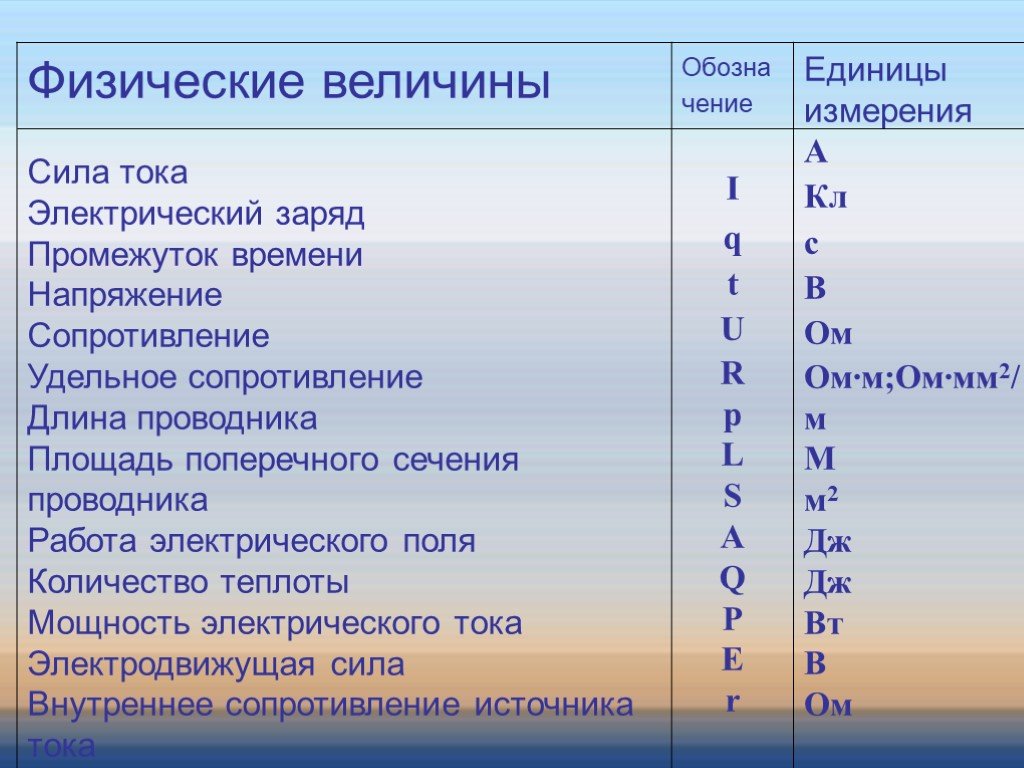 А. Ремнев, Ю.В. Усов
А. Ремнев, Ю.В. Усов Пахтусова, К.В. Пугачев, Я.C. Савченко, С.И. Середняков, З.К. Силагадзе, И.К. Сурин, Ю.В. Усов, А.Г. Харламов, Д.А. Штоль
Пахтусова, К.В. Пугачев, Я.C. Савченко, С.И. Середняков, З.К. Силагадзе, И.К. Сурин, Ю.В. Усов, А.Г. Харламов, Д.А. Штоль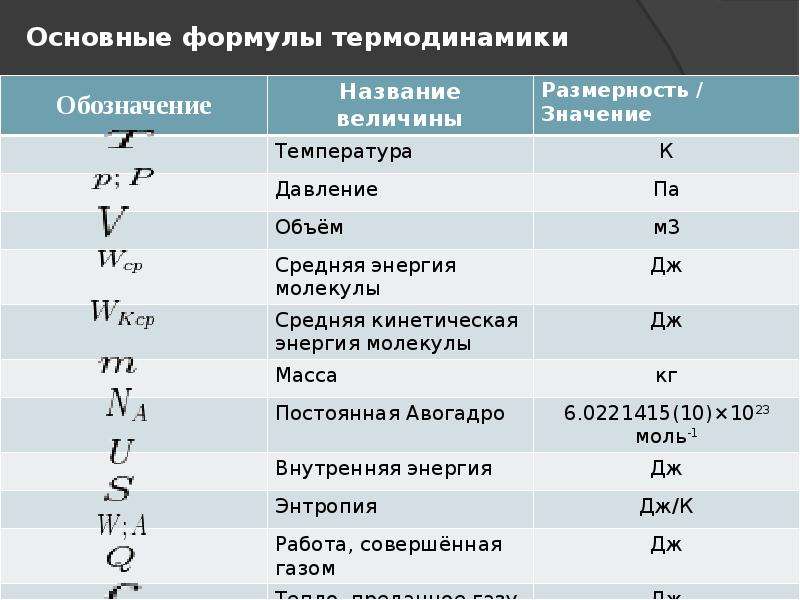 В. Григоренко, Г.Н. Кропачев, Т.В. Кулевой, И.Н. Мешков, С.М. Полозов, А.С. Фомичев, Б.Ю. Шарков, П.Ю. Шатунов, М.И. Явор
В. Григоренко, Г.Н. Кропачев, Т.В. Кулевой, И.Н. Мешков, С.М. Полозов, А.С. Фомичев, Б.Ю. Шарков, П.Ю. Шатунов, М.И. Явор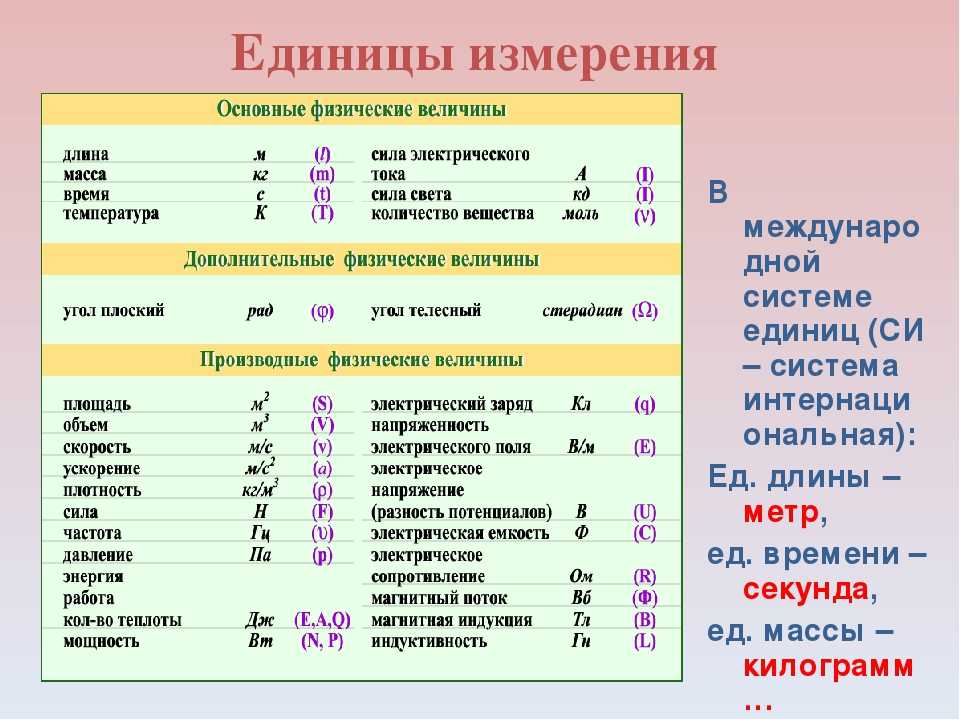 В. Котиков, С. Тебер
В. Котиков, С. Тебер
 Таким образом,
Таким образом,
 α(0,0 с)=-0,6 рад/с2,α(15,0 с)=-0,3 рад/с2 и (30,0 с)=0 рад/с.
α(0,0 с)=-0,6 рад/с2,α(15,0 с)=-0,3 рад/с2 и (30,0 с)=0 рад/с.