Умножение столбиком. Онлайн калькулятор | Математика
- Как умножать столбиком
- Калькулятор умножения столбиком
Как умножать столбиком
Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.
Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить 846 на 5:
Умножить 846 на 5 — значит, сложить 5 чисел, каждое из которых равно 846. Для этого достаточно взять сначала 5 раз по 6 единиц, потом 5 раз по 4 десятка и наконец 5 раз по 8 сотен.
- 5 раз по 6 единиц = 30 единиц, т. е. 3 десятка. Пишем 0 под чертой на месте единиц, а 3 десятка запоминаем.

- 5 раз по 4 десятка = 20 десятков, прибавляем к ним ещё 3 десятка = 23 десятка, т. е. 2 сотни и 3 десятка. Пишем 3 десятка под чертой на месте десятков, а 2 сотни запоминаем:
- 5 раз по 8 сотен = 40 сотен, прибавляем к ним ещё 2 сотни = 42 сотни. Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:
Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить 3826 на 472:
Умножить 3826 на 472 — значит, сложить 472 одинаковых числа, каждое из которых равно 3826. Для этого надо сложить 3826 сначала 2 раза, потом 70 раз, потом 400 раз, т. е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.
2 раза по 3826 = 7652. Пишем полученное произведение под чертой:
Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением. Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.
Умножаем 3826 на 7. Это будет второе частичное произведение (26782):
Умножаем множимое на 4. Это будет третье частичное произведение (15304):
Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение (1 805 872):
Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:
Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.
Например, необходимо вычислить 23 000 · 4500. Сначала умножим 23 на 45, не обращая внимание на нули:
И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится 103 500 000.
Калькулятор умножения столбиком
Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку Вычислить
.
Решётчатое умножение | Наука и жизнь
Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа. В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.
Умножение способом решётки. Иллюстрация из первой печатной книги по арифметике. 1487 год.
Палочки Непера. Этот простой счётный прибор впервые был описан в сочинении Джона Непера «Рабдология». 1617 год.
Этот простой счётный прибор впервые был описан в сочинении Джона Непера «Рабдология». 1617 год.
Джон Непер (1550—1617).
Модель счётной машины Шиккарда. Это не дошедшее до нас вычислительное устройство изготовлено изобретателем в 1623 году и описано им годом позже в письме Иоганну Кеплеру.
Вильгельм Шиккард (1592—1635).
‹
›
Открыть в полном размере
Наследие индусов — способ решётки
Индусы, с давних времён знавшие десятичную систему счисления, предпочитали устный счёт письменному. Они изобрели несколько способов быстрого умножения. Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, — умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Этим способом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения — в Европе. Способ решётки именовали также индийским, мусульманским или «умножением в клеточку». А в Италии его называли «джелозия», или «решётчатое умножение» (gelosia в переводе с итальянского — «жалюзи», «решётчатые ставни»). Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями-жалюзи, которые закрывали от солнца окна венецианских домов.
Суть этого нехитрого способа умножения поясним на примере: вычислим произведение 296 × 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, — по количеству цифр в множителях. Разделим клетки пополам по диагонали. Над таблицей запишем число 296, а с правой стороны вертикально — число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.
Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.
Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
Почему способ решётки приводит к правильному ответу? В чём заключается его «механизм»? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 + 90 + 6 и 70 + 3.
Как видим, в первой косой полосе стоят единицы, во второй — десятки, в третьей — сотни и т.д. При сложении они дают в ответе соответственно число единиц, десятков, сотен и т.д. Дальнейшее очевидно:
Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:
296 x 73 = (200 + 90 + 6) x (70 + 3) = 14 000 + 6300 + 420 + 600 + 270 + 18 = 10 000 + (4000 + 6000) + (300 + 400 + 600 + 200) + (70 + 20 + 10) + 8 = 21 608.
Палочки Непера
Умножение способом решётки лежит в основе простого и оригинального счётного прибора — палочек Непера. Его изобретатель Джон Непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.
Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней — число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек Непера легко умножать многозначные числа, сводя эту операцию к сложению.
В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней — число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек Непера легко умножать многозначные числа, сводя эту операцию к сложению.
Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие — с цифрами 2, 9 и 6 наверху (они должны образовать число 296). Теперь заглянем в третью строку (номера строк указаны на крайней линейке). Цифры в ней образуют уже знакомый нам набор.
Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, рассмотрев седьмую строку, найдём, что 296 x 7 = 2072, тогда 296 x 70 = 20 720. Таким образом,
296 x 73 = 20 720 + 888 = 21 608.

Палочки Непера применялись и для более сложных операций — деления и извлечения квадратного корня. Этот счётный прибор не раз пытались усовершенствовать и сделать более удобным и эффективным в работе. Ведь в ряде случаев для умножения чисел, например с повторяющимися цифрами, нужны были несколько комплектов палочек. Но такая проблема решалась заменой линеек вращающимися цилиндрами с нанесённой на поверхность каждого из них таблицей умножения в том же виде, как её представил Непер. Вместо одного набора палочек получалось сразу девять.
Подобные ухищрения в самом деле ускоряли и облегчали расчёты, однако не затрагивали главный принцип работы прибора Непера. Так способ решётки обрел вторую жизнь, продлившуюся ещё несколько столетий.
Машина Шиккарда
Учёные давно задумывались над тем, как переложить непростую вычислительную работу на механические устройства. Первые успешные шаги в создании счётных машин удалось осуществить только в XVII столетии. Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард. Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру. Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.
Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард. Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру. Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.
По сути, машина Шиккарда представляет собой шестиразрядный механический калькулятор, выполняющий сложение, вычитание, умножение и деление чисел. В ней три части: множительное устройство, суммирующее устройство и механизм для сохранения промежуточных результатов. Основой для первого послужили, как нетрудно догадаться, палочки Непера, свёрнутые в цилиндры. Они крепились на шести вертикальных осях и поворачивались с помощью специальных ручек, расположенных наверху машины. Перед цилиндрами располагалась панель с девятью рядами окошек по шесть штук в каждом, которые открывались и закрывались боковыми задвижками, когда требовалось увидеть нужные цифры и скрыть остальные.
В работе счётная машина Шиккарда очень проста. Чтобы узнать, чему равно произведение 296 x 73, нужно установить цилиндры в положение, при котором в верхнем ряду окошек появится первый множитель: 000296. Произведение 296 x 3 получим, открыв окошки третьего ряда и просуммировав увиденные цифры, как в способе решётки. Точно так же, открыв окошки седьмого ряда, получим произведение 296 x 7, к которому припишем справа 0. Остаётся только сложить найденные числа на суммирующем устройстве.
Придуманный некогда индусами быстрый и надёжный способ умножения многозначных чисел, много веков применявшийся при расчётах, ныне, увы, забыт. А ведь он мог бы выручить нас и сегодня, если бы под рукой не оказалось столь привычного всем калькулятора.
Сможете ли вы пройти этот тест на умственное умножение?
“”
Изображение: Wavebreakmedia Ltd/Wavebreak Media/Getty Images Plus/Getty Images
Обращаемся ко всем любителям математики: если вы любите умножать числа для развлечения, вы получите массу удовольствия, пытаясь умножить числа в этой викторине вместе ! Некоторые вопросы довольно просты, например, 7 умножить на 11 (что равно 77), в то время как другие требуют, чтобы вы знали, как умножать квадратные корни, числа в квадрате и кубе, а также десятичные дроби.
Давайте разогреемся, решим несколько практических задач. Попробуйте угадать, сколько будет 10 умножить на 5. Ответ должен прийти к вам довольно быстро: 50! Теперь как насчет 10 раз -2? Так как мы умножаем одно отрицательное число и одно положительное число вместе, ответ всегда будет отрицательным. Так что в данном случае правильный ответ -20.
Теперь попробуем вместе умножить квадратные корни. Перед умножением квадратных корней важно сначала извлечь фактический квадратный корень из числа. Например, давайте попробуем вычислить, что такое √25, умноженное на √1. Что ж, квадратный корень из 25 равен 5, так как 5 умножить на 5 равно 25. Квадратный корень из 1 равен 1, потому что 1 умножить на 1 равно 1. Итак, задача становится 25 умножить на 1, что равно 25!
Теперь, когда вы познакомились с разминкой, мы думаем, вы готовы пройти этот тест на умножение в уме! Удачи!
Думаешь, ты знаешь, сколько будет 7 умножить на 7?
Если умножить 7 на 7, получится 49. Это означает, что квадратный корень из 49 тоже равен 7.
Это означает, что квадратный корень из 49 тоже равен 7.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Что получится, если умножить 5 и 6?
Когда вы умножаете 5 и 6 вместе, вы получаете 30. Как следует из подсказки, 20 + 10 тоже 30.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Сколько будет 0 умножить на 10?
Ответ равен 0. Когда вы умножаете что-либо на 0, ответ равен 0.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 1 умножить на 20?
20 — правильный ответ. Когда вы умножаете любое число, например 20, 5 или 10, на 1, ответ все равно будет 20, 5 или 10.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Какое число получится, если умножить 3 и 11?
Ответ 33. Другой пример: 11 умножить на 4 будет 44, а 11 умножить на 5 будет 55.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Угадайте, сколько будет 10 умножить на 10?
Если умножить 10 на 10, получится 100. Это означает, что квадратный корень из 100 равен 10.
Это означает, что квадратный корень из 100 равен 10.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Что произойдет, если умножить -1 и 1 вместе?
Невозможно вычислить
-1 правильный ответ. Когда вы умножаете положительное и отрицательное число вместе, ответ всегда отрицательный.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Попробуйте угадать -2 умножить на -2!
2 + 2 равно 4 и -2 умножить на -2 тоже четыре. Когда вы умножаете два отрицательных числа вместе, ответ всегда положительный.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 5 умножить на 5 умножить на 5?
125 — правильный ответ. Другой способ переписать это 5(5)(5) или 25(5).
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 3 раза 2 раза 1?
6 правильный ответ. Другой способ переписать это — 3(2)(1). 3(2) равно 6 и 6(1) равно 6.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Можете ли вы сосчитать, сколько будет 10 умножить на 0,50?
5 правильный ответ. Когда вы умножаете число на 0,5, вы просто делите это число пополам.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 3 раза -3 раза 3?
-27 правильный ответ. Посмотрите на задачу так: 3(-3)(3), что равно -9(3), что равно -27.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Что произойдет, если 24 умножить на 0,25?
6 правильный ответ. Когда вы умножаете 24 на 0,25, вы просто делите это число на четверти или четверти. Другими словами, 6(4) равно 24, то есть 24 умножить на 0,25.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Попробуйте угадать, сколько будет 0,50 на 0,50!
1/4 или 0,25 — правильный ответ. Когда вы умножаете 0,50 и 0,50 вместе, вы получаете меньшее число, равное 0,25.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 25 умножить на 2?
50 — правильный ответ. Когда вы умножаете число на 2, вы просто удваиваете это число.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сможете ли вы вычислить, сколько будет 0,75 умножить на 100?
Ответ: 75. Когда вы умножаете десятичную дробь на 100, вы просто сдвигаете эту десятичную дробь вправо два раза.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 1000 раз 0,15?
Ответ: 150. Когда вы умножаете десятичную дробь на 1000, все, что вам нужно сделать, это переместить десятичную дробь вправо три раза, следовательно, 0,15 станет 150.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Что такое -2 умножить на -4 умножить на -10?
-80 – правильный ответ. Когда вы умножаете три отрицательных числа вместе, ответ всегда отрицательный.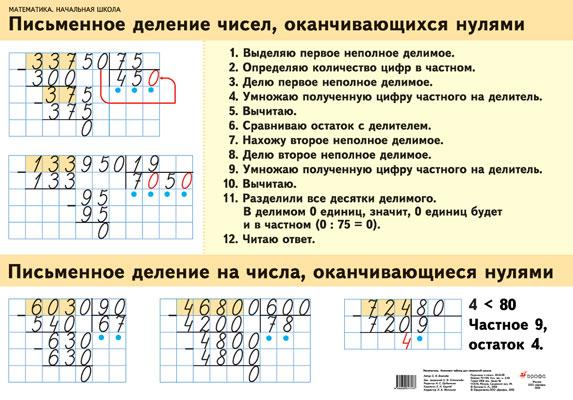
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет √25 умножить на √9?
Ответ 15. И вот почему: квадратный корень из 25 равен 5, а квадратный корень из 9равно 3,5 умножить на 3 равно 15.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Что получится, если умножить √9, √16 и √4 вместе?
Правильный ответ: 24. Квадратный корень из 9 равен 3, квадратный корень из 16 равен 4, а квадратный корень из 4 равен 2. 3 умножить на 4 умножить на 2 равно 24.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет -√4 умножить на -√4?
Правильный ответ: 4. -√4 равно -2, так как квадратный корень из 4 равен 2, но перед ним стоит знак минус, поэтому получается -2. -2 раза -2 равно 4.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Можете ли вы угадать, сколько будет √1 умножить на √0?
Ответ: 0. √1 равно 1 и √0 равно 0, поэтому 1 умножить на 0 равно 0.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет (2²) умножить на (3²)?
36 — правильный ответ. 2² равно 4, а 3² равно 9, поэтому 4 умножить на 9 равно 36.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Думаешь, ты знаешь, сколько будет 3³ умножить на 1³?
27 — правильный ответ. 3³ равно 27, так как это в основном 3(3)(3). 1³ равно 1, поэтому 27 умножить на 1 равно 27.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Что такое -5 раз (5²)?
-125 правильный ответ. 5² равно 25, поэтому 25 умножить на -5 будет -125.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Умножьте эти числа вместе: √4, -4 и (2²).
Если вы угадали -32, вы правы! √4 равно 2, а (2²) равно 4, поэтому задача состоит всего лишь в том, что 2 умножить на -4 умножить на 4, что равно -32.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 20 раз -0,25?
-5 правильно. Умножение числа на 0,25 — это просто четвертование этого числа, поэтому, когда вы четвертуете 20, вы получаете 5. Но поскольку 0,25 отрицательно, оно становится -5.
Умножение числа на 0,25 — это просто четвертование этого числа, поэтому, когда вы четвертуете 20, вы получаете 5. Но поскольку 0,25 отрицательно, оно становится -5.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сможете ли вы вычислить, что такое √100, умноженное на 0,50?
Правильный ответ: 5. √100 равно 10, а 10 умножить на 0,50 равно 5.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет -√25 умножить на -1?
Ответ: 5. -√25 равно -5, потому что квадратный корень из 25 равен 5, но поскольку перед ним стоит знак минус, получается -5. -5 раз -1 равно 5.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 50% умножить на 100?
50 — правильный ответ. 50% можно переписать как 0,50, а 0,50 умножить на 100 равно 50 (это всего лишь половина от 100).
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Угадайте, сколько будет 10% умножить на √36?
Ответ: 0,60. Хотя проблема выглядит сложной, просто разберите ее шаг за шагом. √36 равно 6, так как 6 умножить на 6 равно 36. 10% можно переписать как 0,10, так что теперь проблема 0,10 умножить на 6, что равно 0,6. Вы просто перемещаете невидимый десятичный знак перед 6 влево один раз.
Хотя проблема выглядит сложной, просто разберите ее шаг за шагом. √36 равно 6, так как 6 умножить на 6 равно 36. 10% можно переписать как 0,10, так что теперь проблема 0,10 умножить на 6, что равно 0,6. Вы просто перемещаете невидимый десятичный знак перед 6 влево один раз.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Сколько будет 10 умножить на 10 умножить на 10?
1000 — правильный ответ. 10 умножить на 10 — это 100, а 100 умножить на 10 — это 1000.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Что получится, если умножить 6 и -10 вместе?
-60 правильный ответ. Когда вы умножаете положительное число и отрицательное число вместе, вы получаете отрицательное число.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Попробуйте угадать, сколько будет 10 умножить на 5!
50 — правильный ответ. 10 умножить на 5 будет 50, значит 50/10 будет 5, а 50/5 будет 10.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
Как вы думаете, сколько будет 7 умножить на 11?
77 — правильный ответ. 11 умножить на 7 — это 77, точно так же, как 6 умножить на 11 — это 66, а 5 умножить на 11 — это 55.
ЗАВЕРШЕНИЕ ВИКТОРИНЫ
Реклама
Реклама
Вы получили:
/35
Wavebreakmedia Ltd/Wavebreak Media/Getty Images Plus/Getty Images
Об умственном умножении и возрасте
Сохранить цитату в файл
Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Не удалось загрузить вашу коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Невозможно загрузить делегатов из-за ошибки
Пожалуйста, попробуйте еще раз
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл. адрес:
(изменить)
адрес:
(изменить)
Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день
Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота
Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed
Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
. 1992 декабрь; 7 (4): 536-45.
doi: 10.1037//0882-7974. 7.4.536.
7.4.536.
П А Аллен 1 , М. Х. Эшкрафт, Т. А. Вебер
принадлежность
- 1 Факультет психологии, Кливлендский государственный университет, Огайо 44115.
- PMID: 1466822
- DOI: 10.1037//0882-7974.7.4.536
П.А. Аллен и соавт. Психологическое старение. 1992 Декабрь
. 1992 декабрь; 7 (4): 536-45.
дои: 10.1037//0882-7974.7.4.536.
Авторы
П А Аллен 1 , М. Х. Эшкрафт, Т. А. Вебер
Х. Эшкрафт, Т. А. Вебер
принадлежность
- 1 Факультет психологии, Кливлендский государственный университет, Огайо 44115.
- PMID: 1466822
- DOI: 10.1037//0882-7974.7.4.536
Абстрактный
В 2 экспериментах младшим и пожилым людям предлагались простые задачи на умножение (например, 4 x 7 = 28 и 5 x 3 = 10) для их рассчитанных на время, истинных или ложных суждений. Были получены все эффекты, обычно наблюдаемые в фундаментальных исследованиях ментальной арифметики, то есть время реакции (а) увеличивалось с размером задачи, (б) замедлялось для ответов, лишь незначительно отличающихся от правильного значения, и ( c) замедлялся при представлении связанных (например, 7 x 4 = 21) ответов по сравнению с несвязанными (например, 7 x 4 = 18) ответами. Пожилые люди были медленнее в своих суждениях. Самое главное, что возраст существенно не влиял на размер проблемы или размер разделения. Авторы предполагают, что центральные процессы пожилых людей, такие как восстановление памяти и принятие решений, не демонстрировали типичного возрастного дефицита из-за квалифицированного характера этих процессов в простой арифметике.
Пожилые люди были медленнее в своих суждениях. Самое главное, что возраст существенно не влиял на размер проблемы или размер разделения. Авторы предполагают, что центральные процессы пожилых людей, такие как восстановление памяти и принятие решений, не демонстрировали типичного возрастного дефицита из-за квалифицированного характера этих процессов в простой арифметике.
Похожие статьи
Процессы поиска в арифметическом производстве и проверке.
Кэмпбелл Дж.И., Тарлинг Д.П. Кэмпбелл Дж.И. и др. Мем Когнит. 1996 март; 24(2):156-72. дои: 10.3758/bf03200878. Мем Когнит. 1996. PMID: 8881320
Возрастные различия в умственном умножении: свидетельство периферического, но не центрального упадка.
Аллен П.
83 А., Смит А.Ф., Джердж К.А., Вирес-Коллинз Х.
Аллен П.А. и соавт.
J Gerontol B Psychol Sci Soc Sci. 1997 март; 52 (2): P81-90. doi: 10.1093/geronb/52b.2.p81.
J Gerontol B Psychol Sci Soc Sci. 1997.
PMID:
А., Смит А.Ф., Джердж К.А., Вирес-Коллинз Х.
Аллен П.А. и соавт.
J Gerontol B Psychol Sci Soc Sci. 1997 март; 52 (2): P81-90. doi: 10.1093/geronb/52b.2.p81.
J Gerontol B Psychol Sci Soc Sci. 1997.
PMID:Влияет ли дефицит контроля времени на отсроченное смещение памяти у пожилых людей во время приобретения навыков?
Hertzog C, Touron DR, Hines JC. Герцог С. и соавт. Психологическое старение. 2007 сен; 22 (3): 607-24. дои: 10.1037/0882-7974.22.3.607. Психологическое старение. 2007. PMID: 17874958
Стратегическое превосходство пожилых людей с умственным умножением: оценка эффекта поколения.
Песта Б.Дж., Сандерс Р.Е., Немек Р.Дж. Песта Б.Дж. и др. Exp Aging Res. 1996 г., апрель-июнь; 22(2):155-69.
 дои: 10.1080/03610739608254004.
Exp Aging Res. 1996.
PMID: 8735150
дои: 10.1080/03610739608254004.
Exp Aging Res. 1996.
PMID: 8735150Возрастной дефицит ассоциативной памяти: влияние нарушения стратегического поиска.
Кон М., Эмрих С.М., Москович М. Кон М. и др. Психологическое старение. 2008 март; 23(1):93-103. дои: 10.1037/0882-7974.23.1.93. Психологическое старение. 2008. PMID: 18361659
Посмотреть все похожие статьи
Цитируется
Влияние успеха в выполнении предшествующих задач на когнитивные способности молодых и пожилых людей: оценка гипотезы стратегии.
Лемер П., Брун Ф. Лемер П. и соавт. Дж Когн. 20 фев 2018; 1(1):14. doi: 10.5334/joc.17. Дж Когн. 2018. PMID: 31517188 Бесплатная статья ЧВК.

Обучение арифметике в пожилом возрасте.
Замарян Л., Шерфлер С., Кремсер С., Пертл М.Т., Гижевски Э., Бенке Т., Делазер М. Замарян Л. и др. ПЛОС Один. 28 февраля 2018 г.; 13(2):e0193529. doi: 10.1371/journal.pone.0193529. Электронная коллекция 2018. ПЛОС Один. 2018. PMID: 29489905 Бесплатная статья ЧВК.
Используют ли пожилые люди метод локусов? Результаты исследования ACTIVE.
Гросс А.Л., Брандт Дж., Бандин-Рош К., Карлсон М.С., Стюарт Э.А., Марсиске М., Ребок Г.В. Гросс А.Л. и др. Exp Aging Res. 2014;40(2):140-63. doi: 10.1080/0361073X.2014.882204. Exp Aging Res. 2014. PMID: 24625044 Бесплатная статья ЧВК. Клиническое испытание.
Специфическое для ответа замедление в пожилом возрасте выявляется посредством дифференциального воздействия стимула и ответа на латентный период P300 и время реакции.



 А., Смит А.Ф., Джердж К.А., Вирес-Коллинз Х.
Аллен П.А. и соавт.
J Gerontol B Psychol Sci Soc Sci. 1997 март; 52 (2): P81-90. doi: 10.1093/geronb/52b.2.p81.
J Gerontol B Psychol Sci Soc Sci. 1997.
PMID:
А., Смит А.Ф., Джердж К.А., Вирес-Коллинз Х.
Аллен П.А. и соавт.
J Gerontol B Psychol Sci Soc Sci. 1997 март; 52 (2): P81-90. doi: 10.1093/geronb/52b.2.p81.
J Gerontol B Psychol Sci Soc Sci. 1997.
PMID: дои: 10.1080/03610739608254004.
Exp Aging Res. 1996.
PMID: 8735150
дои: 10.1080/03610739608254004.
Exp Aging Res. 1996.
PMID: 8735150
