Умножение матриц | это… Что такое Умножение матриц?
Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.
Содержание
|
Определение
Пусть даны две прямоугольные матрицы и размерности и соответственно:
Тогда матрица размерностью называется их произведением:
где:
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Следует заметить, что из существования произведения вовсе не следует существование произведения
Иллюстрация
Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений строк матрицы A и столбцов матрицы B. Элемент матрицы AB с индексами i, j есть скалярное произведение i-ой строки матрицы A и j-го столбца матрицы B.
Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы
Значения на пересечениях отмеченных кружочками будут:
В общем случае, произведение матриц не является коммутативной операцией. К примеру:
К примеру:
Элемент произведения матриц приведённых выше вычисляется следующим образом
Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент на пересечении строки и столбца результирующей матрицы является скалярным произведением -й строки первой матрицы и -го столбца второй матрицы. Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.
Мотивировка
Описанное правило матричного умножения прозрачнее всего мотивируется исходя из умножения вектора на матрицу.
Последнее естественно вводится исходя из того, что при разложении векторов по базису действие (любого) линейного оператора A дает выражение компонент вектора v’ = Av:
-то есть линейный оператор оказывается представлен матрицей, векторы – векторами-столбцами, а действие оператора на вектор – матричным умножением вектора-столбца слева на матрицу оператора (это частный случай матричного умножения, когда одна из матриц – вектор-столбец – имеет размер 1х

(Равно переход к любому новому базису при смене координат представляется полностью аналогичным выражением, только в этом случае уже не компоненты нового вектора в старом базисе, а компоненты старого вектора в новом базисе; при этом – элементы матрицы перехода к новому базису).
Далее, рассмотрев последовательное действие на вектор двух операторов: сначала
откуда видно, что композиции BA действия линейных операторов A и B (или аналогичной композиции преобразований базиса) соответствует матрица, вычисляемая по рецепту произведения соответствующих матриц:
Определенное таким образом произведение матриц оказывается совершенно естественным и очевидно полезным (дает простой и универсальный способ вычисления композиций произвольного количества линейных преобразований).
Свойства
Сочетательное свойство:
Распределительное свойство:
- .

Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице:
Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице:
Если и — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.
Умножение матриц в целом некоммутативно:
Если , то матрицы и называются перестановочными или коммутирующими между собой.
Определитель и след произведения не зависят от порядка умножения матриц:
Обратная матрица
Основная статья: Обратная матрица
Квадратная матрица называется неособенной (невырожденной), если она имеет единственную обратную матрицу такую, что выполняется условие:
В противном случае матрица называется особенной (вырожденной).
Матрица порядка является невырожденной в том и только в том случае, если в этом случае есть квадратная матрица того же порядка
где — алгебраическое дополнение элемента в определителе
Алгоритмы быстрого перемножения матриц
Сложность вычисления произведения матриц по определению составляет Θ(n3), однако существуют более эффективные алгоритмы
- Алгоритм Штрассена (1969)
- Первый алгоритм быстрого умножения матриц был разработан В. Штрассеном[2] в 1969. В основе алгоритма лежит рекурсивное разбиение матриц на блоки. На каждом этапе рекурсии выполняется семь умножений вместо восьми. В результате сложность этого алгоритма составляет . Недостатком данного метода является бо́льшая сложность программирования по сравнению со стандартным алгоритмом, численная неустойчивость и большой объём используемой памяти.
- Разработано большое количество алгоритмов на основе метода Штрассена, которые улучшают его численную устойчивость и уменьшают объём используемой памяти.
- Алгоритм Пана (1978)
- В 1978 Пан[3] предложил свой метод умножения матриц, сложность которого составила Θ(n2.78041).
- Алгоритм Бини (1979)
- В 1979 группа итальянских учёных во главе с Бини[4] разработала алгоритм умножения матриц с использованием тензоров.
 Его сложность составляет Θ(n
Его сложность составляет Θ(n
- В 1979 группа итальянских учёных во главе с Бини[4] разработала алгоритм умножения матриц с использованием тензоров.
- Алгоритмы Шёнхаге (1981)
- В 1981 Шёнхаге[5] представил метод, работающий со сложностью Θ(n2.695), который он назвал частичным матричным умножением. Позже ему удалось получить оценку Θ(n2.6087).
- Затем Шёнхаге создал метод, названный методом прямых сумм, сложность которого составляет Θ(n2.548). Романи сумел понизить оценку до Θ(n2.5166), а Пан — до Θ(n2.5161).
- Алгоритм Копперсмита — Винограда (1990)
- В 1990 Копперсмит и Виноград[6] опубликовали алгоритм, умножающий матрицы со сложностью O(n2.3727)

- В 1990 Копперсмит и Виноград[6] опубликовали алгоритм, умножающий матрицы со сложностью O(n2.3727)
- Алгоритмы с использованием теории групп (2003)
- В 2003 Кох и др. рассмотрели в своих работах[8] алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали возможность существования алгоритмов умножения матриц со сложностью Θ(n2)[9].
См. также
- Произведение Кронекера
Литература
- Корн Г., Корн Т. Алгебра матриц и матричное исчисление // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 392—394..
Примечания
- ↑ Кибернетический сборник. Новая серия. Вып. 25. Сб. статей 1983 — 1985 гг.: Пер. с англ. — М.: Мир, 1988 — В.Б. Алекссев. Сложность умножения матриц. Обзор.
- ↑ Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969
- ↑ Pan V. Ya, Strassen’s algorithm is not optimal — trilinear technique of aggregating uniting and canceling for constructing fast algorithms for matrix operations.

- ↑ Bini D., Capovani M., Lotti G., Romani F. — complexity for approximate matrix multiplication. — Inform. Process. Lett., 1979
- ↑ Schonhage A. Partial and total matrix multiplication. – SIAM J. Comput., 1981
- ↑ Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation, 9:251–280, 1990.
- ↑ Williams, Virginia (2011), Breaking the Coppersmith-Winograd barrier.
- ↑ Group-theoretic Algorithms for Matrix Multiplication
- ↑ Toward an Optimal Algorithm for Matrix Multiplication
Матричное умножение. Медленное достижение мифической цели / Хабр
В недавней работе был установлен новый рекорд скорости по умножению двух матриц. Она также знаменует и конец эпохи для метода, который ученые применяли для исследований на протяжении десятилетий.
Математики стремятся к достижению мифической цели — второй степени (exponent two), то есть к умножению пары матриц n х n всего за n2 шагов. Исследователи подбираются все ближе к своей цели, но получится ли у них когда-нибудь достичь ее?
Для специалистов в области Computer Science и математиков сама идея о «второй степени» связана с представлениями о совершенном мире.
«Трудно разграничить научное мышление и беспочвенные мечтания», — признается Крис Уманс из Калифорнийского технологического института. «Я хочу, чтобы степень была равна двум, потому что это красиво».
С точки зрения необходимого количества шагов «вторая степень» — это идеальная скорость выполнения одной из самых фундаментальных математических операций — матричного умножения. Если вторая степень достижима, то матричное умножение получится выполнять максимально быстро, насколько это физически возможно. Если это не так, то мы застряли в мире, который не соответствует нашим мечтам.
Матрицы представляют собой массивы чисел. Когда две матрицы согласованы (число столбцов в первом сомножителе равно числу строк во втором), их можно перемножить, чтобы получить третью. Например, если вы начнете с пары матриц 2 х 2, их произведение также будет матрицей 2 х 2, содержащей четыре элемента. В более общем смысле, произведение пары матриц размером n х n представляет собой другую матрицу размером n х n с n2 элементами.
Поэтому наименьшее возможное количество шагов для умножения пар матриц это n2, то есть количество шагов, необходимое просто для записи ответа. Отсюда и название «вторая степень».
И хотя никто точно не знает, можно ли этого достичь, исследователи продолжают продвигаться в этом направлении.
Статья, опубликованная в октябре, подбирается к цели еще ближе и описывает самый быстрый на данный момент метод умножения двух матриц. Результат, который получили Джош Алман, докторант Гарвардского университета, и Вирджиния Василевска Уильямс из Массачусетского технологического института, уменьшает степень предыдущего лучшего показателя примерно на одну стотысячную. Это действительно большое достижение в данной области, добытое кропотливым трудом.
Это действительно большое достижение в данной области, добытое кропотливым трудом.
Чтобы получше разобраться в этом процессе и понять, как его можно усовершенствовать, давайте начнем с пары матриц 2 х 2, A и B. При вычислении каждого элемента их произведения вы используете соответствующую строку из A и соответствующий столбец из B. Чтобы получить верхний правый элемент, умножьте первое число в первой строке A на первое число во втором столбце B, затем умножьте второе число в первой строке A на второе число во втором столбце B и сложите эти два произведения.
Самуэль Веласко / Quanta Magazine
Эта операция известна как получение «скалярного произведения» строки со столбцом (иногда называется «внутренним произведением»). Чтобы вычислить другие элементы в произведении матриц, повторите процедуру с соответствующими строками и столбцами.
В целом, классический метод умножения матриц 2 х 2 состоит из восьми умножений и нескольких сложений. Как правило, этот способ умножения двух матриц размера n х n требует n3 умножений.
С увеличением размера матриц количество умножений, необходимых для нахождения их произведения, растет намного быстрее, чем количество сложений. Чтобы найти произведение матриц 2 х 2 требуется всего восемь промежуточных умножений, а чтобы найти произведение матриц 4 х 4 их требуется уже 64. Однако количество сложений, необходимых для получения суммы этих матриц, не так значительно отличается. Обычно количество сложений равно количеству элементов в матрице, то есть четыре для матриц 2 х 2 и 16 для матриц 4 х 4. Эта разница между сложением и умножением позволяет понять, почему исследователи измеряют скорость умножения матриц исключительно с точки зрения количества требуемых умножений.
«Умножения — это наше всё, — утверждает Уманс, — Показатель степени в итоге полностью зависит только от количества умножений. Сложения в некотором смысле исчезают».
На протяжении веков люди считали, что n3 — это самый быстрый способ умножения матриц. По имеющимся сведениям, в 1969 году Фолькер Штрассен намеревался доказать, что невозможно умножить матрицы 2 х 2, используя менее восьми умножений. Видимо, он все-таки не смог найти доказательства, а через некоторое время и понял почему: на самом деле, существует способ сделать это с помощью семи умножений!
Видимо, он все-таки не смог найти доказательства, а через некоторое время и понял почему: на самом деле, существует способ сделать это с помощью семи умножений!
Штрассен придумал сложный набор соотношений, которые позволили заменить одно из этих восьми умножений 14 дополнительными сложениями. Может показаться, что разница совершенно незначительна, но она оправдывает себя, так как умножение вносит больший вклад, чем сложение. Найдя способ избавиться от одного умножения для маленьких матриц 2 х 2, Штрассен открыл возможность, которую он мог использовать при умножении бOльших матриц.
«Это крошечное изменение приводит к огромным улучшениям в работе с большими матрицами», — говорит Уильямс.
Вирджиния Василевска Уильямс из Массачусетского технологического института и Джош Алман из Гарвардского университета открыли самый быстрый способ перемножения двух матриц за n2.3728596 шагов. Джаред Чарни; Ричард Т.К. Хоук
Предположим, вы хотите перемножить пару матриц 8 х 8. Один из способов сделать это — разбить каждую большую матрицу на четыре матрицы размером 4 х 4 так, чтобы каждая имела по четыре элемента. Поскольку элементы матрицы также могут являться матрицами, вы можете считать исходные матрицы парой матриц 2 х 2, каждый из четырех элементов которых сам по себе является матрицей 4 х 4. Посредством некоторых манипуляций каждая из этих матриц размером 4 х 4 может быть разбита на четыре матрицы размером 2 х 2.
Один из способов сделать это — разбить каждую большую матрицу на четыре матрицы размером 4 х 4 так, чтобы каждая имела по четыре элемента. Поскольку элементы матрицы также могут являться матрицами, вы можете считать исходные матрицы парой матриц 2 х 2, каждый из четырех элементов которых сам по себе является матрицей 4 х 4. Посредством некоторых манипуляций каждая из этих матриц размером 4 х 4 может быть разбита на четыре матрицы размером 2 х 2.
Смысл этого многократного разбиения больших матриц на более мелкие заключается в том, что можно снова и снова применять алгоритм Штрассена к меньшим матрицам и с помощью его метода сокращать количество шагов на каждом этапе. В целом алгоритм Штрассена увеличил скорость умножения матриц с n3 до n2.81 мультипликативных шагов.
Следующий важный шаг в развитии идеи произошел в конце 1970-х, когда появился принципиально новый подход к решению этой задачи. Он подразумевает перевод матричного умножения в другую вычислительную задачу линейной алгебры с использованием объектов, называемых тензорами. Тензоры, используемые в этой задаче, представляют собой трехмерные массивы чисел, состоящие из множества различных частей, каждая из которых выглядит как небольшая задача на умножение матриц.
Тензоры, используемые в этой задаче, представляют собой трехмерные массивы чисел, состоящие из множества различных частей, каждая из которых выглядит как небольшая задача на умножение матриц.
Умножение матриц и эта задача, связанная с тензорами, в определенном смысле эквивалентны друг другу, но для решения последней исследователи уже имели более быстрые процедуры. Таким образом, перед ними встала задача определить «обменный курс» между ними: Матрицы какого размера можно перемножить при тех же вычислительных затратах, которые требуются для решения тензорной задачи?
«Это очень распространенная в теоретической информатике концепция: преобразовывать задачи и проводить аналогию между ними, чтобы показать, что они одинаково простые или сложные», — сказал Алман.
В 1981 году Арнольд Шёнхаге использовал этот подход, чтобы доказать, что умножение матриц возможно выполнить за n2.522 шагов. Позднее Штрассен назвал этот подход «лазерным методом» (laser method).
За последние несколько десятилетий каждое улучшение в процессе умножения матриц происходило за счет усовершенствования лазерного метода, поскольку исследователи находили все более эффективные способы трансформации задачи. В своем новом доказательстве Алман и Уильямс стирают различие между 2 задачами и показывают, что уменьшить число умножений возможно. «В целом Джош и Вирджиния нашли способ применить машинные вычисления в рамках лазерного метода и получили лучшие на настоящий момент результаты», — сказал Генри Кон из Microsoft Research.
В их статье теоретическое ограничение скорости умножения матриц улучшено до n2.3728596.
Также благодаря этому исследованию Уильямс может вернуть себе корону в области матричного умножения, которую она по праву получила в 2012 году (n2.372873), а затем уступила в 2014 году Франсуа Ле Галлю (n2.3728639).
Но, несмотря на все эти гонки и победы, становится ясно, что в случае с этим подходом действует закон убывающей доходности, или убывающей отдачи. Скорее всего, усовершенствование Алмана и Уильямс почти полностью исчерпало возможности лазерного метода, но так и не позволило достичь конечной теоретической цели.
Скорее всего, усовершенствование Алмана и Уильямс почти полностью исчерпало возможности лазерного метода, но так и не позволило достичь конечной теоретической цели.
«Маловероятно, что получится приблизиться ко второй степени, используя это семейство методов», — отметил Уманс.
Для этого потребуется открытие новых методов и стойкая вера в то, что это вообще возможно.
Уильямс вспоминает один из разговоров со Штрассеном об этом: «Я спросила его, считает ли он, что возможно получить вторую степень для матричного умножения, и он ответил: «Нет, нет, нет, никогда!».
2.2. Умножение матрицы на число
Матрицу любой размерности можно умножить на число . Это значит – умножить на число все элементы матрицы: , т.е.
если , то .
Примеры выполнения заданий:
Задача 1. Даны матрицы: .
Выполните действия: .
Решение:
;
.
Ответ: .
Задача 2. Найдите значение линейной комбинации матриц .
Решение:
.
Ответ: .
Для самостоятельного решения:
Найдите линейные комбинации заданных матриц:
1) .
2) .
3) .
2.3. Умножение матриц
Матрицу A можно умножить на матрицу B только в том случае, когда число столбцов матрицы A равно числу строк матрицы B.
В результате умножения получится матрица C, у которой столько же строк, сколько их в матрице A, и столько же столбцов, сколько их в матрице B, а элементы матрицы C вычисляются по формуле: .
Другими словами: для получения элемента ,
расположенного в i-ой
строке и j-ом столбце
матрицы C надо элементы i-ой строки матрицы A умножить на соответствующие элементы j-го столбца матрицы B и полученные
произведения сложить.
Алгоритм вычисления произведения матрицы на матрицу :
1) Проверить, совпадает ли число столбцов матрицы с числом строк матрицы , («согласованы» ли порядки множителей). Только в этом случае можно умножить A на B. В противном случае вычислить C нельзя.
2) Определить порядок матрицы произведения: имеет порядок , где m – число строк первого множителя A, k – число столбцов второго множителя B.
3) Вычислить каждый элемент матрицы произведения C по формулам:
4) Выписать полученную матрицу C.
Примеры выполнения заданий:
Задача 1. Найдите произведение матриц , если .
Решение:
1. Проверим, совпадает
ли число столбцов матрицы А с числом
строк матрицы B –
совпадают, порядки множителей
«согласованы».
2. Определим порядок матрицы произведения: имеет порядок , где 2 – число строк первого множителя A, 2 – число столбцов второго множителя B.
3. Вычислим каждый элемент матрицы произведения C по формулам:
4. Выписать полученную матрицу C.
Ответ: .
Задача 2. Пусть . Найдите произведения и (если это возможно).
Решение:
Произведение не существует, так как число столбцов матрицы B не совпадает с числом строк матрицы .
Задача 3. Найдите произведение матриц , если ;
Решение:
.
Ответ: .
Задача 4. Найдите произведение матриц , если .
Решение: .
Ответ: 2.
Задача 5. Найдите произведение матриц , если .
Решение:
.
Ответ: .
Задача 6. Найдите произведение матриц , если .
Решение:
.
Ответ: .
Задача 7. Найдите произведение матриц , если
Решение:
.
Ответ: .
Задача 8. Найдите произведение матриц , если
.
Решение:
Ответ: .
Для самостоятельного решения:
Даны матрицы .
Найти и . Докажите, что .
Свойства операции умножения матриц
1. Умножение
матриц не коммутативно, т. е.
,
даже если определены оба произведения.
Однако если для каких-либо матриц
соотношение выполняется, то такие матрицы называются
еще перестановочными.
е.
,
даже если определены оба произведения.
Однако если для каких-либо матриц
соотношение выполняется, то такие матрицы называются
еще перестановочными.
Самым характерным примером может служить единичная матрица E, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка . Очевидно, что для любых матриц выполняется следующее свойство: , где O – нулевая матрица.
2. Операция перемножения матриц ассоциативна, т.е. если определены произведения и , то определены и , и выполняется равенство: .
3. Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения и , то соответственно:
4. Если произведение определено, то для любого числа k верно соотношение: .
Замечание 1. 1. Произведение матриц определено только
в том случае, когда число столбцов первой
матрицы равно числу строк второй матрицы.
Произведение матриц содержит столько
строк, сколько имеет первая матрица,
и столько столбцов, сколько имеет вторая
матрица.
1. Произведение матриц определено только
в том случае, когда число столбцов первой
матрицы равно числу строк второй матрицы.
Произведение матриц содержит столько
строк, сколько имеет первая матрица,
и столько столбцов, сколько имеет вторая
матрица.
Замечание 1.2. В общем случае , даже если оба произведения матриц, и , определены. Матрицы, для которых выполняется условие , называются коммутативными.
5. Как и умножение чисел, произведение матриц подчиняется сочетательному закону: .
Для самостоятельного решения:
Проверьте, коммутируют ли матрицы
1. ; 2. ;
3. ; 4. .
Онлайн калькулятор умножения матриц
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | – | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор дает детальное решение с объяснением умножения двух матриц.
 Умножить две матрицы возможно только в том случае, если количество столбцов первой матрицы, равно количеству строк второй
Умножить две матрицы возможно только в том случае, если количество столбцов первой матрицы, равно количеству строк второйКак умножать матрицы
Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов.
Элементы матрицы обозначаются как aij, где i – номер строки, j – номер столбца.
Две матрицы A и B можно умножить только в том случае, если число столбцов матрицы A равно числу строк матрицы B.
При умножении матрицы А размерности l × m на матрицу В размерности m × n получаем матрицу С размерности l × n
| C = |
|
× |
|
= |
|
Элемент матрицы с индексом Cij находится по формуле
Приведем пример, умножим две матрицы A и B. Размер матрицы A равен 3 ×
2, размер матрицы B равен 2 × 3.
Размер матрицы A равен 3 ×
2, размер матрицы B равен 2 × 3.
| A = |
|
| B = |
|
Даны две матрицы
| A = |
|
где, | a11 = 3 |
|||||||||
| B = |
|
где, | b11 = 0 |
Элемент матрицы с индексом Cij находится по формуле
c11 = a11 ⋅ b11 + a12 ⋅ b21 + a13 ⋅ b31 = 3 ⋅ 0 + 0 ⋅ 3 + 4 ⋅ 12 = 48
c12 = a11 ⋅ b12 + a12 ⋅ b22 + a13 ⋅ b32 = 3 ⋅ (-2) + 0 ⋅ (-1) + 4 ⋅ 3 = 6
c13 = a11 ⋅ b13 + a12 ⋅ b23 + a13 ⋅ b33 = 3 ⋅ 0 + 0 ⋅ 7 + 4 ⋅ 6 = 24
c21 = a21 ⋅ b11 + a22 ⋅ b21 + a23 ⋅ b31 = -1 ⋅ 0 + 2 ⋅ 3 + 0 ⋅ 12 = 6
c22 = a21 ⋅ b12 + a22 ⋅ b22 + a23 ⋅ b32 = -1 ⋅ (-2) + 2 ⋅ (-1) + 0 ⋅ 3 = 0
c23 = a21 ⋅ b13 + a22 ⋅ b23 + a23 ⋅ b33 = -1 ⋅ 0 + 2 ⋅ 7 + 0 ⋅ 6 = 14
c31 = a31 ⋅ b11 + a32 ⋅ b21 + a33 ⋅ b31 = 0 ⋅ 0 + 3 ⋅ 3 + 6 ⋅ 12 = 81
c32 = a31 ⋅ b12 + a32 ⋅ b22 + a33 ⋅ b32 = 0 ⋅ (-2) + 3 ⋅ (-1) + 6 ⋅ 3 = 15
c33 = a31 ⋅ b13 + a32 ⋅ b23 + a33 ⋅ b33 = 0 ⋅ 0 + 3 ⋅ 7 + 6 ⋅ 6 = 57
| C = |
|
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
НОУ ИНТУИТ | Лекция | Параллельные методы умножения матрицы на вектор
< Лекция 12 || Лекция 6: 1234567
Аннотация: В лекции рассматривается задача умножения матрицы на вектор. Приводится постановка задачи и последовательный алгоритм ее решения. Описываются методы разделения матрицы между процессорами вычислительной системы, которые необходимы для параллельной реализации матричных операций. Далее излагаются три возможных подхода к параллельной реализации алгоритма умножения матрицы на вектор
Далее излагаются три возможных подхода к параллельной реализации алгоритма умножения матрицы на вектор
Ключевые слова: операции, матричные вычисления, математика, структуры хранения, метод матричных вычислений, перемножение матриц, параллелизм по данным, параллельные алгоритмы матричных вычислений, скалярное умножение, MPI, эффективность, ускорение, операции передачи данных, вычислительный эксперимент, EM64T, computer cluster, частичный результат, каскадная схема, программная реализация
Матрицы и матричные операции широко используются при математическом моделировании самых разнообразных процессов, явлений и систем. Матричные вычисления составляют основу многих научных и инженерных расчетов – среди областей приложений могут быть указаны вычислительная математика, физика, экономика и др.
С учетом значимости эффективного выполнения матричных расчетов
многие стандартные библиотеки программ содержат процедуры для
различных матричных операций. Объем программного обеспечения для
обработки матриц постоянно увеличивается – разрабатываются новые
экономные структуры хранения для матриц специального типа
(треугольных, ленточных, разреженных и т.п.), создаются различные
высокоэффективные машинно-зависимые реализации алгоритмов,
проводятся теоретические исследования для поиска более быстрых
методов матричных вычислений.
Объем программного обеспечения для
обработки матриц постоянно увеличивается – разрабатываются новые
экономные структуры хранения для матриц специального типа
(треугольных, ленточных, разреженных и т.п.), создаются различные
высокоэффективные машинно-зависимые реализации алгоритмов,
проводятся теоретические исследования для поиска более быстрых
методов матричных вычислений.
Являясь вычислительно трудоемкими, матричные вычисления представляют собой классическую область применения параллельных вычислений. С одной стороны, использование высокопроизводительных многопроцессорных систем позволяет существенно повысить сложность решаемых задач. С другой стороны, в силу своей достаточно простой формулировки матричные операции предоставляют прекрасную возможность для демонстрации многих приемов и методов параллельного программирования.
В данной лекции обсуждаются методы параллельных вычислений для
операции матрично-векторного умножения, в следующей лекции
(
“Параллельные методы матричного умножения”
) излагается более
общий случай – задача перемножения матриц. Важный вид матричных
вычислений – решение систем линейных уравнений – представлен в “Решение систем линейных уравнений”
. Общий для всех
перечисленных задач вопрос разделения обрабатываемых матриц между
параллельно работающими процессорами рассматривается в первом
подразделе лекции 6.
Важный вид матричных
вычислений – решение систем линейных уравнений – представлен в “Решение систем линейных уравнений”
. Общий для всех
перечисленных задач вопрос разделения обрабатываемых матриц между
параллельно работающими процессорами рассматривается в первом
подразделе лекции 6.
При изложении следующего материала будем полагать, что рассматриваемые матрицы являются плотными ( dense ), то есть число нулевых элементов в них незначительно по сравнению с общим количеством элементов матриц.
6.1. Принципы распараллеливания
Для многих методов матричных вычислений характерным является
повторение одних и тех же вычислительных действий для разных
элементов матриц. Данное свойство свидетельствует о наличии параллелизма по данным при выполнении
матричных расчетов, и, как результат, распараллеливание матричных
операций сводится в большинстве случаев к разделению
обрабатываемых матриц между процессорами используемой
вычислительной системы. Выбор способа разделения матриц приводит
к определению конкретного метода параллельных вычислений;
существование разных схем распределения данных порождает целый
ряд параллельных алгоритмов матричных
вычислений.
Выбор способа разделения матриц приводит
к определению конкретного метода параллельных вычислений;
существование разных схем распределения данных порождает целый
ряд параллельных алгоритмов матричных
вычислений.
Наиболее общие и широко используемые способы разделения матриц состоят в разбиении данных на полосы (по вертикали или горизонтали) или на прямоугольные фрагменты ( блоки ).
1. Ленточное разбиение матрицы. При ленточном ( block-striped ) разбиении каждому
процессору выделяется то или иное подмножество строк
( rowwise или горизонтальное разбиение ) или столбцов
( columnwise или вертикальное разбиение ) матрицы
(рис. 6.1). Разделение строк
и столбцов на полосы в большинстве случаев происходит на непрерывной ( последовательной ) основе. При таком
подходе для горизонтального разбиения по строкам, например,
матрица A представляется в виде
(см. рис. 6.1)
рис. 6.1)
| ( 6.1) |
где ai=(ai1,ai2,…,ain), 0<=i<m, есть i -я строка матрицы A (предполагается, что количество строк m кратно числу процессоров p, т.е. m = kxp ). Во всех алгоритмах матричного умножения и умножения матрицы на вектор, которые будут рассмотрены в этой и следующей лекциях, применяется разделение данных на непрерывной основе.
Другой возможный подход к формированию полос состоит в применении той или иной схемы чередования ( цикличности ) строк или столбцов. Как правило, для чередования используется число процессоров p – в этом случае при горизонтальном разбиении матрица A принимает вид
(
6. 2) 2) |
Циклическая схема формирования полос может оказаться полезной для лучшей балансировки вычислительной нагрузки процессоров (например, при решении системы линейных уравнений с использованием метода Гаусса – см. “Решение систем линейных уравнений” ).
2. Блочное разбиение матрицы. При блочном ( chessboard block ) разделении матрица делится на прямоугольные наборы элементов – при этом, как правило, используется разделение на непрерывной основе. Пусть количество процессоров составляет p = sxq, количество строк матрицы является кратным s, а количество столбцов – кратным q, то есть m = kxs и n = lxq. Представим исходную матрицу A в виде набора прямоугольных блоков следующим образом:
где Aij — блок матрицы, состоящий из элементов:
(
6. 3) 3) |
При таком подходе целесообразно, чтобы вычислительная система имела физическую или, по крайней мере, логическую топологию процессорной решетки из s строк и q столбцов. В этом случае при разделении данных на непрерывной основе процессоры, соседние в структуре решетки, обрабатывают смежные блоки исходной матрицы. Следует отметить, однако, что и для блочной схемы может быть применено циклическое чередование строк и столбцов.
В данной лекции рассматриваются три параллельных алгоритма для умножения квадратной матрицы на вектор. Каждый подход основан на разном типе распределения исходных данных (элементов матрицы и вектора) между процессорами. Разделение данных меняет схему взаимодействия процессоров, поэтому каждый из представленных методов существенным образом отличается от двух остальных.
Рис.
6. 1. Способы распределения элементов матрицы между процессорами вычислительной системы
1. Способы распределения элементов матрицы между процессорами вычислительной системы
Дальше >>
< Лекция 12 || Лекция 6: 1234567
Калькулятор умножения матриц – MathCracker.com
Решатели Алгебра
Инструкции:
Используйте этот пошаговый калькулятор для вычисления умножения двух матриц. Следите за тем, чтобы количество столбцов первой матрицы совпадало с количеством строк второй матрицы.
При необходимости измените размер матриц, указав количество строк и количество столбцов. Когда у вас есть правильные размеры, которые вы хотите, вы вводите матрицы (вводя числа и перемещаясь по матрице с помощью “TAB”
Number of Rows A = Number of Cols A =Number of Rows B = Number of Cols B =
The number of rows and columns provided needs to be integers that are greater than 1. The maximum number of rows is 8, and the maximum number of columns is 8
\(A\) = \begin{bmatrix} & \\ & \end{bmatrix}
\(B\) = \begin{bmatrix} & \\ & \end{bmatrix}
Матрицы часто появляются в линейной алгебре из-за их тесной связи с линейными функциями. Но помимо этой связи матрицы — это объекты, которые во многом похожи на числа. Действительно, вы можете складывать, вычитать и умножать матрицы при условии, что размеры совместимы.
Действительно, вы можете складывать, вычитать и умножать матрицы при условии, что размеры совместимы.
Например, чтобы добавить две матрицы нужно, чтобы они имели одинаковые габариты. Это же требование необходимо, когда вы хотите вычесть матрицы .
Как умножать матрицы?
Умножение матриц представляет собой другую проблему, поскольку его определение менее интуитивно понятно, чем способ сложения и вычитания матриц. Кроме того, подходящие размерности для умножения не требуют, чтобы матрицы имели одинаковые размеры, но все же были в другом состоянии.
Кроме того, подходящие размерности для умножения не требуют, чтобы матрицы имели одинаковые размеры, но все же были в другом состоянии.
Итак, начнем с этого: чтобы можно было перемножать матрицы, количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы.
На самом деле это означает, что у вас может быть две матрицы разной формы, которые можно перемножать. Например, матрицу 2×4 можно умножить на матрицу 4×4. Или матрицу 3×3 можно умножить на матрицу 3×6.
Теперь, как вы определяете умножение между двумя матрицами? Вы делаете определение
покомпонентно
следующим образом: Предположим, что \(A\) является матрицей \(m \times n\), а \(B\) является матрицей \(n \times p\). n A_{ik} B_{kj}\]
n A_{ik} B_{kj}\]
Часто эту формулу трудно усвоить, но лучший способ сделать это — думать о ней так: элемент матрицы произведения, который находится в строке i и столбце j, вычисляется путем вычисления скалярного произведения между i- -я строка первой матрицы и j-й столбец второй матрицы.
Что такое свойство единичной матрицы умножения матриц?
Единичная матрица является очень особенным с точки зрения матричного умножения. Действительно, матрица А вообще не меняется при умножении на Единичная матрица (при условии, что размеры допустимы для проведения умножения)
Это калькулятор умножения матриц с шагами?
Да, это так. Все, что вам нужно сделать, это указать матрицы, которые вы хотите перемножить, а калькулятор сделает все остальное. Калькулятор начинает с двух пустых матриц 2×2. Таким образом, вам может потребоваться настроить размеры матриц, чтобы ввести нужные вам матрицы.
Все, что вам нужно сделать, это указать матрицы, которые вы хотите перемножить, а калькулятор сделает все остальное. Калькулятор начинает с двух пустых матриц 2×2. Таким образом, вам может потребоваться настроить размеры матриц, чтобы ввести нужные вам матрицы.
Это калькулятор умножения 3-х матриц?
Не напрямую. Этот калькулятор вычислит произведение двух матриц. Если вы хотите умножить три функции, то вам нужно сначала вычислить умножение первых двух, а затем результат умножить на третью.
калькулятор умножения матриц Калькулятор умножения матриц Калькулятор умножения двух матриц
Интуиция программиста для умножения матриц — BetterExplained
Что означает умножение матриц? Вот несколько общих догадок:
1) Умножение матриц масштабирует/вращает/искажает геометрическую плоскость.
Это полезно при первом изучении векторов: приходят новые векторы, появляются новые. К сожалению, это может привести к чрезмерной зависимости от геометрической визуализации.
Если 20 семей придут к вам на барбекю, как вы оцениваете количество необходимых хот-догов? ( Хм… 20 семей, скажем, по 3 человека в семье, по 2 хот-дога в каждой… примерно 20 * 3 * 2 = 120 хот-догов. )
Вы, наверное, не думаете: “О, мне нужен объем призмы приглашения-семейного-голода!”. С большими матрицами я не думаю о 500-мерных векторах, просто о данных, которые нужно изменить.
2) Умножение матриц составляет линейные операции.
Это технически точное определение: да, умножение матриц приводит к новой матрице, которая составляет исходные функции. Однако иногда обрабатываемая матрица представляет собой не линейную операцию, а набор векторов или точек данных. Нам нужна другая интуиция для того, что происходит.
Я представлю точку зрения программиста:
3) Умножение матриц связано с потоком информации, преобразованием данных в код и обратно.
Я думаю о линейной алгебре как о «математических электронных таблицах» (если вы новичок в линейной алгебре, прочтите это введение):
- Мы храним информацию в различных электронных таблицах («матрицах»)
- Некоторые данные рассматриваются как функции для применения, другие — как точки данных для использования
- При необходимости мы можем переключаться между интерпретацией вектора и функции
Иногда я думаю о данных как о геометрических векторах, а иногда я вижу матрицу как составную функцию. Но в основном я думаю об информации, проходящей через систему. (Некоторых пуристов пугает сведение красивых алгебраических структур в невзрачные таблицы; я спокойно сплю по ночам.)
Интуиция программиста: код — это данные — это код
Возьмите свой любимый рецепт. Если вы интерпретируете слова как инструкции , вы получите пирог, кекс, торт и т. д.
Если вы интерпретируете слова как данные , текст будет прозой, который можно настроить:
- Преобразование измерений в метрические единицы
- Замена ингредиентов из-за аллергии
- Настройка по высоте или другому оборудованию
Результатом является новый рецепт, который можно дополнительно изменить или выполнить как инструкции для приготовления другого пирога, кекса, торта и т. д. (Компиляторы рассматривают программу как текст, модифицируют ее и в конечном итоге выводят «инструкции», которые может быть текстом для другого слоя.)
д. (Компиляторы рассматривают программу как текст, модифицируют ее и в конечном итоге выводят «инструкции», которые может быть текстом для другого слоя.)
Это линейная алгебра. Мы берем необработанную информацию, такую как «3 4 5», обрабатываем ее как вектор или функцию, в зависимости от того, как она написана:
По соглашению вертикальный столбец обычно является вектором, а горизонтальная строка обычно представляет собой функцию:
-
[3; 4; 5]означаетх = (3, 4, 5). Здесьx— это вектор данных (я использую;для разделения каждой строки). -
[3 4 5]означаетf(a, b, c) = 3a + 4b + 5c. Это функция, принимающая три входа и возвращающая один результат.
Ага! момент: данные — это код, код — это данные!
Строка, содержащая горизонтальную функцию, действительно может состоять из трех точек данных (каждая с одним элементом).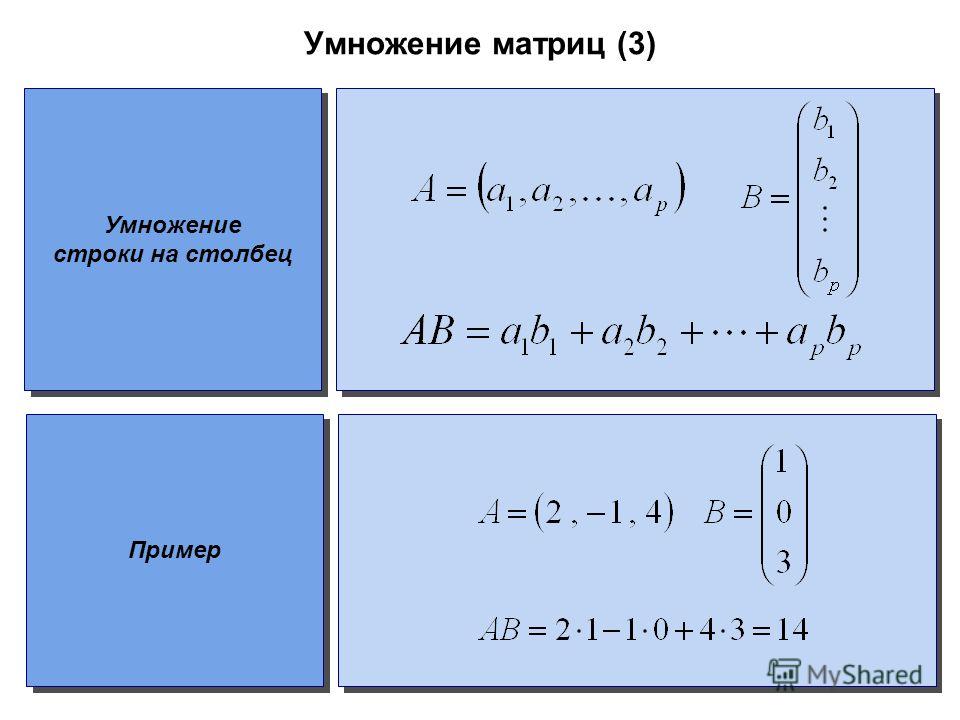 Вертикальный столбец данных действительно может быть тремя отдельными функциями, каждая из которых принимает один параметр.
Вертикальный столбец данных действительно может быть тремя отдельными функциями, каждая из которых принимает один параметр.
Ач. Это становится изящным: в зависимости от желаемого результата мы можем комбинировать данные и код в другом порядке.
Транспонирование матрицы
Транспонирование матрицы меняет местами строки и столбцы. Вот что это означает на практике.
Если x было вектор-столбцом с 3 элементами ( [3; 4; 5] ), то x' равно:
- Функция с 3 аргументами (
[3 4 5]) -
x'может по-прежнему оставаться вектором данных, но в виде трех отдельных записей. Транспонирование «разделило его».
Аналогично, если f = [3 4 5] — наш вектор-строка, тогда f' может означать:
- Один вектор данных в вертикальном столбце.
-
f'разделен на три функции (каждая из которых принимает один вход).
Используем это на практике.
Когда мы видим x' * x , мы имеем в виду: x' (как отдельная функция) работает с x (один вектор). Результатом является скалярное произведение (подробнее). Другими словами, мы применили данные к себе.
Когда мы видим x * x' , мы имеем в виду, что x (как набор функций) работает с x' (набор отдельных точек данных). Результатом является сетка, в которой мы применили каждую функцию к каждой точке данных. Здесь мы смешали данные друг с другом во всех возможных перестановках.
Я думаю о xx как о x(x) . Это «функция x», работающая с «вектором x». (Это помогает вычислить ковариационную матрицу, меру самоподобия данных.)
Использование интуиции
Фу! Как это нам поможет? Когда мы видим такое уравнение (из класса машинного обучения):
, я мгновенно чувствую, что происходит. В первом уравнении мы рассматриваем $\theta$ (обычно это набор параметров данных) как функцию и передаем $x$ в качестве аргумента. Это должно дать нам одно значение.
Это должно дать нам одно значение.
Более сложные производные, такие как:
могут быть проработаны. В некоторых случаях это становится сложно, потому что мы храним данные в виде строк (а не столбцов) в матрице, но теперь у меня есть гораздо лучшие инструменты для отслеживания. Вы можете начать оценивать, когда вы получите одно значение или когда в результате вы получите «сетку перестановок».
Геометрическое масштабирование и линейная композиция имеют место быть, но здесь я хочу подумать об информации. «Информация в x становится функцией, и мы передаем себя в качестве параметра».
Короче говоря, не замыкайтесь на одной интуиции. Умножение эволюционировало от многократного сложения к масштабированию (десятичные числа), к поворотам (мнимые числа), к «применению» одного числа к другому (интегралы) и так далее. Почему не то же самое для умножения матриц?
Счастливая математика.
Приложение: А как насчет других комбинаций?
Вам может быть любопытно, почему мы не можем использовать другие комбинации, такие как x x или x' x' . Проще говоря, параметры не выстраиваются в линию: у нас были бы функции, ожидающие передачи 3 входных данных только с одним параметром, или функции, ожидающие передачи одного входного параметра 3.
Проще говоря, параметры не выстраиваются в линию: у нас были бы функции, ожидающие передачи 3 входных данных только с одним параметром, или функции, ожидающие передачи одного входного параметра 3.
Приложение: интерпретация Javascript
Скалярный продукт x' * x можно рассматривать как следующую команду javascript:
((x, y, z) => x*3 + y*4 + z*5)(3, 4, 5)
Определяем анонимную функцию из 3 аргументов, и сразу передаем ей 3 параметра . Это возвращает 50 (точечный продукт: 3*3 + 4*4 + 5*5 = 50 ).
Математическая запись суперкомпактна, поэтому мы можем просто написать (в октаве/Matlab):
октава:2> [3 4 5] * [3 4 5]'
ans = 50
Помните, что [3 4 5] — это функция, а [3; 4; 5] или [3 4 5]' — это то, как мы запишем вектор данных.
Приложение: Метод ADEPT
Эта статья возникла из TODO в моих заметках по машинному обучению, в которых используется метод ADEPT:
Я хотел объяснить себе — на простом английском языке — почему мы хотели x' x а не наоборот. Теперь простым языком: мы обрабатываем информацию как функцию и передаем ту же информацию в качестве параметра.
Теперь простым языком: мы обрабатываем информацию как функцию и передаем ту же информацию в качестве параметра.
Другие сообщения из этой серии
- Наглядное интуитивное руководство по мнимым числам
- Интуитивная арифметика с комплексными числами
- Понимание того, почему сложное умножение работает
- Интуитивное руководство по углам, градусам и радианам
- Интуитивное понимание формулы Эйлера
- Интерактивное руководство по преобразованию Фурье
- Интуитивное руководство по свертке
- Интуитивное понимание синусоиды
- Интуитивное руководство по линейной алгебре
- Интуиция программиста для умножения матриц
- Мнимое умножение против мнимых показателей
- Интуитивное руководство по гиперболическим функциям
Умножение матриц. ЭТО СОВЕРШЕННО НОВАЯ ОБЛАСТЬ, ПОМИМО… | Соломон Се | Основы линейной алгебры
ЭТО СОВЕРШЕННО НОВАЯ ОБЛАСТЬ ПОМИМО МАТРИЧНЫХ ОСНОВНЫХ ОПЕРАЦИЙ .
Очень сложно в этом разобраться. Но математики просто каким-то образом заставляют это работать, тогда это определенная человеком операция , это не имеет смысла, но вам просто нужно иметь с этим дело.
Если вам просто нужно решить проблему, вам нужно всего 5 минут, чтобы обойти ее, а затем вы можете пропустить все это ниже.
Но если хочешь разобраться, то приготовься на это пару часов или дней.
Необходимо сбить вас с толку приведенной ниже операцией. Потому что большинство учителей начинают с того, чтобы научить вас перемножать матрицы. Не волнуйтесь, мы должны пропустить этот вопрос и найти лучшую перспективу для его решения.
См. статью Академии Хана: Умножение матриц
Обратитесь к 3Blue1Brown: Скалярные произведения и двойственность
Обратитесь к математике — это весело: Как умножать матрицы
Эта тема очень проста в использовании, но очень сложна для понимания!
Но я предпочитаю понять его, а не просто запомнить.
Итак, это Путь обучения этой темы:
- Скалярное произведение
- Линейные преобразования
- Матрично-векторное произведение
- Матрично-матричное произведение 7 Есть так много разных способов понять это,7 чтобы понять это, потому что это так трудно понять.
- Через
Матричное преобразование - Через
Пример из реальной жизни - ~Алгебраическими методами~
- Скалярное произведение: Вектор * Вектор
- Матрично-векторное произведение: Матрица * Вектор
- Матрично-матричное произведение: Матрица * Матрица
- Перемещение: Мы пусть единичный вектор
i = (100, 0), тогда вектор, перемещающийся вправо, становится(-100, 2). - Вращение: пусть единичный вектор
i = (0, 1)иj = (-1, 0), тогда вектор поворачивается на 90° становится(-2, -1). -
График: 1-й справа элемент.
-
Правила: Все остальные матрицы слева отГрафик. - Точка:
(2,3) - Треугольник:
[ (3,0) (0 ,4) (3,4) ] - Прямоугольник:
[ (3,0) (3,4) (0,4) (0,0)] - Любая форма в любом размере…..
- Исходный график
0073 , поэтому после применения нового правилаi & jмы получаем: - Теперь мы можем сделать вектор
умножьте скалярный метод, чтобы получить это: - Тогда мы могли бы сделать
Добавить два вектора: - Итак, после применения правила преобразования мы успешно преобразовали вектор в новую позицию:
(19, -3) - Похоже на задачу
Умножение матрицы - Сначала нам нужно сформировать исходную матрицу, идентифицируя все вершины:
- Draw it out by the result matrix
- Параметры
[in] *pSrcA указывает на первую структуру входной матрицы [in] *pSrcB указывает на вторую структуру входной матрицы [out] *pDst указывает на структуру выходной матрицы - Возвращает
- Функция возвращает либо
ARM_MATH_SIZE_MISMATCH, либоARM_MATH_SUCCESSв зависимости от результата проверки размера.
- Параметры
[в] *PSRCA Точки на структуру первой матрицы [в] *PSRCB . указывает на структуру выходной матрицы - Возвращает
- Функция возвращает либо
ARM_MATH_SIZE_MISMATCH, либоARM_MATH_SUCCESSпо результатам проверки размера.
- Параметры
[в] *PSRCA Точки на структуру первой матрицы [в] *PSRCB . указывает на структуру выходной матрицы - Возвращает
- Функция возвращает либо
ARM_MATH_SIZE_MISMATCH, либоARM_MATH_SUCCESSв зависимости от результата проверки размера.
- Параметры
[in] pSrcA points to the first input matrix structure [in] pSrcB points to the second input matrix structure [out] pDst points на вывод матричной структуры [in] pState указывает на массив для хранения промежуточных результатов - Возвращает
- статус выполнения
- ARM_MATH_SUCCESS : Операция выполнена успешно
- ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась
- Масштабирование и поведение при переполнении
- Разница между функцией arm_mat_mult_q15() и этим быстрым вариантом заключается в том, что быстрый вариант использует 32-битный, а не 64-битный аккумулятор.
 Результат каждого умножения 1,15 x 1,15 усекается до формата 2,30. Эти промежуточные результаты накапливаются в 32-битном регистре в формате 2.30. Наконец, аккумулятор насыщается и преобразуется в результат 1,15.
Результат каждого умножения 1,15 x 1,15 усекается до формата 2,30. Эти промежуточные результаты накапливаются в 32-битном регистре в формате 2.30. Наконец, аккумулятор насыщается и преобразуется в результат 1,15. - Быстрая версия имеет то же поведение при переполнении, что и стандартная версия, но обеспечивает меньшую точность, поскольку отбрасывает младшие 16 бит каждого результата умножения. Чтобы полностью избежать переполнения, входные сигналы должны быть уменьшены. Уменьшите одну из входных матриц на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество добавлений numColsA вычисляется внутренне для каждого выходного элемента.
- Параметры
[in] pSrcA points to the first input matrix structure [in] pSrcB points to the second input matrix structure [out] pDst points для вывода матричной структуры - Возвращает
- статус выполнения
- ARM_MATH_SUCCESS : Операция выполнена успешно
- ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась
- Масштабирование и поведение при переполнении
- Разница между функцией arm_mat_mult_q31() и этим быстрым вариантом заключается в том, что быстрый вариант использует 32-битный, а не 64-битный аккумулятор. Результат каждого умножения 1,31 x 1,31 усекается до формата 2,30. Эти промежуточные результаты накапливаются в 32-битном регистре в формате 2.30. Наконец, аккумулятор насыщается и преобразуется в результат 1,31.

- Быстрая версия имеет то же поведение при переполнении, что и стандартная версия, но обеспечивает меньшую точность, поскольку отбрасывает младшие 32 бита каждого результата умножения. Чтобы полностью избежать переполнения, входные сигналы должны быть уменьшены. Уменьшите одну из входных матриц на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество добавлений numColsA вычисляется внутренне для каждого выходного элемента.
- Параметры
[in] pSrcA указывает на первую структуру входной матрицы [in] pSrcB указывает на вторую структуру входной матрицы pDst указывает на структуру выходной матрицы [in] pState указывает на массив для хранения промежуточных результатов - Возвращает
- статус выполнения
- ARM_MATH_SUCCESS : Операция выполнена успешно
- ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась
- Масштабирование и поведение при переполнении
- Функция реализована с использованием внутреннего 64-битного аккумулятора.
 Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат.
Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат. - Параметры
[in] pSrcA указывает на первую структуру входной матрицы [in] pSrcB указывает на вторую структуру входной матрицы [out] pDst указывает на структуру выходной матрицы [in] pState указывает на массив для хранения промежуточных результатов - Возвращает
- статус выполнения
- ARM_MATH_SUCCESS : Операция выполнена успешно
- ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась
- Масштабирование и поведение при переполнении
- Функция реализована с использованием внутреннего 64-битного аккумулятора.
 Входные данные для умножения имеют формат 1,15, а умножения дают результат 2,30. Промежуточные результаты 2.30 накапливаются в 64-битном аккумуляторе в формате 34.30. Этот подход обеспечивает 33 защитных бита и исключает риск переполнения. Затем результат 34,30 усекается до формата 34,15 путем отбрасывания младших 15 бит, а затем насыщается до формата 1,15.
Входные данные для умножения имеют формат 1,15, а умножения дают результат 2,30. Промежуточные результаты 2.30 накапливаются в 64-битном аккумуляторе в формате 34.30. Этот подход обеспечивает 33 защитных бита и исключает риск переполнения. Затем результат 34,30 усекается до формата 34,15 путем отбрасывания младших 15 бит, а затем насыщается до формата 1,15.
- Обратитесь к arm_mat_mult_fast_q15() за более быстрой, но менее точной версией этой функции.
arm_status arm_mat_mult_q31 ( константа arm_matrix_instance_q31 * ПСРКА , константа arm_matrix_instance_q31 * pSrcB , arm_matrix_instance_q31 * pDst ) - Параметры
[in] pSrcA points to the first input matrix structure [in] pSrcB points to the second input matrix structure [out] pDst points для вывода матричной структуры
- Возвращает
- статус выполнения
- ARM_MATH_SUCCESS : Операция выполнена успешно
- ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась
- Масштабирование и поведение при переполнении
- Функция реализована с использованием внутреннего 64-битного аккумулятора.
 Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат.
Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат.
arm_status arm_mat_mult_q7 ( константа arm_matrix_instance_q7 * ПСРКА , константа arm_matrix_instance_q7 * pSrcB , arm_matrix_instance_q7 * пдст , q7_t * pState ) - Параметры
[in] *pSrcA указывает на первую структуру входной матрицы [in] *pSrcB указывает на вторую структуру входной матрицы . 
- Возвращает
- Функция возвращает либо
ARM_MATH_SIZE_MISMATCH, либоARM_MATH_SUCCESSв зависимости от результата проверки размера.
Масштабирование и режим переполнения:
- Функция реализована с использованием 32-битного внутреннего аккумулятора, насыщенного до формата 1.7.
Дискретная математика – Сколько числовых умножений для произведения трех матриц?
Спросил
Изменено 1 год, 6 месяцев назад
Просмотрено 6к раз
$\begingroup$
Например, у вас есть матрицы $A, (5 х 8), B, (8 х 4), C (4 х 10). $ Вопрос требует, чтобы вы нашли количество умножений, если бы вы умножали эти матрицы, например $(A\times B)\times C$.
Ответ: $5 \times 4 \times 8 + 5 \times 10 \times 4 = 160 + 200 = 360$ умножения.

- матрицы
- дискретная математика
$\endgroup$
5
$\begingroup$
Если у вас есть матрица $5$ на $8$ $A$ и вы умножаете ее на матрицу $8$ на $4$ $B$, вы получите матрицу $5$ на $4$ и каждый элемент в этой матрице $AB$ потребуется умножить в 8 раз. Следовательно, вычисление $AB$ требует $5\times 4\times 8$ умножений.
С остальным справишься?
Давайте посмотрим на корпус поменьше. Скажем, мы умножаем $2\times3$ на $3\times 2 $. Это должно привести к матрице $2 \times 2$. Но во сколько раз я умножу?
$$\Big(\matrix{1 & 2 & 3 \\ 10& 20 & 30} \Big)\Bigg( \matrix{2 & 3 \\ 5 & 7 \\ 11 & 13} \Bigg) $$
$$= \Big( \matrix{1\times 2+2\times 5+3\times 11 & 1\times 3 +2\times 7+3\times 13 \\ 10\times 2+20\times 5+30\умножить на 11 и 10\умножить на 3 +20\умножить на 7+30\умножить на 13 \\} \Большой) $$
$$= \Big( \matrix{45 & 56 \\ 450 & 560 \\} \Big) $$
Таким образом, каждая запись (а их 4$, потому что это матрица $2\times 2$) заняла 3$ $ умножения (Откуда в задаче взялись $3$?).
 Это означает, что всего у нас было $12$ умножений. Если вы действительно обдумаете, почему это число должно быть 12, вы сможете представить, что должно произойти в более крупном случае.
Это означает, что всего у нас было $12$ умножений. Если вы действительно обдумаете, почему это число должно быть 12, вы сможете представить, что должно произойти в более крупном случае.$\endgroup$
5
$\begingroup$
Начнем шаг за шагом. Сколько умножений вам нужно, чтобы умножить $M (1\times 8)$ на $N (8 \times 2)$?
$M$ содержит одну строку из $8$ чисел. Когда мы умножаем это на первый столбец, это $8$ умножения, которые затем складываются. (Это очень похоже на точечный продукт). Затем, когда мы умножаем второй столбец, это еще 8 долларов умножения. Это в общей сложности $16$ числовых умножений.
А если мы возьмем ваши $A, (5 \times 8), B, (8 \times 4)$ и умножим $A\times B$? Для первой строки мы делаем $4 \times 8 = 32$ умножения. И мы делаем это для всех строк по $5$, поэтому общее количество умножений равно $5\times 4\times 8 = 160$.

Как насчет $D (5 \times 4), C (4 \times 10)$ и умножить $D \times C$? Те же рассуждения приводят нас к умножению $5\times 4 \times 10 = 200$.
На самом деле, если мы допустим $D = A\times B$ и добавим количество умножений, мы получим $(A \times B) \times C$, для вычисления которого требуется $360$ числовых умножений.
$\endgroup$
1
$\begingroup$
Для умножения матриц порядка $(m\times n)$ и $(n\times p)$.
Ни одно из задействованных умножений не равно $= m\cdot n\cdot p$.
Нет Дополнений $= m\cdot n\cdot (p-1)$
поэтому здесь для
первое умножение: $5\cdot 8\cdot 4= 160$
Второе умножение: $5\cdot 4 \cdot 10 = 200$
Итого $= 360$
Аналогично Общее добавление составит $=300.$
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Умножение матриц: (2×2) на (2×2)
Предположим, у нас есть 2×2 матрица A, которая имеет 2 строки и 2 столбца:
А = А 11 А 12 А 21 А 22 Предположим, у нас также есть 2×2 матрица B, которая имеет 2 строки и 2 столбца:
Б = Б 11 Б 12 Б 21 Б 22 Чтобы умножить матрицу A на матрицу B, мы используем следующую формулу:
А х В = А 11 *В 11 +А 12 *В 21 А 11 *В 12 +А 12 *В 22 А 21 *В 11 +А 22 *В 21 А 21 *В 12 +А 22 *В 22 Получается матрица 2×2.

В следующих примерах показано, как умножить матрицу 2×2 на матрицу 2×2, используя действительные числа.
Пример 1Предположим, у нас есть 2×2 матрица C, которая имеет 2 строки и 2 столбца:
С = 7 5 6 3 Предположим, у нас также есть 2×2 матрица D, которая имеет 2 строки и 2 столбца:
Д = 2 1 5 1 Вот как умножить матрицу C на матрицу D:
С x Г = 7*2 + 5*5 7*1 + 5*1 6*2 + 3*5 6*1 + 3*1 В результате получается следующая матрица 2×2:
С x Г = 39 12 27 9 Е = -2 4 9 2 Предположим, у нас также есть 2×2 матрица F, которая имеет 2 строки и 2 столбца:
Ф = 3 6 2 4 Вот как умножить матрицу E на матрицу F:
Э х Ф = -2*3 + 4*2 -2*6 + 4*4 9*3 + 2*2 9*6 + 2*4 В результате получается следующая матрица 2×2:
Е х Ф = 2 4 31 62 Г = 2 3 4 5 Предположим, у нас также есть 2×2 матрица H, которая имеет 2 строки и 2 столбца:
Н = 1 2 4 5 Вот как умножить матрицу G на матрицу H:
Г x В = 2*1 + 3*4 2*2 + 3*5 4*1 + 5*4 4*2 + 5*5 В результате получается следующая матрица 2×2:
Ш x В = 14 19 24 33 I = 1 3 5 7 Предположим, у нас также есть 2×2 матрица J, которая имеет 2 строки и 2 столбца:
Дж = 2 4 6 8 Вот как умножить матрицу I на матрицу J:
I x J = 1*2 + 3*6 1*4 + 3*8 5*2 + 7*6 5*4 + 7*8 В результате получается следующая матрица 2×2:
Калькулятор матрицI x J = 20 28 52 76 В приведенных выше примерах показано, как умножать матрицы 2×2 вручную.
Видеоруководство по умножению матриц (2×2) на (2×2) Хороший способ перепроверить свою работу, если вы перемножаете матрицы вручную, — это подтвердить свои ответы с помощью матричного калькулятора. Хотя в Интернете есть много матричных калькуляторов, самый простой в использовании, с которым я столкнулся, — это Math is Fun.
Хороший способ перепроверить свою работу, если вы перемножаете матрицы вручную, — это подтвердить свои ответы с помощью матричного калькулятора. Хотя в Интернете есть много матричных калькуляторов, самый простой в использовании, с которым я столкнулся, — это Math is Fun.Опубликовано Заком
Просмотреть все сообщения от Zach
Как проверить (быстро) умножение матриц | by Haris Angelidakis
Спойлер: случайность помогает (еще раз)
Умножение двух N x N матриц A и B — фундаментальная операция, которая проявляется как подпрограмма во всех видах приложений. Поиск алгоритма, способного умножать две матрицы за время O( N ²) все еще продолжается, с самым быстрым асимптотическим алгоритмом, благодаря Джошу Алману и Вирджинии Василевской Уильямс (2021), в настоящее время время работы
Однако, как отмечено в этой статье Википедии, этот алгоритм является галактическим алгоритмом из-за большие константы и не могут быть реализованы практически.
 Если вам интересно узнать о первом алгоритме, преодолевшем наивный барьер O( N ³) для умножения матриц, вы можете взглянуть на мою предыдущую статью о классическом алгоритме Штрассена.
Если вам интересно узнать о первом алгоритме, преодолевшем наивный барьер O( N ³) для умножения матриц, вы можете взглянуть на мою предыдущую статью о классическом алгоритме Штрассена.Однако в сегодняшней статье мы изучим другой, связанный с этим вопрос. Предположим, что кто-то дает нам N x N матрицы A, B и C, и, кроме того, пусть они утверждают, что C есть произведение A и B , т.е. = АБ . Вопрос теперь в следующем. Можем ли мы проверить, действительно ли C является произведением A и B , не умножая A с B с нуля? Другими словами:
Учитывая N x N матриц A , B и C , как быстро мы можем проверить, является ли C = AB 9?
Тривиальным тестом на поставленный выше вопрос было бы просто умножить A на B и проверить, равно ли произведение C .
 Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь — разработать O( N ²) алгоритм, проверяющий, является ли C = AB . Для этого мы прибегаем к случайности.
Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь — разработать O( N ²) алгоритм, проверяющий, является ли C = AB . Для этого мы прибегаем к случайности.Примечание: Прежде чем продолжить, мы заявляем, что изложение следует главе 11 прекрасной книги «Тридцать три миниатюры: математические и алгоритмические приложения линейной алгебры» Иржи Матоусека.
Основная идея состоит в том, чтобы выбрать случайный N -мерный {0,1} вектор x , где каждая координата независимо установлена в 0 или 1 с вероятностью 0,5, и умножить оба C и AB с х. Если C = AB , то мы будем иметь Cx = (AB)x, для любого вектора x. Однако, если C не равно AB, , то мы надеемся, что существует много векторов, для которых Cx не равно ( AB)x. Формально предлагаемый тест выглядит следующим образом.

Базовый тест
- Выберите N -мерный {0,1} вектор x равномерно случайным образом.
- Вычислить y = Cx и z = ( AB ) x .
- Если y = z , то вернуть «РАВНО», иначе вернуть «НЕ РАВНО».
Очень легко увидеть, что тест всегда будет возвращать «EQUAL», если C действительно равно AB . Итак, единственный интересный случай для анализа — это когда C не равно AB . Но прежде чем сделать это, мы должны уточнить следующее. Предлагаемая идея требует вычисления произведения (АВ)х . Здесь мы должны быть немного осторожны, так как хотим избежать вычисления произведения AB . Чтобы решить эту проблему, мы используем тот факт, что умножение матриц является ассоциативным, и сначала вычисляем Bx , затем умножаем на с результатом Bx , при этом общее время работы равно O( N ²).

Возвращаясь к анализу, предположим, что C не равно AB . Пусть D = C-AB. Ясно, что хотя бы одна запись из D будет ненулевым. Обозначим элемент в i -й строке и j -м столбце D как d(i,j) , и пусть k , t таковы, что d(k, t) не равно нулю. Пусть x(j) обозначает j -ю координату вектора x, и пусть q= Dx . Заметьте, что q = y-z . Теперь у нас есть
Поскольку каждая координата x выбирается независимо случайным образом, мы можем предположить, что координата x(t) является последней, которая будет установлена в 0 или 1. Итак, предположим, что все остальные координаты x были установлены, кроме координаты x(t) . Когда мы собираемся решить, равно ли x(t) 0 или 1, подбрасывая правильную монету, мы уже определили значение выражения
Обратите внимание, что есть два варианта для S ; он либо равен нулю, либо отличен от нуля.
 Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая:
Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая:- с вероятностью 0,5, x(t) = 1, поэтому q(k) = S + d(k,t) .
- с вероятностью 0,5, x(t) = 0, поэтому q(k) = S .
Поскольку d(k,t) не равно нулю, это означает, что S + d(k,t) не равно S . Таким образом, по крайней мере одно из S и S+ d(k,t) не равно нулю, и поэтому мы заключаем, что q(k) не равно нулю с вероятностью не менее 0,5, откуда следует, что y не равно z с вероятностью не менее 0,5. Мы заключаем, что с вероятностью не менее 0,5 наш тест правильно определит, что C не равно AB .
Тем не менее, можно сказать, что вероятность успеха в 50% не очень удовлетворительна. И, действительно, это справедливое беспокойство. Но мы можем использовать стандартный прием, используемый для таких алгоритмов, которые попадают в широкий класс алгоритмов Монте-Карло, а именно повторить их несколько раз.

Основные способы понимания:
Итак,
Матричное преобразование — это лучший способ понять матричное умножение. И оказалось, что это лучший способ для этого, и для всех основных идей
Линейная алгебра .Прежде чем мы начнем, давайте проясним:
векторные произведения как линейные преобразования
В графическом процессоре компьютера
«ВСЕ ГРАФИЧЕСКИЕ ПРОЦЕССОРЫ ЯВЛЯЮТСЯ ТОЛЬКО ЖЕСТКИМИ МАТРИЧНЫМИ МНОЖИТЕЛЯМИ! ВСЕ, ЧТО ОНИ ДЕЛАЮТ, ЭТО ТОЛЬКО УМНОЖАЮТ МАТРИЦЫ!» — САЛ ХАН 9 Линейные преобразования единственный шанс понять это в конце концов.
ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ — ЭТО КЛЮЧ К ОТКРЫТИЮ ВСЕХ ГЕТ В ЛИНЕЙНОЙ АЛГЕБРЕ, ПОТОМУ ЧТО ОНО ОБЛАДАЕТ СОВЕРШЕННЫМ СМЫСЛОМ МАТРИЧНОГО УМНОЖЕНИЯ.
Чтобы понять умножение матриц , линейное преобразование — это самое первое, что вам нужно изучить. Это довольно важно, и от этого не уйти.
Линейное преобразование— это особый вид преобразования, который работает свекторами.
Следует отметить, что 3Blue1Brown преуспел в построении интуиции по этой теме:
См. видео 3Blue1Brown: Линейные преобразования и матрицы
См. то же видео: Как работает линейное преобразование единичных векторов
См. видео 3Blue1Brown: Трехмерные линейные преобразования
См. видео 3Blue1Brown: Умножение матриц как композиция
«Матрицы дают нам язык для описания этих преобразований, где столбцы представляют эти координаты.

А умножение матрицы на вектор — это всего лишь способ вычислить, что это преобразование делает с заданным вектором.
Каждый раз, когда вы видите матрицу, вы можете интерпретировать ее как определенное преобразование пространства.
Как только вы усвоите идею, вы сможете глубоко понять линейную алгебру.
Почти все темы линейной алгебры станут понятными, как только вы начнете думать о матрицах как о преобразованиях пространства. ” — 3Blue1Brown
ВЫ ПРОСТО ДОЛЖНЫ ЗАПОМНИТЬ ЭТО УРАВНЕНИЕ И ПОЛУЧИТЬ ИДЕЮ. ЭТО ПОМОЖЕТ ВАМ ОТ ВСЕХ ИДЕЙ И ПРОБЛЕМ ЛИНЕЙНОЙ АЛГЕБРЫ.
Изменение базисаявляется самой сутью линейной трансформации. Каждое движение основано на этом.
Помните, что вектор (a, b) также может быть представлен в форме единичного вектора как v = ai + bj ,
и единичные векторы равны i = (1, 0) & j = (0 , 1) .
Если мы хотим преобразовать вектор, например, переместить, перевернуть, повернуть, масштабировать , мы сделаем следующее:
ЧТОБЫ ИЗМЕНИТЬ ЕДИНИЧНЫЙ ВЕКТОР и И j .
Например, есть вектор v = (-1, 2) , и он может быть представлен как v = -1i + 2j , тогда мы должны сделать с ним какое-то движение:
ЭТО МАГИЯ!!
Указав, куда должны идти единичных вектора , мы можем создать шаблон, правило сопоставления, так что каждый вектор использует эту карту, это правило, этот шаблон будет иметь одно и то же преобразование!
Другой пример:
Предположим, что есть вектор v=(5,7) , и пусть единичный вектор i=(3,-2) и j=(2,1) , и представим это ШАБЛОН ПРЕОБРАЗОВАНИЯ , как показано ниже:
И мы представляем это Применение преобразования к вектору в форме ниже:
ПОЭТОМУ, КОГДА КОГДА ВЫ ВСТРЕТИТЕСЬ С МАТРИЧНЫМ УМНОЖЕНИЕМ СНОВА, НИКОГДА НЕ ЧИТАЙТЕ ЭТО КАК ДВА ВЕКТОРА ИЛИ ДВЕ МАТРИЦЫ, УМНОЖАЮЩИЕСЯ ВМЕСТЕ!
Есть только ДВЕ части этого умножения матрицы:
График может состоять из одной точки (вектора) или множества точек (векторов), например:
ПОЭТОМУ ВСЕ, ЧТО ВАМ НУЖНО СДЕЛАТЬ, ЭТО ПРОСТО ПРИМЕНЯТЬ ЭТИ ПРАВИЛА ОДНО ЗА ОДНИМ, СЛЕВА ЗА ПРАВОМ И ПОЛУЧИТЬ НОВЫЙ ГРАФИК!!!
Например, мы применяем два правила преобразования к вектору (x, y) :
То же самое с принципами работы: Shear( Rotate(x, y)) .
В правиле преобразования , как показано ниже:
МЫ ДОЛЖНЫ РАЗБИТЬ МАТРИЦЫ НА ОТДЕЛЬНЫЕ ЧАСТИ, ПРЕЖДЕ ЧЕМ НАЧАТЬ ВЫЧИСЛЕНИЕ.
И так как мы сделали правило для i & j , поэтому давайте применим единичный вектор к График :
Обратите внимание, что:
v = 5(3,-2) + 7(2,1)
v = (15,-10) + (14,7)
v = (9009 , -3)
Решить:
- 1 90
Coordinate Matrix :Matrix Multiplication
| arm_status | arm_mat_mult_f16 (const arm_matrix_instance_f16 *pSrcA, const arm_matrix_instance_f16 *pSrcB, arm_matrix_instance_f16 *pDst) |
Умножение матриц с плавающей запятой. More… More… | |
| arm_status | arm_mat_mult_f32 (const arm_matrix_instance_f32 *pSrcA, const arm_matrix_instance_f32 *pSrcB, arm_matrix_instance_f32 *pDst) |
| Floating-point matrix multiplication. Подробнее… | |
| arm_status | arm_mat_mult_f64 (const arm_matrix_instance_f64 *pSrcA, const arm_matrix_instance_f64 *pSrc_ins, arm_ins, arm_instance0633 |
| Умножение матриц с плавающей запятой. More… | |
| arm_status | arm_mat_mult_fast_q15 (const arm_matrix_instance_q15 *pSrcA, const arm_matrix_instance_q15 *pSrcB, arm_matrix_instance_q15 *pDst, q15_t *pState) |
Q15 matrix multiplication (fast variant). Подробнее… Подробнее… | |
| arm_status | arm_mat_mult_fast_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_qinstance_q31 *pSrcB, arm_ins *0633 |
| Умножение матриц Q31 (быстрый вариант). More… | |
| arm_status | arm_mat_mult_opt_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst, q31_t *pState) |
| Q31 matrix multiplication. Подробнее … | |
| ARM_STATUS | ARM_MAT_MULT_Q15 (CONST ARM_MATRIX_INSTANCE_Q15 *PSRCA, CONST ARM_MATRIX_INSTANCE_IMTRIX_INSTANS0633 |
| Умножение матриц Q15. More… | |
| arm_status | arm_mat_mult_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst) |
Q31 matrix multiplication.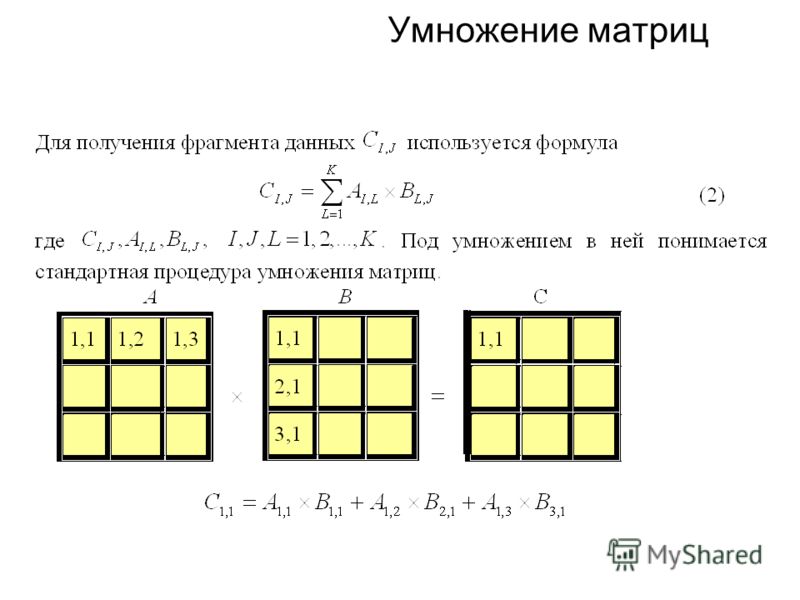 Подробнее… Подробнее… | |
| arm_status | arm_mat_mult_q7 (const arm_matrix_instance_q7 *pSrcA, const arm_matrix_instance_q7 *pst7pSrcB, arm_qStatinstance_q7 *pSt7pSrcB, arm_qStatins)0633 |
| Умножение матриц Q7. Подробнее… | |
Умножает две матрицы.
Умножение двух матриц 3 x 3
Умножение матриц определяется только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы. Умножение матрицы M x N на матрицу N x P дает матрицу M x P . Когда проверка размера матрицы включена, функции проверяют: (1) внутренние размеры pSrcA и pSrcB равны; и (2) что размер выходной матрицы равен внешним размерам pSrcA и pSrcB .
| arm_status arm_mat_mult_f16 | ( | константа arm_matrix_instance_f16 * | ПСРКА , |
| константа arm_matrix_instance_f16 * | pSrcB , | ||
| arm_matrix_instance_f16 * | пдст | ||
| ) |
| arm_status arm_mat_mult_f32 | ( | константа arm_matrix_instance_f32 * | ПСРКА , |
| константа arm_matrix_instance_f32 * | pSrcB , | ||
| arm_matrix_instance_f32 * | пдст | ||
| ) |
| arm_status arm_mat_mult_f64 | ( | константа arm_matrix_instance_f64 * | ПСРКА , |
| константа arm_matrix_instance_f64 * | pSrcB , | ||
| arm_matrix_instance_f64 * | пдст | ||
| ) |
| arm_status arm_mat_mult_fast_q15 | ( | константа arm_matrix_instance_q15 * | ПСРКА , |
| константа arm_matrix_instance_q15 * | pSrcB , | ||
| arm_matrix_instance_q15 * | пдст , | ||
| q15_t * | pState | ||
| ) |
Умножение матриц Q15 (быстрый вариант) для Cortex-M3 и Cortex-M4.
| arm_status arm_mat_mult_fast_q31 | ( | константа arm_matrix_instance_q31 * | ПСРКА , |
| константа arm_matrix_instance_q31 * | pSrcB , | ||
| arm_matrix_instance_q31 * | пдст | ||
| ) |
Умножение матриц Q31 (быстрый вариант) для Cortex-M3 и Cortex-M4.
| arm_status arm_mat_mult_opt_q31 | ( | константа arm_matrix_instance_q31 * | ПСРКА , |
| константа arm_matrix_instance_q31 * | pSrcB , | ||
| arm_matrix_instance_q31 * | пдст , | ||
| q31_t * | pState | ||
| ) |
| arm_status arm_mat_mult_q15 | ( | константа arm_matrix_instance_q15 * | ПСРКА , |
| константа arm_matrix_instance_q15 * | pSrcB , | ||
| arm_matrix_instance_q15 * | пдст , | ||
| q15_t * | pState | ||
| ) |


 Его сложность составляет Θ(n
Его сложность составляет Θ(n





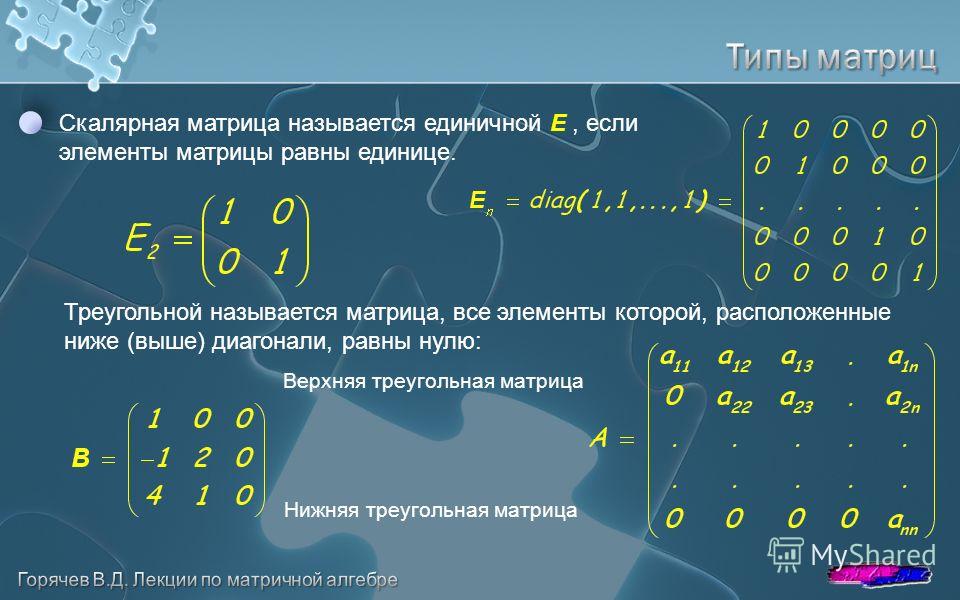


 Результат каждого умножения 1,15 x 1,15 усекается до формата 2,30. Эти промежуточные результаты накапливаются в 32-битном регистре в формате 2.30. Наконец, аккумулятор насыщается и преобразуется в результат 1,15.
Результат каждого умножения 1,15 x 1,15 усекается до формата 2,30. Эти промежуточные результаты накапливаются в 32-битном регистре в формате 2.30. Наконец, аккумулятор насыщается и преобразуется в результат 1,15.
 Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат.
Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат. Входные данные для умножения имеют формат 1,15, а умножения дают результат 2,30. Промежуточные результаты 2.30 накапливаются в 64-битном аккумуляторе в формате 34.30. Этот подход обеспечивает 33 защитных бита и исключает риск переполнения. Затем результат 34,30 усекается до формата 34,15 путем отбрасывания младших 15 бит, а затем насыщается до формата 1,15.
Входные данные для умножения имеют формат 1,15, а умножения дают результат 2,30. Промежуточные результаты 2.30 накапливаются в 64-битном аккумуляторе в формате 34.30. Этот подход обеспечивает 33 защитных бита и исключает риск переполнения. Затем результат 34,30 усекается до формата 34,15 путем отбрасывания младших 15 бит, а затем насыщается до формата 1,15. Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат.
Аккумулятор имеет формат 2.62 и поддерживает полную точность промежуточных результатов умножения, но предоставляет только один защитный бит. На промежуточных добавках насыщения нет. Таким образом, если аккумулятор переполняется, он закручивается и искажает результат. Входные сигналы должны быть уменьшены, чтобы избежать промежуточных переполнений. Таким образом, входные данные уменьшаются на log2(numColsA) битов, чтобы избежать переполнения, так как общее количество сложений numColsA выполняется внутри. Аккумулятор 2,62 сдвигается вправо на 31 бит и насыщается до формата 1,31, чтобы получить окончательный результат.

 Это означает, что всего у нас было $12$ умножений. Если вы действительно обдумаете, почему это число должно быть 12, вы сможете представить, что должно произойти в более крупном случае.
Это означает, что всего у нас было $12$ умножений. Если вы действительно обдумаете, почему это число должно быть 12, вы сможете представить, что должно произойти в более крупном случае.


 Хороший способ перепроверить свою работу, если вы перемножаете матрицы вручную, — это подтвердить свои ответы с помощью матричного калькулятора. Хотя в Интернете есть много матричных калькуляторов, самый простой в использовании, с которым я столкнулся, — это Math is Fun.
Хороший способ перепроверить свою работу, если вы перемножаете матрицы вручную, — это подтвердить свои ответы с помощью матричного калькулятора. Хотя в Интернете есть много матричных калькуляторов, самый простой в использовании, с которым я столкнулся, — это Math is Fun. Если вам интересно узнать о первом алгоритме, преодолевшем наивный барьер O( N ³) для умножения матриц, вы можете взглянуть на мою предыдущую статью о классическом алгоритме Штрассена.
Если вам интересно узнать о первом алгоритме, преодолевшем наивный барьер O( N ³) для умножения матриц, вы можете взглянуть на мою предыдущую статью о классическом алгоритме Штрассена. Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь — разработать O( N ²) алгоритм, проверяющий, является ли C = AB . Для этого мы прибегаем к случайности.
Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь — разработать O( N ²) алгоритм, проверяющий, является ли C = AB . Для этого мы прибегаем к случайности.

 Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая:
Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая: