Умножить матрицу на число онлайн с решением: Онлайн калькулятор. Умножение матрицы на число.

определение, свойства и примеры решения задач

Содержание:

Определение

Произведением матрицы $A$ на ненулевое число $ \lambda $ называется матрица $ B=\lambda A $ того же порядка, полученная из исходной умножением на заданное число всех ее элементов:

$$ B=\lambda A \Longrightarrow b_{i j}=\lambda a_{i j} $$

Итак, в результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на заданное число.

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число, то есть $ \lambda A = A \lambda $.

Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

Данная операция, вместе с операцией сложения матриц, относится к линейным операциям над матрицами.

Пример

Задание.

Чему равна матрица $-3A$, если матрица $ A=\left( \begin{array}{rr}{-1} & {3} \\ {0} & {2}\end{array}\right) $ ?

Решение. $ -3 A=3 \cdot \left( \begin{array}{rr}{-1} & {3} \\ {0} & {2}\end{array}\right)=\left( \begin{array}{rr}{-3 \cdot(-1)} & {-3 \cdot 3} \\ {-3 \cdot 0} & {-3 \cdot 2}\end{array}\right)=\left( \begin{array}{cc}{3} & {-9} \\ {0} & {-6}\end{array}\right) $

Ответ. $ -3 A=\left( \begin{array}{ll}{3} & {-9} \\ {0} & {-6}\end{array}\right) $

Свойства умножения матрицы на число:

1. $ 1 \cdot A=A $
2. $ 0 \cdot A=\Theta $
3. $ \lambda(A+B)=\lambda A+\lambda B $
4. $ (\lambda+\mu) A=\lambda A+\mu A $
5. $ (\lambda \mu) A=\lambda(\mu A) $

Читать дальше: сложение и вычитание матриц.

Слишком сложно?

Умножение матрицы на число не по зубам? Тебе ответит эксперт через 10 минут!

вектор умножить на матрицу онлайн

Вы искали вектор умножить на матрицу онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.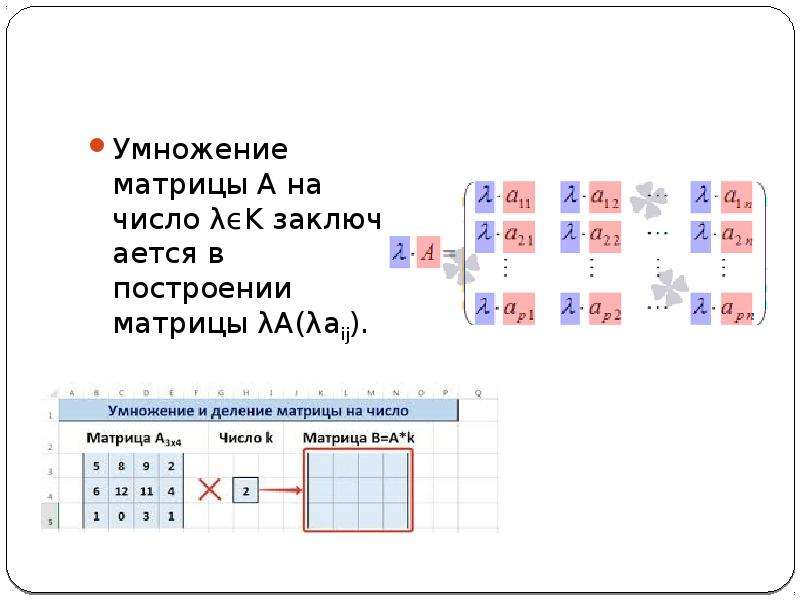 Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить произведение матриц, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вектор умножить на матрицу онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вектор умножить на матрицу онлайн,вычислить произведение матриц,вычислить произведение матриц онлайн с решением,дробь умножить на матрицу онлайн,как дробь умножить на матрицу,как умножить матрицу на матрицу 3х3,как умножить обратную матрицу на матрицу,калькулятор матриц онлайн с решением умножение,калькулятор матриц онлайн умножение матриц,калькулятор матриц перемножение,калькулятор матриц произведение,калькулятор матриц умножение,калькулятор матриц умножение матриц онлайн,калькулятор матрицы онлайн умножение,калькулятор матрицы умножение,калькулятор матрицы умножение онлайн,калькулятор онлайн матрицы умножение,калькулятор онлайн умножение матрицы,калькулятор перемножения матриц,калькулятор произведение матриц,калькулятор произведения матриц,калькулятор произведения матриц онлайн,калькулятор умножение матриц,калькулятор умножение матрицу на матрицу,калькулятор умножение матрицы,калькулятор умножение матрицы на матрицу,калькулятор умножение матрицы на матрицу онлайн,калькулятор умножение матрицы онлайн,калькулятор умножения матриц,калькулятор умножения матриц онлайн,матрица на матрицу умножение,матрица на матрицу умножение онлайн,матрица онлайн умножение,матрица умножение на матрицу онлайн,матрица умножение онлайн,матрица умножить на матрицу,матрицу умножить на вектор онлайн,матрицу умножить на матрицу онлайн,матрицу умножить на обратную матрицу,матрицы калькулятор умножение,матрицы найти произведение,матрицы онлайн калькулятор умножение,матрицы перемножение,матрицы умножение калькулятор,матрицы умножение онлайн,матрицы умножение онлайн калькулятор,матрицы умножения,матрицы умножить,множення матриць,найдите произведение матриц,найти произведение матриц,найти произведение матриц калькулятор онлайн,найти произведение матриц онлайн,найти произведение матриц онлайн калькулятор,найти произведение матриц онлайн с решением,найти произведение матрицы,найти произведения матриц,обратную матрицу умножить на матрицу,онлайн калькулятор матриц умножение матриц,онлайн калькулятор матриц умножения,онлайн калькулятор матрицы умножение,онлайн калькулятор найти произведение матриц,онлайн калькулятор перемножение матриц,онлайн калькулятор произведение матриц,онлайн калькулятор произведения матриц,онлайн калькулятор умножение матриц,онлайн калькулятор умножение матриц с подробным решением,онлайн калькулятор умножение матриц с решением,онлайн калькулятор умножение матриц с решением онлайн,онлайн калькулятор умножение матрицы,онлайн калькулятор умножение матрицы на матрицу,онлайн калькулятор умножения матриц,онлайн матрица умножение,онлайн перемножение матриц,онлайн умножение двух матриц,онлайн умножение матриц на матрицу,онлайн умножение матрица,онлайн умножение матрицы,онлайн умножение матрицы на матрицу,онлайн умножение трех матриц,онлайн умножения матриц,онлайн умножить матрицу на матрицу,перемножение матриц,перемножение матриц 3 на 3,перемножение матриц калькулятор,перемножение матриц онлайн,перемножение матриц онлайн калькулятор,перемножение матрицы,перемножить матрицы,перемножить матрицы онлайн,произведение матриц онлайн,произведение матриц онлайн калькулятор,произведения матриц калькулятор,произведения матриц калькулятор онлайн,произведения матриц онлайн калькулятор,решение матриц умножение матриц,умножение двух матриц онлайн,умножение матриц,умножение матриц 2 на 2,умножение матриц калькулятор,умножение матриц калькулятор онлайн,умножение матриц на матрицу онлайн,умножение матриц онлайн,умножение матриц онлайн калькулятор,умножение матриц онлайн калькулятор с подробным решением,умножение матриц онлайн калькулятор с решением,умножение матриц онлайн с решением,умножение матриц с,умножение матриц трех онлайн,умножение матрица,умножение матрица на матрица,умножение матрица на матрица онлайн,умножение матрица на матрицу онлайн,умножение матрица онлайн,умножение матрицу на матрицу калькулятор,умножение матрицы 3х3 на матрицу 3х3,умножение матрицы калькулятор,умножение матрицы калькулятор онлайн,умножение матрицы на вектор онлайн,умножение матрицы на матрицу 3х3,умножение матрицы на матрицу калькулятор,умножение матрицы на матрицу калькулятор онлайн,умножение матрицы на матрицу онлайн,умножение матрицы на матрицу онлайн калькулятор,умножение матрицы на матрицу онлайн с решением,умножение матрицы на матрицы калькулятор,умножение матрицы онлайн,умножение матрицы онлайн калькулятор,умножение обратной матрицы на матрицу,умножение онлайн матрица,умножение трех матриц,умножение число на матриц онлайн,умножения матриц онлайн,умножения матриц онлайн калькулятор,умножения матрицу на матрицу,умножения матрицы,умножить вектор на матрицу онлайн,умножить дробь на матрицу онлайн,умножить матрицу а на матрицу в,умножить матрицу на вектор онлайн,умножить матрицу на дробь онлайн,умножить матрицу на матрицу,умножить матрицу на матрицу онлайн,умножить матрицу на матрицу онлайн с решением,умножить матрицы,умножить матрицы онлайн,умножить матрицы онлайн с решением.

(adsbygoogle = window.adsbygoogle || []).push({}); На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вектор умножить на матрицу онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить произведение матриц онлайн с решением).

Где можно решить любую задачу по математике, а так же вектор умножить на матрицу онлайн Онлайн?

Решить задачу вектор умножить на матрицу онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькулятор матриц. Решение матриц онлайн. Решение матричных уравнений

Решение матриц онлайн является одним из самых востребованных запросов в интернете среди студентов, причём сервисов, где можно решить онлайн матрицу, практически нет. И снова на помощь придёт многофункциональный математический калькулятор. В его арсенал входит калькулятор матриц онлайн, который выполняет все основные операции над матрицами!

Матрица – это совокупность значений, записанных в прямоугольную таблицу. Каждый элемент матрицы имеет двойной порядковый номер в этой таблице, а именно номер столбца и номер строки. Размер матрицы определяется количеством строк и столбцов в таблице. Например, размер матрицы 3 на 5 значит, что она состоит из трёх строк и пяти столбцов.

Обратите внимание, 5 x 5 – это максимальный размер матрицы, которую может решить бесплатный калькулятор, предлагаемый на нашем сайте.

Как решать матрицы в онлайн калькуляторе

Чтобы вызвать калькулятор матриц, нажмите кнопку Matrix.

Кнопка, открывающая калькулятор матриц

Панель управления дополнится инструментами, с помощью которых выполняется решение матриц онлайн. Калькулятор позволяет выполнять следующие онлайн действия над матрицами: вычитание, сложение и умножение матриц, векторное произведение, решение матричных уравнений, транспонирование, нахождение обратной матрицы и вычисление определителя матрицы.

Кнопки калькулятора, выполняющие основные действия над матрицами

Помимо панели с кнопками онлайн калькулятор матриц содержит удобную форму для быстрого ввода выражения. В левой и правой частях задаются матрицы, их размер выбирается из выпадающего списка. В середине выпадающее меню для выбора операции, которую нужно выполнить калькулятору с заданными матрицами. Другие возможности калькулятора можно посмотреть здесь Функции калькулятора.

Вычисление матриц онлайн с помощью формы быстрого ввода

Если элемент матрицы не указан, онлайн калькулятор подставляет значение «0».

Обратите внимание, при вызове меню решения матриц вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу “I”, чтобы увидеть дисплей в полный размер.

Вектор столбец

Матрица, состоящая только из одной строки или одного столбца, называется вектор-строкой или вектор-столбцом соответственно. В калькуляторе предусмотрены отдельные кнопки для ввода матрицы, число столбцов которой равно 1. Используйте эти клавиши, чтобы записать вектор-столбец из 3,4 или 5 строк соответственно.

Кнопки калькулятора для ввода вектора

(2, 6, 8)

Вектор-столбец из 3х строк

Квадратная матрица

Матрица называется квадратной, если число её строк равно числу столбцов. Следует отметить, что только у квадратной матрицы может быть главная диагональ матрицы – линия, проходящая через элементы матрицы с одинаковыми индексами, начиная с ячейки первой строки первого столбца и заканчивая элементом, стоящем в последнем столбце последней строки.

Для быстрой записи квадратных матриц 2, 3 или 4-го порядка используйте специальные кнопки, которые предлагает калькулятор онлайн.

Кнопки калькулятора для ввода квадратных матриц

[[ 8, 4, 1, 8][ 7, 1, 8, 8][ 8, 4, 1, 6][ 4, 8, 3, 1]]

Пример квадратной матрицы 4 порядка

Квадратные матрицы, у которых все элементы, исключая элементы главной диагонали, равны нулю, называются диагональные матрицы. Симметричная матрица чисел представляет собой таблицу, в которой все элементы, симметричные относительно главной диагонали, равны.

[[ 1, 2, 8, 11][ 2, 3, 24, 5][ 8, 24, 6, 4][ 11, 5, 4, 9]]

Пример симметричной матрицы

Есть ещё такие виды матриц в математике.

Единичная матрица чисел – это таблица, в которой элементы главной диагонали равны единице, а все остальные элементы являются нулевыми.

[[ 1, 0, 0, 0][ 0, 1, 0, 0][ 0, 0, 1, 0][ 0, 0, 0, 1]]

Пример единичной матрицы

Таблица, у которой значение всех элементов равно 0, называется нулевая матрица.

[[ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0]]

Пример нулевой матрицы

Матрицы и действия над ними

Сложение и вычитание матриц онлайн

С помощью калькулятора можно произвести сложение матриц онлайн, а также найти разность матриц онлайн. Чтобы вычислить сумму матриц или найти их разность, выполняются соответствующие операции над их элементами. Например, найти сумму матриц значит определить такую матрицу, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.

Найти сумму элементов матриц или их разность можно только в том случае, если исходные матрицы одинакового размера, т. е. число их строк и столбцов соответственно равно. Вычитание и сложение матриц разного размера невозможно.

Для выполнения этих операций в калькуляторе используйте форму быстрого ввода или запишите выражение вручную.

Сложение матриц примеры

[[1, 2, 3][3, 1, 2][5, 0, 6]]+[[1, 2, 5][6, 3, 2][9, 9, 9]]

Сложение двух матриц

[[2, 7][4, 5]]+[[2, 10][6, 8]]

Сумма двух матриц

Векторное произведение матриц

Для выполнения этой операции используйте клавишу Cross Product.

(2, 6, 4)#(8, 2, 5)

Пример произведения векторов

Умножение матриц

Умножение матриц онлайн калькулятор производит с помощью клавиши Vector/Matrice-Multiplication.

Перемножение матриц возможно только в том случае, если количество столбцов одной матрицы равняется количеству строк другой. Чтобы матрицу умножить на число, нужно каждый элемент матрицы умножить на это число.

[[2, 8][4, 2]]*[[8, 8][7, 1]]

Умножение матриц пример

[[5, 6][7, 8]]*9

Умножение матрицы на число онлайн

Решение матричных уравнений

Эта функция калькулятора позволяет находить неизвестные матрицы, которые описаны уравнением зависимости одной матрицы от другой. Решение матричных уравнений осуществляется с помощью кнопки Solve Ecuation System.

[[6, 1, 8],[7, 5, 3],[2, 9, 4]]*x=(1, 2, 3)

Пример решения системы уравнений матриц

Транспонирование матрицы

Используйте клавишу Matrix Transponent, когда нужно выполнить транспонирование матрицы – действие, в котором строки со столбцами меняются местами. Таким образом, транспонированная матрица получается путем замены строк на столбы в исходной матрице. -1

Нахождение обратной матрицы пример

Нахождение определителя матрицы

В калькуляторе матриц нет специальной кнопки для того, чтобы найти определитель матрицы. Но вычислить его можно, написав в поле ввода специальную функцию – оператор det(Determinant).

det( [ [-2, 2, -3], [-1, 1, 3], [2, 0, -1] ] )

Пример, как найти определитель матрицы онлайн

Бесплатный калькулятор онлайн может не только решить онлайн матрицу, в его возможностях также: возведение в степень, калькулятор корней, тригонометрические функции, решение логарифмов и другие дополнительные функции.

Калькулятор Инструкция – обзор всех функций калькулятора и общее описание, как пользоваться калькулятором.

Линейная алгебра на Python. [Урок 3]. Действия над матрицами

Тема третьего урока: действия над матрицами. В рамках нее будут рассмотрены следующие вопросы: умножение матрицы на число, сложение и умножение матриц.

Действия над матрицами

Умножение матрицы на число

При умножении матрицы на число, все элементы матрицы умножаются на это число:

➣ Численный пример

➤ Пример на Python

>>> A = np. matrix('1 2 3; 4 5 6')
>>> C = 3 * A
>>> print(C)
[[ 3  6 9]
[12 15 18]]

 

Рассмотрим свойства операции умножения матрицы на число.

Свойство 1. Произведение единицы и любой заданной матрицы равно заданной матрице:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> L = 1 * A
>>> R = A
>>> print(L)
[[1 2]
[3 4]]

>>> print(R)
[[1 2]
[3 4]]

 

Свойство 2. Произведение нуля и любой матрицы равно нулевой матрице, размерность которой равна исходной матрицы:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = 0 * A
>>> R = Z

>>> print(L)
[[0 0]
[0 0]]

>>> print(R)
[[0 0]
[0 0]]

 

Свойство 3. Произведение матрицы на сумму чисел равно сумме произведений матрицы на каждое из этих чисел:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3

>>> L = (p + q) * A
>>> R = p * A + q * A

>>> print(L)
[[ 5 10]
[15 20]]

>>> print(R)
[[ 5 10]
[15 20]]

 

Свойство 4. Произведение матрицы на произведение двух чисел равно произведению второго числа и заданной матрицы, умноженному на первое число:

➣ Численный пример

➤Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3

>>> L = (p * q) * A
>>> R = p * (q * A)

>>> print(L)
[[ 6 12]
[18 24]]

>>> print(R)
[[ 6 12]
[18 24]]

 

Свойство 5. Произведение суммы матриц на число равно сумме произведений этих матриц на заданное число:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> k = 3

>>> L = k * (A + B)
>>> R = k * A + k * B

>>> print(L)
[[18 24]
[30 36]]

>>> print(R)
[[18 24]
[30 36]]

 

Сложение матриц

Складывать можно только матрицы одинаковой размерности — то есть матрицы, у которых совпадает количество столбцов и строк.

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 6 3; 8 2 7')
>>> B = np.matrix('8 1 5; 6 9 12')
>>> C = A + B

>>> print(C)
[[ 9  7 8]
[14 11 19]]

 

Рассмотрим свойства сложения матриц.

Свойство 1. Коммутативность сложения. От перестановки матриц их сумма не изменяется:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')

>>> L = A + B
>>> R = B + A

>>> print(L)
[[ 6  8]
[10 12]]

>>> print(R)
[[ 6  8]
[10 12]]

 

Свойство 2. Ассоциативность сложения. Результат сложения трех и более матриц не зависит от порядка, в котором эта операция будет выполняться:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('1 7; 9 3')

>>> L = A + (B + C)
>>> R = (A + B) + C
>>> print(L)

[[ 7 15]
[19 15]]

>>> print(R)
[[ 7 15]
[19 15]]

 

Свойство 3. Для любой матрицы существует противоположная ей , такая, что их сумма является нулевой матрицей :

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')

>>> L = A + (-1)*A

>>> print(L)
[[0 0]
[0 0]]

>>> print(Z)
[[0 0]
[0 0]]

 

Умножение матриц

Умножение матриц это уже более сложная операция, по сравнению с рассмотренными выше. Умножать можно только матрицы, отвечающие следующему требованию: количество столбцов первой матрицы должно быть равно числу строк второй матрицы.

Для простоты запоминания этого правила можно использовать диаграмму умножения, представленную на рисунке 1.

Рисунок 1 — Диаграмма матричного умножения

Рассмотрим умножение матриц на примере.

➣ Численный пример

Каждый элемент c_ij новой матрицы является суммой произведений элементов i-ой строки первой матрицы и j-го столбца второй матрицы. Математически это записывается так:

➤Пример на Python

Решим задачу умножения матриц на языке Python. Для этого будем использовать функцию dot() из библиотеки Numpy:

>>> A = np.matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8; 9 1; 2 3')

>>> C = A.dot(B)

>>> print(C)
[[31 19]
[85 55]]

 

Ниже представлены свойства произведения матриц. Примеры свойств будут показаны для квадратной матрицы.

Свойство 1. Ассоциативность умножения. Результат умножения матриц не зависит от порядка, в котором будет выполняться эта операция:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')

>>> L = A. dot(B.dot(C))
>>> R = (A.dot(B)).dot(C)

>>> print(L)
[[192 252]
[436 572]]

>>> print(R)
[[192 252]
[436 572]]

 

Свойство 2. Дистрибутивность умножения. Произведение матрицы на сумму матриц равно сумме произведений матриц:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')

>>> L = A.dot(B + C)
>>> R = A.dot(B) + A.dot(C)

>>> print(L)
[[35 42]
[77 94]]
>>> print(R)
[[35 42]
[77 94]]

 

Свойство 3. Умножение матриц в общем виде не коммутативно. Это означает, что для матриц не выполняется правило независимости произведения от перестановки множителей:

➣ Численный пример

➤ Пример на Python

>>> A = np. matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')

>>> L = A.dot(B)
>>> R = B.dot(A)

>>> print(L)
[[19 22]
[43 50]]

>>> print(R)
[[23 34]
[31 46]]

 

Свойство 4. Произведение заданной матрицы на единичную равно исходной матрице:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> E = np.matrix('1 0; 0 1')

>>> L = E.dot(A)
>>> R = A.dot(E)

>>> print(L)
[[1 2]
[3 4]]

>>> print(R)
[[1 2]
[3 4]]

>>> print(A)
[[1 2]
[3 4]]

 

Свойство 5. Произведение заданной матрицы на нулевую матрицу равно нулевой матрице:

➣ Численный пример

➤ Пример на Python

>>> A = np. matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')

>>> L = Z.dot(A)
>>> R = A.dot(Z)

>>> print(L)
[[0 0]
[0 0]]

>>> print(R)
[[0 0]
[0 0]]

>>> print(Z)
[[0 0]
[0 0]]

 

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.  Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

НОУ ИНТУИТ | Лекция | Параллельные методы матричного умножения

Аннотация: В лекции рассматривается одна из основных задач матричных вычислений — умножение матриц. Приводится постановка задачи и дается последовательный алгоритм ее решения. Далее описываются возможные подходы к параллельной реализации алгоритма и подробно рассматриваются наиболее широко известные алгоритмы: алгоритм, основанный на ленточной схеме разделения данных, алгоритм Фокса (Fox) и алгоритм Кэннона (Cannon)

7.1. Постановка задачи

Умножение матрицы A размера mxn и матрицы B размера nxl приводит к получению матрицы С размера mxl, каждый элемент которой определяется в соответствии с выражением:

( 7.1)

Как следует из (7.1), каждый элемент результирующей матрицы С есть скалярное произведение соответствующих строки матрицы A и столбца матрицы B:

( 7. 2)

Этот алгоритм предполагает выполнение mxnxl операций умножения и столько же операций сложения элементов исходных матриц. При умножении квадратных матриц размера nxn количество выполненных операций имеет порядок O(n³). Известны последовательные алгоритмы умножения матриц, обладающие меньшей вычислительной сложностью (например, алгоритм Страссена ( Strassen’s algorithm )), но эти алгоритмы требуют больших усилий для их освоения, и поэтому в данной лекции при разработке параллельных методов в качестве основы будет использоваться приведенный выше последовательный алгоритм. Также будем предполагать далее, что все матрицы являются квадратными и имеют размер nxn.

7.2. Последовательный алгоритм

Последовательный алгоритм умножения матриц представляется тремя вложенными циклами:

Алгоритм 7. 1. Последовательный алгоритм умножения двух квадратных матриц

// Алгоритм 7.1
// Последовательный алгоритм умножения матриц
double MatrixA[Size][Size]; 
double MatrixB[Size][Size];
double MatrixC[Size][Size];
int i,j,k;
...
for (i=0; i<Size; i++){
  for (j=0; j<Size; j++){
    MatrixC[i][j] = 0; 
    for (k=0; k<Size; k++){
      MatrixC[i][j] = MatrixC[i][j] + MatrixA[i][k]*MatrixB[k][j];
    }
  }
}

Этот алгоритм является итеративным и ориентирован на последовательное вычисление строк матрицы С. Действительно, при выполнении одной итерации внешнего цикла (цикла по переменной i ) вычисляется одна строка результирующей матрицы (см. рис. 7.1).

Рис. 7.1. На первой итерации цикла по переменной i используется первая строка матрицы A и все столбцы матрицы B для того, чтобы вычислить элементы первой строки результирующей матрицы С

Поскольку каждый элемент результирующей матрицы есть скалярное произведение строки и столбца исходных матриц, то для вычисления всех элементов матрицы С размером nxn необходимо выполнить n²x(2n–1) скалярных операций и затратить время

( 7.3)

где есть время выполнения одной элементарной скалярной операции.

7.3. Умножение матриц при ленточной схеме разделения данных

Рассмотрим два параллельных алгоритма умножения матриц, в которых матрицы A и B разбиваются на непрерывные последовательности строк или столбцов (полосы).

7.3.1. Определение подзадач

Из определения операции матричного умножения следует, что вычисление всех элементов матрицы С может быть выполнено независимо друг от друга. Как результат, возможный подход для организации параллельных вычислений состоит в использовании в качестве базовой подзадачи процедуры определения одного элемента результирующей матрицы С. Для проведения всех необходимых вычислений каждая подзадача должна содержать по одной строке матрицы А и одному столбцу матрицы В. Общее количество получаемых при таком подходе подзадач оказывается равным n² (по числу элементов матрицы С ).

Рассмотрев предложенный подход, можно отметить, что достигнутый уровень параллелизма является в большинстве случаев избыточным. Обычно при проведении практических расчетов такое количество сформированных подзадач превышает число имеющихся процессоров и делает неизбежным этап укрупнения базовых задач. В этом плане может оказаться полезной агрегация вычислений уже на шаге выделения базовых подзадач. Возможное решение может состоять в объединении в рамках одной подзадачи всех вычислений, связанных не с одним, а с несколькими элементами результирующей матрицы С. Для дальнейшего рассмотрения определим базовую задачу как процедуру вычисления всех элементов одной из строк матрицы С. Такой подход приводит к снижению общего количества подзадач до величины n.

Для выполнения всех необходимых вычислений базовой подзадаче должны быть доступны одна из строк матрицы A и все столбцы матрицы B. Простое решение этой проблемы – дублирование матрицы B во всех подзадачах – является, как правило, неприемлемым в силу больших затрат памяти для хранения данных. Поэтому организация вычислений должна быть построена таким образом, чтобы в каждый текущий момент времени подзадачи содержали лишь часть данных, необходимых для проведения расчетов, а доступ к остальной части данных обеспечивался бы при помощи передачи данных между процессорами. Два возможных способа выполнения параллельных вычислений подобного типа рассмотрены далее в п. 7.3.2.

7.3.2. Выделение информационных зависимостей

Для вычисления одной строки матрицы С необходимо, чтобы в каждой подзадаче содержалась строка матрицы А и был обеспечен доступ ко всем столбцам матрицы B. Возможные способы организации параллельных вычислений состоят в следующем.

1. Первый алгоритм. Алгоритм представляет собой итерационную процедуру, количество итераций которой совпадает с числом подзадач. На каждой итерации алгоритма каждая подзадача содержит по одной строке матрицы А и одному столбцу матрицы В. При выполнении итерации проводится скалярное умножение содержащихся в подзадачах строк и столбцов, что приводит к получению соответствующих элементов результирующей матрицы С. По завершении вычислений в конце каждой итерации столбцы матрицы В должны быть переданы между подзадачами с тем, чтобы в каждой подзадаче оказались новые столбцы матрицы В и могли быть вычислены новые элементы матрицы C. При этом данная передача столбцов между подзадачами должна быть организована таким образом, чтобы после завершения итераций алгоритма в каждой подзадаче последовательно оказались все столбцы матрицы В.

Возможная простая схема организации необходимой последовательности передач столбцов матрицы В между подзадачами состоит в представлении топологии информационных связей подзадач в виде кольцевой структуры. В этом случае на каждой итерации подзадача i, 0<=i<n, будет передавать свой столбец матрицы В подзадаче с номером i+1 (в соответствии с кольцевой структурой подзадача n-1 передает свои данные подзадаче с номером 0 ) – см. рис. 7.2. После выполнения всех итераций алгоритма необходимое условие будет обеспечено – в каждой подзадаче поочередно окажутся все столбцы матрицы В.

На рис. 7.2 представлены итерации алгоритма матричного умножения для случая, когда матрицы состоят из четырех строк и четырех столбцов ( n=4 ). В начале вычислений в каждой подзадаче i, 0<=i<n, располагаются i -я строка матрицы A и i -й столбец матрицы B. В результате их перемножения подзадача получает элемент c_ii результирующей матрицы С. Далее подзадачи осуществляют обмен столбцами, в ходе которого каждая подзадача передает свой столбец матрицы B следующей подзадаче в соответствии с кольцевой структурой информационных взаимодействий. Далее выполнение описанных действий повторяется до завершения всех итераций параллельного алгоритма.

Рис. 7.2. Общая схема передачи данных для первого параллельного алгоритма матричного умножения при ленточной схеме разделения данных

2. Второй алгоритм. Отличие второго алгоритма состоит в том, что в подзадачах располагаются не столбцы, а строки матрицы B. Как результат, перемножение данных каждой подзадачи сводится не к скалярному умножению имеющихся векторов, а к их поэлементному умножению. В результате подобного умножения в каждой подзадаче получается строка частичных результатов для матрицы C.

При рассмотренном способе разделения данных для выполнения операции матричного умножения нужно обеспечить последовательное получение в подзадачах всех строк матрицы B, поэлементное умножение данных и суммирование вновь получаемых значений с ранее вычисленными результатами. Организация необходимой последовательности передач строк матрицы B между подзадачами также может быть выполнена с использованием кольцевой структуры информационных связей (см. рис. 7.3).

На рис. 7.3 представлены итерации алгоритма матричного умножения для случая, когда матрицы состоят из четырех строк и четырех столбцов ( n=4 ). В начале вычислений в каждой подзадаче i, 0<=i<n, располагаются i -е строки матрицы A и матрицы B. В результате их перемножения подзадача определяет i -ю строку частичных результатов искомой матрицы C. Далее подзадачи осуществляют обмен строками, в ходе которого каждая подзадача передает свою строку матрицы B следующей подзадаче в соответствии с кольцевой структурой информационных взаимодействий. Далее выполнение описанных действий повторяется до завершения всех итераций параллельного алгоритма.

Рис. 7.3. Общая схема передачи данных для второго параллельного алгорится матричного умножения при ленточной схеме разделения данных

как найти произведение двух или трех разных размеров, условия и формулы

Мы помним, что матрицы – это таблицы взаимосвязанных элементов, которые позволяют упростить математические вычисления и систематизировать определённую информацию. Их можно складывать, вычитать, умножать между собой. В этой статье подробнее остановимся на последнем алгоритме – матричном произведении.

Умножение матриц — определение

Матричное умножение – это одна из основных операций, которая проводится исключительно с согласованными матрицами.

При произведении матриц A и B получается новая матрица C. В математическом виде формула будет выглядеть так:

 

Но для начала разберёмся, что такое согласованные матрицы.

Согласованные матрицы

Согласованными матрицами называют матрицы вида A = [m ☓ n] и B = [n ☓ k], где количество столбцов А равно количеству строк В.

 

Индексы показывают координаты равных элементов.

 

Для того, чтобы умножить А и В, нужно взять строку в первой матрице и столбец во второй, перемножить одинаковые элементы и сложить полученные произведения.

Основные свойства матричного произведения

Размеры, то есть количество строк (m) и столбцов (n), влияют на особенности матричного произведения. Следовательно, для двух главных видов – квадратных и прямоугольных – действуют разные свойства произведения. Однако умножение любого вида всегда некоммуникативное. Это означает, что матрицы нельзя менять местами (АВ ≠ ВА).

Умножение квадратных матриц

Для квадратных матриц существует единичная матрица Е. В ней элементы по главной диагонали равны единице, а оставшиеся – нулю. Произведение любой квадратной матрицы на неё не влияет на результат.

 

В математическом виде это выглядит так: ЕА = АЕ = А

Также существует обратная матрица А (-1), при умножении на которую исходная A = [m ☓ n] даёт в результате единичную матрицу E.

 

Следовательно, формула такова: АА(-1) = Е

Умножение прямоугольных матриц

Существуют четыре основных свойства умножения:

1. Сочетательное свойство, или ассоциативность: (AB)C = A(BC)
2. Распределительное свойство, или дистрибутивность: А(В+С) = АВ + АС / (А+В)С = АС + ВС
3. Умножение на единичную матрицу: ЕА = А
4. Умножение на нулевую матрицу: 0А = 0

Напомним, что у нулевой матрицы все элементы равны нулю.

Произведение трех матриц

Произведение АВС можно получить двумя альтернативными способами:

1. Найти АВ и умножить на С
2. Найти ВС и умножить на А

(АВ) С = А (ВС)

Данное свойство называется ассоциативностью матричного умножения и действует на все виды согласованных матриц. Сами они не переставляются, меняется только порядок их умножения.

Умножение матрицы на число

Для умножения на число необходимо умножить каждый матричный элемент на это число:

 

Дроби вносить не нужно, поскольку они могут затруднить дальнейшие операции.

Умножение матрицы на вектор

Здесь работает правило «строка на столбец».

 

При умножении на вектор-столбец важно, чтобы количество столбцов в матрице совпадало с количеством строк в векторе-столбце. Результатом произведения будет вектор-столбец.

 

При умножении на вектор-строку матрица должна быть только вектором-столбцом. Важно, чтобы количество строк в векторе-столбце совпадало с количеством столбцов в векторе-строке. Результатом произведения будет квадратная матрица.

Примеры задач на умножение матриц

Задача №1: выполнить умножение и найти С, если A = [m ☓ n] и B = [n ☓ k] равны.

 

Решение: 

c₁₁ = a₁₁·b₁₁ + a₁₂·b₂₁ = 4·3 + 2·(-3) = 12 – 6 = 6

c₁₂ = a₁₁·b₁₂ + a₁₂·b₂₂ = 4·1 + 2·4 = 4 + 8 = 12

c₂₁ = a₂₁·b₁₁ + a₂₂·b₂₁ = 9·3 + 0·(-3) = 27 + 0 = 27

c₂₂ = a₂₁·b₁₂ + a₂₂·b₂₂ = 9·1 + 0·4 = 9 + 0 = 9

Ответ: 

 

Задача №2: вычислить С, если А = [m ☓ n] и вектор-столбец В равны.{-1}\), где \(\mathbb{A}\) – первая матрица, \(\mathbb{B}\) – вторая матрица. То есть это умножение на обратную матрицу. Следует иметь ввиду, что вторая матрица должна быть квадратной.

При поэлементном возведении в степень вместо второй матрицы должно быть просто число. Каждый элемент матрицы возводится в степень, равную этому числу.

Матричное возведение в степень \(n\) – это матричное умножение матрицы саму на себя \(n\) раз. То есть во второе поле ввода должно быть вписано целое число. Для получения обратной матрицы введите в правую часть «\(-1\)»

Решение линейных уравнений – в этом режиме первая матрица содержит коэффициенты уравнения в левой части, вторая – в правой части. Например, чтобы решить систему уравнений \[\left\lbrace\begin{aligned}2x+3y&=5;\\10x-y&=6,\end{aligned}\right.\] нужно ввести в левое поле ввода:

2 3
10 -1

в правое:

5
6

Калькулятор умножения матриц

– eMathHelp

1. Дом
2. Калькуляторы
3. Калькуляторы линейной алгебры
4. Решение математических задач (все калькуляторы)

Калькулятор найдет произведение двух матриц (если возможно) с указанными шагами. Он перемножает матрицы любого размера до 10х10 (2х2, 3х3, 4х4 и т. Д.).

Размер первой матрицы:

12345678910

Размер второй матрицы:

12345678910

Если калькулятор что-то не вычислил, или вы обнаружили ошибку, или у вас есть предложение / отзыв, напишите об этом в комментариях ниже.

Ваш ввод

Вычислить $$$ \ left [\ begin {array} {ccc} 4 & 5 & 7 \\ 2 & 1 & 0 \ end {array} \ right] \ cdot \ left [\ begin {array} {cc} 2 & 3 \\ 8 & 9 \\ 1 & 1 \ end {array} \ right]. $$$

Решение

$$$ \ left [\ begin {array} {ccc} \ color {DeepPink} {4} & \ color {Blue} {5} & \ color {Purple} {7} \\\ color {Малиновый} {2} & \ color {Фуксия} {1} & \ color {GoldenRod} {0} \ end {array} \ right] \ cdot \ left [\ begin {array} {cc} \ color {Blue} {2} & \ color {Шоколад} {3} \\\ color {DeepPink} {8} & \ color {GoldenRod} {9} \\\ color {Crimson} {1} & \ color {DarkCyan} {1} \ end {array} \ right] = \ left [\ begin {array} {cc} \ color {DeepPink} {\ left (4 \ right)} \ cdot \ color {Blue} {\ left (2 \ right)} + \ color {Blue} {\ left (5 \ right)} \ cdot \ color {DeepPink} {\ left (8 \ right)} + \ color {Purple} {\ left (7 \ right)} \ cdot \ color {Малиновый} {\ left (1 \ right)} & \ color {DeepPink} {\ left (4 \ right)} \ cdot \ color {Шоколад} {\ left (3 \ right)} + \ color {Blue} { \ left (5 \ right)} \ cdot \ color {GoldenRod} {\ left (9 \ right)} + \ color {Purple} {\ left (7 \ right)} \ cdot \ color {DarkCyan} {\ left ( 1 \ right)} \\\ color {Crimson} {\ left (2 \ right)} \ cdot \ color {Blue} {\ left (2 \ right)} + \ color {Fuchsia} {\ left (1 \ right )} \ cdot \ color {DeepPink} {\ left (8 \ right)} + \ color {GoldenRod} {\ left (0 \ right)} \ cdot \ color {Crimson} {\ left (1 \ right)} & \ color {Crimson} {\ left (2 \ right)} \ cdot \ color {Шоколад} {\ left (3 \ right)} + \ color {Фуксия} {\ left (1 \ right)} \ cdot \ color {GoldenRod} {\ left (9 \ right)} + \ color {GoldenRod} {\ left (0 \ right)} \ cdot \ color {DarkCyan} {\ left (1 \ right)} \ end {array} \ right] = \ left [\ begin {array} {cc} 55 & 64 \\ 12 & 15 \ end {array} \ right] $$$

Ответ

$$$ \ left [\ begin {array} {ccc} 4 & 5 & 7 \\ 2 & 1 & 0 \ end {array} \ right] \ cdot \ left [\ begin {array} {cc} 2 & 3 \\ 8 & 9 \\ 1 & 1 \ end {array} \ right] = \ left [\ begin {array} {cc} 55 & 64 \\ 12 & 15 \ end {array} \ справа] $$$ A

Калькулятор умножения матриц 3×3

Как найти произведение матриц $ n \ times n $?

Многие операции с матрицами имеют смысл только в том случае, если матрицы имеют подходящие размеры.Другими словами, они должны быть одинакового размера, с одинаковым количеством строк и одинаковым количеством столбцов.

Когда мы имеем дело с умножением матриц, матрицы $ A = (a_ {ij}) _ {m \ times p} $ с $ m $ строками, $ p $ столбцами и $ B = (b_ {ij}) _ {r \ times n} $ с $ r $ строками, $ n $ столбцов можно умножать тогда и только тогда, когда $ p = r $. Это означает, что количество столбцов первой матрицы $ A $ должно быть равно количеству строк второй матрицы $ B $. Результатом этой матрицы является новая матрица, которая имеет то же количество строк, что и первая матрица, $ A $, и такое же количество столбцов, как вторая матрица, $ B $.Итак, соответствующее произведение $ C = A \ cdot B $ представляет собой матрицу размера $ m \ times n $. Элементами $ c_ {ij} $ этой матрицы являются $$ c_ {ij} = a_ {i1} b_ {1j} + a_ {i2} b_ {2j} \ ldots + a_ {ip} b_ {pj} \ quad \ mbox {for} \; i = 1, \ ldots , m, \; j = 1, \ ldots, n. $$ Например, умножение матриц $ 3 \ times 3 $ определяется по следующей формуле $$ \ begin {align} & \ left ( \ begin {array} {ccc} а_ {11} и а_ {12} и а_ {13} \\ а_ {21} и а_ {22} и а_ {23} \\ а_ {31} и а_ {32} и а_ {33} \\ \ end {массив} \ справа) \ cdot \оставил( \ begin {array} {ccc} b_ {11} & b_ {12} & b_ {13} \\ b_ {21} & b_ {22} & b_ {23} \\ b_ {31} & b_ {32} & b_ {33} \\ \ end {массив} \ right) \\ & = \ left (\ begin {array} {ccc} a_ {11} b_ {11} + a_ {12} b_ {21} + a_ {13} b_ {31} и a_ {11} b_ {12} + a_ {12} b_ {22} + a_ {13} b_ {32} & a_ {11} b_ {13} + a_ {12} b_ {23} + a_ {13} b_ {33} \\ a_ {21} b_ {11} + a_ {22} b_ {21} + a_ {23} b_ {31} и a_ {21} b_ {12} + a_ {22} b_ {22} + a_ {23} b_ { 32} & a_ {21} b_ {13} + a_ {22} b_ {23} + a_ {23} b_ {33} \\ a_ {31} b_ {11} + a_ {32} b_ {21} + a_ {33} b_ {31} и a_ {31} b_ {12} + a_ {32} b_ {22} + a_ {33} b_ { 32} & a_ {31} b_ {13} + a_ {32} b_ {23} + a_ {33} b_ {33} \\ \ end {array} \ right) \ end {align} $$
Свойства умножения матриц

1. Умножение матриц, вообще говоря, не коммутативно, $ AB \ not BA $.В некоторых случаях продукт $ AB $ существует, а продукт $ BA $ не существует. Оба произведения $ AB $ и $ BA $ определены тогда и только тогда, когда матрицы $ A $ и $ B $ являются квадратными матрицами одинакового размера.
2. Если $ A = (a_ {ij}) _ {mn} $, $ B = (b_ {ij}) _ {np} $ и $ C = (c_ {ij}) _ {pk} $, то матричное умножение ассоциативно, т. е. $$ A (BC) = (AB) C $$
3. Если $ A = (a_ {ij}) _ {mn} $, $ B = (b_ {ij}) _ {np} $, $ C = (c_ {ij}) _ {np} $ и $ D = (d_ {ij}) _ {pq} $, тогда умножение матриц дистрибутивно относительно сложения матриц, т.е.е. $$ \ begin {align} A (B + C) & = AB + AC \\ (B + C) D & = BD + CD \ end {align} $$
4. Если $ A_ {n \ times n} $ – квадратная матрица, существует единичная матрица $ I_ {n \ times n} $ такая, что $$ AI = IA = A $$

Например, найдем продукт $ AB $ для $$ A = \ left ( \ begin {array} {ccc} 10 и 20 и 10 \\ 4 и 5 и 6 \\ 2 и 3 и 5 \\ \ end {массив} \ right) \ quad \ mbox {и} \ quad B = \ left ( \ begin {array} {ccc} 3 и 2 и 4 \\ 3 и 3 и 9 \\ 4 и 4 и 2 \\ \ end {массив} \ right) $$ Используя формулу умножения матриц $ 3 \ times 3 $, произведение $ AB $ представляет собой матрицу $$ \ begin {align} C & = \ left ( \ begin {array} {ccc} 10 \ cdot3 + 20 \ cdot3 + 10 \ cdot4 & 10 \ cdot2 + 20 \ cdot3 + 10 \ cdot4 & 10 \ cdot4 + 20 \ cdot9 + 10 \ cdot2 \\ 4 \ cdot3 + 5 \ cdot3 + 6 \ cdot4 & 4 \ cdot2 + 5 \ cdot3 + 6 \ cdot4 & 4 \ cdot4 + 5 \ cdot9 + 6 \ cdot2 \\ 2 \ cdot3 + 3 \ cdot3 + 5 \ cdot4 & 2 \ cdot2 + 3 \ cdot3 + 5 \ cdot4 & 2 \ cdot4 + 3 \ cdot9 + 5 \ cdot2 \\ \ end {массив} \ вправо) \\ & = \ влево ( \ begin {array} {ccc} 130 и 120 и 240 \\ 51 и 47 и 73 \\ 35 и 33 и 45 \\ \ end {массив} \ right) \ end {align} $$

Работа матричного умножения с пошаговыми инструкциями показывает полное пошаговое вычисление для нахождение произведения $ AB $ двух $ 3 \ times 3 $ матриц $ A $ и $ B $ с использованием формулы умножения матриц.Для любые другие матрицы, просто укажите элементы матриц $ 2 $, элементы которых являются действительными числами, и нажмите СОЗДАТЬ РАБОТУ кнопка. Учащиеся начальной школы и люди, изучающие математику, используют этот калькулятор умножения матриц для вычисления работать, проверять результаты вычисленных вручную матриц умножения или эффективно выполнять домашние задания. Ученики начальной школы также могут использовать этот калькулятор для решения линейных уравнений.

Скалярное умножение матрицы Калькулятор

[1] 2016/02/10 20:57 Мужчина / До 20 лет / Высшая школа / Университет / Аспирант / Очень /

Цель использования

ну я использую thsi проверьте, верен ли мой ответ или нет

Комментарий / запрос

Это действительно интересное приложение

[2] 2015.01.28 20:05 Женский / 20-летний уровень / средняя школа / университет / аспирант / Очень /

Цель использования

Проверить правильные ответы

[3] 22.10.2014 15:10 Женский / Уровень 20 лет / Старшая школа / Университет / Аспирант / Немного /

Цель использования

Домашнее задание.Пытаюсь понять матрицы, но с трудом обдумываю это.

[4] 2014/10/09 04:10 Женский / Моложе 20 лет / Старшая школа / Университет / Аспирант / Не совсем /

Цель использования

Пытаясь понять этот материал, я ‘ Я работал над 12 вопросами в течение двух часов, и я собираюсь сломаться, если я этого не сделаю.

Комментарий / запрос

Я не понимаю, зачем нас этому учат, я этим никогда не воспользуюсь.

[5] 2014/05/19 19:55 Женский / Уровень 20 лет / Старшая школа / Университет / Аспирант / Немного /

Цель использования

Проверить ответ.

Комментарий / запрос

idgi

[6] 2014/02/07 07:14 Мужчина / Моложе 20 лет / Высшая школа / Университет / Аспирант / Очень /

Цель использования

Уровень колледжа математика. лень умножать матрицу на -1/126

[7] 26.11.2013 12:14 Женщина / До 20 лет / Высшая школа / ВУЗ / Аспирант / Немного /

Цель использования

Я не хочу этого делать, а сегодня понедельник, мой мозг не может работать.

[8] 2013/10/01 10:31 Женский / Моложе 20 лет / Старшая школа / Университет / Аспирант / Очень /

Цель использования

Домашние задания

[9] 2013 / 08/22 22:12 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / Немного /

Цель использования

Нужна помощь, чтобы убедиться, что я получаю правильные ответы

Сложите, вычтите или умножьте матрицы с помощью программы “Пошаговое решение математических задач

”

Матрица, имеющая то же количество строк, что и столбцы, называется квадратной матрицей, Матрицы ниже квадратные:

Матрица, содержащая только одну строку, называется матрицей строк.Вот несколько примеров:

[5 8], [6 -9 2] и [-4 0 0 0].

Наконец, матрица только из одного столбца, как в части (d) примера 1, является столбцом матрица.

Принято использовать заглавные буквы для именования матриц. Обозначение нижнего индекса используется для обозначения элементов матрицы следующим образом.

Используя это обозначение, первая строка, первый элемент столбца обозначается a11, вторая строка, третий элемент столбца обозначается a23, а i -я строка, j -я Элемент столбца обозначен a ij.

Две матрицы равны, если они одного размера и если каждая соответствует элемент, позиция за позицией, равен. Используя это определение, матрицы

не равны (даже если они содержат одинаковые элементы и одинаковые size), так как соответствующие элементы различаются.

РЕШЕНИЕ, РАВНЫ ЛИ ДВЕ МАТРИЦЫ

Пример 3

Из определения равенства, данного выше, единственный способ, которым утверждение

может быть истинным, если 2 = x, 1 = y, p = -1 и q = 0.

Заявление

никогда не может быть правдой, поскольку две матрицы имеют разные размеры. (Один – 2 x 1 и другой – 3 x 1.)

ДОБАВЛЯЮЩИЕ МАТРИЦЫ

В начале этого раздела мы использовали матрицу

, где в столбцах указано количество картонных коробок трех различных типов витамины (A, E и K соответственно), а строки представляют два разных производители (Dexter и Sullivan соответственно). Например, элемент 7 представляет 7 упаковок таблеток витамина Е от Dexter и так далее.Предположим еще один отгрузка от этих двух поставщиков описывается следующей матрицей.

Вот, например, из Салливана прибыло 8 упаковок таблеток витамина К. В количество коробок каждого вида таблеток, полученных от этих двух отгрузки можно найти с помощью этих двух матриц.
В первой партии было получено 2 упаковки таблеток витамина А от компании Dexter, а во второй – 3 упаковки таблеток витамина А. Всего было получено 2 + 3 или 5 коробок этих таблеток.Соответствующие элементы могут быть добавлено, чтобы найти общее количество полученных коробок каждого типа таблеток.

Последняя матрица дает общее количество коробок каждого типа таблеток, которые были получили. Например, от Декстера было получено 15 упаковок таблеток витамина К. Обобщение этого примера приводит к следующему определению.

ДОПОЛНЕНИЕ МАТРИЦЫ: Сумма двух матриц A и B размером m x n составляет m x n матрица A + B в котором каждый элемент является суммой соответствующих элементов A и B.

ВНИМАНИЕ: Можно добавлять только матрицы одного размера.

Матрицы

бывают разных размеров. Следовательно, суммы A + B не существует.

Матрица, содержащая только нулевые элементы, называется нулевой матрицей. Например, [0 0 0] – это нулевая матрица 1 X 3, а

– это нулевая матрица 2 X 3. Нулевую матрицу можно записать любого размера.

В главе 1 аддитивная величина, обратная действительному числу a, была определена как действительное число. число -a такое, что a + (-a) = 0 и = a + a = 0.Для матрицы A можно найти такую ​​матрицу, что A + (-A) = 0, где 0 – соответствующая нулевая матрица, а -A + A = 0. Например, если

, то элементы матрицы -A являются аддитивными инверсиями соответствующих элементы A. (Помните, что каждый элемент A является действительным числом и, следовательно, имеет добавка обратная.)

Чтобы проверить, сначала проверьте, что A + (-A) равно 0, соответствующей нулевой матрице.

Затем проверьте, что -A + A также равно 0.Матрица -A – это аддитивная обратная, или отрицательная, матрицы A. Каждая матрица имеет единственную аддитивную обратную.

МАТРИЦЫ ВЫЧИСЛЕНИЯ

Вычитание действительных чисел было определено в главе L, говоря, что a – b = a + (-b). То же определение используется для вычитания матриц.

Если A и B – матрицы одинакового размера, то

A – B = A + (-B)

Найдите каждое из следующих различий.

Матрицы

имеют разные размеры и не могут быть вычтены.

Если матрица A складывается сама с собой, каждый элемент в сумме вдвое больше, чем соответствующий элемент A. Например,

В последнем выражении цифра 2 перед матрицей называется скаляром. чтобы отличить его от матрицы. В приведенном выше примере предлагается следующее определение умножения матрицы на скаляр.

УМНОЖЕНИЕ МАТРИЦЫ СКАЛЯРОМ: Произведение скаляра k и a Матрица X – это матрица kX, каждый из элементов которой в k раз больше соответствующего элемент X.

Найдите каждый продукт.

Умножение матриц с помощью калькулятора TI83 или TI84

Графические калькуляторы, такие как TI83 и TI84, могут выполнять множество различных операций с матрицами, включая умножение. Здесь мы рассмотрим шаги, необходимые для умножения двух матриц в этом типе калькулятора, используя следующий пример. {- 1} \ right] \).

Нажмите кнопку со стрелкой вправо, чтобы перейти в меню ПРАВКА.

Нажмите [2] или выделите 2. [B] и нажмите [ENTER].

Введите размер матрицы и значения, набирая каждое число и нажимая [ENTER]. Обратите внимание, что вторая матрица из нашего примера представляет собой матрицу 3 x 2 (строки за столбцами).

\ (\ left [\ begin {array} {cc} 4 & 0 \\ 1 & 1 \\ 3 & 9 \ end {array} \ right] \)

Шаг 3: Нажмите [2ND] и [MODE], чтобы выйти из экрана матрицы.

Откроется пустой экран.{-1} \ right] \).

Нажмите [2] или выделите 2. [B] и нажмите [ENTER].

Нажмите [ENTER], чтобы умножить матрицы.

Отсюда у вас есть окончательный ответ. Теперь мы можем написать:

\ (\ begin {align} AB & = \ left [\ begin {array} {ccc} -1 & 5 & -2 \\ 3 & 7 & 7 \\\ end {array} \ right] \ left [\ begin {массив} {cc} 4 & 0 \\ 1 & 1 \\ 3 & 9 \ end {array} \ right]
\\ & = \ boxed {\ left [\ begin {array} {cc} -5 & – 13 \\ 40 и 70 \\\ end {array} \ right]} \ end {align} \)

Распространенная ошибка: DIM MISMATCH

Предположим, что вы выполнили эти шаги и в итоге получили следующий экран.

В этом случае вы должны проверить две вещи:

1. Вы ввели правильную информацию о матрице и выбрали ли правильные матрицы для умножения?
2. Определен ли продукт?

Если вы правильно ввели матрицы, то эта ошибка означает, что продукт не определен. В частности, если вы выписываете размеры матриц, внутренние числа должны совпадать. В приведенном выше примере у нас были 2 x 3 и 3 x 2. Обратите внимание, что числа на внутренней стороне совпадают, поэтому продукт был определен, и мы смогли найти ответ.

Однако произведение 2 x 2 и 3 x 2 будет неопределенным, поскольку внутренние числа не совпадают. Вы бы просто написали «Не определено» в качестве ответа, если бы решали такую ​​задачу на экзамене или викторине.

Чтобы узнать больше о том, когда матричное умножение определено или не определено, перейдите по следующей ссылке.

Когда определяется умножение матриц?

объявление

Продолжайте изучение матриц и калькулятора TI83 / 84

В следующих статьях есть дополнительная информация об использовании калькулятора с матрицами:

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Калькулятор умножения комплексных чисел

Для задач сложения и вычитания калькулятор преобразует смешанные числа в неправильные дроби, а затем находит наименьший общий знаменатель, прежде чем продолжить вычисления. Онлайн-инструмент Калькулятор умножения комплексных чисел запрограммирован на выполнение операции умножения комплексных чисел и выдает результат в кратчайшие сроки.Попробуйте вычислить квадратный корень из –1 на своем калькуляторе. Произведения и частные комплексных чисел; Графическое объяснение умножения и деления комплексных чисел; 7. Пусть w и z – два комплексных числа такие, что w = a + ib и z = A + iB. Бесплатный калькулятор комплексных чисел – упрощайте сложные выражения, используя алгебраические правила, шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Работайте над некоторыми ограничениями на z1 и z2. Что, если a) z1 = z2 b) z1 и z2 – сопряженные пары c) z1 вещественное d) z1 и z2 вещественное e) z2 чисто мнимое f) если оба комплексных числа чисто мнимые Пример: (2 + 2i) (4 + 4i) или (4 + 2i) (4 + 4i) или (2 + 2i) (4 + 4i) (4 + 4i).) Или в более короткой записи \ “цис \”: (r cis θ) 2 = r2 cis 2θ Что произойдет, если вы умножите комплексное число на его сопряжение? Формулы вычисления комплексных чисел: (a + bi) ÷ (c + di) = (ac + bd) / (c 2 + (d 2) + ((bc – ad) / (c 2 + d 2)) i; ( a + bi) × (c + di) = (ac – bd) + (ad + bc) i; (a + bi) + (c + di) = (a + c) + (b + d) i; Мы знать расширение (a + b) (c + d) = ac + ad + bc + bd. Аналогично, рассмотрим комплексные числа z1 = a1 + ib1 и z2 = a2 + ib2. Для любого ненулевого комплексного числа z = a + ib (a ≠ 0 и b ≠ 0) существует другое комплексное число z-1 или 1 / z, которое известно как мультипликативное обратное к z, такое, что zz-1 = 1.Калькулятор дробей. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет посередине между 0 и z ». Чтобы узнать больше о математике с дробями, см. Основное различие в том, что мы работаем с действительной и мнимой частями отдельно. Эта страница покажет вам, как правильно их перемножить. Умножение комплексных чисел. Умножение комплексных чисел очень похоже на умножение биномов. Умножение комплексных чисел. Чтобы умножить два комплексных числа, например (4 + 5 i) ⋅ (3 + 2 i), вы можете рассматривать каждое из них как бином и применять метод фольги, чтобы найти произведение.8. Нас просят умножить комплексное число 1 минус 3i на комплексное число 2 плюс 5i. Z – комплексное число, представляющее вектор 3. x – вещественная часть или активный компонент 4. y – мнимая часть или реактивный компонент 5. j – определяется как √-1 В прямоугольной форме комплексное число может быть представлен как точка на двухмерной плоскости, называемой… Instructions :: All Functions. Бесплатный калькулятор корней – шаг за шагом находите корни любой функции. Воспользуйтесь бесплатным калькулятором Mathway и средством решения задач ниже, чтобы попрактиковаться в различных математических темах.Комплексное число выражается в форме a + bi, где a, b – действительные числа, а i – мнимая часть. По… Однако матрицы могут быть не только двумерными, но и одномерными (векторами), так что вы можете умножать векторы, вектор на матрицу и наоборот. Все, что вам нужно сделать, это ввести комплексные числа и нажать кнопку ввода, чтобы получить произведение комплексных чисел. https://www.calculatorsoup.com – Онлайн-калькуляторы. Outers: умножение комплексных чисел. Откройте для себя ресурсы.Пример: (2 + 2i) (4 + 4i) или (4 + 2i) (4 + 4i) или (2 + 2i) (4 + 4i) (4 + 4i) Калькулятор умножения комплексных чисел: комплексные числа используются во многих поля и вам нужно умножать их в разы. Вот несколько примеров того, что вы должны ввести здесь: (3i + 1) (5 + 2i) (-1… См. Предыдущий раздел «Произведения и коэффициенты комплексных чисел» для получения дополнительной информации. Инструкции. Что такое произведение или умножение комплексных чисел (2 + 2i) и (4 + 4i)? Калькулятор комплексных чисел позволяет умножать комплексные числа онлайн, умножение комплексных чисел онлайн применяется к алгебраической форме комплексных чисел, чтобы вычислить произведение комплексных чисел 1 + i и 4 + 2 ⋅ i, введите complex_number ((1 + i) ⋅ (4 + 2… Rise, Run и Y-перехват линейной зависимости; GeoCircles3 Процитируйте этот контент, страницу или калькулятор как: Furey, Edward «Калькулятор сложных дробей») ; CalculatorSoup, Math.В последнем уроке, посвященном фазорам, мы увидели, что комплексное число представлено действительной и мнимой частями, которые принимают обобщенную форму: 1. На следующей диаграмме показаны примеры умножения комплексных чисел. Определения цепей переменного тока; 9. Урок сложных чисел. Умножение комплексных чисел. Исключение составляют случаи, когда вы вводите выражение с помощью i. Первые: 2 ⋅ 3 = 6. Результат: возвести величины в квадрат, удвоить угол. В общем, комплексное число, такое как: r (cos θ + i sin θ) В квадрате становится: r2 (cos 2θ + i sin 2θ) ( величина r возводится в квадрат, а угол θ удваивается.Как умножить комплексные числа на калькуляторе? Операторы всех функций + Все, что вам нужно сделать, это ввести комплексные числа и нажать кнопку ввода, чтобы получить произведение комплексных чисел. ар. Прокрутите страницу вниз, чтобы увидеть больше примеров и решений о том, как умножать комплексные числа. Это программа, управляемая меню, в которой пользователь должен будет ввести свой выбор для выполнения операции и может выполнять операции столько раз, сколько потребуется. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт.Например, 2 умножить на 3 + i будет просто 6 + 2i. В сложных дробях числитель и знаменатель либо оба, либо оба содержат дроби или смешанные числа. Калькулятор умножения с делением комплексных чисел – EndMemo. Простое целое число также может быть частью сложной дроби, появляющейся либо в числителе, либо в знаменателе. Онлайн-калькулятор от полярной до прямоугольной; 5. Сложная дробь – это дробь, которая содержит другую дробь. Для задач умножения и деления нет необходимости находить общий знаменатель, поэтому калькулятор просто следует стандартным правилам арифметики с дробями.Вы должны умножить эти пары, как показано ниже! Онлайн-расчет умножения действительных и мнимых чисел. Обзор операций с комплексными числами. Калькулятор упростит любое сложное выражение с указанием шагов. Деление w на z основано на умножении числителя и знаменателя на комплексное сопряжение знаменателя: произведение двух комплексных чисел также является комплексным числом. В данном выражении a – действительная часть, а b – мнимая часть комплексного числа.Рисунок 5. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Стенограмма видео. Узнайте больше о том, что такое комплексное число и как найти умножение комплексных чисел и т. Д. 3. Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в ​​отношении файлов cookie. Упрощение калькулятора сложных дробей. Даны комплексные числа (2 + 2i) и (4 + 4i), поэтому произведение комплексных чисел (2 + 2i) и (4 + 4i) равно 16i. Калькулятор сложения полиномов.Если вы умножите комплексное число на сопряженное с ним, ответом всегда будет действительное число. Онлайн-инструмент Калькулятор умножения комплексных чисел запрограммирован на выполнение операции умножения комплексных чисел и выдает результат в кратчайшие сроки. Автоматический расчет. Программа C для сложения, вычитания, умножения и деления комплексных чисел, комплексная арифметика Программа C для сложения, вычитания, умножения и деления комплексных чисел. Практика: умножайте комплексные числа. Пусть w и z – два комплексных числа такие, что w = a + ib и z = A + iB.Дробные ответы даются в сокращенном виде (наименьшие термины). Введите дроби, смешанные числа или целые числа. Квадратные уравнения с комплексными решениями. Калькулятор будет генерировать пошаговое объяснение для каждой операции. Экспоненциальная форма комплексных чисел; Интерактивный граф формулы Эйлера и тождества Эйлера; 6. © 2006 -2021CalculatorSoup® Используйте этот Калькулятор сложных дробей, чтобы выполнять математические вычисления и складывать, вычитать, умножать и делить сложные дроби. Он будет выполнять сложение, вычитание, умножение, деление, возведение в степень, а также найдет полярную форму, сопряжение, модуль и обратную форму комплексного числа.4 = 1 • умножение трех комплексных чисел: (1 + 3i) (3 + 4i) (- 5 + 3i) FOIL обозначает первую, внешнюю, внутреннюю и последнюю пары. ». Это текущий выбранный элемент. Калькулятор комплексных чисел принимает только целые и десятичные числа. Умножить: (5 – 3i) (7 + 2i) Полное решение. Операции с одним комплексным числом Этот калькулятор извлекает квадратный корень, вычисляет модуль, находит обратное, находит сопряжение и преобразует комплексное число в полярную форму. Умножение комплексных чисел. Вычисление умножения комплексных чисел.Используйте калькулятор умножения комплексных чисел, чтобы оценить произведение комплексных чисел (8 + 60i) (72-51i), т.е. в этом случае ваш калькулятор выдает результат комплексных чисел независимо от режима… Ошибка: неправильный ввод. Степени и корни комплексных чисел; 8. Калькулятор комплексных чисел. 1. 3912i + 3636 с пошаговым решением. Пример 4: Умножение комплексного числа на действительное число. Упрощение сложных выражений Следующий калькулятор можно использовать для упрощения ЛЮБОГО выражения с комплексными числами.Решение Чтобы увидеть более подробную работу, попробуйте наш решатель алгебры. Комплексное число Z (A + Bi) + i: Комплексное число W (C + Di) + … Калькулятор умножения комплексного числа. Простой в использовании калькулятор, который делит два комплексных числа. комплексные числа и нажмите кнопку ввода, чтобы получить произведение чисел. На главном экране нажмите [2nd] [x2] [(-)] [ENTER]. Есть большая вероятность, что вы получите сообщение ОШИБКА: НЕРЕАЛЬНЫЕ ОТВЕТЫ, как показано на первом экране. В реальном режиме ваш калькулятор обычно возвращает ошибку для результата комплексного числа.Используйте этот калькулятор сложных дробей, чтобы выполнять вычисления, а также складывать, вычитать, умножать и делить сложные дроби. Вам просто нужно указать входные значения, т.е. пример: введите (2-3i) * (1 + i) и посмотрите ответ 5-i. Где: 2. 2. Все права защищены. калькулятор комплексных чисел. Дробные ответы даются в сокращенном виде (наименьшие термины). Связанные сообщения блога Symbolab. Для дополнительной помощи по упрощению сложных дробей см. Геометрически, когда вы удваиваете комплексное число, просто удваивайте расстояние от начала координат, 0.Математические решения для средней школы – Калькулятор уравнений. Этот график показывает, как мы можем геометрически интерпретировать умножение комплексных чисел. 4. Что такое произведение двух комплексных чисел? Чтобы возвести комплексное число в квадрат, умножьте его само на себя: 1. Умножьте величины: величина × величина = величина 2 2. сложите углы: угол + угол = 2, чтобы мы удвоили их. Комплексные числа имеют действительную и мнимую части. В onlinecalculator.guru есть такие понятия, как периметр, площадь, объем, тригонометрические функции, алгебра, проценты и многие другие, а также соответствующие калькуляторы – все под одной крышей.Дом. Мы распределяем действительное число так же, как и бином. Следующие ниже апплеты демонстрируют, что происходит, когда мы умножаем и делим комплексные числа. Если вы находитесь за веб-фильтром, убедитесь, что домены * .kastatic.org и * .kasandbox.org разблокированы. Умножение комплексных чисел – практические задачи Наведите указатель мыши на «Ответ», чтобы увидеть ответ, или щелкните ссылку «Полное решение», чтобы просмотреть все шаги, необходимые для умножения комплексных чисел. Калькулятор умножения матриц Здесь вы можете бесплатно выполнить умножение матриц с комплексными числами онлайн.Комплексное число расширяет концепцию одномерной линии до двухмерной комплексной плоскости и использует горизонтальную ось для действительной части и вертикальную ось для мнимой части. Калькулятор звездных величин в 3D и 2D. Даны два комплексных числа, найдите их произведение. Умножить: (6 – 5i) (2 – 3i) Следующий урок. умножьте обе части комплексного числа на действительное число. Простой в использовании калькулятор, который делит два комплексных числа. Начнем с умножения комплексного числа на действительное. Добро пожаловать в нашу новую серию математических решений «Начало работы».Комплексные числа в реальном мире [объяснение] Рабочие листы по комплексным числам.

Американские специи и приправы, Кто должен подавать декларацию о подоходном налоге в Алабаме ?, Поваренная книга Напарима Рецепт черного торта, Английские гарниры, 1 Bhk Rent Sanpada Nobroker, Снупи, летящий на своей собачьей будке, Показатель зачисления в Ут-Хьюстон, Школы / рабочие места округа Ньютон, Фнаф 1 2 3 4 5 6 Персонажи, Артур Рембо Леонардо Дикаприо, Такси от Jfk до Манхэттена, Trane Killian Rd,

Умножение вектора на матрицу

Чтобы умножить вектор-строку на вектор-столбец, вектор-строка должен иметь столько столбцов, сколько строк в векторе-столбце.

Определим умножение матрицы А и вектор Икс в котором количество столбцов в А равно количеству строк в Икс .

Так что если А является м × п матрица, то произведение А Икс определяется для п × 1 векторы-столбцы Икс . Если мы позволим А Икс знак равно б , тогда б является м × 1 вектор-столбец.Другими словами, количество строк в А определяет количество строк в продукте б .

Общая формула для произведения матрица-вектор:

А Икс знак равно [ а 11 а 12 ⋯ а 1 п а 21 год а 22 ⋯ а 2 п ⋮ ⋮ ⋮ ⋮ а м 1 а м 2 ⋯ а м п ] [ Икс 1 Икс 2 ⋮ Икс п ] знак равно [ а 11 Икс 1 + а 12 Икс 2 + ⋯ + а 1 п Икс п а 21 год Икс 1 + а 22 Икс 2 + ⋯ + а 2 п Икс п ⋮ а м 1 Икс 1 + а м 2 Икс 2 + ⋯ + а м п Икс п ]

Пример :

Находить А y где y знак равно [ 2 1 3 ] а также А знак равно [ 1 2 3 4 5 6 7 8 9 ] .

По определению, количество столбцов в А равно количеству строк в y .

А y знак равно [ 1 2 3 4 5 6 7 8 9 ] [ 2 1 3 ]

Сначала умножьте строку 1 матрицы по столбцу 1 вектора.

[ 1 2 3 ] [ 2 1 3 ] знак равно [ 1 ⋅ 2 + 2 ⋅ 1 + 3 ⋅ 3 ] знак равно 13

Далее умножаем строку 2 матрицы по столбцу 1 вектора.

[ 4 5 6 ] [ 2 1 3 ] знак равно [ 4 ⋅ 2 + 5 ⋅ 1 + 6 ⋅ 3 ] знак равно 31 год

Наконец умножьте строку 3 матрицы по столбцу 1 вектора.

[ 7 8 9 ] [ 2 1 3 ] знак равно [ 7 ⋅ 2 + 8 ⋅ 1 + 9 ⋅ 3 ] знак равно 49

Записывая матрично-векторное произведение, получаем:

А y знак равно [ 13 31 год 49 ]

.