Тест №3
3.1. Площадь поперечного сечения потока, перпендикулярная направлению движения называется
а) открытым сечением;
б) живым сечением;
в) полным сечением;
г) площадь расхода.
3.2. Часть периметра живого сечения, ограниченная твердыми стенками называется
а) мокрый периметр;
б) периметр контакта;
в) смоченный периметр;
г) гидравлический периметр.
3.3. Объем жидкости, протекающий за единицу времени через живое сечение называется
а) расход потока;
б) объемный поток;
в) скорость потока;
г) скорость расхода.
3.4. Отношение расхода жидкости к площади живого сечения называется
а) средний расход потока жидкости;
б) средняя скорость потока;
в) максимальная скорость потока;
г) минимальный расход потока.
3.5. Отношение живого сечения к смоченному периметру называется
а) гидравлическая скорость потока;
б) гидродинамический расход потока;
г) гидравлический радиус потока.
3.6. Если при движении жидкости в данной точке русла давление и скорость не изменяются, то такое движение называется
а) установившемся;
б) неустановившемся;
в) турбулентным установившимся;
г) ламинарным неустановившемся.
3.7. Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени называется
а) ламинарным;
б) стационарным;
в) неустановившимся;
г) турбулентным.
3.8. Расход потока обозначается латинской буквой
а) Q;
б) V;
в) P;
г) H.
а) χ;
б) V;
в) υ;
г) ω.
3.10. Живое сечение обозначается буквой
а) W;
б) η;
в) ω;
г) φ.
3.11. При неустановившемся движении, кривая, в каждой точке которой вектора скорости в данный момент времени направлены по касательной называется
а) траектория тока;
б) трубка тока;
в) струйка тока;
г) линия тока.
3.12. Трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением называется
а) трубка тока;
б) трубка потока;
г) элементарная струйка.
3.13. Элементарная струйка – это
а) трубка потока, окруженная линиями тока;
б) часть потока, заключенная внутри трубки тока;
в) объем потока, движущийся вдоль линии тока;
г) неразрывный поток с произвольной траекторией.
3.14. Течение жидкости со свободной поверхностью называется
а) установившееся;
б) напорное;
в) безнапорное;
г) свободное.
3.15. Течение жидкости без свободной поверхности в трубопроводах с повышенным или пониженным давлением называется
а) безнапорное;
б) напорное;
в) неустановившееся;
г) несвободное (закрытое).
3.16. Уравнение неразрывности течений имеет вид
а) ω1υ2= ω2υ1 = const;
б) ω1υ1 = ω2υ2 = const;
в) ω1ω2 = υ1υ2 = const;
г) ω1 / υ1 = ω2 / υ2 = const.
3.17. Уравнение Бернулли для идеальной жидкости имеет вид
3.18. На каком рисунке трубка Пито установлена правильно
3.19. Уравнение Бернулли для реальной жидкости имеет вид
3.20. Член уравнения Бернулли, обозначаемый буквой z, называется
а) геометрической высотой;
б) пьезометрической высотой;
в) скоростной высотой;
г) потерянной высотой.
3.21. Член уравнения Бернулли, обозначаемый выражением называется
а) скоростной высотой;
б) геометрической высотой;
в) пьезометрической высотой;
г) потерянной высотой.
3.22. Член уравнения Бернулли, обозначаемый выражением называется
а) пьезометрической высотой;
б) скоростной высотой;
в) геометрической высотой;
г) такого члена не существует.
3.23. Уравнение Бернулли для двух различных сечений потока дает взаимосвязь между
а) давлением, расходом и скоростью;
б) скоростью, давлением и коэффициентом Кориолиса;
в) давлением, скоростью и геометрической высотой;
г) геометрической высотой, скоростью, расходом.
3.24. Коэффициент Кориолиса в уравнении Бернулли характеризует
а) режим течения жидкости;
б) степень гидравлического сопротивления трубопровода;
в) изменение скоростного напора;
г) степень уменьшения уровня полной энергии.
3.25. Показание уровня жидкости в трубке Пито отражает
а) разность между уровнем полной и пьезометрической энергией;
б) изменение пьезометрической энергии;
г) уровень полной энергии.
3.26. Потерянная высота характеризует
а) степень изменения давления;
б) степень сопротивления трубопровода;
в) направление течения жидкости в трубопроводе;
г) степень изменения скорости жидкости.
3.27. Линейные потери вызваны
а) силой трения между слоями жидкости;
б) местными сопротивлениями;
в) длиной трубопровода;
г) вязкостью жидкости.
3.28. Местные потери энергии вызваны
а) наличием линейных сопротивлений;
б) наличием местных сопротивлений;
в) массой движущейся жидкости;
г) инерцией движущейся жидкоcти.
3.29. На участке трубопровода между двумя его сечениями, для которых записано уравнение Бернулли можно установить следующие гидроэлементы
а) фильтр, отвод, гидромотор, диффузор;
б) кран, конфузор, дроссель, насос;
в) фильтр, кран, диффузор, колено;
г) гидроцилиндр, дроссель, клапан, сопло.
3.30. Укажите правильную запись
а) hлин = hпот + hмест;
б) hмест = hлин + hпот;
в) hпот = hлин – h
г) hлин = hпот – hмест.
3.31. Для измерения скорости потока используется
а) трубка Пито;
б) пьезометр;
в) вискозиметр;
г) трубка Вентури.
3.32. Для измерения расхода жидкости используется
а) трубка Пито;
б) расходомер Пито;
в) расходомер Вентури;
г) пьезометр.
3.33. Укажите, на каком рисунке изображен расходомер Вентури
3.
34. Установившееся движение характеризуется уравнениями
a) υ =
б)υ = f(x, y, z, t); P = φ(x, y, z, t)
в)υ = f(x, y, z); P = φ(x, y, z, t)
г)υ = f(x, y, z); P = φ(x, y, z)
3.35. Расход потока измеряется в следующих единицах
а) м³;
б) м²/с;
в) м³ с;
г) м³/с.
3.36. Для двух сечений трубопровода известны величины P1, υ1, z1 и z2. Можно ли определить давление P2 и скорость потока υ2?
а) можно;
б) можно, если известны диаметры d1 и d2;
в) можно, если известен диаметр трубопровода d1;
г) нельзя.
3.37. Неустановившееся движение жидкости характеризуется уравнением
a) υ = f(x, y, z,); P = φ(x, y, z)
б)υ = f(x, y, z); P = φ(x, y, z, t)
в)υ = f(x, y, z, t); P = φ(x, y, z, t)
г)υ = f(x, y, z, t); P = φ(x, y, z)
3.
38. Значение коэффициента Кориолиса для ламинарного режима движения жидкости равно
а) 1,5;
б) 2;
в) 3;
г) 1.
3.39. Значение коэффициента Кориолиса для турбулентного режима движения жидкости равно
а) 1,5;
б) 2;
в) 3;
г) 1.
3.40. По мере движения жидкости от одного сечения к другому потерянный напор
а) увеличивается;
б) уменьшается;
в) остается постоянным;
г) увеличивается при наличии местных сопротивлений.
3.41. Уровень жидкости в трубке Пито поднялся на высоту H = 15 см. Чему равна скорость жидкости в трубопроводе
а) 2,94 м/с;
б) 17,2 м/с;
в) 1,72 м/с;
г) 8,64 м/с.
Повторить тему
Ключи к тестам
Наверх страницы
Тесты с ответами к лекциям по гидравлике и пневматике – пройти тест онлайн бесплатно
Авторам
8-800-333-85-44
Оформить заявку
Вход
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Выполним любые типы работ
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Гидравлика и пневматика
Контрольная работа
от 1 дня /
от 100 руб
Курсовая работа
от 5 дней /
от 1800 руб
Дипломная работа
от 7 дней /
от 7950 руб
Реферат
от 1 дня /
от 700 руб
Онлайн-помощь
от 1 дня /
от 300 руб
Оставляй заявку — и мы пройдем все тесты за тебя!
Жидкости: уравнение Бернулли
Жидкости: уравнение Бернулли
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Это еще не все, что нужно знать о жидкостях, гидростатике и гидродинамике. Он задуман как подготовка к уроку.
Когда пистолет находится под давлением и нажат спусковой крючок, давление выталкивает воду. Вода выбрасывается вертикально на максимальную высоту. Как выглядят энергетические карты в определенных местах?
Вода выходит вверху с небольшой скоростью. Нарисуйте энергии, связанные с местами, показанными ниже.
Но вы можете сравнить два места. Особенно два места, где есть разные давления. Это продемонстрировано в трех примерах ниже.
На приведенной выше диаграмме показаны различные высоты, на которые жидкость поднимается в трубках. С какой скоростью движется жидкость под трубой, расположенной справа?
Рассчитайте минимальную скорость воздуха, при которой жидкость достигнет сопла. [Для плотности воздуха используйте ρ воздух =1,29 кг/м 3 ]
Площадь вашей руки 400см 2 . Какая сила действует на вашу руку?Тони Уэйн … (Если вы учитель, не стесняйтесь использовать эти ресурсы в своем обучении.)
Владелец этого веб-сайта не собирает файлы cookie при посещении сайта.
Однако на этом сайте используются и/или встраиваются продукты Adobe, Apple, GoDaddy, Google и YouTube. Эти компании собирают файлы cookie, когда их продукция используется на моих страницах. Нажмите здесь, чтобы перейти к ним и узнать больше о том, как они используют свои файлы cookie. Если вы не согласны с какой-либо из их политик, покиньте этот сайт сейчас.
Вывод уравнения Бернулли
Уравнение Бернулли описывает взаимосвязь между статическим, динамическим и гидростатическим давлением для невязких и несжимаемых жидкостей.
Статическое, динамическое и гидростатическое давление
Из-за давления, действующего в покоящихся жидкостях, на поверхности раздела действует сила. Эта сила способна совершать механическую работу, например, когда сила действует на поршень в цилиндре. В статье об эффекте Вентури уже подробно объяснялось, что поэтому давление можно интерпретировать как объемная удельная энергия . Давление показывает, сколько потенциальной энергии на единицу объема присутствует в жидкости и может быть преобразовано в механическую работу:
\begin{align}
\label{p}
& \boxed{p= \frac{\Delta W} {\Delta V}} \\[5px]
\end{align}
: Давление как удельная объемная потенциальная энергияПокоящаяся жидкость может совершать работу только за счет статического давления, т.е. давления, которое возникает из-за случайного микроскопическое движение молекул при их столкновении с границей раздела (см. статью Давление в газах). Однако, если жидкость течет ( упорядоченное макроскопическое объемное движение ), то жидкость также может совершать работу за счет кинетической энергии, связанной с движением. Если эта кинетическая энергия связана с объемом жидкости, то кинетическая энергия также может быть соотнесена с давлением в соответствии с уравнением (\ref{p}). В отличие от статического давления , в данном случае мы говорим о динамическом давлении . Проще говоря:
Статическое давление связано со случайным микроскопическим движением молекул, а динамическое давление связано с упорядоченным макроскопическим объемным движением текущей жидкости!
В зависимости от исходного уровня жидкость также обладает гравитационной позиционной энергией, которая также может быть преобразована в работу.
Эта энергия используется, например, на гидроэлектростанциях. Согласно уравнению (\ref{p}), потенциальная энергия, содержащаяся в единице объема, соответствует определенному давлению. Это давление называется гидростатическим давлением !
Если к потоку не подводится энергия из внешнего источника, сумма статической энергии («энергия давления»), кинетической энергии и гравитационной потенциальной энергии должна оставаться постоянной из соображений сохранения энергии. Для горизонтальных потоков или для потоков жидкостей с низкой плотностью (например, газов) изменения гравитационных потенциальных энергий отсутствуют или незначительны. Таким образом, в этих случаях увеличение кинетической энергии неизбежно означает уменьшение статической энергии.
Такие случаи бывают с горизонтальными трубами при уменьшении поперечного сечения. Из-за сохранения массы никакая масса не может накапливаться в трубе или уничтожаться. Таким образом, массовый расход одинаков во всех точках трубы.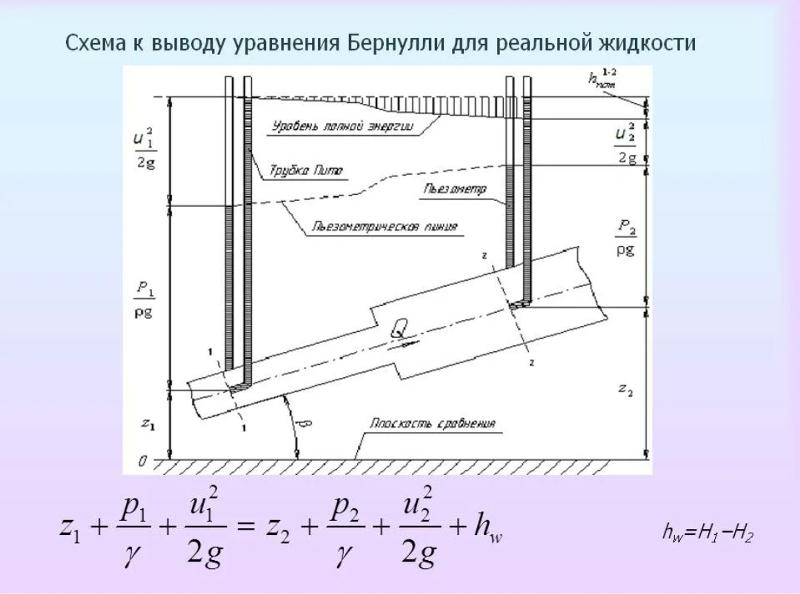
Следовательно, в случае меньших поперечных сечений скорость потока должна быть больше, чтобы одна и та же масса могла протекать в единицу времени.
Таким образом, уменьшение площади поперечного сечения неизбежно означает увеличение скорости потока. Результирующее увеличение кинетической энергии может происходить только за счет статической энергии, если энергия не подается (например, насосом). Таким образом, статическое давление уменьшится в пользу динамического давления. В статье Эффект Вентури это явление снижения давления при увеличении скорости потока уже подробно обсуждалось.
Рисунок: Увеличение скорости потока и связанное с этим снижение давленияКак упоминалось ранее, необходимо учитывать гравитационную позиционную энергию, когда жидкость преодолевает определенную высоту. Соотношение между высотой, скоростью потока и статическим давлением будет получено ниже.
Вывод уравнения Бернулли
Для вывода соотношения рассмотрим несжимаемое невязкое течение в трубе без трения.
Труба имеет переменное сечение и преодолевает определенную высоту.
Энергия давления (энергия выталкивания и выталкивания)
Сначала рассмотрим нижнюю часть сечения трубы в точке 1, где действует статическое давление p 1 . В течение определенного периода времени Δt это давление выталкивает определенную массу жидкости Δm через поперечное сечение трубы A 1 . Расстояние, на которое проталкивается рассматриваемый элемент жидкости, обозначается Δs 1 . Энергия давления W 1 с которым элемент жидкости проталкивается через трубу в точке 1 за счет статического давления («вталкиваемой» энергии) зависит от объема вталкиваемой жидкости ΔV:
\begin{align}
& W_1 = F_1 \cdot \Delta s_1= p_1 \underbrace{A_1 \cdot \Delta s_1}_{\Delta V} \\[5px]
& \underline{W_1 = p_1 \Delta V} ~~~~~\text{“ push-in” energy}\\[5px]
\end{align}
Теперь посмотрим на верхнюю часть трубы в точке 2 , где меньше статическое давление p 2 из-за взаимосвязей, объясненных в предыдущем разделе.
Однако за рассматриваемый период времени Δt ту же массу жидкости необходимо протолкнуть через уменьшенное сечение A 2 (сохранение массы). Поскольку предполагается несжимаемая жидкость, через A 2 протекает тот же объем жидкости ΔV, что и через A 1 .
При уменьшенном поперечном сечении A 2 это означает большее расстояние Δs 2 и, следовательно, более высокую скорость потока! За счет статического давления p 2 действуя там, элемент жидкости проталкивается через трубу в точке 2 со следующей энергией давления W 2 («выталкивающая» энергия):
\begin{align}
& W_2 = F_2 \cdot \ Delta s_2= p_2 \underbrace{A_2 \cdot \Delta s_2}_{\Delta V} \\[5px]
& \underline{W_2 = p_2 \Delta V} ~~~~~\text{“выталкивание” Energy}\\[5px]
\end{align}
Работа, необходимая для ускорения и подъема жидкости
На практике можно заметить, что энергия давления W 1 , с которой элемент жидкости был вдавлен в секцию трубы в точке 1, больше, чем энергия давления W 2 , с которой он вытолкнут в точке 2.
причина этого в том, что часть «вталкиваемой» энергии должна была использоваться для ускорения элемента жидкости (запас кинетической энергии) и для поднятия жидкости против силы тяжести (запас потенциальной гравитационной энергии). Энергия «вталкивания» за вычетом работы, необходимой для ускорения и подъема жидкости, дает оставшуюся энергию «выталкивания». Другими словами, разница в энергии давления есть сумма работы ускорения ΔW a и подъемные работы ΔW h :
\begin{align}
\label{a}
& \boxed{W_1 – W_2 = \Delta W_\text{a} + \Delta W_\text{h} } \\[5px]
\end{align}
Работа, необходимая для ускорения элемента жидкости от v 1 до v 2 , определяется разницей в кинетические энергии в точке 2 и точке 1 (примечание: Δm=ϱ⋅ΔV):
\begin{align}
& \Delta W_\text{a} = W_\text{kin,2} -W_\text{kin ,1} \\[5px] 92} \\[5px]
\end{align}
Работа, необходимая для подъема элемента жидкости с высоты h 1 на высоту h 2 , определяется разностью гравитационных потенциальных энергий в точке 2 и точке 1.
:
\begin{align}
& \Delta W_\text{h} = W_\text{h,2} – W_\text{h,1}\\[5px]
& \underline{\Delta W_\ text{h} =\rho \Delta V \cdot g \cdot h_2 – \rho \Delta V \cdot g \cdot h_1}\\[5px]
\end{align}
Уравнение Бернулли
92 +\rho g h= \text{constant}}=p_\text{tot} \\[5px]\end{align}
Это уравнение также известно как уравнение Бернулли . Все члены уравнения Бернулли имеют размерность давления. Термин ½⋅ϱ⋅v², связанный с кинетической энергией жидкости, называется гидродинамическим давлением или просто динамическим давлением . Член ϱ⋅g⋅h, связанный с потенциальной энергией гравитации, называется гидростатическим давлением. В отличие от этих условий давления, давление p называется статическое давление .
| pressure type | term | energetically linked with |
| static pressure | p | pressure energy (per unit fluid volume) |
| dynamic pressure | ½⋅ ϱ⋅v² | кинетическая энергия (на единицу объема жидкости) |
| гидростатическое давление | ϱ⋅g⋅h | гравитационная потенциальная энергия (на единицу объема жидкости) |
В статье Упражнения с решениями на основе уравнения Бернулли более подробно показаны несколько примеров применения уравнения Бернулли.
Уравнение Бернулли утверждает, что сумма статического давления, динамического давления и гидростатического давления постоянна для невязкой и несжимаемой жидкости (пока энергия не поступает из внешнего источника, например, с помощью насоса). Постоянная сумма этих давлений называется также полным давлением p до . Для применения уравнения Бернулли всегда можно представить любой элемент жидкости, движущийся вдоль линии тока. Затем уравнение Бернулли связывает состояния двух произвольных точек на этой линии тока.
Уравнение Бернулли утверждает, что вдоль линии тока сумма статического давления, динамического давления и гидростатического давления постоянна. В таком виде он применим только к свободному от трения (невязкому) и несжимаемому потоку без внешнего подвода энергии.
Обратите внимание, что из-за вязкости любых жидкостей (внутреннее трение) поток не может быть полностью свободным от трения. На практике это означает рассеяние энергии и связано с дополнительными (статическими) потерями давления.
Подробнее об этом позже.
Важные примечания
Важно понимать, что уравнение Бернулли является уравнением энергии (специфическим для объема). Это связано с переходом от уравнения (\ref{1}) к уравнению (\ref{2}), где различные формы энергии (энергия давления, кинетическая энергия и гравитационная потенциальная энергия) были связаны с объемом жидкости ΔV. Обозначение в виде давления для отдельных слагаемых, входящих в уравнение Бернулли, носит лишь формальный характер, так как каждое из них имеет размерность давления. Однако всегда следует помнить, что эти давления основаны на энергиях.
В противном случае классическая трактовка давления как «силы на единицу площади» часто приводит к недоразумениям, особенно с динамическим давлением. При такой интерпретации очень сложно понять, почему статическое давление уменьшается при увеличении скорости потока. Часто ошибочно полагают, что высокая скорость потока означает большую «силу» и, следовательно, высокое давление.
Однако при интерпретации как энергии сразу становится ясно, что увеличение кинетической энергии может происходить только за счет энергии давления. Следовательно, статическое давление будет уменьшаться с увеличением скорости потока! Это явление также называется эффектом Вентури и более подробно объясняется в связанной статье.
На самом деле термин гидростатическое давление следует понимать в этом контексте иначе, чем, возможно, известное из гидростатического давления водяного столба. В уравнении Бернулли гидростатическое давление не следует интерпретировать как «силу на единицу площади». Что касается уравнения Бернулли, любое гидростатическое давление может быть отнесено к точке потока в зависимости от того, какой опорный уровень выбран для высоты. Однако это, конечно, не меняет сил, действующих в жидкости, только потому, что выбран другой опорный уровень.
В этом случае гидростатическое давление снова следует интерпретировать как энергию, т.е. как гравитационную потенциальную энергию, которая присутствует в единице объема.
Эта гравитационная потенциальная энергия зависит от выбранного опорного уровня и, следовательно, также от определяемого им гидростатического давления.
Расширенное уравнение Бернулли с учетом потерь
Поскольку давление является формой (удельной по объему) энергии, потеря энергии неизбежно означает потерю давления. Такая потеря давления происходит просто потому, что каждая жидкость имеет определенную вязкость. Слои жидкости на стенке трубы прилипают к ней за счет так называемого условие отсутствия проскальзывания , поэтому слои, расположенные дальше внутри, должны быть смещены относительно друг друга, если жидкость должна течь. Это приводит к внутреннему трению жидкости, что в конечном итоге означает потерю энергии и, следовательно, потерю давления (см. также поток Пуазейля).
Дальнейшие потери энергии происходят в турбулентных потоках из-за турбулентности. Здесь большую роль играет шероховатость стенки трубы. Потери потока и, следовательно, потери давления также происходят в компонентах трубопроводной системы, таких как клапаны, отводы труб, переходники и т.
д. (подробнее об этом в статье Потери давления в трубопроводных системах).
Энергия движения потока, определяемая разностью энергии выталкивания W 2 и энергии выталкивания W 1 между входом и выходом рассматриваемого сечения потока, должна поэтому не только ускорять и поднимать течь против силы тяжести, но и компенсировать трение. Следовательно, уравнение (\ref{a}) должно быть дополнено термином потерь энергии ΔW loss :
\begin{align}
& \boxed{W_1 – W_2 = \Delta W_\text{b} + \Delta W_ \text{h} + \Delta W_\text{потеря}} \\[5px] 92 + \rho g h_2 + \Delta p_\text{потеря}}~~~\text{где}~~~\boxed{\Delta p_\text{потеря} = \frac{\Delta W_\text{потеря} }{\Delta V}} \\[5px]
\end{align}
Термин W потери /ΔV соответствует потерям энергии на единицу объема и, следовательно, представляет потери давления Δp потери . Такая потеря давления в основном заметна только в статическом давлении, так как динамическое и гидростатическое давления предопределяются скоростями и высотами потока.