4. Уравнение Бернулли для трубки тока идеального газа
Уравнение Бернулли является математическим выражением закона сохранения энергии для трубки тока несжимаемой идеальной жидкости:
. (1.22)
Здесь первое слагаемое представляет собой объемную плотность кинетической энергии движущегося газа и называется динамическим давлением. Второе слагаемое Р имеет смысл объемной плотности потенциальной энергии и называется статическим давлением. Третье слагаемое представляет собой объемную плотность потенциальной энергии положения и называется геометрическим давлением.
Уравнение Бернулли показывает, что суммарная механическая энергия, т. е. сумма кинетической и потенциальной энергии по длине трубки тока остается постоянной.
В соответствии с
уравнением Бернулли различные виды
энергии могут переходить один в другой.
Например: при горизонтальном движении
газа, т. е. при Z=const, увеличение скорости потока приводит
к уменьшению статическое давления, и
наоборот, при уменьшении скорости
статическое давление возрастает.
Иногда уравнение Бернулли для идеальной среды записывается и в таком виде:
, (1.23)
разделив обе части уравнения (1.22) на удельный вес j=g;
5. Вывод уравнения Бернулли в избыточных давлениях
Мы говорили ранее,
что в металлургической теплотехнике
пользуются давлением, избыточным над
атмосферным. Мы записали уравнение
Бернулли (1.22) в общем виде. Теперь приведем
уравнение Бернулли к такому виду, при
котором все его члены будут выражены в
избыточных давлениях. Для этого представим
канал, окруженный воздухом плотностью
в, по которому
движется газ плотностью
Рисунок 1
Для газа: .
Для воздуха
(считаем, что он в спокойном состоянии,
т.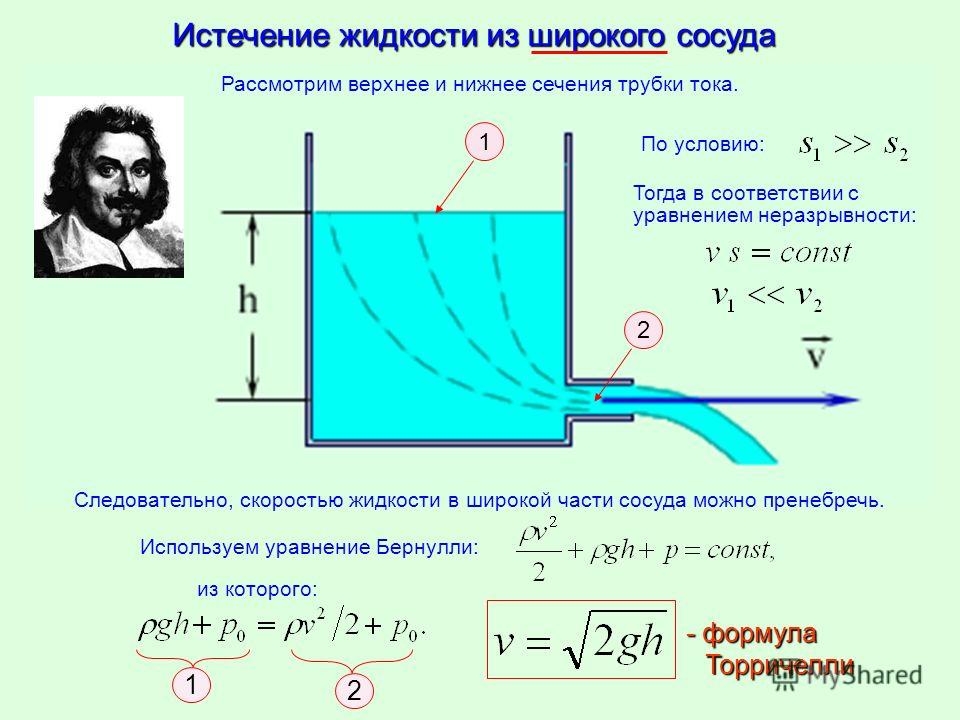 е.Wв=0).
е.Wв=0).
.
Вычитаем из первого уравнения второе и получаем уравнение Бернулли для газа в избыточных давлениях:
.
или окончательно это можно записать так (с учетом ранее принятых обозначений):
. (1.24)
Это равенство справедливо для идеальной среды, лишенной вязкости. При движении реального газа по каналу часть его энергии затрачивается на преодоление различных сопротивлений и происходит потеря энергии. Тогда уравнение Бернулли можно записать так:
. (1.25)
Окончательно закон Бернулли формулируется так: «При установившемся течении несжимаемой жидкости или газа для различных сечений канала сумма давлений всех видов является постоянной.»
Лекция 5: Применение уравнения Бернулли в расчетах
1. Потери давления на предоление местных сопротивленй и на трение.
Рассмотрим, что
представляет собой потерянное давление,
входящее в уравнение Бернулли (1.
Потери давления на местных сопротивлениях возникают при резком изменении величины скорости и направления движения газа. Это может быть резкое изменение сечения канала, поворот канала под всевозможными углами и т. д.
Потери давления на местных сопротивлениях определяют по формуле (Па):
, (1.26)
где Км.с.– коэффициент местных сопротивлений, его величина зависит от формы местного сопротивления и, как правило, определяется опытным путем или по справочным таблицам;
0,W0– плотность и скорость газа при нормальных условиях, т. е. при атмосферном давлении 760 мм. рт. ст. и Т0=273 К;
Т – действительная температура газа, К.
Если при движении
газа по каналу, газопроводу местных
сопротивлений нет, т. е. участок прямой,
то все равно имеют место потери
первоначального давления – это потери
на трение. Потери давления на трение
можно определить по следующей формуле
(Па):
Потери давления на трение
можно определить по следующей формуле
(Па):
, (1.27)
Существуют эмпирические формулы для определения коэффициента трения. При ламинарном движении (Re2100) коэффициент трения зависит отReи не зависит от шероховатости стенок канала:.
При турбулентном движении (Re2300) коэффициент трения зависит не только от критерияRe, но и от относительной шероховатости стенки канала.
Если для гладких стенок при турбулентном движении , то для шероховатой поверхности,
где – абсолютная шероховатость, мм;d– диаметр канала, мм;
При приближенных
практических расчетах можно принимать постоянным и равным
для кирпичных каналов 0,05, для металлических
0,04.
Курс общей физики, Т.1
Курс общей физики, Т.1
ОглавлениеПРЕДИСЛОВИЕМЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ВВЕДЕНИЕ ЧАСТЬ 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ § 1. Механическое движение § 2. Некоторые сведения о векторах § 3. Скорость § 4. Ускорение § 5. Кинематика вращательного движения ГЛАВА II. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ § 6. Классическая механика. Границы ее применимости § 7. Первый закон Ньютона. Инерциальные системы отсчета § 8. Масса и импульс тела § 9. Второй закон Ньютона § 11. Третий закон Ньютона § 12. Принцип относительности Галилея § 13. Силы § 14. Упругие силы § 15. Силы трения. § 16, Сила тяжести и вес § 17. Практическое применение законов Ньютона ГЛАВА III. ЗАКОНЫ СОХРАНЕНИЯ § 18.  Сохраняющиеся величины Сохраняющиеся величины§ 19. Кинетическая энергия § 20. Работа § 21. Консервативные силы § 22. Потенциальная энергия во внешнем поле сил § 23. Потенциальная энергия взаимодействия § 24. Закон сохранения энергии § 25. Энергия упругой деформации § 26. Условия равновесия механической системы § 28. Соударение двух тел § 29. Закон сохранения момента импульса § 30. Движение в центральном поле сил § 31. Задача двух тел ГЛАВА IV. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА § 32. Силы инерции § 33. Центробежная сила инерции § 34. Сила Кориолиса § 35. Законы сохранения в неинерциальных системах отсчета ГЛАВА V. МЕХАНИКА ТВЕРДОГО ТЁЛА § 36. Движение твердого тела § 37. Движение центра масс твердого тела § 38. Вращение тела вокруг неподвижной оси § 39. Момент инерции § 40. Понятие о тензоре инерции § 41. Кинетическая энергия вращающегося твердого тела § 42. Кинетическая энергия тела при плоском движении § 43.  § 44. Гироскопы ГЛАВА VI. ВСЕМИРНОЕ ТЯГОТЕНИЕ § 45. Закон всемирного тяготения § 46. Гравитационное поле § 47. Принцип эквивалентности § 48. Космические скорости ГЛАВА VII. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. Общие сведения о колебаниях § 50. Малые колебания § 51. Комплексные числа § 52. Линейные дифференциальные уравнения § 53. Гармонические колебания § 54. Маятник § 55. Векторная диаграмма § 56. Биения § 57. Сложение взаимно перпендикулярных колебаний § 58. Затухающие колебания § 59. Автоколебания § 61. Параметрический резонанс ГЛАВА VIII. РЕЛЯТИВИСТСКАЯ МЕХАНИКА § 62. Специальная теория относительности § 63. Преобразования Лоренца § 64. Следствия из преобразований Лоренца § 65. Интервал § 66. Преобразование и сложение скоростей § 67. Релятивистское выражение для импульса § 68. Релятивистское выражение для энергии § 69.  Преобразования импульса и энергии Преобразования импульса и энергии§ 70. Взаимосвязь массы и энергии § 71. Частицы с нулевой массой покоя ГЛАВА IX. ГИДРОДИНАМИКА § 72. Линии и трубки тока. Неразрывность струи § 73. Уравнение Бернулли § 74. Истечение жидкости из отверстия § 75. Силы внутреннего трения § 76. Ламинарное и турбулентное течения § 77. Течение жидкости в круглой трубе § 78. Движение тел в жидкостях и газах ЧАСТЬ 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА § 79. Статистическая физика и термодинамика § 80. Масса и размеры молекул § 81. Состояние системы. Процесс § 82. Внутренняя энергия системы § 83. Первое начало термодинамики § 84. Работа, совершаемая телом при изменениях объема § 85. Температура § 86. Уравнение состояния идеального газа § 87. Внутренняя энергия и теплоемкость идеального газа § 88. Уравнение адиабаты идеального газа § 89. Политропические процессы § 90. Работа, совершаемая идеальным газом при различных процессах § 91.  Ван-дер-ваальсовский газ Ван-дер-ваальсовский газ§ 92. Барометрическая формула ГЛАВА XI. СТАТИСТИЧЕСКАЯ ФИЗИКА § 93. Некоторые сведения из теории вероятностей § 94. Характер теплового движения молекул § 95. Число ударов молекул о стенку § 96. Давление газа на стенку § 97. Средняя энергия молекул § 98. Распределение Максвелла § 99. Экспериментальная проверка закона распределения Максвелла § 100. Распределение Больцмана § 101. Определение Перреном числа Авогадро § 102. Макро- и микросостояния. Статистический вес § 103. Энтропия ГЛАВА XII. ТЕРМОДИНАМИКА § 104. Основные законы термодинамики § 105. Цикл Карно § 106. Термодинамическая шкала температур § 107. Примеры на вычисление энтропии § 108. Некоторые применения энтропии § 109. Термодинамические потенциалы ГЛАВА XIII. КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ § 110. Отличительные черты кристаллического состояния § 111. Классификация кристаллов § 112. Физические типы кристаллических решеток § 113.  Дефекты в кристаллах Дефекты в кристаллах§ 114. Теплоемкость кристаллов ГЛАВА XIV. ЖИДКОЕ СОСТОЯНИЕ § 115. Строение жидкостей § 116. Поверхностное натяжение § 117. Давление под изогнутой поверхностью жидкости § 118. Явления на границе жидкости и твердого тела § 119. Капиллярные явления ГЛАВА XV. ФАЗОВЫЕ РАВНОВЕСИЯ И ПРЕВРАЩЕНИЯ § 121. Испарение и конденсация § 122. Равновесие жидкости и насыщенного пара § 123. Критическое состояние § 124. Пересыщенный пар и перегретая жидкость § 125. Плавление и кристаллизация § 126. Уравнение Клапейрона—Клаузиуса § 127. Тройная точка. Диаграмма состояния ГЛАВА XVI. ФИЗИЧЕСКАЯ КИНЕТИКА § 128. Явления переноса § 129. Средняя длина свободного пробега § 130. Диффузия в газах § 131. Теплопроводность газов § 132. Вязкость газов § 133. Ультраразреженные газы § 134. Эффузия ПРИЛОЖЕНИЯ I. Вычисление некоторых интегралов II. Формула Стирлинга III. Симметричные тензоры второго ранга |
гидродинамика – Уравнение Бернулли для потока газа и изменения площади
Задавать вопрос
спросил
Изменено 3 года, 1 месяц назад
Просмотрено 7к раз
$\begingroup$
Моя задача — определить размер трубопровода, необходимого для системы. В этой системе газообразный водород течет горизонтально по $\frac{3}{4}\,\mathrm{inch}$ трубе и в вертикальную трубу большего диаметра. Мое ограничение состоит в том, что скорость водорода не может превышать $1\,\mathrm{м/с}$ после того, как он расширится и пойдет вверх по вертикальной трубе.
В этой системе газообразный водород течет горизонтально по $\frac{3}{4}\,\mathrm{inch}$ трубе и в вертикальную трубу большего диаметра. Мое ограничение состоит в том, что скорость водорода не может превышать $1\,\mathrm{м/с}$ после того, как он расширится и пойдет вверх по вертикальной трубе.
| | (2) | |__________________ (1) <- Газообразный водород
Давление в горизонтальном трубопроводе в точке 1 составляет $2\,\mathrm{psig}$, а давление в вертикальном трубопроводе 2 составляет $0\,\mathrm{psig}$ (отверстие от атмосферы). 92 + gh_2$$
уравнение непрерывности:$$\rho_1A_1V_1 = \rho_2A_2V_2$$
Используя уравнение Бернулли, я получаю очень большой отрицательный корень или скорость около ~550 м/с в секции 1, что кажется очень нелепым. Есть ли более подходящее уравнение для этого приложения? Цель состоит в том, чтобы определить размер трубопровода, необходимого для секции 2.
- гидродинамика
- уравнение Бернулли
$\endgroup$
7
$\begingroup$
Я использовал численную модель для оценки параметров потока. Вот несколько вариантов труб разного диаметра на выходе. Задача нестационарная, интеграл Бернулли явно не сохраняется. Выходная скорость сначала увеличивается, затем достигает максимума и уменьшается. Непонятно, какая скорость должна быть ограничена. На приведенных рисунках скорость потока нормирована на скорость звука на входе, поэтому даже самая маленькая скорость на выходе составляет около 10 м/с. Анимация показывает, как модуль скорости потока изменяется со временем. 92$ в последний момент. Видно, что интеграл Бернулли не сохраняется из-за большой плотности и градиента давления в тонкой трубе.
Вот несколько вариантов труб разного диаметра на выходе. Задача нестационарная, интеграл Бернулли явно не сохраняется. Выходная скорость сначала увеличивается, затем достигает максимума и уменьшается. Непонятно, какая скорость должна быть ограничена. На приведенных рисунках скорость потока нормирована на скорость звука на входе, поэтому даже самая маленькая скорость на выходе составляет около 10 м/с. Анимация показывает, как модуль скорости потока изменяется со временем. 92$ в последний момент. Видно, что интеграл Бернулли не сохраняется из-за большой плотности и градиента давления в тонкой трубе.
И пара картинок, на которых то же самое, но число Рейнольдса увеличено в 10 раз. Видно, что в толстой трубе образовался вихрь, который привел к блокировке части трубы.
$\endgroup$
$\begingroup$
Вы можете попробовать использовать модифицированную форму уравнения Пуазейля. 92}{8 \mu_{av} L} \frac{z_2(p_1+p_2)}{2z_{av}p_2}$$
92}{8 \mu_{av} L} \frac{z_2(p_1+p_2)}{2z_{av}p_2}$$
, где $\frac{z_2(p_1+p_2)}{2z_{av}p_2 }$ — поправочный коэффициент, учитывающий постепенное расширение газа при переходе от входа высокого давления к выходу низкого давления. См. эту ссылку для получения поправочного коэффициента сжимаемости: http://oaktrust.library.tamu.edu/bitstream/handle/1969.1/ETD-TAMU-2010-12-8739/LING-DISSERTATION.pdf. просмотреть страницы с 26 по 34 (из 243).
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
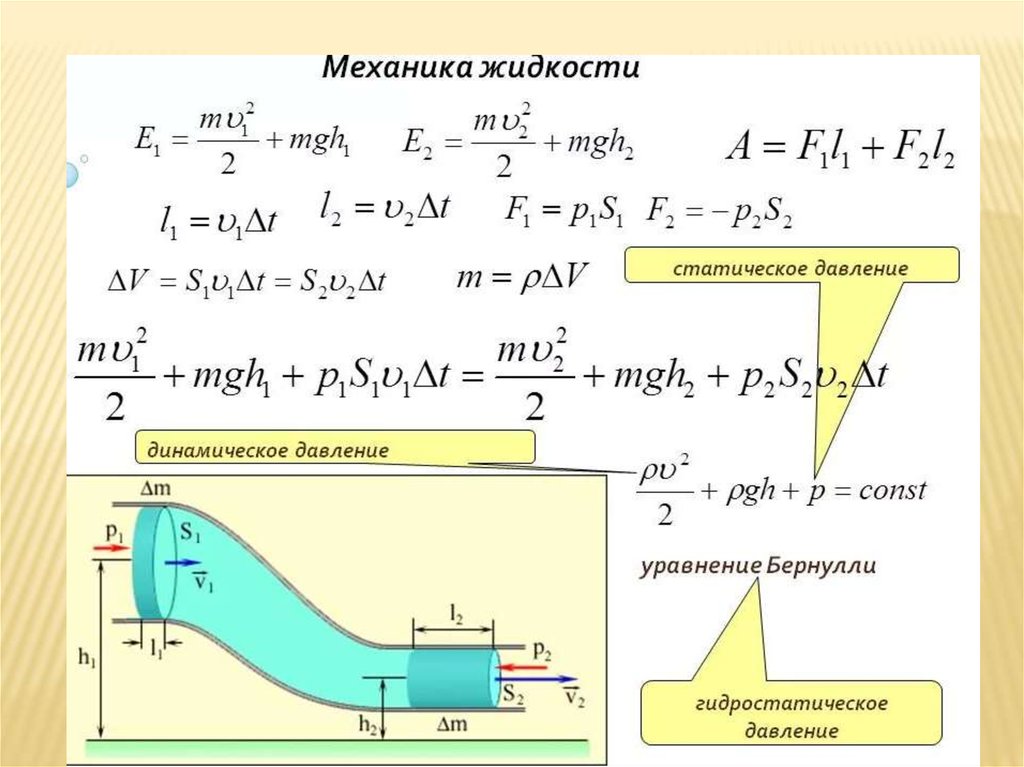
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
17.9: Уравнение Бернулли - Науки о Земле LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10597
- Роланд Стулл
- Университет Британской Колумбии
Рассмотрим стационарный поток (поток, который не меняется со временем), но который может иметь разные скорости в разных местах. Если мы проследим за воздушным пакетом, когда он движется вдоль линии тока, его скорость может измениться по мере его перемещения из одного места в другое. При скорости ветра M ≤ 20 м·с 9{2}+\frac{P}{\rho}+|g| \cdot z=C_{B}\tag{17.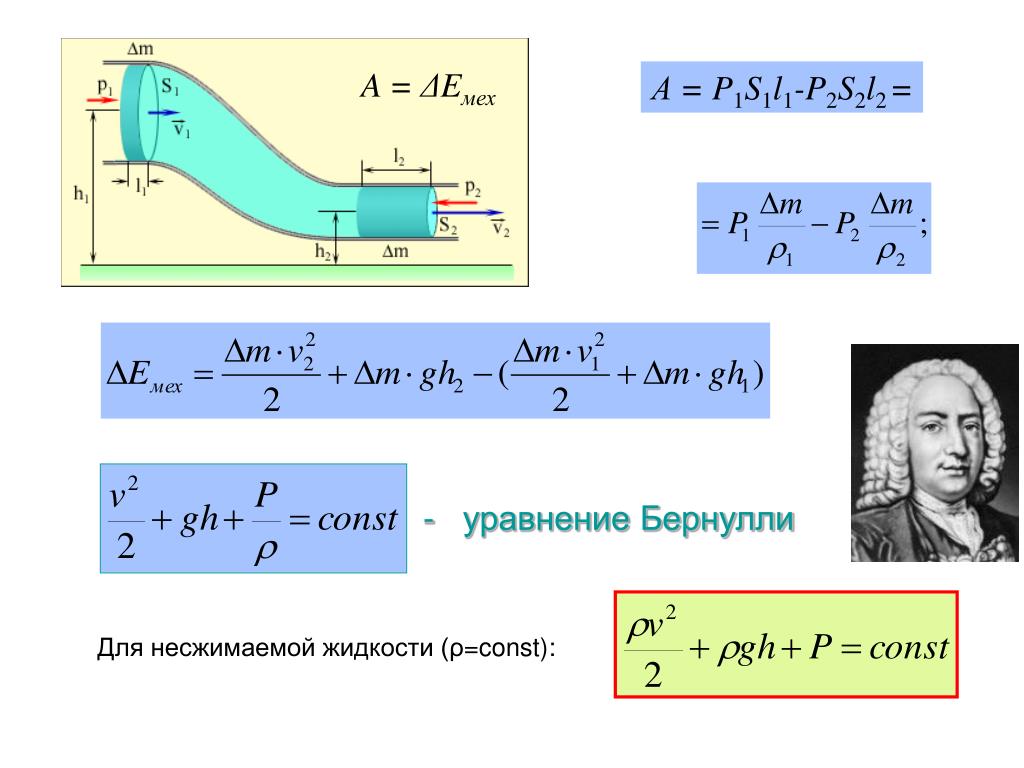 35}\end{align}\)
35}\end{align}\)
\(\ энергия: кинетическая + поток + потенциал = постоянная\)
где M - полная скорость вдоль линии тока, P - статическое давление воздуха, ρ - плотность воздуха, |g| = 9,8 м·с –2 – модуль ускорения свободного падения, z – высота над некоторой точкой отсчета.
Образец заявления
Окружающий воздух вне урагана имеет давление на уровне моря 100 кПа. Найдите подъем уровня моря на глаз, где давление на уровне моря равно 90 кПа. Течениями и ветровыми волнами пренебречь. Найти ответ м, где z — высота над уровнем моря.
Рассмотрим линию тока в воде на поверхности моря. ρ = 1025 кг·м –3 для морской воды.
Используйте Бернулли экв. (17.35) чтобы найти CB для окружающей среды, затем используйте его для глаза:
Env: 0,5·(0 м с –1 ) 2 + (100 000 Па)/(1025 кг·м –3 ) + (9,8 м с –2 )·(0 м) = C B 9 м 2 с –2
Глаз: 0,5·(0 м с –1 ) 2 + (90 000 Па)/(1025 кг·м –3 )0 1 – 9,8 м с (z eye ) = C B = 97. 6 m 2 s –2
6 m 2 s –2
z eye = {(97.6 m 2 s –1 )–[(90,000Pa)/( 1025 кг м –3 )]}/ (9,8 м с –2 ) = 1,0 м .
Проверить: Блоки в норме. Величина в порядке.
Экспозиция: Такое повышение уровня моря представляет собой опасность, называемую штормовым нагоном .
C B — произвольная константа, называемая константой Бернулли или функцией Бернулли . C B постоянно вдоль любой линии тока, но разные линии тока могут иметь разные значения C B .
Уравнение Бернулли фокусируется на сохранении механической энергии вдоль линии тока. Первый член слева — это кинетической энергии на единицу массы. Средний термин — это работа, выполненная над воздухом (иногда называемая 90 126 энергии потока 90 127 на единицу массы), которая хранится в виде давления. Последний член слева — это потенциальная энергия на единицу массы. Вдоль любой линии тока энергия может переходить из одной формы в другую при условии, что сумма этих энергий постоянна.
Последний член слева — это потенциальная энергия на единицу массы. Вдоль любой линии тока энергия может переходить из одной формы в другую при условии, что сумма этих энергий постоянна.
ВЫСШАЯ МАТЕМАТИКА • Вывод Бернулли
Рис. 17.d. Силы, действующие на воздушную посылку (светло-синий прямоугольник), движущуюся по линии тока (темно-синяя кривая).Чтобы вывести уравнение Бернулли, примените второй закон Ньютона (a = F/m) вдоль линии тока s. Ускорение есть полная производная от скорости ветра: a = dM/dt = ∂M/∂t + M·∂M/∂s. Рассмотрим частный случай потока, стационарного в любом месте (∂M/∂t = 0), хотя поток может быть разным в разных местах (∂M/∂s ≠ 0). Таким образом 9{2}+P / \rho+|g| \cdot z=C_{B}\)
, где C B — постоянная интегрирования.
Этот результат применим только к установившемуся несжимаемому течению вдоль линии тока. Не используйте его в ситуациях, когда важны дополнительные силы, такие как турбулентное сопротивление, а также ветряные турбины или вентиляторы.
В гидравлике гравитационный термин определяется изменением глубины воды, особенно при рассмотрении линии тока вдоль поверхности воды. В метеорологии аналогичная ситуация возникает, когда холодный воздух поднимается в более теплую среду; а именно, это плотная жидкость, поднимающаяся против силы тяжести. Однако сила тяжести, ощущаемая поднимающимся холодным воздухом, уменьшается из-за его плавучести в окружающем воздухе. Чтобы компенсировать это, гравитационный фактор в уравнении Бернулли можно заменить на 9{2}+\frac{P}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.36}\end{align}\)
, где ∆θ v — виртуальная потенциальная температура разница между теплым воздухом наверху и холодным воздухом внизу, а T v – абсолютная виртуальная температура воздуха (К). Таким образом, гравитационный член отличен от нуля, когда интересующая линия тока окружена воздухом с различной виртуальной потенциальной температурой для воздуха, текущего вверх или вниз.
Образец заявления
Скорость потока холодного воздуха 10 мс –1 изменяется на 2 мс –1 после прохождения гидравлического прыжка. Этот воздух на 10°C холоднее окружающего. Как высоко может прыгать гидравлический прыжок?
Find the Answer
Given: M 1 = 10 m s –1 , M 2 = 2 m s –1 , ∆T = 10K, z 1 = 0.
Найти: z 2 = ? м выше начальной з.
Предположим: ∆θ v = ∆T и |g|/T v = 0,0333 м·с –2 ·K –1 . P ≈ постоянный на линии тока вдоль кровли холодного воздуха.
Использовать экв. (17.36), учитывая, что C B – P/ρ постоянна:
- В точке 1: 0,5 ·(10 м с –1 ) 2 + 0 = C B – P/ρ = 50 м 2 с –2
- At 2: 0,5·(2 м с –1 ) 2 +(0,0333 м·с –2 ·K –1 )·(10K)·z 2 =50 м9 2с –2
Решение для z 2 : z 2 = [M 1 2 - M 2 2 ] · T V /(2 · * * * * * * * = 144 м
Проверить: Блоки в норме. Величина в порядке.
Величина в порядке.
Экспозиция: Гидравлические прыжки очень турбулентны и могут рассеивать часть механической энергии в виде тепла. Таким образом, фактическая высота прыжка будет меньше.
Для использования экв. (17.36), сначала измерьте все члены в левой части уравнения в некотором начальном (или выше по течению) месте в потоке. Назовите эту точку 1. Используйте ее для расчета начального значения C 9{2}\right]+\Delta\left[\frac{P}{\rho}\right]+\Delta\left[|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot z\right]=0\tag{17,38}\end{align}\)
Внимание: ∆[(0,5)·M 2 ] ≠ (0,5)·[∆M] 2 .
Приведенные выше уравнения Бернулли НЕ работают:
- везде, где поток турбулентный
- за препятствиями, создающими турбулентный след или вызывающими внезапные изменения потока
- в местах подвода или потери тепла
- в местах ввода механической энергии (например, вентилятор) или потерь (например, ветряная турбина)
- у земли, где сопротивление замедляет ветер
- при скорости потока > 20 м с –1
- , где плотность приблизительно не постоянна
Следовательно, существует множество атмосферных ситуаций, для которых приведенные выше уравнения слишком упрощены.
Образец заявки
Ветер на постоянной высоте замедляется с 15 до 10 м/с при прохождении через ветряную турбину. Какая противоположная разность чистого давления вызвала бы такое же замедление при ламинарном течении?
Найдите ответ.
Найти: ∆P = ? Па
Предположим, что ρ = 1 кг м –3 = постоянная.
Решить уравнение (17.38) для ∆P: ∆P = – ρ · ∆[(0,5)·M 2 ]
∆P = – (1 кг м –3 ) · (0,5)·[(10м с – 1 ) 2 – (15 м с –1 ) 2 ] = 62,4 Па
Проверка: Блоки в норме. Величина в порядке.
Экспозиция: Процесс извлечения механической энергии из ветра имеет тот же эффект, что и встречная разность давлений. Эта разница давлений невелика по сравнению с атмосферным давлением окружающей среды P = 100 000 Па.
Фактическое изменение давления на ветряной турбине показано на нижнем рисунке.
17.9.1.2. Сжимаемый поток
Для многих реальных атмосферных условий, когда скорость ветра может быть любой, следует использовать более общую форму уравнения Бернулли, включающую тепловые процессы. 9{2}+\mathfrak{R}_{d} \cdot T_{v} \cdot \ln (P)+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.39}\end{align}\)
, где ℜ d = 287 м 2 ·s –2 ·K –1 – постоянная идеального газа для сухого воздуха, где C B постоянна в процессе (т. е. начальное C B = конечное C B ).
Образец заявки
Воздух с давлением 100 кПа изначально находится в состоянии покоя. Он ускоряется над плоской снежной поверхностью при температуре 0 ° C, когда его всасывает в систему вентиляции дома. Если конечная скорость 10 м с –1 , какое давление воздуха на входе вентилятора? Найти ответ
Найти: P 2 = ? кПа
Предположим, что снег поддерживает постоянную температуру воздуха T v = 0°C. Используйте уравнение (17.39) для изотермического процесса:
Используйте уравнение (17.39) для изотермического процесса:
[0,5M 2 2 – 0] + ℜ d ·T v ·[ln(P 2 )–ln(P 1 )] = 0
Используйте ln(a) – ln(b) = ln(a/b). Затем возьмите exp с обеих сторон и переставьте: P 2 = P 1 ·exp[–0.5M 2 2 / (ℜ d ·T v )] 15 8
3
33
33
3 = = (100кПа)·exp[–0,5(10м с –1 ) 2 /{(287м 2 ·с –2 ·K –1 )·(273K)}] = (100кПа )·exp[–0,000638] = (100 кПа)· (0,9994) = 99,94 кПа.
9{2}+C_{v} \cdot T+\frac{P}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.43}\end{align}\)
энергия: кинетическая + внутренняя + поток + потенциальная = постоянная
Опять же, C B постоянна во время адиабатического процесса.
Образец заявки
Небольшое расстояние за двигателем реактивного самолета, летящего в горизонтальном полете, температура выхлопных газов 400 °C и скорость реактивной струи 200 м с –1 . Какова конечная температура выхлопного воздуха после того, как выхлоп струи замедлится до нуля, если пренебречь проводимостью и турбулентным перемешиванием. 9Найти ответ 2 = ? °С. Предположим, что процесс адиабатический.
Какова конечная температура выхлопного воздуха после того, как выхлоп струи замедлится до нуля, если пренебречь проводимостью и турбулентным перемешиванием. 9Найти ответ 2 = ? °С. Предположим, что процесс адиабатический.
Переставить экв. (17,42): T 2 = T 1 + M 1 2 /(2C P )
T 2 = (673K) + (200m S - 2 2 2 =. /(2· 1004 м 2 ·с –2 ·К –1 )
= 673K + 19,9K = 693K = 420°C
Проверить: Единицы в норме. Величина в порядке.
Описание: Реактивный выхлоп турбулентный и быстро смешивается с более холодным окружающим воздухом, поэтому уравнение Бернулли не подходит. Дополнительную информацию см. в разделе «Динамическое нагревание» далее в этой главе.
17.9.1.
 3. Сохранение энергии
3. Сохранение энергии Поскольку эти несколько предыдущих уравнений также учитывают температуру, мы не можем называть их уравнениями Бернулли. их уравнения сохранения энергии , которые учитывают механическую и тепловую энергию, следующие по линии тока.
Если мы распространим это дальше на бюджет энергии уравнение , то мы можем добавить эффекты чистого добавления тепловой энергии (теплоты на единицу массы) ∆q через излучение, конденсацию или испарение, теплопроводность, горение, и т. д. Мы также можем включить 90 126 работы вала на единицу массы 90 127 ∆SW, выполняемой в воздухе вентилятором, или энергию, извлекаемую из воздуха ветряной турбиной. 9{2}\right]+\Delta\left[C_{p} \cdot T\right]+\Delta\left[|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot z\right]=\Delta q+\Delta S W\tag{17.45}\end{align}\)
Образец приложения
Электрический ветрогенератор мощностью 75 кВт с вентилятором радиусом 2,5 м используется в саду для смешивания воздуха с целью уменьшения повреждения плодов морозом. Вентилятор разгоняет воздух по горизонтали от 0 до 5 м с –1 . Найти изменение температуры на вентиляторе, пренебрегая смешиванием с окружающим воздухом.
Вентилятор разгоняет воздух по горизонтали от 0 до 5 м с –1 . Найти изменение температуры на вентиляторе, пренебрегая смешиванием с окружающим воздухом.
Найдите ответ
Дано: Мощность = 75 кВт = 75000 кг·м 2 ·с –3 , R = 2,5 м, М 1 = 0, М 2 = 1 м2 8 – 90 , ∆z = 0
Найти: ∆T = ? °C
Предположим, что вся электрическая энергия, используемая двигателем вентилятора, уходит на теплоту и работу вала.
Массовый расход через этот вентилятор:
ρ·M 2 ·π·R 2 = (1,225 кг м –3 )·(5м с –1 )·π·(2,5 м) 2 =120 кг с –1
Таким образом: ∆q + ∆SW = мощность/(массовый расход) = 624 м (17.45): ∆T = (1/C p )·[∆q +∆SW –0,5·(M 2 2 –M 1 2 )]
2 = (17.45) м 2 ·с –2 ·К –1 )·[(624 м 2 ·с –2 ) – 0,5·(5м с –1 ) 90 390 90 90 0 90 128 2 2 2 0,61 К = 0,61°С
Проверка: Блоки в норме. Величина в порядке.
Величина в порядке.
Экспозиция: Несмотря на большое энергопотребление электродвигателя, нагрев распространяется на очень большой объем воздуха, проходящего через вентилятор. Следовательно, величина изменения температуры невелика.
17.9.2.1. Динамическое и статическое давление и температура
Рис. 17.34. Линии тока, показывающие застой при приближении воздуха к препятствию. Набегающий поток Атмосферное давление вдали от любых препятствий называется статическое давление P s . Аналогично, пусть T - температура набегающего потока (начальная).
Когда ветер приближается к препятствию, большая часть воздуха обтекает его, как показано на рис. 17.34. Однако для одной линии тока, которая сталкивается с препятствием, воздух замедляется от скорости восходящего потока M начальная = Ms до конечной скорости M final = 0. Эта конечная точка называется точкой торможения .
Когда воздух приближается к точке застоя, скорость ветра уменьшается, а давление увеличивается по мере сближения молекул воздуха. Это вызывает повышение температуры в соответствии с законом идеального газа. Повышенное давление называется динамическое давление P dyn , а повышенная температура называется динамическая температура T dyn . В критической точке, где скорость равна нулю, конечное динамическое давление называется давлением торможения P o , а соответствующая динамическая температура обозначается символом To. Думайте о нижнем индексе «о» как о нулевой скорости ветра относительно препятствия.
Чтобы найти динамические эффекты при стагнации, используйте уравнение сохранения энергии (17.42) для ветра, дующего горизонтально (т. е. без изменения z), и предположите почти адиабатический процесс: 9{2}}{2 \cdot C_{p}}\tag{17.47}\end{align}\)
, где C p = 1004 м 2 ·s –2 ·K –1 для сухого воздуха. уравнение (17.47) действительно для дозвуковых скоростей (см. блок INFO).
уравнение (17.47) действительно для дозвуковых скоростей (см. блок INFO).
Рис. 17.35 Повышение давления (∆P, зеленая сплошная линия) и температуры (∆T, оранжевая пунктирная линия) из-за динамического нагрева, когда воздух со скоростью M s сталкивается с препятствием и застаивается. Условия внешнего набегающего потока для этого расчета: T = 290K и P с = 100 кПа, что дает скорость звука c = 341 м с –1 . Этот эффект называется динамическое нагревание или динамическое нагревание — эффект, который вы должны учитывать при развертывании термометров на ветру, потому что ветер будет застаиваться, когда он ударяет по термометру. Как показано на рис. 17.35, динамический нагрев (∆T = T o – T) пренебрежимо мал (∆T ≤ 0,2°C) для скоростей потока M с ≤ 20 м с –1 .
Тем не менее, для термометров на воздушном судне, движущемся на 100 м с –1 относительно воздуха, или для стационарных термометров, подвергающихся воздействию торнадо ветров М с = 100 мс –1 , динамическое потепление составляет примерно ∆T ≈ 5°C. Для этих экстремальных ветров вы можете внести поправку на динамическое потепление, используя динамическую температуру T o , измеренную термометром, и используя измеренную скорость ветра M s , а затем решив уравнение. (17.47) для температуры набегающего потока T.
Для этих экстремальных ветров вы можете внести поправку на динамическое потепление, используя динамическую температуру T o , измеренную термометром, и используя измеренную скорость ветра M s , а затем решив уравнение. (17.47) для температуры набегающего потока T.
В главе «Бюджеты тепла» представлена зависимость между температурой и давлением для адиабатического процесса сжатия. Используя это с приведенным выше уравнением, мы можем решить для 9{c_{p} / \Re}\tag{17.49}\end{align}\)
, где C p /ℜ ≈ C pd /ℜ d = 3,5 для воздуха, P s равно статическое (набегающее) давление, M s – скорость ветра набегающего потока вдоль линии тока, C p ≈ C pd = 1004 Дж·кг –1 ·K –1 , T – набегающий поток температура, а нижний индекс d обозначает сухой воздух. На рис. 17.35 показано увеличение давления застоя с увеличением скорости потока.
Для скоростей ветра М с 9{2}\tag{17. 50}\end{align}\)
50}\end{align}\)
, где ρ — плотность воздуха. Не используйте экв. (17.50), чтобы найти динамический нагрев в сочетании с законом идеального газа, потому что он пренебрегает большими изменениями плотности, которые происходят в высокоскоростных потоках, которые застаиваются.
Образец заявки
Вихревой ветер со скоростью 100 м с –1 и температурой 30°C дует в гараж и застаивается. Найдите стагнацию T и P. Какая результирующая сила давит на стену гаража размером 3 x 5 м?
Найди ответ
Дано: M s =100 м s –1 , T=30°C, площадь стены A=3x5 =15 м 2
Найти: F net = ? N. Предположим: ρ = 1,2 кг·м –3 , P = 100 кПа.
Использовать экв. (17.47): T o = (30°C)+[(100м с –1 ) 2 /(2 · 1004м 2 ·с –2 ·K –1 ) 4 = 35°С.
Используйте экв. (17.48): P o = (100 кПа)·[(35+273)/(30+273)] 3,5 = 105,9 кПа.
(17.48): P o = (100 кПа)·[(35+273)/(30+273)] 3,5 = 105,9 кПа.
Сравните с ур. (17.50): P o = (100 кПа) + [(0,5 · 1,2 кг м –3 )·(100 м с –1 ) 2 ]·(1 кПа/1000Па)= 106 кПа
F NET = ∆P · A = (6 кН M –2 ) · (15 М 2 ) = 90 кН
6667777777777777777 год. Физика ок. Экспозиция: Эта сила эквивалентна весу более 1000 человек и действует на все стены и крышу. Этого достаточно, чтобы снести всю крышу дома. Потом стены рушатся, а крыша падает на пол.
Спрятаться в подвале. Быстро.
Предыдущие три уравнения показывают, что увеличение давления из-за стагнации (∆P = P o – P s ) мало (∆P < 0,25 кПа) по сравнению с атмосферным давлением окружающей среды (P s = 100 кПа ) для скоростей ветра М с < 20 м с –1 .
Динамические эффекты затрудняют измерение статического давления на ветру. Когда ветер попадает на датчик давления, он замедляется и вызывает увеличение давления. По этой причине приборы статического давления спроектированы таким образом, чтобы свести к минимуму замедление потока и динамические ошибки за счет наличия портов давления (отверстий) по сторонам датчика, где нет потока к датчику или от него.
Динамическое давление можно использовать для измерения скорости ветра. Инструментом, который делает это, является трубка Пито . Авиационные приборы измеряют давление застоя, когда трубка Пито обращена вперед к потоку, и статическое давление, когда другой порт обращен к потоку сбоку, чтобы свести к минимуму динамические эффекты. Затем прибор вычисляет «приведенную воздушную скорость» по уравнению. (17,49 или 17,50) с использованием перепада давления Пито – статического давления .
Во время смерчей и ураганов, если сильный ветер сталкивается с открытой дверью гаража или окном дома, ветер, стремящийся проникнуть в здание, вызывает динамическое увеличение давления внутри здания. Как обсуждается в Примере применения, результирующая разность давлений на крыше и стенах здания может привести к тому, что они взорвутся так быстро, что будет казаться, что здание взорвется. 9{1 / 2}\tag{17.42}\end{align}\)
Как обсуждается в Примере применения, результирующая разность давлений на крыше и стенах здания может привести к тому, что они взорвутся так быстро, что будет казаться, что здание взорвется. 9{1 / 2}\tag{17.42}\end{align}\)
, где k = C p /C v — отношение удельных теплоемкостей воздуха, ℜ — постоянная закона идеального газа, а T является абсолютной температурой. [См. вставку INFO в Главе 3, раздел 3.2.3, для обзора удельных теплоемкостей при постоянном давлении C p и постоянном объеме C v .] Для сухого воздуха константы таковы: k = C pd /C vd = 1,4 и ℜ d = 287,053 (m 2 с –2 )·K –1 . Таким образом, скорость звука увеличивается пропорционально квадратному корню из абсолютной температуры.
Скорость M любого объекта, например самолета или воздушной посылки, можно сравнить со скоростью звука:
\(\ \begin{align} M a=M / c\tag{17.43}\end{align }\)
где Ма - безразмерное число Маха . Таким образом, объект, движущийся со скоростью 1 Маха, движется со скоростью звука.
Таким образом, объект, движущийся со скоростью 1 Маха, движется со скоростью звука.
Рис. 17.д. Скорость звука в сухом воздухе. 17.9.2.2. Эффект Вентури
Уравнение Бернулли говорит, что если скорость увеличивается в области сужения потока, то давление уменьшается. Это называется 9{2}\right]\tag{17.52}\end{align}\)
К сожалению, щелевые потоки часто не имеют постоянной глубины, потому что температурная инверсия, закрывающая эти потоки, является не жесткими крышками.
Образец заявки
Если полоса ветра шириной 20 км и скоростью 5 м с –1 должна сжаться, чтобы пройти через щель шириной 2 км, каково падение давления в щели по сравнению с потоком без щели?
Найдите ответ
Дано: D s = 20 км, D д = 2 км, М с = 5 м с –1 .
Найти: M d = ? м с –1 .
Допустим: ρ = 1,2 кг·м –3 .
3
3 = = (100кПа)·exp[–0,5(10м с –1 ) 2 /{(287м 2 ·с –2 ·K –1 )·(273K)}] = (100кПа )·exp[–0,000638] = (100 кПа)· (0,9994) = 99,94 кПа.
9{2}+C_{v} \cdot T+\frac{P}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.43}\end{align}\)
энергия: кинетическая + внутренняя + поток + потенциальная = постоянная
Опять же, C B постоянна во время адиабатического процесса.
Образец заявки
Небольшое расстояние за двигателем реактивного самолета, летящего в горизонтальном полете, температура выхлопных газов 400 °C и скорость реактивной струи 200 м с –1 . Какова конечная температура выхлопного воздуха после того, как выхлоп струи замедлится до нуля, если пренебречь проводимостью и турбулентным перемешиванием. 9Найти ответ 2 = ? °С. Предположим, что процесс адиабатический.
Какова конечная температура выхлопного воздуха после того, как выхлоп струи замедлится до нуля, если пренебречь проводимостью и турбулентным перемешиванием. 9Найти ответ 2 = ? °С. Предположим, что процесс адиабатический.
Переставить экв. (17,42): T 2 = T 1 + M 1 2 /(2C P )
T 2 = (673K) + (200m S - 2 2 2 =. /(2· 1004 м 2 ·с –2 ·К –1 )
= 673K + 19,9K = 693K = 420°C
Проверить: Единицы в норме. Величина в порядке.
Описание: Реактивный выхлоп турбулентный и быстро смешивается с более холодным окружающим воздухом, поэтому уравнение Бернулли не подходит. Дополнительную информацию см. в разделе «Динамическое нагревание» далее в этой главе.
17.9.1.
 3. Сохранение энергии
3. Сохранение энергииПоскольку эти несколько предыдущих уравнений также учитывают температуру, мы не можем называть их уравнениями Бернулли. их уравнения сохранения энергии , которые учитывают механическую и тепловую энергию, следующие по линии тока.
Если мы распространим это дальше на бюджет энергии уравнение , то мы можем добавить эффекты чистого добавления тепловой энергии (теплоты на единицу массы) ∆q через излучение, конденсацию или испарение, теплопроводность, горение, и т. д. Мы также можем включить 90 126 работы вала на единицу массы 90 127 ∆SW, выполняемой в воздухе вентилятором, или энергию, извлекаемую из воздуха ветряной турбиной. 9{2}\right]+\Delta\left[C_{p} \cdot T\right]+\Delta\left[|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot z\right]=\Delta q+\Delta S W\tag{17.45}\end{align}\)
Образец приложения
Электрический ветрогенератор мощностью 75 кВт с вентилятором радиусом 2,5 м используется в саду для смешивания воздуха с целью уменьшения повреждения плодов морозом. Вентилятор разгоняет воздух по горизонтали от 0 до 5 м с –1 . Найти изменение температуры на вентиляторе, пренебрегая смешиванием с окружающим воздухом.
Вентилятор разгоняет воздух по горизонтали от 0 до 5 м с –1 . Найти изменение температуры на вентиляторе, пренебрегая смешиванием с окружающим воздухом.
Найдите ответ
Дано: Мощность = 75 кВт = 75000 кг·м 2 ·с –3 , R = 2,5 м, М 1 = 0, М 2 = 1 м2 8 – 90 , ∆z = 0
Найти: ∆T = ? °C
Предположим, что вся электрическая энергия, используемая двигателем вентилятора, уходит на теплоту и работу вала.
Массовый расход через этот вентилятор:
ρ·M 2 ·π·R 2 = (1,225 кг м –3 )·(5м с –1 )·π·(2,5 м) 2 =120 кг с –1
Таким образом: ∆q + ∆SW = мощность/(массовый расход) = 624 м (17.45): ∆T = (1/C p )·[∆q +∆SW –0,5·(M 2 2 –M 1 2 )]
2 = (17.45) м 2 ·с –2 ·К –1 )·[(624 м 2 ·с –2 ) – 0,5·(5м с –1 ) 90 390 90 90 0 90 128 2 2 2 0,61 К = 0,61°С
Проверка: Блоки в норме. Величина в порядке.
Величина в порядке.
Экспозиция: Несмотря на большое энергопотребление электродвигателя, нагрев распространяется на очень большой объем воздуха, проходящего через вентилятор. Следовательно, величина изменения температуры невелика.
17.9.2.1. Динамическое и статическое давление и температура
Рис. 17.34. Линии тока, показывающие застой при приближении воздуха к препятствию.Набегающий поток Атмосферное давление вдали от любых препятствий называется статическое давление P s . Аналогично, пусть T - температура набегающего потока (начальная).
Когда ветер приближается к препятствию, большая часть воздуха обтекает его, как показано на рис. 17.34. Однако для одной линии тока, которая сталкивается с препятствием, воздух замедляется от скорости восходящего потока M начальная = Ms до конечной скорости M final = 0. Эта конечная точка называется точкой торможения .
Когда воздух приближается к точке застоя, скорость ветра уменьшается, а давление увеличивается по мере сближения молекул воздуха. Это вызывает повышение температуры в соответствии с законом идеального газа. Повышенное давление называется динамическое давление P dyn , а повышенная температура называется динамическая температура T dyn . В критической точке, где скорость равна нулю, конечное динамическое давление называется давлением торможения P o , а соответствующая динамическая температура обозначается символом To. Думайте о нижнем индексе «о» как о нулевой скорости ветра относительно препятствия.
Чтобы найти динамические эффекты при стагнации, используйте уравнение сохранения энергии (17.42) для ветра, дующего горизонтально (т. е. без изменения z), и предположите почти адиабатический процесс: 9{2}}{2 \cdot C_{p}}\tag{17.47}\end{align}\)
, где C p = 1004 м 2 ·s –2 ·K –1 для сухого воздуха. уравнение (17.47) действительно для дозвуковых скоростей (см. блок INFO).
уравнение (17.47) действительно для дозвуковых скоростей (см. блок INFO).
Этот эффект называется динамическое нагревание или динамическое нагревание — эффект, который вы должны учитывать при развертывании термометров на ветру, потому что ветер будет застаиваться, когда он ударяет по термометру. Как показано на рис. 17.35, динамический нагрев (∆T = T o – T) пренебрежимо мал (∆T ≤ 0,2°C) для скоростей потока M с ≤ 20 м с –1 .
Тем не менее, для термометров на воздушном судне, движущемся на 100 м с –1 относительно воздуха, или для стационарных термометров, подвергающихся воздействию торнадо ветров М с = 100 мс –1 , динамическое потепление составляет примерно ∆T ≈ 5°C. Для этих экстремальных ветров вы можете внести поправку на динамическое потепление, используя динамическую температуру T o , измеренную термометром, и используя измеренную скорость ветра M s , а затем решив уравнение. (17.47) для температуры набегающего потока T.
Для этих экстремальных ветров вы можете внести поправку на динамическое потепление, используя динамическую температуру T o , измеренную термометром, и используя измеренную скорость ветра M s , а затем решив уравнение. (17.47) для температуры набегающего потока T.
В главе «Бюджеты тепла» представлена зависимость между температурой и давлением для адиабатического процесса сжатия. Используя это с приведенным выше уравнением, мы можем решить для 9{c_{p} / \Re}\tag{17.49}\end{align}\)
, где C p /ℜ ≈ C pd /ℜ d = 3,5 для воздуха, P s равно статическое (набегающее) давление, M s – скорость ветра набегающего потока вдоль линии тока, C p ≈ C pd = 1004 Дж·кг –1 ·K –1 , T – набегающий поток температура, а нижний индекс d обозначает сухой воздух. На рис. 17.35 показано увеличение давления застоя с увеличением скорости потока.
Для скоростей ветра М с 9{2}\tag{17. 50}\end{align}\)
50}\end{align}\)
, где ρ — плотность воздуха. Не используйте экв. (17.50), чтобы найти динамический нагрев в сочетании с законом идеального газа, потому что он пренебрегает большими изменениями плотности, которые происходят в высокоскоростных потоках, которые застаиваются.
Образец заявки
Вихревой ветер со скоростью 100 м с –1 и температурой 30°C дует в гараж и застаивается. Найдите стагнацию T и P. Какая результирующая сила давит на стену гаража размером 3 x 5 м?
Найди ответ
Дано: M s =100 м s –1 , T=30°C, площадь стены A=3x5 =15 м 2
Найти: F net = ? N. Предположим: ρ = 1,2 кг·м –3 , P = 100 кПа.
Использовать экв. (17.47): T o = (30°C)+[(100м с –1 ) 2 /(2 · 1004м 2 ·с –2 ·K –1 ) 4 = 35°С.
Используйте экв. (17.48): P o = (100 кПа)·[(35+273)/(30+273)] 3,5 = 105,9 кПа.
(17.48): P o = (100 кПа)·[(35+273)/(30+273)] 3,5 = 105,9 кПа.
Сравните с ур. (17.50): P o = (100 кПа) + [(0,5 · 1,2 кг м –3 )·(100 м с –1 ) 2 ]·(1 кПа/1000Па)= 106 кПа
F NET = ∆P · A = (6 кН M –2 ) · (15 М 2 ) = 90 кН
6667777777777777777 год. Физика ок.Экспозиция: Эта сила эквивалентна весу более 1000 человек и действует на все стены и крышу. Этого достаточно, чтобы снести всю крышу дома. Потом стены рушатся, а крыша падает на пол.
Спрятаться в подвале. Быстро.
Предыдущие три уравнения показывают, что увеличение давления из-за стагнации (∆P = P o – P s ) мало (∆P < 0,25 кПа) по сравнению с атмосферным давлением окружающей среды (P s = 100 кПа ) для скоростей ветра М с < 20 м с –1 .
Динамические эффекты затрудняют измерение статического давления на ветру. Когда ветер попадает на датчик давления, он замедляется и вызывает увеличение давления. По этой причине приборы статического давления спроектированы таким образом, чтобы свести к минимуму замедление потока и динамические ошибки за счет наличия портов давления (отверстий) по сторонам датчика, где нет потока к датчику или от него.
Динамическое давление можно использовать для измерения скорости ветра. Инструментом, который делает это, является трубка Пито . Авиационные приборы измеряют давление застоя, когда трубка Пито обращена вперед к потоку, и статическое давление, когда другой порт обращен к потоку сбоку, чтобы свести к минимуму динамические эффекты. Затем прибор вычисляет «приведенную воздушную скорость» по уравнению. (17,49 или 17,50) с использованием перепада давления Пито – статического давления .
Во время смерчей и ураганов, если сильный ветер сталкивается с открытой дверью гаража или окном дома, ветер, стремящийся проникнуть в здание, вызывает динамическое увеличение давления внутри здания. Как обсуждается в Примере применения, результирующая разность давлений на крыше и стенах здания может привести к тому, что они взорвутся так быстро, что будет казаться, что здание взорвется. 9{1 / 2}\tag{17.42}\end{align}\)
Как обсуждается в Примере применения, результирующая разность давлений на крыше и стенах здания может привести к тому, что они взорвутся так быстро, что будет казаться, что здание взорвется. 9{1 / 2}\tag{17.42}\end{align}\)
, где k = C p /C v — отношение удельных теплоемкостей воздуха, ℜ — постоянная закона идеального газа, а T является абсолютной температурой. [См. вставку INFO в Главе 3, раздел 3.2.3, для обзора удельных теплоемкостей при постоянном давлении C p и постоянном объеме C v .] Для сухого воздуха константы таковы: k = C pd /C vd = 1,4 и ℜ d = 287,053 (m 2 с –2 )·K –1 . Таким образом, скорость звука увеличивается пропорционально квадратному корню из абсолютной температуры.
Скорость M любого объекта, например самолета или воздушной посылки, можно сравнить со скоростью звука:
\(\ \begin{align} M a=M / c\tag{17.43}\end{align }\)
где Ма - безразмерное число Маха . Таким образом, объект, движущийся со скоростью 1 Маха, движется со скоростью звука.
Таким образом, объект, движущийся со скоростью 1 Маха, движется со скоростью звука.
17.9.2.2. Эффект Вентури
Уравнение Бернулли говорит, что если скорость увеличивается в области сужения потока, то давление уменьшается. Это называется 9{2}\right]\tag{17.52}\end{align}\)
К сожалению, щелевые потоки часто не имеют постоянной глубины, потому что температурная инверсия, закрывающая эти потоки, является не жесткими крышками.
Образец заявки
Если полоса ветра шириной 20 км и скоростью 5 м с –1 должна сжаться, чтобы пройти через щель шириной 2 км, каково падение давления в щели по сравнению с потоком без щели?
Найдите ответ
Дано: D s = 20 км, D д = 2 км, М с = 5 м с –1 .
Найти: M d = ? м с –1 .
Допустим: ρ = 1,2 кг·м –3 .

